Abstract
This work deals an experimental and theoretical research about the porous structure and the acoustic performance of cellulose acetate coming from the used cigarette filters. The porous structure was studied through the measurement and the prediction (using an inverse methodology) of some non-acoustic properties (bulk density, fiber size, porosity or flow resistivity and tortuosity). The sound absorption performance was evaluated by comparing experimental measurements using an impedance tube according to ISO 10534-2 with the best-fit approach obtained using some empirical models (Delany and Bazley, Garai-Pompoli, Komatsu and Miki). The accuracy of empirical models to obtain the flow resistivity was relatively high showing differences lower than 8% in the case of the Miki model or lower than 12% in the case of Delany & Bazley model. Regarding the absorption spectra, the errors found were lower than 9% for all the empirical models used in this work. These results showed that using relatively simple models such as empirical models were able to predict accurately the acoustic behaviour of the cellulose acetate. Finally, the sound absorption spectra obtained for cellulose acetate were compared with those obtained for fibrous materials currently used in building sector, suggesting that this fibrous waste could act as a possible substitute to traditional ones, due to the similar relatively high NRC values obtained for both type of fibrous absorber (NRC = 0.65).
Keywords: Sound fibrous absorber, Cellulose acetate, Acoustic properties, Impedance model
Introduction
Sound absorption materials are widely used in building, automotive, aerospace or industrial noise control applications. The form in which these porous absorbers are used is that of acoustic panels which are mainly composed by fibrous, reticulated or granular materials. With respect to the fibrous materials, the most used porous absorbers are made of glass wool or rock wool due to their high efficiency in sound absorption. However and despite that these materials are expensive to produce and efficient in noise reduction, issues like environmental factors or health hazards must be taken into account with respect to their use. This latter have motivated numerous researchers to come up with better and greener alternatives. In the recent decades, the use of natural materials such as kenaf [1], yucca [2], date palm [3] or nettle [4], recycled materials such as end of life tires tyres [5, 6], wool fibers [7] and wastes deriving from other production processes such as cork granulates [8], coffe [9], fruit stones [10] or bagasse from sugar cane [11], have been studied in order to reduce the application of these traditional materials. These works showed that these could be considered as valid raw materials for including in sound absorbing panels at a low cost, showing good sound absorption properties and being available in large quantities often as a by-product of other products.
The materials studied in this paper are the cellulose acetate coming from cigarette butts (CBs). These are one of the most common and numerous types of waste in the world. At least, during the year 2016, 5.7 trillion cigarettes were consumed worldwide [12] being about 97% of the cigarette filters composed by cellulose acetate. CBs are mainly composed of an outer paper (mainly looking like cork), an inner paper wrapper with a polyvinyl acetate emulsion in order to attach the outer paper, tobacco and non-biodegradable cellulose acetate [13]. CBs are considered a hazardous waste. Among their components it can be found more than 4000 toxic substances that can show serious risks to the human health and the environment [13]. The non-recycling of cigarette filters can cause environmental risks where the transmission of contaminants into the environment is a very important issue to take into account. Some of the individual components of the tobacco, trapped in the filter, such as nicotine, heavy metals, acetaldehyde, formaldehyde, benzene, phenol, aromatic hydrocarbons or polycyclic aromatic hydrocarbon among others [13, 14]. Therefore the presence of these contaminants in the streets, urban areas or seacoasts can suppose a serious environmental problem for wildlife and aquatic organisms, plants or citizens.
Thus, a possible recycling of this kind of waste could eliminate a substantial portion of its disposal problems into new materials or applications. Different works have showed that CBs can be applied without previous treatment; the manufacture of bricks [15] or asphalt [16] production. However, other applications needed various processing methods prior to use. Teixeira et al. [17] obtained a methodology to produce cellulose pulp by recycling CBs hydrolyzing the cellulose acetate in the presence of strong alkali. Zhao et al. [18] applied the nicotine present in CBs as corrosion inhibitors for N80 steel at 90 °C in a hydrochloric acid solution. Ghosh et al. [19] obtained a conducting material using CBs with a previous heat treatment. Sabzali et al., [20] obtained a biofilm carrier in the integrated fixed film activated sludge process through waste cigarette filters in tobacco factories. Other many interesting works about recycling solutions of CBs where cited by Marinello et al. [21].
In order to predict the acoustical performance of sound porous absorbers, whatever the material type, it is necessary to use sound absorption models. In these models acoustical variables, such as the characteristic impedance and complex wavenumber, to non-acoustical properties of porous media are related. The number of non-acoustical properties depends on the complexity degree of the model. Many models such as Delany-Bazley [22], Garai-Pompoli [23], Miki [24], Mechel [25] or Komatsu [26] proposed empirical formulas that require just one easily measurable parameter, the airflow resistivity. Other more complex models [27–32] require a larger number of non-acoustic parameters such as porosity, tortuosity, viscous and thermal permeability, static viscous tortuosity and static thermal tortuosity or viscous and thermal characteristic length, being some of them not readily accessible by experimental techniques. Due to this latter and that the materials used in it are highly porous relatively simple and accurate models were preferably used in this paper.
This work provides an experimental and theoretical investigation of the acoustic performance of cellulose acetate fibers coming from CBs. Some initial works about cellulose acetate, only showing the sound absorption spectra of cellulose acetate without previous treatment, were carried out previously by the author of the present paper [33–35]. In order to thoroughly investigate the acoustic performance of this material, the evaluation of the sound absorption coefficient at normal incidence and its non-acoustic properties, were required. For this purpose two methods were used; the direct measurement of the sound absorption coefficient, through an impedance tube, and the prediction of this coefficient using impedance models for sound porous absorbers. The investigation was developed taking into account non-acoustic properties of the cellulose acetate. Physical properties such as porosity, flow resistivity, fiber diameter and skeletal density were obtained. Then, physical properties were introduced in impedance models to evaluate the sound absorption coefficient. Experimental and theoretical sound absorption spectra were compared in order to evaluate the efficiency of models describing the acoustic behaviour of the material. The obtained results showed that a relatively simple model, e.g. Delany-Bazley model or MiKi model could predict the sound absorption coefficient very accurately.
The paper is structured as follows: Materials section presents the sample preparation of the cellulose acetate object of this work; Laboratory measurements section presents the experimental methodology used to obtain the physical and the acoustic properties of the cellulose acetate fibers; Acoustic absorption modelling section briefly presents a review of the impedance models used to predict the flow resistivity and to invert it from experimental data; Results and discussion section reports the comparison between the predicted results from impedance models and the experimental results, and the comparison between cellulose acetate fibers and commercial sound fibrous absorbers; and Conclusions section reports some concluding remarks.
Materials
Sample preparation
The materials used in this work were cigarette filters (CFs) coming from different CBs brands collected from specific dry receptacles (Fig. 1). CFs and remaining tobacco were separated manually from CBs. Subsequently, the outer and inner paper was separated from cellulose acetate and the latter shredded into short fibers (Fig. 2). In order to remove as much as possible the toxic substances present in cellulose acetate, such as metals (iron, nickel, manganese, strontium, lead, copper, chromium, cadmium,…), formaldehyde, benzene, hydrogen cyanide or nicotine [36], the process indicated by Mwaikambo and Ansell [37] was followed. In order to remove non-cellulosic components, the fibers were soaked with distilled water for 1 day. Later they were soaked in a 5 wt.% sodium hydroxide (NaOH) solution at room temperature for 60 min. After this treatment, the fibers were washed with distilled water, neutralized with 1 wt.% acid solution and dried at 80 °C for 24 h. Distilled water was produced by an automatic water distillation apparatus (Elix® Advantage 3 Water Purification System). The main toxic substance removed were nicotine and in less proportion m-cresol and benzene. In order to obtain different porous microstructures, different amounts of cellulose acetate (15 g - 60 g), coming from used cigarette filters, were compacted with the hard back termination of the impedance tube to reach different bulk densities where no specific bonding method was used. Some authors showed that the bonding method had little effects on the sound absorption performance, only included in the bulk density [38, 39]. Nine different samples, having different bulk densities, porosities and thicknesses (Table 1) and therefore different acoustic performance, were used in this work.
Fig. 1.

Photograph of specific dry receptacles to collect cigarette butts
Fig. 2.

Image of cellulose acetate fibers coming from cigarette filters
Table 1.
Physical properties of cellulose acetate samples studied in this work
| Sample | Thickness (cm) |
Bulk density ρm (kg m−3) |
Surface density ρA (kg m−2) |
Porosity ϕ (%) |
Tortuosity |
|---|---|---|---|---|---|
| M#1 | 2.0 | 89.32 | 178.65 | 94.37 | 1.030 |
| M#2 | 4.0 | 92.99 | 371.98 | 94.14 | 1.031 |
| M#6 | 4.8 | 147.42 | 707.62 | 90.71 | 1.051 |
| M#11 | 3.0 | 98.91 | 296.74 | 93.77 | 1.033 |
| M#12 | 5.0 | 76.91 | 384.55 | 95.15 | 1.025 |
| M#14 | 6.5 | 74.53 | 484.47 | 95.30 | 1.025 |
| M#16 | 7.0 | 77.00 | 538.97 | 95.15 | 1.025 |
| M#20 | 3.2 | 77.12 | 246.78 | 95.14 | 1.026 |
| M#21 | 2.2 | 112.17 | 246.78 | 92.93 | 1.038 |
Laboratory measurements
The characterization of sound absorbing materials for building applications requires the evaluation of their acoustic and non-acoustic (namely macroscopic) properties. The first evaluate the material sound absorbing capability whereas the latter allow one to predict the acoustic response of the material for different applications by the use of an appropriate model. The evaluation of non-acoustic properties of fibrous materials can be obtained through the direct measurement of the non-acoustic property, based on its physical definition, through analytical expressions that link the material non-acoustic properties to acoustical measurements (indirect method) and through the best-fit approach used to describe the acoustic impedance and the propagation constant (inverse method) [32].
Measurement of physical properties
Fiber size
Average fibers diameters were determined using an optical microscopy (Leica Leitz Laborlux 12 POL S in transmission) using a 20X and 50X objectives, being the images recorded digitally with a JVC camera model TK-C1480E. At least 30 specimens of fibers were measured and diameters were averaged. The areal density was determined following the ASTM D-3776, Standard Test Method for Mass per Unit Area (Weight) of Fabric [40]. Six samples were weighed using a Mettler Toledo Precision Weighing balance (AX 205).
Porosity
Porous materials can be defined as an elastic or rigid material frame surrounded by air. Open porosity (ϕ), is one of the most relevant non-acoustic parameters that influences the sound absorption capability of a sound porous absorber in which the energy dissipation occurs in its pores. The higher porosity is the higher dissipation of sound energy will occur inside the porous absorber. It is defined as is the relationship between the volumes of the interconnected pores and the porous material. In this work the open porosity was calculated non-acoustically through the next expression:
| 1 |
ρm is the bulk density of the sample (kg m−3) and ρs is the skeletal density of the porous material (kg m−3). Porosity values were obtained according [34].
Flow resistivity
Flow resistivity, beside porosity, is other critical non-acoustic parameters influencing the sound absorption properties of a porous absorber. It is directly related to the capability to absorb sound energy by a material, so the sound absorption value is highly dependent on this parameter. It is defined as the resistance experimented by the air flowing inside a porous material. Therefore it indicates how much sound energy can be lost inside the porous absorber due to viscous and inertia effects when air passes through it. Bulk density determines the flow resistivity value so both are inversely proportional [41–43]. Low values of flow resistivity are associated with low resistance to air flowing through the material while high values can indicate a complex porous structure and therefore high resistance to air flow so low sound absorption values may be expected [44]. In this work, the Ingard and Dear method [45] was used to obtain the flow resistivity of the samples. For each sample, the measurement process was repeated three times and the average value was obtained.
Tortuosity
The tortuosity (α∞), a dimensionless structural parameter, indicates how direct the path is taken by the sound wave inside the porous absorber [41]. It depends only on the pore geometry [46]. A higher fiber density leads to a more complex path inside the porous absorber therefore it implies higher interaction between sound waves and fibers. This results in higher dissipation of the sound energy. Tortuosity can be evaluated by using an empirical formula (3) in terms of porosity ϕ as follows [47]:
| 2 |
In general, tortuosity mainly affects the position and height of the sound absorption spectrum peaks [48].
Measurement of sound absorption coefficient
In order to obtain the acoustic properties of the samples, sound absorption coefficient at normal incidence measurements were carried out according to standard ISO 10534-2 [49]. In this work a Brüel & Kjær impedance tube type 4206 were used. Signals were analysed with a portable Brüel & Kjær PULSE System. In order to accomplish accurate measurements in the frequency range of 50–6400 Hz, two different tubes having different diameters were used. One for measurements over the frequency range 50 Hz - 1600 Hz (100 mm in diameter) and other for frequency range of 500 Hz - 6400 Hz (29 mm in diameter). Previously to start any measurement and after the sample positioning, the influencing environmental parameters (atmospheric pressure, air temperature and relative humidity) were measured and introduced in the software.
In order to evaluate the sound absorption capability of these samples, single number grading methods which are independent of frequencies were used. These indices are useful for a practical evaluation of the performance of sound porous absorbers. For this purpose, the ASTM C423–17 [50] standard defines the NRC (Noise Reduction Coefficient) and the SAA (Sound Absorption Average). NRC is defined as the average of the sound absorption coefficients for 250, 500, 1000 and 2000 Hz rounded off to the nearest multiple of 0.05. SAA is defined as the average of the sound absorption coefficients for 200, 250, 315, 400, 500, 630, 800, 1000, 1250, 1600, 2000 and 2500 Hz, rounded off to the nearest 0.01.
Acoustic absorption modelling
Sound absorbing models are used to predict the sound absorption performance of a porous absorber through the characteristic impedance and the complex wavenumber, using as input parameters, some non-acoustic properties of the porous absorber, such as porosity, tortuosity, airflow resistance, density or fiber size, easily measured. Impedance models are generally differentiated based both on the absorption mechanism and the different type of pores. In this work, the Delany and Bazley (DBM), Miki, Garai-Pompoli and Komatsu models were chosen for their simplicity since the modelling of the sound propagation only requires the determination of a few physical properties having good prediction accuracy.
In order to predict the flow resistivity of the samples a best-fit inverse methodology widely used by some authors was used [2–4, 51–53]. This method requires working with an iterative numerical method to minimize the differences between the measured and the predicted sound absorption spectra, returning the estimated flow resistivity. The following function was used:
| 3 |
where αexp is the measured sound absorption coefficient, αpre is the predicted sound absorption coefficient and fn is the frequency in the range of 50–6400 Hz. The mean error between the measured and the predicted sound absorption spectra could be obtained through the following equation:
| 4 |
Delany-Bazley model (DBM)
The Delany-Bazley model [22] is one of the most used empirical models for sound fibrous absorbers, widely used for sound porous absorbers with porosities close to one, such as rock-wool or fiber-glass, for a specific frequency ranges. The validity of this model is generally considered to be limited to the range 0.01 < ρ0f/σ < 1.00 and sound porous absorbers having flow resistivities in the range of 1000 to 50,000 (Pa s m−2). This model has as unique input parameter the flow resistivity which is highly dependent on the density of the fibrous material. It can be expressed as follow:
| 5 |
| 6 |
| 7 |
| 8 |
where Zc is the characteristic impedance, kc, the complex wavenumber, Zs is the normalized acoustic surface impedance, ρ0 is the air density, d is the thickness of porous materials and ω is the angular frequency, calculated by ω = 2πf. This model shows limitations for low frequencies and for sound absorbers having coarse diameter fibers (higher than 30 μm) [22].
Garai-Pompoli model (GPM)
The Garai-Pompoli model [23], modify the empirical DBM and proposes some changes in order to obtain a more accurate model for coarse fibers and low frequencies. Although the model does not provide any information regarding the range of validity of their expressions, it can be considered to be restricted to the range 0.05 < ρ0f/σ < 8.4, taking into account the results obtained [22]. Nevertheless, the agreement between the measured and the predicted sound absorption coefficients obtained is relatively poor at very low and high frequencies. It can be expressed as follows:
| 9 |
| 10 |
Miki model (MKM)
The Miki Model [24], developed as an improvement to the empirical DBM in order to yield a more accurate sound absorption values across a broader frequency range, mainly at low frequencies. It can be expressed as follows:
| 11 |
| 12 |
| 13 |
where σe is the effective flow resistivity.
Komatsu model (KM)
The Komatsu Model [26] like the two previously cited models, was developed as an improvement to the DBM, increasing effectiveness in the predicted sound absorption coefficient for high density fibrous materials where f/σ < 0.01 m3 kg−1 and low-density ones where f/σ > 0.1 m3 kg−1.
| 14 |
| 15 |
Results and discussion
Measurements based on the optical microscope revealed that the outer diameter of the cellulose acetate fibers were within the range of 25–33 μm. The width of this range could be due to the use of filters coming from different brands. The average fiber diameters obtained were 29 ± 2 μm (Fig. 3). This value was in accordance with previous works which established that synthetic fibers had less irregular shapes and diameters [52]. The skeletal density obtained for cellulose acetate was 1.587 ± 0.072 g cm−3. With this value and the bulk density it was possible to determine the porosity using Eq. (1).
Fig. 3.

Microscopic images of acetate cellulose fiber from used cigarette filter obtained with different objectives: a 20X and b 50X
Open porosity is one of the key factors in acoustic absorption coefficient performance of the materials. The open porosities are showed in Table 1. These values ranged globally from 90.71% to 95.30% showing, as it was obvious, that a significant decrease in bulk density led to a substantial increase in porosity due to higher number of voids in the material. These results were similar to those expected from good quality and most commonly used synthetic and natural sound absorbers, such as glass wool, fiber glass [34] or coconut [52] and hemp [22, 52] for the same thicknesses and frequencies higher than 1500 Hz. Therefore, this suggested that the cellulose acetate fibers, chemically treated as was previously explained, acted as very effective sound absorber.
The Ingard and Dear method [45] was used to obtain the flow resistivity. These values ranged from 24,891 Pa s m−2 to 94,101 Pa s m−2. Figure 4 shows the relationship between the flow resistivity and the bulk density. Figure 5 and Table 2 show the measured and the predicted flow resistivity data for all fibrous samples studied in this work. The difference between measured values was associated to the variation of the bulk density. The higher differences (Table 3) were found in the Garai-Pompoli model for the inversions of all samples with values ranging from −69.7% to 76.1% of the measured value. In the case of the Komatsu model, all the differences were negatives, ranging from −17.9% to −3.4% while for the Delany-Bazley model, these differences were positives, ranging from 5.5% to 19.5%, except the sample M#6 having a difference of −1.7%. However, the flow resistivity values predicted with the Miki model was much similar to the measured values, ranging from −1.6% to 7.3%. Only the sample M#11 showed a higher difference, 18.2%. The results obtained for DBM and MKM were good enough according to Hurrell et al. [53]. These differences could be associated to the uncertainties when measuring experimental values like sound absorption coefficient, porosity or flow resistivity.
Fig. 4.
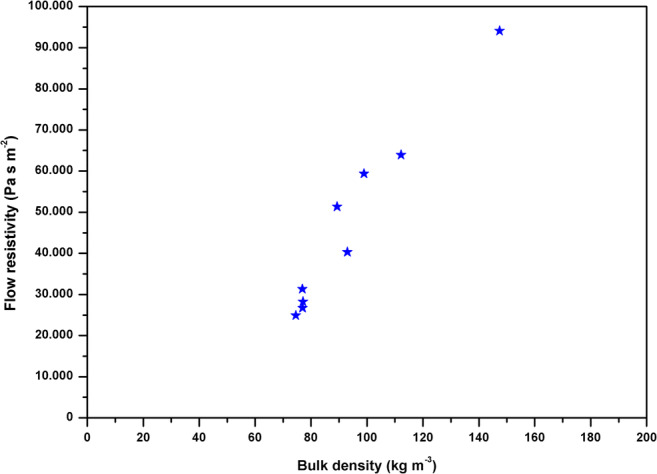
Relationship between bulk density and experimental flow resistivity for the samples
Fig. 5.
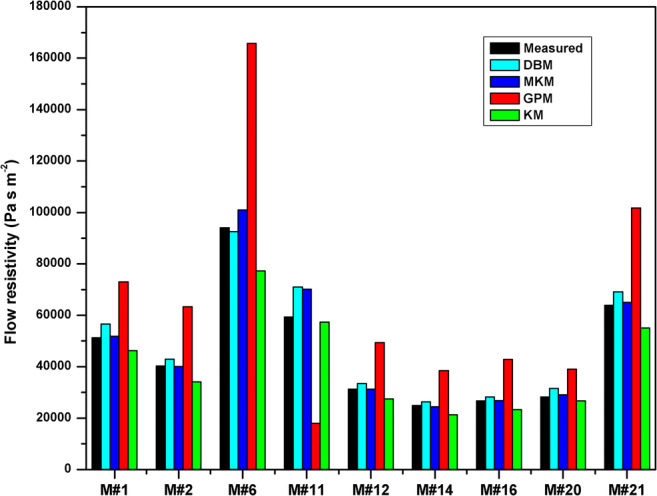
Comparison of experimental and predicted flow resistivity values obtained from impedance models
Table 2.
Measured and predicted flow resistivity values (Pa s m−2) of the cellulose acetate samples
| Sample | Experimental | DBM | MKM | GPM | KM |
|---|---|---|---|---|---|
| M#1 | 51,349 ± 710 | 56,620 | 51,804 | 73,038 | 46,230 |
| M#2 | 40,307 ± 532 | 42,937 | 40,143 | 63,321 | 34,157 |
| M#6 | 94,101 ± 1452 | 92,472 | 100,945 | 165,703 | 77,291 |
| M#11 | 59,356 ± 630 | 70,952 | 70,165 | 17,990 | 57,329 |
| M#12 | 31,306 ± 121 | 33,438 | 31,223 | 49,341 | 27,399 |
| M#14 | 24,891 ± 208 | 26,372 | 24,487 | 38,476 | 21,368 |
| M#16 | 26,737 ± 160 | 28,201 | 26,846 | 42,891 | 23,257 |
| M#20 | 28,261 ± 673 | 31,598 | 29,122 | 38,991 | 26,746 |
| M#21 | 63,937 ± 869 | 69,138 | 64,966 | 101,747 | 55,100 |
Table 3.
Differences (%) between measured and predicted airflow resistivity, σ, for each model, where negative values show results lower than measured, and mean errors, E(%), between measured and predicted sound absorption spectra for each model
| Sample | DBM | MKM | GPM | KM | ||||
|---|---|---|---|---|---|---|---|---|
| σ difference | E | σ difference | E | σ difference | E | σ difference | E | |
| M#1 | 10.3 | 1.5 | 0.9 | 0.8 | 42.2 | 2.6 | −10.0 | 2.2 |
| M#2 | 6.5 | 2.0 | −0.4 | 2.3 | 57.1 | 2.8 | −15.3 | 3.4 |
| M#6 | −1.7 | 1.2 | 7.3 | 1.2 | 76.1 | 8.7 | −17.9 | 4.4 |
| M#11 | 19.5 | 2.8 | 18.2 | 2.2 | −69.7 | 6.0 | −3.4 | 1.5 |
| M#12 | 6.8 | 0.9 | −0.3 | 1.1 | 57.6 | 2.2 | −12.5 | 2.2 |
| M#14 | 5.9 | 1.1 | −1.6 | 1.4 | 54.6 | 1.7 | −14.2 | 2.3 |
| M#16 | 5.5 | 0.9 | 0.4 | 1.4 | 60.4 | 2.0 | −13.0 | 2.3 |
| M#20 | 11.8 | 1.6 | 3.0 | 1.5 | 38.0 | 2.2 | −5.4 | 1.8 |
| M#21 | 8.1 | 2.0 | 1.6 | 1.7 | 59.1 | 4.1 | −13.8 | 3.6 |
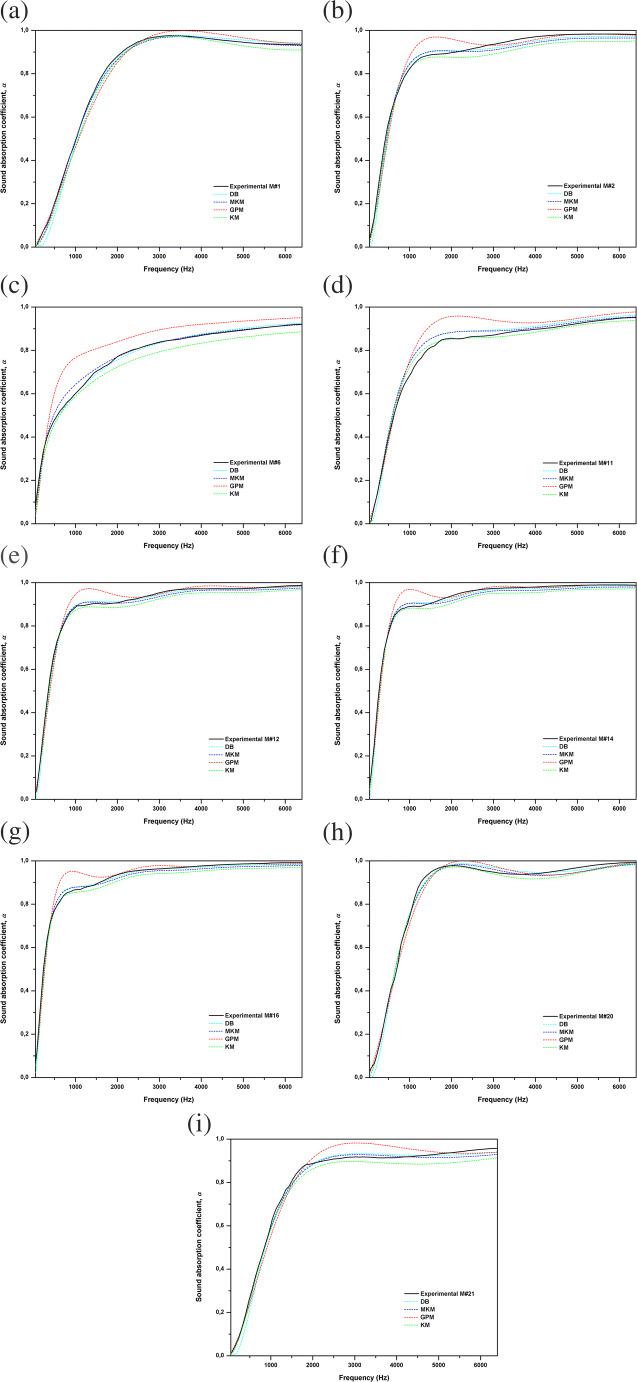
Figure 6 shows the comparison between the measured sound absorption spectra and those predicted with the DBM, MKM, GPM and KM models using as input parameter the optimised value of the flow resistivity. Table 3 shows the mean errors observed between the measured and predicted sound absorption spectra using the impedance models obtained following the Eq. (4). The errors observed for the models DBM, MKM, GPM and KM ranges from 0.8% to 8.7%. In the case of the DBM and MKM models the maximum mean error was below 3%. Nevertheless and as it was expected, at low frequencies, DBM showed higher errors than MKM so with this latter the predictions obtained using optimised flow resistivity were mostly closer with the experimental data than those using DBM, mainly at low frequencies. In the case of the GPM and KM models the maximum mean error was below 9.0%. This can be shown in the Fig. 6 where in the most cases important differences were found in a broader frequency range between the measured and predicted sound absorption spectra. This was in accordance with the differences obtained between the measured and the predicted flow resistivity. Therefore these results suggested that DBM and MKM models were able to predict accurately the acoustic behaviour of the cellulose acetate.
Fig. 6.
Measured and predicted sound absorption spectra for cellulose acetate samples
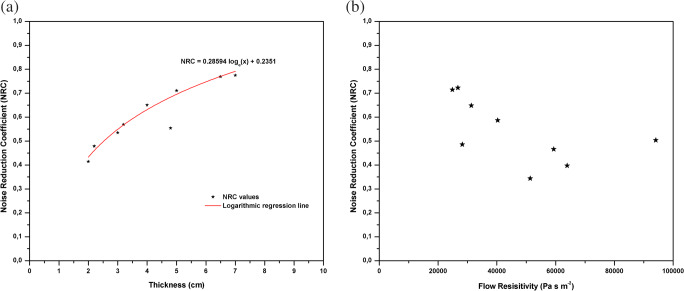
In order to evaluate the acoustic performance of cellulose acetate samples, NRC and SAA were evaluated according ASTM C423–17 [50]. Table 4 shows NRC and SAA values for the cellulose acetate samples. NRC values ranges from 0.40 to 0.80. SAA values ranges from 0.34 to 0.72. Figure 7 shows the relationship between the NRC and the thickness. It could be observed that the NRC increased as the thickness of the sample increased, as it was expected, because of the interaction between the sound waves and fibers of the sound absorber was greater when increasing the thickness of the sample. The higher the thickness was, the higher the thermal-viscous effects were because of friction, so the NRC was higher.
Table 4.
NRC and SAA values for the cellulose acetate samples and some commercial sound fibrous absorbers
| M#1 | M#2 | M#6 | M#11 | M#12 | M#14 | M#16 | M#20 | M#21 | CFM-1 | CFM-2 | CFM-3 | CFM-4 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NRC | 0.40 | 0.65 | 0.55 | 0.55 | 0.70 | 0.80 | 0.80 | 0.55 | 0.50 | 0.60 | 0.60 | 0.65 | 0.60 |
| SAA | 0.34 | 0.59 | 0.50 | 0.47 | 0.65 | 0.71 | 0.72 | 0.49 | 0.40 | 0.58 | 0.56 | 0.60 | 0.57 |
Fig. 7.
(a) Variation of NRC for cellulose acetate fibers having different thicknesses. (b) Relationship between SAA and flow resistivity
For small thicknesses, the rise in NRC seemed to be more steep (ΔNRC = 0.13 between 2 cm and 3 cm) than for greater thicknesses (ΔNRC = 0.06 between 5 cm and 7 cm) and the rate of NRC increments with thickness tended to be logarithmic (Fig.7a) [4]. Therefore, using direct interpolation of the NRC values shown in Fig. 7a it was possible to obtain an empirical expression for NRC as a function of the thickness, d:
| 16 |
The validity of this expression lies only in a thickness range of 0.5 cm to 14.5 cm due to NRC should always lie between 0 and 1 and it is only valid for this material. Figure 7b shows the relationship between SAA and the measured flow resistivity where the higher the SAA the lower the flow resistivity. In both Figures sample M#6 showed anomalous results.
In order to compare cellulose acetate samples with some commercial sound fibrous absorbers, four different fibrous materials (CFM) made of fiber glass; CFM-1 (σ = 41,398 Pa s m−2) and CFM-4 (σ = 38,138 Pa s m−2), and glass wool; CFM-2 (σ = 8248 Pa s m−2) and CFM-3 (σ = 32,503 Pa s m−2) were tested and compared with M#1 and M#20 samples. Data coming from commercial sound fibrous absorbers were obtained from Maderuelo-Sanz et al. [34]. The bulk densities of these commercial fibrous absorbers ranged between 30 kg m−3 to 110 kg m−3, having a fiber diameter ranging between 8 μm to 15 μm. Figure 8 shows the sound absorption spectrums for the commercial samples and the samples M#1 and M#20. These results showed similar absorption spectrum between samples CFM-2 and M#20, and between samples M#2, CFM-1 CFM-3 and CFM-4. Table 4 shows the NRC and SAA values obtained for these samples. Samples CFM-3 and M#2 showed very similar NRC and SAA values. The higher the NRC or the SAA values; the better is the material capability in sound absorption.
Fig. 8.
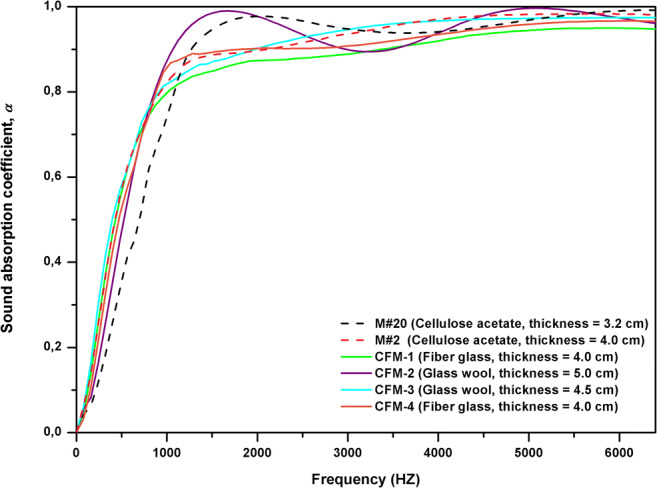
Sound absorption spectra for commercial sound fibrous absorbers and samples M#2 and M#20
Conclusions
This paper shows that the acoustical properties of cellulose acetate can be predicted with relatively simpler models which are mainly based on the flow resistivity. Moreover, experimental and theoretical studies of the acoustic properties of cellulose acetate coming from cigarette butts were carried out. Nine fibrous samples, having different physical properties, were acoustically characterised by means of an impedance tube and optimized using acoustic impedance models (Delany-Bazley, Garai-Pompoli, Miki and Komatsu). Non-acoustic properties such as bulk density, porosity and flow resistivity were firstly measured. Tortuosity was evaluated according a prediction-based equation.
The results suggested that values of the flow resistivity, determined by making use of an inverse calculation method based on the obtained acoustic measurement results, characteristic impedance and complex wavenumber, were more accurate when using the Delany-Bazley and the Miki models than that predicted using Garai-Pompoli and Komatsu models. In absolute terms, the Garai-Pompoli model showed the higher differences of the predicted flow resistivities (38.0% to 76.1%). The flow resistivity values obtained using this model was always higher than those measured values with the exception of the sample M#11. In the case of the Komatsu model, the predicted flow resistivity values were always lower than measured values. These differences were between −17.9% and − 3.4%. The differences between the predicted and measured values of the flow resistivity are smaller using the Delany and Bazley and Miki models (in absolute terms; 1.7%–11.8% and 0.3%–7.3% respectively). Therefore, the Miki model enables to obtain the predicted flow resistivity of this type of fibrous material from measured sound absorption spectrum with better accuracy than 7.3%.
The sound absorption spectra of the cellulose acetate samples using the Miki model were in better agreement with the experimental data than those using Delany-Bazley model, mainly at low frequencies. The errors found for Miki and Delany-Bazley models were relatively low (E < 2.2% and E < 2.8%, respectively). In the case of the Garai-Pompoli and the Komatsu models high error values were found (E < 8.7% and E < 4.4%, respectively).
Moreover, the sound absorption performance of the samples was compared with commercial fibrous absorbers. The NRC and SAA results suggested that cellulose acetate, adequately treated in order to remove the toxic substances, could show similar acoustic performance than those fibrous absorbers used actually in the building sector, even having lower thicknesses. Therefore, cellulose acetate could be considered good sound porous absorber to be used in building construction or in the core of noise barriers.
The growth of fungus and moulds on these panels could be a problem and a possibility to take into account in the future development of these building solutions. As this work is a first approach of recycling this waste, future works must take into account this problem and try to solve through the use of hydrophobic polymers in the manufacture of the sound absorbing panel. Moreover it will be necessary trying to remove as much as possible the toxic substances present in the cigarette butts through other chemical or physical methods in order to obtain a raw material as much as possible cleaner to be used in building.
Development of this high value-added product could solve some important environmental problems; on the one hand, avoiding the possible dispersion of this waste into the environment using it in building construction as an alternative solutions to landfilling and incineration, at same time promoting economic development of the building sector through the development of new building solutions.
Acknowledgements
The author is grateful to INTROMAC and Regional Office of Economics, Science and Digital Agenda of the Government of Extremadura.
Fundings
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Declarations
Conflict of interest
The authors declare that there are no conflicts of interest.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Lim ZY, Putra A, Nor MJM, Yaakob MY. Sound absorption performance of natural kenaf fibres. Appl Acoust. 2018;130:107–114. doi: 10.1016/j.apacoust.2017.09.012. [DOI] [Google Scholar]
- 2.Soltani P, Taban E, Faridan M, Samaei SE, Amininasab S. Experimental and computational investigation of sound absorption performance of sustainable porous material: Yucca Gloriosa fiber. Appl Acoust. 2020;157:106999. doi: 10.1016/j.apacoust.2019.106999. [DOI] [Google Scholar]
- 3.Taban E, Khavanin A, Ohadi A, Putra A, Jafari AJ, Faridan M, Soleimanian A. Study on the acoustic characteristics of natural date palm fibres: experimental and theoretical approaches. Build Environ. 2019;161:106274. doi: 10.1016/j.buildenv.2019.106274. [DOI] [Google Scholar]
- 4.Raj M, Fatima S, Tandon N. An experimental and theoretical study on environment-friendly sound absorber sourced from nettle fibers. J Build Eng. 2020;31:101395. doi: 10.1016/j.jobe.2020.101395. [DOI] [Google Scholar]
- 5.Maderuelo-Sanz R, Nadal-Gisbert AV, Crespo-Amorós JE, Parres-García F. A novel sound absorber with recycled fibers coming from end of life tires (ELTs) Appl Acoust. 2012;73:402–408. doi: 10.1016/j.apacoust.2011.12.001. [DOI] [Google Scholar]
- 6.Khan A, Mohamed M, Al Halo N, Benkreira H. Acoustical properties of novel sound absorbers made from recycled granulates. Appl Acoust. 2017;127:80–88. doi: 10.1016/j.apacoust.2017.05.035. [DOI] [Google Scholar]
- 7.Rubino C, Aracil MB, Liuzzi S, Stefanizzi P, Martellotta F. Wool waste used as sustainable nonwoven for building applications. J Clean Prod. 2021;278:123905. doi: 10.1016/j.jclepro.2020.123905. [DOI] [Google Scholar]
- 8.Maderuelo-Sanz R, Barrigón Morillas JM, Gómez Escobar V. The performance of resilient layers made from cork granulates mixed with resins for impact noise reduction. Eur J Wood Wood Prod. 2014;72:833–835. doi: 10.1007/s00107-014-0845-1. [DOI] [Google Scholar]
- 9.Yun BY, Cho HM, Kim YU, Lee SC, Berardi U, Kim S. Circular reutilization of coffee waste for sound absorbing panels: a perspective on material recycling. Environ Res. 2020;184:109281. doi: 10.1016/j.envres.2020.109281. [DOI] [PubMed] [Google Scholar]
- 10.Gadea Borrell JM, Juliá Sanchis E, Segura Alcaraz J, Montava Belda I. Sustainable sound absorbers from fruit stones waste. Appl Acoust. 2020;161:107164. doi: 10.1016/j.apacoust.2019.107174. [DOI] [Google Scholar]
- 11.Malawade UA, Jadhav MG. Investigation of the acoustic performance of bagasse. J Mater. 2020;9:882–889. doi: 10.1016/j.jmrt.2019.11.028. [DOI] [Google Scholar]
- 12.The Tobacco Atlas. Consumption. https://tobaccoatlas.org/topic/consumption/. 2018 (Accessed 13 October 2019).
- 13.Kurmus H, Mohajerani A. The toxicity and valorization options of cigarette butts. Waste Manag. 2020;104:104–118. doi: 10.1016/j.wasman.2020.01.011. [DOI] [PubMed] [Google Scholar]
- 14.Torkashvand J, Farzadkia M, Sobhi HR, Esrafili A. Littered cigarette butt as a well-known hazardous waste: a comprehensive systematic review. J Hazard Mater. 2020;383:121242. doi: 10.1016/j.jhazmat.2019.121242. [DOI] [PubMed] [Google Scholar]
- 15.Mohajerani A, Kadir AA, Larobina L. A practical proposal for solving the world’s cigarette butt problem: recycling in fired clay bricks. Waste Manag. 2016;52:228–244. doi: 10.1016/j.wasman.2016.03.012. [DOI] [PubMed] [Google Scholar]
- 16.Mohajerani A, Tanriverdi Y, Nguyen BT, Wong KK, Dissanayake HN, Johnson L, Whitfield D, Thomson G, Alqattan E, Rezaei A. Physico-mechanical properties of asphalt concrete incorporated with encapsulated cigarette butts. Constr Build Mater. 2017;153:69–80. doi: 10.1016/j.conbuildmat.2017.07.091. [DOI] [Google Scholar]
- 17.Teixeira MBH, Duarte MAB, Garcez LR, Rubim JC, Gatti TH, Suarez PAZ. Process development for cigarette butts recycling into cellulose pulp. Waste Manag. 2017;60:140–150. doi: 10.1016/j.wasman.2016.10.013. [DOI] [PubMed] [Google Scholar]
- 18.Zhao J, Zhang N, Qu C, Wu X, Zhang J, Zhang X. Cigarette butts and their application in corrosion inhibition for N80 steel at 90° C in a hydrochloric acid solution. Ind Eng Chem Res. 2010;49(8):3986–3991. doi: 10.1021/ie100168s. [DOI] [Google Scholar]
- 19.Ghosh TK, Sadhukhanc S, Ranad D, Sarkarc G, Dase C, Chattopadhyaye S, Chattopadhyay D, Chakraborty M. Treatment of recycled cigarette butts (man-made pollutants) to prepare electrically conducting material. J Indian Chem Soc. 2017;94:863–870. [Google Scholar]
- 20.Sabzali A, Nikaeen M, Bina B. Evaluation of cigarette filters rods as a biofilm carrier in integrated fixed film activated sludge process. World Acad Sci Eng Technol. 2011;5:82–87. doi: 10.5281/zenodo.1069943. [DOI] [PubMed] [Google Scholar]
- 21.Marinello S, Lolli F, Gamberini R, Rimini B. A second life for cigarette butts? A review of recycling solutions. J Hazard Mater. 2020;384:121245. doi: 10.1016/j.jhazmat.2019.121245. [DOI] [PubMed] [Google Scholar]
- 22.Delany ME, Bazley EN. Acoustical properties of fibrous absorbent materials. Appl.Acoust. 1970;3(2):105–116. doi: 10.1016/0003-682X(70)90031-9. [DOI] [Google Scholar]
- 23.Garai M, Pompoli F. A simple empirical model of polyester fibre materials for acoustical applications. Appl Acoust. 2005;66(12):1383–1398. doi: 10.1016/j.apacoust.2005.04.008. [DOI] [Google Scholar]
- 24.Miki Y. Acoustical properties of porous materials-generalizations of empirical models. J Acoust Soc Jpn. 1990;11:25–28. doi: 10.1250/ast.11.25. [DOI] [Google Scholar]
- 25.Mechel FP. Design charts for sound absorber layers. J Acoust Soc Am. 1988;83(3):1002–1013. doi: 10.1121/1.396045. [DOI] [Google Scholar]
- 26.Komatsu T. Improvement of the Delany-Bazley and Miki models for fibrous sound-absorbing materials. Acoust Sci Technol. 2008;29(2):121–129. doi: 10.1250/ast.29.121. [DOI] [Google Scholar]
- 27.Johnson DL, Koplik J, Dashen R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. J Fluid Mech. 1987;176:379–402. doi: 10.1017/S0022112087000727. [DOI] [Google Scholar]
- 28.Champoux Y, Allard JF. Dynamic tortuosity and bulk modulus in air saturated porous media. J Appl Phys. 1991;70(4):1975–1979. doi: 10.1063/1.349482. [DOI] [Google Scholar]
- 29.Pride SR, Gangi AF, Morgan FD. Deriving the equations of motion for porous isotropic media. J Acoust Soc Am. 1992;92:3278–3290. doi: 10.1121/1.404178. [DOI] [Google Scholar]
- 30.Pride SR, Morgan FD, Gangi AF. Drag forces of porous-medium acoustics. Phys Rev B. 1993;47:4964–4978. doi: 10.1103/PhysRevB.47.4964. [DOI] [PubMed] [Google Scholar]
- 31.Lafarge D, Lemarinier P, Allard JF, Tarnow V. Dynamic compressibility of air in porous structures at audible frequencies. J Acoust Soc Am. 1997;102:1995–2006. doi: 10.1121/1.419690. [DOI] [Google Scholar]
- 32.Allard JF, Atalla N. Propagation of sound in porous media: modelling sound absorbing materials. 2nd ed: Wiley; 2009. 10.1007/978-94-011-1866-8.
- 33.Gómez Escobar V, Maderuelo Sanz R. Acoustical performance of samples prepared with cigarette butts. Appl Acoust. 2017;125:166–172. doi: 10.1016/j.apacoust.2017.05.001. [DOI] [Google Scholar]
- 34.Maderuelo-Sanz R, Gómez Escobar V, Meneses Rodríguez JM. Potential use of cigarette filters as sound porous absorber. Appl Acoust. 2018;129:86–91. doi: 10.1016/j.apacoust.2017.07.011. [DOI] [Google Scholar]
- 35.Gómez Escobar V, Rey Gozalo G, Pérez CJ. Variability and performance study of the sound absorption of used cigarette butts. Materials. 2019;12(16):2584. doi: 10.3390/ma12162584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Koutela N, Fernández E, Saru ML, Psillakis E. A comprehensive study on the leaching of metals from heated tobacco sticks and cigarettes in water and natural water. Sci Total Environ. 2020;714:136700. doi: 10.1016/j.scitotenv.2020.136700. [DOI] [PubMed] [Google Scholar]
- 37.Mwaikambo LY, Ansell MP. Chemical modification of hemp, sisal, jute, and kapok fibers by alkalization. J Appl Polym Sci. 2002;84(12):2222–2234. doi: 10.1002/app.10460. [DOI] [Google Scholar]
- 38.Lee Y, Joo C. Sound absorption properties of recycled polyester fibrous assembly absorbers. Autex Res J. 2003;3:78–84. http://www.autexrj.com/cms/zalaczone_pliki/5-03-2.pdf. Accessed 30 June 2020.
- 39.Maderuelo-Sanz R, Martín-Castizo M, Vilchez-Gómez R. The performance of resilient layers made from recycled rubber fluff for impact noise reduction. Appl Acoust. 2011;72:823–828. doi: 10.1016/j.apacoust.2011.05.004. [DOI] [Google Scholar]
- 40.ASTM, ASTM D-3776. Standard test methods for mass per unit area (Weight) of fabric. 2007 Annual book of ASTM standards. 2007. www.astm.org. Accessed 12 May 2020.
- 41.Yang Y, Chen Z, Chen Z, Fu R, Li Y. Sound insulation properties of sandwich structures on glass fiber felts. Fiber Polym. 2015;16:1568–1577. doi: 10.1007/s12221-015-5200-6. [DOI] [Google Scholar]
- 42.Kucuk M, Korkmaz Y. Sound absorption properties of bilayered nonwoven composites. Fiber Polym. 2016;16:941–948. doi: 10.1007/s12221-015-0941-9. [DOI] [Google Scholar]
- 43.Maderuelo-Sanz R, Nadal-Gisbert AV, Crespo-Amorós JE, Barrigón Morillas JM, Parrés-García F, Juliá Sanchís E. Influence of the microstructure in the acoustical performance of consolidated lightweight granular materials. Acoust Aust. 2016;44:149–157. doi: 10.1007/s40857-016-0048-5. [DOI] [Google Scholar]
- 44.Bies DA, Hansen CH. Flow resistance information for acoustical design. Appl Acoust. 1980;13(5):357–391. doi: 10.1016/0003-682X(80)90002-X. [DOI] [Google Scholar]
- 45.Ingard KU, Dear TA. Measurement of acoustic flow resistance. J Sound Vib. 1985;103(4):567–572. doi: 10.1016/S0022-460X(85)80024-9. [DOI] [Google Scholar]
- 46.Johnson DL, Plona TJ, Scala C, Pasierb F, Kojima H. Tortuosity and acoustic slow waves. Phys Rev Lett. 1982;49:1840–1844. doi: 10.1103/PhysRevLett.49.1840. [DOI] [Google Scholar]
- 47.Attenborough K. Models for the acoustical characteristics of air filled granular materials. Acta Acust. 1993;64:27–30. [Google Scholar]
- 48.Attenborough K. Acoustical characteristics of rigid fibrous absorbents and granular materials. J Acoust Soc Am. 1983;73:785–799. doi: 10.1121/1.389045. [DOI] [Google Scholar]
- 49.ISO 10534-2. Acoustics determination of sound absorption coefficient and impedance in impedance tubes. Part 2: Transfer function method. International Organization for Standardization, Geneva 1998.
- 50.ASTM, ASTM C423. Standard test method for sound absorption and sound absorption coefficients by the reverberation room method. 2017 Annual book of ASTM standards. 2017. www.astm.org. Accessed 17 Oct 2020.
- 51.Pelegrinis MT, Horoshenkov KV, Burnett A. An application of Kozeny–Carman flow resistivity model to predict the acoustical properties of polyester fibre. Appl.Acoust. 2016;101:1–4. doi: 10.1016/j.apacoust.2015.07.019. [DOI] [Google Scholar]
- 52.Berardi U, Iannace G. Acoustic characterization of natural fibers for sound absorption applications. Build Environ. 2015;94:840–852. doi: 10.1016/j.buildenv.2015.05.029. [DOI] [Google Scholar]
- 53.Hurrell AI, Horoshenkov KV, Pelegrinis MT. The accuracy of some models for the airflow resistivity of nonwoven materials. Appl Acoust. 2018;130:230–237. doi: 10.1016/j.apacoust.2017.09.024. [DOI] [Google Scholar]