Systematic Parametrization of Divalent Metal Ions for the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models

Abstract

Divalent metal ions play important roles in biological and materials systems. Molecular dynamics simulation is an efficient tool to investigate these systems at the microscopic level. Recently, four new water models (OPC3, OPC, TIP3P-FB, and TIP4P-FB) have been developed and better represent the physical properties of water than previous models. Metal ion parameters are dependent on the water model employed, making it necessary to develop metal ion parameters for select new water models. In the present work, we performed parameter scanning for the 12–6 Lennard-Jones nonbonded model of divalent metal ions in conjunction with the four new water models as well as four previous water models (TIP3P, SPC/E, TIP4P, and TIP4P-Ew). We found that these new three-point and four-point water models provide comparable or significantly improved performance for the simulation of divalent metal ions when compared to previous water models in the same category. Among all eight water models, the OPC3 water model yields the best performance for the simulation of divalent metal ions in the aqueous phase when using the 12–6 model. On the basis of the scanning results, we independently parametrized the 12–6 model for 24 divalent metal ions with each of the four new water models. As noted previously, the 12–6 model still fails to simultaneously reproduce the experimental hydration free energy (HFE) and ion-oxygen distance (IOD) values even with these new water models. To solve this problem, we parametrized the 12–6-4 model for the 16 divalent metal ions for which we have both experimental HFE and IOD values for each of the four new water models. The final parameters are able to reproduce both the experimental HFE and IOD values accurately. To validate the transferability of our parameters, we carried out benchmark calculations to predict the energies and geometries of ion–water clusters as well as the ion diffusivity coefficient of Mg²⁺. By comparison to quantum chemical calculations and experimental data, these results show that our parameters are well designed and have excellent transferability. The metal ion parameters for the 12–6 and 12–6-4 models reported herein can be employed in simulations of various biological and materials systems when using the OPC3, OPC, TIP3P-FB, or TIP4P-FB water model.

Graphical Abstract

INTRODUCTION

Metal ions play significant roles in biology.^1–3 For example, over 25% of all proteins need metal ions.^4–6 As a major category of metal ions, divalent metal ions are not only important for proteins,^7,8 carbohydrates,⁹ nucleic acids,¹⁰ and lipids,¹¹ but are also valuable in the materials sciences.^12–14 Computational chemistry is an effective tool to investigate metal ion-containing systems in biology as well as materials.^15,16 Compared to quantum mechanics-based models, force field models have significant advantages in computational costs. However, simultaneously reproducing the thermodynamics (e.g., hydration free energy) and structural features (e.g., ion–oxygen distance) of metal ions in the aqueous phase is a challenge.¹⁷ The challenge is even bigger for modeling metal ions in more complicated systems such as metalloproteins. A variety of force field models have been developed for metal ion modeling, such as the bonded model,¹⁸ the nonbonded model,¹⁹ the cationic dummy atom model,²⁰ the Drude oscillator model,^21,22 the fluctuating charge model,²³ and ReaxFF.²⁴ A comprehensive review concerning metal ion modeling has been recently provided by Li and Merz.²⁵

The bonded model is widely used for metalloprotein modeling.^18,26–30 In this model, the metal ion is covalently bonded to the coordinating residues. The bond, angle, dihedral, van der Waals (vdW), and electrostatic interactions are described by classical terms. Different schemes have been developed to parametrize these terms.²⁵ Although the bonded model can reproduce experimentally determined structures of metal sites, it cannot simulate ligand exchange or switches in coordination number (CN), which is crucial for modeling catalytic metal centers as well as metal transport. One alternative model is the cationic dummy model proposed by Åqvist and Warshel.^20,31 In this model, dummy particles are distributed around the metal ion with a predefined geometry. These dummy particles are covalently bonded to the ion center, while the rigid cation–dummy particle framework interacts with the coordinating residues through vdW and electrostatic interactions. However, only a few metal ions have been parametrized for this model,^32–36 and it can be biased by the predefined geometry. Moreover, the cationic dummy atom model which works for a certain system may not be suitable for another system.³⁷

The nonbonded model is another widely used model for metal ions. In this model, the metal ion is represented by a soft sphere that usually has an integer charge and interacts with the environment through vdW and electrostatic interactions. The 12–6 Lennard-Jones (LJ) potential³⁸ is the most widely used potential to describe the vdW interactions, although the Born–Mayer potential may be used instead.³⁹ Recently, Li, Merz, and co-workers parametrized various (mono-, di-, tri-, tetra-valent) ions for the 12–6 LJ nonbonded model in conjunction with several explicit water models by targeting the experimental hydration free energies (HFEs) or the ion–oxygen distances (IODs).^17,19,40 Meanwhile, they also found that when a metal ion has a charge of +2 or higher the 12–6 LJ nonbonded model is not able to reproduce the experimental HFE and IOD simultaneously. Moreover, Li and Merz proposed that this deficiency originated from overlook of the ion-induced dipole interaction in the 12–6 model. To solve this problem, they proposed adding a C₄ term to the conventional 12–6 model to take this interaction into account.⁴¹ This was chosen because the ion-induced dipole interaction is proportional to r⁻⁴, where r is the distance between two particles.⁴¹ The new model was named the 12–6-4 LJ-type nonbonded model, and it can reproduce both the experimental HFE and IOD simultaneously for various metal ions.⁴¹ Furthermore, the 12–6-4 model can also simulate ion–ligand interactions. For example, by optimizing the C₄ term between metal ion and ligands, Sengupta et al. showed that the 12–6-4 model can simulate the chelate effect between metal ions and ethylenediamine in the aqueous environment, capturing both the thermodynamic and structural features simultaneously.^19,42 In addition, the 12–6-4 model can accurately model the interactions between nucleic acids and metal ions after parameter optimization.⁴³ Furthermore, inspired by the 12–6-4 model, Liao et al. added the C₄ term into the cationic dummy atom model and parametrized the new model for several divalent and trivalent metal ions.⁴⁴

Because of its speed and accuracy in describing the interactions between metal ions and coordinating ligands, the 12–6-4 model serves as an excellent model for simulating metal ions in molecular dynamics (MD) simulations. Previously, Li, Merz, and co-workers parametrized the 12–6-4 model for metal ions^19,40,41 in conjunction with the popular TIP3P,⁴⁵ SPC/E,⁴⁶ and TIP4P-Ew⁴⁷ water models. Recently, progresses in water model development have been made^48–60 and lead to more accurate simulations for biological systems in explicit water environment.^61,62 For example, the OPC3 and OPC water models were shown to be more accurate in reproducing various liquid bulk properties when compared to the previous three-point and four-point water models, respectively.^54,57 Moreover, predictions of the hydration free energies for small molecules using the OPC water model can achieve chemical accuracy (within ±1 kcal/mol of experimental values).¹⁹ In addition, the TIP3P-FB and TIP4P-FB water models, optimized by the ForceBalance method, can accurately reproduce many physical properties of water.⁵⁵ Our previous studies showed that ion parameters are water model dependent.¹⁷ However, to our best knowledge, no parameters have been reported for simulating divalent metal ions in conjunction with these four new water models. Moreover, nowadays, the particle mesh Ewald (PME) method⁶³ has become a standard protocol for dealing with the long-range electrostatic interactions in MD simulations. Hence, in this work, we parametrized the 12–6 and 12–6-4 models under PME conditions for divalent metal ions in conjunction with the OPC3, OPC, TIP3P-FB, and TIP4P-FB water models independently. Our parameters can accurately reproduce the experimental HFE and/or IOD values, along with an excellent balance between the R_min/2 and ε parameters. Moreover, we also performed benchmark calculations for ion–water clusters and ion transport. These results showed reasonable agreement with quantum mechanical (QM) calculations and experimental data, demonstrating the excellent transferability of the parameters developed in the present study. These parameters will serve the molecular modeling community for simulating various divalent metal ions when using these new water models.

METHODS

The potential function of the 12–6 nonbonded model is

$$\begin{gathered} U_{MW}\left(r_{MW}\right)=\frac{C_{12}^{MW}}{r_{MW}^{12}}-\frac{C_6^{MW}}{r_{MW}^6}+\frac{e^2{Q}_M{Q}_W}{r_{MW}} \\ ={\epsilon }_{MW}\left[{\left(\frac{R_{\min ,MW}}{r_{MW}}\right)}^{12}-2{\left(\frac{R_{\min ,MW}}{r_{MW}}\right)}^6\right]+\frac{e^2{Q}_M{Q}_W}{r_{MW}} \end{gathered}$$ (1)

The first two terms calculate the vdW interactions, and the last term calculates the electrostatic interactions. Herein, M and W represent the metal ion and an atom inside a water molecule, respectively. r_MW is the distance between M and W. Q_M and Q_W are charges of M and W, respectively. Q_M is +2 for the divalent metal ions investigated in the present work. The partial charges of oxygen and hydrogen atoms inside a water molecule are different among various water models, and these values are shown in Table S1. e is the charge of a proton. R_min,MW is the distance between M and W when their LJ potential reaches its minimum, and ε_MW is the corresponding well depth at this minimum. In the present work, ε_MW and R_min,MW are obtained through the Lorentz–Berthelot combining rule

$$R_{\min ,MW}=R_{\min ,M}/2+R_{\min ,W}/2$$ (2)

$${\epsilon }_{MW}=\sqrt{{\epsilon }_M{\epsilon }_W}$$ (3)

Herein, R_min,W and ε_W are the vdW radius and well depth for W, respectively. These parameters of the oxygen and hydrogen atoms in different water models are shown in Table S1. Therefore, in the present work, there are only two parameters that need to be determined for the 12–6 model for a certain metal ion, i.e., ε_M and R_min,M/2. Our previous study showed that there are different combinations of R_min,M/2 and ε_M values which can reproduce the same HFE or IOD value.¹⁷ However, these two parameters have physical meaning and, hence, could not be chosen arbitrarily. To solve this problem, we correlated these two parameters R_min/2 and ε based on fits of the experimentally determined R_min/2 and ε parameters for noble gas atoms.¹⁷ This fitted curve was named the noble gas curve (NGC) and was used to describe the relationship between R_min/2 and ε

$$-\log (\epsilon )=57.36e^{-2.471(\frac{R_{\min }}{2})}$$ (4)

For the 12–6 model parametrization in this study, we performed parameter scanning and determination by treating only R_min,M/2 as the variable, with ε_M calculated according to the NGC, providing an intrinsically one-dimensional problem that needs to be solved.

The potential function of the 12–6-4 nonbonded model is

$$\begin{gathered} U_{MW}\left(r_{MW}\right)=\frac{C_{12}^{MW}}{r_{MW}^{12}}-\frac{C_6^{MW}}{r_{MW}^6}-\frac{C_4^{MW}}{r_{MW}^4}+\frac{e^2{Q}_M{Q}_W}{r_{MW}} \\ ={\epsilon }_{MW}\left[{\left(\frac{R_{\min ,MW}}{r_{MW}}\right)}^{12}-2{\left(\frac{R_{\min ,MW}}{r_{MW}}\right)}^6\right]-\frac{C_4^{MW}}{r_{MW}^4}+\frac{e^2{Q}_M{Q}_W}{r_{MW}} \end{gathered}$$ (5)

In comparison to the 12–6 model, a C₄ term was added to account for the ion-induced dipole interactions between the metal ion and water molecules. Herein, we used the NGC to describe the relationship between R_min,M/2 and ε_M as well. Moreover, we assume the ion-induced dipole interactions between the metal ion and the water oxygen atoms dominate, with the C₄ terms between the metal ion and the water hydrogen atoms set to zero. For the 12–6-4 model, we performed parameter space scanning along the two variables R_min,M/2 and the C₄ term between the metal ion and water oxygen atoms. For the 12–6-4 parameter determination, the number of variables we have (R_min,M/2 and the C₄ term) is equal to the number of target properties (HFE and IOD) we want to reproduce, making this a well-defined parametrization process.

The thermodynamic integration (TI) method was used to calculate the HFE. Herein, we run the TI production runs in the NVT ensemble and assume a negligible contribution of the PdV term to the free energy. In the present study, the free energy change of an alchemical process is calculated as

$$\mathrm{\Delta }G=\mathrm{\Delta }A={\int }_0^1{\langle \frac{\partial U(\lambda )}{\partial \lambda }\rangle }_{\lambda }d\lambda$$ (6)

where U(λ) is the potential function of λ that varies from 0 to 1. λ = 0 corresponds to the initial state, and λ = 1 corresponds to the final state. TI has recently been implemented into the CUDA platform of Amber18,^64,65 and we have employed this implementation in the present study. In this work, four alchemical steps were simulated to obtain the HFE: (1) “turn on” the vdW interactions (and C₄ interactions, if applicable) of a dummy atom in water to obtain ΔG₁, (2) “turn on” the electrostatic interactions of the neutral atom in water yielding ΔG₂, (3) “turn off” the electrostatic interactions of the metal ion in water giving ΔG₃, and (4) “turn off” the vdW interactions (and C₄ interactions, if applicable) of the neutral atom in water to get ΔG₄. Steps (1) and (2) represent the hydration process of a metal ion, and steps (3) and (4) represent the dehydration process of a metal ion. The final HFE values were calculated as (ΔG₁ + ΔG₂ − ΔG₃ − ΔG₄)/2. For the electrostatic scaling steps, i.e., steps (2) and (3), the linear mixing potential function was used

$$U(\lambda )=(1-\lambda )U_0+\lambda U_1$$ (7)

where U₀ and U₁ represent the potential functions of the initial and final states, respectively.

For the vdW scaling steps, i.e., steps (1) and (4), the soft-core potential was used for the 12–6 Lennard-Jones potential to prevent the “end-point catastrophe”

$$U(\lambda )=4\epsilon \lambda \left[\frac{1}{{\left[\alpha (1-\lambda )+{\left(\frac{r_{ij}}{\sigma }\right)}^6\right]}^2}-\frac{1}{\alpha (1-\lambda )+{\left(\frac{r_{ij}}{\sigma }\right)}^6}\right]$$ (8)

where α is 0.5, and σ is the distance at which the LJ potential between atoms i and j equals zero. Specifically, eq 8 is for the vdW appearing step, while for the vdW disappearing step, λ is replaced by 1 − λ.

For each of the vdW scaling steps, three λ windows were used (0.1127, 0.5, and 0.88729). For each of the electrostatic scaling steps, seven λ windows were used (0.02544, 0.12923, 0.29707, 0.5, 0.70292, 0.87076, 0.97455). The free energy change for each step was calculated using the Gaussian quadrature

$$\mathrm{\Delta }G=\sum _i{w}_i{\langle \frac{\partial U(\lambda )}{\partial \lambda }\rangle }_i$$ (9)

where w_i is the weighting factor for window i.

In order to obtain ΔG₁ and ΔG₄, we started from an equilibrated structure for a system which has a divalent ion in a quasicubic water box with a side length of 40 Å. Then, the divalent ion was treated as a dummy/neutral atom mixed state, and the system was prepared for the TI runs through the following procedure with λ equals to 0.1127. First, 5000 steps of minimization using the steepest descent algorithm were carried out followed by 5000 steps of minimization using the conjugate gradient algorithm. Second, 360 ps of NVT was performed to heat the system gradually from 0 to 300 K through following stages: (1) 30 ps simulation was used to heat the system from 0 to 50 K, followed by 30 ps of equilibration at 50 K. (2) 30 ps simulation was performed to heat the system from 50 to 100 K, followed by 30 ps of equilibration at 100 K. (3) 30 ps simulation was performed to heat the system from 100 to 150 K, followed by 30 ps of equilibration at 150 K. (4) 30 ps simulation was performed to heat the system from 150 to 200 K, followed by 30 ps of equilibration at 200 K. (5) 30 ps simulation was performed to heat the system from 200 to 250 K, followed by 30 ps of equilibration at 250 K. (6) 30 ps simulation was performed to heat the system from 250 to 300 K, followed by 30 ps of equilibration at 300 K. Third, a 2 ns NPT equilibration was performed at 300 K and 1 atm. The final structure was used for the initial structure for a set of three-window TI calculations to obtain ΔG₁. TI calculations for the three windows were performed subsequently with λ values of 0.1127, 0.5, and 0.88729, respectively. Each of these windows cover 300 ps in the NVT ensemble at 300 K, with the last 200 ps used to obtain the averaged ∂U(λ)/∂λ value. Afterward, the vdW interactions of the neutral atom was “turned off” by another set of three-window TI calculations to obtain ΔG₄. Each of these windows covered 300 ps in the NVT ensemble at 300 K as well, with the last 200 ps used to obtain the averaged ∂U(λ)/∂λ value.

A similar protocol was used to obtain the ΔG₂ and ΔG₃ values. The same initial structure was used, and then, the divalent ion was treated as a mixture of a neutral atom and a metal ion with a λ value of 0.02544 for the following preparation steps: (1) 5000 steps of minimization using the steepest descent algorithm followed by 5000 steps of minimization using the conjugate gradient algorithm, (2) 360 ps NVT heating to gradually heat the system from 0 to 300 K with different stages as described above, and (3) 2 ns NPT equilibration at 300 K and 1 atm. Afterward, a set of seven-window TI calculations was performed to calculate ΔG₂. The λ values of these windows are 0.02544, 0.12923, 0.29707, 0.5, 0.70292, 0.87076, and 0.97455. Each window covered 300 ps in the NVT ensemble at 300 K, with the last 200 ps used to obtain the averaged ∂U(λ)/∂λ value. Afterward, another set of seven-window TI calculations was performed to obtain ΔG₃ using the same protocol. To test the convergence of the current protocol, we performed benchmark calculations by varying the simulation length for the TI calculations, and the results are shown in Tables S2A and S2B. These benchmark calculations indicate that 300 ps simulations including 200 ps production at each widow are sufficient to provide converged results. In terms of the uncertainties of the calculated HFEs, our previous studies on the 12–6 model¹⁷ and the 12–6-4 model⁴¹ for divalent metal ions showed that the uncertainties are on the order of ~1 kcal/mol. Hence, we expect that the calculated HFEs in the present study are of similar accuracy.

To obtain the IOD and CN values, the same initial structure was used to simulate the metal ion in the aqueous phase. Similarly, 5000 steps of minimization using the steepest descent algorithm followed by 5000 steps of minimization using the conjugate gradient algorithm, 360 ps of NVT heating to gradually heat the system from 0 to 300 K through a series of stages as described above, and 2 ns NPT of equilibration at 300 K and 1 atm were performed to equilibrate the system. Finally, 2 ns of NVT sampling at 300 K was performed with snapshots saved every 0.5 ps. The cpptraj program⁶⁶ was used to generate the radial distribution function (RDF) between the metal ion and water oxygen atoms in the range of 0–10 Å with a resolution of 0.01 Å. Each RDF was generated based on the averaged volume of that specific trajectory. On the basis of the RDF, we obtained the IOD and CN values with the method introduced in our previous study.¹⁹

For all the minimizations and MD simulations, the periodic boundary conditions (PBCs) were used. The PME method⁶³ was used with the nonbonded cutoff treated as 10 Å in the real space, and the size of the charge grid was set as 48 in each dimension. Benchmark calculations varying the size of the charge grid in the PME method were carried out, which indicated that the current setting is able to provide converged results (see Tables S2C and S2D). For all the MD simulations, the Langevin thermostat with a collision frequency of 2 ps⁻¹ was used for the temperature control. The time step was set to 1 fs. The Berendsen barostat with a pressure relaxation time of 1 ps was used for the pressure control in the NPT ensemble. The “three-point” SHAKE algorithm⁶⁷ was used for the water molecules in all the simulations except the minimizations and simulations involved in the protocol to obtain the ΔG₁ and ΔG₄ values. The simulations in the present work were assisted by the IPMach.py program in the AmberTools software package.⁶⁸

RESULTS AND DISCUSSIONS

Target HFE and IOD Values of Divalent Ions.

In the present work, we performed parametrizations for 24 divalent metal ions. The target HFE and IOD values of these 24 ions are shown in Table 1. To keep consistency with our previous study, we used the HFE values from Marcus.⁶⁹ The scatter plot of Figure 1 shows the target HFEs and IODs for these 24 divalent ions.

Table 1.

Target HFE, IOD, and CN Values for 24 Divalent Metal Ions^a

Ions	Electronic structures	HFE (kcal/mol)	IOD (Å)	CN
Be2+	[He]	−572.4	1.67	4
Cu2+	[Ar]3d9	−480.4	2.11	6
Ni2+	[Ar]3d8	−473.2	2.06 ± 0.01	6
Pt2+	[Xe]4f145d8	−468.5	N/A	N/A
Zn2+	[Ar]3d10	−467.3	2.09 ± 0.06	6
Co2+	[Ar]3d7	−457.7	2.10 ± 0.02	6
Pd2+	[Kr]4d8	−456.5	N/A	N/A
Ag2+	[Kr]4d9	−445.7	N/A	N/A
Cr2+	[Ar]3d4	−442.2	2.08	6
Fe2+	[Ar]3d6	−439.8	2.11 ± 0.01	6
Mg2+	[Ne]	−437.4	2.09 ± 0.04	6
V2+	[Ar]3d3	−436.2	2.21	6
Mn2+	[Ar]3d5	−420.7	2.19 ± 0.01	6
Hg2+	[Xe]4f145d10	−420.7	2.41	6
Cd2+	[Kr]4d10	−419.5	2.30 ± 0.02	6
Yb2+	[Xe]4f14	−360.9	N/A	N/A
Ca2+	[Ar]	−359.7	2.46	8
Sn2+	[Kr]4d105s2	−356.1	2.62	6
Pb2+	[Xe]4f145d106s2	−340.6	N/A	N/A
Eu2+	[Xe]4f7	−331.0	N/A	N/A
Sr2+	[Kr]	−329.8	2.64 ± 0.04	8−15
Sm2+	[Xe]4f6	−328.6	N/A	N/A
Ba2+	[Xe]	−298.8	2.83	9
Ra2+	[Rn]	−298.8	N/A	N/A

^aThese HFE, IOD, and CN values are from ref 17, which publication cites the original work.

Figure 1.

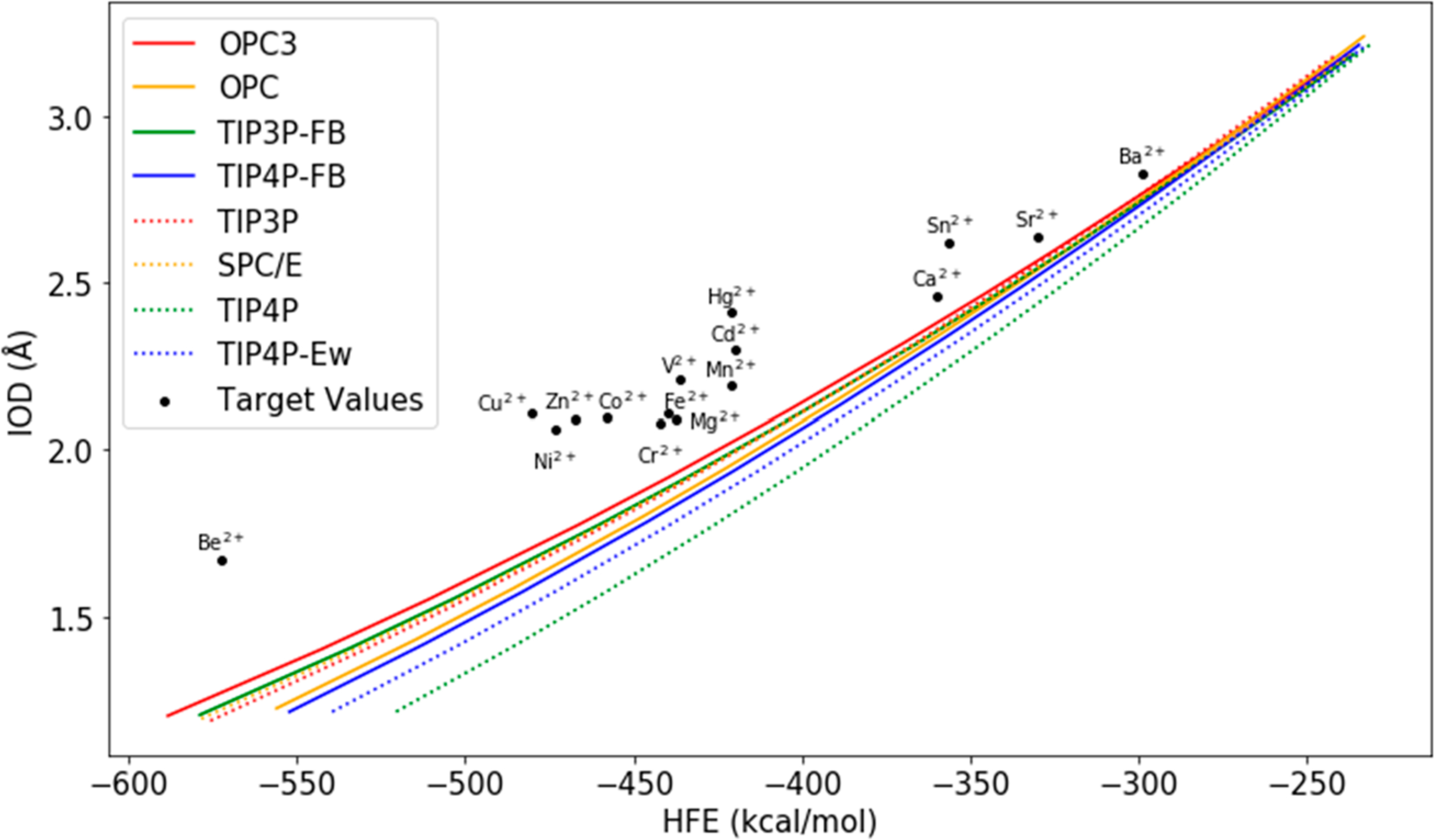
IOD vs HFE quadratic fitting curves based on the scan results of the 12–6 model for each water model and their comparison with the target IOD vs HFE scatter points of divalent metal ions.

In general, there are two different HFEs of ions that have been used in the literature: the real HFE and the intrinsic HFE (or the “absolute” HFE).⁷⁰ The real HFE includes contributions from the phase potential for an ion crossing the air/water interface, while the intrinsic HFE is independent of the interfacial potential and only accounts for the interaction between ion and water molecules.⁷⁰ The real HFE and intrinsic HFE have the following relationship: $\mathrm{\Delta }{G}_{\text{hydr}}^{\text{real}}=\mathrm{\Delta }{G}_{\text{hydr}}^{\text{intr}}+zF\varphi$, where F is the Faraday constant, while ϕ is the interfacial potential, which is negative and water model dependent. In the work of Lamoureux and Roux,⁷⁰ the authors noted that Tissandier et al.⁷¹ obtained a ΔG_hydr for the proton of −264 kcal/mol, and if one interpreted it as $\mathrm{\Delta }{G}_{\text{real}}^{\text{hydr}}$, this would provide a $\mathrm{\Delta }{G}_{\text{intr}}^{\text{hydr}}$ of around −252 kcal/mol. This value is consistent with the work of Grossfield et al.⁷² which gave $\mathrm{\Delta }{G}_{\text{intr}}^{\text{hydr}}$ as −252.5 kcal/mol through free energy simulations using the AMOEBA polarizable force field. Both of the above two values are very close to the value of $\mathrm{\Delta }{G}_0^{\text{hydr}}$ of the proton that was used by Marcus (−252.4 kcal/mol) in the Marcus data set.⁶⁹ In the Marcus data set, Marcus derived the HFE for a cation based on the $\mathrm{\Delta }{G}_0^{\text{hydr}}$ of the proton and the conventional HFE of this cation.⁶⁹ This means that the Marcus data set can be interpreted as the intrinsic HFE set for cations, which is directly comparable to free energy simulations without considering the phase potential, as we did in the present work. However, we are also aware that the HFE of the proton is still debated, and this value may change if more definitive experiments are performed or our understanding about the ion solvation advances in the future. In the present work, we provide all the scanned results in the SI. If anyone wants to derive parameters to target a different HFE, he or she can refer to the SI and refine these parameters to meet the specific needs.

Parameter Scanning Results for the 12–6 Model.

In order to characterize the performance of the 12–6 nonbonded model for divalent metal ions in conjunction with the four new water models, we performed parameter space scanning for each of these water models (OPC3,⁵⁴ OPC,⁵⁷ TIP3P-FB,⁵⁵ and TIP4P-FB⁵⁵). For comparison, we also performed parameter scans for four previous water models (TIP3P,⁴⁵ SPC/E,⁴⁶ TIP4P,⁴⁵ and TIP4P-Ew⁴⁷). The parameter scanning for each of these eight water models was carried out for R_min,M/2 values in the range of 0.9–2.3 Å with an interval of 0.1 Å. The ε_M value was calculated based on the R_min,M/2 value using the NGC. The scanning results are shown in the “C₄ = 0” columns in Tables S3 and S4. In our previous study, we found that the HFE and IOD values are highly correlated with each other: if two sets of parameters reproduce the same HFE value, they would likely to reproduce the same IOD value.¹⁷ Herein, we performed a quadratic fitting between the simulated HFE and IOD values for each water model and illustrate the fitted curves in Figure 1. Interestingly, the fitted curves converge when the ion has a large IOD but diverge when the ion has a small IOD. Moreover, the target points are above the fitting curves in Figure 1, indicating that all the water models underestimate the HFE values of divalent metal ions when reproducing their experimental IOD values, which differs from our previous study of monovalent ions where the experimental scatter points distribute on both sides of the fitted curves.¹⁹ This also agrees with our previous finding that it is challenging to reproduce both experimental HFE and IOD values using the 12–6 model when the cation has a charge of ≥ +2.¹⁷ In general, the OPC3 water model yields the best performance as its curve is the closest to the scatter points of the experimental HFE and IOD values for divalent metal ions. Specifically, the performance of the eight water models are as follows: OPC3 > TIP3P ~ SPC/E ~ TIP3P-FB > OPC ~ TIP4P-FB > TIP4P-Ew > TIP4P. These results are consistent to our previous study which indicated that the four-point water models tend to have larger errors when simulating divalent cations.¹⁷ Moreover, our results also showed that the four new water models can provide improved or similar performance when compared to the previous water models in the same category. In the category of three-point water models, OPC3 provides better performance than the TIP3P-FB model, which showed similar performance to the widely used TIP3P and SPC/E water models. In the category of four-point water models, the two new water models (OPC and TIP4P-FB) showed comparable performance to each other, and both are better than the TIP4P-Ew and TIP4P water models.

In order to further compare the eight water models, we performed curve fitting between the R_min,M/2 and simulated HFE values for each of the water models. These fitted curves are shown in Figure 2A. Similar to the IOD vs HFE fitting curves shown in Figure 1, the fitted curves in Figure 2A converge when R_min,M/2 is large but diverge when R_min,M/2 is small. The eight water models almost yield identical results when R_min,M/2 is ~2.3 Å. In contrast, these water models have significant differences when R_min,M/2 is ~0.9 Å. In general, the OPC3 water model tends to simulate a larger HFE value than the other water models when using the same Lennard-Jones parameters for a divalent metal ion (Figure 2A), especially when R_min,M/2 is smaller than 1.1 Å (Figure 2A inset). For example, when R_min,M/2 is 0.9 Å, the simulated HFE when using the OPC3 water model is more negative than the simulated HFE when using the TIP4P water model by ~68 kcal/mol (see Table S3).

Figure 2.

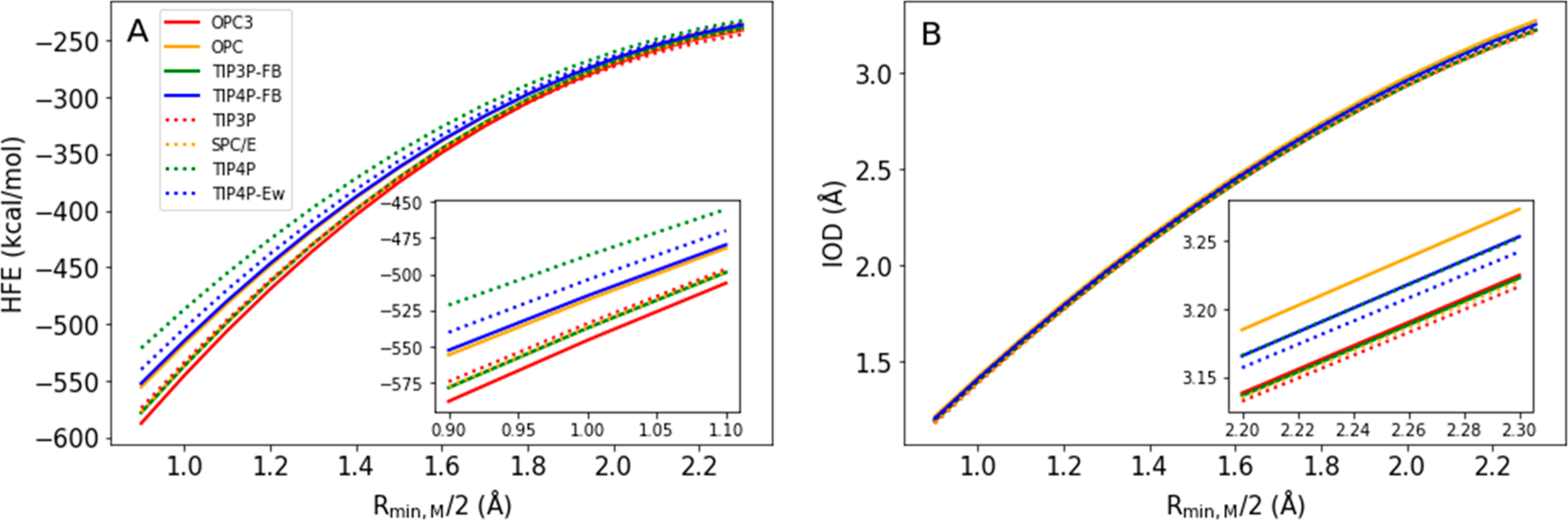
(A) HFE fitting curve for the eight water models. (B) IOD fitting curves for the eight water models. In the panel B insert, the fitting curves for TIP4P and TIP4P-FB overlap with each other, while the fitting curves of the four three-point water models overlap with each other.

Similarly, to compare the performance of the eight water models for simulating IOD values, we performed quadratic fits for IOD vs R_min,M/2 for each water model and illustrate the results in Figure 2B. Unlike Figure 2A, these IOD fitting curves of the eight water models are close to each other, which agrees with our previous studies.^17,19 By checking the figure carefully, we found that the IOD fitting curves for these water models converge when R_min,M/2 is small but diverge when R_min,M/2 is large, which is opposite to the trends of the HFE fitting curves in Figure 2A. Specifically, when R_min,M/2 is larger than 2.1 Å, the three-point water models tend to simulate smaller IOD values than the four-point water models (Figure 2B inset). However, this difference is relatively small: ~0.05 Å at most.

Parameter Determination for the 12–6 Model in Conjunction with the Four New Water Models.

On the basis of the parameter space scanning results, we performed a parametrization for the 12–6 model of divalent metal ions in conjunction with each of the four new water models. Because the 12–6 model has intrinsic errors when modeling divalent metal ions, it is impossible to reproduce both the experimental HFE and IOD values at the same time (Figure 1). Hence, we parametrized different parameter sets to reproduce different target properties, as was done in our previous works.^17,19,40 Specifically, we have parametrized the HFE parameter set to reproduce the target HFE values, the IOD parameter set to reproduce the target IOD values, and the compromise (CM) parameter set to keep a balance of these two properties and to reproduce the experimental relative HFE values. Because only 16 out of 24 divalent metal ions have target IOD values, the IOD parameter set was designed for only 16 divalent metal ions. Herein, we show the HFE, IOD, and CM parameter sets in Tables 2, 3, and 4, respectively. The simulated HFE, IOD, and CN values of these parameter sets are shown in Tables S5, S6, and S7, respectively. The HFE parameter set can reproduce the target HFE values within 1 kcal/mol, while the IOD parameter set can reproduce the target IOD values within 0.01 Å. The CM set was parametrized by systematically shifting the target HFE values by a constant. In this way, the relative HFE values between different divalent metal ions are still reproduced. By considering the differences in the four new water models (Figure 1), the constants of shifting were 20, 25, 25, and 30 kcal/mol for the OPC3, OPC, TIP3P-FB, and TIP4P-FB water models, respectively. For a certain divalent ion, its CM parameter set usually has R_min,M/2 between its HFE and IOD parameter sets.

Table 2.

HFE Parameter Set for 24 Divalent Metal Ions in Conjunction with the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models

	OPC3		OPC		TIP3P-FB		TIP4P-FB
	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)
Be2+	0.935	0.00000204	0.852	0.00000010	0.914	0.00000101	0.840	0.00000006
Cu2+	1.166	0.00060803	1.114	0.00022027	1.153	0.00047746	1.107	0.00019018
Ni2+	1.179	0.00076841	1.132	0.00031773	1.169	0.00064221	1.127	0.00028746
Pt2+	1.195	0.00101467	1.144	0.00040203	1.176	0.00072849	1.139	0.00036479
Zn2+	1.200	0.00110429	1.151	0.00045971	1.179	0.00076841	1.142	0.00038675
Co2+	1.233	0.00188205	1.172	0.00067804	1.220	0.00153342	1.164	0.00058613
Pd2+	1.237	0.00200187	1.175	0.00071558	1.220	0.00153342	1.168	0.00063064
Ag2+	1.284	0.00395662	1.205	0.00120058	1.269	0.00321068	1.200	0.00110429
Cr2+	1.291	0.00435036	1.219	0.00150903	1.278	0.00364281	1.218	0.00148497
Fe2+	1.300	0.00490301	1.229	0.00176831	1.284	0.00395662	1.224	0.00163434
Mg2+	1.306	0.00530214	1.239	0.00206414	1.288	0.00417787	1.238	0.00203280
V2+	1.310	0.00558254	1.244	0.00222695	1.292	0.00440914	1.255	0.00262320
Mn2+	1.353	0.00941798	1.305	0.00523385	1.339	0.00799176	1.300	0.00490301
Hg2+	1.353	0.00941798	1.305	0.00523385	1.339	0.00799176	1.300	0.00490301
Cd2+	1.357	0.00986018	1.309	0.00551135	1.342	0.00828195	1.302	0.00503325
Yb2+	1.534	0.05065033	1.489	0.03566355	1.520	0.04560206	1.485	0.03450196
Ca2+	1.541	0.05330850	1.493	0.03685224	1.525	0.04736426	1.488	0.03537062
Sn2+	1.556	0.05930945	1.506	0.04090549	1.540	0.05292325	1.500	0.03899838
Pb2+	1.624	0.09180886	1.577	0.06841702	1.607	0.08286870	1.574	0.06706518
Eu2+	1.671	0.11928915	1.625	0.09235154	1.653	0.10829364	1.620	0.08965674
Sr2+	1.677	0.12308079	1.631	0.09564656	1.659	0.11189491	1.626	0.09289608
Sm2+	1.683	0.12693448	1.637	0.09900804	1.664	0.11494497	1.632	0.0962022
Ba2+	1.840	0.24650465	1.797	0.21069138	1.824	0.23296929	1.795	0.20907204
Ra2+	1.840	0.24650465	1.797	0.21069138	1.824	0.23296929	1.795	0.20907204

Table 3.

IOD Parameter Set for 16 Divalent Metal Ions in Conjunction with the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models

	OPC3		OPC		TIP3P-FB		TIP4P-FB
	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)
Be2+	1.162	0.00056491	1.136	0.00034392	1.163	0.00057544	1.150	0.00045105
Cu2+	1.413	0.01791152	1.391	0.01430674	1.413	0.01791152	1.400	0.01570749
Ni2+	1.373	0.01179373	1.345	0.00858042	1.373	0.01179373	1.358	0.00997323
Zn2+	1.400	0.01570749	1.373	0.01179373	1.400	0.01570749	1.383	0.01314367
Co2+	1.406	0.01669760	1.382	0.01300356	1.406	0.01669760	1.392	0.01445748
Cr2+	1.391	0.01430674	1.364	0.01067299	1.391	0.01430674	1.375	0.01205473
Fe2+	1.413	0.01430674	1.391	0.01430674	1.413	0.01791152	1.400	0.01570749
Mg2+	1.400	0.01570749	1.373	0.01179373	1.400	0.01570749	1.383	0.01314367
V2+	1.480	0.03308772	1.456	0.02686716	1.480	0.03308772	1.465	0.02909167
Mn2+	1.462	0.02833599	1.444	0.02409615	1.462	0.02833599	1.459	0.02759452
Hg2+	1.584	0.07163727	1.565	0.06311131	1.584	0.07163727	1.572	0.06617338
Cd2+	1.526	0.04772212	1.506	0.04090549	1.520	0.04560206	1.511	0.04254294
Ca2+	1.617	0.08806221	1.590	0.07447106	1.617	0.08806221	1.600	0.07934493
Sn2+	1.746	0.17092614	1.715	0.14850170	1.746	0.17092614	1.731	0.15989650
Sr2+	1.762	0.18304100	1.731	0.15989650	1.762	0.18304100	1.746	0.17092614
Ba2+	1.918	0.31509345	1.883	0.28387745	1.918	0.31509345	1.900	0.29896986

Table 4.

CM Parameter Set for 24 Divalent Metal Ions in Conjunction with the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models

	OPC3		OPC		TIP3P-FB		TIP4P-FB
	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)	Rmin,M/2 (Å)	εM (kcal/mol)
Be2+	0.971	0.00000621	0.921	0.00000128	0.963	0.00000489	0.924	0.00000142
Cu2+	1.228	0.00174080	1.178	0.00075490	1.223	0.00160860	1.181	0.00089969
Ni2+	1.251	0.00247282	1.197	0.00104974	1.257	0.00270120	1.213	0.00136949
Pt2+	1.272	0.00334975	1.219	0.00150903	1.274	0.00344520	1.229	0.00176831
Zn2+	1.280	0.00374505	1.219	0.00150903	1.276	0.00354287	1.234	0.00191142
Co2+	1.306	0.00530214	1.263	0.00294683	1.304	0.00516628	1.277	0.00359255
Pd2+	1.309	0.00551135	1.269	0.00321068	1.308	0.00544088	1.282	0.00384964
Ag2+	1.339	0.00799176	1.305	0.00523385	1.339	0.00799176	1.316	0.00602547
Cr2+	1.349	0.00899152	1.316	0.00602547	1.349	0.00899152	1.327	0.00691068
Fe2+	1.356	0.00974813	1.323	0.00657749	1.356	0.00974813	1.334	0.00752608
Mg2+	1.363	0.01055378	1.330	0.00716930	1.363	0.01055378	1.342	0.00828195
V2+	1.366	0.01091456	1.334	0.00752608	1.366	0.01091456	1.345	0.00858042
Mn2+	1.410	0.01738340	1.381	0.01286460	1.411	0.01755812	1.394	0.01476261
Hg2+	1.410	0.01738340	1.381	0.01286460	1.411	0.01755812	1.394	0.01476261
Cd2+	1.413	0.01791152	1.389	0.01400886	1.415	0.01827024	1.398	0.01538757
Yb2+	1.622	0.09072908	1.602	0.08034231	1.629	0.09454081	1.621	0.09019198
Ca2+	1.628	0.09399072	1.608	0.08337961	1.635	0.09788018	1.627	0.09344247
Sn2+	1.641	0.10128575	1.625	0.09235154	1.652	0.10769970	1.645	0.10359269
Pb2+	1.723	0.15415012	1.707	0.14295367	1.730	0.15917293	1.728	0.15773029
Eu2+	1.772	0.19078645	1.753	0.17618319	1.782	0.19865859	1.782	0.19865859
Sr2+	1.778	0.19549490	1.766	0.18612361	1.789	0.20424131	1.789	0.20424131
Sm2+	1.784	0.20024770	1.766	0.18612361	1.795	0.20907204	1.796	0.20988115
Ba2+	1.966	0.35853865	1.960	0.35308749	1.983	0.37399087	1.992	0.38216886
Ra2+	1.966	0.35853865	1.960	0.35308749	1.983	0.37399087	1.992	0.38216886

Error Analysis.

To better understand the errors in the 12–6 model, we performed an error analysis for the 12–6 model when running simulations using the HFE and IOD parameter sets. By treating the OPC3 and OPC water models as an example, we show the corresponding HFE and IOD errors (as a percentage) for 16 divalent metal ions in Figure 3. The corresponding results for the TIP3P-FB and TIP4P-FB water models are shown in Figure S1. The HFE percent errors were calculated for the IOD parameter set, indicating the percent error of the 12–6 model for simulating the HFE values when reproducing the target IOD values. Similarly, the IOD percent errors were calculated for the HFE parameter set, indicating the percent error of the 12–6 model for simulating the IOD values when reproducing the target HFE values. These results indicate a general trend that the percent error increases when the size of the divalent metal ion decreases, agreeing with our previous study.¹⁷ Figure 3 showed that the biggest divalent ion Ba²⁺ has both the HFE percent error and IOD percent error less than 5%, when using the 12–6 model in conjunction with the OPC3 water model. By comparison, the smallest divalent ion Be²⁺ has the biggest percent errors: the HFE percent error and IOD percent error for Be²⁺ are 16% and 29%, respectively. These errors for Be²⁺ are even larger when using the other three water models (Figure 3 and Figure S1). Moreover, it can be seen that except for the Be²⁺ ion, the alkaline earth metal ions generally have smaller percent errors than the transition metal ions. This is consistent with the fact that the C₆ term in the 12–6 model considers the induced dipole–induced dipole interaction that is isotropic in nature: the alkaline earth metal ions have electronic structures identical to the noble gas atoms, making the point charge representation in the 12–6 model better able to represent these ions relative to the transition metal ions.

Figure 3.

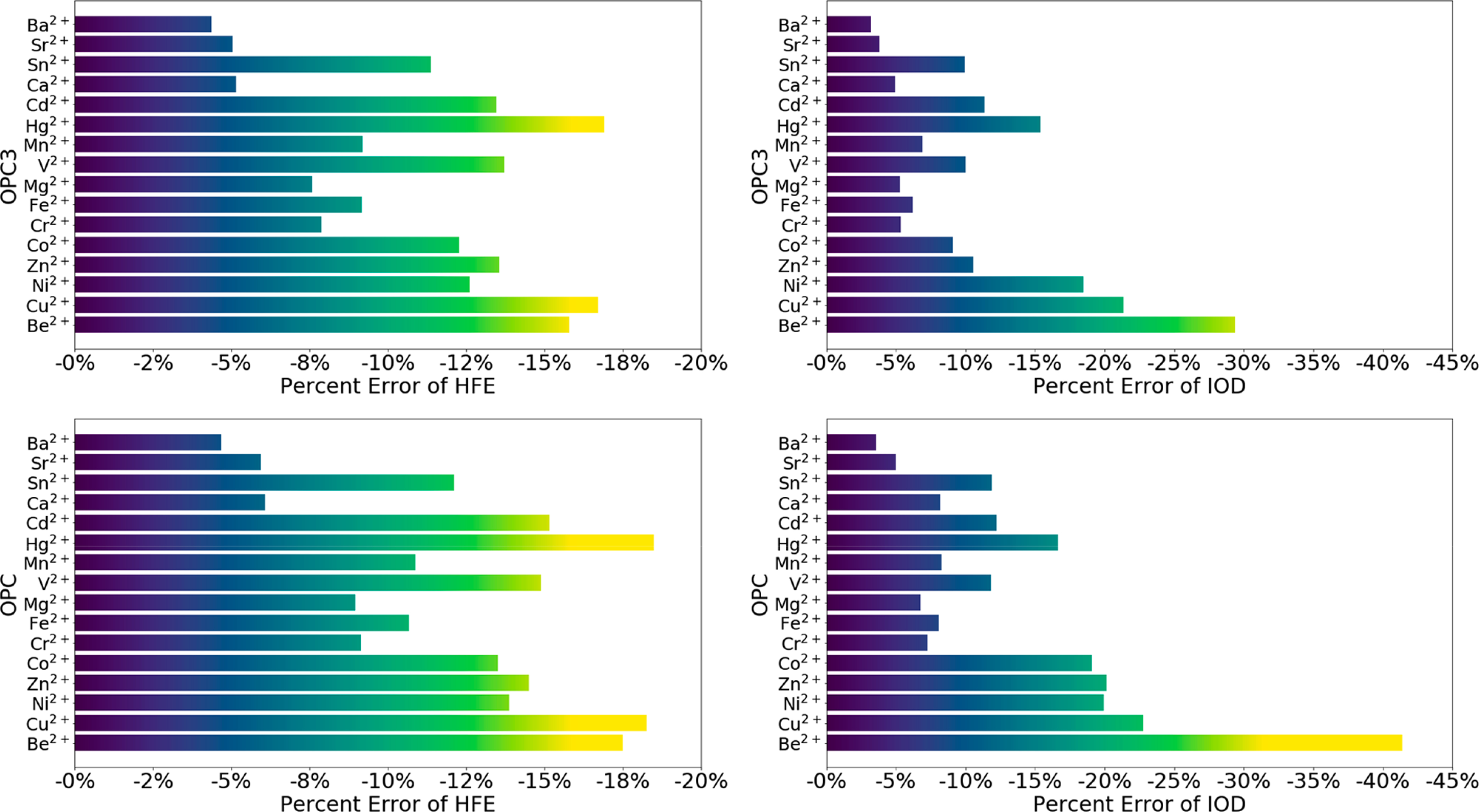
HFE and IOD percent errors for the 12–6 nonbonded model of divalent metal ions in conjunction with the OPC3 or OPC water model. The HFE percent errors were for the 12–6 IOD parameter set that can reproduce the target IOD values (Table 3 and Table S6). The IOD percent errors were for the 12–6 HFE parameter set that can reproduce the target HFE values (Table 2 and Table S5).

In summary, our results indicate that the 12–6 model has significant errors for simulating divalent metal ions in conjunction with the four new water models, as we found for previous water models.¹⁷ Although none of these new water models can reproduce the experimental HFE and IOD values simultaneously when simulating divalent metal ions using the 12–6 model, the performance of the four new water models follows the sequence OPC3 > TIP3P-FB > OPC ~ TIP4P-FB. Previously, we have attributed this error to the absence of ion-induced dipole interactions in the 12–6 model and proposed the addition of a C₄ term into the 12–6 model to take this interaction into account.⁴¹ The new model was named the 12–6-4 model, and it can reproduce experimental HFE and IOD values simultaneously for various ions,^40,41 hence providing significant improvement over the 12–6 model. Herein, in order to solve the intrinsic error of the 12–6 model as well as better simulate divalent metal ions in conjunction with the four new water models, we also parametrized the 12–6-4 model for each of these water models.

Parameter Determination for the 12–6-4 Model.

We performed parameter space scans for the 12–6-4 model and show the results in Tables S3 and S4. On the basis of the parameter scanning results, we performed parametrizations for the 12–6-4 model in conjunction with the four new water models. In these parametrizations, we aim to reproduce both the target HFE and IOD values. Because only 16 out of 24 divalent metal ions have both target HFE and IOD values, we only performed the 12–6-4 parametrization for these 16 divalent metal ions. The final parameters are shown in Table 5, and the simulated HFE, IOD, and CN values obtained by these parameters are shown in Table S8. These parameters can simultaneously reproduce the experimental HFE and IOD values with excellent accuracy; i.e., the experimental HFE are within 1 kcal/mol and the experimental IOD values within 0.01 Å.

Table 5.

12–6–4 Parameter Set for 16 Divalent Metal Ions in Conjunction with the OPC3, OPC, TIP3P-FB, and TIP4P-FB Water Models

	OPC3			OPC			TIP3P-FB			TIP4P-FB
	Rmin,M/2 (Å)	εM (kcal/mol)	C4(kcal/mol•Å4)	Rmin,M/2 (Å)	εM (kcal/mol)	C4(kcal/mol•Å4)	Rmin,M/2 (Å)	εM (kcal/mol)	C4(kcal/mol•Å4)	Rmin,M/2 (Å)	εM (kcal/mol)	C4(kcal/mol•Å4)
Be2+	1.211	0.00132548	186	1.201	0.00112300	214	1.209	0.00128267	193	1.213	0.00136949	227
Cu2+	1.467	0.02960343	269	1.448	0.02499549	291	1.467	0.02960343	279	1.469	0.03012160	313
Ni2+	1.435	0.02215953	207	1.402	0.01603244	212	1.437	0.02257962	223	1.409	0.01721000	218
Zn2+	1.441	0.02343735	199	1.423	0.01975917	225	1.446	0.02454281	217	1.436	0.02236885	239
Co2+	1.443	0.02387506	182	1.426	0.02034021	204	1.445	0.02431873	192	1.433	0.02174524	206
Cr2+	1.416	0.01845160	109	1.400	0.01570749	132	1.433	0.02174524	138	1.424	0.01995146	159
Fe2+	1.441	0.02343735	131	1.423	0.01975917	154	1.454	0.02639002	157	1.451	0.02568588	187
Mg2+	1.433	0.02174524	117	1.405	0.01652939	127	1.433	0.02174524	128	1.409	0.01721000	133
V2+	1.505	0.04058327	201	1.501	0.03931188	239	1.506	0.04090549	212	1.497	0.03806827	234
Mn2+	1.495	0.03745682	137	1.485	0.03450196	175	1.491	0.03625449	149	1.489	0.03566355	181
Hg2+	1.625	0.09235154	276	1.599	0.07884906	289	1.627	0.09344247	289	1.637	0.09900804	331
Cd2+	1.551	0.05726270	200	1.526	0.05292325	219	1.545	0.05486796	201	1.539	0.05253984	227
Ca2+	1.632	0.09620220	76	1.602	0.08034231	86	1.636	0.09844319	92	1.625	0.09235154	109
Sn2+	1.770	0.18922704	188	1.743	0.16869420	199	1.774	0.19235093	205	1.760	0.18150763	215
Sr2+	1.777	0.19470705	85	1.738	0.16500296	87	1.769	0.18844925	91	1.755	0.17769767	103
Ba2+	1.936	0.33132862	77	1.898	0.29718682	78	1.922	0.31869290	78	1.917	0.31419444	95

The 12–6-4 parameter set shows that the three-point water models generally have smaller C₄ terms than the four-point water models. This is consistent with our previous 12–6-4 parametrization efforts for the TIP3P, SPC/E, and TIP4P-Ew water models.⁴¹ Nonetheless, using the 12–6-4 model, we show that each water model is able to reproduce the experimental HFE and IOD values simultaneously.

Parameter Balance.

All of the three parameters in the present study (R_min,M/2, ε_M, and C₄) have physical meanings. On the other hand, all these three parameters are correlated with each other such that unphysical assignment of one can cause overfitting of the others. Balancing these parameters relative to each other is important to ensure their transferability to other systems such as biomolecules and materials. In our present study, we compared our parameters to the vdW radii calculated by the quantum mechanics scaling principle (QMSP) method⁷³ and showed that our parameters, which are obtained based on the NGC, show better agreement with the QMSP results than other parameter sets. Specifically, to analyze the balance of the obtained parameters in the present work, we compared the R_min,M/2 parameters to the QMSP calculated vdW radii. The QMSP calculated vdW radii of four alkaline earth metal ions in the gas phase are shown in Table 6. By treating these four values as the reference, we calculated the average unsigned error (AUE) for each parameter set we obtained herein and show the results in Table S9 and Figure 4. In comparison, we also calculated the AUEs for the parameter sets we obtained previously⁴¹ and the parameter sets developed by Babu and Lim⁷⁴ and Åqvist⁷⁵ These results are illustrated in Table S9 and Figure 4 as well.

Table 6.

vdW Radii Calculated Using the QMSP Method for Divalent Ions Which Have the Same Electronic Structures as the Noble Gas Atoms⁷³

Ion	vdW radii (Å)
Mg2+	1.180
Ca2+	1.480
Sr2+	1.625
Ba2+	1.802

Figure 4.

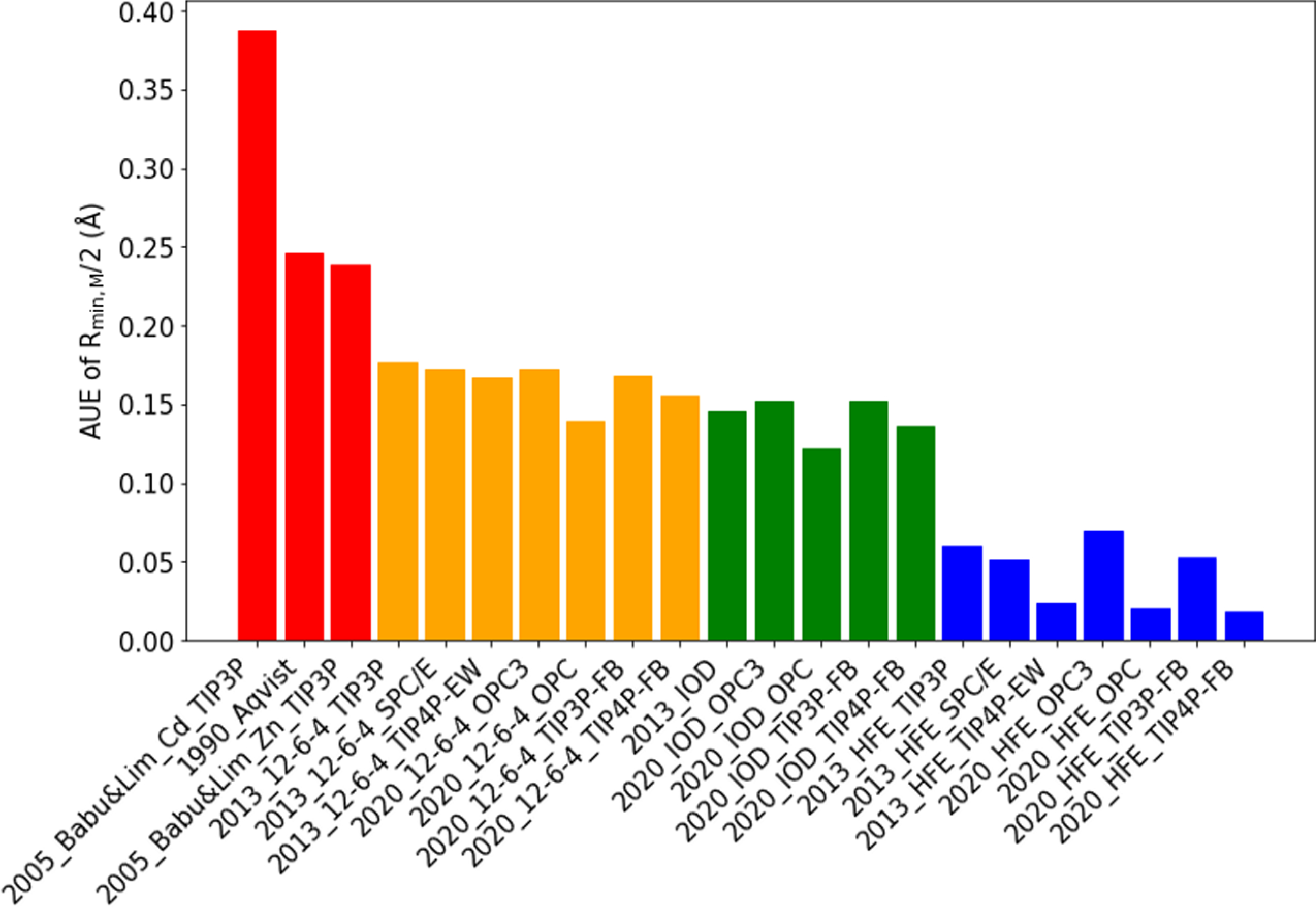
AUEs of the R_min,M/2 parameters in different parameter sets when using Table 6 as the reference.

Figure 4 shows that our parameter sets have smaller AUEs than the parameter sets developed by Babu and Lim⁷⁴ and Åqvist,⁷⁵ indicating the NGC we employed in our parametrization can provide a better balance of the R_min/2 and ε parameters. Interestingly, the Babu and Lim parameter set by treating Zn²⁺ as the reference has a smaller AUE than the analogous parameter set using Cd²⁺ as the reference. Moreover, these results indicated the HFE parameter sets have the smallest AUEs, agreeing with our previous study.¹⁹ However, the QMSP calculated vdW radii are for metal ions in the gas phase rather than the aqueous phase. These radii should be slightly larger when the metal ions are in the aqueous phase due to the more polarizing environment. This may contribute to a slight increase in these radii. When this effect is included, the 12–6-4 and IOD parameter sets may have similar or even smaller AUEs than the HFE parameter set.

Additional Tests and Analyses.

To further evaluate the performance of our parameters, we performed a series of additional tests and analyses. First, to test the transferability of our parameters, we modeled ion–water dimers of Mg²⁺ and Ca²⁺ ions. We obtained the optimized IOD and ion–water interaction energy for each combination of parameter set and water model (see SI for the computational details). The obtained results are shown in Table 7 and Table S10, along with the results based on the Drude oscillator model²¹ as well as density functional theory (DFT) and the AMOEBA polarizable force field.⁷⁶ We can see that although the current parameter sets were designed by targeting liquid phase properties, in general, they provide a reasonable description of ion–water dimers. Encouragingly, the 12–6 HFE parameter set in conjugation with the OPC3/TIP3P-FB water model provides excellent performance for simulating each of the Mg²⁺–water and Ca²⁺–water dimers, which can reproduce the QM calculated ion–water interaction energy and optimized IOD within 1 kcal/mol and 0.1 Å, respectively. However, one certain combination of parameter set and water model which provides excellent performance (when comparing to the QM results) for modeling a certain ion–water dimer may not necessarily provide comparable performance for simulating another ion–water dimer. For example, the 12–6 HFE parameter in conjugation with the TIP4P-FB water model performs reasonably well for modeling the Ca²⁺–water dimer, but it considerably underestimates the IOD value and overestimates the interaction strength for modeling the Mg²⁺–water dimer.

Table 7.

Benchmark Calculations Using the OPC3 Water Model for Ion–Water Dimer Systems Containing Mg²⁺ or Ca²⁺

Ion	Model	Water Model	Interaction Energy (kcal/mol)	IOD (Å)
Mg2+−H2O dimer
Mg2+	12–6 HFE	OPC3	−84.23	1.84
Mg2+	12–6 IOD	OPC3	−71.80	2.00
Mg2+	12–6 CM	OPC3	−76.25	1.94
Mg2+	12–6–4	OPC3	−75.15	2.02
Mg2+	Drude oscillator modela	SWM4-NDPa	−89.4	1.86
Mg2+	AMOEBAb	AMOEBAb	−79.56	1.88
Mg2+	ωB97X-V/def2-QZVPPDb	N/A	−83.12	1.91
Ca2+−H2O dimer
Ca2+	12–6 HFE	OPC3	−58.76	2.23
Ca2+	12–6 IOD	OPC3	−53.57	2.34
Ca2+	12–6 CM	OPC3	−52.89	2.36
Ca2+	12–6–4	OPC3	−55.18	2.34
Ca2+	Drude oscillator modela	SWM4-NDPa	−55.6	2.18
Ca2+	AMOEBAb	AMOEBAb	−54.65	2.22
Ca2+	ωB97X-V/def2-QZVPPDb	N/A	−57.97	2.22

^aFrom ref 21.

^bFrom ref 76.

To further evaluate the performance of our parameter sets to model ion–water clusters, we calculated the energy change of the [Zn(H₂O)_n]²⁺+ H₂O → [Zn(H₂O)_n+1]²⁺ reaction as a function of n. The computational details are described in the SI, and the computed numbers are shown in Table S11. Herein, we depict these values in Figure 5 by comparing our results with the results based on the MP4SDQ(FC)/HUZSP*//RHF/HUZSP* level of theory.⁷⁷ In general, it is challenging to quantitively reproduce the trends illustrated by the QM results; that said, our results showed qualitative agreement with the QM results. Among the different combinations, the 12–6 CM parameter set showed the best performance for reproducing the QM calculated values when used in conjugation with the OPC3/TIP3P-FB/TIP4P-FB water models, providing an AUE of ~7 kcal/mol for these reaction energies (Table S11).

Figure 5.

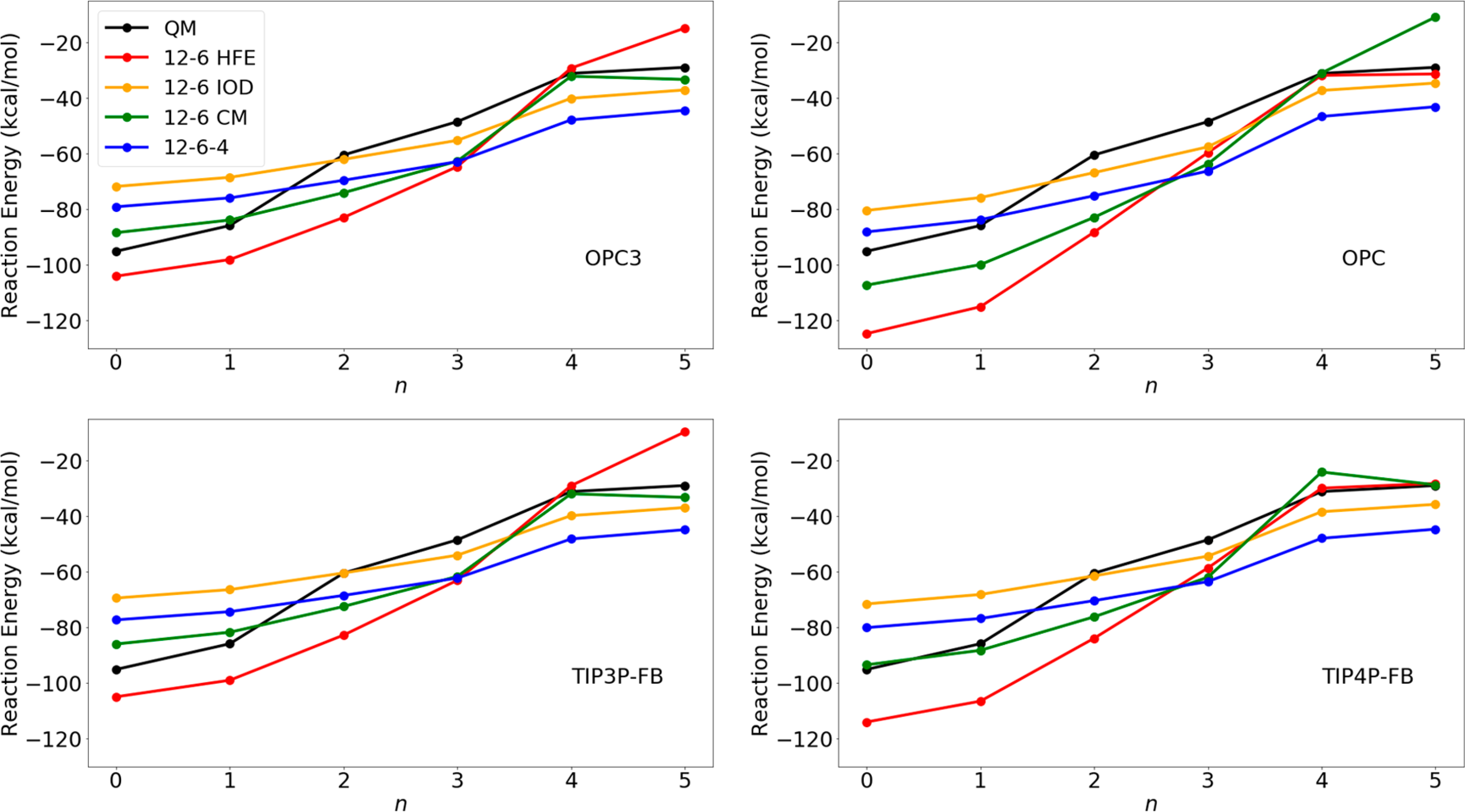
Reaction energies of the [Zn(H₂O)_n]²⁺+ H₂O → [Zn(H₂O)_n+1]²⁺ reaction along with n for different parameter sets in conjugation with different water models. The QM results are shown in black. The data used to generate these figures are given in Table S11.

In addition, to further evaluate the performance of our parameters to simulate the structural properties in the liquid phase, we showed the RDFs and cumulative coordination numbers between Zn²⁺ and water oxygen atoms calculated by different combinations of parameter sets and water models in Figure S2. In comparison to a previous study based on ab initio molecular dynamics (AIMD) and AIMD/MM simulations,⁷⁸ which showed a height of ~12 and a half-width of ~0.2 Å for the first peak in the RDF between Zn²⁺ and water oxygen atoms, our results showed sharper peaks (higher peak heights with smaller half-widths) for the first peak for all the parameter combinations. This is likely because the C₁₂ term generates a more repulsive potential than the ab initio calculations. Moreover, we found that different water models showed different peak heights when using the 12–6 HFE or 12–6 CM parameter set. For example, in terms of the 12–6 HFE parameter set, the OPC3 water model reproduced the same HFE with a significantly larger IOD value than other water models. In comparison, different water models showed similar peak heights when using the 12–6 IOD or 12–6-4 parameter set.

Finally, to assess the performance of our parameters to simulate the ion transport process, we calculated the diffusivity constant of Mg²⁺ using our parameter sets in conjugation with the OPC water model. These values were calculated using a protocol adapted from previous studies (see SI)^57,79 and are shown in Table 8 along with the experimental values. We find that all of these parameter sets can reproduce the experimental diffusivity coefficient of Mg²⁺, showing agreement with a previous benchmark study for several other water models⁷⁹ and illustrating the transferability of the parameters developed in the present study.

Table 8.

Performance of Parameters Sets Developed in the Present Study in Simulating the Diffusivity Coeffcient of Mg²⁺ When Used in Conjugation with the OPC Water Model

Parameter Set	Diffusion coeffcient (10−5 cm2/s)
12–6 HFE	0.742 ± 0.074
12–6 CM	0.771 ± 0.068
12–6 IOD	0.824 ± 0.081
12–6–4	0.810 ± 0.076
Experiment	0.706

In general, these test calculations show that our parameters can simulate properties for which they were not parametrized toward and are transferable across different systems.

CONCLUSIONS

Divalent metal ions play significant roles in various chemical systems. Recently, four new water models (OPC3,⁵⁴ OPC,⁵⁷ TIP3P-FB,⁵⁵ and TIP4P-FB⁵⁵) have been developed to better simulate water molecules in the condensed phase. They showed significant improvement in simulating a variety of properties relative to previous water models.^54,55,57 Previous studies indicated that metal ion parameters are usually water model dependent.²⁵ To facilitate molecular modeling using these new water models, we parametrized the 12–6 and 12–6-4 nonbonded models for various divalent metal ions.

We first investigated the performance of the 12–6 nonbonded model for its ability to simulate divalent metal ions in conjunction with the four new water models as well as four previous water models (TIP3P, SPC/E, TIP4P, TIP4P-Ew). Our results indicated that these four new water models provide comparable or significantly better performance than the previous water models in the same category when simulating divalent metal ions using the 12–6 model. This is consistent with the fact that these new water models were designed to better simulate properties in the aqueous phase.^54,55,57,62 In general, the three-point water models provide better performance than the four-point water models when simulating divalent metal ions using the 12–6 model. Of the three-point water models, OPC3 has the best performance, while the remaining three (TIP3P-FB, TIP3P, and SPC/E) have similar performances relative to each other. Of the four-point water models, OPC and TIP4P-FB provide comparable performances and are better than TIP4P-Ew followed by TIP4P.

Next, we parametrized the 12–6 model for 24 divalent metal ions in conjunction with these four new water models. Although these water models can provide similar or significantly better performance than previous water models when simulating divalent metal ions using the 12–6 model, because of the intrinsic error of the 12–6 model, we still could not reproduce both the experimental HFE and IOD values simultaneously. Hence, as done in our previous study,¹⁷ in order to reproduce different target properties, we designed different parameter sets: the HFE parameter set to reproduce experimental HFE values, the IOD parameter set to reproduce experimental IOD values, and the CM parameter set to keep a balance between HFE and IOD while reproducing the relative experimental HFE values. Moreover, in our previous study,⁴¹ we proposed the 12–6-4 model and showed that it can effectively solve the intrinsic error of the 12–6 model and accurately reproduce both the HFE and IOD values simultaneously. Herein, we also parametrized the 12–6-4 model for 16 divalent metal ions in conjunction with the four new water models. These parameters can reproduce the target HFE within 1 kcal/mol and the target IOD within 0.01 Å simultaneously.

In addition, to test the transferability of our parameters, we performed calculations for ion–water clusters having Mg²⁺, Ca²⁺, or Zn²⁺. By comparing to QM results, our parameters provided reasonable descriptions of ion–water clusters. Moreover, we also evaluated our parameters to simulate the diffusivity coefficient of Mg²⁺. Our results showed that our parameters match experiment reasonably well. All these tests support the idea that our parameters are well designed and are transferable.

In summary, in the present work, we provide 12–6 and 12–6-4 parameters for various divalent metal ions when using four new water models. These parameters are recommended for use for simulating divalent metal ions when using these new water models.