Prediction and error in early infant speech learning: A speech acquisition model

Abstract

In the last two decades, statistical clustering models have emerged as a dominant model of how infants learn the sounds of their language. However, recent empirical and computational evidence suggests that purely statistical clustering methods may not be sufficient to explain speech sound acquisition. To model early development of speech perception, the present study used a two-layer network trained with Rescorla-Wagner learning equations, an implementation of discriminative, error-driven learning. The model contained no a priori linguistic units, such as phonemes or phonetic features. Instead, expectations about the upcoming acoustic speech signal were learned from the surrounding speech signal, with spectral components extracted from an audio recording of child-directed speech as both inputs and outputs of the model. To evaluate model performance, we simulated infant responses in the high-amplitude sucking paradigm using vowel and fricative pairs and continua. The simulations were able to discriminate vowel and consonant pairs and predicted the infant speech perception data. The model also showed the greatest amount of discrimination in the expected spectral frequencies. These results suggest that discriminative error-driven learning may provide a viable approach to modelling early infant speech sound acquisition.

1. Introduction

Young infants can detect fine-grained changes in sensory information, including the acoustic signal used for speech (Hohne & Jusczyk, 1994; Jusczyk et al., 1992; Jusczyk & Derrah, 1987; Morse, 1972). With this broad discrimination ability, infants have the potential to become native speakers of any of the world's languages. Over time, discrimination becomes increasingly honed to the native languages with reduced discrimination of certain non-native sounds (Jusczyk, Luce, & Charles-Luce, 1994; Werker, Cohen, Lloyd, Casasola, & Stager, 1998; Werker, Gilbert, Humphrey, & Tees, 1981; Werker & Tees, 1984). This perceptual narrowing is not limited to speech, but occurs across a variety of domains according to the information and predictive structure available in the infants' environment (Baker, Golinkoff, & Petitto, 2006; Hadley, Rost, Fava, & Scott, 2014; Hannon & Trehub, 2005; Singh, Loh, & Xiao, 2017).

While this general pattern is well documented, what mechanisms lead to this transition is still the focus of much ongoing research. In other domains, a wide variety of learning and adaptation processes have been successfully modelled using error-driven learning models. In this study, we present a new model of infant speech sound acquisition, in which cue weights develop through an error-driven learning process of predicting upcoming acoustic signal from the surrounding acoustic signal. We focus on the first few months of age.

1.1. Statistical learning models

Early accounts proposed that the world's languages consisted of a limited set of discrete sound units. Infants were thought to be born knowing the members of the set and their task in learning language was to determine which of this limited set of sound units or features occurred in their own languages (Eimas, 1985; Eimas & Corbit, 1973). However, increasing evidence suggests that acoustic cues vary continuously rather than discretely across languages and that listeners are sensitive to fine-grained acoustic information (e.g. Beddor, McGowan, Boland, Coetzee, & Brasher, 2013; Fowler, 1984; Roettger, Winter, Grawunder, Kirby, & Grice, 2014). Learning to use continuous perceptual information for discrimination entails different learning mechanisms compared to observing the occurrence vs. non-occurrence of members of a known set. It has been proposed that rather than having innate knowledge of speech sounds, listeners might instead learn from the input, based on the statistical distribution of acoustic cues (Guenther & Gjaja, 1996; Maye & Gerken, 2000; Maye, Werker, & Gerken, 2002). Maye et al. (2002) proposed that infants determine how many and which sounds occur in their language according to the cue clusters they hear. After a surge of statistical learning studies, the speech acquisition community has become increasingly accepting of the idea that an innate inventory is not required to explain speech acquisition and that infants can instead learn speech sounds through interaction with the world and the ambient language.

While there is clear evidence that learners pick up on statistical regularities in some way, there have been a number of challenges to models based on learning directly from the summary statistics, per se. Several recent studies have failed to find differences in categorisation behaviour between unimodal vs. bimodal distributions (Terry, Ong, & Escudero, 2015; Wanrooij, Boersma, & van Zuijen, 2014; Wanrooij, de Vos, & Boersma, 2015; Werker, Yeung, & Yoshida, 2012). Moreover, computational models have also suggested that distributional learning models, which are generally based on unsupervised clustering, may not sufficiently account for speech acquisition.¹ In some cases, there is too much overlap between speech sound categories (Feldman, Griffiths, Goldwater, & Morgan, 2013a) and without competition models fail to converge on the right number of categories (McMurray & Hollich, 2009).

1.2. Discriminative error-driven learning vs. generative models

Learning algorithms can be divided into two broad classes, discriminative and generative (Bröker & Ramscar, 2020; Ng & Jordan, 2002). Generative models attempt to find the underlying distribution of the population from a sample distribution. Distributional learning (e.g. Maye et al., 2002) is based on this idea. Bayesian models, including Kullback–Leibler (K-L) divergence models, are also generative models. Error-driven learning models are discriminative (Bröker & Ramscar, 2020; Ramscar, Dye, & McCauley, 2013b; Ramscar, Yarlett, Dye, Denny, & Thorpe, 2010a). Natural language processing networks typically use Hidden-Markov Models (HMMs; Jurafsky & Martin, 2008). HMMs trained to recognize speech (e.g. in speech to text applications) learn by calculating the probability of acoustic features P(feature), the probabilities of words P(word), and the joint probabilities of features and words P(word, feature). Once trained, the model can provide classifications based on Bayes' rule P(word| features). In other words, HMMs are Bayesian learners that learn on the basis of positive evidence. While this method has proven highly effective as an engineering tool, there is evidence that humans learn discriminatively and learn not only from positive evidence but also from negative evidence (Bröker & Ramscar, 2020; Ramscar et al., 2010a, 2013b, see also Ng & Jordan, 2002, who compared discriminative and Bayesian classifiers).

Discriminative, error-driven learning (Baayen, Milin, Đurđević, Hendrix, & Marelli, 2011; Baayen, Willits, & Ramscar, 2016; Ramscar, Dye, & McCauley, 2013b; Ramscar & Yarlett, 2007; Ramscar, Yarlett, Dye, Denny, & Thorpe, 2010b) has a number of assumptions that distinguish it from other learning models (see also Nixon, 2020, for comparison with statistical learning and other forms of associative learning). Firstly, learning occurs both when cues co-occur with outcomes (positive evidence) and when cues occur without particular outcomes (negative evidence). When an outcome event occurs, connection strength from the present cues to that outcome event increases; when a particular outcome event does not occur, connection strength from present cues to that outcome is weakened. This differs from associative models that emphasise positive-evidence only (see Bröker & Ramscar, 2020, for discussion). Secondly, a number of recent studies suggest that learning is a predictive process, in which perceived sensory information (cues) predicts future events (outcomes; Ramscar et al., 2010b; Nixon, 2020; Hoppe, van Rij, Hendriks, & Ramscar, 2020b). That is, the order of cues vs. outcomes affects what is learnt. Thirdly, the amount of change in connection strength depends on how expected the outcome is. The occurrence of an unexpected item or the non-occurrence of an expected item is surprising and, therefore, more learning (i.e. more weight adjustment) occurs, in comparison to the occurrence of a highly expected item or the non-occurrence of a highly unexpected item. Thus, current learning depends on prior learning. Fourthly, when adjustments are made to cue-outcome connection weights, the adjustment is shared equally between all present cues. This means cues compete for relevance in predicting outcomes. For a detailed description of how error-driven learning predicts learning in different cue-to-outcome constellations, see Hoppe, Hendriks, Ramscar, and van Rij (2020a).

This formulation of learning means that learners develop expectations that are not necessarily proportional to co-occurrence counts. Rather, learning mirrors cue informativity, which depends on the positive and negative evidence the cues provide about an outcome (Ramscar, Dye, & Klein, 2013a). Due to cue competition, cues which predict multiple outcomes are less informative about these outcomes than cues that are unique to an outcome. Learning leads to an increased ability to use cues to predict and discriminate outcomes. In the process, different cues become more or less informative about various outcomes. When cues have been experienced frequently as predicting e.g. the occurrence of an outcome they become informative about that outcome. When encountering these highly predictive cues the amount of uncertainty is small - the outcome is highly expected. The error - the difference between the level of expectation and the maximum association strength of the outcome - is small. This happens as learning approaches asymptote. If, at this stage, new cues begin to co-occur with cues that already predict an outcome, learning of the new cues will be blocked (Kamin, 1968). This blocking effect has been found in second language speech sound acquisition (Nixon, 2020).

Some neural networks such as Recurrent Neural Networks (Graves, Mohamed, & Hinton, 2013) or Long Short-Term Memory (Graves & Schmidhuber, 2005) incorporate negative evidence through back propagation. However, these models often have many hidden layers. While they may achieve high accuracy for engineering applications, their lack of transparency is problematic as a tool for understanding cognitive processes. The Delta rule or Rescorla-Wagner learning equations are a mathematically simple implementation that allows for relatively transparent modelling of learning. Furthermore, the Rescorla-Wagner learning equations have repeatedly proven to be effective in modelling language processing at various levels, including modelling child language acquisition (Ramscar et al., 2010b; Ramscar, Dye, & Klein, 2013a), for disentangling linguistic maturation from cognitive decline over the lifespan (Ramscar, Hendrix, Shaoul, Milin, & Baayen, 2014; Ramscar, Sun, Hendrix, & Baayen, 2017), for predicting reaction times in the visual lexical decision task (Baayen et al., 2011; Baayen & Smolka, 2020) and self-paced reading (Milin, Feldman, Ramscar, Hendrix, & Baayen, 2017), as well as for auditory comprehension (Arnold, Tomaschek, Sering, Ramscar, & Baayen, 2017; Baayen, Shaoul, Willits, & Ramscar, 2016a; Shafaei-Bajestan & Baayen, 2018), for predicting the performance of learning of morphology (Divjak, Milin, Ez-zizi, Józefowski, & Adam, 2020; Ramscar, Dye, Popick, & O'Donnell-McCarthy, 2011; Ramscar & Yarlett, 2007), for predicting fine phonetic detail during speech production (Tomaschek, Plag, Ernestus, & Baayen, 2019) and for predicting second-language learning of speech sounds (Nixon, 2020).

1.3. Error-driven learning in the brain

The neural processes of error-driven learning are not the focus of this article. However, we will briefly mention some of the literature on this topic as general background. The last two decades have seen growing interest in and evidence for the role of prediction in language (reviewed in Den Ouden, Kok, & De Lange, 2012). For example, how highly expected a word is predicts neural activity as measured by N400 amplitude (DeLong, Urbach, & Kutas, 2005, see also Ito, Martin, & Nieuwland, 2017; DeLong, Urbach, & Kutas, 2017; Yan, Kuperberg, & Jaeger, 2017, Nieuwland et al., 2018 for further discussion and debate), MEG response (Dikker & Pylkkänen, 2013) and fMRI BOLD response (Willems, Frank, Nijhof, Hagoort, & Van den Bosch, 2016). Willems et al. (2016) show that the information theoretic measures entropy and surprisal both affect the bold signal in an fMRI experiment, but that the effects emerge in different brain areas, providing support for prediction in the sense of preactivation, rather than simply post-stimulus integration (or ‘post-diction’). Examination using all three neural measures provides evidence that how expected a word is modulates activity in the left anterior temporal cortex (Lau, Weber, Gramfort, Hämäläinen, & Kuperberg, 2016). Using fMRI, Tremblay, Baroni, and Hasson (2013) found that the supratemporal plane was sensitive to predictability of auditory input streams, suggesting that brain regions around the primary auditory cortex may play a role in prediction and prediction error related to auditory sequences. Because the responses occurred for both speech and non-speech stimuli, with no regions showing responses to speech alone, this suggests a general learning mechanism, rather than a specialised mechanism for speech.

Studies of electrical activity on the scalp (electro-encephalogram, EEG) have discovered various neural markers associated with expectation and error, such as the P3, error negativity and N400 components (Falkenstein, Hohnsbein, Hoormann, & Blanke, 1991; Kopp & Wolff, 2000; Kutas & Hillyard, 1980; Polich, 2011; Sutton, Braren, Zubin, & John, 1965), which differ in the task, the sensory modality and the complexity of the stimuli (e.g. from low-level sensory-perceptual processes to higher-level semantic processing). The component most often used to investigate speech sounds is the mismatch negativity (Näätänen, Gaillard, & Mäntysalo, 1978; Näätänen & Kreegipuu, 2011; Winkler et al., 1999). Lentz, Nixon, and van Rij (under review) show that error-driven learning models are able to predict trial-by-trial fluctuations in the EEG response during learning of sequences of speech sounds.

How error-driven sensory learning occurs at the neuronal level is not yet well established in the literature. However, two main hypotheses have been put forward. Firstly, although dopamine was initially associated with reinforcement (reward and punishment) learning and found to be released in response to unexpected reward outcomes (see Schultz, 1998, Schultz, 2019, for reviews), or to unexpected occurrence but not unexpected non-occurrence of sensory outcomes within a reward context (Kobayashi & Schultz, 2014), dopaminergic responses have recently also been proposed to occur in response to unexpected sensory outcomes more generally (Gardner, Schoenbaum, & Gershman, 2018; Suarez, Howard, Schoenbaum, & Kahnt, 2019; Takahashi et al., 2017). If this is the case, dopamine could play a role in error-driven sensory learning and language learning. Secondly, rather than a distinct, explicit error signal generated by separate, specialised population of neurons, prediction error may be driven by a temporal difference error signal; that is, prediction error is detected as the difference over time in activation states, with a prediction state followed by a sensory outcome state (Maes et al., 2020; O'Reilly, Russin, Zolfaghar, & Rohrlich, 2020).

In the present study, numerical measures of expectation are derived from error-driven learning. Expectations in error-driven learning are closely related to information theoretic measures of uncertainty (Ðurđević & Milin, 2019). Also like information theory, error-driven learning is discriminative. Importantly, as discussed in more depth below, error-driven learning is dynamic and nonlinear, with expectations continually developing with each new learning event, and with learning dependent on previous learning. We propose that, with the system of learning from experienced events relative to expectations outlined below, infants can learn about the sound system of their native language by developing a sense of the likelihood of occurrence of various streams of acoustic information.

1.4. The Rescorla-Wagner learning equations

The present study uses the Delta rule or Rescorla-Wagner learning equations, developed independently by Widrow and Hoff (1960) and Rescorla and Wagner (1972), to model early infant learning from the acoustic signal (for simplicity hereinafter we use the term Rescorla-Wagner equations). The learning algorithm estimates the connection strength between the set of input cues and a set of outcomes. When the network is initiated, connections between cues and outcomes have a strength of zero. During training, the connection strength is iteratively updated using the learning algorithm in Eqs. (1), (2), (3). At the end of training with k cues and n outcomes, the network consists of a k × n matrix of connection weights. The learning algorithm iterates across all learning events. A learning event is any event that may potentially lead to a change in expectations or connection strength (also called ‘association weight’). Traditionally this was typically an experimental trial, hence it is denoted by t. In the present study, a learning event occurs in each time step in a moving window. In each learning event, the algorithm calculates the adjustment to connection strength for each individual cue-outcome combination. Connection strength at the end of the current learning event is equal to the connection strength at the end of the previous learning event, plus any change in connection strength during the current learning event, as shown in Eq. (1):

$$V_{\mathit{ij}}^t=V_{\mathit{ij}}^{t-1}+\mathrm{\Delta }{V}_{\mathit{ij}}^t$$ (1)

with V representing the connection strength, ΔV representing adjustment to the connection strength, t representing the current learning event, and iterating across all connections between all cues i present in the learning event and all previously encountered outcomes j. Adjustments are calculated separately for each outcome.

The level of expectation of each outcome in each learning event is measured in activation. Activation is calculated by summing the connection strength from all cues present in the learning event to each previously encountered outcome, as shown in Eq. 2:

$$A_j^t=\sum _{\mathit{Present}\left(C_i,t\right)}{V}_{\mathit{ij}}$$ (2)

in which A_j^t is the activation of outcome j in the current learning event and Present(C_i,t) represents all cues present in the current learning event.

The adjustments to connection weights in each learning event, ΔV_ij^t, are given in Eq. (3):

$$\mathrm{\Delta }{V}_{\mathit{ij}}^t=\left\{\begin{array}{ll}a)0& \mathit{if\; Absent}\left(C_i,t\right)\\ b)\eta \left(\lambda -A_t\right)& \mathit{if\; Present}\left(C_i,t\right)\&\mathit{Present}\left(O_j,t\right)\\ c)\eta \left(0-A_t\right)& \mathit{if\hspace{0.17em}Present}\left(C_i,t\right)\&\mathit{Absent}\left(O_j,t\right)\\ d)0& \mathit{if\; Unobserved}\left(O_j,t\right)\end{array}\right)$$ (3)

in which O represents the outcomes, the constants η and lambda represent the learning rate and the maximum connection strength of the outcome, respectively. Changes in connection weights depend on the occurrence and non-occurrence of cues and outcomes: a) for any cues that do not occur in the current learning event, no adjustment is made; b) for all cues and outcomes that occur in the same learning event, connection strength is increased; c) connection strength between cues that occur and outcomes that do not occur in the current learning event is decreased; d) for outcomes not yet encountered, no adjustment is made.

In b) and c) the adjustment of the connection strength depends on the current activation, A_t. For present outcomes, the adjustment to connection strength is the maximum connection strength minus the current activation, multiplied by the learning rate. For absent outcomes, the adjustment to connection strength is zero minus the current activation, multiplied by the learning rate. The total adjustment to connection strength is shared between all present cues, resulting in cue-competition. Cues compete for predicting outcomes.

2. Training the model

2.1. Training materials

To train the model, we used a two-hour recording of German child -directed speech from the Szagun Corpus (File ID: 010329; Szagun, 2001 l) in CHILDES (MacWhinney, 2000). The recording contains the audio of a toy play situation during which primarily the mother but also the experimenters interact with the child. The typically developing child – Lisa – was 1 year and 3 months old at the date of recording. This recording was selected because this was the youngest age for which recordings were available for German-learning children in the CHILDES database. In addition to this recording we also replicated the training and test with recordings from three other children (see the Supplementary Material https://osf.io/f79cq/). According to the transcription, the mother exchanged 4467 words with the child, the child uttered 385 words and 180 words were uttered by the experimenter. However, inspection of the recording revealed that the transcription did not cover all recorded utterances. In particular, much of the conversation between the mother and experimenter as well as when the experimenter addressed the child was missed. Utterances directed toward the child used infant directed speech (Trainor & Desjardins, 2002). This is most apparent in the prosody, which differed from the prosody of speech between the mother and experimenter. In addition to speech, the recording also contains noises and sounds of the child playing. We regard this as reflecting a realistic day-to-day situation, as the child not only hears infant directed speech but also adult-directed speech and other sounds. Although experiments show that changes in sensitivity and expectation can occur in a short training period (Ramscar, Dye, & Klein, 2013a), the two-hour recording we use for training is not equivalent to two hours of an infant's learning. Rather, the learning rate in our model is set such that it learns quickly, even when it is provided with a relatively small data set.

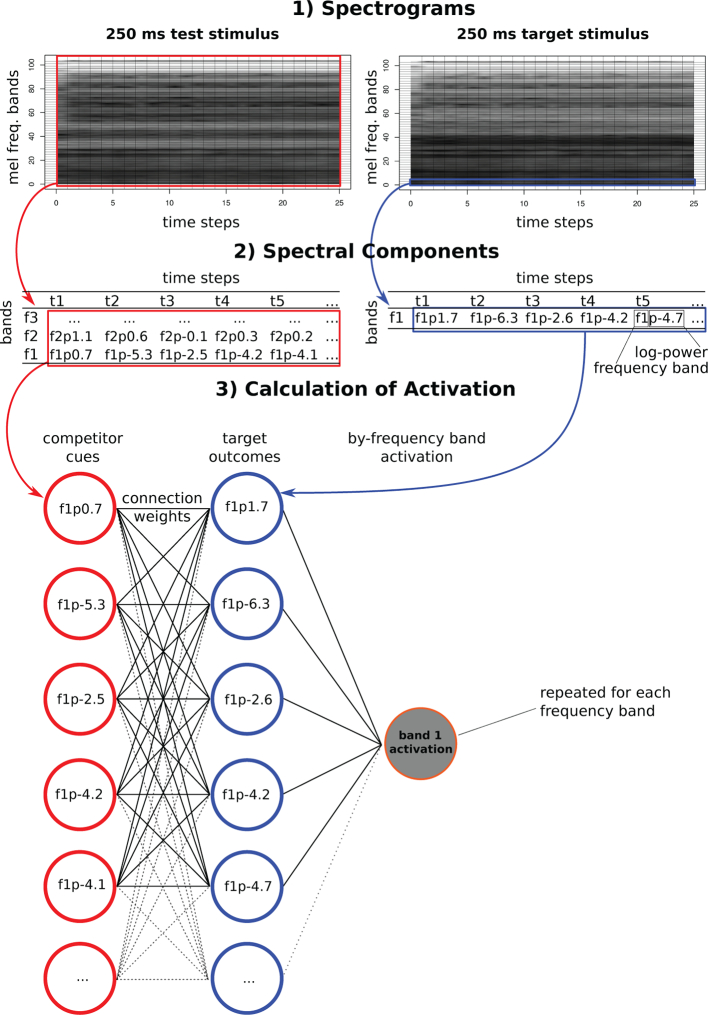
Because the Rescorla-Wagner model operates on discrete cues and outcomes, we needed to create discrete spectral components from the continuous speech signal. The left panel of Fig. 1 is a schematic illustration of the procedure we used to create the spectral components, which served as both cues and outcomes in the network. The speech signal was divided into temporal windows of 25 ms duration (vertical lines in Fig. 1). The temporal windows had an overlap of 15 ms (e.g. Chapaneri & Jayaswal, 2013). The right panel of Fig. 1 shows how the training window moves across the audio file. Most information conveyed in speech occurs below 10,000 Hz (Shannon, Zeng, Kamath, Wygonski, & Ekelid, 1995). Therefore, following common practise in natural language processing (Jurafsky, 2000), we used only frequencies up to 10,200 Hz to reduce the processing cost of running the training simulations.

Fig. 1.

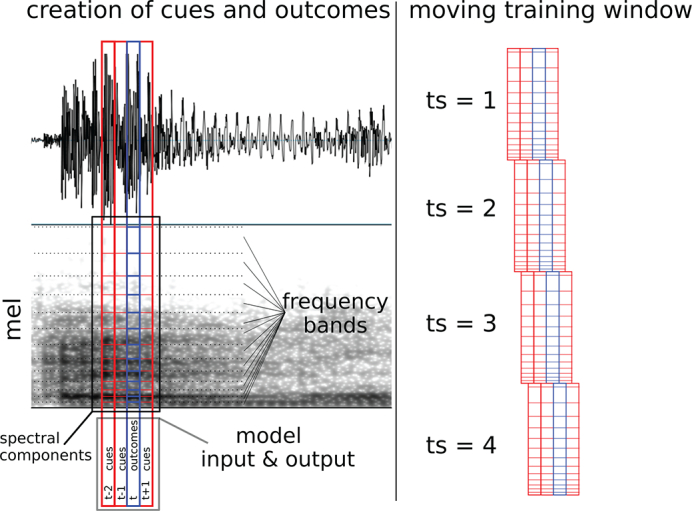
Left: Schematic illustration of the generation of the spectral components that were used as cues (red columns) and outcomes (blue column). In each time step, all 104 spectral component cues from each of the three temporal windows (312 cues in total) predict each individual spectral component outcome. This leads to a total of 104 outcomes in each time step. Note: the spectral components are not to scale. Right: Schematic illustration of how a moving training window was used to generate time steps (‘ts’) for training. Each temporal window is 25 ms. The window moves to the right 10 ms in each time step. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

In each 25 ms window, the spectral frequencies were divided into 104 equal mel steps (0 to 49 mel, equivalent to 0 Hz to 10,200 Hz). The mel scale was used to reflect the non-linearity in sensitivity of the human cochlea over spectral frequencies (Allen, 2008). The number of spectral frequency steps (104) was the maximum number possible with the spectral resolution of 0.47 mel that resulted from the 25 ms duration of the window. Finally, for each 25 ms by 0.47 mel cell of the grid, we calculated the log power (rounded to one decimal place) as a measure of intensity. An illustration of the spectral components is also shown in Fig. 3, Fig. 2, for one set of test stimuli that will later be used to evaluate the trained model.

Fig. 3.

Schematic illustration of calculating activations in a frequency band for target outcomes (blue) from test cues (red). See text for detailed explanation. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

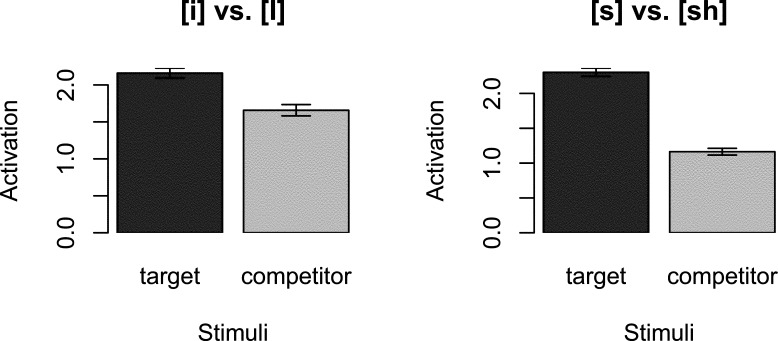
Fig. 2.

Activation of target's spectral components as outcomes by the target's spectral components as cues (target) and by the competitor's spectral components as cues (competitor). Each speech sound in the pair (left: [i] vs. [i]; right: [s] vs. [ʃ]) was tested once as the target and once as the competitor.

Due to this discretisation process, the numerical value of neither the spectral frequency nor the intensity was available to the model. Each spectral component was coded according to its frequency band value and power log value, deriving a unique spectral component for each unique combination of these values. This procedure generated roughly 28,000 unique spectral components, which occurred in the model as both cues and outcomes.

2.2. Model specification

We trained the model using the Rescorla-Wagner learning algorithm, implemented in the Naive Discriminative Learning (NDL) package (Arppe et al., 2015; Shaoul et al., 2014) in R (R Development Core Team, 2018). The model is a simple two-layer network with no hidden layers. The input layer consists of cues; the output layer outcomes. Note that this use of the term ‘cue’ differs somewhat compared to common usage in phonetics or speech perception research, where it is often used to refer to established acoustic-phonetic patterns that are proposed to affect perception, such as voice-onset time or place of articulation. Here we use the term ‘cue’ to refer to model input.

Infant learning from the acoustic speech signal was simulated by sliding a moving window over the input sound file in 10 ms time steps (right panel of Fig. 1). One learning event occurs in each time step. Each time step consisted of four consecutive 25 ms temporal windows. In each time step, spectral components from the first, second and fourth windows acted as cues (red columns in Fig. 1); spectral components from the third window acted as the outcomes (blue column in Fig. 1). Thus, 312 cues (104 spectral frequency bands × three temporal windows) were used to predict the outcomes in each of the 104 spectral frequency bands in the outcome temporal window. Apart from the spectral components in the first two temporal windows, all spectral components acted as both cues and outcomes. Using cues from the fourth window accounted for effects of anticipatory coarticulation (Magen, 1997; Öhman, 1966). Repetitions of identical cues were permitted, if they occurred. Connection weights from the input cues to occurring and non-occurring outcomes were updated in each learning event according to the Rescorla-Wagner learning equations (Eq. (1), (3)). The maximum association strength of the outcomes (λ) was set to 1. The learning rate (η) was set to 0.0001. The data and source code for this procedure can be found in the Supplementary Material (https://osf.io/f79cq/).

In summary, the network used low-level acoustic cues to predict low-level acoustic outcomes. The final model represents the level of expectation of hearing the various possible upcoming acoustic events depending on the incoming acoustic cues.

3. Model evaluation

To evaluate model performance, we simulated infant responses in one of the most common experimental paradigms for investigating speech perception in young infants, the high-amplitude sucking (HAS) paradigm (e.g. Siqueland & Delucua, 1969; Stevens, Libermann, Studdert-Kennedy, & Öhman, 1969; Swoboda, Morse, & Leavitt, 1976). In the HAS task, infants' rate of sucking is measured by means of a nonnutritive artificial nipple set up to record infant sucking behaviour. The infants are exposed to a repeated sequence of a single speech sound. After each infant's baseline sucking rate has been established, sounds are played in response to the infant's high-amplitude sucking. This leads to a gradual increase in sucking rate for the first few minutes, after which sucking rate then gradually declines as the infants start to lose interest in – habituate to – the sound. At this point, the sound either changes to a new sound (change condition) or continues as before (control condition). If the infant detects the change in the stimulus, this generally leads to an increase in sucking again, while the sucking rate continues to fall in response to the same sound or if no change is detected. From an error-driven learning perspective, repeated presentation of the same sound following the infant's sucking behaviour is likely to lead to the infant increasingly expecting to hearing that sound after their sucking. When the sound changes, this leads to surprise or an increase in prediction error, compared to when the same sound is presented, because the new sound was less expected. The increased prediction error results in the infant's increased sucking rate. Note that using discrimination of sound pairs to evaluate our model is not to make the claim that infants represent sounds in discrete units. On the contrary, we aim to show that a model that is trained without such units is nevertheless able to simulate infant behaviour in such speech perception experiments.

We chose the HAS paradigm for two reasons. Firstly, the task is used with infants of a few months of age, the age range we aim to model. Secondly, the task is a relatively direct measure of infant discrimination abilities. As described above, the task involves training the infants that their sucking produces an effect: the sounds are played in response to the infants' high-amplitude sucking behaviour. However, the infants are not given different training for different types of sounds as they are in some other paradigms, such as, for example, the Head Turn paradigm. This by-stimulus training may affect infants' discrimination behaviour and would likely require another layer of training of the model.

In the present paper, we simulate two HAS experiments. The first is from Swoboda et al. (1976) who used the HAS task to investigate infant vowel perception.² They were interested in whether infants perceive vowels categorically or continuously. Their experiment had three between-participant conditions: following the habituation phase, either the sound changed to what the authors call a different sound category, [i] to [i] or [i] to [i] (between-category condition) or to a variant of the same category [i] to [i] or [i] to [i] (within-category condition) or the identical sound continued to be presented (control condition). In the within-category condition, the two tokens of the same category varied in the values of the first to third formants (F1 to F3) in equal logarithmic steps, such that the four between- and within-category tokens formed a 4-step vowel continuum. Their results showed that infants were able to discriminate both within- and between-category vowels equally well. That is, perception was continuous or linear. In both change conditions, infants' high-amplitude sucking rate increased (to an average of approximately 37 sucks per minute; approximately 73% of the baseline level of approximately 48 sucks per minute).³ When the same sound continued, the high-amplitude sucking rate declined (to approximately 27 sucks per minute; approximately 56% of its maximum).

The second set of data that we model is from Eilers and Minifie (1975) who investigated infants' discrimination of fricatives. Eilers and Minifie tested three different fricative contrasts ([s] vs. [v], [s] vs. [ʃ], [s] vs. [z], in a CV syllable). We focus here on discrimination of [s] vs. [ʃ]. Unlike Swoboda et al. (1976), Eilers and Minifie (1975) did not use a continuum but tested just a sound pair. Their results showed that when a sound switched from [s] to [ʃ] or [ʃ] to [s], infants' high-amplitude sucking rate returned to over 80% of its maximum. There were no significant differences in the direction of the change. In contrast, when the same sound continued ([ʃ] to [ʃ]), the high-amplitude sucking rate fell to approximately 45% of its maximum.

3.1. Modelling infant discrimination of sound pairs in the high-amplitude sucking paradigm

Our first test simulates discrimination between two speech sounds (Eilers & Minifie, 1975). We test the sound pairs [i] vs. [i] and [s] vs. [ʃ].

3.1.1. Test stimuli

We tested the vowels [i] – [i] as investigated in Swoboda et al. (1976) and the fricatives [s]–[ʃ] as in Eilers and Minifie (1975) The stimuli were recorded by the second author, embedded in disyllabic German words ‘biete’ [bi:tǝ], ‘bitte’ [bitǝ], ‘Meister’ articulated as [maistɐ] and [maiʃtɐ] (both variants are possible in the dialect of the second author). The [i] vowel had F1 = 220 Hz, F2 = 2090 Hz and F3 = 3290 Hz. The [i] vowel had F1 = 240 Hz, F2 = 1600 Hz and F3 = 2400 Hz. The test stimuli were 250 ms in duration. Discretised 25 ms-by-0.47 Hz spectral components were then created for the test stimuli in the same manner as above for the training stimuli.

3.1.2. Calculating response estimates

For each sound pair, we simulated discrimination of the sounds by calculating and comparing the activation for the same sound (the target) compared to the different sound (the competitor). The connection weights from the spectral component cues in the test stimulus are used to calculate activation of the spectral component outcomes in the target, where the test stimulus may be either the target (for the same sound, simulating control trials) or the competitor (for the different sound, simulating change trials). The connection weights are those that developed during the moving window training; the test phase does not involve further training of the model connection weights.

The degree of expectation of a particular outcome is measured in activation. As shown above, activation is calculated by summing the connection weights from all present cues to the individual outcomes in question. In previous studies, outcomes were individual items such as words (Arnold et al., 2017; Baayen et al., 2011), speech tokens in a distributional learning paradigm (Lentz et al., under review) or morphological functions (Tomaschek et al., 2019). However, in the present study, because we are interested in learning from the acoustic signal, we aim to model more complex target stimuli. Rather than single outcome units, targets contain multiple spectral component outcomes. The test and target stimuli consisted of 104 spectral frequency bands and 25 temporal windows, yielding 2600 spectral components. Therefore, first, connection weights were calculated and summed from the 2600 spectral components as cues in the test stimulus to each of outcomes to get the individual outcome activations. This was iterated over the 2600 outcomes. Then, the activations of the 2600 outcomes were summed to give the total activation from the test stimulus to the target stimulus. In this model evaluation, the cues in the stimulus were integrated into one percept.

To estimate how well the spectral components of the target stimulus activate the spectral components of the target stimulus (thus itself), the target stimulus served as a test stimulus. This approach established the target as equivalent to the control stimulus and the competitor as the change stimulus in the HAS task.

3.1.3. Results

Fig. 2 shows the total activation from each test stimulus (target, competitor) to the target vowel [i] or [i] (left panel) and fricative [s] or [ʃ] (right panel). The figure shows that activation of the target is higher than that of the competitor.⁴

The difference in activation between the target and the competitor reflects the prediction error that occurs when the infant hears the sound change. In the experiments with infants, this led to an increase in high-amplitude sucking. Fig. 2 shows a greater difference in activation between the target and competitor for the fricatives than the vowels. Our model thus predicts that a change between [s] and [ʃ] leads to greater surprise or prediction error than a change between [i] and [i].

3.2. Infant discrimination over a continuum in the high-amplitude sucking paradigm

While many infant studies have tested discrimination of sound pairs, some infant studies (e.g. Kuhl, 1991; Swoboda et al., 1976) and most adult studies use a continuum between two speech sounds to investigate discrimination (e.g. Boll-Avetisyan et al., 2018; Lotto, Kluender, & Holt, 1998; Nixon et al., 2018; Nixon & Best, 2018; Nixon, van Rij, Mok, Baayen, & Chen, 2016; Pisoni & Lazarus, 1974; Tomaschek, Truckenbrodt, & Hertrich, 2015). Therefore, we were also interested in deriving predictions for a continuum. Predictions for the vowel continuum are tested against the data reported in Swoboda et al. (1976). We are not aware of any study that has yet tested perception of fricative continua in infants. However, we present the model predictions, which may be tested in future research.

3.2.1. Test stimuli

The same stimuli used for the vowel and fricative categories were used as the endpoint stimuli in two 20-step continua. We created a vowel continuum between [i] and [i] in Praat (Boersma & Weenink, 2015) by synthesising intermediate steps with interpolated formant frequencies between the two endpoint vowels (Winn, 2014). Manual adjustments of formants for left and right endpoint stimuli were necessary during synthesis to make the target vowels more prototypical. The fricative continuum between [s] and [ʃ] was created by linearly increasing/decreasing and adding the wave forms of [s] and [ʃ] in a step-wise manner. Stimuli were 250 ms in duration. Finally, discretised 25 ms-by-0.47 Hz spectral components were then created for the stimuli along the continuum in the same manner as above for the training stimuli.⁵

3.2.2. Calculating response estimates

For each step on the continuum, we calculated the activation of the left and right endpoints (which we refer to respectively as [i] and [i] for the vowels, [s] and [ʃ] for the fricatives) as targets, using the same method as above for the sound pairs. Above, we used the summed activations from all cues in the test stimulus to all outcomes in the target stimulus. Here, in order to get more insight into which cues are most discriminative, we also examine the activations in the different spectral frequencies. To do this, we calculated by-frequency band activations for the target stimulus.

Fig. 3 shows the whole procedure, from converting the speech file to spectral components to calculating the by-frequency band activations. First, the log power information in each frequency band and each time step in the test stimulus and the log power information in the target stimulus (Fig. 3, Fig. 1, left and right) were transformed into the spectral components (Fig. 3, Fig. 2, left and right). Activation was obtained by summing the connection weights from all spectral component cues of a test stimulus to the spectral component outcomes within a single frequency band in the target stimulus (Fig. 3, Fig. 2). The network is schematically demonstrated in Figs. 3, 3. The left (red) column contains the spectral component cues from the test stimulus, the right (blue) column contains the spectral components components from target stimulus. Connection lines between the circles represent the connection weights estimated during the training of the network with the CHILDES recording. This process was replicated for each frequency band in the target stimulus, yielding a vector of 104 activations (one for each frequency band).

We used Generalised Additive Models (GAM, Wood, 2011) to analyse the by-bandwidth activation of the left and right endpoint stimuli. GAMs fit nonlinear relations between dependent variables and predictors, using smooths to fit univariate and tensor product smooths to fit multivariate nonlinear relations.⁶ For each sound pair, we fitted two models, one for each of the endpoint stimuli, with a continuum step × spectral frequency tensor product interaction. Visualisation was carried out using functions from the itsadug package (van Rij, Wieling, Baayen, & van Rijn, 2016).

In addition to the gradient level of activation within each spectral frequency band, we also calculated the predicted probability of selecting the left endpoint (i.e. [i] or [s] as the target) in an AXB task. In the AXB task, human participants hear three sounds and are asked if the second is the same as the first or the third. In our simulated AXB task, A and B represent the endpoints and X represents the continuum steps. To simulate the use of the cues in X to discriminate between A and B, we calculated the proportion of the 104 spectral frequency bands that had higher activation for A. This process was done for each continuum step. We fitted the results using a binomial GAM model with a smooth for continuum step.

3.2.3. Results

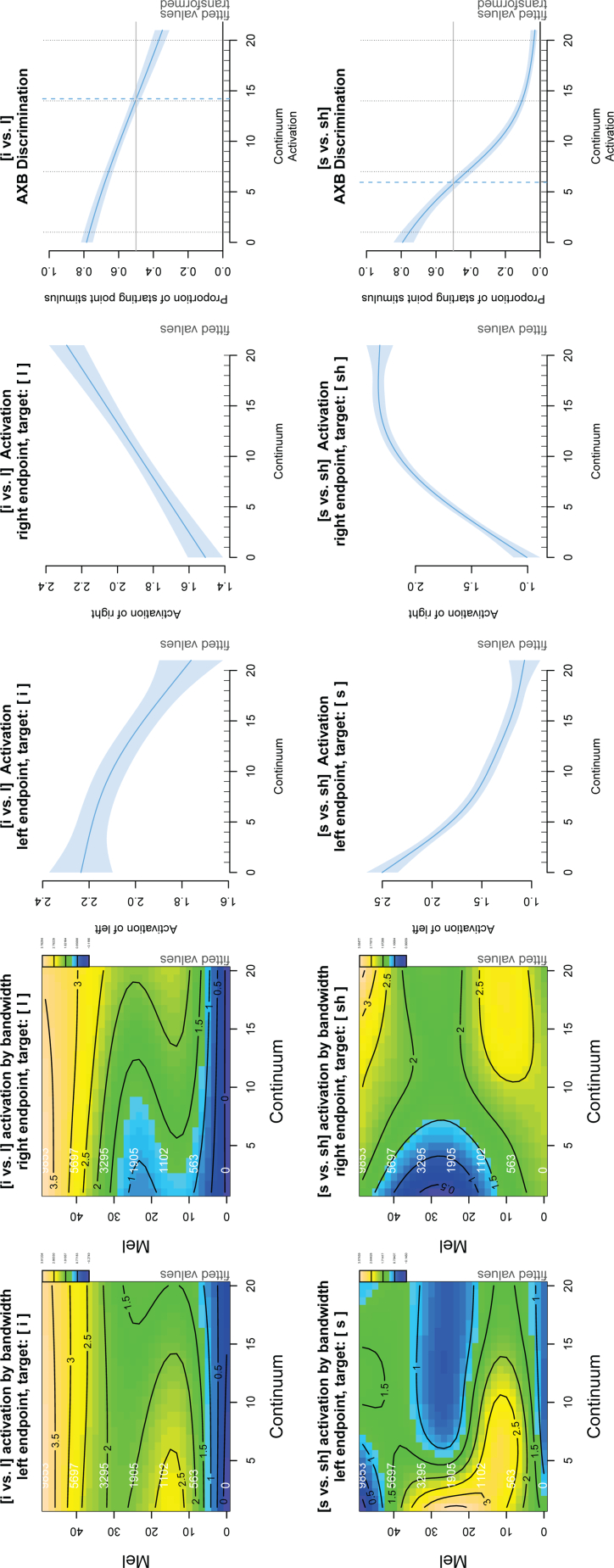
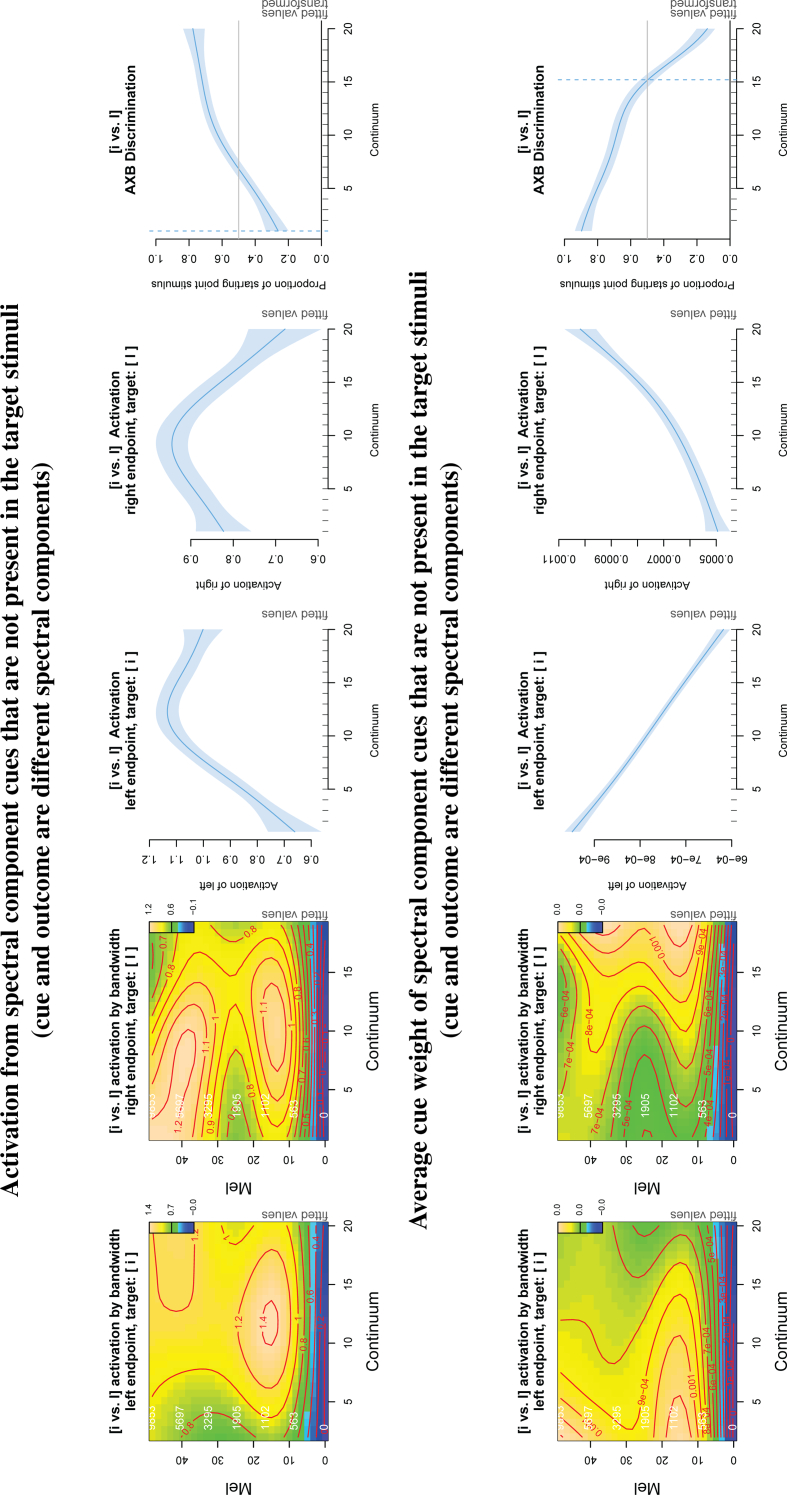
Fig. 4 illustrates the simulation results for the [i - i] (top) and [s - ʃ] continua (bottom). The first and second columns show the estimated effects of the interaction between continuum step and spectral frequency on the activation of the left and right endpoint stimuli, respectively. The x-axis represents the continuum step, the y-axis represents the spectral frequency. Activation is on the z-axis, represented by contour lines and colour coding: blue represents low activation; green, mid activation; and yellow, high activation. The third and fourth columns show the average activation over all spectral frequency bands for the left and right endpoints, respectively. The rightmost column shows the result of the simulated AXB task.

Fig. 4.

Simulation results for infant discrimination of the vowels [i - i] (top row) and fricatives [s - ʃ] (bottom row). First and second columns: the topographic plots show the estimated effect of the interaction between continuum step and spectral frequency on the activation of the left and right endpoint stimuli. The x-axis represents the continuum step. The y-axis represents the spectral frequency (mel: outer axis label in black; Hz: inner axis label in white). Activation is represented by means of contour lines and colour coding, where blue represents low activation; green, mid activation and yellow, high activation. Note that the z-limits differ between sound pairs. For both the vowels and the fricatives, activation is highest close to the target and gradually decreases over the continuum (first column: yellow areas gradually change to green/blue; second column: blue areas gradually change to green/yellow). Effects are greatest in the expected spectral frequency ranges for these speech sounds. Third and fourth column: Average activation (y-axis) across the continuum (x-axis). Rightmost column: the smooth illustrates the probability (y-axis) of perceiving the left endpoint stimulus in the AXB classification test along the continuum (x-axis). Black dotted vertical lines show the four continuum steps tested in Swoboda et al. Y-axis values were back-transformed to probabilities. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

In the top left plot ([i] target), activation starts out relatively high (yellow area) then decreases (changes to green) from left to right along the continuum. This occurs mainly between 10 and 30 mel (roughly 500–3000 Hz). The inverse occurs for the [i] target (top row, second column). The model predicts that the stimulus will become gradually less likely to be perceived as the target the further away it is on the continuum. The cues that lead to these changes in activation are in the expected frequency bands for these vowels, the second and third formants.

The bottom row of Fig. 4 shows the results for the fricatives. The bottom left plot shows for target [s] that changes in activation occur over a broad range of spectral frequencies, with the most prominent changes in the two frequency bands between 5 and 15 mel (335 and 1000 Hz) and between 15 and 35 mel (1000 and 3950 Hz). A similar effect can be observed for [ʃ] as the target.

The third and fourth columns demonstrate the average activation across all bandwidths along the continuum, fitted with a GAM smooth (i.e a non-linear regression spline). The activation steadily decreases along the continuum for [i] (increases for [i]), as the distance from the target increases (decreases). The decrease in activation along the continuum with increasing distance from the target predicts that the greater the acoustic distance between target and competitor, the greater the infant's prediction error will be.

The rightmost column in Fig. 4 illustrates the results for the AXB test. Y-axis values were back-transformed from logit to probabilities. The vertical blue dashed line represents the point where classification is 50% for each endpoint. The vertical dotted lines represent the continuum steps tested by Swoboda et al. for the vowels. The two points on the left and the two points on the right represent the within-category stimuli and the two central points represent the between-category stimuli. The model predicts a linear classification pattern for the vowel pairs [i - i] and a non-linear classification curve for the fricative pairs [s -ʃ]. The model predictions for the vowels match the experimental data from Swoboda et al. (1976), who found that infants discriminate within- and between-category stimuli equally well on a 4-step [i] to [i] continuum. Infant perception of the fricatives has not yet been tested with a continuum. However, the model predicts that infants' discrimination along the fricative continuum will be nonlinear, as has been found in adults (Mann & Repp, 1980).

3.3. Inspection of cue weights

Because we discretised the speech cues in order to use the Rescorla-Wagner equations, we wanted to ensure that the observed effects did not emerge due to artefacts in the discretisation process. It is possible that artefacts could emerge from the discrete differences in log power values and frequency bands. For example, depending on the grain size, connection weights between a particular spectral component and itself might become artificially high during the moving window training process. If this were the case, then when the same spectral component served as both cue and outcome in the test phase, there could potentially be inflated activation compared to when the cue and outcome are different spectral components. Consequently, our finding of a gradient decrease in activation across the continuum with increasing distance from the target might emerge simply from a decreasing number of identical cues with distance from the target. To rule out this possibility, we divided the cues into those for which the same spectral component occurred both as cue in the test stimulus and outcome in the target stimulus (identical cues) and those which occurred in the test stimulus but did not occur in the target stimulus (non-identical cues). If our effects are found only in the identical cues, this would suggest that the higher activation for continuum steps close to the competitor occurred simply because these continuum steps contained more identical cues. If we find that the effects occur not only in the identical cues, but also in the non-identical cues, this would provide further support for our model.

In the previous calculations, all test stimuli contained the same number of cues, allowing us to make comparisons using our summed measure, activation. However, dividing the cues into identical and non-identical may result in different spectral frequencies in different continuum steps having different numbers of cues. Therefore, to facilitate comparison between these stimuli, in addition to activation, we also calculated the average cue weight.

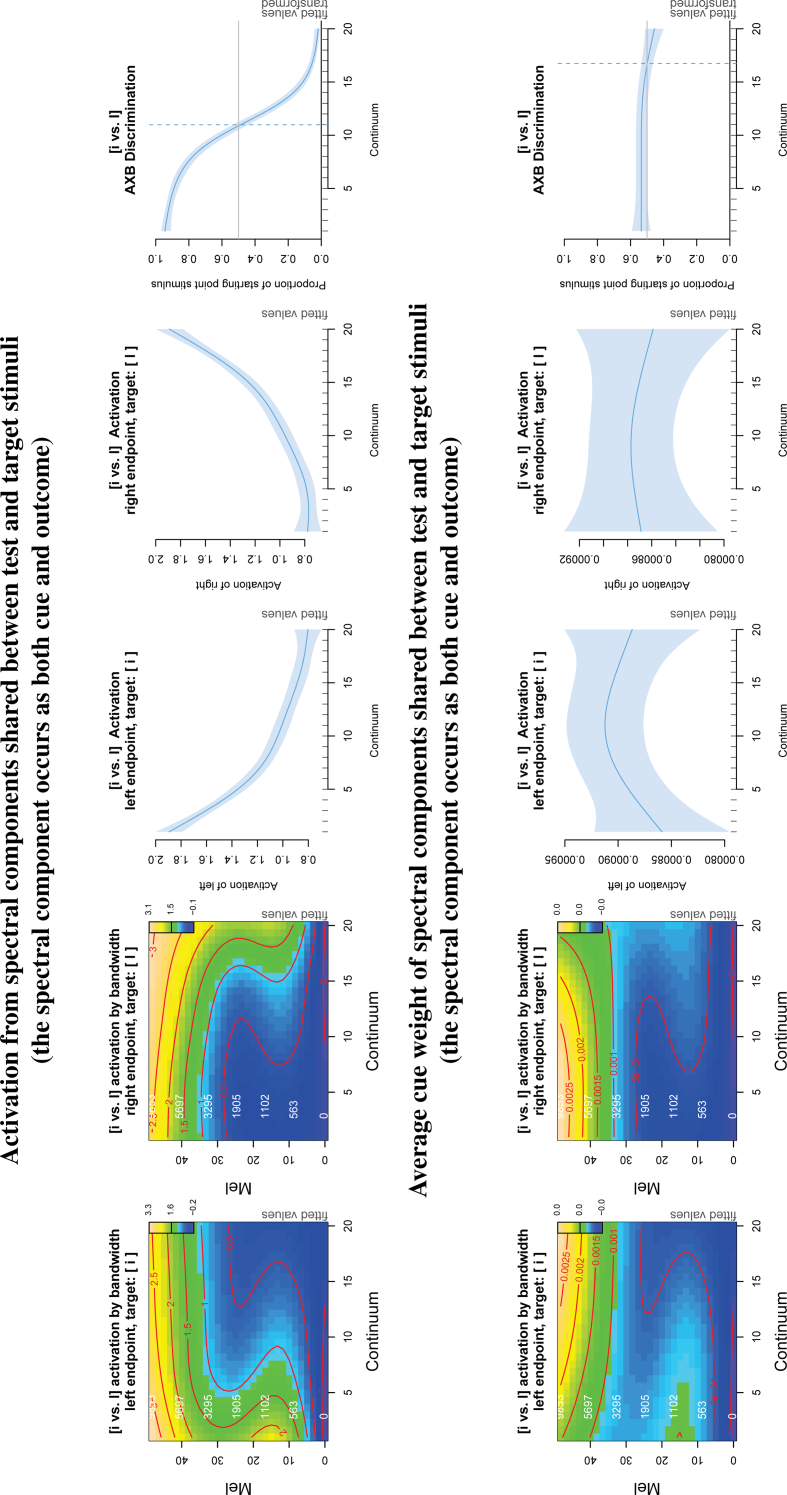
In Fig. 5, the top and bottom rows show the activation and average cue weight, respectively, for all spectral components that occurred both as cues in the test stimulus and outcomes in the target stimulus (identical cues) for the [i-i] pair. In Fig. 6, the top and bottom rows show the activation and average cue weight, respectively, for the all cues in the test stimulus that did not occur in the target stimulus (non-identical cues). As in Fig. 4, the first and second columns show topographic plots of the activation per spectral frequency band to the left and right endpoints, respectively. The third and fourth columns show the activation summed over all spectral frequency bands to the left and right endpoints, respectively. The rightmost column shows the AXB discrimination between the left and right endpoints.

Fig. 5.

Inspection of activations for the [i-i] pair for the identical cues. Activation (top row) and average cue weight (bottomrow) for only those cues which are identical to the target. See Fig. 4 for how to read the GAM plot. The activation (top) shows a similar pattern to the main results in Fig. 4. Activation gradually decreases over the continuum in the expected spectral frequency range. Average cue weight (bottom) does not change across the continuum.

Fig. 6.

Inspection of activations for the [i-i] pair for the non-identical cues. Activation (top row) and average cue weight (bottom row) for only those cues which are not identical to the target. See Fig. 4 for how to read the GAM plot. Activation (top row) seems to go in the opposite to expected direction. However, this is because there are a greater number of non-identical cues for continuum steps further from the target. The average cue weight (bottom row) shows a similar pattern to the main results in Fig. 4: there is a gradient change in activation over the continuum. This result shows that the change in activation across the continuum is not limited to identical cues, but also occurs for spectral components that differ between the test stimulus and target stimulus.

The activation plots for the identical cues (top row, first and second columns) look similar to the main discrimination results above. Although the activation values are a little lower due to the smaller number of cues, the pattern is similar: there's a decrease in activation with distance from the target, especially in the F2 to F3 spectral frequency range. The summed activations (third and fourth columns) still show gradient activation over the continuum. The AXB plot (rightmost column) still shows discrimination of the endpoints. In contrast, the average weight of the identical cues (second row, all panels) now looks very flat. Together, the activation and average cue weight results show that, within the identical cues, the decreasing support for the target with increasing distance from the target on the continuum results from a larger number of identical cues for continuum steps closer to the target.

The non-identical cues (Fig. 6) show a different pattern. At first glance, the activation results (top row) look as if the effects go in the opposite to expected direction: the AXB plot (top row, rightmost column) predicts increasing support for the target [i] with increasing distance on the continuum. However, of course, there are fewer non-identical cues for continuum steps close to the target, so this is not surprising. Probably the most interesting and important results for the present study are the average cue weights for the non-identical cues (bottom row). Here we see a pattern that is very similar to the overall main results. Cue weight is high close to the target and decreases with distance from the target: even when the cues are not identical to the target, the model still captures the gradient decrease in activation with distance from the target. This shows that, during training, the model learned greater connection strength between similar cues, despite not having any representation of acoustic similarity.

4. Discussion

We present a model of early first language speech sound acquisition which does not assume innate knowledge of phonological units, such as phonemes or phonetic features. Rather, speech sound acquisition occurs through error-driven learning of the acoustic signal based on predictions from incoming acoustic signal. After training on a corpus of spontaneous speech, the model was able to simulate infant discrimination behaviour in a common speech perception task, the high-amplitude sucking paradigm. Because cues competed for prediction strength, any cues that either did not reliably occur with a given outcome or that occurred often with many other outcomes were downweighted. By this mechanism, certain cues that were good predictors of one vowel or fricative, say [i] or [s], became poor predictors of another [I] or [ʃ]. Separate inspection of spectral components in the continuum steps that were shared between the test stimulus and target stimulus (identical cues) vs. those that differed between the test stimulus and target stimulus (non-identical cues) showed that even for the non-identical cues, the model had developed cue weights that decreased over the continuum. This shows that cues more similar to the target generally had greater connection strength, even though the model did not have access to information about acoustic similarity. These cue weights developed through the cues' predictiveness during training.

In a recent review of speech learning models, Räsänen (2012) concludes that, unless we assume phonetic knowledge is innate, word learning is possible from an acoustic speech signal with sequences of spectral cues; however, models have only limited success if they first learn phone-like units from which words are learnt. The present model demonstrates how speech sounds may be learned from acoustics without assuming phone-like units. Taking the acoustic input as the starting point allows for the continuous variability of speech cues across languages and listeners' sensitivity to fine-grained acoustic information, as discussed in the introduction (Beddor et al., 2013; Fowler, 1984; Hohne & Jusczyk, 1994; Jusczyk et al., 1992; Jusczyk & Derrah, 1987; Morse, 1972; Roettger et al., 2014). An error-driven learning approach is compatible with listeners' senstitivity to statistical regularities (Feldman, Griffiths, et al., 2013a; Guenther & Gjaja, 1996; Maye et al., 2002; Maye & Gerken, 2000; McMurray & Hollich, 2009; Nixon et al., 2016; Nixon & Best, 2018; Schatz, Feldman, Goldwater, Cao, & Dupoux, 2019) and effects of prediction found in the literature (DeLong et al., 2005; Den Ouden et al., 2012; Dikker & Pylkkänen, 2013; Lau et al., 2016; Willems et al., 2016; Yan et al., 2017), and also makes specific predictions about when learning diverges from the statistics (Hoppe, Hendriks, et al., 2020a; Nixon, 2020; Ramscar et al., 2010b).

As experience grows, infants also learn to use acoustic cues to predict events other than the acoustic signal. For example, over time, certain acoustic cues might come to predict objects, such as food or toys, actions or people, perceived through visual or other senses (McMurray, Horst, & Samuelson, 2012; Ramscar, Dye, & Klein, 2013a; Yu, 2008; Yu & Smith, 2012). This process of learning words is likely in turn to also play a role in further development of speech discrimination (Feldman, Griffiths, et al., 2013a; Feldman, Myers, White, Griffiths, & Morgan, 2013b; Hadley et al., 2014). Baayen, Shaoul, Willits, and Ramscar (2016b) used discriminative, error-driven learning to model how children learn to segment an ongoing speech stream into words. They propose that segmentation develops from high prediction error at low-probability transitions (i.e. word boundaries).

Discriminative, error-driven learning is a general learning mechanism. As such, we do not see this model as being restricted only to German-learning infants, but should apply broadly across languages. Similarly, error-driven learning processes are likely to also be involved in adaptation processes in adult perception, such as dimension-based statistical learning (Idemaru and Holt, 2011, Idemaru and Holt, 2014, Idemaru and Holt, 2020), and perceptual learning (Kraljic and Samuel, 2005, Kraljic and Samuel, 2007; Samuel & Kraljic, 2009). Although it has not yet been tested, in principle, the model presented here should also apply to these kinds of adaptation processes in adults. However, in adults there may be additional factors that affect discrimination. For instance, adults have decades of experience with their languages, with the world they live in and with the relationship between language and the world. By this time, they have developed much stronger expectations about the world than infants have and have learned to discriminate on many levels, which affects the learning process. Importantly, literate children and adults are affected by the orthographic system in which they read and write. By the time they start school, children are already learning to use acoustic cues to discriminate between letters of the alphabet (or other orthographic symbols) and to use letters (or other orthographic symbols) to predict speech sounds. Adults also have lexical knowledge, which interacts with the writing system in its effects on speech perception. All these factors mean that in addition to acoustic information, adults have already learned to discriminate on multiple other levels. This has implications for determining the appropriate cue and outcome representations. The goal of the present study was to present a possible mechanism by which young infants' learning of speech sounds could occur in the absence of these more concrete, discrete, often multi-modal outcomes. Nevertheless, adults continue to learn about speech sounds through error-driven learning (Lentz et al., under review; Nixon, 2020; Olejarczuk, Kapatsinski, & Baayen, 2018). So some form of the present model might also be used to model speech adaptation and learning processes in adults. We leave this question to future research.

4.1. Limitations of the model and future directions

We present the current instantiation of the model as an initial proof of concept. Some aspects will require further development. Firstly, for practical reasons, we only addressed the acoustic signal in the present study. However, given the multisensory nature of learning (Lewkowicz, 2014; Mason, Goldstein, & Schwade, 2019), a more complete model would need to take other sensory modalities and other levels of discrimination into account.

Because the Rescorla-Wagner equations operate on discrete cues and outcomes, it was necessary to discretise the continuous acoustic speech signal. This was a practical necessity. We do not make any theoretical claim that human hearing or speech perception is discretised in the same way. Human hearing has access to gradient degrees of distance between sounds. Nevertheless, this limitation seems to provide a strong test of the model. Despite the fact that the model did not have access to acoustic distance information, it was still able to learn gradient degrees of expectation that corresponded to gradient acoustic changes over the continuum. In the present study, we focused on discrimination of speech sounds. An interesting follow-up would be to test the model with different experimental paradigms, such as the Head Turn paradigm, in which infants are trained to respond differently to same vs. different stimuli, to test the perceptual narrowing effects observed in young infants (Werker & Hensch, 2015).

Due to the discretisation of the signal, it was necessary to select a specific temporal and spectral resolution for the spectral components. Although these choices were based on common practice, they may not necessarily be optimal for human infant learning and it is possible that different choices might have led to different results. We have not explored the effects of these parameters in the present study. In addition, in its current instantiation, the model does not encode temporal information. Therefore, the model may not deal well with speech cues that rely heavily on duration information, such as vowel length and in some cases voice-onset time. Future instantiations of the model will need to address the question of temporal cues.

4.2. Conclusion

In summary, after training on a corpus of spontaneous infant-directed speech, our model was able to discriminate vowel and consonant pairs. Different activation patterns in different spectral frequencies showed that discrimination was based on the expected spectral information for the different sound pairs. The model showed increased activation for stimuli more similar to the target, despite having no representation of acoustic similarity. This effect of similarity on activation resulted from the predictiveness of cues during training. We therefore propose that error-driven learning of the acoustic signal may constitute a viable account of early infant speech sound acquisition.

Appendix

In this section, we provide a technical description of the algorithm used to calculate the by-frequency band activations for target and competitor stimuli, as demonstrated in Fig. 3.

Table 1.

Illustration of a p × p sized cue-to-outcome network with p cues and p outcomes, in which spectral components (sc) are used as cues (rows) and outcomes (columns). spectral components are grouped to k frequency bands (B), with m spectral components within each frequency band (m may vary by frequency band). Each u-th spectral component cue is associated with each v-th outcome by a weight w_{u, v}, representing their connection strength, where u = 1, 2, …, p and v = 1, 2, …, p. The table demonstrates the calculation of the j^th by-frequency band activation for a target and a competitor, where a hypothetical target stimulus has the spectral components sc_{1, 1}, sc_{1, 3} and sc_{2, 1}, and a hypothetical competitor stimulus has the spectral components sc_{1, 2}, sc_{2, 2}, sc_{2, 3}. Cells marked in dark blue represent the afferent weights between the target's cues and the target's outcomes. Cells marked in dark red represent the afferent weights between the competitor's cues and the target's outcomes. The bottom lines represent the by-frequency band activation vectors a for the target and the competitor, with activations a_j representing the summed weights between cues and outcomes, as calculated in Eq. 4.

		B1			B2				Bk
		sc1, 1	sc1, 2	sc1, 3	sc2, 1	sc2, 2	sc2, 3	...	sck, m
Target	sc1, 1	w1, 1	w1, 2	w1, 3	w1, 4	w1, 5	w1, 6	...	w1, v
Competitor	sc1, 2	w2, 1	w2, 2	w2, 3	w2, 4	w2, 5	w2, 6	...	w2, v
Target	sc1, 3	w3, 1	w3, 2	w3, 3	w3, 4	w3, 5	w3, 6	...	w3, v
Target	sc2, 1	w4, 1	w4, 2	w4, 3	w4, 4	w4, 5	w4, 6	...	w4, v
Competitor	sc2, 2	w5, 1	w5, 2	w5, 3	w5, 4	w5, 5	w5, 6	...	w5, v
Competitor	sc2, 3	w6, 1	w6, 2	w6, 3	w6, 4	w6, 5	w6, 6	...	w6, v
	...	...	...	...	...	...	...	...
	sck, m	wu, 1	wu, 2	wu, 3	wu, 4	wu, 5	wu, 6	...	wp, p
Target activation		a1			a2			...	ak
Competitor activation		a1			a2			...	ak

Table 1 illustrates a p × p cue-to-outcome weight network with p cues and p outcomes that is trained as illustrated in Fig. 1. Each u-th cue is associated with each v-th outcome by a weight w_{u, v}, representing their connection strength, where u = 1, 2, …, p and v = 1, 2, …, p. Spectral components are grouped into k frequency bands (B), with m spectral components within each frequency band (m may vary by frequency band). k in the present study is 104. The table schematises the calculation of the j^th by-frequency band activation for a target and a competitor, where a hypothetical target stimulus has the spectral components sc_{1, 1}, sc_{1, 3} and sc_{2, 1}, and a hypothetical competitor stimulus has the spectral components sc_{1, 2}, sc_{2, 2}, sc_{2, 3}. The spectral components are independent of time.

To calculate by-frequency band activation from the competitor to the target, the spectral components (sc) of the competitor are used as cues (rows) and the spectral components of the target are used as outcomes (columns). To calculate by-frequency band activation from the target to the target, the spectral components of the target are used as both cues (rows) and outcomes (columns).

Cells marked in dark blue represent the afferent weights between the target's cues and the target's outcomes. Cells marked in dark red represent the afferent weights between the competitor's cues and the target's outcomes.

The calculation of activation for all frequency bands produces an activation vector a with a length of k. The j^th activation in the a vector is calculated using Eq. (4),

$$a_j=\sum _{i=1}^l\sum _{s\in B_j}{w}_{\mathit{is}}$$ (4)

where a represent a vector of activations (equivalent to the bottom two lines in Table 1); j = 1, 2, …k iterates across all the spectral frequency bands B_j in the stimulus (columns B₁, B₂, … B_k in Table 1); i = 1, 2, …l iterates across all cues in all temporal windows and all spectral frequency bands (all rows in Table 1); s ∈ B_j iterates across the spectral outcomes of the j^th spectral frequency band B_j in the target stimulus (equivalent to sc_{1, 1}, sc_{1, 2}, sc_{1, 3}, etc.); w represents the afferent weight between the i^th cue (the rows in Table 1) and the s^th outcome (the columns in Table 1).

The two bottom lines in Table 1 represent the by-frequency band activation vectors a for the target and the competitor (target activation, competitor activation), with activations a_j representing the summed weights between cues and outcomes, as calculated in Eq. (4).