Abstract
Objectives:
Leeds Test Object Ten (TO.10) is routinely used to subjectively estimate Threshold Contrast Detail Detectability (TCDD) as a measure of image quality in fluoroscopy. However, manufacturer guidance provides calibrated contrasts for only limited peak voltage and copper filtration thickness combinations. Prescribed testing conditions are often difficult to attain as modern flat panel fluoroscopic systems independently determine voltage and copper filtration thickness settings. This work aims to extend the range of TO.10 contrasts available for routine testing at peak voltage and copper thickness settings likely to be encountered.
Methods:
Two methods are described for generalising the calculation of target contrasts: a three-dimensional interpolation/extrapolation model in MATLAB®, and a multivariate log-polynomial function. Both methods utilise the available calibrated contrasts to estimate contrasts at voltage and copper thickness combinations routinely encountered.
Results:
Results are presented as Threshold Detection Index curves fit by a second-order polynomial of log to log . Results are found to be more accurate at unprescribed conditions while also reproducible for relatively consistent input air kerma rate (IAKR) expected from automatic dose rate controls (ADRC).
Conclusions:
The calculation of TO.10 contrasts at non-standard conditions aids in the determination of an absolute estimate of image quality in fluoroscopy with greater accuracy, reproducibility and efficiency.
Advances in knowledge:
TO.10 detail contrasts for TCDD testing of fluoroscopy units have been significantly extended beyond those previously available. The described methods will aid the clinical physicist in absolute assessments of fluoroscopic image quality and facilitate inter system comparisons.
Introduction
Leeds Test Object Ten (TO.10) is routinely used to provide a subjective estimate of Threshold Contrast Detail Detectability (TCDD) and signal-to-noise ratio (SNR) as a surrogate for image quality in fluoroscopy. 1,2 Originally intended for Image Intensifier (II) systems, 3 the application to Flat Panel Detector (FPD) systems has been documented. 1
Limited calibrated contrasts are provided by the manufacturer. 4 However, modern automatic dose rate controls (ADRC) automatically vary peak voltage (kVp) and copper filter thickness (mm Cu) settings in order to deliver a consistent image quality. 5 It is, therefore, often difficult to attain prescribed settings necessary for image quality testing. Calibrated detail contrasts vary by up to 15% between prescribed voltages and 10% between prescribed filtration thicknesses. The combined effect from variations in both voltage and copper thickness is as high as 20%, demonstrating the range in uncertainty for contrast values at unprescribed settings.
Some operators may attempt to increase the accuracy of their measurements by adding light element attenuators, Perspex, to the X-ray beam, forcing voltages towards higher prescribed values up to 80 kVp. However, this introduces systematic error into the assessment and is not recommended. 5 Others may limit analysis to “counting dots”. Observer precision error of ~15%, associated with the subjective nature of TO.10 use, 6,7 must also be considered. Combined, the total error in contrast values has potential to exceed 25%.
Recent Leeds Test Objects Manuals state that:
“For greater accuracy, interpolated [contrast] values can be calculated, i.e. where the kVp is not exactly 65, 70, 75 or 80 kVp but some intermediate value”. 5 We are unaware of any publications in which this has been attempted. Thus, we present two methods of calculating unprescribed contrasts for Threshold Detection Index calculations, both of which use the available calibrated contrasts to generalise the calculation of TCDD values, and hence : (a) a computational model using interpolation/extrapolation functions in MATLAB®, and (b) a multivariate log-polynomial function.
Methods and materials
Threshold detection index
Threshold Detection Indexes are the standard format for TO.10 results and based on the Rose Model. 8 Rose’s Equation states:
| (1) |
where is a constant denoting the signal-to-noise ratio required for reliable detection of an object against a uniform background of white noise. denotes contrast, given as the relative difference between signal and background number of quanta per unit area, is the area of the object and is the average number of quanta per unit area in the background. is analogous to noise equivalent quanta (NEQ). 9
The threshold detection index is defined as:
| (2) |
Therefore, using Rose’s equation (1):
| (3) |
Thus, scales with as a surrogate estimate of image SNR that is theoretically constant and independent of area if the detector is uniformly exposed to . Put differently, depends on IAKR only, with no spatial frequency dependence. However, in practice, values are not constant, instead producing a curve that exhibits a characteristic shape when plotted against . curves drop sharply at smaller detail areas due to the inherent unsharpness of the imaging system and drop more gradually at larger detail areas due to the eye’s decreased response to low spatial frequencies. 10
The Curve Fitting
A smooth curve can be produced when numerous experienced observers independently score TO.10 images multiple times and the results are averaged. However, this requires significant time and staff resources. At our hospital, two experienced observers each score images twice and threshold contrast uncertainty is manifest as a spread in data points. The characteristic shape exhibited by curves is subsequently modelled by a second-order polynomial fit of the log of values to the log of detail root area
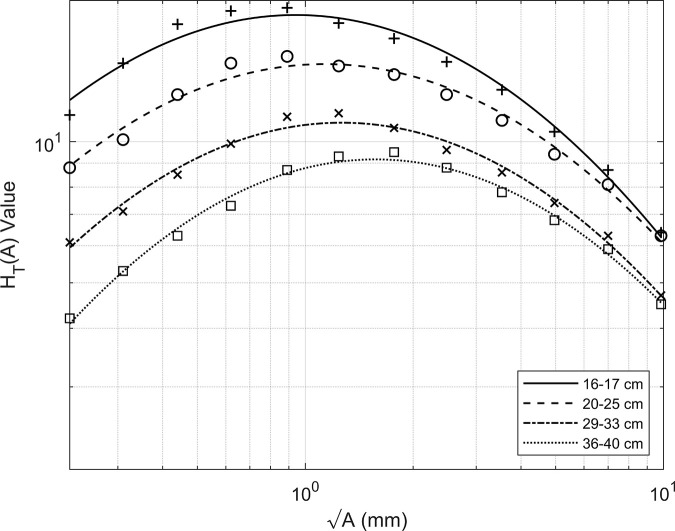
Figure 1 plots the KCARE fluoroscopy reference values (markers) for various field sizes. 11 The curve fitting applied to these data results in the solid, dashed, dash-dot and dotted lines also presented. Table 1 compares the KCARE reference values with the fitted values at detail . The average difference between experimentally achieved and model fitted values is only 2.9%.
Figure 1.
KCARE reference threshold detection index values (markers) with second order polynomial fitted curves of to (solid–dotted lines) depicted in log-space.
Table 1.
KCARE Reference and Fitted values with respective percentage differences
| 16–17 cm | 20–25 cm | 29–33 cm | 36–40 cm | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Detail | KCARE | Model Fit. | % diff. | KCARE | Model Fit. | % diff. | KCARE | Model Fit. | % diff. | KCARE | Model Fit. | % diff. |
| A | 6.4 | 6.3 | −1.6% | 6.3 | 6.1 | −3.2% | 4.7 | 4.7 | 0.0% | 4.5 | 4.5 | 0.0% |
| B | 8.7 | 8.4 | −3.4% | 8.1 | 7.9 | −2.5% | 6.3 | 6.1 | −3.2% | 5.9 | 5.8 | −1.7% |
| C | 10.5 | 10.8 | 2.9% | 9.4 | 9.7 | 3.2% | 7.4 | 7.5 | 1.4% | 6.8 | 7.0 | 2.9% |
| D | 12.9 | 13.2 | 2.3% | 11.1 | 11.5 | 3.6% | 8.6 | 8.7 | 1.2% | 7.8 | 8.0 | 2.6% |
| E | 14.8 | 15.5 | 4.7% | 12.6 | 13.1 | 4.0% | 9.6 | 10.0 | 4.2% | 8.8 | 8.8 | 0.0% |
| F | 16.6 | 17.2 | 3.6% | 13.9 | 14.1 | 1.4% | 10.7 | 10.7 | 0.0% | 9.5 | 9.1 | −4.2% |
| G | 17.9 | 18.3 | 2.2% | 14.5 | 14.6 | 0.7% | 11.5 | 11.0 | −4.3% | 9.3 | 9.1 | −2.2% |
| H | 19.3 | 18.6 | −3.6% | 15.2 | 14.5 | −4.6% | 11.3 | 10.7 | −5.3% | 8.7 | 8.6 | −1.1% |
| J | 19.0 | 18.0 | −5.3% | 14.7 | 13.7 | −6.8% | 9.9 | 9.9 | 0.0% | 7.3 | 7.7 | 5.5% |
| K | 17.8 | 16.6 | −6.7% | 12.6 | 12.4 | −1.6% | 8.5 | 8.8 | 3.5% | 6.3 | 6.5 | 3.2% |
| L | 14.7 | 14.6 | −0.7% | 10.1 | 10.7 | 5.9% | 7.1 | 7.4 | 4.2% | 5.3 | 5.3 | 0.0% |
| M | 11.4 | 12.3 | 7.9% | 8.8 | 8.9 | 1.1% | 6.1 | 5.9 | −3.3% | 4.2 | 4.1 | −2.4% |
Gallacher et al, 12 suggest the use of a quality index, , to describe the image quality given by a system as:
| (4) |
The calculated values for the fitted curves to the reference data are 1.002, 1.001, 0.999, and 1.002, respectively.
Thus, while in routine testing, individual estimates of values may exhibit large uncertainty, the curve fit to these data reduces the overall level of uncertainty in the underlying response function. We, therefore, define a quality index, , analogous to Gallacher et al, but in which the fitted values and reference values give:
| (5) |
As such, the second-order polynomial fit of the log of calculated values to the log of aims to reduce the impact of observer precision error.
The Normalised Quality Index ( modified to incorporate the above) can thus be given as:
| (6) |
where is the pulsed fluoroscopy correction factor, is the radiation beam quality factor, is the measured IAKR and is the IAKR of the reference system at a stated field size.
The interpolation and extrapolation model
Within our model, the Leeds provided calibrated contrasts are sorted into a 3D grid with axes i) disk index (1–14), ii) prescribed voltage (65, 70, 75 and 80 kVp) and iii) copper thickness (1.0, 1.5, 2.0 mm Cu). The peak voltage and total copper filtration are input by the user with the average number of disks scored in each row (A-M). The model interpolates/extrapolates the TCDD for each detail area and iterates until contrasts for all details are determined. values are calculated and is determined. Optional inputs for field size, pulse rate and IAKR are available for the determination of .
The interpolation/extrapolation function used is based on the Akima cubic Hermite polynomial interpolation in MATLAB®. This method avoids overshoots with less undulations than other interpolative methods producing smooth contrast curves that intercept the available calibrated contrasts precisely. While we utilise the MATLAB® function directly, detailed documentation of the interpolation algorithm is freely available from MathWorks. 13 As such, the algorithm is easily adoptable into other programming languages.
The multivariate log-polynomial formula
Where coding is not an option the formula calculation of detail contrasts can be given as:
| (7) |
where
| (8) |
is a contrast detail index (1-14), kV is the peak voltage and mm Cu is the total copper filtration.
Equation (8) calculates the location of a point on a peak voltage versus copper thickness contrast surface. The log of this point defines the intercept at detail index one in a log of detail contrast versus detail index fit of the calibrated contrasts. Equation (7) estimates the contrast at each detail index.
Figure 2a shows the log of calibrated contrasts for 65, 70, 75 and 80 kVp with 1.0 mm Cu. Applying a linear fit, a value for the slope can be calculated. The average slope for all calibrated settings gives . For comparison, the approximated log of contrasts using this method are shown in Figure 2b.
Figure 2.
Comparison of the Leeds provided log of calibrated contrasts for 65–80 kVp and 1.0 mm Cu (a) and formula calculated contrasts for identical settings (b). Contrasts are approximated from a linear equation in log-space with varying intercept.
Fluoroscopy testing set up
Image quality tests were performed on three flat panel detector fluoroscopy systems (two Siemens Artis Zee and one Philips Allura FD20) located in our hospital. The antiscatter grid was removed and a varying distance protocol was adopted with low levels of ambient light. The amount of system added filtration, as well as user added filtration, and peak voltage were recorded. In all cases, the details visible under fluoroscopy were scored by two experienced observers and the results averaged. The resulting curves, using the methods described, were plotted and quality indexes calculated using equation (5).
Results and discussion
Reproduction of calibrated contrast values at prescribed settings
Figure 3 compares calibrated contrasts for rows K,L,M at 70 kVp and 1.0 mm Cu (□) with model (+) and formula (o) calculated contrasts. The interpolation of contrasts between details is shown by the solid and dashed lines, respectively. Table 2 summarises the calibrated, modelled and formula calculated contrasts at these settings. The greatest divergence between calibrated and formula calculated contrasts occurs at detail three where the difference is 0.056 or 9.8%. This demonstrates that the calibrated contrasts do not follow a purely exponential path and is likely attributable to the design characteristics of the contrast details and X-ray beam being poly- rather than monochromatic.
Figure 3.
Comparison of the Leeds provided calibrated contrasts at 70 kVp and 1.0 mm Cu (□), model calculated values (+) and formula calculated values (o). The model interpolation of contrasts is shown as a solid line while the formula interpolation of contrasts is shown as a dashed line.
Table 2.
Leeds, Model and Formula Calculated Contrasts for 70 kVp and 1.0 mm Cu
| Detail | Leeds | Model | Formula |
|---|---|---|---|
| 1 | 0.9540 | 0.9540 | 0.9543 |
| 2 | 0.7260 | 0.7260 | 0.7318 |
| 3 | 0.5730 | 0.5730 | 0.5170 |
| 4 | 0.3600 | 0.3600 | 0.3841 |
| 5 | 0.2380 | 0.2380 | 0.2588 |
| 6 | 0.1670 | 0.1670 | 0.1659 |
| 7 | 0.1280 | 0.1280 | 0.1054 |
| 8 | 0.0876 | 0.0876 | 0.0773 |
| 9 | 0.0674 | 0.0674 | 0.0817 |
Nevertheless, the model reproduces the calibrated contrasts exactly at prescribed settings while the exponential fit of contrasts generated by the formula provides a reasonable approximation of the values. Similar graphs are produced at other settings.
Interpolation of at unprescribed conditions
Two IAKR settings of a nominally low-dose cardiac protocol on a Siemens Artis Zee system were selected. 1 mm Cu was placed at the X-ray tube while the ADRC added 0.6 and 0.3 mm Cu, respectively, and the images scored. Peak voltages of 67.7 kVp and 69.2 kVp were recorded.
Figure 4a compares results obtained when interpolated contrasts calculated for 67.7 kVp (an intermediate voltage setting) and 1.6 mm Cu are compared with calibrated values for 60 and 65 kVp with 1.5 mm Cu. Figure 4b compares contrasts calculated for 69.2 kVp and 1.3 mm Cu (an intermediate copper filter thickness) with calibrated values for 1.0 and 1.5 mm Cu at 70.0 kVp. Table 3 presents the values determined for each curve.
Figure 4.
plots for two IAKR on a Siemens Artis Zee system (a) and (b). Model results are presented as solid lines with + markers, formula results as dashed lines with o markers and prescribed settings as dash dot and dotted lines, respectively. In both cases, the model and formula produce interpolated values between prescribed settings.
Table 3.
obtained for two IAKR investigating interpolative capabilities on a Siemens AZ-25 system
| (a) | (b) | |
|---|---|---|
| Model: | 0.66 | 0.79 |
| Formula: | 0.66 | 0.79 |
| Calibrated (dash-dot setting): | 0.61 | 0.76 |
| Calibrated (dotted setting): | 0.69 | 0.83 |
Note the quality index is shown to vary not insignificantly between the calibrated peak voltages and calibrated copper filter thickness settings, by 13 and 9%, respectively. This demonstrates the necessity for accurate calculation of contrasts at the voltage and copper thickness settings encountered if the testing desired is for more than image quality consistency.
However, results shown in Figure 4 confirm that both methods successfully interpolate detectability index curves between those at calibrated settings, as expected. Both model and formula calculate values that are within 1% of each other and in the range bounded by calibrated settings resulting from the more accurate calculation of contrasts.
Extrapolation of at unprescribed conditions
Two IAKR settings on a Philips Allura Xper FD20 system were selected. 1 mm Cu was placed at the X-ray tube head while the ADRC added 0.5 and 0.2 mm Cu, respectively, and the images scored. Peak voltages of 60 kVp and 61 kVp were recorded with 1.5 mm Cu and 1.2 mm Cu.
Figure 5a compares results from extrapolated contrasts for 60 kVp and 1.5 mm Cu with calibrated values for 65 kVp and 1.5 mm Cu, being the closest available calibrated data set. Figure 5b compares extrapolated contrasts for 61 kVp and 1.2 mm Cu with calibrated values for 65 kVp with 1.0 and 1.5 mm Cu. As such, in Figure 5b, the methods extrapolate for peak voltage settings while simultaneously interpolating copper thickness values.
Figure 5.
plots for two IAKR on a Philips Allura Xper FD20 system (a) and (b). Model results are presented as solid lines with + markers, formula results as dashed lines with o markers and prescribed settings as dash dot and dotted lines, respectively. In all cases, the model and formula produce extrapolated results at values below prescribed settings.
Given the lower voltage settings, contrasts are expected to increase, thus forcing the measured curve below the curve at calibrated settings. The results shown in Figure 5 confirm that both methods extrapolate detectability index curves in line with these expectations. Table 4 summarises the values for each curve shown.
Table 4.
obtained for two IAKR investigating extrapolative capabilities on a Philips Allura Xper FD20 system
| (a) | (b) | |
|---|---|---|
| Model: | 0.49 | 0.63 |
| Formula: | 0.50 | 0.66 |
| Calibrated (dash-dot settings): | N/A | 0.66 |
| Calibrated (dotted settings): | 0.54 | 0.72 |
In extrapolating for peak voltage settings, the model and formula calculate similar quality indexes within 2% of each other that are 9 and 7%, respectively, lower than the quality index calculated using the nearest calibrated settings. In extrapolating for peak voltage while simultaneously interpolating for copper thickness the quality indexes determined by the model and formula differ by 4.8%.
The necessity for accurate contrasts at varying copper filter thickness is again demonstrated in the 9% variation between the quality indexes determined at the closest calibrated copper filtration thickness settings. It is also worth noting that while the curve generated from calibrated settings at 65 kVp and 1.0 mm Cu produces a result similar to the formula at 61 kVp and 1.2 mm Cu, this is only achieved by a coincidental balancing of an over represented voltage against an under represented copper filter thickness. As such, confidence in an experimental result obtained in this manner during routine quality assurance would be low, while results obtained by the methods described provide additional confidence.
Reproducibility of at unprescribed conditions
A single low-dose protocol on a second Siemens Artis Zee system was selected. 0.1 mm Cu was initially placed at the X-ray tube while the ADRC added 0.9 mm Cu. The TO.10 was scored sequentially under fluoroscopy with an additional 0.5 mm Cu being added to the beam in a series of five tests. Thus, a range of peak voltage and copper thickness settings were obtained.
Model resulting curves are shown in Figure 6a, while formula results are presented in Figure 6b. A curve for calibrated settings that most closely approach an experimentally obtained set, at 80 kVp and 2.0 mm Cu, is also plotted for comparison. For clarity, individual data points are omitted and the images are magnified. The corresponding quality indexes are shown in Table 5.
Figure 6.
plots for single protocol on a Siemens Artis Zee system with varying voltage and copper thickness. Model results are presented in (a), formula results are presented in (b). Error bars are calculated as the standard deviation in scores at .
Table 5.
obtained for consistent IAKR on a Siemens Artis Zee system with varying peak voltage and copper filtration thickness settings. *Excluded from calculation of mean and standard deviation
| Test | Settings | Model (a) |
Dev. from mean |
Formula (b) |
Dev. from mean |
|---|---|---|---|---|---|
| 1 | 66.4 kVp, 1.0 mm Cu | 0.73 | 0.01 | 0.75 | 0.00 |
| 2 | 73.8 kVp, 1.5 mm Cu | 0.75 | 0.01 | 0.74 | 0.01 |
| 3 | 80.4 kVp, 2.0 mm Cu | 0.73 | 0.01 | 0.72 | 0.03 |
| 4 | 86.7 kVp, 2.5 mm Cu | 0.75 | 0.01 | 0.80 | 0.05 |
| 5 | *86.7 kVp, 3.0 mm Cu | 0.66 | 0.08 | 0.83 | 0.08 |
| Cal: 80.0 kVp, 2.0 mm Cu | 0.73 | 0.01 | 0.72 | 0.03 | |
| Mean | 0.74 | ±0.01 | 0.75 | ±0.03 | |
| Std. Deviation | (±1.35%) | (±4%) |
The results confirm that for varying voltages and copper thicknesses between 1.0 and 2.5 mm, (tests 1–4), the model successfully reproduces similar results. For these tests, with the addition of copper, the ADRC preferentially increased the kV while delivering a relatively consistent IAKR, (max: 0.206 μGys−1, min: 0.182 μGys−1) to the detector. This is consistent with the expected performance of the ADRC. 5 The maximum difference between the quality indexes obtained is only 3%, even at 86.7 kVp and 2.5 mm Cu, demonstrating the models capacity to extrapolate contrasts beyond the current maximum prescribed settings.
However, with 3.0 mm Cu, (test 5), the ADRC did not increase the voltage above 86.7 kV. The tube current also plateaued. Thus, the IAKR and image quality as indicated by the curve shifted downwards. For this reason, these results are excluded from the calculation of the mean and standard deviation but are still presented to demonstrate the sensitivity of the testing to changing conditions.
The formula results confirm that for varying voltages and copper thicknesses between 1.0 and 2.0 mm the formula also successfully reproduces similar results. Within this range the maximum difference between the calculated quality indexes is only 4%. However, it is found that for copper filtration thicknesses at and above 2.5 mm, the formula underestimates the contrast values of the smaller TO.10 details. This results in exaggerated values that artificially increase the calculated quality index.
Overall, it is found that the model maintains stability for voltages between 50 and 95 kVp for 0.5 to 2.5 mm Cu while the formula provides reasonable contrast estimates between 60 and 80 kVp and 1.0 to 2.0 mm Cu. As such for extrapolated conditions, the model performs better than the formula, but within the limits provided by the manufacturer guidance, there is little difference between the two methods.
Figure 7 trends model and formula obtained values against total copper filtration demonstrating that both methods maintain stability for voltage and copper values likely to be routinely encountered.
Figure 7.
Trending of values determined by model and formula for various peak voltage and copper thickness combinations at consistent IAKR up to 2.5 mm Cu.
Conclusion
A recent publication, Shaw et al 1 , suggested that while the TO.10 is still in routine use today, the focus of testing has shifted to a consistency check, for which the peak voltage can invariably fall outside of the available kVp range. Yet, it is with relative ease that the range of contrast values available for TO.10 testing can be significantly extended. This is accomplished not only for varying peak voltage but also for the varying spectral filtration utilised on modern fluoroscopy systems.
While the human observer remains the dominant source of error in this subjective analysis, the error associated with experimental inaccuracies should not be ignored, as minor changes in testing conditions can lead to significant changes in contrast values. As such, methods to minimise both errors should be adopted, especially if more in-depth analysis, or intersystem comparisons at local level are desired. The described tools presented will thus aid the clinical physicist in such assessments until fluoroscopic image quality techniques fully adopt the use of more quantitative methods. 14,15
Contributor Information
Dean McCarthy, Email: deanmccarthy@mater.ie.
Patrick Kenny, Email: pkenny411@gmail.com.
REFERENCES
- 1. Shaw D, Worrall M, Baker C, Charnock P, Fazakerley J, Honey I, et al. IPEM topical report: an evidence and risk assessment based analysis of the efficacy of quality assurance tests on fluoroscopy units-part II; image quality. Phys Med Biol 2020; 65: 225037. doi: 10.1088/1361-6560/abb92f [DOI] [PubMed] [Google Scholar]
- 2. Institute of Physics and Engineering in Medicine .Recommended standards for the routine performance testing of diagnostic X-ray imaging systems. IPEM report 91; 2005. [Google Scholar]
- 3. Hay GA, Clarke OF, Coleman NJ, Cowen AR. A set of X-ray test objects for quality control in television fluoroscopy. Br J Radiol 1985; 58: 335–44. doi: 10.1259/0007-1285-58-688-335 [DOI] [PubMed] [Google Scholar]
- 4. Cowen AR, Clarke OF, Coleman NJ, Craven DM, McArdle S, Hay GA. Leeds X-ray test objects instruction manual (man. 097c. Leeds: FAXIL, The General Infirmary; 2011. [Google Scholar]
- 5. Lin P-JP. The operation logic of automatic dose control of fluoroscopy system in conjunction with spectral shaping filters. Med Phys 2007; 34: 3169–72. doi: 10.1118/1.2752576 [DOI] [PubMed] [Google Scholar]
- 6. Cohen G, McDaniel DL, Wagner LK. Analysis of variations in contrast-detail experiments. Med Phys 1984; 11: 469–73. doi: 10.1118/1.595539 [DOI] [PubMed] [Google Scholar]
- 7. Marshall NW, Faulkner K, Kotre CJ, Robson K. Analysis of variations in contrast-detail measurements performed on image intensifier-television systems. Phys Med Biol 1992; 37: 2297–302. doi: 10.1088/0031-9155/37/12/011 [DOI] [Google Scholar]
- 8. Rose A. The sensitivity performance of the human eye on an absolute Scale*. J Opt Soc Am 1948; 38: 196–208. doi: 10.1364/JOSA.38.000196 [DOI] [PubMed] [Google Scholar]
- 9. Cunningham IA, Shaw R. Signal-To-Noise optimization of medical imaging systems. J. Opt. Soc. Am. A 1999; 16: 621–32. doi: 10.1364/JOSAA.16.000621 [DOI] [Google Scholar]
- 10. Workman A, Cowen AR, Signal CAR. Signal, noise and SNR transfer properties of computed radiography. Phys Med Biol 1993; 38: 1789–808. doi: 10.1088/0031-9155/38/12/007 [DOI] [Google Scholar]
- 11. Evans DS, Mackenzie A, Lawinski CP, Smith D. Threshold contrast detail detectability curves for fluoroscopy and digital acquisition using modern image intensifier systems. Br J Radiol 2004; 77: 751–8. doi: 10.1259/bjr/16707499 [DOI] [PubMed] [Google Scholar]
- 12. Gallacher DJ, Mackenzie A, Batchelor S, Lynch J, Saunders JE. Use of a quality index in threshold contrast detail detection measurements in television fluoroscopy. Br J Radiol 2003; 76: 464–72. doi: 10.1259/bjr/82965103 [DOI] [PubMed] [Google Scholar]
- 13. MathWorks. Makima piecewise cubic interpolation. 2019. Available from: https://blogs.mathworks.com/cleve/2019/04/29/makima-piecewise-cubic-interpolation/.
- 14. Goode AR, Snyder C, Snyder A, Collins P, DeLorenzo M, Lin P-J. Signal and contrast to noise ratio evaluation of fluoroscopic loops for interventional fluoroscope quality control. J Appl Clin Med Phys 2019; 20: 172–80. doi: 10.1002/acm2.12734 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Kenny P, Costello D, McCarthy D, Kenny E. A novel quantitative measure of image quality in fluoroscopy. Phys Med 2020; 71: 150–60. doi: 10.1016/j.ejmp.2020.02.002 [DOI] [PubMed] [Google Scholar]