Flow-induced segregation and dynamics of red blood cells in sickle cell disease

Abstract

Blood flow in sickle cell disease (SCD) can substantially differ from normal blood flow due to significant alterations in the physical properties of the red blood cells (RBCs). Chronic complications, such as inflammation of the endothelial cells lining blood vessel walls, are associated with SCD, for reasons that are unclear. Here, detailed boundary integral simulations are performed to investigate an idealized model flow flow in SCD, a binary suspension of flexible biconcave discoidal fluid-filled capsules and stiff curved prolate capsules that represent healthy and sickle RBCs, respectively, subjected to pressure-driven flow in a planar slit. The stiff component is dilute. The key observation is that, unlike healthy RBCs that concentrate around the center of the channel and form an RBC-depleted layer (i.e. cell-free layer) next to the walls, sickle cells are largely drained from the bulk of the suspension and aggregate inside the cell-free layer, displaying strong margination. These cells are found to undergo a rigid-body-like rolling orbit near the walls. A binary suspension of flexible biconcave discoidal capsules and stiff straight (non-curved) prolate capsules is also considered for comparison, and the curvature of the stiff component is found to play a minor role in the behavior. Additionally, by considering a mixture of flexible and stiff biconcave discoids, we reveal that rigidity difference by itself is sufficient to induce the segregation behavior in a binary suspension. Furthermore, the additional shear stress on the walls induced by the presence of cells is computed for the various cases. Compared to the small fluctuations in wall shear stress for a suspension of healthy RBCs, large local peaks in wall shear stress are observed for the binary suspensions, due to the proximity of the marginated stiff cells to the walls. This effect is most marked for the straight prolate capsules. As endothelial cells are known to mechanotransduce physical forces such as aberrations in shear stress and convert them to physiological processes such as activation of inflammatory signals, these results may aid in understanding mechanisms for endothelial dysfunction associated with SCD.

I. INTRODUCTION

Blood is composed primarily of red blood cells (RBCs) suspended in plasma, with the hematocrit (i.e. volume fraction of RBCs) ranging from 0.1 − 0.3 in the microcirculation to 0.4 − 0.5 in large vessels such as arteries [1]. Two other major types of cells in blood, white blood cells (WBCs) and platelets, are both considerably outnumbered by RBCs, by ~ 500 − 1000 : 1 and 12 − 32 : 1, respectively [2]. In addition to the drastic difference in population density, these three cellular components exhibit distinct contrasts shape, size, and rigidity [3]. Typically, RBCs are fluid-filled biconcave discoids with a radius of ~ 3.8 − 4.0 μm, WBCs are approximately spherical and slightly larger than RBCs, while platelets are the smallest. Healthy RBCs are highly flexible, while both WBCs and platelets are much stiffer. Under pathological conditions, diseased RBCs often display substantial alterations in physical properties compared to healthy RBCs. This is particularly pertinent in blood disorders such as sickle cell disease (SCD), as all SCD patients have a small percentage (1−10%) of RBCs that are permanently stiffened and misshapen [4]. These alterations may lead to significant aberrance in the behavior of blood flow, and further cause complications. The insufficient understanding of both the dynamics of blood flow in SCD and the mechanism for complications associated with SCD forms the principal motivation of the present work.

A significant feature of blood flow in the microcirculation, the network of microvessels (5 − 200 μm in diameter [5]) consisting of arterioles, capillaries, and venules, is that all types of blood cells display a non-uniform distribution across the vessels. Flexible RBCs tend to migrate away from the vessel wall and form an RBC-depleted region termed the cell-free layer next to the wall [6–10]. In contrast, the stiffer WBCs and platelets are found to reside near the vessel walls, a phenomenon known as margination [7, 9, 11–14]. Many prior experimental [11, 12, 15–23] and computational [14, 24–33] studies have attempted to characterize the effects of a variety of parameters, such as cell stiff ness, shear rate, channel width, hematocrit, and RBC aggregation, on the strength of margination of WBCs and platelets. For example, recent experiments by Fay et al. [21] showed that WBC margination was substantially attenuated after treatment with dexamethasone or epinephrine, both of which were found to greatly reduce the stiffness of WBCs. Furthermore, margination-based cell separation has been realized using lab-on-a-chip devices. Examples include separation of WBCs from whole blood [13], and of stiffened RBCs such as those infected in malaria from the healthy ones [34–36].

A series of recent computational efforts have examined the individual roles of various cell properties in the segregation behavior. Using direct simulations, Kumar et al. [37, 38] determined the role of stiff ness difference by considering a confined binary suspension of capsules that differ only in deformability. Here the stiff ness (or deformability) of a capsule is characterized by the dimensionless capillary number, which represents the ratio of viscous stresses on the particle to elastic restoring stresses. In both simple shear flow and pressure-driven flow, when the stiffer capsules are the dilute component, they display substantial margination. In contrast, flexible capsules tend to enrich around the centerline of the channel when they are dilute, a behavior termed demargination. The effect of size contrast was also revealed [38]: in a mixture of large and small capsules with equal capillary number, the small capsules marginate while the large particles demarginate, in their respective dilute suspensions. Similarly, Sinha and Graham [39] explored the shape-mediated segregation behavior in binary suspensions of spherical and ellipsoidal capsules in flow, and showed that the effect of shape (aspect ratio) contrast depends on whether the equatorial radius or the volume of the capsules is held constant.

A number of phenomenological theories have also been developed for the segregation behavior in flowing multicomponent suspensions of deformable particles [38, 40–43]. These incorporate the two key sources of cross-stream particle fluxes in flowing suspensions under confinement: wall-induced migration flux of deformable particles away from walls [44], and shear-induced diffusive flux due to hydrodynamic pair collisions between particles. An example is a recent theory developed by Henríquez Rivera et al. [45, 46] that consists of a set of drift-diffusion equations. Predictions of cell-free layer thickness are found [46] to agree well with the values reported in other experimental [47], numerical [38] and theoretical [42] studies. Moreover, several regimes of segregation arise in both simple shear flow and pressure-driven flow, depending on the value of a so-called “margination parameter”, which charactierizes the relative significance of the wall-induced migration and the collisional fluxes. Furthermore, a sharp “drainage transition”, characterized by complete depletion of one component from the bulk flow toward the walls, is also identified.

In light of these advances, in this work we investigate the dynamics of blood flow in SCD, an inherited blood disorder characterized by abnormal sickle hemoglobin. Under deoxygenated conditions, sickle hemoglobin molecules self-assemble inside RBCs, forming long rigid polymers, a process termed sickling. These polymers mechanically alter and damage the membrane of RBCs, leading to the classic “sickled” (or crescent-like) shape [48, 49] for sickle cells. In fact, in addition to this characteristic sickle shape, a large variation in cell morphology has been observed within the population of sample sickle cells. Byun et al. [50] recently performed optical measurements of individual sickle RBCs, and classified them into echinocytes, discocytes, and the typical crescent-shaped irreversibly sickled cells (ISCs) based on their morphological features, similar to the observations in a prior study by Kaul et al. [51]. Here ISCs refer to cells afflicted with irreversible membrane damage after repeated intracellular sickling-unsickling cycles, which have permanently lost membrane elasticity and remain sickle-shaped even when exposed to extensive oxygenation [48, 52, 53]. In SCD patients, ISCs take up a small percentage (1−10%) of RBCs [4] due to the much shorter life span (~15 days [54]) than healthy RBCs (~115 days [55]). ISCs also have a much smaller volume than healthy RBCs due to dehydration [56, 57]. In addition, a general increase in membrane rigidity has been determined for sickle cells compared to that of healthy RBCs, although the extent of stiffening varies greatly from cell to cell [50, 58–62].

The pathophysiology of SCD has canonically been thought to lie in the acute vaso-occlusive crisis, in which diseased RBCs, upon deoxygenation, tend to obstruct microvessels due to the sickled shape and increased stiff ness, resulting in restricted local blood flow and subsequent tissue ischemia accompanied by acute pain. However, this view of SCD pathophysiology overlooks a common yet important complication of SCD, chronic sickle vasculopathy, in which the endothelial cells that line the blood vessels are dysfunctional and in a pro-inflammatory state in most regions in the circulation. Of particular clinical importance in understanding SCD vasculopathy is its association with stroke, one of the leading yet least understood causes of mortality in SCD. Indeed, the fact that vasculopathy pervasively occurs even in the oxygenated conditions in both small and large vessels necessitates a new understanding of SCD pathophysiology that extends beyond, and is independent of, vaso-occlusion, which, occurs only under the deoxygenated conditions in microvessels. Specifically, how the abnormality in physical properties of sickle cells, such as the distorted shape and increased stiff ness, alters the dynamics of blood flow, and ultimately, how this alteration may be linked to the underlying mechanism for the endothelial inflammation in SCD and subsequent complications such as stroke, are important issues to address.

Endothelial cells mechanotransduce the shear forces of the hemodynamic microenvironment into cellular biological signals [63–65]. Bao et al. [66] measured the mRNA expression of MCP-1 and PDGF-A, two genes related to endothelial inflammation, by endothelial cells subjected to laminar flows with different well-defined wall shear stress profiles, namely (1) ramp flow in which shear stress was smoothly changed from zero to a maximum value and then sustained, (2) step flow in which shear stress was abruptly applied at flow onset followed by steady shear stress for a sustained period, and (3) impulse flow in which shear stress was abruptly applied and then removed. A steady shear stress profile was also considered for comparison. They showed that rapid changes in shear stress (as in impulse flow and the onset of step flow) and steady shear stress (as in ramp flow and the steady component of step flow) stimulate and diminish the expression of both genes, respectively. In particular, the impulse flow case was found to induce the highest level endothelial expression of the pro-infammatory signals compared to the other profiles. Other studies [63, 67–75] have also elucidated a variety of shear stress-induced signal transduction pathways of the endothelium, and revealed the opposing effects of steady and unsteady shear stresses on endothelial dysfunction.

While well-studied in the context of cardiovascular disease, this issue has yet to be explored in SCD. To the best of our knowledge, there exist only a limited number of computational studies of the behavior of sickle cells in suspensions in association with mechanisms for SCD complications. Examples are [76–78], which aimed to investigate the mechanism for vaso-occlusive crisis. In these studies, simulations were performed for suspensions containing sickle cells in a cylindrical tube of diameter D = 10 μm, mimicking post-capillary flow, to quantify the consequences of adhesive interactions between sickle cells and the endothelium (tube wall) during flow, and determine the effects of cell morphology and rigidity. However, given their particular focus on blood flow in post-capillaries, these studies considered suspensions with only a very small number of cells under strong confinement, so that characteristic dynamics of multicomponent suspensions such as flow-induced segregation and margination were not incorporated.

The aim of the present study is to take a first step toward understanding these phenomena in SCD. Using large-scale direct simulations, we investigate a number of binary suspensions containing primarily flexible healthy RBCs with a small fraction of stiff cells with different rest shapes in confined pressure-driven flow at zero Reynolds number. WBCs and platelets are not included in the suspensions due to their extremely small number fractions in blood flow. We predict that sickle cells display strong margination toward the walls due to their increased rigidity and reduced size compared to healthy RBCs. The effects of shape, size, and rigidity differences between the components on the behavior of different suspensions are studied. We also characterize the orbital dynamics of single cells in the suspensions. Furthermore, the hydrodynamic effects of the cell suspensions on the walls, particularly the additional wall shear stress induced by the marginated cells are quantified to establish a connection with issues in SCD such as shear-induced endothelial dysfunction.

The rest of the paper is organized as follows: in Section II we describe the models for the cells and suspension systems considered in this work, as well as the numerical methods and algorithms employed to compute the flow field and cell motion; in Section III we present detailed results and discussion on the behavior of different suspensions and the dynamics of single cells, followed by a characterization of the hydrodynamic effects of the suspensions on the walls. Concluding remarks are presented in Section IV

II. MODEL FORMULATION

A. Model and discretization

We consider a flowing suspension of deformable fluid-filled elastic capsules in a planar slit bounded by two parallel rigid walls (FIG. 1). In the wall-normal (y) direction, no-slip boundary conditions are applied to the two rigid walls at y = 0 and y = 2H, where H is the distance from each wall to the centerplane of the slit domain. In the flow (x) and the vorticity (z) directions, periodic boundary conditions are imposed, with spatial periods L_x and L_z, respectively. The suspension is subjected to a unidirectional pressure-driven (Poiseuille) flow, and the undisturbed flow velocity field is given by

$$u^{\infty }(x,y,z)=2U_0\frac{y}{H}\left(1-\frac{y}{2H}\right)e_x,$$ (1)

where U₀ is the undisturbed flow velocity at the centerplane of the channel, and e_x is the unit vector in the x direction. In the present study a constant pressure drop is imposed, which is equivalent to fixing the mean wall shear rate at ${\dot{\gamma }}_w=2U_0/H$. We take the fluids outside and within the capsules to be incompressible and Newtonian with viscosity η and λη, respectively, so λ denotes the viscosity ratio between the fluids inside and outside the capsules.

FIG. 1:

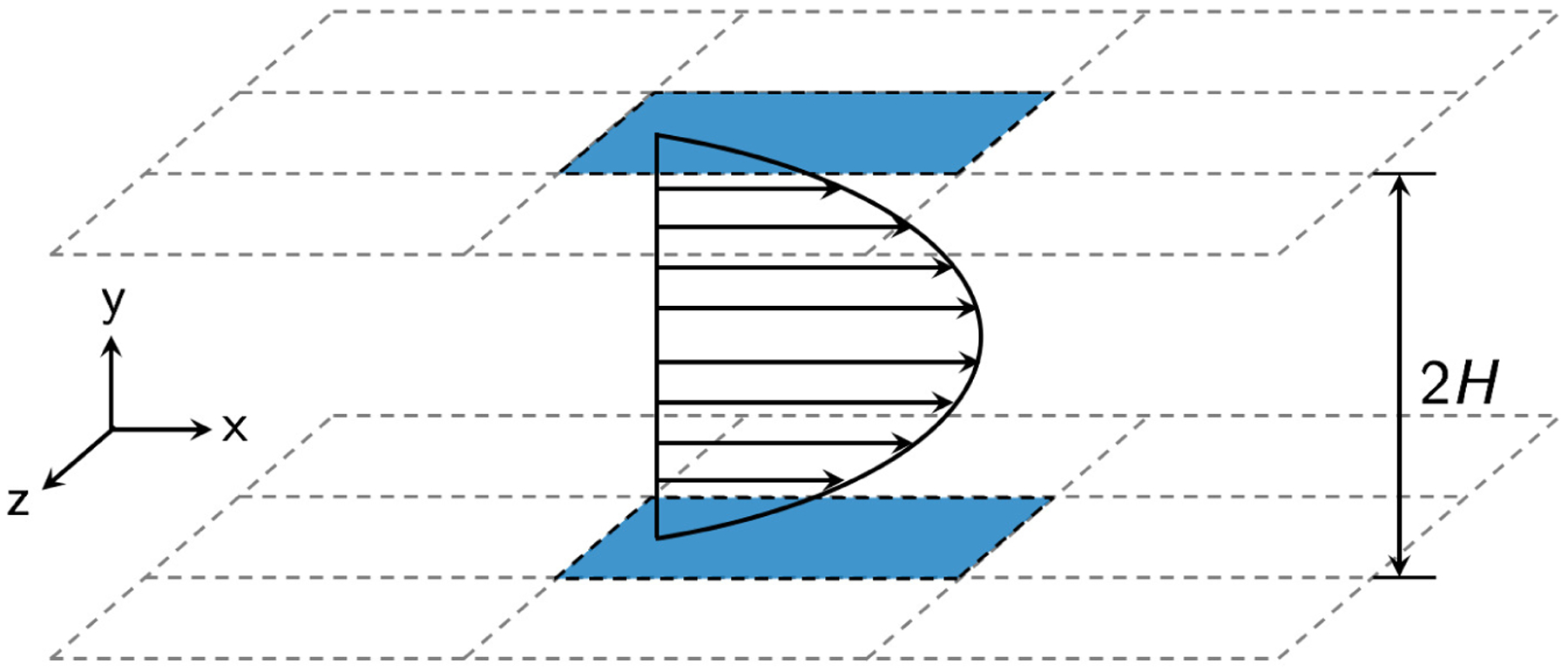
Schematic of the simulation domain.

Different suspension systems comprising various types of cells are investigated in this work. Figure 2 shows the rest shapes of the cell models. A healthy RBC is modeled as a flexible capsule with a biconcave discoidal rest shape [79, 80], with the geometry given by

$$y=\frac{a}{2}\sqrt{1-r^2}\left(C_0+C_2{r}^2+C_4{r}^4\right),$$ (2)

where r² = x² + z² ⩽ 1, C₀ = 0.2072, C₂ = 2.0026, and C₄ = −1.1228; a denotes the radius of the biconcave discoid, which is ~ 3.8 − 4.0 μm for human RBCs. In contrast to a healthy RBC, a typical ISC is crescent-shaped with a characteristic length c slightly greater than a [50, 81]. In this study, an ISC is modeled as a stiff capsule with a curved prolate spheroidal rest shape. This shape is constructed by first polar stretching and equatorial compression of a spherical capsule with radius a, which results in a slender prolate capsule with polar radius a₁ = c = 1.2a and equatorial radius a₂ = 0.25a (aspect ratio AR = a₁/a₂ = 4.8). The resulting straight prolate capsule is then subjected to a quadratic unidirectional displacement of membrane points perpendicular to the polar axis of the capsule, which eventually generates a curved prolate capsule. Details regarding the transformation procedure for the sickle RBC model are found in [82]. For our models, the volume of a straight or curved prolate capsule is ~ 20% that of a biconcave discoid.

FIG. 2:

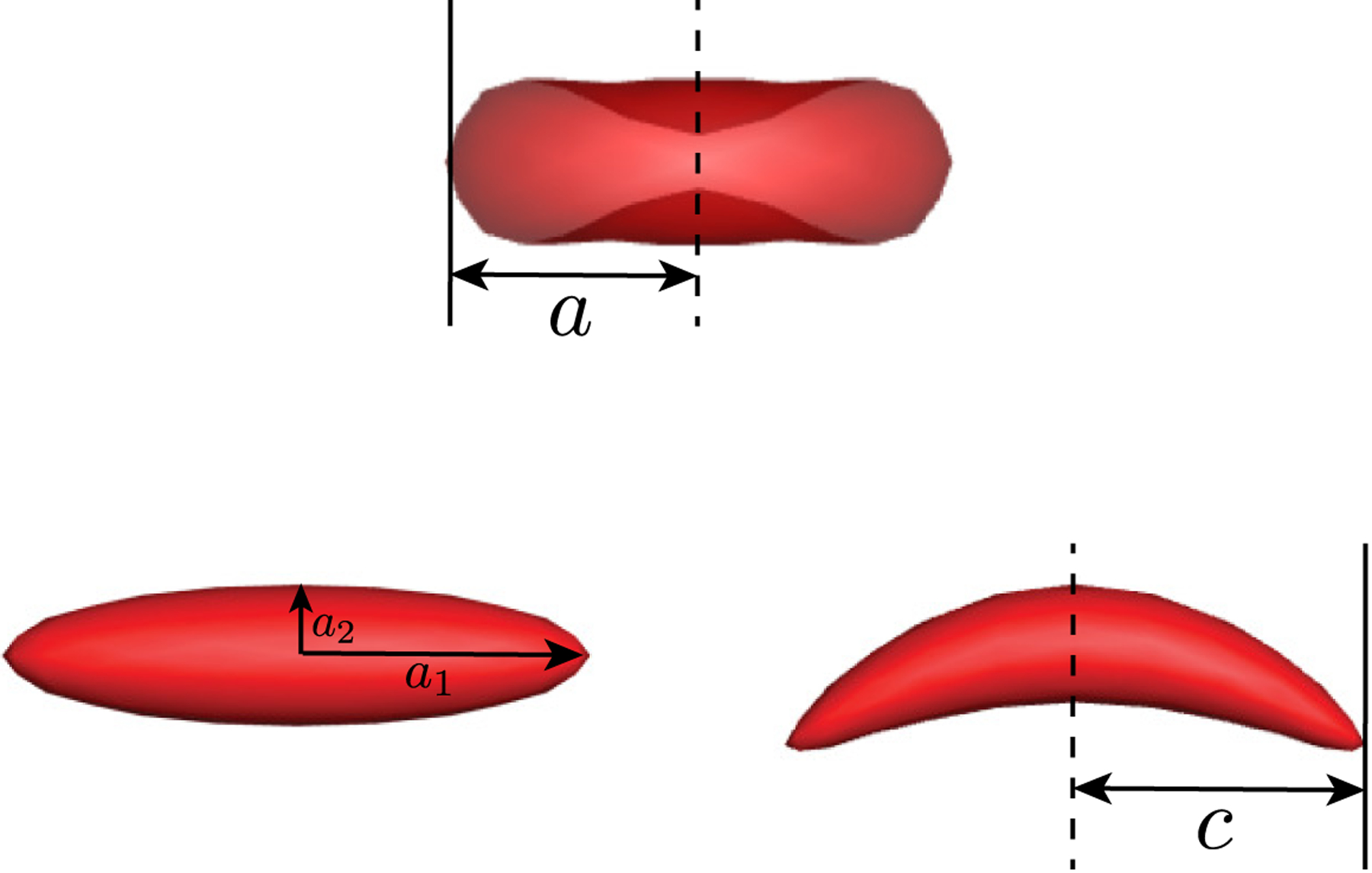
Rest shapes of a biconcave discoidal capsule (top) as a model for healthy RBCs, a straight prolate capsule (bottom left), and a curved prolate capsule (bottom right) as a model for typical sickle cells.

Having introduced the models for the morphologies of different cells, we now describe the membrane mechanics of the capsules. In this work, the capsule membrane is modeled as an isotropic and hyperelastic surface that incorporates shear elasticity, area dilatation, and bending resistance. For an arbitrary capsule, the total energy E of the capsule membrane S is:

$$E=\frac{K_B}{2}{\int }_S{\left(2{\kappa }_H+c_0\right)}^{2}dS+\overline{K_B}{\int }_S{\kappa }_{G}dS+{\int }_{S}WdS,$$ (3)

where K_B and $\overline{K_B}$ are the bending moduli, and W is the shear strain energy density; κ_H and κ_G are the mean and Gaussian curvature of the membrane surface, respectively; c₀ = −2H₀ is the spontaneous curvature, H₀ being the mean curvature of the spontaneous shape. In this equation, the first two terms represent the Canham-Helfrich bending energy [83, 84], and the third term corresponds to the shear strain energy. The behavior of the capsule membrane in response to the in-plane shear elastic force is described using a membrane model by Skalak et al. [85], in which the shear strain energy density W is given by

$$W_{\text{SK}}=\frac{G}{4}\left[\left(I_1^2+2I_1-2I_2\right)+C_a{I}_2^2\right],$$ (4)

where G is the in-plane shear modulus of the membrane, and C_a characterizes the energy penalty for area change of the membrane. The strain invariants I₁ and I₂ are functions of the principal stretch ratios λ₁ and λ₂, defined as

$$I_1={\lambda }_1^2+{\lambda }_2^2-2, I_2={\lambda }_1^2{\lambda }_2^2-1.$$ (5)

Barthès-Biesel et al. [86] showed that for C_a ≳10, the tension of a Skalak membrane becomes nearly independent of C_a under a simple uniaxial deformation, so C_a is set to 10 for all capsules in our simulations. Sinha and Graham [80] have validated this model for the membrane mechanics of a healthy RBC, showing that the strain hardening behavior of the membrane predicted by this model agrees very well with the experimentally determined response of an RBC membrane to optical tweezer stretching by Mills et al. [87].

The deformability of a capsule in pressure driven flow is characterized by the dimensionless wall capillary number $\text{Ca}=\eta {\dot{\gamma }}_{w}l/G$, where l is the characteristic length of the capsule. The bending modulus of a capsule is expressed nondimensionally by ${\widehat{\kappa }}_B=K_B/l^{2}G$, which is ~ O(10⁻⁴ − 10⁻²) in the physiological context [88, 89]; here we set ${\widehat{\kappa }}_B=0.04$ for all capsules, which also prevents the cell membranes from any buckling instabilities. Taking the first variation of the total membrane energy E in Eq. 3 gives the total membrane strain force density:

$$f^m=f^b+f^s,$$ (6)

where f^b and f^s are bending and shear elastic force densities, respectively. For any capsule in this work, unless noted otherwise, the natural shape for shear and the spontaneous shape for bending elasticities of the capsule membrane are both chosen to be the same as the rest shape of the capsule, so that any in-plane or out-of-plane deformation would lead to an increase in the membrane energy and thus to an elastic restoring force. The capsule membrane is discretized into N_Δ piecewise flat triangular elements; in this work N_Δ = 320, resulting in 162 nodes. We have verified that increasing the number of nodes makes no difference to the cell dynamics, and this mesh resolution keeps the computational cost manageable given that very long simulation times are required for the dynamics of the suspensions to reach steady state. Note that in this work, steady state refers to the state in which the suspension dynamics are statistically invariant or stationary. Based on this discretization, the calculation of the total membrane force density f^m follows the work of Kumar and Graham [90] and Sinha and Graham [80] using approaches given by Charrier et al. [91] for the in-plane shear force density f^s and Meyer et al. [92] for the out-of-plane bending force density f^b, respectively. Details regarding these calculations are found in [90] and [80].

Now we describe the suspension systems considered in this work. A base case is a homogeneous suspension of flexible biconcave discoidal capsules representing purely healthy RBCs. In our simulations Ca is always set to 1.6 for flexible biconcave discoids in all suspensions, which is in accordance with the biomechanical properties of the membrane of a healthy RBC within the physiological ranges, assuming the shear rate of blood flow in the microcirculation ${\dot{\gamma }}_w~O\left({10}^2-{10}^3\right){\text{s}}^{-1}$ [93], the viscosity of plasma η ~ 1.2 mPa s [94], and the in-plane shear modulus of a healthy RBC membrane G ~ 7.1 ±1.6 μN/m [50].

One of the major aims of this study is to understand the effects of deformability, shape, and size contrast on the dynamics of a flowing suspension of capsules. To this end, different cases of binary suspensions are considered. The “primary” component, i.e., the component with a larger population, is always the flexible biconcave discoids (healthy RBCs), and denoted as ‘p’. The other component is stiff, termed “trace” and denoted as ‘t’. The number fractions for the capsules of these two components in all binary suspensions considered in this work are set to X_p = 0.9 and X_t = 0.1, respectively, with a number density ratio n_p/n_t = 9.These values are within the physiological ranges in the context of SCD [4]. In the first binary suspension, the ‘t’ component is stiff biconcave discoidal capsules with the same rest shape as the flexible (healthy) ones to investigate the isolated role of rigidity difference in the dynamics of the binary suspension. In the second case, we study a binary suspension with the ‘t’ component being stiff curved prolate capsules that represent typical sickle cells, and this system serves as an idealized model for blood flow in SCD. For comparison, we also consider a suspension containing stiff straight prolate capsules with no curvature to illustrate the effect of curvature on the behavior of the suspension. In all cases of the binary suspensions, Ca_t is always set to 0.4 for the ‘t’ component to control variables. Indeed, this value is physiological given that the membrane shear modulus of a typical sickle cell is experimentally determined to be roughly four times that of a healthy RBC [50].

In this study, the total volume fraction of the capsules is ϕ ≈ 0.15 for all suspensions, with ϕ being slightly lower for the cases containing curved and straight prolate capsules due to their smaller volume than a biconcave discoid, as noted above. This volume fraction is consistent with the physiological hematocrit in small vessels (~ 40 μm across) in the microcirculation [95, 96]. The domain is periodic in x and z with lengths L_x = L_z = 2H = 10a, where a again is the radius of a biconcave discoid as described above. The domain height H = 5a so the confinement ratio C = H/a = 5. We have verified that changing the domain period in the x direction from L_x = 10a to L_x = 20a makes negligible difference in the cross-stream distribution and dynamics of capsules (not shown). Furthermore, the suspending fluid and the fluid inside the capsules are always assumed to have the same viscosity, i.e., λ = 1 for all suspensions, to keep the computational cost manageable. This is different than the physiological viscosity ratio of ~ 5. However, our previous investigations have revealed that the dynamics of a single sickle cell [82] or straight prolate capsule [97] remain qualitatively unchanged as the viscosity ratio λ is increased from 1 to 5. Furthermore, as shown by the simulation results below (Section III A 1), the dynamics of single healthy RBCs in the suspensions assuming λ = 1 are consistent with the orbital behavior observed in a number of prior experimental [98–100] and numerical [101, 102] studies with λ = 5.

B. Fluid motion

In our simulations, the particle and channel Reynolds numbers, defined as ${\text{Re}}_p=\rho {\dot{\gamma }}_w{l}^2/\eta$ and ${\text{Re}}_c=\rho {\dot{\gamma }}_w{H}^2/\eta$, respectively, both have magnitude of ~O(10⁻³ − 10⁻²) based on the physiological range of the parameter values for blood flow in the microcirculation as noted in Section II A. The Reynolds numbers are assumed to be sufficiently small so that the fluid motion is governed by the Stokes equation. To determine the velocity field at each time instant, we use an accelerated boundary integral method of Kumar and Graham [90] for simulations of capsule suspensions. The fluid velocity u at any point x₀ in the simulation domain can be written as:

$$u_j\left(x_0\right)=u_j^{\infty }\left(x_0\right)+\sum _{m=1}^{N_p}{\int }_{S^m}{q}_i(x)G_{ji}\left(x_0,x\right)dS(x),$$ (7)

where the single layer density q(x₀) satisfies

$$q_j\left(x_0\right)+\frac{\lambda -1}{4\pi (\lambda +1)}{n}_k\left(x_0\right)\sum _{m=1}^{N_p}{\int }_{S^m}{q}_i(x)T_{jik}\left(x_0,x\right)dS(x)=-\frac{1}{4\pi \mu }\left(\frac{\Delta f_j\left(x_0\right)}{\lambda +1}+\frac{\lambda -1}{\lambda +1}{f}_j^{\infty }\left(x_0\right)\right).$$ (8)

Here u^∞(x₀) is the undisturbed fluid velocity at a given point x₀, S^m denotes the surface of capsule m; f^∞(x₀) is the traction at x₀ due to the stress generated in the fluid corresponding to the undisturbed flow u^∞(x₀); Δf(x₀) is the hydrodynamic traction jump across the membrane interface, which relates to the total membrane force density by Δf(x₀) = −f^m assuming the membrane equilibrium condition; G and T are the Green’s function and its associated stress tensor.

The acceleration in this implementation is achieved by the use of the General Geometry Ewald-like Method (GGEM) by Hernandez-Ortiz et al. [103]. The key idea is to decompose the overall problem into a local and a global problem, specifically by splitting the Green’s function for the Stokes equation into a singular but exponentially-decaying (short-ranged) part and a smooth but long-ranged part. The solution associated with the local problem is obtained assuming free-space boundary conditions, i.e., it is independent of the geometry of interest. The solution associated with the global problem, on the other hand, is nonsingular and ensures that the boundary conditions for the overall problem are satisfied. In this work, we compute the global solution by employing the discrete Fourier series approximation in the periodic x (flow) and z (vorticity) directions and the discrete Chebyshev polynomial approximation in the y (wall-normal) direction. This approach ensures that the simulations in this work are performed at constant pressure drop. The overall solution for the velocity or stress field is the sum of the local and global solutions. For a flowing suspension in a slit geometry as considered in the present study, the computational cost of the algorithm scales as O(NlogN), where N is proportional to the product of the total number of capsules N_p and the number of triangular elements N_Δ upon surface discretization. Details of the numerical method and algorithm are found in [90].

Once the flow field is determined, the positions of the element nodes on the discretized capsule membrane are advanced in time using the second-order explicit Adams-Bashforth method with adaptive time step Δt = 0.02Cad, where d is the minimum node-to-node distance. Time is nondimensionalized with the wall shear rate ${\dot{\gamma }}_w$, and in this work, t always represents dimensionless time.

III. RESULTS AND DISCUSSION

In this section, we first present and discuss simulation results for the dynamics of different suspension systems as described above (Section III A). Specifically, we focus on understanding the flow-induced segregation behavior as well as determining the orbital dynamics of single cells, especially the stiff cells, in each suspension. Substantial margination of the stiff cells is observed in all binary suspensions. Following these results, we further characterize the hydrodynamic effects of the suspensions on the walls, particularly the additional wall shear stress induced by the marginated stiff cells (Section III B). We reveal that compared to the small fluctuations in wall shear stress observed in the case of a homogeneous suspension of healthy RBCs, the marginated cells in the binary suspensions induce intermittent local wall shear stress peaks. We further discuss the implications of these findings on the mechanism for endothelial inflammation in SCD.

A. Cross-stream distribution and dynamics of cells in different suspensions

1. Homogeneous suspension of healthy (flexible) RBCs

We first consider the base case with a homogeneous suspension of flexible biconcave discoidal capsules representing purely healthy RBCs, and assume that the spontaneous shape of the capsules is the same as their rest shape, i.e., a biconcave discoid. The effect of spontaneous shape will be discussed shortly. To obtain the cross-stream distribution for the cells of component α in a general suspension, we compute the normalized number density profile of the cells based on their wall-normal center-of-mass positions, given by ${\widehat{n}}_{\alpha }(y)=n_{\alpha }(y)/n_{\alpha }^0$ where $n_{\alpha }^0$ is the mean number density of the cells of component α in the suspension; for a uniform distribution, ${\widehat{n}}_{\alpha }(y)=1$ at all y positions. Figure 3(a) shows the time-averaged wall-normal number density distribution profile for healthy RBCs in a homogeneous suspension. The error bars represent estimated error using the “blocking” method [104]. A cell-free layer is evidently observed next to the wall (y/a = 0), which is a consequence of the competition between the effects of wall-induced migration [44] and hydrodynamic pair collisions. The two substantial peaks in the profile, which have been observed in prior experiments [105], simulations [38, 39, 106–108], and theoretical predictions [46, 105] for suspensions of RBCs and other deformable capsules, indicate that the healthy RBCs accumulate both around the centerplane of the channel and near the wall right beyond the cell-free layer. In addition, we also determine the hematocrit profile by computing the local volume fraction of the RBCs. The time-averaged hematocrit profile is shown in FIG. 3(b). We note that this profile closely resembles those in a previous numerical study by Zhao, Shaqfeh and Narsimhan [29] for an RBC suspension with similar parameters.

FIG. 3:

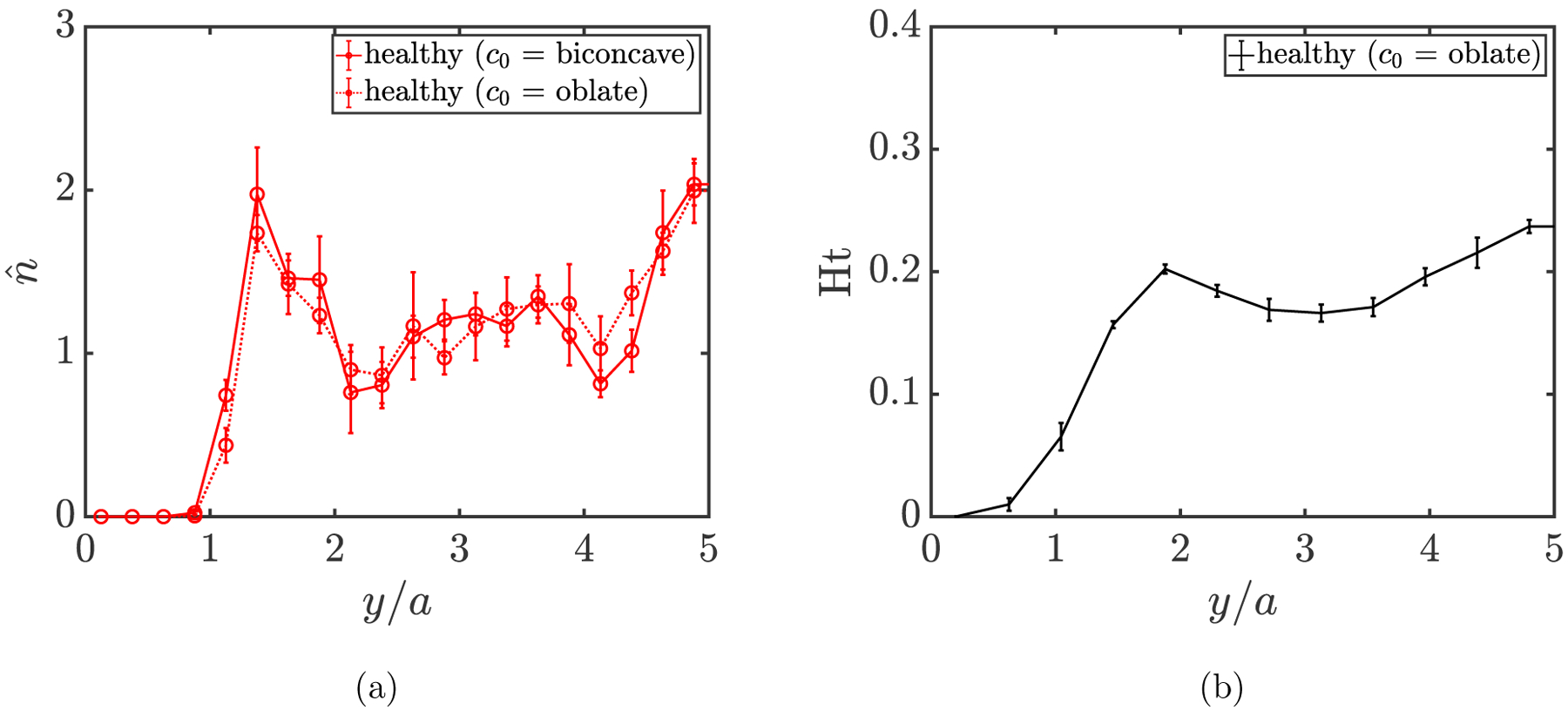
(a) Wall-normal number density profile $\widehat{n}$ for healthy RBCs assuming different spontaneous shapes (c₀) in a homogeneous suspension at steady state. (b) Hematocrit profile for the healthy RBC suspension. The two positions at y/a = 0 and y/a = 5 correspond to the wall and centerplane of the channel, respectively.

Furthermore, in the near-wall region where the local shear rate is high, healthy RBCs approximate a “rolling” orientational motion, where the axis of symmetry (the short axis in the case of an oblate object) orients in the z-direction and the cell rolls like a wheel, as observed in the simulation snapshot (FIG. 4(a)). Two periods of the simulation domain are shown in both x and z directions in this snapshot as well as all future snapshots for other suspensions. This rolling orbit assumed by an RBC at high shear rate, or a transition of the cell dynamics toward the rolling orbit upon increasing shear rate, has also been revealed in both experimental [98–100] and numerical [101, 102, 109] studies for single RBCs under physiological conditions in which the viscosity ratio between the fluids inside and outside the cell is typically λ ≈ 5, although the viscosity ratio is set to λ = 1 in this work, again, to make the computational cost manageable. We note, though, that the spontaneous shape (c₀) has a nontrivial effect on the dynamics of single RBCs. For example, as shown in FIG. 4, the near-wall healthy RBCs reorient from a rolling orbit into a “tank-treading” configuration when their spontaneous shape is changed from a biconcave discoid to an oblate spheroid, consistent with the findings in a prior numerical investigation by Sinha and Graham [80]. (In tank-treading, points on the surface of the cell move but the cell shape itself remains nearly time-independent.) In spite of the change in orientational dynamics when the spontaneous shape is changed, no substantial change is observed in the wall-normal number density profile for healthy RBCs (FIG. 3(a)). Indeed, we have further verified that for the binary suspensions that will be presented next, the segregation behavior and dynamics of stiff cells are only weakly affected by the orientational dynamics of healthy (flexible) RBCs.

FIG. 4:

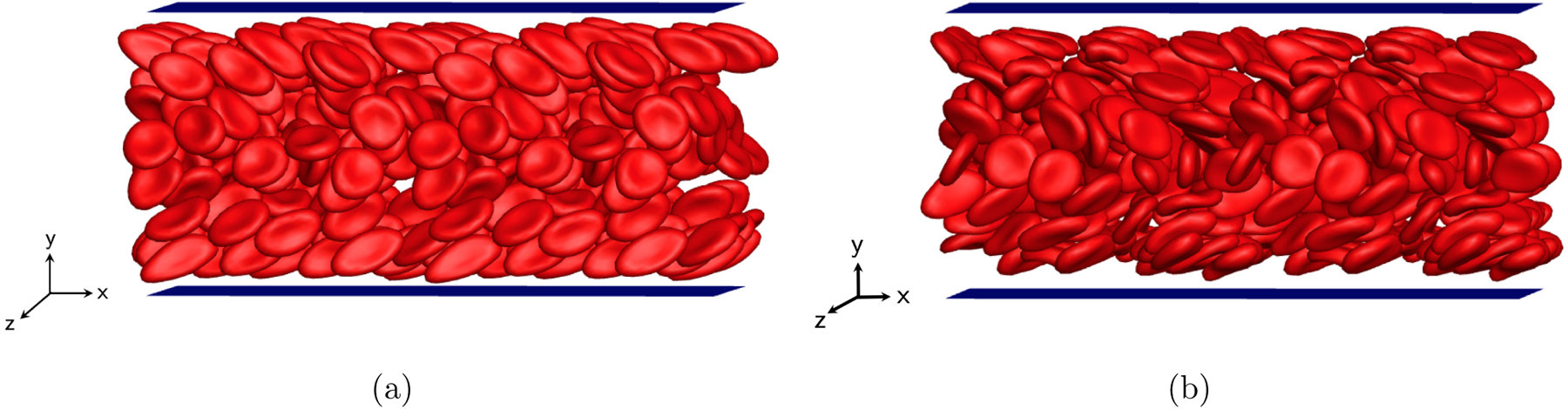
Simulation snapshots for a homogeneous suspension at steady state of flexible biconcave discoidal capsules (healthy RBCs) with Ca = 1.6 assuming either a biconcave discoidal (a) or an oblate spheroidal (b) spontaneous shape.

2. Binary suspension of flexible and stiff RBCs: isolated effect of rigidity difference

We now consider a binary suspension of flexible (Ca_p = 1.6) and stiff (Ca_t = 0.4) RBCs with a number density ratio n_p/n_t = 9. To characterize the collective dynamics of the cells of each component, we define a parameter $s={\langle {\left(y_{cm}-H\right)}^2\rangle }^{1/2}/a$, which measures the root-mean-square (RMS) distance of the cells from the centerplane of the channel; here y_cm is the center-of-mass position of an arbitrary cell in the wall-normal direction. The time evolution of s for the cells of each component is plotted in FIG. 5(a). It is obvious that though starting with comparable values for both components, s decreases for flexible RBCs while increasing for stiff RBCs, before reaching a plateau (steady state) at s_p ≈ 2.2 and s_t ≈ 3.2, respectively, indicating a segregation behavior in the binary suspension.

FIG. 5:

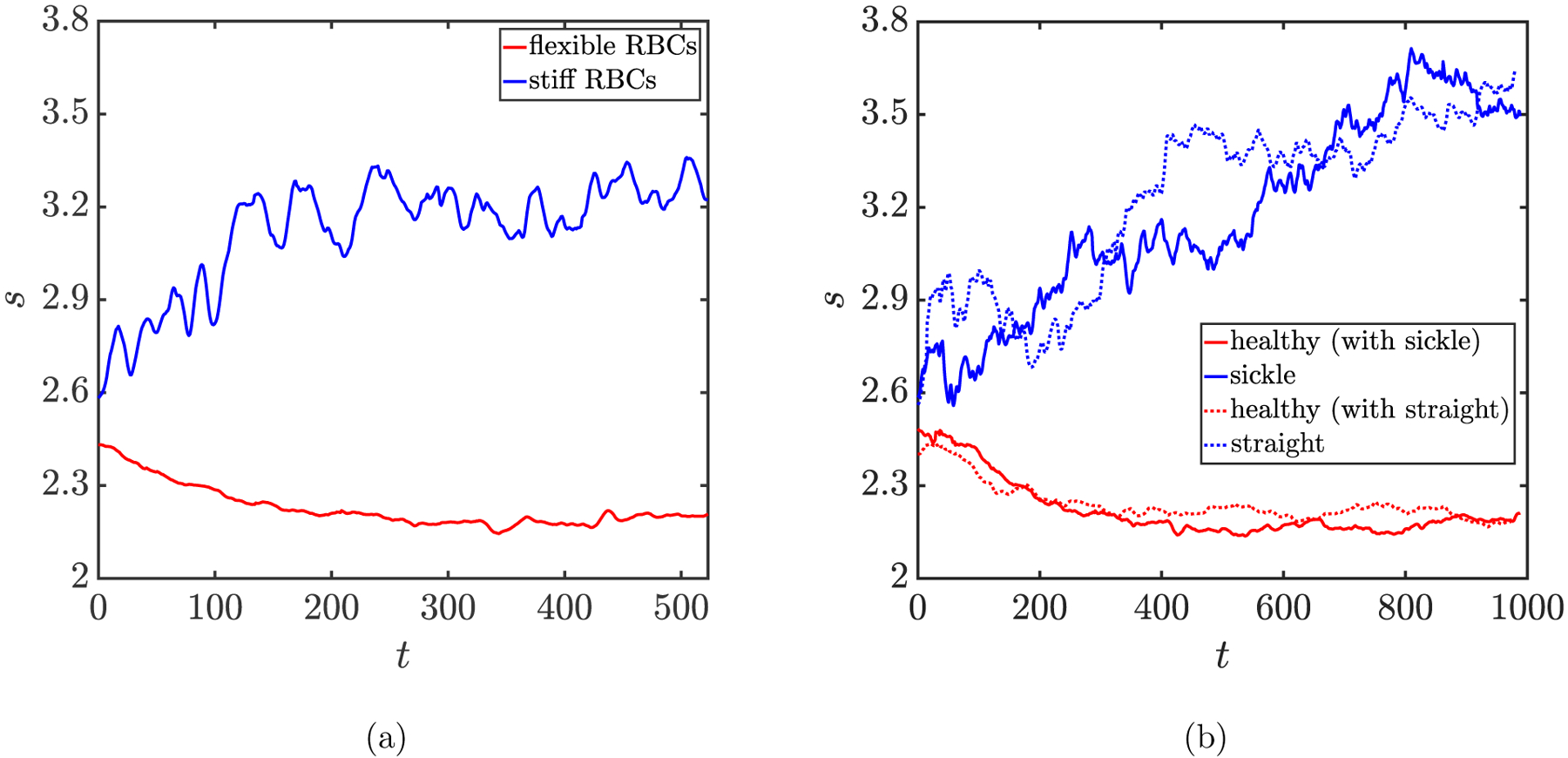
Time evolution of the parameter $s={\langle {\left(y_{cm}-H\right)}^2\rangle }^{1/2}/a$ for (a) flexible (i.e. healthy) RBCs in suspension with stiff RBCs, and for (b) healthy RBCs in suspension with sickle cells and straight prolate capsules, respectively.

Furthermore, to quantify the cell distributions, the steady-state wall-normal number density profiles $\widehat{n}(y)$ are computed for both components and shown in FIG. 6. In this case where stiff RBCs are dilute, the key observation is that, in contrast to flexible RBCs that exhibit a profile similar to that in their pure suspension, a majority of stiff RBCs are drained from the center of the channel and aggregate in the near-wall region, undergoing substantial margination. This margination and segregation behavior is also evident in snapshots from simulation for this binary suspension (FIG. 7). These results demonstrate that rigidity difference by itself is sufficientto induce the segregation behavior in a binary suspension, which is consistent with the findings in prior studies [37, 38, 46] considering a suspension of spherical capsules that differ only in rigidity. The marginated stiff RBCs are found to take an approximate in-plane “tumbling” orbit near the walls: i.e. the axis of symmetry undergoes as an approximately circular trajectory in the x-y plane. In addition, we have verified that the existence of a small number fraction of stiff RBCs makes little difference to the orientational dynamics of flexible RBCs (not shown).

FIG. 6:

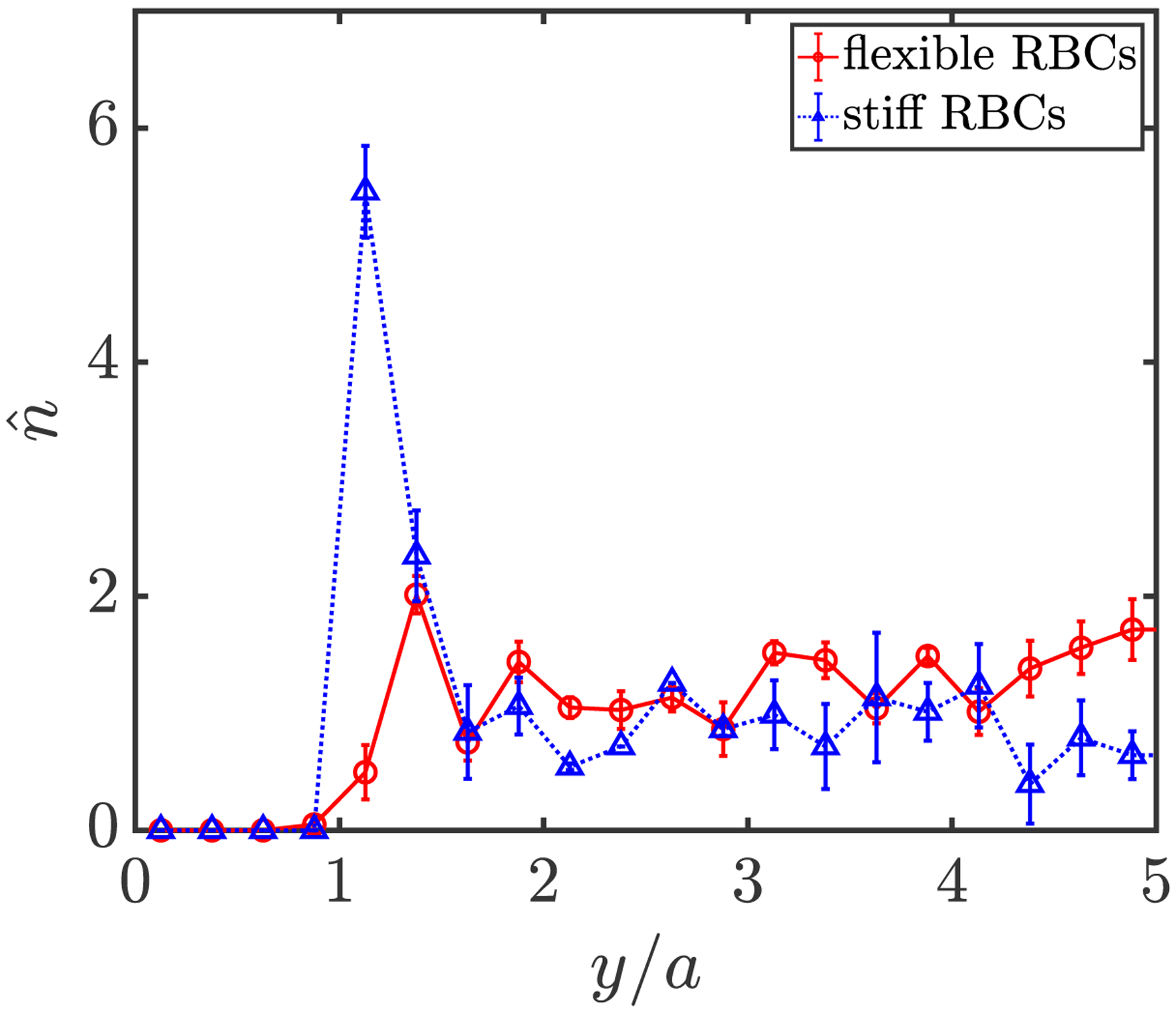
Wall-normal number density profiles $\widehat{n}$ for flexible (solid red) and stiff (dotted blue) RBCs in a binary suspension at steady state.

FIG. 7:

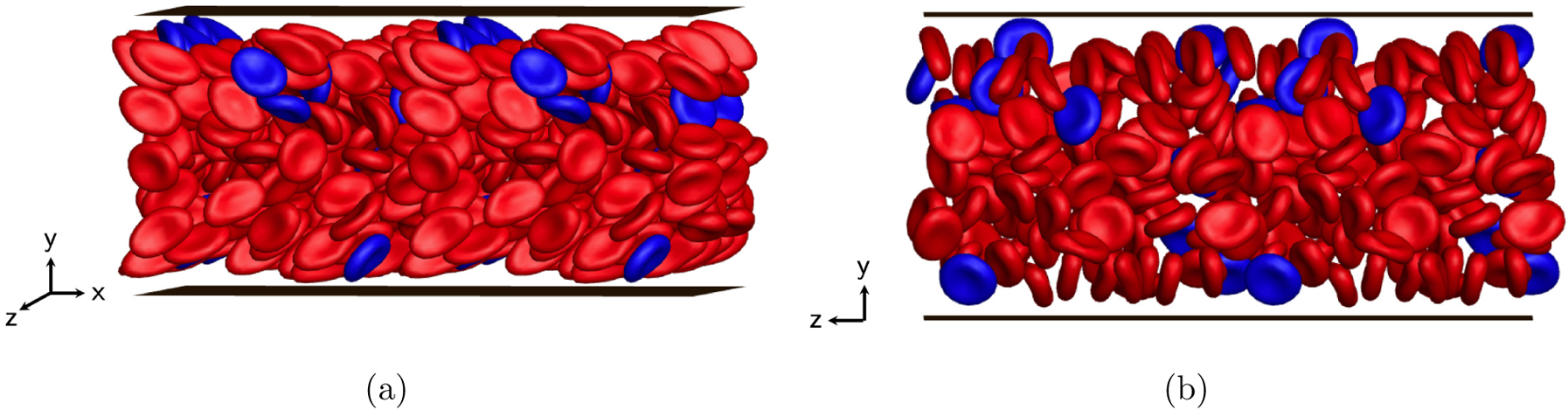
Simulation snapshots ((a) side view, (b) front view) for a binary suspension of flexible (red) and stiff (blue) RBCs at steady state.

3. Binary suspension of healthy and sickle RBCs: combined effect of rigidity, shape, and size differences

In this section we present simulation results for a binary suspension of healthy and sickle RBCs (specifically ISCs), which is the focus of this work. Again, healthy RBCs are modeled as exible biconcave discoidal capsules (Ca_p = 1.6), while sickle cells as stiff curved prolate capsules (Ca_t = 0:4); the number density ratio between these two components is n_p = n_t = 9. In the meantime, results for the case in which sickle cells, the trace component, are replaced by stiff straight prolate capsules (Ca_t = 0:4 and X_t = 0.1) are also presented for comparison to illustrate the effect of curvature for the trace component.

Figure 5(b) shows the time evolution of the parameter $s={\langle {\left(y_{cm}-H\right)}^2\rangle }^{1/2}/a$ for each component in both suspensions. Segregation behavior is observed for both cases. The trends of increase in s display minor differences for sickle cells and straight prolate capsules, both reaching a plateau (steady state) at s_t ˇ 3.6. This steady-state value is greater than that for stiff RBCs (s_t ≈ 3.2). We also note that compared to the case with stiff RBCs, the cases with sickle cells and straight prolate capsules take a longer time to reach steady state.

More details can be revealed by computing the cross-stream distribution profiles for each component in both suspensions. In FIG. 8(a), a cell-free layer is observed in the wall-normal number density profiles $\widehat{n}$ for healthy RBCs in both cases, as well as the two peaks both around the centerplane of the channel and right beyond the cell-free layer. In general, the $\widehat{n}$ profiles for healthy RBCs in these two suspensions are similar to those in previous cases. For sickle cells and straight prolate capsules, the profiles both show a high near-wall peak inside the cell-free layer (FIG. 8(b)), which suggests that the trace component in both cases is largely drained from the bulk of the suspension, displaying strong margination as seen in the simulation snapshots in FIG. 9. No substantial differences are observed in the $\widehat{n}$ profiles for both cases. We also show in FIG. 10 that when the spontaneous shape (c₀) of healthy RBCs is changed from a biconcave discoid to an oblate spheroid, although an orientational transformation is observed for the dynamics of healthy RBCs (FIGs. 10(a) and 10(b)), insignificant differences are found in the distribution profiles for both healthy RBCs and sickle cells in a binary suspension (FIGs. 10(c) and 10(d)).

FIG. 8:

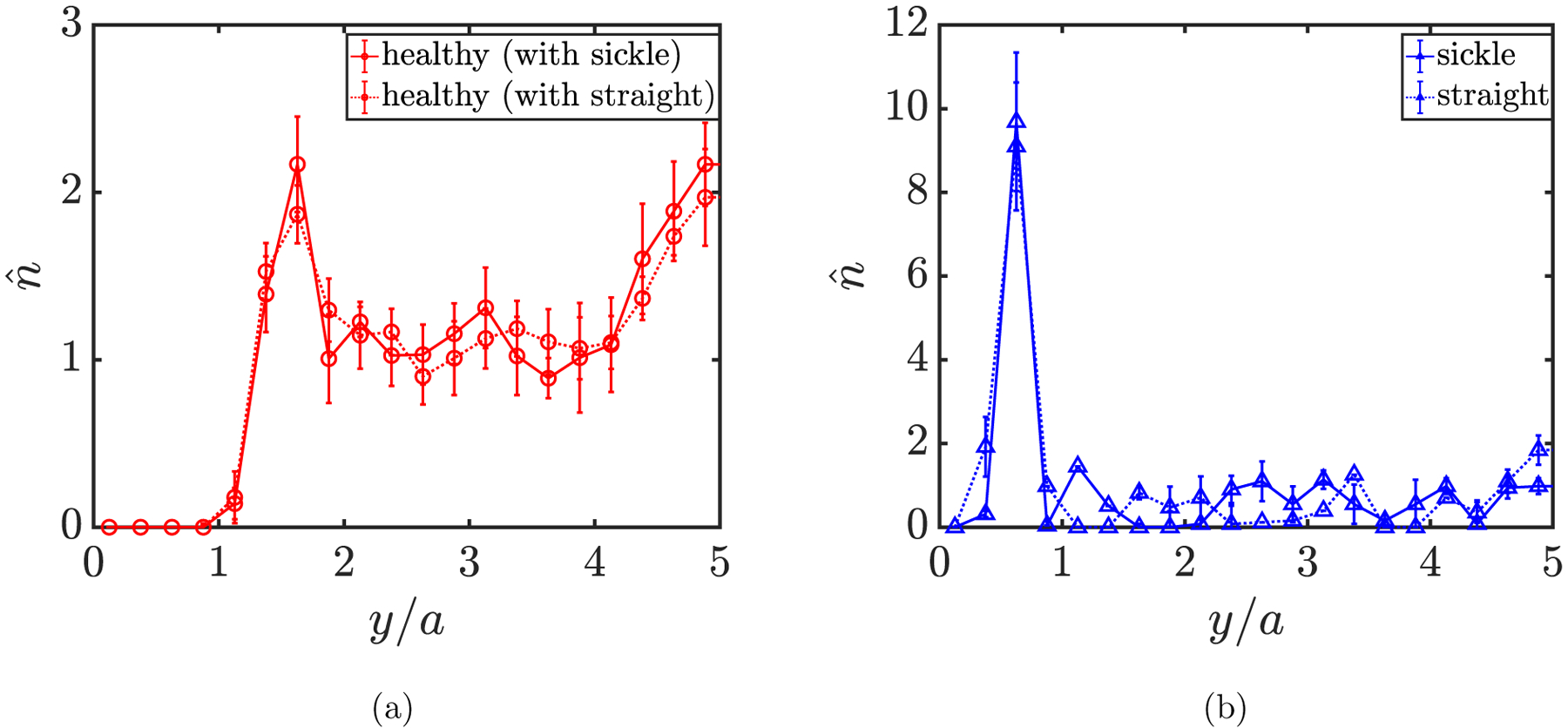
Wall-normal number density profiles $\widehat{n}$ for (a) healthy RBCs in suspension with sickle cells (solid red) and straight prolate capsules (dotted red), and (b) for sickle cells (solid blue) and straight prolate capsules (dotted blue) in suspension with healthy RBCs, respectively.

FIG. 9:

Simulation snapshots (left: side view; right: front view) for binary suspensions of healthy RBCs with sickle cells (a,b) and straight prolate capsules (c,d), respectively, at steady state.

FIG. 10:

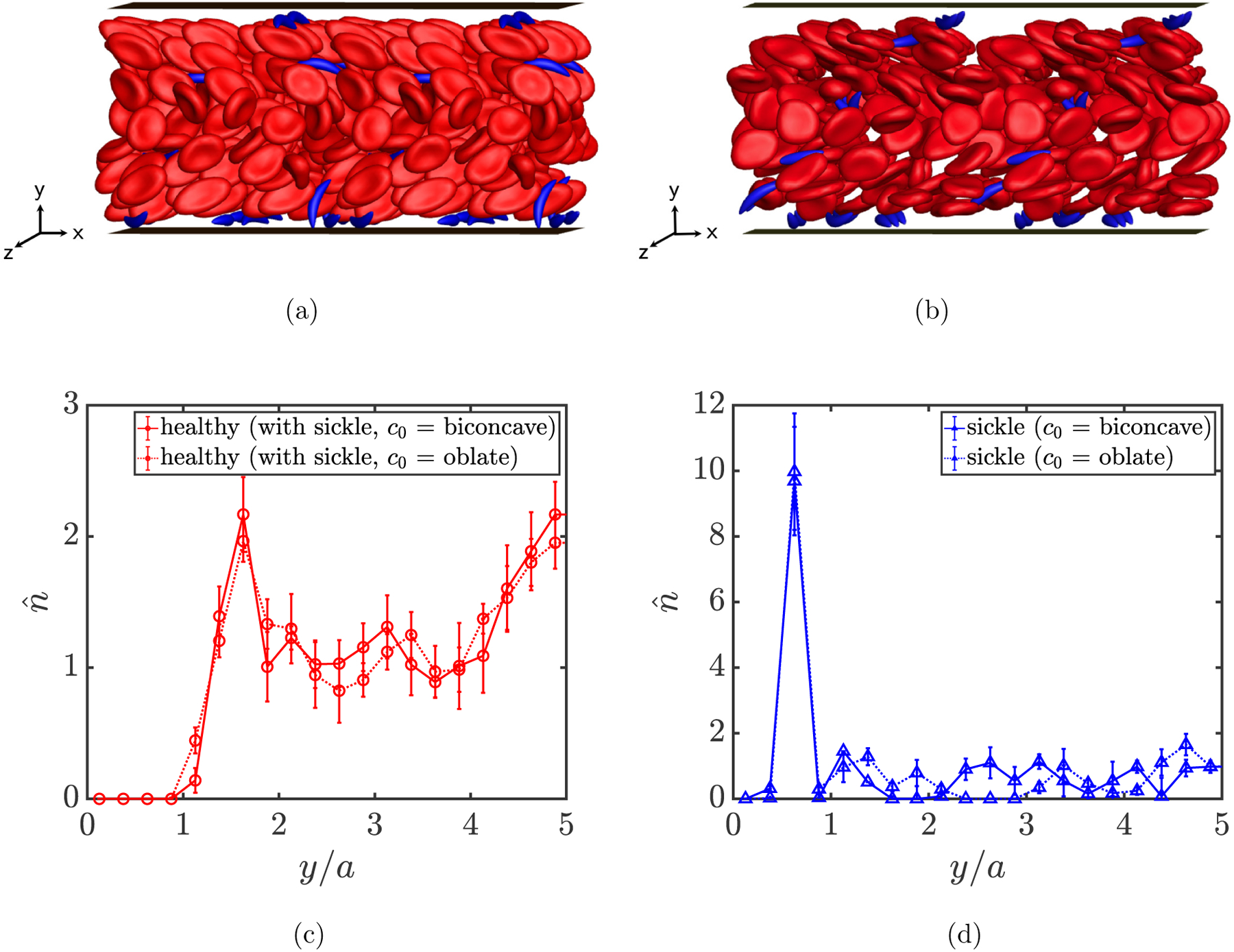
Simulation snapshots (a,b) for a steady-state binary suspension of healthy RBCs with sickle cells, as well as wall-normal number density profiles $\widehat{n}$ (c,d) for both components, assuming a biconcave discoidal (a) and an oblate spheroidal (b) spontaneous shape (c₀) for healthy RBCs, respectively.

It is noteworthy that the near-wall peaks in the $\widehat{n}$ profiles for sickle cells and straight prolate capsules (FIG. 8(b)) are both of greater magnitude and closer to the wall compared to that in the profile for stiff RBCs (FIG. 6). To explain this, we first characterize the orbital dynamics of sickle cells and straight prolate capsules in the respective suspension. Here the cells (capsules) are classified into two groups based on their wall-normal center-of-mass positions: one for the cells inside the cell-free layer, and the other for those in the bulk of the suspension. The instantaneous orientation of a single sickle cell or straight prolate capsule in flow is given by a unit end-to-end vector p that connects the two tips of the cell (capsule). We then define a tensor S to quantify the ensemble-averaged orientation of the cells in each group, given as

$$S=\langle pp\rangle =\left(\begin{array}{lll}\langle p_x{p}_x\rangle \hfill & \langle p_x{p}_y\rangle \hfill & \langle p_x{p}_z\rangle \hfill \\ \langle p_y{p}_x\rangle \hfill & \langle p_y{p}_y\rangle \hfill & \langle p_y{p}_z\rangle \hfill \\ \langle p_z{p}_x\rangle \hfill & \langle p_z{p}_y\rangle \hfill & \langle p_z{p}_z\rangle \hfill \end{array}\right).$$ (9)

In particular, we care about the magnitude of the components 〈p_xp_x〉, 〈p_xp_y〉 (= 〈p_yp_x〉), 〈p_yp_y〉 and 〈p_zp_z〉, assuming that the values for the other components are essentially zero given the equal probability of p_z being positive or negative for an arbitrary cell. The steady-state magnitude of each of these components is presented using a bar graph in FIG. 11 for sickle cells and straight prolate capsules inside the cell-free layer and in the bulk of the suspension, respectively. We observe that for the cells inside the cell-free layer, the component 〈p_zp_z〉 dominates with the magnitude close to 1, while the other components are vanishingly small. This suggests that the marginated sickle cells and straight prolate capsules tend to approximate a log-rolling orbital motion inside the cell-free layer, with the end-to-end vector p nearly aligned with the z axis, which is in agreement with the observations from the simulation snapshots in FIG. 9. Compared to the marginated stiff RBCs that approximate a tumbling motion, the near-wall sickle cells or straight prolate capsules are able to approach closer to the walls owing to a minimal volume exclusion effect because of their near-rolling orbits, smaller volume, and slenderness in shape, which leads to a near-wall peak in the $\widehat{n}$ profile that is both greater in magnitude and closer to the wall.

FIG. 11:

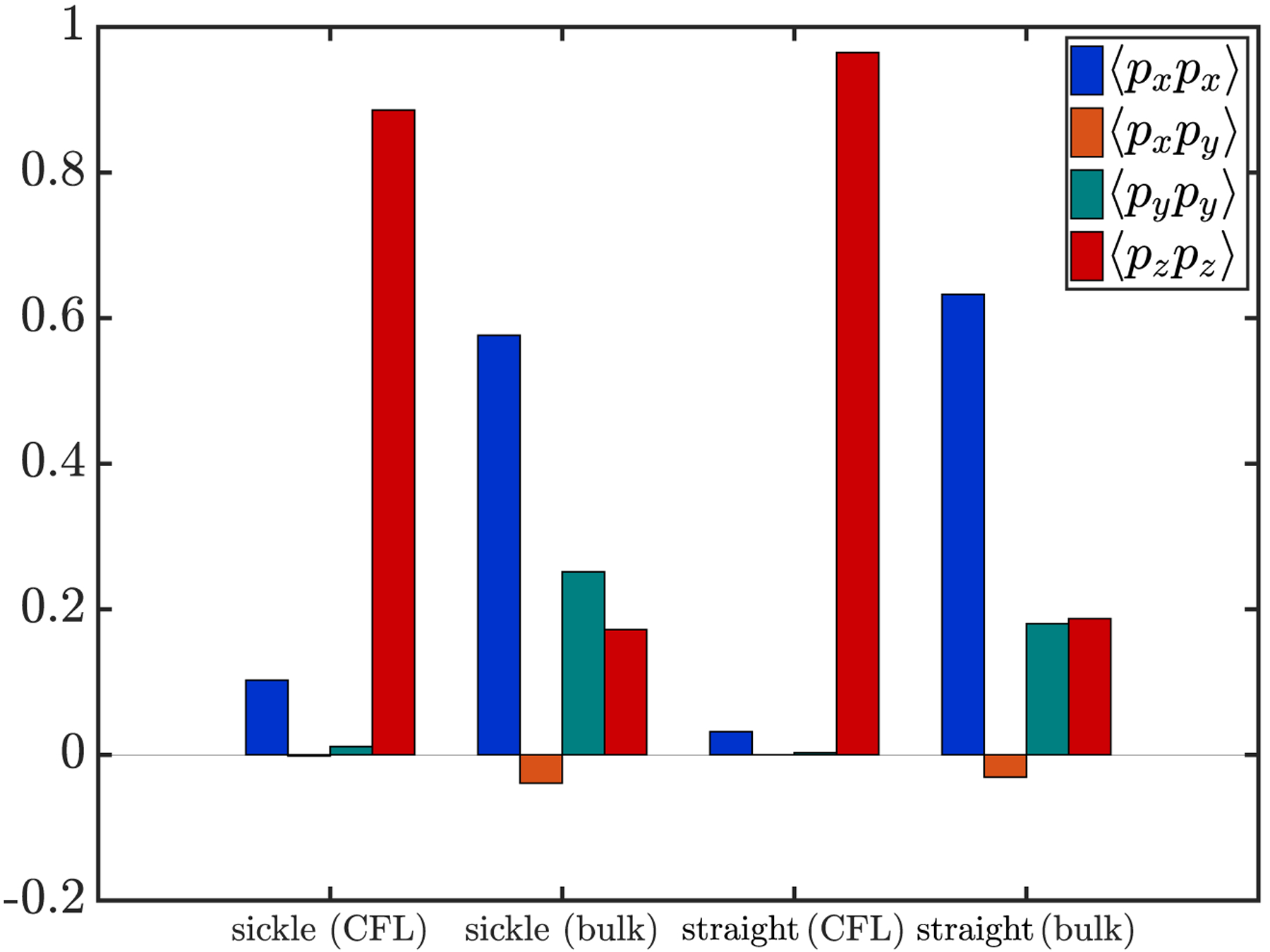
Magnitude of the x-x, x-y, y-y, and z-z components of the tensor S = 〈pp〉 for sickle cells and straight prolate capsules inside the cell-free layer (labelled “CFL”) and in the bulk of the suspension (labelled “bulk”), respectively.

For sickle cells and straight prolate capsules in the bulk of the suspension, in contrast, 〈p_xp_x〉 dominates, with 〈p_yp_y〉 and 〈p_zp_z〉 being smaller but non-zero, indicating that the cells in the bulk generally take a “kayaking” orbit (in which the long axis of the cell lies out of the x-y plane but is not fully aligned along the z-axis). Here the long axis is only slightly out of the shear (x-y) plane, consistent with our previous findings on the dynamics of a single sickle cell in unbounded simple shear flow [82]. During the evolution of the suspension dynamics, this orbit becomes favorable for these slender cells with a high aspect ratio, given limited space between cells (primarily healthy RBCs) in suspension. The dynamics of the healthy RBCs do not show much difference compared to previous cases.

B. Effect of marginated cells on the walls in binary suspensions

Having determined the cross-stream distribution and cell dynamics in different suspensions, in this section we characterize the hydrodynamic effects of the suspensions on the walls, and compare the results for the binary suspensions with the case containing purely healthy RBCs to illustrate the impact of the marginated stiff cells in the binary suspensions. Particularly, we compute the shear stress at the walls associated with different suspensions. For an undisturbed planar pressure-driven flow in the absence of the capsules confined by two walls at y = 0 and y = 2H, the mean wall shear stress is given by ${\tau }_w=2\eta U_0/H$. In the case of a flowing suspension of capsules, however, additional wall shear stress ${\tau }_w^{\prime }$ can be induced by the presence of the capsules. In this work ${\tau }_w^{\prime }$ is computed numerically using an accelerated boundary integral method [90], as introduced in Section II B. It is worth emphasizing, though, that since the simulations are performed at constant pressure drop, the mean wall shear stress is the same for all suspensions considered here, and is equal to the undisturbed wall shear stress τ_w, which is nondimensionalized to 2. Figure 12 shows examples of the spatial distribution of ${\widehat{\tau }}_w={\tau }_w^{\prime }/{\tau }_w$ on the bottom wall (y = 0) induced by different suspensions at steady state. Note that this quantity and all the wall shear stress quantities reported below have been normalized by the undisturbed wall shear stress τ_w unless noted otherwise. It is clear that except for the case with purely healthy RBCs in which barely any fluctuations in wall shear stress are observed, the binary suspensions all induce local shear stress peaks on the wall, which is certainly accredited to the marginated cells in each suspension.

FIG. 12:

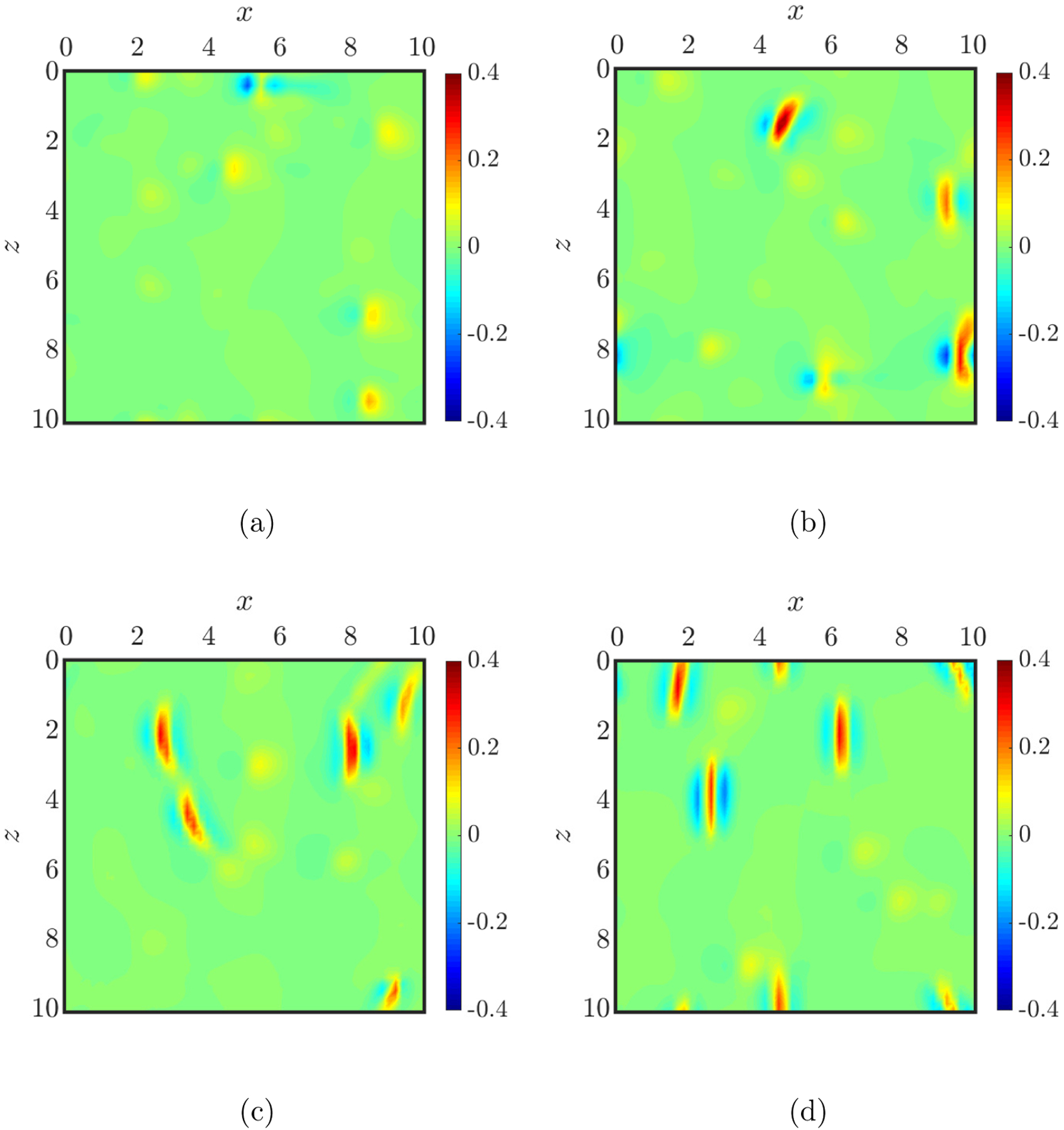
Examples of the spatial distribution of the additional wall shear stress ${\widehat{\tau }}_w$ on the bottom wall (y = 0) induced by a homogeneous suspension of healthy RBCs (a) and binary suspensions of healthy (flexible) RBCs with stiff RBCs (b), sickle cells (c), and straight prolate capsules (d), respectively, at steady state.

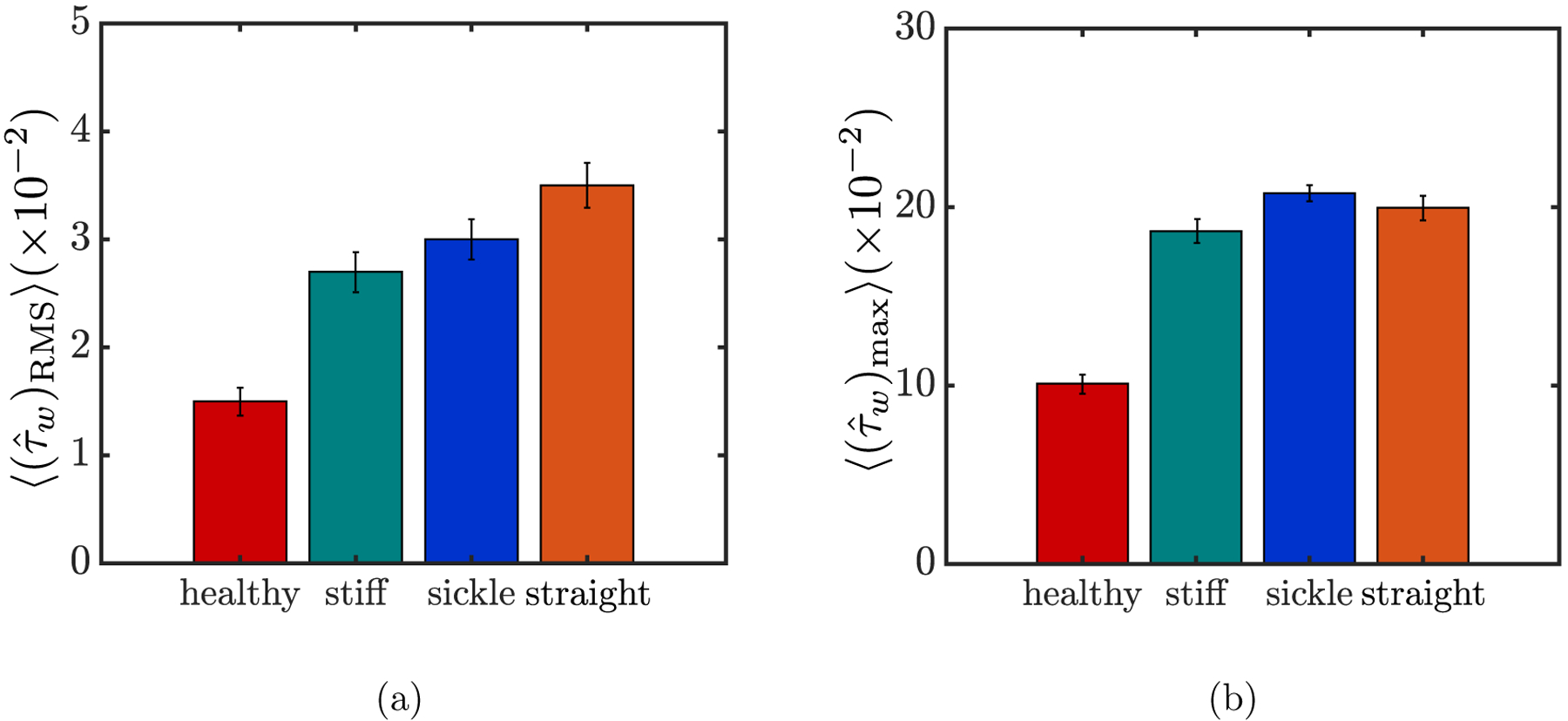
In general, an arbitrary wall position can experience dramatic fluctuations in ${\widehat{\tau }}_w$ due to the dynamical motion of the near-wall cells in a flowing suspension. Examples are shown in FIG. 13 for the evolution of ${\widehat{\tau }}_w$ experienced at a fixed wall position (x, y, z) = (0.74a, 0, 1.67a) for different suspensions at steady state. A number of peaks with large magnitude are observed in each case of the binary suspensions, suggesting that this wall position experiences high additional shear stress intermittently. We now detailedly characterize the hydrodynamic effect of each suspension on the walls. First, we compute the RMS of the additional wall shear stress ${\widehat{\tau }}_w$ for each wall position, and the results for the spatially-averaged RMS wall shear stress, $\langle {\left({\widehat{\tau }}_w\right)}_{\text{RMS}}\rangle$, are plotted in FIG. 14(a) for different suspensions. It is observed that all three types of cells as the trace component, i.e., stiff RBCs, sickle cells, and straight prolate capsules, cause an increase (of approximately two folds) in the averaged RMS wall shear stress in the case of the corresponding binary suspension compared to the case with purely healthy RBCs. The magnitude of the increase is the greatest for the case with straight prolate capsules, though the differences are small among the binary cases. In addition, the spatially-averaged maximum additional wall shear stress $\langle {\left({\widehat{\tau }}_w\right)}_{\text{max}}\rangle$, is also computed for differ ent cases (FIG. 14(b)). Again, no substantial differences are observed among the binary cases, although the magnitude of this quantity is slightly greater for the case with sickle cells than with stiff RBCs or straight prolate capsules.

FIG. 13:

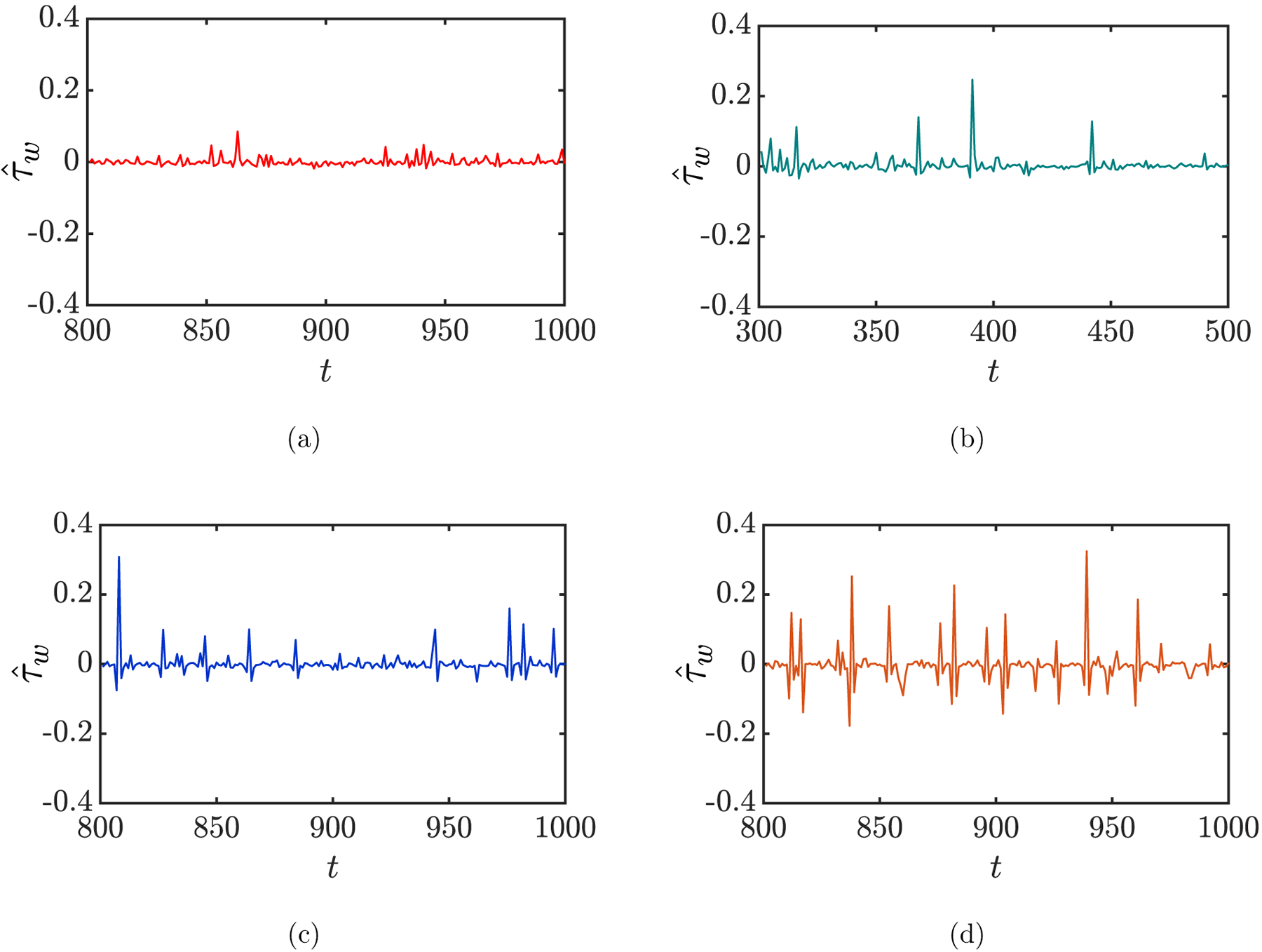
Time evolution of the additional wall shear stress ${\widehat{\tau }}_w$ at a fixed wall position (x, y, z) = (0.74a, 0, 1.67a) for the cases of a homogeneous suspension of healthy RBCs (a) and binary suspensions of healthy (flexible) RBCs with stiff RBCs (b), sickle cells (c), and straight prolate capsules (d), respectively, at steady state.

FIG. 14:

The spatially-averaged RMS $\langle {\left({\widehat{\tau }}_w\right)}_{\text{RMS}}\rangle$ (a) and maximum $\langle {\left({\widehat{\tau }}_w\right)}_{\text{max}}\rangle$ (b) of the additional wall shear stress for different suspensions at steady state. For each quantity, the error bars represent standard error.

However, despite the general indications, neither the RMS nor the maximum is able to reveal the influence of the marginated cells in a binary suspension on the walls in detail. Indeed, it is mainly these near-wall cells that generate the intermittent peaks in the additional wall shear stress, as shown in the examples in FIG. 13. To this end, we now compute three quantities for each of the suspensions: the ensemble-averaged magnitude, duration, and frequency of the peaks in the additional wall shear stress. To do this, we consider only those wall shear stress peaks in each case that are greater than the expected maximum value for the healthy case, and the associated quantities are denoted using the subscript “pk”. The ensemble-averaged magnitude, duration, and frequency of these peaks are then computed, which gives $\langle {\left({\widehat{\tau }}_w\right)}_{pk}\rangle$, 〈Δt_pk〉 and 〈f_pk〉, respectively. Note that an arbitrary peak in ${\widehat{\tau }}_w$, as defined above, is always characterized by a spike and two dips right before and after it (FIG. 13). Accordingly, the duration of a peak is defined as the time difference between the onset of the dip before the spike and the end of the one after. Finally, we take the product A_pk of these three quantities, defined as

$$A_{pk}=\langle {\left({\widehat{\tau }}_w\right)}_{pk}\rangle \times \langle \Delta t_{pk}\rangle \times \langle f_{pk}\rangle ,$$ (10)

which quantifies the overall effect of each suspension on the wall shear stress.

The results are summarized in FIG. 15. It is obvious that compared to the case with purely healthy RBCs where A_pk is vanishingly small, all three binary suspensions exert a substantial overall effect on the wall shear stress (FIG. 15(d)). The averaged magnitude and duration of the wall shear stress peaks, $\langle {\left({\widehat{\tau }}_w\right)}_{pk}\rangle$ and 〈Δt_pk〉 show minor differences among the cases of binary suspensions, although both are slightly greater for the case with stiff RBCs than with sickle cells or straight prolate capsules. Significant differences, however, are observed in the averaged frequency of the wall shear stress peaks, with 〈f_pk〉 being the greatest when the trace component is straight prolate capsules. As a result, the product A_pk also yields the greatest value for the case with straight prolate capsules, while being slightly greater for the case with sickle cells than with stiff RBCs.

FIG. 15:

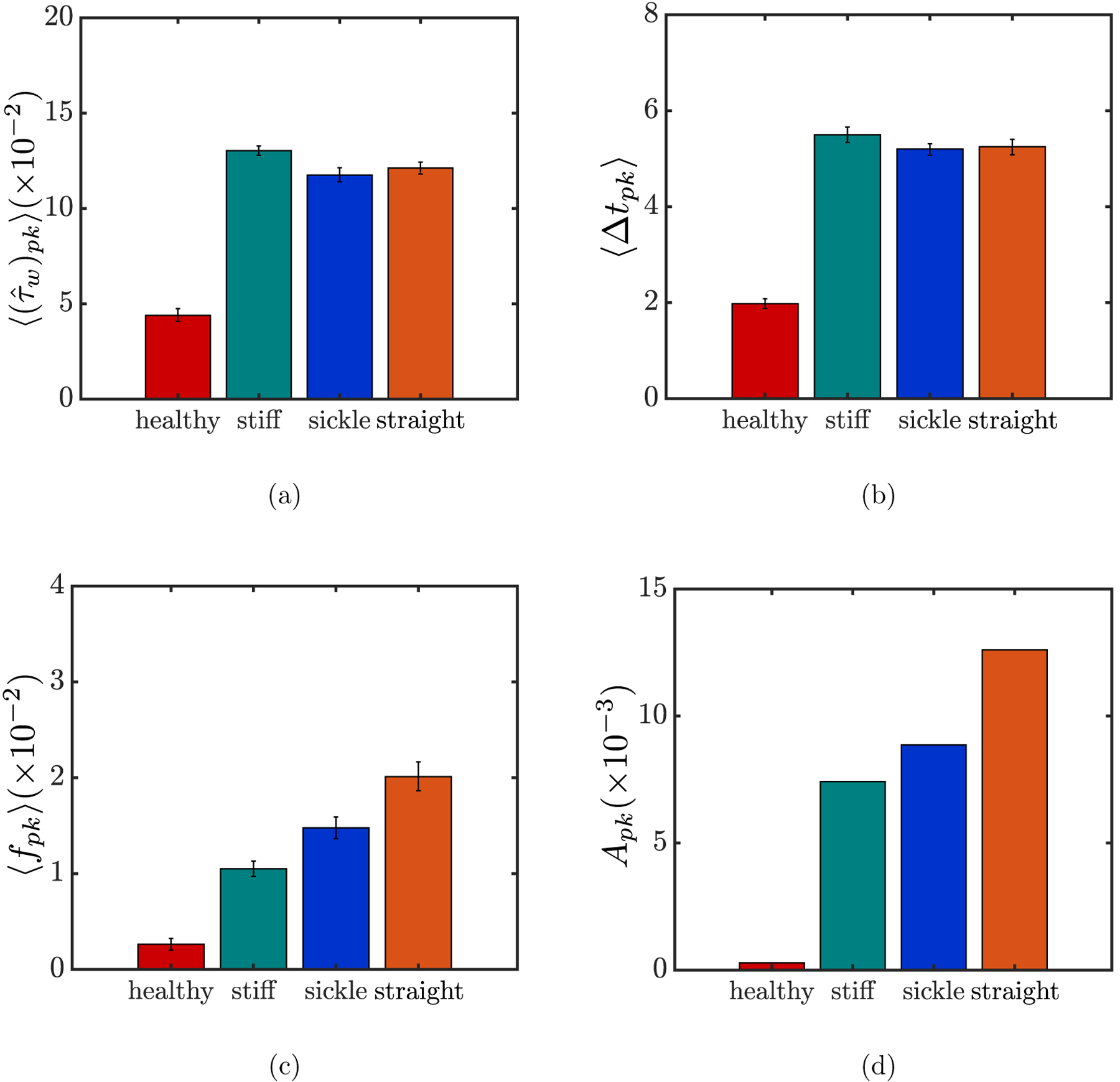
The ensemble-averaged magnitude $\langle {\left({\widehat{\tau }}_w\right)}_{pk}\rangle$ (a), duration 〈Δt_pk〉 (b), and frequency 〈f_pk〉 (c), respectively, of the wall shear stress peaks experienced by all wall positions for different suspensions at steady state, and the product A_pk of these three quantities (d). The error bars in (a), (b), and (c) represent standard error for each quantity.

The differences in 〈f_pk〉 among the binary suspension cases, as shown in FIG. 15(c), may be explained by the orbital dynamics of the marginated cells. As determined in Section III A 2, marginated stiff RBCs tend to approximate an in-plane tumbling orbit. Theoretically, substantial additional wall shear stress is induced when the cell is oriented per pendicular to the wall with a minimal distance between the edge of the cell and the wall. However, during the periodic orbital motion of the cell, this orientation is transient before the cell is quickly flipped by the shear effect of the flow and spend longer time at the edge of the cell-free layer becoming parallel with the wall, which conversely leads to negligible additional wall shear stress and, as a consequence, the lowest frequency of the wall shear stress peaks among the binary suspension cases. The difference in 〈f_pk〉 between the cases with sickle cells and straight prolate capsules, on the other hand, is majorly an effect of curvature: the steady rolling motion of marginated straight prolate capsules inside the cell-free layer, with negligible fluctuations in the wall-normal position of the cell body compared to the larger fluctuations for near-wall rolling sickle cells caused by curvature, ensures that at any wall position, a peak in wall shear stress is induced whenever a straight prolate capsule goes by.

As mentioned in Introduction, in this work WBCs and platelets are not considered in the suspensions assuming negligible effects due to their extremely small number fractions in blood. To justify this assumption, we have tested the case in which one stiff spherical capsule slightly larger than a biconcave discoid, which serves as a model for the WBC, is placed near the wall in suspension with healthy RBCs (X_p = 0.99, X_t = 0.01). We reveal that the overall effect of this suspension on wall shear stress, characterized by A_p as defined above, is indeed negligible compared to that for the case containing sickle cells; note that this number fraction of WBCs is even higher than the physiological range [2]. Therefore, it is reasonable to exclude WBCs in our simulations. Similarly, we expect that platelets should also have a negligible effect on wall shear stress due to both the small number fraction and the tumbling motion taken near the walls [29] as noted above for stiff RBCs.

The findings in the present work may aid in understanding the pathophysiology of chronic endothelial inflammation in SCD from a biophysical perspective. Indeed, the intermittent peaks in wall shear stress induced by the marginated stiff sickle cells, as observed in this work, resemble the spiky wall shear stress profile considered in Bao et al. [66] on flow-mediated endothelial mechanotransduction. This spiky profile, characterized by abrupt onset and termination of shear stress, was found to induce the greatest upregulation of pro-inflammatory signals compared to the other shear stress profiles. More generally, rapid changes in shear stress, as opposed to steady shear stress, have been demonstrated to contribute to endothelial inflammation and subsequent atherogenesis via specific mechanotransduction pathways of the endothelium [63, 68, 72–74]. In this sense, our results provide a possible mechanism for chronic SCD vasculopathy.

The present work does not incorporate adhesive interactions between diseased cells and vessel walls. While these play a significant role in the acute vaso-occlusive crisis [76, 77, 110–112], which in turn, may cause endothelial dysfunction, our aim here was to address the question of whether non-adhesive effects may also lead to a pro-inflammatory state of the endothelium via mechanotransductive mechanisms. In fact, the aforementioned experimental studies on shear stress-induced endothelial expression were all performed in the absence of adhesive events. Hence, this work suggests that purely physical (non-adhesive) interactions between endothelial cells and sickle cells may be sufficient to cause endothelial inflammation, which provides innovative and vital insight into SCD pathophysiology that extends beyond, and is independent of, vaso-occlusion. In the case where adhesive events become important, the phenomena revealed here would still be of prime importance, as the strong sickle cell margination demonstrated here brings the cells into the vicinity of the walls, which is of course a prerequisite for adhesion to them.

IV. CONSLUSION

In this study, we investigated different flowing suspensions of deformable capsules subjected to pressure-driven flow in a planar slit using boundary integral simulations, assuming that the flow is in the Stokes regime. The focus of this study is a binary suspension of healthy RBCs and sickle cells, which describes the microvascular blood flow in sickle cell disease. The parameter regime is based on the range of experimentally determined values for RBCs and blood flow in the microcirculation.

We first characterized the cross-stream distributions and orientational dynamics of different types of capsules in each suspension (Section III A), and revealed a number of key features.

(i) In a homogeneous suspension of healthy (flexible) RBCs, a cell-free layer is formed next to the channel walls. The spontaneous shape of RBCs plays a nontrivial role in the orientational dynamics of single cells in the suspension, but has a negligible effect on the number density distribution. In a binary suspension of flexible and stiff RBCs with the same rest shape but large contrast in membrane rigidity, the dilute stiff RBCs are largely drained from the center of the channel and display substantial margination toward the walls. This suggests that rigidity contrast by itself is sufficient to induce the segregation behavior in a binary suspension. The marginated stiff RBCs assume an approximate in-plane tumbling orbit.

(ii) In a binary suspension of healthy RBCs and sickle cells, the dilute stiff sickle cells are almost completely drained from the bulk of the suspension, and strongly aggregate inside the cell-free layer. The marginated sickle cells tend to roll in flow with the major axis aligned with the vorticity (z) direction. Curvature plays a minor role in the segregation behavior and orientational motion of the stiff capsules.

Furthermore, we quantified the physical effect of each suspension on the walls (Section III B). In particular, the additional wall shear stress induced by the capsules was computed for each suspension. We found that, compared to the small fluctuations in wall shear stress for the case with purely healthy RBCs, large local peaks in wall shear stress are induced by all binary suspensions, a hydrodynamic effect of the marginated cells on the walls. Detailed quantification showed that the shape and size of the stiff component have a secondary role, even though for the parameter space considered in this study, straight prolate capsules seem to have a greater overall effect on the wall shear stress than do stiff RBCs and sickle cells.

Overall, all these results represent an effort to gain an improved understanding of the behavior of flowing suspensions of cells or capsules in complex scenarios, particularly the blood flow in SCD which is the focus of the current study. More importantly, this work is of essential interest from the medical point of view in that the results may help explain the mechanism for complications associated with SCD, such as endothelial inflammation, that are still poorly understood. In particular, this work addresses how circulating stiffened and misshapen RBC subpopulations may directly contribute to vasculopathy in SCD, not via vaso-occlusion or cell adhesion as canonically depicted, but via biophysical effects due to the margination of diseased cells.

One limitation of this work is that the properties of cells of each type were identical and unchanging – physiologically, sickle cells vary considerably in cell morphology and membrane stiff ness, which should be addressed in future studies. Other parameters of the suspensions, such as the total volume fraction and the number fraction of each component in a binary system, can also be altered in extended studies to investigate the effects of these parameters on the suspension dynamics. Furthermore, it has been observed in experiments [113] that the flow of a suspension of sickle cells around an acute corner of a triangular pillar or a bifurcation leads to an enhanced deposition and aggregation of cells. Therefore, complex geometries of the flow domain other than a planar slit should be considered in future simulations. Finally, future experimental studies are needed to elucidate to what extent the cross-stream distribution of RBCs in SCD would be adversely altered in the microcirculation, and if so, how this process may contribute to SCD vasculopathy. Such work could directly lead to a new paradigm of biophysical therapeutic strategies by mitigating the potential margination of aberrant sickle RBCs in SCD.