Distributed Fiber Optic Measurements of Strain and Temperature in Long-Span Composite Floor Beams with Simple Shear Connections Subject to Compartment Fires

Abstract

This study explores an instrumentation strategy using distributed fiber optic sensors to measure strain and temperature through the concrete volume in large-scale structures. Single-mode optical fibers were deployed in three 12.8 m long steel and concrete composite floor specimens tested under mechanical or combined mechanical and fire loading. The concrete slab in each specimen was instrumented with five strain and temperature fiber optic sensors along the centerline of the slab to determine the variation of the measurands through the depth of the concrete. Two additional fiber optic temperature sensors were arranged in a zigzag pattern at mid-depth in the concrete to map the horizontal spatial temperature distribution across each slab. Pulse pre-pump Brillouin optical time domain analysis (PPP-BOTDA) was used to determine strains and temperatures at thousands of locations at time intervals of a few minutes. Comparisons with co-located strain gauges and theoretical calculations indicate good agreement in overall spatial distribution along the length of the beam tested at ambient temperature, while the fiber optic sensors additionally capture strain fluctuations associated with local geometric variations in the specimen. Strain measurements with the distributed fiber optic sensors at elevated temperatures were unsuccessful. Comparisons with co-located thermocouples show that while the increased spatial resolution provides new insights about temperature phenomena, challenges for local temperature measurements were encountered during this first attempt at application to large-scale specimens.

1. Introduction

Structural response to fires has been widely studied using physical experiments and numerical models [1,2]. Measured or calculated temperature distributions are often used to evaluate structural response using coupled thermal-mechanical analysis [3-5]. However, it remains cumbersome to measure temperature distributions with high spatial resolution in structural materials such as concrete under fire conditions [6]. Historically, discrete (point) temperatures have been measured using thermocouples; however, dozens, or even hundreds, of thermocouples must be placed in the concrete formwork prior to casting to get even a coarse indication of the horizontal and through-depth temperature variation in concrete during heating for large structures. This is cost and time intensive. Although infrared cameras provide valuable information about temperature distribution over large areas, they are not suited for measurements of temperature variation through the depth of a material and can be susceptible to error caused by changes in surface conditions as well as the presence of flames in the field of view of the camera [7].

Fiber optic sensors for measuring temperature have seen increased use in structural fire research due to their ability to survive harsh environmental conditions [8]. For example, fiber Bragg grating (FBG) sensors [9] have been used to measure strain and temperature up to approximately 300 °C, the temperature at which traditional gratings are annealed (erased). Huang et al. [10,11] used long-period fiber grating (LPFG) sensors to measure strain and temperature up to 700 °C. To extend the temperature range further, regenerated FBG (rFBG) sensors were used by Rinaudo et al. [12] to record strain and temperature up to 970 °C. Although grating-based sensors can measure high strain and temperature, they provide measurements only at a single location; i.e. the location of the gratings. More recently, measurements that are distributed along the length of an optical fiber, without the need for a grating, have become feasible due to developments such as Brillouin optical time domain analysis (BOTDA) and Brillouin optical time domain reflectometry (BOTDR). For example, pulse pre-pump BOTDA (PPP-BOTDA) has been developed with spatial resolution of 2 cm over 500 m of fiber length. Using this emerging technology in structural condition monitoring to measure strain distributions and detect cracks at ambient temperature has been explored [13,14]. PPP-BOTDA technology used for temperature and strain measurement under fire conditions is still limited. Bao et al. [15,16] studied and calibrated temperature-dependent strain and temperature sensitivities of PPP-BOTDA sensors and went on to use the sensors for strain and temperature measurements in simply-supported steel beams under fire conditions [17]. Additionally, Bao et al. [18] studied temperature measurement and damage detection in concrete beams exposed to fire using PPP-BOTDA sensors and the conducted experiments on the deployment of the technique in small (1.2 m × 0.9 m) steel-concrete composite slabs [19]. Their results showed that one single-mode optical fiber can achieve temperature measurements with accuracy better than 12 %, compared to the readings of thermocouples at the same locations.

In this study, distributed fiber optic sensors (DFOS) were deployed for the first time in full-scale steel-concrete composite floor slabs tested under mechanical loading or combined mechanical and fire loading. Under mechanical loading at ambient temperature, the mid-span strains measured in the concrete slab using PPP-BOTDA were compared with those linearly interpolated or extrapolated from two strain gauges installed in the same cross section. Under combined mechanical loading and fire conditions, the temperatures measured in the concrete slabs using PPP-BOTDA were compared with values linearly interpolated or extrapolated from nearby thermocouples. Due to undocumented uncertainties in temperature measurement that is required to compensate the discrimination of strain measurements, strain data under the combined mechanical and fire conditions are not reported in this paper.

2. Distributed Fiber Optic Sensor

2.1. Working principles of PPP-BOTDA

PPP-BOTDA measures temperature and strain changes by relating them to the change in the refractive index of an optical fiber and the speed of acoustic wave traveling along the optical fiber. Their relations are associated with the electrostrictive effect of the fiber that tends to compress materials in the presence of an electrical field. Through electrostriction, the density and thus refractive index of the optical fiber are modulated when a pump pulse wave and a counter-propagating continuous probe (Stokes) wave propagate from two ends of the optical fiber and encounter at various points of the optical fiber. As a result of the light interaction with the molecular structure of the fiber, an energy exchange with acoustic phonons occurs to form a back-propagating acoustic wave or a ‘traveling grating’ in analogy with FBG sensors. At a speed of sound in the fiber material, the acoustic wave energizes the reflected light power of the pump wave. The reflected pump wave is downshifted by the frequency difference between the pump wave and the probe wave due to the Doppler effect, and thus, adds power to the Stokes wave to be detectable. In this case, the acoustic wave is referred to as stimulated Brillouin scattering [20]. The Brillouin gain can be determined as a function of position by the time-varying probe wave. As a result, the location of Brillouin frequency shift can be determined.

The Brillouin scattering behavior is influenced by the material properties of the fiber, which are in turn affected by the applied temperature and strain on the fiber creating a sensor. Compared with the traditional BOTDA, PPP-BOTDA greatly improves the spatial resolution with a pre-pump pulse by stimulating the phonon before a narrow bandwidth pulse arrives. For silica-based single-mode optical fibers, the Brillouin frequency v_B typically varies from 9 GHz to 13 GHz for light wavelengths of 1.3 μm to 1.6 μm and can be calculated by Equation (1):

$$v_B=\frac{2v_0}{C}n{V}_a$$ (1)

where v₀ denotes the frequency of an incipient light wave, n represents the refractive index of the optic fiber, V_a represents the speed of an acoustic wave in the fiber, and C represents the speed of light in a vacuum, which is equal to 3.0 × 10⁸ m/s. The speed of the acoustic wave V_a in the optical fiber is given by [17]:

$$V_a=\sqrt{\frac{(1-\mu )E}{(1+\mu )(1-2\mu )\rho }}$$ (2)

where μ, π, and E represent the Poisson’s ratio, density and Young’s modulus of the optic fiber, respectively.

The density and refractive index are affected by both strain (ε) and temperature (T), while the Young’s modulus and Poisson’s ratio are affected by temperature only. Therefore, strain and temperature changes in the optical fiber cause a shift in the Brillouin frequency. For a change in strain and temperature from reference values obtained during calibration, the Brillouin frequency shift (Δv_B) can be expressed as:

$$\Delta v_B=C_{\epsilon }\Delta \epsilon +C_T\Delta T$$ (3)

where C_ε and C_T represent the strain and temperature sensitivity coefficients, respectively.

2.2. Fiber optic sensor calibration

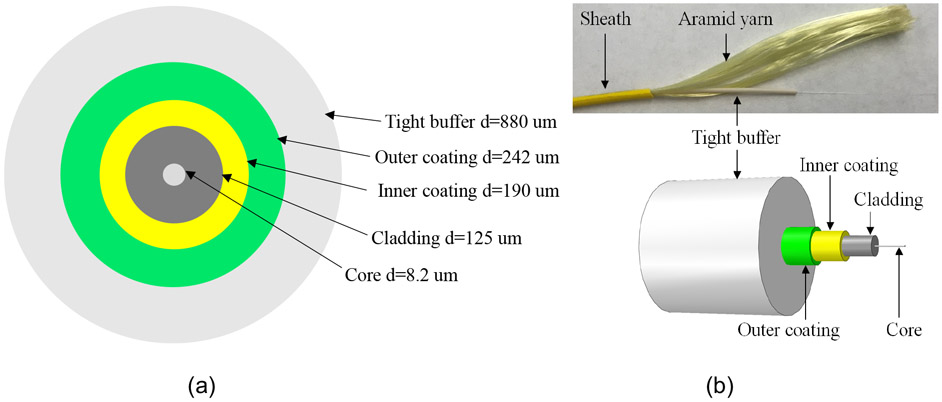
Telecommunication-grade, single-mode optical fiber cable was used as a distributed temperature sensor. The temperature sensor (Figure 1) has a polymer outer sheath (diameter: 3 mm), a layer of aramid yarn, a tight polymer buffer (diameter: 880 μm), a polymer outer coating (outer diameter: 242 μm), a polymer inner coating (outer diameter: 190 μm), a silica glass cladding (outer diameter: 125 μm), and a silica glass core (diameter: 8.2 μm). The polymer of the inner and outer coatings as well as the tight buffer is composed of mixtures of monomers, oligomers, photoinitiators, and additives. The outer sheath protects the temperature sensor from abrasion. The polymer buffer and coatings protected the glass from mechanical impact and from undesired environmental exposure. The aramid yarn significantly reduces the transfer of axial strain from the outer sheath to the measurement fiber at a room temperature (approximately 22 °C) based on the tests of 1.2 m × 0.9 m steel-concrete composite slabs [19]. However, the efficacy of the yarn to eliminate axial strain over long distances (> 4 m with multiple 180° turns) at elevated temperature (> 22 °C) and embedded in concrete where the fiber path is torturous, was not verified. The cost of the sensor cable was approximately $0.40 USD per m. A similar optical fiber without the outer sheath and aramid yarn was used as a distributed strain sensor; i.e., the concrete was in direct contact with the polymer buffer allowing transfer of mechanical strain from the concrete to the optical fiber core. It is assumed that sheathing, buffer and coatings have a glass transition temperature of less than 180 °C. The silica glass core and cladding can sustain temperatures above 1000 °C.

Figure 1.

Single-mode optical fiber used as temperature sensors: (a) overall composition excluding the aramid yarn and sheath and (b) photo of cross section with annotation (not to scale)

For an optical fiber that is free of strain change, the Brillouin frequency shift is dependent on temperature change only. However, this relationship is nonlinear when a large change in temperature occurs. Based on the results in [15], [16], [18], and [21], a relationship between the temperature sensitivity coefficient and temperature for the investigated fiber optic temperature sensors is given in Equation (4). It is noted that any transient reduction of temperature when the sensor coatings melt is neglected. When both strain and temperature change, an additional fiber that is (approximately) free of strain can be incorporated for temperature compensation. Equation (3) can then be rearranged to find the change in strain after the strain sensitivity coefficient C_ε has been determined empirically with temperature up to 800 °C as shown in Equation (5). This is the strain sensitivity of bare optical fiber sensors, which should not be applied for strain sensing at elevated temperature unless the behavior of strain transfer between the fiber and its surrounding base material (concrete) is well understood and taken into account. The temperature unit in equations (4) and (5) is °C.

$$C_T=-6.928\times {10}^{-7}T+1.110\times {10}^{-3}$$ (4)

$$C_{\epsilon }=-1.228\times {10}^{-5}T+4.97\times {10}^{-2}$$ (5)

3. Experimental program

3.1. Test specimens

Three 12.8 m long composite floor beams that were part of a larger study of the performance of composite construction in fire [22] were instrumented with distributed fiber optic sensors. These unique large-scale composite specimen experiments were leveraged to explore the advantages and disadvantages of distributed fiber optic sensing technology compared to conventional sensors. The specimens were designed with double angle end (shear) connections in accordance with current codes and standards [23, 24] in the United States. The first beam with no slab end continuity as a baseline to the other beams, designated as CB-DA-AMB, was tested to failure under mechanical loading at ambient temperature to understand its ultimate strength. Identical to the first beam, the second specimen, designated as CB-DA, was tested to failure under combined mechanical loading and fire. The third beam with slab end continuity, designated as CB-DA-SC, was tested to failure under combined mechanical loading and fire. Design details for the specimens are presented in [25, 26]. The magnitude of mechanical loading applied on the second and third beams corresponded to 45 % of the ultimate moment capacity of the first beam [27]. The fire was generated using natural gas burners with a maximum total heat release rate of 4 MW.

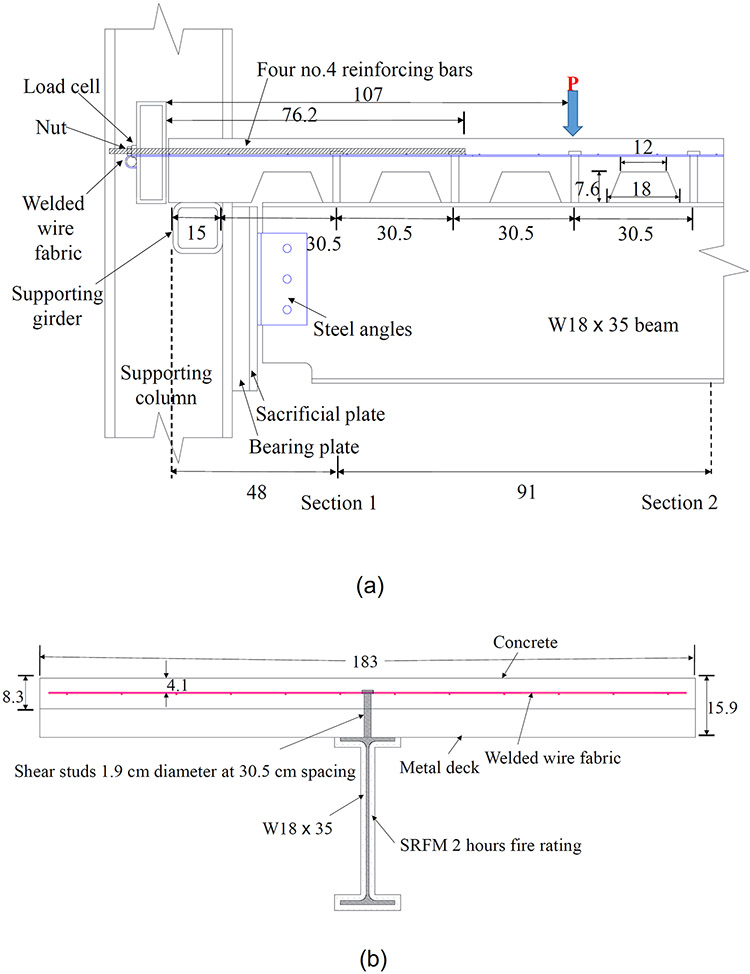
Figures 2(a) and (b) give the end connection with double angles and slab continuity (using four no. 4 reinforcing bars), and the cross section of the CB-DA-SC specimen, respectively. A 1.83 m wide by 12.8 m long lightweight aggregate concrete slab with polypropylene microfibers was cast on 20-gauge profiled metal decking above a W18×35 steel beam. Headed studs (19 mm shaft diameter) were welded to the steel beam with a spacing of 305 mm. The degree of composite action between the concrete and the beam achieved by the studs was approximately equal to 82 % of the ambient yield strength of the steel cross section (W18×35). Welded wire fabric (6×6 W1.4×W1.4) was embedded at 42 mm below the top surface of the concrete to satisfy minimum shrinkage and temperature cracking control requirements in Steel Deck Institute Standard C-2011 [28]. The bottom flange of the steel beam was coped at both ends (Figure 2(a)) to accommodate the double angles during construction. For CB-DA-SC, four additional no. 4 steel reinforcing bars were embedded in the negative bending moment region near the end supports and anchored to a hollow steel section to simulate the slab continuity. The steel beam was coated with sprayed fire resistive materials (SFRM) to achieve a 2-hour fire resistance rating along the member and a 3-hour fire rating at the connections.

Figure 2.

Scale drawings of (a) the specimen-to-column connection and (b) the transverse cross-section of specimens (Units: cm)

3.2. Material properties

A full description of the specimen material properties is available in [22]. Select properties relevant to the distributed fiber optic sensors are provided here. All material properties were determined in accordance with the relevant ASTM standards [29-37]. Polypropylene microfiber reinforced lightweight aggregate concrete with a water-to-binder ratio of 0.46 was used for the test specimens. The sand used was a natural product comprised of silica grains. High-range water reducer was added to achieve a design slump of 216 mm and limit the required mechanical vibration of the concrete. This was intended to prevent breakage of the distributed optical fiber sensors during casting. The polypropylene microfibers (25 mm long and 40 μm in diameter at a dosage of 2.37 kg/m³) were used to reduce the likelihood of spalling of the concrete under fire conditions [38]. The mean 28-day concrete cylinder compressive strength was 45.4 MPa. After curing for 6 months, internal relative humidity in the concrete dropped to about 80 %. The fire experiments were conducted about 12 months after the concrete placement. For the W18×35 beams, the measured yield and ultimate tensile strengths were 360 MPa and 470 MPa, respectively. The modulus of elasticity of the steel beams was 203 GPa. The measured ultimate strength for bolts, shear studs, and welded wire fabrics was 960 MPa, 510 MPa, and 760 MPa, respectively.

3.3. Test setup and instrumentation

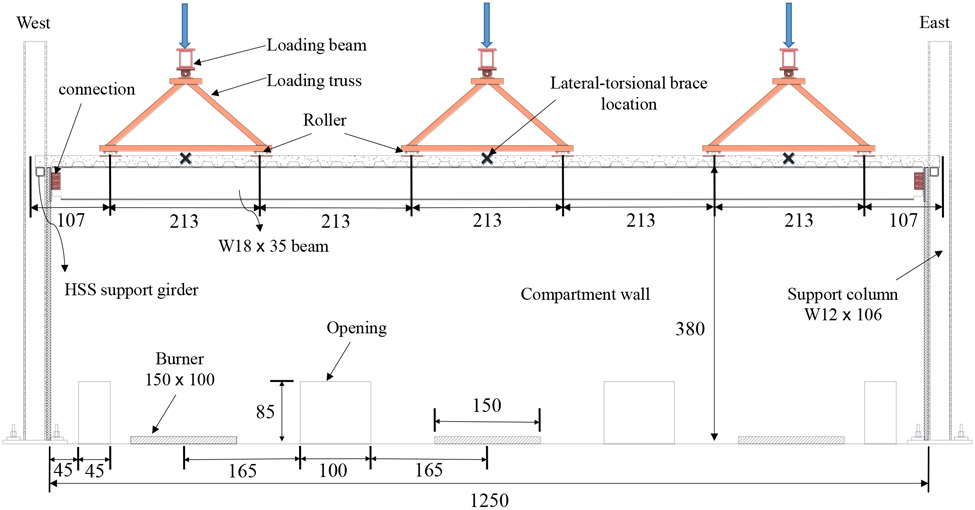
The test setup is shown in Figure 3. The test specimen, for which the soffit of the slab was elevated 3.8 m above the laboratory floor, was attached to longitudinally braced W12x106 steel columns at the west and east ends. Six equally distributed point loads were applied to the specimen along its centerline using three pairs of servo-hydraulically controlled actuators attached to the ends of loading beams coupled with triangular loading trusses. To confine the fire below the specimen, enclosure walls were constructed below the specimen using cold-formed steel framing and sheet steel. The fire-exposed wall surfaces were protected with two layers of 25 mm thick ceramic fiber blankets. Three natural gas diffusion burners with servo-controlled gas mass flow were arranged along the center of the compartment floor and were used to heat the specimen. This setup replicated a 1.83 m wide strip of a building around the beam-column centerline for which a realistic fire and design gravity load could be simultaneously applied at full-scale.

Figure 3.

Scale drawing of longitudinal section of the experimental setup (Units: cm)

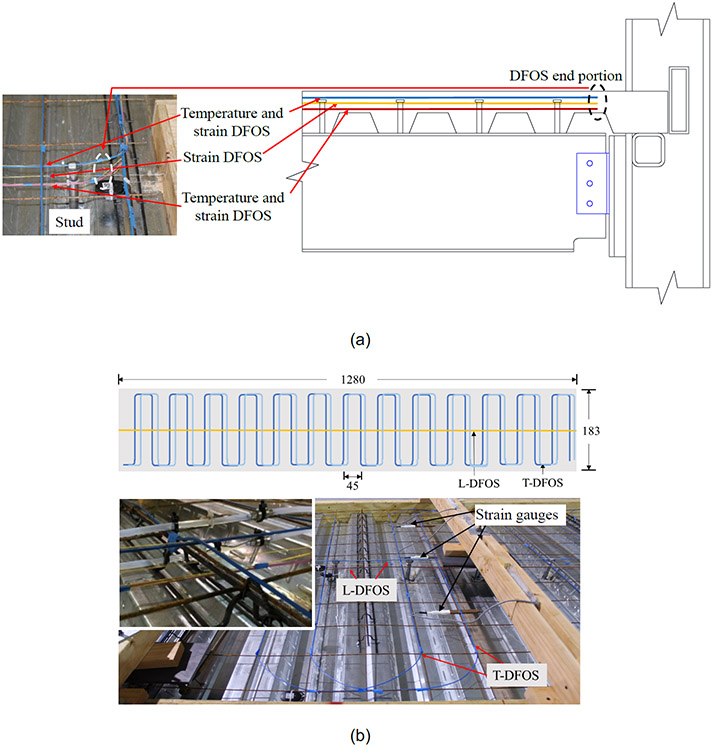
Three strain distributed fiber optic sensors (L-DFOS) were placed longitudinally along the centerline of the beam at approximately 32 mm, 51 mm, and 70 mm below the top surface of the concrete as shown in Figure 4(a). Two temperature fiber optic cables were co-located with the top and bottom strain sensors. The longitudinal sensors were taped to thin wires spanned from end-to-end in the slab so that they could maintain their position during casting of the concrete. As shown in the excerpt of Figure 4(a), all five L-DFOS were collected and turned by 90° to an exit point for data acquisition during tests. Additionally, two transverse distributed fiber optic sensors (T-DFOS) were deployed in a zig-zag pattern on the weld wire fabric (reinforcement) to measure the temperature distribution in the concrete slab approximately 41 mm from its top surface (Figure 4(b)). Since the top L-DFOS was placed prior to the installation of the T-DFOS, the transverse fibers were raised for about 10 mm in elevation near the centerline of the specimen as detailed in the insert of Figure 4(b). Several of the sensors were spliced together in series outside of the concrete so their data could be acquired simultaneously on a single analyzer. The strain and temperature distributed fiber optic sensors have a 95 % confidence interval of ± 1.63 % and ± 3.66 %, respectively, based on the coefficient of variation of nine adjacent measurement points.

Figure 4.

Specimen instrumentation: (a) longitudinal distributed fiber optic sensors (L-DFOS) for temperature and strain and (b) transverse distributed fiber optic sensors (T-DFOS) and strain gauges (Units: cm)

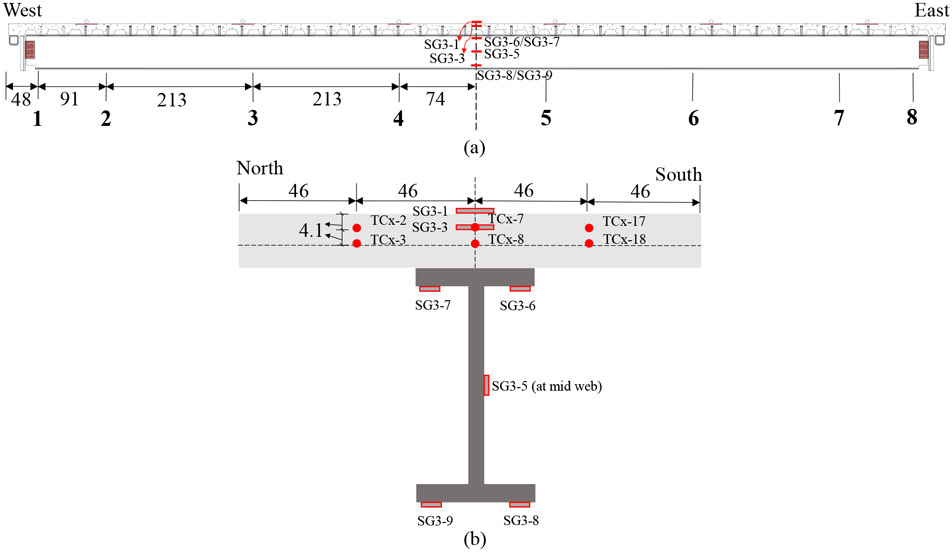
To validate the spatially-distributed temperature measurements from the distributed fiber optic sensors, six glass-sheathed 24-gauge Type K thermocouples (TC) were deployed on the welded wire fabric and top of the metal decking at each of the eight sections (x = 1 through 8) as shown in Figure 5. At each section, two thermocouples (TCx-7 and TCx-8) were installed right above the steel beam in centerline, two (TCx-2 and TCx-3) were located at 46 cm north of the beam centerline and two (TCx-17 and TCx-18) at 46 cm south of the beam centerline. At mid-span section of the CB-DA-AMB specimen, two strain gauges were deployed in the concrete slab: one on the top surface and the other at 4.1 cm below in the concrete. Additional strain gauges were installed at the top and bottom flanges as well as the mid-height web of the steel beam.

Figure 5.

Locations and labels of Type K thermocouples (TC) mounted on each specimen: (a) cross section numbers (x=1 through 8) and (b) TC designations at each cross section and strain gauges (SG) at mid-span cross section (Units: cm)

The location where each optical fiber run entered and exited the concrete as detected by the PPP-BOTDA analyzer was determined immediately prior the fire testing. This was done by placing an ice cube on points of interest on the fiber which provided a measurable localized temperature decrease. The position of the fibers inside the concrete had been mapped prior to concrete casting.

3.4. Test protocols

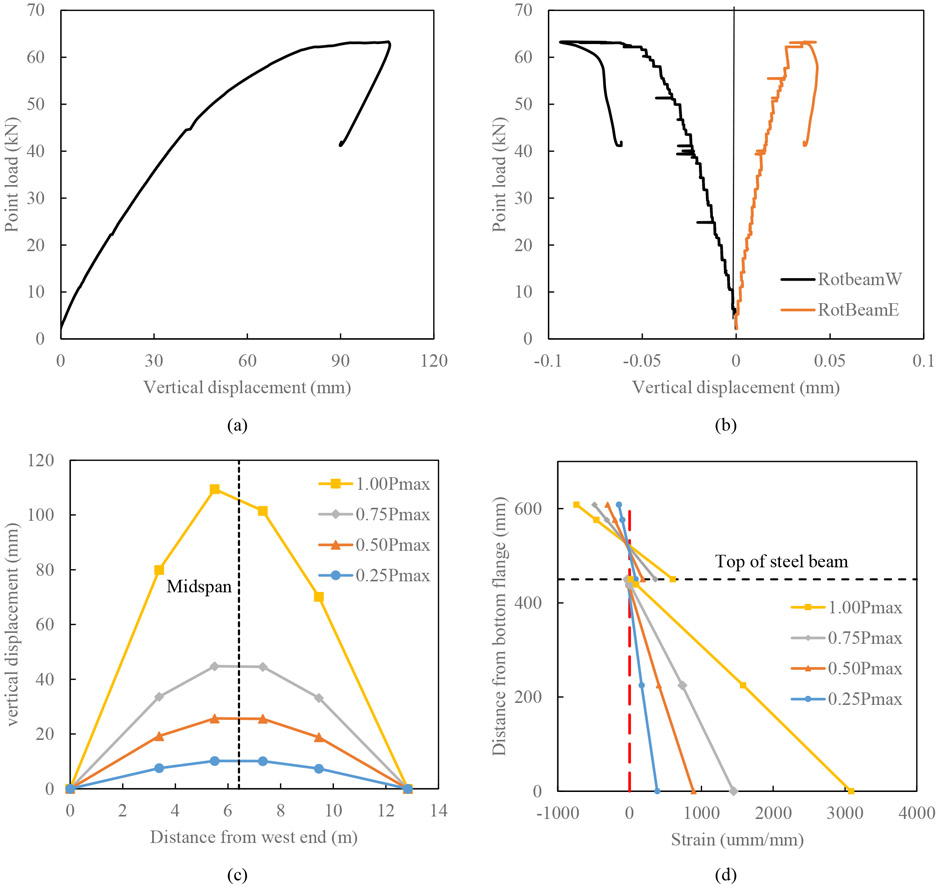
To establish the baseline specimen behavior and understand the performance of strain DFOS at ambient temperature, the CB-DA-AMB specimen with no slab continuity was tested to failure under six point-loads as positioned in Figure 3. Figure 6 presents the load-deflection curve at midspan, beam rotations at two ends, deflection curves, and strain distribution in mid-span cross section during the first cycle of point loading up to P_max equal to 63 kN (maximum load). It can be seen from Figure 6 that both the end rotations and the deflection curves indicated more severe displacement on the west end of the specimen even under six well-controlled point loads symmetric about the mid-span. Based on two measurements in the concrete slab and two measurements in the steel beam, the strain distribution in the cross section at mid-span shows discontinuity at the slab-beam interface, which is indicative of partial slip particularly at a load of 0.75P_max or higher. At 0.25P_max, the strain discontinuity or slip at the interface is negligible. The neutral axis of the concrete cross section under various load levels ranged from 125 mm to 155 mm from the top surface of the concrete slab and near the top flange of the steel beam at mid-span.

Figure 6.

Test results of CB-DA-AMB specimen: (a) point load versus mid-span deflection, (b) beam rotation at two ends, (c) deflection curves, and (d) strain distribution in mid-span cross section during the first cycle of loading up to P_max

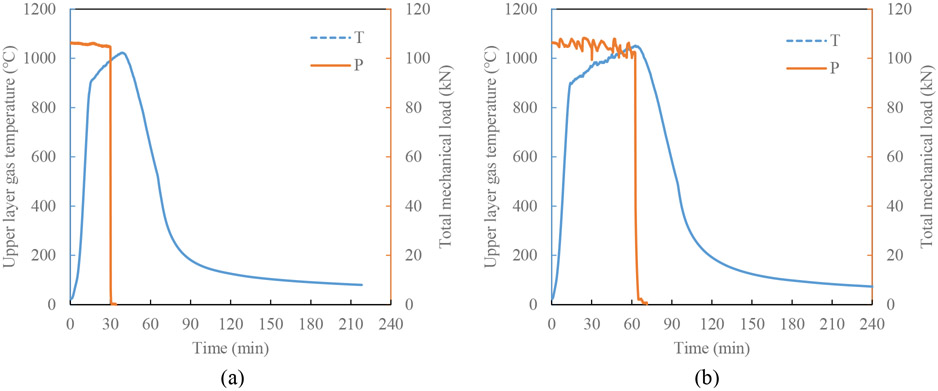
The experimental protocol used for CB-DA and CB-DA-SC specimens was as follows: (1) a total mechanical load of 106 kN (17.7 kN/point load or 45 % of the ultimate moment) was applied and held constant at ambient temperature, (2) the heat release rate in the compartment under the beam was increased to 4 MW over a period of 15 min and held constant, and (3) a cooling phase was initiated by linearly decreasing the heat release rate over 30 min. The applied total mechanical loading and compartment upper layer gas temperature histories for the specimens instrumented with distributed fiber optic sensors are shown in Figure 7. Note that the applied point load (17.7 kN) is slightly higher than 0.25P_max = 15.75 kN in Figure 6.

Figure 7.

Gas temperature (T) measured 81 cm below concrete slab and total applied mechanical load (P) for (a) CB-DA specimen and (b) CB-DA-SC specimen

4. Results and discussion

4.1. Strain distribution from longitudinal DFOS at ambient temperature

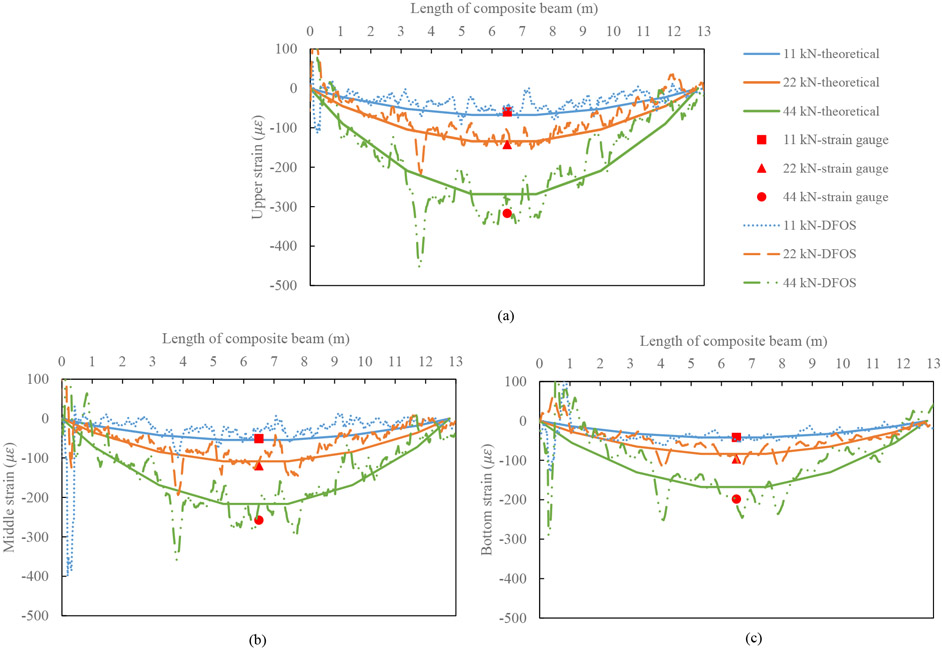
Typical fiber optic strain measurements along the centerline of specimen CB-DA-AMB at ambient temperature under applied mechanical loads of 11 kN, 22 kN, and 44 kN are presented in Figure 8. To account for potential misalignment of the position of fibers, a moving average of nine points was applied to increase the effective sensor gauge length to 10 cm, which was deemed to be appropriate for the investigated trapezoidal decking dimensions. Idealized strain predictions based on simple elastic analysis with the neutral axis located at 135 mm from the top surface of the thin concrete slab and ignoring slip within the cross section are also shown in Figure 8 at the corresponding depths. Because six point-loads were applied on the simply supported beam, the elastic strain distribution follows a piecewise linear line that resembles a parabolic curve. The theoretical predictions and the measured strain distributions from the DFOS agree reasonably well in terms of overall shape. Figure 8 also shows measurements from the resistance-based strain gauges at mid-span (with required linear interpolations or extrapolations), which closely resemble the DFOS strains at these locations. The advantage of the DFOS measurements are that they provide information about the continuous strain distribution along the length of the specimen whereas the conventional strain gauges provide information only at single points. The causes of the local variations in the DFOS strain in this large test specimen may be ascribed to local strain concentrations around the headed studs, spatial variations of the slab depth in conformance with the metal decking, concrete material heterogeneity, or local variation in the optical fiber path. The authors believe however that many of the variations are associated with the periodic change of the headed studs and slab depth as evidenced by the fact that peaks appear at the same locations in all three fibers with varying amplitude. Note that the longitudinal DFOS readings at the ends of the specimen (before Section 1 and after Section 8 as indicated in Figure 5(a)) are misrepresentative because the longitudinal sensors at different elevations were bundled together during a 90° turn as shown in the insert of Figure 4(a) and thus not considered in the following analysis both for strain and temperature measurements.

Figure 8.

Strain distributions measured from the DFOS system in CB-DA-AMB at ambient temperature along with theoretical predictions and interpolation/extrapolation from strain gauge measurements: (a) upper, (b) middle, and (c) lower

4.2. Temperature distribution from longitudinal DFOS in fire conditions

Figure 9 compares concrete temperatures measured at different times from the longitudinal DFOS and thermocouples deployed along the centerline of the CB-DA specimen that was tested under simultaneous mechanical and fire loads. The fiber optic temperature sensors were located 32 mm (Top) and 70 mm (Bottom) below the top surface of the concrete slab. Their closest thermocouples were positioned at 41 mm and 82 mm from the top surface of the slab. Therefore, the thermocouple temperatures were linearly interpolated or extrapolated to obtain the temperatures at the locations of the fiber optic sensors for comparison.

Figure 9.

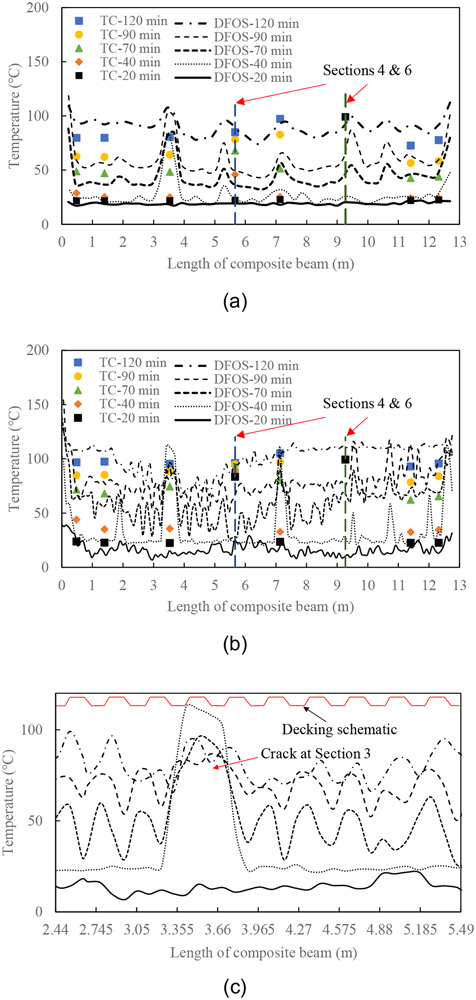
Concrete slab temperatures measured from thermocouple (TC) and distributed fiber optic sensors (DFOS) in CB-DA specimen at various times after fire ignition: (a) 32 mm and (b) 70 mm below the top surface of the slab, and (c) 70 mm below the top surface of the slab (between 2.44 m and 5.49 m) in (b)

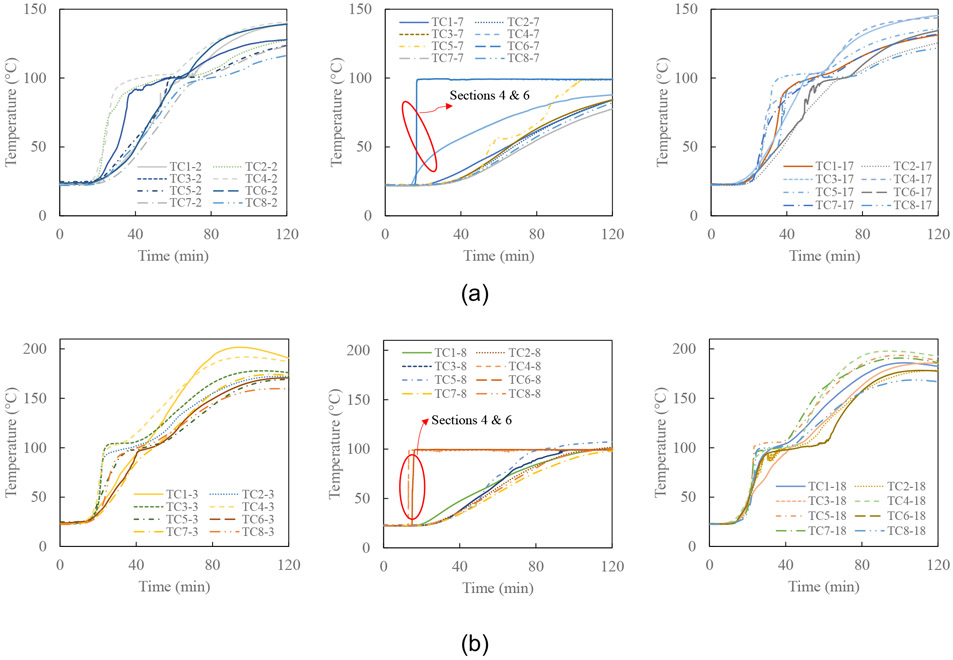
The thermocouple temperatures in Figure 9(a, b) at a given time follow a roughly horizontal line along the length of the specimen; except at Section 4 (Bottom) and Section 6 (Top and Bottom) where temperatures jump suddenly to 100 °C by 20 min into the test. This is more clearly illustrated by Figure 10, which shows the complete thermocouple temperature-time histories; refer to Figure 5 for thermocouple locations. As moisture is driven out of the concrete during heating (desiccation), it will maintain a temperature of 100 °C as the water is vaporized. This results in a plateau in the time versus temperature curve until the water is driven off. A temperature plateau at 100 °C is also visible in many thermocouples to the north and south of the centerline, however, the rise to 100 °C is gradual. Thus while amplitude of 100 °C at Sections 4 and 6 is likely caused by water vaporization, the rise time is clearly erroneous – possibly caused by multi unintended junctions in the lead wires – and these data are disregarded in the subsequent analysis. It is also noted from Figure 10 that along the centerline of the beam specimen, the heating of the concrete is slower than to the north and south due to the thermal shadowing from the beam underneath.

Figure 10.

Concrete slab temperatures versus time measured from thermocouples (TC) in CB-DA specimen along the centerline (TCx-7 and TCx-8) and 46 cm to the north (TCx-2 and TCx-3) and south (TCx-17 and TCx-18) of the centerline at Sections 1 to 8: (a) 41 mm and (b) 82 mm below the top surface

The DFOS also exhibits an overall horizontal temperature distribution along the specimen, particularly the top temperature sensor; however, the curves show prominent local temperature peaks. The large, non-periodic singular peaks in the DFOS temperature are likely associated with the formation of cracks in the concrete. There are also smaller amplitude periodic variations visible in the DFOS readings. Due to the trapezoidal shape of the metal decking, the concrete cover to the bottom optical fiber from the fire varies from 13 cm to 89 cm over a length of 30.5 cm (refer to Figure 2(a)). This results in periodic local temperature fluctuation along the length of the composite beam as can be seen most clearly in the data extracted from Figure 9(b) between 2.44 m and 5.49 m shown in Figure 9(c). The local maxima represent the locations of the thinner concrete cover (13 cm) to the heated surface of the slab; however, this behavior is complicated by the presence of the cracks in the concrete which cause prominent singular temperature variations. This amplitude fluctuation at 30.5 cm spacing is most pronounced at 70 min, i.e., during the controlled cooling phase of a fire, and then gradually disappears.

The minimum, average, and maximum section-by-section differences in the temperature readings between the DFOS and thermocouples are compared in Table 1 at the locations of thermocouples. Any difference below 20% in Table 1 are highlighted in bold face. The temperature difference at a single location ranges from zero to 232 % with an average value less than 26 % for specimen CB-DA except at the peak of gas temperature right after mechanical unloading. The reasons for the large maximum differences may include variation in the position of the measurement locations in the concrete (up to several cm), heat transfer (or cooling) along the fiber and sheathing, required acquisition time (e.g., 2 min) to sweep the range of Brillouin frequency, and the inherent uncertainty of the two measurement techniques.

Table 1.

Longitudinal distributed fiber optic sensor (DFOS) and thermocouple (TC) temperature readings and their relative difference (Rel. Diff.)

Specimen	CB-DA				CB-DA-SC
Location	Top		Bottom		Top		Bottom
Parameter	DFOS/TC (°C)	Rel. Diff.	DFOS/TC (°C)	Rel. Diff.	DFOS/TC (°C)	Rel. Diff.	DFOS/TC (°C)	Rel. Diff.
20 min after the ignition of fire
Average		8%		10%		17%		15%
Maximum	21/23	9%	27/24	13%	33/64	48%	35/72	51%
Minimum	21/22	5%	23/22	5%	23/23	0%	24/24	0%
40 min after the ignition of fire
Average		51%		87%		11%		57%
Maximum	83/25	232%	111/36	208%	32/26	23%	82/34	141%
Minimum	26/24	8%	30/35	14%	26/27	4%	42/41	2%
70 min after the ignition of fire
Average		22%		15%		36%		31%
Maximum	81/48	68%	95/75	27%	81/46	76%	119/74	60%
Minimum	44/44	0%	70/65	8%	73/83	12%	77/87	11%
90 min after the ignition of fire
Average		18%		13%		35%		40%
Maximum	102/64	59%	102/79	29%	153/89	72%	206/97	112%
Minimum	62/63	2%	103/97	6%	79/73	9%	109/101	8%
120 min after the ignition of fire
Average		26%		10%		39%		59%
Maximum	107/75	43%	112/96	17%	224/98	129%	258/112	130%
Minimum	93/95	2%	94/96	2%	94/92	2%	144/118	22%

Note: The Rel. Diff. value was calculated as ∣DFOS-TC∣ / TC x 100%. The minimum, average, and maximum values were determined from six TC readings for CB-DA (Sections 4 & 6 excluded) and six TC readings for CB-DA-SC (Sections 1 & 8 excluded) at the height of the DFOS. The maximum value represents the largest error among all individual sections in each specimen. Its corresponding temperatures are given.

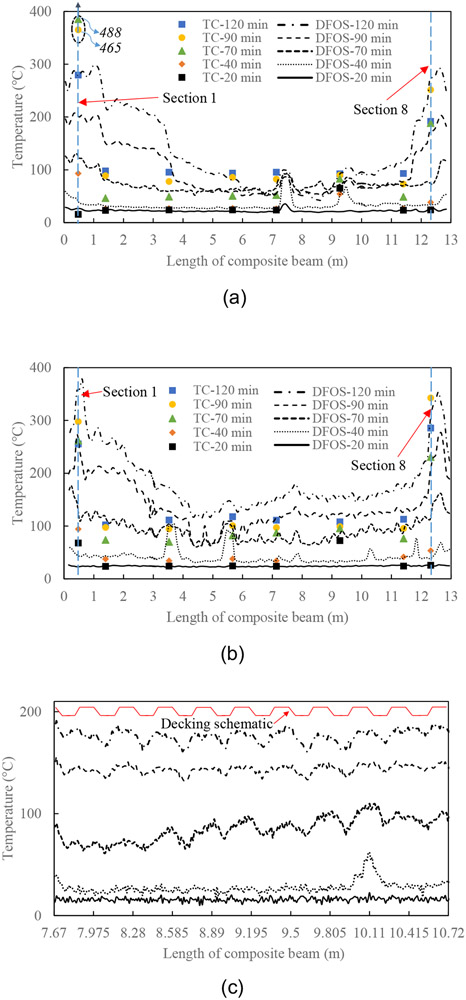
Figure 11 shows the test data for the CB-DA-SC specimen. Like the CB-DA specimen, the unique information provided by the DFOS that is not apparent in the thermocouple data is the local spatial variation of temperature. A prominent example of this can be seen between Section 3 and Section 6. There are indications of significant cracks formed at the bottom of concrete slab near Sections 3 and 4, and at the top of the slab near Sections 5 and 6. Once the concrete has been fully desiccated at the sensor location after 70 min of burning, the local temperature variation at the cracks becomes less prominent as shown for the lower fiber in Figure 11(b). Note that minor cracks likely occur between Section 5 and 8 closing to the lower fiber. As with specimen CB-DA, low-amplitude periodic temperature variations are visible along the optical fiber between 7.67 m and 10.72 m resulting from the varying concrete cover thickness to the heat source (Figure 11(c)).

Figure 11.

Concrete slab temperatures measured from TC and DFOS in CB-DA-SC specimen at various times after fire ignition: (a) 32 mm, (b) 70 mm below the top surface, and (c) 70 mm below the top surface of the slab (between 7.67 m and 10.72 m) in (b)

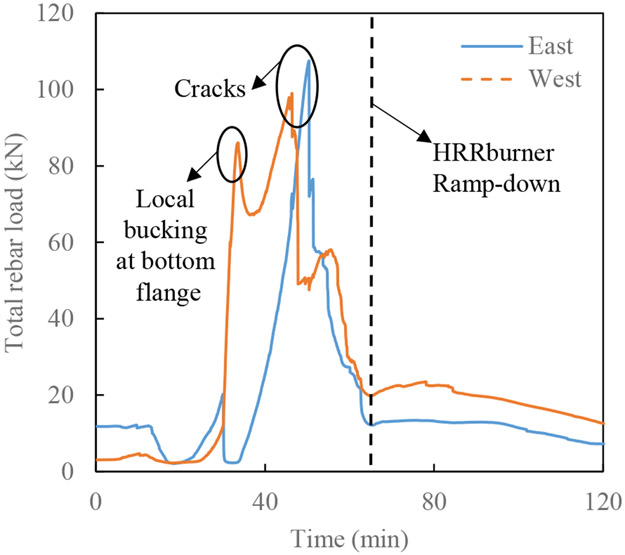
Unlike the CB-DA specimen, both the thermocouple data and the DFOS data of the CB-DA-SC specimen indicate a temperature rise near the ends of the slab compared to the middle of the slab. This is due to the pronounced cracking in these portions of the slab, which provided additional paths for moisture transport out of the concrete. For the CB-DA specimen, the end temperature rise is not prominent because the heating of the slab was stopped 40 min after burner ignition before the moisture had been driven out of the concrete at the sensor locations. For specimen CB-DA-SC, the end continuity provided by four reinforcing bars in this specimen and longer heating time, leading to larger bending deformation of the specimen, led to multiple large cracks observed at the top side of concrete slab as shown in Figure 12(a). It was observed during the experiment that the concrete slab above the west angle connection cracked at 43 min, and released black smoke on top of concrete at 48 min and visible flames at 54 min. The concrete slab near the east support cracked at 50 min, and released black smoke at 52 min and visible flames at 60 min. This is further evidenced by the concrete discoloration along the crack surface seen in Figure 12(b). These observations are supported by the measured tensile forces in the reinforcing bars as presented in Figure 13. Thus, the thermocouple readings at the end portion of the concrete slab are indicative of flame/hot air temperature through penetrated cracks, resulting in a temperature difference of over 200 °C between two closely spaced thermocouples (e.g., TCx-7 and TCx-8) at 65 min. as shown in Figure 10. As a result, thermocouple data at Sections 1 and 8 are not used for comparison with the DFOS data in the following analysis.

Figure 12.

Photographs of damage to specimen CB-DA-SC after cool-down: (a) concrete cracks (top view) and (b) fractures at east end (cross section)

Figure 13.

Total tensile loads in east and west reinforcing bars of the CB-DA-SC specimen

The combined effect of the opening of metal deck seams and multiple penetrated concrete cracks caused the end temperature rise. The heat radiation through metal decking and heat convection through seam opening and concrete cracks are combined to create the complicated mechanical and thermal field in the CB-DA-SC specimen. While the thermocouple measurement indicates cooling of the slab between 90 min and 120 min at the ends of the slab as a result of completing moisture evaporation, the DFOS indicates continued increase in temperatures. This inconsistency is likely attributed to the unintended strain induced along the distributed temperature sensor by multiple cracks (both top and bottom of the concreate slab) in addition to other factors as discussed for the CB-DA specimen. As shown in Table 1, the temperature difference between the two methods ranges from zero to 130 % at single sections with an average value of less than 59 % in the CB-DA-SC specimen.

4.3. Temperature distribution from transverse DFOS in fire conditions

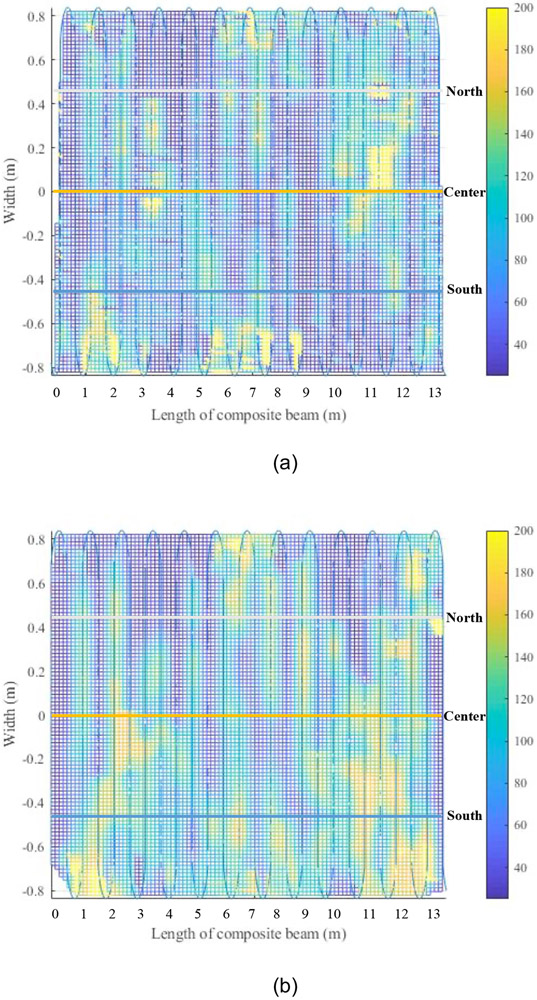
Figures 14(a) and 14(b) show measured temperature distributions at 90 min after ignition in the slabs of CB-DA and CB-DA-SC, respectively. The vertical axis represents the width of the slab and the horizontal axis represents the length of the slab (not to scale). The measured temperatures were calculated from the results of two transverse fiber optic sensors (T-DFOS) as shown in Figure 4(b) for CB-DA, and the second T-DFOS only for CB-DA-SC (the first T-DFOS was broken prior to testing). Figure 14 shows some regionally periodic temperature variations due to the varying slab thickness although the transverse fibers were deployed with a varying longitudinal spacing of 15 cm to 45 cm, which is insufficient to resolve the full resolution of spatial periodicity (30.5 cm) in the concrete slab. It is notable that the T-DFOS data for specimen CB-DA-SC does not indicate a temperature increase near the end of the slab at the centerline of the beam as suggested by the L-DFOS data. This is because the cracks at the ends of the slab did not penetrate through the transverse fibers on the north and south side of the centerline as evidenced in Figure 12(a).

Figure 14.

Transverse temperature distribution in the slab of (a) CB-DA and (b) CB-DA-SC 90 min after ignition measured from the DFOS

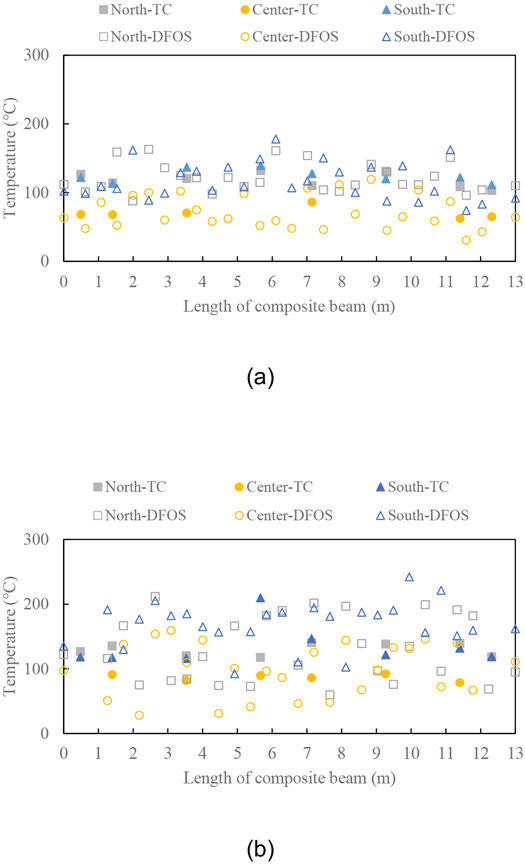
Figures 15(a) and Figure 15(b) compare the T-DFOS and thermocouple data for the slabs of CB-DA and CB-DA-SC specimens, respectively. In each figure, the temperatures along the centerline, north and south sides of the beam are presented. In general, the concrete temperature at the centerline is lower than that on the side lines due to the thermal shading effect of the steel beam and the temperatures on the north and south sides are roughly symmetric. This agrees with the observation from the thermocouples presented in Figure 10. The quantitative section-by-section comparison between the T-DFOS and thermocouple data is summarized in Table 2. For the CB-DA specimen, the average difference is within 19 % along the north and south lines and 29 % along the centerline (thermocouple data at Sections 4 and 6 are excluded as discussed when compared with the L-DFOS readings). The maximum difference at single sections is 54 %. For the CB-DA-SC specimen, the average difference is within 35 % (thermocouple data at Sections 1 and 8 are excluded). The maximum difference at single sections is 59 % along the north and south lines and 78 % along the centerline.

Figure 15.

Transverse temperatures measured from TC and DFOS in the slab of (a) CB-DA (b) CB-DA-SC 90 min after ignition at select locations

Table 2.

Transverse distributed fiber optic sensor (DFOS) and thermocouple (TC) temperature readings and their relative difference (Rel. Diff.)

Specimen	CB-DA		CB-DA-SC
Parameter	DFOS/TC (°C)	Rel. Diff.	DFOS/TC (°C)	Rel. Diff.
	North Line
Average		17%		29%
Maximum	159/108	47%	182/118	54%
Minimum	121/120	1%	120/127	6%
	Center Line
Average		29%		33%
Maximum	31/67	54%	139/78	78%
Minimum	52/62	16%	96/89	8%
	South Line
Average		19%		35%
Maximum	74/113	35%	185/116	59%
Minimum	150/139	8%	151/132	14%

Note: The Rel. Diff. value was calculated as ∣DFOS-TC∣ / TC x 100%. The minimum, average, and maximum values were determined from all TC readings for CB-DA (Sections 4 & 6 excluded at Center Line) and CB-DA-SC (Sections 1 & 8 excluded at Center Line) at 41 mm from the top surface of concrete. The maximum value represents the largest error among all individual sections in each specimen.

5. Conclusions

This study applied pulse pre-pumped Brillouin optical time domain analysis along a single-mode optic fiber for strain and temperature measurements in large-scale concrete composite structures. For strain measurements at ambient temperature, the high spatial resolution in the concrete slab with a profile decking above a steel beam is promising to shed light on the presence of shear studs and cross-section thickness variations. The measured strains at mid-span of the CB-DA-AMB specimen compared well with the linear interpolation and extrapolation of readings from strain gauges in the concrete slab. For temperature measurements under simultaneous mechanical loading and fire, the effectiveness of distributed fiber optic sensors was verified against thermocouples. Unlike thermocouples, unique peaks relevant to the concrete cracks and regionally periodic temperature variation due to the varying slab thickness can be captured by the distributed sensors under high temperatures.

From longitudinal distributed fiber optic sensors, the measured temperature increases with time from ignition as observed from co-located thermocouples. For the CB-DA specimen with no end slab continuity, the average temperatures from the two measurement techniques differ by less than 26 % except at the peak of gas temperature right after mechanical unloading. Most distributed sensor readings (averaged over 10 cm in length) are lower than those from thermocouples (point measurement). For the CB-DA-SC specimen with end slab continuity, the average temperatures from the two techniques differ by 59 %. The different measurement accuracies between the two specimens mainly result from the prolonged loading and fire duration as well as end slab continuity, causing complex degradation (damage) near two ends of the specimens under combined mechanical and fire conditions.

From transverse distributed fiber optic sensors, the average difference in measured temperatures between the fiber optic sensors and thermocouples is within 19 % along sidelines and 29 % along centerline of the CB-DA specimen. For the CB-DA-SC specimen, the average difference is within 35 %.

The above comparisons between optical sensors and their adjacent thermocouples are made at individual cross sections of the tested floor beam. They are sensitive to any misalignment of the two types of sensors. Nevertheless, challenges still exist to uncouple the effects of temperature and strain when multiple cracks penetrate through distributed fiber optic sensors deployed in long distances. Future studies will be directed to further understand the bond between distributed strain sensors and concrete under high temperatures, and the local anchor effect on the performance of distributed temperature sensors when deployed with a zigzag pattern including multiple 180° turns.