An Iterative Diffeomorphic Algorithm for Registration of Subdivision Surfaces: Application to Congenital Heart Disease

Abstract

In this paper, we present a new diffeomorphic registration algorithm for the registration of 3D models to 3D points. A biventricular template is iteratively fitted to the data by a series of implicitly constrained diffeomorphic linear least squares fits with decreasing regularization weights before performing an explicitly constrained diffeomorphic fit. The algorithm has been tested on a set of manual contours from 20 patients with a variety of congenital heart disease. Registration accuracy was assessed by calculating the mean point-to-point distance and the Dice overlap metric. Results showed that the method was able to accurately fit the biventricular model to 3D points and that the deformable model was able to fit all the pathologies while being diffeomorphic. The algorithm took approximately 5 minutes to fit each case, with an average of 52,580 points per case.

I. Introduction

Evaluation of cardiac function is indispensable for the diagnosis and treatment of any cardiovascular disease. Both left ventricular (LV) and right ventricular (RV) function are important to maintaining overall cardiovascular function. Using model-driven or model-based analysis, a prior or template is registered to the patient images by minimizing an objective function defined between the model parameters and the patient image. The segmentation process is therefore constrained by the model, avoiding errors due to the sparse nature of the image data. Both the LV and RV models can be expressed as a small number of parameters allowing simultaneous image processing and shape modelling. One such parameterization is called a subdivision surface introduced by Catmull and Clark [2], which has received increasing attention for cardiac modelling [15, 10, 12].

Subdivision surfaces are a mathematical tool for generating smooth surfaces by means of polygonal meshes. Legget et al. [10] and Sheehan et al. [15] developed a piecewise smooth subdivision surface algorithm to reconstruct both LV and RV geometries from manually traced contours in 3D ultrasound images. Shape-prior and physical constraints were integrated to allow sharp edges, which are commonly found at the mitral annulus and apex [9]. Stebbing et al. [17] have developed a morphable model of the RV using Loop subdivision surfaces. The model was expressed as a linear combination of a set of basis shapes and was able to model the RV by only using a four-parameter statistical model.

A key challenge when fitting a 3D model to a patient’s data, such as magnetic resonance images (MRI), is to satisfy a diffeomorphic constraint where the mapping between the model and the data is invertible, continuous and differentiable. Diffeomorphism preserves the topology of the model and prevents surface folding. A penalty function can be used to avoid surface folding [10, 15, 1], but it does not ensure a diffeomorphic transformation. Large Deformation Diffeomorphic Metric Mapping (LDDMM) [6] and Demons algorithm [18] are two popular diffeomorphic registration algorithms for medical images. In cardiac imaging, Mansi et al. [11] incorporated the information of incompressibility of the myocardium as a constraint within the diffeomorphic demon algorithm. De Craene et al. [4] also proposed a temporal diffeomorphic free form deformation framework incorporating incompressibility of the myocardium. The main drawback of LDDMM and Demon is a high computational time to complete the registration process. Another approach to diffeomorphic registration is based on B-splines control point displacements [3], which was applied to medical images by [14].

We have developed a registration framework by which 3D diffeomorphic displacement fields were generated, ensuring both anatomically realistic results and minimal registration error. This algorithm deforms a finite element model under the combination of implicit and explicit diffeomorphic constraints. Each transformation is guaranteed to be bijective by preventing the determinant of the Jacobian matrix of each element from falling below zero and by limiting the displacement of the coarse mesh within each iteration under explicit constraints. We validated the flexibility and accuracy of this algorithm on 20 patients with cyanotic and acyanotic congenital heart disease (CHD).

II. Methods

A. Template

Our biventricular model was comprised of the LV, the RV and four valves: aortic, mitral, tricuspid and pulmonary (see Fig. 1). At the coarse level, the model consisted of 388 vertices $V^0\in {ℝ}^3$, of which 22 were extraordinary [7]. We modified the model by adding 25 elements using Blender¹ to allow more flexibility around the tricuspid corner and the pulmonary valve. Specific knowledge of the final heart shape was incorporated in the coarse model with sharp edges around the valve and at the RV insertion points [9]. The final surface model was obtained after subdividing the coarse mesh twice using the Catmull-Clark subdivision method [2, 5, 16], resulting in 5,806 vertices.

Figure 1.

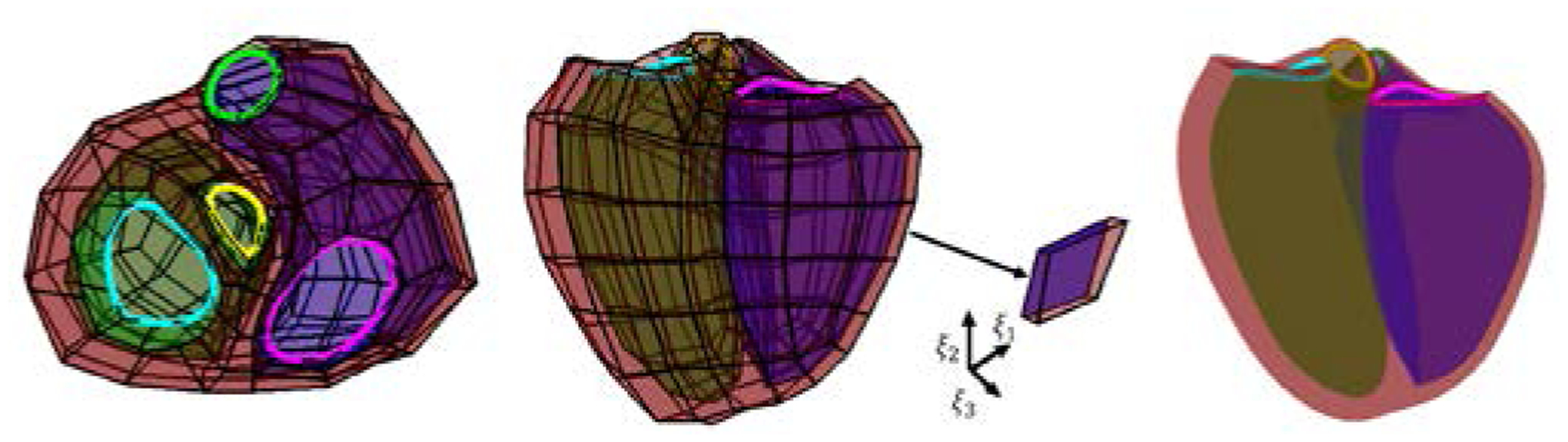
Biventricular coarse mesh (left: basal-apex view and middle: longitudinal view) and its Catmull Clark subdivision (right) with an element extracted showing interpolation directions (ξ1, ξ2, ξ3). Green surface: LV endocardium, blue surface: RV endocardium, red surface: epicardium. The mitral valve is shown in cyan, the aortic valve in yellow, the tricuspid valve in magenta and the pulmonary valve in green.

Catmull-Clark surfaces are a generalization of uniform B-splines and each surface point can be expressed as a linear combination of the coarse mesh, weighted by cubic B-spline coefficients using Stam’s parameterization [16]. Let (u,v) ∈ [0,1] be a location on an element of the coarse mesh. The corresponding surface point is parameterized by

$$p\left(u,v\right)={\sum }_{i=1}^{16}{b}_i\left(u,v\right)V_i$$ (1)

where b_i(u,v) is a bicubic B-spline basis function evaluated at (u,v) and $V_{\text{i}}\in {ℝ}^3$ are the control points. The coarse points and subdivided points were used to generate a B-splines finite element mesh (FEM). The FEM consisted of 187 elements with the local coordinate system defined by (ξ₁, ξ₂,ξ₃). Each element was defined using Bi-cubic spline interpolation along the circumferential ξ₁ and longitudinal direction ξ₂, and a linear interpolation along the transmural outward direction ξ₃. These interpolation directions are shown in Figure 1. Each surface point with the Cartesian coordinates (x,y,z) was expressed as a linear combination of the coarse points V⁰ as:

$$p_i\left(x,y,z\right)=B_i\left({\xi }_1,{\xi }_2,{\xi }_3\right)V^0$$ (2)

B. Implicitly constrained linear least-squares optimization

Diffeomorphic registration is a time consuming process. To increase the speed of our algorithm, a series of implicitly constrained stiff linear least-square fits were first performed in order to provide a closer solution to the data before performing a constrained diffeomorphic fit. The model was fitted to the data by minimizing the following objective function:

$$E=E_{reg}+{\sum }_{g=1}^n{w}_g{\Vert x\left({\xi }_g\right)-x_g\Vert }^2$$ (3)

where ${\text{x}}_{\text{g}}\in {ℝ}^{n\times 3}$ are the data points, x(ξ_g) are the surface points at element coordinates ξg corresponding to the closest point on the model. E_reg is a regularization term. In this work, a D-Affine regularization term [8] was used to penalize deviation in strain from affine transformation of the prior and to ensure smooth and physically plausible deformation fields. Hence, E_reg is defined as:

$$E_{reg}=\sum _{k\in \left(x,y,z\right)}{\int }_{\Omega }{\eta }_k{\Vert \frac{\partial J}{\partial {\xi }_k}\Vert }_F^{2}d\Omega$$ (4)

where ||·||^F is the Frobenius norm, η_k the smoothing weight in the k^th direction and J the Jacobian of the transformation. To discourage self-interaction and folding, the initial smoothing weights used were η₁ = η₂ = η₃ = 10¹⁰. To make sure that an iteration does not lead to a nonbijective transformation, implicit constraints based on the determinant of the Jacobian matrix J were added. The sign of the determinant of J gives information about the mapping from the reference template shape (χ₁, χ₂, χ₃) to the patient-shaped model. The deformation, or displacement, from the template’s shape is u = x − χ. Therefore, J is given by:

$$\begin{gathered} J_{ij}=\frac{\partial \left(x_i=u_i+{\chi }_i\right)}{\partial {\chi }_j}=\sum _{l=1}^3\frac{\partial u_i}{\partial {\xi }_l}\frac{\delta {\xi }_l}{\delta {\chi }_j}+{\delta }_{ij} \\ =\sum _{l=1}^3\frac{\partial {\sum }_{k=1}^{16}{b}_k{u}_k}{\partial {\xi }_l}\frac{\delta {\xi }_l}{\delta {\chi }_j}+{\delta }_{ij} \end{gathered}$$ (5)

Where u_k is the displacement of the B-spline patch point and can be expressed as a linear combination of the displacement of the coarse mesh and b_k, the basis functions. At each iteration, a least-square fit was performed and the determinant of the Jacobian matrix on 4×4×4 Gaussian quadrature points per element was calculated. If all values were positive, the subdivision surface was deformed by updating its control points, x(ξ_g) were recalculated and η_k were decreased. As long as the deformation is diffeomorphic, the smoothing weights are decreased. If one or more intersections were detected, the model was not updated and explicit diffeomorphic constraints were added.

C. Optimization with explicit diffeomorphic constraints

Minimizing (3) only with D-affine regularization does not lead to diffeomorphic transformations if η_k is too small, as seen Fig. 2. However, in order to fit a large variety of shapes, a highly deformable model and therefore a small η_k is required while keeping D-Affine constraints. Rohde et al. [13] derived sufficient conditions for bijectivity based on the magnitude of the derivatives of displacement. The sufficient condition to guarantee positivity of the Jacobian determinant was derived from Neumann series arguments. They showed that the minimum Jacobian determinant is positive if the magnitude of each gradient is bounded by $\frac{1}{3}$. Therefore, the following equation assures the bijectivity of the transformation:

$$\left|\frac{\partial u_i}{\partial {\chi }_j}\right|=\left|\sum _{l=1}^3\frac{\partial u_i}{\partial {\xi }_l}\frac{\partial {\xi }_l}{\partial {\chi }_j}\right|=\left|\sum _{l=1}^3{B}_i^{(1)}\frac{\partial {\xi }_l}{\partial {\chi }_j}{U}^0\right|<\frac{1}{3}$$ (6)

where ${\text{B}}_{\text{i}}^{\left(1\right)}\in {ℝ}^{\text{n}\times 338}$ can be pre-calculated for each Gaussian quadrature point for which we want to check det(J). $\text{s}=\frac{\partial {\xi }_{\text{l}}}{\partial {\chi }_{\text{j}}}$ is the scale factor between the template and the deformed model. Equation 3 can be then replaced by a quadratic programming problem with linear constraints. As the maximum displacement was constrained by Equation 6, an iterative process was used. At each iteration the optimization was performed and the model was updated. The scale factor s was then recalculated and the solution found was used as an initial guess for the next iteration. Weights along ξ₁, ξ₂ and ξ₃ were set to 10⁴. The optimization library IBM ILOG CPLEX Optimization Studio² was used. Fig. 3 presents the overview of the algorithm.

Figure 2.

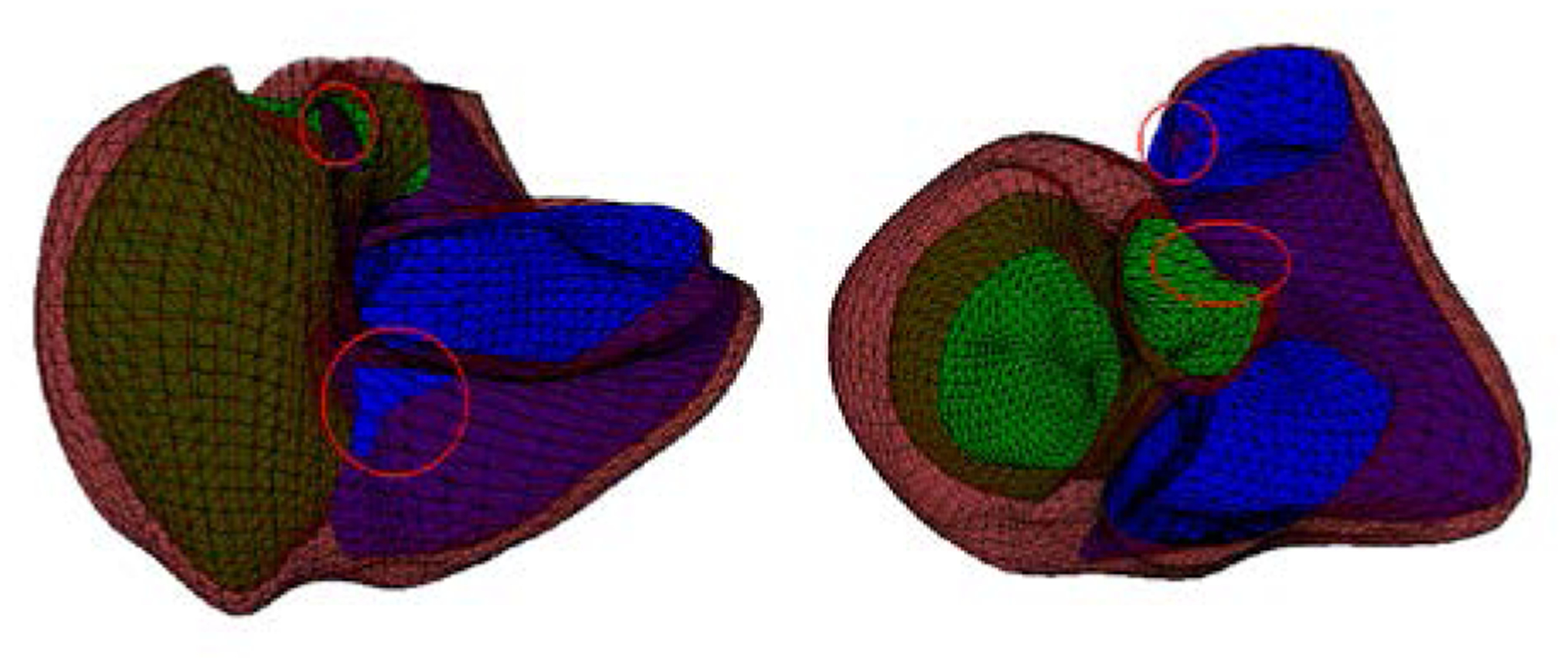
Linear least squares optimization without diffeomorphic constraints for two cases. Surface intersections are circled in red

Figure 3.

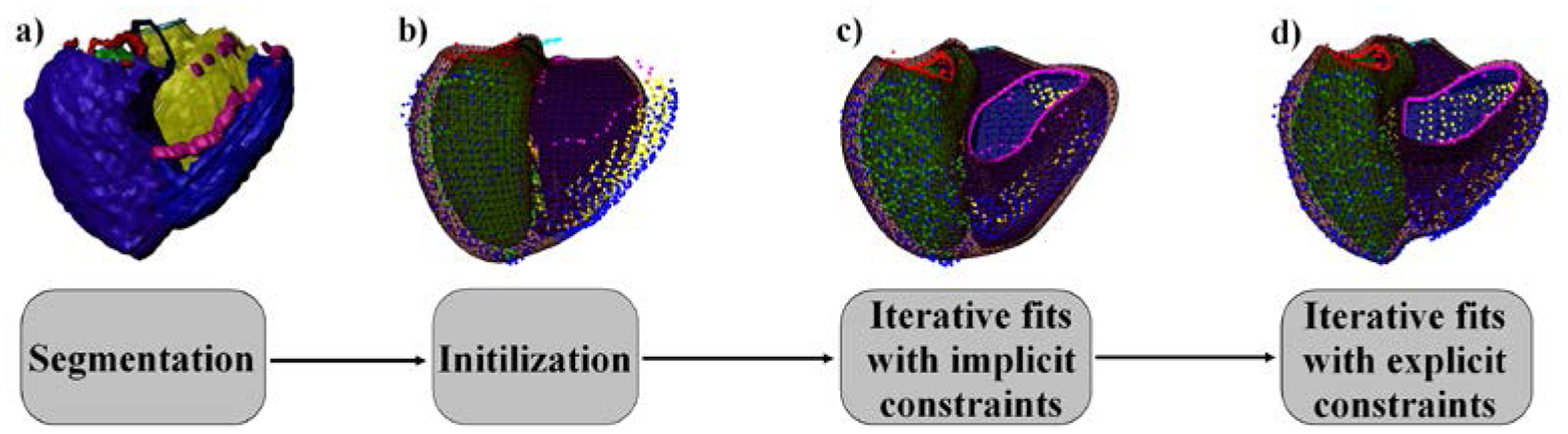
Algorithm overview. LV chamber: green, RV chamber: yellow, epicardium: blue. The mitral valve is shown in red, the aortic valve in black, the tricuspid valve in magenta and the pulmonary valve in cyan

III. Results

A. Data

We validated the proposed algorithm on 3D MRI acquisition of 20 patients with congenital heart disease, including three transposition of the great arteries, five tetralogies of Fallot, one Ebstein’s anomaly, two Marfan’s Syndromes, three bicuspid aortic valves, four coarctations and two double outlet right ventricles. To get an accurate valve orientation, the 3D MR images were re-oriented using Syngo.via (Syngo MR 2004V, Siemens Healthcare, Erlangen, Germany), which produced a range of parallel images to the aortic and the pulmonary valves. Manual segmentation was performed using ITK-Snap [19]. These 3D segmentations were loaded into Blender and separated into surfaces to be projected onto the template. Fig. 4 shows an example of the 3D segmentation image with surface labelling.

Figure 4.

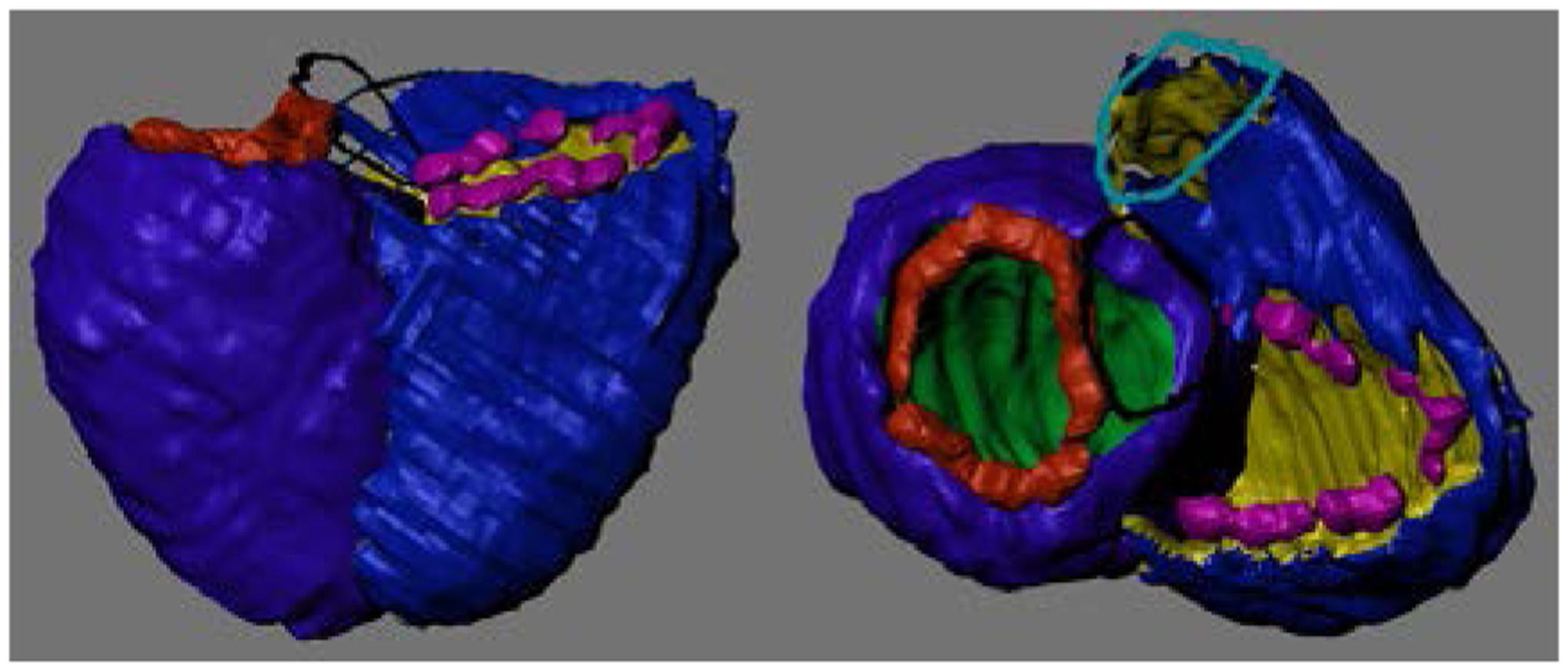
3D segmentation of a heart. The epicardium is shown in blue, RV cavity in yellow, LV cavity in green, pulmonary valve in light blue, tricuspid valve in pink, mitral valve in red and aorta in black

B. Accuracy of registration

Registration accuracy was assessed by using the mean point-to-point distance and the Dice overlap metric. The point-to-point distance was calculated as the distance between a data point and its closest vertex on the surface. Table I lists the mean point-to-point distances and the Dice metric for the RV chamber, the LV chamber and the epicardium. The Dice overlap metric was over 0.88 for each surface, demonstrating a good overlap after fitting. The mean point-to-point distance was smaller than 2 mm, similar to [17]. Fig. 5 shows the results of three different CHD patients.

TABLE I.

Evaluation of the registration accuracy

	Mean point-to-point distance (mm)	Dice metric
LV chamber	1.38 ± 0.18	0.95 ± 0.014
RV chamber	1.55 ± 0.22	0.92 ± 0.014
Epicardium	1.66 ± 0.18	0.88 ± 0.024

Figure 5.

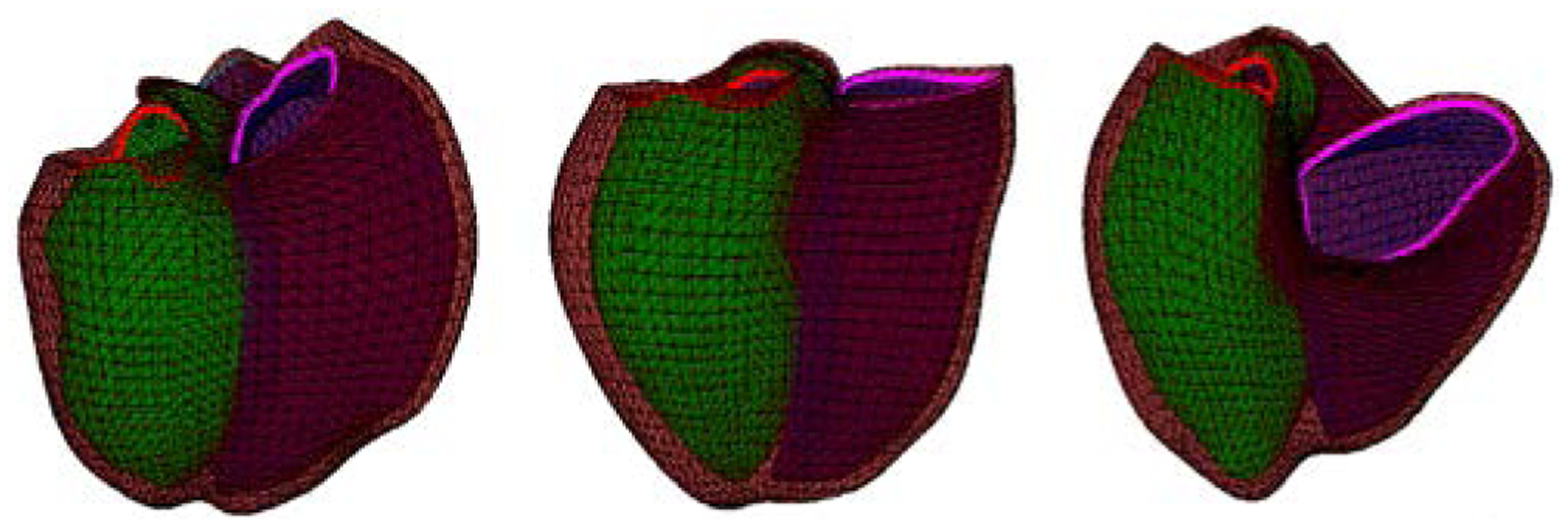
Fit to CHD patient anatomy. Left: Tetralogy of Fallot. Middle: Marfan’s Syndrome, Right: Ebstein’s anomaly

IV. Discussion and conclusion

We have proposed a method for generating diffeomorphic deformation fields. This method is based on the decomposition of deformations, preventing the determinant of the Jacobian matrix falling below zero. Each transformation is guaranteed to be bijective by limiting the displacement of the coarse mesh within each iteration. Topology-preserving registration is a time consuming process. Furthermore, constraining the magnitude of the displacement does not necessarily allow large deformations. Although we added a series of least-square fits compared to the original diffeomorphic fit, the algorithm showed a fast convergence, with an average processing time of 4.8 ± 2.4 minutes (implemented with python programming language) and an average of 52,580 ± 1,463 points to fit. The succession of least-square fits has an important effect on the rate of convergence as it provided a good initialization at a lesser cost. Our results have shown that this technique was able to achieve good registration accuracy while generating diffeomorphic displacement fields. The surface modelling also achieved a good performance as it was able to fit all the CHD pathologies present in our dataset.