Abstract
In the present study, the adsorptive removal of organophosphate diazinon pesticide using porous pumice adsorbent was experimentally investigated in a batch system, modelled and optimized upon response surface methodology (RSM) and artificial neural network-genetic algorithm (ANN-GA), fitted to isotherm, kinetic and thermodynamic models. The quantification of adsorbent elements was determined using EDX. XRD analysis was utilized to study the crystalline properties of adsorbent. The FT-IR spectra were taken from adsorbent before and after adsorption to study the presence and changes in functional groups. The constituted composition of the adsorbent was determined by XRF. Also, the ionic strength and adsorbent reusability were explored. The influences of operational parameters like pH, initial pesticide concentration, adsorbent dosage and contact time were investigated systematically. ANN-GA and RSM techniques were used to identify the optimal process variables that result in the highest removal. Based on the RSM approach, the optimization conditions for maximum removal efficiency is obtained at pH = 3, adsorbent dosage = 4 g/L, contact time = 30 min, and initial pesticide concentration = 6.2 mg/L. To accurately identify the parameters of nonlinear isotherm and kinetic models, a hybrid evolutionary differential evolution optimization (DEO) is applied. Results indicated that the equilibrium adsorption data were best fitted with Langmuir and Temkin isotherms and kinetic data were well described by pseudo-first and second-order kinetic models. The thermodynamic parameters such as entropy, enthalpy and Gibbs energy were evaluated to study the effect of temperature on pesticide adsorption.
Subject terms: Climate sciences, Environmental sciences
Introduction
The enormous growth in population was putting the world under stress, to meet their global food demand. To cater this demand, food production has to be increased many folds, and crop losses due to pests should be reduced. Around the globe every year more than 800 different agricultural pesticides are produced. Among them, organophosphate pesticides are extensively used due to their significant effect on a wide range of pests, high durability, and low cost1. Unfortunately, the excessive use of these pesticides will accumulate in the soil and subsequently end up in water bodies during the rainfall-runoff, thus polluting water and the environment. Chlorpyrifos, malathion, chlorpyriphos-methyl, and diazinon are among the essential organophosphate pesticides that are commonly found in the surface and underground water resources2. Organophosphate pesticides pose a severe threat to human health due to central nervous system dysfunction and cholinesterase activity. According to global statistics, the highest mortality due to pesticides is associated with organophosphate pesticides. Diazinon pesticide is one of the extensively used organophosphate pesticides for agricultural purposes around the world1,3,4. Typically, the half-life of the insecticide in natural water is around 180 days at pH = 7.4. However, diazinon quickly hydrolyze in the aquatic environment within 12 h under acidic environment (pH = 3.1). Diazinon is non-polar, slightly water-soluble, and resistant to decomposition in soil. A lethal dose of diazinon for humans has been reported 90–444 mg/kg of body weight. Thus, the concerns on surface and groundwater pollution and ultimately endangering the human health and aquatic creatures are a global issue, which force the global researchers to further explore their mitigation3.
So far, various methods have been investigated for removing recalcitrant organic pollutants from an aqueous environment, including photocatalytic processes5,6, oxidation7, electrochemical decomposition8, membrane separation9, and adsorption10,11. Some of these methods are complex processes, which incur a high cost as well as higher consumption of chemicals. In this regard, researchers have found that the adsorption process is a more efficient method, and its operating costs can be reduced by using various natural as well as synthetic adsorbents12.
Among the various natural and low-cost adsorbents, Pumice was considered as a natural adsorbent for adsorption process as it is a lightweight material (density ~ 0.5—1 kg/L) with a high porosity (φ = 85%)13. It is structurally composed of a series of irregular cavities, some of them connected to each other, and volcanic gases like sulfur-based are being confined in them. Pumice stone has a porous structure and large surface to volume ratio that make it a potential candidate as a natural and low-cost adsorbent14. Till today, many studies have been conducted on the performance of pumice for the removal of water pollutants13,15,16, but the removal of organophosphate diazinon pesticides using pumice has not been reported so far in the open literature.
Therefore, the prime objective of this research study is to evaluate the performance of pumice as an adsorbent for organophosphorus diazinon pesticide removal from water bodies. In this study, the influence of independent process variables (initial diazinon concentration, pH, contact time, and adsorbent dosage) on the overall efficiency is investigated systematically. To capture the intrinsic features of the pumice adsorption process and minimize the experiments, response surface methodology (RSM) is used. To further predict the natural pumice removal at different operating conditions and identify the optimal process variable values, backpropagation artificial neural network (ANN) is used as a data-driven model. Also, the interaction effect of process variables is thoroughly investigated, and these variables are optimized using RSM and artificial neural network-genetic algorithm (ANN-GA). To understand the mechanism involved in pesticide adsorption by pumice, isotherms and kinetic modelling are examined separately. To accurately identify the parameters of nonlinear isotherm and kinetic models, a hybrid evolutionary differential evolution optimization (DEO) is applied. To minimize the use of pumice, regeneration studies are conducted to validate its performance in removing diazinon for multiple cycles. Also, an ionic strength study was conducted to simulate the real condition of aquatic environments during the adsorption process.
Experimental section
Materials and chemicals
The laboratory-grade chemicals like NaOH, H2SO4, HNO3 used in this study are purchased from Merck Company (Germany), and diazinon pesticide (60% purity) purchased from Partonar Company, Iran. Natural Pumice (Fig. S1) was obtained from Tekmeh Dash, East of Azerbaijan. The constituted components of pumice used in this study were found to be SiO2 (71.75%), Al2O3 (12.33%), Fe2O3 (1.98%), CaO (0.7%), MgO (0.12%), Na2O (3.59%), K2O (4.47%), and SO3 (0.18%).
Adsorbent preparation
Initially, solid pumice was crushed and sieved through a mesh size of 10–70 (200 to 2000 μm) and was rinsed with distilled water several times to remove unwanted impurities. In order to increase the porosity of the adsorbent, pumice was placed in 1 N H2SO4 at room temperature for two days. Then, it was washed thoroughly until the effluent turbidity is reduced to be clear and can read under spectrometer, as well as pH reaches neutral conditions. Then, the adsorbent was dried in an oven for about 8 h at 105 °C17.
Adsorbent characterization
The porosity and density of pumice were measured according to the following procedure. The saturation and Buoyancy technique was employed for pumice porosity and density, which conforms to the standard suggested by ISRM and ASTM18. The mass of pumice sample was 50 g and irregular in form. The pumice bulk volume (V) was determined by measurement of the saturated‐submerged mass (Msub) and the saturated mass (Msat) of the pumice sample. Initially, the pumice sample is immersed in water to be saturated under vacuum conditions of less than 800 Pa for 1 h. Regular mixing was done to remove trapped air. The mass of saturated‐submerged pumice was measured to determine Msub. The pumice sample is taken out of the water and the mass of the pumice plus container (B) is measured with an accuracy of 0.01 g. The pumice sample is then dried in the open container located in an oven for 24 h at the temperature of 105 °C to reach the constant mass. The container, with the dry pumice, was cooled in a desiccator for 30 min, and the mass (C) of the dry sample with the container is again measured with an accuracy of 0.01 g. Also, the mass of the container (A) was determined separately. The following calculations were done to obtain the porosity and dry density of the pumice sample.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
Here, V and VV represent the total volume and pore volume, respectively, of the pumice sample (cm3). ρd and ne stand for dry density (g/ cm3) and porosity percent, respectively. Ms, Msub, and Msat show the dry, saturated‐submerged, and saturated masses, respectively, of the pumice sample (g). A, B, and C are the mass of the container, dried pumice sample plus container, and saturated pumice sample plus container, respectively, (g). Geometries, morphology, and structural characteristics of pumice adsorbent were analyzed using field electron emission microscopy (SU-3500 model, HITACHI). The quantification of adsorbent elements was determined using an Energy dispersive X-ray spectroscopy device (EDX, Ametext, Oktane prime model). X-ray diffraction (XRD) analysis (Rigaku miniflex diffractometer device) was utilized to study the crystalline properties of pumice. The FT-IR spectra were taken from pumice before and after adsorption by using Perkin-Elmer Spectrophotometer to investigate the presence and changes in functional groups. The constituted composition of the pumice was determined by a Philips X-ray fluorescence (XRF) analysis (Philips PW1480 model). pH at the point of zero charge (pHZPC) was determined by the pH drift method for pumice adsorbent. 180 mL of 0.01 M NaCl solution was added in 650 mL beakers, and the pH of solutions was adjusted by NaOH/H2SO4 to be within the range of 2 to 12. Then, 0.25 g of the adsorbent was added to each Erlenmeyer and was mixed for 24 h at 120 rpm, and the final pH is recorded.
Batch experiments
All batch experiments on diazinon adsorption by pumice adsorbent were performed in Erlenmeyer flasks with a volume of 250 mL. The stock solution of 50 mg/L was prepared by liquifying 0.025 g of diazinon in 500 mL deionized water. The process parameters like initial diazinon concentration, pH, contact time, and pumice dosage were explored in the adsorption process at the levels given in Table S1 and the experiment design given in Table S2. The sample was filtered with a 0.45 μm syringe filter, and the remaining diazinon in the solution was measured using DR 5000™ UV–Vis spectrophotometer at 248 nm wavelengths12. Then, the efficiency of diazinon removal and adsorption capacity by pumice adsorbent was determined. For every experimental run according to the experiment design (Table S2), one sample was conducted under the designed experiment conditions without adding the pumice. Its UV absorption was measured at 248 nm after filtration using 0.45-micron filter paper. By comparing the UV absorption between the samples and the standard curve, no reasonable change in the UV absorption was identified, indicating that there was no self-settling of pesticide due to its limited solubility. Moreover, the designed experiments were repeated by adding the pumice to the samples without having the pesticide to identify whether UV absorption at 248 nm occurs by the added pumice. After shaking and filtering the samples, it confirmed that there was no background resulted from pumice powder at 248 nm.
Experimental design
In the current study, central composite design (CCD) in RSM was employed for designing the experiments. Applying this method via a statistical approach optimizes the number of required experimental runs and hence reduces the wastage of chemicals and lowers the total budget19. Furthermore, this method identifies the relationship between the process variables and removal efficiency, as well as identifies the interactive effects within the variables and overall influence on the removal efficiency. The process variables that influence the removal efficiency were identified as initial diazinon concentration, contact time, pH, and pumice dosage. Therefore, these process variables were considered within the ranges, which were categorized as five levels (Table S1), and thus, results in an experimental matrix of 30 experimental runs (Table S2) with different values of process variables. Each experiment was performed thrice to minimize the measurement/experimental error and to check the variation among the outcomes. It was observed that the variability of these outcomes is less than 2%; hence the average value was used for further analysis studies and reported in Table S2.
Implementation of a hybrid ANN-GA algorithm
The multivariate modeling of the experimental design was performed by the ANN modeling, which can establish a data-driven model which can capture the interdependency of process parameters and their effect on the response20–22. Here, a three-layered (hidden, input, and output layers) ANN model was implemented with the Levenberg–Marquardt backpropagation algorithm with 1000 epochs. Tansig and Purelin transfer functions were employed at the hidden and output layer, respectively23. Among the total data, a set of 70%, 15% and 15% data were randomly segregated for training, validation, and testing, respectively. The number of neurons in the hidden layer remarkably influences the model structure and hence the predicted values. Therefore, the best number of neurons (1 ~ 14) in the hidden layer was verified via well-known statistical metrics called mean squared error (MSE) and coefficient of determination (R2). The best optimum number of neurons will result in a lower value of MSE and the higher value of R2 (close to 1.0).
The performance of ANN depends on the appropriate choice of the weights and bias in the ANN architecture. Instead of the manual trial & error method, these weights can be more estimated (optimized) by suitable optimization techniques. In this study, a genetic algorithm is used to optimize the weights, which can find the exact or estimated relation between the response (removal efficiency) and input process variables. In this method, computing solutions are based on the population and get updated at every iteration if it is better than the former one. This procedure is continued until the best solution or fit is achieved. GA utilizes individual populations obtaining from different combinations of process variables, thus explores all search space for the best solution. This configuration is denoted as a hybrid ANN-GA technique24–26.
Isotherms, kinetics, and Thermodynamics studies
The study of adsorption isotherms can better understand the mechanisms involved in the diazinon adsorption onto pumice. Hence, the adsorption equilibrium data were fitted with six well-known adsorption equilibrium isotherms. The model expressions of these isotherms are presented in Table S3. Also, four kinetics models (Table S4) are evaluated and fitted in order to understand the inherent kinetics further and interpret the rate of adsorption of solute onto the adsorbent surface.
Temperature being an essential factor in the adsorption process, so to understand its effect on the performance of natural pumice adsorbent for diazinon removal, the experimental studies are conducted at 20, 30, 40, and 50 °C. The thermodynamic parameters such as entropy change (ΔS°), enthalpy change (ΔH°) and Gibbs energy change (ΔG°), were evaluated to study the effect of temperature on the diazinon adsorption27,28. The expression to calculate the parameters was given in supplementary material.
Evaluation of isotherms and kinetic models
Usually, most researchers evaluate the isotherm and kinetic model parameters by linearizing the non-linear equation. However, linearization will misinterpret the adsorption mechanisms as well as the adsorption rate. So, to use the same non-linear model expression, the model parameters are evaluated by well-known differential evolution optimization (DEO). The features of DEO and its implementation are provided in ESM as well as from previous studies29. The performance of DEO based model predictions are validated with important statistical metrics, as shown below:
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
where n and p is the number of experimental runs and parameters; are the qe values of the experimental, average and predicted values, respectively”;
Results and discussion
Adsorbent characterization
The porosity and density of pumice were measured to be in the range of 50–85% and 0.7–1.2 g/cm3 according to the saturation and Buoyancy technique. SEM image (Fig. 1) of pumice adsorbent showed a porous surface with large grains and sharp edges on the adsorbent.
Figure 1.
SEM graphs of pumice adsorbent.
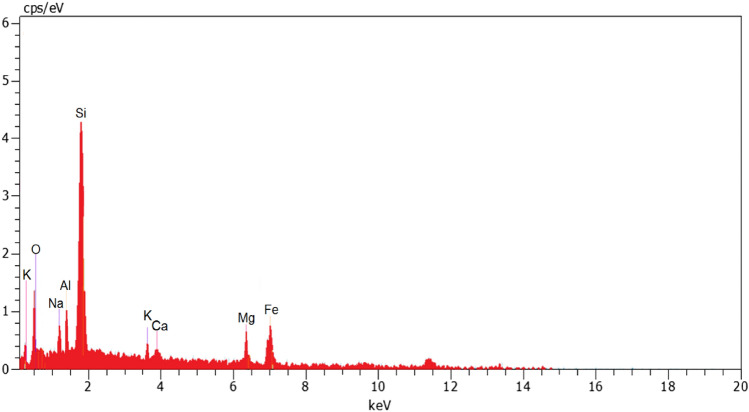
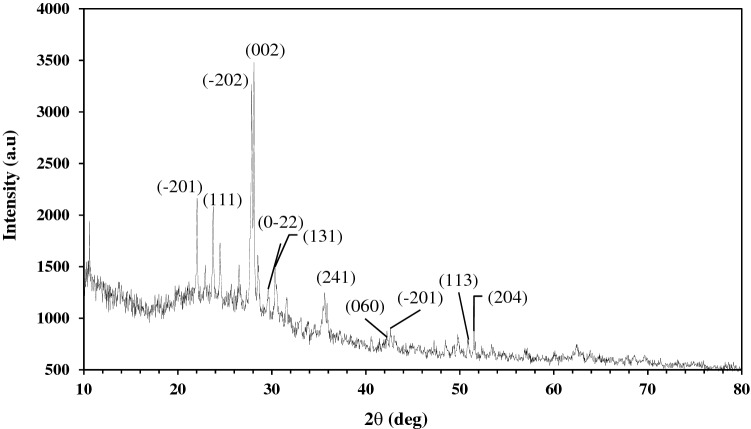
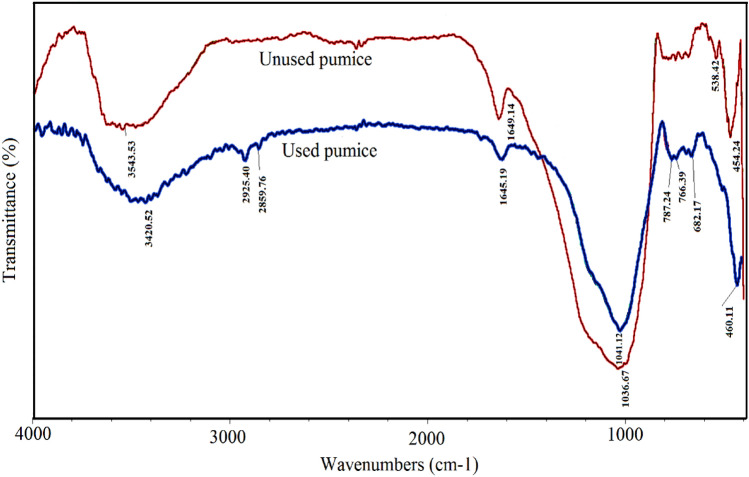
The results of the EDX analysis shown in Fig. 2 elucidated that the elemental composition of pumice are O (45.08%), Si (34.47%), Al (7.13%), K (3.17%), Mg (2.59%), Fe (2.55%), Na (2.53%) and Ca (1.48%). XRD pattern for pumice was depicted in Fig. 3. The results show that some diffraction peaks at the crystalline pattern of the pumice have appeared at 2θ of 22.1, 23.7, 27.8, 28.1, 30.1, 30.4, 35.8, 50.3, and 52.3, which belong to (100), (002), (101), (102), (110), (103), (200), (112) and (201) crystalline planes and correspond to the reference XRD pattern with the standard JCPDS code of 00–041-1481. Accordingly, the main component of pumice was found to be anorthite (Na.25Ca.71(Al2Si2O8)), a kind of natural zeolite constituted from sodium, calcium, aluminum, and silicate30. In addition, the background line has formed a broad peak in the 20°–30° range, points out amorph substance. Figure 4 depicts FTIR spectra of pumice before and after adsorption. The bands that appeared at 3543.53 cm-1 are ascribed to the stretching vibration of the H–O group. The peaks around 1649.14 cm-1 can also be allocated to the stretching vibration of H–O groups arising from water absorbed31. The peaks that appeared at 1035–1045 cm-1 bonds are assigned to stretching vibrations of Si–O and Al-O, and between 400 and 500 cm-1 bonds are related to their bending modes. The Si–O-Al stretching vibration is found around 787–788 cm -1 bonds32. By making a comparison between the FTIR spectra of used and unused pumice, the peaks at 3543.53 cm-1 and 1649.14 cm-1 bonds, which are related to the OH group, although could be observed, were found to be weaker and shifted to 3420.52 cm-1 and 1645.19 cm-1 bonds, respectively. The results reveal that electrostatic interactions play a key role in the adsorption of diazinon in acidic pHs owing to the existence of positively charged pumice33. It also observed that two new peaks had been appeared at 2925.40 cm-1 and 2859.76 cm-1 bands of FTIR spectrum of used pumice, corresponding to asymmetric and symmetric stretching vibrations of C–H bonds, respectively. This confirms the residues of adsorbed diazinon onto the pumice surface34.
Figure 2.
EDX analysis of pumice.
Figure 3.
The XRD pattern of natural pumice.
Figure 4.
FTIR spectrum for used and unused pumice.
Model fitting and statistical analysis
Based on the RSM-CCD framework, a quadratic model (Eq. 12) is developed that shows the connection between the output response and process variables. Based on the analysis of variance (ANOVA) approach, the following quadratic expression is obtained.
| 12 |
The Pareto effect of each process variable (factor) on the removal efficiency was obtained according to Eq. (13), which is shown in Fig. S2.
| 13 |
where b shows the regression coefficient of each term. As displayed in Fig. S2, the initial diazinon concentration has the highest effect (about 51.8%) on the removal efficiency.
The statistical results of the analysis of variance (Table S5) indicate a well-fitted model, and most of the factors in the model have a substantial effect on the outcome. The R2 value for this model was 0.9997, which concludes the high capability of the model in predicting the response variability. The residuals are situated near/on the 45° line, confirming the normality of error (Fig. S3a). Also, the residuals vs. predicted (Fig. S3b) plot signifies that the residuals are erratically scattered around the baseline and do not follow any specified trend.
Data-driven modelling by ANN
To configure optimal ANN topology, the different number of neurons (1–14) in the hidden layer is initially verified. Simulation runs indicate that the 8-neuron hidden layer model results in the lowest mean square error. Therefore, these eight neurons are chosen as an optimum number of neurons in this ANN topology. Hence, a three-layered feed-forward network with a 4:8:1 topology (Fig. S4) was employed for modeling the process. The performance of the ANN model is displayed in Fig. S5. It can be observed that most of the predicted values are close to 45° line, which thus resulted in R2 of 0.999, 0.995, and 0.976 for training, validation, and testing, respectively. The model predictions are in good compatibility with the experimental values and also better than RSM model predictions, thus indicating the higher capability of capturing the non-linear dynamics of the adsorption system.
Performance of model predictions by RSM and ANN approaches
Based on the quadratic model (Eq. 8), the pesticide removal efficiency by pumice adsorbent is estimated, and the performance of model predictions against the experimental values is shown in Fig. S6a. These RSM predictions are in good fit with the experimental values, resulting in an R2 of 0.986. Similarly, the three-layered 4:8:1 topology ANN model predictions were compared against the experimental values, as shown in Fig. S6b. It can be noticed that these predictions are as good as experimental values, hence resulted in a higher R2 of 0.992. To evaluate the performance of both RSM and ANN, their residual errors (model predictions – experimental values) were calculated and plotted for each experimental run, as shown in Fig. S6c. These residual errors further confirm that the superior performance of the data-driven model derived from ANN.
Effect of pHZPC for pumice adsorbent
The final pH value of the solution is compared to the initial pH to determine pHZPC for pumice adsorbent (Fig. S7). In the figure, the point where the final pH value is equal to the initial pH is considered as pHZPC. In this research, the obtained value of pHZPC for pumice adsorbent was equal to 6. When the pH of the solution < pHZPC, the adsorbent surface charge is positive and vice versa35. The surface of pumice is +ve charged at a solution pH values below 6 (pHZPC) and would, therefore, be prone to the electrostatic attraction of diazinon molecules10. At pH over 6, the surface charge would be negative. These negative charges on the sites decrease the adsorption of anionic diazinon because of electrostatic repulsion. This finding is similar to those reported by other studies13,36. Therefore, at the solution, pHs are less than pHZPC (3 <6) and more than pKa of diazinon, the adsorbent surface has a positive charge.
In contrast, diazinon molecules begin to decompose into anionic species and are adsorbed by electrostatic adsorption on active sites of pumice adsorbent36,37. Therefore, the maximum removal of diazinon occurs under acidic pH conditions, and these outcomes in this study are consistent with the results of other studies38. The mechanism for adsorption of diazinon on pumice can also be in the interlayer adsorption space of pumice as well as its surface. This is consistent with the results of previous works39.
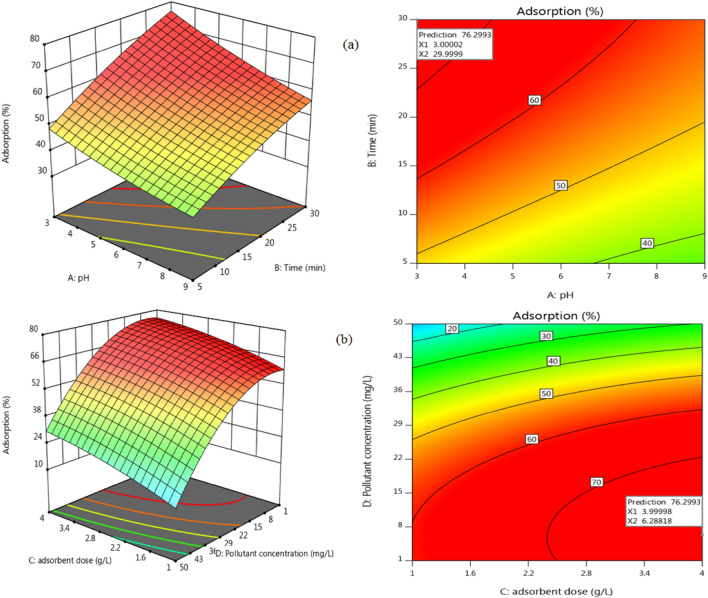
Interaction effect of process variables
To better visualize the interaction effect of process variables on the overall diazinon removal efficiency, the contour plots and 3D surface plots are produced as given in Fig. 5. As seen in Fig. 5a, the maximum removal efficiency of diazinon was observed in acidic conditions, and by increasing pH, the removal of diazinon exhibits a reducing trend. This behaviour can be attributed to various reasons: 1) rapid hydrolysis of diazinon under acidic conditions and 2) a pKa of 2.6 of diazinon40.
Figure 5.
The 3D response surface and contour plots for diazinon removal by pumice, (a) pH -contact time on adsorption (initial diazinon concentration = 6.28 mg/L, and pumice dosage = 4 g/L), (b) pumice dosage—initial diazinon concentration on adsorption (pH = 3 and contact time = 30 min).
Contact time is one of the essential variables in the uptake of diazinon pesticide by pumice adsorbent. As seen in Fig. 5a, the amount of diazinon removal increased rapidly at the early stages and then gradually reached a steady state. With increasing contact time from the start of the process to longer times, diazinon removal increased. This fact could be due to the presence of empty adsorption sites on the adsorbent during initial contact time and the increased rate of transfer of diazinon molecules from the solution to the adsorbent surface. It must be noted that the removal rate at a prolonged time is relatively lower than the initial times because the sites on the adsorbent are saturated at the extended contact time, and fewer sites are available to adsorb the pollutant41. These results are consistent with the results reported in other studies on the diazinon removal by other adsorbents, as well as the use of pumice to remove other pollutants than diazinon16.
The amount of diazinon adsorption at different initial concentrations of diazinon is shown in Fig. 5b. According to the trends shown in this figure, it is observed that with increasing the concentration of diazinon from 1 to 7 mg/L, diazinon removal by pumice has increased, then with increasing the concentration, the removal efficiency of diazinon gradually reduced. This can be due to the fact that with increasing the concentration of diazinon, competition has been increased to adsorb diazinon in the adsorbent active sites, and adsorption capacity increased, but adsorption reduced due to increased diazinon molecules in the environment42. This result is consistent with the trend reported in another study16.
The adsorbent dosage is also one of the key variables in determining the quantity of removal of a selected pollutant41,43. Figure 5b shows the amount of Diazinon adsorption as a function of pumice adsorption dosage. According to the trends seen in this figure, it is found that diazinon removal increased with increasing the pumice dosage. This increase can be attributed to enhanced active sites while increasing the adsorbent dosage; hence the amount of diazinon adsorption increased. Also, the continuous reduction in adsorption capacity with increasing the dosage may be due to the lower access adsorbate molecules to the adsorbent surface in higher doses44.
Optimization studies by RSM-GA approaches
Keeping the maximization of removal efficiency as a desirable goal, the process variables were optimized. Using the RSM-CCD approach, along with the quadratic model, the optimal values of process variables are evaluated. As observed in Fig. S8, the max diazinon removal efficiency is 76.3% which can be attained at the optimal values of 6.28 mg/L, 4 g/L, 3, and 30 min for initial diazinon concentration, pumice dosage, pH and contact time, respectively.
Optimization by the genetic algorithm was carried out for each parameter within the range given in Table S6. The optimization can result in maximum pesticide adsorption. Figure S8 depicts the significant statistical factors in the implementation of the GA technique. By implementing GA, the optimized values that are obtained for initial diazinon concentration, pumice dosage, pH, and contact time are 6.266 mg/L, 4 g/L, 3, and 30 min, respectively. At these conditions, the maximum pesticide removal was obtained as 76.5%. These findings were consistent with the optimization values that resulted in the RSM technique. To validate the consistency of the optimal predicted responses by both RSM and GA approaches, three experiments were conducted at these optimum conditions (as per RSM), and the average adsorption efficiency was found to be 77.0% (± 1.7) (Table S6). These results are close to the predicted responses of RSM and GA approaches. Moreover, at the optimum operational parameters and neutral pH values in the range of 6 to 8, removal efficiency changed from 64.9 to 59.3%.
Effect of ionic strength
The existence of various salts in the effluent might affect the adsorption efficiency. Since various salts exist in aqueous solutions, one of the important propose of the present study was to examine the adsorption efficiency of diazinon onto the pumice in the presence of the different electrolytes including NaCl, Na2SO4, and KNO3 at acidic, neutral and basic pHs. The results (Fig. 6) elucidate that the removal efficiency is suppressed significantly at acidic pH, whereas it exhibits no significant decrease at neutral and basic pHs. The considerable reduction in removal efficiency at acidic pH indicates that electrostatic attraction potentially contributes to the diazinon adsorption onto the pumice. The electrostatic interaction indeed occurs between the adsorbed H+ groups and the anionic form of diazinon molecules at acidic pH45. Theoretically, when the electrostatic attraction prevails between adsorbent and adsorbate, the added salts compete with adsorbate for the occupation of the vacant sites on the adsorbents, thus decreasing the overall adsorption efficiency46. The results also confirm that the adsorption at the system at acidic pH is of outer-sphere surface complexation. As stated, no significant decrease of removal efficiency was found at neutral and basic pH’s, when the salts were added to the solution, signifying inner-sphere surface complexation, largely covalent in character, dominated47.
Figure 6.
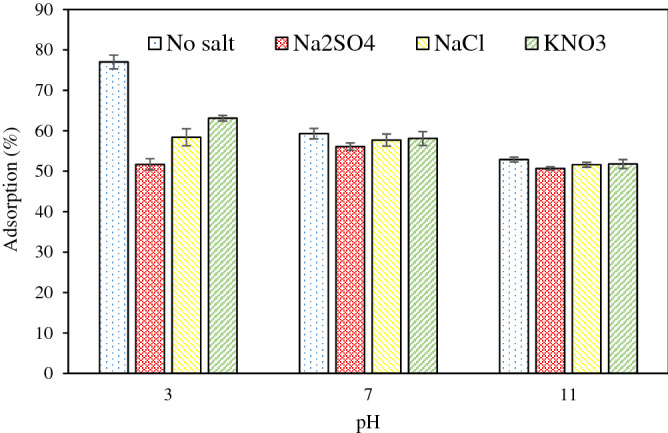
Effect of inorganic salts on diazinon adsorption on pumice (initial diazinon concentration = 6.28 mg/L, pumice dosage = 4 g/L, and contact time = 30 min, electrolyte salt concentration = 500 mg/L).
Desorption and regeneration studies
To minimize the overall operating cost, the usage of spent adsorbent has to be reduced. This can be done by regenerating the adsorbent from the treated effluent. So, desorption tests were conducted, which provides useful information for evaluating the nature of the adsorption process and the regeneration of the spent adsorbent. Usually, these desorption tests are carried using desorbing agents like CaCl2, HNO3, HCl, EDTA, NaOH, etc., which can desorb the adsorbed ions48. In this study, the desorption of diazinon and regeneration of spent pumice was investigated by eluting the diazinon adsorbed pumice with NaOH.
For desorption tests, 0.1 M NaOH was used on the adsorbed pumice adsorbent. In order to saturate the adsorbent, the first adsorption experiment is conducting by adding 0.75 g of pumice into a 250 ml conical flask containing 5 mg/L of diazinon solution. Then, the flask was placed in a shaker (120 rpm) for 80 minutes to make sure that the adsorbent is completely saturated. The removal percentage of the regenerated pumice was studied in the three cycles of adsorption-desorption processes. The adsorption/desorption study given in Fig. 7 illustrates that adsorption decreased from 76.4 to 43.6%, and desorption reduced from 61.3 to 37.8% after three consecutive cycles. These experimental results indicate that the regenerated pumice adsorbent can be used up to 3 cycles with 43.6 % removal efficiency at the last cycle. So, to minimize the total operation cost (usage of pumice adsorbent), the fresh diazinon polluted water can be treated first with the regenerated adsorbent then get into contact with fresh pumice adsorbent for maximum removal performance.
Figure 7.
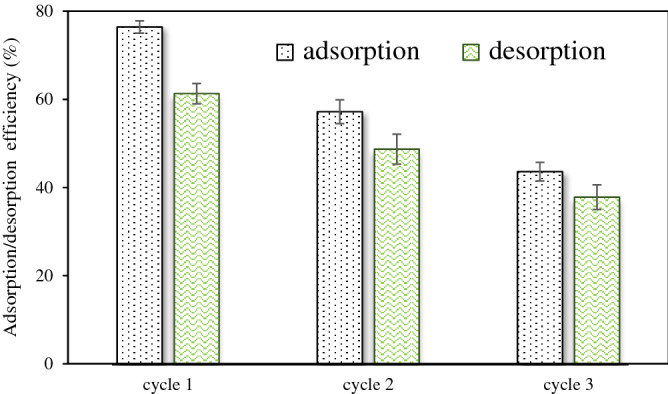
Adsorption–desorption and regeneration studies of pumice.
Comparison with other adsorbents
In this study, a low-cost and abundant natural adsorbent was used for the diazinon pesticide removal from an aqueous solution, and the performance was found to be excellent. To further validate its performance, the diazinon pesticide removal efficiency was compared with other reported adsorbents. Applications of different adsorbents in the diazinon removal are given in Table 1. As shown in this table, pumice as a natural adsorbent shows a reasonable adsorption capacity for diazinon. Many features like low cost and abundance, availability, and promising adsorption capacity evidence the superiority of pumice over many adsorbents for diazinon removal from aqueous solution.
Table 1.
Comparison of diazinon adsorption efficiency of different adsorbents.
| Adsorbent | Maximum adsorption capacity (mg/g) | References |
|---|---|---|
| Ca-montmorillonite | 9.5 | 39 |
| FeOH-modified | 16.4 | |
| Fe-modified | 17.9 | |
| Nanocrystalline MgO | 20 | 52 |
| Commercial MgO | 12 | |
| Magnetic guar gum | 47.17 | 50 |
| Magnetic guar gum-montmorillonite | 80 | |
| Acid treated zeolite | 15.1 | 51 |
| Cu2O nanoparticles modified zeolite | 61.73 | |
| Activated coconut shell biochar | 9.65 | 53 |
| Phosphoric acid modified coconut shell biochar | 10.33 | |
| Chitosan/Carbon nanotube | 222.86 | 54 |
| Pumice | 20.65 | This study |
Isotherms modelling and adsorption kinetics
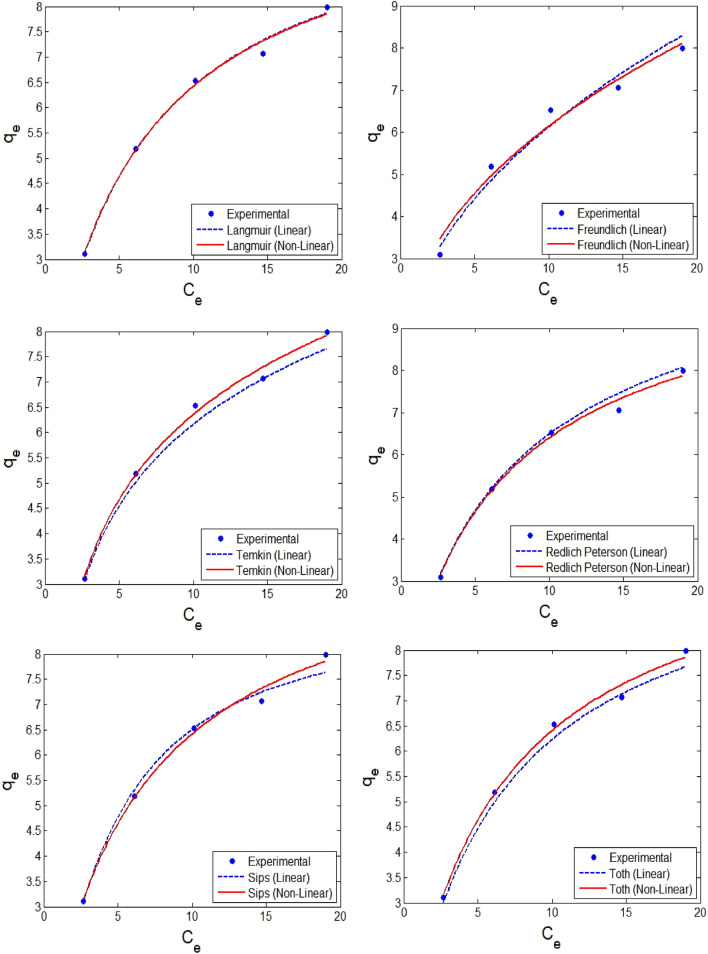
The adsorption isotherms describe the relationship between the adsorbent and the amount of analyte present in the solution49. In order to better interpret the adsorption of diazinon on pumice, the six well-known isotherm models (2 and 3 parameters models) are evaluated and fitted with the equilibrium adsorption data. As mentioned in “Evaluation of isotherms and kinetic models” section, the model parameters were achieved from both linear and non-linear expressions of adsorption isotherm models. Hence, the isotherm information obtained from the conventional linear method and DEO-based non-linear approach for the equilibrium data for diazinon adsorption onto pumice adsorbent is presented in Fig. 8. These results confirm that the model parameters evaluated from non-linear expression better represent the equilibrium isotherms. It is observed that diazinon adsorption onto pumice follows Langmuir and Temkin models, indicating that the monolayer adsorption takes place on the surface, and the adsorption is characterized by a uniform distribution of binding energies. The DEO-based model parameters of Langmuir and Temkin models represent the actual adsorption process and hence resulted in a higher R2 of 0.995 and 0.994, respectively. These outcomes are very similar to the results reported by Nikzad et al.50, who studied the diazinon adsorption using magnetic guar gum-montmorillonite.
Figure 8.
Performance of parameters estimated by linear and non-linear approaches to fit isotherm models that interpret the adsorption of diazinon by pumice (pumice dosage = 1 g/L, and contact time = 30 min, and pH = 3).
Even though the R2 value is the metric that is used by most researchers to validate the model predictions, but this metric cannot be representing the true error residuals. Hence, this cannot be the only metric to appraise the performance. Sometimes, researchers calculate another statistical metric like RMSE. This metric definitely provides good information on the overall error residuals but does not give enough information on the error distribution like overfitted or underfitting. Therefore, other important metrics like SAE, SSE and ARE should be determined. These metrics for the isotherm models that were employed to represent the diazinon adsorption onto pumice adsorbent are evaluated and shown in Table 2. It can be observed that the RMSE values for Langmuir and Temkin models are the lowest for optimized non-linear model parameters, thus further confirming that the non-linear model captures the inherent mechanisms. The lower values of other metrics also confirm the same. These results depict that a monolayer adsorption phenomenon occurs, and uniform distribution of binding energies at the adsorbent surface occurs during the adsorption of diazinon by pumice from an aqueous solution.
Table 2.
Isotherm models for adsorption of diazinon onto pumice*.
| Models → | Freundlich | Langmuir | Temkin | Redlich–Peterson | Sips | Toth | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Statistical metrics ↓ | L | NL | L | NL | L | NL | L | NL | L | NL | L | NL |
| Parameters → |
qe: 20.65 bF: 0.472 |
KF: 20.27 bF: 0.433 |
KL: 10.48 bL: 0.159 |
KL: 10.42 bL: 0.161 |
BT: 1.412 KT: 2.33 |
BT: 1.370 KT: 2.43 |
KR: 1.813 aR: 0.220 α: 0.923 |
KR: 1.763 aR: 0.191 α: 0.964 |
Ks: 8.923 bs: 0.1592 ns: 0.814 |
Ks: 10.54 bs: 0.162 ns: 0.962 |
Kth: 10.35 bth: 0.159 nth: 0.986 |
Kth: 10.73 bth: 0.180 nth: 0.947 |
| R2 | 0.972 | 0.981 | 0.993 | 0.995 | 0.989 | 0.994 | 0.982 | 0.989 | 0.978 | 0.986 | 0.983 | 0.989 |
| SAE | 1.474 | 1.258 | 0.533 | 0.529 | 0.882 | 0.540 | 0.580 | 0.584 | 0.661 | 0.564 | 0.989 | 0.573 |
| SSE | 0.458 | 0.366 | 0.097 | 0.095 | 0.264 | 0.084 | 0.104 | 0.094 | 0.178 | 0.096 | 0.247 | 0.096 |
| ARE | 12.883 | 12.762 | 3.917 | 3.882 | 6.769 | 4.342 | 4.629 | 4.664 | 4.725 | 4.343 | 6.346 | 4.489 |
| RMSE | 0.338 | 0.282 | 0.156 | 0.149 | 0.257 | 0.145 | 0.161 | 0.154 | 0.211 | 0.155 | 0.248 | 0.155 |
*Linear (L); non-linear (NL).
are qe values of experimental and predicted values respectively. p is the number of parameters; n is the number of experimental runs.
Units: Langmuir: KL (mg/g). bL (L/mg). Freundlich: KF (mg1-(1/n) L(1/n) g-1) and bF is dimensionless. Temkin: KT (L/mg). bT (J/mol). Redlich – Peterson: KR (L/g) and aR(L/mg) nP and nR is dimensionless. Sips: KS,(mg/g). bs (L/mg)n and ns is dimensionless. Toth: Kth (L/g). bth (mg/L)n and nth is dimensionless exponent.
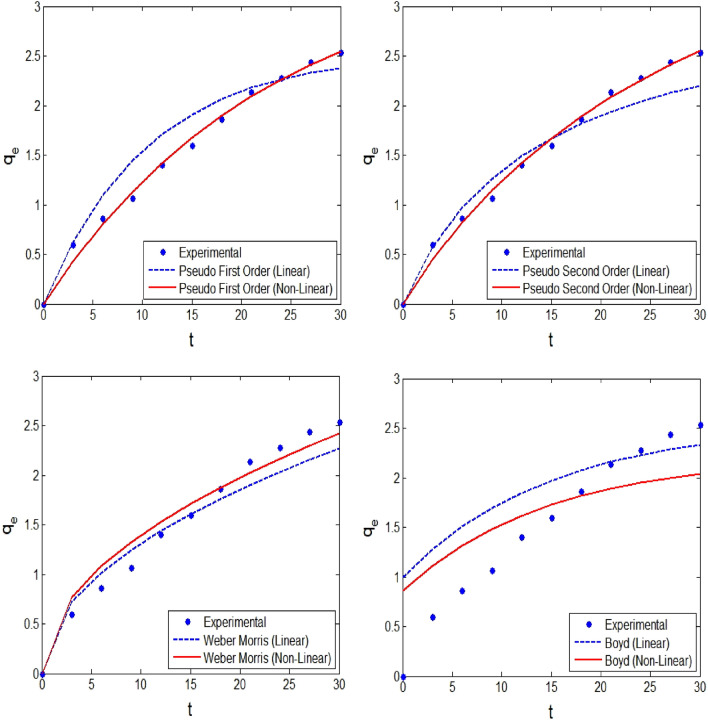
The adsorption rate of the adsorbent in the solution for diazinon can be understood by investigating the kinetic behaviour of the adsorption process. The adsorption kinetics were analyzed using the conventional and inter-molecular diffusion kinetic models. The experiments are conducted in the range of 3–30 min. These kinetic models are generally non-linear expressions, but most researchers linearize these models to evaluate the respective model parameters using the least square regression fit. As mentioned in recent literature29, the model parameters evaluated will under/overestimate and hence misinterpret the mechanisms in the adsorption process. Therefore, in this study, DEO is implemented to evaluate the model parameters from the non-linear kinetic models. The performance “of these optimized model parameters (non-linear model) against the conventional least square fit is shown in Fig. 9. It is evident that DEO-based model parameters better represent the kinetic behaviour and hence can be used to interpret the adsorption rate and kinetics involved in the diazinon adsorption onto pumice. From the result presented in Fig. 9, it is seen that the diazinon adsorption onto pumice follows pseudo 1st and 2nd order kinetics, which resulted in R2 > 0.99. These outcomes are very similar to the reported results for diazinon removal from aqueous solutions50,51.
Figure 9.
Kinetic plots for the adsorption of diazinon by pumice (initial diazinon concentration = 50 mg/L, pumice dosage = 1 g/L, and pH = 3).
The important statistical metrics that appraise the significance of linear and non-linear approaches for interpreting kinetics using various kinetic models are presented in Table 3. It is seen that the DEO-based kinetic parameters better capture the inherent kinetic behaviour in diazinon adsorption onto pumice, and hence, resulted in higher R2 and lower ARE, SSE, SAE, and RMSE. Therefore, these statistical metrics further confirm the praiseworthy and creditability of the DEO approach.
Table 3.
Kinetic models for diazinon removal by pumice**.
| Models → | PFO | PSO | Weber—Morris | Boyd | ||||
|---|---|---|---|---|---|---|---|---|
| Statistical metrics ↓ | L | NL | L | NL | L | NL | L | NL |
| Parameters → |
K1: 0.0012 qe: 84.32 |
K1: 0.044 qe: 3.49 |
K2: 0.022 qe: 3.233 |
K2: 0.0054 qe: 5.4342 |
Kid:0.415 | Kid:0.442 |
B: 0.0675 qe: 2.533 |
B: 0.068 qe: 2.210 |
| R2 | 0.9368 | 0.9910 | 0.9623 | 0.9914 | 0.9796 | 0.9852 | 0.9515 | 0.9709 |
| SAE | 64.835 | 27.126 | 47.137 | 25.581 | 53.080 | 51.808 | 164.801 | 133.266 |
| SSE | 0.460 | 0.048 | 0.371 | 0.044 | 0.346 | 0.229 | 1.711 | 1.320 |
| ARE | 1.758 | 0.524 | 1.622 | 0.514 | 1.622 | 1.372 | 3.410 | 3.292 |
| RMSE | 0.339 | 0.109 | 0.305 | 0.105 | 0.294 | 0.239 | 0.654 | 0.574 |
**Linear (L). Non-linear (NL). Pseudo first order (PFO) and Pseudo second-order (PSO).
are the qe values of the experimental and predicted values, respectively.
p is the number of parameters. n is the number of experimental runs.
Pseudo-first-order model (PFO) & pseudo-second-order model (PSO).
Units: qe (mg/g), K1 (min−1), K2 (g mg−1 min-1), Kid (mg/g min0.5), Di (cm2).
Thermodynamic studies of diazinon pesticide adsorption using pumice adsorption
In this work, thermodynamic studies were performed at the optimal conditions of the process variables and temperatures of 293, 303, 318, and 323 K. The thermodynamic equilibrium constant (Ke°) is calculated from the Eq. (a.3). From the isotherm studies, it was observed that diazinon onto pumice follows the Langmuir isotherm model; hence the KL is the Langmuir equilibrium constant. After that, (L/mol) is calculated by multiplying with a molecular weight of adsorbate and translating it into appropriate units. This value is multiplied with the unitary standard concentration of the adsorbate (1 mol/L) and dividing with the activity coefficient (γ). Since the adsorbate solution in this study is much diluted, hence the activity coefficient can be assumed as unity. The important parameters like standard enthalpy (ΔH°), Gibbs free energy (ΔG°) and standard entropy (ΔS°) are obtained from the thermodynamic relations given in Eq. (a.1) & Eq. (a.2) are presented in Table S7. The computed values of ΔG° were negative, showing a natural adsorption process, and it is decreasing with the increase of temperature. Thus, higher temperatures supported the diazinon adsorption onto pumice due to a greater force of adsorption. The positiveness of ΔH° depicts that the endothermic nature of the adsorption process. Also, the positive values of ΔS° indicate the increase in randomness at the solid–liquid interface during the adsorption process, as well as a greater affinity between diazinon and adsorbent.
Conclusions
A low-cost and natural pumice adsorbent was used to remove organophosphorus diazinon pesticide from water bodies. The characterization of pumice adsorbent before and after the adsorption process is investigated by analytical instruments. To understand the influence of independent process variables like pH, initial diazinon concentration, pumice adsorbent, and contact time on the diazinon pesticide removal, a systematic statistical approach is used, and the experimental design matrix is developed. The RSM-CCD framework modeled diazinon removal, and the interactive effects of process variables on the removal percentage are examined. To predict the diazinon removal (%) at different process conditions, a quadratic model is developed using ANOVA in RSM. The model validation indicated that this quadratic model is well-fitted model with R2 = 0.9997, p-value < 0.001, and Lack of fit = 0.872. ANN approach was used to develop a data-driven model. This approach suggested a topology of 4:8:1 with backpropagation ANN, whose model predictions resulted in R2 = 0.9991. To identify the optimum process variables that result in the highest removal efficiency, GA and RSM techniques are used. RSM based optimization results showed the maximum diazinon removal efficiency of 76.3% is obtained at initial diazinon concentration = 6.288 mg/L, pH = 3, pumice dosage = 4 g/L, and contact time = 30 min. The GA optimization results were very similar to the RSM technique. The pumice showed a promising result of regeneration. The ionic strength results showed that the removal efficiency is suppressed significantly at acidic pH, whereas it exhibits no significant decrease at neutral and basic pH’s. Diazinon adsorption isotherms were also investigated, and the experimental data follows Langmuir isotherm. It was found that the diazinon adsorption could be well described by the pseudo-first and second-order kinetic models. Diazinon removal by pumice showed the favourable, spontaneous endothermic nature of the adsorption process. Therefore, pumice can be considered as a potential efficient adsorbent for the removal of pesticides from aqueous solutions.
Supplementary Information
Acknowledgements
This research has been supported by the Islamic Azad University and the Tehran University of Medical Sciences.
Author contributions
M.H.D., A.H.H., B.Y.: conceptualization, methodology, software, supervision. M.H.D., A.H.H., B.Y.: writing—review and editing. M.H.D., A.H. H., B.Y.: data curation, writing—original draft. M.H.D., A.H. H., M.Y., Z.H.: visualization, investigation. R.R.K., M.S., M.S., A.Z.: software, validation. M.H.D., B.Y., R.R.K.: Writing—re-view and editing.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Mohammad Hadi Dehghani, Email: hdehghani@tums.ac.ir.
Bahareh Younesi, Email: b_unesei@yahoo.com.
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-021-91178-3.
References
- 1.Ehrampoush MH, Sadeghi A, Ghaneian MT, Bonyadi Z. Optimization of diazinon biodegradation from aqueous solutions by Saccharomyces cerevisiae using response surface methodology. AMB Express. 2017;7:68. doi: 10.1186/s13568-017-0366-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Shayeghi M, Khobdel M, Bagheri F, Abtai M. Azynfosmethyl and diazinon residues in Qarasu River and Gorganrood in Golestan Province. J. Public Health Health Res. Inst. 2008;6:75–82. [Google Scholar]
- 3.Toolabi A, Malakootian M, Ghaneian MT, Esrafili A, Ehrampoush MH, AskarShahi M, et al. Modeling photocatalytic degradation of diazinon from aqueous solutions and effluent toxicity risk assessment using Escherichia coli LMG 15862. AMB Express. 2018;8:59. doi: 10.1186/s13568-018-0589-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Arfaeinia H, Rezaei H, Sharaf K, Moradi M, Pasalari H, Hashemi SE. Application of ozone/magnetic graphene oxide for degradation of diazinon pesticide from aqueous solutions. Desalin. Water Treat. 2018;107:127–135. doi: 10.5004/dwt.2018.22158. [DOI] [Google Scholar]
- 5.Mahour R, Khan MF, Forbes S, Perez-Estrada LA. Pesticides and herbicides. Water Environ. Res. 2014;86:1545–1578. doi: 10.2175/106143014X14031280668777. [DOI] [Google Scholar]
- 6.Gao Y, Wu J, Wang J, Fan Y, Zhang S, Dai W. A Novel Multifunctional p-Type Semiconductor@ MOFs Nanoporous Platform for Simultaneous Sensing and Photodegradation of Tetracycline. ACS Appl. Mater. Interfaces. 2020;12:11036–11044. doi: 10.1021/acsami.9b23314. [DOI] [PubMed] [Google Scholar]
- 7.Hossaini H, Moussavi G, Farrokhi M. Oxidation of diazinon in cns-ZnO/LED photocatalytic process: Catalyst preparation, photocatalytic examination, and toxicity bioassay of oxidation by-products. Sep. Purif. Technol. 2017;174:320–330. doi: 10.1016/j.seppur.2016.11.005. [DOI] [Google Scholar]
- 8.Vlyssides A, Arapoglou D, Mai S, Barampouti EM. Electrochemical detoxification of four phosphorothioate obsolete pesticides stocks. Chemosphere. 2005;58:439–447. doi: 10.1016/j.chemosphere.2004.09.037. [DOI] [PubMed] [Google Scholar]
- 9.Plakas KV, Karabelas AJ. Removal of pesticides from water by NF and RO membranes—a review. Desalination. 2012;287:255–265. doi: 10.1016/j.desal.2011.08.003. [DOI] [Google Scholar]
- 10.Ouznadji ZB, Sahmoune MN, Mezenner NY. Adsorptive removal of diazinon: kinetic and equilibrium study. Desalin. Water Treat. 2016;57:1880–1889. doi: 10.1080/19443994.2014.978386. [DOI] [Google Scholar]
- 11.Zhou Y, Yu L, Gao Y, Wu J, Dai W. Effective capture of cefradines in water with a highly stable Zr (IV)-based bimetal–organic Framework. Ind. Eng. Chem. Res. 2019;58:19202–19210. doi: 10.1021/acs.iecr.9b03815. [DOI] [Google Scholar]
- 12.Abedi-Koupai J, Nasri Z, Talebi K, Mamanpoush A, Mousavi S. Investigation of Zayandehrud water pollution by diazinon and its assimilative capacity. JWSS Isfahan Univ. Technol. 2011;15:1–10. [Google Scholar]
- 13.Salman JM, Njoku VO, Hameed BH. Adsorption of pesticides from aqueous solution onto banana stalk activated carbon. Chem. Eng. J. 2011;174:41–48. doi: 10.1016/j.cej.2011.08.026. [DOI] [Google Scholar]
- 14.Sharbatmaleki M, Borghei SM. Performance of pumice stone as a packing in fixed-bed aerobic bioreactor. J. Water Wastewater. 2005;56:62–71. [Google Scholar]
- 15.Babakhani N, Reyahi-Khoram M, Sobhanardakani S. Kinetic study of heavy metal ions removal from aqueous solutions using activated pumice stone. Environ. Health Eng. Manag. J. 2016;3:47–53. [Google Scholar]
- 16.Ouardi ME, Alahiane S, Qourzal S, Abaamrane A, Assabbane A, Douch J. Removal of carbaryl pesticide from aqueous solution by adsorption on local clay in Agadir. Am. J. Anal. Chem. 2013;4:72–79. doi: 10.4236/ajac.2013.47A010. [DOI] [Google Scholar]
- 17.HajiBagher S, Tehrani M, Nourisepehr M, Zarabi M, Rahimzadeh M. Investigation of cephalexin absorption using pumice from aqueous solution and the effect common ions in water in removal it. Alborz Univ. Med. J. 2017;6:241–256. doi: 10.29252/aums.6.4.241. [DOI] [Google Scholar]
- 18.Anikoh G, Adesida P, Afolabi O. Investigation of physical and mechanical properties of selected rock types in Kogi State using hardness tests. J. Min. World Express MWE. 2015;4:37. doi: 10.14355/mwe.2015.04.004. [DOI] [Google Scholar]
- 19.Hadi N, Alizadeh R, Niaei A. Synthesis and characterization of MFI zeolite nanosheets for optimizing the dominant operational conditions of methanol to propylene process. J. Nanostruct. 2019;9:51–73. [Google Scholar]
- 20.Asfaram A, Ghaedi M, Azqhandi MA, Goudarzi A, Dastkhoon MJRA. Statistical experimental design, least squares-support vector machine (LS-SVM) and artificial neural network (ANN) methods for modeling the facilitated adsorption of methylene blue dye. RSC Adv. 2016;6:40502–40516. doi: 10.1039/C6RA01874B. [DOI] [Google Scholar]
- 21.Krishna D, Sree RP. Artificial neural network and response surface methodology approach for modeling and optimization of chromium (VI) adsorption from waste water using Ragi husk powder. J. Indian Chem. Eng. 2013;55:200–222. [Google Scholar]
- 22.Cao R, Fan M, Hu J, Ruan W, Wu X, Wei X. Artificial intelligence based optimization for the Se (IV) removal from aqueous solution by reduced graphene oxide-supported nanoscale zero-valent iron composites. Materials. 2018;11:428. doi: 10.3390/ma11030428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kim Z, Shin Y, Yu J, Kim G, Hwang S. Development of NOx removal process for LNG evaporation system: Comparative assessment between response surface methodology (RSM) and artificial neural network (ANN) J. Ind. Eng. Chem. 2019;74:136–147. doi: 10.1016/j.jiec.2019.02.020. [DOI] [Google Scholar]
- 24.Mitra T, Bar N, Das SK. Rice husk: Green adsorbent for Pb (II) and Cr (VI) removal from aqueous solution—column study and GA–NN modeling. SN Appl. Sci. 2019;1:486. doi: 10.1007/s42452-019-0513-5. [DOI] [Google Scholar]
- 25.Dil EA, Ghaedi M, Ghezelbash GR, Asfaram A, Ghaedi AM, Mehrabi F. Modeling and optimization of Hg2+ ion biosorption by live yeast Yarrowia lipolytica 70562 from aqueous solutions under artificial neural network-genetic algorithm and response surface methodology: kinetic and equilibrium study. RSC Adv. 2016;6:54149–54161. doi: 10.1039/C6RA11292G. [DOI] [Google Scholar]
- 26.Mohan S, Singh Y, Verma DK, Hasan SHJPS, Protection E. Synthesis of CuO nanoparticles through green route using Citrus limon juice and its application as nanosorbent for Cr (VI) remediation: process optimization with RSM and ANN-GA based model. Process. Saf. Environ. Prot. 2015;96:156–166. doi: 10.1016/j.psep.2015.05.005. [DOI] [Google Scholar]
- 27.Lima EC, Hosseini-Bandegharaei A, Moreno-Piraján JC, Anastopoulos I. A critical review of the estimation of the thermodynamic parameters on adsorption equilibria. Wrong use of equilibrium constant in the Van't Hoof equation for calculation of thermodynamic parameters of adsorption. J. Mol. Liq. 2019;273:425–434. doi: 10.1016/j.molliq.2018.10.048. [DOI] [Google Scholar]
- 28.E.C. Lima, A. Hosseini-Bandegharaei, I. Anastopoulos, Response to some remarks on a critical review of the estimation of the thermodynamic parameters on adsorption equilibria Wrong use of equilibrium constant in the van't Hoff equation for calculation of thermodynamic parameters of adsorption. J. Mol. Liq.273 (2019) 425–434., J. Mol. Liq.280 (2019) 298-300.
- 29.Hairuddin MN, Mubarak NM, Khalid M, Abdullah EC, Walvekar R, Karri RR. Magnetic palm kernel biochar potential route for phenol removal from wastewater. Environ. Sci. Pollut. Res. 2019;26:35183–35197. doi: 10.1007/s11356-019-06524-w. [DOI] [PubMed] [Google Scholar]
- 30.P. Pookmanee, A. Wannawek, S. Satienperakul, R. Putharod, N. Laorodphan, S. Sangsrichan, et al., editors. Characterization of diatomite, leonardite and pumice. Materials Science Forum; 2016: Trans Tech Publ.
- 31.Shokoohi R, Salari M, Safari R, Zolghadr Nasab H, Shanehsaz S. Modelling and optimisation of catalytic ozonation process assisted by ZrO2-pumice/H2O2 in the degradation of Rhodamine B dye from aqueous environment. Int. J. Environ. Anal. Chem. 2020 doi: 10.1080/03067319.2019.1704748. [DOI] [Google Scholar]
- 32.Sepehr MN, Sivasankar V, Zarrabi M, Kumar MS. Surface modification of pumice enhancing its fluoride adsorption capacity: An insight into kinetic and thermodynamic studies. Chem. Eng. J. 2013;228:192–204. doi: 10.1016/j.cej.2013.04.089. [DOI] [Google Scholar]
- 33.Li J, Li B, Huang H, Lv X, Zhao N, Guo G, et al. Removal of phosphate from aqueous solution by dolomite-modified biochar derived from urban dewatered sewage sludge. Sci. Total Environ. 2019;687:460–469. doi: 10.1016/j.scitotenv.2019.05.400. [DOI] [PubMed] [Google Scholar]
- 34.Körlü AE, Yapar S, Perinçek S, Yılmaz H, Bağıran C. Dye removal from textile waste water through the adsorption by pumice used in stone washing. Autex Res. J. 2015;15:158–163. doi: 10.1515/aut-2015-0012. [DOI] [Google Scholar]
- 35.Mohammadi AA, Zarei A, Alidadi H, Afsharnia M, Shams M. Two-dimensional zeolitic imidazolate framework-8 for efficient removal of phosphate from water, process modeling, optimization, kinetic, and isotherm studies. Desalin. Water Treat. 2018;129:244–254. doi: 10.5004/dwt.2018.22813. [DOI] [Google Scholar]
- 36.Moussavi G, Hosseini H, Alahabadi A. The investigation of diazinon pesticide removal from contaminated water by adsorption onto NH4Cl-induced activated carbon. Chem. Eng. J. 2013;214:172–179. doi: 10.1016/j.cej.2012.10.034. [DOI] [Google Scholar]
- 37.Farmany A, Mortazavi SS, Mahdavi H. Ultrasond-assisted synthesis of Fe3O4/SiO2 core/shell with enhanced adsorption capacity for diazinon removal. J. Magn. Magn. Mater. 2016;416:75–80. doi: 10.1016/j.jmmm.2016.04.007. [DOI] [Google Scholar]
- 38.Jonidi-Jafari A, Shirzad-Siboni M, Yang J-K, Naimi-Joubani M, Farrokhi M. Photocatalytic degradation of diazinon with illuminated ZnO–TiO2 composite. J. Taiwan Inst. Chem. Eng. 2015;50:100–107. doi: 10.1016/j.jtice.2014.12.020. [DOI] [Google Scholar]
- 39.Kabwadza-Corner P, Matsue N, Johan E, Henmi T. Mechanism of Diazinon adsorption on iron modified montmorillonite. Am. J. Anal. Chem. 2014;5:70. doi: 10.4236/ajac.2014.52011. [DOI] [Google Scholar]
- 40.Kalantary RR, Shahamat YD, Farzadkia M, Esrafili A, Asgharnia H. Heterogeneous photocatalytic degradation of diazinon in water using nano-TiO2: Modeling and intermediates. Eur J Exp. Biol. 2014;4:186–194. [Google Scholar]
- 41.Liu T, Xu S, Lu S, Qin P, Bi B, Ding H, et al. A review on removal of organophosphorus pesticides in constructed wetland: performance, mechanism and influencing factors. Sci. Total Environ. 2018;651:2247–2268. doi: 10.1016/j.scitotenv.2018.10.087. [DOI] [PubMed] [Google Scholar]
- 42.Rani M, Shanker U. Effective adsorption and enhanced degradation of various pesticides from aqueous solution by Prussian blue nanorods. J. Environ. Chem. Eng. 2018;6:1512–1521. doi: 10.1016/j.jece.2018.01.060. [DOI] [Google Scholar]
- 43.Moghaddam MH, Nabizadeh R, Dehghani MH, Akbarpour B, Azari A, Yousefi M. Performance investigation of Zeolitic Imidazolate Framework–8 (ZIF-8) in the removal of trichloroethylene from aqueous solutions. Microchem. J. 2019;150:104185. doi: 10.1016/j.microc.2019.104185. [DOI] [Google Scholar]
- 44.Bootharaju M, Pradeep T. Understanding the degradation pathway of the pesticide, chlorpyrifos by noble metal nanoparticles. Langmuir. 2012;28:2671–2679. doi: 10.1021/la2050515. [DOI] [PubMed] [Google Scholar]
- 45.Heibati B, Rodriguez-Couto S, Amrane A, Rafatullah M, Hawari A, Al-Ghouti MA. Uptake of Reactive Black 5 by pumice and walnut activated carbon: chemistry and adsorption mechanisms. J. Ind. Eng. Chem. 2014;20:2939–2947. doi: 10.1016/j.jiec.2013.10.063. [DOI] [Google Scholar]
- 46.Al-Degs YS, El-Barghouthi MI, El-Sheikh AH, Walker GM. Effect of solution pH, ionic strength, and temperature on adsorption behavior of reactive dyes on activated carbon. Dyes Pigm. 2008;77:16–23. doi: 10.1016/j.dyepig.2007.03.001. [DOI] [Google Scholar]
- 47.Zhang Y, Zhu C, Liu F, Yuan Y, Wu H, Li A. Effects of ionic strength on removal of toxic pollutants from aqueous media with multifarious adsorbents: a review. Sci. Total Environ. 2019;646:265–279. doi: 10.1016/j.scitotenv.2018.07.279. [DOI] [PubMed] [Google Scholar]
- 48.Zulfikar M, Novita E, Hertadi R, Djajanti S. Removal of humic acid from peat water using untreated powdered eggshell as a low cost adsorbent. Int. J. Environ. Sci. Technol. 2013;10:1357–1366. doi: 10.1007/s13762-013-0204-5. [DOI] [Google Scholar]
- 49.Tomczak E. Application of ANN and EA for description of metal ions sorption on chitosan foamed structure—equilibrium and dynamics of packed column. Comput. Chem. Eng. 2011;35:226–235. doi: 10.1016/j.compchemeng.2010.05.012. [DOI] [Google Scholar]
- 50.Nikzad S, Amooey AA, Alinejad-Mir A. Adsorption of diazinon from aqueous solutions by magnetic guar gum-montmorillonite. Chem. Data Collect. 2019;20:100187. doi: 10.1016/j.cdc.2019.100187. [DOI] [Google Scholar]
- 51.Gunasekara AS, Rubin AL, Goh KS, Spurlock FC, Tjeerdema RS. Environmental fate and toxicology of carbaryl. Rev. Environ. Contam. Toxicol. 2008;196:95–121. doi: 10.1007/978-0-387-78444-1_4. [DOI] [PubMed] [Google Scholar]
- 52.Armaghan M, Amini MM. Adsorption of diazinon and fenitrothion on nanocrystalline magnesium oxides. Arab. J. Chem. 2017;10:91–99. doi: 10.1016/j.arabjc.2014.01.002. [DOI] [Google Scholar]
- 53.Atikah Baharum N, Mohmad Nasir H, Yusoff Ishak M, Mohd Isa N, AliHassan M, ZaharinAris A. Highly efficient removal of diazinon pesticide from aqueous solutions by using coconut shell-modified biochar. Arab. J. Chem. 2020;13:6106. doi: 10.1016/j.arabjc.2020.05.011. [DOI] [Google Scholar]
- 54.Firozjaee TT, Mehrdadi N, Baghdadi M, Bidhendi G. The removal of diazinon from aqueous solution by chitosan/carbon nanotube adsorbent. Desalin. Water. Treat. 2017;79:291–300. doi: 10.5004/dwt.2017.20794. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.