Patient-Specific 3D Bioprinted Models of Developing Human Heart

Abstract

The heart is the first organ to develop in the human embryo through a series of complex chronological processes, many of which critically rely on the interplay between cells and the dynamic microenvironment. Tight spatiotemporal regulation of these interactions is key in heart development and diseases. Due to suboptimal experimental models, however, there is little knowledge on the role of microenvironmental cues in the heart development. This study investigates the use of 3D bioprinting and perfusion bioreactor technologies to create bioartificial constructs that can serve as high-fidelity models of the developing human heart. Bioprinted hydrogel-based, anatomically accurate models of the human embryonic heart tube (e-HT, day 22) and fetal left ventricle (f-LV, week 33) were perfused and analyzed both computationally and experimentally using ultrasound and magnetic resonance imaging. Results demonstrated comparable and precise flow hemodynamic patterns within the 3D space. We demonstrated human endothelial cell growth and endothelialization within the bioprinted e-HT and f-LV constructs, which varied significantly in varying cardiac geometries and under flow. This study introduces the first generation of anatomically accurate, 3D functional models of developing human heart at different stages. This platform enables precise tuning of microenvironmental factors, such as flow and geometry, thus allowing the study of normal developmental processes and underlying diseases.

1. Introduction

The human heart – the first organ to form during embryogenesis – is foundational to the development and survival of a growing fetus. Cardiac morphogenesis is highlighted by seminal stages where cardiac precursor cells migrate and expand to form two endocardial tubes by day 20 of development.^{[1, 2]} The endocardial tubes merge into a singular linear heart tube (HT) by day 22, which folds into a primitive atrium and ventricle by day 28 capable of contracting.^{[2, 3]} Valvular features and arterial trunks arise as the heart septates into four chambers by day 56.^[4] The architecture for this dynamic, synchronized mechanical pump of four interdependent chambers is now framed to scale in size and support a new life. This complex and delicate process of formation has been shown to be, in part, dependent upon a strict coordination of a variety of biomechanical and chemical stimuli (signaling and transcriptional networks) within time-sensitive windows.^[5] If these are absent or disturbed, structural and, eventually, functional abnormalities may occur.^[6] However, the balance between these mechanisms that sustain normal human heart development are not well known. Therefore, studying the intricate interplay of various cell–cell and cell–extracellular matrix (ECM) interactions that are active during heart development can help unravel the mechanisms underlying various congenital cardiac anomalies.^{[6, 7]}

Ex vivo and in vivo (animal) models of heart development have been extensively explored, including zebrafish,^[8] chick,^[9] and mouse^[10] models. Using these models, much of the heart looping processes were delineated. Cardiac tissue mechanics and hemodynamic literature have described fluid and solid motion and forces at different stages.^[11] The extra and intra cellular composition of tissue types have also been traced as the developing heart evolves.^[12] However, these animal models cannot be assumed to be fully analogous with human heart development.^[13] Ethical principles and technological limitations have made early human cardiogenesis difficult to observe.^[14] Furthermore, the pumping mechanism that drives flow in the linear heart tube and looping stages is not fully known.^[15] Therefore, the need for in vitro models that can faithfully and accurately recapitulate the tissue, cellular, and molecular- level mechanisms of heart development is prominent.^{[16, 17]}

Cardiovascular tissue engineering has grown dramatically since the advent of techniques to differentiate various pluripotent stem cell sources into cardiomyocytes (CMs) and other cardiac cells, hence generating 3D structures that resemble the native cardiac muscle tissue.^[18] Engineered in vitro models of cardiac development have been used to study early cardiac development via stem cell differentiation to cardiac progenitor cells or CMs.^{[17, 19, 20]} Despite the strides to produce fetal-like cardiac tissues, these in vitro models lack the ability to recapitulate the native three-dimensional (3D) environment.^[21] Most reports explore planar sheets of cardiac tissues with thicknesses of only a few cells, due to the nutrient and spatial patterning constraints caused by inadequate vasculature and diffusion.^[22] Additionally, these studies often do not mimic the temporal changes in mechanical and chemical stimuli that precisely shape the developing heart, particularly during the folding and septation stages.

3D bioprinting technologies have recently emerged and evolved alongside the cardiovascular tissue engineering field, offering great promise to overcome many obstacles in the in vitro modeling of functional cardiovascular tissues.^{[23–26, 27]} 3D printing is an additive manufacturing technique that enables spatial patterning of materials into a 3D construct. Bioprinting emerged when 3D printing technology was adapted for biological purposes. This often involves biologically derived materials (i.e. bioinks), consisting of living cells, biomaterials (hydrogels), and a variety of small molecules (e.g. growth factors), to replicate specific 3D tissue geometries.^{[28, 29]} For cardiovascular purposes, 3D bioprinting has been applied toward creating various components, including myocardium,^{[26, 30]} heart valves,^[31] endovascular stents,^[32] and their associated disease states.^[33] Advantages of 3D bioprinting include its ability to selectively pattern multiple biomaterials and/or cell types.^{[23, 25]} Hybrid bioinks, such as gelatin methacrylate (gelMA), that merge beneficial natural and artificial characteristics enable heightened control of construct stiffness. Limitations of 3D bioprinting include a lack of repeatability, construct stability, and cell viability. Mechanical stability of constructs, even with sacrificial supports, is weak, easily breaks, and limits geometric complexity. Maintaining sufficient sterility, temperature, nutrients, and mechanical shielding for cell viability complicates 3D bioprinting approaches.

In this study, we examined 3D models of the human heart at multiple developmental stages: linear heart tube at embryonic day 22 (e-HT) and the left ventricle at fetal week 33 (f-LV). With synthetic models, we investigated the fluid mechanics within patient-derived geometries at these stages. 3D ultrasound and 4D magnetic resonance imaging (MRI) techniques were used to generate temporal and 3D spatial visualizations of flow, to recapitulate various stages of cardiac morphogenesis. Computational fluid dynamic (CFD) models were simultaneously produced to compare with physical flow parameters. Tissue engineered e-HT and f-LV models were also 3D bioprinted using hydrogels and seeded with endothelial cells, demonstrating significant cell viability and growth under both static and dynamic flow conditions. This study demonstrates a novel platform for studying and validating flows in complex, patient-derived geometries to visualize early mechanical flow patterns in developing human hearts. Further, we demonstrate that the bioprinted models maintain high fidelity compared to the reference (clinical) data. Adapting these capabilities to complex, 3D bioprinted constructs enables a new – and necessary – level of controlled tissue engineering, especially in tissues dictated by flow.

2. Results and Discussion

Many of the critical processes of the human heart development rely on the close interplay between cells and the dynamic cardiac tissue microenvironment.^[34] A tight spatiotemporal regulation of these interactions is key in heart development and various diseases.^[35] Due to suboptimal experimental models, however, there is little knowledge about the effects of microenvironmental cues on heart development. In this study, we aimed to establish anatomically accurate, 3D in vitro models of the developing human heart as a platform to study the complex interplay between tissue geometry, flow hemodynamics, and cellular response. Incorporation of medical imaging, 3D bioprinting, perfusion bioreactors, CFD modeling, and experimental flow imaging and analysis tools enabled us to create biological replicates of embryonic and fetal human heart at high precision, consistency, and through-put.

2.1. Fabrication of Patient-Derived 3D Models of Embryonic and Fetal Heart

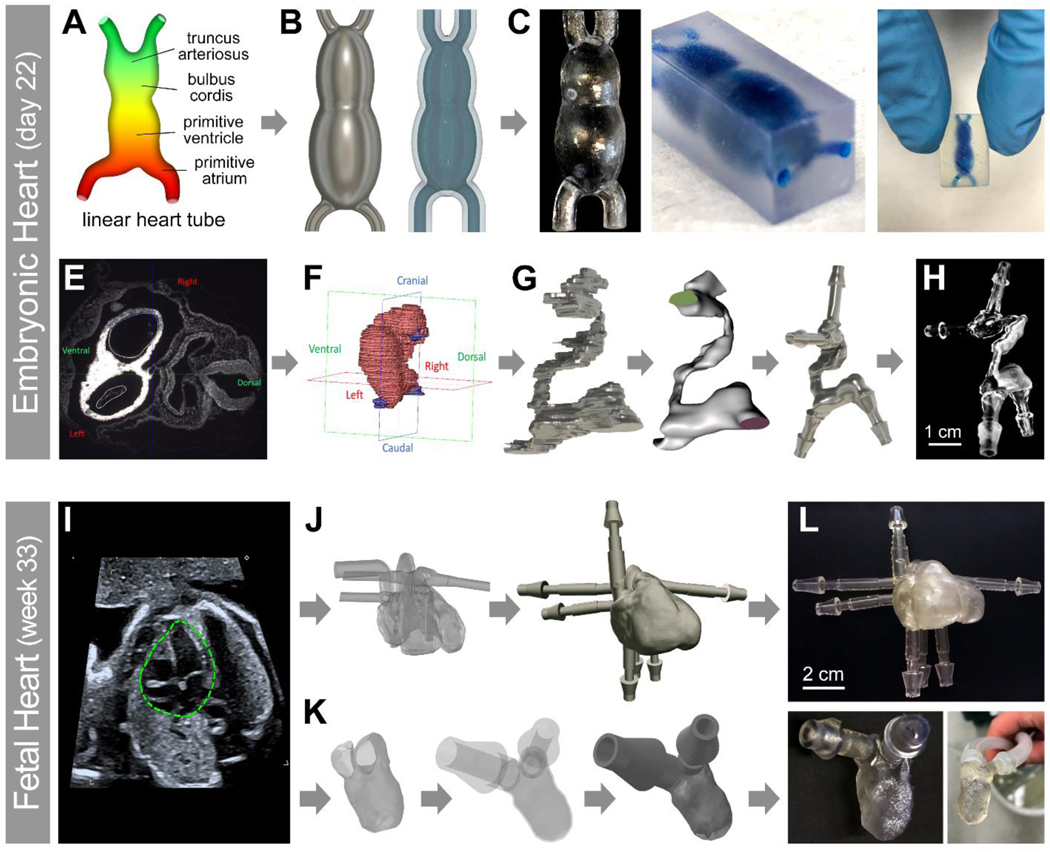
We used two different methods to create human e-HT constructs. First, a CAD model and subsequently an STL file with simplified geometry were designed to closely mimic the shape and geometry of a linear e-HT (Figure 1A–B). Briefly, hollowed and smoothed STL models were 3D printed using a clear resin with resolution that allowed for linear tube reconstruction in both hollowed from (positive model) and embedded within a resin block (negative model) (Figure 1C, left and right panels, respectively). In second approach, 3D reconstructed histological data of a developing human heart at Carnegie stage 10 (21–23 days old) was used (collaboration with the 3D Atlas of Human Embryology) to create a patient-derived STL model of e-HT (Figure 1E–G).^[36] The 3D printed anatomically accurate e-HT model showed adequate resolution, recapitulating the complex in vivo geometry (Figure 1H). A similar approach was used to reconstruct patient specific 3D STL models and 3D print a 30-week fetal human heart (both the 4-chamber heart and the isolated LV) using the patient’s echocardiography data (Figure 1I–L).^[37]

Figure 1: Experimental workflow used to create patient-derived 3D printed heart models at varying developmental stages.

A-H: A 3D model of an embryonic human heart at Carnegie stage 10 (21–23 days old, e-HT) was made either through CAD modeling of an idealized structure (A-C), or using the actual human data obtained in collaboration with the 3D Atlas of Human Embryology^[36] (E-H). The anatomical heart tube model contained the primitive cardiovascular system (E) which was trimmed (F-H) to only include the linear heart structure. I-L: A patient specific fetal left ventricle (f-LV) was acquired from fetal echocardiography of the human heart (week 33).^[37] The full heart model (I) was trimmed (J-L) at the mitral and aortic valves to only include the inner surface of the LV. For both models, the geometries were optimized, hollowed, and smoothed using the Meshmixer. Flow extensions were appended using AutoDesk Fusion 360 at the trimmed inlets and outlets to simulate adjacent vasculature. Different scales of e-HT (C,H) and f-LV (L) constructs were 3D printed by a Form 2 printer using the Clear Resin.

Generated STL models of the two heart anatomies were first printed, using synthetic (resin-based) inks, to optimize print processes, visualize each anatomy, and conduct the flow visualization and analyses (ultrasound and MR imaging). Multiple resin-based models were reliably printed for simplified and patient-derived e-HT and f-LV models with minimal post-processing required, while still maintaining high fidelity structures. The 3D reconstruction and prints highlighted the complex external and internal hollow structures of the developing human heart at different stages, including the sinus venosus (flow inlets) and truncus arteriosus (flow outlets) in the e-HT model (Figure 1C, H) and the mitral valve (flow inlet) and aortic valve (flow outlet) in the f-LV construct (Figure 1L). The protocol to generate these synthetic phantoms was streamlined to take less than 2 days to complete, starting with the clinical data, through 3D model design and optimization and concluding with testing the manufactured vasculature mimics for retained perfusion capabilities. This proposed pipeline is within the timeframe to be suitable for use as a clinical aid in future planning surgical interventions. The Clear Resin that was chosen as the main synthetic material to print the heart models allowed for visualization of the internal cavities and flow.

2.2. Ultrasound Imaging of Flow in Bioprinted Developing Heart Models

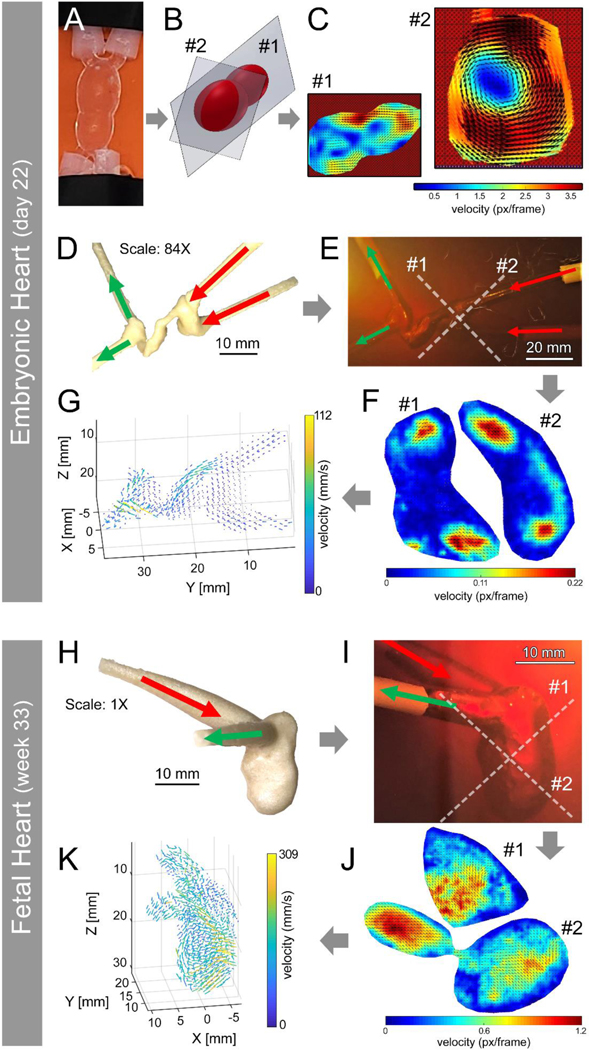
Two experimental (ultrasound and 4D MRI) and one computational (CFD modeling) approaches were used in this study to visualize and analyze 3D flow hemodynamics within the printed human heart models. Notably, due to the limited resolution of the ultrasound probe, both e-HT and f-LV models required further scale up for adequate imaging, to the scales that were not feasible for bioprinting using our experimental setup (84X for e-HT and 1X for f-LV). Thus, we utilized a water-soluble PVA resin to print the positive molds and cast gelatin (negative) molds to create the ultrasound models. The ultrasound images were acquired at 2 cross sections of the idealized e-HT model (Figure 2B and SI Figure S1). The results indicated the feasibility of extracting the flow velocity vector from ultrasound images of the 3D printed e-HT model using PIV analysis (Figure 2C). The velocity vectors in section #1 indicate the fluid flowed from the larger chamber into the smaller chamber of the idealized e-HT. The flow exhibited an acceleration when it reached the narrowed junction between the two chambers, which is indicated by the heat map of the flow amplitude (Figure 2C, section #1). The velocity vectors indicated the presence of a vortex in section #2, in which the velocity increased with increasing distance from the center of the chamber.

Figure 2: 3D ultrasound visualization and quantification of flow within 3D printed developing heart models.

A-C: Ultrasound imaging of flow in idealized embryonic heart tube (e-HT), demonstrating the velocity distribution within two selected planes (#1 and 2) (B-C). D-G: Flow analysis in the anatomical e-HT construct (at 84X scale), demonstrating velocity patterns within the selected planes #1 and 2 (E-F). Flow velocity was further mapped in 3D space (G). H-K: Ultrasound of flow in the patient-derived 3D printed fetal left ventricle (f-LV, 1X scale). Again, velocity heatmaps were generated for two selected planes (#1 and 2) (I-J), and the velocity in the 3D space was also mapped (K).

The geometry of the e-HT at Carnegie stage 10 (21–23 days old) was successfully reconstructed in the gelatin-based tissue-mimicking phantom (Figure 2E). The 2D velocity map was extracted from 2 orthogonal imaging planes (Figure 2F). The full 3D velocity vector field was reconstructed using 42 slices of 2D velocity maps. After the reconstruction of the full 3D velocity fields, the direction and velocity magnitude could be visualized (Figure 2G) with a spatial resolution of 1.4 mm (i.e. the spacing between vectors). The net flow direction in the model was along the positive direction of the Y-axis, which is consistent with the introduced flow direction (Figure 2D and 2E). The local flow velocity direction was regulated by the geometry of the e-HT as the fluid passed through the e-HT, with locally elevated velocity visible at locations of increased narrowing and curvature, specifically at approximately y = 20 mm and y = 30 mm. The peak velocity (0.112 m/s) was observed at the latter of these two locations, in the narrow throat of the e-HT.

The geometry of the f-LV was also reconstructed in the gelatin-based phantom (Figure 2I). By using the same method as the e-HT measurements, the 2D velocity map was obtained at 2 orthogonal imaging planes. Subsequently, 36 slices of the 2D velocity map were used to reconstruct the 3D velocity vector field of the f-LV (Figure 2K), exhibiting a peak velocity of 0.309 m/s. The flow dynamics in the f-LV are more complicated than that in the e-HT. There appeared to be a vertical flow in the chamber (Z = 20 mm) where the flow is redirected towards the outlets.

2.3. CFD Modeling of Flow in Bioprinted Heart Models

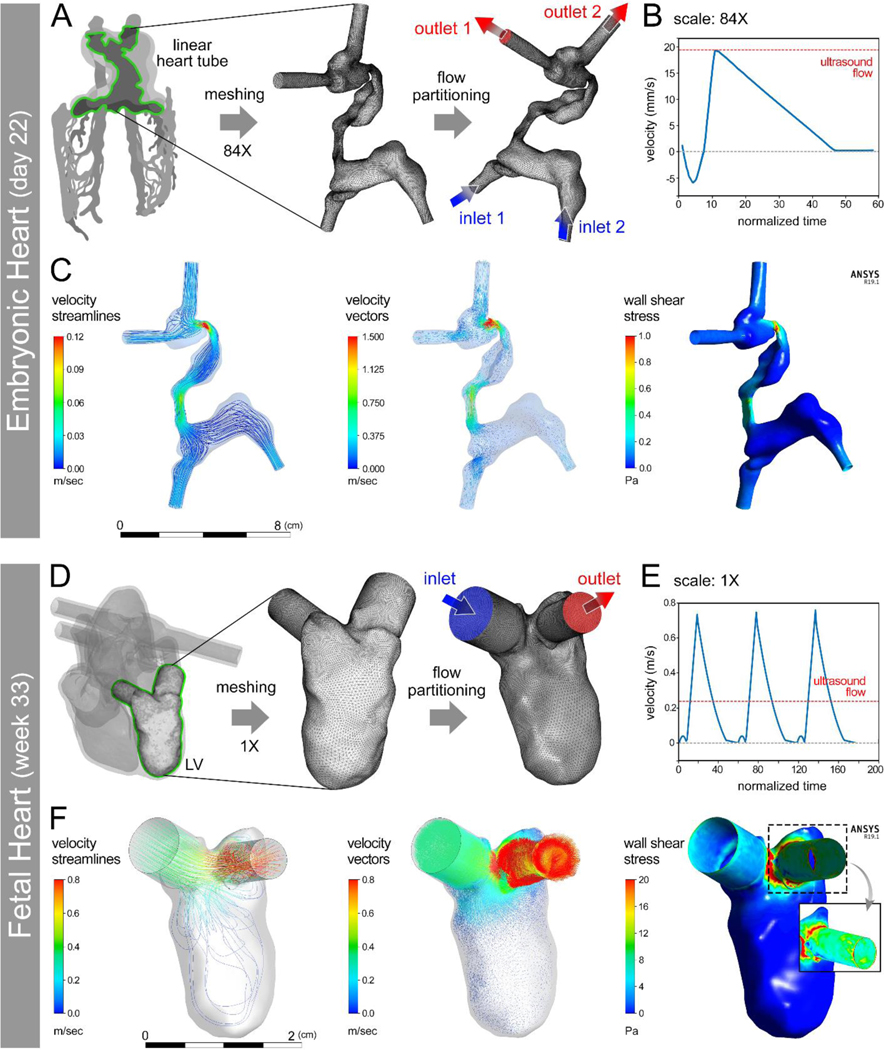
Computational models were next analyzed for the e-HT and f-LV to juxtapose with the experimental (3D ultrasound and 4D MRI) datasets. We conducted CFD modeling at two scales: 1) the scale used for ultrasound imaging (84X for e-HT and 1X for f-LV); and 2) the scale used for bioprinting (21X for e-HT and 0.25X for f-LV). To compare with the ultrasound measurements, we first conducted the CFD modeling of flow on the e-HT model scaled to 84X of its anatomical size at day 22 of development (Figure 3A–C). At peak velocity of the waveform, fluid velocity peaked in the narrow, tortuous regions while remaining relatively slow in the wide, non-tortuous regions (Figure 3C and SI Videos S1–2). Consistent with velocity predictions, wall shear stresses demonstrated higher levels along the narrow, tortuous regions (Figure 3C and SI Video S3). The flow profile of f-LV constructs were modeled at anatomical (1X) scale at week 33 of development (Figure 3D–F). At peak velocity of the waveform, fluid velocity was highest near the aortic outlet while lowest within the ventricle, indicating the formation of an attached flow around the apex (Figure 3F and SI Videos S5–6). Wall shear stresses were greatest where fluid was funneled to the aortic outlet (Figure 3F and SI Video S7). Combined, these results show anatomically accurate flow regimes at the aortic outlet, specifically the ability of the presented model to mimic shear stress spikes, which are implicated in heart development, as well as in pathologies of the cardiovascular system.

Figure 3: Computational fluid dynamics (CFD) modeling of hemodynamics in developing human heart constructs.

(A) Conversion of an anatomical embryonic heart tube (e-HT, 84X) geometry into a meshed boundary for CFD analysis performed with anatomically appropriate flow wavefront (B). CFD results demonstrated the velocity and wall shear stress at peak flow (C). D-F: Conversion of a patient-specific 3D printed fetal left ventricle (f-LV, 1X scale) geometry into a meshed boundary for CFD analysis (D) performed using an anatomically appropriate flow wavefront (E). CFD results demonstrated velocity and wall shear stress at peak flow (F). The inset in (F – right panel) shows zoomed in views of peak wall shear stress with higher values at the aortic outflow tract.

In both constructs, the general flow patterns predicted by CFD modeling (Figure 3) were consistent with those measured by the ultrasound (Figure 2) and 4D MRI (SI Figure S3 and SI Video S4), demonstrating highest levels of velocity and wall shear stress along the more constricted regions (narrowed areas in the e-HT and inlet and outlets in the f-LV). In contrast, lowest velocity and shear stress levels were observed within components of the 3D constructs with larger volumes (i.e., inflow tract and common atrium of e-HT and the f-LV chamber), where fluid swirls and mixes. Considering Bernoulli’s principle, these findings are expected as narrowed regions should behave like a nozzle. Though these printed tissue constructs were static (no contractile function), these observations may reflect the anatomical results particularly near the aortic valve for the LV. The disparate mechanical stresses along the e-HT and LV structures reflect the importance of mechanotransduction signals in proper heart development,^[38] especially during the embryonic stage when rapid morphological changes occur.^[39]

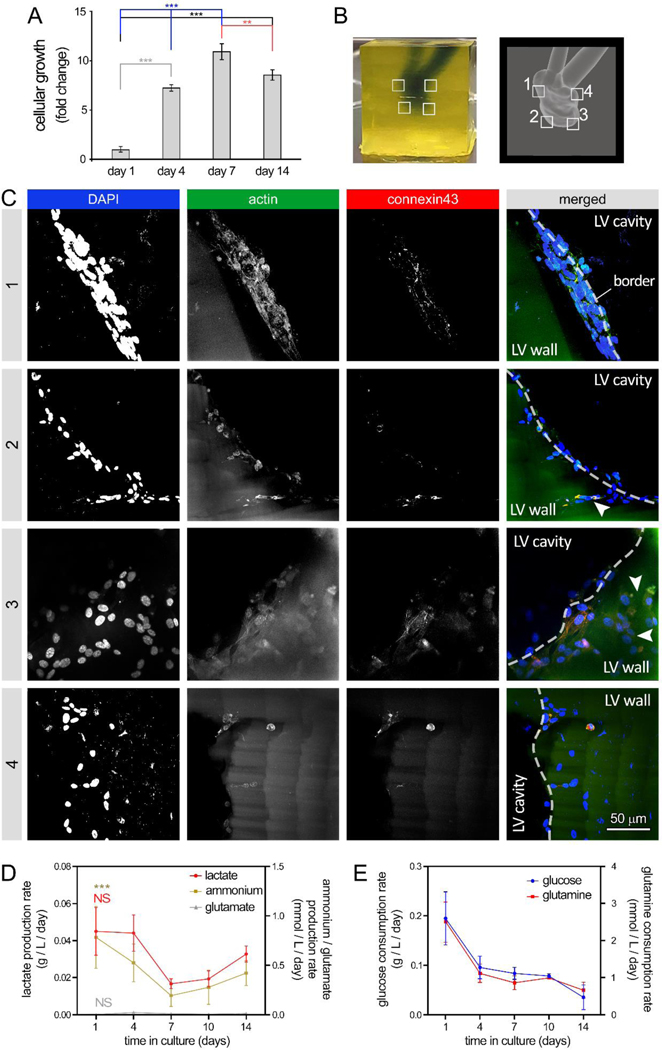
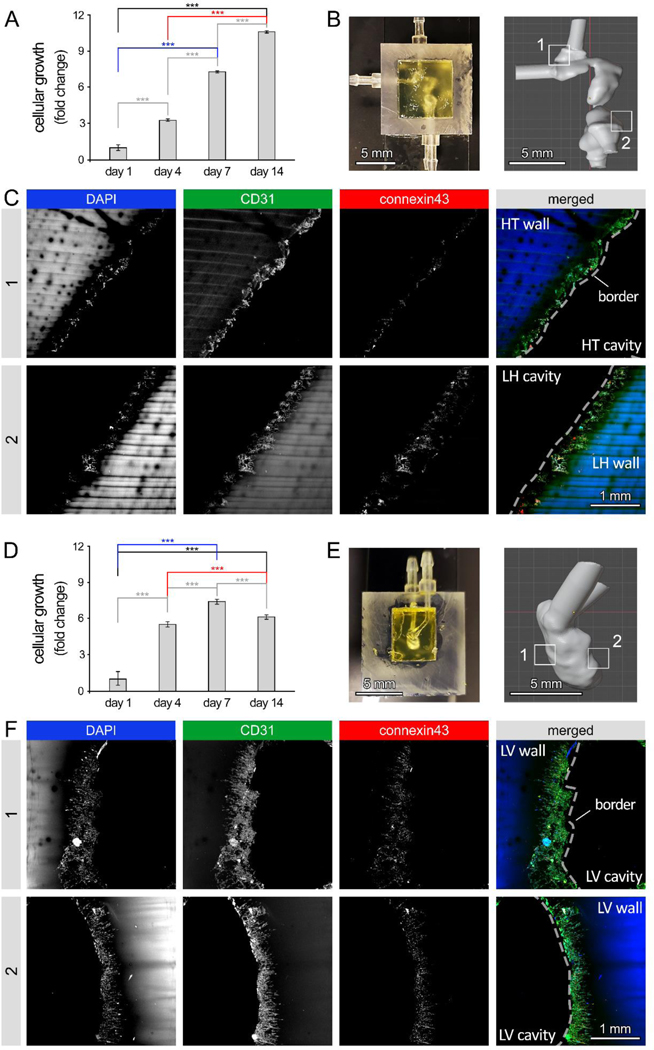
Figure 4: 3D bioprinting of human embryonic heart tube (e-HT) constructs and their endothelization.

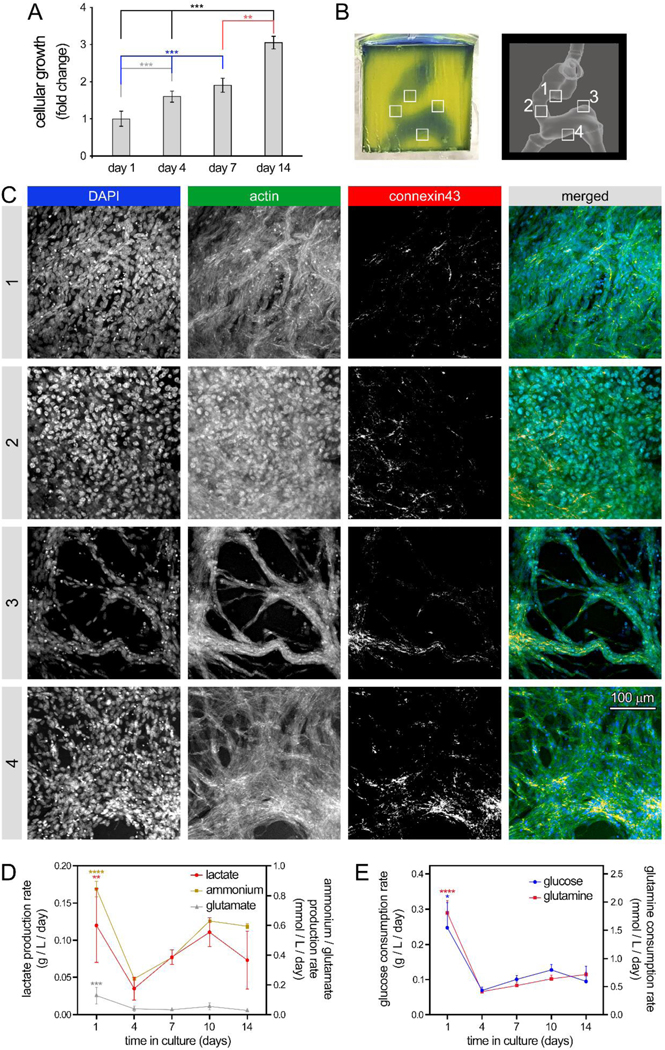
A: AlamarBlue metabolic activity assay used to assess endothelial cell (EC) growth seeded onto the luminal space of the bioprinted e-HT constructs. B-Left: A bioprinted e-HT construct, made using gelMA-based bioinks and perfused with PBS (a blue food coloring used for visualization). B-Right: corresponding CAD model used to bioprint the e-HT constructs. The four insets in panel (B) highlight the areas in which the cellular constructs were fixed, sliced, and imaged using immunohistochemical (IHC) assay. C: IHC imaging of bioprinted, cellular e-HT constructs performed after 14 days of in vitro 3D culture. Rows 1 to 4 correspond to the windows 1–4 depicted in the panel (B). From left to right, columns show immunostaining results for DAPI, actin, connexin43, and merged, respectively. D-E: Rate of metabolite production (D) and nutrient consumption (E) throughout the 2-week 3D culture of ECs in bioprinted constructs. There was significantly higher lactate/glutamate/ammonium production and glucose/glutamine consumption at the beginning of the culture (day 1). Metabolic activity was higher at the beginning of the culture (both glycolysis and glutamine metabolism). Note: * p < 0.05; ** p < 0.01; *** p < 0.001; and **** p < 0.0001. p value demonstrates statistically significant difference compared to value in the same group at day 1. An n = 4 of e-HT constructs per condition were used.

The CFD and ultrasound flow patterns showed agreement both qualitatively and quantitatively. Notably, there was a close agreement between the CFD predicted flow velocities, ranging from 0 to 120 mm/sec in e-HT and 0 to 800 mm/sec in f-LV (Figure 3C,F), with those measured by ultrasound, ranging from 0 to 110 mm/sec and 0 to 310 mm/sec in the e-HT and f-LV constructs, respectively (Figure 2G,K). The observed differences in the f-LV velocity ranges, obtained by CFD versus ultrasound, could be attributed to multiple simplifying adjustments made in ultrasound assays (e.g., applying a constant flow different from the waveform used in CFD, geometric differences due to molding technique limitations, and possible differences in inlet/outlet boundary conditions). Of particular note, at the time step when the inlet flow velocity was equal to that used in the ultrasound assay (~0.22 m/sec), the CFD-predicted flow velocity range (0–310 mm/sec) and pattern in the f-LV highly overlapped with those obtained by the ultrasound (SI Figure S4).

We also performed the CFD analysis at the scale used for tissue bioprinting (21X for e-HT and 0.25X for f-LV) to enable direct comparison of flow hemodynamics with the cell behavior obtained from dynamic culture assays. The similarity in the range of wall shear stress (0–1 Pa) between the CFD models at different scales was used as one criterion to adjust the flow parameters while scaling. Enforcing consistent range of shear stress across different scales enabled us to adequately correlate the cellular behavior observed in the perfused bioprinted models to that in the native tissue at the anatomical scale. Results demonstrated flow hemodynamic trends consistent with those predicted above for the greater scales (SI Figure S5). Flow velocities ranged from 0 to 30 mm/sec in e-HT and 0 to 500 in f-LV (SI Figure S5B, D, left panels). Wall shear stress also ranged from 0 to 0.45 Pa in e-HT and 0 to 20 Pa in the f-LV structures (SI Figure S5B, D, right panels). These were the (predicted) ranges of shear stress that will be exposed to the endothelial cell culture in the dynamic flow experiments. We also performed CFD modeling of flow in the e-HT at natural-size (1X) scale to determine the range of wall shear stress in the native tissue (SI Figure S6).

Simultaneous use of these experimental and computational tools enables comparison and verification of the efficacy of these methods, especially in such complex geometries and flow scenarios.^[40] The accuracy of scaling each construct to different sizes and the prescribed flow parameters was verified through CFD modeling and calculation of the wall shear stress at each scale. Our results showed an adequate agreement and consistency in the wall shear stress ranges generated at all different scales of the two models, when compared to the range obtained for the natural-size (1X) structures (0–1 Pa for e-HT structures and 0–20 Pa for f-LV constructs). Utilizing this hybrid approach also enables a more quantitative view of the mechanical interactions between flow and the tissue microenvironment. Based on these measurements, there is a strong correlation between the flow patterns in all examined scales.

2.4. Cellularization of Bioprinted Embryonic and Fetal Heart Models

Conventional, typically 2D, cardiac tissue culture systems have enabled generating high-throughput cellular models to study cell-cell and cell-ECM interactions contributing to the development and disease.^[41] However, such cellular platforms are often non-perfusable and have shown limited capacity to recapitulate complex and dynamic processes of heart development. 3D bioprinting technologies are ideally suited to generate such complex tissue structures and evaluate the crosstalk between ECM microenvironment and cells.^{[29, 42]} Through bioprinting, the tissue architecture can be precisely controlled, using patient’s own data, 3D printing also enables fabrication of vascular tissue constructs that can be perfused using bioreactor systems.^{[23, 24, 43]}

At the next step of this study, we aimed to assess bioactivity of the bioprinted, anatomically accurate 3D scaffolds, to support vascular cell growth and homeostasis using the well-characterized HUVEC cell line. Using a digital light processing (DLP) 3D bioprinter, we created gelMA constructs that closely mimicked the e-HT and f-LV anatomies. Due to the dimensional limitations of the DLP bioprinting platform, the heart structures were bioprinted at scales smaller than those used for the ultrasound imaging (21X scale for e-HT and 0.25X scale for f-LV). Comparison with the CAD design demonstrated acceptable structural fidelities for the bioprinted heart constructs, ranging from ~93% to 97% (n = 4) (Table 1 and SI Figure S7).

Table 1.

External and internal dimensional measurements for 3D bioprinted vs. CAD designs, used to assess the printing fidelity for the e-HT and f-LV constructs.

Dimension	HT-X	HT-Y	HT-Z	HT cavity area	LV-X	LV-Y	LV-Z	LV cavity area
Measured	14.4mm	14.2mm	13.7mm	10.7mm2	9.4mm	9.4mm	9.4mm	5.7mm2
CAD	15.0mm	15.0mm	15.0mm	11.4mm2	10.0mm	10.0mm	10.0mm	6.1mm2
Agreement	96.7±2%	95.8±3%	94.5±7%	93.7±8%	95.3±2%	94.6±2%	95.2±2%	93.7±6%

Seeding 10×10⁶ cells/ml of HUVECs into bioprinted e-HT constructs demonstrated significantly increasing cellular viability and growth during the 2-week 3D cell culture (~3-fold increase in metabolic activity, Figure 4A), with media changes every 2 days. Immunohistochemical staining and confocal imaging of the embryonic tube at 4 different regions in the construct confirmed the significant cellular growth, achieving a rather uniform endothelialization of the inner luminal cavities (Figure 4B–C, SI Figure S3, and SI Videos 8–9). Dense networks of ECs with noticeable connexin43 expression were observed in regions #1 to 4 throughout the 3D construct. Although, the more spatially constricted areas (region 3) showed relatively lower cell densities, possibly due to lower accessibility to the seeded cells and the effect of gravity (Figure 4C). Bioprofiling of the supernatants taken during the culture time course revealed that from day 4 through day 14 of culture, lactate and ammonium metabolite production increased and retained an upward trend while glutamate remained constant (Figure 4D); in contrast, the consumption rate of glucose and glutamine nutrients remained constant (Figure 4E). A significant drop was observed in both metabolite production and nutrient consumption at the beginning of culture, from day 1 to 4.

In the f-LV constructs, HUVECs showed a significant increase in cellular growth up until day 7 (~11-fold increase in growth), following by a slight decline at day 14 (Figure 5A). The diminished growth in f-LV at longer time points may be attributed to the more constricted geometry of these constructs, with single inlet and outlet, which could impede the circulation of culture media in the f-LV chamber, in comparison to the relatively straight e-HT geometry with two inlets and two outlets. Confocal images of the f-LV constructs at 4 different regions, revealed rather uniform cellularization of f-LV tissues (Figure 5B–C and SI Videos 10–11), consistent with the results from e-HT constructs. HUVECs formed continuous chains onto the surface of cavities, with noticeable connexin43 expression, and occasionally demonstrated inward migration into the gelMA wall (white arrows, Figure 5C). Bioprofiling analysis of f-LV cultures demonstrated that production of lactate and ammonium metabolites decreased from day 1 to 7, followed by a gradual increase in the second week of culture (Figure 5D). Consumption of nutrients (glucose and glutamine) displayed a continuous decline throughout the 14-day culture (Figure 5E). For both geometries, glutamate levels remained consistent and low across the entire two-week culture period (Figures 4D and 5D).

Figure 5: 3D bioprinting of human fetal left ventricle (f-LV) constructs and their endothelization.

A: AlamarBlue metabolic activity assay used to assess endothelial cell (EC) growth seeded onto the luminal space of the bioprinted f-LV structures. B-Left: A bioprinted f-LV construct, made using gelMA-based bioinks and perfused with PBS (a blue food coloring used for visualization). B-Right: corresponding CAD model used to bioprint the f-LV constructs. The four insets in panel (B) highlight the areas in which the cellular constructs were fixed, sliced, and imaged using immunohistochemical (IHC) assay. C: IHC imaging of bioprinted, cellular f-LV constructs performed after 14 days of in vitro 3D culture. Rows 1 to 4 correspond to the windows 1–4 depicted in the panel (B). From left to right, columns show immunostaining results for DAPI, actin, connexin43, and merged, respectively. D-E: Rate of metabolite production (D) and nutrient consumption (E) throughout the 2-week 3D culture of ECs in bioprinted constructs. There was significantly higher lactate/glutamate/ammonium production and glucose/glutamine consumption at the beginning of the culture (day 1). Metabolic activity was higher at the beginning of the culture (both glycolysis and glutamine metabolism). Note: * p < 0.05; ** p < 0.01; *** p < 0.001; and **** p < 0.0001. p value demonstrates statistically significant difference compared to value in the same group at day 1. An n = 4 of f-LV constructs per condition were used.

In both models, HUVECs exhibited significant amount of connexin43 expression, suggesting that the cells were capable of functional performance, such as tight junction formation and intercellular communication within bioprinted heart models. ECs in e-HT constructs demonstrated approximately four times greater level of onnexin43 expression compared to the f-LV samples (SI Figure S3C), which could be attributed to the relatively higher cell density (~3 times higher, Figure S3D) and facilitated media (oxygen and nutrients) exchange in the linear tube structure. These results confirm the applicability of the bioprinted models developed here as a perfusable platform to study endothelial (and other cardiac) cell behavior in response to geometric and flow perturbations in developing cardiac constructs as well as in healthy or diseased adult heart.

The bioprofiling results of both models were in agreement with the cell viability and growth assay (Figures 4A and 5A). The initial declines in metabolite production and nutrient consumption at the beginning of culture in both constructs could be attributed to the transition phase for the seeded cells to settle into the 3D hydrogel and resume their normal functions. The AlamarBlue and metabolite profiles of both constructs suggested that cells were actively dividing and metabolically active (not quiescent) at two weeks post-seeding, forming conformal sheets along the entire bioprinted cavities and showing high expression of the mature endothelial marker, connexin43.^[44]

To examine the effect of flow on cellular responses in varying cardiac geometries, we next conducted a dynamic culture of endothelialized e-HT and f-LV constructs using a bioreactor. Physiological flow rates were selected and scaled to ensure that biologically relevant levels of wall shear stress (verified by CFD) will be generated at each 3D bioprinted model, namely 0.4 ml/min for the e-HT (21X) and 12 ml/min for the f-LV (0.25X) constructs. A customized bioreactor chamber and perfusion system enabled applying homeostatic flow rates in complex anatomical models (SI Figure S8).

We observed increasing metabolic activity within the constructs over the span of the two-week dynamic culture assay as shown by the AlamarBlue metabolic assay (Figure 6). Confocal imaging of constructs revealed high cell retention within both e-HT and f-LV constructs, with confluent HUVEC cell layer (i.e. endothelization) visible in different imaged areas (Figure 6B and 6D; SI Video 12). Comparison between static versus dynamic cultures demonstrated a notable improvement in endothelialization degree of lumens in both e-HT (Figure 4C and Figure 6C) and f-LV constructs (Figure 5C and Figure 6F). Further, significantly greater (~3X) levels of tight junction marker connexin43 expression were observed in the perfused e-HT and f-LV constructs compared to those in the static culture, suggesting enhanced cellular maturation and function by the introduction of flow in the 3D LV constructs (Figure 5C, Figure 6F, and SI Figure S9).^[45] In addition, we observed that applying flow in the f-LV constructs resulted in morphological alteration in the HUVECs, compared to the static group, where the cells appear to migrate inward more extensively into the surrounding gelMA tissue (SI Figure S9A, Figure 6F, and SI Video 12).

Figure 6: Cellular response to flow in human embryonic heart tube (e-HT) and fetal left ventricle (f-LV) constructs.

A: AlamarBlue reduction assay was used to measure viability and growth of endothelial cells (ECs), seeded onto the luminal space of the bioprinted e-HT constructs under flow. B-Left: Bioprinted e-HT construct integrated in a custom-printed bioreactor housing. B-Right: CAD model of the e-HT structure. Zones 1 and 2 highlight the areas used for immunohistochemical (IHC) analysis. C: IHC imaging of zones 1 (top) and 2 (bottom) within the bioprinted cellular e-HT constructs, performed after 14 days of in vitro dynamic culture. From left to right, columns show immunostaining results for DAPI, CD31, connexin43, and merged, respectively. D: AlamarBlue assay demonstrating EC viability and growth on the luminal space of bioprinted e-HT constructs under dynamic flow. B-Left: Bioprinted f-LV construct in the bioreactor housing. B-Right: CAD model of the f-LV structure. Zones 1 and 2 highlight the areas used for the IHC analysis. C: IHC imaging of zones 1 (top) and 2 (bottom) in the bioprinted cellular f-LV constructs after 14 days of dynamic culture. From left to right, columns show immunostaining results for DAPI, CD31, connexin43, and merged, respectively. Note: * p < 0.05; ** p < 0.01; *** p < 0.001; and **** p < 0.0001. p value demonstrates statistically significant difference compared to value in the same group at day 1. Results are based on n = 4 constructs for the AlamarBlue assay and n = 3 per group for IHC.

The results presented for the static and dynamic culture of ECs in the bioprinted platforms demonstrate the feasibility of the patient-derived 3D structures to be bioprinted and seeded with cells under flow to resemble simplified cardiac microenvironments. However, to establish a more robust in vitro model of the developing heart, several other aspects should be incorporated into these models. These include multiple patient-derived cardiovascular cell types (e.g., cardiomyocytes, smooth muscle cells, and cardiac fibroblasts), tuning tissue stiffness and composition to approximate those at the varying stages of heart development, and applying more realistic flow hemodynamics.

3. Conclusion

In summary, the new generation of live and functional, patient-derived models of human heart, at different stages of the development, could serve as a robust, high fidelity platform for studying a variety of cell-microenvironment interactions under static and dynamic flow conditions. Perfusion of bioprinted cellular constructs at physiological flow rates would provide a unique opportunity to examine the real-time response of cardiovascular cells to geometric and flow perturbations. These cellular platforms enable precise tuning of microenvironmental cues, including geometry, flow hemodynamics, ECM composition, and biomechanics (e.g. tissue stiffness), allowing to study the normal organ and tissue developmental processes and their underlying diseases. While we demonstrated the application of this platform to study endothelial cell behavior in various cardiac geometries, future studies are needed to further enhance the efficacy and accuracy of this system in recapitulating the developing human heart. Incorporation of multiple cardiac lineages into the bioprinted models, for instance, would enable conducting mechanistic studies that could shed light on the complex physiological and pathological processes of heart development and disease.

4. Experimental Section

Digital Model Development of Developing Human Heart:

Starting with an anatomical model of either an embryonic heart tube (e-HT), or a fetal left ventricle (f-LV), we generated a digital 3D model (STL file) of the target anatomy using a formerly established process flow as previously described.^[33]. A 3D model (.STL) of a developing human heart at Carnegie stage 10 (21–23 days old, e-HT) was obtained in collaboration with Dr. Jensen on behalf of the 3D Atlas of Human Embryology.^[36] The model contained the primitive cardiovascular system but was trimmed to only include the linear HT from the sinus venosus (“flow inlets”) to the truncus arteriosus (“flow outlets”). Similarly, a patient-specific 30 week fetal human heart model (.STL) acquired from fetal echocardiography was obtained in collaboration with Dr. Roldán-Alzate.^[37] The full heart model was trimmed at the mitral valve (“flow inlet”) and aortic valve (“flow outlet”) to only include the inner surface of the f-LV. For both models, the geometries were optimized, hollowed, and smoothed (Meshmixer). Flow extensions were appended (AutoDesk Fusion 360, Meshmixer) at the trimmed inlets and outlets to simulate adjacent vasculature. We performed Boolean subtraction to generate cavities that mimicked each anatomy in a solid cube block. Scaled up e-HT and f-LV constructs were first 3D printed by a Form 2 printer using the Clear Resin (FormLabs).

3D Printing of Patient-Derived Developing Human Heart Models:

Scaled up 3D models (84X e-HT and 1X f-LV) were extruded to include a shell thickness of ≥1 mm extended from inner wall surfaces to maintain internal volume, but also provide structural stability of the 3D prints during flows. Importantly, we made sure that the internal dimensions were accurate per the ascribed scaling. Transparent models were printed (Clear Resin, Form 2 SLA printer; Formlabs, MA, US). Post processing included washes (x3, 20 mins each) in pure isopropanol to remove residual non-crosslinked resin, drying, UV curing (20 mins), and a clear outer varnish coating to improve transparency, rigidity, and waterproof for any potential leaks.

Flow Scaling of Heart Models for Experimental Perfusion Assays:

For the e-HT, flow measurements were adapted from zebrafish studies at the same twisting heart tube developmental stage.^[46] However, due to print resolution and image acquisition limitations, the e-HT model was proportionally scaled by pressure – assuming Hagen-Poiseuille, low Reynolds number flow:

$$\Delta P=\mathrm{ }\frac{{\mu }_1{Q}_1{L}_1}{{r_1}^4}=\frac{{\mu }_2{Q}_2{L}_2}{{r_2}^4}$$

where $\Delta P$ is change in pressure, ${\mu }_1,\mathrm{ }{\mu }_2$ are dynamic viscosities, $Q_1$,$\mathrm{ }{Q}_2$ are volumetric flow rates, $L_1,\mathrm{ }{L}_2$ are characteristic z-length (end-to-end height), and $r_1,\mathrm{ }{r}_2$ are radii of circular inlets. Using known values and estimates, this pressure-based scaling was solved for $Q_2$ to calculate an average volumetric flow rate. Specific cardiac flow waveforms were then adapted to reflect $Q_2$.

The ultrasound flow acquisition for the e-HT was scaled to 84X its original size. A calculated average flow rate of 27 mL/min was prescribed using a syringe pump. For 4D MR acquisition, an e-HT model was scaled to x246 its original size. A calculated average flow rate of 386 mL/min was prescribed using a custom flow system capable of recreating cardiac waveforms.

For the f-LV, no scaling was needed for the ultrasound imaging, as the actual model size was large enough for 3D printing and flow visualization purposes. Perfusion was performed at a 291 mL/min flow rate. Anatomical size was maintained and flows were simulated to replicate pressures and velocities at the mitral and aortic valves from fetal ultrasounds.^[47] For the bioprinted f-LV models, a 0.25X scale of the model was used. A flow rate of 12 ml/min was prescribed for perfusing the bioprinted f-LV constructs to maintain the consistent range of wall shear stress (0–20 Pa).

The accuracy of scaling was verified by calculating wall shear stress values at each scale using CFD modeling. First, we performed CFD modeling of flow at anatomical (1X) scale of each structure to identify the wall shear stress range experienced by the cells under physiological conditions. Next, we calculated wall shear stress at each scaled model with the adjusted the flow parameters ($Q_2$), to verify that consistent level of shear stress will be generated under the adjusted flow.

3D Ultrasound Imaging of e-HT and f-LV Constructs

A. 2D velocity measurements:

Ultrasound contrast agents, which are lipid-shelled microbubbles synthesized in the lab following an established protocol^[48] were utilized as tracers at a concentration of ~10⁵ microbubbles/mL. The idealized e-HT model was imaged using a high frame rate (1000 frame/s) ultrasound system (Verasonics, Kirkland, WA, USA). 2D velocity maps were extracted from 2D ultrasound images using a particle image velocimetry (PIV) analysis toolbox.^[49]

B. 3D velocity measurements:

Based on the pilot test of 2D velocity measurement capability, 3D velocity vector measurements were acquired on 3D printed e-HT and f-LV constructs. To improve the compatibility of printed models for ultrasound scanning and optimize the image quality, tissue mimicking gel phantoms were built based on the 3D printed models and used to perform 3D ultrasound imaging and velocity measurements.

For flow experiments, the e-HT and f-LV constructs were created using a 3D printer (Ultimaker 2+) with sacrificial polyvinyl alcohol (PVA) ink. Due to the very small sizes of e-HT model, we needed to scale it up to 81X bring it into the resolution range to allow for 3D printing and ultrasound measurements. The tissue mimicking gel phantom was fabricated using degassed water (91% V/V), gelatin powder (6% W/V, 300 bloom), 1-propanol (5% V/V), and 25% glutaraldehyde aqueous solution (4% V/V). The 3D printed constructs were embedded in the phantom, with tubing connected to the inlets and outlets of the printed constructs. The phantom solution solidified within 30 seconds after the glutaraldehyde solution was mixed with gelatin. After the phantom was stored for 10 hours at ~4 °C, tap water was infused through the constructs to slowly dissolve the PVA material. The geometry of the printed e-HT and f-LV models was preserved in the tissue mimicking phantom. A syringe pump (PHD 2000, Harvard Apparatus, Holliston, MA) was used to introduce flow through the phantom. We also scaled up the appropriate flows to maintain a similar range of wall shear stress across the different scales. These adjusted flow rates were 27 mL/min for the e-HT and 291 mL/min for the f-LV.

A custom 3D ultrasound velocimetry setup comprised of a 3-axis motion stage (XPS-Q8, Newport, Irvine, CA, USA) and a programmable ultrasound system (Verasonics, Kirkland, WA, USA) with a linear array probe (L11–5, ATL, Bothell, WA, USA) was utilized to acquire ultrasound imaging data and estimate flow velocities (SI Figure S1). During the data acquisition process, degassed water mixed with ultrasound contrast agents (~10⁵ microbubbles/mL) was infused through the e-HT or f-LV gel phantom. 2D high frame rate (1000 frame/s) ultrasound images were acquired at multiple orthogonal imaging planes (SI Figure S1A). A custom-made rotational ultrasound probe holding device was used to acquire orthogonal-plane data sets by ensuring ultrasound probe rotation by exactly 90°. The flow rate was kept the same for each acquisition at each plane. 2D velocity maps were extracted from 2D ultrasound images acquired in individual planes using the particle image velocimetry analysis toolbox.^[49] A full 3D velocity map was reconstructed at the intersection of the orthogonal planes by combining two sets of 2D flow velocity vectors on the orthogonal planes. A similar ultrasound velocimetry method was previously developed.^[50]

4D Flow MRI of e-HT Constructs:

4D flow acquisitions were obtained on a 3.0 Tesla scanner (Siemens PRISMA, Malvern, PA).^[51] The time-resolved 3D velocity field was used to trace fluid particles motion through the e-HT. A 246X scale e-HT model was printed with Clear Resin to create a hollow flow conduit. The larger scale was chosen due to 4D MR spatial resolution limitations.^[52] An in-house cardiac flow system was used to prescribe a custom cardiac flow waveform representative of the e-HT pulsations. An acquisition with 1.6×1.6×1.6 mm voxel spatial resolution and 380 ms time resolution was conducted with water as the flow medium. A velocity encoding (VENC) of 100 cm/s was applied. Data were visualized (Siemens 4DFLOW software) to view particle traces and velocity vectors.

GelMA Bioink Preparation for Digital Light Processing (DLP) Bioprinting:

GelMA bioink was prepared as previously described,^[53] with amendments to the protocol to optimize its use for DLP bioprinting. Briefly, porcine gelatin (Sigma) was incubated with methacrylic anhydride (MAA, Sigma) at 50 °C for 3 hours. Functionalized gelatin was then dialyzed to remove the unreacted MAA via reverse osmosis, lyophilized, and stored away from light at −20 ºC until use.^[53] The gelMA bioink formulation that was then used to print the e-HT and f-LV models used 4 grams of gelMA resuspended in 20 ml of sterile 1X phosphate buffered saline (PBS) for a final concentration of 20% (w/v) solution. Lithium phenyl-2,4,6-trimethylbenzoylphosphinate (LAP; Sigma-Aldrich) photoinitiator was used at a final concentration of 0.5% (w/v). The mixture was heated at 37 ºC for 60 minutes to fully dissolve the gelMA and LAP into the PBS. Once fully dissolved, the bioink pH was adjusted to ~7.4. Subsequently, 1.5 mM tartrazine photoabsorber (Sigma) was used to allow for high resolution DLP bioprinting with the Lumen X 3D bioprinter (CELLINK). The prepared bioink was vortexed to mix all ingredients again and spun down briefly. This gelMA-DLP bioink was then stored away from ambient light at 4ºC and used for bioprinting experiments within a week post preparation. The constructs were printed at 100-μm layer heights, using 10sec blue light exposure per layer. Post-printing, they were washed for 2 days in 1X PBS to remove excess non-crosslinked gelMA from the internal cavities and prepare them for cell seeding.

Endothelial Cell Culture:

Human umbilical vein endothelial cells (HUVECs), expressing endogenous green fluorescent protein (GFP) were plated on 0.5% gelatin coated T75 flasks and maintained in complete HUVEC Media (VascuLife® VEGF Endothelial Medium Complete Kit), supplemented with 1% pen/strep (Gibco) until they were at 90% confluency. Cell cultures were split at ~1:20 and full media changes were done every 3 days until 90% confluency was reached again. Cells were passaged using 2 mL of 0.05% Trypsin (Invitrogen), incubating at 37°C for 10 minutes to detach the cells. Cells were fully detached using 5 mL of HUVEC Media by pipetting up and down until all cells came off and confirmed via visual observation under a microscope. Cell viability and density were ascertained with a 1:1 mix of cell suspension and of Trypan Blue solution (Invitrogen. Cells were maintained at 37°C and 5% CO₂ incubator.

Bioprinting Fidelity Assessment:

Structural accuracy measurements of the outer XYZ lengths and measurements of the major internal cavities and inlet/outlet regions were performed to assess the fidelity of bioprinted models in reference to the CAD/STL design. Our exclusion criterion was an anatomical accuracy lower than 85% in any of the structural parameters. Detailed measurement plan is shown in SI Figure S7. An n = 4 was used for all fidelity measurements.

3D Bioprinting of Developing Heart Constructs – Cellularization of 3D Bioprinted Heart Models:

The constructs were bioprinted using a Lumen X DLP bioprinter (CELLINK) with optimized crosslinking parameters: 15 sec/layer; 1X burn-in; 67% projector strength, which took approximately 35 minutes to bioprint each heart construct. Printed structures featured a solid block of gelMA for stability with a cavity that mimicked closely a scaled-up model of either the anatomical heart tube or the left ventricle.

In preparation to cellularize the constructs, we resuspended HUVEC cells in 10 ml of fresh 1X PBS and spun them down at 500 rpm for 5 minutes at room temperature. All the PBS was aspirated off the pellet and the cells were then resuspended in 2 ml of fresh HUVEC media. Cell viability and numbers were determined using Trypan Blue and the final cell concentration was adjusted to 10 million cells/mL. The bioprinted constructs were then seeded with HUVECs suspended in media, using one of the inlets of the model, while closing the other outlets to ensure that the cell suspension did not leak out. For this purpose, 400 and 200 μL of the cell suspension were added to the e-HT and f-LV constructs, respectively. The cellularized constructs were then incubated at 37 ºC in complete HUVEC cell media for 2 hours to ensure cell attachment, and then moved to a fresh well to minimize cell attachment to the outside of the constructs, containing fresh HUVEC media in the 37 °C and 5% CO₂ incubator. Downstream experiments were started 24 hours after this final wash step (n > 4). Briefly, cells were maintained in the constructs for two weeks, with regular media changes every 2–3 days and supernatant collection for metabolic activity and bioprofiling assay at defined time points.

Bioreactor Perfusion and Dynamic 3D Culture of Bioprinted Endothelialized Heart Models:

Following 2 days of static culture (to ensure EC attachment and initial growth), constructs were transferred to custom-printed perfusion chambers that specifically designed to fit and seal the e-HT and f-LV constructs. A microscopic glass slide was used as a lid to cover and seal the open surface of the chamber, while allowing to have visual access to the embedded samples (SI Figure S7). Four housed constructs were then connected to a 4-channel bioreactor system (Ismatec® IPC Digital Peristaltic Pumps, US) and perfused in parallel at defined flow rates (27 mL/min for e-HT and 291 mL/min for f-LV) for a 2-week duration. At serial time points, non-invasive AlamarBlue assays were conducted while the perfusion continued. At the end of the dynamic culture, printed samples were harvested from perfusion chambers, fixed and examined using IHC.

Metabolic Activity Assessment of Cellular Bioprinted Heart Models:

Non-invasive AlamarBlue assay was performed over a two-week timecourse (days 1, 4, 7 and 14) to measure metabolic activity of the seeded cells within printed constructs.^{[17, 20, 54]} Cell-free bioprinted constructs were used as control. Briefly, the AlamarBlue reagent was prepared as a 10% v/v mixture with HUVEC media and added to each tissue culture well, containing the e-HT and f-LV constructs. Tissues were incubated in the AlamarBlue mixture for 4 hours at 37°C. Subsequently, 100-μl samples were collected from each well and loaded into a microplate reader (Synergy 2, Biotek) to measure absorbance at 550 and 600 nm wavelengths. AlamarBlue reduction % was calculated using a previously established protocol.^[55] To perform AlamarBlue assay during the dynamic culture, culture media was replaced with the media + AlamarBlue reagents (same ratios as above) and perfused for a 4-hour incubation period.

Bioprofiling Analysis of 3D Endothelial Cell Culture in Bioprinted Cardiac Structures:

For the e-HT samples: Supernatants were collected from 3D printed constructs (n=4) at various time points throughout the culture period (D1, D4, D7 D10, D14). 400 microliters of sample supernatant was used for analysis using the NovaFlex Bioprofile 2 (NovaBiomedical), which generated data of metabolite concentrations (glucose, glutamine, ammonium, glutamate, lactate), ion concentrations (K+, Na+, Ca++), and pH measured in the spent media from the samples. The data were normalized to fresh media samples (n=3) to demonstrate production/consumption of metabolites and changes to pH/ion concentrations as a function of culture time. Cumulative changes in metabolite production/concentration were determined and compared across each individual construct to show variability in the cumulative changes of metabolites during the culture period. Rates of metabolite production and consumption were calculated by dividing the production/consumption of metabolites by the time between media exchanges to reveal rate of metabolite concentration changes per day. Finally, statistical significance was determined using two-way ANOVA (GraphPad Prism) to reveal trends in metabolite consumption/production, pH variability and ion variability throughout the culture period.

For the f-LV samples: Supernatants were collected from 3D printed constructs (n=5) at various time points throughout the culture period (D1, D4, D7 D10, D14). At each time point, 400 μL of sample supernatant was used for analysis using the NovaFlex Bioprofile 2; this generated data regarding metabolite concentrations (glucose, glutamine, ammonium, glutamate, lactate), ion concentrations (K+, Na+, Ca++) and pH measured in the spent media from the samples throughout the time period. This data was normalized to fresh media samples (n=3) to measure production/consumption of metabolites and changes to pH/ion concentrations as a function of the culture time. Cumulative changes in metabolite production/concentration were determined and compared across each individual construct to show variability in the cumulative changes of metabolites across the culture period. Rate of metabolite production and consumption was calculated by dividing the production/consumption of metabolites by the time between media exchanges to reveal rate of metabolite concentration changes per day. Finally, statistical significance was determined using two-way ANOVA (GraphPad Prism) to reveal trends in metabolite consumption/production, pH variability and ion variability throughout the culture period.

Computational Modeling of Flow in Developing Heart Constructs:

Computational fluid dynamic (CFD) models were run at two different scales relative to the anatomical sizes for the e-HT and f-LV: 1) 84X scale of e-HT and 1X scale of f-LV were used to perform CFD analysis of flow in the constructs used for the ultrasound imaging (to allow direct comparison of experimental versus computational flow measurements); 2) 21X scale of e-HT and 0.25X scale of f-LV were used for CFD modeling of flow in the constructs used for bioprinting and cellular assays, to enable direct correlation of cell behavior in bioprinted structures to the flow hemodynamics. For each set of modeling, digital STL models were meshed and analyzed (ANSYS Fluent). Inlet and outlet diameters of e-HT model (anatomical scale) were set at ~35 μm using a patient-specific geometry. A mesh of 120k elements was constructed (CellCut assembly method). A Navier-Stokes based laminar viscous flow solver was used. It was evaluated with whole fetal blood rheological properties including: constant mass density (1.06 g/cm³)^[56] with a nonlinear Carreau viscosity model (Time Constant: 3.313 s, Power-Law Index: 0.3568, Zero Shear Viscosity 0.056 P; Infinite Shear Viscosity: 0.0035 P).^[57] Boundary conditions assigned included inlet velocities (custom waveform) and pressure outlets (0.28 mmHg) ^[58]. A custom time varying, pulsatile velocity waveform was prescribed based upon characteristic waveforms in zebrafish and chicks of similar developmental stages.^{[46, 58]}

For the f-LV model, inlet (0.75 cm) and outlet diameters (0.52 cm) were applied from a patient-derived geometry (1X scale). A mesh of 418k elements was constructed (CellCut assembly method). A turbulent flow large eddy simulation (LES) solver was used (with Wall-Adapting Local Eddy-viscosity as the sub-grid scale model). The same whole fetal blood rheological properties were used as described for the e-HT. Prescribed boundary conditions included a pulsatile velocity at the outlet representative of Doppler waveform at the aortic outflow tract in a normal 33-weeks fetal heart.^{[47, 59]}

In both e-HT and f-LV models, three cardiac cycles (60 timesteps/cycle) were run to optimize calculation stability and accuracy. Vascular walls were assumed rigid with no-slip boundary conditions. Mesh solutions were considered convergent when successive mesh velocities differed by less than 5%.

Statistical Analysis:

Data was normalized to day 1 for the AlamarBlue and the bioprofiling assays and then presented as an average ± standard deviation for each time point. Significant differences were determined with one-way ANOVA or two-way ANOVA if applicable. A post-hoc Tukey-Kramer test was performed for multiple comparisons and a p-value of <0.05 was considered statistically significant (*p-value < 0.05, **p-value < 0.01, ****p-value < 0.0001). We used samples sizes of at least 4 for each statistical analysis, including AlamarBlue metabolic assays and bioprofiling. Least square means connecting letters reports were also used to show significant differences between multiple comparisons.

Nonstandard Abbreviations and Acronyms

gelMA

gelatin methacrylate

STL

stereolithography

MAA

methacrylic anhydride

PVA

polyvinyl alcohol

SLA

stereolithography

MRI

magnetic resonance imaging

e-HT

embryonic heart tube

f-LV

fetal left ventricle

ECM

extracellular matrix

CM

cardiomyocyte

HUVEC

human umbilical vein endothelial cell

CFD

computational fluid dynamics

PIV

particle image velocimetry

PBS

phosphate buffered saline

LAP

Lithium phenyl-2,4,6-trimethylbenzoylphosphinate

DLP

digital light processing

GFP

green fluorescent protein

LES

large eddy simulation