A review of machine learning in obesity

Summary

Rich sources of obesity-related data arising from sensors, smartphone apps, electronic medical health records and insurance data can bring new insights for understanding, preventing and treating obesity. For such large datasets, machine learning provides sophisticated and elegant tools to describe, classify and predict obesity-related risks and outcomes.

Here, we review machine learning methods that predict and/or classify such as linear and logistic regression, artificial neural networks, deep learning and decision tree analysis. We also review methods that describe and characterize data such as cluster analysis, principal component analysis, network science and topological data analysis. We introduce each method with a high-level overview followed by examples of successful applications. The algorithms were then applied to National Health and Nutrition Examination Survey to demonstrate methodology, utility and outcomes. The strengths and limitations of each method were also evaluated.

This summary of machine learning algorithms provides a unique overview of the state of data analysis applied specifically to obesity.

Introduction

Today, obesity researchers and healthcare professionals have access to a wealth of data. Sensor and smartphone app data, electronic medical records, large insurance databases and publically available national health data like those collected by the Centers for Disease Control and Prevention give rise to a growing need for advanced mathematical analysis in the field.

Machine learning represents a powerful set of algorithms that can characterize, adapt, learn, predict and analyse data, amplifying our understanding of obesity and our capacity to predict with unprecedented precision. To this end, there have been increasing applications of machine learning in the obesity research field (1-10). To demonstrate the effectiveness of machine learning for a broadly trained interdisciplinary readership, we provide here a general description of several of the most recognized methods along with a history of previous successful applications. Each machine learning technique was applied to the National Health and Nutrition Examination Survey (NHANES) to demonstrate methodology and outcomes.

In addition to the standard machine learning methods, network science and topological data analysis (TDA) were reviewed. Network science’s relation to data analysis results from models that define data structure using connections between data elements. TDA is an emerging data analytic method that identifies data features from the shape of the data. While the software tools and methods are not as well developed as long-standing methods, TDA provides an exciting new data analytic method with promising early results (11,12).

Subjects

The NHANES 1999–2006 dataset provided a nationally representative sample of US adult (age ≥ 18 years) participants among three race/ethnic groups including non-Hispanic (NH) Whites, NH Blacks and Mexican Americans. The NHANES protocol was approved by the National Center for Health Statistics (NCHS) of the Centers for Disease Control and Prevention, and written informed consent was provided by all participants.

Measurements

Height and weight were measured using standardized procedures and calibrated measurement devices. Body mass index (BMI) was calculated using the measurements weight (kg) and height (m) within the formula, weight/height.

Blood pressure

Rigorously controlled blood pressure measurements were made in NHANES (13). Systolic and diastolic blood pressures were each calculated as the average of three measurements.

Body composition

Whole-body dual-energy X-ray absorptiometry scans (Hologic, Inc., Bedford, MA, USA) were used to evaluate adiposity that was quantified as percent body fat (14). Participants wore examination gowns for the scan and were asked to remove objects such as jewellery from their body. The manufacturer recommended calibration, and acquisition procedure was followed for the evaluation of each subject’s scan. Details of the imaging protocol are reported in the NCHS technical documentation (15).

Data distribution

Owing to the relatively large number of missing dual-energy X-ray absorptiometry values, the NCHS released five datasets in which the missing measurements were derived using a multiple-imputation procedure (16). We restricted our analyses to the first imputation dataset. This is not a concern here because we are using the NHANES dataset to illustrate model application, and additionally, our past analysis indicates that the variability between imputed datasets is relatively small.

Certain race/ethnicities were oversampled to gain more insight into the health status in these populations (17). This oversampling scheme needs to be accounted for if one is conducting an analysis to make an overall conclusion about the United States. To this end, the NCHS NHANES study team has provided weights to account for oversampling. However, as we are using the data mainly to illustrate model methodology and utility, we did not re-weight the data.

Overview of mathematical models and data analytic software

Predictive versus descriptive machine learning methods

Machine learning and data analytic methods typically have two different purposes. The first and probably more well-known purpose is prediction. Clearly, it is important for effective clinical practice to predict patient outcomes or predict risk. Machine learning methods that are reviewed under the prediction category are linear regression/logistic regression, decision trees, neural networks and deep learning. Some of these methods can only be used to classify outcomes (like whether a patient is likely to lose 5% of their body weight) rather than predict a continuous variable (like end of intervention body weight). Logistic regression and decision trees are solely used for classification. Neural networks and deep learning can enable classification but can also be applied to predict a continuous variable, as in linear regression.

The second purpose of machine learning models is to describe or characterize the data. For example, in large datasets, several variables may be related to each other. Finding these relations are important when making personalized patient treatment recommendations or identifying how to appropriately target community-wide interventions. Descriptive methods can also be used as a precursor to application of predictive methods because the outcome of the description could generate hypotheses. The methods that are descriptive in nature are principal component analysis (PCA), cluster algorithms, network science and TDA.

Software

Newer modelling techniques like deep learning, network science and TDA are often not included in standard data analysis software. In these cases, programs need to be coded or semi-coded by the investigator. Other more well-established methods like PCA and regression are readily accessible through commercial software like spss. As the need for model comparison increases, software, like Alteryx, that supports the simultaneous comparison of models becomes more accessible and user friendly. Owing to this diversity in software, our study used a mixture of off the shelf software and self-developed code.

NHANES variables

In some cases, the machine learning methods have the same construct and are comparable. In these cases, we standardized the variables used. However, some machine learning methods have specialized purposes. For example, PCA is designed to identify related variables in large datasets and aggregate them on what is referred to as components. If all explanatory or input variables are related, only one component would be identified, and as a result, PCA would be irrelevant. In such cases, we selected NHANES variables that best illustrated method usefulness.

Predictive machine learning algorithms

Regression

Introduction to regression

Linear regression is the most commonly used model for characterizing the relationship between a dependent variable and one or more explanatory variables (18). Logistic regression differs from linear regression by predicting categorical outcomes or classifying outcomes. In obesity, this is most relevant to classification of obesity-related disease states or risks.

Applications of regression

In obesity and/or nutrition research, linear regression is a well-used modelling technique (19-21). Regression was used to derive what is known as the 3,500-calorie rule, that 3,500 kcal is the equivalent of 1 lb of body weight (22). Regression is used to make predictions about future trends in obesity prevalence (23) and estimate resting metabolic rate in individuals (24). Logistic regression has been used to classify long-term response to dietary interventions (25) or to classify obesity-related health status as we do here (26).

Methods

The NHANES-recorded variables of race, gender, waist circumference (cm), education level, BMI (kg m⁻²) and age (years) were used as explanatory (also referred to as independent or input) variables. After removing records with missing data, a final dataset comprising 25,367 patient records was used. Predicted (also referred to as dependent, outcome or output) variables were categorical binary classifications for high blood pressure and percent body fat levels. Appropriate cut-offs for these measurements were set using the American Heart Association (blood pressure) and the World Health Organization (percent body fat) (27). These thresholds differed for men (systolic blood pressure 140 mmHg, diastolic blood pressure 90 mmHg, percent body fat 25) and women (systolic blood pressure 120, diastolic blood pressure 80, percent body fat 35).

To evaluate model quality, receiver operating characteristic (ROC) curves and the area under the curve (AUC) were computed. All analyses were performed in Alteryx 10.4 (Irvine, CA, USA, 2017).

Results

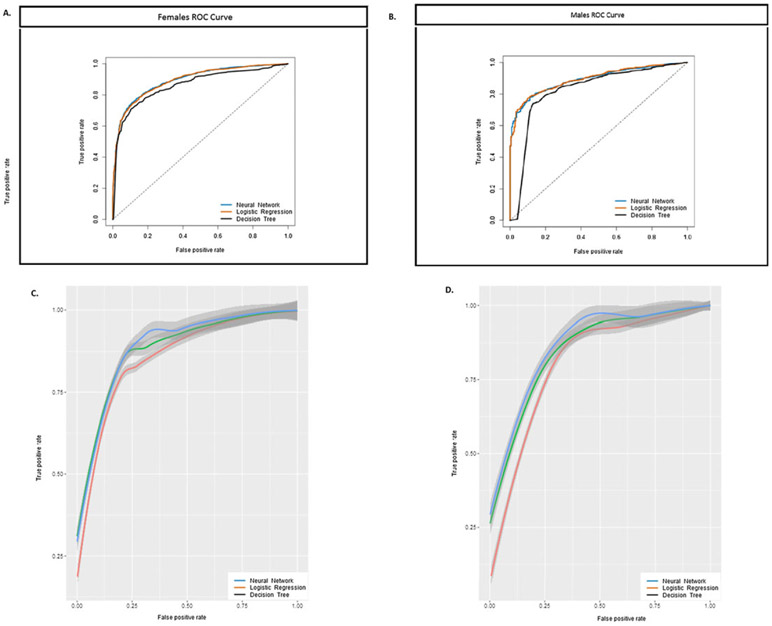
Table 1 (first column) contains the resulting AUC for men and women. As one sees from Table 1, race, gender, waist circumference (cm), education level, BMI (kg m⁻²) and age (years) classify high blood pressure and high percent body fat with good accuracy. Figure 1A,B demonstrates the capacity for logistic regression as a classification model in comparison with neural networks and decision tree analysis, which are described in the next two sections. Figure 1C,D represents the leave-one-out cross-validation ROC curves for all outcomes combined. That is, NHANES subjects were classified at risk if they were above the blood pressure or percent body fat cut-offs. Typically, for validity, we would expect that Figure 1A,B is similar in shape to Figure 1C,D.

Table 1.

Area under the curve that evaluates the accuracy of logistic regression, decision tree analysis, neural networks and deep learning to predict high blood pressure and body fat percentages

Method	Area under the curve
	Logistic regression	Decision tree		Neural networks	Deep learning
			Men
High systolic pressure	0.87	0.82		0.87	0.88
High diastolic pressure	0.79	0.80		0.82	0.87
High body fat	0.89	0.92		0.94	0.94
			Women
High systolic pressure	0.89	0.85		0.89	0.88
High diastolic pressure	0.72	0.71		0.77	0.81
High body fat	0.95	0.93		0.95	0.95

Figure 1.

ROC curves displayed for three predictive machine learning algorithms: logistic regression, neural networks and decision tree analysis. Each algorithm used NHANES anthropometric input data to diagnose whether NHANES individuals are classified with high blood pressure or high levels of percent body fat. ROC curve for (A) women and (B) men. While the curves are very close, neural networks perform slightly better than did decision trees and logistic regression. This is observed in the 95% confidence intervals that overlap in the cross-validations for (C) women and (D) men. NHANES, National Health and Nutrition Examination Survey; ROC, receiver operating characteristic.

Strengths of regression

The strength of regression is that it has a long-standing, well-understood theoretical and computational background. Nearly every scientist receives training in performing a regression analysis, and the language discussing regression is universally accepted. Statistical packages standardize output that allows for fluid movement between software outputs. This would not be the case for TDA (last section) where different software yields a variety of different summaries.

Limitations of regression

When regression methods are employed, model conditions like normally distributed data must be assumed a priori. Additionally, either an iterative check of model terms or an assumed functional form must be determined. Specifically, modellers relying on regression or curve fitting approaches must have a good knowledge of both data properties and model capabilities before the models can be successfully applied.

Neural networks

Introduction to neural networks

An artificial neural network (or simply, neural network) is a mathematical representation of the architecture of the human neurological system and hence falls under the field of artificial intelligence. Neural networks mimic the underlying learning capability of the human brain. The neural network is modelled such that a series of neurons (or nodes) are organized in layers where each neuron in one layer is connected to neurons of other layers with associated weights.

Neural networks are used to predict both continuous numerical and categorical data. There are two phases for effective neural network development. The first phase is what is known as training or learning. What occurs during the training phase is weights that are associated with connections between nodes are adjusted until the model performs well. This completed model is then applied to new data in order to make a prediction. This application of the model is called the testing phase. There are many variations of neural networks that are adopted for different conditions and applications. We refer the reader to the literature for more broad descriptions (18).

Applications of neural networks

Neural networks have been developed to diagnose diseases like tuberculosis (28), malignant melanoma (29), and neuroblastoma (30). Their use has been rarer in obesity research (26,31,32) but could potentially be very valuable in enhancing predictive accuracy when model forms and inter-connections between variables may be non-linear or unknown. For example, neural networks enhanced the capacity to predict long-term success (33) from preoperative data in bariatric surgery patients substantially over linear (34) and logistic regression (35). Neural networks may have similar potential to amplify predictions of long-term weight loss success during lifestyle interventions and long-term behavioural adherence to physical activity.

Methods

For the neural network analysis, we applied the same NHANES variables used in logistic regression; race, gender, waist circumference (cm), education level, BMI (kg m⁻²) and age (years). We also used the same reference database formed after removing missing data. Training data were formed by separating out 70% while the remaining 30% was used for testing. Output variables also remained the same categorical binary outcome of health risk using blood pressure and percent body fat levels, as used for logistic regression.

Results

The comparative model table, Table 1, contains the resulting AUC for neural network classification (second column). While it may not be readily observable from the AUC statistic, ROC analysis (Fig. 1A,B) demonstrates that neural network performs as well as or better than do the other methods (note the confidence intervals overlap in Fig. 1C,D).

Strengths of neural networks

The primary advantage of modelling using neural networks is that they are self-adaptive models that adjust their internal architecture to the data without specification of functional or distributional form (36). Network models have the capacity to approximate any functional form as closely as desired (36,37).

Limitations of neural networks

Neural networks can be prone to overfitting with small sample sizes. Therefore, they are better suited for large datasets as opposed to smaller single-site experimental clinical trial data.

Additionally, where the final developed regression and decision tree models (next section) are easily explained, neural networks are more complex and less readily accessible. Unless the model is coded into a user-friendly app, it is unlikely that a neural network is immediately ready for clinical application. However, with the advent of electronic medical health records and other advances to more technologically advanced health care, it is foreseeable that unified apps can be developed that provide clinicians and healthcare providers with evidenced-based predictions, no matter how complex.

Decision tree analysis

Introduction

Decision tree learning is a predictive algorithm that uses both categorical and numerical data with the goal of assigning samples to specific classes (18). Here we will use decision trees to group NHANES subjects based on their individual characteristics into classes of varying health risks based on blood pressure and percent body fat cut-offs. Unlike regression models, which rely on minimization of error through least squares, decision tree analysis determines thresholds derived from input data. For example, falling above or below the threshold for patient age moves the patient into the appropriate class. While decision trees are standalone effective models for classification, the algorithm’s performance is in some cases improved by using random forests, which aggregate the results of randomly generated decision trees to produce a more effective model (18).

Applications of decision trees

Decision trees have a well-documented history in supporting diagnosis in the medical field. In fact, the method is particularly well suited for diagnosis owing to the transparency of the decision rules determined by the algorithm (38). In obesity, decision trees have already been applied to classify which patients are at risk for metabolic syndrome (39), in which behaviours lead to long-term success in bariatric surgery patients (40), and predicting childhood obesity from early age factors (3). Unlike methods such as neural networks, the thresholds and subsequent class predictions determined by decision trees often have practical interpretation that may be used to draw logical medical conclusions to support clinical decisions. Specifically, the categorical thresholds that dictate splits between predicted classifications provide intuitive decision making rules for clinicians (38).

Methods

The same NHANES input (race, gender, waist circumference [cm], education level, BMI (kg m⁻²) and age [years]) and output (categorical binary outcome of health risk using blood pressure and percent body fat levels) variables were used as in logistic regression and neural networks. Statistics of ROC curves and AUC values were calculated. All simulations were performed in Alteryx 10.4 (2017).

Results

Table 1 contains the resulting AUC for decision trees (third column). The AUC table (Table 1) and ROC curves in Figure 1A,B allow for direct comparison of all three machine learning algorithms. This type of head-to-head comparison is critical for investigators who are analysing large datasets and interested in optimal predictions and minimizing computational time/complexity. Additionally, predictions can be combined into a super-classifier, which may be another neural network to enhance the quality of predictions even further (41).

Strengths of decision tree analysis

As noted earlier, decision trees are particularly well suited for classification of health status using a mixture of categorical and continuous valued input data.

Limitations

Solving an implementation of a decision tree application with optimal thresholds falls into the most difficult class of algorithms with respect to computational complexity. This is referred to as non-polynomial complete or NP-Complete (42). As a result, we must determine thresholds and subsequently patient classification, employing what is known as a greedy algorithm. The greedy algorithm produces only an approximation of the optimal decision tree and is highly sensitive to changes in input data.

Decision tree methods vary, and all methods are not equal. For example, classification algorithms and regression trees (43) suffer from selection bias. This is when predictors with a higher number of distinct values are preferred over predictors with a lower number of distinct values (44). This creates even more problems if there are noisy variables, because the splitting into compartments can be dictated by the noisy variables (45). This bias is not present in other types of decision tree methods such as the classification rule with unbiased interaction selection and estimation (46). Unbiased decision tree methods may be more complicated and computationally complex to implement, and the choice of which method to use should be selected judiciously.

Deep learning

Introduction

Deep learning is one of the more recent entrants to the machine learning domain and involves learning data representations (47) as opposed to constructing task or domain specific features. Unlike the aforementioned neural networks, deep neural networks (DNNs) use a cascade of many layers of neurons (nodes) for feature extraction and transformation. The assumption is that observed data are generated by the interactions of layered factors. This is similar to the layer approach used in network science, described later. Typically, a greedy layer-by-layer method is implemented, where each successive layer uses the output from the previous layer as input. This allows hierarchical generation of low-level features (akin to principal components; see next section), which in turn are combined to form higher-level features and so on.

Typical supervised training of the DNN uses input data and labels to activate nodes and generate weights at each layer of the network. Once the data reach the output (outer-most) layer, the DNN uses all extracted features and hierarchical representations to generate a combined classification. A cost function measures the classification error, which is then fed back (‘backpropagated’) through the DNN to optimize the weights of each neuron and layer. To improve generalization performance, DNNs are typically implemented with regularization (48). For example, in dropout regularization (49), nodes are randomly selected in the DNN to be ignored during training to ensure nodes do not become overly interdependent on each other. For more specifics on deep learning architectures, we refer the reader to (50).

Applications

The most popular and widely recognized applications of DNNs have been in computer vision, recognizing images and objects (51) as well as natural language and speech processing (52). Natural language and speech processing is becoming more important with the advent of obesity research and social media (53). Within genomics, DNNs have been designed for accurate classification of cancer types based on somatic point mutations (54). DNNs have also been able to predict alternative RNA splicing patterns in different types of tissues (55). In the field of biomedical informatics, DNNs have successfully classified human age based on blood biochemistry (56) and early patient readmission to hospitals (57). To our knowledge, they have not been specifically utilized in obesity research thus far; however, there is increasing opportunity to utilize large datasets obtained from three-dimensional (3D) body shape modelling to predict risk of obesity-related mortality and morbidity (58). Specifically, body geometry collected by 3D laser technology provides hundreds of anthropometric measurements on the human body within seconds. These data could be paired with obesity-related medical measurements such as blood pressure, resting heart rate and even injuries in which DNNs can be used to predict risk from scanned images. Additionally, DNNs perform particularly well in genomics as noted earlier. The wealth of genomic related data in obesity provides novel opportunities to predict obesity-related outcomes.

Methods

The same input variables as for logistic regression (education, age year, ethnicity, BMI and waist circumference) were used to construct DNN models to predict the same three categorical output variables as earlier (mean systolic blood pressure, mean diastolic blood pressure and percent body fat). Additionally, the same reference dataset after removal of missing data was used. Models were implemented using Keras, a high-level artificial neural network library written in Python, using Theano as a backend (59).

Results

Each algorithm was evaluated in terms of AUC on the hold-out testing data. We evaluated gender-specific DNN models (Table 1), similar to experiments for logistic regression, neural networks and decision trees. Deep learning can be seen to be the only algorithm to achieve the highest AUCs for all three output variables, as compared with other predictive models. We also examined the performance of a gender-agnostic DNN (where gender was an input variable). While performance during training optimization was comparable for all three output variables for both types of models, the gender-specific DNNs showed a marked improvement in AUC compared with the gender-agnostic DNN for the blood pressure variables (0.83 increased to 0.88). The percent body fat prediction AUC was relatively consistent across both gender-specific and gender-agnostic DNNs.

Strengths of deep learning

In general, deep learning algorithms are popular for their ability to extract abstract features and trends from data that would otherwise be hard to identify via manual observation and perhaps not identified by neural networks. The multi-layer architecture of deep learning neural networks allows deep learning algorithms to condense multi-dimensional data into simpler representations (60). Moreover, deep learning algorithms can be thought to be self-correcting to a certain extent. Through various methods, such as backpropagation and stochastic gradient descent, deep learning algorithms can automatically optimize learned parameters in a fashion that would be more laborious to attempt when developing task-specific features.

Limitations of deep learning

Deep learning algorithms typically perform best with very large training datasets. Similar to the case of neural networks, small sample sizes may lead to overfitting, significantly worsening the generalization performance of the algorithm. Moreover, raw input data cannot be used for training. Typically, datasets need to undergo preprocessing and standardization, which can be time-consuming (60). Additionally, there is no methodical way for determining hyperparameters (multi-dimensional weights) (60). Currently, adjusting hyperparameters is dominated by trial and error, which can be computationally expensive and time-consuming. However, hyperparameter optimization is necessary, as algorithms will not be able to generalize well to other unknown datasets. Similar to neural networks, deep learning is considered a ‘black box’. It is still unknown which nodes, or group of nodes, are responsible for decisions during the training process or why they were selected. In the context of image recognition, research has been performed on visualizing and understanding the low-level deep learning features at each layer; however, this is still an effort in progress. Thus, it is difficult to gather evidence that explains the performance of deep learning algorithms (60), which makes it hard to gauge points of failure.

Finally, unlike the other methods already described, DNN requires either user-developed code as we have done here or coding through specialized software like matlab. As a result, the learning curve for implementation is high.

Descriptive machine learning models

Principal component analysis

Introduction

Principal component analysis is a data collapsing method that groups interrelated variables into what is referred to as components. Each component contains variables that are related to each other. For example, it is well known that BMI is associated with waist circumference (61). Using the NHANES database, we would expect that a PCA would combine BMI and waist circumference into a single component. Components are additionally rank ordered, with the most strongly related variables placed on the first component. The second component would contain the second most strongly related variables that are not related to variables on the first component, and so forth. The end purpose of PCA is to reduce the dataset with many variables to a smaller set of new ‘variables’ called components.

Applications

Principal component analysis is primarily applied to problems where there are a large number of variables measured, which are referred to as high-dimensional problems. Typically, the goal is to reduce the dimensionality by focusing only on the most important components and dropping components of lesser importance.

One important and illustrative application involves facial recognition. The intuitive approach is to develop a library of facial images. When presented with a face to be recognized, an algorithm would then try to match the shape of the eyes and other facial features. Unfortunately, this method is not easily scalable, is computationally intense and is unreliable. Instead of dictating which facial features are important, PCA can determine important components of facial features and then represent any face as a combination of these components (62). That is, every face is essentially a unique combination of components. The number of components is smaller than the original measurements contained in the large image database. To recognize a presented face, the weights of each component in the new face are matched to weights of the components in the database.

Methods

The two main assumptions that must be satisfied to apply PCA is that the data are normally distributed and that the variables considered should not be all correlated to each other (63). If they are, then PCA will only yield one component.

To apply the method to the NHANES dataset, several known related variables and additional variables, which may or may not be related, were considered. Specifically, the variables age (years), weight (kg), height (cm), waist circumference (cm), mean systolic blood pressure (mmHg), mean diastolic blood pressure (mmHg), percent fat for the left and right legs, percent fat for the left and right arms, trunk fat (g), total percent fat, thigh circumference, arm circumference, head area and head bone mineral density.

Analysis was performed in SPSS 24 (IBM, Armonk, NY, 2011). To ensure that the dataset was suitable for PCA, a Kaiser–Meyer–Olkin (KMO) test and Bartlett test of sphericity (63) were performed. The KMO measure of sampling adequacy was used to determine whether the sample was large enough to conduct a PCA. KMO values should generally be above 0.60 for sampling adequacy. The Bartlett test of sphericity determines whether there are indeed at least one set of correlated values, which is determined by statistical significance.

A scree plot was applied to determine how many components to retain. The rule of thumb is to retain the components up to the ‘elbow’ of the plot (63), which appears by the second or third component. Factor loadings that define which variables are contained in each component were obtained from the rotated component matrix.

Results

The resulting KMO measure was 0.85, which is above the rule-of-thumb cut-off for KMO. Bartlett’s test of sphericity was statistically significant (p < 0.001). There were potentially three points in the scree plot including the elbow (Fig. 2). Thus, we retained three components. Of the three components, 47% of the variance in the data was explained by the first component, 71% of the variance was explained by the first and second components, and 80% of the variance was explained by the first three components.

Figure 2.

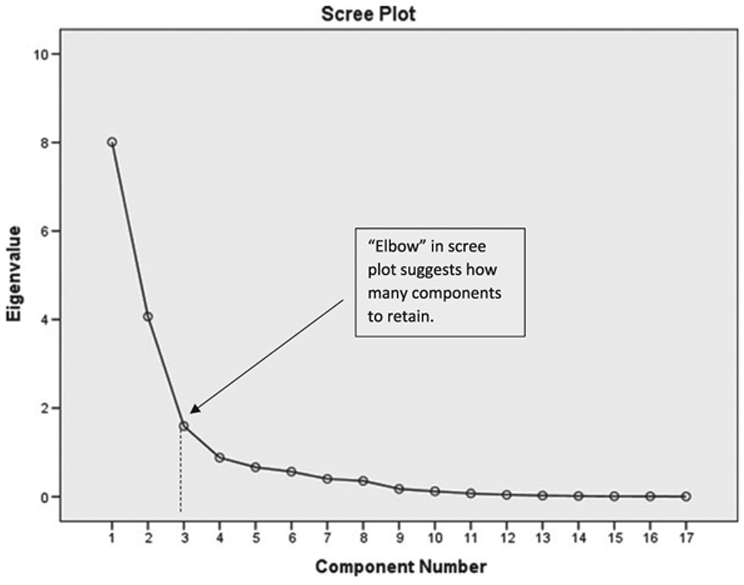
The scree plot relates each eigenvalue in order of magnitude to its component number. The figure is used to determine how many components to retain. Typically, this is right at the ‘elbow’ indicated by the dashed line.

The rotated component matrix (Table 2) identified the first principal component to contain the variables weight (kg), thigh circumference (cm), arm circumference (cm), BMI (kg m⁻²), waist circumference (cm), trunk fat (g), height (cm) and head bone mineral density. The second component contained percent fat in the left and right legs, percent fat in the left and right arms, total percent fat and head area. The third component consisted of age (years), mean systolic blood pressure (mmHg) and mean diastolic blood pressure (mmHg).

Table 2.

The rotated component matrix provides the factor loadings for each variable. Variables in each component are identified by holding the largest magnitude factor loadings (outlined in dark grid lines).

Component	1	2	3
Weight (kg)	0.962	0.012	0.223
Thigh circumference (cm)	0.921	0.163	−0.023
Arm circumference (cm)	0.918	0.130	0.222
BMI (kg/m2)	0.869	0.357	0.192
Waist circumference (cm)	0.847	0.236	0.343
Trunk fat (g)	0.791	0.453	0.283
Height (cm)	0.614	−0.555	0.206
Bone mineral density	0.443	0.019	0.357
Left leg (% fat)	0.163	0.939	−0.041
Left arm (% fat)	0.241	0.938	0.080
Right leg (% fat)	0.172	0.938	−0.033
Right arm (% fat)	0.256	0.934	0.092
Total % fat	0.361	0.911	0.125
Head area (cm2)	0.283	−0.624	−0.202
Age (years)	0.169	0.159	0.835
Systolic blood pressure (mmHg)	0.162	0.062	0.823
Diastolic blood pressure (mmHg)	0.233	−0.046	0.649

BMI, body mass index.

Strengths

The strength of PCA comes from its simple implementation, well-developed mathematical background and application to characterize and distill very large datasets.

Limitations

Direct PCA cannot be applied to categorical data such as gender or race; however, there are categorical variable versions of PCA (63). PCA is also not a prediction method but rather a data aggregation method. Often, PCA is a precursor to prediction after the components are identified.

Cluster analysis

Introduction

Clustering methods are not directly predictive in nature; rather they are descriptive and reveal inherent structure that may be hidden within the data. Unlike regression, applying clustering methods does not require a hypothesis. In some sense, clustering algorithms generate hypotheses by revealing how the data aggregates along with group-specific features. This is particularly important in obesity research where often a single food type (64) or lifestyle behaviour (65) is evaluated for causal effects. The interaction of nutrients in a complex diet and the mixture of non-homogenous lifestyle behaviours in industrialized countries challenge investigators in identifying one sole food type or behaviour as a root cause of obesity. Clustering analysis can identify groups of foods and/or behaviours associated with higher health risks, which can lead to more informed policy decisions and public health recommendations.

Applications of clustering

Within the field of obesity research, clustering is less employed when compared with some of the more traditional predictive methods of analysis. However, there are several interesting applications that are of note (66,67). Analysis of the National Weight Control Registry identified four different subpopulations that successfully lose and maintain long-term weight loss (66). Schuit et al. found that individuals with higher BMI cluster in risky health behaviours, namely, smoking, low vegetable and fruit consumption, excessive alcohol intake and low physical activity (67). A study by Green et al. applied clustering analysis to identify groups with BMI over 30 kg m⁻² (68). The study examined a large health survey database, the Yorkshire Health Study, and found that six distinct group were associated with obesity. Namely, the distinct groups identified were men who consume high volumes of alcohol, young and otherwise healthy women, affluent and otherwise healthy elderly, physically ill and happy elderly, unhappy and anxious middle-aged adults and a subpopulation with the poorest health indicators.

There are a number of different clustering algorithms, each with their own benefits and limitations (18). The most common algorithms are hierarchical clustering, k-means clustering and mean-shift clustering. Hierarchical and mean-shift clustering each produce more accurate and refined results, but large datasets can reduce quality and performance time. For this reason, here, we will focus on a k-means clustering algorithm and refer the reader to (18) for additional algorithms.

Methods

All analyses were performed in the statistical package r (R Core Team, Vienna, Austria, 2013).

NHANES variables

Similar to the published applications, we are interested in clustering groups of individuals by population characteristics with physiological measures. To achieve this, we considered input variables of socioeconomic (education levels), demographic (race, gender and age) and clinical measurements (BMI and waist circumference). Additional NHANES variables could be included, but in order to illustrate the utility of clustering, we restricted to fewer variables.

Data standardization

The first step in the algorithm requires standardizing data. This prevents one characteristic from dominating the clustering algorithm. Some statistical packages, such as spss, automatically standardize data, and the user should review the package descriptions to determine whether an additional transformation is required. Here, we applied ‘scale’ function in r, which subtracts the mean of a particular variable from each observation and divides it by its standard deviation.

Determination of optimal number of clusters

The next step is to determine the optimal number of clusters to identify. As the goal of clustering is to identify subpopulations that share characteristics, a good clustering algorithm should decrease the amount of variation within the clusters with the fewest number of clusters. Obviously, the more clusters that are employed, the less variation will appear in each cluster; however, too many clusters will not be informative. To determine the optimal clusters, we developed a plot that depicts the total variation explained by each additional cluster similar to the scree plot in PCA. We applied r’s kmeans function to determine how many clusters are relevant. The kmeans function requires selection of initial seeds that are anticipated centroids of the clusters. With more information about a dataset, we could judiciously select initial seeds at hypothesized centroids of clusters; however, as we do not have any information to hypothesize where clusters may aggregate in the NHANES dataset, we simply applied 100 random initial guesses. We ran the algorithm for two through 30 clusters, and the percent total variance within clusters was retained.

Results

Optimal number of clusters.

Figure 3 demonstrates the accounted variance as we increase our clusters. The more clusters we have, the more variance is accounted for. Similar to the PCA scree plot, the number of clusters at the ‘elbow’ of the graph at which the variance gains is minimal. In Figure 3, the elbow appears at approximately six clusters.

Figure 3.

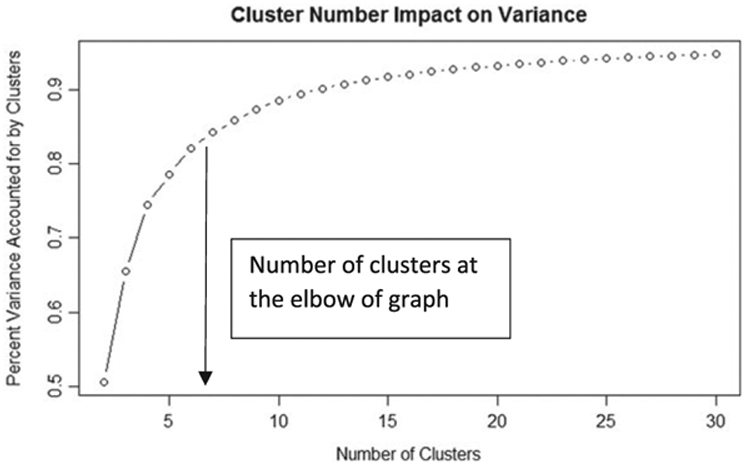
Total percent variance in the dataset plotted on the y-axis versus the number of clusters. As the number of clusters increases, the percent variance increases and plateaus to total variance explained. An optimal number of clusters to consider is where the rate of change of the graph begins to dwindle, implying less return for additional clusters considered.

Cluster descriptions.

The kmeans function in r provides a vector of integers called ‘cluster’, indicating the cluster to which each point is allocated. r output also provides the centroid of each cluster (Table 3). The number of observations in each cluster is high, suggesting that all clusters are important. The centroids reveal the predominant characteristics of each cluster. Cluster 1 can be characterized as older, educated White women, cluster 2 as high-school-educated White women, cluster 3 as middle-aged Hispanic/Asian populations, cluster 4 as high-school-educated men, cluster 5 as individuals effected with higher levels of obesity and cluster 6 as older, educated men.

Table 3.

Each of the six clusters identified by the cluster kmeans algorithm

Cluster	Education ≤ 3 HS or less	Gender 1 = Female 2 = Male	Age (years)	Race*	BMI (kg m −2)	Waist (cm)	N
1	3.709	2.000	50.294	1.325	25.892	88.375	4,205
2	1.610	2.000	16.069	2.285	21.557	74.940	4,340
3	2.167	1.367	42.525	3.225	28.492	97.36	4,229
4	1.529	1.000	15.487	2.181	20.682	73.458	5,223
5	2.890	1.695	42.470	1.837	38.986	118.974	2,676
6	3.691	1.000	49.623	1.246	27.310	98.833	4,693

The centroids identify each cluster as a subpopulation.

HS, high school.

^*1 = non-Hispanic White, 2 = non-Hispanic Black, 3 = Mexican American, 4 = other.

Clusters 1 and 6 distinguish between men and women around the age of 50 with similar education levels. In these clusters, men seem to have a slightly higher BMI and larger waist. Clusters 2 and 4 are also similar in education level (high school); however, differences in BMI and waist circumference are not as pronounced. Clusters 3 and 5 separate by race. Cluster 3 appears to consist mostly of Hispanic and other races, while cluster 5 consists mostly of African–Americans. While the education levels are similar in both clusters, African–Americans were identified with higher BMI and waist circumference.

Illustrating the clusters graphically relays how clusters appear visually as a partition of the dataset. We re-ran the analysis for only three variables (BMI, age and waist circumference) so that we can form a 3D plot of the clusters. Figure S1 visually demonstrates how the clusters partition the dataset.

Strengths

Clustering allows you to look at smaller groups of like data points for analysis. The clustering analysis we present here suggests several different paths that one can act on. As clustering identifies groups as in (66), a targeted anti-obesity marketing campaign or focused community-wide intervention within a cluster would permit interventionists to target communities in a feasible and cost-effective manner with the greatest potential impact.

While our selection of variables did not result in small-sized clusters, clustering can also be effective in identifying extreme observations. For example, if we had found a cluster in the NHANES dataset that is substantially smaller sized, then it is probably worth investigating this distinction, as it may identify a unique set of features that align with a relatively small population. This may be of even more importance when testing the effect of weight loss pharmaco-therapy, which may work better for some subpopulations than for others.

Limitations

Most modelling is used for prediction. Direct clustering is not predictive, but descriptive. While most prediction models require a hypothesis, clustering analysis does not. However, clustering can be used as a precursor to predictive modelling to form a hypothesis. For example, the analysis here suggests that six linear regression models could be developed within each cluster that can predict other NHANES variables we may be interested in. Developing a regression model within a cluster will yield a more accurate model than using a single generic model for the entire dataset.

Network science

Introduction

Network science models inform the understanding of complex systems through representation of data as graphs, which are ordered pairs of nodes and arcs (69). A network is a graph with information associated with the nodes and/or arcs (69). Nodes represent objects such as individuals and locations. Arcs represent the way in which nodes are connected or related to each other. For example, arcs could represent roads between cities. Arcs could also connect something less tangible. For example, two individuals could share an arc if they had similar BMI or education levels.

After developing the network model, we may analyse the topology (or structure) of the network. There are many descriptors, statistics and metrics to describe networks including, but not limited to, centrality measures, density, average path length, average degree, size, number of components and community (69). These quantities describe the data similar to PCA, cluster analysis or TDA (next section) but also can be applied to make predictions.

Applications of network science

Network science has been applied to study a variety of complex systems including social networks (70), the brain and other biological systems (71), the Internet (72), logistics operations (73) and dark networks like terrorist organizations (74). Obesity is a complex problem that is influenced by a variety of factors, making it a natural candidate for network science study (75).

Most commonly, the analysis is of a single-layer network that models social interaction and may assign additional known information about nodes as attributes. Homophily quantifies the tendency for individuals to aggregate under common attributes (69) and can then be used to analyse the connection between social structure and a particular attribute. In 2007, Christakis and Fowler published an analysis of a social network that examined the spread of obesity through social connections (70). In this case, the authors used social networks for prediction, namely, through an examination of homophily effects using different attributes in a social network predicting who is at risk to becoming obese. More recently, network science has been applied to understand how social connections are formed in children affected by obesity (76). On the horizon is the application of network science to develop effective and targeted large-scale interventions as opposed to the one-size-fits-all approach used to date (77).

The traditional approach using single-layer networks has shown utility in understanding obesity trends and potential interventions (75). The single-layer model shows that individuals are related to each other. Multi-layered networks network models and, similar to the concept behind DNN, can account for each of the characteristics that define the system being observed.

A ‘vocation’ layer may represent a specific vocational characteristic. In this case, an arc would connect the nodes representing, e.g. two teachers in a vocation layer. A physical characteristic layer, on the other hand, may consist of individuals in the same BMI classification (normal weight, overweight, etc.). Two nodes representing individuals would be connected by an arc in this layer if they fall into the same category. Naturally, some layers may be more useful or important than others, and so each layer is weighted accordingly.

After building the multi-layer network, we may leverage network science analysis tools to optimize intervention strategies (78).

Finally, a multiplex network consists of multiple layers, which are constructed based on different relationships between the same nodes (79). For example, we may disaggregate a social network into friendship, familial and professional ties, adding even greater fidelity to the multi-layer network model.

Methods

Although there are many network analysis tools and algorithms, this model construction and analysis focuses solely on community detection (80) in NHANES. In general, community detection and clustering are used interchangeably in academia to refer to a process of reducing a network dataset into subsets. The main difference between clustering and community detection lies in the network construction approach and the chosen algorithm to find the subsets. Related to clustering and necessary for community detection is the concept of network modularity. Modularity compares the density of connections inside the identified communities to the density of connections between communities. The community detection algorithm chosen for this section of the paper is the Louvain method (81), which optimizes network modularity with the least computational expense of commonly used algorithms. All simulations were performed in self-written code in the programming language PYTHON (version 2.7). Graphical visualization was developed in gephi (version 0.9.1).

Variables used for network analysis

We developed layers in a category titled ‘demographics’ by using collected demographic data, specifically gender, race, age and education. We applied anthropometric measurements, specifically BMI (kg m⁻²) and waist circumference (cm), to the development of layers within the health category.

Determining network layers

We connected two nodes in the gender layer if the two individuals represented by those nodes were the same gender (e.g. for any two nodes that represent men, an arc connects those nodes in the gender layer). Similarly for the race layer, we connected two nodes if the two individuals represented by those nodes are of the same race, which resulted in four cliques. For the age layer, we developed a more interesting process. We connected two nodes if the younger individual’s age is greater than or equal to one half of the older individual’s age plus seven, or within 2 years’ age of each other, whichever is greater. This relationship takes into account that older individuals are more likely to associate with individuals of broader age range than do younger individuals, and demonstrates that connections can be made using any appropriate criteria.

Similarly, we developed a clique for each education level (i.e. five education layers) such that a person with a given education level is connected to all others with that education level or with a level offset by one. Nodes representing all individuals with education level 1 are connected to all others with levels 1 and 2. Additionally, all nodes representing individuals with education level 2 are connected to all others with levels 1, 2 and 3. Similarly, individuals with education levels 2, 3 and 4 are connected; individuals with education levels 3, 4 and 5 are connected; and individuals with education levels 4 and 5 are also connected.

For anthropometric variables, we developed sets of BMI connections in which two nodes are connected if the individuals represented by them have a BMI that are within 5 kg m⁻² of one another. We defined two individuals to share a waist circumference connection if their waist circumference was within 5 cm of one another. A descriptive diagram of the education layers from the phantom data (Table S1) is depicted in Fig. S2.

Results

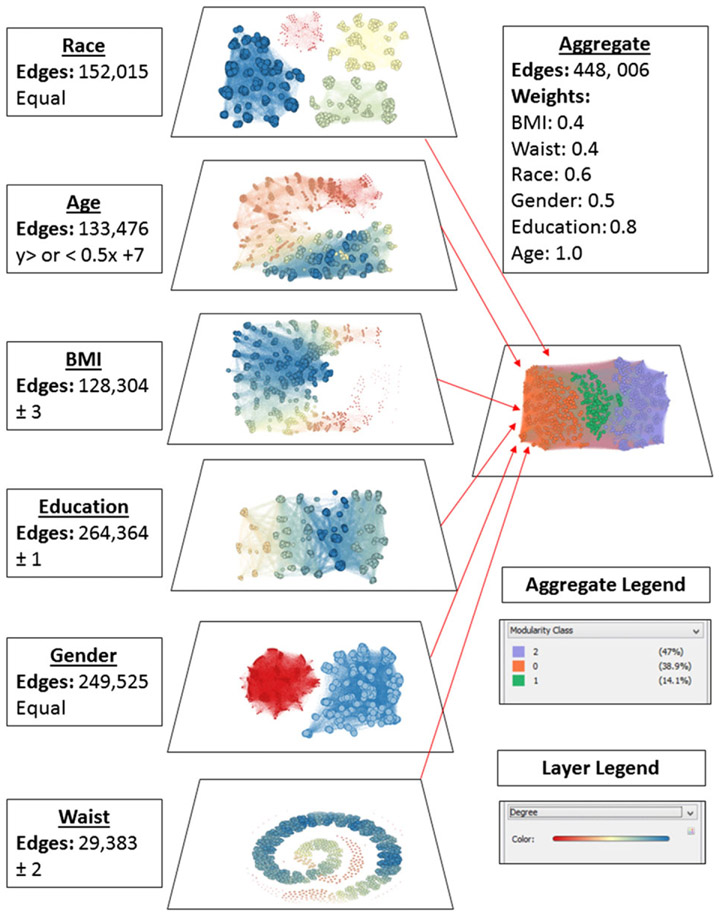
The resultant network structure and community identification are depicted in Fig. 4. Each of the seven attributes is represented separately as a layer within the network to demonstrate each layer’s contribution to the weighted graph labelled ‘aggregate’. In addition to the aggregate network, we can describe the properties of each community in the network. Some of the community properties are summarized in Table 3. Based upon centrality scores, we conclude that the individuals labelled as node 984 and node 49 may be community leaders for communities orange and purple, respectively. This analysis allows us to employ the ‘identification’ intervention strategy by targeting the community leaders, which have the ability to influence change in the rest of the community. Examining other community properties has the potential to guide the use of ‘segmentation’ intervention strategies. For example, the majority of the purple community is highly educated, middle aged, predominantly woman and White with an average BMI of 27.8 kg m⁻² and average waist circumference of 122.7 cm. Knowing these attributes about this community allows us to develop a strategy that is designed specifically for this community.

Figure 4.

NHANES 1000 node sample network and community structure. Each layer depicts the connections of nodes that share attributes, which is described next to the layer. These are then combined to form the aggregate layer, which revealed three communities. BMI, body mass index; NHANES, National Health and Nutrition Examination Survey.

Strengths

Community detection on a multi-layered network, which we applied here, is one of many network science approaches to understanding obesity networks. Similar to cluster analysis, partitioning the network into communities allows us to further study and identify characteristics of each community to personalize an intervention strategy strategically tailored to each community. For example, one community may exhibit a negative attitude towards physical activity that requires a unique intense fitness intervention. Additionally, centrality measures enable the identification of key leaders within each community to focus on ascribing to obesity intervention plans. We can also identify and target key brokers through betweenness centrality to potentially effect multiple communities at once. A third approach could use the idea of community centrality to focus efforts on effecting the most important community in the hopes of influencing the other communities.

Limitations

The approach used in this paper only illustrated the potential for community detection to help inform obesity intervention strategies. The available NHANES data served to build a pseudo-social network. More layers concerning social connections and behaviours are necessary for a more complete analysis to determine proper community assignment. With the advent of natural language processing applied to social media, the potential for building and analysing networks make including social data more promising.

A second important limitation is that the structure of the network layers must be specifically designated. This requires some experience with the data or population or a strong hypothesis, and the final network may be biased by the dictated input structure.

Topological data analysis

Introduction

One of the new methods on the horizon of machine learning is TDA. Unlike the other methods described here, the theory and algorithms for TDA have only been formally applied within the last decade (82). The implications of such a recent development is that user interface software has only been in existence for a few years and has not had the lead time for testing that other machine learning algorithms have had involving varied investigators and applications. Despite these challenges, we included TDA in this review owing to initial successful applications and the potential use to obesity-related high-dimensional noisy data that is becoming increasingly more common in the field.

The premise behind TDA is that data have a ‘shape’ that can be quantified using an area of mathematics called topology. Application of TDA describes the features of the data’s shape, e.g. the number of aggregated data components and/or the number of holes in each group. TDA is best equipped to analyse large data sources like genetic information linked to an individual. This type of data is called high-dimensional data and may be noisy. Many obesity-related data sources such as sensor and genetic data fall into this category.

Applications

To date, the most well-known application of TDA has been to detecting the presence of breast cancer using breast cancer transcriptional data (12). In this study, the authors developed a topologically based algorithm called MAPPER, which relies on a mixture of topological classifications. The study analysed a database consisting of genetic profiles of breast cancer tumours from different subjects. Using MAPPER, the investigators identified and classified a new tumour subtype that had more positive outcomes compared with other tumours. Others have focused on a concept of persistence of topological properties to also examine breast cancer (83). In the case of persistence, analysis can be conducted in freely available software developed by Ulrich Bauer programmed in C++ titled ripser (84).

Methods

Similar to the network science, there are numerous methods and algorithms that fall under TDA. We are employing the persistence topology (PT) method (83).

The NHANES dataset is not a high-dimensional, noisy-enough dataset to warrant comparison through TDA, and the application here is for illustration. If data are already linearly correlated, then similar to PCA, there would be nothing to detect. Thus, we looked at two variables, total bone mineral content (g) and fat mass (kg), that have some correlation, but the correlation appears to have scatter. The entire dataset yielded similar results, but patterns are more easily visualized with a smaller portion of the dataset, which we randomly selected (N ~ 5,000).

The data were first normalized, so all values were between zero and one. To do this, we divided each value by the maximum measurement that appeared in the dataset. Next, we covered each data point with a circle that increased in radius beginning with radius zero and ending when only one component was left (Fig. 5). Components die when the circles overlap and therefore are merged as one component. Figure 5 illustrates a schematic diagram of the intermediate steps in the TDA process using three height and body mass data points from NHANES.

Figure 5.

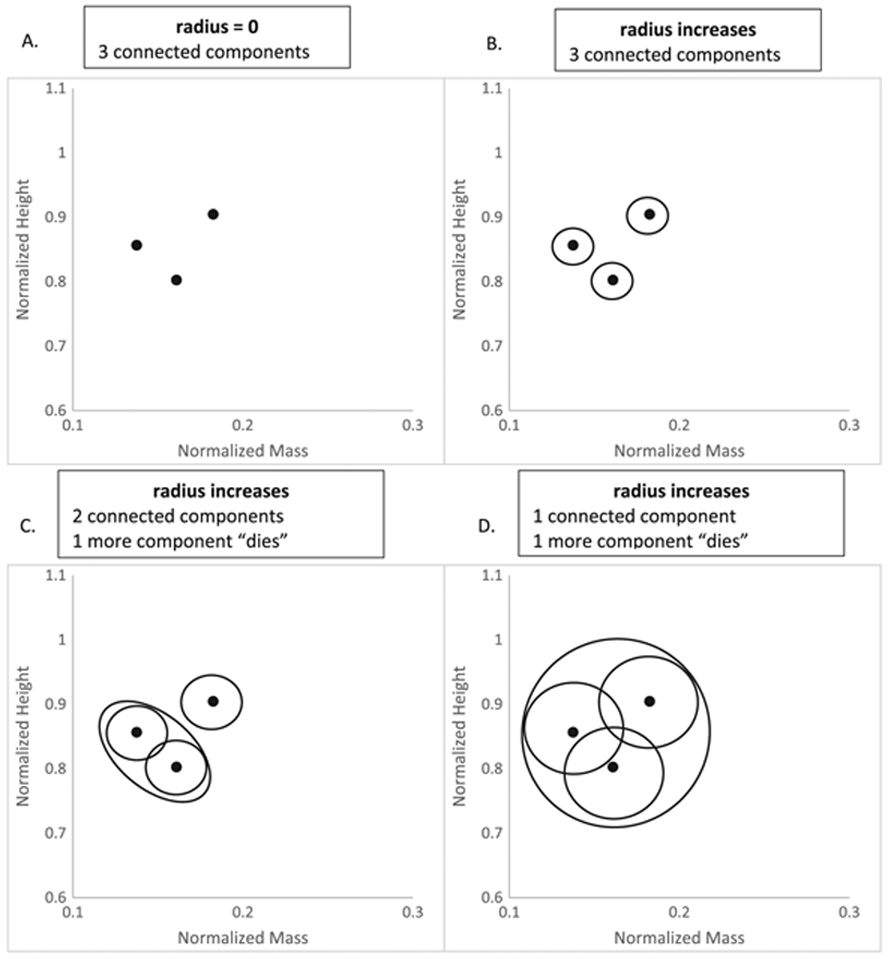
(A–C) TDA ‘death’ process of components as the radius of the circles that cover data points increases. (A) consists of three data points, which by themselves represent three connected components. As the radius increases, they remain as three components (B), until eventually two circles overlap each other (C). The overlapping circles are combined as one, and therefore, one component that used to be alive now dies. (D) The radius has increased sufficiently to cover all three data points so that only one component remains. TDA, topological data analysis.

All simulations were performed in ripser (84), and an add-on program was coded in the programming language PYTHON (version 2.7). Output was exported and graphed in Microsoft Excel (Seattle, WA, 2011).

Results

Figure 6 is a plot of the radius values at which a connected component dies. Most components die quickly until a radius of 0.022. At this point, we see gaps in death time as the radius expanded. Closer examination of the data revealed that the remaining connected components were out-lying data points.

Figure 6.

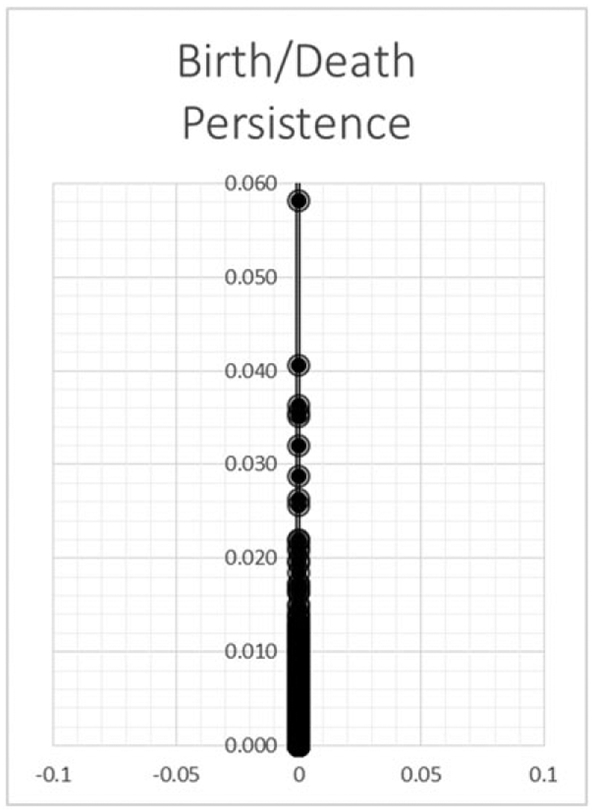
The graph demonstrates the persistence of a connected component. The y-axis represents the radius at which a connected component merges with another (death). As the radius increases, more components merge until all components become one.

Strengths

As described earlier, TDA is equipped to characterize some of the most challenging data that are high dimensional and noisy. The relatively new application of TDA on these types of datasets stands to reveal data descriptions that may not have been already observed with our existing data analysis tools.

Limitations

The biggest limitation to immediate widespread application of TDA, specifically persistence topology, is the lack of standardized software. Software implementations of TDA have recently been developed, such as ripser or MAPPER, but they are not as simple as well-established software such as SPSS. Similar to other new machine learning methods like deep learning, we opted to write our own add-on program in Python. As a result, some thought needs to be put in to determine whether TDA may be useful for a particular dataset and potentially with an expert who has successfully performed TDA. There are currently relatively few individuals with this expertise, but we anticipate that this will change with the rapid growth of successful TDA applications.

Discussion

Here, for the first time, we have put together some of the most common machine learning methods that are currently being applied to understand large and diverse datasets that we are increasingly encountering. We also included a review of DNN, network science and TDA, which are emerging methods that are demonstrating high potential for application in obesity. All methods were applied to the familiar NHANES database for illustration on steps involved, available software and potential output.

We have not included all possible data analysis methods and point out that much more exists in statistics, agent-based models and systems dynamic models. Indeed, to include all tools would be excessive and take away from providing an overview as we have done here.

Conclusions

New and exciting data sources in obesity are requiring innovative and sophisticated mathematical methods for analysis. Existing and emerging methods in machine learning are meeting the need for sophisticated high-level prediction and description. General knowledge of what tools are available will advance the goals of interdisciplinary teams involved in the study of obesity.

Supplementary Material

Supplementary figures

Figure S1: 3D visualization of 400 observations of the six clusters in NHANES projecting on variables age, BMI, and waist circumference. Each color represents a cluster which is observable by sight.

Table S1: Phantom data used to create Figure 2 Supplemental Material.

Figure S2: Schematic diagram depicting education connections from phantom data in Table 1 Supplemental Material.

Abbreviations:

AUC

area under the curve

BMI

body mass index

DNN

deep neural network

KMO

Kaiser–Meyer–Olkin

NCHS

National Center for Health Statistics

NHANES

National Health and Nutrition Examination Survey

PCA

principal component analysis

ROC

receiver operating characteristic

TDA

topological data analysis.