Membrane-curvature-mediated co-endocytosis of bystander and functional nanoparticles

Abstract

Efficient cellular uptake of nanoparticles (NPs) is necessary for the development of nanomedicine in biomedical applications. Recently, the coadministration of functionalized NPs (FNPs) was shown to stimulate the cellular uptake of nonfunctionalized NPs (termed bystander NPs, BNPs), which presents a new strategy to achieve synergistic delivery. However, a mechanistic understanding of the underlying mechanism is still lacking. In this work, the bystander uptake effect was investigated at the cell membrane level by combining the coarse-grained molecular dynamics, potential of mean force calculation and theoretical energy analysis methods. The membrane internalization efficiency of BNPs was enhanced by co-administered FNPs, and such activity depends on the affinity of both NPs to the membrane and the resultant membrane deformation. The membrane-curvature-mediated attraction and aggregation of NPs facilitated the membrane uptake of BNPs. Furthermore, quantitative suggestions were given to modulate the BNP internalization through controlling the FNP properties such as size, concentration and surface-ligand density. Our results provide insight into the molecular mechanism of the bystander uptake effect, and offer a practical guide to regulate the cellular internalization of NPs for targeted and efficient delivery to cells.

Graphical Abstract

A mechanistic understanding and efficient modulation of the bystander uptake effect are given for synergistic delivery of NPs to cells.

1. Introduction

Enormous efforts have been taken over the past decades to develop novel nanoparticle (NP)-based nanomedicines due to the huge potential of NPs in varying applications such as bioimaging,^1-3 therapeutic drug/gene delivery^4-7 and cell tracking.^{8, 9} For these biomedical applications, the entry of NPs into the target cells is a critical but challenging step.^{10, 11} NPs enter cells by several distinct pathways^12-15 with endocytosis being dominant.¹⁶ The endocytic process of cells is extremely complex.^17-21 It is usually initiated by chemo-targeting that relies on NP surface functional ligands, which specifically bind to the cell membrane-embedded receptors in a molecular “lock-and-key” form.²² The process is further modulated by the characteristic properties of NPs, such as type,^22-27 shape,^28-34 elasticity,^35-37 and surface properties.^38-42 However, due to the complexity of the corresponding biological processes, more promising strategies are still required to regulate the cell entry of NPs, which currently limits their use for many advanced and diverse clinical applications.^43-45

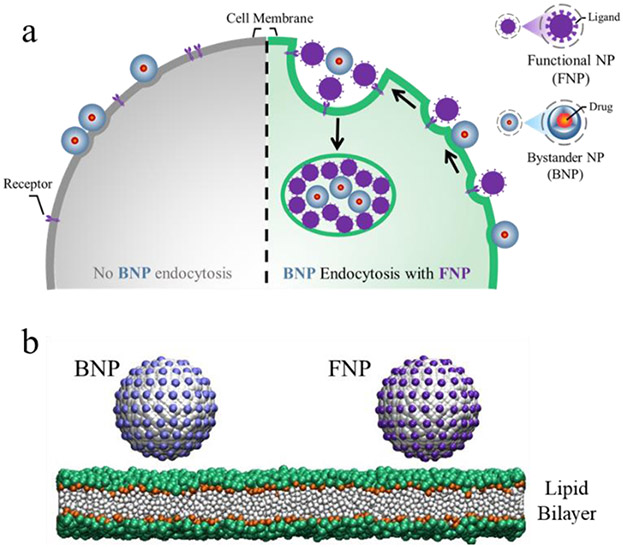
It was recently reported that the cellular internalization of NPs functionalized with transactivator of transcription (TAT) peptides (i.e., FNPs) triggers the cell entry of bystander NPs (BNPs), that cannot be taken up by the cell alone through a receptor-dependent micropinocytosis pathway (Fig. 1a).⁴⁶ Additionally, Xiang et al reported that the co-administration of peptosomes can act like FNP to improve the delivery efficiency of BNPs to tumours.⁴⁷ Such an enhanced cellular uptake activity of BNPs, described as the bystander uptake effect herein, promises an efficient manner to regulate the cellular uptake of cargo NPs or a new strategy to realize NP delivery to target cells. However, a mechanistic understanding of this cellular endocytosis behaviour, such as the physical origin behind the FNP-triggered BNP-uptake process, remains largely unknown.

Fig. 1.

Schematic illustration of the bystander uptake effect (a) and simulation models (b). Colour codes used in (b): the core of the NP in grey, ligands on FNP and BNP surface in purple and light blue, respectively, NC₃ and PO₄ groups of lipids in green, GL1 and GL2 groups of lipids in orange, lipid tails in white.

In this work, the bystander uptake effect was investigated using a coarse-grained (CG) molecular dynamics (MD) simulation and theoretical modelling. The FNPs (mimicking the TAT-coated NPs used in the experiments) and BNPs were constructed and their interactions with the lipid bilayer membrane was performed (Fig. 1). Simulations showed that the membrane internalization of BNPs is dependent on the membrane interaction with both NPs, and thus such an effect could be effectively modulated by controlling the FNP properties such as surficial ligand density and particle size and number. Moreover, calculations of the potential of mean force (PMF) and theoretical energy analysis revealed that the co-endocytosis of BNPs and FNPs can be ascribed to the membrane-curvature-mediated attraction and aggregation of the particles. These results provide insight into the molecular mechanism of the bystander uptake effect of NPs and can guide development of means to regulate the cellular uptake behaviour of NPs as well as novel strategies for targeted delivery of NPs to cells.

2. Methods

2.1. Simulation system and details

The Dry Martini force field was used in the simulations considering the large spatio-temporal scale involved in the cellular endocytosis process. The force field includes four main types of beads (i.e., P: polar, C: apolar, N: nonpolar, Q: charged), and each type has four or five subtypes (such as Q₀, Qd and Nda). More details of the Dry Martini force field can be found in the paper of Arnarez et al.⁴⁸ All simulations were performed with a time step of 30 fs. The second-order stochastic dynamics (SD) integrator with the friction in the Langevin equation (τ_t = 4.0 ps) was used in the simulations. The temperature was set to 310 K. In the simulations, the Berendsen and MTK barostats were used to control the system pressure in the equilibrium and production processes, respectively. Specifically, the compressibility was set to 0 bar⁻¹ in the direction normal to the bilayer surface and 3 × 10⁻⁴ bar⁻¹ in the directions along the bilayer plane with a time constant of τ_p = 12.0 ps. Accordingly, the tensionless state of the membrane in the pure lipid bilayer system or the membrane system containing FNP and BNP could be well controlled in the simulations (Fig. S1). Each system experienced an equilibrium process of 1 μs, after which a production run of 12 μs was performed. All simulations were performed using GALAMOST (version 4.0) package for a full use of computational power of GPUs.^{49, 50}

2.2. Simulation models

Lipid DLPC (1,2-dodecanol-sn-glycerol-3-phosphocholine) was applied to build the planar lipid bilayer membrane with insane.py script⁵¹ (Fig. 1b), and some lipids were chosen as receptors with a special affinity between their head-groups and the ligands coated on the NP surface. Initially, the bilayer had a size of 50 x 50 nm² unless stated otherwise. The NP was constructed by arranging the Nda-type beads on a face-cantered cubic (FCC) lattice with the nearest distance of 0.37 nm. The spherical diameter ranged from 6 to 10 nm where D_F and D_B represent the diameters of FNP and BNP, respectively. The ligand beads (Qd1 for FNP and Qd2 for BNP) were evenly decorated on the NP surface at a density of ρ (ρ_F and ρ_B referring to FNP and BNP, respectively, Fig. 1b). In the simulations, the receptor-ligand interaction was demonstrated by a non-bonded interaction between the Qd1 or Qd2 bead and Q₀ bead (i.e., the head-group of the receptor), as U_r−l = 4ε[(σ/r)¹² − (σ/r)⁶]. Accordingly, the strength of U_r−l could be easily modulated by adjusting the parameter, ε. Noted that in our experiments, FNPs and BNPs differ mainly in their chemical properties or membrane affinities; as a result, unlike FNPs, BNPs are not taken up by cells alone.⁴⁶ Therefore, to realize such behaviour in the simulations (Fig. S2), for FNP, U_r−l was set to have a larger ε = ε_F (e.g., ε_F = 3.5 kJ/mol) due to its stronger membrane affinity; while for BNP, its weaker affinity with receptors was achieved with a smaller ε = ε_B (e.g., ε_B = 1.5 kJ/mol). In addition, the time for membrane wrapping of NPs is on the order of a second,⁵² which is well much beyond the simulation timescale. To overcome this limitation, a high density (30% or 100%) was used as in previous simulations.^{23, 34, 53-55} Additionally, it was found that even with a low total receptor density of 30%, the local number density grew quickly upon FNP binding to more than 80% around the membrane bound particles (Fig. S3a). In the cases with varying receptor percentages, the membrane internalization degrees of NPs were still similar (Fig. S3b). Thus, to improve the computational efficiency, all lipids were considered as receptors in the simulations except where noted to mimic the situations with sufficient receptors in the system. However, this necessary compromise is due to the current limitation of computational ability. The actual membrane internalization rate of NPs, including the occurrence time, is still influenced by the receptor density as well as their diffusion behaviour in the membrane (e.g., Fig. S3b).

2.3. Potential of mean force calculation

The PMF as a function of the distance between FNP and BNP, L, was calculated based on the umbrella sampling method following the most-used protocol (see ESI for details).^56-58 In short, the initial FNP-BNP distance was divided into the configuration windows spaced by 0.2 nm. Then in each window, the system was simulated for 400 ns with a spring force using a constant of 1000 J/mol/nm² applied between BNP and FNP to restrain the special NPs’ configuration on the membrane. The last 300 ns of such trajectories was then used for the Weighted Histogram Analysis Method with the program g_wham in the GROMACS package.⁵⁹ In each window for sampling, the membrane morphology remained stable without obvious change under the NPs’ interactions (Fig. S4).

2.4. Data analysis

The membrane internalization degree of a NP could be described by the extent to which the nanoparticle is wrapped by the membrane, denoted as η = n/N. Here, n is the number of the surface beads in the membrane deformation region, and N is the total number of the surface beads of NP. As such, a larger value of η corresponds to a higher membrane internalization degree. To quantitatively describe the bystander uptake effect, the relative membrane internalization degree of a BNP, η_R = η_B1/η_B0, was used in our simulations, where η_B0 is the membrane internalization degree of the BNP alone (without FNPs) and η_B1 is the internalization degree of the BNP with the help of FNPs. For each system, the last 1 μs trajectory was used for the calculation of η or η_R.

3. Results and discussion

3.1. FNP-triggered membrane internalization of BNPs

The affinity between ligands and receptors drives the receptor-mediated endocytosis of NPs. For the BNPs with a weak membrane affinity (i.e., ε_B = 1.5 kJ/mol), the particles only adsorb to the membrane surface without internalization throughout the simulations (Fig. S2a). However, for the FNPs with ε_F = 3.5 kJ/mol, a strong membrane deformation occurs due to FNP actions in the same simulation conditions (Fig. S2b). As a result, the FNPs are mostly wrapped by the membrane (η ≈ 70 %). These observations agree well with previous studies.³⁴ Moreover, an effective membrane internalization of BNPs could be realized with the help of FNPs, when both of them were placed on the membrane surface (Figs. 2a and S5). The internalization was also dependent on ε_F and ε_B. When ε_B ≥ 1.5 kJ/mol, the BNP spontaneously moves towards the FNP (Fig. 2b), which energetically causes lipid membrane deformation (Fig. S5). Eventually, the BNP is wrapped by the membrane together with the FNP (Figs. 2a and S5). The simulation thus provides a plausible mechanism for the promotion of BNPs internalization by FNPs that is also corroborates experimental observations.⁴⁶ Prior to associating with FNP, BNPs undergoes lateral surface diffusion with the duration dependent on the value of ε_B (Fig. S7). That is, large values promote FNP-BNP association, but if the BNP-membrane affinity is too weak (e.g., ε_B = 1.0 kJ/mol), the BNP remain distant (Fig. 2b) or even detach from the surface (Fig. S5). In these latter situations, little bystander uptake is observed. This is also consistent with experimental observation of TAT-NPs, where little or no bystander activity to solute tracers was seen (the tracer has no affinity to the cell membrane).³⁹

Fig. 2.

Dependence of the membrane internalization of BNPs on ε_B and ε_F. (a) Representative NPs-membrane interaction states (side-view snapshots) under the various ε_B and ε_F (kJ/mol). All the snapshots in the table are obtained at 12 μs. (b) Evolution of BNP-FNP distance during the membrane interaction process. ε_F = 3.5 kJ/mol. (c) Change of the relative membrane internalization degree (η_R) of BNPs with ε_B and ε_F. In all cases, ρ_F = ρ_B = 1.6 nm⁻², D_F = D_B = 8 nm.

The relative membrane internalization degree of the BNPs, η_R, provides a quantitative measure of the bystander uptake effect the value of η_R is determined by both ε_B and ε_F. For most values, η_R > 100% suggesting an enhanced membrane internalization (i.e., cellular uptake) of BNPs with the help of FNPs. With a certain ε_B, η_R increases with the increase of ε_F (Fig. 2c), indicating that a stronger ligand-receptor affinity of the FNPs would further improve the membrane internalization efficiency of BNPs. The influence of ε_B on the BNP internalization behaviour is more complicated. On the one hand, η_R decreases with an increase in ε_B, and when ε_B is sufficiently strong (e.g., ε_B = 2.7 kJ/mol), individual BNPs without FNPs can be enveloped by the membrane to some extent (e.g., η > 50%, Fig. S5 and S6). In this case, the enhancing role of FNPs is effectively reduced. On the other hand, when ε_B is rather weak, η_R is less than 100% (e.g., η_R < 80% with ε_B = 1.0 kJ/mol, dashed columns in Fig. 2c and Fig. S5). It appears that the ensuing large perturbation of membrane due to FNP adsorption interferes with BNP membrane association and/or binding to FNP, which results in a small η_R value (Fig. S8). Overall, our simulations indicate that the bystander uptake effect occurs only when the BNP-membrane affinity exceeds a threshold value (e.g., ε_B ≥ 1.5 kJ/mol) and a larger discrepancy in membrane affinity between BNPs and FNPs would further enhance such effect.

3.2. Influence of FNP properties on the bystander uptake effect

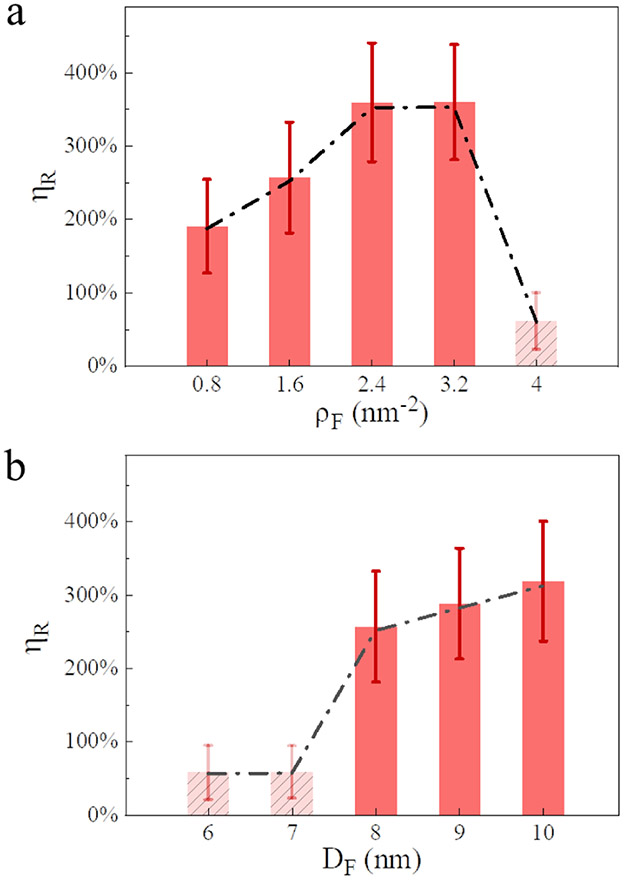
The density of ligands on the FNP surface, ρ_F, is an important factor determining the FNP-membrane interaction process and thereby the bystander activity. Fig. 3a shows that η_R increases monotonically (from ~200% to ~360%) with an increase of ρ_F when ρ_F ≤ 2.4 nm⁻², and then reaches a plateau value with 2.4 ≤ ρ_F ≤ 3.2 nm⁻². However, when ρ_F is further increased (e.g., ρ_F = 4.0 nm⁻²), η_R drops significantly (to ~60%). That is, there appears to be an optimal ligand density for the bystander uptake effect. It may be that with the increase of ligand density, the membrane deformation under FNP actions becomes more dramatic, which significantly facilitates the membrane internalization of FNPs and enhances the cellular uptake efficiency of BNPs. However, for large ρ_F values, the FNP would be rapidly internalized by the membrane (e.g., <0.2 μs), and the BNP is thus left on the membrane without internalization (Fig. S9).

Fig. 3.

Influences of ligand density (a) and particle size (b) of FNPs on the relative membrane internalization degree of BNPs (η_R). ε_F = 3.5 kJ/mol, ε_B = 1.5 kJ/mol. In (a), ρ_B = 1.6 nm⁻² while ρ_F varies, D_F = D_B = 8 nm; In (b), ρ_F = ρ_B = 1.6 nm⁻², D_B = 8 nm while D_F varies. Dashed lines are used to guide eyes.

The size of FNPs also affects the bystander uptake effect, although to a lesser extent than that of ρ_F. As shown in Fig. 3b, for BNPs with D_B = 8 nm, FNPs with a size similar to or larger undergo enhanced membrane internalization. Specifically, η_R increases from 50% (D_F = 6 or 7 nm) to more than 260% (D_F = 8~10 nm). In contrast, FNPs smaller than the BNP undergo little or no enhancement effect. As opposed to the large FNPs, the smaller FNP do not induce significant membrane perturbation (Fig. S10) most likely due to the higher energy required for membrane wrapping of the small NP. Additionally, it is shown by our simulations that the initial FNP-BNP distance only has a minor influence on the bystander uptake effect (Fig. S11). In general, it is obviously demonstrated that the bystander uptake effect can be effectively regulated by modulating the properties of FNPs.

3.3. Association between the bystander uptake effect and membrane curvature change

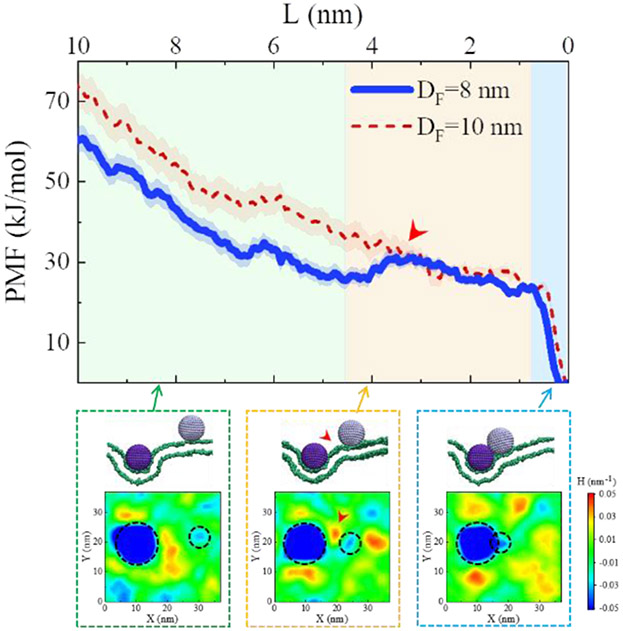
The potential mean force was calculated using the distance between FNP and BNP, L, as the reaction coordinate. Using the case of D_F = 8 nm as an example, the PMF exhibited a complicated, stage-like decline with L (Fig. 4). The PMF displays a rapid decrease when the BNP and FNP are far away from each other (i.e., L > ~4.5 nm); and then the decrease becomes slower, even with a small increase in the middle stage; after that, a dramatic drop in PMF appears at L~0.8 nm, reflecting the aggregation of the two NPs in membrane (Fig. 4). Insofar as no specific affinity is assigned between the BNP and FNP (see Fig. S12c for the detailed interaction energy analysis), the decline of the calculated PMF profile with L suggests a membrane-mediated attraction between NPs. Moreover, at different FNP-BNP distances, the varying membrane deformation or membrane wrapping degrees of NPs occur under the NP-membrane interactions (Fig. S13). In a closer examination, the PMF was noted to be closely correlated to the change membrane curvature. As shown in Fig. 4, the decreasing of PMF exactly corresponds to the merging process of two membrane regions with negative curvatures induced by the membrane-bound FNP and BNP, respectively (the blue parts highlighted by dashed circles, Fig. 4). Even, a small membrane protrusion with positive curvature (indicated by red arrowheads in Fig. 4) appears during the approaching of the NPs, referring to the increase of the PMF profile observed in the middle stage. In addition, in the case of D_F = 10 nm, the L-dependent decrease of PMF is even steeper and more smoothly, corresponding to the stronger membrane deformation and higher NP internalization efficiency. Similar membrane curvature changes around the NPs were also observed in the unbiased simulations with spontaneous movement of BNP towards FNP (Fig. S12a, b). In addition, the systems containing FNPs with varying ρ_F values also demonstrated a similar tendency in the PMF profile (Fig. S14). All these results suggest that the bystander uptake effect is a result of the membrane-curvature-mediated attraction and aggregation of the NPs.^{53, 55, 60-62}

Fig. 4.

Change of the PMF profile with the BNP-FNP distance (L). Dashed boxes show the representative snapshots during the NP-membrane interactions with different L and the corresponding membrane curvature patterns (bottom). For clarity, only lipid heads (green beads) are shown in the snapshots. ε_F = 3.5 kJ/mol, ε_B = 1.5 kJ/mol, ρ_F = ρ_B = 1.6 nm⁻², D_B = 8 nm, D_F = 8 or 10 nm.

3.4. Cooperation of FNPs regulates the bystander activity

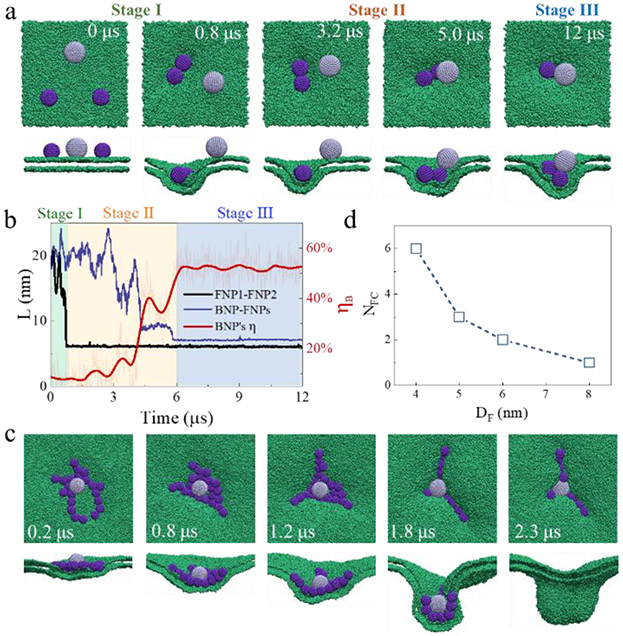
In the simulations above, the simplest situation consisting of a single FNP and a BNP was considered. However, the FNP number (N_F), i.e., the relative concentration of FNPs to BNPs, also plays a role in determining the NP-membrane interactions. For example, as shown in Fig. 3b, it is difficult for a small FNP with D_F = 6 nm to activate the membrane internalization of a BNP with D_B = 8 nm due to the weak membrane actions of the FNP. However, at a higher FNP number, e.g., from one to two, the bystander uptake became obvious (Fig. 5a). In this case, the occurrence of the BNP internalization is followed by the aggregation of the two small FNPs (Fig. 5a). This point is also reflected by the close association between the changes of η_R and that of the BNP-FNP distance (Fig. 5b): the two small FNPs aggregate together rapidly (Stage I), which triggers the gradual approaching of the BNP (Stage II), and the final FNP-BNP aggregation is accompanied by a much-enhanced membrane internalization degree of the particles (Stage III).

Fig. 5.

FNP number and size dependence. (a) Representative simulation snapshots showing the membrane internalization of a BNP with the help of two FNPs. (b) Time-evolutions of the NP-NP distance and the membrane internalization degree of a BNP. Background colours refer to the three stages. (c) Representative simulation snapshots showing the membrane internalization of a BNP with the help of 21 FNPs. In this case, the membrane size is 70 nm × 70 nm. (d) Correlation between the critical number of FNPs required for the internalization of a BNP and the FNP size. In all cases, ε_F = 3.5 kJ/mol, ε_B = 1.5 kJ/mol, ρ_F = ρ_B = 1.6 nm⁻², D_B =8 nm; in (a-c), D_F = 6 nm.

An increased FNP number in the system would also further strengthen the degree of membrane deformation and facilitate the bystander uptake effect. Fig. 5c shows the events associated with a FNP number of N_F = 21, in which a large-scale membrane deformation occurs (even like the vesiculation observed in experiments),⁴⁶ along with a strong membrane wrapping of the BNP closely surrounded by the FNPs.

In addition, the effect of FNP number is dependent on FNP size. We calculated the minimum number of FNPs (N_Fc) needed to activate the bystander uptake of a BNP with D_B = 8 nm (i.e., η_R ≥ 200%). As shown in Fig. 5d, with the decrease of D_F, more FNPs are required, but the initial locations of FNPs relative to the BNP only have a minor effect on η_R of the BNP (Fig. S15). Generally, all these results suggest the complicated cooperative effect of FNPs, which is influenced by the particle size and number (i.e., concentration), in activating the membrane uptake of BNPs.

3.5. Theoretical energy analysis of the NP-membrane interactions

A theoretical energy analysis of the interaction between the membrane and particles (i.e., FNPs and BNP) and the possible membrane wrapping situations were examined based on the Helfrich model (Fig. 6a).⁶³ For such a multiple-NP-membrane system, the total energy E could be taken as:

$$E=E_{bind}+E_{bend}+E_{rim}.$$ (1)

Fig. 6.

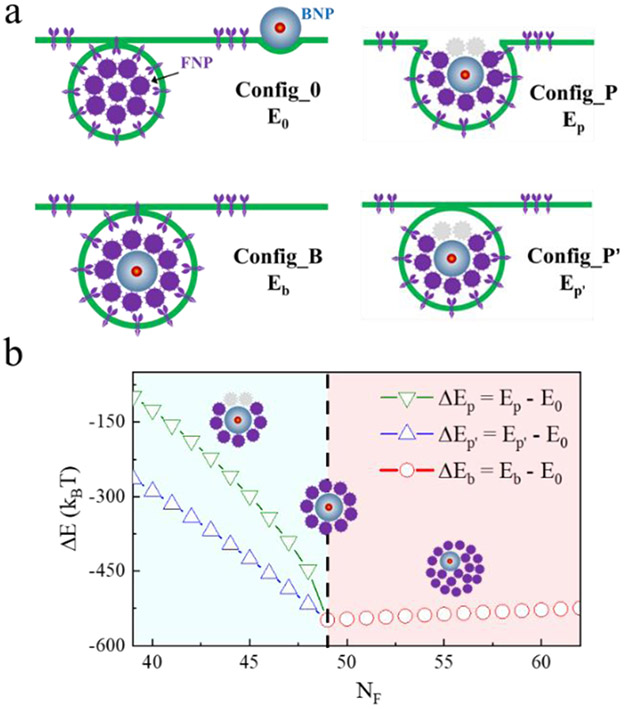
Energy analysis of the bystander uptake effect. (a) Sketches showing some typical interaction states between the NPs (i.e., FNPs and BNPs) and the membrane. (b) Changes of energy differences between the different states with the FNP number N_F. Insets show the possible covering situations of FNPs around BNPs. N_B = 1, r_F = 10 nm, r_B = 25 nm.

Here, E_bind = −N_pair μ, in which N_pair is the number of ligand-receptor pairs and μ is the energy released upon the binding of a ligand-receptor pair, whose value is on the order of 20k_BT based on experimental measurements.⁶⁴ Usually, the cross-sectional area of a receptor is about a₀ ≈ 192 nm².⁶⁴ For a NP with the radius r partially wrapped by the membrane, its contact area with membrane is 4πr²η, where η is the membrane wrapping degree of the NP. Thus, η = 1 refers to the fully membrane-wrapping state of the NP, η = 0 is the slight membrane-adhesion state of the NP, and 0 < η < 1 corresponds to the partially membrane-wrapping state of the NP. Accordingly, N_pair could be taken as N_pair = 4πr²η/a₀. The bending energy, E_bend, of the membrane was calculated as E_bend = 1/2κA(H₁ + H₂)² where the bending rigidity κ is typically on the order of 20 k_BT,⁶⁵ H₁ and H₂ are the local principal curvatures of the deformed membrane region, and A is the area of the deformed membrane. For a membrane-wrapped spherical NP, $H_1=H_2={}^1∕_r$, and A = 4πr²η. E_rim = γL is the line energy of the rim of the deformed membrane region, in which γ is the line tension(γ~ k_B T/nm) and L is the length of the rim.⁶⁶ Similarly, L was taken as $L=2\pi r\sqrt{4\eta (1-\eta )}$. Thus, for a simple NP-membrane interaction system, the associated energy could be written as:

$$E=-4\pi \mu r^2\eta ∕a_0+8\kappa \pi \eta +\gamma 2\pi r\sqrt{4\eta (1-\eta )}.$$ (2)

Due to the complexity of the membrane wrapping process in the bystander uptake activity, the energy differences between some typical states (ΔE) associated with the bystander uptake effect was the focus. That is, the bystander uptake or non-bystander uptake states shown in Fig. 6a were examined to determine the energetically favourable state, instead of the wrapping pathway. The system contained multiple FNPs (note that N_F is a variable here) with a radius of r_F = 10 nm and one BNP with the radius of r_B = 25 nm. As shown in Fig. 6a, the Config_0 state refers to the state without the bystander effect, that is, all FNPs are wrapped by the membrane while the BNP remains at the membrane surface. For simplification, the membrane-wrapped FNPs are regarded approximately as a “big NP” with the radius of R₀, which has the same volume as that of the membrane-wrapped FNPs (i.e.,$\frac{4}{3}\pi R_0^3=N_F\frac{4}{3}\pi r_F^3$). The membrane wrapping degree of the BNP was assumed to be η_B0. Thus,

$$\begin{gathered} E_0=\left(-\frac{4\pi R_0^2}{a_0}{\mu }_F+8\kappa \pi \right) \\ +\left(-\frac{4\pi r_B^2{\eta }_{B0}}{a_0}{\mu }_B+8\kappa \pi {\eta }_{B0}+\gamma 2\pi r_B\sqrt{4{\eta }_{B0}(1-{\eta }_{B0})}\right). \end{gathered}$$ (3)

The first term on the right of (3) stems from the energy contribution of the FNP-membrane interactions and the second term is for the BNP. It is noted that there is also a ligand-receptor binding energy for BNP, although μ_B ≪ μ_F. Here, we assume μ_F = 20 k_BT, μ_B = 4 k_BT, and γ_B0 = 20%.

In contrast, the Config_B state could be considered as an ideal bystander uptake state (Fig. 6a). Based on the simulation (e.g., the snapshots in Fig. 5c) and experimental observations,⁴⁶ we assume that, in this state, the BNP is always surrounded by the FNPs, and then they are wrapped by the membrane completely. Also, all these wrapped NPs (including both FNPs and BNP) are considered as a “big NP” with the same volume. Thus,

$$E_b=\left(-\frac{4\pi R_1^2}{a_0}{\mu }_F+8\kappa \pi \right).$$ (4)

In (4), R₁ the radius of the equivalent “NP”, whose volume $\frac{4}{3}\pi R_1^3=N_F\frac{4}{3}\pi r_F^3+\frac{4}{3}\pi r_B^3$.

The partial bystander uptake state probably exists, if there are not enough FNPs or the BNP is too large. Under this situation, only part of the BNP surface could be covered by the FNPs, and the coverage ratio is approximately ${\eta }_c=N_F\pi r_F^2∕4\pi (r_F+r_B{)}^2$. Two possibilities were taken into consideration (Fig. 6a). One, the membrane is only able to wrap the part of the BNP which is covered by the FNPs (i.e., Config_P). In this case, the system energy is about:

$$E_p=-\frac{4\pi R_2^2{\eta }_c}{a_0}{\mu }_F+8\kappa \pi {\eta }_c+\gamma 2\pi R_2\sqrt{4{\eta }_c(1-{\eta }_c)}.$$ (5)

The other, the BNP and the surrounding FNPs are still able to be internalized by the membrane completely, if the binding between the BNP and the membrane is considered and η_c is large enough (Config_P’, Fig. 6a). Accordingly, the energy is:

$$E_{p^{{}_{\prime }}}=-\frac{4\pi R_{2\prime }^2{\eta }_c}{a_0}{\mu }_F-\frac{4\pi R_{2^{\prime }}^2(1-{\eta }_c)}{a_0}{\mu }_B+8\kappa \pi .$$ (6)

Also, R₂ or R₂, is the radius of the equivalent “NP”. For simplification, we only consider the situation with a large η_c (η_c > 80%), namely a large part of the BNP surface is covered by the FNPs. Thus, R₂ or R₂, is approximately equal to R₁. Based on these considerations, the energy difference between the states associated with the bystander activity could be calculated as ΔE_b = E_b – E₀, ΔE_p = E_p – E₀, and ΔE_p′ = E_p′ – E₀.

As shown in Fig. 6b, the calculated values of all three ΔE are less than zero. This indicates that the co-endocytosis of BNP with FNPs is more energy favourable compared with the non-bystander uptake state (i.e., Config_0 state). Moreover, with the increase of N_F, both ΔE_p and ΔE_p′ decrease rapidly, suggesting that an increased FNP number would effectively facilitate the bystander uptake behaviour, being consistent with the simulation observations (Fig. 5). With a further increased in N_F (e.g., N_F ≥ 49 here, with which the FNPs are more than enough to fully cover the BNP surface), ΔE_b increases slowly with N_F, although is still less than zero. This is mainly ascribed to the decrease in the surface area gain of the membrane-wrapped NPs with N_F (ΔS, see Fig. S16). These results demonstrate that an optimal FNP number (i.e., relative concentration of FNPs to BNPs) is suggested in improving the bystander uptake efficiency.

For simplification, the shape of the vesicle containing wrapped NPs is assumed to be spherical in the energy analysis above. However, based on previous theoretical models and especially experimental observations,^{46, 67-70} both spherical and tube-like endocytic vesicles are possibly formed. Therefore, energy analysis of the energy differences between some typical states in the bystander uptake activity with tube-like vesicle forms was also performed (see ESI for details). Similarly, it is found that, compared with the non-bystander uptake state, the bystander uptake states are more energetically favourable (Fig. S17) although the membrane is deformed in a tube-like form.

4. Conclusion

The bystander uptake effect is one of the newly found pathways for NPs entrance into cells.⁴⁶ We investigated the underlying molecular mechanism by combining the MD simulations with theoretical model analysis. The simulations revealed that the membrane wrapping of FNPs will enhance the membrane internalization of BNPs, consistent with experimental observations. From PMF calculations and membrane curvature analysis, the bystander uptake effect was closely correlated with the FNP/BNP-membrane interactions and the resultant membrane-curvature-mediated attraction and aggregation of the NPs. The FNP properties of size, number (i.e., relative concentration of FNPs to BNPs), and the number density of ligands coated on the FNP surface, play complicated roles in regulating the bystander uptake effect. Note that the cooperative wrapping behaviours of NPs by the membrane have been reported before, which, however, were mostly concentrated on the NPs with the same or similar properties.^{53, 55, 60, 69-71} It was clearly demonstrated by our simulations and energy analysis that membrane-mediated cooperation of NPs could also occur between NPs with distinct properties. Furthermore, the strong dependence of the bystander uptake effect on the properties of BNPs and especially FNPs, such as the cargo selectivity effect or the quantitative modulating ability of the membrane internalization degree of BNPs by the FNP number and size, provides a larger parametric space to control the cooperation or cellular uptake of NPs. Moreover, the stage-like internalization process of BNP with multiple FNPs also provides a deeper insight into the complexity of the membrane-mediated cooperation of NPs. In all, our results provide a mechanistic insight into the bystander uptake effect, and suggest the practical ways to regulate such a new cellular uptake behaviour for applications.