Errors in reported ages and dates in surveys of adult mortality: a record linkage study in Niakhar (Senegal)

Abstract

Sibling survival histories are a major source of adult mortality estimates in countries where death registration is incomplete. We evaluate age and date reporting errors in sibling histories collected during a validation study in the Niakhar Health and Demographic Surveillance System (Senegal). Participants were randomly assigned to the questionnaire used in Demographic and Health Surveys or to a questionnaire incorporating an event history calendar, recall cues and increased probing strategies. We linked 60–62% of survey reports of siblings to the reference database using manual and probabilistic approaches. Both questionnaires had high sensitivity (>96%) and specificity (>97%) in recording the vital status of siblings. Respondents underestimated the ages of living siblings, ages at death, and the time since deaths. These reporting errors introduced downward biases in mortality estimates. The revised questionnaire improved the reporting of ages of living siblings but not the reporting of ages at death or the timing of deaths.

1. Introduction

In most countries in Sub-Saharan Africa and Asia, death registration systems are deficient (Mikkelsen et al., 2015). To compensate for the lack of reliable vital statistics, mortality trends are derived from survey or census data on the survival of close relatives and household members. Full birth histories collected in Demographic and Health Surveys (DHS) are the primary source of estimates of under-five mortality (You et al., 2015). Similarly, sibling survival histories (SSHs) are a major source of data on adult mortality (Dicker et al., 2018). In sibling histories, women aged 15–49 years are asked to list all their siblings born to the same mother by birth order, and to report on their gender, survival status, current age when alive, or ages at death and years since death when deceased. Sibling histories are also a key data source for the monitoring of trends in maternal mortality, as questions are asked to identify sisters who died from pregnancy-related causes (Wilmoth et al., 2012; Alkema et al., 2016).

Sibling histories are subject to reporting bias that may affect the accuracy of mortality estimates. Evaluations of data have been based on consistency checks (Stanton et al., 2000; Masquelier, 2014; Saiffudin et al., 2014), comparisons of mortality trends across successive surveys (Obermeyer et al., 2010; Timæus and Jasseh, 2004) or with other sources, such as estimates generated by UN agencies (Feeney, 2001; Reniers et al., 2011). These approaches can only give a sense of the direction of the biases because different types of reporting errors are at play in sibling histories. Some live and deceased siblings can be omitted and ages at survey or at death can be misreported. The time of death can also be affected by heaping or systematic misstatement. Some errors have similar effects on mortality estimates but other errors can in part cancel each other out. For example, survey respondents might omit to list some of their deceased siblings, introducing downward biases in mortality levels but omissions could be counterbalanced to a certain degree by ages at death being under-estimated. The identification of reporting errors and evaluation of their effects on mortality estimates require direct evaluation studies−comparing survey reports of siblings’ survival to prospective records of these siblings’ vital events.

Direct evaluation studies are rare because they require that high-quality independent mortality data be available to be used as reference; that genealogical data are sufficiently detailed to provide reasonably complete lists of siblings; and that record linkages between independent data sources are feasible. This latter requirement is rarely met because datasets collected in low and middle-income countries seldom include shared unique identifiers (e.g., a social security number) that allow the convenient matching of records. We thus know of only two direct evaluation studies of sibling data based on record linkages at the sibling level, all conducted in Health and Demographic Surveillance Systems (HDSS). HDSS sites are study areas where the population is monitored through regular household visits (Pison, 2005). After an initial census, an open cohort is followed, with new members entering through birth or in-migration, and members exiting through death or out-migration. Data are collected on vital events, marriages, migrations and pregnancies since the last household visit. Causes of deaths are determined through verbal autopsies (Nichols et al., 2018).

The previous direct evaluation studies of sibling histories have been conducted in Bangladesh in the Matlab HDSS, and in Senegal in the Bandafassi HDSS. In the Matlab study, respondents were selected among surviving siblings of women who had died of pregnancy-related causes (Shahidullah, 1995). This study highlighted negative bias in maternal mortality estimates due to omissions and misclassification of maternal deaths. However, the accuracy of ages at death and the timing of death were not examined. In the Bandafassi study, sibling histories were collected through the standard DHS questionnaire and manually linked to the HDSS dataset (Helleringer et al., 2014a). Respondents omitted 4% of their sisters still alive, 9% of their deceased sisters, and 17% of their sisters who had migrated out of the HDSS area. Respondents also systematically underestimated the age at death of their deceased siblings, particularly for siblings who died at older ages (≥45 years).

Both studies were based on manual linkages between survey reports and HDSS records: researchers visually compared first and last names, as well as other fields from the two databases (e.g., reported gender), then they assigned the same ID number to the cases for which these fields matched. In most instances of manual linkages, two reviewers attempt to link each survey report to the HDSS data, and then discrepancies are resolved by a third reviewer. This process of manual review was the standard approach in the past, before the development of probabilistic record linkage techniques based on the Fellegi and Sunter (1969) framework (Alvey and Jamerson, 1997). It is still regularly used for linking small databases or in settings without common identifiers (Wallis et al., 2015; Van der Maas et al., 2017; Carter et al., 2011; Hufanga et al., 2012). It has however important drawbacks. Manual record linkages are difficult to conduct in larger samples, due to costs and time constraints; it was only feasible in the Matlab and Bandafassi studies because they had relatively small samples (respectively 384 and 268 respondents). In addition, manual linkages often lack replicability since they depend on judgments made by the researchers involved in reviewing data fields.

Another approach to record linkages exists that addresses these limitations: it uses an algorithm to calculate the probability that the same value obtained on common variables in two databases for a pair of records refers to the same person (Jaro, 1995). This probabilistic approach has been used to match HDSS data with other data sets. Kabudula and colleagues (2014a) linked mortality data between the national civil registration and vital statistics (CRVS) system and the Agincourt HDSS in South Africa. In a subset of records that were linked using the South African national identity number, they obtained high sensitivity (90.0%) and positive predictive value (98.5%) for the probabilistic approach. Records from health care facilities have also been successfully matched with HDSS to advance research on the uptake of health services and the prevalence of some diseases (Kabudula et al. 2014b, Rentsch et al., 2017).

In this paper, we re-analyze data from a third direct evaluation study of sibling histories conducted in 2013 in the Niakhar HDSS, in Senegal. This study was much larger than the studies conducted in Matlab and Bandafassi. It also evaluated a new questionnaire, the siblings’ survival calendar (SSC), which incorporated an event history calendar, additional recall cues and increased probing strategies (Helleringer et al. 2014b). This questionnaire reduced the tendency to round ages to the nearest multiple of 5 or 10 (digit preference). It also reduced the omission of female deaths. However, until now, the survey data from this study had not been linked to the HDSS dataset at the sibling level. Thus age and date errors have not be measured precisely. We extend previous work in three directions. First, we link data from the Niakhar study at the sibling level using both manual and probabilistic approaches, and we compare the resulting links. If successful, the probabilistic approach to record linkages could be employed in other evaluation studies of mortality data collected during surveys, such as birth histories for under-five mortality. Second, we use the linked datasets to examine distributions and covariates of reporting errors on ages and dates. Third, we investigate the effects of reporting errors on mortality estimates using simple simulations applied to the most recent set of sibling histories collected in a DHS in Senegal.

2. Methods

Reference dataset

The Niakhar HDSS is located in Senegal (West Africa), 135km southeast of Dakar (Delaunay et al., 2013; 2018). It is one of the oldest HDSS, with 8 villages under demographic surveillance since 1962. The study zone was extended in 1983 to cover 30 villages comprising about 44 000 inhabitants in 2013. The main religious groups in the area are Muslims (74%) and Christians (18%). The educational level is low: in 2015, 57% of women aged 15–49 in the HDSS population had never attended primary school. The area has experienced a rapid mortality decline, with under-five mortality rates declining from 182 per thousand in 1984–8 to 34 per thousand in 2014–17 (Trape et al., 2012; Delaunay et al., forthcoming). Fertility rates remain high (with TFR around 6 in 2014), resulting in sustained population growth.

In the HDSS, each resident is attributed a unique ID number, which he/she maintains after migration within the HDSS area. Individuals also retain their ID number after episodes of migration outside of the HDSS area. Residents are attributed a maternal and a paternal ID numbers, which identify their biological parents in the HDSS population. This information allows rapidly generating a list of the siblings of any population member, by looking up which other HDSS members shared the same maternal/paternal ID numbers. In Niakhar, some HDSS members have a missing mother/father ID number, either because the biological mother/father was never part of the HDSS and is thus unknown, or because the information collected during household visits was insufficient to establish a link between mother/father and child. Sibship lists can also be incomplete if a mother gave birth to children outside of the HDSS and these siblings have never been resident in the area. At the time of the 2013 mortality survey, a mother ID number was available for 96% of residents alive at the last HDSS round, 65% of previous residents that had left the area under surveillance, and 38% of residents who had died prior to the last round. Due to these missing ID numbers, we cannot measure the completeness of the lists of siblings reported in sibling histories. Instead, we focus on assessing the accuracy of the information on vital status, ages and dates for siblings that can be matched to a HDSS record. The age of siblings who are residents of the HDSS is known with varying accuracy, depending on how they were first registered. 44% of adult siblings that could be matched to a survey record were born in the area between two household visits; their age is known with great precision. 9% of siblings migrated into the area and 47% of siblings were already present in the HDSS at the time of the initial census (1962 in 8 villages or 1983 in 22 villages). Particular attention is devoted to establishing accurate dates of birth at the time of first registration, including by using historical calendars, administrative documentation such as immunization cards, and the reconstruction of birth and marital histories of women of reproductive age (Garenne et al., 2000). Even for the latter two groups of HDSS records, age data is thus likely of high quality.

Collection of sibling survival histories

Between January and March 2013, a total of 1,189 participants from Niakhar HDSS were recruited for the validation study. Participants were selected among individuals aged 15 to 59 years who had ever been registered by the HDSS. Individuals who had experienced at least one adult death among their maternal siblings were oversampled. Members of the HDSS population who had no known siblings or who had a missing, invalid or inconsistent mother ID number were excluded. Absent residents and migrants were followed-up in the cities of Dakar and Mbour and their suburbs, and in a tracing area within a 80-km radius of the HDSS. In total, we interviewed 609 respondents who had been randomly assigned to the standard DHS module on adult mortality and 580 respondents who had been assigned to the SSC questionnaire. The study design is described extensively elsewhere (Helleringer et al., 2014b).

The 1189 respondents reported on 8025 siblings. They provided information on the name of each of their sibling, his/her sex, survival status, current age or age at death and the timing of death (years since the death). They also reported on the last residence of the sibling, the name of the head of the compound in which he/she last lived, the name of his/her spouse for married siblings, and nicknames. These questions were aimed at enabling the linkages with the HDSS dataset.

Record linkages

Both manual and probabilistic record linkage techniques were used to match survey reports on siblings to HDSS records on the same individuals. For manual linkages, a spreadsheet presented each SSH report alongside lists of siblings born to the same mother and extracted from the HDSS databases. Two members of the study team working independently assigned an HDSS ID number to each reported siblings. The variables used were (1) name, (2) sex, (3) the name of the head of the compound, (4) other names used or nicknames, (5) the name of the partner, and (6) the last known residence of the sibling. Vital status, ages at survey and ages at death were not used as we evaluate the quality of reporting on these items. When two team members had not assigned the same identification number, a third investigator reviewed the linkage and determined which to choose.

For probabilistic linkages, we formed pairs of records by associating each sibling reported in the survey with all the siblings of the respondent known in the HDSS database. Thus if a respondent reported 6 siblings in the survey, and had 5 known siblings in the HDSS, we formed 5 × 6 pairs (with the aim to identify at most 5 of them as links). The variables used to build comparison patterns were the same as for manual linkages. We first corrected entry errors and spelling variations in names and nicknames and compared these for each pair of records, using the Jaro-Winkler index as the string comparison metric (Winkler, 1990). A threshold of 0.8 was used to designate a match. We estimated 2 marginal probabilities, m and u. The m-probability is the probability that a given pair of records agrees on a field if the pair refers to the same sibling. The u-probability is the probability that an identifier in two elements of a non-matching pair agrees purely by chance. We calculated an agreement weight w_i for each matching variable such that w_i = ln(m_i/u_i). In case of disagreement, the weight was computed as w_i = ln((1-m_i)/(1-u_i)). Weights were calculated based on an expectation maximization (EM) algorithm, using the RecordLinkage package in R (Sariyar and Borg, 2010). For each pair of records, a score was obtained as the sum of the individual agreement weights w_i for each i^th matching variable. Based on the total score, all pairs were classified into three categories: links, non-links or possible links necessitating manual review. Predefined errors rates were set to compute weight thresholds minimizing the number of pairs that need to be assigned to manual review (Fellegi and Sunter, 1969). This procedure assumes that conditional independence holds for all combinations of variables used for the linkage. We set the error bounds at 0.05 for false positives (that is, 1- positive predictive value) and 0.10 for false negatives (that is, specificity). Possible links also included pairs initially classified as links but for which either survey or HDSS record had already been matched to another record with a higher matching weight.

Ethical statement

This study was approved by the Columbia University Medical Center institutional review board (Protocol AAAI9159) and by the Ethics committee of Senegal’s Ministry of Health and Social Action (SEN 12/11). Study participants provided informed consent in writing prior to participating in the study.

3. Results

In the survey, respondents reported on 6.7 siblings on average; the HDSS database contained information on 5.3 siblings for each respondent. Thus 46,384 pairs of records were established ≈ 6.7 × 5.3 × 1189. Table 1 presents the linkage outcomes from the two approaches for these pairs of records. With manual linkages, 4,781 (60%) of the 8,025 maternal siblings reports from the survey were matched to records in the Niakhar HDSS. Using the probabilistic approach, 62% (n=4,979) of records in the survey were matched to the HDSS.

Table 1:

Record linkage outcomes in the manual and probabilistic approaches (N=46,384)

		Probabilistic linkages
		Non-links	Possible links	Links
Manual linkages	Non-links	29,954	11,036	613
	Links	54	361	4,366

Using the reviewers’ decisions as a gold standard, we evaluated the quality of records matched through the probabilistic approach using sensitivity and positive predictive value (PPV). The probabilistic approach has a sensitivity of 99.8% and a PPV of 87.7%. We exclude possible links here; if we had not performed a manual linkage on all pairs, these possible links would have been submitted to human review and be re-classified as links or non-links. 24.6% of all record pairs were classified as possible links in Niakhar through the probabilistic approach. This suggests that probabilistic record linkages can substantially reduce the workload and provide links that are highly consistent with those obtained manually. For the sake of conciseness, we report below on results based on the probabilistic sample, unless otherwise indicated. All tables present results for both approaches.

In Table 2, we compare the characteristics of matched and non-matched records using Pearson’s chi-square tests. In both linked datasets, the matching rates do not differ by gender of the respondent or by type of questionnaire administered. Survey reports that are successfully matched to HDSS records come disproportionately from respondents who are younger (p<0.001) or have the same biological father as the reported sibling (p<0.001). Of note, about three quarters (75%) of records of siblings reported to be alive are matched, whereas less than half (43%) of records of deceased siblings are matched. These differentials point to the incompleteness of maternal identifiers in the HDSS as the main obstacle to higher matching rates. Imprecisions in the sibling’s names and other details could also be at play as fewer siblings were linked when the respondent was less educated (p<0.001) or reported more than six siblings (p<0.001). We compared the quality of age reporting in matched and unmatched cases, considering the percentage of siblings whose age at death or age at survey ended in 0 and 5. Matching rates were not associated with heaping on current age (p>0.1); however, siblings with a reported age at death ending in 0 or 5 were less likely to be matched (p<0.001). This indicates that misreporting errors could be smaller in our sample of matched cases. Further analyses are based on matched records of adolescent and adult siblings (≥15 years) who died in the HDSS area or were still living in the area at the time of the survey (n=2,926 probabilistic; n=2,794 manual).

Table 2:

Characteristics of respondents and their siblings (N=8,025)

	Probabilistic			Manual
	Matched n=4,979	Unmatched n=3,046	P value	Matched n=4,781	Unmatched n=3,244	P value
Respondent characteristics
Age			<0.001			<0.001
<25 years	1,602 (76%)	519 (24%)		1,610 (76%)	511 (24%)
25–34 years	1,538 (66%)	799 (34%)		1,506 (64%)	831 (36%)
35–44 years	984 (57%)	752 (43%)		899 (52%)	837 (48%)
≥45 years	855 (47%)	976 (53%)		766 (42%)	1,065 (58%)
Sex			0.4			0.6
Male	2,396 (62%)	1,493 (38%)		2,306 (59%)	1,583 (41%)
Female	2,583 (63%)	1,553 (37%)		2,475 (60%)	1,661 (40%)
Education			<0.001			<0.001
No schooling	2,667 (58%)	1,918 (42%)		2,537 (55%)	2,048 (45%)
Primary schooling	1,061 (63%)	634 (37%)		1,009 (60%)	686 (40%)
Secondary schooling or higher	1,234 (72%)	482 (28%)		1,216 (71%)	500 (29%)
Unknown	17 (59%)	12 (41%)		19 (66%)	10 (34%)
Questionnaire			0.3			0.2
SSC	2,441 (63%)	1,459 (37%)		2,485 (60%)	1,640 (40%)
DHS	2,538 (62%)	1,587 (38%)		2,296 (59%)	1,604 (41%)
Sibling characteristics(1)
Family size			<0.001			<0.001
≤6 siblings	1,684 (65%)	891 (35%)		1,615 (63%)	960 (37%)
>6 siblings	3,295 (60%)	2,152 (40%)		3,166 (58%)	2,281 (42%)
Same biological father			<0.001			<0.001
Yes	4,695 (64%)	2,628 (36%)		4,516 (62%)	2,807 (38%)
No	253 (41%)	368 (59%)		230 (37%)	391 (63%)
Unknown	31 (38%)	50 (62%)		35 (43%)	46 (57%)
Vital status			<0.001			<0.001
Alive	3,584 (75%)	1,170 (25%)		3,431 (72%)	1,323 (28%)
Deceased	1,394 (43%)	1,868 (57%)		1,348 (41%)	1,914 (59%)
Current age of living siblings			<0.001			<0.001
<25 years	1,332 (80%)	341 (20%)		1,334 (80%)	339 (20%)
25–34 years	1,017 (82%)	223 (18%)		988 (80%)	252 (20%)
35–44 years	710 (76%)	223 (24%)		652 (70%)	281 (30%)
≥45 years	515 (58%)	380 (43%)		447 (50%)	448 (40%)
Heaping on current age			0.7			0.9
Ending in round digit (0,5)	713 (75%)	239 (25%)		686 (72%)	266 (29%)
Not ending in round digit	2861 (76%)	928 (24%)		2735 (72%)	1054 (29%)
Age at death of deceased siblings			<0.001			<0.001
<25 years	921 (36%)	1,671 (64%)		920 (36%)	1,672 (65%)
25–34 years	203 (73%)	76 (27%)		189 (68%)	90 (32%)
35–44 years	167 (76%)	53 (24%)		149 (68%)	71 (32%)
≥45 years	102 (66%)	53 (34%)		89 (57%)	66 (43%)
Heaping on age at death			<0.001			<0.001
Ending in round digit (0,5)	380 (35%)	708 (65%)		361 (33%)	727 (67%)
Not ending in round digit	1013 (47%)	1145 (53%)		986 (46%)	1172 (54%)
Sex			<0.001			<0.001
Male	2,738 (65%)	1,504 (35%)		2,643 (62%)	1,599 (38%)
Female	2,241 (60%)	1,480 (40%)		2,136 (57%)	1,585 (43%)

SSC: siblings’ survival calendar. DHS: demographic and health surveys.

⁽¹⁾Sibling characteristics as reported in the SSH. Pearson’s chi-square tests and tabulations for sibling characteristics exclude cases with unknown values: 9 siblings (8 unmatched) for vital status, 14 siblings (3 unmatched) for current age, 16 siblings (15 unmatched) for age at death, and 62 siblings (all unmatched) with unknown sex (most of these cases with unknown sex were infant deaths with no name reported).

Among events reported in the survey, we computed specificity and sensitivity to assess the validity of sibling histories in identifying the vital status of adult siblings compared to the HDSS. Sensitivity is defined as the proportion of adult deaths according to the HDSS that are correctly reported as such during the survey. Specificity is defined as the proportion of living adult siblings that are correctly reported as alive during the survey. We reiterate that these parameters are only estimated here on our matched samples, and capture the effects of misreporting on vital status, but not the omissions. Sibling histories have high sensitivity and specificity, conditional on being matched. Compared to the HDSS, 96% of deceased siblings were correctly identified as such by respondents, while 98% of surviving siblings were correctly identified as such (Table 3). The SSC and DHS perform equally well in terms of sensitivity and specificity, and there are no differences by linking approach.

Table 3:

Performance of the SSH at identifying adult deaths from the HDSS dataset by linking approach, among matched cases

	Probabilistic			Manual
	n	Sensitivity (95% CI)	Specificity (95% CI)	n	Sensitivity (95% CI)	Specificity (95% CI)
SSH	2,926	96.4 (94.4 – 97.7)	98.2 (97.5 – 98.7)	2,794	97.3 (95.4 – 98.4)	98.4 (97.8 – 98.9)
SSC	1,413	96.4 (93.3 – 98.1)	98.0 (96.9 – 98.7)	1,317	97.2 (94.3 – 98.7)	97.9 (96.8 – 98.7)
DHS	1,513	96.4 (93.2 – 98.1)	98.4 (97.4 – 99.0)	1,477	97.3 (94.5 – 98.7)	98.8 (98.0 – 99.3)

SSH: sibling survival history. SSC: siblings’ survival calendar. DHS: demographic and health surveys. CI: 95% confidence interval.

Using regression, we examined the association between respondent and sibling characteristics and disagreement between reported vital status in the survey and the HDSS (Table 4). As siblings are nested by respondent, we used a mixed-effects logistic model with the respondent included as a random effect. The following model was estimated:

$$\ln \left(\frac{y_{i,r}}{1-y_{i,r}}\right)={\beta }_1{X}_{i,r}+{\beta }_2{X}_r+U_r$$ (1)

$$U_r\sim N(0,{\sigma }_r^2)$$

where y_i,r is a categorical variable coded 1 in case of disagreement on vital status of sibling i reported by respondent r and 0 otherwise, X_i,r and X_r are vectors of sibling and respondent characteristics and βs are vectors of coefficients. U_r refers to the random effects that are assumed to be normally distributed. In the probabilistically linked records, the odds of disagreement are 2.88 times greater when the respondent reported on a deceased sibling (according to the HDSS) than when the respondent reported on a living sibling (95% CI: 1.63–5.08). The odds of disagreement are not associated with the type of questionnaire. There are fewer discrepancies on the survival status of siblings registered in the HDSS at the time of the initial census than among those born in the area during the demographic surveillance (OR 0.41, 95% CI: 0.22–0.76). Additional regression models reveal that this is because these siblings are less likely to be reported as deceased when in fact they are still alive (p < 0.05), rather than the other way around. These models also indicate that older respondents are less likely to report their deceased siblings as alive (p < 0.05) (results not shown).

Table 4:

Factors associated with disagreement on vital status of siblings

	Probabilistic (N=2,926)		Manual (N=2,794)
	OR	aOR	OR	aOR
Respondent characteristics
Age
15–24 years	Reference		Reference
25–34 years	0.74 (0.38 – 1.44)		0.53 (0.25 – 1.11)
35–44 years	0.62 (0.28 – 1.37)		0.49 (0.20 – 1.18)
≥45 years	0.57 (0.24 – 1.33)		0.44 (0.17 – 1.16)
Sex
Male	Reference		Reference
Female	1.10 (0.64 – 1.89)		1.52 (0.82 – 2.83)
Education
No schooling	0.94 (0.47 – 1.88)		0.70 (0.34 – 1.48)
Primary schooling	1.15 (0.51 – 2.60)		0.79 (0.32 – 1.92)
Secondary schooling or higher	Reference		Reference
Questionnaire
DHS	Reference	Reference	Reference	Reference
SSC	1.15 (0.65 – 2.05)	1.22 (0.68–2.20)	1.42 (0.75 – 2.71)	1.51 (0.78 – 2.90)
Sibling characteristics(1)
Vital status
Alive	Reference	Reference	Reference	Reference
Deceased	2.18 (1.28 – 3.71)	2.88 (1.63–5.08)	1.78 (0.98 – 3.24)	2.31 (1.23 – 4.35)
Sex
Male	Reference		Reference
Female	0.97 (0.56 – 1.66)		1.21 (0.67 – 2.20)
Same biological father
Yes	Reference	Reference	Reference	Reference
No	2.41 (0.94 – 6.15)	2.38 (0.86–6.63)	2.44 (0.88 – 6.76)	2.88 (0.99 – 8.41)
Family size(2)
≤6 siblings	Reference	Reference	Reference	Reference
>6 siblings	1.78 (0.94 – 3.35)	1.86 (0.98–3.52)	1.38 (0.71 – 2.71)	1.39 (0.70 – 2.76)
First registration in the HDSS
Birth	Reference	Reference	Reference	Reference
HDSS initial census	0.53 (0.30 – 0.94)	0.41 (0.22–0.76)	0.37 (0.19 – 0.74)	0.30 (0.14 – 0.61)
In-migration	0.63 (0.23 – 1.75)	0.49 (0.17–1.42)	0.84 (0.29 – 2.39)	0.64 (0.21 – 1.90)

OR: odds ratio. aOR: adjusted odds ratio. CI: 95% confidence interval. SSC: siblings’ survival calendar. DHS: demographic and health surveys.

⁽¹⁾Sibling characteristics as reported in the SSH, except for the first registration in the HDSS.

⁽²⁾In manual linkages, the sibship size was not significantly associated with the outcome variable in the bivariate regression but we included it among the predictors of the adjusted model to be consistent with probabilistic linkages.

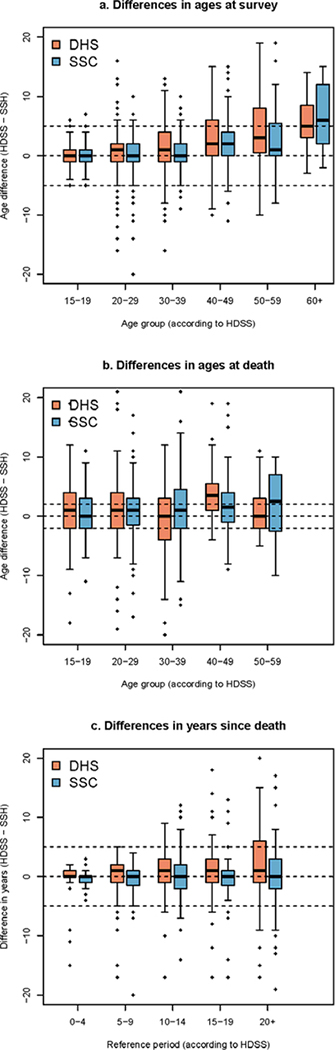
We calculated differences in HDSS and SSH values for current age of living siblings, age at death and time since death of deceased siblings. The mean absolute difference in current ages between the HDSS and the sibling histories is 2.8 years (95% CI: 2.7–3.0) in the probabilistically matched sampled (Table 5). Absolute differences are significantly lower in sibling histories collected with the SSC questionnaire (2.5 years, 95% CI: 2.2–2.7), when compared to the standard DHS questionnaire (3.2 years, 95% CI: 2.9–3.4). Still, both questionnaires show a pattern of systematic underestimation of ages (Figure 1a). In young adults (siblings aged 15–39 years), age misreporting appears to be broadly symmetric and ages are underestimated by only 0.8 years on average with the sibling history module used in the DHS questionnaire and 0.4 years with the SSC. Beyond the age of 40 years, errors are characterized by net age understatement, by 3.6 years on average with the DHS questionnaire and 2.5 years with the SSC.

Table 5:

Differences in reported current age, age at death and time since death of siblings

		Current age of living siblings (years)	Age at death of deceased siblings (years)	Time since death of deceased siblings (years)
Probabilistic	HDSS	32.8 (32.0–33.6)	29.6 (28.6–30.6)	11.5 (10.7–12.2)
	SSH	31.5 (30.8–32.3)	28.4 (27.3–29.5)	11.7 (10.9–12.6)
	SSC	32.0 (30.8–33.1)	28.0 (26.6–29.5)	12.4 (11.3–13.6)
	DHS	31.2 (30.1–32.3)	28.7 (27.2–30.3)	11.0 (9.9–11.2)
	Pearson’s correlation	0.95	0.85	0.78
	Absolute differencea	2.8 (2.7–3.0)	4.4 (4.0–4.8)	3.0 (2.6–3.4)
	SSC  DHS	2.5 (2.2–2.7) 3.2 (2.9–3.4)	4.2 (3.7–4.7) 4.6 (4.0–5.2)	2.7 (2.2–3.2) 3.4 (2.8–4.0)
Manual	HDSS	32.3 (31.5–33.1)	29.0 (28.0–29.9)	11.6 (10.8–12.4)
	SSH	31.1 (30.3–31.9)	27.7 (27.7–28.8)	11.7 (10.8–12.5)
	SSC	31.5 (30.4–32.7)	27.5 (26.0–29.0)	12.5 (11.2–13.7)
	DHS	30.7 (29.6–31.8)	27.9 (26.4–29.5)	10.9 (9.8–12.1)
	Pearson’s correlation	0.95	0.85	0.78
	Absolute differencea	2.8 (2.6–2.9)	4.1 (3.8–4.4)	3.1 (2.7–3.5)
	SSC  DHS	2.4 (2.2–2.7) 3.1 (2.8–3.3)	4.0 (3.5–4.4) 4.2 (3.8–4.7)	2.9 (2.3–3.5) 3.2 (2.7–3.8)

^aBetween HDSS and SSH.

SSC: siblings’ survival calendar. DHS: demographic and health surveys. All values except the Pearson’s correlation coefficients refer to mean and 95% confidence intervals.

Figure 1: Difference in the reported ages at survey of live siblings, ages at death of deceased siblings, and time elapsed since the death (DHS versus SSC).

Note: only results referring to patterns of misreporting errors observed in our probabilistic sample are presented here

Similarly, survey respondents tend to underestimate the age at death of deceased siblings (Figure 1b). The mean absolute difference between the HDSS and survey reports (4.4 years, 95% CI: 4.0–4.8) is greater than for the current age of living siblings. Age misreporting, however, is symmetric in young adults. Siblings who died before age 40 have their age underestimated by less than one year (0.5, 95% CI: 0.1–1.0), while above age 40, net age understatement is 2.6 years on average (95% CI: 1.6–3.5). The mean absolute error in ages at death in the SSC (4.2, 95% CI: 3.7–4.7) is not significantly different from the error in reports collected through the questionnaire used in DHS (4.6, 95% CI: 4.0–5.2).

The mean reported time since death was similar in both sources, and there was a significant but small difference by questionnaire (SSC 12.4 years (11.3–13.6) and DHS 11.0 years (9.9–11.2) against 11.5 (10.7–12.2) in the HDSS). The absolute difference was also larger with the DHS questionnaire than with the SSC, but confidence intervals around the estimates overlap (3.4 (2.8–4.0) against 2.7 (2.2–3.2)). Unsurprisingly, absolute errors are larger for deaths that occurred in the distant past (Figure 1c). For example, when considering deaths that occurred more than 15 years prior to the survey, the difference between the HDSS and survey reports on the timing of deaths is larger than 5 years in 38% of the cases with the DHS questionnaire, and 23% of cases with the SSC.

To assess factors associated with age errors, we estimated multilevel linear models. These models were similar to the one detailed in Eq.1, except that the mean absolute age difference was the outcome variable. Increasing age of reported sibling and decreasing education level of the respondent are associated with a larger error in the current age of living siblings (Table 6). Respondents reporting on few siblings (<7) make larger errors on the age of living siblings, presumably because smaller sibships point to lower quality of recall. The SSC questionnaire significantly improves the reporting of current ages. For the age at death of deceased siblings, age errors increase as the age of the deceased and time since death increase (Table 7). Compared to respondents with secondary education or higher, respondents with no schooling are more likely to misreport age at death. Again, respondents who report on fewer siblings make larger errors. The type of questionnaire has no significant effect on errors in the age at death. Lastly, we assessed factors associated with errors in the time since death for deceased siblings (Table 8). Respondents who had no schooling make larger errors in the time since death. Errors are also larger for deaths that occurred more than 5 years prior to the survey. The difference in the error in time since death between the SSC and DHS questionnaire is not significant.

Table 6:

Factors associated with errors in the reported current age of living siblings

	Probabilistic (n=2,103)		Manual (n=2,027)
	Unadjusted model β (95% CI)	Adjusted model β (95% CI)	Unadjusted model β (95% CI)	Adjusted model β (95% CI)
Respondent characteristics
Age
15–24 years	Reference	Reference	Reference	Reference
25–34 years	0.39 (0.03 – 0.75)	−0.02 (−0.39 – 0.36)	0.59 (0.24 – 0.94)	0.16 (−0.21 – 0.53)
35–44 years	0.80 (0.38 – 1.22)	0.02 (−0.43 – 0.48)	1.00 (0.58 – 1.42)	0.18 (−0.27 – 0.63)
≥45 years	1.64 (1.17 – 2.11)	0.23 (−0.29 – 0.75)	1.68 (1.21 – 2.14)	0.15 (−0.39 – 0.69)
Sex
Male	Reference		Reference
Female	0.07 (−0.21 – 0.36)		0.19 (−0.10 – 0.48)
Education
No schooling	0.87 (0.50 – 1.23)	0.46 (0.06 – 0.85)	0.86 (0.50 – 1.23)	0.35 (−0.05 – 0.74)
Primary schooling	0.34 (−0.09 – 0.78)	0.19 (−0.25 – 0.62)	0.29 (−0.14 – 0.72)	0.10 (−0.33 – 0.53)
Secondary schooling or higher	Reference	Reference	Reference	Reference
Questionnaire
DHS	Reference	Reference	Reference	Reference
SSC	−0.75 (−1.12 – − 0.38)	−0.73 (−1.07 – −0.40)	−0.72 (−1.08 – −0.36)	−0.73 (−1.06 – −0.40)
Sibling characteristics(1)
Current age of sibling
15–24 years	Reference	Reference	Reference	Reference
25–34 years	0.75 (0.45 – 1.05)	0.58 (0.26 – 0.90)	0.57 (0.28 – 0.86)	0.38 (0.07 – 0.69)
35–44 years	1.40 (1.04 – 1.75)	1.04 (0.61 – 1.48)	1.40 (1.05 – 1.75)	1.01 (0.58 – 1.45)
≥45 years	2.74 (2.33 – 3.14)	2.29 (1.78 – 2.80)	2.62 (2.21 – 3.02)	2.12 (1.60–2.64)
Sex
Male	Reference		Reference
Female	−0.02 (−0.26 – 0.23)		−0.09 (−0.34 – 0.16)
Same biological father(2)
Yes	Reference	Reference	Reference	Reference
No	0.60 (−0.05 – 1.26)	0.36 (−0.26 – 0.98)	0.34 (−0.31–1.00)	0.12 (−0.51 – 0.75)
Family size
≤6 siblings	Reference	Reference	Reference	Reference
>6 siblings	−0.88 (−1.20 – − 0.55)	−0.71 (−1.02 – − 0.40)	−0.73 (−1.06 – − 0.41)	−0.13 (−0.49 – 0.22)
First registration in the HDSS
Birth	Reference	Reference	Reference	Reference
HDSS initial census	1.29 (1.01 – 1.57)	0.32 (−0.03 – 0.66)	1.32 (1.05 – 1.60)	0.41 (0.06 – 0.76)
In-migration	0.81 (0.32 – 1.31)	0.13 (−0.37 – 0.63)	0.92 (0.43 – 1.42)	0.36 (−0.14 – 0.87)

SSC: siblings’ survival calendar. DHS: demographic and health surveys. CI: 95% confidence interval

⁽¹⁾Sibling characteristics as reported in the SSH, except for the first registration in the HDSS.

⁽²⁾In manual linkages, having the same biological father was not significantly associated with the outcome variable in the bivariate regression but we included it among the predictors of the adjusted model to be consistent with probabilistic linkages.

Table 7:

Factors associated with errors in the reported age at death of deceased siblings

	Probabilistic (n=741)		Manual (n=705)
	Unadjusted mode β (95% CI)	Adjusted mode β (95% CI)	Unadjusted mode β (95% CI)	Adjusted mode β (95% CI)
Respondent characteristics
Age
15–24 years	Reference		Reference	Reference
25–34 years	0.49 (−0.41 – 1.40)	−0.58 (−1.55 – 0.40)	0.57 (−0.32 – 1.46)	−0.57 (−1.51 – 0.38)
35–44 years	0.75 (−0.19 – 1.70)	−0.70 (−1.79 – 0.39)	0.65 (−0.30 –1.60)	−0.94 (−2.02 – 0.14)
≥45 years	1.91 (0.99 – 2.83)	−0.06 (−1.23 – 1.12)	2.14 (1.20 – 3.08)	0.18 (−0.98 – 1.34)
Sex
Male	Reference		Reference
Female	0.12 (−0.49 – 0.73)		0.10 (−0.52 – 0.72)
Education
No schooling	1.23 (0.39 – 2.06)	1.04 (0.14 – 1.94)	1.43 (0.57 – 2.28)	1.23 (0.32 – 2.14)
Primary schooling	0.41 (−0.58 – 1.39)	0.35 (−0.64 – 1.34)	0.55 (−0.44 – 1.53)	0.61 (−0.38 – 2.60)
Secondary schooling or higher	Reference	Reference	Reference	Reference
Questionnaire
DHS	Reference	Reference	Reference	Reference
SSC	−0.25 (−0.89 – 0.38)	−0.27 (−0.87 – 0.33)	−0.32 (−0.98 – 0.34)	−0.34 (−0.96 – 0.29)
Sibling characteristics(1)
Age at death of sibling
15–24 years	Reference	Reference	Reference	Reference
25–34 years	0.98 (0.22 – 1.74)	0.87 (0.03 – 1.70)	1.15 (0.38 – 1.92)	0.92 (0.08 – 1.77)
35–44 years	0.67 (−0.24 – 1.58)	0.62 (−0.45 – 1.70)	0.86 (−0.07 – 1.79)	0.60 (−0.48 – 1.68)
≥45 years	0.96 (−0.02 – 1.95)	1.09 (−0.19 – 2.38)	0.63 (−0.42 – 1.67)	0.69 (−0.65 – 2.03)
Time since death
<5 years	Reference	Reference	Reference	Reference
5–9 years	0.55 (−0.31 – 1.41)	0.75 (−0.11 – 1.61)	0.70 (−0.19 –1.58)	0.93 (0.04 – 1.82)
10–14 years	1.60 (0.60 – 2.59)	2.07 (1.02 – 3.11)	1.30 (0.28 – 2.33)	1.67 (0.59 – 2.75)
≥15 years	2.18 (1.34 – 3.02)	2.36 (1.35 – 3.38)	2.38 (1.51 – 3.25)	2.42 (1.35 – 3.47)
Sex
Male	Reference	Reference	Reference	Reference
Female	−0.71 (−1.40 – −0.02)	−0.42 (−1.09 – 0.26)	−0.96 (−1.67 – −0.25)	−0.65 (−1.35 – 0.05)
Same biological father
Yes	Reference		Reference
No	0.39 (−0.88 – 1.65)		0.64 (−0.63 – 1.91)
Family size
≤6 siblings	Reference	Reference	Reference	Reference
>6 siblings	−0.85 (−1.48 – −0.23)	−0.68 (−1.29 – −0.08)	−0.72 (−1.36 – −0.08)	−0.50 (−1.12 – 0.12)
First registration in the HDSS
Birth	Reference	Reference	Reference	Reference
HDSS initial census	1.75 (1.02 – 2.48)	0.55 (−0.33 – 1.43)	1.89 (1.16 – 2.63)	0.74 (−0.15 – 1.62)
In-migration	1.76 (0.63 – 2.89)	1.05 (−0.13 – 2.23)	1.95 (0.80 – 3.11)	1.19 (−0.02 – 2.41)

SSC: siblings’ survival calendar. DHS: demographic and health surveys. CI: 95% confidence interval

⁽¹⁾Sibling characteristics as reported in the SSH, except for the first registration in the HDSS.

Table 8:

Factors associated with errors in the reported time since death of deceased siblings

	Probabilistic (n=741)		Manual (n=705)
	Unadjusted model β (95% CI)	Adjusted model β (95% CI)	Unadjusted model β (95% CI)	Adjusted model β (95% CI)
Respondent characteristics
Age
15–24 years	Reference	Reference	Reference	Reference
25–34 years	0.33 (−0.80 – 1.46)	−0.48 (−1.70 – 0.73)	0.52 (−0.54 – 1.58)	−0.26 (−1.40 – 0.88)
35–44 years	0.91 (−0.28 – 2.09)	−0.05 (−1.40 – 1.31)	0.45 (−0.70 – 1.61)	−0.50 (−1.81 – 0.82)
≥45 years	2.05 (0.89 – 3.22)	1.28 (−0.19 – 2.74)	2.56 (1.39 – 3.73)	1.80 (0.38 – 3.22)
Sex(1)
Male	Reference	Reference	Reference	Reference
Female	−0.83 (−1.59 – −0.08)	−0.75 (−1.50 – −0.01)	−0.33 (−1.07 – 0.40)	−0.34 (−1.08 – 0.39)
Education
No schooling	1.56 (0.51 – 2.61)	1.69 (0.56 – 2.82)	1.54 (0.49 – 2.59)	1.57 (0.44 – 2.69)
Primary schooling	0.91 (−0.32 – 2.14)	0.93 (−0.31 – 2.18)	0.71 (−0.49 – 1.91)	0.94 (−0.28 – 2.16)
Secondary schooling or higher	Reference	Reference	Reference	Reference
Questionnaire
DHS	Reference	Reference	Reference	Reference
SSC	−0.67 (−1.47 – 0.14)	−0.70 (−1.46 – 0.05)	−0.20 (−1.08 – 0.67)	−0.26 (−1.06 – 0.54)
Sibling characteristics(2)
Age at death of sibling
15–24 years	Reference	Reference	Reference	Reference
25–34 years	−0.47 (−1.43 – 0.49)	−1.18 (−2.23 – −0.14)	−0.02 (−1.02 – 0.98)	−0.71 (−1.78 – 0.35)
35–44 years	0.69 (−0.43 – 1.82)	−0.07 (−1.41 – 1.27)	0.88 (−0.29 – 2.05)	0.01 (−1.33 – 1.36)
≥45 years	−1.71 (−2.95 – −0.47)	−2.59 (−4.20 – −0.99)	−1.78 (−3.12 – 0.44)	−2.60 (−4.27 – − 0.92)
Time since death
<5 years	Reference	Reference	Reference	Reference
5–9 years	1.72 (0.64 – 2.79)	1.47 (0.40 – 2.55)	2.23 (1.10 – 3.35)	1.92 (0.80 – 3.04)
10–14 years	2.47 (1.21 – 3.72)	1.78 (0.47 – 3.10)	2.82 (1.51 – 4.13)	2.04 (0.68 – 3.40)
≥15 years	3.08 (2.03 – 4.14)	1.95 (0.68 – 3.22)	3.22 (2.11 – 4.33)	1.92 (0.63 – 3.29)
Sex
Male	Reference	Reference	Reference	Reference
Female	−0.75 (−1.62 – 0.13)	−0.58 (−1.43 – 0.26)	−0.89 (−1.82 – 0.04)	−0.63 (−1.51 – 0.25)
Same biological father
Yes	Reference		Reference
No	−0.27 (−1.86 – 1.32)		−0.42 (−1.98 – 1.15)
Family size
≤6 siblings	Reference		Reference
>6 siblings	−0.59 (−1.37 – 0.19)		−0.53 (−1.33 – 0.27)
First registration in the HDSS
Birth	Reference	Reference	Reference	Reference
HDSS initial census	1.28 (0.34 – 2.22)	0.86 (−0.25 – 1.97)	1.50 (0.53 – 2.48)	1.01 (−0.11 – 2.13)
In-migration	0.41 (−1.05 – 1.87)	0.55 (−0.92 – 2.03)	0.72 (−0.80 – 2.24)	0.75 (−0.78 – 2.27)

SSC: siblings’ survival calendar. DHS: demographic and health surveys. CI: 95% confidence interval

⁽¹⁾In manual linkages, the sex of respondents was not significantly associated with the outcome variable in the bivariate regression but we included it among the predictors of the adjusted model to be consistent with probabilistic linkages.

⁽²⁾Sibling characteristics as reported in the SSH, except for the first registration in the HDSS.

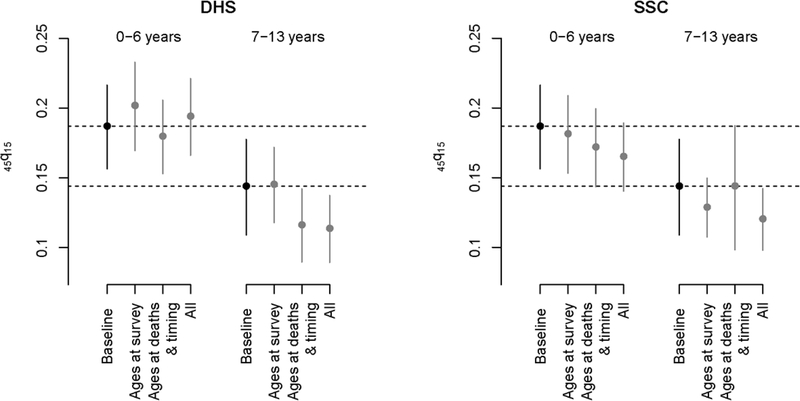
Results presented above suggest that reporting errors in sibling histories can be large when considering gross errors, but net understatement of ages at survey and at death remains limited, especially for young siblings. Errors on the timing of deaths are frequent but estimates are usually computed for large reference periods in adult mortality surveys. To evaluate the impact of reporting errors on mortality estimates derived from a typical DHS survey, we extracted sibling histories from the 2010–2011 DHS conducted in Senegal and assumed that the data were unbiased and reflected actual mortality rates. We estimated from the DHS the probability ₄₅q₁₅ for two periods (0–6 years and 7–13 years prior to the survey). Standard errors were computed with stratified jackknife. We then distorted these reports based on the errors observed in our study. For each surviving sibling in the 2010–2011 DHS, we randomly sampled from our survey data a surviving sibling of the same age group and sex and used the age difference between the HDSS and SSH reports to shift backwards or forwards the date of birth in the DHS record. For deceased siblings, we estimated the joint effects of errors on ages at death and years since death on mortality estimates, rather than considering them separately. This is because dates of birth and death are imputed when the age at death or the number of years since death is unknown in DHS surveys, taking into consideration the sibling’s birth order. In the 2010–2011 Senegalese DHS, imputation was required for 5.8% of all deceased siblings. For each deceased sibling in the 2010–2011 DHS, we randomly sampled a deceased sibling in the Niakhar survey with a similar time elapsed since death and a similar age at death (using 5-year age groups or reference periods). We shifted both the imputed dates of death and of birth according to errors made on the timing of deaths, and shifted only the imputed dates of birth based on errors made on ages at death. We recalculated mortality rates from the real and modified sibling histories and compared point estimates and confidence intervals. Figure 2 presents the probability ₄₅q₁₅ extracted from the survey (henceforth the “baseline sample”), and those obtained after reporting errors are added (for two periods and using errors captured in the two questionnaires). Only results based on our probabilistically matched dataset are presented since patterns of errors are similar in the manual linkages.

Figure 2: Estimates of the probability ₄₅q₁₅ derived from the 2010–2011 DHS and estimates obtained when errors in the reported current age, age at death and the timing of death are factored in sibling histories (DHS versus SSC questionnaires).

Note: all estimates are derived from the 2010–2011 DHS in Senegal. The black dots refer to estimates obtained conventionally from SSH, using only the sampling weights, without any modification. The grey dots refer to the estimates obtained from the same set of SSH data after distorting the reports based on the patterns of errors observed in the Niakhar study. Only results referring to patterns of misreporting errors observed in our probabilistic sample are presented here.

Biases introduced in the probability ₄₅q₁₅ by errors on ages at survey vary depending on the questionnaire, but these changes are small when considering the width of the confidence intervals around estimates calculated from a typical DHS. The underestimation of ages at death and years since death result in downward biases. For example, introducing errors observed in the DHS questionnaire leads to a 4% underestimate of ₄₅q₁₅ relative to the baseline sample in the most recent period, and a 19% underestimate in the period 7–13 years before the survey. When considered together, reporting errors on ages of living siblings, ages at death and the timing of death result in a downward bias in three out of four cases. The largest difference emerges for the period 7–13 years prior to the survey with errors observed in the standard DHS questionnaire, with a 21% underestimate of ₄₅q₁₅.

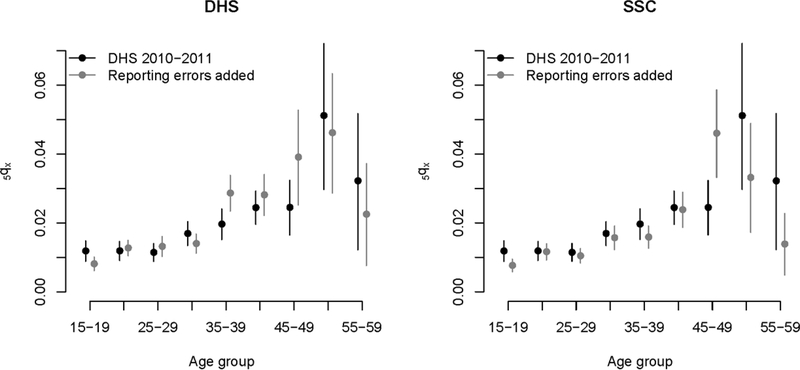
The probability ₄₅q₁₅ from the baseline sample (187 per thousand) is contained in the 95% confidence intervals around the ₄₅q₁₅ values distorted by reporting errors in the most recent period (166–221 in the DHS study arm and 140–189 in the SSC). However, in the period 7–13 years prior to the survey, the “true” probability (144 per thousand) falls above the upper bound of these confidence intervals (89–137 in the DHS study arm and 98–142 in the SSC). Patterns of age misstatement observed in the Niakhar study also introduce distortions in age-specific mortality rates (ASMRs). Figure 3 presents the ASMRs extracted from the baseline sample (for the period 0–6 years before the survey) with those obtained after including all types of reporting errors in the sibling histories. Confidence intervals around the ASMRs usually overlap, but in several instances, the estimate obtained from the baseline sample is not contained in the 95% confidence intervals from the sample altered by reporting errors.

Figure 3: Age-specific mortality rates derived from the the 2010–2011 DHS (for the period 0–6 years before data collection) (in black), and age-specific mortality rates obtained when errors in the reported current age, age at death and the timing of death are factored in sibling histories (DHS versus SSC questionnaires).

Note: all estimates are derived from the 2010–2011 DHS in Senegal. The black dots refer to estimates obtained conventionally from SSH, using only the sampling weights, without any modification. The grey dots refer to the estimates obtained from the same set of SSH data after distorting the reports based on the patterns of errors observed in the Niakhar study. Only results referring to patterns of misreporting errors observed in our probabilistic sample are presented here.

4. Discussion

Since their introduction in DHS in the early 1990s, sibling histories have become the most common data source of adult mortality estimates in countries with incomplete death registration. Sibling histories are relatively easy to collect and offer the possibility to reconstruct past trends and age patterns of mortality. The Global Burden of Disease (GBD) Study (Dicker et al., 2018) and the World Population Prospects (United Nations, 2019) use sibling histories to model trends in ₄₅q₁₅. More than 80% of the data used by the WHO to estimate maternal mortality in Africa also come from sibling histories (Wilmoth et al., 2012). However, evidence is accumulating that reporting errors might affect the estimates. In this study, we observed large absolute errors in ages at survey or at death, and the time elapsed since death. These errors have offsetting effects in young adults and result only in a slight understatement of current ages and ages at death in older siblings. The time elapsed since death is also underestimated, shifting some deaths in the most recent reference periods. Our simulations indicate that taken together, these reporting errors introduce downward biases in adult mortality estimates. Even if confidence intervals around the probability ₄₅q₁₅ are large in a typical DHS, the patterns of errors observed in our study can shift these intervals downwards to such an extent that they no longer include the “true” value of ₄₅q₁₅. This was observed in our simulation for estimates referring to the period 7–13 years before data collection, irrespective of the questionnaire used. These results call for caution when reconstructing trends in adult mortality based on a single survey. Statistical models have been developed to produce robust estimates of under-five mortality by combining multiple surveys with other data sources and modelling biases in data series. This is the case, for example, of the Bayesian B-spline Bias-reduction model (B3) developed by Alkema and New (2014). Similar models should be developed for adult survival and explicitly account for omissions and age misreporting errors in sibling histories.

Our results are consistent with our previous validation study conducted in Bandafassi, another HDSS in Senegal (Helleringer et al., 2014a). Respondents also underestimated the ages at death of siblings reported in this study, especially those who died at older ages (≥45). However, our results related to improvements in the questionnaire are quite mixed and do not all confirm our preliminary analysis carried out at the sibship level on the Niakhar survey (Helleringer et al., 2014b). In the linked records analyzed here, respondents of the SSC questionnaire made significantly fewer errors in the reported age of living siblings. Nonetheless, the SSC did not significantly improve reporting of the age at death or the timing of death. We did not observe any significant difference in the accuracy of survey reports on vital status when comparing the two questionnaires. It is important to keep in mind that we looked here only at matched cases and matching rates among deceased siblings were low (42%). We were not able to capture omissions of deceased siblings in this study, while the SSC questionnaire has been shown to improve the reporting of female deaths (Helleringer et al., 2014b).

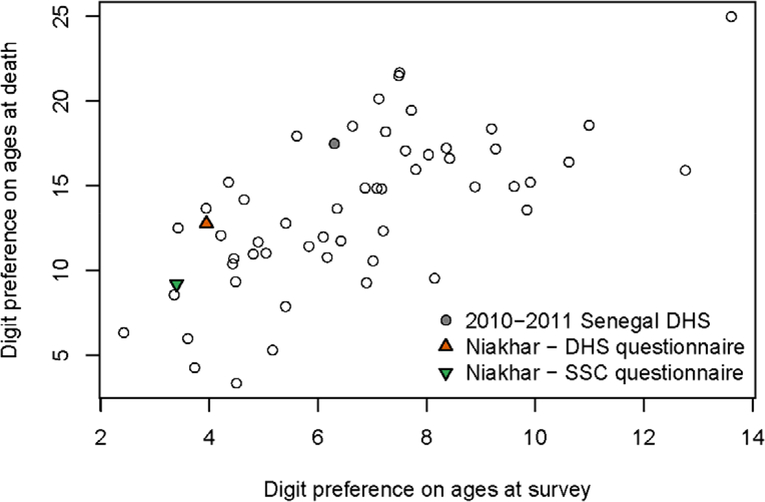
Our study has some limitations. First, there could be errors in the reference dataset, although ages and dates are very precise for those born between HDSS rounds and we did not find larger errors in reports referring to siblings who migrated into the area or those present in the HDSS at the initial census. A second limitation is that respondents in Niakhar are regularly contacted by interviewers to participate in surveys or in the demographic follow-up. They may have a better knowledge of ages and dates referring to their siblings than in the general population. This could reduce the generalizability of our results. Figure 4 compares values of Myer’s index for age heaping in the Niakhar survey, against those computed on all DHS with sibling histories conducted in 2010 or after. There is less heaping on ages at survey in our survey than in most national DHS, including the 2010–2011 Senegalese survey. Heaping on ages at death, however, is as pervasive as in national DHS. The Myers’ blended index measured on our sample interviewed with the DHS questionnaire (12.8) is close to the median value of the 54 DHS used as a comparison (13.9). The SCC questionnaire reduces the heaping (9.2), but we noted that ages at death are still systematically understated. Third, generalizability could be further reduced if patterns of age and date misstatement differ in various cultural and epidemiological contexts. Additional validation studies are needed in other countries to investigate variations in misreporting errors. A fundamental cause of poor age data is the limited registration of vital events. In Senegal, according to the 2013 census, less than 65% of adults had a birth certificate and fewer than 35% of deaths were registered. Other countries with low registration might experience similar age/date errors in sibling histories. But age and date errors do not come solely from respondents; some errors are introduced in the interaction with the interviewers. As DHS surveys are highly standardized (in terms of questionnaires, training protocols, procedures for interviewer recruitment and supervision), some patterns of errors are likely shared across all surveys.

Figure 4:

Digit preference in the reporting of age at survey of surviving siblings and age at death of deceased siblings, according to Myer’s blended index (DHS surveys conducted in 2010–2018 and Niakhar study)

Finally, an important limitation of this study is that we could not consider omissions of live and deceased siblings because of incomplete genealogical data. These omissions are likely to inflate the downward bias introduced by errors on ages and dates. In Bandafassi, omissions were more frequent among deceased sisters (9.1%) than live sisters (3.8%) (Helleringer et al., 2014a). The combined impact of errors on ages, dates and omissions can be illustrated by utilizing the 2010–2011 DHS in Senegal, (1) distorting the reports on ages and dates based on patterns observed in this study and (2) removing a fraction of siblings assumed to be unreported, based on percentages cited above. In this scenario, the baseline probability for the most recent period (187) would still be contained in the 95% confidence intervals around the estimate biased by omissions and errors on ages and dates (159–214). By contrast, the probability ₄₅q₁₅ estimated for the more distant period (144 per thousand), reduced to 114 (95% CI: 89–137) by misstatements of ages and dates, would be further reduced to 109 (95% CI: 84–133) when factoring in omissions (a 24% underestimate). More detailed simulations are required before drawing firm conclusions because the proportions of deaths omitted should be allowed to vary by date, age at death and possibly the age of respondents and their educational level. Microsimulations have been used to explore selection biases in sibling data (Masquelier, 2013) and could help in assessing the various effects of recall errors.

Our study calls for improvements in the DHS questionnaire. In 2017, the DHS questionnaire was revised to include a list of probing questions to ensure that all siblings have been recorded (DHS Program, 2017). These additional recall cues targeted half-brothers or sisters, siblings who did not live with the respondent as a child, and deceased siblings, in line with evidence gathered in previous validation studies. These additional questions aimed at limiting omissions, but our study shows that further improvements are required to elicit better information on ages and dates.

Finally, this is the first study linking retrospective reports on the survival of close relatives to a reference dataset on such a large sample of respondents. Our results based on probabilistic linkages were very similar to manual linkages. Probabilistic record linkages could be employed in future validation studies of mortality surveys. HDSS sites have been used as references to assess the accuracy of mortality estimates derived from surveys (Rerimoi et al., 2019), but comparisons can be conducted at the individual level when names and other identifiers are available. Without the cost of new surveys, linking HDSS records to national censuses is also a promising avenue to evaluate the quality of reporting of recent household deaths and children ever born and surviving. Eventually, these studies should lead to improvements in the collection of mortality data through surveys and censuses, which will remain essential until countries ensure that all deaths are counted in functional systems of death registration.

Data availability statement

The dataset of the Niakhar survey is available in the OPENICPSR repository (https://www.openicpsr.org/openicpsr/project/100112/version/V1/view, DOI: https://doi.org/10.3886/E100112V1)