Joint analysis of days to flowering reveals independent temperate adaptations in maize

Abstract

Domesticates are an excellent model for understanding biological consequences of rapid climate change. Maize (Zea mays ssp. mays) was domesticated from a tropical grass yet is widespread across temperate regions today. We investigate the biological basis of temperate adaptation in diverse structured nested association mapping (NAM) populations from China, Europe (Dent and Flint) and the United States as well as in the Ames inbred diversity panel, using days to flowering as a proxy. Using cross-population prediction, where high prediction accuracy derives from overall genomic relatedness, shared genetic architecture, and sufficient diversity in the training population, we identify patterns in predictive ability across the five populations. To identify the source of temperate adapted alleles in these populations, we predict top associated genome-wide association study (GWAS) identified loci in a Random Forest Classifier using independent temperate–tropical North American populations based on lines selected from Hapmap3 as predictors. We find that North American populations are well predicted (AUC equals 0.89 and 0.85 for Ames and USNAM, respectively), European populations somewhat well predicted (AUC equals 0.59 and 0.67 for the Dent and Flint panels, respectively) and that the Chinese population is not predicted well at all (AUC is 0.47), suggesting an independent adaptation process for early flowering in China. Multiple adaptations for the complex trait days to flowering in maize provide hope for similar natural systems under climate change.

Introduction

Domesticated plants and animals are an excellent model for understanding the genetic consequences of adaptation to rapidly changing environments, since humans first started to move domesticates from their native ranges starting 10,000 years ago. One of the easiest ways for a plant to adapt to a new environment is to modulate the time until flowering, avoiding obstacles to reproductive success. Maize (Zea mays ssp. mays) was domesticated from the tropical grass teosinte (Zea mays ssp. parviglumis) during the mid-Holocene maximum (9000–5000 BP) (Matsuoka et al. 2002; Piperno et al. 2009; van Heerwaarden et al. 2011), where annual temperatures were higher than any time before the industrial era (Metcalfe et al. 2000). After domestication in central Mexico, humans moved maize across the Americas, reaching the southern Andes by at least 3600 BP (Perry et al. 2006) and moving northward to southern Ontario, Canada by 1500 BP (Smith and Crawford 2002). After Spanish contact with the Americas in the late 1400s, maize was quickly established across the world (Ho 1955; Anderson 1988; Revilla et al. 2003; Rebourg et al. 2003; Dubreuil et al. 2006). Modern breeding in the last 100 years has further complicated these histories with the development of inbred lines, heterotic groups, and the intentional introgression of exotic germplasm into global maize, particularly from the historical US Dent germplasm (Barrière et al. 2006). The resulting global modern maize germplasm is highly diverse, and days to flowering in inbred lines varies from 35 to 120 days (Bennetzen and Hake 2008).

Changes in flowering lead to reproductive isolation, structuring populations so that subsequently selected loci are nested within the historical source population (Rebourg et al. 2001; Brown et al. 2011; Swarts et al. 2017). This study seeks to refine our understanding of the genetic architecture underlying maize flowering by jointly analyzing diverse populations genotyped using whole-genome resequencing data.

Flowering time traits have received much attention in maize due to the quantitative nature of inheritance, high heritabilities (up to 0.96 for days to silking in the USNAM population (Buckler et al. 2009)), and ease of scoring (Thornsberry et al. 2001; Salvi et al. 2002, 2007, 2009; Chardon et al. 2004, 2005; Buckler et al. 2009; Coles et al. 2010; Wang et al. 2010; Xu et al. 2012; Durand et al. 2012; Hung et al. 2012; Romay et al. 2013; Giraud et al. 2014). Only a handful of loci, mostly in the autonomous flowering pathway, have confirmed effects for modulating days to flowering either through mutagenesis or positional cloning, including Rap2.7 (Salvi et al. 2007) and the MITE insertion (Castelletti et al. 2014) at the Vgt1 locus (Ducrocq et al. 2008; Salvi et al. 2002), ZCN8 (Meng et al. 2011; Guo et al. 2018), ID1 (Kozaki et al. 2004; Colasanti et al. 2006), conz1 (Miller et al. 2008), df1 (Muszynski et al. 2006), zfl1 and zfl2 (Bomblies and Doebley 2006), ZmMADS69 (Liang et al. 2019) and the major photoperiod locus, ZmCCT (Hung et al. 2012; Huang et al. 2018). However, independent days to flowering quantitative trait loci (QTL) have been mapped in tens of biparental, recombinant inbred line (RIL), and other structured population designs that mitigate the effects of linked background population structure (Chardon et al. 2004; Salvi et al. 2009), including four NAM populations (Buckler et al. 2009; Lehermeier et al. 2014; Li et al. 2015). Within natural diversity populations (the largest being the Ames Diversity Panel (Romay et al. 2013)), only Vgt1, ZCN8, and ZmCCT of the confirmed loci have common standing variation and are routinely detected in mapping populations (Salvi et al. 2009; Buckler et al. 2009; Coles et al. 2010).

Previous studies (Chardon et al. 2004; Salvi et al. 2009; Buckler et al. 2009; Xu et al. 2012; Mace et al. 2013; Lehermeier et al. 2014; Li et al. 2016) have confirmed that days to flowering is quantitative and highly additive in maize, and that many of the effects target common loci, with allelic series present at many loci; a meta-analysis of 22 linkage mapping and ANOVA studies record a total of 313 QTL that collapsed into 62 consensus regions of the genome (Chardon et al. 2004). Synteny mapping to rice and Arabidopsis resulted in 19 overlapping associations (Chardon et al. 2004), and synteny mapping with sorghum revealed that 92.5% of QTL found in sorghum were <10 Mbp from a corresponding QTL in USNAM (Mace et al. 2013). A later meta-analysis including 29 studies (Salvi et al. 2009) found that 441 significant QTL could be collapsed into 59 genomic regions. Similarly, days to flowering in the first NAM population, USNAM, found over 50 genomic regions with significance, and additionally confirmed the existence of allelic series at common loci. A large multi-environment evaluation of maize flowering in the USNAM, Ames diversity panel, and a newly developed Chinese NAM (CNNAM) (Li et al. 2015) population using low-density genotyping-by-sequencing (GBS) markers identified 130 QTL from linkage mapping in USNAM and CNNAM, of which 40 overlapped between the two populations (Li et al. 2016). This suggests that genetic control for flowering is conserved, and allelic variation evolved early and is at least partially differentiated across populations.

Genomic prediction using Genotypic Best Linear Unbiased Predictors (GBLUP) predicts trait values based on relatedness to phenotyped individuals, and cross-population prediction is typically impossible without shared genetic ancestry (Meuwissen 2009). The EUNAM-Dent and EUNAM-Flint populations, which were developed from European parents selected to be from genetically divergent pools, have little overlap in QTL for flowering (Giraud et al. 2014) and evidence for selection on different pathways between the two panels (Unterseer et al. 2016). Cross heterotic pool predictive accuracies were correspondingly typically close to zero or even negative in most families (Lehermeier et al. 2014). Here, we capitalize on the linkage between selection for time to flowering and source population structure to investigate the genetic architecture underlying flowering in regionally distinct global maize populations.

Materials and methods

Datasets

Five publicly available maize datasets were reanalyzed for this analysis, four Nested Association Mapping (NAM) designs—US (USNAM) (Buckler et al. 2009; McMullen et al. 2009), Chinese (CNNAM) (Li et al. 2015), and two European panels based on the major European heterotic groups, Flint (EUNAM-Flint) and Dent (EUNAM-Dent) (Lehermeier et al. 2014; Giraud et al. 2014)—and one diversity panel (Ames) (Romay et al. 2013) (Table 1). Phenotypes—flowering Days to Anthesis (DTA) for male reproductive parts and Days to Silking (DTS) for female—used were genotypic estimates reported in the original studies; spatially corrected BLUPs from per se evaluations in the Ames, CNNAM, and USNAM populations and spatially corrected BLUEs from testcrosses between the EUNAM-Flint and EUNAM-Dent panels. All of the populations were genotyped at low density in their original study, which we used to anchor whole-genome projection for all individuals. The EUNAM panels were genotyped using an Illumina MaizeSNP50 BeadChip (Ganal et al. 2011), and the other panels were genotyped with genotyping-by-sequencing (GBS) (Elshire et al. 2011). Whole-genome genotypes from maize Hapmap 3.2.1 (Bukowski et al. 2016) were imputed using K-Nearest Neighbor imputation (KNNi) (Money et al. 2015) with an overall accuracy of 0.988 and a minor allele imputation accuracy of 0.94 for imputed genotypes, then haplotypes projected onto all populations. Hapmap 3.21 (Bukowski et al. 2016) was called on 1268 inbred genotypes from across the world, with highly variable depth of coverage, and paralogous sites were retained, as they provide signal in GWAS. Because paralogous sites were retained in Hapmap 3.21, we used KNNi (Money et al. 2015) to impute, which was robust to high error rates in genotype calling, but KNNi over-imputes missing data to the major allele.

Table 1.

Population information.

Population	Type (N families)	Filt. KNNi sites	N taxa (DTA)	N taxa (DTS)	Trial locations and years
USNAM	NAM (25)	39,302,149	4758	4758	Clayton, North Carolina, USA—(35.39°N, 78.27°W)—2006, 2007; Aurora, New York, USA—(42.45°N, 76.42°W)—2006, 2007; Columbia, Missouri, USA—(38.95°N, 92.33°W)—2006, 2007; and Urbana, Illinois, USA—(40.11°N, 88.21°W)—2006, 2007
Ames	Diversity	34,967,601	2312	2279	Ames, Iowa, USA—(42.01°N, 93.37°W)—2010; Clayton, North Carolina, USA—(35.39°N, 78.27°W)—2010; Aurora, New York, USA—(42.45°N, 76.42°W)—2010
CNNAM	NAM (11)	27,047,718	1928	1928	Beijing, Beijing, China—(39.48°N, 116.28°E)—2009, 2010; Xinxiang, Henan, China—(35.19°N, 113.53°E)—2009,2010; Urumqi, Xinjiang, China—(43.47°N, 87.39°E)—2009, 2010
EUNAM-Dent	NAM (10)	23,766,799	841	841	Mons, France—(43.41°N, 6.42°E)—2011; Einbeck, Germany—(51.49°N, 9.52°E)—2011; Wadersloh, Germany—(51.44°N, 8.15°E)—2011; Roggenstein, Germany—(49.38°N, 12.15°E)—2011
EUNAM-Flint	NAM (11)	25,388,592	811	811	Ploudaniel, France—(48.32°N, 4.18°E)—2011; Eckartsweier, Germany - (48.31°N, 7.51°E)—2011; Wadersloh, Germany—(51.44°N, 8.15°E)—2011; Roggenstein, Germany—(49.38°N, 12.15°E)—2011; La Coruña, Spain—(43.21°N, 8.42°E)—2011

GBS-genotyped populations were projected using FILLIN (Swarts et al. 2014), and EUNAM was projected using a custom implementation of FSFHap (Swarts et al. 2014). KNNi, FILLIN, and FSFHap all use implementations in TASSEL (Bradbury et al. 2007). For GBS populations, projection was anchored by 465,085 consensus sites—where the physical positions match and the major/minor alleles are shared—between Hapmap 3 and GBS. Projection accuracy as calculated by the correlation between masked known and imputed consensus SNPs was r = 0.99 overall between masked and subsequently imputed genotypes (0.96 for minor alleles). For EUNAM, the parental haplotype breakpoints were imputed for each of the progeny using FSFHap. TASSEL used those breakpoints to project the Hapmap 3.21 genotypes of the parents onto the progeny. While most of the parents of these NAM populations were completely inbred, there were a minority that had residual heterozygosity, which can produce families with three haplotypes segregating. Projected datasets were then filtered using appropriate parameters for the family structure of each population, to ensure a minimum of at least ten minor alleles for any given site in a population; NAM populations were filtered so that one family must have a minimum minor allele frequency (MAF) of 0.1 (which controls for the parental residual heterozygosity), giving a minimum MAF of 0.02 for the population as a whole, and Ames was filtered for minimum MAF of 0.015. Any sites with a maximum heterozygosity above 0.02 or coverage below 0.3 were removed. Before calculating kinships, any residual missing genotypes were assigned a homozygous genotype randomly drawn from the genotypic frequency distribution at each site, by family if appropriate.

Multidimensional scaling (MDS) of American landraces and NAM parents

It is often unclear how inbred lines fit within an adaptive evolutionary context, since breeding programs cross and select on progeny from unrelated individuals. We performed joint MDS analysis with American landraces from Takuno et al. (2015) spanning the two American temperate–tropical gradients with the parents of the four NAM populations to understand the distributions of the parents across American temperate adaptation. Each landrace individual was included ten times in the IBS distance matrix used to calculate the MDS coordinates so that the first two coordinates reflect the relatedness between landrace individuals. Landraces and parents for CNNAM were natively genotyped using GBS, and EUNAM and USNAM projected in Hapmap 3.21 coordinates. MDS was based on 465,085 consensus sites between Hapmap 3 and GBS (cmdscale() in R, using an IBS distance matrix generated in TASSEL)

Cross-population prediction

Cross-population prediction was performed to better understand how populations were related to each other with respect to shared genetic architecture for days to flowering. Cross-population prediction was performed using GBLUP as implemented in TASSEL (Bradbury et al. 2007). The training and test populations were combined in a single kinship (similarity) matrix, calculated using the Centered-IBS implementation in TASSEL (Endelman and Jannink 2012) and phenotypes for the test population masked so that the model was trained solely from the training population phenotypes. This method scales such that the mean diagonal elements estimate 1 + f, accommodating the divergence from Hardy–Weinberg equilibrium inherent in structured populations. Predictions from the resulting model for the test phenotypes were then correlated with the true phenotypes (the “predictive ability”) in R using the Pearson method in cor.test() in the stats package. We use predictive ability, rather than prediction accuracy, the predictive ability divided by the square of the heritability, because heritabilities for flowering traits are quite high (all greater than 0.8) and it is more conservative. Predictive ability based on genomic subsets—coding sequence, three and five prime regions, introns and intergenic—were calculated following Rodgers-Melnick et al. (2016).

Genome-wide Association Study (GWAS)

To determine associations between individual SNPs and flowering traits, we ran a series of genome-wide association models with increasing control for population structure, which is highly confounded with biological association for days to flowering. All models were conducted in TASSEL (Bradbury et al. 2007). Model A was a fixed effects model using the unmodified phenotypes from the original publications, uncontrolled for population structure, because flowering is not only correlated with population structure, but it acts to differentiate populations. Thus, many of the regions that differentiate populations may also control regions important for temperate adaptation and we captured these in the uncorrected model. We also lightly controlled for population structure in another fixed effects model, model B, by fitting five MDS coordinates calculated from an IBS distance matrix in TASSEL for the Ames panel, or fitting a family term for the structured populations in a TASSEL GLM for the NAM populations. Models C and D used a two-step modified mixed linear model framework for computational efficiency. We first calculated residuals in the TASSEL MLM from models incorporating (1) only a kinship matrix calculated in TASSEL using the Centered-IBS method (VanRaden 2008; Endelman and Jannink 2012) as a random effect (model C), or (2) both a kinship matrix as random and five MDS coordinates (for Ames) or a family term (for NAM populations) as fixed effects (model D). The residuals from these models were used as the response in a TASSEL GLM. We do not include the two-step GLM results in machine learning analyses because we found that, due to the high correlation between population structure and flowering time, fully controlling for population structure reduced power to detect even well-known flowering loci such as Vgt1 or ZmCCT. Models A and B were used for subsequent machine learning as the “no population-structure correction” GWAS (model A) and the “population-structure-corrected” GWAS (model B).

Machine learning analyses with GWAS results as the response

We employ the RandomForestClassifier method in Spark (Zaharia et al. 2010) in a Databricks environment, classifying additive p values from GWAS results for model training such that the smallest 1% are classified as 1, or true positives, and, to not overwhelm the true positives, only two million random results from the bottom 95% are classed as 0, or true negatives. We cross-validated by using the other nine chromosomes to predict the tenth. A classifier rather than a regression-based approach was chosen, because we are only interested in how the top regions rank relative to all the others, and a regression approach gives more weight to the insignificant results because they vastly outnumber the top hits. P values for SNPs not reaching filtering criteria in a given dataset were assigned to 1, before ranking results, because a SNP that does not meet MAF filtering criteria will not be highly significant, even if biologically causative. Accuracy is reported as area under the curve (AUC), the integration of the receiver operating characteristic (ROC) curve (for receiver operating characteristic). ROC curves display the false positive rate on the x-axis against the true positive rate on the y-axis for each unique raw predicted value reported by the classifier model, as the prediction for each classified instance is reported on a continuous random variable. An AUC of 0.5 is equivalent to guessing. Overall AUC is simply the average AUC for the ten chromosomal tests. Top predictors were reported as the average mean ranking across all ten tests. Within a given test, predictors are ranked by which splits they participate in for a given tree, averaged across all trees.

Results

This study combines five populations, four NAM designs, and a diversity panel, totaling over ten thousand individuals (Table 1). These populations were previously genotyped using GBS or an Illumina array and imputed with whole-genome resequencing using FILLIN and FSFHap, respectively. This resulted in 70 million segregating markers across all populations (Table 1). The populations have variable genetic overlap based on the first two MDS coordinates, where Ames, as expected of a diversity panel, shows the greatest genetic diversity and CNNAM and EUNAM-Flint are the most isolated (Fig. 1). Only half of the SNPs that survive filtering are shared between study populations (Fig. S1), and the allele frequencies at those loci are highly variable (Fig. S2).

Fig. 1. Relatedness between the five study populations.

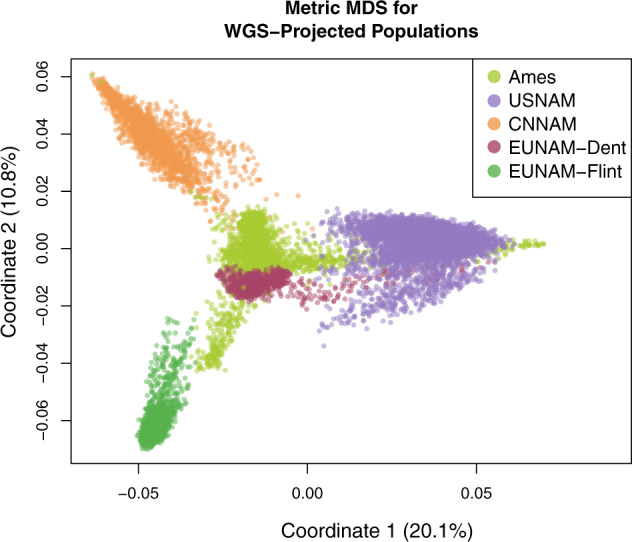
Metric multidimensional scaling (MDS) of study populations from 70 million projected Hapmap 3.21 segregating SNPs (generating with cmdscale function in R, using an isolation-by-state (IBS) distance matrix generated in TASSEL).

Evaluation of relatedness between populations by MDS analysis and phenotypic comparison

To better understand the global genetic relationships between the founders of the four NAM populations, Fig. 2 shows the genetic relatedness of the NAM-type population parents to a panel of GBS-genotyped landraces from across the Americas (Ames includes all of the USNAM parents). In this context, the NAM founders overwhelmingly cluster on the North American temperate–tropical gradient, rather than the South American gradient. CNNAM and EUNAM-Dent panel show a more restricted geographic origin for the founder germplasm, while the other populations contain parents with a greater mix of American tropical and temperate origins.

Fig. 2. MDS of GBS genotypes of American landraces from Takuno et al. (Takuno et al. 2015), replicated 10X each to drive the first two coordinates, and NAM population parents.

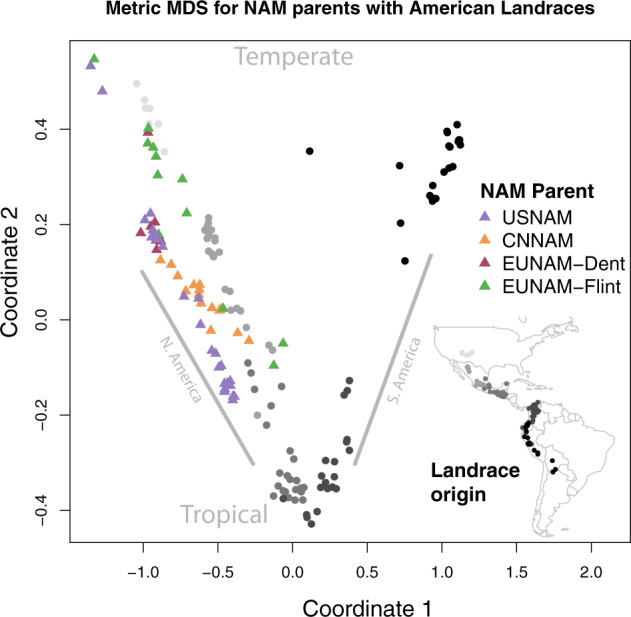
The closest USNAM parents to EUNAM-Dent are the temperate US Dents, including B73, B97, Oh7B, Ky21, and MS71, while the nearest US inbreds to CNNAM parents are South African inbreds M162W, M37W, and the Texas US line, Tx303. All of these are more proximal to the tropical Mexican landraces. The EUNAM-Flint recurrent parent, the Iodent/Iowa Stiff Stalk Synthetic EUNAM-Dent line UH007, clusters with the majority of the EUNAM-Flint parents. The Spanish lines EP44, EZ5, and the French line F64 are the most tropically associated lines in the EUNAM-Dent population.

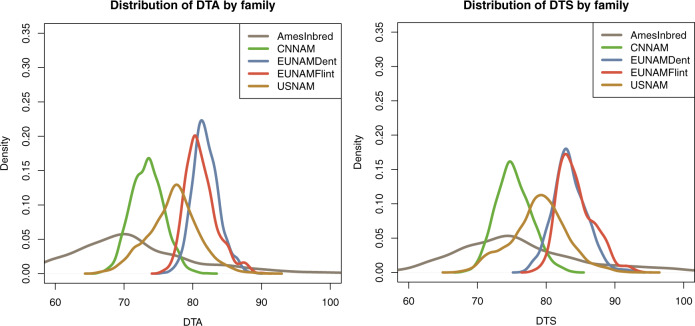
The five populations vary with respect to both the mean and the total variance for flowering (Fig. 3). This is the result of both genetic variance within the populations, and environmental effects of the evaluation regions. Because normalizing heat unit measures such as growing degree days are not available for all populations, we limit GWAS analyses to within population measures. For additive cross-population prediction, the differences across population are less relevant because accuracy is a function of the Pearson correlation between real and predicted values and are not scale dependent.

Fig. 3. Distribution of reported spatially corrected phenotypes for days to anthesis.

The distributions are affected by the trial locations, e.g. EUNAM was grown in Europe which has less heat units and thus as a population takes longer to flower than it would if it were grown in China. Because of the lack of shared trial locations, the means and variances cannot be directly compared but ather serve to demonstrate that all of the populations have variation for days to flowering, and highlight that the highest diversityAmesInbred panel contains the most phenotypic variance, overlapping with the four NAM families.

Cross-population prediction of days to flowering

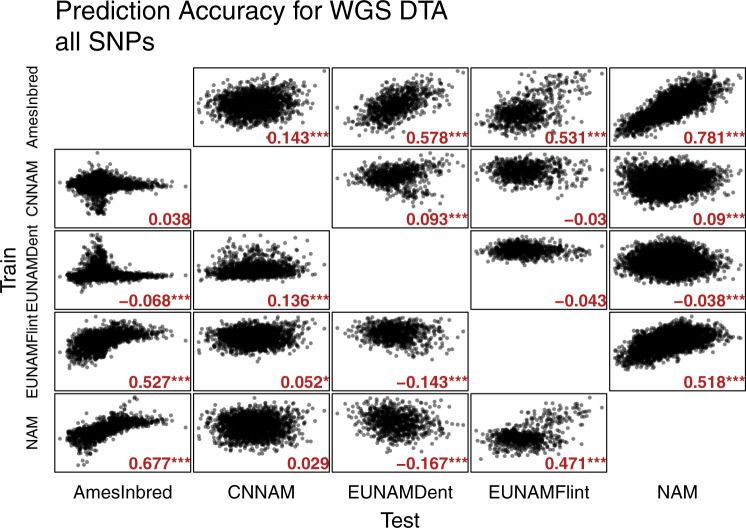
We performed cross-population prediction to better understand how the genetic basis for flowering is structured across these populations. Cross-population predictions were generated pairwise with GBLUP in TASSEL across all genomic SNPs (Fig. 4). GBLUP integrates over all of the SNPs in a covariance structure modeling relatedness between individuals to explain variation in the trait of interest (Meuwissen 2009). Thus, for high predictive ability, the phenotypic variation must be closely correlated with the relatedness between individuals. In addition, high predictability requires that the test contains a subset of the diversity represented in the training set.

Fig. 4. GBLUP cross-population predictive abilities for DTA using all 70 million segregating SNPs in Hapmap 3.21.

Genetic similarity matrix generated using the Centered-IBS method in TASSEL. Predictive abilities are noted in gray text within plots.

Ames has the best cross-population predictive abilities (given throughout as the Pearson correlation between observed and predicted) overall, and unsurprisingly given the close relationship between Ames and USNAM, the best predictive ability is when the model is trained on Ames and predicts DTA in USNAM (r = 0.78; 0.67 for the reverse). Ames predicted all of the populations better than the others, with the exception of CNNAM, which might be expected since Ames is a diversity panel and suggests that Ames is a superset to everything but CNNAM (Chinese lines are present, but poorly represented in Ames (Romay et al. 2013)). CNNAM, uniquely, not only was predicted poorly by the other populations but also did not predict any population well. The EUNAM-Dent population also had poor cross-population predictive ability, but was well predicted by Ames. Both of these populations also show a marked non-linear correlation in predicting Ames, suggesting that a large subset of the Ames population is not represented in these panels. The EUNAM-Flint population is well predicted by Ames and USNAM, but especially when predicted by USNAM, the high overall correlation is especially driven by a relatively small set of lines in the top right of the plot descended from primarily three families descending from the Spanish lines EP44, EZ5, and the French line F64. These three parents are the most “tropical” of the EUNAM-Flint lines on the N. American gradient (Fig. 2).

Theoretically, including only causal polymorphisms should generate stable predictions independent of population specific linkage patterns if the test and training population share a genetic basis (Meuwissen 2009). To this end, we looked at predictions using only SNPs from the functionally annotated regions of the genome as defined in Rodgers-Melnick et al. (2016) and Wallace et al. (2014), and found that subsets can sometimes improve predictions if genomic predictive ability was low, but never if the accuracy was already high (Fig. S3). An exception where a well predicted population is further improved by a subset is when the EUNAM-Flint population predicts Ames or USNAM; in both of these cases predictive ability is already high, and genic or open chromatin subsets further increased accuracy.

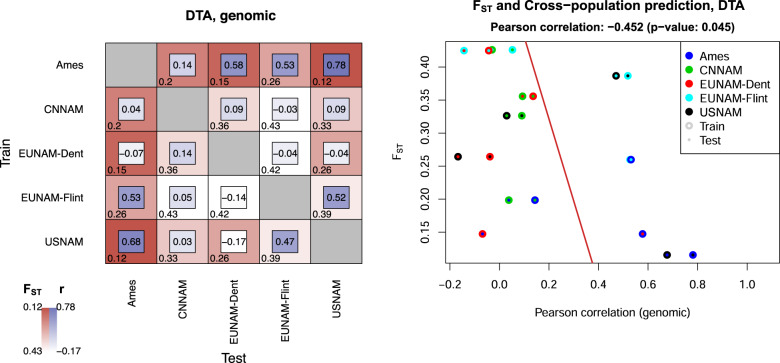
Because predictive ability is a function of relatedness, we calculated F_ST statistics using the Weir and Cockerham method in vcftools (Danecek et al. 2011) for all pairs of populations. Figure 5 shows a correlation of −0.41 for F_ST and predictive ability for DTA across all markers, confirming a relationship between close relatedness and high predictive ability, but there are outliers that do not fit the expected pattern. Figure 5 shows that CNNAM and EUNAM-Dent generally have lower cross-population predictions than expected by population relatedness, with the exception that EUNAM-Dent is predicted similar to expectation by Ames. In contrast, EUNAM-Flint has higher than expected predictive ability with USNAM.

Fig. 5. Pairwise population differentiation, F_ST and cross-population predictive ability (r) for DTA.

High predictive ability is significantly correlated (α < 0.05) with low population differentiation, but many population pairs have higher or lower predictive ability than expected based on relatedness.

Random forest predictions of GWAS for flowering loci across the genome by population

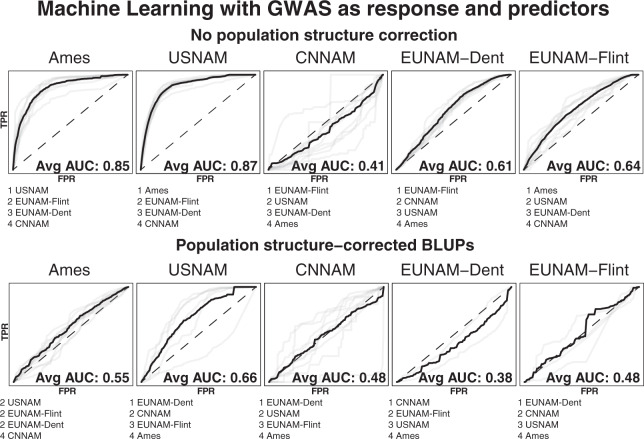
To maximize the influence of selection from background drift on prediction, we examine cross-population predictability using a Random Forest Classifier where only the top GWAS results are coded as “true” (SNPs not segregating in a given population were given a p value of 1 and coded as “false”). GWAS results were run for each population, and because changes in flowering time generate population structure (Swarts et al. 2017), we performed GWAS with no population-structure correction and minimal population-structure correction (a family term for NAM populations, and five MDS coordinates for Ames), which is designed to further enrich top GWAS loci for biological (rather than population-structure artifacts) loci underlying flowering (Figs. 6 and S4). Without population-structure control the results are similar to the cross-population predictions, where Ames and USNAM are well predicted, mostly by each other. EUNAM-Flint is predicted to a lesser extent by Ames, followed by USNAM, and EUNAM-Dent is predicted equally well, but by EUNAM-Flint. CNNAM is predicted less well than by chance. After accounting for population structure, no population is well predicted by the others, and only Ames has a positive predictability.

Fig. 6. Average area under the curve (AUC, in bold)—the false positive rate (FPR) to true positive rate (TPR) ratio—and predictor rankings across all chromosomes from Random Forest Classifier for GWAS results between populations to evaluate overlap in GWAS results between populations.

The heavy line represents the mean of the chromosomal receiver operating characteristic curves, sampled at 0.01 intervals. Predictors are equivalent GWAS (with or without population-structure correction) for the other populations. Trained on nine chromosomes and tested on the 10th. Not all chromosomes for the population-structure-corrected results have top predictors, and are excluded from average AUC calculations.

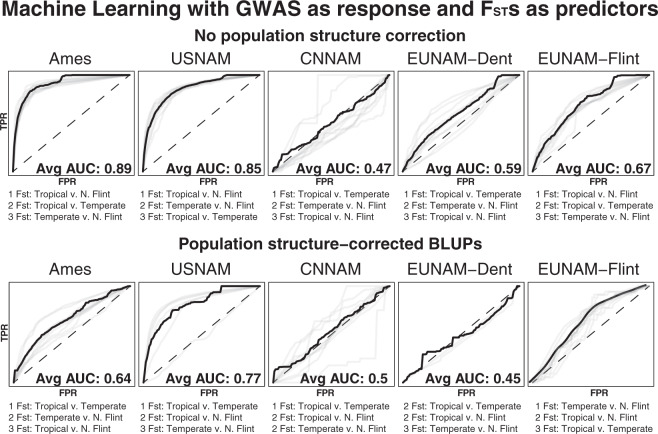
To explicitly test if the North American early flowering adaptation (Swarts et al. 2017) was the source germplasm for early flowering, we also tested the GWAS results against measures of population differentiation between three different N. American germplasm pools, tropical, temperate, and Northern Flint; the temperate germplasm results from the admixture between the southern Dent and N. Flint pools (Figs. 7 and S5). Confirming the inference from the cross-population predictions, Ames is predicted very well (overall AUC of 0.89) by the tropical contrasts, followed closely by USNAM (0.85), with EUNAM-Flint well predicted at 0.67, EUNAM-Dent rather poorly predicted at 0.59 and CNNAM slightly negatively predicted with an AUC score of 0.47. Population-structure control with a family term for the NAMs and five MDS coordinates for Ames reduced predictive ability by population differentiation, but did not eliminate the effects, confirming that flowering time is closely tied to population structure.

Fig. 7. Average area under the curve (AUC, in bold)—the false positive rate (FPR) to true positive rate (TPR) ratio—and predictor rankings across all chromosomes from Random Forest Classifier with GWAS additive p values as the response, and N.

American F_STs as the predictors. The heavy black line represents the mean of the chromosomal receiver operating characteristic curves, sampled at 0.01 intervals. Predictors are equivalent GWAS (with or without population-structure correction) for the other populations. Trained on nine chromosomes and tested on the 10th. Not all chromosomes for the population-structure-corrected results have top predictors, and are excluded from average AUC calculations.

Discussion

Complex traits, such as yield, are well-known to aggregate fitness effects across all pathways and systems of a plant, but this study highlights that this is also true for days to flowering (Li et al. 2016). When a plant is induced to flower depends on the alleles present at ZmCCT, ZCN8, and Vgt1, but it also depends on the pleiotropic response of hundreds of other loci responding to signals for heat, circadian signaling, light quality, moisture availability, starch accumulation, and others (Tian et al. 2011; Brown et al. 2011). Limited overlap in mapping results suggests that, as maize spread across the world during improvement and modern hybrid breeding, complex population dynamics may have led to differential selection for secondary pathways implicated in temperate adaptation.

These patterns are found in Arabidopsis thaliana as well. Fournier-Level et al. find evidence for selection on different, pleiotropic QTL in different environments across Europe in a common garden experiment (Fournier-Level et al. 2013). Additionally, Kover et al. (2009) find that adaptation to early flowering is partially conditional on other conditions in the selection environment. Finally, only two out of a total of 10 QTL were shared between Swedish and Italian RIL populations (Dittmar et al. 2014), similar to findings in maize.

That some populations, namely EUNAM-Flint and CNNAM, do not predict Ames as expected based on population differentiation suggests more complicated population dynamics than simple relatedness (Fig. 5). What better explains the patterning in predictive ability is the spread of the population founders on the North American temperate/tropical gradient (Fig. 2). The two populations with a localized geographic origin on this gradient, CNNAM and EUNAM-Dent, are the two populations with more limited cross-population predictive ability, and low predictive ability for GWAS results in machine learning. In contrast, EUNAM-Flint, which has higher than expected cross-population predictive ability when predicting USNAM, has parents spanning the tropical/temperate North American gradient, and F_STs between Northern Flints and tropical American germplasm from Hapmap 3.21 are top predictors in machine learning against uncorrected GWAS results. Lower than expected predictive ability relative to population differentiation could be interpreted in two ways; a narrow germplasm base or, if the population has high variance for flowering time, that these populations contain novel temperate adaptation not captured on either American temperate/tropical axis.

The history of germplasm introduction can shed light on the discrepancies between predictive ability and population differentiation especially for the EUNAM-Dent and CNNAM. The earliest germplasm in Europe was Caribbean in origin, and subjected to selection for early flowering upon entry into Spain (Rebourg et al. 2003). However, it was only after the introduction of the Northern Flint landraces in the mid-1600s from the northeast of the modern US that maize agriculture spread to European climates north of the Pyrenees (Revilla et al. 2003; Rebourg et al. 2003; Dubreuil et al. 2006). Genetic evidence from European maize suggests that most of the early flowering adaptation was acquired from the North American Northern Flint germplasm introduced in the 1600s (Rebourg et al. 2003; Dubreuil et al. 2006), but also that there are unique rare alleles in the Southern European (Spanish and Portuguese) germplasm (Revilla et al. 2003). Finally, in the past century, the development of the European heterotic groups introduced primarily American Iodent, Stiff Stalk, Lancaster, and Minnesota germplasm into Europe, captured primarily in the EUNAM-Dent panel (Dubreuil et al. 2006; Troyer and Hendrickson 2007).

The recurrent parent of the EUNAM-Dent population is representative of the agronomically important Iodent germplasm (derived from an Iodent/Iowa Stiff Stalk Synthetic cross), and the additional lines in the EUNAM-Dent panel derive from the US Stiff Stalk, US Lancaster, and Hohenheim Dent populations (Doebley et al. 1988; Bauer et al. 2013). The Hohenheim Dents were bred from US temperate germplasm, and especially the early flowering Minnesota lines (Technow et al. 2014), which result from crosses between the US Southern Dents and Northern Flints, followed by selection for extreme temperate adaptation, with early flowering contributed by the Northern Flints (Troyer and Hendrickson 2007).

EUNAM-Dent is well predicted by Ames, but not USNAM; Ames is enriched for temperate US germplasm, including Iodent and Minnesota lines (Romay et al. 2013), while USNAM is not (McMullen et al. 2009). It is not surprising that Ames then predicts the EUNAM-Dent panel, as it is a superset, but it is perhaps surprising that the Ames GWAS results predict the EUNAM-Dent germplasm so poorly in machine learning, given that the pedigree suggests that temperate adaptation in the EUNAM-Dent panel is Northern Flint in origin. EUNAM-Dent has low narrow-sense heritabilities for flowering relative to Ames (0.92 for DTA (Romay et al. 2013)) or USNAM (0.94 for DTA and DTS (Buckler et al. 2009)), 0.7 (DTS) and 0.61 (DTA), which can result from fixation of alleles in a population and may explain this discrepancy. In addition, Giraud et al. (2014) found fewer QTL in the EUNAM-Dent relative to the EUNAM-Flint panel, and these QTL explain less variance. In our results, the machine learning using both cross-population and F_ST results find no significant loci on many chromosomes, especially in EUNAM-Dent after population-structure correction (Supplementary Figs. S4 and S5), suggesting that many of the flowering loci are fixed in the population. Alternately, poor overlap and machine learning prediction could be a result of recent selection for temperate adaptation in the development of the Minnesota germplasm and subsequent selection in Europe, which is not sufficiently represented in the other datasets.

Like early European germplasm, the first maize introduced into China was tropical in origin. The most likely first point of entry for maize to China was by Spanish and Portuguese traders through the Port of Macau, and these are reported to have been humid, tropical adapted varieties (Ho 1955; Anderson 1988). A regular trading route between Acapulco and Manila, which started in CE 1565, could have introduced western lowland Mexican maize to Asia (Schurz 1939). Although Chinese maize now contains both early and late flowering varieties, unlike the European germplasm, there is no record of later introduction of American temperate adapted material until the past century.

Almost all of the CNNAM parents derive from Chinese sources across heterotic groups, and the recurrent parent is a derivative of the temperate Chinese landrace TangPiSingTou (Lu et al. 2009). While most of the CNNAM parents are temperate adapted (Li et al. 2016), they are significant at the major photoperiod locus ZmCCT, confirming that the population contains tropical alleles. In addition, broad sense heritabilities for CNNAM were high (0.91 and 0.90 for DTA and DTS, respectively), so the genetic basis for days to flowering is not narrow. High heritability and broad phenotypic variability suggest that the CNNAM population does not suffer from a narrow germplasm base. Thus, poor cross-population prediction across all populations indicates that CNNAM contains novel alleles for temperate adaptation. Although novel targets are consistent with these data, Li et al. (2016) find that 40 out of 130 independently identified QTL overlap between between CNNAM and USNAM, suggesting that many of these novel variants are allelic variants at common loci, consistent with the “common gene” mode of adaptation inferred from USNAM alone (Buckler et al. 2009).

As the CNNAM panel is dominated by lines whose origins likely predate modern hybrids of the 20th century, these results suggest an indigenous temperate adaptation to China of independent origin relative to the other four populations. As CNNAM germplasm is not extensively utilized outside of China, this study highlights a potential source of novel alleles for breeding programs. Moreover, maize suggests a roadmap for understanding the characteristics important for resiliency in natural species subject to changing climate. Per these results, there is evidence for independent adaptation in maize in the Americas and China, and partial adaptation in Europe (Rebourg et al. 2003) but why was maize able to accomplish these feats? Maize is historically highly outcrossing resulting in large effective population sizes, with high levels of genetic diversity (Hufford et al. 2012), which theoretically allows for efficient selection (Bürger and Lande 1994). To better understand the impacts of climate change on a diversity of natural systems, understanding past adaptations in other domesticates will provide a clearer picture of the population parameters underlying resiliency.

Data archiving

Phenotypes and imputed genotypes will be made available upon request.

Compliance with ethical standards

Conflict of interest

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41437-021-00422-z.