Optimal resilience of modular interacting networks

Significance

In real-world scenarios, many subnetworks interact with other subnetworks to form a modular interacting network system. In previous models, it was assumed that all subnetworks may be linked pairwise; however, in real systems, only some pairs of subnetworks are connected. Understanding how to develop theoretical frameworks and study system resilience of general coupling patterns of the subnetworks is of significant importance for designing and optimizing economic, social, and infrastructure networks. Here we present two frameworks for such systems having specific coupling patterns to investigate their resilience. Specifically, we find an optimal level of interaction between subnetworks, which maximizes the system’s resilience to failures. Our findings highlight the need to consider real-world coupling patterns and possible optimizations for designing resilient systems.

Abstract

Coupling between networks is widely prevalent in real systems and has dramatic effects on their resilience and functional properties. However, current theoretical models tend to assume homogeneous coupling where all the various subcomponents interact with one another, whereas real-world systems tend to have various different coupling patterns. We develop two frameworks to explore the resilience of such modular networks, including specific deterministic coupling patterns and coupling patterns where specific subnetworks are connected randomly. We find both analytically and numerically that the location of the percolation phase transition varies nonmonotonically with the fraction of interconnected nodes when the total number of interconnecting links remains fixed. Furthermore, there exists an optimal fraction $r^{*}$ of interconnected nodes where the system becomes optimally resilient and is able to withstand more damage. Our results suggest that, although the exact location of the optimal $r^{*}$ varies based on the coupling patterns, for all coupling patterns, there exists such an optimal point. Our findings provide a deeper understanding of network resilience and show how networks can be optimized based on their specific coupling patterns.

Network science has been applied to study resilience of complex systems including infrastructures, financial systems, and others (1–6). Real-world networks have distinct modular structures where groups of nodes are tightly connected to others within their same group, while being loosely connected to other modules (7–13). The current modular network models for these situations typically assume all of the modules have the same probability to be connected to one another, yet in real networks modules may connect only to some specific modules. Understanding the topological structures of real-world networks enables researchers to better reveal their intrinsic behaviors from different perspectives (14–22). Real-world networks are not homogeneous and often composed of modules, with nodes more densely connected to other nodes within the same module than to the rest of the network (23–26). In other cases, subnetworks of one kind (e.g., a power grid, energy system) interact with subnetworks of other types (e.g., communications systems, social networks), leading to an encompassing network of networks that incorporates different kinds of subnetworks with different types of interactions within and between them (27–29). Such interconnected networks can take various forms based on the specific coupling patterns between the various subnetworks. For the case of interdependent networks, where the interactions between subnetworks involve dependencies, different coupling patterns such as a tree, a loop, etc., have been investigated (30, 31). These studies revealed that the resilience of coupled interdependent networks often depends on the specific coupling patterns and also suggest possible methods to mitigate the collapse of real systems (29–37).

However, a precise understanding of how interconnected networks and how the specific nodes with the interconnections (interconnected nodes) affect the resilience of the overall interconnected network has been lacking. Most studies on interconnected networks (38, 39) have considered all-to-all coupling where the subnetworks could all be interconnected to one another as opposed to having a specific coupling pattern. Such patterns can include a deterministic coupling pattern, where coupling between given pairs of subnetworks is predefined to attain some larger overarching structure, and random coupling where specific pairs of subnetworks are chosen randomly to have connections between one another.

Furthermore, in interconnected networks since each link has a cost and the interconnected links tend to be most costly (e.g., if they are long-distance power lines or long highways connecting disparate cities), it is often impractical to increase the number of such connections and rather it is preferable to more optimally allocate a fixed number of connections (25, 26). Such optimization could, for example, improve resilience of a power grid in the face of a weather storm or other failures.

Here, we develop two analytical frameworks for understanding the resilience of a modular interacting network with different coupling patterns of the subnetworks, including deterministic coupling patterns like a star, a tree, etc., and random coupling patterns like a random regular (RR) pattern, a pattern following a Poisson distribution, and one that follows a power-law distribution. Surprisingly, for all of these various coupling patterns, we find that there exists an optimal coupling point at which the system shows remarkable resilience and is best able to withstand failures at the level of the entire system. Our results generalize known results and provide theoretical support for efforts at optimizing system resilience.

Theory

Real systems are often composed of numerous subnetworks with different attributes coupled together to maintain functioning. Here we present a model based on a modular interacting network (MIN), where each subnetwork has connections to other specific subnetworks. In this manner, we have a network of networks, where we can consider the larger network of connections between the subnetworks as a typical network where each node represents a subnetwork as shown in Fig. 1. The model can use diverse coupling patterns, which include deterministic coupling patterns between subnetworks and random coupling patterns where subnetworks connect randomly or follow some distribution.

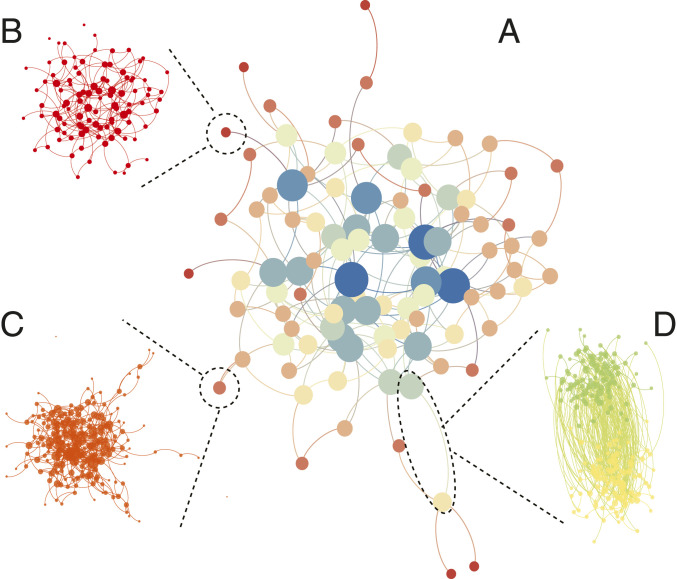
Fig. 1.

Demonstration of a modular interacting network. (A) The degree distribution of the overall network follows a power-law distribution with some subnetworks connecting to many others, whereas most subnetworks connect to only a few others. (B and C) Within the subnetworks, the degree distribution can follow, e.g., a Poisson distribution (B) or a power-law distribution (C), respectively. (D) The links between any two connected subnetworks follow some interdegree distribution with some subset of predefined nodes in each subnetwork connecting to nodes, called interconnected nodes, in the other subnetwork.

To understand this model from a theoretical perspective, we use generating functions, which have been widely applied in studying percolation problems including epidemic spreading and cascading failures (36, 38–41). These generating functions can be used to incorporate information on the degree distribution $p_k$ using a concise power series. Beginning with the appropriate generating function of the degree distribution, one can analytically obtain solutions for the size of the giant component and determine the percolation threshold, i.e., the maximum fraction of failures, $\left(1-p\right)$, for which the network collapses and becomes disconnected (see SI Appendix for details). For a deterministic coupling pattern, the coupling between given pairs of subnetworks is predefined to take a certain form, e.g., a star or tree pattern of a network of networks (SI Appendix). The connectivity links within each subnetwork and between subnetworks are assumed to be described by independent degree distributions. For convenience, we provide a summary of all variables and their meanings in Table 1.

Table 1.

Variables and their definitions

Variable	Definition
$P_s\left(k^i\right)$	The degree distribution of a node with intradegree $k^i$ in subnetwork $i$
$P_c\left(k^{ji}\right)$	The degree distribution of a node with interdegree $k^{ji}$ between subnetworks $i$ and $j$
$P_u\left(K\right)$	The degree distribution of the subnetworks with degree $K$ in the MIN system
$m$	No. of subnetworks
$M$	No. of links in the MIN system
$N_i$	No. of nodes in subnetwork $i$
$Ñ$	No. of nodes in the whole MIN system, $Ñ=m\cdot N_i$
$k_i$	The mean intradegree of nodes in the subnetwork $i$ and for simplify let $k_i=k$, $i=1,\dots ,m$
$k_{ij}$	The mean interdegree of nodes between subnetworks $i$ and $j$ and for simplify let $k_{ij}=\overline{k}$, $i,j=1,\dots ,m$, and $i\ne j$
$K$	The average degree of a subnetwork in the random coupling pattern
$\tilde{K}$	The average degree of nodes in the whole MIN system and $\tilde{K}=\frac{2M}{Ñ}$
$\lambda$	The power-law exponent of MIN follows the power-law coupling pattern
$r_i$	The fraction of interconnected nodes within subnetwork $i$ that have both intra- and interlinks, and for simplify let $r=r_1=r_2=\cdots =r_m$
$r^{*}$	The $r$ value, at which $p_c$ has the minimum value
$S_i$	The fraction of giant component in subnetwork $i$ after undergoing failures
$\overline{S}$	The fraction of largest (giant) component composed of vertices (subnetworks) for the original MIN system
$S$	The fraction of giant component composed of nodes in the whole MIN system after undergoing failure

Next, we determine the appropriate generating function of the degree distribution for our case to be

$$\begin{array}{cc}\hfill G_i\left(x_{ii},x_{ji}\right)=& \left(1-r_i\right)\sum _{k^i}{P}_s\left(k^i\right)x_{ii}^{k^i}+\hfill \\ \hfill & r_i\sum _{k^i}{P}_s\left(k^i\right)x_{ii}^{k^i}\prod _{j\in {\mathrm{\Gamma }}_i}\sum _{k^{ji}}{P}_c\left(k^{ji}\right)x_{ji}^{k^{ji}},\hfill \end{array}$$ [1]

where $r_i$ represents the fraction of nodes within subnetwork $i$ that can have links to the other subnetworks. For simplicity in analyzing the resilient properties of the system, we let $r_i=r$, $i=1,\dots ,m$ in Eqs. 1 and 2 and continue with that assumption for the remainder of the derivations. The above equation, Eq. 1, can be understood to consist of two parts that consider whether a given node within subnetwork $i$ has solely connections within $i$ or whether it also has connections to subnetwork $j$. First, the term $\left(1-r_i\right){\sum }_{k^i}{P}_s\left(k^i\right)x_{ii}^{k^i}$ defines the distribution for the $\left(1-r_i\right)$ fraction of nodes that do not have any links to other subnetworks and thus follow a degree distribution according to $P_s\left(k^i\right)$ within subnetwork $i$. The second term, $r_i{\sum }_{k^i}{P}_s\left(k^i\right)x_{ii}^{k^i}{\prod }_{j\in {\mathrm{\Gamma }}_i}{\sum }_{k^{ji}}{P}_c\left(k^{ji}\right)x_{ji}^{k^{ji}}$, describes the case for the $r_i$ fraction of nodes that also have connections to other subnetworks. These nodes are still connected within their own subnetwork according to the same degree distribution, $P_s\left(k^i\right)$, but they also connect to other subnetworks according to a degree distribution $P_c\left(k^{ji}\right)$, where $j$ is another subnetwork among the ${\mathrm{\Gamma }}_i$ set of subnetworks that are neighbors of subnetwork $i$.

For the case of a random coupling pattern between subnetworks following a distribution $P_u\left(K\right)$, the term ${\prod }_{j\in {\mathrm{\Gamma }}_i}{\sum }_{k^{ji}}{P}_c\left(k^{ji}\right)x_{ji}^{k^{ji}}$ can be similarly simplified by considering it as a term within an appropriate generating function. In this case, Eq. 1 can be written as

$$\begin{array}{cc}\hfill G_i\left(x_{ii},x_{ji}\right)& \hspace{0.17em}=\hspace{0.17em}\left(1-r_i\right)\sum _{k^i}{P}_s\left(k^i\right)x_{ii}^{k^i}+\hfill \\ \hfill & r_i\sum _{k^i}{P}_s\left(k^i\right)x_{ii}^{k^i}\sum _K{P}_u\left(K\right){\left[\sum _{k^{ji}}{P}_c\left(k^{ji}\right)x_{ji}^{k^{ji}}\right]}^K,\hfill \end{array}$$ [2]

where $P_s\left(k^i\right)$ is the degree distribution within each subnetwork, and $P_c\left(k^{ji}\right)$ is the interdegree distribution between subnetwork $i$ and subnetwork $j$. The first term $\left(1-r_i\right){\sum }_{k^i}{P}_s\left(k^i\right)x_{ii}^{k^i}$ is the same as in Eq. 1 and describes the connections of the $1-r_i$ fraction of nodes within subnetwork $i$ that do not connect to other subnetworks. The second term is for the $r_i$ fraction of nodes which also have interconnections to subnetwork $j$, where the number of subnetworks, $K$ that $i$ connects to follows a distribution $P_u\left(K\right)$. Here, $\left[{\sum }_{k^{ji}}{P}_c\left(k^{ji}\right)x_{ji}^{k^{ji}}\right]$ is similar to the state variable $x$ in the generating function of a single network. After randomly removing a $1-p$ fraction of nodes from the system, the size of the giant component within the random coupling pattern can be described as

$$S=\overline{S}\cdot S_i,$$ [3]

where $\overline{S}$ is the fraction of subnetworks that remain connected to one other in the overall giant component (this is determined based on $P_u\left(K\right)$) for a random coupling pattern, and $S_i$ is the fraction within each subnetwork within the giant component. $S_i$ is given by

$$S_i=p\left[1-G_i\left(1-p\left(1-f_{ii}\right),1-p\left(1-f_{ji}\right)\right)\right],$$ [4]

where $f_{ii}$ and $f_{ji}$ are the probabilities that a randomly chosen inner link within subnetwork $i$ and interlink between subnetworks $i$ and $j$ do not belong to the giant component of the MIN, respectively. Here, if $i=2$ (two interacting subnetworks), Eq. 4 reduces to equation 3 in ref. 38. Furthermore, the critical threshold $p_c$ at which the system fails and connectivity is lost can be obtained from the limit of Eq. 4 at $S=0$.

Coupling between subnetworks can significantly affect the resilience of the system in that it increases the resilience, since even if a single subnetwork is internally disconnected, there can still be sufficient connectivity among the various subnetworks, allowing the system to remain resilient at what was the original transition point for a single network (38).

Results

Deterministic Coupling Patterns.

The first basic pattern we consider is the star coupling pattern as shown in SI Appendix, Fig. S1A. For the star coupling pattern consisting of $m$ subnetworks, we obtain the analytical expression of $S$ from Eqs. 1 and 4,

$$S=p\left[1-\frac{1}{m}{f}_{ii}-\frac{m-1}{m}{f}_{jj}\right],$$ [5]

where $m$ is the total number of subnetworks. The result of Eq. 5 is general for any degree distribution within and between subnetworks; however, to better demonstrate the result, we consider a specific case where $\tilde{K}$ is the average degree of the MIN system, and the degree distributions within and between subnetworks follow Poisson distributions with inner average and interaverage degrees $k$ and $\overline{k}$, respectively (more details in SI Appendix for the case of power-law distributions). For this case, the expressions of $f_{ii}$ and $f_{ji}$ are shown in SI Appendix, Eq. 7. One can observe that simulation results agree well with analytical results in SI Appendix, Fig. S2 for different values of parameters. Finding the limit of Eq. 5, with the appropriate values of $f_{ii}$ and $f_{ij}$, at $S=0$ we can obtain the critical threshold $p_c$ numerically. For the limiting case $r_i=r=1$ for all $i=1,\dots ,m$ and $k=\overline{k}$, the critical threshold $p_c$ can be expressed as

$$p_c=\frac{\sqrt{m-1}-1}{\left(m-2\right)k}$$ [6]

(SI Appendix, Eqs. 10–14).

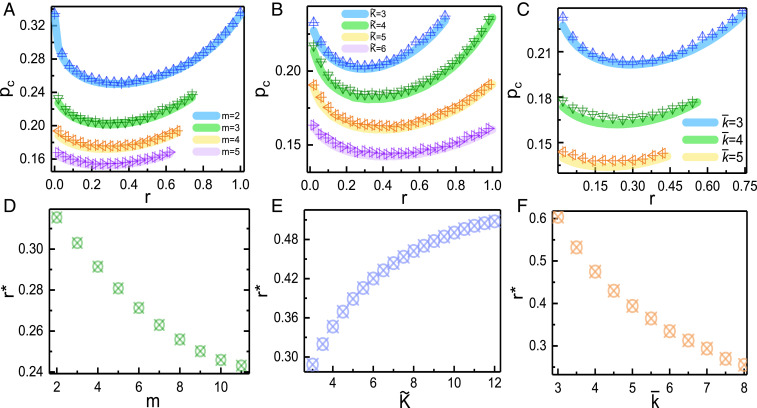
The nature of the coupling between subnetworks is controlled by $r$, the fraction of nodes that are predefined to have interconnection links. From Fig. 2A, one can observe that $p_c$, defined by the location $p$ of the maximum in the size of the second largest component $S_2$ (as shown in SI Appendix, Fig. S2B), becomes gradually smaller as $r$ increases from near 0 to around $r=0.2$ for different $m$. As $r$ increases, an increasing number of interconnected nodes act as hubs, which allows the system to become more resilient. System connectivity here not only is maintained via the links within the subnetworks, but also begins to be more impacted by the links connecting to the other subnetworks via the interconnected nodes. Thus, even if there is no path between two nodes in the same subnetwork, it is still possible have a path between them via their connections to other subnetworks. As $r$ increases to the optimal transition value $r^{*}$, the system reaches the minimal $p_c$, where it is optimal, i.e., most resilient to withstand random failures or perturbations.

Fig. 2.

(A–C) Analytical predictions (thick lines) compared with simulation results (symbols) for $p_c$ as a function of $r$ for different $m$, $\tilde{K}$, and $\overline{k}$ for a star coupling pattern. Analytical results are from Eq. 5 and SI Appendix, Eq. 12. The parameters are $\tilde{K}$ = $\overline{k}$ = 3 in A, $m=3$ and $\overline{k}=3$ in B, and $m=3$ and $\tilde{K}=3$ in C, respectively. D–F show the results of $r^{*}$ as functions of $m$, $\tilde{K}$, and $\overline{k}$. The parameters are the same as for A–C. Simulation results are averaged over 1,000 independent realizations with $N_i=N=10^7$ for each subnetwork $i=\mathrm{1,2},\dots ,m$.

When $r$ further increases, for $r>r^{*}$, the system becomes more vulnerable since $p_c$ increases. For this stronger coupling case, more nodes become interconnected nodes, but due to the fixed number of total links there are fewer intralinks within the subnetworks. Thus, the network connectivity within these subnetworks eventually becomes small to the point that they may collapse internally.

Similarly, this optimal transition can also be observed for different values of $\tilde{K}$ and $\overline{k}$, as shown in Fig. 2 B and C. We also plot the optimal transition point $r^{*}$ as a function of $m$, $\tilde{K}$, and $\overline{k}$ in Fig. 2 D–F, respectively. The results indicate that $r^{*}$ decreases as $m$ increases for fixed $\tilde{K}$ and $\overline{k}$. As $\tilde{K}$ increases, $r^{*}$ also increases for fixed $m$ and $\overline{k}$. This is because as $\tilde{K}$ increases, the system becomes more resilient, and $p_c$ for all values of $r$ becomes smaller. Finally, as $\overline{k}$ increases, $r^{*}$ decreases for fixed $m$ and $\tilde{K}$.

The binary-tree coupling pattern is another important case where a general expression of $S$ can be obtained from Eqs. 1, 3, and 4. The simplified solution is

$$S=\frac{\sum _{l=1}^L{2}^{l-1}{S}_i}{2^L-1},$$ [7]

where $L$ ($L=2$ also corresponds to a star coupling pattern with $m=3$) is the number of layers of the binary tree, $l$ represents the layer, and $S_i$ is described in SI Appendix, Eqs. 27 and 28. For this case, we consider the resilience of the system with Poisson and power-law degree distributions within and between the subnetworks (more details in SI Appendix). Just as for the star coupling pattern, here too we also observe the existence of an optimal $r^{*}$ for various sets of parameters (further details in SI Appendix, Fig. S4 C–E).

Aside from these two cases, the general framework developed above allows for studying the structural robustness of any deterministic coupling patterns. Our results here suggest that the existence of an optimal $r^{*}$ is general for most, if not all, deterministic coupling patterns and highlights the importance of carrying out optimization in real systems.

Random Coupling Patterns.

We now turn our attention to coupling patterns based on random coupling. Specifically, we study the system resilience for RR, Poisson, and power-law coupling patterns.

RR coupling pattern.

For the RR coupling pattern, we assume that each subnetwork is connected to exactly $K$ other subnetworks. We present here the case where connections within and between subnetworks follow the Poisson degree distribution with average degrees $k$ and $\overline{k}$, respectively (see SI Appendix for the case of power-law distributions), such that $k_i=k$ and $k_{ij}=\overline{k}$, $i,j=1,\dots ,m$ in Eqs. 3 and 4. The analytical expression that is obtained is (SI Appendix, Eq. 39)

$$S=p\left(1-f_{ii}\right),$$ [8]

$$f_{ji}=e^{kp\left(f_{ii}-1\right)+K\overline{k}p\left(f_{ji}-1\right)}.$$ [9]

Comparisons between analytical and simulation results for $S$ as a function of $p$ are shown in SI Appendix, Fig. S6 for different parameters. One could find that simulation results agree well with analytical results. The expressions for $p$ with respect to $f_{ii}$ can be found from the formulas of $f_{ii}$ and $f_{ij}$ (see SI Appendix, Eqs. 39 and 41 for more details), and the critical threshold is found when $f_{ii}\to 1$,

$$p_c=\frac{\left(k+\overline{k}K\right)-\sqrt{{\left(k-\overline{k}K\right)}^2+4k\overline{k}Kr}}{2k\overline{k}K\left(1-r\right)}.$$ [10]

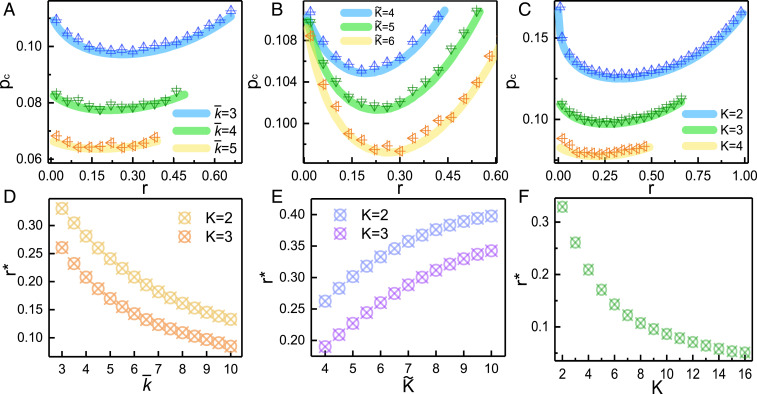
For keeping the number of links fixed, it can be determined that $\tilde{K}=k+r\overline{k}K$ (SI Appendix, Eq. 43). As shown in Fig. 3 A–C, $p_c$ decreases, and the system becomes more resilient as $\overline{k}$, $\tilde{K}$, or $K$ increases. There, it is also observed that there exist optimal values of $r$ for all of the different parameter sets of $\overline{k}$, $K$, and $k$. For $r<r^{*}$, when the total number of links is fixed, as the interlinks between subnetworks increase, hubs appear and the resilience is enhanced. When $r=r^{*}$, the system is at its most resilient point. If $r$ is further increased to $r>r^{*}$, the system becomes more vulnerable and $p_c$ increases. In this case, the optimal transition point, $r^{*}$, which corresponds to the minimum $p_c$ value,

$$r^{*}=\left\{r|min\left(p_c\right)\right\}.$$ [11]

Fig. 3.

(A–C) Analytical predictions (thick lines) compared to simulation results (symbols) for the RR coupling pattern. We show $p_c$ as a function of $r$ for different $\overline{k}$, $\tilde{K}$, and $K$ based on Eq. 10. The parameters are (A) $\tilde{K}=6$ and $K=3$, (B) $K=3$ and $\overline{k}=3$, and (C) $\overline{k}=3$ and $\tilde{K}=6$, respectively. (D–F) $r^{*}$ as a function of $\overline{k}$, $\tilde{K}$, and $K$ from Eq. 11. The parameters correspond to those in A–C. The value of $p_c$ is determined by the location of the peak value of $S_2$, as shown in SI Appendix, Fig. S6C. Simulation results are averaged over 1,000 independent realizations with $m\cdot N_i=10^4\cdot 10^6$, where $m$ and $N_i$ are the number and size of the subnetworks, respectively.

The value of $r^{*}$ as a function of $\overline{k}$, $K$, and $k$ is shown in Fig. 3 D–F. The results demonstrate that the system becomes more resilient when increasing interconnectivity or total system connectivity. Furthermore, $r^{*}$ decreases as $\overline{k}$ increases and as $\tilde{K}$ decreases, as shown in Fig. 3 D and E. While for increasing $K$ the system becomes more robust, the corresponding $r^{*}$ decreases as $K$ increases, as shown in Fig. 3 C and F.

Poisson coupling pattern.

Another example of coupling according to a random degree distribution is the Poisson coupling pattern where we assume that each subnetwork is connected to an average of $K$ other subnetworks. We present here the case where the connections within and between the subnetworks also follow the Poisson degree distribution with average degrees $k$ and $\overline{k}$, respectively (see SI Appendix for the case of power-law distributions); the analytical expressions derived from Eqs. 3 and 4 (SI Appendix, Eqs. 46 and 47) are

$$\begin{array}{cc}\hfill & \overline{S}=1-e^{-K\overline{S}},\hfill \\ \hfill & S=p\left(1-f_{ii}\right)\overline{S},\hfill \end{array}$$ [12]

and

$$\begin{array}{cc}\hfill & f_{ii}=\left(1-r\right)e^{kp\left(f_{ii}-1\right)}+r{e}^{kp\left(f_{ii}-1\right)}{e}^{K\left(e^{\overline{k}p\left(f_{ji}-1\right)}-1\right)},\hfill \\ \hfill & f_{ji}=e^{kp\left(f_{ii}-1\right)}{e}^{K\left(e^{\overline{k}p\left(f_{ji}-1\right)}-1\right)}{e}^{\overline{k}p\left(f_{ji}-1\right)},\hfill \end{array}$$ [13]

where $k$ and $\overline{k}$ are the average degree within each subnetwork and the average degree between the subnetworks, respectively. SI Appendix, Fig. S8 shows that analytical results for $S$ as a function of $p$ match the simulation results. Similarly, the critical threshold $p_c$ can be found numerically via the limit where $S\to 0$ using Eqs. 12 and 13, as shown in Fig. 4 A–C. For the limiting case of $r=1$, we obtain

$$p_c=\frac{\left(k+\overline{k}+\overline{k}K\right)-\sqrt{{\left(k+\overline{k}+\overline{k}K\right)}^2-4k\overline{k}}}{2k\overline{k}}.$$ [14]

Assuming the total number of links to be constant, we can define $\tilde{K}=k+r\overline{k}K$ (details in SI Appendix, Eq. 43) and find the optimal coupling value $r^{*}$ from Eqs. 12 and 13.

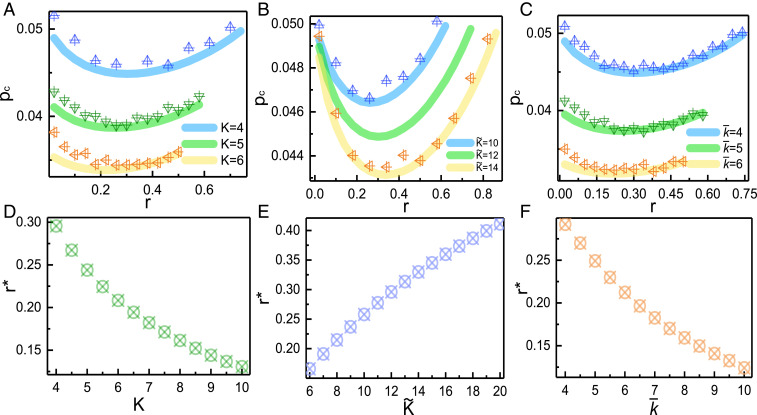
Fig. 4.

(A–C) Analytical predictions (thick lines) in comparison with simulation results (symbols) for the Poisson coupling pattern. We show $p_c$ as a function of $r$ for different $\overline{k}$, $\tilde{K}$, and $K$ based on Eqs. 12 and 13. The parameters are (A) $\tilde{K}=12$ and $\overline{k}=4$, (B) $K=4$ and $\overline{k}=4$, and (C) $\tilde{K}=12$ and $K=4$. (D–F) $r^{*}$ as a function of $K$, $\tilde{K}$, and $\overline{k}$, for parameters corresponding to those of A–C. Simulation results are averaged over 1,000 realizations with the network size given by $m\cdot N_i=10^4\cdot 10^6$.

Fig. 4 A–C shows that the system exhibits an optimal transition point at $r^{*}$ for all values of parameters of $K$, $\tilde{K}$, and $\overline{k}$. As $K$ increases, $r^{*}$ gradually decreases. A similar trend is seen with $\overline{k}$ increasing but as $\tilde{K}$ increases, the opposite occurs and $r^{*}$ actually increases as shown in Fig. 4 D–F. The results again demonstrate the existence of an optimal resilience that is valid for all parameter values. Here, for the simulation results, the value of $p_c$ is determined by the largest negative slope of $S$ as a function of $p$ (42).

Power-law coupling pattern.

The final case we consider is a power-law coupling pattern with a power-law exponent $\lambda$. Each subnetwork is connected to an average of $K$ other subnetworks, although some will be connected to far more due to the power-law distribution. Here we present results for the case where the connections within and between subnetworks follow a Poisson distribution with average degrees $k$ and $\overline{k}$. The analytical results can be found from Eqs. 3 and 4, respectively (see SI Appendix, Eqs. 54–56 and Fig. S10 for more details). The resulting solution is

$$\left\{\begin{array}{c}{S}_i=p\left[1-G_i\left(1-p\left(1-f_{ii}\right),1-p\left(1-f_{ji}\right)\right)\right],\hfill \\ S=\overline{S}\cdot S_i,\hfill \end{array}\right.$$ [15]

where $f_{ii}$ and $f_{ji}$ are described in SI Appendix, Eq. 54. We observe excellent agreement between the analytical and simulation results for different parameters in SI Appendix, Fig. S10. For the case of connections within and between subnetworks both following power-law distributions, see SI Appendix, Eqs. 57–59 and Fig. S11. The value of $p_c$ can be numerically obtained from Eq. 15 for $f_{ii}\to 1$. We observe a similar phenomenon to that of the previous cases, with an optimal $r^{*}$ existing for all values of $\lambda$, $\overline{k}$, and K, as shown in Fig. 5 A–C. In this case, we see that as $\lambda$ decreases, $r^{*}$ increases (Fig. 5D). The value of the optimal $r^{*}$ is shown for different values of the parameters $\overline{k}$ and $K$ in Fig. 5 E and F.

Fig. 5.

(A–C) Analytical predictions (thick lines) compared with simulation results (symbols) for a power-law coupling pattern with minimum degree $k_{\mathrm{m}\mathrm{i}\mathrm{n}}=2$ and maximum degree $k_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{1,000}$. The value of $p_c$ from Eq. 15 is shown as a function of $r$ for different parameters $\lambda$, $\tilde{k}$, and $K$. The parameters are (A) $\tilde{K}=6$, $\overline{k}=2.5$, and $K=2.0$; (B) $\tilde{K}=6$, $\lambda =4.5$, and $K=2.0$; and (C) $\tilde{K}=6$, $\lambda =4.5$, and $\overline{k}=2.5$. (D–F) We show $r*$ as a function of $\lambda$, $\overline{k}$, and $K$, with the other parameters as in A–C. Simulation results are averaged over 100 independent realizations with networks of size $m\cdot N_i=10^5\cdot 10^5$.

We note a discrepancy between simulation and theoretical results for this case in Fig. 5. This is because our analytical results assume a perfect power law, but the simulations rely on an approximation using defined limits. Furthermore, there also exist finite-size effects since the number of modules that can be formed is limited (due to limited computation power) since we need each module to have a reasonable large size.

Analysis of a Real Network.

We next consider an example of a real-world network of merger and acquisitions (M&A). Due to geopolitical factors, and economic frictions, financial acquisitions are often easiest to carry out locally. At the same time, with the increasing spread of capital on a global scale, most nations view greater openness as a vital component of the path to prosperity. Therefore, a critical question is how much global economic development should be supported as opposed to maintaining local development. This has become even more acute for policymakers due to the current coronavirus pandemic, which has dramatically interrupted international travel and highlighted risks of globalization (43–47). Furthermore, due to limited capital, companies and organizations are constantly forced to assess risks and benefits of M&A between and within regions to maximize synergies and growth.

Based on the above motivation, we applied our model to the two largest M&A regions, Asia and America, over the past 18 y. Here, we focus on the largest cluster of the M&A network, reflecting the key economic relationships. In this M&A network, nodes denote global companies or organizations and links represent M$\&$A transactions. (General information and statistics on this network are summarized in SI Appendix, Table S1). As in our theoretical model, we find a strong optimally resilient point for the M&A network between Asia and America (Data and Methods).

To keep the total number of connections in the network fixed, we rewire links from being within subnetworks to be between subnetworks. This changes the fraction of interconnected nodes, $r$, in the original network to be $r+\mathrm{\Delta }r$ (for details see Data and Methods). The inverse, i.e., changing links between the subnetworks to being within the subnetworks, will decrease the value of $r$ by $\mathrm{\Delta }r$. Fig. 6A shows $p_c$ as a function of $\mathrm{\Delta }r$ for the real M&A network and the network model with similar parameters. The results clearly show an optimal $r^{*}\approx 0.133$, which is consistent with the corresponding network model. This implies that the optimal resilience $r^{*}$ can be predicted from the simulations. The value of $p_c$ has been determined by the peak value of $S_2$, as shown in Fig. 6B. The comparison of $S$ and $S_2$ as a function of $p$ with different $\mathrm{\Delta }r$ for the network model is shown in SI Appendix, Fig. S13. Although economists have often promoted the superiority of open economic borders over closed ones, the question of exactly “how much to open up globally” has become a pivotal and divisive issue. From the perspective of resilience, we hope that our results offer decision makers some approaches to making a suitable decision between openness and protectionism.

Fig. 6.

(A) Comparison of simulation results on the real M&A network (red) and a network model for the critical threshold $p_c$ as a function of $\mathrm{\Delta }r$ for the same parameters. For the network model, the average $p_c$ value (light blue), the maximum value (pink), and the minimum value (blue) are obtained from 5,000 independent realizations. The simulation results for $p_c$ are determined using the location of the peak in $S_2$. (B) $S_2$ as a function of $p$ for different $\mathrm{\Delta }r$ for the real network. The parameters of the network model are similar to those of the real network. The simulated results of the real network are averaged over 5,000 independent realizations.

Discussion

We have introduced a modular interacting network, where a large number of subnetworks interact together following specific coupling patterns, where only some fraction, $r$, of nodes in each subnetwork are interconnected nodes, i.e., nodes that can have links to nodes in other subnetworks. We consider two general cases of coupling between the subnetworks, deterministic coupling patterns and random coupling patterns following some distribution. We determined analytically and via simulations the resilience of the systems having these various coupling patterns. Our results show that if the number of links is unchanged, there exists an optimal fraction of interconnected nodes, $r^{*}$, for which the system is most resilient. This optimal phenomenon exists for all of the coupling patterns we considered. Finally, an optimal coupling was also found in the real M&A network between Asia and North America. These results may provide theoretical support for decision makers to build robust economic systems. Additionally, we bridged the analytical framework from a single network to a modular interacting network from a more realistic perspective. Although our theory here is for studying the resilience of interconnected networks, it can be extended to study the resilience of broader coupling relationships like interdependent networks or multiplex networks.

Data and Methods

The real data are obtained from the Zephyr M&A database (48). The data mining and analysis are processed using the igraph package of the R software (49). To simulate changes in the real network, we randomly choose a $\mathrm{\Delta }r$ fraction of nodes that were not interconnected to become interconnected nodes or vice versa. We then update the fraction of interconnected nodes to be $r$ = $r_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}+\mathrm{\Delta }r$, with $r=r_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}$ for $\mathrm{\Delta }r=0$. To maintain a fixed number of total links, we rewire intralinks to become interlinks by replacing the intralinks of the $\mathrm{\Delta }r>0$ fraction of nodes within each subnetwork to randomly connect to the $r$ fraction of interconnected nodes in the other subnetwork. Similarly, for $\mathrm{\Delta }r<0$, total links are kept fixed by randomly rewiring interlinks connecting the $\left|\mathrm{\Delta }r\right|$ fraction of nodes to become intralinks. We then built the network model to match the parameters of the real network. The datasets generated and analyzed in the current study follow the database utilization guide of the data provider (50).

Data Availability

Some study data are available upon request.