COVID-19 pandemic decision support system for a population defense strategy and vaccination effectiveness

Abstract

The year 2020 ended with a significant COVID-19 pandemic, which traumatized almost many countries where the lockdowns were restored, and numerous emotional social protests erupted. According to the World Health Organization, the global epidemiological situation in the first months of 2021 deteriorated. In this paper, the decision-making supporting system (DMSS) is proposed to be an epidemiological prediction tool. COVID-19 trends in several countries and regions, take into account the big data clouds for important geophysical and socio-ecological characteristics and the expected potentials of the medical service, including vaccination and restrictions on population migration both within the country and international traffic. These parameters for numerical simulations are estimated from officially delivered data that allows the verification of theoretical results. The numerical simulations of the transition and the results of COVID-19 are mainly based on the deterministic approach and the algorithm for processing statistical data based on the instability indicator. DMSS has been shown to help predict the effects of COVID-19 depending on the protection strategies against COVID-19 including vaccination. Numerical simulations have shown that DMSS provides results using accompanying information in the appropriate scenario.

1. Introduction

The status of decisions accepted by countries to minimize the effects of COVID-19 pandemic is determined by the use of information-modeling tools (Varotsos et al., 2018, Das et al., 2021) which helps in the range of risks depending on the administrative and social resources. The decision-making system as one of the possible statistical tools can promote the successful implementation of pandemic trend management according to the accepted strategy of minimizing losses within the existing socio-economic capacities of a country or region (Krapivin et al., 2017). The administrative level of decision-making in each country is to support the appropriate response recommended by the decision making system, the operation of which is based on epidemiologically verified monitoring data whose architecture is represented as a multi-scale stochastic process with a detailed structure. All officially recorded data cover potential COVID-19 results as statistical series, the analysis of which helps to test and predict a trend in each pandemic. Unfortunately, many efforts made by many countries to reduce the number of infections at present have little effect, not depending on vaccination (Wang et al., 2020).

Early diagnosis and understanding of the reasons for making decisions to control the pandemic situation requires operational statistical analysis of the delivered information using algorithms for episodic situations when there are limited statistics for some unpredictable variables. In this case, classical statistical methods are used when the statistical data have fixed characteristics and sequential procedure is used in the opposite case (Krapivin et al., 2012, Krapivin et al., 2015). Many governments extend or reduce the administrative control of socio-economic processes according to the increase or decrease of previously defected peoples, respectively. Algorithms and models developed by many authors are used in practice to analyze limited demonstrative causes, when the diagnosis and prediction of the spread of coronavirus disease are evaluated in the context of the administrative role in controlling management parameters [Ivorra et al., 2020, Varotsos and Krapivin, 2020, Varotsos et al., 2021a, Varotsos and Cracknell, 2020]. The complexity of pandemic responses is determined by the variety of geographical location, political system, economic development, demographic difference, and social orientation (Renzaho, 2020, Tuncer et al., 2021). Many authors use existing universal indicators such as Human Development Index (HDI), Food Production Index (FDI), Gross Domestic Product (GDP), Gender Parity Index (GPI), etc. to take these parameters into account (Lippi et al., 2020).

Paul et al. (2021) examined the modeling aspects of the corona pandemic and showed the uncertainties of epidemiological dynamic models whose equation has unknown or incorrect parameters. Effective delimitation between the lockdown and unlock phases in government decisions is achieved by using two values SSIT (steady state initiation time) and SSIS (steady state initiation size) whose values help identify the inherent phase. Gupta et al. (2021) considered an emotion care model using COVID-19 pandemic situation in India. This model helps health organizations understand people’s emotional health and interpret people’s reactions to government solutions. Muñoz-Fernández et al. (2021) show that a non-autonomous SIR type model with non-constant parameters helps to assess the mortality rate and to search for asymptotic value depending on population mobility, social distancing and massive use of protection material.

Coronavirus vaccines aim to reduce the spread rate of the virus, which can help to improve the lifestyle of people in many countries. Menon et al. (2021) developed a nonlinear deterministic model describing correlations between susceptible, exposed, quarantined, infected, isolated and recovered components that helps to analyze the effect of vaccination in the case of Pakistan. Mahrouf et al. (2021) demonstrated how complex mathematical model with deterministic and stochastic components provides narrow possibilities for predicting epidemiological trends. The search of an effective decision is usually made by producing scenarios what is most likely to happen.

The main contribution of this paper is how to use official COVID-19 pandemic data to predict trends in virus spreading. The method is designed to create a decision-making support system (DMSS) based on the sequential analysis procedure to assess the corona virus transition probability between sites and the mathematical model.

2. Materials and method

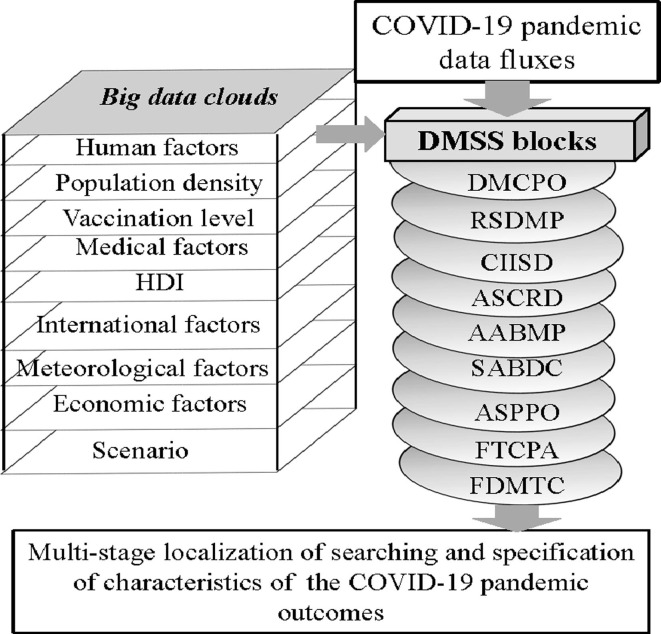
Analysis of existing epidemic data in many countries confirms the weak effectiveness of different social restrictions that depend mainly on financial capabilities. It is obvious that forecasting the results of the COVID-19 pandemic by statistical analysis of data sets requires additional knowledge of different indicators to reflect the socio-economic characteristics of human society and to take into account geophysical, demographic and medical aspects. The decision-making supporting system (DMSS) analyzes current statistical data on the epidemiological situation in the study area using the method of sequential analysis (Efstathiou and Varotsos, 2012, Krapivin et al., 2012, Sukov et al., 2008, Varotsos et al., 2013, Varotsos et al., 2019, Varotsos et al., 2020). Fig. 1 represents the DMSS structure and its functions. The DMSS foresees the existence of adequate statistics on COVID-19 outcomes and the big data clouds recorded by various sources and reflect environmental, demographic, economic and medical factors. As shown in Table 1 , the DMSS items solve specific tasks that assess trends in COVID-19 results. Big data clouds and the technology for processing them to minimize the level of uncertainty and improve predictive features (Varotsos, Krapivin, 2017).

Fig. 1.

Principal functional structure of the decision-making supporting system aimed at forecasting the COVID-19 pandemic outcomes.

Table 1.

The block-functional structure of DMSS.

Block	The block function
DMCPO	Dynamic model for COVID-19 pandemic outcomes.
AABMP	Algorithm for assessing basic management parameters.
RSDMP	Realization of the sequential decision-making procedure.
SABDC	Synchronization algorithm for big data clouds.
CIISD	Calculation of instability indicator for statistical data fluxes.
ASPPO	Assessment of statistical parameters for the pandemic outcomes using the randomized approximation.
ASCRD	Analysis of statistical characteristics for the reported data during a given time period and their possible renewal with consideration of other time period.
FTCPA	Forecasting trend COVID-19 pandemic aftereffects.
FDMTC	Final decision making on trends in COVID-19 pandemic outcomes over a given time period and in a selected scenario.

Official traditional statistics on the effects of the COVID-19 pandemic on human society covers population groups not depending on the region, but the classification of individuals differs when forecasting algorithms are proposed. Ndaïrou et al. (2021) suggested eight epidemiological classes of individuals that could be key components for the appropriate model. An analysis of other publications shows that such detailed classification of individuals exposed to COVID-19 requires additional, sometimes inaccessible information, which may reduce the reliability of the expected results (Gupta et al., 2021, Muñoz-Fernández et al., 2021, Paul et al., 2021, Varotsos et al., 2021a, Memon et al., 2021). Traditional fractional pandemic models cover the following classification groups of individuals, which promotes decision makers to select effective set of national restrictions depending on the resources available.

Susceptible individuals (S) are peoples who have not hide immunity against COVID-19 obtained at the expense of vaccination or natural existence antibodies. The dynamics of susceptible individuals S_Ξ in country Ξ is represented by the following equation:

$$S_{\mathrm{\Xi }}\left(t+\mathrm{\Delta }t\right)=S_{\mathrm{\Xi }}\left(t\right)-\frac{S_{\mathrm{\Xi }}\left(t\right)}{M_{\mathrm{\Xi }}}\nu p\mathrm{\Delta }t$$ (1)

where ν ∈ [0,1] quantifies the immunization coefficient, p is the probability of the human-to-human transitions at time t per unit time (days) per person, Δt is the time step for calculations, M_Ξ = N_Ξ(1-τ_Ξ), N_Ξ is the total number of individuals in the population of the country Ξ, τ_Ξ is a vaccination indicator.

Infected individuals (I) are people who have detectable symptoms of the virus. Some people become infected and do not develop any symptoms or feel unwell. Their dynamics can be described by the traditional equation:

$$I_{\mathrm{\Xi }}\left(t+\mathrm{\Delta }t\right)=I_{\mathrm{\Xi }}\left(t\right)\left\{1+p\frac{S_{\mathrm{\Xi }}\left(t\right)}{M_{\mathrm{\Xi }}}-c\left(t\right)\right\}{J}_{\mathrm{\Xi }}\left(t\right)\mathrm{\Delta }t$$ (2)

where c is the recovery rate at time t (c = R_Ξ /I_Ξ), J _Ξ is instability indicator reflecting the statistical character of official COVID-19 pandemic data.

Recovered individuals (R_Ξ) are the category of individuals that are transmitted to susceptible individuals and hence, change their status to infectious. This category of individuals is supposed to have an antibody level that is medically acceptable at time t. The modelling representation of the recovery process is performed through a digital equation:

$$R_{\mathrm{\Xi }}\left(t+\mathrm{\Delta }t\right)=R_{\mathrm{\Xi }}\left(t\right)+c\left(t\right)q\left(t\right)\frac{I_{\mathrm{\Xi }}\left(t\right)}{M_{\mathrm{\Xi }}\left(t\right)}\mathrm{\Delta }t$$ (3)

where q(t) indicates the medical support indicator at time t.

Dead individuals (D _Ξ) determine the death rates of the COVID-19 pandemic per country Ξ reflecting the effectiveness of socio-economic and management solutions for the defense of the population through appropriate decisions concerning the probability of reducing p. Finally, the following equation describes the total number of dead individuals:

$$D_{\mathrm{\Xi }}\left(t+\mathrm{\Delta }t\right)=D_{\mathrm{\Xi }}\left(t\right)+d\left(t\right)\left[1-q\left(t\right)\right]\frac{I_{\mathrm{\Xi }}\left(t\right)}{M_{\mathrm{\Xi }}\left(t\right)}\mathrm{\Delta }t$$ (4)

Official statistics series Z= (S, I, R, D) represent typical data with deterministic and stochastic components that need to introduce the instability factor J_Ξ for country Ξ to correct the model results. To formalize this procedure the algorithm for evaluating these instability data is proposed:

$$J_{\mathrm{\Xi }}=\frac{1}{s(T-N)}\sum _{j=1}^{T-N}\sum _{i=1}^s{\beta }_i{\mu }_i(t_j)$$ (5)

where N is the quasi-stationary time interval for calculating the average values of the official statistics; T is the time interval for evaluating the indicator J_Ξ ; s is the number of registered parameters (in considered case s = 4); β_i indicates the weight coefficient for the i-th characteristic;

$${\mu }_i\left(t_j\right)=\left\{\begin{array}{c}1\text{when}\mathrm{\Delta }{z}_i\left(t_j\right)·\mathrm{\Delta }{z}_i\left(t_{j+1}\right)⩽0,\hfill \\ 0\text{when}\mathrm{\Delta }{z}_i\left(t_j\right)·\mathrm{\Delta }{z}_i\left(t_{j+1}\right)>0\hfill \end{array}\right)$$ (6)

where

$$\mathrm{\Delta }{z}_i\left(t_j\right)=\frac{1}{N}\sum _{l=T\left(k-1\right)+t_j}^{T\left(k-1\right)+t_j+N-1}{z}_i\left(t_l\right)-z_i\left(T\left(k-1\right)+t_j+N\right)$$ (7)

$$\mathrm{\Delta }{z}_i\left(t_{j+1}\right)=\frac{1}{N}\sum _{l=T\left(k-1\right)+t_j+1}^{T\left(k-1\right)+t_j+N}{z}_i\left(t_l\right)-z_i\left(T\left(k-1\right)+t_j+N+1\right)$$ (8)

An overview of the situation with the spread of COVID-19 in different countries and territories helps to understand this solution of the main task to assess the effectiveness and usefulness of government actions needs in conjunction with dynamic and statistical tools. The mathematical model as the DMSS component demonstrates a trend in the appropriate statistical row. Under this, the {Z_ij} rows of official data on infected, recovered and dead represent formal statistical analysis samples whose traditional methods allows us to parameterize their trends over a limited time interval kΔt. Therefore, corrected components in equations (1)-(4) are

$$\mathrm{\Delta }{Z}_{\mathit{kj}}=Z_{k+1j}-\frac{1}{k}\sum _{i=1}^k{Z}_{\mathit{ij}}=\mathrm{\Delta }{T}_{\mathit{kj}}+\frac{1}{k}\sum _{i=1}^k\mathrm{\Delta }{\xi }_{\mathit{ij}}$$ (9)

where the j index corresponds to one of the COVID-19 components (S,I,R,D) and T_kj and ξ_ij are deterministic and stochastic components, respectively.

3. Results and discussion

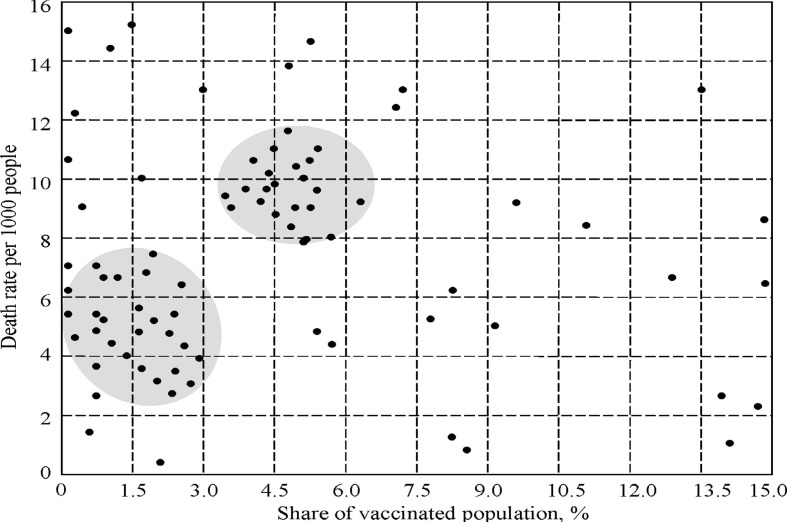
The availability of coronavirus data helps to use the deterministic and statistical tools for spatio-temporal modeling of existing epidemic phenomena and to assess the effectiveness of management efforts to reduce losses, including vaccination. The DMSS provides an estimate of quarantine parameters and management strategies when considering a specific scenario. It is expected that the proper eradication of COVID-19 is possible only through successful vaccinations in the entire human population. The results of Fig. 2 show that the correlation between the level of the vaccinated population and deaths is not consistently dependent. Indeed, there are two specific clusters that are distinguished by the controversial parameters. The comparison of these clusters allows the conclusion that the disease status of the specific country depends on both the vaccination level and other indicators such as Gross Domestic Product (GDP) and Human Development Index (HDI) (Khazaei et al., 2020, Lippi et al., 2020). For example, the relations between death rates, GDPs and HDIs between India and Romania are 0.52, 0.29 and 0.77, respectively, confirming the diverse relationship between the clinical outcome of COVID-19 and socio-economic resources of country. Varotsos et al. (2021) have shown that the correlation between the number of deaths and HDI is approximately linear: D(HDI) = -26.16 + 79.32 HDI. On the other hand, the disproportionately high COVID-19 outcomes in countries examined in Fig. 2 need more detailed analysis that can help improve the conclusion about vaccination efficacy (Singh et al., 2021).

Fig. 2.

Dependence of the death rate on the level of the population vaccination.

The DMSS functions enable cumulative data generation in COVID-19 taking into account big data clouds and official coronavirus pandemic data. The specific examination of the pandemic situation in a given country requires the synthesis of a scenario that regulates all restrictions, including internal and external movements, masks use, travel and transportation services, quarantine, remote work, etc. Many authors pay close attention to the role of passenger flows at the pandemic level. It is estimated that passengers arriving in a country explain about 14.2% of the variance in the distribution of COVID-19 outcomes per million inhabitants (Ribeiro et al., 2020). Further results of this study correspond to the following PEP scenario:

• passengers who arrived in a country are directed to quarantine, not depending on the positive test.

• education structures, many services and industrial organizations operate without restrictions, only equally binding for all.

• public health inspectors examine individuals locally and when COVID-19 symptoms are detected the person is quarantined.

A statistical perspective to take into account various COVID-19 pandemic data when conducting simulation experiment is provided by the instability indicator J_Ξ (t) the dynamics of which certainly reflects COVID-19 pandemic trends. Table 2 shows the trends in the pandemic instability indicator for different countries. The instability level does not exceed almost 50% in many countries for a long time. The instability of the pandemic data is increasing worldwide in 2021 by 8.5 ± 3.7% which warns and suggests a more detailed analysis of the big data related to COVID-19 pandemic cases. The calculation and interpretation of pandemic data requires knowledge of different indicators, the values of which depend on many factors. Table 3 represents the evaluations of the indicators used in equations (1)-(4).

Table 2.

COVID-19 pandemic instability indicator J_Ξ as a precursor to the range of outcomes.

Country, Ξ	Date 2021
	25.01	15.02	25.02	15.03	30.03	15.04	30.04	15.05
Australia	0.135	0.167	0.293	0.262	0.199	0.175	0.168	0.171
Brazil	0.312	0.344	0.487	0.496	0.463	0.517	0.525	0.529
Canada	0.232	0.261	0.354	0.373	0.387	0.302	0.309	0.312
France	0.263	0.288	0.391	0.392	0.377	0.408	0.427	0.444
Germany	0.403	0.451	0.498	0.523	0.496	0.493	0.501	0.488
Italy	0.254	0.366	0.398	0.401	0.399	0.404	0.434	0.469
Japan	0.202	0.197	0.203	0.312	0.334	0.279	0.207	0.198
Russia	0.299	0.303	0.326	0.349	0.472	0.488	0.491	0.511
Spain	0.417	0.399	0.422	0.386	0.433	0.393	0.453	0.442
Turkey	0.176	0.201	0.217	0.249	0.279	0.282	0.276	0.269
USA	0.354	0.389	0.453	0.476	0.512	0.532	0.541	0.554
World	0.389	0.395	0.401	0.422	0.433	0.485	0.576	0.583

Table 3.

Average values of the COVID-19 transition indicators from different regions.

Region	p	c	ν	q
Australia	0.059	0.058	0.37	0.77
Belarus	0.087	0.012	0.72	0.82
Brasil	0.084	0.054	0,34	0.58
China	0.068	0.021	0.63	0.75
France	0.088	0.032	0.39	0.79
Germany	0.089	0.021	0.42	0.81
Greece	0.087	0.111	0.54	0.76
Italy	0.097	0.130	0.44	0.72
Japan	0.088	0.014	0.45	0.79
Russia	0.077	0.019	0.68	0.74
South Africa	0.086	0.012	0.41	0. 57
USA	0.096	0.019	0.31	0.72
World	0.095	0.008	0.45	0.68

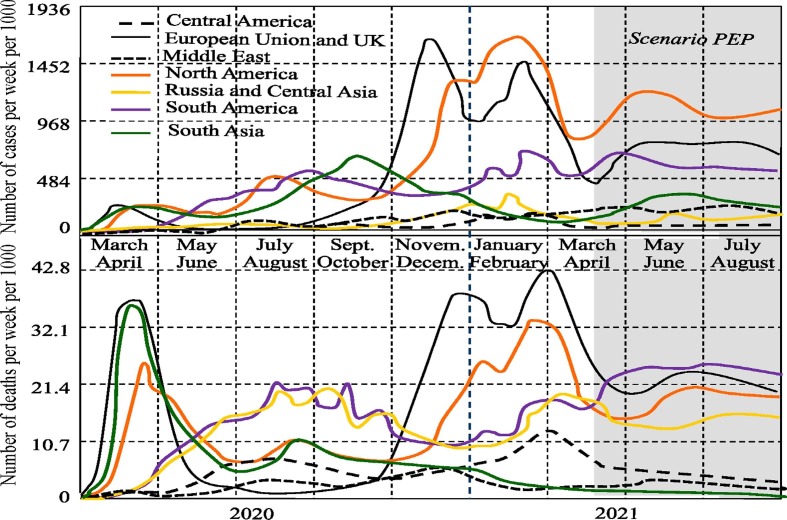
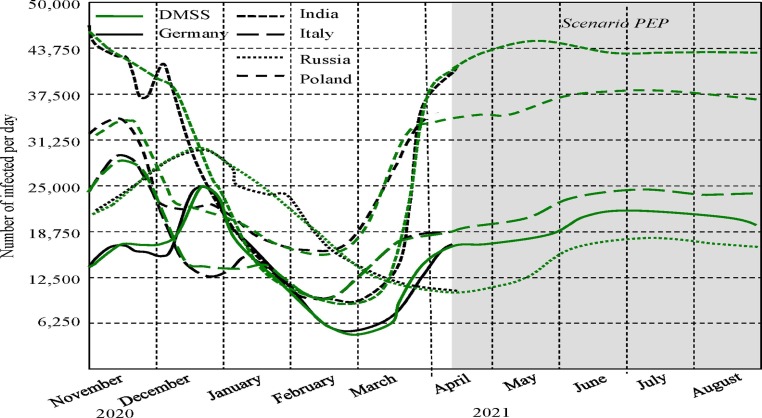
Let us consider and analyze the modeling results for the initial data on March 23, 2021 and assess the forecast trends in COVID-19 spread when all the examined regions follow the PEP scenario. Fig. 3 shows that in this case the changes in the pandemic outcomes stabilize significantly and the booms of results are not expected until September 2021. The detailed analysis of the modeling results shows that this stabilized period occurred due to vaccination and quarantine for airline-passengers. Medical control also plays a key role in limiting the spread of virus. Finally, the results of PEP scenario demonstrate that the transmission of the COVID-19 pandemic is mainly caused by human contacts, the restrictions of which contribute significantly to reducing aftereffects. The calculations reveal the disparity between the restrictions covered by PEP and human-to-human contacts in traditional life.

Fig. 3.

Trends in the number of cases and deaths from areas with a prognosis in the nearest future.

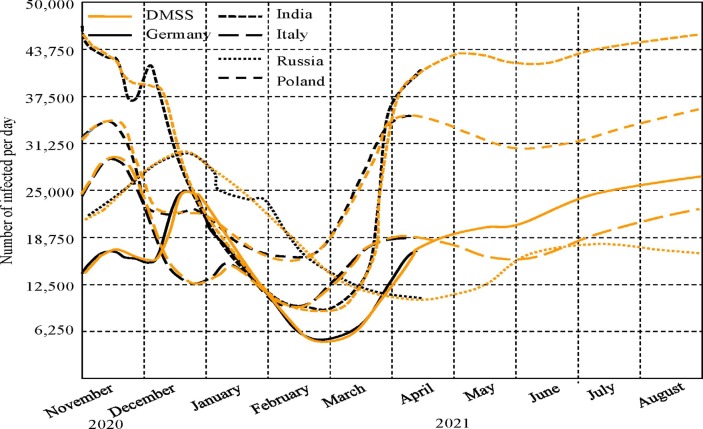
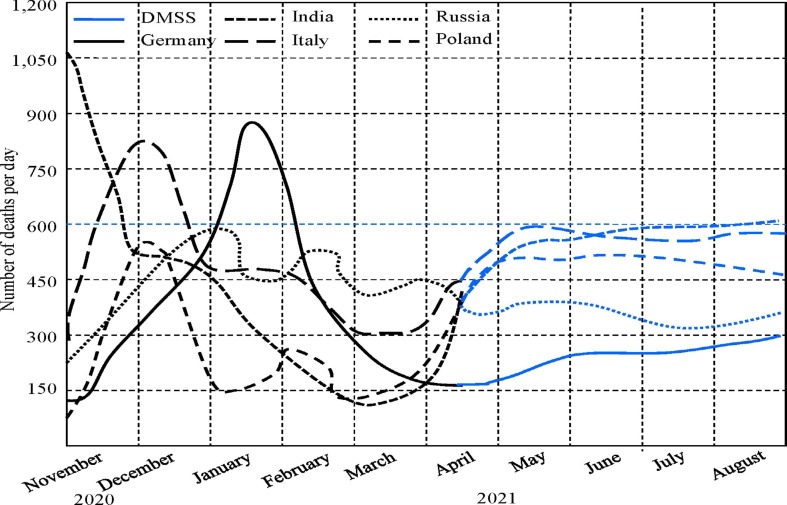
Unfortunately, many countries follow the traditional strategy of reducing the effects of the COVID-19 pandemic, which always gives similar results. Fig. 4 characterizes such results for many countries provided that traditional restrictions are followed. For example, on March 31, 2021 the French government announced a third national lockdown that began on April 3, 2021. Other national restrictions related to the COVID-19 pandemic make virtually no distinction except for restaurants, school closures, children organizations, museums, etc.

Fig. 4.

DMSS verification and forecast by August 2021 at individual vaccination levels from countries: Germany 5.2%, India 0.7%, Italy 5.7%, Russia 4.4% and Poland 5.5%.

The lockdown restrictions set in Poland include closure parks, boulevards, beaches, hairdressers and beauty salons, Legends accepted in countries considered in Fig. 4 are taken into account by the DMSS. The comparison of simulation results depicted in Fig. 5 shows that total lockdown restrictions in practice do not improve the pandemic results provided by the DMSS in the PEP scenario. Moreover, in the case of Fig. 4 the symptoms of the next wave are shown in contrast to the results illustrated in Fig. 5.

Fig. 5.

The prognosis of infected cases occurred after April 2021, when the examined countries decide to use the PEP scenario.

One of the expected effective measures to end the pandemic is the vaccination using a vaccine production technology that requires significant discussions between countries, which in fact does not start positive results from the beginning of 2021. The results of Fig. 2 show the existence of high uncertainty in the possible conclusions related to the COVID-19 outcomes depending on the vaccination level. This uncertainty also arises from the data in Table 4 which show the existence of countries where the effects of the pandemic are minimal.

Table 4.

Comparison of some population characteristics and effects of the COVID-19 pandemic.

Country	GDP per capita	HDI	Population density, humans/km2	Vaccination level, % (April)	Number of infected per day, 2021
					May	June	July	August
USA	66,678	0.92	36	32.15	34,932	34,987	35,078	35,145
Germany	49,548	0.939	235	11.98	20,000	21,625	25,000	26,250
Canada	48,137	9.922	4	15.47	8091	8326	8402	8531
France	43,959	0.891	119	13.64	14,697	14,946	15,623	15,391
Japan	43,597	0.915	334	0.76	2522	2714	3047	3082
United Kingdom	42,915	0.92	281	46.52	3947	3894	3956	4083
Italy	34,629	0.883	200	12.85	16,875	16,875	20,000	21,875
South Korea	34,000	0.906	512	1.95	506	568	597	602
Greece	22,226	0.872	79	11.73	1863	1904	2032	1912
Spain	32,026	0.893	92	12.60	13,419	13,564	13,607	13,924
Poland	17,149	0.872	121	0.01	16,740	17,354	18,196	17,492
Russia	11,428	0.824	9	5.19	12,475	16,875	18,125	16,875
China	10,710	0.758	149	38.8	23	22	21	16
Brazil	9,638	0.761	25	8.07	28,645	32,183	31,672	30,801
Turkey	9,519	0.806	109	11.62	30,021	32,163	31,291	32,208
Peru	7,319	0.759	26	1.75	14,624	15,033	14,632	14,944
Morocco	3,456	0.676	84	11.79	575	603	608	614
Vietnam	2,876	0.693	296	0.05	3	2	1	0
India	2,338	0.647	424	5.24	48,750	48,375	50,169	51,221

4. Conclusions

Understanding the results of the status of the COVID-19 spread around the world requires an examination of the country's set of characteristics, such as political system, geography, population size, and economic development, which allows for the improvement of the tools used for the study of this status. . This paper proposes the DMSS, a novel decision making system for the regional and global strategy for dealing with the COVID-19 pandemic, taking into account existing information resources on specific national and sub-national situations and capacities expressed in different social restrictions such as physical distancing, masks, movement restrictions, vaccination, etc. The numerical results of this study show that the existing negative tendencies could be redirected to the favorable status at the expense of the weighed revision of the restrictions. The use of DMSS helps to achieve very realistic outcomes and to produce predictions in several countries, which supports a motivation to use the PEP scenario where many restrictions are considered unjustified (Varotsos et al., 2021b). A confirmation of this conclusion is given in Fig. 6 and Table 4.

Fig. 6.

Number of deaths when the vaccination level of individuals in the country increases linearly up to 25% during April-August 2021.

Numerous existing publications on the COVID-19 pandemic suggest useful models and conclusions about pandemic outcome trends, but the constructive results of these publications are not considered by many government as a rational guideline for step-by-step decision-making on choosing an effective strategy for the population defense. Coronavirus trends continue to bring significant disruptive changes to the lives of people in many countries.

The mathematical model and the big data processing algorithm as DMSS components provide the analysis of complex uncoordinated data fluxes that help to find the more informative data packages and speed up the integration process for understanding trends in COVID-19 results. The availability of coronavirus data helps to use deterministic and stochastic tools for spatio-temporal modeling of existing epidemic phenomena and to assess the effectiveness of management efforts to reduce losses including vaccination. The results presented here show how DMSS provides both the reconstruction and the prognosis of pandemic data when an accompanying information is immediately taken into account and in total volume.

Certainly, the deterministic and stochastic tools developed in this study to predict pandemic trends need to be improved due to the use of optimal control theory methods, including the modernization of the instability indicator and its immediate use for formal data classification on the range of their reliability. One of main task solution required in the near future is to evaluate the effectiveness of vaccination taking into account different levels of this action in different countries.

In conclusion, the results of this study demonstrate that DMSS helps to understand and predict how an infectious disease spreads in the world and how control of restricting factors affects the dynamics of COVID-19 outcomes. Moreover, the DMSS results confirm that COVID-19 pandemic trends are not directly dependent on the country’s economic status. This problem needs further research.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.