Skip to main content
PMC home page
Chemical Science logoLink to Chemical Science
. 2021 Jan 29;12(10):3489–3496. doi: 10.1039/d0sc04978f

A microscopic description of SARS-CoV-2 main protease inhibition with Michael acceptors. Strategies for improving inhibitor design†

Carlos A Ramos-Guzmán 1, J Javier Ruiz-Pernía 1,✉, Iñaki Tuñón 1,✉
PMCID: PMC8179461  PMID: 34163622

Abstract

The irreversible inhibition of the main protease of SARS-CoV-2 by a Michael acceptor known as N3 has been investigated using multiscale methods. The noncovalent enzyme–inhibitor complex was simulated using classical molecular dynamics techniques and the pose of the inhibitor in the active site was compared to that of the natural substrate, a peptide containing the Gln–Ser scissile bond. The formation of the covalent enzyme–inhibitor complex was then simulated using hybrid QM/MM free energy methods. After binding, the reaction mechanism was found to be composed of two steps: (i) the activation of the catalytic dyad (Cys145 and His41) to form an ion pair and (ii) a Michael addition where the attack of the Sγ atom of Cys145 to the Cβ atom of the inhibitor precedes the water-mediated proton transfer from His41 to the Cα atom. The microscopic description of protease inhibition by N3 obtained from our simulations is strongly supported by the excellent agreement between the estimated activation free energy and the value derived from kinetic experiments. Comparison with the acylation reaction of a peptide substrate suggests that N3-based inhibitors could be improved by adding chemical modifications that could facilitate the formation of the catalytic dyad ion pair.

Inhibition of SARS-CoV-2 3CL protease by a Michael acceptor is studied using classical and QM/MM simulations. Results point out to a transition state with a key water molecule stabilizing the catalytic dyad and assisting the protonation step.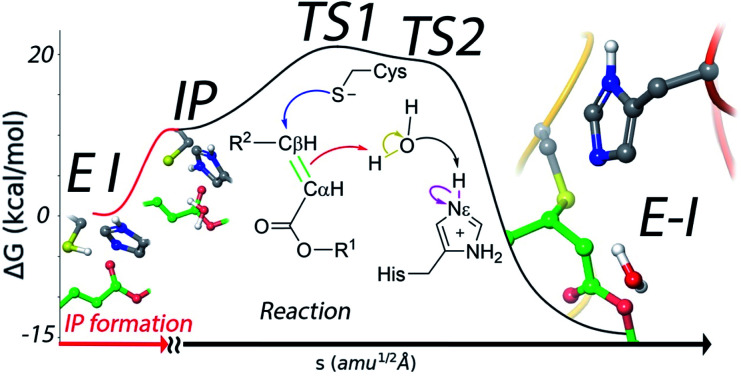graphic file with name d0sc04978f-ga.jpg

Introduction

A powerful strategy to fight against infectious diseases is the development of drugs to inhibit the activity of one of those enzymes that are crucial in the life cycle of the pathogenic agents. This is the case of the main protease, or 3CL protease (3CLpro), of coronaviruses in general and of SARS-CoV-2 in particular. The 3CLpro cleaves the polyproteins translated into the infected cells to produce functional proteins for the coronavirus.1 As in other cysteine proteases, the proteolysis is performed in the active site of 3CLpro by a Cys/His catalytic dyad, the substrate cleavage taking place between Gln at the P1 position of the peptide chain and a Gly/Ala/Ser at the P1′ one.2 This enzyme plays an essential role during the replication of the virus and has no closely related homologues in human cells, making it in an attractive drug target.3

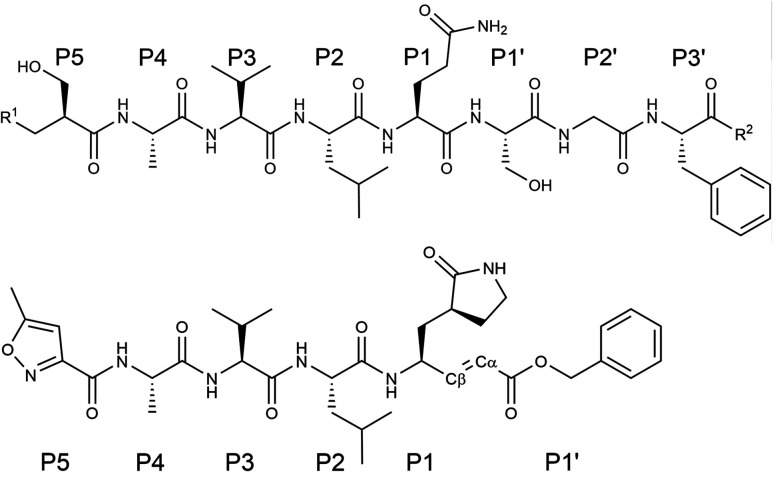
Several lead compounds have already been demonstrated to be effective at inhibiting the activity of SARS-CoV-2 3CLpro, including Michael acceptors,4 α-ketoamides,5 carbamoyl derivatives6 and aldehydes.7 N3 is a Michael acceptor, an α,β-unsaturated carbonyl compound, that was designed as an inhibitor of the 3CLpro of several coronaviruses, including SARS-CoV and MERS-CoV8 and that has been demonstrated to have inhibitory activity against the ortholog enzyme of SARS-CoV-2.4 This compound has a chemical structure similar to that of a peptide, the natural substrate of the enzyme (see Fig. 1). However, the microscopic details of 3CLpro inhibition by N3 are still unclear.

Fig. 1. Chemical structure of a peptide substrate of SARS-CoV-2 3CLpro (top) and of the N3 inhibitor (bottom). The scissile bond of the peptide is placed between Gln-P1 and Ser-P1′.

Fig. 1

Open in a new tab

Kinetic experiments showed that N3 is a potent time-dependent irreversible inhibitor of SARS-CoV-2 3CLpro that follows the next kinetic scheme:4

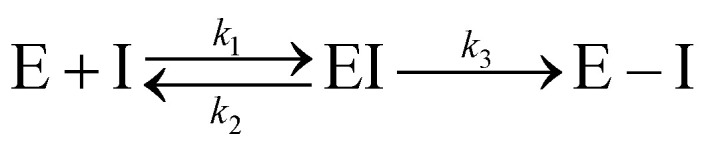graphic file with name d0sc04978f-t1.jpg 1

In a first stage, the inhibitor reversibly binds into the active site of the enzyme forming a noncovalent complex (EI) with a dissociation constant (KI = k2/k1). Afterwards, the inhibitor irreversibly reacts with the enzyme, with a rate constant k3, to give a stable acylenzyme (E–I). This acylenzyme is characterized by the formation of a covalent bond between the Sγ atom of Cys145 and the Cβ atom of the inhibitor, as observed in the X-ray structure of the inhibited enzyme.4

N3, or any of the other 3CLpro inhibitors characterized until now, can be used as a starting point for the development of an efficient drug for the treatment of COVID-19. One of the steps in this development is the optimization of the thermodynamic (binding) and kinetic properties of the inhibitor. This improvement should be based in the microscopic knowledge of the inhibition process, which in part relies on the details provided by simulations of the enzyme and the complex formed with the inhibitor. The analysis of the reaction step requires of the use of QM/MM potentials, which are adequate to describe bond forming and breaking processes. QM/MM techniques have been already employed to study, at microscopic level, the SARS-CoV-2 3CLpro hydrolysis mechanism with a natural peptide9 and a modified peptide having a fluorescent tag as leaving group10 as substrates. We here use these methods to investigate the inhibition process of this enzyme by N3. The atomistic details provide here could be applied to improve the design of future drugs based in this compound.

Results and discussion

As detailed in the Methods section (see ESI†), we carried out classical Molecular Dynamics (MD) simulations of the non-covalent enzyme–inhibitor (EI) complex built from the 7BQY PDB structure.4 A total of 4.0 μs (2 replicas) of classical MD simulation were run using the AMBER19 GPU version of pmemd.11,12 We then explored the reaction mechanism for the formation of the covalent acylenzyme complex (E–I, see eqn (1)) using QM/MM simulation methods at the hybrid B3LYP/MM level,13,14 including D3 dispersion corrections,15 with the 6-31+G* basis set, as explained in Methods section. The string-method16,17 was employed to find the reaction minimum free energy paths (MFEP) on multidimensional free energy surfaces defined by a set of Collective Variables (CVs) in which we included those geometrical parameters (bond lengths) suffering noticeable changes during the process. A path-CV (s) that measures the advance along the MFEP was defined to trace the corresponding free energy profiles. Umbrella sampling18 along a distinguished coordinate was used to obtain the free energy difference between the neutral and ion pair (IP) forms of the catalytic dyad (Cys145/His41) within the same QM/MM approach. This methodological combination was previously used in the study of the acylation and de-acylation steps of a natural peptide substrate by SARS-CoV-2 3CLpro with results in excellent agreement with experiments.9 In that work we used the string method to explore the reaction mechanism, with different starting points and initial guesses for the path. In the string method, the initial and final nodes are allowed to evolve until they reach free energy minima while the rest of nodes trace a MFEP between them. After all our attempts, we found two kinds of mechanisms: either the reaction goes through a metastable IP intermediate, where the Cys–His proton transfer precedes the dyad attack on the substrate or the reaction proceeds without formation of the ion pair by means of a direct proton transfer from the catalytic cysteine to the substrate; presenting this last mechanism a significantly higher activation free energy.9 The existence of an IP dyad is compatible with the experimental observations made during the kinetic characterization of the homologue protease of SARS-CoV (96% identical), in which a proteolysis mechanism involving the IP formation was proposed on the basis of the pH-inactivation profile and the analysis of solvent isotope effects.19 We have then here explored similar reaction mechanisms for the SARS-CoV-2 3CLpro protease inactivation with N3. It must be also noticed that, in a recent work published during the revision of this manuscript, Moliner and coworkers explored SARS-CoV-2 inhibition by N3 and related inhibitors finding also a reaction mechanism that involves first the formation of the IP followed by the formation of the enzyme–inhibitor covalent bond.20

The noncovalent EI complex

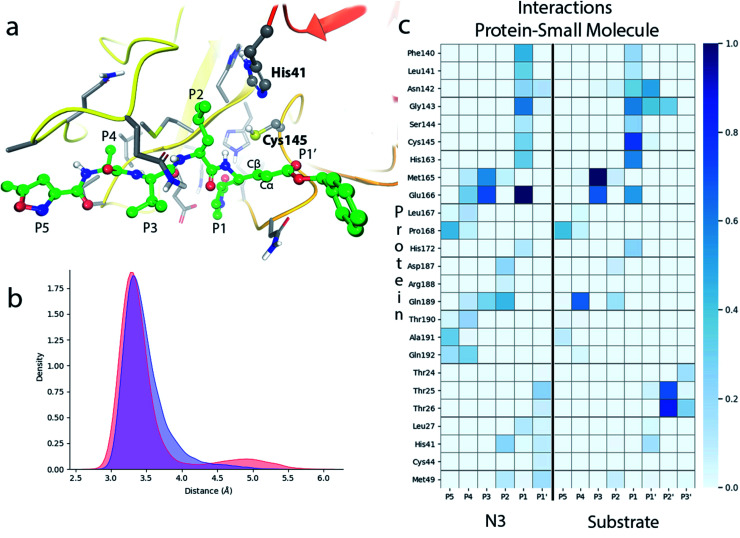
N3 has a chemical structure that resembles that of a peptide substrate (see Fig. 1). As such, the pose found for N3 in the active site of SARS-CoV-2 3CLpro during our MD simulations is also quite similar to that described for the peptide.9Fig. 2a shows the N3 inhibitor in the active site of one of the protomers of the dimeric enzyme. Analysis of root-mean-square-deviation (RMSD) of the protein and the inhibitor shows that this configuration of the system was stable during the simulated time (see Fig. S1†). In this complex, the Sγ atom of Cys145 remains close to the Cβ atom of N3. According to the probability distribution shown in Fig. 2b, the most probable distance between these two atoms is 3.3 Å (there is a small fraction of configurations with larger distances, about 5 Å, that corresponds to a configurational change of the side chain of Cys145 from trans to gauche conformation). In the enzyme–inhibitor complex the catalytic dyad remains hydrogen bonded with the sulfhydryl proton pointing towards the Nε atom of His41 (the most probable donor–acceptor distance is 3.3 Å, see Fig. 2b). This configuration suggests a mechanism for the formation of the acylenzyme (E–I) in which the catalytic dyad could be activated by means of a proton transfer from Cys145 to His41 to form an ion pair (IP). This activation mechanism of the catalytic dyad was found to be the first step in the acylation of the natural substrate9 and it is compatible with experimental kinetic observations on the ortholog enzyme of SARS-CoV, which is highly similar to the 3CLpro of SARS-CoV-2.19

Fig. 2. Molecular dynamics simulation of the noncovalent EI complex between N3 and SARS-CoV-2 3CLpro. (a) N3 in the active site of the enzyme, showing the location of the catalytic dyad. (b) Probability densities of the distances from the Cys145-Sγ atom to the Cβ carbon atom of the substrate, in red, and to the Nε atom of His41, in blue. (c) Fraction of hydrogen bond contacts between residues of N3 and a peptide substrate9 and those of the protease. A hydrogen bond contact is counted when the donor–acceptor distance is <3.8 Å and the hydrogen bond angle is >120°.

Fig. 2

Open in a new tab

Fig. 2c displays the fraction of hydrogen bond interactions established between protein residues and the different groups of the inhibitor and the peptide substrate. 3CLpro presents an absolute requirement for Gln at P1 position.21 As seen in Fig. 2c the P1 residue of the peptide substrate is the one establishing more hydrogen bond interactions with the enzyme.9 In particular, main chain atoms of Gln-P1 form hydrogen bonds with residues Gly143, Ser144 and His164, while the side chain is accommodated through hydrogen bond contacts with Phe140, Leu141, His163 and Glu166. In N3, the Gln residue is substituted by a γ-lactam ring at P1 position, which essentially reproduces the same hydrogen bond interactions. The interaction pattern of the P2–P5 groups is also quite similar in the inhibitor and the peptide substrate, which could explain the affinity between the enzyme and the inhibitor. Important differences appear at the P1′ site, where the serine residue of the peptide substrate is substituted in the inhibitor by a benzyl ester group. While the main chain O atom of Ser-P1′ forms hydrogen bonds with the amide group of Gly143 and the side chain of Asn142, the hydroxyl group of its side chain can contact the catalytic dyad (Cys145 and His41). In the inhibitor, the carbonyl O atom of the P1′ group can form a hydrogen bond contact with the main chain NH of Gly143. The terminal benzyl group can establish a CH⋯π interaction with the methyl group of Asn142 side chain, while the other side of the ring remains solvent exposed. Because of its mobility, this benzyl ester group can also establish interactions with threonine residues placed at positions 24–26 and nearby residues. It is also noticeable to remark that the strong interactions established by Gly-P2′ of the peptide substrate with Thr25 and Thr26 are significantly weakened or absent in the inhibitor, opening a way to improve the binding affinity between the protease and N3.

Formation of the covalent E–I complex

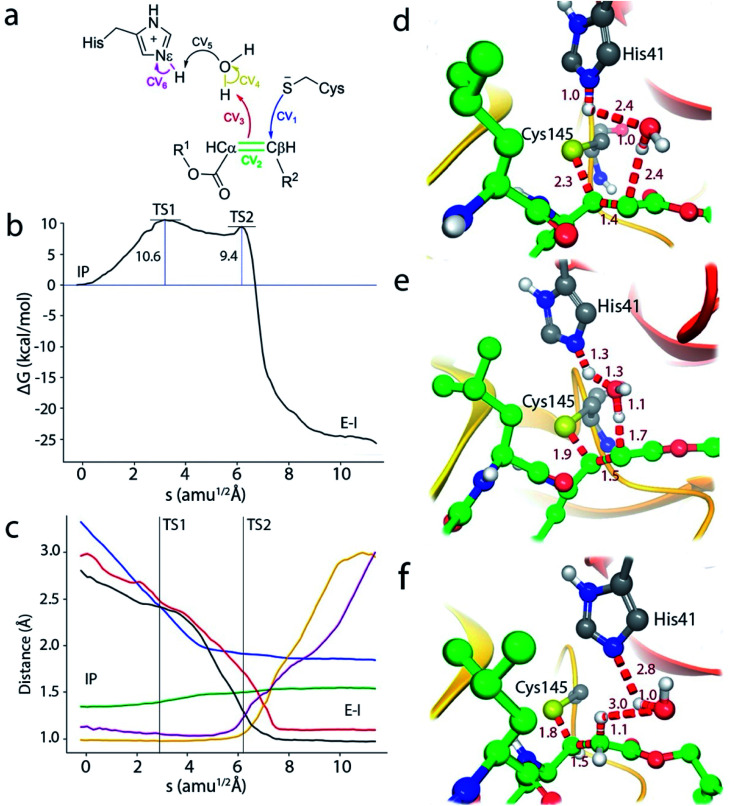
According to the analysis performed on the noncovalent EI complex, we investigated a possible activation of the catalytic dyad via IP formation. With this purpose, we obtained the B3LYPD3/6-31+G*/MM free energy profile associated to the proton transfer from the Sγ atom of Cys145 to the Nε atom of His41 using an antisymmetric transfer coordinate (d(Sγ-H)–d(Nε–H)). Fig. 3a shows the profile obtained with N3 present in the active site; as well as the free energy profiles corresponding to the same proton transfer in the apo enzyme and when a peptide substrate is present in the active site.9 The free energy cost to form the IP from the neutral catalytic dyad is the lowest (2.9 kcal mol−1) for the apo enzyme, because the charged residues (CysS− and HisH+) can be stabilized by solvent molecules (see Fig. 3c). The free energy cost is increased up to 4.8 kcal mol−1 when the peptide substrate is present in the active site. In this case the hydroxyl group of Ser-P1′ can contribute to stabilize the negative charge on Cys145, but the accessibility of water molecules to the ion pair dyad is significantly reduced when compared to the apo form. In the case of the N3 inhibitor the free energy cost of forming the IP is increased up to 10.7 kcal mol−1, a value obtained as the average between the forward (11.1 kcal mol−1) and backward (10.3 kcal mol−1) profiles. The ionized catalytic dyad is stabilized by a single water molecule that enters into the active site and is placed in between the inhibitor and His41, being hydrogen bonded to the two residues of the dyad (see Fig. 3b). It must be noticed that the barrier for the proton transfer back from His41 to Cys145 from the IP is very small, which suggest that this protonation state is not very stable and that could only appear as a transient species during the acylation process.9 Recently, Warshel and coworkers, using an Empirical Valence Bond method, reported an identical value, 2.9 kcal mol−1, for the formation of the IP in the apo enzyme and a similar increase when an α-ketoamide inhibitor is bound in the active site, 7.3 kcal mol−1.22 Altogether, these values indicate that desolvation of the active site upon ligand binding can destabilize the IP form. In fact, formation of the IP, where two charged residues are found at short distance, results in a large dipole moment (about 14 D at the B3LYP/6-31+G* level) that can be stabilized by solvent molecules. This result also suggests that binding of the ligand into the active site after IP formation could have associated a large energy penalty due to the need to remove water molecules from the active site. Classical MD simulations of the noncovalent complex with the catalytic dyad in the IP form show a trend for the ligand to slowly depart from the active site after several hundred nanoseconds (see Fig. S2†), being the active site then occupied by water molecules. In the recent work of Moliner and coworkers, in which a combination of AM1 dynamics and M06-2X energies are used to describe the QM region and the Amber ff03 force field for the MM region, the IP was found to be only 1.3 kcal mol−1 above the neutral dyad when N3 is present in the active site.20 As discussed below, this value leads to an estimated activation energy for the covalent inhibition of 3CLpro by N3 which seems to be too small when compared to the reference values derived from the inhibition rate constant of closely related enzymes.8

Fig. 3. Proton transfer from Cys145 to His41 in SARS-CoV-2 3CLpro. (a) Free energy profile for the transformation from the neutral catalytic dyad (left) to the ion pair (IP, right) in the EI complex with N3 (red line); in the complex with the peptide substrate9 (blue line) and in the apo enzyme9 (green line). (b) Snapshot of the IP configuration in the EI complex showing a water molecule placed between His41 and the inhibitor. (c) Snapshot of the IP configuration in the apo enzyme.

Fig. 3

Open in a new tab

Because of the comparatively larger free energy cost of forming the IP from the noncovalent EI complex with the N3 inhibitor found in our study, we investigated first the possibility of a reaction mechanism for the formation of the covalent E–I complex that does not involve a proton transfer from Cys145 to His41. In such a mechanism the sulfhydryl proton is directly transferred to the Cα atom of N3 while the Sγ atom attacks on the Cβ one (see Fig. S3†). However, the activation free energy found for this mechanism (about 50 kcal mol−1) is too high and incompatible with the observed inhibition rates (see below).

We thus explored a reaction mechanism for the formation of the E–I acylenzyme from the IP form. This mechanism implies the proton transfer from the Nε atom of His41 to the Cα atom of the inhibitor, mediated by the water molecule placed in between, and the nucleophilic attach of the Sγ atom of Cys145 to the Cβ atom of N3 (see Fig. 4a). The results obtained for the MFEP corresponding to this mechanism at the B3LYPD3/6-31+G*/MM level are shown in Fig. 4b and c. According to the free energy profile the reaction proceeds via two Transition States (TS1 and TS2) separated by a shallow intermediate (see Fig. 4b). TS1 is the rate-limiting one with a free energy 10.6 kcal mol−1 higher than the IP, while the free energy difference corresponding to TS2 is 9.4 kcal mol−1. The evolution of the CVs used to define the multidimensional free energy surface (Fig. 4c) shows that TS1 is associated to the nucleophilic attack of the Sγ atom to the Cβ atom and the change of the bond between Cα and Cβ atoms from double to single. The Sγ–Cβ distance at TS1 has been reduced from 3.3 to 2.33 Å, while the Cβ–Cα distance has been slightly increased from 1.34 to 1.41 Å (see Fig. 4d). TS2 corresponds to the proton transfer from His41 to the neighbor water molecule and from this to the Cα atom, being the first proton transfer more advanced than the second one (see Fig. 4e). At TS2 the Sγ–Cβ bond is significantly shorter (1.91 Å) while the Cβ–Cα distance has been elongated up to a value close to that of a single bond (1.50 Å). Note that in this mechanism the sequence of nucleophilic attack and proton transfer is just the reverse of that observed for the acylation mechanism of the peptide substrate, where the proton transfer to the N atom of the scissile bond precedes the nucleophilic attack on the carbonyl carbon atom.9 Finally, the reaction product, where a proton has been transferred to the Cα atom, is shown in Fig. 4f. The Sγ–Cβ bond distance found at the E–I complex (1.85 Å) is close to the value found in the X-ray structure of the inhibited enzyme (1.77 Å).4 The overlap between the QM/MM and X-ray structures is shown in Fig. S4.†

Fig. 4. Simulation of the reaction from the ion pair (IP) to the covalent complex E–I. (a) Collective Variables (CVs) employed to explore the MFEP. (b) B3LYPD3/6-31+G*/MM free energy profile along the path-CV for the formation of the covalent E–I complex from the IP. (c) Evolution of the distances selected as CVs along the MFEP. The color code corresponds to those shown in (a). (d) Representation of TS1. The values of the distances correspond (in Å) to the coordinates of the MFEP where TS1 is located. (e) Representation of TS2 and values of key distances. (f) Representation of the reaction product, the acylenzyme E–I.

Fig. 4

Open in a new tab

In order to check the robustness of our mechanistic proposal, the string calculation was repeated using the M06-2X functional with the same basis set and D3 corrections. The resulting free energy profile was almost identical to the B3LYP one, both from the energetic and structural points of view: the geometries and energies of the transition states were very similar at both theoretical levels, as can be seen in Fig. S5.† This result confirms the adequacy of the B3LYP functional for the present Michael addition, in spite of the reported limitations of this functional to correctly describe some enolate or carbanion intermediates.23,24 Note that these species are not strictly found in the proposed mechanism because of the proton transfer from His41 to the substrate. It must be also stressed that at both theoretical levels, the string converges to a mechanism evolving from the IP to the covalent product, confirming that, in agreement with our previous work,10 the IP is a metastable species from which the most favorable mechanism may proceed.

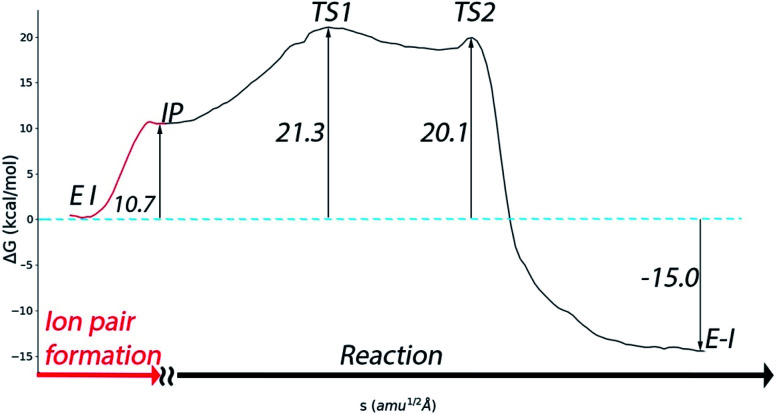
A complete representation of the free energy path from the noncovalent complex (EI) to the covalent one (E–I) is provided in Fig. 5. According to this free energy profile, resulting from the combination of those presented in Fig. 3 and 4, the transformation from the noncovalent EI complex to the covalent one (E–I) is an exothermic process. The free energy difference between E–I and IP (Fig. 4b) is −25.7 kcal mol−1, while the free energy difference between IP and EI is 10.7 kcal mol−1 (Fig. 3a). Combining these two values, our simulations predict that the covalently bonded E–I complex is −15.0 kcal mol−1 more stable than the noncovalent EI complex, which agrees with the observed irreversibility of the inhibition process of 3CLpro by N3.4

Fig. 5. Free energy profile for the whole transformation of the noncovalent complex (EI) into the covalent one (E–I) through formation of the IP.

Fig. 5

Open in a new tab

Regarding the inactivation rate (k3 in eqn (1)), our simulations predict that the associated activation free energy results also from the sum of two contributions: the free energy cost of creating the IP form from EI (10.7 kcal mol−1, Fig. 3a) plus the activation free energy of TS1 relative to IP (10.6 kcal mol−1, Fig. 4b). This gives in a total activation free energy of 21.3 kcal mol−1, which according to Transition State Theory (see eqn (S1) in SI†) corresponds to a rate constant of 1.9 × 10−3 s−1 at 300 K. Unfortunately, only the second-order rate constant (k3/KI) and not the inactivation rate constant of SARS-CoV-2 3CLpro by N3 has been estimated.4 However, the inactivation rate constant by N3 (k3) was determined for the highly similar ortholog protease of SARS-CoV.8 In this case the activation free energy derived from the rate constant measured at 303 K (3.1 × 10−3 s−1) is 21.2 kcal mol−1. Comparison between SARS-CoV and SARS-CoV-2 main proteases seems appropriate considering that they present identical active sites, the same substrate specificity and very similar reaction rate constants for the hydrolysis of peptides.25 The order of magnitude predicted for the k3 rate constant seems also correct when compared to the values determined for the main proteases of other coronaviruses.8 Even if the rate constant for SARS-CoV-2 inhibition would be one order of magnitude faster, which could account for the rapid inhibition reported experimentally,4 the resulting activation free energy for the SARS-CoV-2 enzyme would only be 1.4 kcal mol−1 smaller than the reported value for the SARS-CoV one. Lastly, our prediction for the rate constant is compatible with the experimental estimation of k3/KI for the SARS-CoV-2 enzyme (11 300 M−1 s−1).4 Combination of our predicted k3 with the reported estimation for k3/KI gives a KI of ∼0.2 μM, a value similar to those determined for the inhibition of other coronaviruses's proteases with N3.8 The excellent agreement between the experimental values and our theoretical estimation strongly supports our mechanistic proposal for the inhibition of SARS-CoV-2 3CLpro by a Michael acceptor.

The QM/MM study of Moliner and coworkers found an activation free energy of 11.2 kcal mol−1 and a reaction free energy of −17.9 kcal mol−1.20 While the latter value is close to our findings (−15.0 kcal mol−1), the former departs significantly from our estimation (21.3 kcal mol−1). Their activation free energy provides a rate constant of ∼104 s−1, significantly larger than the aforementioned value measured for the homologous SARS-CoV protease. In their mechanistic proposal the proton transfer from His41 to the inhibitor is direct and not water-mediated. However, this mechanistic difference does not explain the gap between their and ours calculated activation free energies. In their simulations the rate-limiting TS corresponds, as in our case, to the Sγ–Cβ bond formation and the free energy difference with the IP is 9.9 kcal mol−1, very close to our value of 10.6 kcal mol−1 (see Fig. 4b). The main difference between our results and those reported by Moliner and coworkers is found in the first part of the process, the free energy cost of forming the IP from the EI complex, 10.7 and 1.3 kcal mol−1, respectively. Differences between the two works may arise from the different QM levels of theory, MM forcefields or to the sampling of different enzymatic configurations (their exploration of the mechanism started from the E–I complex while we started from the noncovalent EI complex); factors that could affect the relative stability of the neutral and ionic forms of the catalytic dyad. According to our previous discussion, we think that our simulations provides a general picture (see Fig. 5) in better agreement with current experimental results.

Roughly speaking, in our simulations the two steps presented in Fig. 3 and 4, IP formation and Michael addition, contribute similarly to the activation free energy of the inhibition process (about 10 kcal mol−1 each of them). This suggests that the kinetic properties of inhibitors can be improved also by stabilizing the ligand-bound ion pair state. It has been already suggested for other related 3CL proteases (from MERS and SARS-CoV) that stabilization of a charged catalytic dyad could promote catalysis.26 For the SARS-CoV-2 protease it has been shown that inhibitors can shift the protonation state of some residues, not only the catalytic dyad but also other residues found in the vicinity of the active site.27 In principle, a possible strategy is the introduction of chemical groups in the inhibitor structure that imitate the role played by Ser-P1′ in the natural substrate. The hydroxyl group of this residue can make contacts with the catalytic dyad that, together with the presence of solvent molecules, can contribute to stabilize the IP.9 Interestingly, the position of the water molecule in the rate limiting TS structure found in this work (TS1, see Fig. 4d) could be useful to assist in the design of inhibitors that favor this stabilization process. In this sense, a recently reported potent inhibitor of SARS-CoV-2 3CLpro (PF-00835231)28 presents a hydroxyl group that matches the position of the water molecule in TS1 (see Fig. S6† for an overlap of the X-ray structure of the enzyme inhibited by PF-00835231and TS1). This observation illustrates the insights offered by mechanistic studies for the design of new inhibitors.

Conclusions

We have here presented the results of microscopic simulations of SARS-CoV-2 3CL protease inhibition by N3, a Michael acceptor. Classical and hybrid QM/MM simulations were performed to investigate the noncovalent and the covalent enzyme–inhibitor complexes, respectively.

Molecular dynamics simulations of the noncovalent EI complex show that the inhibitor mimics the interactions established by the P1–P5 residues of the natural substrate. Our analysis also shows that an interesting strategy to improve a potential inhibitor based in N3 could be the introduction of chemical changes in the benzyl ester group in such a way that could restore the interactions that the P2′ group of the peptide substrate establishes with Thr25, Thr26 and Gly143. This change could increase the affinity between the inhibitor and the protein, reducing the dissociation constant KI.

Regarding the formation process of the covalent E–I complex, our simulations show that the inhibition mechanism of SARS-CoV-2 3CLpro by a Michael acceptor involves two steps after binding the inhibitor: (i) the activation of the catalytic dyad by means of the formation of an ion pair and (ii) a Michael addition process where Cys145 attacks to the Cβ atom of the Michael acceptor and a proton is transferred, water mediated, from His41 to the Cα atom of the inhibitor. The contribution of each of the two steps to the activation free energy of the inhibition process is roughly the same (about 10 kcal mol−1) and thus inhibition kinetics can be favored by reducing either of the two contributions. The free energy cost to form the IP is substantially smaller in the enzymatic complex with the peptide substrate than when N3 is present in the active site (about 5.9 kcal mol−1, according to Fig. 3a) and the activation free energy for the acylation of a peptide substrate is also significantly smaller than for the N3 inhibitor (by about the same quantity reflected in Fig. 3a).9 This clearly suggests that, in order to improve the kinetic behavior of newly designed inhibitors (increasing k3), attention must be paid to the formation of the IP. In this sense, the structures found along our reaction path, an in particular the rate-limiting transition state, could be useful to guide that design.

Conflicts of interest

The are no conflicts to declare.

Supplementary Material

SC-012-D0SC04978F-s001

Acknowledgments

The authors acknowledge financial support from Feder funds and the Ministerio de Ciencia, Innovación y Universidades (project PGC2018-094852-B-C22) and Generalitat Valenciana (GVCOV19/Decreto180/2020). We also acknowledge Barcelona Supercomputing Center (BSC) for awarding us access to MareNostrum and Servei d'Informàtica de la Universitat de València for the use of Tirant. The support of Alejandro Soriano from Servei d'Informàtica de la Universitat de València, and the staff from BSC is gratefully acknowledged. Authors also deeply acknowledge Dr Kirill Zinovjev for assistance in the adaptation of the code and helpful discussions during about the use of the string method.

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc04978f

References

  1. Bangham C. R. M. J. Gen. Virol. 2003;84:3177–3189. doi: 10.1099/vir.0.19334-0. [DOI] [PubMed] [Google Scholar]
  2. Hilgenfeld R. FEBS J. 2014;281:4085–4096. doi: 10.1111/febs.12936. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Pillaiyar T. Manickam M. Namasivayam V. Hayashi Y. Jung S.-H. J. Med. Chem. 2016;59:6595–6628. doi: 10.1021/acs.jmedchem.5b01461. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Jin Z. Du X. Xu Y. Deng Y. Liu M. Zhao Y. Zhang B. Li X. Zhang L. Peng C. Duan Y. Yu J. Wang L. Yang K. Liu F. Jiang R. Yang X. X. X. You T. Liu X. X. X. X. Yang X. X. X. Bai F. Liu H. Liu X. X. X. X. Guddat L. W. Xu W. Xiao G. Qin C. Shi Z. Jiang H. Rao Z. Yang H. Nature. 2020;582:289–293. doi: 10.1038/s41586-020-2223-y. [DOI] [PubMed] [Google Scholar]
  5. Zhang L. Lin D. Sun X. Curth U. Drosten C. Sauerhering L. Becker S. Rox K. Hilgenfeld R. Science. 2020;368:409–412. doi: 10.1126/science.abb3405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Jin Z. Zhao Y. Sun Y. Zhang B. Wang H. Wu Y. Zhu Y. Zhu C. Hu T. Du X. Duan Y. Yu J. Yang X. Yang X. Yang K. Liu X. Guddat L. W. Xiao G. Zhang L. Yang H. Rao Z. Nat. Struct. Mol. Biol. 2020;27:529–532. doi: 10.1038/s41594-020-0440-6. [DOI] [PubMed] [Google Scholar]
  7. Dai W. Zhang B. Jiang X.-M. Su H. Li J. Zhao Y. Xie X. Jin Z. Peng J. Liu F. Li C. Li Y. Bai F. Wang H. Cheng X. Cen X. Hu S. Yang X. Wang J. Liu X. Xiao G. Jiang H. Rao Z. Zhang L.-K. Xu Y. Yang H. Liu H. Science. 2020;368:1331–1335. doi: 10.1126/science.abb4489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Yang H. Xie W. Xue X. Yang K. Ma J. Liang W. Zhao Q. Zhou Z. Pei D. Ziebuhr J. Hilgenfeld R. Kwok Y. Y. Wong L. Gao G. Chen S. Chen Z. Ma D. Bartlam M. Rao Z. PLoS Biol. 2005;3:1742–1752. doi: 10.1371/journal.pbio.0030324. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ramos-Guzmán C. A. Ruiz-Pernía J. J. Tuñón I. ACS Catal. 2020;10:12544–12554. doi: 10.1021/acscatal.0c03420. [DOI] [PubMed] [Google Scholar]
  10. Świderek K. Moliner V. Chem. Sci. 2020;11:10626–10630. doi: 10.1039/D0SC02823A. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Le Grand S. Götz A. W. Walker R. C. Comput. Phys. Commun. 2013;184:374–380. doi: 10.1016/j.cpc.2012.09.022. [DOI] [Google Scholar]
  12. Salomon-Ferrer R. Götz A. W. Poole D. Le Grand S. Walker R. C. J. Chem. Theory Comput. 2013;9:3878–3888. doi: 10.1021/ct400314y. [DOI] [PubMed] [Google Scholar]
  13. Becke A. D. J. Chem. Phys. 1993;98:5648–5652. doi: 10.1063/1.464913. [DOI] [Google Scholar]
  14. Lee C. Yang W. Parr R. G. Phys. Rev. B: Condens. Matter Mater. Phys. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  15. Grimme S. Antony J. Ehrlich S. Krieg H. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  16. Zinovjev K. Tuñón I. Proc. Natl. Acad. Sci. U. S. A. 2017;114:12390–12395. doi: 10.1073/pnas.1710820114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Maragliano L. Vanden-Eijnden E. Chem. Phys. Lett. 2007;446:182–190. doi: 10.1016/j.cplett.2007.08.017. [DOI] [Google Scholar]
  18. Torrie G. M. Valleau J. P. J. Comput. Phys. 1977;23:187–199. doi: 10.1016/0021-9991(77)90121-8. [DOI] [Google Scholar]
  19. Solowiej J. Thomson J. A. Ryan K. Luo C. He M. Lou J. Murray B. W. Biochemistry. 2008;47:2617–2630. doi: 10.1021/bi702107v. [DOI] [PubMed] [Google Scholar]
  20. Arafet K. Serrano-Aparicio N. Lodola A. Mulholland A. J. González F. V. Świderek K. Moliner V. Chem. Sci. 2021 doi: 10.1039/D0SC06195F. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Fan K. Wei P. Feng Q. Chen S. Huang C. Ma L. Lai B. Pei J. Liu Y. Chen J. Lai L. J. Biol. Chem. 2004;279:1637–1642. doi: 10.1074/jbc.M310875200. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Mondal D. Warshel A. Biochemistry. 2020;59:4601–4608. doi: 10.1021/acs.biochem.0c00782. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Awoonor-Williams E. Isley W. C. Dale S. G. Johnson E. R. Yu H. Becke A. D. Roux B. Rowley C. N. J. Comput. Chem. 2020;41:427–438. doi: 10.1002/jcc.26064. [DOI] [PubMed] [Google Scholar]
  24. Smith J. M. Jami Alahmadi Y. Rowley C. N. J. Chem. Theory Comput. 2013;9:4860–4865. doi: 10.1021/ct400773k. [DOI] [PubMed] [Google Scholar]
  25. Vuong W. Khan M. B. Fischer C. Arutyunova E. Lamer T. Shields J. Saffran H. A. McKay R. T. van Belkum M. J. Joyce M. A. Young H. S. Tyrrell D. L. Vederas J. C. Lemieux M. J. Nat. Commun. 2020;11:4282. doi: 10.1038/s41467-020-18096-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Wang H. He S. Deng W. Zhang Y. Li G. Sun J. Zhao W. Guo Y. Yin Z. Li D. Shang L. ACS Catal. 2020;10:5871–5890. doi: 10.1021/acscatal.0c00110. [DOI] [PubMed] [Google Scholar]
  27. Pavlova A. Lynch D. L. Daidone I. Zanetti-Polzi L. Smith M. D. Chipot C. Kneller D. W. Kovalevsky A. Coates L. Golosov A. A. Dickson C. J. Velez-Vega C. Duca J. S. Vermaas J. V. Pang Y. T. Acharya A. Parks J. M. Smith J. C. Gumbart J. C. Chem. Sci. 2021 doi: 10.1039/D0SC04942E. [DOI] [Google Scholar]
  28. Hoffman R. L. Kania R. S. Brothers M. A. Davies J. F. Ferre R. A. Gajiwala K. S. He M. Hogan R. J. Kozminski K. Li L. Y. Lockner J. W. Lou J. Marra M. T. Mitchell L. J. Murray B. W. Nieman J. A. Noell S. Planken S. P. Rowe T. Ryan K. Smith G. J. Solowiej J. E. Steppan C. M. Taggart B. J. Med. Chem. 2020;63:12725–12747. doi: 10.1021/acs.jmedchem.0c01063. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

SC-012-D0SC04978F-s001
SC-012-D0SC04978F-s001.pdf (3.9MB, pdf)

Articles from Chemical Science are provided here courtesy of Royal Society of Chemistry

RESOURCES