Abstract
Modern machine learning techniques (such as deep learning) offer immense opportunities in the field of human biological aging research. Aging is a complex process, experienced by all living organisms. While traditional machine learning and data mining approaches are still popular in aging research, they typically need feature engineering or feature extraction for robust performance. Explicit feature engineering represents a major challenge, as it requires significant domain knowledge. The latest advances in deep learning provide a paradigm shift in eliciting meaningful knowledge from complex data without performing explicit feature engineering. In this article, we review the recent literature on applying deep learning in biological age estimation. We consider the current data modalities that have been used to study aging and the deep learning architectures that have been applied. We identify four broad classes of measures to quantify the performance of algorithms for biological age estimation and based on these evaluate the current approaches. The paper concludes with a brief discussion on possible future directions in biological aging research using deep learning. This study has significant potentials for improving our understanding of the health status of individuals, for instance, based on their physical activities, blood samples and body shapes. Thus, the results of the study could have implications in different health care settings, from palliative care to public health.
Keywords: deep learning, biological age, bioinformatics, biomarkers, anthropometry, locomotor activity, electronic health records, health indices, artificial intelligence
1 Introduction
Aging is a gradual process experienced by all living organisms. Human aging is a complex process that depends on different types of tissues that are comprised of billions of cells. Aging leads to diseases, functional performance deterioration and both physical and physiological damage over time. Age estimation is an important medical and public health challenge. The major challenge is that most measures used to characterize age, for instance, biological markers vary significantly from person to person, even for people with the same chronological age (CA). The reason is that, the multi-faceted nature of aging with its many unknowns (example, genetics, nutrition, body shape, health condition, cardiorespiratory fitness, social conditions and life style) contribute to influence the perceived age of an individual. CA is based on the date of birth. However, biological age (BA) is a conceptual idea that a person’s true age can be different from his/her CA. Although BA is a loosely used concept and lacks precise definition, it is often viewed as the true age of an individual [24]. Thus, BA provides a better measure of the life expectancy of an individual than his or her CA. The common idea is to calculate BA based on some age-dependent variables [3, 8, 21, 47], where CA may or may not be a required variable depending on the application. In this article, we provide a technical overview of the recent and future applications of deep learning techniques for estimating BA. In particular, we investigate the performance of different deep learning architectures applied on data modalities such as biomarkers, body measurements and physical locomotor activity (recorded by a wearable device) for reliable estimation of BA in adults.
Levine[30] compared the performance of five BA estimation algorithms and identified the Klemera and Doubal (KD) method [24] as the most reliable predictor for mortality. Cho et al. [8] studied various BA estimation methods to examine the relation with work ability index (WAI). WAI is a measure that reflects present health condition rather than how it changes over age. The KD method on PCA features produced relatively reliable results. Mitnitski et al. [34] compared performance of frailty index (FI) with biomarker-based measures of BA. They employed the KD algorithm in predicting mortality. In another work, Belsky et al. [6] compared different methods of BA estimation, including genomic, epigenetic and blood biomarker measures. Two other recent work on BA estimation used the notions of phenotypic age [31] and age neighborhoods [43]. These studies did not use deep learning techniques.
Putin et al. [38] studied the use of biomarkers in a deep learning framework for CA prediction. They utilized an ensemble of multiple deep neural networks (DNNs) and trained on blood biomarkers. They employed a variation of the implementation of permutation feature importance [2] technique to evaluate the relative importance of each blood biochemistry marker to ensemble accuracy. The best performance by a DNN was a mean absolute error (MAE) of 6.07 years in predicting CA and the ensemble learning produced an MAE of 5.55 years. They identified the five most important biomarkers for predicting human CA: albumin, glucose, alkaline phosphatase, urea and erythrocytes. Fischer et al. [13] earlier identified four biomarkers: alpha-1-acid glycoprotein, albumin, very-low-density lipoprotein particle size and citrate for predicting all-cause mortality by applying biomarker profiling via nuclear magnetic resonance spectroscopy. They also showed that these four biomarkers can predict healthy people that may be at a short-term risk of dying within 5 years from heart disease, cancer and other illness. Findings from these studies suggest that particular biomarkers can be related to aging and mortality (for example albumin). Cole et al. [10] studied the use of structural neuro-imaging magnetic resonance imaging (MRI) under a Gaussian process regression framework. The predicted age was identified as ‘brain-predicted age’ or brain age for short. They combined DNA-methylation with brain age and showed that the combination improves mortality risk prediction. On the contrary, they also combined brain age with grey matter and cerebrospinal fluid volumes but that did not improve mortality risk prediction. Bobrov et al. [7] proposed a DNN-based model to estimate BA using eye corner images (called PhotoAgeClock). Their method resulted in an MAE of 2.3 years and 95% correlation with CA; however, they did not consider BA. Mamoshina et al. [32] used a multilayer DNN model and showed population specific aging patterns for Canadian, Korean and Eastern European subjects. In a recent paper, Rahman and Adjeroh [44] applied a deep convolutional long short-term memory (ConvLSTM) model on a week-long physical activity data measured per minute to estimate BA. They also compared the estimated BAs with the KD method applied on biomarkers in a common data set. Estimating BA using different feature sets is interesting and brings in different perspectives. Pyrkov et al. [40] applied a 1-dimensional convolutional neural network (CNN) on the physical activity data to estimate BA. Cole et al. [9] studied a deep learning framework using 3D-CNN-based approach with raw MRI data. They showed that their model can predict CA for healthy individuals. They also showed brain predicted age is heritable and can be used in genetic studies of brain aging.
Miotto et al. [33] discussed applications of deep learning in medicine highlighting the major aspects that significantly impact health care. Their study is limited to biomedical data, especially those that originated from clinical imaging, electronic health records, genomes and wearable devices. Ravi et al. [45] presented a review of deep learning in health informatics. The study focuses on applications of deep learning in translational bioinformatics, medical imaging, pervasive sensing, medical informatics and public health. However, these studies did not cover aging (neither chronological nor biological).
Zhavoronkov et al. [53] discussed recent advances and perspectives in using artificial intelligence (AI) for studying aging and longevity. Specifically, they discussed studies related to deep learning, transfer learning and reinforcement learning. They also discussed different data modalities often used in BA estimation such as biomedical images (e.g. MRI), genetic markers and epigenetic attributes. Although this is a comprehensive study on aging and longevity describing machine learning (ML) algorithms that are used in different aging research, the paper did not discuss the issue of quantification of BA. Generally, survival models based on mortality status are used to compare/quantify these estimated BAs. Further, there was no discussion on how the different methods compare for instance, when applied on healthy individuals and on those that suffer from chronic diseases (e.g. diabetes, kidney disease, cardiovascular disease, etc.).
Given that deep learning provides newer architectures and stronger performance in various domains, we strongly believe that deep learning have much to offer in the area of biological aging and aging acceleration. In this review, we do not provide a comprehensive discussion on technical details on the deep learning (DL) architectures, rather we provide an overview of the DL techniques used to estimate BA. One of the major challenges is quantifying the estimated BA; we discuss how to approach the quantification problem. We describe the advances and opportunities that are brought in with the DL algorithms, over traditional ML algorithms.
The remainder of this paper is organized as follows: in Section 2, we describe different DL architectures relevant to BA estimation. Section 3 describes the different data modalities used for studying biological aging. Section 4 provides metrics for performance evaluation and for quantifying BA. Section 5 shows comparative results for BA estimation methods in terms of mortality models. In Section 6, we discuss several interesting observations, such as, the connection between BA and general health status, relation with known health indices, and relation with disease status. Section 7 concludes the paper and describes potential directions for future work in this area. Table 14 lists the key terms and definitions used in this paper.
Table 14.
Key terms and definitions used in the paper
| DNN | Deep neural network | KM plots | Kaplan–Meier plots |
|---|---|---|---|
| CNN | Convolutional neural network | Cox PH | Cox proportional hazard model |
| BA | Biological age | CA | Chronological age |
| KD | Klemera doubal method |
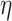
|
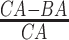
|
| LSTM | Long short-term memory |
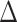
|

|
| RNN | Recurrent neural network |
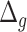
|
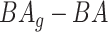
|
| ConvLSTM | Convolutional LSTM |
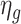
|
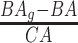
|
| SBSI | Surface-based body shape index |
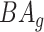
|
BA age, gender-matched cohort |
| MAE | mean absolute error | AUC | Area under the curve |
|
Pearson correlation coefficient | HR | Hazard ratio |
2 DL architectures
Machine learning (ML) is a general method of AI where a computer can learn from the data with/without a specifically designed algorithm. DL is a sub-field of ML that uses hierarchical/layered learning [29]. DL varies from traditional ML in how they learn representations from the data. DL typically consists of many layers (hence deep) of non-linear computational units. The idea is to glean complex and meaningful information from the data in successive layers. Each layer sends the output to its next layer. This is also known as layered representation learning based on stacked neural networks. The term ‘deep’ is used to denote more than a single layer. Here we briefly describe the popular DL architectures that have been used in age estimation. More detailed descriptions can be found in [29, 32, 38, 40, 44, 53].
2.1 Deep neural network
An artificial neural network (ANN) consists of a single hidden layer. ANN provides the basis for the deep (or dense) neural network with the inclusion of more layers. Given the input data, a layer learns from the data and stores the information as numeric weights. Technically, weights are the parameters of a layer. Training a DNN revolves around the following: (i) layers of the network, (ii) input data and the target/output, (iii) the loss function and (iv) the optimizer, that determines how the learning occurs. The network of layers chained together learns/maps the input data to the target. The loss function compares these predictions to the output. The optimizer updates the network’s weights based on the value from the loss function. Figure 1A shows a general structure of a DNN. This deep architecture can be used for a regression or classification problem and is widely used in different areas. The learning/training process sometimes can be very slow depending on the data dimension and the number of layers. DNNs [32, 38] have been used for CA estimation.
Figure 1.
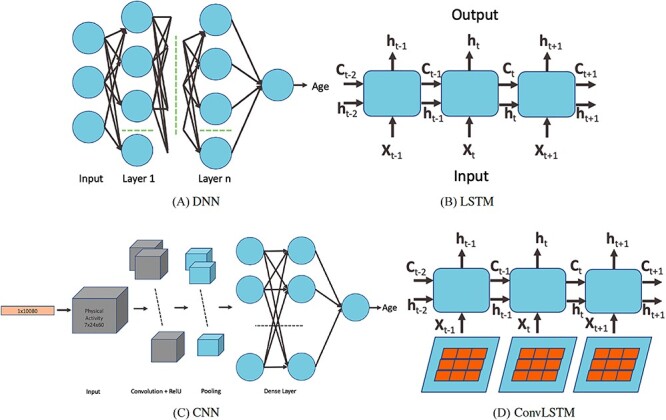
DL architectures used in BA estimation (A) dense (or deep) neural network (DNN), (B) long short-term memory (LSTM) cells (LSTM updates for timestep  given the input
given the input  and the previous state
and the previous state  and previous cell output
and previous cell output 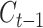 ), (C) convolutional neural network (CNN) and (D) convoutional LSTM cell. Here (A) and (C) show the network while (B) and (D) show the basic structure; to use the models for age estimation, we add dense layers and a single unit output.
), (C) convolutional neural network (CNN) and (D) convoutional LSTM cell. Here (A) and (C) show the network while (B) and (D) show the basic structure; to use the models for age estimation, we add dense layers and a single unit output.
2.2 Recurrent neural network
A recurrent neural network (RNN) has a ‘state’ that stores the information pertaining to what it has observed/processed thus far, and it processes sequential data through a number of iterations. So, an RNN is basically a neural network containing an internal loop and the state of the RNN is changed/reset between two sequences. The RNN, however, suffers from the problem of propagating vanishing gradients [17]. The long short-term memory (LSTM) is one of the most popular RNNs developed by Hochreiter and Schmidhuber [17] that adds a way to carry information across sequences. This saves information for later and prevents older signals from vanishing gradually. RNNs are good for memorizing sequential events and time dependencies. However, they suffer from the vanishing gradient problem and are about the slowest of the DL architectures. LSTM improves the performance over RNN but does not entirely solve the problem of vanishing gradient. Zhang et al. [52] used an attention-based LSTM network for fine-grained age estimation. Rahman and Adjeroh [44] combined an LSTM and a CNN to estimate BA from physical activity data.
2.3 Convolutional neural network
The convolutional neural network (CNN) [29] is probably the most popular architecture currently used for image analysis. The single most compelling reason for this is that the feature extraction is done by the network itself and is much better than the traditional feature extraction algorithms. CNN is a specific type of neural network that is generally composed of convolution and pooling layers. The convolution operation extracts patches from its input feature map and applies the same transformation to all of these patches, producing an output feature map. Convolutions are defined by two key parameters: (i) size of the patch (e.g., 3 3, 3
3, 3 3
3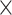 3) and (ii) number of filters. The convolution operation works by sliding these windows over the input feature map from every accessible/possible location. Each patch is now transformed via a tensor product with learned weight matrix called convolution kernel. The convolution layer uses filters that perform a convolution operation. The pooling layer performs down-sampling, typically immediately after convolution. Max and average pooling are common where maximum and average values are taken, respectively. The reason for pooling is to introduce spatial invariance to the convolution operation. Similar to DNN [38], a fully connected layer operates on a flattened input where all the inputs are connected to all the neurons. 1D-CNN [40] works with the input layer over a single spatial (or temporal) dimension. 2D-CNN [27] and 3D-CNN [22] use different representations compared with the 1D CNN. The structure in the sequence of 2D and 3D representations of the daily activities makes it easier to learn valuable patterns from the activity data. This may be difficult using 1D CNN or DNN. For 2D-CNN, we consider the data as an image of size 168
3) and (ii) number of filters. The convolution operation works by sliding these windows over the input feature map from every accessible/possible location. Each patch is now transformed via a tensor product with learned weight matrix called convolution kernel. The convolution layer uses filters that perform a convolution operation. The pooling layer performs down-sampling, typically immediately after convolution. Max and average pooling are common where maximum and average values are taken, respectively. The reason for pooling is to introduce spatial invariance to the convolution operation. Similar to DNN [38], a fully connected layer operates on a flattened input where all the inputs are connected to all the neurons. 1D-CNN [40] works with the input layer over a single spatial (or temporal) dimension. 2D-CNN [27] and 3D-CNN [22] use different representations compared with the 1D CNN. The structure in the sequence of 2D and 3D representations of the daily activities makes it easier to learn valuable patterns from the activity data. This may be difficult using 1D CNN or DNN. For 2D-CNN, we consider the data as an image of size 168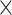 60 (DH
60 (DH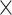 M) ignoring the days as temporal information. However, for 3D-CNN we consider the data as a 3D volume with temporal information across the days, where each day has 24 h and an hour is 60 min. So to break it down, we represent it as a 3D information of 7
M) ignoring the days as temporal information. However, for 3D-CNN we consider the data as a 3D volume with temporal information across the days, where each day has 24 h and an hour is 60 min. So to break it down, we represent it as a 3D information of 7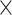 24
24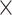 60 (D
60 (D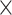 H
H M) min. Both the 2D (DH
M) min. Both the 2D (DH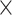 M) and 3D representation (D
M) and 3D representation (D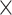 H
H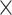 M) of the 1D physical activity data expose different feature dimensions that cannot be observed easily using a 1D CNN architecture. In particular, using the 24
M) of the 1D physical activity data expose different feature dimensions that cannot be observed easily using a 1D CNN architecture. In particular, using the 24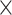 60 matrix representation of physical activity, records at minute 1 and minute 61 are neighbors (when considered as 2D in a matrix form), while in a 1D sequential view they will be 60 timesteps apart. Two important factors here are that the spatial structure is changed and that the sequence of 2D and 3D information is very different from that of the original 1D time series (especially the information gathered from the 1D CNN and DNN).
60 matrix representation of physical activity, records at minute 1 and minute 61 are neighbors (when considered as 2D in a matrix form), while in a 1D sequential view they will be 60 timesteps apart. Two important factors here are that the spatial structure is changed and that the sequence of 2D and 3D information is very different from that of the original 1D time series (especially the information gathered from the 1D CNN and DNN).
The CNN + LSTM architecture uses CNN layers on the input data and combines with LSTMs for extracting improved temporal sequence information. This architecture is suitable for both spatial and temporal feature extraction. CNN + LSTMs were developed for time series prediction problems and for the application of generating textual descriptions from videos (sequence of images). Another application is to generate a textual description of activity in a sequence of images. This architecture has also been used in speech recognition and natural language processing problems where CNNs perform the job of feature extractions for the LSTMs on audio and textual input data. If the input has a 2D structure (e.g. image) or 1D structure (e.g. text), this approach can be applied. CNN + LSTM architecture was applied to BA estimation in [44].
Another variation in combining CNN and LSTM is ConvLSTM [44, 50]. Under this architecture, the convolution structures are applied at both the input-to-state transition and at the state-to-state transitions. The ConvLSTM differs from simple CNN+LSTM in that, for CNN+LSTM, the convolution structure (CNN) is applied as the first layer and sequentially the LSTM layer is applied in the second layer. Similar to CNN, fully connected dense layers are used after ConvLSTM. Unlike CNN+LSTM, the ConvLSTM approach provides a 3D view of the data, thus making it easier to identify temporal patterns in the data. Recently, authors in [44] used ConvLSTM for BA estimation using physical activity data.
2.4 Generative adversarial network
Generative adversarial networks (GANs) [15] are unsupervised, probabilistic models that generate data similar to the original data set that the GANs are trained on. GANs are a way of training a generative model to perform supervised learning with two sub-models– (i) the generator and (ii) the discriminator. The generator network takes the input as a random point in latent space and tries to decode it into a synthetic data (e.g. image). The discriminator network takes an input (real or synthetic) and predicts if it is from the training set (real input) or generator network (fake or synthetic input). The generator network tries to fool the discriminator network evolving towards generating more realistic synthetic data while the discriminator network tries to adapt constantly to match with the advanced capabilities of the generator network. Once the training is done, the generator is capable of converting any point in input space to a compelling synthetic point. The caveat is that, there is no explicit guarantee of meaningful structure, and it is not continuous. GAN was applied in [49] using face images to study CA.
2.5 Transfer learning
Transfer learning (TL) is an ML approach where a model learned from a task is re-purposed or reused on a different but related task [37]. The idea is to improve the learning for the second task based on the knowledge gathered from the first task. TL tends to work if both the tasks are general in principle. That is, if the features are specific to the base task and unrelated to the second task, the TL will probably not work well. TL can be used as a pre-trained model or as a develop model approach. A number of pre-trained models on large and challenging data sets are now available from different research institutes. We can select them from the pool for suitable cause. We can either reuse the model or tune the model for the specific task. However, when pre-trained models are not available, we can develop our own custom model for the base task, which can later be re-purposed for a model on the second task.
From the foregoing, various neural network models use very different architectures. However, to compare the performance of the DL methods described above, we need to consider some of the parameters. For instance, how deep the networks are (number of layers), number of filters in each layer, learning rate, loss function, weight initialization, dropout percent, optimization techniques, etc.
3 Data modalities
Here we consider the basic data modalities or types of data that have been used as inputs for BA estimation algorithms. These have ranged from blood biomarkers [38, 43] to images [9] to physical activity data [40, 44] to genomic or epigenetic data [19]. The National Health and Human Nutrition Examination Surveys (NHANES) provides biomarkers for different years from 1999–2015 (https://wwwn.cdc.gov/nchs/nhanes/). NHANES employs a complex cluster design to sample members of the civilian USA population who are not institutionalized. NHANES uses stratified multistage probability to sample the data. Ethnicity included white, black, Hispanic and others. The NHANES data set provides information on biomarkers, anthropometry and physical activity on individuals from the civilian US population. We obtained 21,451 individuals with 1,664 deaths during the 5–16 years of follow-up (1999–2015) from NHANES. Human Ageing Genomic Resources provides a collection of tools and databases in the area of genetics of human ageing (http://genomics.senescence.info/). For instance, this provides data sets for GenAge, GenDR, GeneExpression, LongevityMap, DrugAge and CellAge. Below we describe some of the larger data sets of different modalities that are used for age estimation.
Biomarkers
From the NHANES data set, we identified 21,451 individuals with information on their biomarkers. Biomarkers are used for both CA and BA estimation. For aging biomarkers, some of the biomarkers used are C-reactive protein, glycated hemoglobin, albumin, total cholesterol, urea nitrogen, alkaline phosphatase, systolic blood pressure, diastolic blood pressure, pulse, high density lipoprotein, hemoglobin, lymphocyte percent, white blood cell count, hematocrit, red blood cell count and platelet count. Table 1 shows the key biomarkers used in this study. Subsets of these have been used in earlier work as key biomarkers of BA, however, using non-deep learning methods [5, 24, 30, 43, 47]. Putin et al. [38] used a DL framework for CA prediction. Similarly, Mamoshina et al. [32] used a DL framework and studied physiological meaning of biomarkers for human aging.
Table 1.
Key anthropometric and biomarker attributes for study participants using the NHANES data set
| Anthropometric attributes |
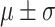
|
Biomarkers |
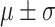
|
|---|---|---|---|
| Anthropometric | Average 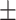 SD SD |
Biomarkers | Average 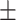 SD SD |
| Weight(W)(kg) | 75.49 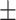 16.54 16.54 |
C-reactive protein | 0.37 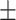 0.80 0.80 |
| Height(H)(cm) | 167.83 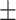 10.14 10.14 |
Glycated hemoglobin | 5.51 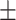 0.90 0.90 |
BMI(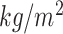 ) ) |
26.72 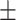 4.95 4.95 |
Serum albumin | 4.29 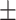 0.37 0.37 |
| Arm length (cm) | 37.16 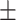 2.75 2.75 |
Total cholesterol | 196.58 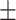 42.03 42.03 |
| Arm circumference (cm) | 31.57 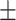 4.19 4.19 |
Serum urea nitrogen | 13.14 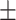 5.63 5.63 |
| Waist circumference (cm) | 93.56 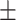 13.62 13.62 |
Serum alkaline phosphatase | 71.98 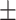 26.50 26.50 |
| Triceps skinfold (cm) | 17.92 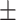 8.01 8.01 |
Systolic blood pressure | 123.99 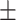 20.33 20.33 |
| Subscapular skinfold (cm) | 19.95 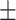 7.80 7.80 |
Diastolic blood pressure | 69.24 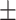 13.55 13.55 |
| Vertical trunk circumference (VTC) (cm) | 159.00 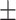 10.28 10.28 |
Pulse | 71.93 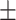 12.36 12.36 |
| Neck circumference (NC)(cm) | 39.67 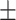 2.70 2.70 |
High density lipoprotein | 53.87 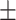 16.13 16.13 |
A body shape index (ABSI)(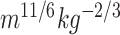 ) ) |
0.08 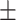 0.01 0.01 |
Hemoglobin | 14.31 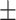 1.53 1.53 |
Body surface area (BSA)(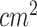 ) ) |
18235.73 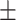 2223.73 2223.73 |
Lymphocyte percent | 30.08 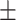 8.64 8.64 |
| Surface-based body shape (SBSI) | 0.12  0.01 0.01 |
White blood cell count | 7.19 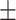 2.49 2.49 |
| Waist-to-height ratio (WHtR) | 0.56 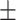 0.08 0.08 |
Hematocrit | 42.05 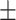 4.45 4.45 |
| BSA to VTC ratio (BSTC) | 114.28 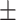 6.73 6.73 |
Red blood cell count | 4.68 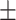 0.52 0.52 |
| VTC to NC ratio (VTNR) | 4.01 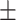 0.08 0.08 |
Platelet count | 259.14 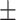 67.33 67.33 |
| VTC to H ratio (VTHR) | 0.95 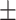 0.05 0.05 |
||
| VTC to WC ratio (VTWR) | 1.72 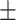 0.18 0.18 |
Age (years) | 46.45 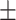 19.87 19.87 |
3.1 Anthropometry
Human body measurements represent a simple and easy-to-acquire group of features often used in health profiling. Anthropometric measurements generally include weight, height, body mass index (BMI), arm length, arm circumference, waist circumference, tricep skinfold, subscapular skinfold, vertical trunk circumference, neck circumference, body shape index, body surface area, surface-based body shape index (SBSI) and waist-to-height ratio (WHtR). Similar to biomarkers, we obtained data for 21,451 individuals from NHANES. Table 1 also shows the key body measurements used in this study and their statistics. Adjeroh et al. [1] studied correlation and predictability in human anthropometric measurements. Rahman and Adjeroh [41] showed that different anthropometric attributes are correlated with age and thus used them to predict all cause mortality. In more recent studies, they showed that anthropometric measurements can be used to estimate both CA and BA [42].
Another popular data set for human anthropometric measurements is the Civilian American and European Surface Anthropometry Resource (CAESAR) [46] data set (http://store.sae.org/caesar/). This data set includes manual hand measurements of the various anthropometric attributes, recorded as both 3D and 1D data. The 1D data sets from the CEASAR survey contains 2400 US and Canadian civilians, aged 18–65. Key measurements shared by both NHANES and CAESAR data sets tend to have similar general statistics. For example, the mean and standard deviation were observed as follows: height (NHANES 167.83 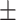 10.1; CAESAR 170.5
10.1; CAESAR 170.5 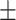 10.2), waist circumference (NHANES 93.56
10.2), waist circumference (NHANES 93.56 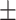 13.6; CAESAR 84.8
13.6; CAESAR 84.8 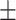 14.4), weight (NHANES 75.5
14.4), weight (NHANES 75.5 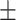 16.5; CAESAR 77
16.5; CAESAR 77 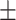 19.8), BMI (NHANES 26.7
19.8), BMI (NHANES 26.7 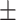 4.9; CAESAR 26.3
4.9; CAESAR 26.3 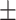 5.7).
5.7).
3.2 Physical activity
Human physical activity can be measured by an accelerometer. The intensity of the accelerometer can be used to estimate BA. Locomotor physical activity is also related to cardiorespiratory fitness (CRF) that has been linked to mortality [20]. NHANES provides physical (locomotor) activity for a 7-day continuous tracking of activity counts that is sampled every minute and recorded using a physical activity monitor (ActiGraph AM-7164 piezoelectric accelerometer). Intensity of the physical activity (also called device intensity value) is recorded by the physical activity monitor. The devices were worn on the right hip by the individuals using an elastic belt. The NHANES physical activity data set contained information on 14,631 study participants (7,176 in 2003–04 and 7,455 in 2005–06). Rahman and Adjeroh [44] and Pyrkov et al. [40] showed different convolutional architectures along with DNN to calculate BA from locomotor physical activity data. Pyrkov et al. [39] also studied physical activity data and their relationship with frailty, morbidity and mortality, however, without using DL methods.
3.3 Images
Different types of images have been used to estimate age for instance face, gait and brain MRI. Age estimation from face is probably the most popular. It remains a challenging problem because face aging is a complex process and involves many factors. Detailed surveys of methods for face-based age estimation can be found in Fu et al. [14] and Han et al. [16]. Bobrov et al. [7] showed a DNN-based model (called PhotoAgeClock) to estimate CA using image patches of eye corners. Their method resulted in an MAE of 2.3 years and 95% correlation with CA. However, none of the face image-based methods considered BA. MRI of the brain has been used to predict CA. Cole et al. [9] studied ‘brain predicted age’ as a biomarker from MRI data. They used a CNN-based network to estimate the brain age and showed that brain-predicted age represents a reliable and genetically influenced phenotype that could be used as a biomarker.
3.4 Genetic and epigenetic profiles
The epigenome is characterized by its ability to respond to cellular stimuli. Epigenetic modifications are often associated with certain health changes and disease status. Thus, epigenetic biomarkers are increasingly being used for early symptoms/detection of diseases, and hence as a predictor of future risk of disease development. Epigenetic changes are a complex combination of chemical, molecular and biological factors along with the genome. DNA methylation is perhaps the most popular and most studied epigenetic biomarker, and has been shown to be associated with aging [19]. Different research groups have studied the use of epigenetic factors, such as DNA methylation as a basis for age prediction [12, 19, 51]. Recently, Belsky et al. [6] compared different methods of BA estimation, including genomic, epigenetic and blood biomarker measures.
3.5 Electronic medical records
Electronic medical records (EMRs) provide a detailed health information about an individual. These records typically contain vital signs, laboratory test variables (essentially biomarkers) and many other features. Wang et al. [48] used EMR data from Mount Sinai Health System, involving over 4 million patient records from 1980 to 2015. After performing necessary refinement, they used data from 385,918 individuals. Their study covered 85 vital signs and 2,968 unique laboratory test variables. They showed that combining vital signs and laboratory tests predicted CA better than using each component separately.
4 Performance evaluation
Evaluation of CA is straight forward and well defined, but evaluation of BA is a less studied problem. With the increasing interest in BA, and the expanding number of approaches for its estimation, there is now an urgent need for effective methods to evaluate the BA estimation algorithms. In this work, we consider evaluation of BA estimation algorithms from four viewpoints, namely error in CA estimation, BA acceleration, mortality modeling and connection with health status. Since BA is said to be a better predictor of functional age when compared with CA, a good BA estimate should be able to separate individuals based on their disease status or overall health. The last three considerations are closely related to the general health of an individual or of a population.
4.1 CA performance
The following metrics have been used to evaluate accuracy in age estimation:
(1) Pearson correlation coefficient between x and y: 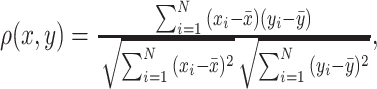 where
where 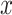 and
and 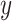 are different attributes,
are different attributes, 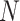 is number of samples.
is number of samples.
(2) Mean absolute error: 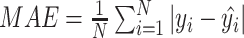 , where
, where 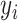 is the original value and
is the original value and 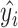 is the estimated value. In this work, MAE shows the average change/error between the CA and the estimated age.
is the estimated value. In this work, MAE shows the average change/error between the CA and the estimated age.
(3) Root mean square error (RMSE): 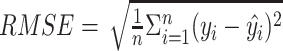 , where
, where 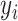 is the original value and
is the original value and 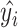 is the estimated value.
is the estimated value.
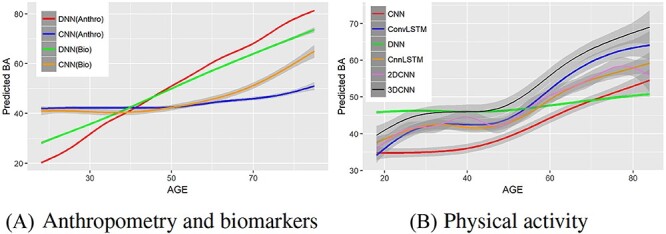
4.2 BA acceleration
Age acceleration is associated with problems in health. Age acceleration can be used to evaluate BA estimation methods. In general, age acceleration is defined as the difference between CA and BA: 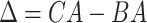 , where BA denotes the estimated age and CA denotes the chronological age. However, in a recent work, Rahman and Adjeroh [44] showed two new variations of aging acceleration. They proposed a normalized biological age acceleration (NBAA), denoted
, where BA denotes the estimated age and CA denotes the chronological age. However, in a recent work, Rahman and Adjeroh [44] showed two new variations of aging acceleration. They proposed a normalized biological age acceleration (NBAA), denoted 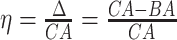 . The normalized form is used to reduce the effect of low values or high values of CA. However, when the loss function used in the DL method is based on the mean square error (as was used in this work), the required fitting minimization during learning will imply that this definition of
. The normalized form is used to reduce the effect of low values or high values of CA. However, when the loss function used in the DL method is based on the mean square error (as was used in this work), the required fitting minimization during learning will imply that this definition of 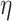 may still suffer from the known problem of ‘regressing to the mean’ [28]. To address this problem, they calculated the difference between an individuals’ BA and the average for a corresponding age and gender-matched cohort, defined as
may still suffer from the known problem of ‘regressing to the mean’ [28]. To address this problem, they calculated the difference between an individuals’ BA and the average for a corresponding age and gender-matched cohort, defined as 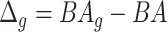 and
and 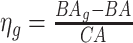 , where
, where 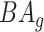 is the average for the age-gender matched cohort.
is the average for the age-gender matched cohort.
4.3 Mortality modeling
For validation and comparisons of the BA estimation algorithms, survival models, such as Cox proportional hazard model (Cox PH) and Kaplan–Meier (KM) curves can be used. Log-rank test is performed to quantify the KM plots. Log-rank test provides chi-square distances. Rahman and Adjeroh [43] also used receiver operating characteristics (ROC) curves to examine the sensitivity and specificity of CA and the predicted BAs in mortality modeling. They have applied estimators of cumulative and incident/dynamic area under curve (AUC). These estimators are given by the areas under the time dependent ROC curves estimated by sensitivity and specificity.
4.4 Connection with health status
Another way to investigate the performance of the estimated BAs in capturing health risks is to consider their possible relationship with known indicators of health risk or how the estimated BA differentiates between subjects with known diseases and those without.
Relationship with known health indices. For general indices of health status, various popular indices, e.g. the BMI, WHtR or the more recently introduced SBSI [41] or ABSI [26] can be used. Rahman and Adjeroh [44] studied the variation of the BA acceleration with variations in the WHtR and in SBSI categories. The idea is to observe the pattern of the performances from first quartile to the fourth quartile (in terms of estimated age). For a good BA estimator, we should expect a clear separation as we move from the lowest end to the highest end.
Relation with disease status. Another way is to analyze whether the proposed measure of BA acceleration would show any difference between healthy subjects and those with certain known chronic diseases such as diabetes, cardiovascular diseases (CVD) and kidney diseases. On average 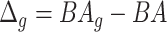 should be supposedly lower for the individuals having chronic diseases when compared with those for all subjects or those without any chronic disease. Also positive
should be supposedly lower for the individuals having chronic diseases when compared with those for all subjects or those without any chronic disease. Also positive 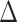 and
and 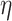 correspond to lower BA than the CA (more healthy), while negative values correspond to higher BA than the CA (less healthy). Ideally, subjects with no chronic disease should have the lowest proportion of negative
correspond to lower BA than the CA (more healthy), while negative values correspond to higher BA than the CA (less healthy). Ideally, subjects with no chronic disease should have the lowest proportion of negative  s.
s.
5 Results
In this study, we have used three different types of data modalities, namely biomarkers, anthropometry and locomotor physical activity. For the individuals that have biomarkers (21,451 subjects with 18 features) and anthropometry (21,451 subjects with 16 features), we used 1D CNN and DNN techniques. For the physical activity data (7,104 individuals with 10,080 features), however, we applied six different methods [DNN, CNN (1D, 2D, 3D), ConvLSTM and CNN+LSTM]. The 2D architectures (e.g. 2D CNN, CNN+LSTM) and 3D architectures (3D CNN, ConvLSTM) are not applicable for 1D biomarker and anthropometric features.
5.1 CA performance
Table 2 shows the comparative performance of the methods. We observe that applying DNN on biomarkers have the lowest MAE and highest correlation, whereas applying DNN on the anthropometry data resulted in estimated BAs with the lowest correlation with the CA. Table 3 shows the comparative performance of the DL methods applied on the physical activity. Figure 2A shows the results for the estimated ages applying DNN and CNN on biomarkers and anthropometric features, and Figure 2B shows the estimated BAs applied on human physical activity data.
Table 2.
Performance of DL age estimation methods in CA estimation, using anthropometric and biomarker features
| Anthropometry | Biomarkers | |||
|---|---|---|---|---|
| CNN | DNN | CNN | DNN | |
| MAE | 18.35 | 22.06 | 20.88 | 8.99 |
| RMSE | 22.44 | 27.08 | 28.19 | 12.01 |
Corr (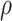 ) ) |
0.15 | 0.10 | 0.22 | 0.80 |
Table 3.
Performance of DL age estimation methods in CA estimation using physical activity data
| 1D CNN | DNN | ConvLSTM | CNN+LSTM | 2D CNN | 3D CNN | |
|---|---|---|---|---|---|---|
| MAE | 15.49 | 15.92 | 13.4 | 13.58 | 14.19 | 14.08 |
| RMSE | 18.81 | 18.38 | 16.74 | 16.45 | 17.48 | 19.40 |
Corr (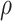 ) ) |
0.45 | 0.45 | 0.55 | 0.54 | 0.48 | 0.48 |
Figure 2.
Comparison of estimated age with CA for various DL methods using anthropometry, biomarkers and physical activity over the age range 18–84. Estimated BA against CA using (A) biomarkers and anthropometric features, (B) locomotor physical activity data.
We can observe that DNN outperformed CNN with respect to the MAE (a measure of CA estimation performance) using the biomarker data set. Different DL models tend to perform well on different data modalities. The nature of the data has a significant impact on the performance of a DL model. Typically, CNN (especially 2D-CNN) tends to do best on image data, which tends to capture important spatial relations in the data or data where the sequence ordering (e.g. temporal information) is significant. The anthropometric data and biomarker data used in this work are 1D data and captured neither temporal nor spatial information. Thus, we do not expect CNN to do very well on these (especially in terms of MAE, given our loss function). The activity data contains temporal information, which can easily be exploited by CNN, as we will see later, the CNN models performed better than the other models on this data set. However, we note that good performance with respect to MAE, may not always translate to very good performance in terms of BA estimation. For instance, as we will see below, CNN did better than DNN on biomarker data, with respect to BA, even though DNN had a smaller MAE.
5.2 Mortality modeling
To evaluate the estimated BAs, we have applied two statistical models from survival analysis, namely Cox proportional hazard model (CoxPH) [11, 25] and KM curves [23].
Cox PH. Under the Cox model, the relationship between hazard and the covariates is described by considering the logarithm of the hazard as a linear function of the variables. Here we calculate the hazard ratio (HR) for each BA estimation algorithm. We estimated BA using three different sets of data using different architectures, namely (i) anthropometry (CNN, DNN), (ii) biomarkers (CNN, DNN) and (iii) physical activity (1D CNN, DNN, CNN+LSTM, ConvLSTM, 2D CNN and 3D CNN models). Then we calculated  for each BA estimation algorithm.
for each BA estimation algorithm.
We applied 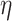 as the co-variate in the Cox model. Results for 1D CNN and DNN applied to the anthropometry and biomarkers data are shown in Table 4. Applying CNN the HR value is 1.13 for both anthropometry and biomarker features while applying DNN the HR is 1.62 for anthropometry and 1.10 for biomarkers. Similarly, Table 5 shows the results for Cox PH models applied on the estimated ages using physical activity data. We found that the BA estimation methods have generally similar performance on this modality. Best overall results using physical activity were obtained using 3D CNN, with HR = 1.14 (P-value 1.91E-16) using the normalized BA acceleration,
as the co-variate in the Cox model. Results for 1D CNN and DNN applied to the anthropometry and biomarkers data are shown in Table 4. Applying CNN the HR value is 1.13 for both anthropometry and biomarker features while applying DNN the HR is 1.62 for anthropometry and 1.10 for biomarkers. Similarly, Table 5 shows the results for Cox PH models applied on the estimated ages using physical activity data. We found that the BA estimation methods have generally similar performance on this modality. Best overall results using physical activity were obtained using 3D CNN, with HR = 1.14 (P-value 1.91E-16) using the normalized BA acceleration, 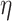 .
.
Table 4.
Results of the Cox proportional hazard (Cox PH) models applied on the normalized BA acceleration 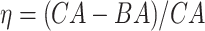 for estimated BAs using blood biomarkers and anthropometric data
for estimated BAs using blood biomarkers and anthropometric data
| HR | P-value | |
|---|---|---|
| Anthropometry | ||
| CNN | 1.13 ( 1.12, 1.14 ) | 2.11E-16 |
| DNN | 1.62 ( 1.58, 1.68 ) | 1.23E-16 |
| Biomarkers | ||
| CNN | 1.13 ( 1.12, 1.14 ) | 1.63E-16 |
| DNN [42] | 1.10 ( 1.09, 1.11 ) | 2.00E-09 |
Table 5.
Results of the Cox proportional hazard (Cox PH) models applied on the normalized BA acceleration 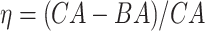 for estimated BAs using human locomotor physical activity data
for estimated BAs using human locomotor physical activity data
KM plots and log-rank test. Another way to study the performance of the estimated BAs is to analyse the KM survival curves [23] obtained using the quantile factored NBAA ( ). A given variable is a good mortality predictor if the KM curves are easily distinguishable (more distance between them), and the variable gives lower survival rates from low to high levels, with less crossing between curves. Figure 3 shows the KM plots for the BA estimation methods using anthropometry and biomarkers. In general, each method of predicting BA performed well in distinguishing the proportion of survivors. Among the DL BA estimation methods, distinction between the four quartiles using CNN on biomarkers was not as good as the other three methods. Similarly, Figure 4 shows the KM plots for BA estimation methods using different DL architectures on physical activity data.
). A given variable is a good mortality predictor if the KM curves are easily distinguishable (more distance between them), and the variable gives lower survival rates from low to high levels, with less crossing between curves. Figure 3 shows the KM plots for the BA estimation methods using anthropometry and biomarkers. In general, each method of predicting BA performed well in distinguishing the proportion of survivors. Among the DL BA estimation methods, distinction between the four quartiles using CNN on biomarkers was not as good as the other three methods. Similarly, Figure 4 shows the KM plots for BA estimation methods using different DL architectures on physical activity data.
Figure 3.
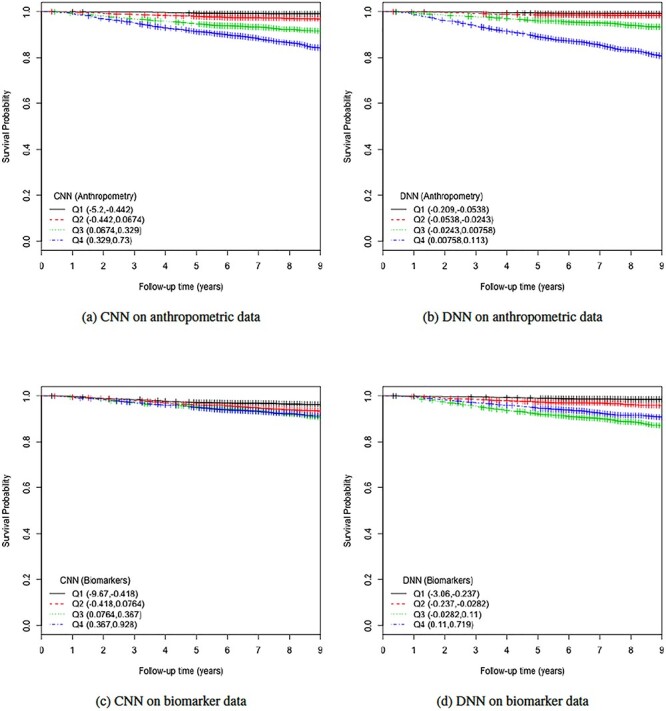
The KM curves for estimated BAs using two DL architectures on biomarker data and anthropometric data. Results are based on normalized BA acceleration 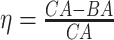 , using the estimated BAs. Q1, Q2, Q3and Q4 denote 1st, 2nd, 3rd and 4th quartiles, respectively.
, using the estimated BAs. Q1, Q2, Q3and Q4 denote 1st, 2nd, 3rd and 4th quartiles, respectively.
Figure 4.
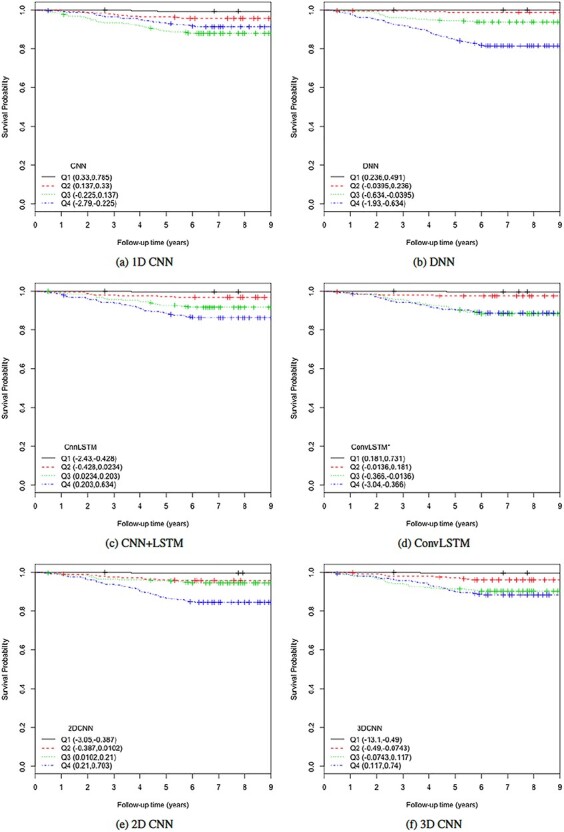
The KM curves for estimated BAs using six DL architectures on physical activity data applying 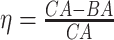 for estimated BAs. Q1, Q2, Q3 and Q4 denote 1st, 2nd, 3rd and 4th quartiles, respectively.
for estimated BAs. Q1, Q2, Q3 and Q4 denote 1st, 2nd, 3rd and 4th quartiles, respectively.
To further quantify the performance, we used the log-rank test to compare the survival distributions obtained using the different BA algorithms. The log-rank test compares the KM curves to check if they are statistically equivalent. The output of the test is a 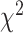 -distance and the P-value associated with the distance. Higher
-distance and the P-value associated with the distance. Higher 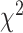 -distances and low P-values indicate a better separation between the curves and hence a better performance in mortality modeling. The difference among the BA estimation methods is more evident using quantitative measures, e.g. the
-distances and low P-values indicate a better separation between the curves and hence a better performance in mortality modeling. The difference among the BA estimation methods is more evident using quantitative measures, e.g. the 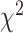 -distance between their respective KM curves, as captured by the log-rank test (Tables 6 and 7). DNN using anthropometric features for BA estimation has the best
-distance between their respective KM curves, as captured by the log-rank test (Tables 6 and 7). DNN using anthropometric features for BA estimation has the best 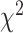 -distance in Table 6. For physical activity data, 3D CNN estimated BA has the highest
-distance in Table 6. For physical activity data, 3D CNN estimated BA has the highest 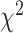 -distance followed by CNN+LSTM (see Table 7).
-distance followed by CNN+LSTM (see Table 7).
Table 6.
Results of the log-rank test applied on the normalized BA acceleration 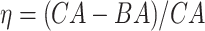 using the estimated BAs. Results are for the anthropometric data set and the biomarker data set
using the estimated BAs. Results are for the anthropometric data set and the biomarker data set
| DL architecture | Chi-Sq | P-value |
|---|---|---|
| Anthropometry | ||
| CNN | 375.71 | 6.22E-17 |
| DNN | 642.42 | 2.19E-16 |
| Biomarkers | ||
| CNN | 226.16 | 1.29E-16 |
| DNN [42] | 56.64 | 3.07E-12 |
Table 7.
Results of the log-rank test applied on the normalized BA acceleration 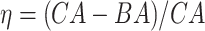 using the estimated BAs. Results are for the human physical activity data set
using the estimated BAs. Results are for the human physical activity data set
5.3 Connection with general health status
As discussed in [44], another way to investigate the performance of the different BA estimation methods is to consider their possible relationship with known indicators of health risk or how the estimated BA differentiates between subjects with known diseases and those without. Below we consider these two perspectives in evaluating the DL-based BA estimation methods introduced so far.
Relation with known health indices. For this evaluation, we selected two general indices of health status, namely the WHtR and the SBSI. WHtR is known to be a better measure of health status [35] when compared with the BMI. Rahman and Adjeroh [41] made a similar observation on the superiority of SBSI over BMI. Thus, we studied the variation of the proposed normalized BA acceleration (NBAA, denoted 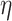 ) computed using the estimated BA from each method with variations in the WHtR and in SBSI categories. For biomarkers and anthropometric features, we applied CNN and DNN. Table 8 shows the log-rank test on the SBSI quartiles using biomarkers and anthropometric features. The results are shown using
) computed using the estimated BA from each method with variations in the WHtR and in SBSI categories. For biomarkers and anthropometric features, we applied CNN and DNN. Table 8 shows the log-rank test on the SBSI quartiles using biomarkers and anthropometric features. The results are shown using 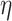 , for each SBSI category. We observe that, in general the
, for each SBSI category. We observe that, in general the 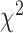 values increase from first quartile to fourth quartile. For instance, using CNN for both biomarkers and anthropometry and using DNN for biomarkers
values increase from first quartile to fourth quartile. For instance, using CNN for both biomarkers and anthropometry and using DNN for biomarkers 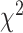 distance increases monotonically (from Q1 to Q4) while using DNN for anthropometry
distance increases monotonically (from Q1 to Q4) while using DNN for anthropometry 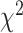 distance increases from Q1 to Q2, then decreases from Q2 to Q3, respectively. Correspondingly, Table 9 shows results for WHtR. Using CNN for both biomarkers and anthropometry
distance increases from Q1 to Q2, then decreases from Q2 to Q3, respectively. Correspondingly, Table 9 shows results for WHtR. Using CNN for both biomarkers and anthropometry 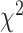 distance increases monotonically (from Q1 to Q4). Using DNN
distance increases monotonically (from Q1 to Q4). Using DNN 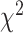 distance increases from Q1 to Q2, then decreases from Q2 to Q3, while the general trend is an increase from Q1 to Q4.
distance increases from Q1 to Q2, then decreases from Q2 to Q3, while the general trend is an increase from Q1 to Q4.
Table 8.
Log rank results applying the normalized BA acceleration (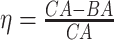 ) for different SBSI categories using anthropometric data and biomarker data, respectively. Q1, Q2, etc. denote 1st quartile, 2nd quartile, etc.
) for different SBSI categories using anthropometric data and biomarker data, respectively. Q1, Q2, etc. denote 1st quartile, 2nd quartile, etc.
| DL architecture |
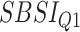
|
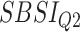
|
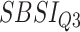
|
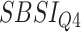
|
||||
|---|---|---|---|---|---|---|---|---|
| Chi-sq | P-value | Chi-sq | P-value | Chi-sq | P-value | Chi-sq | P-value | |
| Anthropometry | ||||||||
| CNN | 86.81 | 2.03E-16 | 219.15 | 1.92E-15 | 305.79 | 2.07E-14 | 727.11 | 3.03E-16 |
| DNN | 9.58 | 0.02 | 40.23 | 9.52E-09 | 10.96 | 0.01 | 36.93 | 4.77E-08 |
| Biomarkers | ||||||||
| CNN | 130.63 | 1.29E-16 | 159.84 | 4.03E-11 | 317.14 | 2.29E-13 | 764.68 | 7.03E-12 |
| DNN | 15.63 | 0.001 | 32.68 | 3.75E-07 | 108.06 | 0.00 | 340.97 | 0 |
Table 9.
Log rank results applying normalized BA acceleration (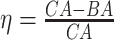 ) for different WHtR quartiles using anthropometric data and biomarker data, respectively. Q1, Q2, etc. denote 1st quartile, 2nd quartile, etc.
) for different WHtR quartiles using anthropometric data and biomarker data, respectively. Q1, Q2, etc. denote 1st quartile, 2nd quartile, etc.
| DL architecture |
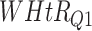
|
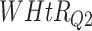
|
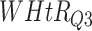
|
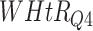
|
||||
|---|---|---|---|---|---|---|---|---|
| Chi-sq | P-value | Chi-sq | P-value | Chi-sq | P-value | Chi-sq | P-value | |
| Anthropometry | ||||||||
| CNN | 205.12 | 1.31E-07 | 388.57 | 6.20E-11 | 405.55 | 6.21E-09 | 687.06 | 8.03E-13 |
| DNN | 11.98 | 0.007 | 28.93 | 2.31E-06 | 15.68 | 0.001 | 13.77 | 0.003 |
| Biomarkers | ||||||||
| CNN | 233.26 | 7.34E-08 | 342.22 | 2.41E-11 | 414.40 | 3.72E-10 | 556.95 | 4.04E-16 |
| DNN | 35.37 | 1.02E-07 | 122.66 | 5.93E-06 | 117.62 | 2.94E-17 | 226.82 | 9.21E-09 |
Similar to biomarkers and anthropometric features, we applied different DL approaches to physical activity data. Table 10 shows the log-rank test on SBSI quartiles for human physical activity. We observed that, in general the 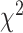 values increase from first quartile to fourth quartile. For instance, using CNN+LSTM method, the
values increase from first quartile to fourth quartile. For instance, using CNN+LSTM method, the 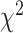 distance increases monotonically (from Q1 to Q4), while using DNN, CNN and ConvLSTM, the
distance increases monotonically (from Q1 to Q4), while using DNN, CNN and ConvLSTM, the 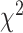 distance decreases from Q1 to Q2, then increases from Q2 to Q3 and Q3 to Q4, respectively. Correspondingly, with respect to the WHtR quartiles, we observe a similar trend in general for all the methods. Using CNN and ConvLSTM methods, the
distance decreases from Q1 to Q2, then increases from Q2 to Q3 and Q3 to Q4, respectively. Correspondingly, with respect to the WHtR quartiles, we observe a similar trend in general for all the methods. Using CNN and ConvLSTM methods, the 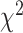 distances increased monotonically (from Q1 to Q4), whereas using DNN and CNN+LSTM show a decrease of
distances increased monotonically (from Q1 to Q4), whereas using DNN and CNN+LSTM show a decrease of 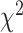 distances from Q3 to Q4. Table 11 shows the detailed results for log-rank test applied on the WHtR quartiles.
distances from Q3 to Q4. Table 11 shows the detailed results for log-rank test applied on the WHtR quartiles.
Table 10.
Log rank results applying normalized BA acceleration (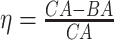 ) for different SBSI categories using activity data. Q1, Q2, etc. denote 1st quartile, 2nd quartile, etc.
) for different SBSI categories using activity data. Q1, Q2, etc. denote 1st quartile, 2nd quartile, etc.
| DL architecture |
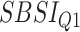
|
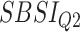
|
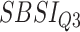
|
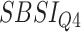
|
||||
|---|---|---|---|---|---|---|---|---|
| Chi-sq | P-value | Chi-sq | P-value | Chi-sq | P-value | Chi-sq | P-value | |
| CNN | 11.13 | 0.01 | 10.22 | 0.02 | 23.47 | 3.22E-05 | 63.80 | 9.06E-14 |
| DNN | 42.27 | 3.51E-09 | 22.95 | 4.14E-05 | 71.61 | 1.89E-15 | 131.52 | 1.49E-11 |
| CNN+LSTM | 22.16 | 6.04E-05 | 27.16 | 5.45E-06 | 38.57 | 2.14E-08 | 96.32 | 2.07E-16 |
| ConvLSTM | 13.25 | 4.12E-03 | 8.57 | 3.55E-02 | 13.37 | 3.90E-03 | 38.01 | 2.81E-08 |
| 2D CNN | 13.88 | 3.07E-03 | 18.98 | 2.76E-04 | 31.91 | 5.46E-07 | 78.28 | 1.11E-16 |
| 3D CNN | 10.37 | 1.57E-02 | 7.06 | 7.01E-02 | 17.75 | 4.95E-04 | 48.95 | 1.34E-10 |
Table 11.
Log rank results applying normalized BA acceleration (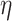 ) for different WHtR quartiles using activity data. Q1, Q2, etc. denote 1st quartile, 2nd quartile, etc.
) for different WHtR quartiles using activity data. Q1, Q2, etc. denote 1st quartile, 2nd quartile, etc.
| DL architecture |
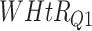
|
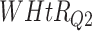
|
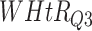
|
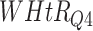
|
||||
|---|---|---|---|---|---|---|---|---|
| Chi-sq | P-value | Chi-sq | P-value | Chi-sq | P-value | Chi-sq | P-value | |
| CNN | 26.73 | 6.71E-06 | 29.97 | 1.40E-06 | 36.53 | 5.79E-08 | 38.92 | 1.81E-08 |
| DNN | 70.01 | 4.22E-15 | 93.30 | 3.18E-07 | 123.10 | 2.09E-08 | 91.77 | 9.17E-16 |
| CNN+LSTM | 51.67 | 3.52E-11 | 35.41 | 9.99E-08 | 68.72 | 7.99E-15 | 58.24 | 1.40E-12 |
| ConvLSTM | 15.01 | 1.81E-03 | 23.94 | 2.57E-05 | 24.93 | 1.60E-05 | 26.73 | 6.70E-06 |
| 2D CNN | 29.67 | 1.61E-07 | 49.04 | 1.28E-10 | 54.48 | 8.84E-12 | 55.87 | 4.49E-12 |
| 3D CNN | 9.13 | 2.76E-02 | 14.90 | 1.9E-03 | 28.79 | 4.02E-06 | 28.28 | 3.17E-06 |
Relation with disease status. We also considered the performance of the proposed measure of BA acceleration in terms of differences between healthy subjects and those with certain known diseases. Tables 12 and 13 show the results grouped for subjects having chronic diseases, such as diabetes, CVD and kidney diseases. Table 12 shows the results for estimated BAs based on biomarkers and anthropometry using CNN and DNN. On average 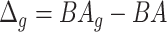 is lower for the individuals having chronic diseases than for all subjects. Subjects that do not suffer from any chronic disease have a lower
is lower for the individuals having chronic diseases than for all subjects. Subjects that do not suffer from any chronic disease have a lower 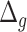 on average for all methods. Positive and negative refer to average of the subjects having positive and negative
on average for all methods. Positive and negative refer to average of the subjects having positive and negative 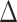 , respectively. Positive
, respectively. Positive 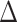 and
and 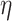 corresponds to lower BA than the CA (more healthy), while negative values correspond to higher BA than the CA (less healthy). In general, % of negative
corresponds to lower BA than the CA (more healthy), while negative values correspond to higher BA than the CA (less healthy). In general, % of negative 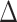 is higher for subjects with disease, compared with all subjects. Subjects with no chronic disease have the lowest proportion of negative
is higher for subjects with disease, compared with all subjects. Subjects with no chronic disease have the lowest proportion of negative 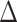 s. For both the anthropometric and biomarkers data set, CNN appears to perform better than DNN on this measure of differentiating between healthy subjects and those that have a given disease (highlighted as bold for average and % positive). Correspondingly, Table 13 shows the results for DL methods on human physical activity data. In general, the performances of the methods are similar. Based on the average
s. For both the anthropometric and biomarkers data set, CNN appears to perform better than DNN on this measure of differentiating between healthy subjects and those that have a given disease (highlighted as bold for average and % positive). Correspondingly, Table 13 shows the results for DL methods on human physical activity data. In general, the performances of the methods are similar. Based on the average 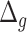 and % positive or % negative, for human activity data, best results were produced using 1D-CNN (highlighted) followed by CNN+LSTM, 3D-CNN and ConvLSTM.
and % positive or % negative, for human activity data, best results were produced using 1D-CNN (highlighted) followed by CNN+LSTM, 3D-CNN and ConvLSTM.
Table 12.
Performance of estimated BA for subjects with different chronic diseases using different DL models. Results are shown for BA acceleration (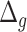 ) estimated using anthropometric data and blood biomarkers, respectively
) estimated using anthropometric data and blood biomarkers, respectively
| DNN (anthropometry) | CNN (anthropometry) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Diabetes | Kidney | CVD | All | Others | Diabetes | Kidney | CVD | All | Others | |
| Average | –0.96 | –0.73 | –0.67 | –0.01 | 0.20 | –4.89 | –4.58 | –2.62 | –0.82 | –0.18 |
| Positive | 0.66 | 0.81 | 0.60 | 0.78 | 0.81 | 8.34 | 8.24 | 8.39 | 8.90 | 9.05 |
| Negative | –1.69 | –1.78 | –1.64 | –1.54 | –1.45 | –12.49 | –12.90 | –11.16 | –10.55 | –10.22 |
| % Pos | 30.86 | 40.67 | 43.26 | 65.98 | 73.36 | 36.51 | 39.33 | 43.68 | 50.02 | 52.07 |
| % Neg | 69.14 | 59.33 | 56.74 | 34.02 | 26.64 | 63.49 | 60.67 | 56.32 | 49.98 | 47.93 |
| DNN (biomarkers) | CNN (biomarkers) | |||||||||
| Diabetes | Kidney | CVD | All | Others | Diabetes | Kidney | CVD | All | Others | |
| Average | –4.42 | –3.67 | –2.91 | 0.29 | 1.32 | –12.79 | –25.10 | –4.97 | –0.96 | 0.86 |
| Positive | 2.73 | 4.39 | 3.14 | 4.65 | 4.83 | 9.33 | 11.24 | 11.47 | 12.24 | 12.45 |
| Negative | –5.47 | –6.03 | –5.05 | –4.54 | –4.19 | –20.12 | –35.75 | –16.51 | –14.04 | –12.50 |
| % Pos | 12.87 | 22.67 | 26.11 | 52.51 | 61.09 | 24.87 | 22.67 | 41.26 | 49.77 | 53.54 |
| % Neg | 87.13 | 77.33 | 73.89 | 47.49 | 38.91 | 75.13 | 77.33 | 58.74 | 50.23 | 46.46 |
Table 13.
Performance of estimated BA for subjects having different chronic diseases using different DL models. Results are shown for BA acceleration (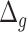 ) estimated using physical activity data
) estimated using physical activity data
| CNN | DNN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Diabetes | Kidney | CVD | All | Others | Diabetes | Kidney | CVD | All | Others | |
| Average | –8.59 | –9.89 | –6.39 | –3.17 | –1.95 | –2.94 | –3.29 | –1.87 | –1.02 | –0.68 |
| Positive | 5.61 | 12.74 | 9.00 | 9.17 | 9.34 | 0.70 | 1.70 | 0.72 | 0.82 | 0.83 |
| Negative | –11.90 | –10.79 | –11.27 | –10.04 | –9.5 | –4.31 | –5.13 | –3.27 | –2.47 | –2.04 |
| % Pos | 18.87 | 3.85 | 24.04 | 35.78 | 40.1 | 27.36 | 26.92 | 34.97 | 44.11 | 47.71 |
| % Neg | 81.13 | 96.15 | 75.96 | 64.22 | 59.9 | 72.64 | 73.08 | 65.03 | 55.89 | 52.29 |
| ConvLSTM | CNN+LSTM | |||||||||
| Diabetes | Kidney | CVD | All | Others | Diabetes | Kidney | CVD | All | Others | |
| Average | –5.18 | –3.66 | –2.92 | –0.67 | 0.25 | –6.47 | –6.20 | –3.27 | –1.62 | –0.83 |
| Positive | 7.49 | 9.20 | 7.89 | 8.84 | 8.98 | 5.80 | 10.58 | 6.28 | 7.05 | 7.20 |
| Negative | –9.51 | –10.47 | –8.33 | –8.07 | –7.67 | –9.32 | –10.19 | –8.53 | –8.46 | –8.29 |
| % Pos | 25.47 | 34.62 | 33.33 | 43.75 | 47.58 | 18.87 | 19.23 | 35.52 | 44.11 | 48.19 |
| % Neg | 74.53 | 65.38 | 66.67 | 56.25 | 52.42 | 81.13 | 80.77 | 64.48 | 55.89 | 51.81 |
| 2D-CNN | 3D-CNN | |||||||||
| Diabetes | Kidney | CVD | All-Subjects | Others | Diabetes | Kidney | CVD | All-Subjects | Others | |
| Average | –6.42 | –5.50 | –3.82 | –0.84 | 0.41 | –4.06 | –4.11 | –2.10 | 0.90 | 2.05 |
| Positive | 5.59 | 5.37 | 6.11 | 8.07 | 8.53 | 7.84 | 9.50 | 8.59 | 10.69 | 11.12 |
| Negative | –11.16 | –11.25 | –9.55 | –9.53 | –9.21 | –7.17 | –8.19 | –6.47 | –6.60 | –6.51 |
| % Pos | 28.30 | 34.62 | 36.61 | 49.37 | 54.23 | 20.75 | 23.08 | 28.96 | 43.39 | 48.55 |
| % Neg | 71.70 | 65.38 | 63.39 | 50.63 | 45.77 | 79.25 | 76.92 | 71.04 | 56.61 | 51.45 |
6 Discussion
In this work, we have investigated DL approaches on different types of data (e.g. biomarkers, anthropometry, locomotor physical activity) to estimate BA. To quantify how well the estimated BA captures the health risk, we applied the Cox proportional hazard model and KM curves for analysis of all-cause mortality. The DL models such as DNN, CNN, ConvLSTM, CNN+LSTM were trained to exploit the dependence of the physiological/activity changes with age. In all cases, the DL approaches were trained to minimize the MSE between the CA and estimated BA.
6.1 Comparison
We have shown comparative performance of different data modalities using survival models (Cox PH, KM plots and log-rank test). We then observed performance of the estimated BA in terms of connection with health status (relations with popular health indices and in relation with disease status for chronic diseases such as diabetes, kidney diseases and CVD). Methods discussed in this study use supervised learning that learn by minimizing the MSE. For the data set that contains both biomarkers and anthropometry, we applied two DL methods (CNN and DNN). DNN applied on anthropometric data has the lowest MAE of 8.99 and highest correlation (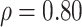 ). Applying CoxPH and log-rank test DNN with anthropometry data has the highest HR (1.62) and highest
). Applying CoxPH and log-rank test DNN with anthropometry data has the highest HR (1.62) and highest 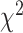 -distance. Using log-rank test for SBSI quartiles, applying CNN for both biomarkers and anthropometry,
-distance. Using log-rank test for SBSI quartiles, applying CNN for both biomarkers and anthropometry, 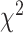 -distance increases monotonically from Q1 to Q4. Similarly, using WHtR quartiles, applying CNN for both biomarkers and anthropometry,
-distance increases monotonically from Q1 to Q4. Similarly, using WHtR quartiles, applying CNN for both biomarkers and anthropometry, 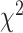 -distance increases monotonically from Q1 to Q4. For anthropometric data set, CNN appears to perform better than DNN on this measure of differentiating between healthy subjects and those that have a given disease. Between anthropometry and biomarker data sets, applying CNN on the blood biomarkers produced the best result on these two data modalities.
-distance increases monotonically from Q1 to Q4. For anthropometric data set, CNN appears to perform better than DNN on this measure of differentiating between healthy subjects and those that have a given disease. Between anthropometry and biomarker data sets, applying CNN on the blood biomarkers produced the best result on these two data modalities.
For the physical activity data, we applied six different methods (DNN, 1D-CNN, 2D-CNN, 3D-CNN, ConvLSTM, CNN+LSTM). Table 3 shows the comparative performance of the different methods. Among the methods, ConvLSTM and CNN+LSTM produced lowest MAE of 13.40, 13.58 and highest correlation (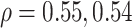 ), respectively. Applying
), respectively. Applying 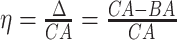 in CoxPH model as the co-variate, for all the DL techniques, we observe similarity in their HRs. However, for log-rank test, 3D-CNN has the highest
in CoxPH model as the co-variate, for all the DL techniques, we observe similarity in their HRs. However, for log-rank test, 3D-CNN has the highest 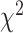 -distance followed by CNN+LSTM. Using log-rank test for SBSI quartiles applying CNN+LSTM and 3D-CNN
-distance followed by CNN+LSTM. Using log-rank test for SBSI quartiles applying CNN+LSTM and 3D-CNN 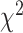 -distance increases monotonically from Q1 to Q4. With respect to WHtR quartiles, applying CNN and ConvLSTM
-distance increases monotonically from Q1 to Q4. With respect to WHtR quartiles, applying CNN and ConvLSTM 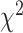 -distance increases monotonically from Q1 to Q4. Based on the average
-distance increases monotonically from Q1 to Q4. Based on the average 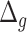 and % positive or % negative, for human activity data, we obtain best results using 1D-CNN followed by CNN+LSTM, 3D-CNN and ConvLSTM.
and % positive or % negative, for human activity data, we obtain best results using 1D-CNN followed by CNN+LSTM, 3D-CNN and ConvLSTM.
DL methods (DNN, CNN) applied for biomarkers and anthropometric features do not have a clear cut winner with respect to MAE, CoxPH, KM plots and 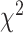 -distances. With respect to connections with general health status, CNN-based methods perform better than DNN. Similarly, for the physical activity data, ConvLSTM has the lowest MAE and highest correlation, 3D-CNN has the highest HR, and 2D-CNN gives the highest
-distances. With respect to connections with general health status, CNN-based methods perform better than DNN. Similarly, for the physical activity data, ConvLSTM has the lowest MAE and highest correlation, 3D-CNN has the highest HR, and 2D-CNN gives the highest 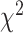 -distance among the methods. With respect to relations with known health indices, 2D-CNN-based method has best performance and with respect to relation with disease status 1D-CNN has the best overall performance.
-distance among the methods. With respect to relations with known health indices, 2D-CNN-based method has best performance and with respect to relation with disease status 1D-CNN has the best overall performance.
The methods learn in the form of minimizing the difference between estimated BA and the CA. This difference has been called BA acceleration [34] in the literature. Pyrkov et al. [40] suggested that an improvement in CA estimation can affect the significance of BA acceleration for a particular test that may involve health risks. This also relates to the issue of ‘paradox of biomarkers’ as described by Klemera and Doubal [24] and Hochschild [18]. These results seem to suggest that improved CA estimation may not always lead to a deterioration in BA estimation. The issue might be in how the estimated BA is used for further analysis, rather than the accuracy of the initial CA estimation. This clearly warrants further investigation.
7 Conclusion and future directions
In this work, we studied BA estimation methods using human biomarkers, human anthropometry and locomotor activity. From a public health perspective, aging can be a critical risk factor for various pathologies such as many forms of cancers and type II diabetes. The use of EMR systems has greatly increased in hospitals and most hospitals have now adopted at least a basic EMR system. Estimated BA based on the EMR features can be used for disease susceptibility in public health, health management and by insurance companies. We applied several different DL models to estimate and compare BA using these methods. We established that different modalities can be used to exploit 1D features and temporal patterns (3D CNN, ConvLSTM) in human locomotor physical activity to estimate BA. The paper used four different measures to compare performance in BA estimation, including the traditional measures of prediction error, (namely, MAE, RMSE and correlation). We also used relation with known health indices (WHtR and SBSI) and relation with disease status (CVD, diabetes and kidney diseases), in addition to traditional mortality modeling using Cox PH, 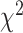 -distance from the log-rank test and KM curves.
-distance from the log-rank test and KM curves.
DL methods are rapidly emerging and are starting to deliver encouraging results in biological aging and longevity research. Possible future work includes use of GANs in CA and BA estimation (using physical activity data), use of 3D human modeling combined with geometric DL [29], use of attention-based models [4] and of domain adaptation [36] (use transfer learning from a set of features to a different set). Methods discussed in this work can either be used as standalone approaches or integrated within learning pipelines for solving more complex tasks. These pipelines can capture efficient feature selection. Deep networks can be used to learn features over multiple modalities. In cross modality feature learning, better feature for one modality can be learned if multiple modalities are present at learning time. While using physical activity, blood biomarkers and anthropometric data separately performs reasonably well for CA estimation alone, fusing these multimodal information can substantially improve performance of BA estimation. We can also observe that different methods seem to perform better on different data modalities. Thus, performing such multimodal fusion can be best done by considering the DL method(s) that worked best on a given data modality, and then combine these best results, for instance, using score-level, or decision-level fusion. Another potential future work will be to perform population specific studies and observe performance on different ethnic groups, while using these multimodal approaches.
Cardio respiratory fitness (CRF) is related to numerous physiological systems, including cardiovascular, respiratory and musculoskeletal systems [20]. Similar to biological age, CRF is also considered as one other reflection of whole-body health and function, and hence one of the predictors of all-cause mortality [20]. Thus, another potential future work will be to study the relationship between BA and CRF, for instance, using a DL framework.
Another interesting challenge and potential extension of this work is to study how the estimated BA can be used as a tool for general health profiling. For instance, the DL-based methods can be applied for public health campaign, and general health monitoring, by analyzing the estimated BA at a population scale. The results of such analysis could also serve as an early indicator of patients that may require palliative care, and hence could provide a tool for health-care providers and policy makers for preparing for such patients.
8 Appendix
9 Competing interests
There is NO competing interest.
Supplementary Material
Acknowledgments
The authors thank the anonymous reviewers for their valuable suggestions.
Syed Ashiqur Rahman, PhD is a researcher in the Lane Department of Computer Science and Electrical Engineering at West Virginia University. His research interests focus on the application of machine learning and data analytics to health sciences.
Peter Giacobbi, PhD is an associate professor in the College of Physical Activity and Sport Sciences with a joint appointment with the School of Public Health at West Virginia University.
Lee A. Pyles, MD, MS is an associate professor in the Department of Pediatrics, School of Medicine at West Virginia University. His specialty is in pediatric cardiology.
Charles J. Mullett, MD, PhD is an associate professor and chairman in the Department of Pediatrics at West Virginia University. His clinical focus is on critical care medicine and congenital heart disease.
Gianfranco Doretto, PhD is an associate professor in the Lane Department of Computer Science and Electrical Engineering at West Virginia University. He has research interests in computer vision, machine learning, deep learning, medical imaging and virtual reality.
Donald Adjeroh, PhD is a professor and associate department chair in the Lane Department of Computer Science and Electrical Engineering at West Virginia University. He has research interests in data structures, machine learning and biomedical informatics.
10 Key Points
We provide a survey on existing deep learning (DL) architectures that have been used for biological age (BA) estimation.
We showed results of existing DL techniques for BA estimation on different data modalities and compared their performances.
We showed performance evaluation based on different techniques, including some techniques we introduced in the paper.
Funding
This work is supported in part by funds from the National Science Foundation (NSF: # 1636933 and # 1920920).
References
- 1. Adjeroh D, Cao D, Piccirilli M, et al. Predictability and correlation in human metrology. In: IEEE International Workshop on Information Forensics and Security (WIFS), 2010. pp. 1–6. Seattle, WA, USA: IEEE.
- 2. Altmann A, Toloşi L, Sander O, et al. Permutation importance: A corrected feature importance measure. Bioinformatics 2010; 26(10): 1340–7. [DOI] [PubMed] [Google Scholar]
- 3. Anstey KJ, Lord SR, Smith GA. Measuring human functional age: a review of empirical findings. Exp Aging Res 1996; 22(3): 245–66. [DOI] [PubMed] [Google Scholar]
- 4. Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate. arXiv 2014; 1–15.
- 5. Belsky DW, Caspi A, Houts R, et al. Quantification of biological aging in young adults. Proc Natl Acad SciU S A 2015; 112(30): E4104–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Belsky DW, Moffitt TE, Cohen AA, et al. Eleven telomere, epigenetic clock, and biomarker-composite quantifications of biological aging: do they measure the same thing? Am J Epidemiol 2017; 187(6): 1220–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Bobrov E, Georgievskaya A, Kiselev K, et al. PhotoAgeClock: Deep learning algorithms for development of non-invasive visual biomarkers of aging. Aging (Albany NY) 2018; 10(11): 3249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Cho IH, Park KS, Lim CJ. An empirical comparative study on biological age estimation algorithms with an application of Work Ability Index (WAI). Mech Ageing Dev 2010; 131(2): 69–78. [DOI] [PubMed] [Google Scholar]
- 9. Cole JH, Poudel RPK, Tsagkrasoulis D, et al. Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. NeuroImage 2017; 163:115–24. [DOI] [PubMed] [Google Scholar]
- 10. Cole JH, Ritchie SJ, Bastin ME, et al. Brain age predicts mortality. Mol Psychiatry 2018; 23: 1385–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Cox DR Oakes D. Analysis of Survival Data, vol. 21. Boca Raton, Florida, USA: CRC Press, 1984. [Google Scholar]
- 12. Eipel M, Mayer F, Arent T, et al. Epigenetic age predictions based on buccal swabs are more precise in combination with cell type-specific DNA methylation signatures. Aging 2016; 8(5):1034–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Fischer K, Kettunen J, Würtz P, et al. Biomarker profiling by nuclear magnetic resonance spectroscopy for the prediction of all-cause mortality: an observational study of 17,345 persons. PLoS Med 2014; 11(2):e1001606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Fu Y, Guo G, Huang TS. Age synthesis and estimation via faces: A survey. IEEE Pattern Anal 2010; 32(11): 1955–76. [DOI] [PubMed] [Google Scholar]
- 15. Goodfellow I, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. In: Advances in Neural Information Processing Systems. Montreal, Quebec, Canada: NIPS, 2014, 2672–80.
- 16. Han H, Otto C, Liu X, et al. Demographic estimation from face images: human vs. machine performance. IEEE Pattern Anal 2015; 37(6): 1148–61. [DOI] [PubMed] [Google Scholar]
- 17. Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput 1997; 9(8): 1735–80. [DOI] [PubMed] [Google Scholar]
- 18. Hochschild R. Improving the precision of biological age determinations. Part 1: a new approach to calculating biological age. Exp Gerontol 1989; 24(4): 289–300. [DOI] [PubMed] [Google Scholar]
- 19. Horvath S. DNA methylation age of human tissues and cell types. Genome Biol 2013; 14(10): 3156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Imboden MT, Harber MP, Whaley MH, et al. Cardiorespiratory fitness and mortality in healthy men and women. J Am Coll Cardiol 2018; 72(19): 2283–92. [DOI] [PubMed] [Google Scholar]
- 21. Jackson SHD, Weale MR, Weale RA. Biological age–what is it and can it be measured? Arch Gerontol Geriatr 2003; 36(2): 103–15. [DOI] [PubMed] [Google Scholar]
- 22. Ji S, Xu W, Yang M, et al. 3D convolutional neural networks for human action recognition. IEEE Pattern Anal 2012; 35(1): 221–31. [DOI] [PubMed] [Google Scholar]
- 23. Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. J Am Stat Assoc 1958; 53(282): 457–81. [Google Scholar]
- 24. Klemera P, Doubal S. A new approach to the concept and computation of biological age. Mech Ageing Dev 2006; 127(3): 240–8. [DOI] [PubMed] [Google Scholar]
- 25. Kom EL, Graubard BI, Midthune D. Time-to-event analysis of longitudinal follow-up of a survey: choice of the time-scale. Am J Epidemiol 1997; 145(1): 72–80. [DOI] [PubMed] [Google Scholar]
- 26. Krakauer NY, Krakauer JC. A new body shape index predicts mortality hazard independently of Body Mass Index. PLoS ONE 2012; 7(7):e39504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. In: Advances in Neural Information Processing Systems. Lake Tahoe, NV, USA: NIPS, 2012, 1097–105.
- 28. Krøll J, Saxtrup O. On the use of regression analysis for the estimation of human biological age. Biogerontology 2000; 1(4): 363–8. [DOI] [PubMed] [Google Scholar]
- 29. LeCun Y, Bengio Y, Hinton G. Deep learning. Nature 2015; 521(7553): 436. [DOI] [PubMed] [Google Scholar]
- 30. Levine ME. Modeling the rate of senescence: can estimated biological age predict mortality more accurately than chronological age? J Gerontol A Biol Sci Med Sci 2012; 68(6): 667–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Liu Z, Kuo P-L, Horvath S, et al. Phenotypic age: a novel signature of mortality and morbidity risk. BioRxiv 2018,. 363291. [Google Scholar]
- 32. Mamoshina P, Kochetov K, Putin E, et al. Population specific biomarkers of human aging: a big data study using South Korean, Canadian, and Eastern European patient populations. J Gerontol A 2018; 73(11): 1482–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Miotto R, Wang F, Wang S, et al. Deep learning for healthcare: review, opportunities and challenges. Brief Bioinform 2017; 19(6): 1236–46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Mitnitski A, Howlett SE, Rockwood K. Heterogeneity of human aging and its assessment. J Gerontol A Biol Sci Med Sci 2016; 72(7): 877–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Mørkedal B, Romundstad PR, Vatten LJ. Informativeness of indices of blood pressure, obesity and serum lipids in relation to ischaemic heart disease mortality: the HUNT-II study. Eur J Epidemiol 2011; 26(6): 457–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Motiian S, Piccirilli M, Adjeroh DA, et al. Unified deep supervised domain adaptation and generalization. In: Proceedings of the IEEE International Conference on Computer Vision. Venice, Italy: IEEE, 2017, 5715–25.
- 37. Murphy KP. Machine learning: a probabilistic perspective. Cambridge, MA, USA: MIT Press, 2012. [Google Scholar]
- 38. Putin E, Mamoshina P, Aliper A, et al. Deep biomarkers of human aging: Application of deep neural networks to biomarker development. Aging 2016; 8(5): 1–021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Pyrkov TV, Getmantsev E, Zhurov B, et al. Quantitative characterization of biological age and frailty based on locomotor activity records. Aging (Albany NY) 2018; 10(10): 2973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Pyrkov TV, Slipensky K, Barg M, et al. Extracting biological age from biomedical data via deep learning: Too much of a good thing? Sci Rep 2018; 8(1): 5210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Rahman SA, Adjeroh D. Surface-based body shape index and its relationship with all-cause mortality. PLoS ONE 2015; 10(12):e0144639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Rahman SA, Adjeroh D. Centroid of age neighborhoods: A generalized approach to estimate biological age. In: 2019 IEEE EMBS International Conference on Biomedical & Health Informatics (BHI), 2019, pp. 1–4. Chicago, IL, USA: IEEE. [DOI] [PMC free article] [PubMed]
- 43. Rahman SA, Adjeroh D. Centroid of age neighborhoods: A new approach to estimate biological age. IEEE J Biomed Health 2019; 1–4. (published online). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Rahman SA, Adjeroh DA. Deep learning using convolutional LSTM estimates biological age from physical activity. Sci Rep 2019; 9(1): 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Ravì D, Wong C, Deligianni F, et al. Deep learning for health informatics. IEEE J Biomed Health 2016; 21(1): 4–21. [DOI] [PubMed] [Google Scholar]
- 46. Robinette KM, Daanen H, Paquet E. The CAESAR Project: a 3-D surface anthropometry survey. In: Second International Conference on 3-D Digital Imaging and Modeling, 1999. pp. 380–6. Ottawa, Ontario, Canada: IEEE.
- 47. Sebastiani P, Thyagarajan B, Sun F, et al. Biomarker signatures of aging. Aging Cell 2017; 16(2): 329–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Wang Z, Li L, Glicksberg BS, et al. Predicting age by mining electronic medical records with deep learning characterizes differences between chronological and physiological age. J Biomed Inform 2017; 76:59–68. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Wang Z, Tang X, Luo W, et al. Face aging with identity-preserved conditional generative adversarial networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Long Beach, CA, USA: IEEE, 2018, 7939–47. [Google Scholar]
- 50. Xingjian SHI, Chen Z, Wang H, et al. Convolutional lstm network: a machine learning approach for precipitation nowcasting. In: Advances in Neural Information Processing Systems. Montreal, Quebec, Canada: NIPS, 2015, 802–10.
- 51. Xu C, Qu H, Wang G, et al. A novel strategy for forensic age prediction by DNA methylation and support vector regression model. Sci Rep 2015; 5:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Zhang K, Liu N, Yuan X, et al. Fine-grained age estimation in the wild with attention LSTM networks. arXiv 2019; 1–12.
- 53. Zhavoronkov A, Mamoshina P, Vanhaelen Q, et al. Artificial intelligence for aging and longevity research: recent advances and perspectives. Ageing Res Rev 2019; 49:49–66. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


