Porous shape-persistent rylene imine cages with tunable optoelectronic properties and delayed fluorescence

Abstract

A simultaneous combination of porosity and tunable optoelectronic properties, common in covalent organic frameworks, is rare in shape-persistent organic cages. Yet, organic cages offer important molecular advantages such as solubility and modularity. Herein, we report the synthesis of a series of chiral imine organic cages with three built-in rylene units by means of dynamic imine chemistry and we investigate their textural and optoelectronic properties. Thereby we demonstrate that the synthesized rylene cages can be reversibly reduced at accessible potentials, absorb from UV up to green light, are porous, and preferentially adsorb CO₂ over N₂ and CH₄ with a good selectivity. In addition, we discovered that the cage incorporating three perylene-3,4:9,10-bis(dicarboximide) units displays an efficient delayed fluorescence. Time-correlated single photon counting and transient absorption spectroscopy measurements suggest that the delayed fluorescence is likely a consequence of a reversible intracage charge-separation event. Rylene cages thus offer a promising platform that allows combining the porosity of processable materials and photochemical phenomena useful in diverse applications such as photocatalysis or energy storage.

Chiral rylene imine cages combine porosity and tunable optoelectronic properties. They adsorb CO₂ over N₂ with good selectivity and can show an efficient delayed fluorescence.

Introduction

Shape-persistent organic cages opened up new possibilities to form various supramolecular hosts and porous materials with well-defined, tunable internal cavities.¹ The porosity of organic cages originates from the presence of the internal cavity, which is responsible for the intrinsic porosity of the material along with other accessible pores that emanate from the extrinsic voids created through the packing of cage molecules in the solid-state. Unlike other porous materials such as zeolites,² metal–organic frameworks³ (MOFs), covalent organic frameworks⁴ (COFs) and porous organic polymers,⁵ the solution processability of porous organic cages^1,4b (POCs) represents an important advantage. It should, however, be noted that the packing of cage molecules has a profound impact on the porosity of POCs. For example, different polymorphs have been shown to result in different porosity.⁶ Similar to COFs, POCs are typically synthesized from highly preorganized organic building blocks via dynamic covalent chemistry⁷ utilizing reversible condensation and addition reactions or alkyne methathesis. The most prominent examples are the condensation reactions of boronic acids with alcohols and aldehydes with amines. This approach circumvents the problems of multi-step synthesis that relies on kinetically controlled reactions with low overall yields. Although the resulting structures are often not chemically stable, post-synthetic modification strategies to convert organic cages into stable materials have recently emerged.⁸ The porosity of some POCs has been shown to match that of COFs.^1,6b,9 Accordingly, POCs have been exploited in applications that rely on their porous nature, such as gas sorption and separation,¹⁰ molecular sieving,¹¹ sensing,¹² catalysis¹³ or transport of ions.¹⁴

However, contrary to COFs, studies that explore the electronic properties of POCs are rather scarce. Yet, organic cages represent well-defined molecular architectures with building blocks arranged spatially with high precision, which is an important requirement for electronic materials. As a result, properties that typically arise from the interplay of the intermolecular electronic coupling between molecules in the solid-state could potentially emerge within a single cage due to its three-dimensional structure. Importantly, the incorporation of chromophores or redox-active molecules could also allow the investigation of their mutual electronic communication both in a solution or in the solid-state.

Two examples of POCs incorporating porphyrin moieties have recently been shown to exhibit interesting optoelectronic properties. Porphyrin boxes¹⁶ can possess relatively high Brunauer–Emmett–Teller (BET) surface areas (1370 m² g⁻¹) and show a good selectivity towards CO₂ over N₂ and CH₄. The ability to incorporate different metal centers into porphyrins transforms porphyrin POCs into promising heterogeneous CO₂ or O₂ reduction catalysts.^16b,c The co-crystallization of a cube-shaped porphyrin cage with fullerenes allows for a photoinduced charge-separation^16d with a biphasic decay of the charge-separated state due to the anisotropy of the porphyrin–fullerene interaction that cannot be achieved in the co-crystals of fullerenes with monomeric porphyrin units. Recently,¹⁷ the first porphyrin heterogeneous POC photocatalyst has been reported. It generates singlet oxygen with high-efficiency and facilitates photo-oxidation of primary amines with conversion efficiencies >99% under visible light irradiation. Other examples of luminescent or diradicaloid organic cages also exist but they are accessed via kinetically controlled reactions or the porosity of these cages has not yet been determined.¹⁸

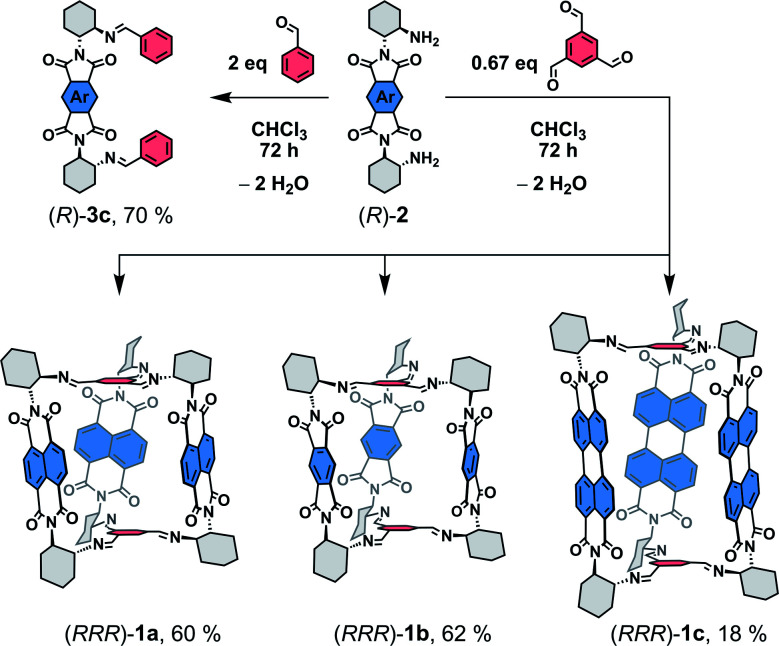
We have recently reported¹⁹ the first example from a series of chiral imine organic cages 1 (Scheme 1) with built-in redox-active rylene units. Cage 1a is composed of three naphthalene-1,4:5,8-bis(dicarboximide)s (NDIs), a well-known electron acceptor, which endowed 1a with unique optoelectronic properties such as the ability to store up to six electrons, intracage electron hopping and photoinduced charge-separation with prolonged excited state lifetimes. Encouraged by these initial results, herein, we explore the structural variability of rylene cages 1 and complete the series by the synthesis of 1b and 1c that consist of three pyromellitic diimide (PMDI) and perylene-3,4:9,10-bis(dicarboximide) (PDI) units, respectively. These cages demonstrate the ability to tune their redox or optical properties with chromophores absorbing from UV to visible. We discovered an intriguing excited state behavior of 1c, which displays a delayed fluorescence in solution. The measured steady-state optical spectra, quantum yields, time-correlated single photon counting, transient absorption, and electrochemical data suggest that photoexcited cage 1c undergoes a reversible intra-cage charge separation between two PDI units. Moreover, we also explored the porosity and affinity of these cages towards small gases. Notably, we showed that rylene cages 1 are porous and possess a good CO₂ selectivity over N₂ and CH₄. The interplay between the textural and electronic properties of these cages could pave the way for the development of highly efficient porous photocatalysts or optoelectronic materials.

Scheme 1. Synthesis of 1a–c and 3 from diamines 2.¹⁵.

Results and discussion

Synthesis and properties

The structure of the cages 1 requires that a ditopic amine and a tritopic aldehyde react in a [3 + 2] condensation reaction (Scheme 1). Previously,¹⁹ we synthesized 1a by refluxing the diamine 2a with benzene-1,3,5-tricarbaldehyde in toluene under Dean–Stark conditions. However, this approach was not suitable for the synthesis of 1c because the corresponding diamine 2c has a very low solubility in toluene. Although, the cage formation could be detected by MALDI-TOF, a majority of 2c formed an insoluble film leading to negligible yield and impure samples. Generally, PDIs have a lower solubility compared to the NDI or PMDI derivatives. Therefore, we performed DFT calculations to estimate the relative stabilities of 1b and 1c using an isodesmic reaction shown in Scheme S1† prior to the synthesis. We found that all cages display similar stability (Table S1†) even when the solvent environment was included, which promised a successful synthesis of 1b and 1c. The thermodynamic control of imine formation demands that the starting compounds are soluble to drive the equilibrium to the products. We therefore tried to synthesize 1a in dry chloroform, in which the diamines 2 possess a sufficient solubility. We observed a full conversion and a clean formation of 1a in 72 hours at 80 °C in 60% yield after purification by HPLC. It suggests that 1a is the thermodynamic product in chloroform. The PMDI cage 1b was then synthesized from 2b formed in situ from its ditosyl salt, which allowed an easier handling and synthesis, in the presence of excess triethylamine in 62% yield after purification. Finally, PDI cage 1c was prepared from 2c in 18% yield. The three-dimensional shape of the cages improved their solubility in chlorinated solvents, THF, toluene or nitrobenzene when compared to simple PMDI, NDI, and PDI derivatives with cyclohexyls in imide positions. However, cage 1c possesses the lowest solubility in the series, which complicated its purification and affected the isolated yield. The structure of cages 1 was confirmed by ¹H, ¹³C and 2D homo- and heteronuclear correlation NMR spectroscopy, HR-ESI mass spectrometry (see the ESI†) and single crystal X-ray diffraction analysis (XRD, vide infra).

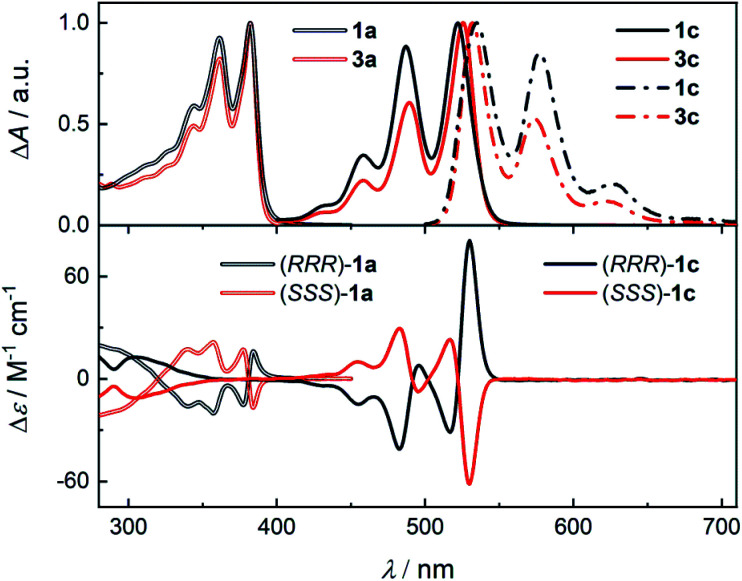
Enantiopure samples of (RRR)- or (SSS)-1 are obtained when the synthesis commences from enantiopure diamines 2 as evidenced by the mirror images of the circular dichroism spectra of each pair of enantiomers (Fig. 1 and S45†). The Cotton effects with the zero-crossing are located at the absorption maxima in 1a and 1c. This reveals a chiral exciton coupling between the chromophores due to the helical twist of the cage structure, which is absent in 3a¹⁹ and 3c (Fig. S47†). The Cotton effect in the visible absorption range of the PDI's S₀–S₁ transition (λ_max = 522 nm) in 1c is markedly stronger than that observed for the structurally similar 1a (λ_max = 381 nm). The center-to-center and the edge-to-edge distances (DFT, Fig. 2a) between two rylene units are shorter in 1c than in 1a by ≈0.2–0.4 Å. This, together with the higher oscillator strength of the PDI, results in a stronger exciton coupling in 1c. Further evidence is provided by UV-Vis absorption spectra that show clearly that the change in the ratio of the intensities of the individual vibronic bands with respect to monomeric reference compounds 3 is larger for 1c than for 1a (Fig. 1). The R_abs, the ratio of the oscillator strengths of the first and the second vibronic bands, I_0–0/I_0–1, decreases to 1.13 in 1c and to 1.08 in 1a from 1.65 and 1.21 found in 3c and 3a, respectively. Despite an increase in the long-range Coulomb coupling, the short-range charge-transfer coupling is small and it does not manifest in the electrochemical measurements in CH₂Cl₂. In each cage 1, no splitting in the first or the second reduction wave can be observed in the cyclic voltammograms (see the ESI†). As in 1a,¹⁹ each cathodic wave in both 1b and 1c corresponds to an electron transfer event that involves three electrons.

Fig. 1. (Top) The normalized absorption (solid or double line) spectra of 1a, 1c, 3a, and 3c and fluorescence spectra (dash dot line, see the ESI† for details) of 1c and 3c in CH₂Cl₂. (Bottom) The circular dichroism spectra of 1a (double line) and 1c (single line) in CH₂Cl₂.

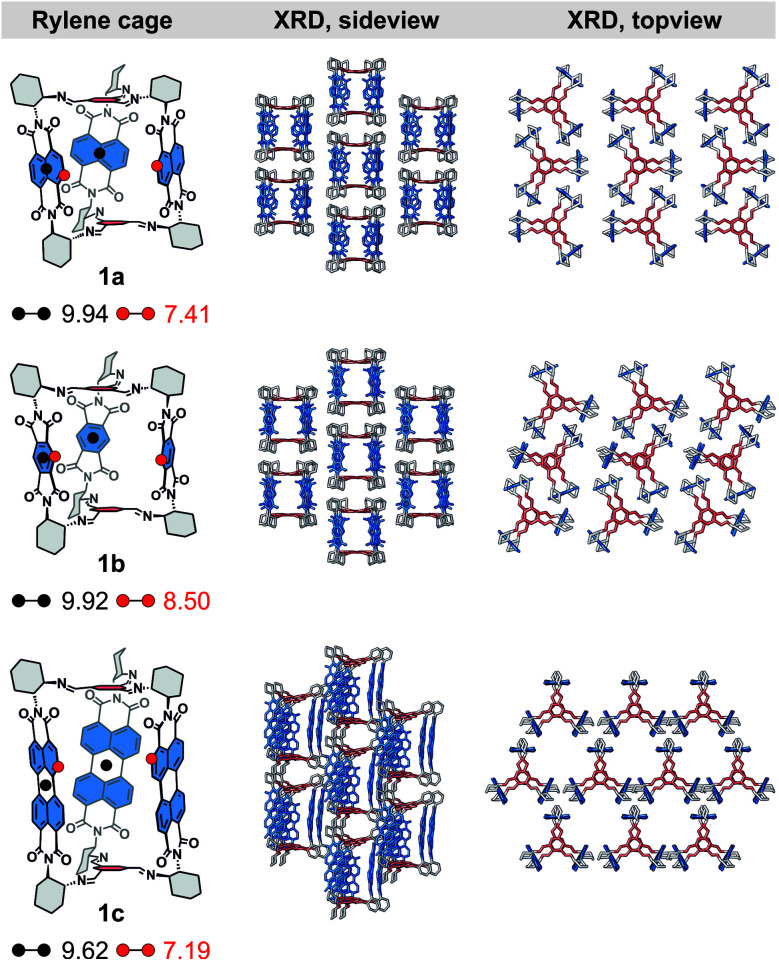
Fig. 2. (Left) The center-to-center (black dots) and edge-to-edge (red dots) distances (in Å, DFT) in cages 1, (middle) the side view and (right) the top view of their solid-state superstructure determined by single crystal XRD. Hydrogen atoms and nitrobenzene solvent molecules are omitted for clarity.

Solid-state structure

We were able to grow single crystals of rylene cages 1 and we unequivocally confirmed their structures. We obtained crystals of 1b and 1c by a slow diffusion of methanol vapors into nitrobenzene solutions of (RRR)- or (SSS)-1b and 1c, respectively. The cages crystallize in a monoclinic space group C₂ (see the ESI†) unlike 1a that crystallizes from the same solvent in an orthorhombic C222₁ space group.¹⁹Fig. 2 compares the single crystal XRD solid-state superstructures of all cages. The symmetry of individual cages in the crystal structure decreases compared to the models obtained from DFT calculations, which predict that the lowest energy geometries of all cages 1 possess a D₃ symmetry in agreement with their NMR spectra. The structural distortion due to packing must be accompanied by an energy penalty. We estimated this energy by DFT calculations where the crystal structure geometries were partially optimized by fully relaxing the coordinates of all hydrogens and the bond lengths between the heavy atoms (C, O, N). The calculated energies (Table S3†) suggest that the cages are rather flexible in a solution and sample the conformational space faster than the NMR time scale at room temperature. Each rylene cage displays an analogous packing (Fig. 2, side view) with the individual molecules assembled into a series of columns. These columns are mutually displaced by a similar length in 1a and 1b, which have a comparable aspect ratio, while the displacement increased in 1c as a result of its elongated structure. The solvent molecules fill both intrinsic and extrinsic voids in all crystal structures. The latter consists of the pockets created by six cyclohexanediyl and two tris(iminomethyl)-benzene units, i.e., pockets between two bridging units of a pair of cages in a column. The larger aspect ratio of 1c allows for a different rylene–rylene interaction and affects the packing as can be observed when the solid-state superstructure is investigated from a different perspective (Fig. 2, top view). In cages 1a and 1b, the edge-to-face NDI–NDI and PMDI–PMDI interaction leads to blocking of window-to-window packing between the cages, which partially closes the intrinsic voids. On the contrary, no edge-to-face orientation of PDI units is present in 1c. Instead, prismatic columns with a slipped stack of tilted PDI units pervade the crystal structure. Consequently, a full window-to-window packing is permitted creating a new hexagonal extrinsic void, orthogonal to the now fully accessible intrinsic voids.

For other solvents, however, the quality of the single crystal X-ray diffraction data exhibited a significant disorder irrespective of the measurement temperature because of the residual solvent molecules. This allowed us to confirm the structure of the cage and the unit cell of the crystal in such cases but with a worse resolution of the individual cage structure (1b, toluene: R₁ ≈ 18%; 1c, nitrobenzene: R₁ ≈ 14%). Comparison of the crystal structures obtained from nitrobenzene and toluene reveals that the electronic nature of the solvent molecules determines the molecular packing. An electron rich guest, such as toluene, prefers to be incorporated in the cavity of the cage, while nitrobenzene of similar size is held less tightly (Fig. S58†). This phenomenon is observed for both 1a and 1b, although the electron affinity of PMDI is markedly lower than that of NDI (Table S2†). This generally allows controlling the solid-state morphology by host–guest interactions in rylene cages 1. The absence of a strong host–guest interaction between nitrobenzene and the rylene cage results in crystal structures that possess both intrinsic and extrinsic voids. Therefore, we decided to grow single crystals from THF, a solvent that is expected to have no appreciable host–guest interaction with the rylenes but with a much lower boiling point than nitrobenzene. Despite the large size and a good quality of the single crystals that we obtained for 1a and 1b by crystallization from THF, a very poor diffraction could only be observed at wide angles, which prevented us from acquiring sufficient data and resolving the crystal structure in this case.

Gas adsorption and porosity

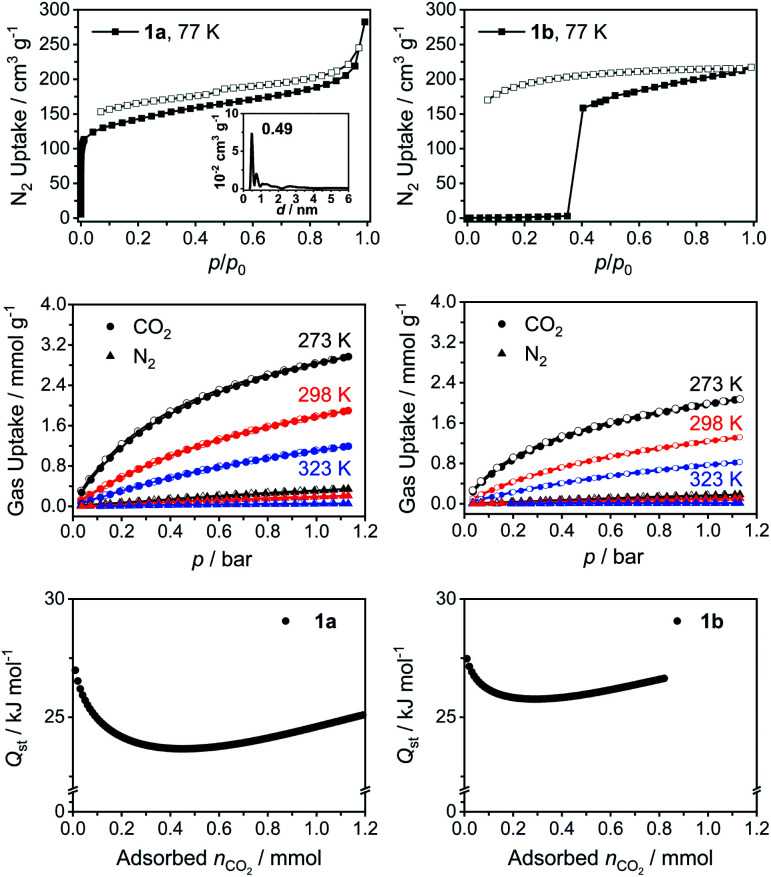
The presence of both intrinsic and extrinsic voids in the crystal structures of 1 motivated us to explore the porosity of the cages. Only cages 1a and 1b could be synthesized in a large enough quantity to perform these studies. Initial gas sorption analysis using Ar or N₂ at 77 K with samples obtained from nitrobenzene displayed a low porosity (Fig. S60†). We attribute this result to the residual nitrobenzene molecules blocking the voids even after the activation of the samples under dynamic vacuum at 120 °C for 24 h because of the high boiling point of nitrobenzene (Fig. S64†). We reasoned that the cages crystallized from THF would allow us to remove the solvent molecules from the pores more effectively. Indeed, we observed a significant increase in the BET surface areas (Fig. 3 and S60†). Cage 1a showed a characteristic type I gas adsorption profile, an indication for a highly microporous structure, with a BET surface area of 522 m² g⁻¹ (Table 1). Further analysis of the adsorption isotherm revealed that the micropores and external pores are responsible for ≈60% and ≈40% of the total BET surface area, respectively. Interestingly, we observed almost no N₂ uptake at low relative pressures for the PMDI cage 1b until the pressure reached a value of p/p₀ ≈ 0.35, at which point a fast uptake of N₂ occurred. Therefore, the BET surface area could not be quantified in this case. In addition, we observed a non-closed desorption isotherm without mesopore hysteresis for 1b. The behavior of 1b thus points to a gate opening phenomenon related to kinetic gas trapping, which is generally observed for soft porous crystals and flexible porous cages.²⁰ The empty voids in the activated material are initially closed at low pressures at 77 K and a necessary structural rearrangement is achieved only with increasing the external pressure to a point when a gate opening takes place. This was accompanied by a substantial increase in the pore volume (0.34 cm³ g⁻¹, Table 1). We observed this gate opening phenomenon also for Ar adsorption isotherms at 77 K (Fig. S60†). We speculate that the difference between the N₂ adsorption behavior of 1a and 1b originates from the intrinsic flexibility of these cages. Whereas 1b adopts a closed-form at low pressures due to its flexibility,²¹ it can transform into an open-form once the threshold pressure (p/p₀ ≈ 0.35) is reached. However, 1a displayed a shape-persistent adsorption due to the limited rotation of the NDI linker in the solid-state. This is supported by the difference in barriers of rotation around the imidic C–N bond in models of NDI and PMDI obtained by DFT calculations (ΔE ≈ 11 kcal mol⁻¹, Table S11†).

Fig. 3. (Top) N₂ adsorption (filled) and desorption (empty) isotherms at 77 K of 1a (inset: pore size distribution) and 1b, (middle) CO₂ and N₂ adsorption of 1a (left) and 1b (right), and (bottom) CO₂ heat of adsorption (Q_st) in 1a and 1b.

Textural properties of 1a and 1b.

Cage	BETa (m2 g−1)	S micro b (m2 g−1)	S ext. c (m2 g−1)	V total d (cm3 g−1)	V micro e (cm3 g−1)	V ext. f (cm3 g−1)	n N2 g (mmol g−1)	n CO2 g (mmol g−1)	Q st h	CO2/N2 (IAST)i
1a	522	312	210	0.44	0.2	0.24	0.31	2.91	27.0	26.9
1b	—j	—j	189	0.34	0.14	0.20	0.16	2.00	27.5	45.5

^aBrunauer–Emmett–Teller (BET) surface area calculated over the pressure range (p/p₀) of 0.01–0.11.

^bMicropore surface area calculated using the t-plot method.

^c S _ext. = S_total − S_micro.

^dTotal pore volume obtained at p/p₀ = 0.99.

^eMicropore volume calculated using the t-plot method.

^f V _ext. = V_total − V_micro.

^gGas uptake (1 bar, 273 K).

^hAt zero coverage.

ⁱSelectivity (IAST, 273 K) of CO₂ over N₂ adsorption.

^jNot available.

In order to probe the affinity of small gases towards the cages, we performed CO₂, CH₄ and N₂ gas uptake experiments at 273, 298 and 323 K up to 1 bar (Fig. 3, S61, S62 and Tables S4, S5†). Both cages 1a and 1b showed higher affinity towards CO₂ with a similar isosteric binding enthalpy (Q_st) of ≈27 kJ mol⁻¹ at zero coverage and a relatively high CO₂ uptake capacities of 2.91 and 2.00 mmol g⁻¹, respectively, at 273 K and 1 bar (for comparison with other POCs, see Table S6†). The N₂ uptake capacities of 1a and 1b are 0.31 and 0.16 mmol g⁻¹ (273 K, 1 bar), respectively. The high CO₂ affinity of the cages prompted us to calculate the CO₂/N₂ selectivity using ideal adsorbed solution theory (IAST), which is used to determine the selectivity for binary gas mixtures using the experimental pure gas isotherms. Cages 1a and 1b exhibited good IAST CO₂/N₂ selectivities of 26.9 and 45.5 (Fig. S61 and Table S4†), respectively. We also observed a good affinity towards CH₄ with uptake capacities (Fig. S62 and Table S5†) of 1.09 and 0.65 mmol g⁻¹ (273 K, 1 bar) and Q_st values of 21.6 and 22.6 kJ mol⁻¹ for 1a and 1b, respectively, which is expected due to the hydrophobic nature of the cage cavity. Considering the rich chemistry of rylene diimides,²² one can imagine that their functionalization through the aromatic core to introduce heteroatoms could further boost the CO₂ uptake capacities. Therefore, rylene cages provide a versatile platform, wherein the porosity, electronic properties, and chemical functionality could be tuned simultaneously to improve the gas uptake and selectivity.

Excited-state behavior and delayed fluorescence in 1c

The presence of three PDI units in the structure of 1c endows the cage with bright photoluminescence. A close inspection of the excited state properties of 1c, however, reveals a different excited-state behavior than that observed for monomeric PDI diimine 3c. The absorption and fluorescence spectra of 1c and 3c are similar (Fig. 1) and do not display solvatochromism in solvents of different polarity such as toluene, CH₂Cl₂, and benzonitrile (Fig. S43 and S44†). However, the fluorescence quantum yield (Φ_em, Table 2) of 1c decreases with increasing polarity of the solvent unlike in 3c, for which both the measured quantum yields (Φ_em = 0.89–0.86, Table S7†) and the excited state lifetimes (τ ≈ 4 ns, Table S8†) are insensitive.

Photophysical parameters determined for samples of 1c in toluene, CH₂Cl₂, and benzonitrile.

Solvent	Toluene	CH2Cl2	Benzonitrile
Φ em a	0.83	0.75	0.40
τ prompt b (ns)	6.27	3.00	1.10
τ delayed c (ns)	—l	10.2	55.9
k proc d (107 s−1)	—l	17.4	75.0
Φ proc e	—l	0.52	0.82
Φ prompt f	—l	0.40	0.15
Φ delayed g	—l	0.35	0.25
k −proc h (107 s−1)	—l	16.70	3.79
ΔGproci (kcal mol−1)	—l	−0.02	−1.77
J Coul j (cm−1)	265	69	25
ΔGCSk (kcal mol−1)	—l	−7.10	−8.92

^aQuantum yield of emission (see Table S7).

^bExcited state lifetime from the prompt fluorescence signal decay (see Table S8).

^cExcited state lifetime from the delayed fluorescence signal decay.

^d S ₁ → S^† rate constant.

^eQuantum yield of S₁ → S^† process.

^fQuantum yield of prompt fluorescence.

^gQuantum yield of delayed fluorescence.

^h S ^† → S₁ rate constant.

ⁱGibbs free energy of the S₁ ⇌ S^† equilibrium.

^jLong-range Coulomb coupling calculated from eqn (3).

^kGibbs free energy of the PDI–PDI photoinduced electron transfer calculated from eqn (4).

^lNot available.

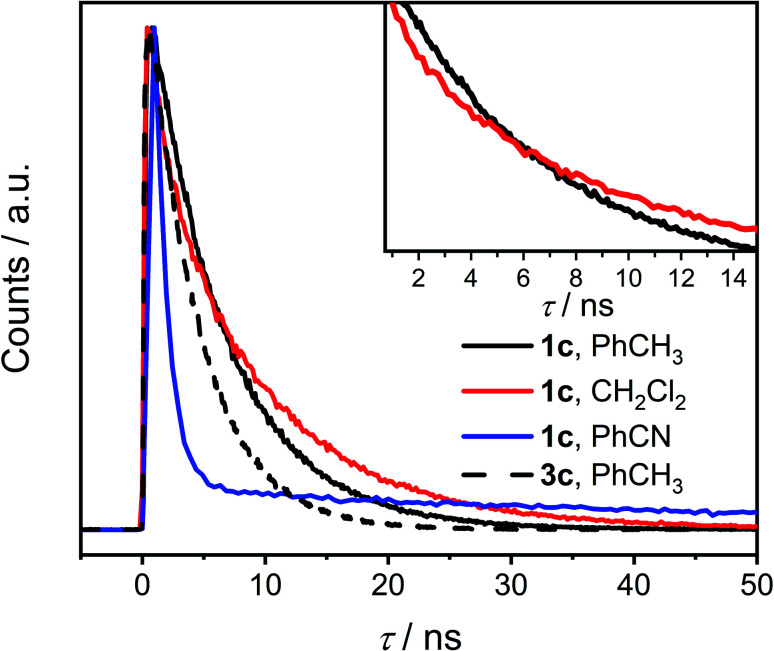
The time-correlated single photon counting (TCSPC) data (Fig. 4 and Tables S7, S8†) show clearly that τ of excited 1c in toluene is longer than that of 3c and it increases further in CH₂Cl₂. This result is surprising because a presence of an additional non-radiative process typically leads to a decrease of both the fluorescence quantum yield and the lifetime of the excited state. This contradiction is resolved by the analysis of the fluorescence kinetics of 1c in benzonitrile. The data show clearly a biexponential emission signal decay with a prompt and a delayed component with the lifetimes τ_prompt = 1.10 ns and τ_delayed = 55.9 ns, respectively. In fact, the analysis of the TCSPC data collected for 1c in toluene and CH₂Cl₂ (Fig. 4, inset) reveals that biexponential decay is already present in the latter. While τ = 6.27 ns in toluene, the τ_prompt = 3.0 ns and τ_delayed = 10.2 ns in CH₂Cl₂. Emission detected at the maximum of each vibronic band provided the same kinetic data. A ten-fold increase in the concentration did not affect either the measured Φ_em or τ of photoexcited 1c excluding the involvement of bimolecular processes. Although we could not acquire the individual prompt and delayed emission spectra, the determined quantum yields and the kinetic data for 1c in benzonitrile show that the prompt and the delayed fluorescence contribute comparably to the overall emission (see below). Because the steady-state optical spectra of 1c and 3c are alike in all the studied solvents, we concluded that the prompt and the delayed fluorescence emanate from the same emissive species in 1c, i.e., from an excited state localized on a single PDI unit (S₁ state, Scheme 2). Therefore, a new process, absent in 3c, exists in 1c and equilibrates²³ the emissive and a non-emissive excited state that we denote here S^†. The markedly lower Φ_em of 1c compared to 3c suggests that this process is present in CH₂Cl₂ and benzonitrile, but likely not in toluene, and the S₁ ⇌ S^† equilibrium is dictated by the solvent polarity. We attribute the longer excited state lifetime and a slightly lower Φ_em observed for 1c compared to 3c in toluene to the weak H-type coupling between the PDI chromophores in 1c (see below), which decreases the k_rad, the rate constant of luminescence.

Fig. 4. Time-resolved fluorescence decay of 1c (solid line) in toluene, CH₂Cl₂ and benzonitrile and of 3c (dashed line) in toluene (see the ESI† for data of 3c in CH₂Cl₂ and benzonitrile). Inset: the crossing of the fluorescence decay curves of 1c in toluene and CH₂Cl₂.

Scheme 2. Schematic diagram for the photoprocesses and the associated rate constants in excited 1c.

TCSPC does not allow to directly observe a spectroscopic signature of the S^† state or the recovery of the ground state absorption. Therefore, we do not provide a full kinetic analysis by solving the necessary set of kinetic equations. Nevertheless, the quantum yields and the large difference of τ_prompt and τ_delayed of 1c in polar solvents allowed us to determine the relative energy of S^† and the individual rate constants of its formation and decay semi-quantitatively (Table 2). In the following, we assume that the τ and the Φ_em in 1c in the absence of the S^† state would be identical to those determined for 1c in toluene. Note, that both the τ and the Φ_em of 3c are invariant to the solvent polarity. Thus, k_proc = 75.0 × 10⁷ s⁻¹ (Scheme 2) can be calculated directly from τ_prompt considering k_rad = 13.2 × 10⁷ s⁻¹ and k_nr = 2.71 × 10⁷ s⁻¹ that we determined from τ and Φ_em of 1c in toluene (Table 2). The quantum yield of the forward process Φ_proc is given by eqn (1):

1

where Φ_proc represents the excited state population initially transferred from S1 to S†. In benzonitrile, Φ_proc = 0.82. As a result, the Φ_prompt of the prompt fluorescence can be obtained from (1 − Φ_proc), and Φ_delayed of the delayed fluorescence from (Φ_em − Φ_prompt). Their values in benzonitrile (Table 2), after correction for the non-radiative decay of the S₁ state, are Φ_prompt = 0.15 and Φ_delayed = 0.25, respectively. Clearly, prompt fluorescence is responsible for less than half of the overall luminescence quantum yield (Φ_em = 0.40). It follows that Φ_delayed represents the total excited state population in the S^† state that decays radiatively by repopulating the bright S₁ state. There must be other deactivation channels from the S^† state that account for ≈50% of the quenching of the initially excited cages. Considering the individual quantum yields and the value of τ_delayed, the corresponding rate constant for the reverse process, k_−proc, that repopulates the S₁ state could be derived^24a,b according to eqn (2):

2

where k_prompt and k_delayed are the observed rate constants that correspond to the experimentally determined lifetimes τ_prompt and τ_delayed, respectively. The calculated values of k_−proc in benzonitrile and CH₂Cl₂ are listed in Table 2. The rate constants of the forward and the reverse process in the S₁ ⇌ S^† equilibrium provide an apparent equilibrium constant in benzonitrile K = 19.8 and the corresponding Gibbs free energy of ΔG_proc = −1.77 kcal mol⁻¹ at 298 K (Table 2). The same line of arguments gives ΔG_proc = −0.02 kcal mol⁻¹ at 298 K in CH₂Cl₂. Note, however, that the difference between k_proc and k_−proc, which forms the basis of our kinetic analysis, is small in CH₂Cl₂ and, as a consequence, provides a less accurate value for the energy difference between the S₁ and S^† states in this solvent.

Although fluorescent organic cages were previously reported,¹⁸ cage 1c represents the first example of a covalent organic cage that displays a delayed fluorescence. This demonstrates the unique interplay of the PDI chromophores in its structure that promotes an unusual but very useful property that is typically observed in compounds with very different structural design incorporating twisted electron donor and acceptor motifs. For example, compounds with delayed fluorescence are important light-emitting materials used in organic light-emitting diodes.²⁴ What is, however, the likely nature of the new non-emissive S^† state and the process by which it forms? There are three feasible scenarios to consider: (a) a formation of an excimer or an intramolecular H-type aggregate, (b) multiexciton generation, or (c) intracage charge-separation.

Formation of an excimer or an intramolecular H-type aggregate

A large electronic coupling is necessary between PDI units to form an excimer. This typically requires a cofacial orientation of the PDIs with a short intermolecular distance that can be achieved by a structural rearrangement in the solution. As a result, the excimer state, ¹(PDI–PDI)*, may display enhanced excited state lifetime, a diminished fluorescence quantum yield and a partial charge-transfer (CT) character but it shows a markedly displaced and featureless fluorescence spectrum. There is no sign of an excimer emission in the steady-state fluorescence spectrum of 1c in any solvent. The distance of the PDI units in the DFT optimized structure of 1c (Fig. 2a) is too large to allow a sufficient coupling to form an excimer. In addition, the structural rearrangement would require the PDIs in the cage to rotate significantly (>30°) around the N–C bond connecting the PDI and the cyclohexyl connector to adopt a cofacial geometry. This rotation is, however, hindered and slow even on the NMR time scale because we observed four doublets for the PDI aromatic core protons in the ¹H NMR of 1c at room temperature (Fig. S8†).

A comparison of the absorption spectra reveals that absorption maxima of 1c are slightly blue-shifted compared to the spectra of the monomeric 3c. The relative intensities of the individual vibronic bands also deviate as already discussed above. The ratio of the oscillator strengths of the first and the second vibronic bands, I_0–0/I_0–1, decreases from 1.65 in 3c to 1.13 in 1c (Fig. 1), suggesting the presence of an H-type coupling in 1c.²⁵ Its magnitude is, however, small and can be estimated assuming a point-dipole interaction between transition dipole moments of two PDIs:

3

In this expression, μ_0→1 is the transition dipole moment (3.50 × 10⁻²⁹ Cm, Table S9†) that is parallel with the long PDI axis, ε is the absolute solvent permittivity, r₁₂ is the center-to-center PDI–PDI distance (9.62 Å, Fig. 2) obtained from the DFT-optimized geometry of 1c, and φ is the tilt angle between the two PDIs in the cage (≈10°). In CH₂Cl₂, we obtain an interaction energy J_Coul = 69 cm⁻¹ that agrees well with J_Coul = 70 cm⁻¹ calculated from the vibronic bands intensity ratio R_abs according to Spano and co-workers.²⁶ Our TD-DFT calculations predict a somewhat higher coupling (≈180 cm⁻¹, Table S9†). Both the experiment and theory show that J_Coul does not vary correctly with the solvent polarity (Table 2) and, therefore, it is inconsistent with the excited state behavior that we observe for samples of 1c in different solvents. In addition, rapid excited state symmetry-breaking is induced by solvent field (polar medium) or structural (non-polar medium) fluctuations when the interchromophore coupling is very small²⁷ and, therefore, the exciton must quickly localize on a single PDI unit in 1c. Nevertheless, the presence of this small coupling is sufficient to reduce the k_rad and Φ_em in 1c (toluene, Table 2) when compared to 3c in the three studied solvents (Tables S7 and S8†).

Intracage charge-separation (CS) and multiexciton (ME) generation

Rylene diimides are known as excellent electron acceptors in their ground or excited states. We reported previously¹⁹ that 1b serves as a strong oxidant and transfers an electron from the tris(iminomethyl)benzene bridge on an ultrafast time scale when excited with UV light. NDIs and PDIs have similar redox potentials but the excited state of 1c has a considerably lower energy than that of 1a (Table S2†). Indeed, we do not observe quenching of fluorescence in 3c, which confirms that the tris(iminomethyl)benzene bridge is electrochemically innocent in the excited 1c. However, an initially delocalized exciton in PDI dimers or higher aggregates is known²⁸ to undergo a symmetry-breaking CS where two PDIs disproportionate to a pair of radical ions, PDI˙⁻ and PDI˙⁺. Recombination of these radical ions might repopulate the bright singlet excited state and result in a delayed fluorescence.

A kinetically equivalent event involves formation of a rather exotic species, a ME state, which is an intermediate in a process called singlet fission.²⁹ Singlet fission has attracted considerable interest of scientific community in recent years because the incorporation of singlet fission compounds into solar cells could raise their theoretical efficiency limit. In a singlet fission, an excited singlet state transforms into a correlated triplet pair, the ME state, with an overall singlet spin character. Its fate in molecular dimers/oligomers is typically twofold, (a) it splits into two independent triplet states if the process is exergonic or (b) it recombines back to the excited singlet state.³⁰ Both processes can lead to a delayed fluorescence. The former via a triplet–triplet annihilation (TTA) with a rate comparable to the lifetime of an independent triplet state, while the latter with lifetimes typically in nanoseconds. Singlet fission has been observed in solid samples of PDI derivatives.³¹ A strong electronic coupling in cofacial PDI dimers typically leads to the formation of unproductive excimer³² or charge-separated states^28,33 and a slipped stack geometry, observed in PDI thin films, is believed³¹ to be crucial for a singlet fission to occur in PDI derivatives. Very recently, Hong et al. proposed^34a that the singlet fission can occur also in PDI dimers in solution. The dimers displayed two distinct fluorescence lifetimes in 1,1,2,2-tetrachloroethane but the longer lifetime was attributed to the emission of an excimer state.^34b The dimers exhibited a strong J_Coul (>500 cm⁻¹) and a short-range CT coupling of a similar magnitude but of the opposite sign (J_CT ≈ −500 cm⁻¹). The ME generation process occurred with τ_ME = 370 and 20 ps in toluene and benzonitrile, respectively, after an initial structural or solvent reorganization enhancing the CT character in the excited dimers. The results corroborate the CT-mediated singlet fission mechanism observed previously in structurally related terrylene diimides (TDIs).³⁵

The CS and ME generation can both be described by the diagram in Scheme 2 and they are, therefore, kinetically indistinguishable. The former process may be facile only when the corresponding Gibbs free energy of the photoinduced electron transfer, ΔG_CS, is negative. To quantify the ΔG_CS for 1c, we applied eqn (4):³⁶

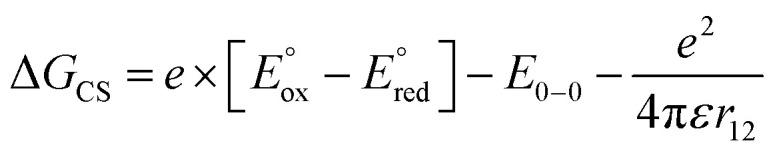4

where 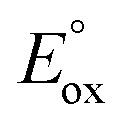and 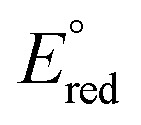are the first oxidation and reduction potentials, respectively, E_0–0 is the excited state energy, and ε and r₁₂ are as described above. We obtained the redox potentials and the excited state energies by cyclic voltammetry³⁷ and optical spectroscopy (Table S2†), respectively. The resulting Gibbs free energy of the electron transfer in CH₂Cl₂ is 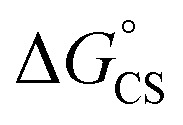= −7.10 kcal mol⁻¹ at 298 K. The value of 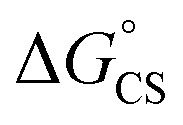= −8.92 kcal mol⁻¹ is obtained for the electron transfer in polar benzonitrile by correcting the redox potentials with solvation energies calculated by DFT (Table S10†). Both values are negative and predict a productive charge separation event. The ΔG_proc determined from the kinetic data is, however, considerably higher, even if the last term in eqn (4) was ignored. In fact, the calculated 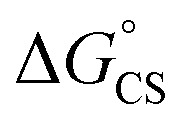values suggest that the electron transfer is too exergonic to allow efficient charge recombination to repopulate the bright S1 state on the observed time scale. In such a case, a charge-separated state typically decays rapidly to the ground or to a triplet state, ³1c. This was observed previously in a macrocycle with weakly coupled PDIs^33a or in 1a.¹⁹ No delayed emission was detected in the former case and the charge recombination was rapid in the latter. In addition, electrogenerated chemiluminescence that was observed in PDI derivatives in CHCl₃/CH₃CN solvent mixture by Bard and co-workers³⁸ showed that the population of the emissive excited state occurred exclusively via a TTA mechanism because of the insurmountable energy required for the direct PDI˙⁻ and PDI˙⁺ recombination to reach a singlet excited PDI. A TTA process is excluded in our case because tenfold increase in the concentration of 1c had no impact on the kinetic data or the quantum yields. The luminescence signal of 1c decays in several nanoseconds in all solvents, similar to endothermic singlet fission observed in tetracene dimers.³⁹ Despite the singlet fission being slightly endergonic in PDI solids due to strong PDI–PDI coupling, the reported triplet energy of PDI in a solution is E_T ≈ 1.1–1.2 eV (ref. 40) (DFT: 1.22 eV, see the ESI†). Considering the E_0–0 = 2.35 eV in 1c, the resulting energy change is nearly isoergic and admixture of a CT character into S† state, as revealed recently by Hong et al.,^34a can lead to a slightly exoergic process in accord with ΔG_proc. Nevertheless, eqn (4), which is based on a hard spheres model, has been shown to break down in some macrocyclic compounds that contain substituted PDI chromophores^33b and the actual values of 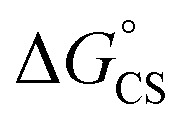are in fact less negative than the values predicted with eqn (4). Note, however, that the difference in 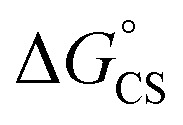in different solvents matches the experimentally determined difference in ΔG_proc remarkably well. Overall, sole thermodynamic considerations are not conclusive in our case.

We then tested the effect of molecular oxygen on the excited state lifetime of 1c by saturating its benzonitrile solution (Table S8†). Indeed, we observed a reduction of τ_delayed and Φ_em from 55.9 to 10.7 ns and from 0.4 to 0.27, respectively. However, τ of 3c was affected, too, although to a smaller extent (2.7 times less), which suggests that superoxide species could be generated instead of singlet oxygen.

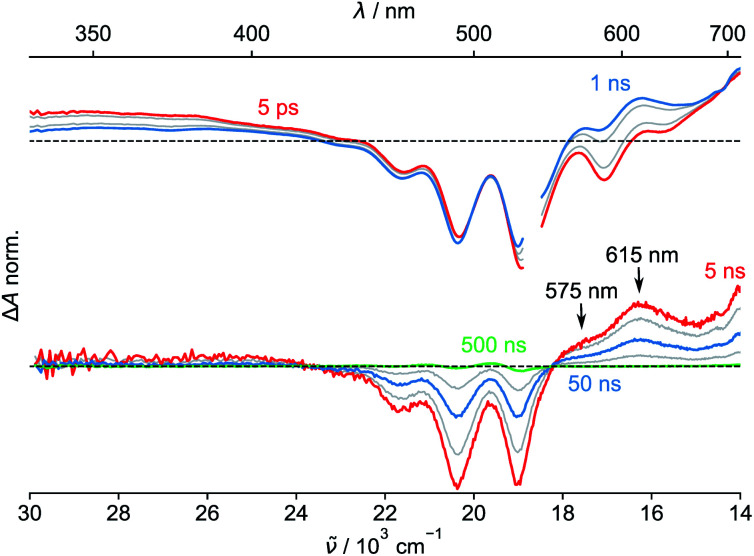
Finally, we performed transient absorption spectroscopy of 1c and followed the evolution of the excited state processes from a few picoseconds to hundreds of nanoseconds in benzonitrile. Fig. 5 shows the obtained transient absorption spectra. An intermediate with a maximum of absorption at 615 nm and a shoulder at 575 nm, which we assign to S†, formed (1.50 ns) and decayed (50.9 ns; Fig. S68†) with time constants that matched very well the τ_prompt and τ_delayed, respectively, from the TCSPC measurements. The delayed fluorescence and the recovery of the ground state bleach parallel kinetically the S^† disappearance and confirm that this intermediate both repopulates the S₁ state and decays directly to the ground state of 1c, respectively. Our results suggest that no or little of PDI triplets form. The signal of S^† in toluene is absent. In order to assign the nature of S^† state, we performed a chemical reduction of 3c with cobaltocene in dry benzonitrile and measured the absorption spectrum (Fig. S69†) of the ensuing radical anion, PDI˙⁻. The absorption maxima of PDI˙⁻ do not match the absorption band observed in our time-resolved experiments and are located outside our detection window. Since oxidation of 1c or 3c is not reversible, we could not measure the absorption spectrum of the corresponding PDI˙⁺. Nevertheless, PDI˙⁺ generated from related PDI derivatives^33,34 possess an absorption that matches the observed spectroscopic signature of the generated transient. Hong et al.^34a attributed a similar transient feature at 615 nm to the ME state. We assign the observed absorption of S^† to PDI˙⁺ generated by a CS process because a CT-mediated singlet fission mechanism requires a virtual intermediary CT state, which, in our case, represents a shallow energy trap (Scheme 3; see both the 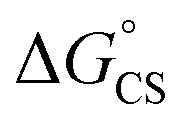or ΔG_proc). Note, however, that we do not fully discard a possibility that the observed intermediate also involves a ME state in an equilibrium. The complex and intriguing photochemical behavior of 1c requires a detailed time-resolved spectroscopic analysis including NIR and IR domains. Such work is currently ongoing in our laboratories and will be communicated in a follow-up report.

Fig. 5. Transient absorption spectra (temporal resolution: ps – top, ns – bottom) measured at various time delays after 532 nm excitation of 1c in benzonitrile. The break in the spectra (top) is due to scattering of the pump light.

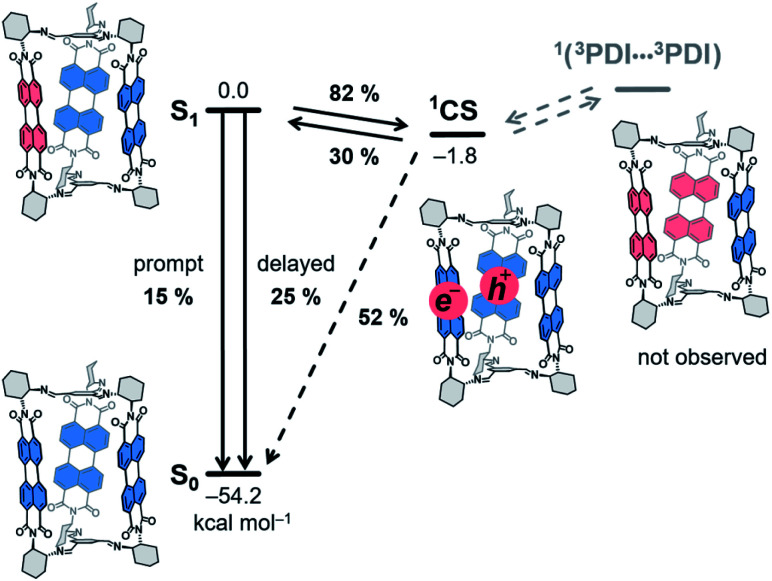
Scheme 3. Energy-level schematic (kcal mol⁻¹) for photoprocesses in 1c. Quantum yields obtained for benzonitrile solutions are given. CS: charge-separated state. Dashed arrows: not observed.

Conclusions

We synthesized a series of chiral imine organic cages that incorporate three redox-active rylene units in their structures and explored their textural and optoelectronic properties. Thereby, we showed that the rylene cages are porous and their optoelectronic properties can easily be tuned by synthesis. NDI and PMDI cages 1a, b showed a good selectivity for adsorption of CO₂ over N₂ an CH₄ and the flexible nature of PMDI cage 1b in the solid state resulted in a gate opening phenomenon during adsorption of N₂ and Ar at 77 K. In addition, we discovered that the PDI cage 1c is the first organic cage that displays a delayed fluorescence, a consequence of the precise spatial arrangement of the PDI units in its structure. Our spectroscopic and electrochemical data suggest that a rapid (pseudo)equilibrium establishes between the singlet excited state of 1c and the intracage charge-separated state where two PDI units disproportionate into radical ions. The delayed fluorescence emanates by re-population of the bright singlet excited state of 1c when the PDI radical ions recombine.

Thus, we demonstrate that rylene cages integrate the advantages of both porous and electronic materials, a feature typically observed in nanoscale materials, such as covalent organic frameworks, but rare in porous organic cages. The three-dimensional arrangement of the rylene units in the studied cages promises a development of new porous materials that incorporate photochemical phenomena, such as excited state symmetry-breaking charge separation, that, when combined together, may lead to useful applications in photocatalysis or solar energy storage.

Author contributions

T. Š. conceived the research idea, designed the compounds and performed all calculations. T. Š., A. C. and H.-H. H. designed the experiments and H.-H. H., T. Š. and R. M. synthesized the compounds. A. P. performed the XRD analysis. K. S. S and A. C. investigated the porosity and analyzed the data. H.-H. H. performed electrochemistry, photochemical steady state and TCSPC experiments and analyzed the data with T. Š. Transient absorption spectroscopy was performed by A. A., G. C., and E. V. The manuscript was written by T. Š., H.-H. H., and A. C. with contributions from all authors.

Conflicts of interest

The authors declare no competing financial interest.