The structural changes in the signaling mechanism of bacteriophytochromes in solution revealed by a multiscale computational investigation

Abstract

Phytochromes are red-light sensing proteins, with important light-regulatory roles in different organisms, which are capturing an increasing interest in bioimaging and optogenetics. Upon absorption of light by the embedded bilin chromophore, they undergo structural changes that extend from the chromophore to the protein and finally drive the biological function. Up to now, the underlying mechanism still has to be characterized fully. Here we investigate the Pfr activated form of a bacterial phytochrome, by combining extensive molecular dynamics simulations with a polarizable QM/MM description of the spectroscopic properties, revealing a large structure relaxation in solution, compared to the crystal structure, both in the chromophore-binding pocket and in the overall structure of the phytochrome. Our results indicate that the final opening of the dimeric structure is preceded by an important internal reorganization of the phytochrome specific (PHY) domain involving a bend of the helical spine connecting the PHY domain with the chromophore-binding domain, opening the way to a new understanding of the activation pathway.

A combination of MD simulations and a polarizable QM/MM description of a bacteriophytochrome in solution reveals the changes in the chromophore-binding pocket and in the overall structure of the phytochrome involved in the signaling mechanism.

1. Introduction

Phytochromes are a large family of photoreceptor proteins used by very different organisms, from bacteria to fungi and plants, to sense light and control a variety of cellular processes connected to light exposure.^1–4 Their function is activated through red and far-red light absorption by a bilin cofactor, which results in a signal transduction through a cascade of structural rearrangements, initially localized in the cofactor but then propagating into various parts of the phytochrome structure up to the output domains.^5–8

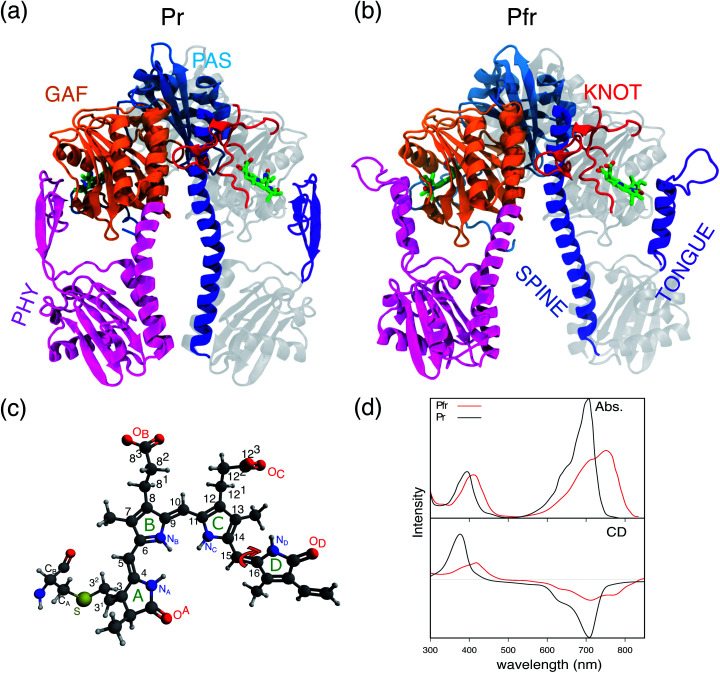
In the most common phytochromes of bacteria (often indicated as canonical), a remarkable modularity is present in the photosensory module (PSM) which is composed of three domains, PAS (Per/Arndt/Sim), GAF (cGMP phosphodiesterase/adenyl cyclase/FhlA), and PHY (phytochrome-specific), see Fig. 1a. The bilin cofactor, here biliverdin IXα (BV), is placed in a binding pocket provided by the GAF domain and is typically covalently linked to a conserved cysteine of the PAS N-terminus by addition to the vinyl group of ring A (see Fig. 1c). In the dark state (or Pr), the BV adopts a 5Zsyn, 10Zsyn, 15Zanti conformation, but, upon absorption of red light, it undergoes an isomerization at its C15 C16 double bond which results in D-ring rotation (see Fig. 1c). This initial photochemical reaction is followed by conformational changes of the protein finally leading to the light-adapted (Pfr) state. Due to their modularity and the red-shifted spectra of BV, bacteriophytochromes have recently received a large attention for possible applications in bioimaging and in the field of optogenetics.^9–12

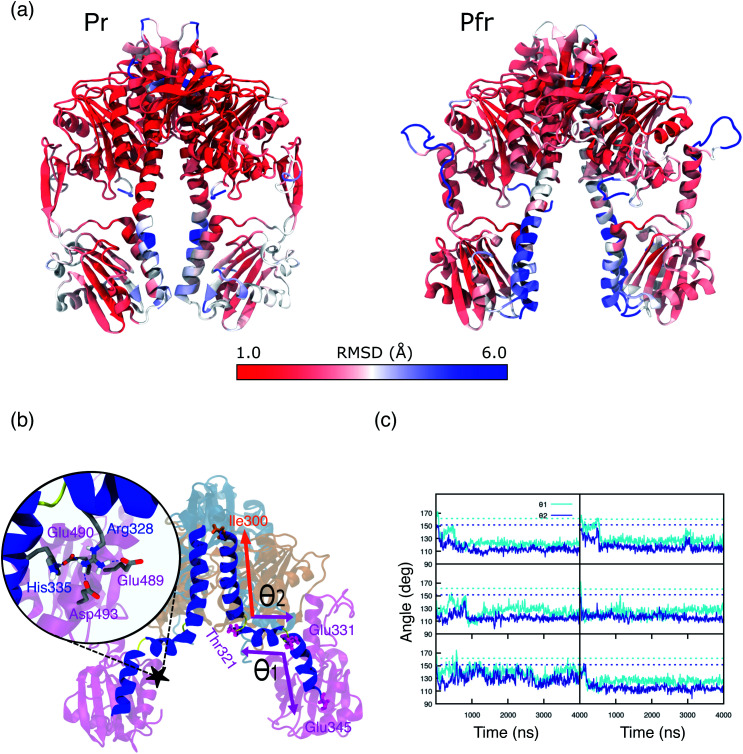
Fig. 1. (a and b) Crystal structure of Pr (a) and Pfr (b) structure for the DrBph photo-sensory module (PSM) in the Pfr form. The chromophore (represented in green) is also reported in the inset to change in the dihedral angles in the Pfr form. (c) Chemical structure of the BV chromophore and main atoms numbering. (d) Measured absorption and CD spectra of the two forms.

In spite of this large interest, many fundamental aspects of their photoactivation remain obscure. In the literature different models have been proposed for the Pr-to-Pfr photoreaction, possibly involving one or more intermediates.^6,13–19 The first guess about the photo-induced isomerization process in the Deinococcus radiodurans bacteriophytochrome (DrBph) was given when crystal structures were firstly published for both Pr and Pfr PSM isomers.²⁰ By a structural X-ray comparison, it was possible to see that the largest difference between the two states is represented by the tongue secondary structure and the straightening of the spine, with the latter directly implicating a larger distance between the PHY domains in the Pfr state (see Fig. 1a and b). Based on these structural data, it was assumed that the PHY-domains opening is due to the tongue shortening consequent to its refolding.^20–22 More recently, a time-resolved FT-IR spectroscopy study¹⁶ on the DrBph has proposed that the photochemically induced D-ring rotation leads to a first intermediate (Lumi-R) characterized by an high disorder in the hydrogen bonds (H-bonds) to the carbonyl of the same ring. Lumi-R evolves in a second intermediate (Meta-R) in which the interactions of the D-ring carbonyl are largely weakened if not lost: this is followed by a destabilization of the β-hairpin conformation of the PHY-tongue which is finally refolded into an α-helix only in the last step, upon Pfr formation. In 2020, a solution-NMR study¹⁹ on the monomeric form of the DrBph PSM (both Pr and Pfr states) suggested a different mechanism going from the chromophore along the figure-of-eight-knot (knot) and the spine helix in DrBph, up to the output domains. In the same study, however, it was also proposed that this pathway is not the only active one, but it could work together with others, such as the one through the PHY tongue.

All these studies have largely enriched the knowledge of the system and of its photoactivation but many fundamental aspects have still to be clarified. In fact, the combination of protein dynamics, the multi-domain organization and their dimeric nature make bacteriophytochromes extremely challenging systems for obtaining structural information of the different functionally relevant states. Within this framework, a very important role can be played by Molecular Dynamics (MD) simulations. In fact, X-ray structures can deviate from solution structures as a consequence of crystal packing, especially in multi-domain proteins.²³ MD simulations can help elucidate the solution structures of proteins or reveal new conformations not seen by X-ray crystallography.^24,25 In the case of phytochromes, they allow achieving the still missing atomistic details of the Pr and Pfr states in their solution environment. Moreover, the results may be used to define important structure–property relationships for revealing the real mechanisms of activation. However, probably due to the complexity and large size of phytochromes, MD studies on the whole PSM are still scarce,^21,26–28 and most of the computational studies have been focused on the calculation of absorption spectra and/or structural determination.^29–34

In this study we used an integrated computational approach which combines extensive MD simulations of the solvated phytochrome with hybrid quantum mechanics/molecular mechanics (QM/MM) calculations to investigate the changes governing the Pr-to-Pfr conversion of DrBph, which are not only structural, but also spectroscopic (see Fig. 1d). Starting from the results we have recently obtained for the dark (Pr) state²⁸ we could connect the changes induced in the protein binding-pocket by the bilin isomerization with the larger-scale structural rearrangement of the PSM, and finally propose a hypothesis for the Pr-to-Pfr activation. Our hypothesis is that the Pr-to-Pfr tongue re-folding, consequent to the chromophore isomerization, causes an overall rotation of the PHY domain and thus a change in the relative GAF/PHY orientation. Due to a tight connection between the spine and the adjacent residues in the PHY and GAF domains through H-bonds, the spine is forced to bend to adapt to the new configuration. The effect of such a PSM internal reorganization is the separation of the PHY-domains and the dimer opening.

2. Methods and computational details

2.1. Crystal structure preparation and molecular dynamics setup

Initial atomic coordinates for the crystal preparation were extracted from the 5C5K³⁵ entry of the protein data bank (PDB), which corresponds to the W469F variant of the phytochrome photo-sensory module (PSM) in the Pfr state. In particular, the PDB chains A and B (chain A and chain B) were selected for this study. To compare the crystal to biological sequences we used the ALIGN program, while MODELLER³⁶ was used to add the missing residues, and to replace some residues adjacent to them for a better structural fit. We added (or replaced) residues 1 to 9, 450 to 463 for chain A and residues 1 to 9, 342 to 350 and 456 to 462 for chain B. In order to simulate the wild-type PSM, we then replaced Thr469 with Phe in both crystal chains. The protein was protonated at physiological pH 6.5 conditions using the H++ program³⁷ For the chromophore we applied the same force-field as obtained for simulating the phytochrome in the Pr form²⁸ and it is reported in the ESI.† All hydrogens and added residues were then minimized with AMBER18.^38,39

After refinement of the crystal structure, we performed three simulations of DrBph in the Pfr state. The refined structure was immersed in a water box, ensuring a 40 Å minimum separation between protein periodic images. The system was neutralized adding sodium ions. For replica one and two (Rep1, Rep2) we used a cubic water box, while a octahedric one for replica three (Rep3). Following details are the same for all replicas.

The solvated system was subjected to 4000 steps of energy minimization (800 steps using steepest descent and other 3200 steps using conjugate gradient). The system was then slowly heated to 300 K for 800 ps in a NVT ensemble, in which we restrained the movement of the whole chromophores, the crystal water oxygens and protein backbone applying a 4 kcal mol⁻¹ Å⁻² harmonic potential. Successively, two NPT equilibrations were run in order to slowly release the restrains: a 2000 ps one in which the chromophores and all the protein backbone were restrained; a second one of 1600 ps in which only the added residues and some of the adjacent residues were released from the previous restraint. The production run was run without any restraint for 4 μs in the NPT ensemble. All simulations were performed applying the particle mesh Ewald (PME) truncation method (with a short-range cut-off of 10 Å), an integration step of 2 fs, the SHAKE algorithm, a Langevin thermostat with a friction coefficient of 1 ps⁻¹, the Monte Carlo barostat for NPT simulations. All molecular dynamics simulations were run with AMBER18.^38,39

2.2. Geometry optimizations and electronic spectra calculation

For the optimization, we used the Gaussian 16 suite of programs⁴⁰ applying a QM/MM ONIOM scheme.⁴¹ Geometry optimizations were performed on chain A and chain B crystal structure, and on solvated 250 MD monomer-geometries extracted from Rep1, Rep2 and Rep3. For the MD structure, a 18 Å sphere of water molecules around the chromophore and a monomer was considered in the MM subsystem. The B3LYP functional in combination with 6-31G(d) basis set and D3 empirical dispersion⁴² was used to treat the QM subsystem (BV). The solvent and the protein were kept frozen, with the exception of C_A and S atoms of CYS24 (covalently bonded to the chromophore) that were flexible and included in the QM part, by cutting the C_A–C_B covalent bond. We simulated electronic spectra applying a QM/MMpol scheme,^43,44 in which the previously optimized QM subsystem (BV) was treated at CAM-B3LYP/6-31+G(d) level of theory. For the MD frames, the protein matrix (all dimer) and the solvent within 40 Å of BV were part of the MMpol model; for the crystal structure only chain A or chain B and the crystal water were part of it. All calculations were performed with a locally modified version of Gaussian 16 (ref. 40) where the QM/MMpol approach has been implemented.⁴⁵

The homogeneous and inhomogeneous broadening to the calculated spectra was included as described previously.²⁸ Briefly, the homogeneous lineshape was calculated, within the second-order cumulant expansion formalism,⁴⁶ on the basis of normal-mode calculations performed on the two crystal chains. The final absorption and CD spectra were obtained by convoluting the homogeneous lineshape with the inhomogeneous distribution of excitation energies and, respectively, transition dipoles and rotatory strength.

3. Results and discussion

In the following, we firstly determine whether the crystal protein-binding pocket structure is representative of the solvated PSM in the Pfr state by investigating possible relationships between intermolecular interactions, structure and spectroscopic properties. Successively we widen the focus to the Pr-to-Pfr secondary and tertiary changes in solution and their connection to H-bond and salt-bridge interactions among the different domains. Finally, we suggest a possible mechanism for the Pr-to-Pfr activation.

3.1. The binding pocket

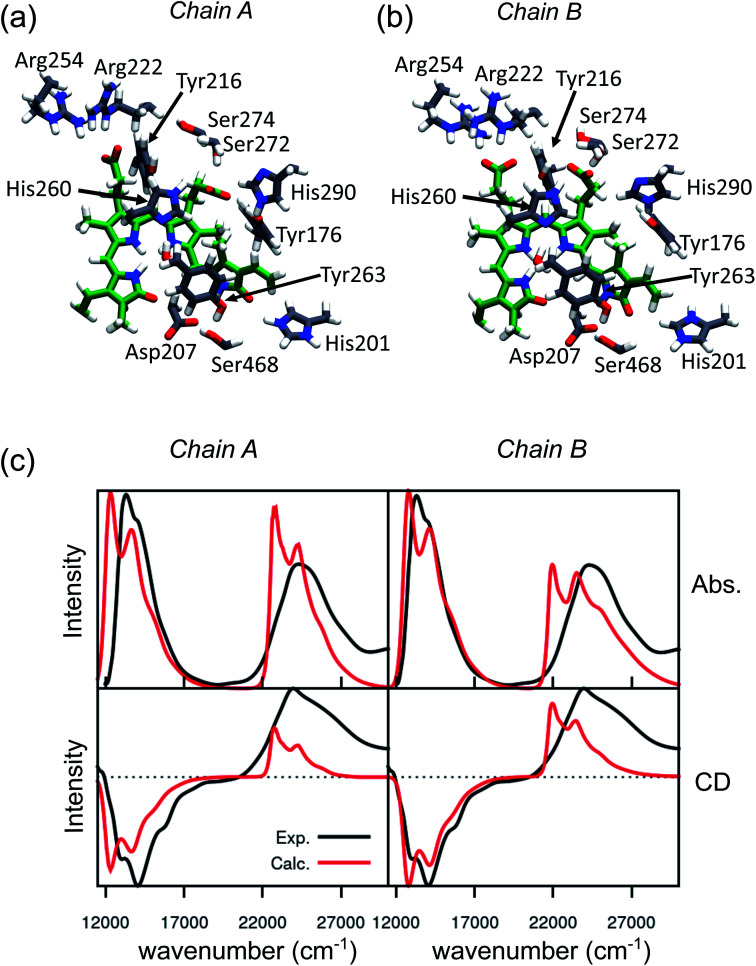
An effective way to investigate the binding pocket embedding the chromophore is through the absorption and circular dichroism (CD) spectra. According to our previous study on Pr, the crystal structure well represents the spectroscopic properties of the Pr state. Here, a parallel analysis is repeated for Pfr, for which the crystal shows that the two binding pockets of chain A and chain B differ in the conformation of several residues and the in chromophore structure (see Fig. 2a and b). In particular, the B-ring and C-ring propionates are differently oriented, and thus show different H-bond networks. Moreover, some differences are observed in the residues close to the D-ring, where for example His201 is H-bonded to the carbonyl in chain A, but positioned farther in chain B.

Fig. 2. Binding pocket and spectroscopic properties of the Pfr crystal structure. (a and b) Zoom-in of the protein-binding pocket in the crystal chain A (a) and chain B (b) with the most important amino acids interacting with BV and pyrrole water. (c) Absorption (Abs., top) and circular dichroism (CD, bottom) electronic spectra calculated on chain A (left panel) and chain B (right panel). All spectra were calculated at the CAM-B3LYP/6-31+G(d) level and shifted by −0.16 eV, to be comparable with our previous calculations on the Pr crystal.²⁸.

We expect these differences to reflect on the spectroscopic properties of the two chains. Indeed, the absorption and CD spectra calculated for the two chains (Fig. 2c) differ both in the position and in the relative intensity of the two typical bands of biliverdin, the lowest energy Q band and the higher energy Soret band. Comparing these results with experiments,²² we note significant differences. Qualitatively, the red shift from Pr is reproduced for the Q-band by crystal calculations, but the shift is overestimated in chain A. On the contrary, for chain B, the calculated Soret band is too red shifted. For both chains, the lineshape of the Soret band is also not well reproduced.

The higher difficulty in reproducing the Soret band was not unexpected, since we found a similar result for Pr in our previous study.²⁸ There, we concluded that TDCAM-B3LYP inverted the order of the two higher-lying states (namely S₂ and S₃), since a very good agreement with experiments was recovered by switching the second and third electronic states. However, for Pfr, the results do not improve by exchanging the two excited states. The reason for this behavior is that in Pfr S₂ and S₃ excitations appear as a mixture of the corresponding ones in Pr. A detailed comparison in terms of natural transition orbitals (NTOs) is reported in Fig. S4 of the ESI.† We also note that the measured Abs–CD shift is less pronounced in the Pfr than the Pr, indicating that the two Soret states are closer in energy for the Pfr isomer.

A qualitative red-shift from the Pr structure was previously predicted by simply rotating the D ring around the C₁₅ C₁₆ double bond of biliverdin.⁴⁷ Instead, the differences between chains A and B in the Pfr crystal, which arise from a different geometry of the chromophore around ring A (Fig. S5 in the ESI†), do not allow a simple understanding of the connection between structure and spectroscopy in the Pfr state. In any case, the differences between the two crystal chains suggest that the Pfr form is a more disordered system than the Pr form, and this disorder is reflected in a spectroscopic heterogeneity.

To confirm the structural heterogeneity of Pfr also for the solvated system, we simulated three MD replicas of 4 μs each, as described in Section 2. Pfr crystal chain A and chain B are respectively the starting structures for monomer A and monomer B of each MD replica.

As said, the largest difference in the chromophore between the crystal chains A/B is given by the propionate orientations, which in turn determine a different H-bond network. Therefore, at first, we analyzed the distributions of the propionate dihedral angles for all MD replicas and compared with the crystal structure (Fig. S6–S9 in the ESI†). We find that propionate dynamics is independent of the initial structure, indicating high mobility and labile (or competitive) interactions with the environment. The largest difference between chain A and chain B propionates is in the C-ring dihedral angle C₁₂–C₁₂¹–C₁₂²–C₁₂³ (see Fig. 1c for C atoms labeling), but the conformation found in the chain B crystal structure is the most populated one in our MD for both chains.

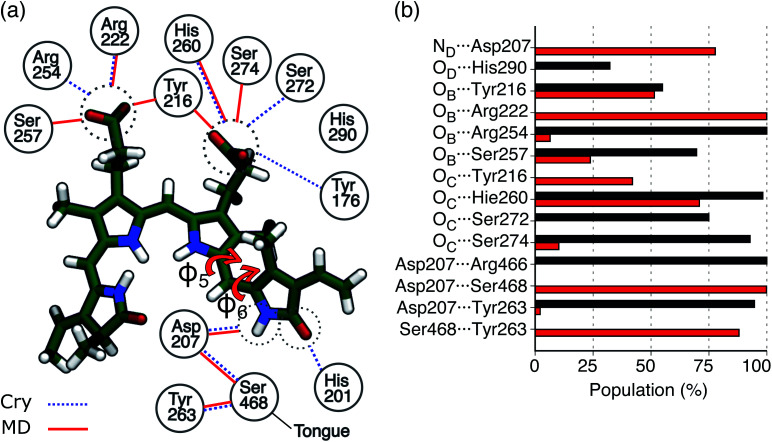
In Fig. 3a the analysis of the changes observed when moving from the crystal structure to the MD simulation is extended to the H-bond network of the whole binding pocket. As it can be seen, some of the H-bonds to the propionates found in the crystal structure are lost, and replaced by H-bonds to Tyr216 and Ser274. In the crystal chain A His201 acts as a H-bond donor to the D-ring carbonyl, but this interaction is missing in chain B: the MD simulations confirm the H-bond breaking of His201 which is replaced by a water molecule.

Fig. 3. H-bond interactions in the Pfr binding pocket. (a) Schematic picture of the protein-binding pocket in the Pfr state. Water molecules were excluded from this analysis. Hydrogen bonds present in the crystal (chain A or chain B) are represented as blue dashed lines, whereas the H-bonds observed in MD are represented as red solid lines. The two torsions between rings C and D are indicated as φ₅ and φ₆, respectively. (b) Probabilities for H-bonds involving the chromophore in Pr and Pfr simulations. The Pfr analysis was performed on 150 000 frames, while the Pr analysis was performed on 60 000 frames. Probabilities were calculated averaging over monomer A and monomer B of Rep1 and Rep2 and over monomer B of Rep3 in the case of Pfr. Hydrogen bonds with less than 10% occupancy are not shown. For the Pfr, the error is less than 1 × 10⁻³, while for Pr it is less than 2 × 10⁻³.

In Fig. 3b, the same H-bond network is compared to that previously found for Pr.²⁸ For both systems we report the probabilities for H-bonds obtained along the MD trajectories. As shown in the graph, in the Pfr state, the chromophore has more H-bond partners than in the Pr state, but with generally lower occupancy. In Pfr, several pocket residues are able to make labile hydrogen bonds with the chromophore, in order to stabilize the rotated isomer of the BV.

FTIR experiments¹⁶ have revealed a change occurring in the carbonyl region between Pr and Pfr, which was ascribed to the carbonyl stretch in ring D. We calculated IR spectra on Pr and Pfr optimized MD snapshots, and computed the difference IR spectrum (Pfr-minus-Pr, Fig. S10 in the ESI†), which shows a good qualitative agreement with the experiment and reproduces the downshift of the carbonyl stretch.

We expect that these changes in the H-bond pattern will reflect on the electronic spectra as well.

To confirm this hypothesis, we calculated the absorption and CD spectra by convolution of excitation energies and transition dipoles/rotatory strength calculated on 250 optimized MD-snapshots (see Section 2).

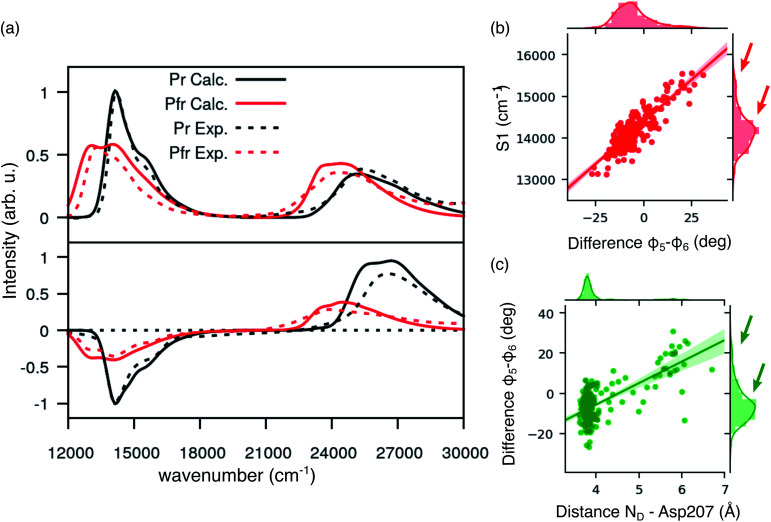
Comparing Fig. 4a and 2c, where the spectra were obtained using the crystal structure, it is evident that including structural disorder through MD largely improves the agreement with experiment for both bands, in both absorption and CD spectra. The relative positions and band shape of the two CD bands, which were not reproduced in Fig. 2c, are here well described by the MD-based calculations. In particular, the increased broadening arises, at least in part, from the heterogeneous distribution of excitation energies observed for the Pfr state.

Fig. 4. Spectroscopic properties of BV in the Pfr state. (a) Absorption and CD spectra computed for Pr (results from previous work) and Pfr state. For the latter, spectra have been obtained as an average over 250 MD configurations. All the calculated spectra have been homogeneously shifted by −0.19 eV to match the experimental lowest energy Q band. All spectra are normalized to the Q-band maximum (minimum in the case of CD). (b) Distribution for the φ₅ − φ₆ difference (right) and for the D2 distance between the D ring and Asp207 (top); dcatter plot for the energy of the φ₅ − φ₆ difference vs. D2 (center). (c) Distribution for the S₁ excitation energy (right) and for the φ₅ − φ₆ difference (top); scatter plot for the energy of S₁ energy (shifted by −0.19 eV) vs. φ₅ − φ₆ (center).

In the same figure we also report a comparison with the results previously obtained for the Pr form by using the same computational strategy. This further comparison clearly shows the accuracy of our results in reproducing the spectroscopic changes due to the Pr-to-Pfr activation. Moreover, the fact that the spectroscopic properties of the Pr state were correctly reproduced simply from the crystal structure, strongly suggests a large spectral heterogeneity of the Pfr state. Among these new interactions, an important one is the H-bond between D-ring NH and Asp207. The latter in fact is connected to the tongue through Ser468. This H-bond pattern is absent in Pr, where Ser468 is replaced by Arg466.

In order to investigate the origin of this heterogeneity in Pfr, we have investigated the lowest-energy transition S₁, which determines the Q band. The S₁ excitation energy might be tuned by a direct electrostatic effect of the protein matrix, or, indirectly, through a distortion of the chromophore geometry. In order to understand which factor plays a major role in the Pfr state of the phytochrome, we performed a cluster analysis based on distances involving ring D (see Section S1 and Fig. S1 in the ESI†), which allowed us to sample structures characterized by different environments around the chromophore. On these structures (after QM/MM optimization), we calculated the excitation energies with the atomistic MMPol environment and (i) replacing the atomistic environment with a continuum solvent description, or (ii) in gas phase (see Fig. S2 and S3 in the ESI†). By comparing the gas-phase and QM/MMPol data, it is clear that the protein environment gives a systematic red-shift of the excitation energies. In addition, excitation energies computed with atomistic and continuum environments correlate almost perfectly, meaning that the variation in excitation energies depends almost only on the internal coordinates of the chromophore. This is not surprising, given that the S₀ → S₁ transition of BV has a local character (see Fig. S4†), for which we do not expect a large direct effect of the environment.

Given the importance of the D-ring rotation in the Pr–Pfr conversion, we considered, as internal coordinates of the chromophore, the torsions around the bonds connecting rings C and D (φ₅ and φ₆Fig. 3a). We found that the variation in S₁ excitation energy is best explained by the difference φ₅ − φ₆ (Fig. 4b) which represents an out-of-plane distortion of the methine group (C₁₅) connecting rings C and D. This out-of-plane distortion is reminiscent of the hula-twist motion proposed as a possible isomerization coordinate in various photoactive systems, including phytochromes.⁴⁸ The strong correlation shown in Fig. 4b highlights that the methine distortion alone can explain the large variability of excitation energies. Moreover, the same figure shows a skewed distribution for the S₁ energies, with a small population of blue-shifted structures, characterized by a large distortion of the methine group. In order to understand whether the protein environment plays a role in the methine distortion, we analyzed the excitation energies on the cluster data (Section S1 in the ESI†). A large variation in the excitation energy was determined by the H-bond related distance between D-ring NH and Asp 207 oxygen (D2). Indeed, when D2 is small, φ₅ − φ₆ values are less or equal to ∼10°, while when D2 is larger φ₅ − φ₆ can assume larger values (see Fig. 4c), and, in turn, at larger values of φ₅ − φ₆ (larger D2) the chromophore has a blue-shifted absorption. Our analysis shows that Asp207 has a unique role in determining the absorption lineshape of phytochromes in the Pfr state. The H-bond between D-ring NH and Asp207 oxygen induces a distortion of the chromophore (in particular around the φ₅ and φ₆ dihedral angles). This distortion, in turn, tunes the S₁ excitation energy. To ensure that the classical force field gives a reasonable description of the chromophore geometry fluctuations, we have compared the aforementioned dihedral angles (φ₅ and φ₆) between MD (non-optimized) structures and QM/MM optimized structures. Fig. S11 in the ESI† shows that the value of φ₅ (panel a) is very similar before and after optimization, whereas φ₆ (panel b) becomes slightly more planar after optimization, yet its value is still correlated with the MD value. The structural heterogeneity of the Pfr binding pocket, and in particular of Asp207, is reflected in the presence of a sub-population with blue-shifted excitation energy (arrows in Fig. 4b), which absorbs at the same wavelengths as the Pr state. For this reason, the relative population of blue-shifted and red-shifted spectral bands may not be directly related to the population of Pr and Pfr forms, as is usually assumed when calculating the photoconversion yield of phytochromes.^14,49

These analyses on the binding pocket suggest that the interactions between the biliverdin and the protein are governed by a very dynamic H-bond pattern which mainly involves the propionate groups and the D ring. In particular, the latter is responsible of the H-bond interaction with Asp207 which represents a fundamental link between the conformation of the chromophore and the rest of the protein through the tongue. However, this H-bond is weak enough to allow a large heterogeneity in the BV-Asp207 distance and in the BV dihedral distortion. We have also shown that this heterogeneity also explains the shift and the enhanced broadening of the spectra with respect to the Pr state.

3.2. Structural changes in the photosensory module

In the previous section we have analyzed the differences between the dynamic description given by the MD and the crystal structure for the binding pocket. Now, we move to analyze the overall structure of the PSM for which even larger deviations are found.

A substantial root mean square displacement (RMSD) from the crystal structure is observed for PAS (∼3 Å), PHY (∼4 Å), spine (∼3 Å) and tongue (oscillating between values of ∼3.5 and ∼6.5). On the contrary, the GAF domain and the knot show a small displacement (∼1 and 0.5 Å respectively) and they are very stable along all the trajectories (see Fig. S12, S13 and Table S1 in the ESI).† These results are in line with recent NMR measurements of the Pfr form in solution¹⁹ which revealed differences from the Pr form not seen in the two crystal structures. In addition, SAXS measurements on Pfr in solution strongly diverge from the signal expected from the crystal structure.²⁰

Overall, we can see that the crystal structure of Pr is essentially reproduced by the MD, whereas the Pfr crystal is not representative of the conformations observed in the MD. These findings are in line with what previously observed for the chromophore with its binding pocket and the resulting spectra. The most striking deviations from the crystal of Pfr are seen in the long spine α-helix, up to the connection with PAS/GAF.

In particular, the α-helix consistently breaks, in all of our replicas, around residues 330, 331 and 321, 322 (Fig. S14 and S15 in the ESI†), causing kinks in the spine structure (Fig. 5b). The degree of spine kinking is measured by two angles centered on the turns, indicated as θ₁ and θ₂Fig. 5b. These angles deviate from the initial values of ∼160° and stabilize around 120° within 1 μs in most replicas (see Fig. 5c).

Fig. 5. (a) Representation of Pr (left panel) and Pfr PSM (right panel). Colors are indicative of the MD-averaged RMSD value of each residue using as a reference the crystal geometry. The RMSD was calculated aligning each monomer separately to the one of the crystal structure. (b) MD-representative structure for the DrBph photo-sensory module (PSM) in the Pfr form. The spine-angles formed between residues Thr321, Glu331, Glu345 (θ₁) and Ile300, Thr321, Glu331 (θ₁) are indicated. The color scheme is the same as used in Fig. 1. The zoom-in shows the salt bridges and H-bond interactions between the spine and the PHY domain. (c) Spine-angles θ₁ and θ₂ are analyzed along the simulation time for Rep1, Rep2, Rep3 (from top to bottom) and separately for monomer A and monomer B (left and right). The dashed lines indicate the crystal chain A and chain B values for θ₁ (∼160°) and θ₂ (∼150°), which correspond to the initial structures for monomer A and monomer B, respectively.

The spine bend corresponding to θ₁ occurs also in the crystal structure of the Pr form^20,22 and was observed in MD simulations performed with both AMBER³⁸ and CHARMM⁵⁰ force fields.^27,28 By contrast, crystal structures of the Pfr form show an essentially straight helical spine.^20,22 Based on this comparison, it was proposed that the photoactivation involves a straightening of the helical spine, which forces a separation of the two PHY domains of the dimer.²² In striking contrast with this picture, our simulations indicate that the spine is significantly bent also in the Pfr state. The domain separation, however, is maintained during our simulations. In fact, the PHY domains of the two monomers stay at an average distance of 40–45 Å (Fig. S16†), close to the crystal value. Also the distance between PHY and GAF domains (Fig. S17†) remains in between the values observed in the two chains of the Pfr crystal, and it is reduced compared to the Pr state.

MD refinement of the crystal structure, guided by solution SAXS measurements, revealed a hinge region around residue 318, corresponding to our θ₂.²⁰ Our simulations, without imposing any constraint, independently confirm the existence of a flexible region in the spine helix. In ref. 20, the structures with a bent spine helix and increased PHY domain separation better fit the difference in SAXS curves between Pr and Pfr states. The resulting PHY–PHY separation of ∼45–50 Å is essentially in agreement with our results. The striking discrepancy between crystal and solution structures was ascribed to the strong packing contacts made by the PHY domains, which stabilize a more closed structure.

In our simulations, we observe two groups of salt bridges between the spine and other domains (see Table S2 of the ESI† for details) that can stabilize a spine bent conformation. A first group keeps the GAF-part of the spine rigid within the whole GAF domain. The second group connects the spine to the adjacent region of the PHY domain (see Fig. 5b, zoom), around the kink at θ₁. The spine–PHY salt bridge interactions are completely formed only during the MD due to the movement of Arg328 (spine) toward Asp493 (PHY) (Fig. S18†). At the same time, the salt bridge between His335 (spine) and Glu490 (PHY) is formed and stable. Notably, the same interactions are observed and stable also in Pr simulations (Fig. S19†). As it is clear from Fig. 5b, the interaction of both Arg328 and His335 with the negatively charged PHY surface (Glu489, Glu490, Asp493) can only occur when the spine is significantly bent at θ₁.

Secondary structure analysis of the tongue (Fig. S20†) reveals two strikingly different regions, corresponding to the α-helix interacting with GAF and the random-coil loop. While the helical part is very stable, the 20-residue loop preceding the α-helix in the sequence is disordered, as also seen in Fig. 5a. However, this region is not completely unstructured. These residues form an important connection between the tongue and the PHY domain through H-bonds, which are especially formed in the Pfr conformation and in part preserved in the Pr one (Table S3†).

It is known that the β-hairpin to α-helix refolding observed in the Pr-to-Pfr transformation implies a significant shortening of the tongue.²⁰ Here, we find that such a refolding changes the interactions within the tongue stem and with the GAF domain, forcing a reduction of the GAF–PHY distance (Fig. S17†). This finally leads to the opening of the PHY domains (Fig. S16†).

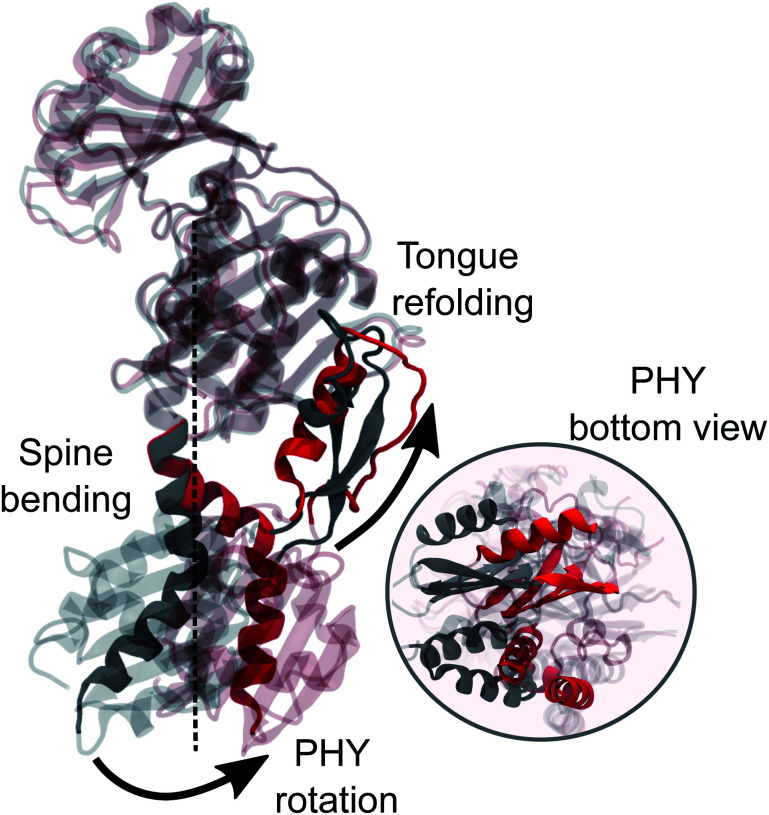
However, we also see that the structural strain posed by the tongue shortening affects the spine bending. While in the crystal the spine is almost straight, in the MD simulations a significant bend is found (θ₂ ∼ 120, Fig. 5c). We note that a bend was already present in the Pr structure but less pronounced (θ₂ ∼ 150, Fig. S21†) and in fact, the interactions between the spine and GAF/PHY domains are generally preserved in both Pr and Pfr simulations (Table S2†). When the tongue changes its conformation in Pfr, however, these interactions also induce a rotation of the entire PHY domain leading to the opening. All these findings are summarized in Fig. 6 where we graphically represent the steps in the large-scale structural change involved in the Pr-to-Pfr transformation.

Fig. 6. MD average-structure of the PSM in the Pr (grey) and Pfr state (red). The two structures were aligned to each other on the backbone of the GAF domain. The part of the spine that is not superimposable in the two states and the tongue are highlighted. A zoom-in bottom-view of the PHY-domain is shown.

We conclude this analysis by recalling that a single-point mutation of the conserved Tyr263 residue resulted in a decoupling between the chromophore state and the conformation of the PSM.^17,18 In fact, the Y263F mutant PSM could adopt a Pfr-like overall structure and a α-helix conformation for the tongue, with the chromophore in the Pr state. These experimental results suggest that the entire opening mechanism of the PSM is controlled by the tongue conformation, and not by the chromophore directly.

4. Conclusions

We combined an extensive MD simulations on the Pfr PSM with a polarizable QM/MM description of absorption and CD spectra.

As a preliminary important element, we found that the Pr-to-Pfr change induces a much more dynamic H-bond network in the protein binding pocket combined with a more dynamic structure of the chromophore. This is in line with the thermal stability of Pr and the possible thermal relaxation from Pfr to Pr and also explains their spectroscopic differences. In fact, while a static picture of the Pr state (for example the crystal geometry) is enough to properly reproduce its spectroscopic response, a dynamic description is essential in the case of the PSM in the Pfr state. In particular, we assigned the blue-shifted region of the Pfr spectra to distorted chromophore-structures (rather than co-existence of Pr-like BV-geometries) which are a clear reflection of the Pfr dynamic nature.

However, the most striking finding of this work is a large bend of the spine of the solvated Pfr, while in the crystal structure the spine is bent in the Pr state but it is straight in the Pfr. Indeed, the straightening of the helical spine was proposed to cause the PHY domains separation of the dimer in Pfr.²² Our results, instead, indicate that the opening follows an overall rotation of the PHY domain (caused by the tongue refolding) and a change in the relative GAF/PHY orientation. In this internal reorganization, the spine is forced to bend due to its tight H-bonding connection with the adjacent residues in the PHY and GAF domains. These results pave the way towards an atomistic understanding of the activation mechanism of bacterial phytochrome through collective variable techniques. Work in this direction is being carried out in our group.

In conclusion, our findings show that the comparison of crystal structures cannot fully explain the Pr-to-Pfr conversion, but a dynamic picture of the Pfr in solution can give further insight into the phytochrome activation. In such a picture, the different “mobile” parts of the PSM are coupled mostly through H-bonds and salt bridges. The coupling however is weak enough to leave some freedom in the motions of the various parts. In particular, we have shown that the connection between the conformation of the chromophore and the following large-scale changes in the secondary and tertiary structure of the PSM is not univocal thus allowing the phytochrome to exploit redundant routes for its activation.^17,18

Author contributions

V. M., L. C. and B. M. designed the study. B. M. acquired funding for the work. V. M. ran the MD simulations. V. M. and G. S. analysed the MD simulations and ran the QM/MM and QM/MMPol calculations. L. C. oversaw the MD analysis and the QM calculations. V. M., L. C. and B. M. wrote the first version of the manuscript. All authors contributed to writing the final version.

Conflicts of interest

There are no conflicts to declare.