Abstract
O-Acetylation of carbohydrates such as sialic acids is common in nature, but its role is not clearly understood due to the lability of O-acetyl groups. We demonstrated previously that 9-acetamido-9-deoxy-N-acetylneuraminic acid (Neu5Ac9NAc) is a chemically and biologically stable mimic of the 9-O-acetyl-N-acetylneuraminic acid (Neu5,9Ac2) of the corresponding sialoglycans. Here, a systematic nuclear magnetic resonance (NMR) spectroscopic and molecular dynamics (MD) simulation study was undertaken for Neu5,9Ac2-containing GM3 ganglioside glycan (GM3-glycan) and its Neu5Ac9NAc analog. GM3-glycan with Neu5Ac as the non-O-acetyl form of Neu5,9Ac2 was used as a control. Complete 1H and 13C NMR chemical shift assignments, three-bond 1H-13C trans-glycosidic coupling constants (3JCH), accurate 1H-1H coupling constants (3JHH), nuclear Overhauser effects and hydrogen bonding detection were carried out. Results show that structural modification (O- or N-acetylation) on the C-9 of Neu5Ac in GM3 glycan does not cause significant conformational changes on either its glycosidic dihedral angles or its secondary structure. All structural differences are confined to the Neu5Ac glycerol chain, and minor temperature-dependent changes are seen in the aglycone portion. We also used Density Functional Theory (DFT) quantum mechanical calculations to improve currently used 3JHH Karplus relations. Furthermore, OH chemical shifts were assigned at −10°C and no evidence of an intramolecular hydrogen bond was observed. The results provide additional evidence regarding structural similarities between sialosides containing 9-N-acetylated and 9-O-acetylated Neu5Ac and support the opportunity of using 9-N-acetylated Neu5Ac as a stable mimic to study the biochemical role of 9-O-acetylated Neu5Ac.
Keywords: ab initio calculations, acetylated GM3 glycan, conformational analysis, molecular dynamics, NMR
Introduction
Sialic acids (Sias) are common terminal monosaccharides of cell surface glycoconjugates. These monosaccharides are a diverse family of naturally occurring polyhydroxyketoaldonic acids and are involved in many physiological and pathological processes. More than 50 structurally different Sia forms including N-acetylneuraminic acid (Neu5Ac), N-glycolylneuraminic acid (Neu5Gc), 2-keto-3-deoxy-nonulosonic acid (Kdn), and their modified forms have been identified in nature (Angata and Varki 2002; Varki and Varki 2007; Chen and Varki 2010). Among the diverse sialic acid modifications, O-acetylation is the most common one, which can be found at the C-4, C-7, C-8 and C-9 positions in Neu5Ac (Figure 1), Neu5Gc and Kdn, as well as the N-glycolyl hydroxyl group in Neu5Gc and the C-5 hydroxyl group in Kdn (Klein and Roussel 1998; Zhu et al. 1999; Schauer 2000; Kooner et al. 2019). O-Acetylated Sias have been shown to play important roles in the regulation of immune responses to bacterial polysaccharides (Deszo et al. 2005; Berti et al. 2018), sialidase recognition and activity, cellular apoptosis and tumor immunology (Varki and Kornfeld 1980; Kelm et al. 1994; Sjoberg et al. 1994; Shi et al. 1996). 9-O-Acetyl-N-acetylneuraminic acid (Neu5,9Ac2) is the most abundant modified Sia form in mammals (Schauer 1982). It plays a regulatory role in tissue morphogenesis (Klotz et al. 1992), serves as an effective biomarker for acute lymphoblastic leukemia and visceral leishmaniasis (Klein and Roussel 1998), is required for influenza C and D virus hemagglutinin binding, masks the recognition of influenza A virus hemagglutinin (Klein and Roussel 1998; Liu et al. 2020) and is a better binder for Salmonella enterica serovar Typhi toxin binding (Nguyen et al. 2020).
Fig. 1.
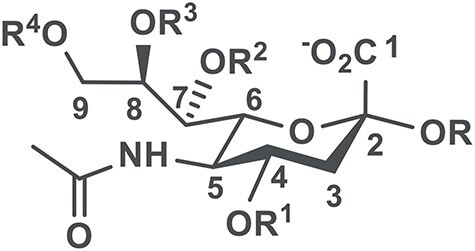
N-Acetylneuraminic acid (Neu5Ac where R1 = R2 = R3 = R4 = H) and its O-acetylated forms (R1, R2, R3, R4 = H or Ac) in α-linked sialosides.
Nevertheless, more detailed understanding of the roles of Neu5,9Ac2 and its applications lags behind due to the instability of the O-acetyl (ester) group, even with small pH changes and in the presence of esterases in biological systems (Herrler et al. 1985; Khedri et al. 2017). The O-acetyl group on C-7 can spontaneously migrate to C-9 (Schauer 1978; Schauer 1982; Kamerling et al. 1987), which further complicates the study and characterization of sialic acid O-acetylation at a position other than C-9. Thus, the mechanisms and the influence of O-acetyl addition, dissociation and migration from the C-7 to the C-9 position remain an open question. Indeed, our previous studies showed that even with the most careful precautions, cleavage of the 9-O-acetyl group in 9-O-acetylated sialoglycans occurred during glycan microarray preparation and assays (Khedri et al. 2017).
We aim to study the importance of sialic acid 9-O-acetylation in gangliosides, a group of sialic acid-containing glycosphingolipids that are ubiquitous in vertebrate cells and enriched in nerve cells (Schnaar 2016). The glycan components of gangliosides are believed to be the major recognition sites for other molecules such as glycan-binding proteins (Lopez and Schnaar 2009). To avoid spurious data resulting from cleavage of the 9-O-acetyl group, we developed 9-acetamido-9-deoxy-N-acetylenuraminic acid (Neu5Ac9NAc) as a chemically and biologically stable mimic of Neu5,9Ac2 and synthesized Neu5Ac9NAc-sialosides using an efficient one-pot multienzyme (OPME) strategy. Similarities and some differences of sialosides containing Neu5Ac9NAc and Neu5,9Ac2 were shown by glycan microarray, mammalian cell incorporation and surface expression, as well as sialidase substrate specificity studies (Khedri et al. 2017; Li et al. 2017). The conformations of GM3 ganglioside glycans containing Neu5Ac9NAc and Neu5,9Ac2 were analyzed by computational molecular dynamics (MD) simulations (2.5 μs trajectories) and showed high similarity except for some minor hair pin conformations observed only for Neu5,9Ac2-glycan. Nevertheless, experimental determination was not available (Khedri et al. 2017).
GM3 is a ganglioside that is overexpressed by different types of tumors and is ranked #48 on a list of 75 prioritized cancer antigens in a 2009 National Cancer Institute Pilot Project report (Cheever et al. 2009). Its enzymatic synthesis and structural study were reported by Paulson, Prestegard and co-workers (Aubin et al. 1993; Ito and Paulson 1993). In early structural studies reported by Dabrowski and co-workers (Siebert et al. 1992) as well as Prestegard and co-workers (Aubin et al. 1993), the conformations of GM3 were studied in dimethyl sulfoxide (DMSO), probably due to the fact that in these pioneering works, the GM3 glycan was covalently attached to fairly hydrophobic ceramide moieties, which are likely only sparingly soluble in water. Thus, their conformational analysis may significantly differ from those examined in the present study. Herein, we report extensive, systematic experimental nuclear magnetic resonance (NMR) spectroscopic studies of ganglioside GM3 glycan containing Neu5Ac9NAc, Neu5,9Ac2, or Neu5Ac (used as a control) in water at two different temperatures (25 and −10 °C). These studies include 1H-13C NMR chemical shift assignment, solution conformations defined by three-bond 1H-13C trans-glycosidic coupling constants (3JCH), three-bond 1H-1H coupling constants in the glycerol chains of Neu5Ac (3JHH), 1H-1H nuclear Overhauser effects (nOes) and hydrogen bonding (Hbonding) experiments. Furthermore, MD simulations in explicit water were extended to 20 μs to provide more detailed interpretations. Additional insights for NMR studies were obtained via computed coupling constants and interatomic distances determined from MD data at 25 and −10 °C. DFT calculations of low-energy conformations were carried out to provide 3JCH values to which the experimental data were compared. Altogether, these studies provide additional evidence regarding structural similarities between sialosides containing 9-N-acetylated and 9-O-acetylated Neu5Ac and support the use of 9-N-acetylated Neu5Ac as a stable mimic to study the biochemical role of 9-O-acetylated Neu5Ac.
Results and discussion
One-pot multienzyme (OPME) synthesis of GM3 glycans containing Neu5Ac, Neu5,9Ac2 or Neu5Ac9NAc (Scheme 1)
Scheme 1.

One-pot multienzyme (OPME) chemoenzymatic synthesis of GM3 glycans containing Neu5Ac, Neu5,9Ac2 or Neu5Ac9NAc (4–6).
To synthesize GM3 glycans, one-pot multienzyme (OPME) sialylation systems were used. As shown in Scheme 1, GM3 glycans containing Neu5Ac and Neu5Ac9NAc (Khedri et al. 2017) were synthesized from N-acetylmannosamine (ManNAc, 1) and 2,6-diacetamido-2,6-dideoxy-D-mannose (ManNAc6NAc, 2), respectively, using a one-pot three-enzyme sialylation system (Yu et al. 2006) containing Pasteurella multocida sialic acid aldolase (PmAldolase) (Cheng et al. 2008), Neisseria meningitidis CMP-sialic acid synthetase (NmCSS) (Yu et al. 2004) and Pasteurella multocida sialyltransferase 1 M144D mutant (PmST1 M144D) (Yu et al. 2005; Sugiarto et al. 2012). GM3 glycans Neu5Acα2-3LacβProN3 (4) and Neu5Ac9NAcα2-3LacβProN3 (5) were obtained in 95 and 84% yields, respectively.
By comparison, GM3 glycan containing Neu5,9Ac2 was synthesized from chemically produced Neu5,9Ac2 (3) (Yu et al. 2009) using a one-pot two-enzyme sialylation system containing NmCSS and PmST1 M144D. A solution containing Tris-HCl buffer controlled at pH 7.0 was used to minimize de-O-acetylation. About 5% deacetylated product, which was separated from Neu5,9Ac2α2-3LacβProN3 (6) on a C18 reverse phase column, was observed during the reaction.
MD and computations: comparison of GM3 glycans containing Neu5Ac, Neu5,9Ac2, or Neu5Ac9NAc
Molecular dynamics (MD) simulations for GM3 glycans 4–6 were carried out using the AMBER18 simulation package (Case et al. 2018). These simulations used a combination of the GLYCAM06 (Kirschner et al. 2008) and GAFF (Wang et al. 2004) force fields, with customized parameters for the N-acetylated and O-acetylated sialosides. Each of the glycans was simulated for 30.0 μs in the NVT ensemble at 298.15 K and 263.15 K. Full details of the simulation setup are provided in the Materials and methods section.
Chemical Shift Assignment of GM3 Glycans Containing Neu5Ac, Neu5,9Ac2, or Neu5Ac9NAc
The NMR portion of this study was designed to probe potential 3D conformational differences among the GM3 glycans. Since these molecules are potentially flexible, chemical modifications may skew the populations and cause the observed chemical shifts and trans-glycosidic coupling constants to change. This would result in different population weighted averages, which should change with temperature, under most circumstances. Thus, we measured spectra, coupling constants and nOes at two different temperatures, where a change in populations should be apparent. Moreover, chemical modifications made herein may impact potential intramolecular Hbonding. Therefore, we ran NMR experiments at −10 °C, where these hydrogen bonds (Hbonds) are most likely to be detected.
1H and 13C NMR chemical shifts of Neu5Acα2-3LacβProN3 at room temperature in D2O were reported previously (Cheng et al. 2008). However, in the previous work, there were difficulties in assigning the H4, H5 and H6 of Neu5Ac residue; H2, H3, H4 and H5 of galactose residue; and H2, H3, H4 and H5 of glucose residue due to similar 1H-1H three-bond coupling constants (3JHH) and spectral overlap (Gilbert et al. 2000). In the present study, these problems (Gilbert et al. 2000) were overcome by exploiting the additional resolution provided in the 13C dimension in HSQC-TOCSY spectra acquired with a 10 ms and 90 ms mixing times (Figure S1) (Lerner and Bax 1986; Lerner and Bax 1987), as well as HSQC (Bodenhausen and Ruben 1980) and PIP-HSQMBC (Castañar et al. 2014) experiments at 25 and −10 °C. 1H-13C HSQC-TOCSY with a 10 ms mixing time yielded through-bond correlations from a 13C-attached 1H to its J-coupled vicinal 1Hs on adjacent carbons, while the 90 ms HSQC-TOCSY provided through-bond correlations between a 13C attached 1H and all other coupled 1Hs within a spin system (e.g., within a monosaccharide residue). This strategy allowed complete 1H and 13C chemical shift assignments of GM3 glycans Neu5Acα2-3LacβProN3 (4), Neu5Ac9NAcα2-3LacβProN3 (5) and Neu5,9Ac2α2-3LacβProN3 (6) at 25 and −10 °C (Table I) which are in general agreement with previous reports (Gilbert et al. 2000; Cheng et al. 2008).
Table I.
1H and 13C NMR chemical shifts (in ppm measured to +/− 0.3) of GM3βProN3 (4), 9NAcGM3βProN3 (5) and 9OAcGM3βProN3 (6) at 25 and −10 °C (results are in parentheses)
| Chemical shift | GM3βProN3 (4) | 9NAcGM3βProN3 (5) | 9OAcGM3βProN3 (6) | ||||
|---|---|---|---|---|---|---|---|
| H | C | H | C | H | C | ||
| Neu5Ac | 1 | N.A. | 173.92 (174.02) | N.A. | 173.86 (173.97) | N.A. | 173.82 (173.99) |
| Residue III | 2 | N.A. | 99.85 (99.64) | N.A. | 99.94 (99.76) | N.A. | 99.80 (99.61) |
| 3 | 1.79 (1.81) | 39.71 (39.53) | 1.80 (1.81) | 39.69 (39.55) | 1.81 (1.81) | 39.77 (39.64) | |
| 3 | 2.75 (2.75) | 2.75 (2.75) | 2.77 (2.76) | ||||
| 4 | 3.68 (3.67) | 68.42 (68.48) | 3.69 (3.66) | 68.38 (68.45) | 3.70 (3.66) | 68.39 (68.50) | |
| 5 | 3.84 (3.87) | 51.76 (51.56) | 3.85 (3.87) | 51.74 (51.58) | 3.87 (3.88) | 51.72 (51.57) | |
| 6 | 3.63 (3.61) | 72.95 (72.78) | 3.66 (3.64) | 72.81 (72.68) | 3.67 (3.64) | 72.74 (72.62) | |
| 7 | 3.59 (3.59) | 68.17 (67.92) | 3.49 (3.50) | 69.66 (69.52) | 3.65 (3.67) | 68.21 (67.96) | |
| 8 | 3.88 (3.91) | 71.84 (71.77) | 3.92(3.94) | 70.02 (69.96) | 4.11 (4.13) | 69.38 (69.31) | |
| 9 | 3.64 (3.63) | 62.65 (62.39) | 3.28(3.25) | 42.19 (42.12) | 4.20 (4.18) | 65.78 (65.59) | |
| 9 | 3.87 (3.87) | 3.61 (3.62) | 4.42(4.42) | ||||
| CH3 on 5 | 2.03 (2.02) | 22.11 (21.96) | 2.03 (2.02) | 22.10 (22.00) | 2.04 (2.03) | 22.11 (22.02) | |
| C=O on 5 | N.A. | 175.06 (174.81) | N.A. | 174.97 (174.79) | N.A. | 175.01 (174.78) | |
| CH3 on 9 | N.A. | N.A. | 2.03 (2.03) | 21.89 (21.75) | 2.14 (2.14) | 20.32 (20.25) | |
| C=O on 9 | N.A. | N.A. | N.A. | 174.43 (174.44) | N.A. | 174.36 (174.25) | |
| Gal | 1 | 4.52 (4.54) | 102.71 (102.46) | 4.52 (4.53) | 102.68 (102.47) | 4.54 (4.54) | 102.70 (102.49) |
| Residue II | 2 | 3.57 (3.57) | 69.44 (69.35) | 3.57 (3.56) | 69.43 (69.40) | 3.58 (3.57) | 69.42 (69.39) |
| 3 | 4.11 (4.13) | 75.56 (75.31) | 4.09 (4.11) | 75.63 (75.41) | 4.12 (4.12) | 75.59 (75.38) | |
| 4 | 3.95 (3.95) | 67.54 (67.31) | 3.95 (3.94) | 67.54 (67.36) | 3.95 (3.94) | 67.46 (67.26) | |
| 5 | 3.70 (3.71) | 75.23 (75.14) | 3.70 (3.70) | 75.22 (75.17) | 3.71 (3.70) | 75.23 (75.17) | |
| 6 | 3.73 (3.73) | 61.09 (61.07) | 3.74 (3.73) | 61.08 (61.10) | 3.75 (3.73) | 61.08 (61.09) | |
| Glc | 1 | 4.48 (4.50) | 102.20 (102.12) | 4.49 (4.50) | 102.19 (102.14) | 4.50 (4.50) | 102.19 (102.14) |
| Residue I | 2 | 3.31 (3.30) | 72.87 (72.74) | 3.31 (3.30) | 72.8 7 (72.78) | 3.32 (3.30) | 72.87 (72.78) |
| 3 | 3.65 (3.65) | 74.42 (74.25) | 3.66 (3.65) | 74.41 (74.28) | 3.66 (3.65) | 74.40 (74.28) | |
| 4 | 3.65 (3.67) | 78.33 (77.71) | 3.66 (3.68) | 78.26 (77.67) | 3.67 (3.67) | 78.31 (77.75) | |
| 5 | 3.59 (3.60) | 74.84 (74.75) | 3.59 (3.59) | 74.85 (74.81) | 3.60 (3.59) | 74.88 (74.83) | |
| 6 | 3.82 (3.83) | 60.13 (59.80) | 3.82 (3.83) | 60.10 (59.80) | 3.83 (3.82) | 60.12 (59.82) | |
| 6 | 3.98 (3.99) | 3.99 (3.99) | 4.00 (3.99) | ||||
| ProN3 | OCH2CH2CH2N3 | 3.76 (3.76) | 67.43 (67.26) | 3.77 (3.76) | 67.42 (67.28) | 3.77 (3.76) | 67.41 (67.28) |
| aglycon | 3.99 (4.02) | 4.00 (4.02) | 4.01 (4.02) | ||||
| OCH2CH2CH2N3 | 1.91 (1.90) | 28.30 (28.21) | 1.92 (1.91) | 28.2 9 (28.23) | 1.92 (1.90) | 28.29 (28.24) | |
| OCH2CH2CH2N3 | 3.45 (3.46) | 47.95 (47.69) | 3.46 (3.47) | 47.94 (47.72) | 3.47 (3.46) | 47.93 (47.72) | |
Cross-peaks between C2 of Neu5Ac and H3 of galactose and C1 of galactose and H4 of glucose confirmed the linkages and sequences of the trisaccharide. PIP-HSQMBC (Castañar et al. 2014) experiments provided coupling constants within each spin system and yielded 1H-13C three-bond trans-glycosidic coupling constants (3JCOCH) between neighboring monosaccharide residues.
According to the 1H and 13C chemical shift assignments (Table I), 9-N-acetyl and 9-O-acetyl modifications on C9 of Neu5Ac in the GM3 glycan affect only the chemical shift of 1H and 13C in the glycerol chain of Neu5Ac, where the most significant difference took place at C9 and H9/H9’ (Figure S2). The effects on NMR chemical shifts decrease dramatically with increasing number of bonds from C9. For all atoms separated by three or more chemical bonds from C9, i.e., beyond C7 and H7, the 1H and 13C chemical shift differences in the three analogs were less than 0.03 ppm and 0.2 ppm, respectively. As expected, the chemical shift difference at C9, H9 and H9’ between GM3 glycans with 9-N-acetyl and 9-O-acetyl modification correlates with the electronegativity of the substituents. In terms of 1H chemical shifts on the glycerol chain, there was less than 0.25 ppm variation in H7 or H8 among GM3βProN3, 9NAcGM3βProN3 and 9OAcGM3βProN3. H9 and H9’ of 9NAcGM3βProN3 and 9OAcGM3proN3 were 0.3–0.4 ppm and 0.5 ppm shielded, respectively, as compared to the H9 and H9’ of GM3βProN3. 13C chemical shifts of C7 and C8 of the glycerol chain differed by < 2.5 ppm among GM3βProN3, 9NAcGM3βProN3 and 9OAcGM3βProN3. C9 chemical shifts in 9NAcGM3βProN3 and 9OAcGM3βProN3 were ~ 20 ppm more shielded and 3 ppm less shielded, respectively, than the C9 of GM3βProN3. In general, N-acetylation causes less de-shielding than O-acetylation on C9, H9 and H9’, which, as stated above, could be explained by the electronegativity differences of substituents (i.e., the N is less electronegative than O and the N-acetyl group is less electronegative than the O-acetyl group). Consequently, N-acetylation results in more shielding than O-acetylation or hydroxylation (OH group). Although this relative shielding trend caused by N-acetyl substitution was most significant at C9, H9, C8 and C7, H8 and H7 did not follow this trend. This suggests that N-acetylation or O-acetylation of GM3 induces only relatively subtle structural and conformational differences in the glycerol chain in these compounds.
Nevertheless, to ensure that subtle conformational effects of N-acetylation did not cause any unintended conformational changes, the following experiments were conducted to further understand the conformation of GM3 glycan with C-9 N-acetylation or O-acetylation. First, temperature-dependent HSQC spectra at 25 and −10 °C were taken with the goal of tracking the chemical shifts: significant changes in chemical shifts with temperature would indicate conformational averaging. Table I shows that temperature did not significantly alter the chemical shifts of all 1H’s and 13C’s.
Trans-Glycosidic Torsions From 3JCH at 25 and −10 °C
Chemical shifts of glycan residues and changes therein are not always reliable reporters of conformational changes. Typically, three-dimensional glycan structure is expressed as the relative orientation of monosaccharide residues and is therefore discussed in terms of the glycosidic bond torsional angles, ϕ and ψ, between these residues (IUPAC-IUB Joint Commission on Biochemical Nomenclature 1983). Using NMR, ϕ and ψ (Figure 2) can be directly related to the long-range 1H-13C spin-spin coupling constants (3JCH), which can be measured by various NMR techniques (Battistel et al. 2014; Hadad et al. 2017).
Fig. 2.
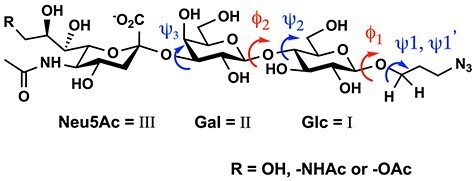
Torsional angles (dihedral angles) ϕ and ψ between Neu5Ac (III) and Gal (II), Gal and Glc (I), as well as Glc and aglycon in GM3 type glycans (ϕ2 = H1II—C1II—O—C4I, ϕ1 = H1I—C1I—O—C1ProN3; ψ3 = C2III—O—C3II—H3II, ψ2 = C1II—O—C4I—H4, ψ1, ψ1’ = C1I—O—C1ProN3—H1ProN3).
To measure the long-range 1H-13C coupling constants through the glycosidic linkages, we used the pure in-phase HSQMBC (PIP-HSQMBC) NMR experiment (Castañar et al. 2014). The extraction of 3JCH was achieved by recording two separate in-phase (IP) and anti-phase (AP) datasets and overlaid “alpha” (IP + AP) and “beta” (IP-AP) multiplets obtained after IPAP data combination in an IPAP experiment, as shown in Figure S4.
Trans-glycosidic 3JCH values between Neu5Ac and galactose (Gal), galactose and glucose (Glc) and Glc and aglycon (Table S1) show virtually no temperature dependence (Figure 3), indicating that the modifications on C-9 do not cause changes in the average glycosidic torsional angles in the GM3 glycans studied here.
Fig. 3.
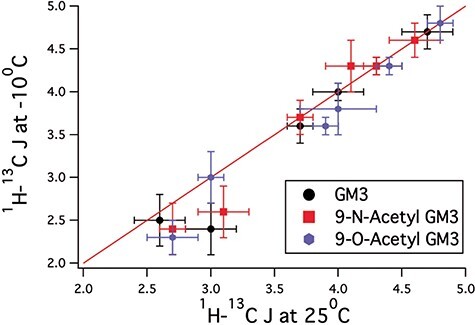
Comparison of trans-glycosidic J-couplings for the three GM3 derivatives, GM3 (black circles), 9-N-acetylated GM3 (red squares) and 9-O-acetylated GM3 (blue circles). The plot shows that trans-glycosidic J-couplings obtained for these three derivatives at −10 °C closely match those measured 25 °C, indicating that there is no change in average structure over this temperature range.
In addition, the 3JCH (Figure 4, Table SI) indicate that there are no major differences in the 3JCH within experimental error among the three analogs.
Fig. 4.

Plots comparing the trans-glycosidic J-values in GM3 and 9NAcGM3 vs their 9-O-acetyl analog. The graphs show that all trans-glycosidic J-values are within experimental error, indicating that their conformations are unchanged regardless of substitution pattern.
MD simulations (details in the Experimental section) were used to complement experimental results for glycosidic torsions. Figure 5 describes the Neu5Ac–Gal glycosidic linkage in simulations of GM3βProN3 and its 9NAc/9OAc modifications. The ψ3 (y-axis) corresponds to the 3JH3-C2; however the ϕ3 torsion angle (x-axis) is not accessible via NMR experiments because Neu5Ac contains no anomeric 1H and therefore is not shown in Figures 3 and 4. The 2D free energy map of the glycosidic angles is characterized by three main peaks located at (ϕ3, ψ3) = (−45°, −15°), (+45°, −60°) and (+60°, 0°), consistent with previous simulation studies (Khedri et al. 2017). The present results are not in agreement with previous studies (Siebert et al. 1992; Aubin et al. 1993). In these two pioneering studies, the authors examined the structure of the intact ganglioside, which contains a ceramide head group. These studies were carried out in DMSO, probably due to the nonpolar ceramide and sphingosine groups, and this change in NMR solvent may change the conformation of the ceramide-bound ganglioside as compared to the present studies, which are carried out in water. It is important to note that the present study compares the effects of N-acetyl substitution on the non-ceramide derivative of GM3 to the O-acetylated and non-acetylated attached GM3, all of which do not contain a ceramide moiety.
Fig. 5.
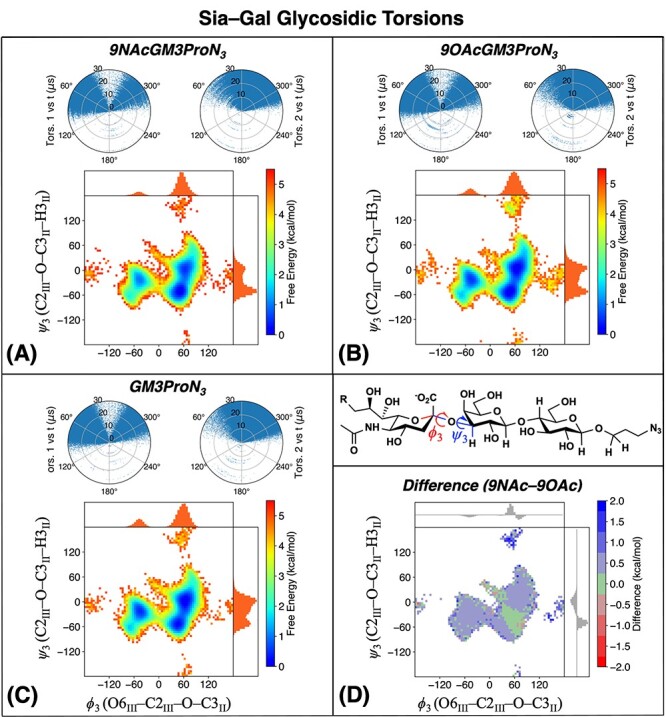
Simulated ϕ3 and ψ3 torsion angles for the Neu5Ac–Gal glycosidic linkage for (A) 9NAcGM3βProN3, (B) 9OAcGM3βProN3, (C) GM3βProN3. The polar plots show values of ϕ3 (left) and ψ3 (right) as a function of simulation time. The heat map is a free energy surface computed as F = –kBT ln P(ϕ, ψ), where P(ϕ, ψ) is the 2-D histogram of torsion angles computed from trajectory frames. The marginal distributions and are shown at the top and right sides of each heat map. (D) Heat map showing the free energy difference between 9-NAc and 9-OAc forms. Normalized differences in the marginal distributions are shown at the top and right sides.
The polar plots show that conformational transitions occur many times over the simulation trajectory, indicating that a given torsion is flexible. The shapes of the free energy maps are highly similar among all three forms. Figure 5D shows that the free energy of 9NAcGM3βProN3 is higher than that of 9OAcGM3βProN3 by ~0.5 kcal/mol in most areas except for the minimum at (+45°, −60°). This small free energy difference in the MD calculations is within the error of this method (±1 kcal/mol) and likely is not indicative of a true energy difference. The increased tendency of 9OAcGM3βProN3 to populate multiple minima, as indicated by the free energy surfaces, indicates that it may be slightly more flexible than 9NAcGM3βProN3; however, this is only a minor effect as the free energy differences are mostly within kBT at room temperature. Another minor cluster of structures, located near (+60°, +150°), favors 9OAcGM3βProN3 over 9NAcGM3βProN3, consistent with our previous simulation findings.15 These extended MD simulations indicate that the differences between N-acetylation and O-acetylation could become more pronounced for conformations out of equilibrium in aqueous solvent, which may be important if these conformations are involved in binding to proteins.
Fitting trans-glycosidic torsional angles, ϕ and ψ, calculated from MD simulations to parameterized Karplus-type equations should result in possible 3JCH constants which could be compared with experimental 3JCH constants measured by NMR and provide experimental verification of previously obtained theoretical models (Coxon 2009; Hackbusch et al. 2017; Khedri et al. 2017). For C-O-C-H type coupling, three different parameterized Karplus relations were employed to explore the possible ϕ and ψ torsional angle and 3JC-O-C-H, which are the Mulloy parameterization (3JC-O-C-H = 5.5cos2(θ) − 0.7cos(θ) + 0.6) (Mulloy et al. 1988), Tvaroska parameterization (3JC-O-C-H = 5.7cos2(θ) − 0.6cos(θ) + 0.5) (Tvaroska et al. 1989) and Anderson parameterization (3JC-O-C-H = 7.6cos2(θ) − 1.7cos(θ) + 1.6) (Anderson and Ijeh 1994). Our MD simulation results were used to further interpret the experimentally measured 3JC-O-C-H coupling constants by comparing simulated coupling constants with experiment.
Simulated values of the 3JC-O-C-H couplings were evaluated as: 3J = <A cos2(ϕ) − B cos(ϕ) + C>. For each structure sampled in the MD trajectory, the dihedral angle of interest, ϕ, is mapped to a coupling using the parameterized Karplus relation, and the final ensemble-averaged value is computed by taking the mean over all trajectory frames. Table II provides a comparison of simulated 3JC-O-C-H values with experiment, using the three sets of Karplus parameters described above. The simulated couplings are in good agreement with experiment, but there are significant differences in the simulated values (and the deviations vs. experiment) depending on which parameterization is used.
Table II.
Trans-glycosidic 3JC-O-C-H resulting from MD simulations. Italicized values correspond to simulations performed at −10°C. Deviations from experiment calculated as J(sim)–J(exp) are given in parentheses. Values in bold correspond to the Karplus parameterizations that agree more closely with DFT-computed couplings
| Karplus parameterization | Torsion | GM3βProN3 (4) | 9NAcGM3βProN3 (5) | 9OAcGM3βProN3 (6) | |||
|---|---|---|---|---|---|---|---|
| 25°C | −10°C | 25°C | −10°C | 25°C | −10°C | ||
| Mulloy | 3 J(C2 III , H3 II ) | 4.1 (−0.6) | 4.2 (−0.5) | 3.6 (−1.0) | 3.6 (−1.0) | 3.9 (−0.9) | 4.0 (−0.8) |
| 3 J(C1 II , H4 I ) | 4.9 (+0.9) | 5.0 (+1.0) | 4.9 (+0.8) | 5.0 (+0.7) | 4.9 (+0.9) | 5.0 (+1.2) | |
| 3 J(H1II, C4I) | 2.9 (−0.8) | 2.8 (−0.8) | 2.8 (−0.9) | 2.7 (−1.0) | 2.9 (−1.0) | 2.7 (−0.9) | |
| 3 J(H1I, C1ProN3) | 3.2 (−1.1) | 3.2 (−1.1) | 3.2 (−1.1) | 3.2 (−1.1) | 3.3 (−1.1) | 3.2 (−1.2) | |
| 3 J(C1 I , H1 ProN3 ) | 3.1 (+0.5) | 3.0 (+0.5) | 3.1 (+0.4) | 3.0 (+0.6) | 3.1 (+0.4) | 3.0 (+0.3) | |
| 3 J(C1 I , H1’ ProN3 ) | 2.8 (−0.2) | 2.7 (+0.3) | 2.8 (−0.3) | 2.7 (+0.1) | 2.8 (−0.2) | 2.7 (−0.3) | |
| RMSD | 0.74 | 0.77 | 0.80 | 0.82 | 0.84 | 0.86 | |
| Tvaroska | 3 J(C2 III , H3 II ) | 4.2 (−0.5) | 4.4 (−0.4) | 3.7 (−0.9) | 3.8 (−0.9) | 4.0 (−0.8) | 4.2 (−0.6) |
| 3 J(C1 II , H4 I ) | 5.1 (+1.1) | 5.2 (+1.2) | 5.1 (+1.0) | 5.2 (+0.9) | 5.1 (+1.1) | 5.2 (+1.4) | |
| 3 J(H1II, C4I) | 3.0 (−0.8) | 2.8 (−0.8) | 2.9 (−0.8) | 2.8 (−0.9) | 2.9 (−1.0) | 2.8 (−0.8) | |
| 3 J(H1I, C1ProN3) | 3.3 (−1.0) | 3.3 (−1.1) | 3.3 (−1.0) | 3.2 (−1.1) | 3.3 (−1.1) | 3.3 (−1.1) | |
| 3 J(C1 I , H1 proN3 ) | 3.1 (+0.5) | 3.0 (+0.5) | 3.1 (+0.4) | 3.0 (+0.6) | 3.1 (+0.4) | 3.0 (+0.3) | |
| 3 J(C1 I , H1’ proN3 ) | 2.8 (−0.2) | 2.7 (+0.3) | 2.8 (−0.3) | 2.7 (+0.1) | 2.8 (−0.2) | 2.7 (−0.3) | |
| RMSD | 0.74 | 0.77 | 0.78 | 0.80 | 0.82 | 0.86 | |
| Anderson | 3 J(C2III, H3II) | 5.8 (+1.1) | 6.0 (+1.3) | 5.2 (+0.6) | 5.2 (+0.6) | 5.5 (+0.7) | 5.7 (+0.9) |
| 3 J(C1II, H4I) | 6.9 (+2.9) | 7.0 (+3.0) | 6.9 (+2.8) | 7.0 (+2.7) | 6.9 (+2.9) | 7.0 (+3.2) | |
| 3 J(H1 II , C4 ) | 4.3 (+0.6) | 4.1 (+0.5) | 4.2 (+0.5) | 4.0 (+0.3) | 4.2 (+0.3) | 4.1 (+0.5) | |
| 3 J(H1 I , C1 ProN3 ) | 4.8 (+0.5) | 4.7 (+0.4) | 4.8 (+0.5) | 4.7 (+0.4) | 4.9 (+0.5) | 4.8 (+0.4) | |
| 3 J(C1I, H1ProN3) | 4.9 (+2.3) | 4.8 (+2.3) | 4.9 (+2.2) | 4.8 (+2.4) | 4.9 (+2.2) | 4.8 (+2.1) | |
| 3 J(C1I, H1’ProN3) | 4.3 (+1.3) | 4.2 (+1.8) | 4.3 (+1.2) | 4.2 (+1.6) | 4.3 (+1.3) | 4.2 (+1.2) | |
| RMSD | 1.70 | 1.81 | 1.59 | 1.65 | 1.62 | 1.71 | |
We carried out DFT calculations on selected structures from the MD simulations (Figure 5) to study the relationships between the torsion angles and the 3JC-O-C-H-couplings and provide more insight into these results (full details in the Experimental section). It is clear that the DFT calculations predict different trends in the couplings for different torsion angles, and no single parameterization is the most accurate for all torsions considered (Figure 6).
Fig. 6.

Parameterized Karplus relations mapping dihedral angles to 3JC–O–C–H couplings. Each color represents a different torsion, while each shape represents a different substitution. The Mulloy and Tvaroska parameterizations provide similar curves, while the Anderson parameterization is shifted towards more positive couplings. The colored symbols show DFT calculations of couplings based on structures sampled from the MD trajectories.
For ψ3 that is probed by 3JH3II-C2III, the sampled structures span a range of (−60°, +30°), and the DFT calculations (red symbols) overlap closely with the Mulloy/Tvaroska (M/T) curve, whereas the Anderson (A) curve overestimates the values. Moreover, the computed couplings do not have an observable dependence on acetylation at the C9 position. Based on the DFT results, we may assume the M/T curves give better comparison with experiment for this torsion angle. From Table II, the ensemble-averaged couplings using the M/T parameterizations are lower than experiment by 0.5–1 Hz. Assuming the J-couplings from DFT calculations are accurate, this indicates that the MD simulations (Figure 7) slightly underestimate the populations of conformations with higher values of the coupling, i.e., structures in the vicinity of (−30°, +30°).
Fig. 7.
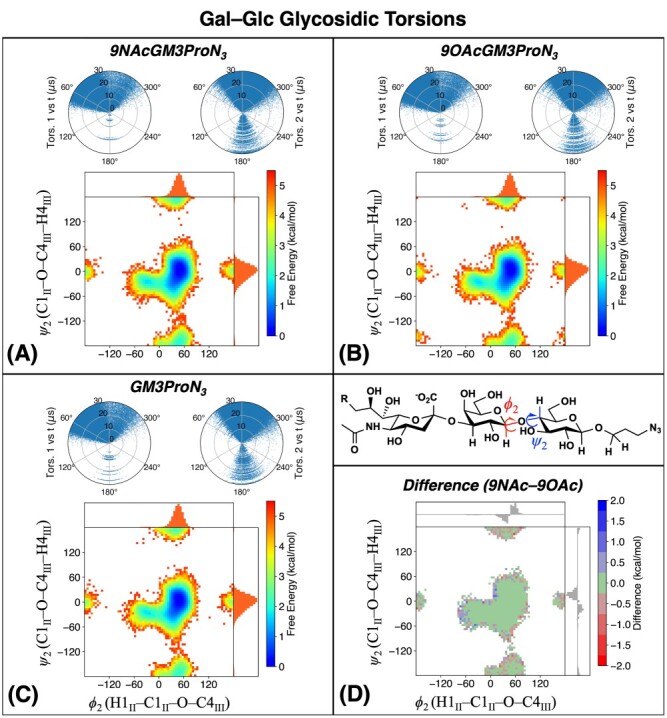
Torsion angle distributions resulting from MD simulations of 9NAcGM3βProN3 including (A) Gal–Glc glycosidic linkage, (B) Glc–ProN3 linkage and, on the glycerol chain, (C) H6–H7 and H7–H8 and (D) H8–H9-pro-S and H9-pro-S–C(NAc). The labeled H8–H9-pro-S torsion angle is 120° smaller than the other H8–H9-pro-R torsion. The polar plots, free energy map and marginal distributions are the same as in Figure 5.
The simulated ψ2 torsion angles are sharply peaked in the (−30°, 30°) range, and the DFT calculations (blue symbols) yield coupling constant values intermediate between the M/T and A curves. This torsion angle is probed by 3JH4I-C1II, and the ensemble-averaged couplings from MD simulations are higher than the experimental value, regardless of which parameterization is used. The overestimation of the simulated couplings is likely due to the overly tight distribution of this torsion; broadening of the distribution would allow more positive and negative values of the angle to be sampled, lowering the average coupling and improving agreement with experiment. This hypothesis aligns with previous studies where we showed that refitting the force field to a large quantum chemical dataset has the effect of broadening energy basins and lowering barriers in proteins (Wang et al. 2017). For ϕ2 that is probed by 3JH1II-C4I, the sampled structures occupy a narrow range of (30°, 60°), and the DFT computed values (purple symbols) overlap more closely with the Anderson curve. Using the Anderson curve, the simulated couplings are 0.3–0.6 Hz higher than experiment. The MD simulations show that this torsion angle is dominated by one major peak. Thus, one possible origin of the overestimation is that the simulated distribution of this torsion is shifted with respect to the experimental distribution by 4–8° corresponding to the slope of ~0.08 Hz/° in this region.
The ϕ3 data points are largely clustered around 15°–75° with a minor peak at 150°–210°. The DFT calculations align more closely with the A curve, which also agrees more closely with experiment for the ensemble-averaged couplings (the simulated values are 0.5 Hz higher on average). Finally, the ψ3 and ψ3’ torsion angles are more broadly distributed in the simulations with DFT-computed couplings (green symbols) that span a broad range. The majority of structures have H1ProN3 and H1’ProN3 in gauche conformations relative to C1I corresponding to torsion angles of +60° and −60°. These conformations are characterized by very small couplings that are better described by the M/T curves. We also observe that the ensemble-averaged couplings computed using M/T curves are in closer agreement with experiment compared to the A curves, with errors in the −0.3–0.6 Hz range. In summary, the M/T parameterizations agree more closely with DFT for ψ angles, the A parameterization agrees more closely with DFT for ϕ angles, and choosing the one that agrees more closely with DFT tends to improve the agreement of ensemble-averaged couplings with experiment.
In terms of temperature dependence, our simulations predicted that none of the couplings are shifted by more than 0.2 Hz when lowering the temperature from 25 to −10 °C. This is broadly consistent with the experimental observations and indicates that entropic effects are mostly insignificant in this temperature range, as they would have affected the relative heights of peaks and by extension the ensemble-averaged couplings. The only inconsistency we observed between simulation and experiment is for 3JH1’proN3-C1I, where the experimental coupling decreased by 0.5–0.6 Hz upon lowering the temperature but simulations did not predict this trend.
3 J HH of Neu5Ac Glycerol Chain at 25 and −10°C
From the above analysis of experimental and theoretical results, we concluded that the conformations about the glycosidic torsions are similar. We now examine the glycerol chain conformation in the Neu5Ac moiety and its intramolecular interactions in each of the analogs.
We used coupled HSQC experiments to measure the vicinal coupling constants (3JH-C-C-H) between H9, H9’, H8 and H7 of the Neu5Ac, on the 9-hydroxy, 9-O-acetylated and 9-N-acetylated GM3 glycans (Compounds # 4, 5 and 6) at 25 and −10 °C. These NMR experiments are reminiscent of those used by Bodenhausen, Freeman and Reynolds, which yield accurate JHH values even when they are strongly coupled because they are measured from a weakly coupled 13C satellite (Bodenhausen et al. 1977; Freeman et al. 1977; Reynolds et al. 1997; Mazzola et al. 2011). The results of these experiments should report on the local conformation of Neu5Ac’s glycerol chain in the three analogous compounds (Table III).
Table III.
3 J H-C-C-H in the Neu5Ac side chain of GM3βProN3, 9NAcGM3βProN3 and 9OAcGM3βProN3 oligosaccharides at 25 and −10°C (in parentheses)*
| J coupling (Hz) | H9’-H9** | H8-H9 | H8-H9’ | H8-H7 | H7-H6 |
|---|---|---|---|---|---|
| GM3βProN3 | −11.8 ± 0.1 (−11.7 ± 0.2) |
2.4 ± 0.1 (2.2 ± 0.1) |
6.3 ± 0.2 (6.7 ± 0.2) |
9.7 ± 0.2 (9.3 ± 0.3) |
1.4 ± 0.2 (1.3 ± 0.3) |
| 9NAcGM3βProN3 | −14.0 ± 0.2 (−14.4 ± 0.4) |
2.9 ± 0.2 (2.3 ± 0.1) |
7.9 ± 0.1 (8.4 ± 0.3) |
8.9 ± 0.1 (9.4 ± 0.3) |
1.5 ± 0.1 (1.5 ± 0.1) |
| 9OAcGM3βProN3 | −11.7 ± 0.1 (−11.7 ± 0.3) |
2.0 ± 0.1 (1.6 ± 0.3) |
6.4 ± 0.1 (6.5 ± 0.3) |
8.8 ± 0.3 (9.1 ± 0.2) |
1.6 ± 0.3 (1.3 ± 0.3) |
* Experimental errors are based repeated measurements. The errors are within the digital resolution (± 0.3 Hz).
** H9’-H9 is 2 J H-C-H.
Table III lists the torsional angles between the two hydrogens in H8-H9, H8-H9’, H8-H7 and H7-H6, as reported by 3JH-C-C-H. A difference in the 3JH-C-C-H would indicate a structural difference of torsions in the glycerol chain of Neu5Ac. The relationship between torsional angle and the 3JHH acquired from coupled HSQC can be calculated by Karplus equation specifically derived for 1H-1H coupling. The most notable difference in Table III shows about a 2 Hz difference in 2JH-C-H of H9’-H9 between GM3βProN3 and 9NAcGM3βProN3 or 9OAcGM3βProN3 and 9NAcGM3βProN3. This is not a coupling that informs on a torsional angle and is therefore likely due to the different substitution on C-9 (Haasnoot et al. 1980). In 9NAcGM3βProN3, the nitrogen atom of the N-acetyl group in 9NAcGM3βProN3 is bonded to C-9. In contrast, in the other two analogs, GM3βProN3 or 9OAcGM3βProN3, it is the oxygen atom of the hydroxyl or O-acetyl group that is directly bonded to C-9.
We also analyzed the torsion angles of the glycerol chain from our MD simulations. Figure 8 shows two parameterized Karplus curves using the Durette-Horton and Bothner-By parameterizations. The parameterized Karplus curves deviate significantly from DFT-computed couplings, particularly in regions where many of the computed couplings are < 2.0 Hz. We developed and tested a new set of Karplus parameters by least-squares fitting to these data points, given by A = 10.18, B = −0.03 and C = 0.48. We observed no significant dependence of the computed couplings on the acetylation at the C9-position, which is notable given the proximity of this chemical modification to the coupled protons.
Fig. 8.

Parameterized Karplus relations mapping dihedral angles to 3JH–C–C–H couplings. DFT calculations of coupling values based on structures sampled from MD simulations are shown as colored symbols.
Figure S5, panels C–D, shows the distribution of simulated glycerol chain torsion angles from our MD simulations, and Table IV provides ensemble-averaged values of the 3JH-C-C-H couplings. These simulated values generally have larger deviations compared to experiment. For the H8-H9 and H8-H9’ torsions, the experiment shows a significant gap between the larger and smaller coupling on the order of 4–6 Hz, but the simulations tend to predict a smaller gap on the order of 1–3 Hz. According to the simulations, these two torsions tend to occupy three free energy minima located at −60, +60 and 180°, and the Karplus curves and DFT calculations predict the coupling to be about 6 Hz larger at 180° than at −60° and +60°. Thus, the large difference in the couplings is likely because the most probable torsion angle for one of the two hydrogens is the minimum at 180°. In the case of 9NAcGM3βProN3, the most populated conformations have the two H8-H9 torsions at −60° and +60°, respectively, which explains why the difference in the simulated couplings is smaller than the experimentally measured value. Further studies are needed to explain why this torsion angle gives relatively large differences vs. experiment, especially given that the potential parameters were carefully fitted to high-level QM calculations. One possible explanation is that the QM calculations for parameter fitting were carried out in the gas phase, which is biased towards forming overly strong intramolecular noncovalent interactions particularly in charged systems such as Neu5Ac.
Table IV.
3 J H-C-C-H values resulting from MD simulations for the glycerol chain. Italicized values correspond to simulations performed at −10°C. Deviations from experiment calculated as J(sim)-J(exp) are given in parentheses. H8–H9’ is always given as the larger of the two couplings
| Karplus parameters | Torsion | GM3βProN3 (4) | 9NAcGM3βProN3 (5) | 9OAcGM3βProN3 (6) | |||
|---|---|---|---|---|---|---|---|
| 25°C | −10°C | 25°C | –10°C | 25°C | –10°C | ||
| Durette-Horton | 3 J(H8-H9) | 5.9 (+3.5) | 5.9 (+3.7) | 5.2 (+2.3) | 4.8 (+2.5) | 5.5 (+3.5) | 5.4 (+3.8) |
| 3 J(H8-H9’) | 7.3 (+1.0) | 7.0 (+0.3) | 6.2 (−1.7) | 6.4 (−2.0) | 8.7 (+2.3) | 8.7 (+2.2) | |
| 3 J(H8-H7) | 8.5 (−1.2) | 8.7 (−0.6) | 8.2 (−0.7) | 9.0 (−0.4) | 10.0 (+1.2) | 9.9 (+0.8) | |
| 3 J(H7-H6) | 3.9 (+2.5) | 3.9 (+2.6) | 4.0 (+2.5) | 3.9 (+2.4) | 4.3 (+2.7) | 4.1 (+2.8) | |
| RMSD | 2.31 | 2.26 | 1.91 | 2.01 | 2.56 | 2.65 | |
| Bothner-By | 3 J(H8-H9) | 5.3 (+2.9) | 5.2 (+3.0) | 4.6 (+1.7) | 4.3 (+2.0) | 4.9 (+2.9) | 4.8 (+3.2) |
| 3 J(H8-H9’) | 6.6 (+0.3) | 6.3 (−0.4) | 5.5 (−2.4) | 5.7 (−2.7) | 7.8 (+1.4) | 7.8 (+1.3) | |
| 3 J(H8-H7) | 7.7 (−2.1) | 7.8 (−1.5) | 7.4 (−1.5) | 8.1 (−1.3) | 9.0 (+0.2) | 8.9 (−0.2) | |
| 3 J(H7-H6) | 3.5 (+2.1) | 3.5 (+2.2) | 3.5 (+2.0) | 3.5 (+2.0) | 3.9 (+2.3) | 3.7 (+2.4) | |
| RMSD | 2.07 | 2.01 | 1.94 | 2.06 | 1.97 | 2.13 | |
| This work (DFT) | 3 J(H8-H9) | 4.3 (+1.9) | 4.3 (+2.1) | 3.4 (+0.5) | 3.1 (+0.8) | 3.9 (+1.9) | 3.9 (+2.3) |
| 3 J(H8-H9’) | 5.1 (−1.2) | 4.9 (−1.8) | 4.6 (−3.3) | 4.8 (−3.6) | 6.2 (−0.2) | 6.2 (−0.3) | |
| 3 J(H8-H7) | 6.0 (−3.7) | 6.2 (−3.1) | 5.9 (−3.0) | 6.5 (−3.0) | 7.2 (−1.6) | 7.1 (−2.0) | |
| 3 J(H7-H6) | 2.2 (+0.8) | 2.1 (+0.8) | 2.3 (+0.8) | 2.3 (+0.8) | 2.6 (+1.0) | 2.4 (+1.1) | |
| RMSD | 2.18 | 2.12 | 2.29 | 2.39 | 1.34 | 1.62 | |
The experimentally measured H6-H7 coupling is in the 8.5–10 Hz range. According to the parameterized Karplus relations and DFT calculations, such high values of the coupling are only possible for torsion angles of ~0° and 180°. The simulations indicate three free energy minima located at −60°, +60° and 180°; this indicates the most likely conformation has the H7–H8 torsion angle distributed around 180°. The tendency of the MD simulations to predict a lower coupling is attributed to the increased probability of sampling the free energy minima at −60° and +60° relative to experiment. Finally, the experimentally measured H6-H7 coupling is in the 1.5 Hz range, which is below the accessible range of both the Durette-Horton and Bothner-By curves. On the other hand, our DFT calculations indicate that such small couplings are attainable for torsion angles in the range of (−90°, −60°) and (+60°, +90°). The MD simulations predict that the H6-H7 torsion angle largely populates a single minimum centered at −60° with a minor peak at +60°, yielding a coupling constant that agrees with experiment to within 1 Hz.
Figures S5 and S7 compare the glycerol chain torsion angles across the three GM3 glycans at 25°C. The H6-H7 torsion angle distribution is predicted to be largely similar for all three forms with a single peak centered near −75°, though the GM3βProN3 distribution has a “shoulder” that extends toward −120°. The similarity of these distributions in the simulation is consistent with the small variations of the measured coupling in experiment. The simulated H7-H8 and H8-H9 torsion angles have more significant variations for the three analogs, largely characterized by differences in the relative heights of three peaks at −60°, +60° and 180°. Although the simulated couplings do not agree well with experiment, we think that differences in population for the three possible conformations are also responsible for the variation in the measured couplings seen in experiment.
The temperature dependence of the simulated couplings is small for the most part. The largest shifts in the couplings that we observed were for 3JH8-H7 of 9NAcGM3βProN3, towards more positive values by 0.6–0.8 Hz depending on the Karplus parameterization. In the MD simulations, the shift towards more positive 3JH8-H7 coupling values is largely due to an increase in the population of the torsion angle at 180° and narrowing of the distribution there. This dependence is highlighted in Figure S6.
Structural data from the nOe
To further verify conformational data, we utilized NOESY-HSQC (13C edited NOESY) experiments to measure 1H-1H nOe’s and determine intramolecular distances in 9-OH, 9-O-acetylated and 9-N-acetylated GM3 glycans (Neuhaus and Williamson 1989). We used these data qualitatively because the flexibility indicated by the MD simulations is certain to average the nOes and could yield virtual structures. Detected nOes across glycosidic bonds were similar in all three compounds at 25 and −10°C (Table SII), providing further support that the structures of the three compounds are highly similar.
Similar to the results from J-coupling and MD simulations, the nOe results for the Neu5Ac residue in 9NAcGM3βProN3, 9OAcGM3βProN3 and GM3βProN3 indicate that these GM3-type glycans have similar conformations at 25 and −10 °C. According to Table SII, the axial H on the C3-Neu5Ac (III) is close to H3-Gal (II), but not H4-Gal (II) or H5-Gal (II). Consistent with this observation, the MD simulation results for GM3βProN3 feature a bimodal distribution of H···H distances (Figure S8). The structures in the cluster with small H···H distances (≤ 3.0 Å) are characterized by glycosidic torsion angles (ϕ1, ψ1) near (−45°, −15°) with no intramolecular Hbonds. These structures correspond to one of the free energy minima in Figure 5. By contrast, H4-Gal (II) and H5-Gal (II) are relatively distant from the Neu5Ac axial H3 in the MD simulations, with H4-Gal (II) approaching within 2.5 Å for only ~1% of structures. H1 of galactose is close to H4-Glc (I), H5-Glc (I) and H6-Glc (I), but not H3-Glc (I); one area of disagreement with the MD simulations is the distance between the H1-Gal (II) and H5-Glc (I), where the simulated distance only drops below 3.0 Å for <1% of structures. H1-Glc (I) is close to H1 of the propyl azide chain.
Intramolecular Hbonding experiments
The distribution of ψ1 occupies a range between −60° and +15°, with a significant population in the eclipsed conformation. Figure S9 shows the distribution of Neu5Ac ring positions and orientations relative to Gal-III over a 5 μs portion of the trajectory. With the structures thus aligned, three distinct clusters of intramolecular inter-residue Hbonds are readily visible, indicating how inter-residue Hbonding may play a role in modulating the torsion angle distribution.
In earlier reports, MD simulations indicated that there may be a sub-population of conformations with an Hbond (Khedri et al. 2017). This is also true for the present simulations. We detected similar Hbonds in different glycans in previous studies (Battistel et al. 2013; Battistel et al. 2015). Because Hbonding could impact three-dimensional solution structure, we investigated any potential intramolecular Hbonding interactions that might exist in the modified GM3 glycans. We used samples dissolved in H2O and assigned hydroxyl group 1H for Neu5Ac, Neu5,9Ac2 and Neu5Ac9NAc-GM3 glycans using HSQC-TOCSY experiments (Battistel et al. 2013) with 10 ms and 30 ms mixing times, at −10 °C (Table V), where Hbonds would be stabilized.
Table V.
1H NMR chemical shift of -OH’s in GM3βProN3, 9NAcGM3βProN3 and 9OAcGM3βProN3 oligosaccharides at −10°C in H2O with 10% D2O (pH = 6.5)
| Chemical shift* (ppm) | GM3βProN3 (4) | 9NAcGM 3βProN3 (5) |
9OAcGM 3βProN3 (6) |
|
|---|---|---|---|---|
| OH | OH | OH | ||
| Neu5Ac | 4-OH | 6.44 | 6.44 | 6.44 |
| Residue I | 5-NH | 8.23 | 8.22 | 8.22 |
| 7-OH | 5.84 | 5.89 | 5.99 | |
| 8-OH | 6.20 | 6.22 | 6.58 | |
| 9-OH/NH | 5.81 | 8.25 | N.A. | |
| Gal | 2-OH | 5.98 | 5.95 | 5.96 |
| Residue II | 4-OH | 6.03 | 6.02 | 6.02 |
| 6-OH | 6.11 | 6.12 | 6.11 | |
| Glc | 2-OH | 6.63 | 6.63 | 6.63 |
| Residue III | 3-OH | 6.09 | 6.10 | 6.09 |
| 6-OH | 5.88 | 5.88 | 5.86 |
In previous studies, LR-HSQMBC spectra showed correlations where Hbonding was present. In the current study, LR-HSQMBC experiments, using a 700 MHz cryoprobe, showed no correlation to or from OH groups. This lack of direct signal for intramolecular Hbonding among GM3βProN3, 9NAcGM3βProN3 and 9OAcGM3βProN3 indicates that no Hbonds can be directly detected in these compounds. However, it is still possible that the sought-after Hbonds cannot be detected due to their low population, which in turn results in a low signal-to-noise ratio of the correlation peaks. It is also possible that some type of conformational exchange or nuclear relaxation process interferes with the observation of said correlation peak.
The structural analysis presented in this report relies on parameterized Karplus relations, the measurements of ϕ and ψ torsional angles and MD simulations. Recently, it has been proposed that torsions in glycans should be defined by as many coupling constants as possible (Hadad et al. 2017) and that these couplings be used together with DFT calculations to derive glycan structure (Zhang et al. 2017; Serianni 2019; Zhang et al. 2019a; Zhang et al. 2019b). Furthermore, application of this method typically requires the chemical synthesis of specifically labeled glycans to permit for the measurement of these coupling constants; synthesis of such specifically labeled molecules was not possible for this study. Altogether, the NMR data, MD simulations and DFT results provide further evidence that 9-N-acetylation or 9-O-acetylation of Neu5Ac in the GM3 glycans does not affect the three-dimensional structure.
Conclusion
Overall, this thorough investigation shows that there are no detectable differences among the three synthetic analogs GM3βProN3, 9NAcGM3βProN3 and 9OAcGM3βProN3 by NMR and computational studies. To reach these conclusions, we conducted systematic NMR spectroscopic studies, including complete 1H and 13C NMR chemical shift assignment, three bond 1H-13C glycosidic coupling constants (3JC-O-C-H), 1H-1H coupling constants of the glycerol chain of Neu5Ac (3JH-C-C-H), nOe’s and Hbonding experiments for Neu5Ac-, Neu5Ac9NAc- and Neu5,9Ac2-containing GM3 glycans. Results measured at −10 and 25 °C show that modifications on the C9 of Neu5Ac in GM3 glycans do not cause detectable conformational change of torsional angles nor any difference in secondary structure. Only the local structure of glycerol chain of Neu5Ac may be affected by different C9-modification.
Our MD simulations confirm the main experimental results of this study, namely, that 9NAcGM3βProN3 is an excellent structural mimic of 9OAcGM3βProN3. According to the simulation studies, acetylation at the C9-position does not significantly affect the glycosidic torsion angles and introduces some differences in the torsion angle distribution for the glycerol chain. While the MD simulations provide a valuable interpretation of the experimental NMR data, we obtained mixed results for quantitative comparison of simulation with experiment; in particular, no single Karplus parameterization for the glycosidic torsions gave uniformly good agreement with the experimentally measured or DFT-computed couplings, and computed couplings for the glycerol chain still shows some disagreement with experiment. Further research is needed to bring simulations into more quantitative agreement with experiment, which in turn should yield more accurate predictions.
Materials and methods
All starting materials were obtained from commercial suppliers and used without further purification. All NMR measurements were performed on Avance III 500 MHz spectrometer equipped with a z-gradient QXI room temperature probe or a 700 MHz Bruker Avance III HD equipped with a TCI xyz-gradient CryoProbe™. High-resolution electrospray ionization (ESI) mass spectrometric data were obtained using a Thermo Electron LTQ-Orbitrap Hybrid MS at the Mass Spectrometry Facility in the University of California, Davis. Column chromatography was performed using RediSep Rf silica columns or an ODS-SM column (51 g, 50 mm, 120 Å, Yamazen) on the Combi-Flash® Rf 200i system. Analytical thin-layer chromatography was performed on silica gel plates 60 GF254 (Sorbent technologies) using an anisaldehyde stain for detection. Gel filtration chromatography was performed using a column (100 cm × 2.5 cm) packed with BioGel P-2 fine resins (Bio-Rad, Hercules, CA, USA). Pasteurella multocida sialic acid aldolase (PmAldolase), Neisseria meningitidis CMP sialic acid synthetase (NmCSS) and Pasteurella multocida sialyltransferase 1 M144D mutant (PmST1M144D) were expressed and purified as described previously. Neu5Acα2–3LacβProN3, Neu5Ac9NAcα2–3LacβProN3 and Neu5Ac9OAcα2–3LacβProN3 were synthesized similar to that reported previously (Khedri et al. 2017; Li et al. 2017).
NMR data acquisition and processing
All NMR experiments were performed on 40 mM samples at pH 6.5 containing 0.5 mM DSS. The samples were dissolved either in 100% D2O or in 90%/10% H2O/D2O. The pH of each sample was measured using a pH meter connected to a thin pH probe that was inserted directly into the NMR sample tube. The pH was adjusted to 6.5 at 25 °C using NaOH and HCl solutions. NMR experiments were run using the parameters described below, unless otherwise noted.
The carrier frequency, spectral window and number of points for the direct and indirect dimensions were set to 4.7 ppm, 62 ppm; 10 ppm, 106 ppm; and 8192, 2048, respectively.
NMR data were processed with Topspin 3.5 and analyzed with CCPNMR Analysis (Vranken et al. 2005). Data were processed using a Gaussian window function (GB = 0.1, LB = −5.0) in the direct dimension, while the indirect dimension was processed using a cosine square function. The direct dimension was referenced based to the DSS 1H signal, while 13C was referenced indirectly from the 1H DSS reference frequency. Data were acquired at −10 and 25 °C. The temperature for each sample was internally calibrated by adjusting the probe temperature such that it would match the water-to-DSS frequency difference reference at the desired temperature.
Assignments
Spin systems were assigned with HSQC-TOCSY experiments (Lerner and Bax 1986; Lerner and Bax 1987) collected on an Avance III 500 MHz spectrometer, utilizing DIPSI-2 as the mixing sequence with mixing times of 10 ms and 90 ms. The sequential assignments of Neu5Ac (I), Gal (II) and Glc (III) were confirmed by PIP-HSQMBC experiments (Castañar et al. 2014).
Molecular dynamics simulations
Parameterization of Glycan Force Field
The MD simulations of glycans 4–6 used a combination of the GLYCAM06 (Case et al. 2018) force field for the monosaccharide building blocks and GAFF (Wang et al. 2004) for the ProN3 aglycon, with customized parameters to describe the N-acetylated and O-acetylated glycans in a consistent manner. The procedure for deriving the new simulation parameters was designed to be maximally consistent with the original GLYCAM procedure.
Two separate sets of atomic partial charges were derived for Neu5Ac modified with an O-acetyl or N-acetyl group at C-9 (we use Neu5Ac9NAc as the representative example in the following). The procedure involves averaging over an ensemble of structures, sampled using a MD simulation of Neu5Ac9NAc2αOMe in TIP3P water using a modular residue definition for the NAc group described previously (Herler et al. 1985). These simulations did not account for variations in charge with the acetylation site and lacked optimized parameters for the glycerol chain but were deemed sufficient for sampling the charge derivation structures. The system was equilibrated for 10 ns at 298.15 K, 1.0 atm (NPT), followed by a 200 ns production run at 298.15 K (NVT). One hundred structures of Neu5Ac9NAc2-OMe were saved at 2 ns intervals. Each of these structures was energy-minimized at the HF/6-31G* level of theory with all of the exocyclic dihedral angles constrained to their MD-sampled values. The bond lengths, angles and dihedral angles of the hexapyranose ring were constrained to the GLYCAM residue definitions as they were derived from neutron diffraction experiments.
For each the 100 constrained energy-minimized structures, electrostatic potential (ESP) calculations were computed on a rectilinear grid of points using the Gaussian16 software (Frisch MJ, et al. 2016. Gaussian, Inc., Wallingford CT.) using the Pop = chelpg option in the route file. This ESP data was used in a single-stage restrained ESP fitting (RESP) calculation with a restraint weight of 0.01 applied to all atoms using the resp program from AmberTools and with charges on the OMe group fixed to the original GLYCAM values. An arithmetic average over the 100 sets of fitted charges yielded the final set of charges in the model. Our derived charges for unmodified Neu5Ac closely matched the original GLYCAM charges with a root-mean-square difference (RMSD) of 0.038 and a maximum unsigned difference of 0.104.
The GLYCAM and GAFF force fields lacked torsional parameters to describe the torsional energy profiles about the flexible glycerol chain, the ProN3 functional group and Glc–ProN3 linkage; these parameters were derived by fitting to reproduce torsional profiles from DFT. In order to generate data for fitting the torsional profiles, constrained optimized geometries were obtained at the HF/6-31G* level of theory with the selected torsional degree of freedom constrained to values on a 30-degree grid. We used the TeraChem quantum chemistry software (Ufimtsev and Martinez 2008; Ufimtsev and Martinez 2009a; Ufimtsev and Martinez 2009b; Wang and Song 2016) for the energy minimizations and the torsiondrive software (Wang et al. 2017) to scan over the dihedral angles recursively. The optimized geometries were used for single-point energies and atomistic forces calculated at the ωB97X-D3/6–31++G(2d,2p) level of theory (Kesharwani et al. 2016). We chose a different DFT functional from what was used in the original GLYCAM procedure because dispersion-corrected DFT functionals have become the standard for accurate conformational energy calculations over the past decade (Lin et al. 2013; Frisch MJ, et al. 2016.Gaussian, Inc., Wallingford CT. 2016; Kesharwani et al. 2016; Řezáč et al. 2018). We also do not expect differences in the torsional parameterization procedure to cause incompatibilities with the rest of the GLYCAM force field, because the effect of parameter optimization on the potential energy surface is localized to the glycerol chain. The parameters were optimized by fitting to the quantum chemical energies using the ForceBalance optimization software (Wang et al. 2014; Wang et al. 2017). Bond stretching and angle bending parameters for the Glc–ProN3 linkage were copied from analogous parameters available in GLYCAM06. The values of optimized parameters and simulation-ready parameter files are provided in the Supporting Information Table SIII.
Details of MD Simulation Setup
The simulations were set up and carried out in the AmberTools18 and AMBER18 software packages (Wang et al. 2017). Two MD simulations were carried out for each of the three glycans, for a total of six simulations. The sialoside was solvated in a truncated octahedral water box with ~1300 water molecules, which ensures a distance of 8.0 Å to the simulation cell edge and prevents interaction of the solute with its periodic images. Water molecules were modeled using the TIP3P potential. Electrostatics were treated using the particle-mesh Ewald method with a 8.0 Å real-space cutoff, and the same cutoff was applied to Lennard-Jones interactions that describe dispersion and short-range repulsion. The initial structure was energy-minimized with 500 steepest-descent steps, followed by an equilibration run of 20 ns at constant temperature and pressure (NPT), employing a time step of 2.0 fs, a Langevin thermostat with set temperature of 298.15 K (25°C) and collision frequency of 5.0 ps−1 and a Berendsen barostat with set pressure of 1.0 bar and relaxation time of 1.0 ps. Solute bonds involving hydrogen were constrained using SHAKE, and water molecules were held rigid.
Following equilibration, a production run was carried out for 30.0 μs in the NVT ensemble. Structures were saved every 100 ps for analysis (300,000 structures total). The equilibration and production runs were carried out using the pmemd.CUDA program running on NVIDIA GTX 980 Ti or 1080 Ti hardware, with simulation speeds in the range of 500–750 ns/day. An independent set of simulations was carried out at 263.15 K (−10 °C) corresponding to the two experimental temperatures, for a total of six simulated systems each with 30 μs of trajectory data. Trajectory analyses were carried out using Python scripts that used the mdtraj simulation analysis package (McGibbon et al. 2015) and matplotlib plotting software package. As no significant differences in the conformational distributions were observed after 10.0 μs, we deemed the results to be converged with respect to simulation length.
Computation of NMR 3J-Couplings Using Density Functional Theory
A small number of structures (2–4) were manually sampled from the MD simulations of all three acetylated forms of GM3 for each of the free energy minima in the torsion angles of interest. These structures were energy-minimized with the torsion angles constrained to their MD values using the B3LYP-D3(BJ)/def-TZVP level of theory and PCM continuum solvent with ε = 78.4 (aqueous solvent). Each energy-minimized structure was used in a single-point calculation of the internuclear spin-spin coupling constants (Ufimtsev and Martinez 2008; Ufimtsev and Martinez 2009a) using the B3LYP functional and pcJ-1 basis set (Wang et al. 2017) in the gas phase; we chose this level of theory because it was previously shown to reproduce the full set of 3J-couplings in strychnine with a RMS error of 0.2 Hz (Helgaker et al. 2016). Our single-point calculations used truncated disaccharide models of the full GM3 structures due to limitations of computer memory. The NMR calculations were performed using the Q-Chem 5.0 quantum chemistry package (Shao et al. 2014).
Funding
This work was supported by the United States National Institutes of Health grant R01AI130684.
Conflict of interest statement
None declared.
Supplementary Material
Acknowledgements
We gratefully acknowledge Robert Woods, Xiaocong Wang and B. Lachele Foley at the Complex Carbohydrate Research Center and Ajit Varki at the UC San Diego School of Medicine for insightful discussions regarding the reproduction of GLYCAM atomic partial charges.
Abbreviations
3 J CH, three-bond 13C-1H coupling constants; 3JHH, three-bond 1H-1H coupling constants; DFT, density functional theory; DMSO, dimethyl sulfoxide; GM3-glycan, ganglioside glycan; Hbonding, hydrogen bonding; Hbond, hydrogen bond; Kdn, 2-keto-3-deoxy-nonulosonic acid; PmST1 M144D, Pasteurella multocida sialyltransferase 1 M144D mutant; ManNAc, N-acetylmannosamine; ManNAc6NAc, 2,6-diacetamido-2,6-dideoxy-D-mannose; MD, molecular dynamics; Neu5,9Ac2, 9-O-acetyl-N-acetylneuraminic acid; Neu5Ac, N-acetylneuraminic acid; Neu5Ac9NAc, 9-acetamido-9-deoxy-N-acetylneuraminic acid; Neu5Gc, N-glycolylneuraminic acid; NmCSS, Neisseria meningitidis CMP-sialic acid synthetase; NMR, nuclear magnetic resonance; nOes, nuclear Overhauser effects; OPME, one-pot multienzyme; PmAldolase, Pasteurella multocida sialic acid aldolase; Sia, sialic acid
References
- Anderson JE, Ijeh AI. 1994. Eclipsed ground-state conformations for methoxycyclohexanes with adjacent methyl-group substitution - an NMR criterion and molecular mechanics calculations. J Chem Soc - Perkin Trans. 2:1965–1967. [Google Scholar]
- Angata T, Varki A. 2002. Chemical diversity in the sialic acids and related α-keto acids: An evolutionary perspective. Chem Rev. 102:439–470. [DOI] [PubMed] [Google Scholar]
- Aubin Y, et al. 1993. Structure and dynamics of the Sialic-acid moiety of GM3-Ganglioside at the surface of a magnetically oriented membrane. Biochemistry. 32:13405–13413. [DOI] [PubMed] [Google Scholar]
- Battistel MD, et al. 2013. Direct evidence for hydrogen bonding in glycans: A combined NMR and molecular dynamics study. J Phys Chem B. 117:4860–4869. [DOI] [PubMed] [Google Scholar]
- Battistel MD, et al. 2014. NMR of polysaccharides: Shedding new light on old problems. Prog NMR Spec. 79:48–68. [DOI] [PubMed] [Google Scholar]
- Battistel MD, et al. 2015. Uncovering non-conventional and conventional hydrogen bonds in oligosaccharides through NMR experiments and molecular modeling: Application to Sialyl Lewis-X. J Am Chem Soc. 137:13444–13447. [DOI] [PubMed] [Google Scholar]
- Berti F, et al. 2018. Role of O-acetylation in the immunogenicity of bacterial polysaccharide vaccines. Molecules. 23:1340–1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bodenhausen G, et al. 1977. Proton-coupled carbon-13 J spectra in the presence of strong coupling. II J Magn Reson. 28:17–28. [Google Scholar]
- Bodenhausen G, Ruben DJ. 1980. Natural abundance Nitrogen-15 NMR by enhanced Heteronuclear spectroscopy. Chem Phys Lett. 69:185–189. [Google Scholar]
- Case D, et al. 2018. Amber 2018. San Francisco: University of California. [Google Scholar]
- Castañar L, et al. 2014. Pure in-phase Heteronuclear correlation NMR experiments. Angew Chem Int Ed. 53:8379–8382. [DOI] [PubMed] [Google Scholar]
- Cheever MA, et al. 2009. The prioritization of cancer antigens: A national cancer institute pilot project for the acceleration of translational research. Clin Cancer Res. 15:5323–5337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Varki A. 2010. Advances in the biology and chemistry of sialic acids. ACS Chem Biol. 5:163–176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng J, et al. 2008. Multifunctionality of campylobacter jejuni sialyltransferase CstII: Characterization of GD3/GT3 oligosaccharide synthase, GD3 oligosaccharide sialidase, and trans-sialidase activities. Glycobiology. 18:686–697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coxon B. 2009. Developments in the Karplus equation as they relate to the NMR coupling constants of carbohydrates. Adv Carbohydr Chem Biochem. 62:17–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deszo EL, et al. 2005. Escherichia coli K1 polysialic acid O-acetyltransferase gene, neuO, and the mechanism of capsule form variation involving a mobile contingency locus. Proc Natl Acad Sci U S A. 102:5564–5569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman R, et al. 1977. Proton-coupled carbon-13 J spectra in the presence of strong coupling I. J Magn Reson. 26:373–378. [Google Scholar]
- Frisch MJ, et al. 2016. Gaussian Revision C.01. Wallingford, CT, USA: Gaussian, Inc. [Google Scholar]
- Gilbert M, et al. 2000. Biosynthesis of ganglioside mimics in campylobacter jejuni OH4384 identification of the glycosyltransferase genes, enzymatic synthesis of model compounds, and characterization of nanomole amounts by 600-MHz 1H and 13C NMR analysis. J Biol Chem. 275:3896–3906. [DOI] [PubMed] [Google Scholar]
- Haasnoot CAG, et al. 1980. The relationship between proton-proton NMR coupling-constants and substituent Electronegativities .1. An empirical generalization of the Karplus equation. Tetrahedron. 36:2783–2792. [Google Scholar]
- Hackbusch S, et al. 2017. Development of a Karplus equation for 3JCOCH in ester-functionalized glucopyranoses and methylglucuronate. ARKIVOC. 2017:268–292. [Google Scholar]
- Hadad MJ, et al. 2017. NMR spin-couplings in saccharides: Relationships between structure, conformation and the magnitudes of JHH, JCH and JCC values, Chapter 2. In: NMR in Glycosciences and Glycotechonology. Cambridge (UK): Royal Society of Chemistry. [Google Scholar]
- Helgaker T, et al. 2016. Calculation of NMR spin–spin coupling constants in strychnine. J Org Chem. 81:11496–11500. [DOI] [PubMed] [Google Scholar]
- Herrler G, et al. 1985. The receptor-destroying enzyme of influenza C virus is neuraminate-O-acetylesterase. EMBO J. 4:1503–1506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ito Y, Paulson JC. 1993. A novel strategy for synthesis of ganglioside GM3 using an enzymically produced sialoside glycosyl donor. J Am Chem Soc. 115:1603–1605. [Google Scholar]
- IUPAC-IUB Joint Commission on Biochemical Nomenclature . 1983. Symbols for specifying the conformation of polysaccharide chains, recommendations 1981. Eur J Biochem. 131:5–7. [DOI] [PubMed] [Google Scholar]
- Kamerling JP, et al. 1987. Migration of O-acetyl groups in N, O-acetylneuraminic acids. Eur J Biochem. 162:601–607. [DOI] [PubMed] [Google Scholar]
- Kelm S, et al. 1994. Modifications of cell surface sialic acids modulate cell adhesion mediated by sialoadhesin and CD22. Glycoconj J. 11:576–585. [DOI] [PubMed] [Google Scholar]
- Kesharwani MK, et al. 2016. Benchmark ab initio conformational energies for the Proteinogenic amino acids through explicitly correlated methods. Assessment of Density Functional Methods J Chem Theory Comput. 12:444–454. [DOI] [PubMed] [Google Scholar]
- Khedri Z, et al. 2017. A chemical biology solution to problems with studying biologically important but unstable 9-O-acetyl Sialic acids. ACS Chem Biol. 12:214–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirschner KN, et al. 2008. GLYCAM06: A generalizable biomolecular force field. Carbohydrates J Comput Chem. 29:622–655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein A, Roussel P. 1998. O-acetylation of sialic acids. Biochimie. 80:49–57. [DOI] [PubMed] [Google Scholar]
- Klotz FW, et al. 1992. Binding of plasmodium falciparum 175-kilodalton erythrocyte binding antigen and invasion of murine erythrocytes requires N-acetylneuraminic acid but not its O-acetylated form. Mol Biochem Parasitol. 51:49–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kooner AS, et al. 2019. Synthesis of N-glycolylneuraminic acid (Neu5Gc) and its glycosides. Front Immunol. 10:2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lerner L, Bax A. 1986. Sensitivity-enhanced two-dimensional heteronuclear relayed coherence transfer NMR-spectroscopy. J Magn Reson. 69:375–380. [Google Scholar]
- Lerner L, Bax A. 1987. Application of new, high-sensitivity 1H-13C-N.M.R.- spectral techniques to the study of oligosaccharides. Carbohydr Res. 166:35–46. [DOI] [PubMed] [Google Scholar]
- Li W, et al. 2017. Chemoenzymatic synthesis of Neu5Ac9NAc-containing α2–3-and α2–6-linked sialosides and their use for sialidase substrate specificity studies. Carbohydr Res. 451:51–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin YS, et al. 2013. Long-range corrected hybrid density functionals with improved dispersion corrections. J Chem Theory Comput. 9:263–272. [DOI] [PubMed] [Google Scholar]
- Liu R, et al. 2020. Influenza D virus diverges from its related influenza C virus in the recognition of 9-O-acetylated N-acetyl- or N-glycolyl-neuraminic acid-containing glycan receptors. Virology. 545:16–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez PH, Schnaar RL. 2009. Gangliosides in cell recognition and membrane protein regulation. Curr Opin Struct Biol. 19:549–557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mazzola EP, et al. 2011. Utility of coupled-HSQC experiments in the intact structural elucidation of three complex saponins from Blighia sapida. Carbohydr Res. 346:759–768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGibbon RT, et al. 2015. MDTraj: A modern open library for the analysis of molecular dynamics trajectories. Biophys J. 109:1528–1532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulloy B, et al. 1988. Long-range carbon—proton coupling constants: Application to conformational studies of oligosaccharides. Carbohydr Res. 184:39–46. [DOI] [PubMed] [Google Scholar]
- Neuhaus D, Williamson M. 1989. The Nuclear Overhauser Effect in Structural and Conformational Analysis. New York: VCH. [Google Scholar]
- Nguyen T, et al. 2020. The role of 9-O-acetylated glycan receptor moieties in the typhoid toxin binding and intoxication. PLoS Pathog. 16:e1008336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds WF, et al. 1997. Comparison of 13C resolution and sensitivity of HSQC and HMQC sequences and application of HSQC-based sequences to the Total 1H and 13C spectral assignment of Clionasterol. Magn Reson Chem. 35:455–462. [Google Scholar]
- Řezáč J, et al. 2018. Toward accurate conformational energies of smaller peptides and medium-sized macrocycles: MPCONF196 benchmark energy data set. J Chem Theory Comput. 14:1254–1266. [DOI] [PubMed] [Google Scholar]
- Schauer R. 1978. Characterization of Sialic Acids. Methods Enzym. New York (NY): Academic Press. p. 64–89. [DOI] [PubMed] [Google Scholar]
- Schauer R. 1982. Chemistry, Metabolism, and Biological Functions of Sialic Acids. San Diego (CA): Elsevier. p. 131–234. [DOI] [PubMed] [Google Scholar]
- Schauer R. 2000. Achievements and challenges of sialic acid research. Glycoconj J. 17:485–499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnaar RL. 2016. Gangliosides of the vertebrate nervous system. J Mol Biol. 428:3325–3336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serianni A.S. 2019. Conformational equilibria and dynamics of saccharides using circular statisticsAbstract ACS Natl mtg. San Diego. [Google Scholar]
- Shao Y, et al. 2014. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol Phys. 113:184–215. [Google Scholar]
- Shi W-X, et al. 1996. Sialic acid 9-O-acetylation on murine erythroleukemia cells affects complement activation, binding to I-type lectins, and tissue homing. J Biol Chem. 271:31526–31532. [DOI] [PubMed] [Google Scholar]
- Siebert HC, et al. 1992. Solution conformations of GM3 gangliosides containing different sialic acid residues as revealed by NOE-based distance mapping, molecular mechanics, and molecular dynamics calculations. Biochemistry. 31:6962–6971. [DOI] [PubMed] [Google Scholar]
- Sjoberg ER, et al. 1994. Natural ligands of the B cell adhesion molecule CD22 beta can be masked by 9-O-acetylation of sialic acids. J Cell Biol. 126:549–562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugiarto G, et al. 2012. A sialyltransferase mutant with decreased donor hydrolysis and reduced sialidase activities for directly sialylating LewisX. ACS Chem Biol. 7:1232–1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tvaroska I, et al. 1989. An attempt to derive a new Karplus-type equation of vicinal proton carbon coupling constants for C-O-C-H segments of bonded atoms. Carbohydr Res. 189:359–362. [Google Scholar]
- Ufimtsev IS, Martinez TJ. 2008. Quantum chemistry on graphical processing units. 1. Strategies for two-electron integral evaluation. Journal of Chemistry Theory Computation. 4:222–231. [DOI] [PubMed] [Google Scholar]
- Ufimtsev IS, Martinez TJ. 2009a. Quantum chemistry on graphical processing units. 3. Analytical energy gradients, geometry optimization, and first principles molecular dynamics. J Chem Theory Comput. 5:2619–2828. [DOI] [PubMed] [Google Scholar]
- Ufimtsev IS, Martinez TJ. 2009b. Quantum chemistry on graphical processing units. 2. Direct self-consistent-field implementation. J Chem Theory Comput. 5:1004–1015. [DOI] [PubMed] [Google Scholar]
- Varki A, Kornfeld S. 1980. An autosomal dominant gene regulates the extent of 9-O-acetylation of murine erythrocyte sialic acids. A probable explanation for the variation in capacity to activate the human alternate complement pathway. J Exp Med. 152:532–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varki NM, Varki A. 2007. Diversity in cell surface sialic acid presentations: Implications for biology and disease. Lab Invest. 87:851–857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vranken WF, et al. 2005. The CCPN data model for NMR spectroscopy: Development of a software pipeline. Proteins. 59:687–696. [DOI] [PubMed] [Google Scholar]
- Wang J, et al. 2004. Development and testing of a general amber force field. J Comput Chem. 25:1157–1174. [DOI] [PubMed] [Google Scholar]
- Wang LP, et al. 2014. Building force fields: An automatic, systematic, and reproducible approach. The Journal of Physical Chemistry Letters. 5:1885–1891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang LP, et al. 2017. Building a more predictive protein force field: A systematic and reproducible route to AMBER-FB15. J Phys Chem B. 121:4023–4039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang LP, Song C. 2016. Geometry optimization made simple with translation and rotation coordinates. J Chem Phys. 144:214108. [DOI] [PubMed] [Google Scholar]
- Yu H, et al. 2004. Chemoenzymatic synthesis of CMP–sialic acid derivatives by a one-pot two-enzyme system: Comparison of substrate flexibility of three microbial CMP–sialic acid synthetases. Bioorg Med Chem. 12:6427–6435. [DOI] [PubMed] [Google Scholar]
- Yu H, et al. 2005. A multifunctional Pasteurella multocida sialyltransferase: A powerful tool for the synthesis of sialoside libraries. J Am Chem Soc. 127:17618–17619. [DOI] [PubMed] [Google Scholar]
- Yu H, et al. 2006. One-pot three-enzyme chemoenzymatic approach to the synthesis of sialosides containing natural and non-natural functionalities. Nat Protoc. 1:2485–2492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu H, et al. 2009. Chemoenzymatic synthesis of GD3 oligosaccharides and other disialyl glycans containing natural and non-natural sialic acids. J Am Chem Soc. 131:18467–18477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, et al. 2017. Conformational populations of beta-(1-->4) O-glycosidic linkages using redundant NMR J-couplings and circular statistics. J Phys Chem B. 121:3042–3058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang W, et al. 2019a. Use of circular statistics to model alphaMan-(1-->2)-alphaMan and alphaMan-(1-->3)-alpha/betaMan O-glycosidic linkage conformation in (13)C-labeled disaccharides and high-mannose oligosaccharides. Biochemistry. 58:546–560. [DOI] [PubMed] [Google Scholar]
- Zhang W, et al. 2019b. Synthesis and O-glycosidic linkage conformational analysis of (13)C-labeled oligosaccharide fragments of an antifreeze glycolipid. J Org Chem. 84:1706–1724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J, et al. 1999. Structural characterization of gangliosides isolated from mullet milt using electrospray ionization-tandem mass spectrometry. Glycobiology. 9:985–993. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


