Abstract
The dialogue between cortex and hippocampus is known to be crucial for sleep-dependent memory consolidation. During slow wave sleep, memory replay depends on slow oscillation (SO) and spindles in the (neo)cortex and sharp wave-ripples (SWRs) in the hippocampus. The mechanisms underlying interaction of these rhythms are poorly understood. We examined the interaction between cortical SO and hippocampal SWRs in a model of the hippocampo–cortico–thalamic network and compared the results with human intracranial recordings during sleep. We observed that ripple occurrence peaked following the onset of an Up-state of SO and that cortical input to hippocampus was crucial to maintain this relationship. A small fraction of ripples occurred during the Down-state and controlled initiation of the next Up-state. We observed that the effect of ripple depends on its precise timing, which supports the idea that ripples occurring at different phases of SO might serve different functions, particularly in the context of encoding the new and reactivation of the old memories during memory consolidation. The study revealed complex bidirectional interaction of SWRs and SO in which early hippocampal ripples influence transitions to Up-state, while cortical Up-states control occurrence of the later ripples, which in turn influence transition to Down-state.
Keywords: network model, NREM sleep, sharp wave-ripple, slow oscillation
Introduction
Coordination between thalamo-cortical and hippocampal (TH-CX-HC) networks during slow-wave sleep is implicated in the process of memory consolidation. The theory of two-stage memory formation (Squire and Alvarez 1995) assumes that newly acquired memory traces created during recent experience initially depend on the hippocampal structures but become hippocampus independent during the following stage of consolidation (Frankland and Bontempi 2005, McClelland et al.1995). Hippocampus may still preserve an index code to link together elements of more complex memories (Nadel et al. 2007, Teyler and DiScenna 1986, Winocur et al. 2010). The underlying mechanisms mediating memory consolidation during sleep are not well understood, but hippocampal sharp-wave ripples (SWRs) coordinated by the cortical slow oscillation (SO) were shown to participate in the consolidation process (Ego-Stengel and Wilson 2010, Girardeau et al. 2009, Nakashiba et al. 2009, Wang et al. 2015). Indeed, a complex nesting of different sleep graphoelements was recently reported in vivo (Latchoumane et al. 2017, Staresina et al. 2015). While a phase preference for SWR with respect to ongoing SO was reported in several studies (Isomura et al. 2006, Mölle et al. 2006, Peyrache et al. 2011, Sirota et al. 2003), SWR complexes can be detected at any SO phase and it remains unclear if SWRs happening at different phase of the SO cycle are performing different functions (Maingret et al. 2016).
A classic picture of the hippocampo-cortical interaction in memory consolidation suggests that new declarative memories are first formed in hippocampus and transferred to cortex over the periods of subsequent NREM sleep (Diekelmann and Born 2010); however, recent studies revealed a more complex bi-directional model of the interaction between hippocampal and cortical networks (Helfrich et al. 2019, Rothschild et al. 2017). The key component here is cortical input to hippocampus that can influence its activation and ultimately define the timing and the replay context of the hippocampal activity; resulted hippocampal input then influences cortical activation. These new data lead to the idea that cortical activation during sleep may influence hippocampal SWRs and therefore define identity of the memories that are replayed (Rothschild 2019). In this new study, we ask two related questions: how ongoing SOs affect ripple occurrences and vice-versa how ripples shape the spatiotemporal pattern of Up and Down cortical states—the alternating activity in the cortical neurons during sleep SO (Sanchez-Vives and McCormick 2000, Steriade et al. 1993b).
To study interaction of SWRs and SO, we bring together biophysical models of the thalamo-cortical network that reproduces SO-like activity during NREM stage-3 sleep (Bazhenov et al. 2002, Krishnan et al. 2016, Wei et al. 2018), and hippocampal CA1-CA3 circuitry producing SWR events (Malerba and Bazhenov 2019, Malerba et al. 2016). Both networks were connected within a cortico-hippocampal synaptic feedback loop. We observed that the cortical input was driving SO-ripple coupling. At the same time, ripples influenced the spatiotemporal pattern of the slow waves subtly—depending on the phase of SO, ripple could either anticipate or postpone transitions between Up- and Down-states, as well as change the initiation site and synchronization properties of the slow waves in the population of cortical neurons. We observed that a cortical site receiving ripple input at a given cycle of SO would likely lead the cortical spatiotemporal pattern in subsequent SO cycles. Finally, we show that the SO–ripple interaction can influence cortical synaptic plasticity and hence shape sequential spike reactivation among cortical cells, as reported previously in vivo (Euston et al. 2007, Ji and Wilson 2007, Peyrache et al. 2009). Our study supports the notion of bilateral cortico-hippocampal dialogue where both sites reciprocally influence the opponent’s transitions and in which ripples occurring at different phases of SO engage in functionally different tasks.
Materials and Methods
Hippocampal module
The model was tuned to show appropriate stochasticity in the spontaneous occurrence of sharp-wave ripples and large irregular activity in the interleaving times. The firing rates of excitatory and inhibitory cells in the system were consistent with experimental in vivo data. The CA1-CA3 model activity in isolation from cortical input was previously studied in terms of the ripple generation mechanism (Malerba et al. 2016), the synaptic connections role on reactivation during ripples (Malerba and Bazhenov 2019), and the relation between reactivation during sleep and synaptic changes induced by awake learning (Malerba et al. 2018). Technically, the model closely followed that of (Malerba and Bazhenov 2019, Malerba et al. 2016) with a slight difference in CA3 connectivity and projections to CA1, which leads to a single main excitable region in CA3 generating all the sharp waves, rather than sharp waves being initiated at random locations in CA3 (which was observed in previous models). Here we briefly describe the basic properties of the model. CA1 model consisted of 800 excitatory and 160 interneurons, and CA3 had 1200 excitatory cells and 240 interneurons. Each neuron was described by the following equations:
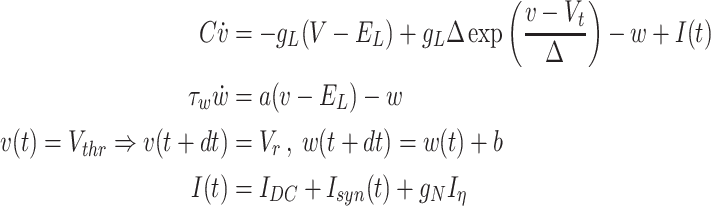 |
where 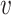 is membrane potential and
is membrane potential and 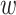 slow variable. For CA1 pyramidal (Py) cells
slow variable. For CA1 pyramidal (Py) cells 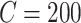 pF,
pF, 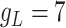 nS,
nS, 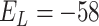 mV,
mV, 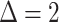 mV,
mV, 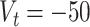 mV,
mV, 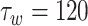 ms,
ms, 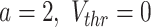 mV,
mV, 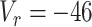 mV,
mV, 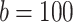 pA; for CA3 pyramidal cells
pA; for CA3 pyramidal cells 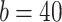 pA; for both CA1/CA3 inhibitory interneurons (Ins) these parameter change:
pA; for both CA1/CA3 inhibitory interneurons (Ins) these parameter change: 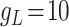 nS,
nS, 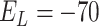 mV,
mV, 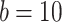 pA,
pA, 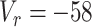 mV,
mV, 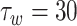 ms.
ms.
Each cell in the hippocampal model received two separate components of independent input: an OU-process (which by definition has zero mean, and whose standard deviation value is parameterized in the model) and a constant DC component, which is randomly selected as an occurrence of a normal distributed (mean and standard deviation parameterized) random variable. Intuitively, one can think of this cell-independent background noise as representing all the synaptic inputs that in vivo cell would be receiving, and indeed data suggest that an OU-process is a good fit for sub-threshold voltage fluctuations in both hippocampal and cortical cells. Having a non-zero mean in this noise input (provided by the DC component) allows for a properly randomized behavior in a population of cells, where some neurons are sitting closer to spiking threshold and others further. It is of note that all the cells were still kept in a noise-driven spiking regime (as opposed to an oscillatory regime perturbed by noise), which allows for the stochasticity in sharp-wave initiation and for flexible response to cortical input (the input dependence of sharp waves in the CA3 portion of the model is analyzed in detail in (Malerba et al. 2019)).
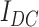 input was a constant different for each cell selected from Gaussian distribution, mean
input was a constant different for each cell selected from Gaussian distribution, mean 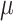 (in pA), and standard deviation
(in pA), and standard deviation 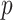 expressed as a percent of the mean value was different for each populations of excitatory (
expressed as a percent of the mean value was different for each populations of excitatory (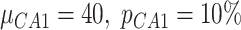 ,
, 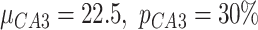 ) and inhibitory (
) and inhibitory (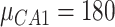 ,
, 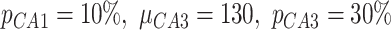 ) cells.
) cells.
We constructed the background noise by generating two incoming surrogate spike trains (one excitatory and one inhibitory) and convolving each spike train with an exponential decay, and finally combining the two into a current signal  . The two spike trains were built as process, by finding the time of the next surrogate spike using an exponential random variable (note that exponential inter-arrival times are markings of memoryless Poisson processes). To numerically obtain the exponential inter-arrival times of the surrogate spikes, we used a well-known conversion from uniform random variables to random variables of a given distribution (inverse transform sampling). Practically, the next time a surrogate spike was defined as
. The two spike trains were built as process, by finding the time of the next surrogate spike using an exponential random variable (note that exponential inter-arrival times are markings of memoryless Poisson processes). To numerically obtain the exponential inter-arrival times of the surrogate spikes, we used a well-known conversion from uniform random variables to random variables of a given distribution (inverse transform sampling). Practically, the next time a surrogate spike was defined as 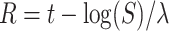 , where
, where 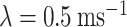 is the rate of incoming spikes, t is the current simulation time, and S is a uniformly sampled random variable. Next, we defined two surrogate spike trains (with the same high rate) and we convolved each of them with a exponential decay time (
is the rate of incoming spikes, t is the current simulation time, and S is a uniformly sampled random variable. Next, we defined two surrogate spike trains (with the same high rate) and we convolved each of them with a exponential decay time (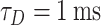 ), shaping two noisy signals with a small standard deviation. Finally, we subtracted the inhibitory signal from the excitatory signal and scaled the resulting signal (noisy, with one pole decay after the
), shaping two noisy signals with a small standard deviation. Finally, we subtracted the inhibitory signal from the excitatory signal and scaled the resulting signal (noisy, with one pole decay after the 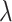 rate, and with small standard deviation) by a constant coefficient that was tuned to induce, when the current was added to a mildly hyperpolarized single cell, a standard deviation in voltage fluctuations of about 2 mV. Technically, this was obtained by scaling the noise added to excitatory cells by
rate, and with small standard deviation) by a constant coefficient that was tuned to induce, when the current was added to a mildly hyperpolarized single cell, a standard deviation in voltage fluctuations of about 2 mV. Technically, this was obtained by scaling the noise added to excitatory cells by 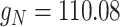 and to inhibitory cells by
and to inhibitory cells by 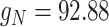 .
.
The synaptic current from excitatory (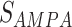 ) and inhibitory(
) and inhibitory(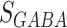 ) synapses to neuron
) synapses to neuron 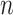 was defined as follows:
was defined as follows:
 |
where reversal potentials were 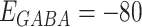 mV and
mV and 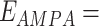 0 mV,
0 mV, 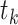 are the spikes times from the presynaptic cell
are the spikes times from the presynaptic cell 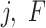 is a normalization coefficient, set so that every spike in the double exponential within parentheses peaks at one, and
is a normalization coefficient, set so that every spike in the double exponential within parentheses peaks at one, and 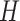 is the Heaviside function, ensuring that the effect of each presynaptic spike affects the post-synaptic current only after the spike has happened. Decay and rise constants were
is the Heaviside function, ensuring that the effect of each presynaptic spike affects the post-synaptic current only after the spike has happened. Decay and rise constants were 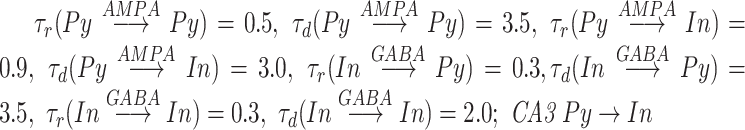 synapses had distinct constants
synapses had distinct constants 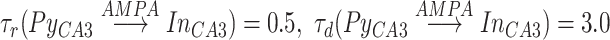 .
.
Synaptic weights were sampled from Gaussian distributions with variance 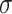 given by percent of the mean
given by percent of the mean 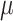 :
: 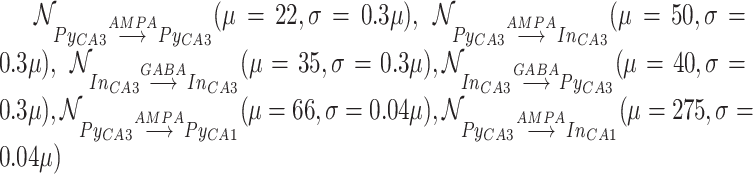 .
.
The rationale for the choice of the equations and parameters is discussed in length in (Malerba and Bazhenov 2019, Malerba et al. 2017, 2016).
Thalamo-cortical module
Our TH-CX module was similar to the previous models (Bazhenov et al. 2002, Krishnan et al. 2016, Wei et al. 2016) aimed at modeling NREM stage-3 sleep. The firing rate of pyramidal cells during Up-state in the model was relatively high compared with in vivo data. The main reason to increase firing in the model, as well as in our previous models of SO, was limited number of connections each pyramidal cell received in the model, which was much lower than in vivo (20 vs thousands). While this is a limitation of the model, it does not prevent it from being able to show replay during Up-states in pure cortical model without hippocampus (see, e.g., González et al. 2019, Wei et al. 2020). Neuromodulatory changes for different sleep stages and synaptic plasticity (except for short-term) were not employed in the model used in this new study.
All neurons followed Hodgkin–Huxley kinetics, and cortical neurons included dendritic and axo-somatic compartments:
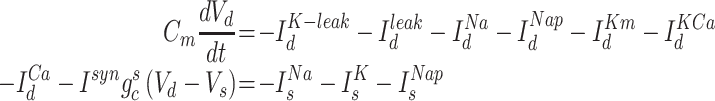 |
where the subscripts  and
and  correspond to axo-somatic and dendritic compartments,
correspond to axo-somatic and dendritic compartments, 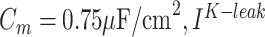 is the potassium leak current,
is the potassium leak current, 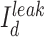 is
is 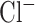 leak currents,
leak currents, 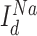 is fast
is fast  currents,
currents,  is persistent sodium current,
is persistent sodium current,  is fast delayed rectifier
is fast delayed rectifier  current,
current, 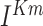 is slow voltage-dependent non-inactivating
is slow voltage-dependent non-inactivating 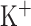 current,
current, 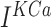 is slow
is slow 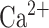 -dependent
-dependent 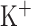 current,
current, 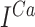 is high-threshold
is high-threshold 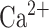 current, and
current, and 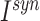 is the sum of all synaptic currents to the neuron. The intrinsic currents had generally the form
is the sum of all synaptic currents to the neuron. The intrinsic currents had generally the form 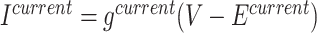 . Details of individual currents can be found in the previous publications (Bazhenov et al. 2002, Chen et al. 2012, Wei et al. 2016). The conductances of the leak currents were
. Details of individual currents can be found in the previous publications (Bazhenov et al. 2002, Chen et al. 2012, Wei et al. 2016). The conductances of the leak currents were 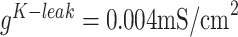 and
and 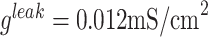 . The maximal conductances for the voltage and ion-gated intrinsic currents were
. The maximal conductances for the voltage and ion-gated intrinsic currents were 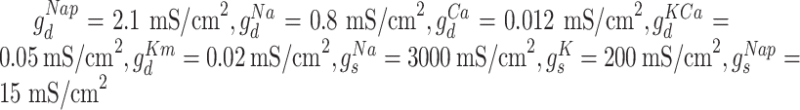 . For inhibitory neurons, persistent sodium current was not present (
. For inhibitory neurons, persistent sodium current was not present (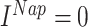 ) and conductances of the leak currents were
) and conductances of the leak currents were 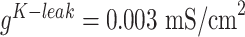 and
and 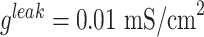 . The maximal conductances for the voltage and ion-gated intrinsic currents were
. The maximal conductances for the voltage and ion-gated intrinsic currents were 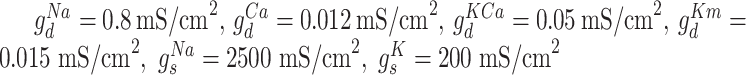 .
.
Thalamic neurons were single-compartmental neurons following the equation:
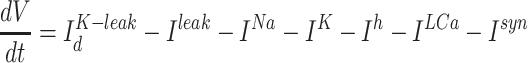 |
where 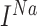 and
and 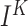 are fast
are fast 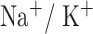 currents, and
currents, and 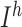 is hyperpolarization-activated depolarizing current. For thalamocortical (TC) neurons leak currents conductances were
is hyperpolarization-activated depolarizing current. For thalamocortical (TC) neurons leak currents conductances were 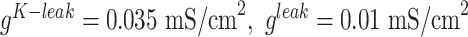 , and maximal conductances for other currents were
, and maximal conductances for other currents were 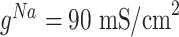 ,
, 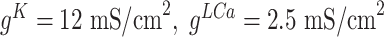 ,
, 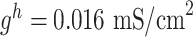 . For thalamic reticular (RE) neurons
. For thalamic reticular (RE) neurons 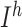 current was not present (
current was not present (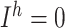 ), and conductances were
), and conductances were 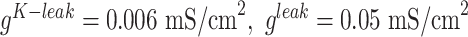 ,
, 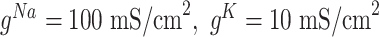 ,
, 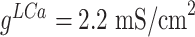 .
.
The synaptic currents for AMPA, NMDA, GABAA, and GABAB synapses were described by first-order activation schemes in the form of  where
where 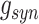 is maximum conductance, [O] is the fraction of open channels, and
is maximum conductance, [O] is the fraction of open channels, and 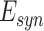 is the reversal potential, the details for each synaptic current is described in (Wei et al. 2016).
is the reversal potential, the details for each synaptic current is described in (Wei et al. 2016).
The maximal conductances were 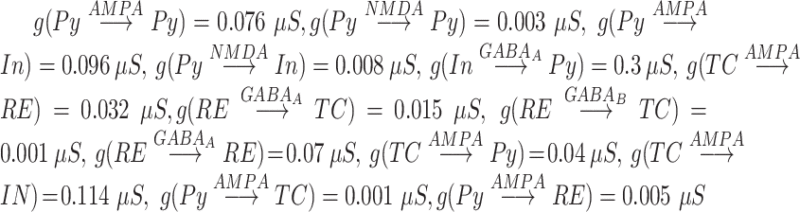 .
.
The synapses between hippocampus and cortex were modeled as AMPA-type synapses as described above with the possibility of signal transmission delay. The maximum conductances were 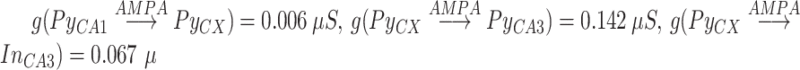 . (Connectivity will be described in the next section.) The default synaptic delays were 16 ms (Ferino et al. 1987) for CA1->CX and 30 ms for CX->CA3 connections (functionally mimicking several synaptic hops needed for the cortical layer 5 signal to reach CA3). The smaller delays of CA1->CX connections did not have a strong effect on the results, and we set them to 0 ms later in the study to have equal sampling distance when the effect of synaptic delays was explored (see Fig. 10).
. (Connectivity will be described in the next section.) The default synaptic delays were 16 ms (Ferino et al. 1987) for CA1->CX and 30 ms for CX->CA3 connections (functionally mimicking several synaptic hops needed for the cortical layer 5 signal to reach CA3). The smaller delays of CA1->CX connections did not have a strong effect on the results, and we set them to 0 ms later in the study to have equal sampling distance when the effect of synaptic delays was explored (see Fig. 10).
Additionally in Py->Py, Py<->In cortical connections miniature EPSP/IPSP (Redman 1990, Salin and Prince 1996) were present, their arrival times were modeled by Poisson processes with time-dependent mean rate 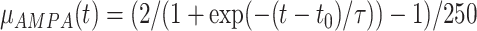 and
and 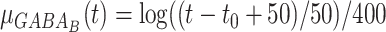 with
with 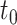 is a time of last presynaptic spike,
is a time of last presynaptic spike, 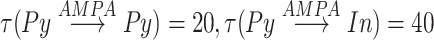 . The maximal conductances for minis were
. The maximal conductances for minis were 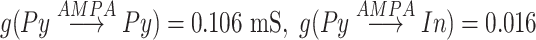 mS,
mS, 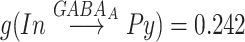 mS.
mS.
Network connectivity
The global topology of connections between the different modules can be seen in Figure 1A, the connectivity between different neuronal types can be seen in Figure 1B. Network connectivity of thalamocortical module is similar to the previous studies (Wei et al. 2018, 2020); it is local in nature, meaning we used dense connectivity in close neighborhood and no connectivity outside a defined radius. This connectivity has been shown to allow replicating properties of the SOs in vivo (Bazhenov et al. 2002, Krishnan et al. 2016). Cortex (CX) consisted of 1200 layer-5 Pys and 240 Ins, and thalamus consisted of 240 TC and 240 RE cells. Each neuronal type had local one-dimensional single-layer connectivity determined by the radii of connections (Fig. 1D,E). The radii of cortical and thalamic connections were 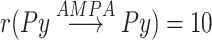 (meaning each cortical excitatory cell connects to its closest 20 neighboring neurons),
(meaning each cortical excitatory cell connects to its closest 20 neighboring neurons), 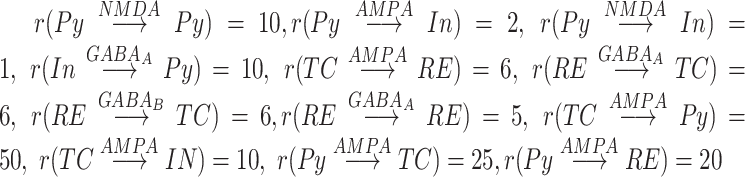 . TC neuron projections to the cortex had a radius of 50, compare with a radius of 10 between cortical pyramidal neurons, and, therefore, TC->CX projections helped to synchronize cortical activity. Effectively, the contribution of thalamus is visible as more synchronized transitions between Up/Down-states.
. TC neuron projections to the cortex had a radius of 50, compare with a radius of 10 between cortical pyramidal neurons, and, therefore, TC->CX projections helped to synchronize cortical activity. Effectively, the contribution of thalamus is visible as more synchronized transitions between Up/Down-states.
Figure 1 .
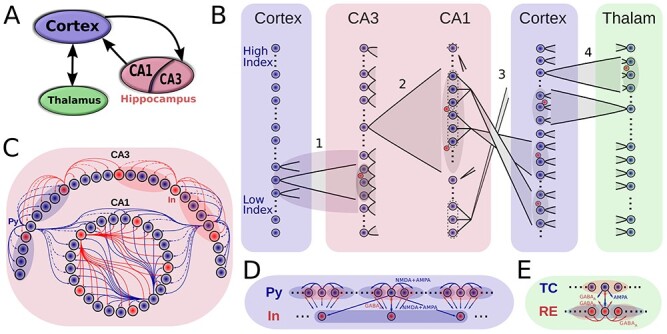
Model connectivity. A. The model consists of the thalamocortical loop that generates slow oscillation (SO), and the hippocampal circuit (consisting of CA1 and CA3 regions) that generates sharp wave-ripples (SWRs). The two components are connected via cortical input to CA3 and hippocampal output from CA1. B. Details of network connectivity. (1) Cortex->CA3: a small contiguous population of cortical excitatory cells targets a restricted part of CA3, which is highly responsive to incoming excitation. Both CA3 excitatory (blue dots) and inhibitory (red dots) cells were targeted. (2) CA3->CA1 (Schaffer collaterals): CA3 pyramidal cells broadly target CA1 excitatory and inhibitory neurons. (3) CA1->Cortex: Each small patch of CA1 cells projects to a small focal region in Cortex. (4) Cortex<->Thalamus: Cortical pyramidal neurons target both thalamic RE and TC cells, TC cells project back to both Pys and Ins of cortex. Cells in each region are linearly arrayed, with connectivity between regions generally being topographically organized, with the sole exception of the CA1-> Cortex where CA1 cells at the top of the array project to the cortical cells a the bottom, and vice-versa. C-E. Intra-area connectivities. Blue circles/arrows are excitatory cells/connections, and the red are inhibitory ones. The shaded area designates the target region of a projecting neuron. Connectivity of the thalamocortical circuity closely follows (Wei et al. 2018), and hippocampal connectivity is similar to the connectivity used in (Malerba and Bazhenov 2019).
Network connectivity of hippocampal module was similar to (Malerba and Bazhenov 2019), see Figure 1C. CA3 consisted of 1200 excitatory cells and 240 interneurons and had one-dimensional topology. The probability of connection from CA3 pyramidal cell with index 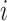 to other CA3 pyramids and interneurons was proportional to
to other CA3 pyramids and interneurons was proportional to 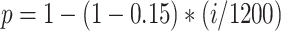 , that is, the subnetwork with smaller index numbers was more densely connected to increase the probability of SWR initiation in this region. The probability of connection from CA3 interneurons to CA3 pyramids was uniform,
, that is, the subnetwork with smaller index numbers was more densely connected to increase the probability of SWR initiation in this region. The probability of connection from CA3 interneurons to CA3 pyramids was uniform, 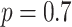 . The connectivity of Schaffer collaterals from CA3 pyramids with index
. The connectivity of Schaffer collaterals from CA3 pyramids with index 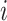 to CA1 pyramids and interneurons was inversely proportional, that is,
to CA1 pyramids and interneurons was inversely proportional, that is, 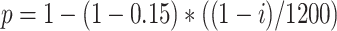 , so that more interconnected CA3 regions project less to CA1 and vice-versa. Within CA1, connectivity was all-to-all (including both Py and In), but synapses that were sampled at zero or less weight were removed from the connectivity, yielding to approximately 50% of CA1 Py-Py connections being removed (details in the next section).
, so that more interconnected CA3 regions project less to CA1 and vice-versa. Within CA1, connectivity was all-to-all (including both Py and In), but synapses that were sampled at zero or less weight were removed from the connectivity, yielding to approximately 50% of CA1 Py-Py connections being removed (details in the next section).
In order to couple only the subdivision of the cortical network with hippocampus, only a subset of cortical pyramidal cells with index 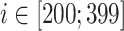 projected to subset of CA3 neurons using radii
projected to subset of CA3 neurons using radii 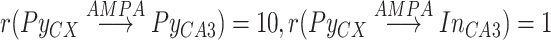 . For the opposite direction flow from hippocampus to cortex, continuous groups (chunks) of 100 CA1 pyramidal neurons were targeting small continuous chunks of 5 cortical Pys. CA1 chunks were partially overlapping (each subsequential one being shifted by 20 neurons), and cortical chunks were non-overlapping with the gap of 33 neurons. Within the single CA1-CX chunk pair, every CA1 neuron projected to all neurons of a cortical chunk. The pairing between the chunks was linear and flipped, so that CA1 chunks with small index targeted chunks with high CX index and vice-versa. Although based on connectivity, CA1 region targeted distinct loci of the whole cortical network, effectively most of the ripple input (see the histogram of firing across CA1 cells in Fig. 2, left top) was received by cortical sites opposite to the subregion projecting to CA3, thanks to the flip. Although far from real anatomical connectivity, this topology was chosen in order to be compatible with the following properties: (a) CA1 projects to frontal part of cortex (mPFC) (Cenquizca and Swanson 2007), (b) CA1 projections target only subset of cortical cells (Dégenètais et al. 2003, Laroche et al. 1990, Thierry et al. 2000), (c) global traveling waves tend to start in the frontal region and travel towards the temporal region (Nir et al. 2011), (d) spiking activity in the temporal lobe is synaptically closer to the enthorhinal cortex, a main gate to the hippocampal structures (Ranganath and Ritchey 2012) and is more probable to directly influence its activity. Translated to our model: subdivision of cortical network (“temporal” part) tends to influence SWR generation in the preferable region of CA3, which is transmitted to topologically similar region of CA1, which in turn projects to another part of the cortex (“frontal” part).
. For the opposite direction flow from hippocampus to cortex, continuous groups (chunks) of 100 CA1 pyramidal neurons were targeting small continuous chunks of 5 cortical Pys. CA1 chunks were partially overlapping (each subsequential one being shifted by 20 neurons), and cortical chunks were non-overlapping with the gap of 33 neurons. Within the single CA1-CX chunk pair, every CA1 neuron projected to all neurons of a cortical chunk. The pairing between the chunks was linear and flipped, so that CA1 chunks with small index targeted chunks with high CX index and vice-versa. Although based on connectivity, CA1 region targeted distinct loci of the whole cortical network, effectively most of the ripple input (see the histogram of firing across CA1 cells in Fig. 2, left top) was received by cortical sites opposite to the subregion projecting to CA3, thanks to the flip. Although far from real anatomical connectivity, this topology was chosen in order to be compatible with the following properties: (a) CA1 projects to frontal part of cortex (mPFC) (Cenquizca and Swanson 2007), (b) CA1 projections target only subset of cortical cells (Dégenètais et al. 2003, Laroche et al. 1990, Thierry et al. 2000), (c) global traveling waves tend to start in the frontal region and travel towards the temporal region (Nir et al. 2011), (d) spiking activity in the temporal lobe is synaptically closer to the enthorhinal cortex, a main gate to the hippocampal structures (Ranganath and Ritchey 2012) and is more probable to directly influence its activity. Translated to our model: subdivision of cortical network (“temporal” part) tends to influence SWR generation in the preferable region of CA3, which is transmitted to topologically similar region of CA1, which in turn projects to another part of the cortex (“frontal” part).
Figure 2 .
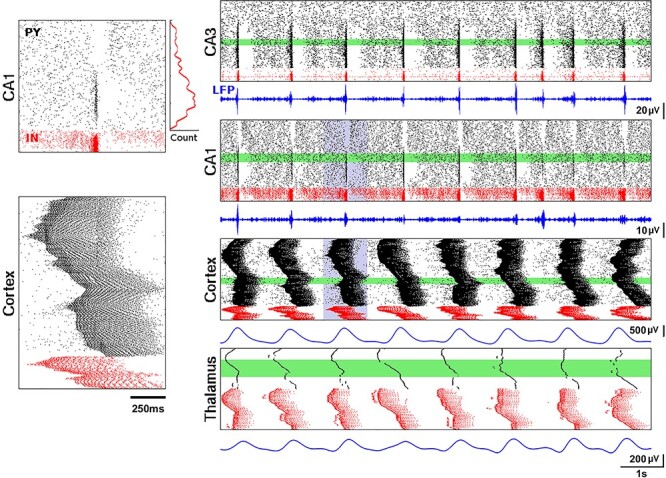
Closed-loop network dynamics. Spiking activity of excitatory pyramidal (black) and local inhibitory (red) neurons, LFP traces (blue). Left panels: representative ripple event in CA1 (top) and Up-state in cortical network (bottom), correspond to the violet region on the right. Histogram next to the ripple event plot shows average spike count of CA1 excitatory cells during ripples. Right panels from top to bottom show 10 seconds of full network activity: spiking rastergrams for CA3, CA1, cortical, and thalamic (RE and TC cells) networks. Average LFPs from 100 neurons (green areas) are shown below rasterplots. LFP for CA1 was filtered from 120 to 200 Hz, for CA3 from 90 to 200 Hz, and for both cortical and thalamic cells from 0.5 to 2 Hz.
Computational methods
All simulations used fourth-order Runge–Kutta integration method with a time step of 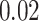 ms. Custom written parallel C++ code was run on Intel Xeon Phi Cooprocessors; parts requiring exhaustive parameter search were run on linux clusters through the NSG project (Sivagnanam et al. 2013). For the basic results (Figs 3, 4, 6) 20 trials were run, each simulating 50 s of SO activity. Each trial had a different random seed for initial condition of network connectivity (hippocampus) and minis generation.
ms. Custom written parallel C++ code was run on Intel Xeon Phi Cooprocessors; parts requiring exhaustive parameter search were run on linux clusters through the NSG project (Sivagnanam et al. 2013). For the basic results (Figs 3, 4, 6) 20 trials were run, each simulating 50 s of SO activity. Each trial had a different random seed for initial condition of network connectivity (hippocampus) and minis generation.
Figure 3 .
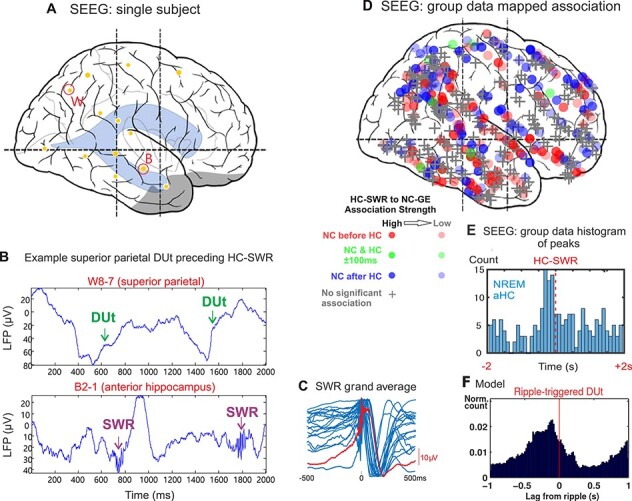
Experimental data and model prediction. A. Position of hippocampal (B) and parietal (W) electrodes in the example subject B. Top. Raw LFP trace (transcortical bipolar SEEG derivation) from an example parietal lobe electrode showing alternating Up/Down-states with the Down to Up transition (DUt) marked. Bottom. Raw LFP trace from depth electrode (bipolar SEEG) from the anterior hippocampus, showing sharpwave-ripples following DUt at the top panel. C. The blue waveforms are the template averages for the SWR in the 17 aHC sites. They range in amplitude from 35-300  V peak-to-peak and are normalized for display. The red waveform is the grand average. D. Locations of the NC electrodes where DUt were detected to correlate with HC SWR. Shape codes if there was a significant temporal relationship (circle: significant, +: not significant); color codes order (red: DUt before SWR; blue: SWR before DUt; green: within 100ms); intensity codes association strength. Significant associations are evident in all cortical areas sampled. E. The number of NC-HC electrode-pairs with peak DUt-SWR association latency in each 100ms bin around the time of the SWR is plotted. F. DUt-triggered ripple histogram for the model. To get a smooth distribution, the transition event in each cell is measured separately. Red vertical line -
V peak-to-peak and are normalized for display. The red waveform is the grand average. D. Locations of the NC electrodes where DUt were detected to correlate with HC SWR. Shape codes if there was a significant temporal relationship (circle: significant, +: not significant); color codes order (red: DUt before SWR; blue: SWR before DUt; green: within 100ms); intensity codes association strength. Significant associations are evident in all cortical areas sampled. E. The number of NC-HC electrode-pairs with peak DUt-SWR association latency in each 100ms bin around the time of the SWR is plotted. F. DUt-triggered ripple histogram for the model. To get a smooth distribution, the transition event in each cell is measured separately. Red vertical line -  ms.
ms.
Figure 4 .
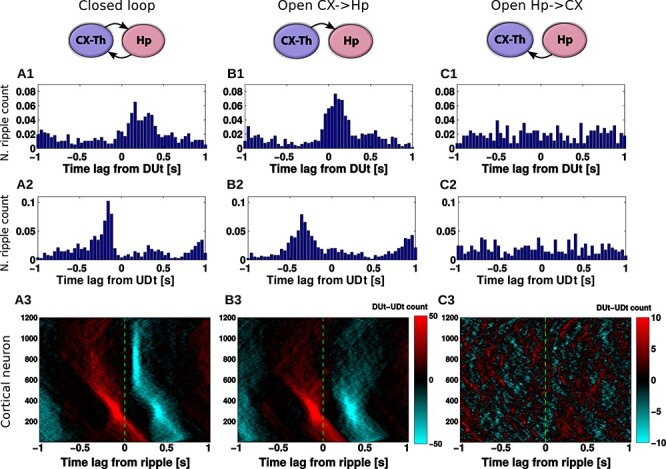
Effect of network connectivity on DUt/UDt-ripple coordination. Left column (A): closed CX-HC loop, middle column (B): open loop (HC does not project back to CX), right column (C): open loop (CX does not project back to HC). 1: DUt triggered ripple count. 2: UDt triggered ripple count. 3: Spatiotemporal profile of ripple triggered DUt (red) and UDt (blue) count for all Py neurons in the CX. Colormap: DUt-UDt count (red indicates mainly DUt events, blue—mainly UDt events); y-axis—index of Py cells. Note the different color-scale used for C3. Corresponding cumulative histograms are shown in Supplementary Figure 7. Data were averaged across 20 trials.
Figure 6 .
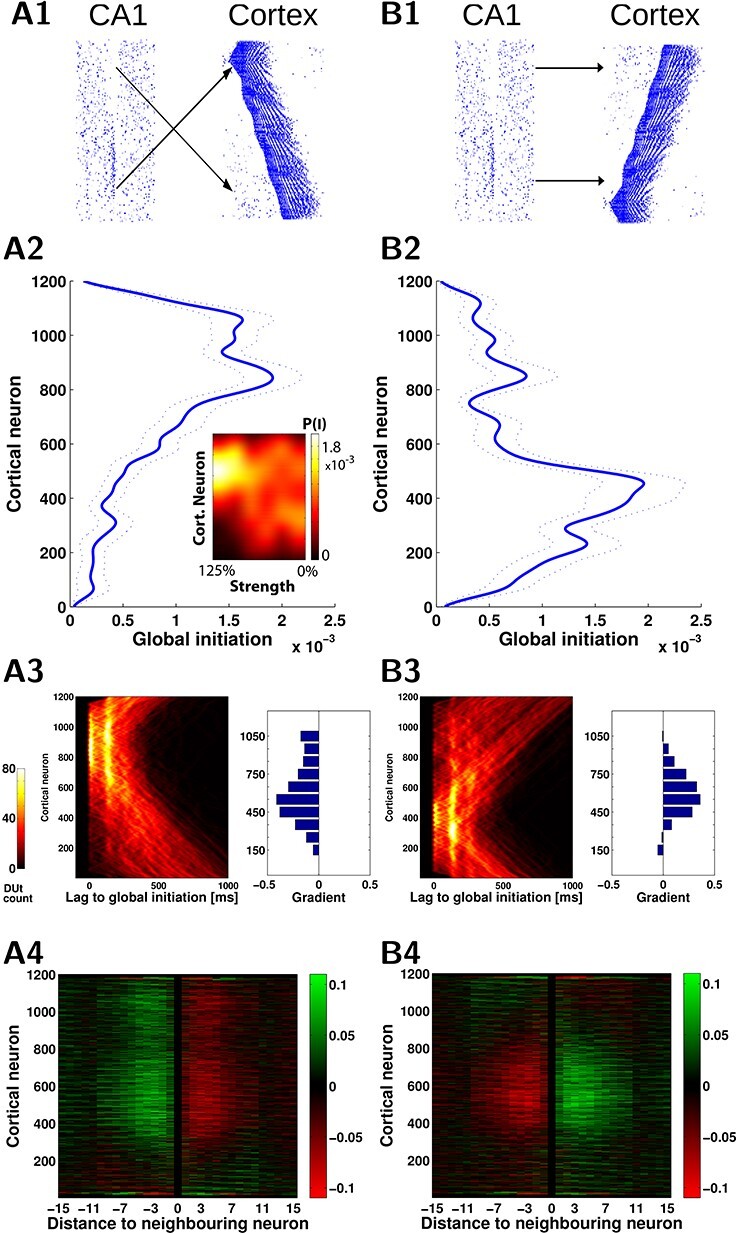
Hippocampal ripples shape spatiotemporal pattern of the slow waves. A1, B1. Two wiring models (A1, mirror) and (B1, direct) reveal different spatiotemporal patterns of the cortical slow waves. A2, B2. Probability of Up-state global initiation for each neuron in the network. In A1 ripples target the “top” region of the cortex (cells [601-1200]) and this causes higher Up-state initiation likelihood in that region (A2, blue). In B1 ripples target the “bottom” region ([1-600]) and this causes higher initiation in that region (B2, blue). Average across 20 simulations, dotted lines show standard error of the mean. A2 inset: Impact of ripples depends on the strength of CA1->CX connections. Color map codes probability of global Up-state initiation for each neuron in A1 wiring scenario. The preference for the upper region initiation dissolved as CA1->CX connectivity strength decreased (100%—baseline, 0%—no CA1 input). A3,B3. The pattern of the Up-state initiation probability is reflected in the shape of the DUt traveling waves. A3/B3, left. Probability of DUt for each neuron as a function of time (lag) with respect to the time moment of a global DUt (zero lag). A3/B3, right. The difference of the gradient (“slope” in radians) of the DUt traveling wave in the mirror and direct map models compared with the cortex-only (no hippocampal input) model, each bar corresponds to restricted region of 100 neurons. Positive values indicate a higher tendency of waves to propagate from the bottom to the top of the network when compared with the cortex-only model, while the negative values show the opposite tendency. A4,B4. Change of “incoming” synapses strength (X-axis—relative index of a presynaptic neuron in respect to the index of a fixed postsynaptic neuron) calculated using offline STDP. The neurons in the middle of the network show an opposite trend for strengthening/weakening of synapses, corresponding to preferred slope gradients as shown A3/B3. The effect starts weakening for the distances over 10 neighboring neurons (X-axis), which was due to the increasing time delay.
At the start of the simulations, both the thalamocortical loop and hippocampal networks were allowed to run independently for a few seconds, to get their stable state before synaptically coupling the two models.
Data processing was done in MATLAB (MathWorks). Down-to-Up transitions (DUt) and Up-to-Down transition (UDt) were computed separately for each cell based on the membrane voltage, and the global transition was defined as the time when most of the cells go through the transition period (peak of cells transition density). SWR event was detected for the whole CA1 network. To estimate LFP, the average synaptic current input across all pyramidal cells in CA1 was calculated, and then rescaled by 1 mS to represent a potential, such that 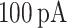 of synaptic current produce a
of synaptic current produce a 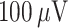 LFP change. SWR was found when the filtered LFP (50–350 Hz) exceeded a threshold of five standard deviations of the mean computed in one SWR-free second of activity, see (Malerba et al. 2016) for details.
LFP change. SWR was found when the filtered LFP (50–350 Hz) exceeded a threshold of five standard deviations of the mean computed in one SWR-free second of activity, see (Malerba et al. 2016) for details.
Human data collection and graphoelement analysis
Patients (N=17, 10 females) with long-standing drug-resistant partial seizures underwent SEEG depth electrode implantation in order to localize seizure onset and thus direct surgical treatment. Patients were from 16 to 58 years old (mean 29.9), with globally typical SEEG rhythms in most channels (i.e., absence of diffuse slowing, widespread interictal discharges, highly frequent seizures, etc.) with no previous excision of brain tissue or other gross pathology. Analyzed HC contacts were not involved in the initiation of seizures, and in five did not evince interictal spikes. Electrode targets and implantation durations were chosen entirely on clinical grounds (Gonzalez-Martinez et al. 2013). All patients gave fully informed consent for data usage as monitored by the local institutional review board, in accordance with clinical guidelines and regulations at the Cleveland Clinic.
After implantation, electrodes were located by aligning post-implant CT to preoperative structural MRI (Dykstra et al. 2012). Because SWR are more prominent in anterior HC, and spindle-ripples in posterior HC (Jiang et al. 2019a,b), only anterior HC leads (N=20, 11 left) were analyzed in this study. Electrode contacts were rejected from analysis if they were involved in the early stages of the seizure discharge and had frequent interictal activity or abnormal spontaneous local field potentials, leaving 371 transcortical pairs (18.2 per patient) accepted for further analysis.
Continuous recordings from SEEG depth electrodes were made with cable telemetry system (Nihon Kohden) across 1 to 6 nights (mean, 3.6). NREM was identified by previously described methods utilizing clustering of first principal components of delta-to-spindle and delta-to-gamma power ratios across multiple LFP-derived signal vectors (Gervasoni et al. 2004, Jiang et al. 2017). Total NREM sleep duration varied from 2.2–7.1 hr (mean 4.5).
HC-SWR were identified using previously described methods (Jiang et al. 2020), which required at least three peaks at ˜85Hz (the “ripple”), on the peak of a characteristic sharpwave, and followed by a slower wave of opposite polarity. Characteristic sharpwave waveforms were established for each channel by hand selection of 100–400 HC-SWR with typical waveforms (as established in primates and rodents), which were averaged to establish a template. The similarity of each putative HC-SWR to the template was quantified as their dot product, with a threshold set to reject at least 95% of putative HC-SWR without visually observable sharpwaves. HC-SWR were distinguished from epileptiform activity using adaptive thresholding of one-dimensional wavelet decomposition and 200 Hz high-passed filtering, set and confirmed with visual inspection of each HC channel. Down-states (DS) and Up-states (US) were identified by filtering from 0.1 to 4 Hz, selecting consecutive zero crossings of opposite slope separated by 250 to 3000 ms, and retaining the top 10% of peaks. DS were surface negative and confirmed with a high gamma (70–190 Hz) power decrease exceeding 1 dB within 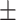 250 ms of the negative NC-DS peaks. DUt were identified as the midpoint between the peaks of a DS-US pair (with US immediately following DS), with the two peaks being at most 3000 ms apart.
250 ms of the negative NC-DS peaks. DUt were identified as the midpoint between the peaks of a DS-US pair (with US immediately following DS), with the two peaks being at most 3000 ms apart.
Peri-stimulus time histograms were constructed for each hippocampo-neocortical (HC-NC) channel pair, comprising the occurrence times of DUt during the 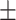 2 s interval surrounding midpoints of HC-SWR (see Fig. 3 for examples). The significance of peaks and troughs in each histogram was tested by comparing them to distributions derived from histograms constructed under the null hypothesis of no relationship between the NC-DUt and HC-SWR using the following randomization procedure. Null-hypothesis histograms (N=1000) were constructed of NC-DUt occurrences relative to a number of random times equal to the number of HC-SWR. For each 200 ms time bin with 100 ms overlap comprising the 4-second trial duration, the actual counts are then compared with the distribution under the null hypothesis, followed by FDR correction (Benjamini and Hochberg 1995) resulting in
2 s interval surrounding midpoints of HC-SWR (see Fig. 3 for examples). The significance of peaks and troughs in each histogram was tested by comparing them to distributions derived from histograms constructed under the null hypothesis of no relationship between the NC-DUt and HC-SWR using the following randomization procedure. Null-hypothesis histograms (N=1000) were constructed of NC-DUt occurrences relative to a number of random times equal to the number of HC-SWR. For each 200 ms time bin with 100 ms overlap comprising the 4-second trial duration, the actual counts are then compared with the distribution under the null hypothesis, followed by FDR correction (Benjamini and Hochberg 1995) resulting in 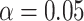 post-FDR correction. Altogether, there were 204 unique HC-NC pairs that showed significant HC-SWR to DUt relationship. A total of 731124 DUt-SWR events were used for histogram construction. The latencies of the largest significant peaks identified in the individual histograms constructed as described above were used to create summary histograms. To test if, overall, DUt significantly precedes or follows HC-SWR, two-tailed binomial tests with chance probability of 0.5 were performed on the number of channel pairs with peak latencies in the 500 ms before versus the 500 ms after the reference HC-SWR. We also tested with Kolmogorov–Smirnov tests whether, overall, the distribution of peak DUt latencies significantly related to HC-SWR differs from chance.
post-FDR correction. Altogether, there were 204 unique HC-NC pairs that showed significant HC-SWR to DUt relationship. A total of 731124 DUt-SWR events were used for histogram construction. The latencies of the largest significant peaks identified in the individual histograms constructed as described above were used to create summary histograms. To test if, overall, DUt significantly precedes or follows HC-SWR, two-tailed binomial tests with chance probability of 0.5 were performed on the number of channel pairs with peak latencies in the 500 ms before versus the 500 ms after the reference HC-SWR. We also tested with Kolmogorov–Smirnov tests whether, overall, the distribution of peak DUt latencies significantly related to HC-SWR differs from chance.
Results
Organization and properties of the network model
Sleep SOs are generated in the thalamocortical network (Mohajerani et al. 2010, Sheroziya and Timofeev 2014, Steriade et al. 1993b, Timofeev et al. 2000, Volgushev et al. 2006) and significantly interact and coordinate with hippocampal SWRs (Buzsáki 2015). Our model is build upon the two major network blocks (see Fig. 1)—an oscillating thalamocortical (TH-CX) network generating slow (˜0.7 Hz) cortical oscillation (Bazhenov et al. 2002, Krishnan et al. 2016, Wei et al. 2018), and a hippocampal (HC) network spontaneously generating SWRs with an average oscillation frequency within a ripple ˜155 Hz (Malerba and Bazhenov 2019). A single layer of cortical (CX) neurons displays alternating Up- and Down-states and is further synchronized by the activity of thalamic TC-RE cells (Lemieux et al. 2014). The connectivity between cortex and hippocampus in the model resembles the biological circuitry where global Up-states tend to travel from medial prefrontal cortex to the medial temporal lobe and hippocampus (Nir et al. 2011). The output side of hippocampal processing—CA1/subiculum—then projects one of its streams back to mPFC via the fornix system (Cenquizca and Swanson 2007) (apart from major feedback connectivity back to the entorhinal cortex, which we do not model here). Thus, in our implementation, a restricted region of the cortical network projects to a subset of CA3 cells in hippocampus and affects the probability of sharp-wave generation there. CA3 region is consequently connected to the CA1 region, which displays ripple events as a consequence of large excitatory events occurring in CA3. The major part of CA1 output is then fed back to the cortical region different from the location projecting back to CA3. For specific details and justification of the connectivity, please see Methods. We did not tune the network so that the Up-states would start at a specific region; however, as we show later, the “frontal” part of the cortex tends to start Up-states as a result of CA1 output activity targeting this region in the model.
Figure 2 shows the spiking rastergrams and LFPs of all the network components when coupled into a “close-loop” large-scale network. The most prominent hippocampal features are sharp-wave events internally generated in CA3 and ripples in CA1 (LFP is filtered for better visibility of ripples). By design, the neurons in the bottom region (i.e., with low index number) of CA3 had higher strength of lateral connections and thus were more prone to initiate a sharp-wave event (note Fig. 2, top right panel, with majority of excitatory spikes located in the bottom region during the sharp-wave). Due to the connectivity from CA3 to CA1, CA3 sharp-waves triggered CA1 ripples in the topologically equivalent (in terms of cell indexes, see Fig. 1B) region of the CA1 (Fig. 2, second right panel). Figure 2, left top, shows detailed view of a single ripple event and a histogram of probability of CA1 cell to become part of a ripple. In order to avoid a problem that the same region of cortex both receives the majority of ripple events from CA1 (see histogram in Fig. 2 top left) and targets CA3 network, CA1->CX connections were “flipped” (see Fig. 1B), such that the low CA1 region projected to the upper region of the cortical network and vice-versa (we also consider network model without flipping in later sections).
The cortical network generated a regular SO pattern (Fig. 2, third right panel) in which pyramidal (Py) cells and inhibitory interneurons (Ins) alternated between Up- and Down-states with an approximate frequency of 0.7 Hz. A single Up-state is detailed in Figure 2, left bottom, and shows cortical spiking activity propagating throughout the network.
Coordination of SO-SWR in model and experimental data
To measure coordination between the prime network activities — SO and SWRs — we determined the temporal relationship between the cortical Down-to-Up transition (DUt) and SWR event times in model simulations and experimental data. Recordings were done in 17 long-standing drug-resistant epileptic patients with intracranially implanted electrodes (see details in Methods, additional intracranial data from humans similar to the presented data were studied in depth in (Jiang et al. 2019a,b)). Electrodes were recorded in the hippocampus and neocortex (NC) during NREM sleep. An example recording from the sites shown in Figure 3A is displayed in Figure 3B. Surface negative deflections in the superior parietal transcortical lead indicate Down-states; their transition to the following Up-state is marked DUt. Simultaneous HC recordings from the hippocampus show prominent ripples a short time later (Fig. 3B, lower panel). Examination of 371 such pairs found 204 with significant temporal association between HC-SWR and NC-DUt. The locations of the NC electrodes are plotted on lateral view of the brain in Figure 3D, which shows that cortical DUt across all lobes are significantly associated with hippocampal SWR, with no definite preference between cortical areas. Clearly, there is a wide variation in association strength and relative times of occurrence, as would be expected given that DUt are not synchronous phenomena across the entire cortex in humans (Mak-McCully et al. 2014). However, when the peak times of this association for each pair are plotted as a histogram, the DUt are seen to predominantly occur prior to the SWR (Fig. 3E). Considering only all significant channel-pair DUt occurrence peaks with latencies in the 500 ms before versus the 500 ms after the reference HC-SWR, their mean latency was 42 ms prior to the HC-SWR peak. If a gaussian is fit to the DUt peak distribution, the mean of the fitted distribution is 33 ms prior to the HC-SWR. This distribution of peak DUt latencies significantly related to HC-SWR differed from chance Kolmogorov–Smirnov test, 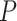 < 0.0002). Critically, the DUt peaks were significantly before the HC-SWR, using a two-tailed binomial test (
< 0.0002). Critically, the DUt peaks were significantly before the HC-SWR, using a two-tailed binomial test (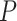 < 0.0483). The timing of the pre-SWR peak of DUt occurrence observed empirically (Fig. 3E) is comparable to that found in the model (Fig. 3F), where DUt peaked 100 ms before SWR (significantly different from chance, Kolmogorov–Smirnov test,
< 0.0483). The timing of the pre-SWR peak of DUt occurrence observed empirically (Fig. 3E) is comparable to that found in the model (Fig. 3F), where DUt peaked 100 ms before SWR (significantly different from chance, Kolmogorov–Smirnov test, 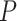 < 0.001).
< 0.001).
Global coordination of SO-SWR rhythms is set by cortical drive
Next we investigated the mechanisms driving the relationship between cortical and hippocampal events reported in the previous section. In Figure 4A1 we plotted the DUt-triggered ripple-count histogram where most of the ripples followed onset of an Up-state. To find what determines this relationship, we considered two open-loop model configurations — one where only CX targets HC and no connections are fed back from HC to CX (column B) and another one where only HC targets CX (column C). The network model with CX targeting HC preserved the phenomenon of DUt preceding the ripple event (Fig. 4B1).
In contrast, in the model where HC targeted CX but no feedback projections were implemented, no obvious coordination pattern was observed (Fig. 4C1). We thus conclude that the global coordination of rhythms is set by the cortical drive to the HC network. Nonetheless, additional important differences to the closed loop model were found (see discussion of Fig. 4A/B3 and Fig. 5 below), rendering the influence of hippocampus on cortex more subtle. Removing HC->CX projections simplified the temporal profile of ripple events that only revealed one peak (compare Fig. 4B1 and A1). Two-sample Kolmogorov–Smirnov test comparing the distributions of time-lags confirmed that the lags were derived from different distributions,  <0.001, suggesting different behavior of the closed loop model especially near the time of UDt, presumably caused by CA1 activity. Analysis of the ripple event histogram using UDt as a reference point found a sharp peak of ripple activity immediately preceding UDt in closed loop model (Fig. 4A2), while this peak was observed earlier and less visible in the model missing CA1 input (Fig. 4B2, a Kolmogorov–Smirnov test confirmed that the lags were derived from different distributions,
<0.001, suggesting different behavior of the closed loop model especially near the time of UDt, presumably caused by CA1 activity. Analysis of the ripple event histogram using UDt as a reference point found a sharp peak of ripple activity immediately preceding UDt in closed loop model (Fig. 4A2), while this peak was observed earlier and less visible in the model missing CA1 input (Fig. 4B2, a Kolmogorov–Smirnov test confirmed that the lags were derived from different distributions,  <0.001).
<0.001).
Figure 5 .
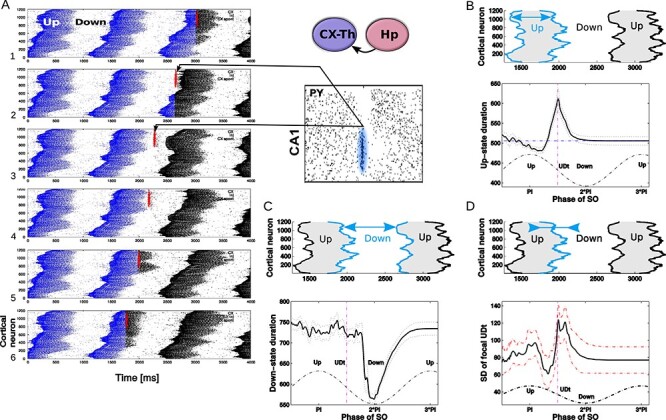
Ripple effect within a single SO cycle, open loop scenario. A. A trace of a single representative ripple event was saved from the closed loop simulation and delivered to the isolated thalamocortical network at the different phases of the SO oscillatory cycle. Red dots show spikes of CA1 cells projected to the region of the cortical network. Blue dots are spikes of cortical cells in the network before ripple stimulation; black dots are cortical spikes after the ripple was delivered. The effect of a ripple on the spatiotemporal pattern of DUt/UDt transitions depended on the exact timing of the event. We tested 100 independent trials using identical networks (note, cortical spiking patterns before ripple arrival (blue) are identical in all five panels) with the ripple delivered at different times: 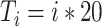 ms for i-th trial. Animation for this experiment is shown in Supplementary Figure 8, effect of SWR magnitude is shown in Supplementary Figure 9. B–D. Average effects of a ripple event. Each stimulation condition was repeated 10 times using different initial seed values hereby creating different cortical dynamics (see animation); the results were averaged. Cortical activity was analyzed in the region receiving most of the ripple input (top 601–1200 cortical cells). B. Effect of a ripple on the Up-state duration. Top. Schematic diagram of cortical activity showing two Up-states (shaded) and single Down-state. Duration of the first Up-state (blue envelope lines) was measured for each trial (i.e., different stimulation phase). Bottom. Average effect of a ripple on the Up-state length from 10 simulations for each phase condition. X-axis—timing of a ripple rescaled to SO cycle (reference cycle for each trial was defined by the run where no ripple was delivered). Dashed vertical line shows time of UDt. C. Effect of a ripple on the Down-state duration. Top. Schematic diagram of cortical activity. Duration of the Down-state (blue-line envelope) was measured. Bottom. Average effect of a ripple on the Down-state duration. D. Effect of ripple on the synchrony of the UDt events. Top: Schematic diagram of cortical activity. Timing of the UDt events (blue-line envelope) across population of cortical neurons was measured. Bottom: Average effect of a ripple on the synchronization of UDt events measured as a standard deviation of UDt events timing.
ms for i-th trial. Animation for this experiment is shown in Supplementary Figure 8, effect of SWR magnitude is shown in Supplementary Figure 9. B–D. Average effects of a ripple event. Each stimulation condition was repeated 10 times using different initial seed values hereby creating different cortical dynamics (see animation); the results were averaged. Cortical activity was analyzed in the region receiving most of the ripple input (top 601–1200 cortical cells). B. Effect of a ripple on the Up-state duration. Top. Schematic diagram of cortical activity showing two Up-states (shaded) and single Down-state. Duration of the first Up-state (blue envelope lines) was measured for each trial (i.e., different stimulation phase). Bottom. Average effect of a ripple on the Up-state length from 10 simulations for each phase condition. X-axis—timing of a ripple rescaled to SO cycle (reference cycle for each trial was defined by the run where no ripple was delivered). Dashed vertical line shows time of UDt. C. Effect of a ripple on the Down-state duration. Top. Schematic diagram of cortical activity. Duration of the Down-state (blue-line envelope) was measured. Bottom. Average effect of a ripple on the Down-state duration. D. Effect of ripple on the synchrony of the UDt events. Top: Schematic diagram of cortical activity. Timing of the UDt events (blue-line envelope) across population of cortical neurons was measured. Bottom: Average effect of a ripple on the synchronization of UDt events measured as a standard deviation of UDt events timing.
To further explore the interaction between SWRs and Up/Down-state transitions, we plotted ripple-triggered DUt-UDt count histograms for all cortical neurons as a rastergram (Fig. 4A3, B3, C3, the cumulative histograms are shown in Supplementary Fig. 7). Both Figure 4A3 and B3 show similar UDt/DUt activity in the bottom region of the network (low indexes). The highly consistent DUt activity (note, red dots indicate high count of DUt events) can be explained by the fact that a DUt transition increases probability of the ripple events, and CA3 receives input from CX in this region (see Fig. 1B, left). Therefore, ripples could likely be triggered by DUt events. Consistent UDt activity (blue dots indicate high count of UDt events) in the same network region would then follow because the Up-state duration tends to be consistent across different cycles of SO in this model. What makes Figure 4A3 and B3 visibly distinct is the pattern of events in the top region (high cell indexes). This pattern was very consistent in the closed-loop network (Fig. 4A3), where UDt (blue dots) typically followed a ripple in the region receiving most of the CA1 input. This structure disappeared in the open-loop network (Fig. 4B3), suggesting that hippocampal input to CX is able to synchronize the UDt events across neurons and across many cycles of SO. In the following section, we will discuss the mechanism that may lead to increased synchrony of UDt in the closed loop network model.
Diverse effect of ripples on the cortical SO
To better understand the impact of a ripple event on the cortical slow-wave dynamics, we tested a simplified scenario. The thalamocortical network was simulated in isolation with an input that was identical to a single hippocampal ripple (the exact spiking of CA1 neurons was saved from simulation of the full TH-CX-HC model) and that ripple was applied at different times corresponding to different phases of SO. Thus, for each trial, the cortical network was targeted only at one specific phase of SO. We ran a set of such trials that uniformly spaced a full cycle of SO, and we repeated this for many cycles of SO to get the average response. Figure 5A shows a representative example of six trials when stimulation was applied at a different phase to the same cycle of SO (so as to allow for a direct comparison between trials). Cortical spiking before (after) ripple injection is labeled in black (blue). The red spikes interposed between blue and black spikes show CA1 spikes representing ripple event. Comprehensive animation of this experiment is provided in Supplementary Figure 8. As we performed this experiment for many cycles of SO, several consistently repeating phenomena could be observed. First, the ripple arriving at the very end of the Up-state was capable of increasing its duration (compare Fig. 5A5 vs A1). Second, the ripple arriving approximately in the middle of the Down-state phase was capable of shortening that Down-state and to cause DUt to start sooner (compare Fig. 5A3 vs A1). Finally, the ripple arriving in the middle of the Up-state phase was capable of improving synchronization of the UDt and mildly shortening Up-state (compare Fig. 5A6 vs A1). We confirmed these observations by quantification across many trials (Fig. 5B–D), including (1) an increase of Up-state duration (the peak in Fig. 5B), (2) a decrease of Down-state duration (the dip in Fig. 5C), and (3) a decrease in the standard deviation for UDt times across neurons in the region receiving the ripple input (the dip in Fig. 5D).
The dip in the midst of a Down-state (Fig. 5C) suggests that ripples arriving during the middle or later phases of a Down-state (note that Down-state duration curve is skewed to the right) can increase the probability of a network transition to an Up-state. This effect was not directly visible in the full closed-loop network analysis (Fig. 4), likely because a sharp increase in the ripple probability during Up-states tends to hide the relatively small number of ripples that occurred during Down-states. In other words, since most of the ripples occurred during an Up-state, statistically a single ripple was much more likely to be followed by a Down-state than an Up-state; note however a small peak in DUt probability ˜200 ms after the ripple in Figure 3F.
The dip in the midst of Up-state and the peak around UDt in Figure 5D correspond to the dip/peak in Figure 5B, suggesting that ripples occurring during an Up-state generally promote a synchronous transition to the Down-state except when precisely targeted at the very end of a Down-state when it can extend its duration (see animations in Supplementary Fig. 8). The increase in synchrony of UDt across cortical neurons during this simplified open-loop experiment suggests the possible cause of the network synchronization observed in the close-loop model. Indeed, the highlighted blue region in Figure 4A3 shows synchronized UDt in the area of the network receiving ripple input (˜#600-1000) following a ripple triggered in the late part of Up-state.
The last observation from the simplified model was further confirmed by running the following experiment. In complete closed-loop TH-CX-HC simulation, we varied the delay from CA1 to CX pyramidal cells, thus effectively changing the phase of SO at which cortex tends to receive a ripple. We observed that the pronounced (synchronized) structure of UDt in the top region of the network (blue dots in Fig. 4A3) appeared mainly for short synaptic delays between CA1 to cortical pyramidal cells (see Supplementary Fig. 10 second/third column, row 1) but disappeared for longer delays (Supplementary Fig. 10 second/third column, e.g., row 3). It is worth noting that UDt-triggered ripple-count histogram in the scenario of shorter delays reveals a peak of ripples ahead of UDt (see Fig. 4A2) suggesting ripple “as a cause of the Down-state.”However, at least in the case of our model, it was mainly the synchronization of transition times to the Down-state across population of cortical cells rather than transition to the Down-state itself (which would occur nevertheless just with higher dispersion) what created the sharper peak in the ripple distribution.
The observation that ripples arriving in the midst of a Down-state can shorten its duration (trigger DUt) from the simplified model (Fig. 5) was also found in the closed-loop model. When CA1->CX axonal delay became (unrealistically) long so that most of the ripples tended to arrive at the midst of the Down-state following the Up-state (which helped to initiate the sharp-wave events), we observed a highly synchronized region of DUt (Supplementary Figure 10, first column, e.g., fourth row, pronounced DUt blob after ripple) initiated by the ripple events occurring in the late phase of a Down-state.
Ripples influence Up-state initiation probability
We described above how ripple events targeting cortical neurons during specific phase of the SO are capable of influencing the structure and duration of Up- and Down-states. To better understand the cumulative effect of the ripples targeting a specific region of the cortical network, we considered two versions of synaptic wiring differing in the connectivity pattern between the hippocampus and cortex (Fig. 6A1, B1). This included the original (mirror) wiring (Fig. 6A1), in which a majority of the ripples targets the region of cortex distant from the cortical region projecting to CA3, which was contrasted with direct (non-mirror) mapping, in which the ripple-active CA1 region projects to roughly the same cortical region that targets CA3 (Fig. 6B1). Simulations of both models revealed that the region receiving most of the ripple input tended to become a global initiator of the cortical Up-states. It is interesting to note that effect of a single ripple was relatively weak. This was likely because the network slow wave activity has some refractoriness (Wei et al. 2016), so a single ripple event could not instantly trigger global slow-wave initiation. Several (3–5) cycles of SO with ripples targeting the same area were typically required for the target cortical region to become slow-wave initiator. Figure 6A2/B2 shows histogram profiles of the global Up-state initiation (two-sample Kolmogorov–Smirnov test confirmed that they were derived from different distributions, 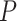 <0.001). The inset heatmap in Figure 6A2 shows that this bias in the initiation preference (yellow region) rapidly decreased as the connectivity strength of CA1->CX connections (X-axis) decreased. The mean spatial profile of the DUt is displayed as a heatmap in Figure 6A3/B3 where for each DUt “wave” a zero time lag indicates that it was the global ignition site (i.e., the first cortical cell that passed through the DUt transition in a given SO cycle). Since in the mirror mapping model Up-states are more likely to start in the top region of the cortex (and conversely in the direct-mapping model Up-states tend to start in the bottom region), this defines a preferred direction of the traveling DUt wave. This observation was further confirmed by measuring an average (over all SO cycles) gradient of the traveling wave for each local neighborhood of neurons that revealed an opposite traveling wave direction for the two network topologies (Fig. 6A3/B3 , histograms). This phenomenon was robust with respect to the phase of SO being hit by the ripple, see Supplementary Figure 10, fourth column, since varying the time delay of CA1->CX projections did not change the overall shape of DUt traveling wave.
<0.001). The inset heatmap in Figure 6A2 shows that this bias in the initiation preference (yellow region) rapidly decreased as the connectivity strength of CA1->CX connections (X-axis) decreased. The mean spatial profile of the DUt is displayed as a heatmap in Figure 6A3/B3 where for each DUt “wave” a zero time lag indicates that it was the global ignition site (i.e., the first cortical cell that passed through the DUt transition in a given SO cycle). Since in the mirror mapping model Up-states are more likely to start in the top region of the cortex (and conversely in the direct-mapping model Up-states tend to start in the bottom region), this defines a preferred direction of the traveling DUt wave. This observation was further confirmed by measuring an average (over all SO cycles) gradient of the traveling wave for each local neighborhood of neurons that revealed an opposite traveling wave direction for the two network topologies (Fig. 6A3/B3 , histograms). This phenomenon was robust with respect to the phase of SO being hit by the ripple, see Supplementary Figure 10, fourth column, since varying the time delay of CA1->CX projections did not change the overall shape of DUt traveling wave.
Preferential direction of the DUt activity propagation could have an impact on synaptic strength via spike-timing dependent plasticity (STDP). In our network model, each cortical pyramidal neuron was projecting symmetrically on both sides to its close (within a radius) neighbors. Thus, for each preferred direction of wave traveling, STDP would lead to synaptic connections decreasing strength in one direction and increasing in the opposite direction. We estimated synaptic changes by calculating STDP offline from spike traces recorded in the simulation. Figure 6A4/B4 shows changes to synaptic weights in close vicinity (X-axis) of each pyramidal neuron (Y-axis) for mirror (left) and direct (right) connectivity models. In the mirror model (Fig. 6A4), synapses from neurons with higher index to the neurons with lower index (which corresponds to the traveling wave direction) were generally increased in strength and opposite direction synapses decreased. Thus, comparing Figure 6A4 and B4 revealed that the two wiring scenarios tend to produce symmetrically opposite synaptic changes as consequence of the opposite preferential directions of the traveling waves.
Discussion
The hippocampo-cortical dialogue is critical for consolidation of memories (Preston and Eichenbaum 2013). Coordination between the prominent activities during NREM sleep — cortical SO and hippocampal ripples — was proposed to be the primary orchestrating mechanism in the memory consolidation process (Buzsáki 1996, Maingret et al. 2016). In this new study, we investigated the reciprocal influence of the slow waves and ripples in the large-scale computational model implementing SO in the thalamo-cortical network (Bazhenov et al. 2002, Wei et al. 2018) and SWRs in the CA3-CA1 hippocampal network (Malerba and Bazhenov 2019, Malerba et al. 2016). Our study revealed a complex pattern of interactions between the rhythms. Hippocampal ripples were able to bias cortical network to initiate Down- to Up-state transitions at specific cortical network locations as well as to synchronize Up- to Down-state transitions. Cortical input to hippocampus defined a pattern of CA3-CA1 activation and ultimately selected which SWRs are replayed. These predictions may help to understand mechanisms behind the role of hippocampal ripples in defining cortical spike sequences replay (Inostroza and Born 2013) and the influence of the cortical activation on the hippocampal SWRs (Helfrich et al. 2019, Rothschild et al. 2017) during sleep-related memory consolidation.
Many specific details of the functional connectivity between (m)PFC and hippocampus are not fully known. Anatomically, the existence of connections from hippocampus to PFC is well established — CA1/subiculum connections to PFC were independently described in mice (Parent et al. 2009), rhesus monkey (Averbeck and Seo 2008, Barbas and Blatt 1995, Goldman-Rakic et al. 1984), cats (Cavada et al. 1983, Irle and Markowitsch 1982), and in greater detail in rats (for review see Cenquizca and Swanson (2007)), where CA1 makes monosynaptic connections to (m)PFC to both excitatory and inhibitory cells (Gabbott et al. 2002) with latency in the order of 15–20 ms (Dégenètais et al. 2003, Ferino et al. 1987, Laroche et al. 1990, Tierney et al. 2004). In line with anatomical findings, recordings during sleep found that CA1-mPFC unit interactions were distributed widely but not uniformly across the cells and showed about 10 ms latency between CA1 and mPFC followers (Wierzynski et al. 2009). Furthermore, there is a converging evidence that hippocampo-cortical pathway is plastic and activated during memory consolidation (Binder et al. 2019, Laroche et al. 2000).
Projections from PFC (anterior cingulate, ACC) back to CA1 were found in mice (Rajasethupathy et al. 2015), but parallel recordings of ACC and CA1 units during slow-wave sleep suggest a rather multisynaptic pathway (Wang and Ikemoto 2016). A weak projection between (o)PFC and CA1 was also described in rhesus monkey (Carmichael and Price 1995), but its existence remains questionable (Cavada et al. 2000). Thus, communication from PFC to hippocampus is likely to be mediated through the main input gate—entorhinal cortex (Lavenex and Amaral 2000, Preston and Eichenbaum 2013).
In agreement with these empirical studies, in our model, the CA1 region projected widely into the “prefrontal” cortex network, but the connectivity was not uniform, instead CA1 was parceled into small regions, which targeted specific focal points in the cortical network (see diagram in Fig. 1B). In the opposite direction, a small patch of the cortical network projected directly to CA3. Thus, effectively during slow-wave sleep, cortical input to the hippocampus was activated only when a traveling wave of Down- to Up-state transition (Luczak et al. 2007, Massimini et al. 2004, Murphy et al. 2009, Nir et al. 2011) reached that cortical location.
We focused our study on sleep SO, defined as quasi-periodic transitions between Up- and Down-states with frequencies below 1 Hz (Steriade et al. (1998, 1993a, b). Recent work (Kim et al. 2019) suggested that cortical SO (defined by presence of an Up-state preceding the Down-state) is needed for consolidation of memories, while delta activity (isolated Down-states) weakens memory reactivation. This finding is consistent with our modeling, which suggests a casual link between an Up-state and SWRs. Further support for this view is found in (Todorova and Zugaro 2019) showing that rat prefrontal cells that fire at the bottom of the Down-state are preferentially tied to the SWRs. Models implementing both SO and delta activity are needed to explore specific role of delta in weakening memory consolidation.
Because of its limited size, the model used in this study simulated slow-wave dynamics in a small cortical patch. Thus, what we refer to in our model as a global initiation site can be considered initiation in a “local” site from the perspective of the whole brain dynamics. Indeed, in vivo many Down-states are isolated in distant areas and may propagate only locally (Mak-McCully et al. 2015). Without explicit modeling of dentate gyrus/rhinal cortices, we considered this simplified model as a functional approximation of the intricate mechanism of how cortical input enters and affects hippocampus in vivo (Hahn et al. 2007). Other important pathways omitted in the model included the nucleus reuniens (NR) known to play a role in coordinating slow-wave activity (Hauer et al. 2019), where NR targets both CA1 & mPFC (Hoover and Vertes 2012, Varela et al. 2014), and mPFC -> NR -> CA1 pathways (Vertes 2006, Vertes et al. 2007) possibly gating mPFC->hippocampal flow, which was shown to be important for memory consolidation (Ito et al. 2015).
While our cortical model shows oscillatory dynamics between Up- and Down-states, recent analysis (Levenstein et al. 2019) of rodent data suggested that NREM sleep may involve neocortical stable Up regime in which brief inactivating inputs bring the system to transitory Down-state; with increased power in delta band the system moves towards oscillatory regime. Up-states in our model had rather stereotyped duration 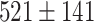 ms, which was shorter than typical Up-state duration in vivo in humans (
ms, which was shorter than typical Up-state duration in vivo in humans (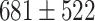 ms) and non-anesthetized rodents (˜1 sec) (Levenstein et al. 2019). Within the context of these results, our cortical model may represent the deep sleep or anesthesia states when network oscillatory dynamics is quasi-regular.
ms) and non-anesthetized rodents (˜1 sec) (Levenstein et al. 2019). Within the context of these results, our cortical model may represent the deep sleep or anesthesia states when network oscillatory dynamics is quasi-regular.
Hippocampal SWRs were hypothesized to be a mediator of the hippocampo-cortical dialogue during deep sleep (Buzsáki 1996) and indeed experimental studies revealed that cortical cells may fire in coordination with hippocampal ripples (Siapas and Wilson 1998). Unlike short SWR events (50–100 ms), cortical slow waves (0.2–1 Hz) are characterized by relatively smooth transitions between Up- and Down-states, so direct comparison of the timing of the SWR and SO events across the published studies is difficult. In many studies, SWRs preferably occur during an Up-state (Isomura et al. 2006, Mölle et al. 2006, Nir et al. 2011), but see also (Battaglia et al. 2004, Hahn et al. 2007). Another common reference points of the SO are transitions between Up- and Down-states; it was reported that SWRs commonly follow transition from Down- to Up-state in the cortical network (Battaglia et al. 2004, Isomura et al. 2006, Mölle et al. 2006, Sirota et al. 2003). There is also evidence that SWRs precede cortical Down-state (Maingret et al. 2016, Peyrache et al. 2011, 2009).
To study interaction between SO and SWRs, we used the biophysical TH-CX-HC model and observed realistic coupling behaviour between cortically generated SO and hippocampally generated ripples. In agreement with (Isomura et al. 2006), we observed clear biasing of the SWR probability by DUt. SWRs affected both UDt and DUt. Thus, UDt transition probability increased following the ripple and causal effect of ripples was confirmed by cutting CA1->CX projections in the open-loop experiment. While only a small fraction of SWRs occurred in the model during cortical Down-states, these events could still bias location of an UP state initiation site. Open-loop (CA1->CX) simulations, where SWR was artificially triggered at different pre-defined phases of SO, revealed that effect of SWR fundamentally depends on the phase of SO, namely we observed that (i) UDt events could be both delayed or advanced by SWR; (ii) synchronization of UDt events could be both improved or reduced; (iii) DUt events could be only advanced; and (iv) in general Up-state initiation could not be directly triggered by a single SWR event unless it occurred in very close proximity to DUt where local initiation could then be observed. That is in line with experimental findings (Isomura et al. 2006) where SWR event during the Down-state was sometimes capable to trigger spiking but the network returned back to the Down-state without transition to the Up-state. Similar observations led Buzsáki (2015) to suggest that in anesthesia conditions SWRs do not routinely bias the phase of SO. Our simulations suggest that while no immediate Up-state typically follows SWR events occurring during Down-state, the duration of the ongoing Down-state changes and thus the phase of SO may be affected as well.
The model prediction that the ripple, occurring in the mid-late phase of an Up-state, is capable of advancing and synchronizing UDt may explain data showing visible peak of ripple probability before Down-state in the UDt-triggered ripple count histogram (Maingret et al. 2016, Peyrache et al. 2011) and may shed light on the mechanisms behind apparently more synchronized UDt compared with DUt events in vivo (Chen et al. 2012, Volgushev et al. 2006). The dependence of the SWR effect on the SO phase reported here is also in line with the experimental work of (Batterink et al. 2016), showing the existence of optimal timing (with respect to SO phase) for the auditory input in targeted memory reactivation that improves memory consolidation in sleep. Jiang et al. (2019a) suggested that anterior HC SWRs are more suited, due to their density (0.2 Hz) and timing (Down-state/transition to Up-state), to influence the general context of neocortical network evolution, while posterior HC ripples (trains phase-locked to local spindles during Up-state) are more suited to detailed influence on neocortical firing. In agreement with this proposal both Figure 5C and Supplementary Figure 9B render Down-state as a sensitive phase for influencing global SO dynamics by the ripple input and possibly linking it to the setting up the general context via selecting Up-state initiation points (compare multiple local initiation sites of an Up-state in Figure 5A1 (no ripple) to more global initiation by earlier ripple input in Figure 5A3; also see animation in Supplementary Fig. 8). The effect of the ripple during Up-state is globally less visible and suggests that it would be suitable for more nuanced changes in the structure of cortical spatiotemporal firing.
Analysis of spindles, though an important component of NREM sleep, was omitted as it would substantially go beyond the scope of this study. Studies show ripple-spindle locking (Clemens et al. 2007, Mölle et al. 2006, Sirota et al. 2003, Wierzynski et al. 2009); a recent work reported phase-locking between SWR, SO and spindles (Latchoumane et al. 2017), and their nesting within hippocampus (Staresina et al. 2015). While it is clear that spindle density is an important marker for memory consolidation processes (Mednick et al. 2013), the exact mechanisms remain unknown. A recent proposal suggests SO as the leader of active memory consolidation while spindles are functionally deafferenting cortical circuitry from SWR input (Genzel et al. 2014) thus helping (selective) reorganization during Up-state following SWR reactivation-Down-state complex (Jiang et al. 2019b, Maingret et al. 2016). Jiang et al. (2019a,b) suggests that SWRs are typical for anterior hippocampus and interact with widespread cortical areas and waves, but preferentially fronto-central areas and Down-Up states. In contrast, spindle-ripples are typical for posterior hippocampus and are tightly coupled to spindles in inferior parietal cortex. These empirical studies suggest that the hippocampal SWRs and spindle-ripples represent distinct phenomena, especially with respect to their interactions with the cortex, and would need to be modeled separately.
The question about temporal coordination of DUt/UDt and SWRs, as explored in our new work, is directly related to the hypothesis of the cortical and hippocampal spike sequences replay during sleep, which is believed to be necessary for stabilizing recent memory traces (Nakashiba et al. 2009, Valero et al. 2017, van de Ven et al. 2016, Wilson and McNaughton 1994). Cortical replay occurs during Up-state (Johnson et al. 2010), peaking close to the transition points (Isomura et al. 2006, Peyrache et al. 2011). Hippocampal replay occurs in CA1 during the ripple events (Kudrimoti et al. 1999); it is known to be concurrent with cortical replay and both pre-cortical (PFC) (Peyrache et al. 2009) and post-cortical (visual cortex) (Ji and Wilson 2007) coupling was observed, leading to the discussion whether the CA1 sequences are driven by SO or SWR drives replay in PFC (Buzsáki 2015, Genzel et al. 2014). In (Rothschild et al. 2017) it was shown that there is a bilateral dialogue between the auditory cortex (AC-CX) and CA1, where AC-CX pre-SWR firing predicted SWR content, which in turn predicted post-SWR AC-CX activity, thus suggesting a possible scenario in which ripples are first triggered by the cortex and intermediately influence the cortex back within a single oscillation cycle (Rothschild 2019). Existence of similar bilateral dialogue was recently suggested in humans (Helfrich et al. 2019), the loop started by precisely coupled SO-spindle complex, in turn triggering a ripple event, subsequently followed by increased information flow back to PFC and delayed enough to skip the triggering spindle event.
In this study, we did not attempt to model spike sequence replay. We observed, however, that repeated ripple events targeting a specific cortical region can reshape spatiotemporal patterns of Up-state initiation. This led to consistent change in how Up-state waves travel across the cortical network. SO firing patterns were found to be supportive for induction of long-term synaptic plastic changes (Chauvette et al. 2012), so we assessed how spike-time dependent plasticity (Bi and Poo 2001) during slow-waves would shape the synaptic connectivity on the cortical site. We found that the spatial location/distance to the cortical cells that are targets of the hippocampal ripples determined whether STDP would render the synapses weakened or strengthened, thus allowing the mechanisms that select the ripple content to influence plasticity on the cortical site. Different hippocampal assemblies representing distinct memory sequences participating in the ripple event(s) could project into various cortical targets leading to parallel reorganization (consolidation) at the different cortical sites. Observed reorganization by SWRs is consistent with experimental results of (Maingret et al. 2016) in which properly timed SWRs (with respect to cortical Down-state) are able to reorganize mPFC firing patterns, which would otherwise stay stable (Luczak et al. 2007).
Supplementary Material
Contributor Information
Pavel Sanda, Department of Medicine, University of California, San Diego, La Jolla, CA 92093, USA; Institute of Computer Science of the Czech Academy of Sciences, Prague 18207, Czech Republic.
Paola Malerba, Department of Medicine, University of California, San Diego, La Jolla, CA 92093, USA; Battelle Center for Mathematical Medicine, Abigail Wexner Research Institute at Nationwide Children’s Hospital, Columbus, OH 43215, USA; Department of Pediatrics and Biophysics Graduate Program, Ohio State University, Columbus, OH 43215, USA.
Xi Jiang, Neurosciences Graduate Program, University of California, San Diego, La Jolla 92093, USA; Canadian Centre for Behavioural Neuroscience, University of Lethbridge, Lethbridge, AB T1K4G9, Canada.
Giri P Krishnan, Department of Medicine, University of California, San Diego, La Jolla, CA 92093, USA.
Jorge Gonzalez-Martinez, Epilepsy Center, Cleveland Clinic, Cleveland, OH 44195, USA.
Eric Halgren, Neurosciences Graduate Program, University of California, San Diego, La Jolla 92093, USA; Department of Radiology, University of California, San Diego, La Jolla, CA 92093, USA.
Maxim Bazhenov, Department of Medicine, University of California, San Diego, La Jolla, CA 92093, USA; Neurosciences Graduate Program, University of California, San Diego, La Jolla 92093, USA.
Notes
Conflicts of Interest: None declared.
Funding
Office of Naval Research (Multidisciplinary University Research Initiatives: N00014-16-1-2829); Lifelong Learning Machines program from Defense Advanced Research Projects Agency/Microsystems Technology Office (HR0011-18-2-0021); and National Institute of Health (RF1MH117155).
References
- Averbeck BB, Seo M. 2008. The statistical neuroanatomy of frontal networks in the macaque. PLoS Comput Biol. 4:e1000050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbas H, Blatt GJ. 1995. Topographically specific hippocampal projections target functionally distinct prefrontal areas in the rhesus monkey. Hippocampus. 5:511–533. [DOI] [PubMed] [Google Scholar]
- Battaglia FP, Sutherland GR, McNaughton BL. 2004. Hippocampal sharp wave bursts coincide with neocortical “Up-state” transitions. Learn Memory. 11:697–704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batterink LJ, Creery JD, Paller KA. 2016. Phase of spontaneous slow oscillations during sleep influences memory-related processing of auditory cues. J Neurosci. 36:1401–1409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bazhenov M, Timofeev I, Steriade M, Sejnowski TJ. 2002. Model of thalamocortical slow-wave sleep oscillations and transitions to activated states. J Neurosci. 22:8691–8704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini Y, Hochberg Y. 1995. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J Royal Stat Soc Ser B (Methodological). 57:289–300. [Google Scholar]
- Bi GQ, Poo MM. 2001. Synaptic modification by correlated activity: Hebb’s postulate revisited. Annu Rev Neurosci. 24:139–166. [DOI] [PubMed] [Google Scholar]
- Binder S, Mölle M, Lippert M, Bruder R, Aksamaz S, Ohl F, Wiegert JS, Marshall L. 2019. Monosynaptic hippocampal–prefrontal projections contribute to spatial memory consolidation in mice. J Neurosci. 39:6978–6991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G. 1996. The hippocampo–neocortical dialogue. Cereb Cortex 6:81–92. [DOI] [PubMed] [Google Scholar]
- Buzsáki G. 2015. Hippocampal sharp wave-ripple: a cognitive biomarker for episodic memory and planning. Hippocampus. 25:1073–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmichael S, Price JL. 1995. Limbic connections of the orbital and medial prefrontal cortex in macaque monkeys. J Comp Neurol. 363:615–641. [DOI] [PubMed] [Google Scholar]
- Cavada C, Compañy T, Tejedor J, Cruz-Rizzolo RJ, Reinoso-Suárez F. 2000. The anatomical connections of the macaque monkey orbitofrontal cortex. A review. Cereb Cortex. 10:220–242. [DOI] [PubMed] [Google Scholar]
- Cavada C, Llamas A, Reinoso-Suárez F. 1983. Allocortical afferent connections of the prefrontal cortex of the cat. Brain Res. 260:117–120. [DOI] [PubMed] [Google Scholar]
- Cenquizca LA, Swanson LW. 2007. Spatial organization of direct hippocampal field CA1 axonal projections to the rest of the cerebral cortex. Brain Res Rev. 56:1–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chauvette S, Seigneur J, Timofeev I. 2012. Sleep oscillations in the thalamocortical system induce long-term neuronal plasticity. Neuron. 75:1105–1113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JY, Chauvette S, Skorheim S, Timofeev I, Bazhenov M. 2012. Interneuron-mediated inhibition synchronizes neuronal activity during slow oscillation. J Physiol. 590:3987–4010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clemens Z, Mölle M, Erőss L, Barsi P, Halász P, Born J. 2007. Temporal coupling of parahippocampal ripples, sleep spindles and slow oscillations in humans. Brain. 130:2868–2878. [DOI] [PubMed] [Google Scholar]
- Dégenètais E, Thierry AM, Glowinski J, Gioanni Y. 2003. Synaptic influence of hippocampus on pyramidal cells of the rat prefrontal cortex: an in vivo intracellular recording study. Cereb Cortex. 13:782–792. [DOI] [PubMed] [Google Scholar]
- Diekelmann S, Born J. 2010. The memory function of sleep. Nat Rev Neurosci. 11:114. [DOI] [PubMed] [Google Scholar]
- Dykstra AR, Chan AM, Quinn BT, Zepeda R, Keller CJ, Cormier J, Madsen JR, Eskandar EN, Cash SS. 2012. Individualized localization and cortical surface-based registration of intracranial electrodes. Neuroimage. 59:3563–3570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ego-Stengel V, Wilson MA. 2010. Disruption of ripple-associated hippocampal activity during rest impairs spatial learning in the rat. Hippocampus. 20:1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Euston DR, Tatsuno M, McNaughton BL. 2007. Fast-forward playback of recent memory sequences in prefrontal cortex during sleep. Science. 318:1147–1150. [DOI] [PubMed] [Google Scholar]
- Ferino F, Thierry A, Glowinski J. 1987. Anatomical and electrophysiological evidence for a direct projection from ammon’s horn to the medial prefrontal cortex in the rat. Exp Brain Res. 65:421–426. [DOI] [PubMed] [Google Scholar]
- Frankland PW, Bontempi B. 2005. The organization of recent and remote memories. Nat Rev Neurosci. 6:119–130. [DOI] [PubMed] [Google Scholar]
- Gabbott P, Headlam A, Busby S. 2002. Morphological evidence that CA1 hippocampal afferents monosynaptically innervate PV-containing neurons and NADPH-diaphorase reactive cells in the medial prefrontal cortex (areas 25/32) of the rat. Brain Res. 946:314–322. [DOI] [PubMed] [Google Scholar]
- Genzel L, Kroes MC, Dresler M, Battaglia FP. 2014. Light sleep versus slow wave sleep in memory consolidation: a question of global versus local processes? Trends Neurosci. 37:10–19. [DOI] [PubMed] [Google Scholar]
- Gervasoni D, Lin SC, Ribeiro S, Soares ES, Pantoja J, Nicolelis MA. 2004. Global forebrain dynamics predict rat behavioral states and their transitions. J Neurosci. 24:11137–11147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girardeau G, Benchenane K, Wiener SI, Buzsáki G, Zugaro MB. 2009. Selective suppression of hippocampal ripples impairs spatial memory. Nat Neurosci. 12:1222–1223. [DOI] [PubMed] [Google Scholar]
- Goldman-Rakic P, Selemon L, Schwartz M. 1984. Dual pathways connecting the dorsolateral prefrontal cortex with the hippocampal formation and parahippocampal cortex in the rhesus monkey. Neuroscience. 12:719–743. [DOI] [PubMed] [Google Scholar]
- González OC, Sokolov Y, Krishnan GP, Bazhenov M. 2020. Can sleep protect memories from catastrophic forgetting? Elife. 9:e51005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonzalez-Martinez J, Bulacio J, Alexopoulos A, Jehi L, Bingaman W, Najm I. 2013. Stereoelectroencephalography in the “difficult to localize” refractory focal epilepsy: early experience from a north American epilepsy center. Epilepsia. 54:323–330. [DOI] [PubMed] [Google Scholar]
- Hahn TT, Sakmann B, Mehta MR. 2007. Differential responses of hippocampal subfields to cortical up–down states. Proc Natl Acad Sci. 104:5169–5174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hauer BE, Pagliardini S, Dickson CT. 2019. The reuniens nucleus of the thalamus has an essential role in coordinating slow-wave activity between neocortex and hippocampus. eNeuro. 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Helfrich RF, Lendner JD, Mander BA, Guillen H, Paff M, Mnatsakanyan L, Vadera S, Walker MP, Lin JJ, Knight RT. 2019. Bidirectional prefrontal–hippocampal dynamics organize information transfer during sleep in humans. Nat Commun. 10:1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoover WB, Vertes RP. 2012. Collateral projections from nucleus reuniens of thalamus to hippocampus and medial prefrontal cortex in the rat: a single and double retrograde fluorescent labeling study. Brain Struct Funct. 217:191–209. [DOI] [PubMed] [Google Scholar]
- Inostroza M, Born J. 2013. Sleep for preserving and transforming episodic memory. Annu Rev Neurosci. 36:79–102. [DOI] [PubMed] [Google Scholar]
- Irle E, Markowitsch H. 1982. Widespread cortical projections of the hippocampal formation in the cat. Neuroscience. 7:2637–2647. [DOI] [PubMed] [Google Scholar]
- Isomura Y, Sirota A, Özen S, Montgomery S, Mizuseki K, Henze DA, Buzsáki G. 2006. Integration and segregation of activity in entorhinal–hippocampal subregions by neocortical slow oscillations. Neuron. 52:871–882. [DOI] [PubMed] [Google Scholar]
- Ito HT, Zhang SJ, Witter MP, Moser EI, Moser MB. 2015. A prefrontal–thalamo–hippocampal circuit for goal-directed spatial navigation. Nature. 522:50. [DOI] [PubMed] [Google Scholar]
- Ji D, Wilson MA. 2007. Coordinated memory replay in the visual cortex and hippocampus during sleep. Nat Neurosci. 10:100. [DOI] [PubMed] [Google Scholar]
- Jiang X, Gonzalez-Martinez J, Cash SS, Chauvel P, Gale J, Halgren E. 2020. Improved identification and differentiation from epileptiform activity of human hippocampal sharp wave ripples during NREM sleep. Hippocampus. 30:610–622. [DOI] [PubMed] [Google Scholar]
- Jiang X, Gonzalez-Martinez J, Halgren E. 2019a. Coordination of human hippocampal sharpwave ripples during NREM sleep with cortical theta bursts, spindles, downstates, and upstates. J Neurosci. 39:8744–8761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang X, Gonzalez-Martinez J, Halgren E. 2019b. Posterior hippocampal spindle ripples co-occur with neocortical theta bursts and downstates-upstates, and phase-lock with parietal spindles during NREM sleep in humans. J Neurosci. 39:8949–8968. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang X, Shamie I, Doyle WK, Friedman D, Dugan P, Devinsky O, Eskandar E, Cash SS, Thesen T, Halgren E. 2017. Replay of large-scale spatio-temporal patterns from waking during subsequent NREM sleep in human cortex. Sci Rep. 7:1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson LA, Euston DR, Tatsuno M, McNaughton BL. 2010. Stored-trace reactivation in rat prefrontal cortex is correlated with Down-to-Up state fluctuation density. J Neurosci. 30:2650–2661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim J, Gulati T, Ganguly K. 2019. Competing roles of slow oscillations and delta waves in memory consolidation versus forgetting. Cell. 179:514–526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan GP, Chauvette S, Shamie I, Soltani S, Timofeev I, Cash SS, Halgren E, Bazhenov M. 2016. Cellular and neurochemical basis of sleep stages in the thalamocortical network. Elife. 5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kudrimoti HS, Barnes CA, McNaughton BL. 1999. Reactivation of hippocampal cell assemblies: effects of behavioral state, experience, and EEG dynamics. J Neurosci. 19:4090–4101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laroche S, Davis S, Jay TM. 2000. Plasticity at hippocampal to prefrontal cortex synapses: dual roles in working memory and consolidation. Hippocampus. 10:438–446. [DOI] [PubMed] [Google Scholar]
- Laroche S, Jay TM, Thierry AM. 1990. Long-term potentiation in the prefrontal cortex following stimulation of the hippocampal CA1/subicular region. Neurosci Lett. 114:184–190. [DOI] [PubMed] [Google Scholar]
- Latchoumane CFV, Ngo HVV, Born J, Shin HS. 2017. Thalamic spindles promote memory formation during sleep through triple phase-locking of cortical, thalamic, and hippocampal rhythms. Neuron. 95:424–435. [DOI] [PubMed] [Google Scholar]
- Lavenex P, Amaral DG. 2000. Hippocampal–neocortical interaction: a hierarchy of associativity. Hippocampus. 10:420–430. [DOI] [PubMed] [Google Scholar]
- Lemieux M, Chen JY, Lonjers P, Bazhenov M, Timofeev I. 2014. The impact of cortical deafferentation on the neocortical slow oscillation. J Neurosci. 34:5689–5703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levenstein D, Buzsáki G, Rinzel J. 2019. NREM sleep in the rodent neocortex and hippocampus reflects excitable dynamics. Nat Commun. 10:2478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luczak A, Barthó P, Marguet SL, Buzsáki G, Harris KD. 2007. Sequential structure of neocortical spontaneous activity in vivo. Proc Natl Acad Sci. 104:347–352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maingret N, Girardeau G, Todorova R, Goutierre M, Zugaro M. 2016. Hippocampo-cortical coupling mediates memory consolidation during sleep. Nat Neurosci. 19:959–964. [DOI] [PubMed] [Google Scholar]
- Mak-McCully RA, Deiss SR, Rosen BQ, Jung KY, Sejnowski TJ, Bastuji H, Rey M, Cash SS, Bazhenov M, Halgren E. 2014. Synchronization of isolated downstates (k-complexes) may be caused by cortically-induced disruption of thalamic spindling. PLoS Comput Biol. 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mak-McCully RA, Rosen BQ, Rolland M, Régis J, Bartolomei F, Rey M, Chauvel P, Cash SS, Halgren E. 2015. Distribution, amplitude, incidence, co-occurrence, and propagation of human k-complexes in focal transcortical recordings. eNeuro. 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malerba P, Bazhenov M. 2019. Circuit mechanisms of hippocampal reactivation during sleep. Neurobiol Learn Memory. 160:98–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malerba P, Jones MW, Bazhenov M. 2017. Defining the synaptic mechanisms that tune CA3-CA1 reactivation during sharp-wave ripples. bioRxiv. Page 164699.
- Malerba P, Krishnan GP, Fellous JM, Bazhenov M. 2016. Hippocampal CA1 ripples as inhibitory transients. PLoS Comput Biol. 12: e1004880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malerba P, Rulkov NF, Bazhenov M. 2019. Large time step discrete-time modeling of sharp wave activity in hippocampal area CA3. Commun Nonlinear Sci Numer Simul. 72:162–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malerba P, Tsimring K, Bazhenov M. 2018. Learning-induced sequence reactivation during sharp-wave ripples: a computational study. In Advances in the Mathematical Sciences: AWMRS 2017, vol. 15, p. 173–204. Springer. [Google Scholar]
- Massimini M, Huber R, Ferrarelli F, Hill S, Tononi G. 2004. The sleep slow oscillation as a traveling wave. J Neurosci. 24:6862–6870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McClelland JL, McNaughton BL, O’Reilly RC. 1995. Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychol Rev. 102:419. [DOI] [PubMed] [Google Scholar]
- Mednick SC, McDevitt EA, Walsh JK, Wamsley E, Paulus M, Kanady JC, Drummond SP. 2013. The critical role of sleep spindles in hippocampal-dependent memory: a pharmacology study. J Neurosci. 33:4494–4504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohajerani MH, McVea DA, Fingas M, Murphy TH. 2010. Mirrored bilateral slow-wave cortical activity within local circuits revealed by fast bihemispheric voltage-sensitive dye imaging in anesthetized and awake mice. J Neurosci. 30:3745–3751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mölle M, Yeshenko O, Marshall L, Sara SJ, Born J. 2006. Hippocampal sharp wave-ripples linked to slow oscillations in rat slow-wave sleep. J Neurophysiol. 96:62–70. [DOI] [PubMed] [Google Scholar]
- Murphy M, Riedner BA, Huber R, Massimini M, Ferrarelli F, Tononi G. 2009. Source modeling sleep slow waves. Proc Natl Acad Sci. 106:1608–1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadel L, Winocur G, Ryan L, Moscovitch M. 2007. Systems consolidation and hippocampus: two views. Debate Neurosci. 1:55–66. [Google Scholar]
- Nakashiba T, Buhl DL, McHugh TJ, Tonegawa S. 2009. Hippocampal CA3 output is crucial for ripple-associated reactivation and consolidation of memory. Neuron. 62:781–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nir Y, Staba RJ, Andrillon T, Vyazovskiy VV, Cirelli C, Fried I, Tononi G. 2011. Regional slow waves and spindles in human sleep. Neuron. 70:153–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parent MA, Wang L, Su J, Netoff T, Yuan LL. 2009. Identification of the hippocampal input to medial prefrontal cortex in vitro. Cereb Cortex. 20:393–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyrache A, Battaglia FP, Destexhe A. 2011. Inhibition recruitment in prefrontal cortex during sleep spindles and gating of hippocampal inputs. Proc Natl Acad Sci. 108:17207–17212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peyrache A, Khamassi M, Benchenane K, Wiener SI, Battaglia FP. 2009. Replay of rule-learning related neural patterns in the prefrontal cortex during sleep. Nat Neurosci. 12:919. [DOI] [PubMed] [Google Scholar]
- Preston AR, Eichenbaum H. 2013. Interplay of hippocampus and prefrontal cortex in memory. Curr Biol. 23:R764–R773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajasethupathy P, Sankaran S, Marshel JH, Kim CK, Ferenczi E, Lee SY, Berndt A, Ramakrishnan C, Jaffe A, Lo M, et al. 2015. Projections from neocortex mediate top-down control of memory retrieval. Nature. 526:653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranganath C, Ritchey M. 2012. Two cortical systems for memory-guided behaviour. Nat Rev Neurosci. 13:713. [DOI] [PubMed] [Google Scholar]
- Redman S. 1990. Quantal analysis of synaptic potentials in neurons of the central nervous system. Physiol Rev. 70:165–198. [DOI] [PubMed] [Google Scholar]
- Rothschild G. 2019. The transformation of multi-sensory experiences into memories during sleep. Neurobiol Learn Memory. 160:58–66. [DOI] [PubMed] [Google Scholar]
- Rothschild G, Eban E, Frank LM. 2017. A cortical–hippocampal–cortical loop of information processing during memory consolidation. Nat Neurosci. 20:251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salin PA, Prince DA. 1996. Spontaneous Gabaa receptor-mediated inhibitory currents in adult rat somatosensory cortex. J Neurophysiol. 75:1573–1588. [DOI] [PubMed] [Google Scholar]
- Sanchez-Vives MV, McCormick DA. 2000. Cellular and network mechanisms of rhythmic recurrent activity in neocortex. Nat Neurosci. 3:1027. [DOI] [PubMed] [Google Scholar]
- Sheroziya M, Timofeev I. 2014. Global intracellular slow-wave dynamics of the thalamocortical system. J Neurosci. 34:8875–8893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siapas AG, Wilson MA. 1998. Coordinated interactions between hippocampal ripples and cortical spindles during slow-wave sleep. Neuron. 21:1123–1128. [DOI] [PubMed] [Google Scholar]
- Sirota A, Csicsvari J, Buhl D, Buzsáki G. 2003. Communication between neocortex and hippocampus during sleep in rodents. Proc Natl Acad Sci. 100:2065–2069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sivagnanam S, Majumdar A, Yoshimoto K, Astakhov V, Bandrowski A, Martone M, Carnevale NT. 2013. Introducing the neuroscience gateway. CEUR Workshop Proceedings, CEUR-WS.org, vol. 993 of IWSG. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Squire LR, Alvarez P. 1995. Retrograde amnesia and memory consolidation: a neurobiological perspective. Curr Opin Neurobiol. 5:169–177. [DOI] [PubMed] [Google Scholar]
- Staresina BP, Bergmann TO, Bonnefond M, Van Der Meij R, Jensen O, Deuker L, Elger CE, Axmacher N, Fell J. 2015. Hierarchical nesting of slow oscillations, spindles and ripples in the human hippocampus during sleep. Nat Neurosci. 18:1679–1686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Amzica F, et al. 1998. Coalescence of sleep rhythms and their chronology in corticothalamic networks. Sleep Res Online. 1:1–10. [PubMed] [Google Scholar]
- Steriade M, Nuñez A, Amzica F. 1993a. Intracellular analysis of relations between the slow (1 hz) neocortical oscillation and other sleep rhythms of the electroencephalogram. J Neurosci. 13:3266–3283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steriade M, Nunez A, Amzica F. 1993b. A novel slow (1 hz) oscillation of neocortical neurons in vivo: depolarizing and hyperpolarizing components. J Neurosci. 13:3252–3265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teyler TJ, DiScenna P. 1986. The hippocampal memory indexing theory. Behav Neurosci. 100:147. [DOI] [PubMed] [Google Scholar]
- Thierry AM, Gioanni Y, Dégénétais E, Glowinski J. 2000. Hippocampo-prefrontal cortex pathway: anatomical and electrophysiological characteristics. Hippocampus. 10:411–419. [DOI] [PubMed] [Google Scholar]
- Tierney PL, Dégenetais E, Thierry AM, Glowinski J, Gioanni Y. 2004. Influence of the hippocampus on interneurons of the rat prefrontal cortex. Eur J Neurosci. 20:514–524. [DOI] [PubMed] [Google Scholar]
- Timofeev I, Grenier F, Bazhenov M, Sejnowski T, Steriade M. 2000. Origin of slow cortical oscillations in deafferented cortical slabs. Cereb Cortex. 10:1185–1199. [DOI] [PubMed] [Google Scholar]
- Todorova R, Zugaro M. 2019. Isolated cortical computations during delta waves support memory consolidation. Science. 366:377–381. [DOI] [PubMed] [Google Scholar]
- Valero M, Averkin RG, Fernandez-Lamo I, Aguilar J, Lopez-Pigozzi D, Brotons-Mas JR, Cid E, Tamas G, de la Prida LM. 2017. Mechanisms for selective single-cell reactivation during offline sharp-wave ripples and their distortion by fast ripples. Neuron. 94:1234–1247. [DOI] [PubMed] [Google Scholar]
- van de Ven GM, Trouche S, McNamara CG, Allen K, Dupret D. 2016. Hippocampal offline reactivation consolidates recently formed cell assembly patterns during sharp wave-ripples. Neuron. 92:968–974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varela C, Kumar S, Yang J, Wilson M. 2014. Anatomical substrates for direct interactions between hippocampus, medial prefrontal cortex, and the thalamic nucleus reuniens. Brain Struct Funct. 219:911–929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vertes RP. 2006. Interactions among the medial prefrontal cortex, hippocampus and midline thalamus in emotional and cognitive processing in the rat. Neuroscience. 142:1–20. [DOI] [PubMed] [Google Scholar]
- Vertes RP, Hoover WB, Szigeti-Buck K, Leranth C. 2007. Nucleus reuniens of the midline thalamus: link between the medial prefrontal cortex and the hippocampus. Brain Res Bull. 71:601–609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volgushev M, Chauvette S, Mukovski M, Timofeev I. 2006. Precise long-range synchronization of activity and silence in neocortical neurons during slow-wave sleep. J Neurosci. 26:5665–5672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang DV, Ikemoto S. 2016. Coordinated interaction between hippocampal sharp-wave ripples and anterior cingulate unit activity. J Neurosci. 36:10663–10672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang DV, Yau HJ, Broker CJ, Tsou JH, Bonci A, Ikemoto S. 2015. Mesopontine median raphe regulates hippocampal ripple oscillation and memory consolidation. Nat Neurosci. 18:728–735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Y, Krishnan GP, Bazhenov M. 2016. Synaptic mechanisms of memory consolidation during sleep slow oscillations. J Neurosci. 36:4231–4247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Y, Krishnan GP, Komarov M, Bazhenov M. 2018. Differential roles of sleep spindles and sleep slow oscillations in memory consolidation. PLoS Comput Biol. 14: e1006322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei Y, Krishnan GP, Marshall L, Martinetz T, Bazhenov M. 2020. Stimulation augments spike sequence replay and memory consolidation during slow-wave sleep. J Neurosci. 40:811–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wierzynski CM, Lubenov EV, Gu M, Siapas AG. 2009. State-dependent spike-timing relationships between hippocampal and prefrontal circuits during sleep. Neuron. 61:587–596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson MA, McNaughton BL. 1994. Reactivation of hippocampal ensemble memories during sleep. Science. 265:676–679. [DOI] [PubMed] [Google Scholar]
- Winocur G, Moscovitch M, Bontempi B. 2010. Memory formation and long-term retention in humans and animals: convergence towards a transformation account of hippocampal–neocortical interactions. Neuropsychologia. 48:2339–2356. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


