Abstract
The role of quantum-mechanical coherences in the elementary photophysics of functional optoelectronic molecular materials is currently under active study. Designing and controlling stable coherences arising from concerted vibronic dynamics in organic chromophores is the key for numerous applications. Here, we present fundamental insight into the energy transfer properties of a rigid synthetic heterodimer that has been experimentally engineered to study coherences. Quantum non-adiabatic excited state simulations are used to compute X-ray Raman signals, which are able to sensitively monitor the coherence evolution. Our results verify their vibronic nature, that survives multiple conical intersection passages for several hundred femtoseconds at room temperature. Despite the contributions of highly heterogeneous evolution pathways, the coherences are unambiguously visualized by the experimentally accessible X-ray signals. They offer direct information on the dynamics of electronic and structural degrees of freedom, paving the way for detailed coherence measurements in functional organic materials.
Coherences during the non-adiabatic dynamics of a bichromophoric molecules are probed via stimulated X-ray Raman signals. They survive for several hundred femtoseconds, despite highly heterogeneous contributions across the molecular sampling space.
Introduction
Organic electronic materials are currently drawing a broad interest due to the morphological organization and crystallinity1–3 of molecular chromophores that can be synthetically engineered to tune their electronic properties. For example, in the area of organic solar cells, significant improvements in power conversion efficiencies have been recently achieved by using materials with fused aromatic units4 that create delocalized electronic states with subsequent localization and charge separation in the course of their photoinduced excited state dynamics. A notable feature of this complex process is a frequent appearance of concerted dynamics of coupled electronic and vibrational degrees of freedom. They give rise to persisting phase relations or coherences across a variety of systems, including conjugated organics,5,6 carbon nanotubes and graphenes,7–9 organo–metallic complexes,10,11 semiconductor nanostructures12,13 and biological photosynthetic light harvesters,14–18 to name a few. The coherence during photoexcited dynamics in these materials arises as a result of strong vibronic (i.e. electron-vibrational) couplings that overcome the effects of temperature-dependent static (structural defects) and dynamic (phonon bath coupling) disorder.19,20 For large molecules embedded in protein complexes, there is a vast source of possible decoherence processes arising from the many nuclear degrees of freedom or impacts of the densely arranged protein environment. Nevertheless, light-harvesting complexes have been found to exhibit picosecond coherence times21,22 that are robust to structural and vibronic modifications.23 The nature of these coherences, their mechanistic influence and necessity are under active research and debate.17,18,24
The ubiquitous phenomenon of coherence involves a fixed phase relation between different excited states, potentially enabling manipulation of photoexcited non-radiative pathways to achieve desired efficient transfer of energy and charges, or laser control of chemical dynamics and reactions. Attaining this goal requires fundamental insights into the coherence creation and destruction mechanisms, as a general property of relatively rigid and densely packed multichromophore molecular systems. Over the years, a number of sophisticated experimental techniques such as 2D electronic spectroscopy25,26 were developed to deliver detailed temporal signatures of coherent dynamics.27 The recent arrival of X-ray free electron laser beam sources offers unprecedented spatial and temporal scales probes of matter,28,29 being an ideal tool to monitor coherences. Design of suitable experimental schemes and interpretation of observed signals are nontrivial and would highly benefit from the guiding by atomistic modeling of the underlining electronic and structural dynamics. Such simulations, however, are a daunting task for conventional quantum chemistry since the dynamics typically occurs beyond the Born–Oppenheimer regime30,31 and involves the passages through conical intersection (CoIns), controlling pathways and yields of many photo-initiated processes.32–34 Moreover, conversion of dynamical trajectories into specific spectroscopic signals directly mimicking experiment is nontrivial as well.
In the present study, we employ non-adiabatic excited state molecular dynamics to track the energy transfer in the molecular heterodimer depicted in Fig. 1(a) upon optical excitation. This system is a representative prototype of coupled multichromophoric systems described by a Frenkel exciton model with sufficient static and dynamic disorder that compete with the interchromophore vibronic coupling, as reported in ref. 35. Two differently substituted fluorescing monomers—5,6-dichloro-2′,7′-dimethylfluorescein (monomer A) and 4,5,6,7-tetrachloro-2′,7′-dimethylfluorescein (monomer B)—are linked with a rigid piperazine unit. Our simulation protocol is based on direct quantum molecular simulations using the ab initio multiple cloning (AIMC) approach,36,37 that is a controllable approximation to non-adiabatic dynamics and naturally includes electronic decoherence. Our modeling results are then used to predict nonlinear X-ray signals that track its coherent behavior.
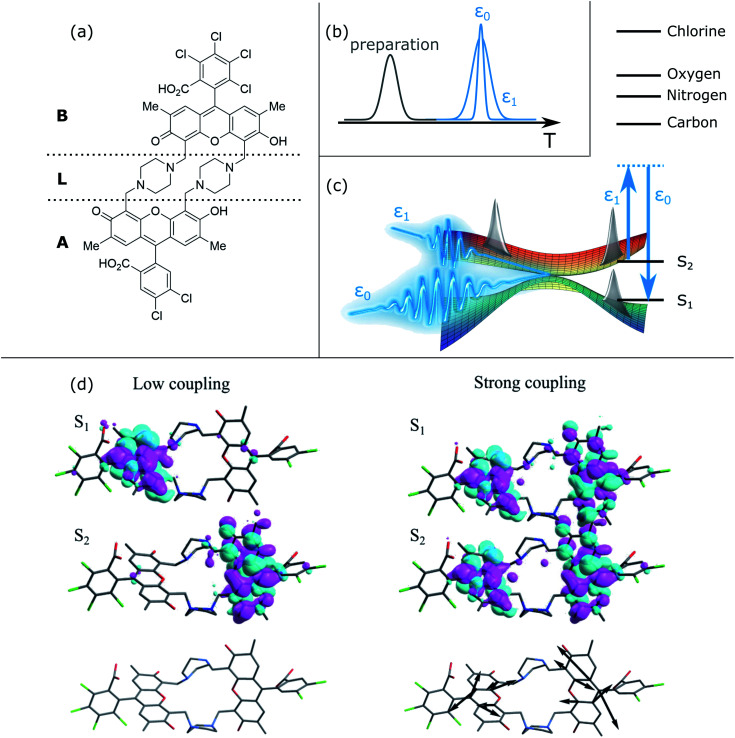
Fig. 1. X-ray stimulated Raman spectroscopy of a heterodimer to monitor coherences. (a) Chemical structure of the heterodimer. The two chromophore moieties are labeled A and B, with the linker L between them. (b) Pulse sequence of the TRUECARS measurement. At time delay T after preparation, the hybrid broadband (500 attosecond) and narrowband (3 fs) X-ray fields ε0 and ε1 probe the molecular dynamics via a stimulated Raman process. Both have Gaussian envelopes centered around T, and their relative phase needs to be controlled. (c) Sketch of the stimulated Raman process that probes coherences between the S2 and S1 electronic states, created due to nuclear wavepacket bifurcation in conical intersection regions. The level scheme shows the valence and core state energies. The probing process should be off-resonant to any core transitions. (d) Orbital representation of electronic transition densities in regions of low (left) and high (right) non-adiabatic coupling. In the former, the density is located on the different monomers A and B in the two electronic states. In the latter, both state densities overlap significantly, giving rise to vibronic coherences and thus the TRUECARS signal. The bottom panel shows the non-adiabatic coupling vector, which is very small (not visible) for low coupling. In the high-coupling region, the excess kinetic energy due to the conical intersection passage is funneled into this motion, being located on both aromatic units of the monomers.
Many linear and non-linear X-ray signals have been proposed to monitor the time-resolved evolution of molecular systems, each with their own properties and advantages.38 A unique example is TRUECARS, which in contrast to other techniques is not dominated by population contributions, but is solely induced by coherences. It has been originally demonstrated in ref. 39 on an ideal model system of two electronic states coupled to two vibrational degrees of freedom, a minimal requirement for CoIns.31 There, after a free evolution time of a nuclear wavepacket in an electronically excited state, a CoIn is reached. The wavepacket, initially located only in one of the two states that form the CoIn, then branches. There is now an overlap of nuclear wavepackets between two electronic states, i.e., a vibrational coherence (compare to Fig. 1(c)). This signature is significantly weaker than the population contributions, and thus hard to detect. TRUECARS employs a hybrid broadband/narrowband X-ray probing scheme39 that is sensitive only to these coherences. Both probe fields have a Gaussian pulse envelope and are centered at the same time delay, with their phases precisely controlled. While a single probe pulse would only be able to give a high temporal (broadband) or spectral (narrowband) resolution, the hybrid probing setup ensures both. This is required in order to resolve both the ultrafast timings of CoIns, as well as the energy range of few tens of eV that the vibronic coherence spans. TRUECARS is measured by counting the frequency-resolved time-integrated rate of change of photon numbers in the broadband field due to Stokes- and Antistokes-type Raman processes.39 Recently, TRUECARS was extended by an application to the ultrafast molecular process of photorelaxation in uracil.40 Using fully ab initio molecular quantities, and a Hamiltonian that has been proven to reproduce kinetic rates of the corresponding experiment,41 the signal was shown to be visible beyond the initial ideal model. Additionally, the Wigner representation of the signal was introduced,40 revealing fundamental physical properties about the non-adiabatic passage. In the meantime, several other studies have emphasized the possibilities of state of the art XUV and X-ray lasers, accessing the necessary temporal and spectral windows for tracing non-adiabatic events.34,42–46
All of the aforementioned studies focus on the fundamental physics that can be potentially accessed by various novel techniques. They are either introduced on model systems to highlight their advantages over other techniques in a certain aspect, or applied to small molecules, offering a clear interpretation to verify that they are feasible. The present study goes significantly beyond this in that we apply the TRUECARS technique to the large bichromophoric heterodimer shown in Fig. 1(a), and demonstrate how X-ray free-electron lasers28,46 can be exploited from a material design perspective by gaining insight into the coherence evolution in such systems. The interpretation of nonlinear optical signals used to probe coherences is not straightforward since especially for a molecule of this size, several pathways contribute and interfere.18 TRUECARS offers a background-free measurement in the respect that it is solely induced by coherences.
The most significant difference to the previous TRUECARS studies39,40 is that we include not two but all 360 nuclear degrees of freedom in the organic heterodimer shown in Fig. 1(a), and that we include many different initial conditions over a large equilibrated conformational sampling at room temperature. Coherent evolution in this heterogeneous sample, or how it can be probed, poses a significantly more complicated challenge. However, this is a major issue from a material design perspective, where coherent energy transport over larger temporal and spectral scales is crucial. While no direct practical usage of this specific heterodimer has been reported, fused aromatic units currently find application in the design of organic solar cells.4 Our most important result is that the TRUECARS measurement is able to resolve coherent behaviour at different parts of the conformational space, and even for the strongly heterogeneous dynamics in the ensemble of trajectories.
Results
The excited state molecular dynamics of the heterodimer shown in Fig. 1(a) was calculated using the AIMC approach as implemented into the Non-adiabatic EXcited state Molecular Dynamics (NEXMD) package.36,37 This has been successfully applied to the modeling of photoinduced energy flow in many other multichromophoric molecules.47,48 Details are given in the method section and ESI.† AIMC naturally includes decoherence by so called cloning events. If a trajectory reaches a point where the wavepacket evolution in both electronic states is very different, and thus must be described separately, a clone of this trajectory is generated. Each of the two clones is now dominated by one of the two respective electronic states, and they start to evolve differently. This leads to decoherence due to the decreasing overlap of the nuclear wavepackets in the two electronic surfaces. The absence of cloning events thus indicates a strong coherence, while their repeated occurrence is an evidence for decoherence due to different excited state topology.
The dimer in Fig. 1(a) consists of two chemically non-equivalent chromophores connected by non-conjugated linkers. We focus on the dynamics of two lowest electronically excited states, S1 and S2 (Fig. 1(c)). During the photoexcited dynamics, these states are either spatially localized on their parent monomers or become delocalized in the vicinity of CoIns (Fig. 1(c)) as will be analyzed in detail below. All of the AIMC trajectories start in S2 and follow the dynamical passage of the photoexcited wavepacket to S1 through a CoIn seam, following the protocol described in the Methods section.
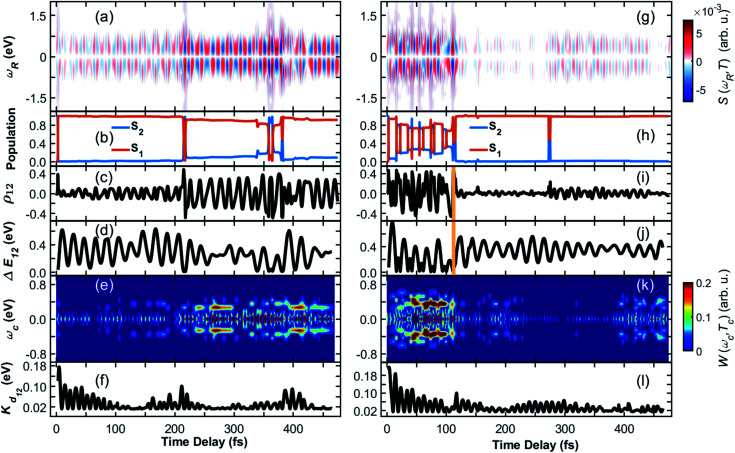
The TRUECARS signal (eqn (4)) was calculated for each trajectory. TRUECARS uses a hybrid broadband/narrowband probing scheme employing two X-ray pulses (Fig. 1(b)). The process is off-resonant to any molecular transition, and the signal is only finite when there is an overlap of nuclear wavepackets in two electronic states. Only the average signal over all trajectories is observable experimentally. However, it is useful to first examine individual trajectories to illustrate the different decoherence scenarios. Trajectory 1 as depicted in Fig. 2(a)–(f) is one example of the evolution of all relevant quantities. The TRUECARS signal (eqn (4)) is shown in Fig. 2(a). We observe an immediate population transfer to S1 (Fig. 2(b)), followed by a free evolution period with no significant coherence magnitude (Fig. 2(c)) until after 200 fs, where the molecule enters a CoIn region with strong non-adiabatic coupling. A vibronic coherence is created, as indicated by the growing coherence magnitude ρ12 in Fig. 2(c). This manifests in the emergence of a strong TRUECARS signal (Fig. 2(a) and eqn (4)). It exhibits characteristic oscillations between a gain and loss for positive (ωR > 0) as well as negative (ωR < 0) Raman shifts. When the signal is negative at ωR > 0 and positive at ωR < 0, energy flows from the molecule to the pulse, and is a Stokes-type process. The inverse situation corresponds to an anti-Stokes process. Once created, the TRUECARS signal does not decay anymore. This is in accordance with the coherence magnitude, surviving the passage through the CoIn. Another strong electron/nuclear coupling region is reached around 350 to 400 fs, involving population transfer between the electronic S1 and S2 states. The coherence survives this event as well. This trajectory has no cloning events and reflects the coherent evolution in both states as found in the experiment.35
Fig. 2. (Left column) Coherence in trajectory 1 of the heterodimer. (a) TRUECARS signal according to eqn (4). (b) Population in the S2 and S1 electronic states. (c) Coherence magnitude ρ12 between the S2 and S1 state according to eqn (3). (d) Energy splitting between the two participating electronic states. (e) Wigner spectrogram (eqn (5)), which is extracted from the TRUECARS signal in (a) by taking a temporal trace at ωR = 0.4 eV. It correctly maps the energy splitting shown in (d), and is directly accessible from the TRUECARS signal. (f) Kinetic energy along the direction of the coupling. Right column (g)–(l) same as (a)–(f) but for trajectory 2. The yellow vertical line indicates a cloning event.
Fig. 2(a)–(c) shows another strength of the TRUECARS signal compared to population-based techniques. If only population transfer was monitored, a signal would light up or change features at 200 fs and 350 fs, where there is strong population transfer happening. No information about the coherences would be available for the time in between. From a material design perspective, coherent energy transport over a longer temporal and spatial scale is essential, rather than short periods of coherent behavior at specific times. We show that the TRUECARS technique is sensitive to this behavior and can be used as a tool to monitor it, in addition to revealing other fundamental physical properties, as will be discussed below.
The electronic transition densities shown in Fig. 1(c) reveal the connection of the TRUECARS signal to the energy transfer. In low coupling regions, the electronic density of S1 and S2 is located at the different monomers A and B. In the region of strong coupling, the electron densities have overlapping contributions at both monomer sites. This gives rise to vibronic coherences and the TRUECARS signal. The excess energy resulting from the electron–nuclei coupling is funneled into the motion drawn with the black arrows in Fig. 1(c), entailing minor distortions at both monomer aromatic units.
The transient energy splittings between the states participating in the coherence is encoded in the temporal gain/loss oscillations in the TRUECARS signal (Fig. 2(a)).40 To extract the former from the signal, we present in Fig. 2(e) the Wigner spectrogram (eqn (5)) of a signal trace at constant ωR 0.4 eV. It gives the instantaneous frequency of the oscillation at each point in time, following the evolution of the vibronic states. Starting from ≃250 fs, which is the time where a vibronic coherence emerges, a strong feature is visible at ωcoh = 0.35 eV. This agrees with Fig. 2(d), where the energy splitting between the two electronic states in the trajectory is drawn, and which oscillates around 0.35 eV as well.
To identify the vibrational motions that modulate the magnitude of the coherence (and the TRUECARS signal), Fig. 2(f) shows the time evolution of the kinetic energy, Kd12, in the direction of the non-adiabatic coupling d12 (see eqn (S2)†). The projection of d12 on the basis of equilibrium normal modes calculated in S1 (see Fig. S1†) reveals that the main contributions to the vibronic couplings come through a bundle of high-frequency vibrations with frequencies of 1650–1880 cm−1 (i.e., with corresponding classical periods of 20.2–17.7 fs).47 Therefore, Kd12 experiences ∼20 fs oscillations, like the coherence ρ12. The amplitude of motion in this direction increases with ρ12 that is observed in the TRUECARS signal (compare panel (f) with panels (a) and (c) in Fig. 2). Thus, this TRUECARS signal monitors the electronic coherence built up during the evolution of the molecular systems in phase space regions close to the CoIn seam (i.e., relatively low values of ΔE12 at ∼220 and 350 fs). This corresponds to an increasing ρ12 and transient accumulations of excess of energy in the direction of the vibronic coupling. We find that the TRUECARS signal is sensitive to these changes. A further inspection of the structural distortions introduced by the transient increases in the amplitude of nuclear motion in the direction of d12 can be seen in the bottom right of Fig. 1(c), where a typical d12 in the region of strong coupling is depicted. It implies vibrations localized primarily at the fused aromatic units of anthracenes for both monomers.
From Fig. 2, we can draw the following conclusions about the time evolution: the molecule starts in the S2 state, following the absorption of a visible 450–500 nm photon (compare to the absorption spectra in ref. 35 and 47). Upon wavepacket bifurcation at the CoIn (compare Fig. 1(c)), the S2/S1 coherence lasts throughout the propagation time (500 fs). Both the absence of cloning events, and the repeated occurrence of population transfer due to strong non-adiabatic couplings, corroborate the concerted evolution of the nuclear wavepackets in both states and thus the strength and longevity of the coherence. The energy splitting between the two states fluctuates between peaks at 0.1 eV and 0.6 eV and transient accumulation of excess energy in the vibrations that mainly contribute to the vibration coupling can be observed. This information provided by the AIMC simulations is directly accessible experimentally by the TRUECARS signal and its Wigner spectrogram.
A different trajectory is depicted in Fig. 2(g)–(l). In contrast to trajectory 1, where the vibronic coherence emerges only late in the dynamics due to CoIn passage, the molecule starts in a region of strong coupling with initial coherence. The latter is not created directly by the excitation, i.e. by a laser pulse that covers both the S0 to S1 and the S0 to S2 transition. It rather emerges because this specific trajectory is excited at a geometry with strong coupling between S2 and S1, and the system immediately undergoes a non-adiabatic passage. The TRUECARS signal (Fig. 2(g)) is strong at the beginning, and there is constant population transfer (Fig. 2(h)) and high vibrational excitation in the direction of the non-adiabatic coupling (Fig. 2(l)) before 100 fs. At 110 fs, a cloning event occurs, as indicated by the vertical yellow line in Fig. 2(i) and (j). Immediately after this event, the coherence and the TRUECARS signal fade out, the molecular system is no longer excited in the direction of the vibronic coupling, and there is no additional population transfer. This is an example of a short-lived coherence, interrupted by a cloning event, and the subsequent individual evolution of the separate populations in S2 and S1. However, a cloning event does not necessarily imply vanishing coherence. This is demonstrated in Fig. S2† in the evolution of trajectory 3. Despite many cloning events (9 in total), the coherence is surprisingly persistent throughout the trajectory. The absence of cloning events does not necessarily mean that the coherence never vanishes, as demonstrated in trajectory 1. Analysis of all 476 trajectories shows a highly heterogeneous molecular dynamics and coherence evolution (see ESI for more examples of representative trajectories in Fig. S2–S4).† The previously discussed trajectories are exemplary cases that contribute to the total ensemble, with many of them exhibiting a strong instantaneous vibronic coherence, and others where it only emerges in the region of CoIns. We observe almost no trajectory where the coherence is absent over the entire 500 fs.
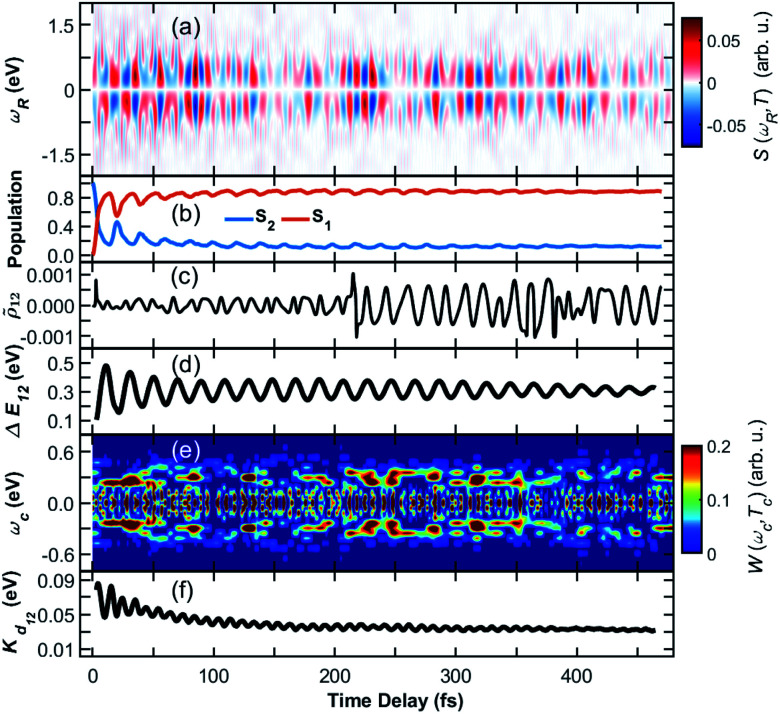
Only the average signal summed over all contributions is experimentally observable, while the individual trajectories represent possible scenarios. The TRUECARS signal in all 476 trajectories, and averaged over all of them with equal weights, is depicted in Fig. 3(a). Despite the highly heterogeneous contributions of the individual trajectories, the TRUECARS signal is visible over the entire simulation time, with stronger magnitudes at e.g. 200–250 fs, where the coherence magnitude spikes, and weaker ones at e.g. 150 fs and 500 fs. This average signal is a balanced mix of the discussed example trajectories, i.e., between excitation in a strong coupling region with immediate coherence, and contributions where there first is a free wavepacket evolution in a single electronic state, and the non-adiabatic passage occurs after few tens or hundred fs. We further observe that the transient excess of energy localized in the direction of the non-adiabatic coupling is gradually damped with time (Fig. 3(f)).
Fig. 3. Coherence in the ensemble of trajectories of the heterodimer. (a) Average TRUECARS signal. Individual trajectory contributions were computed according to eqn (4), with subsequent averaging with equal weights. (b) Combined population in the S2 and S1 electronic states in all trajectories. (c) Average coherence 12 between the S2 and S1 state. Individual trajectory contributions were calculated according to eqn (3). (d) Energy splitting between the two participating electronic states. (e) Wigner spectrogram according to eqn (5), which is extracted from the TRUECARS signal in (a) by taking a temporal trace at ωR = 0.3 eV. The energy splitting starts with contributions at ωc > 0.4 eV, from where it narrows and decays to ωc = 0.4 eV. This corresponds to the evolution of the energy splitting in (d). (f) Average kinetic energy along the direction of the non-adiabatic coupling.
The population is clearly distributed with a large fraction in S1 and a smaller one in the S2 state, initially starting in the S2, with stronger fluctuations at the beginning (compare Fig. 3(b)). The average coherence magnitude 12 (Fig. 3(c)) peaks once at the start of the propagation, followed by a weaker period until 200 fs. At this time, there is a significant increase, meaning that a large fraction of the trajectory ensemble enters a region of strong coupling here. The coherence magnitude stays large after this time, indicating a longer period of coherent evolution until 500 fs. As Fig. 3(e) shows, the Wigner spectrogram of the average signal can correctly map the evolution of the energy splitting between S2 and S1, with the main feature being located around 0.3 eV throughout the 500 fs. This evolution is in agreement with the averaged energy splitting shown in Fig. 3(d).
The different panels in Fig. 3 exhibit varying oscillation patterns, which are connected in the following way. The relative phase of the two electronic states evolves according to their energy difference. A splitting of 0.3 eV corresponds to an oscillation period of around 14 fs. Such oscillations are visible both in the coherence magnitude 12 (Fig. 3(c)), and the temporal evolution of the TRUECARS signal 12 (Fig. 3(a)). The energy splitting in 12 (Fig. 3(d)) evolves with a different frequency, that is determined by the vibrational motion of the molecule, entering and exiting higher and lower splitting regions on the potential energy hypersurface. Whenever the energy splitting is low, there is a higher chance for population transfer. Thus, the oscillations in Fig. 3(b) correspond to this evolution. The excess kinetic energy in Fig. 3(b) in direction of the non-adiabatic coupling oscillates with similar frequencies as the TRUECARS signal and the coherence magnitude. Indeed, the majority of this energy is contained in modes which match this frequency, being located on the fused aromatic units as shown in Fig. 1(c). The TRUECARS signal is directly sensitive to this feature.
To implement the TRUECARS measurement in its current form, phase-control of the two probe field is required. Using e.g. a 354 eV probe field,40i.e. a carrier field with an 11.7 attosecond oscillation period, would require zeptosecond-scale delay control to achieve phase control.49 Energy requirements entirely depend on the molecular properties, i.e. the energetic location of electronic states. Significantly lower energies can be used as long as the process is off-resonant. A phase-locked free-electron laser pulse pair has been achieved recently at 47.5 eV,50 which is an important advance in this direction. A possibility to circumvent the necessity of phase-control is to directly use currently available, stochastic X-ray pulses. There, the signal is measured in covariance with the probe field, considering the spectrally uncorrelated fluctuations in each repetition of the experiment.51 Efforts to formulate a stochastic version of the TRUECARS have recently been made.52
Other than phase-control, the TRUECARS signal primarily depends on three parameters: the intensity of the X-ray probe fields ε0 and ε1 in eqn (4), the amount of molecules in the X-ray focal volume, and the coherence magnitude ρKL, or, more specifically, the magnitude of the expectation value of the transition polarizability.39 While the maximum pulse intensity will be limited by X-ray photoionization, the signal strength can be maximized via a suitable choice of the molecule and by optimizing its density in the experiment. Near-resonant probe pulses can be employed to increase the transition probability, as observed recently for resonant X-ray Raman scattering in the NO molecule.53 A completely resonant version of TRUECARS has been proposed recently,54 where population contributions start to dominate the coherences. Element-specificity in resonant Raman schemes is a key feature that can be exploited to obtain local chemical information around a single X-ray chromophore, but retrieving coherence contributions is difficult due to the dominating population features. Tuning the probe field slightly off-resonance and finding a reasonable trade-off between the competing parameters can be a key factor in realizing a TRUECARS experiment. Off-resonant TRUECARS offers the background-free detection of coherences across the whole molecule, at the cost of a lower experimental cross section due to lower transition probabilities. Specifically in the equilibrated ensemble of the large heterodimer investigated here, energy levels of valence and core states will fluctuate significantly across the vast conformational space. If a certain near-resonant probe pulse frequency is chosen, there might already be some outliers in the ensemble where the transition is resonant, creating additional contributions to the signal that make it more ambiguous. Since the molecule contains several X-ray chromophores, all with different local environments, there are many possible near-resonant transitions that can be chosen. Finding the optimal trade-off between having a large transition polarizability (and thus experimental cross section) and no population contributions will be a highly interesting topic for future simulations and measurements.
Conclusions
We have simulated the excited state photophysics of the heterodimer shown in Fig. 1. Our modeling relies on the AIMC protocol that captures vibronic coherences evolving in non-Born–Oppenheimer dynamics of several electronic states. The coherence between excited states developing over many hundred femtoseconds, as reported in experiments,35 is reproduced. We discussed how current developments in X-ray sources make crucial progress toward realizing a TRUECARS experiment, and potential trade-offs that might be beneficial or necessary. The calculated TRUECARS signal probes the coherence between the S2 and S1 electronic states via a stimulated Raman process, as sketched in Fig. 1(c). Importantly, the vibronic coherence is visible throughout the entire propagation time and survives the ensemble averaging over all trajectories, with highly heterogeneous evolution and properties in different parts of the conformational space. Such dynamics and vibronic signatures are expected to be observed in future experiments at X-ray free-electron laser facilities. Our modeling illustrates the power and potential of X-ray sources, where coherences can be probed unambiguously and sensitively, without the background of population contributions. The signal is found to be sensitive to essential physical properties. The energy splitting between the states involved in the coherence could be extracted. Strong coupling regions, where the S2 and S1 electron densities overlap at both monomers, are captured by the signal.
The heterodimer investigated here was designed to mimic the coherent dynamics in more complicated multi-chromophoric systems. It is expected that the TRUECARS technique could be used to probe dynamics across a broad variety of biological and man-made materials in a similar fashion. This is enabled by the off-resonant probing process, which is universal. The signal does not require any specific core property, and directly probes a coherence between electronic states. Phase-controlled X-ray pulses, necessary for the TRUECARS signal, are currently being developed.50 A very recent study demonstrates that the signal, in a slightly reformulated formalism involving post-processing, can be measured using noisy free-electron laser pulses.52 Our modeling results are thus within reach of current experimental capabilities. Measuring the coherences in this way in different multichromophore molecular systems will increase our understanding of how the coherence is related to the electronic and vibrational energy relaxation fluxes involving multiple passages through the vicinity of conical intersections. The question whether coherences are required for efficient energy transport, and the mechanisms by which they are enabled and act, is an open and controversial debate.17,18,24 We show that the TRUECARS signal is sensitive to these features. X-ray probes backed by direct atomistic non-adiabatic molecular dynamics simulations would enable precise characterization of fundamental interactions in the material resolving collective dynamics of its constituent atoms and electrons.
Methods
Ab initio multiple cloning (AIMC) has been developed as an extension of the Multi-Configurational Ehrenfest (MCE). It uses the idea of adaptive basis sets from ab initio multiple spawning (AIMS),55 to which it is similar in that respect. Ensembles of individual Ehrenfest trajectories, i.e. configurations ψn(t), are used as a basis set to represent the full quantum wave function of electrons and nuclei Ψ(t):
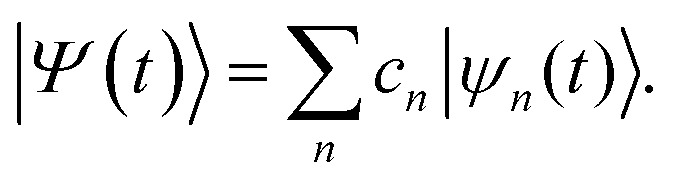 |
1 |
Each configuration is factorized into a nuclear part χn(t) and an electronic part given by a linear combination of adiabatic states ϕI(n):
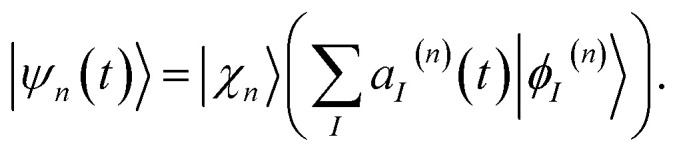 |
2 |
χ n(t) is given by coherent states,56,57 which in the coordinate representation are Gaussian functions centered in the Ehrenfest trajectories. Population transfer between excited states occurs in regions of phase space close to conical intersections, where the Born–Oppenheimer approximation breaks down and the motion of electron and nuclei occurs on the same timescale and is therefore strongly coupled. When reaching such regions, the original nuclear wave packet branches into multiple parts, and a coherence is created. The excess energy flow can follow different relaxation pathways, each dominated by a single electronic state. In such cases, the average Ehrenfest potential energy surface could no longer provide a faithful representation of its individual contributions. AIMC quantifies these cases and replaces the configuration, corresponding to the original Ehrenfest trajectory, by two new configurations, each having the same nuclear wave function but different electronic populations and, therefore, its own distinct mean-field. This splitting is called a cloning event. After that, the two new trajectories evolve independently. Such cloning events allow to naturally account for decoherence of vibronic wavepackets evolving on the sufficiently different potential energy surfaces. More details and technical implementations of the AIMC method can be found elsewhere.36,37,58 We extract from our simulations the coherence between electronic states:
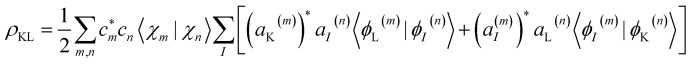 |
3 |
Both the electronic and the nuclear parts carry their own phases, that evolve according to the time-dependent Schrödinger equation for the respective subsystem. Both types of coherences are needed in order to see the overall coherent effect, and their mixing is accounted for in the molecular wave function when calculating the vibronic coherence magnitude ρKL.
The TRUECARS signal is given by
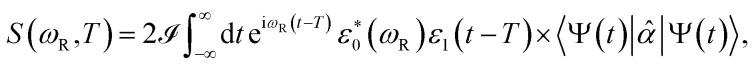 |
4 |
where ε0 is a broadband 500 attosecond and ε1 is a narrowband 3 fs pulse, ωR is the observed Raman frequency (using the narrowband as a reference), and  denotes the imaginary part. The relevant time-dependent material quantity is the expectation value of the polarizability operator
. Populations do not contribute to the signal, since
is zero on the diagonal, and only the transition polarizabilities between electronic states are finite. Following the original TRUECARS formulation,39 we set
to be constant over the nuclear space, reducing 〈Ψ(t)|
|Ψ(t)〉 to the overlap between the two involved electronic states. This is the coherence magnitude ρKL extracted from the AIMC calculations (eqn (3)). Since
is multiplicative, the shape of the TRUECARS signal may depend on the polarizabilities used, but qualitative statements of whether coherences are visible in the signal should still hold. This has been demonstrated in ref. 40, where the TRUECARS signal was calculated with fully ab initio polarizabilities. The signal was visible in all cases, and the physical information extracted was of equal quality in all cases.
denotes the imaginary part. The relevant time-dependent material quantity is the expectation value of the polarizability operator
. Populations do not contribute to the signal, since
is zero on the diagonal, and only the transition polarizabilities between electronic states are finite. Following the original TRUECARS formulation,39 we set
to be constant over the nuclear space, reducing 〈Ψ(t)|
|Ψ(t)〉 to the overlap between the two involved electronic states. This is the coherence magnitude ρKL extracted from the AIMC calculations (eqn (3)). Since
is multiplicative, the shape of the TRUECARS signal may depend on the polarizabilities used, but qualitative statements of whether coherences are visible in the signal should still hold. This has been demonstrated in ref. 40, where the TRUECARS signal was calculated with fully ab initio polarizabilities. The signal was visible in all cases, and the physical information extracted was of equal quality in all cases.
The Wigner spectrogram of the TRUECARS signal is given by
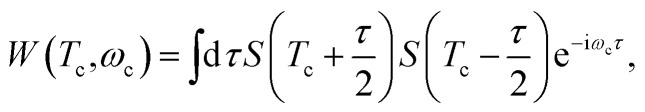 |
5 |
where S(T) is a temporal trace of the frequency-dispersed signal at ωR = 0.4 eV. S(T) oscillates with a frequency that corresponds to the energy splitting between the states participating in the vibronic coherence, and the Wigner spectrogram reveals the transient energy splitting along the trajectory.
In summary, the simulation protocol works as follows (more computational details are provided at ESI†): AIMC simulations of the heterodimer (Fig. 1(a)) have been performed at constant energy using a 0.05 fs time step. Initial conditions were obtained from a previous 1 ns ground state dynamics equilibrated at room temperature (T = 300 K) using the Langevin thermostat with a friction coefficient γ = 2 ps−1. A classical time step of 0.5 fs has been used for this ground state dynamics. A total of 476 initial positions and momenta were collected for excited state dynamics. The AIMC simulations started by a vertical excitation of the molecular system to the second excited state S2 for all trajectories. The populations for S2 and S1 states and coherences according to eqn (3) are tracked throughout the simulation. Cloning events and the evolution of each cloned trajectory are included. The TRUECARS signal is calculated using ρ12 for each trajectory (see Fig. 1(c) for a sketch and level scheme of the probing process). The average signal over all trajectories, corresponding to the experimentally observable scenario, is then calculated, along with the Wigner spectrograms.
Conflicts of interest
There are no conflicts to declare.
Supplementary Material
Acknowledgments
D. K. and S. M. acknowledge support from the Chemical Sciences, Geosciences, and Bio-Sciences Division, Office of Basic Energy Sciences (OBES), Office of Science, U.S. Department of Energy, through award no. DE-SC0019484. H. S. and S. T. acknowledge support from the U.S. DOE, Office of Science, Office of Basic Energy Sciences under contract no. KC0301031. This work was performed in part at the Center for Integrated Nanotechnology (CINT) at Los Alamos National Laboratory (LANL), a U.S. DOE and Office of Basic Energy Sciences user facility. This research used resources provided by the LANL Institutional Computing Program. D. K. gratefully acknowledges the support of the Alexander von Humboldt foundation through the Feodor Lynen program. S. F.-A. and V. M. F acknowledge support of CONICET, UNQ and ANPCyT (PICT-2018-02360).
Electronic supplementary information (ESI) available: Detailed technical information about the simulation technique and results for additional trajectories. See DOI: 10.1039/d0sc06328b
Notes and references
- Bonasera A. Giuliano G. Arrabito G. Pignataro B. Molecules. 2020;25:2200. doi: 10.3390/molecules25092200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin H. Yan C. Hu H. Ho J. K. W. Zhan X. Li G. So S. K. Mater. Sci. Eng., R. 2020;140:100542. [Google Scholar]
- Lee C. Lee S. Kim G.-U. Lee W. Kim B. J. Chem. Rev. 2019;119:8028–8086. doi: 10.1021/acs.chemrev.9b00044. [DOI] [PubMed] [Google Scholar]
- Coughlin J. E. Henson Z. B. Welch G. C. Bazan G. C. Acc. Chem. Res. 2014;47:257–270. doi: 10.1021/ar400136b. [DOI] [PubMed] [Google Scholar]
- Collini E. Scholes G. D. Science. 2009;323:369–373. doi: 10.1126/science.1164016. [DOI] [PubMed] [Google Scholar]
- Nelson T. R. Ondarse-Alvarez D. Oldani N. Rodriguez-Hernandez B. Alfonso-Hernandez L. Galindo J. F. Kleiman V. D. Fernandez-Alberti S. Roitberg A. E. Tretiak S. Nat. Commun. 2018;9:2316. doi: 10.1038/s41467-018-04694-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gambetta A. Manzoni C. Menna E. Meneghetti M. Cerullo G. Lanzani G. Tretiak S. Piryatinski A. Saxena A. Martin R. L. Bishop A. R. Nat. Phys. 2006;2:515–520. [Google Scholar]
- Gaufrès E. Izard N. Noury A. Le Roux X. Rasigade G. Beck A. Vivien L. ACS Nano. 2012;6:3813–3819. doi: 10.1021/nn204924n. [DOI] [PubMed] [Google Scholar]
- Jensen K. L. Shabaev A. Lambrakos S. G. Finkenstadt D. Petillo J. J. Alexander A. M. Smedley J. Moody N. A. Yamaguchi H. Liu F. Neukirch A. J. Tretiak S. J. Appl. Phys. 2020;128:015301. [Google Scholar]
- Atkins A. J. González L. J. Phys. Chem. Lett. 2017;8:3840–3845. doi: 10.1021/acs.jpclett.7b01479. [DOI] [PubMed] [Google Scholar]
- Henwood A. F. and Zysman-Colman E., in Luminescent Iridium Complexes Used in Light-Emitting Electrochemical Cells (LEECs), ed. N. Armaroli and H. J. Bolink, Springer International Publishing, Cham, 2017, pp. 25–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kilina S. Kilin D. Tretiak S. Chem. Rev. 2015;115:5929–5978. doi: 10.1021/acs.chemrev.5b00012. [DOI] [PubMed] [Google Scholar]
- Kamat P. V. ACS Energy Lett. 2017;2:1128–1129. [Google Scholar]
- Lee H. Cheng Y.-C. Fleming G. R. Science. 2007;316:1462–1465. doi: 10.1126/science.1142188. [DOI] [PubMed] [Google Scholar]
- Akimov A. V. Prezhdo O. V. J. Phys. Chem. Lett. 2013;4:3857–3864. doi: 10.1021/jz301878y. [DOI] [PubMed] [Google Scholar]
- Engel G. S. Calhoun T. R. Read E. L. Ahn T.-K. Mančal T. Cheng Y.-C. Blankenship R. E. Fleming G. R. Nature. 2007;446:782–786. doi: 10.1038/nature05678. [DOI] [PubMed] [Google Scholar]
- Scholes G. D. Fleming G. R. Chen L. X. Aspuru-Guzik A. Buchleitner A. Coker D. F. Engel G. S. van Grondelle R. Ishizaki A. Jonas D. M. Lundeen J. S. McCusker J. K. Mukamel S. Ogilvie J. P. Olaya-Castro A. Ratner M. A. Spano F. C. Whaley K. B. Zhu X. Nature. 2017;543:647–656. doi: 10.1038/nature21425. [DOI] [PubMed] [Google Scholar]
- Cao J. Cogdell R. J. Coker D. F. Duan H.-G. Hauer J. Kleinekathöfer U. Jansen T. L. C. Mančal T. Miller R. J. D. Ogilvie J. P. Prokhorenko V. I. Renger T. Tan H.-S. Tempelaar R. Thorwart M. Thyrhaug E. Westenhoff S. Zigmantas D. Sci. Adv. 2020;6:eaaz4888. doi: 10.1126/sciadv.aaz4888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cicoira F. and Santato C., Organic electronics: emerging concepts and technologies, John Wiley & Sons, 2013 [Google Scholar]
- Brédas J.-L. Sargent E. H. Scholes G. D. Nat. Mater. 2017;16:35–44. doi: 10.1038/nmat4767. [DOI] [PubMed] [Google Scholar]
- Collini E. Wong C. Y. Wilk K. E. Curmi P. M. G. Brumer P. Scholes G. D. Nature. 2010;463:644–647. doi: 10.1038/nature08811. [DOI] [PubMed] [Google Scholar]
- Panitchayangkoon G. Hayes D. Fransted K. A. Caram J. R. Harel E. Wen J. Blankenship R. E. Engel G. S. Proc. Natl. Acad. Sci. U. S. A. 2010;107:12766–12770. doi: 10.1073/pnas.1005484107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes D. Wen J. Panitchayangkoon G. Blankenship R. E. Engel G. S. Faraday Discuss. 2011;150:459. doi: 10.1039/c0fd00030b. [DOI] [PubMed] [Google Scholar]
- Duan H.-G. Prokhorenko V. I. Cogdell R. J. Ashraf K. Stevens A. L. Thorwart M. Miller R. J. D. Proc. Natl. Acad. Sci. U. S. A. 2017;114:8493–8498. doi: 10.1073/pnas.1702261114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukamel S. Annu. Rev. Phys. Chem. 2000;51:691–729. doi: 10.1146/annurev.physchem.51.1.691. [DOI] [PubMed] [Google Scholar]
- Jonas D. M. Annu. Rev. Phys. Chem. 2003;54:425–463. doi: 10.1146/annurev.physchem.54.011002.103907. [DOI] [PubMed] [Google Scholar]
- Brixner T. Stenger J. Vaswani H. M. Cho M. Blankenship R. E. Fleming G. R. Nature. 2005;434:625–628. doi: 10.1038/nature03429. [DOI] [PubMed] [Google Scholar]
- Pellegrini C. Marinelli A. Reiche S. Rev. Mod. Phys., T. 2016;88:015006. [Google Scholar]
- Bennett K. Zhang Y. Kowalewski M. Hua W. Mukamel S. Phys. Scr.,T. 2016;169:014002. [Google Scholar]
- Worth G. A. Cederbaum L. S. Annu. Rev. Phys. Chem. 2004;55:127–158. doi: 10.1146/annurev.physchem.55.091602.094335. [DOI] [PubMed] [Google Scholar]
- Domcke W. Yarkony D. R. Annu. Rev. Phys. Chem. 2012;63:325–352. doi: 10.1146/annurev-physchem-032210-103522. [DOI] [PubMed] [Google Scholar]
- Polli D. Altoè P. Weingart O. Spillane K. M. Manzoni C. Brida D. Tomasello G. Orlandi G. Kukura P. Mathies R. A. Garavelli M. Cerullo G. Nature. 2010;467:440–443. doi: 10.1038/nature09346. [DOI] [PubMed] [Google Scholar]
- Oliver T. A. A. Fleming G. R. J. Phys. Chem. B. 2015;119:11428–11441. doi: 10.1021/acs.jpcb.5b04893. [DOI] [PubMed] [Google Scholar]
- Timmers H. Zhu X. Li Z. Kobayashi Y. Sabbar M. Hollstein M. Reduzzi M. Martínez T. J. Neumark D. M. Leone S. R. Nat. Commun. 2019;10:3133. doi: 10.1038/s41467-019-10789-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayes D. Griffin G. B. Engel G. S. Science. 2013;340:1431–1434. doi: 10.1126/science.1233828. [DOI] [PubMed] [Google Scholar]
- Freixas V. M. Fernandez-Alberti S. Makhov D. V. Tretiak S. Shalashilin D. Phys. Chem. Chem. Phys. 2018;20:17762–17772. doi: 10.1039/c8cp02321b. [DOI] [PubMed] [Google Scholar]
- Makhov D. V. Glover W. J. Martinez T. J. Shalashilin D. V. J. Chem. Phys. 2014;141:054110. doi: 10.1063/1.4891530. [DOI] [PubMed] [Google Scholar]
- Kowalewski M. Fingerhut B. P. Dorfman K. E. Bennett K. Mukamel S. Chem. Rev. 2017;117:12165–12226. doi: 10.1021/acs.chemrev.7b00081. [DOI] [PubMed] [Google Scholar]
- Kowalewski M. Bennett K. Dorfman K. E. Mukamel S. Phys. Rev. Lett. 2015;115:193003. doi: 10.1103/PhysRevLett.115.193003. [DOI] [PubMed] [Google Scholar]
- Keefer D. Schnappinger T. de Vivie-Riedle R. Mukamel S. Proc. Natl. Acad. Sci. U. S. A. 2020;117:24069–24075. doi: 10.1073/pnas.2015988117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keefer D. Thallmair S. Matsika S. de Vivie-Riedle R. J. Am. Chem. Soc. 2017;139:5061–5066. doi: 10.1021/jacs.6b12033. [DOI] [PubMed] [Google Scholar]
- Neville S. P. Chergui M. Stolow A. Schuurman M. S. Phys. Rev. Lett. 2018;120:243001. doi: 10.1103/PhysRevLett.120.243001. [DOI] [PubMed] [Google Scholar]
- von Conta A. Tehlar A. Schletter A. Arasaki Y. Takatsuka K. Wörner H. J. Nat. Commun. 2018;9:3162. doi: 10.1038/s41467-018-05292-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kobayashi Y. Chang K. F. Zeng T. Neumark D. M. Leone S. R. Science. 2019;364:79–83. doi: 10.1126/science.aax0076. [DOI] [PubMed] [Google Scholar]
- Makhija V. Veyrinas K. Boguslavskiy A. E. Forbes R. Wilkinson I. Lausten R. Neville S. P. Pratt S. T. Schuurman M. S. Stolow A. J. Phys. B: At., Mol. Opt. Phys. 2020;53:114001. [Google Scholar]
- Young L. Ueda K. Gühr M. Bucksbaum P. H. Simon M. Mukamel S. Rohringer N. Prince K. C. Masciovecchio C. Meyer M. Rudenko A. Rolles D. Bostedt C. Fuchs M. Reis D. A. Santra R. Kapteyn H. Murnane M. Ibrahim H. Légaré F. Vrakking M. Isinger M. Kroon D. Gisselbrecht M. L'Huillier A. Wörner H. J. Leone S. R. J. Phys. B: At., Mol. Opt. Phys. 2018;51:032003. [Google Scholar]
- Freixas V. M. Tretiak S. Makhov D. V. Shalashilin D. V. Fernandez-Alberti S. J. Phys. Chem. B. 2020;124:3992–4001. doi: 10.1021/acs.jpcb.0c01685. [DOI] [PubMed] [Google Scholar]
- Malone W. Nebgen B. White A. Zhang Y. Song H. Bjorgaard J. A. Sifain A. E. Rodriguez-Hernandez B. Freixas V. M. Fernandez-Alberti S. Roitberg A. E. Nelson T. R. Tretiak S. J. Chem. Theory Comput. 2020;16(9):5771–5783. doi: 10.1021/acs.jctc.0c00248. [DOI] [PubMed] [Google Scholar]
- Cerullo G. Garavelli M. Proc. Natl. Acad. Sci. U. S. A. 2020;117:26553–26555. doi: 10.1073/pnas.2018651117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wituschek A. Bruder L. Allaria E. Bangert U. Binz M. Borghes R. Callegari C. Cerullo G. Cinquegrana P. Giannessi L. Danailov M. Demidovich A. Di Fraia M. Drabbels M. Feifel R. Laarmann T. Michiels R. Mirian N. S. Mudrich M. Nikolov I. O'Shea F. H. Penco G. Piseri P. Plekan O. Prince K. C. Przystawik A. Ribič P. R. Sansone G. Sigalotti P. Spampinati S. Spezzani C. Squibb R. J. Stranges S. Uhl D. Stienkemeier F. Nat. Commun. 2020;11:883. doi: 10.1038/s41467-020-14721-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tollerud J. O. Sparapassi G. Montanaro A. Asban S. Glerean F. Giusti F. Marciniak A. Kourousias G. Billè F. Cilento F. Mukamel S. Fausti D. Proc. Natl. Acad. Sci. U. S. A. 2019;116:5383–5386. doi: 10.1073/pnas.1821048116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavaletto S. M. Keefer D. Mukamel S. Phys. Rev. X. 2021;11:011029. [Google Scholar]
- O'Neal J. T. Champenois E. G. Oberli S. Obaid R. Al-Haddad A. Barnard J. Berrah N. Coffee R. Duris J. Galinis G. Garratt D. Glownia J. M. Haxton D. Ho P. Li S. Li X. MacArthur J. Marangos J. P. Natan A. Shivaram N. Slaughter D. S. Walter P. Wandel S. Young L. Bostedt C. Bucksbaum P. H. Picón A. Marinelli A. Cryan J. P. Phys. Rev. Lett. 2020;125:073203. doi: 10.1103/PhysRevLett.125.073203. [DOI] [PubMed] [Google Scholar]
- Cho D. Rouxel J. R. Mukamel S. J. Phys. Chem. Lett. 2020;11:4292–4297. doi: 10.1021/acs.jpclett.0c00949. [DOI] [PubMed] [Google Scholar]
- Ben-Nun M. Quenneville J. Martínez T. J. J. Phys. Chem. A. 2000;104:5161–5175. [Google Scholar]
- Shalashilin D. V. Child M. S. Chem. Phys. 2004;304:103–120. doi: 10.1063/1.1650299. [DOI] [PubMed] [Google Scholar]
- Symonds C. Kattirtzi J. A. Shalashilin D. V. J. Chem. Phys. 2018;148:184113. doi: 10.1063/1.5020567. [DOI] [PubMed] [Google Scholar]
- Makhov D. V. Saita K. Martinez T. J. Shalashilin D. V. Phys. Chem. Chem. Phys. 2015;17:3316–3325. doi: 10.1039/c4cp04571h. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.