Shotgun: A Bayesian seamless phase I-II design to accelerate the development of targeted therapies and immunotherapy

Abstract

Drug development of novel antitumor agents is conventionally divided by phase and cancer indication. With the advent of new molecularly targeted therapies and immunotherapies, this approach has become inefficient and dysfunctional. We propose a Bayesian seamless phase I-II “shotgun” design to evaluate the safety and antitumor efficacy of a new drug in multiple cancer indications simultaneously. “Shotgun” is used to describe the design feature that the trial begins with an all-comer dose finding phase to identify the maximum tolerated dose (MTD) or recommended phase II dose (RP2D), and then is seamlessly split to multiple indication-specific cohort expansions. Patients treated during dose finding are rolled over to the cohort expansion for more efficient evaluation of efficacy, while patients enrolled in cohort expansion contribute to the continuous learning of the safety and tolerability of the new drug. During cohort expansion, interim analyses are performed to discontinue ineffective or unsafe expansion cohorts early. To improve the efficiency of such interim analyses, we propose a clustered Bayesian hierarchical model (CBHM) to adaptively borrow information across indications. A simulation study shows that compared to conventional approaches and the standard Bayesian hierarchical model, the shotgun design has substantially higher probabilities to discover indications that are responsive to the treatment in question, and is associated with a reasonable false discovery rate. The shotgun provides a phase I-II trial design for accelerating drug development and to build a more robust foundation for subsequent phase III trials. The proposed CBHM methodology also provides an efficient design for basket trials.

1. Introduction

Drug development of novel antitumor agents is conventionally divided by phase and cancer indication. Phase I trials typically evaluate the safety of a new drug and determine the maximum tolerated dose (MTD) or recommended phase 2 dose (RP2D), while tumor-specific phase II trials evaluate the short-term efficacy (e.g., tumor response) of the drug at the MTD/RP2D. If the drug demonstrates sufficient safety and efficacy in that specific indication, a randomized phase III trial is initiated to evaluate the long-term efficacy (e.g., overall or progression free survival) of the drug. To expand the drug to another indication, a separate set of trials, typically phase II and III studies, are conducted.

In the era of precision medicine, including molecularly targeted therapies and immunotherapies, the conventional trial paradigm has been increasingly inefficient and dysfunctional. Targeted therapy treats cancer by modulating a specific biological pathway or molecular aberration. This may provide the scientific rationale to assess the new drug in tumor agnostic indications based on a common molecular aberration. For example, pembrolizumab, which targets programmed cell death protein 1 (PD-1), has been approved by the U.S. Food and Drug Administration (FDA) for the treatment of any unresectable or metastatic solid tumors with DNA mismatch repair deficiencies or a microsatellite instability-high state. Larotrectinib was recently approved by FDA for the treatment of patients with NTRK fusion cancers (Drilon et al., 2017).

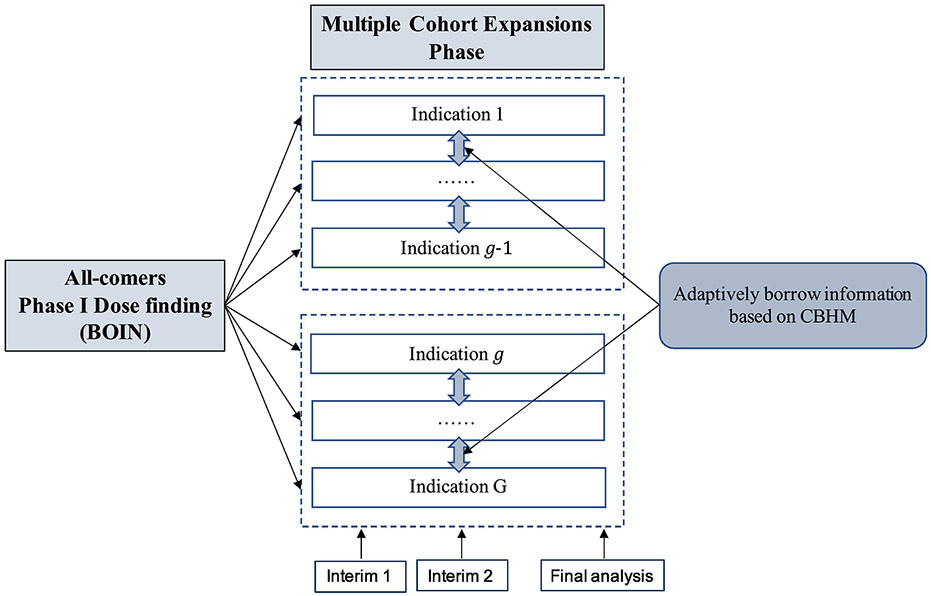
To accelerate the development of novel targeted therapies and immunotherapies, we propose a Bayesian seamless phase I-II design to efficiently evaluate a new drug in multiple indications. In the phase I portion of the design, the trial enrolls all comers and pool all the toxicity information to evaluate safety and tolerability, and establish the MTD/RP2D. In phase II portion of the trial, separate cohorts are formed to evaluate the efficacy of the drug in different indications. We refer to the proposed design as a “shotgun” design to highlight its feature of seamlessly expanding from a single “all-comers” cohort to multiple indication-specific cohorts (see Figure 1). Compared to conventional paradigms, the shotgun design is more efficient in that: (1) the efficacy data collected in the phase I portion of the trial are used for decision making in the phase II portion, and (2) in the phase II portion, information is adaptively borrowed across indications. This is achieved by first clustering the indications into responsive and non-responsive subgroups based on Bayesian posterior probability, and then using a Bayesian hierarchical model to borrow information within each subgroup to minimize the potential bias and inflated type I errors. The methodology developed for phase II portion can also be directly used to design basket trials.

Figure 1:

Schema of the shotgun design, starting with all-comers dose finding and then splitting into J indication-specific cohort expansions. At each interim, indications are adaptively clustered into subgroups (shown in the boxes with broken lines), and information are borrowed within each subgroup based on the clustered Bayesian hierarchical model (CBHM) method.

Our design is motivated by a phase I-II trial to evaluate the safety and clinical activity of a novel phosphatidylinositol 3-kinase (PI3K) inhibitor, combined with olaparib, in patients with advanced solid tumors. Due to confidentiality, a disguised version of the trial is described. Four doses of the PI3K inhibitor are to be investigated, and olaparib is administered at its monotherapy RP2D of 300 mg twice daily. The objective of the trial is to identify the combination maximum tolerated dose with a target toxicity rate of 30%, and to evaluate its safety and efficacy in five indications, including ovarian cancer, breast cancer, prostate cancer, cholangiocarcinoma, and other solid tumors. Toxicities will be assessed according to the National Cancer Institute-Common Terminology Criteria for Adverse Events (NCI-CTCAE) version 5.0. Tumor response will be assessed every 2 cycles (28 days per cycle) or 8 weeks (±7 days) by Response Evaluation Criteria in Solid Tumors (RECIST) version1.1 criteria. For all indications, the null response rate is 5%, and the alternative response rate is 30%. Because the drug may be effective only in some of the indications being tested, the design challenge is how to efficiently identify the indications that are responsive to the treatment.

Numerous phase I-II trial designs have been proposed to use toxicity and efficacy jointly to optimize the dose. Thall and Russell (1998) developed a phase I-II trial design that characterizes patient outcomes using a trinary ordinal variable to account for both toxicity and efficacy. Braun (2002) proposed the bivariate continual reassessment method, in which the MTD is based jointly on toxicity and disease progression. Thall and Cook (2004) described a Bayesian design based on tradeoffs between toxicity and efficacy probabilities. Yin et al. (2006) proposed a Bayesian phase I-II design based on the odds ratio of efficacy and toxicity. Yuan and Yin (2009) developed a phase I-II design for time-to-event endpoints. Jin et al. (2014) proposed a Bayesian design to accommodate late-onset efficacy and toxicity using data augmentation. Liu and Johnson (2016)developed a phase I-II design without assuming parametric dose-toxicity and dose-efficacy curves. Liu et al. (2018) proposed a Bayesian phase design for immunotherapy based on the utility of risk-benefit tradeoff. Comprehensive coverage of phase I-II designs is provided in the book written by Yuan et al. (2017). Most existing phase I-II designs focus on testing a drug in single indication at a time. In contrast, the shotgun design focuses on testing the drug in multiple indications.

The rest of this paper is organized as follows. In Section 2, we introduce the shotgun design, including its statistical model and adaptive decision rule. In Section 3, simulation studies are carried out to assess the performance of the proposed design. A brief discussion is presented in Section 4.

2. Methods

Consider a phase I-II trial with J prespecified doses, d₁ <⋯< d_J, under investigation. Let Y_T and Y_E denote the toxicity and efficacy indicators, respectively, with Y_T = 1 indicating toxicity, and Y_E = 1 indicating response. The objective of the trial is to assess whether the drug is safe and effective in each of G indications to warrant randomized phase III trials. The shotgun design consists of two seamless connected parts. Phase I takes an all-comer approach. All G indications are eligible for enrollment, and the toxicity data are pooled over indications to guide dose escalation and identify the MTD or RP2D. The rationale for this all-comers approach is that the toxicity profile of the drugs are likely to be similar across the indications being tested. This approach has been routinely used in phase I trials, but is not binding to the shotgun design. If different indications are expected to have different toxicity profiles, indication-specific dose finding (based on the data from that specific indication) may be employed to find indication-specific MTD or RP2D. Alternatively, we can take a hybrid approach: use the all-comers approach as a run-in to achieve fast dose escalation, and then switch to indication-specific dose finding once the dose escalation reaches a certain dose level (e.g., the middle dose level). In addition, when clinically appropriate, other indications that will be not investigated in phase II can also be enrolled during phase I to increase the accrual and speed up the trial.

2.1. Phase I dose escalation

The phase I dose escalation phase is carried out using the Bayesian optimal interval (BOIN) design because of its ease of implementation and competitive performance (Zhou et al., 2018). Other designs, such as the continual reassessment method (O’Quigley et al., 1990) can also be used. At the current dose level j, let ϕ_T denote the target toxicity rate, n_j denote the number of patients treated, and y_j denote the number of patients who experienced toxicity. The dose escalation is carried out as follows:

1. Treat the first cohort of patients at the lowest dose or prespecified starting dose.

2. Let ${\widehat{p}}_{{}_j}=y_{{}_j}∕n_{{}_j}$ denote the observed toxicity rate at the current dose, to assign a dose to the next cohort of patients:

   • if ${\widehat{p}}_{{}_j}\le {\lambda }_{{}_e}$, escalate the dose to level j+1,
   • if ${\widehat{p}}_{{}_j}>{\lambda }_{{}_d}$, de-escalate the dose to level j−1,
   • otherwise, stay at the current dose level j,
     where λ_e and λ_d are the optimal dose escalation and de-escalation boundaries that minimize the decision error of dose escalation and de-escalation. Table 1 shows the values of λ_e and λ_d for commonly used ϕ_T.

3. Repeat Step 2 until reaching the maximum sample size N₁. At that point, select the MTD as the dose whose isotonic estimate of toxicity probability is closest to ϕ_T, and then move forward to the phase II portion.

Table 1:

Optimal dose escalation boundary λ_e and de-escalation boundary λ_d of the BOIN design.

	Target toxicity rate ϕT
Boundaries	0.15	0.2	0.25	0.3	0.35	0.4
λe	0.118	0.157	0.197	0.236	0.276	0.316
λd	0.179	0.238	0.298	0.358	0.419	0.479

During the trial conduct, the BOIN design imposes a dose elimination (or overdose control) rule as follows: if Pr(p_j > ϕ_T∣n_j, y_j) > 0.95 and n_j ≥ 3, dose level j and higher are eliminated from the trial, and the trial is terminated if the lowest dose is eliminated, where Pr(p_j > ϕ_T∣n_j, y_j) is evaluated based on the Beta-Binomial model y_j∣p_j ~ Binomial(p_j) and p_j ~ Uniform(0,1). Of note, although the dose escalation is based only on toxicity data, efficacy data will be collected and used in phase II. In addition, depending on the testing agents, the RP2D is not necessarily the MTD, and may be selected based on the totality of clinical evidence, including pharmacokinetics, pharmacodynamics and early efficacy biomarker data, from the doses that are not higher than the MTD.

2.2. Phase II with multiple cohort expansions

2.2.1. Clustered Bayesian hierarchical model

After the RP2D/MTD is determined, indication-specific cohort expansions are initiated to assess the efficacy of the drug in each of the G indications. Suppose that at an interim time, n_g patients from indication g are enrolled. Among them, x_g patients responded to the treatment, and y_g patients experienced toxicity. The n_g patients include the patients who were treated at the RP2D/MTD in phase I, making the proposed design more efficient than the design with an independent phase I and phase II. Of note, the phase II part of the shotgun design can be viewed as a basket trial. Thus, the methodology introduced below is directly applicable to design basket trials, with performance comparable or better than existing basket trial designs as described later.

One well-known approach used to borrow information across indications is the Bayesian hierarchical model (BHM) proposed by Thall et al. (2003). One important assumption of BHM is an exchangeable treatment effect across indications. This assumption, however, is not always appropriate, and it is not uncommon that some indications are responsive to the treatment, while others are not. For example, BRAF-mutant melanoma and hairy-cell leukemia are associated with a high response rate to the BRAF inhibitor PLX4032 (vemurafenib), whereas BRAF-mutant colon cancer is not (Flaherty ey al., 2010; Tiacci et al., 2011; Prahallad et al., 2012). Trastuzumab is effective for treating human epidermal growth factor receptor 2 (HER2)-positive breast cancer, but shows little clinical benefit for HER2-positive recurrent endometrial cancer (Fleming et al., 2010) or HER2-positive non-small-cell lung cancer (Gatzemeier et al., 2004). In this case, as shown in our simulation study, using the BHM will lead to inflated type I errors. This issue is also noted by previous research (Freidlin and Korn, 2013; Chu and Yuan, 2018).

To address this issue, we propose a precision information-borrowing approach, called clustered BHM (CBHM). The basic idea is, based on the interim data, we first cluster the indications into responsive (sensitive) and non-responsive (insensitive) subgroups; and we then apply BHM to borrow information within each subgroup. We allow a subgroup to be empty to accommodate the homogeneous case that all indications are responsive or non-responsive. We here focus on the two subgroups based on the practical consideration that targeted therapy is often either effective (i.e., hit the target) or ineffective (i.e., miss the target), and the number of indications is typically small (2 – 6), and thus it is not practical to form more than two subgroups. Nevertheless, our method can be readily extended to more than two subgroups. The idea of clustering indications and then borrowing information was investigated by Chu and Yuan (2018), Hobbs and Landin (2018), Liu et al. (2017) and Chen and Lee (2020) for basket trials, which are based on sophistically joint modeling or Bayesian nonparametric methodology. As shown in the simulation provided in Section 3.4, our proposed CBHM yields comparable performance as some of these methods, but is more intuitive, simple to implement, and easy to explain to non-statisticians.

Let q_g denote the response rate in indication g, q_0,g denote null response rate that is deemed futile, and q_1,g denote the target response rate that is deemed promising. q_0,g and q_1,g can be different across indications. We propose the following Bayesian rule to cluster indications: an indication is allocated to the responsive cluster $\mathcal{R}$ if it satisfies

$$Pr(q_g>\frac{q_{0,g}+q_{1,g}}{2}\mid x_g,n_g)>\psi (\frac{n_g}{N_{g,2}}{)}^{\omega },$$ (1)

otherwise allocated to the non-responsive cluster $\overline{\mathcal{R}}$, where N_g,2 is the prespecified maximum sample size of indication g for phase II, and ψ and w are positive tuning parameters. We recommend default values ψ = 0.5 and ω = 2 or 3, which can be further calibrated to fit a specific trial requirement in operating characteristics. One important feature of this clustering rule is that its probability cutoff is adaptive and depends on the subgroup interim sample size n_g. At the early stage of the trial, where n_g is small, we prefer to use a more relaxed (i.e., smaller) cutoff to keep an indication in the responsive subgroup to avoid inadvertent stopping due to sparse data and to encourage collecting more data on the indication. When a trial proceeds, we should use a more strict (i.e., larger) cutoff to avoid incorrectly classify non-responsive indications to a responsive subgroup. Through simulation study, we find that this adaptive cutoff improves the performance. In the above Bayesian clustering rule, the posterior probability $Pr(q_{{}_g}>\frac{q_{{}_{0,g}}+q_{{}_{1,g}}}{2}\mid x_{{}_g},n_{{}_g})$ is evaluated based on the Beta-Binomial model,

$$\begin{gathered} x_g\mid q_g\sim Binomial(q_g), \\ {q}_g\sim Beta(a_1,b_1), \end{gathered}$$ (2)

where a₁ and b₁ are hyperparameters, typically set at a small value (e.g., a₁ = b₁ = 0.1) to obtain a vague prior. As a result, the posterior distribution of q_g is given by Beta(x_g + a₁, n_g − x_g + b₁). The proposed method is certainly not the only way to cluster the indications. Other clustering methods (e.g., K-means or hierarchical clustering methods) can also be entertained. However, because the number of indications is often small and the interim data are sparse, we found that using these alternative (often more complicated) methods often worsens, rather than improves performance.

After clustering, we apply the following BHM to subgroups $\mathcal{R}$ and $\overline{\mathcal{R}}$ independently.

$$\begin{gathered} x_g\mid q_g\sim Binomial(q_g), \\ {\theta }_g=\log (\frac{q_g}{1-q_g})-\log (\frac{q_{0,g}}{1-q_{0,g}}), \\ {\theta }_g\mid \theta ,{\sigma }^2\sim N(\theta ,{\sigma }^2), \\ \theta \sim N({\mu }_0,{\tau }_0^2),{\sigma }^2\sim IG(a_0,b_0), \end{gathered}$$ (3)

where IG(·) denotes inverse-gamma distribution, μ₀, ${\tau }_0^2$, a₀ and b₀ are hyperparameters. Typically, we set μ₀ = 0 and ${\tau }_0^2$ at a large value (e.g, ${\tau }_0^2={10}^6$), and a₀ and b₀ at a small value (e.g., a₀ = b₀ = 10⁻⁶), which is known to favor borrowing information (Chu and Yuan, 2018). In the BHM, we use $\log (\frac{q_{0,g}}{1-q_{0,g}})$ as the offset to account for the different baseline response rates for different indications. Depending on the application, $\log (\frac{q_{1,g}}{1-q_{1,g}})$ can also be used as the offset.

If subgroup $\mathcal{R}$ and $\overline{\mathcal{R}}$ only has one member, we replace the above BHM with the Beta-Binomial model (2). As indications within subgroup $\mathcal{R}$ and $\overline{\mathcal{R}}$ are relatively homogenous, the exchangeable assumption required by BHM is more likely to hold. As a result, CBHM yields better performance, as shown by simulation later. Because that the treatment effect θ_g in $\mathcal{R}$ should be better than that in $\overline{\mathcal{R}}$, one might consider imposing this order constraint when fitting the BHM for $\mathcal{R}$ and $\overline{\mathcal{R}}$. This, however, is not necessary and does not improve the estimation of θ_g (see simulation result Table A1 in Appendix). This is because the order on θ_g has been (implicitly) incorporated by the clustering procedure, that is, the indications showing high treatment effect (i.e., large θ_g) are clustered into the responsive cluster, whereas indications showing low treatment effect (i.e., low θ_g) are clustered into the non-responsive cluster. During phase II, we continue collecting the toxicity data to evaluate the safety of the drug in each indication using a Beta-Binomial model similar to (2).

2.2.2. Interim go/no-go rule

The design for phase II is described as follows. There are K_g prespecified interims for each indication, occurring when the sample size of the indication reaches n_g1, ⋯, n_gKg , with n_gKg ≡ N_g,2 . The shotgun design allows the total number of interims K_g and interim times varying from one indication to another. This is a particularly appealing feature, as the accrual rates for various indications are often different. Once an indication reaches its planned interim sample size, interim analysis can be immediately performed in that indication. Given the observed interim data D, we make the go/no-go decision based on the following rule: stop the accrual to indication g if

$$(Futilitystoppingrule)Pr(q_g\le q_{0,g}\mid D)>C(n_g)\text{or}$$ (4)

$$(Toxicitystoppingrule)Pr(p_g>{\varphi }_T\mid D)>C_T,$$ (5)

where C_T and C(n_g) are probability cutoffs calibrated by simulation. A reasonable range for C_T is C_T ∈ (0.7, 0.95). For C(n_g), we adopt the optimal probability cutoff proposed by then Bayesian optimal phase II (BOP2) design (Zhou et al., 2017), that is $C(n_{{}_g})=1-\lambda (\frac{n_{{}_g}}{N_{{}_{g,2}}}{)}^{{}^{\gamma }}$, where the positive tuning parameters λ and γ are calibrated to maximize the power while controlling type I error at a prespecified level α (e.g., α = 10%). The values of λ and γ can be easily obtained using the online BOP2 app available at www.trialdesign.org. Strictly speaking, the optimal values of λ and γ obtained under the BOP2 design are not necessarily optimal for the proposed design because of the information borrowing across indications, but our simulation shows that they lead to satisfactory operating characteristics. In principle, the optimal values of λ and γ can be obtained for our design using the same grid searching strategy as Zhou et al. (2017), but that is time consuming due to more complicated CBHM used here. In addition, due to the information borrowing induced by CBHM, when directly using the values of λ and γ from the BOP2 app, the type I error of each indication may deviate (typically slightly) from α under the global null (i.e., all indications are non-responsive). If it is desirable, we can slightly calibrate λ, while keeping γ fixed, to control type I error of each indication at α under the global null.

2.3. Bayesian model averaging approach

An alternative, statistically more sophisticated approach to do cluster-then-borrow is to use the Bayesian model averaging (BMA), along the line of Hobbs and Landin (2018). With G indications, there are a total of L = 2^G ways to partition the indications into $\mathcal{R}$ and $\overline{\mathcal{R}}$. Let M_ℓ denote the ℓ th partition, ℓ = 1,…,L. Given the interim data D, the posterior probability of M_ℓ is given by

$$Pr(M_{\ell }\mid D)=\frac{L(D\mid M_{\ell })Pr(M_{\ell })}{{\sum }_{\ell =1}^{L}L(D\mid M_{\ell })Pr(M_{\ell })},$$

where Pr(M_ℓ) is the prior of M_ℓ. In general, we apply the non-informative prior, i.e., Pr(M_ℓ) = 1 / L, when there is no preference for any specific partition. L(D∣M_ℓ) is the likelihood of M_ℓ, given by

$$L(D\mid M_{\ell })=\prod _{g=1}^G\left(\begin{array}{c}\hfill n_g\hfill \\ \hfill x_g\hfill \end{array}\right)q_{[\ell ]g}^{x_g}(1-q_{[\ell ]g}{)}^{n_g-x_g},$$

where q_[ℓ]g is the response rate for indication g given the ℓ th partition, i.e., q_[ℓ]g = q_1,g if $g\in \mathcal{R}$ and q_[ℓ]g = q_0,g if $g\in \overline{\mathcal{R}}$.

Given the ℓ th partition (i.e., M_ℓ), the members of $\mathcal{R}$ and $\overline{\mathcal{R}}$ are known, and we apply the BHM (3) to $\mathcal{R}$ and $\overline{\mathcal{R}}$ independently to calculate Pr(q_g ≤ q_0,g ∣ D, M_ℓ), g = 1,…,G and ℓ = 1,…,L. Then, the futility go/no-go rule (4) can be calculated as follows:

$$Pr(q_g\le q_{0,g}\mid D)=\sum _{\ell =1}^{L}Pr(q_g\le q_{0,g}\mid D,M_{\ell })Pr(M_{\ell }\mid D).$$

The BMA approach is statistically sophisticated and computationally intensive, but the simulation (see Table A2 in Appendix) shows that it has similar performance as the CBHM with the simple Bayesian clustering rule (1) described above. The reason is that given the small number of indications and the limited interim (binary) data in each indication, the complicated BMA method introduces more noise (e.g., accounting for 2^G possible partitions or models) and thus often fails to improve the performance. Hence, we recommend the Bayesian clustering rule (1) for practical use because it is much more transparent and easy to understand and implement, especially for non-statisticians.

2.4. Determine sample size N₁ and N_g,2

To determine phase I sample size N₁ and phase II sample size N_g,2, the general approach is to use simulation to calibrate N₁ and N_g,2 such that desirable operating characteristics are obtained (e.g., correct selection of the MTD, power, and type I errors). We provide some rules of thumb to facilitate such calibration. For N₁, we recommend N₁ = 6×J (i.e., six patients per dose). For N_g,2, we recommend using the BOP2 software to obtain an initial value ${\tilde{N}}_{{}_{g,2}}$, given a desirable type I error and power. As BOP2 does not borrow information (thus computationally is much faster), N_g,2 should be smaller than ${\tilde{N}}_{{}_{g,2}}$. We can use $0.5\times {\tilde{N}}_{{}_{g,2}}$ as the starting value to calibrate N_g,2.

3. Simulation studies

3.1. Simulation setting

We evaluated the operating characteristics of the shotgun design and compared it to the “conventional” design that first identifies the MTD using the 3+3 design, followed by multiple cohort expansions. In the latter, each cohort expansion is carried out independently using the Simon optimal two-stage design (Simon, 1989). For fair comparison, the same toxicity stopping rule (5) is used to monitor toxicity for each indication. To investigate the functionality of the proposed CBHM, we also considered the BHM design that is the same as the shotgun design, but replaced the CBHM with the standard BHM (i.e., directly apply the BHM to all indications without clustering).

We consider J = 4 doses and G = 5 indications. To reflect this in practice, accrual rates of indications may be different; we set the accrual rates for 5 indications at 3, 2.5, 2, 1.5, and 2 patients per month, respectively. During the dose finding phase, the target toxicity rate ϕ_T = 0.3, the cohort size is three, and the maximum sample size is N₁ = 24. For conventional designs, the 3+3 design often terminates the trial early (e.g., when 2/3 patients experience toxicity) before reaching the maximum sample size N₁. In that case, following common practice, an all-comers cohort expansion will be performed at the selected MTD so that the total sample size for the phase I portion is N₁.

At the multiple cohorts expansion phase, we consider one interim analysis and one final analysis (e.g., K = 2). The null response rate q_0,1 = ⋯ = q_0,5 = 0.05, and target response rate q_1,1 = ⋯ = q_1,5 = 0.3. For conventional design, applying the Simon optimal two-stage design leads to the total sample size N_g,2 = 12 with an interim at 5 for each indication, assuming a type I error rate of 10% and 80% power. For the shotgun and BHM designs, we set N_g,2 = 12 with an interim at 8. For fair comparison, the tuning parameters in the futility stopping rule (4) are calibrated to control the type I error rates at similar level of those in conventional design in the null case where all indications are ineffective at target dose (i.e., scenario 1 in Table 2).

Table 2:

Ten toxicity-efficacy scenarios with different MTD locations and various numbers of promising indications. The MTD and promising indications are in bold.

Scenario	Dose	Pr(toxicity)	Response rate of five indications
			1	2	3	4	5
MTD is the last dose
1	1	0.05	0.01	0.01	0.01	0.01	0.01
	2	0.09	0.02	0.02	0.03	0.02	0.03
	3	0.16	0.04	0.04	0.05	0.03	0.05
	4	0.30	0.05	0.05	0.05	0.05	0.05
2	1	0.04	0.01	0.01	0.01	0.01	0.01
	2	0.13	0.05	0.09	0.06	0.10	0.12
	3	0.18	0.18	0.20	0.18	0.16	0.19
	4	0.30	0.30	0.30	0.30	0.30	0.30
3	1	0.06	0.01	0.01	0.01	0.01	0.01
	2	0.10	0.05	0.05	0.05	0.02	0.05
	3	0.16	0.14	0.16	0.20	0.04	0.05
	4	0.30	0.30	0.30	0.30	0.05	0.05
4	1	0.05	0.01	0.01	0.01	0.01	0.01
	2	0.12	0.05	0.02	0.03	0.05	0.03
	3	0.18	0.13	0.04	0.05	0.05	0.04
	4	0.30	0.30	0.05	0.05	0.05	0.05
MTD is the middle dose
5	1	0.14	0.01	0.01	0.01	0.01	0.01
	2	0.30	0.30	0.30	0.30	0.30	0.05
	3	0.47	0.40	0.43	0.40	0.48	0.26
	4	0.65	0.49	0.52	0.47	0.48	0.35
6	1	0.12	0.01	0.01	0.01	0.01	0.01
	2	0.30	0.30	0.30	0.30	0.05	0.05
	3	0.48	0.40	0.43	0.40	0.30	0.22
	4	0.62	0.45	0.50	0.40	0.46	0.35
7	1	0.10	0.01	0.01	0.01	0.01	0.01
	2	0.30	0.30	0.30	0.05	0.05	0.05
	3	0.48	0.45	0.48	0.20	0.21	0.16
	4	0.60	0.54	0.57	0.36	0.24	0.30
MTD is the first dose
8	1	0.30	0.30	0.30	0.30	0.05	0.05
	2	0.48	0.45	0.48	0.46	0.20	0.26
	3	0.56	0.50	0.54	0.58	0.38	0.39
	4	0.62	0.50	0.62	0.67	0.45	0.48
9	1	0.30	0.30	0.30	0.30	0.30	0.05
	2	0.45	0.48	0.47	0.43	0.41	0.23
	3	0.52	0.52	0.55	0.54	0.48	0.38
	4	0.60	0.52	0.65	0.63	0.56	0.46
10	1	0.30	0.30	0.30	0.30	0.30	0.30
	2	0.46	0.42	0.38	0.46	0.44	0.45
	3	0.55	0.48	0.43	0.54	0.50	0.45
	4	0.65	0.56	0.58	0.60	0.58	0.45

We considered three toxicity profiles with the true MTD located at the middle, first, and last dose, respectively. Nested each toxicity profile, we considered three to four efficacy profiles where different numbers of indication were responsive to the treatment, resulting a total of 10 scenarios, as shown in Table 2. Under each scenario, we conducted 10,000 simulations.

3.2. Performance metrics

The objective of the shotgun design is to discover promising indications to be further studied in phase III studies, where “promising indications” is defined as the indications for which the treatment is both safe and effective. In what follows, we define several discovery-centered metrics to summarize the overall performance of the design.

(I) Correct discovery rate (CDR), defined as

$$\text{CDR}=\frac{\text{Number of correct discoveries}}{\text{Number of promising indications}},$$

where “Number of correct discoveries” is the number of promising indications identified by the design at the end of the trial. The CDR is closely related to power, but is more relevant here as the primary objective of the trial is to discover promising indications from multiple indications.

(II) False discovery rate (FDR), defined as

$$\text{FDR}=\frac{\text{Number of false discoveries}}{\text{Number of indications claimed as promising by the design}},$$

where “Number of false discoveries” is the number of indications claimed as promising by the design, but actually are not. For example, in scenario 4, if a design claims that indications 1 and 2 are promising at the end of the trial, then the FDR = 1/2, because indication 2 actually is not promising (i.e., there is no dose that is safe and effective for treating indication 2).

(III) Adjusted discovery rate (ADR), defined as

$$\text{ADR}=\frac{\text{Number of correct discoveries-Number of false discoveries}}{\text{Number of promising indications}}.$$

ADR is an overall performance measure that accounts for the tradeoff between correct discovery and false discovery.

3.3. Simulation results

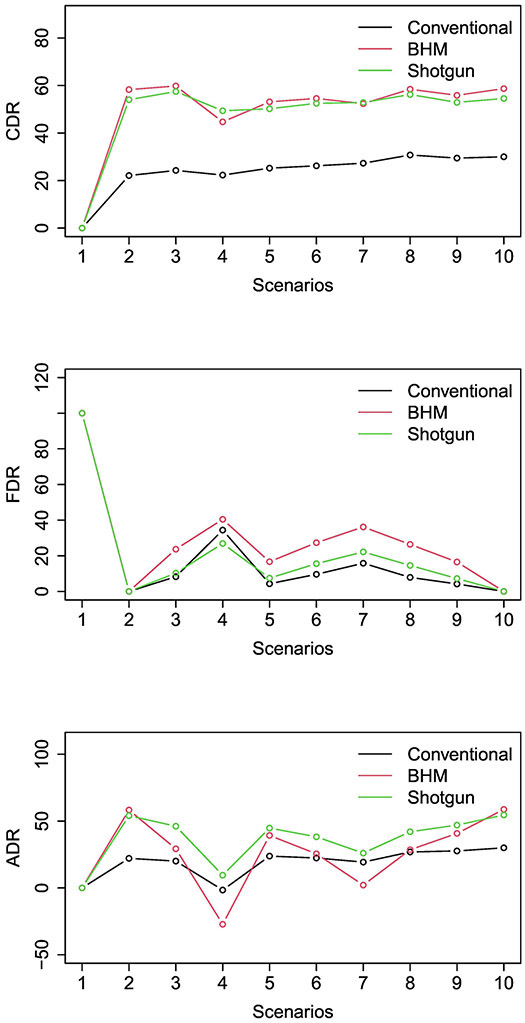
Figure 2 and Table 3 show the simulation results of the three designs. Scenarios 1-4 consider that the true MTD is dose level 4, with various numbers of promising indications. Scenario 1 is the global null where all indications are non-responsive. All designs control the type I error rate < 10%. Because of the safety stopping, the type I error is slightly lower than the normal value of 10%. As expected, CDR=ACDR=0 and FDR=100 for all designs. Scenario 2 is the global alternative where all indications are responsive. The shotgun design and the BHM design outperform the conventional design with higher CDR. For example, the CDR of the shotgun design is 54.0%, more than doubling the CDR of the conventional design (i.e., 22.1%). The BHM design has higher CDR than the shotgun design, but it leads to substantially higher type I error and FDR when some indications are non-response, as described below. In scenario 3, there are three promising indications (indications 1, 2, and 3). The CDR of the shotgun design is more than doubling that of the conventional design (57.5% versus 24.3%), indicating that the shotgun design is twice more likely to discover the promising indications than the conventional design. Because the shotgun design made substantially more discoveries, its FDR is slightly higher (i.e., 2%) than the conventional design. After accounting for the tradeoff between correct discovery and false discovery, the shotgun design substantially outperforms the conventional design with 26.1% higher ADR. The BHM design has comparable CDR to the shotgun design, but has a 13.4% higher FDR, suggesting the ability of the proposed CBHM to reduce the false positive rate. In scenario 4, there is one promising indication (indication 1). The shotgun design outperforms the conventional design with 27.1% higher CDR and 11.1% higher ADR. Compared to the BHM design, the shotgun design has 4.7% higher CDR, and yields 36.7% higher ADR (after adjusting for the false discovery). Scenarios 5-7 consider that the true MTD is dose level 2 with various numbers of promising indications. The results are generally consistent with scenarios 1-4 and support that the shotgun design outperforms the other two designs. For example, in scenario 5, there are four promising indications (indications 1, 2, 3, and 4). The CDR of the shotgun design is 25% higher than the conventional design. After adjusting for the false discovery, the ADR of the shotgun design is 21% higher than the conventional design. The BHM design yields good CDR, but it fails to control FDR and, as a result, its ADR is 5.5% lower than the shotgun design. Scenario 7 has two promising indications (indications 1 and 2). After adjusting for false discovery, the shotgun design ADR is 6.7% and 23.9% higher than the conventional and BHM designs, respectively. Scenarios 8-10 simulate the cases that the lowest dose is the MTD with 3-5 promising indications. The shotgun design has the best performance. Compared to the conventional design, the CDR of the shotgun design is 25.4%, 23.4%, and 24.5% higher, respectively, and the ADR of the shotgun design is 15.1%, 19.3%, and 24.5% higher, in scenarios 8-10. Compared to the BHM design, the shotgun design has comparable CDR, but yields higher ADR (e.g., 13.5% higher in scenario 8), after adjusting for false discovery.

Figure 2:

Simulation results, including (a) correct discovery rate (CDR), (b) false discovery rate (FDR) and (c) adjusted discovery rate (ADR) for the conventional design, Bayesian hierarchical model (BHM) design, and shotgun design.

Table 3:

Simulation results of conventional, BHM and shotgun designs.

Method	Selection (%) of target dose	Power/type I error (%) for indication					CDR (%)	FDR (%)	ADR (%)
		1	2	3	4	5
Scenario 1		0.05	0.05	0.05	0.05	0.05
Conventional	31.8	8.1	9.0	7.9	7.9	8.7	0.0	100	0.0
BHM	69.0	8.1	8.9	8.0	8.0	8.7	0.0	100	0.0
Shotgun	69.0	7.9	8.7	7.8	8.1	8.5	0.0	100	0.0
Scenario 2		0.30	0.30	0.30	0.30	0.30
Conventional	28.2	77.5	79.6	77.2	78.6	78.7	22.1	0.0	22.1
BHM	62.4	91.6	92.6	93.6	95.5	93.7	58.3	0.00	58.3
Shotgun	62.4	85.6	85.6	86.6	88.6	86.4	54.0	0.00	54.0
Scenario 3		0.30	0.30	0.30	0.05	0.05
Conventional	31.0	78.3	79.0	77.3	8.2	9.3	24.3	8.3	20.1
BHM	67.8	87.5	88.1	89.2	50.1	51.3	59.8	23.7	29.3
Shotgun	67.8	85.0	84.8	84.7	18.0	16.5	57.5	10.3	46.2
Scenario 4		0.30	0.05	0.05	0.05	0.05
Conventional	28.6	78.0	8.7	8.0	8.1	9.2	22.3	34.4	−1.6
BHM	63.2	70.7	23.5	21.5	20.9	22.3	44.7	40.5	−27.2
Shotgun	63.2	78.1	11.8	10.4	10.3	11.5	49.4	26.9	9.5
Scenario 5		0.30	0.30	0.30	0.30	0.05
Conventional	31.9	79.0	78.2	79.5	79.4	8.2	25.2	4.3	23.8
BHM	58.2	90.5	91.0	91.5	92.2	73.1	53.1	16.7	39.3
Shotgun	58.2	85.7	85.6	86.7	86.9	18.2	50.2	7.5	44.8
Scenario 6		0.30	0.30	0.30	0.05	0.05
Conventional	33.2	79.1	78.4	79.2	8.2	8.3	26.2	9.6	22.4
BHM	61.7	87.7	88.7	88.9	50.0	52.3	54.6	27.3	25.5
Shotgun	61.7	85.1	85.0	85.2	18.2	17.3	52.5	15.6	38.2
Scenario 7		0.30	0.30	0.05	0.05	0.05
Conventional	34.6	79.3	78.5	9.4	7.9	8.0	27.3	15.8	19.3
BHM	63.5	81.8	83.3	33.9	34.8	37.1	52.4	36.2	2.1
Shotgun	63.5	83.4	83.2	13.0	14.2	14.7	52.8	22.2	26.0
Scenario 8		0.30	0.30	0.30	0.05	0.05
Conventional	38.9	78.9	79.2	78.8	8.3	8.3	30.8	7.9	26.9
BHM	64.9	90.5	90.9	88.7	50.4	52.1	58.4	26.4	28.5
Shotgun	64.9	87.5	87.6	84.8	18.8	16.6	56.2	14.6	42.0
Scenario 9		0.30	0.30	0.30	0.30	0.05
Conventional	37.2	78.7	79.4	78.4	80.3	8.4	29.5	4.2	27.7
BHM	60.5	92.2	93.3	91.1	92.8	73.9	55.9	16.5	40.8
Shotgun	60.5	88.0	88.1	86.0	87.5	17.7	52.9	7.2	47.0
Scenario 10		0.30	0.30	0.30	0.30	0.30
Conventional	38.0	78.5	79.2	78.6	79.8	78.8	30.0	0.0	30.0
BHM	62.1	94.8	95.2	93.5	95.1	94.3	58.7	0.0	58.7
Shotgun	62.1	88.2	88.3	86.5	88.7	87.8	54.5	0.0	54.5

3.4. Using CBHM for basket trials

As described previously, the proposed CBHM methodology for the phase II part of the shotgun design can be used independently for designing basket trials. We evaluated the performance of the CBHM for basket trials, and compare it to the Bayesian nonparametric method (BNP) proposed by Chen and Lee (2020) and the method proposed by Liu et al. (2017). For each comparison, we used the simulation settings considered by these authors.

Specifically, for the comparison with the BNP, taking the simulation setting of Chen and Lee (2020), the null and target response rates are q_0,g = 0.1 and q_1,g = 0.3, respectively, for 10 indications. No interim analysis was considered and the maximum sample size for each indication was 25. Five scenarios were considered: global null (the response rates of all indications are 0.1), global target (the response rates of all indications are 0.3), equal mixture (the response rates in half indications are 0.1 and in the other half are 0.3), mostly target (the response rates in 80% indications are 0.3 and in 20% are 0.1), mostly null (the response rates in 20% indications are 0.3 and in 80% are 0.1). The treatment is claimed to be effective in indication g , if Pr(q_g > q_0,g + δ ∣ D) > C, where δ = 0.1 and C is calibrated to control type I error at 5% in each indication in the global null case. Under each scenarios, we conducted 2000 simulations. The simulation results are shown in Table 4. CBHM and BNP have comparable performance, and both have higher power than the independent approach, where no information is borrowed across the indications. BNP has slightly higher power in the scenario of global target, whereas the CBHM has slightly higher power in the scenarios of equal mixture and mostly null. In addition, under the scenario of mostly target, the type I error of CBHM is lower than that of BNP. One important advantage of the CBHM is that it is substantially simpler than the BNP. The BNP involves complicated Dirichlet process and computation.

Table 4:

Average power and average type I error of BCHM, BNP and independent methods for basket trials.

Scenario	Method	Average power (%)	Average type I error (%)
Global null	Independent	4.8	NA
	BCHM	4.5	NA
	CBHM	4.8	NA
Global target	Independent	NA	77.8
	BCHM	NA	95.0
	CBHM	NA	90.8
Equal mixture	Independent	4.8	77.8
	BCHM	9.6	88.2
	CBHM	9.5	90.8
Mostly target	Independent	4.8	77.8
	BCHM	14.4	92.2
	CBHM	10.2	90.8
Mostly null	Independent	4.8	77.8
	BCHM	7.0	86.6
	CBHM	9.5	89.1

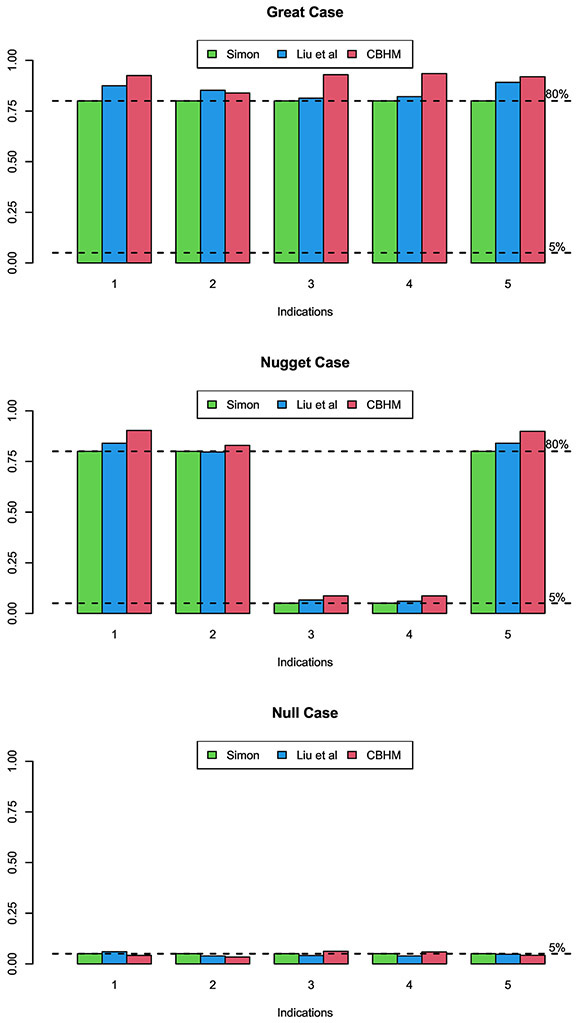
When comparing the CBHM to the method proposed by Liu et al. (2017), we used the simulation setting considered by these authors. There are 5 indications, with null response rates (0.15, 0.25, 0.2, 0.2, 0.15) and target response rates (0.4, 0.5, 0.4, 0.4, 0.4). Following Liu et al. (2017), we also include independent approach for comparison, which evaluates the treatment effect in each indication independently by using Simon two-stage design. Assuming power of 80% and type I error rate of 5%, Simon two-stage design requires total sample sizes of N_g = 25,24,43,43 and 25 for 5 indications, which are used as the total sample sizes in the CBHM with one interim at 12,12,21,21 and 12 , respectively. The accrual rate for each indication is set at 2 patients per month. Three scenarios were considered by Liu et al. (2017): null (treatment is ineffective in all indications), nugget (treatment is effective only in indications 1, 4, 5), and great (treatment is effective in all indications). Under each scenarios, we conduct 1000 simulations, and the simulation results are shown in Figure 3. In general, CBHM has better performance than other two designs. In “great” scenario, CBHM yields higher power than Liu’s design and Simon’s design in indications 1-5 (especially in indications 3-4). In “nugget” scenario, CBHM has higher power in indications 1, 2 and 5, and slightly higher type I error rates in indications 3-4, than other two designs.

Figure 3:

Power and type I error of the CBHM, the method of Liu et al. (2017), and the independent Simon two-stage design for basket trials.

4. Discussion

We propose a Bayesian seamless phase I-II shotgun design to efficiently evaluate the treatment effects of a new drug in multiple indications simultaneously. By using the seamless phase I-II design framework, the shotgun design eliminates the white space between phase I and phase II, thus speeding up the trial. In addition, this framework also allows the use of efficacy data collected from phase I in phase II. The shotgun design is flexible, allowing the total number of interim analyses and interim times to vary from one indication to another. By classifying indications into responsive and non-responsive subgroups and borrowing information within the subgroups using the Bayesian hierarchical model, the shotgun design has a substantially higher probability of discovering promising indications, after adjusting for false discoveries, than the conventional approach.

The proposed CBHM methodology for the phase II portion of the shotgun design can be used independently to design basket trials. The simulation study shows that the CBHM yields comparable or better performance than some existing basket trial designs, e.g., Bayesian nonparametric method (Chen and Lee, 2020) and multisource exchangeability model with Bayesian model averaging (Hobbs and Landin, 2018), but the CBHM is substantially simpler and easy to implement. The reason that these complicated methods do not deliver better performance is that in typical basket trials, the number of indications is often small (e.g., < 6) and the interim data in each indication are limited. The data simply cannot provide enough information to reliably estimate complicated models. Actually, the extra noise introduced by the complicated models often hurts the performance.

It is worth noting that for any information methods, there is intrinsic conflict between improving power and controlling type I error. This is because with a finite sample, even when the treatment effect is heterogeneous across indications (e.g., some indications are responsive and others are non-responsive), there is a non-zero probability that the observed response rate is similar across the indications, which triggers (inappropriate) information borrowing and thus the type I error inflation for non-responsive indications (e.g., scenario 3 in Table 3). In other words, in finite samples, we cannot have power of 1 to distinguish if the treatment effect of any two indications is truly homogeneous or heterogeneous. One may attempt to calibrate the probability cutoff in the decision rule (4) to control type I error rate strictly at the nominal value. That, however, will prohibit any information borrowing in all cases (e.g., the homogeneous case, scenario 2 in Table 3). This phenomenon not only occurs in the CBHM, but any information-borrowing methods. In other words, as long as we intend to borrow information, the inflation of type I error is inevitable. Jiang et al. (2020) discussed this issue and proposed using the utility to account for the power-type-I-error tradeoff and then optimize the utility.

In this paper, we mainly consider a binary endpoint. Our proposed design can also be extended for ordinal, continual, and survival endpoints. In addition, with the advent of novel molecularly targeted therapies and immunotherapies, the endpoints become more complicated, such as those seen with nested endpoints, co-primary endpoints, etc. How to deal with these complicated endpoints, while adaptively borrowing information across different indications at multiple cohorts expansion phases warrants further research.

In addition, although we do not formally investigate it, the dose used in the cohort expansion may be modified based on accumulative data collected. For example, if the additional data collected during cohort expansion suggest that the RP2D/MTD identified in dose finding is overly toxic for some indications (e.g., the observed toxicity rate is higher than the de-escalation boundary of the BOIN design), then we could de-escalate the dose for that indication. Conversely, if the additional data suggest that the dose is particularly safe (e.g., the observed toxicity rate is lower than the escalation boundary of the BOIN design), then we could escalate the dose. We may therefore continue to employ the BOIN dose escalation/de-escalation rule adaptively to modify the dose during cohort expansion. However, in practice, as the sample size of the cohort expansion is often limited and such dose modification inevitably increases the sample size and complicates clinical operations, such decisions are best made based on the totality of clinical evidence and logistical considerations, rather than statistical rule.

Appendix

Table A1:

Power and type I error of CBHM and CBHM with order constraint, for five indications with null response rate q_g = 0.1, target response rate q_g = 0.3, and total sample size N = 25 without interim analysis.

Scenario	Method	Power/type I error (%)for indication
		1	2	3	4	5
1	Response rate	0.1	0.1	0.1	0.1	0.1
	CBHM	10.54	10.46	9.94	10.36	9.52
	CBHM with constraint	10.54	10.46	9.94	10.36	9.52
2	Response rate	0.3	0.3	0.3	0.3	0.3
	CBHM	90.56	91.52	91.06	91.64	90.48
	CBHM with constraint	90.56	91.52	91.06	91.64	90.48
3	Response rate	0.1	0.1	0.3	0.3	0.3
	CBHM	10.54	10.46	91.06	91.64	90.48
	CBHM with constraint	10.54	10.46	91.06	91.64	90.48

Table A2:

Power and type I error of CBHM using Bayesian model averaging (denoted as CBHM-BMA) and CBHM using the proposed Bayesian clustering rule (denoted as CBHM), for three indications with null response rate q_g = 0.1, target response rate q_g = 0.3, and total sample size N = 20 without interim analysis.

Scenario	Method	Power/type I error (%) for indication
		1	2	3
1	Response rate	0.1	0.1	0.1
	CBHM-BMA	9.97	9.80	9.50
	CBHM	10.37	9.33	9.47
2	Response rate	0.3	0.3	0.3
	CBHM-BMA	89.17	90.27	89.83
	CBHM	88.63	90.00	89.33
3	Response rate	0.1	0.3	0.3
	CBHM-BMA	15.30	90.13	89.33
	CBHM	14.13	89.63	88.97
4	Response rate	0.1	0.3	0.1
	CBHM-BMA	14.67	83.97	13.50
	CBHM	13.67	84.33	12.50