Abstract
We compare the calibration and variability of risk prediction models that were estimated using various approaches for combining information on new predictors, termed “markers”, with parameter information available for other variables from an earlier model, that was estimated from a large data source. We assess the performance of risk prediction models updated based on likelihood ratio (LR) approaches that incorporate dependence between new and old risk factors as well as approaches that assume independence (“naive Bayes” methods). We study the impact of estimating the LR by a) fitting a single model to cases and non-cases when the distribution of the new markers is in the exponential family or b) fitting separate models to cases and non-cases. We also evaluate a new constrained maximum likelihood method. We study updating the risk prediction model when the new data arise from a cohort and extend available methods to accommodate updating when the new data source is a case-control study. To create realistic correlations between predictors, we also based simulations on real data on response to antiviral therapy for hepatitis C. From these studies, we recommend the LR method fit using a single model or constrained maximum likelihood.
Keywords: Calibration, Independence Bayes, Discrimination, Model updating, Risk prediction
1. Introduction
Large cohorts or population-based surveys that are linked to disease incidence or mortality data, e.g. the National Health and Nutrition Examination Survey (NHANES) [1], collect risk factor information that can be used to build risk prediction models for incidence of disease or mortality. When novel risk factors become available from new data, it is desirable to combine their information with information from existing prediction models, to improve predictions and risk stratification. That is particularly relevant for rare outcomes, and for new molecular markers, e.g. serum markers, measured on relatively small case-control studies, and when risk estimates from large studies are available for some well established risk factors. For example, estimates of the effects of many reproductive risk factors such as age at menarche, or parity on breast cancer incidence are known from previous studies; it is desirable to utilize this information when updating a risk prediction model, e.g. the NCI's well established and publicly available absolute breast cancer risk model, the Breast Cancer Risk Assessment Tool (BCRAT; http://www.cancer.gov/bcrisktool) or “Gail model” [2], to include additional risk factors, such as mammographic density or circulating hormone measures.
Here we study the performance of various methods in the literature for combining data on a new predictor with parameter estimates from an existing model with “standard” factors. Some authors refer to this approach as “model updating”. We consider likelihood ratio approaches, that incorporate dependence [3, 4, 5, 6], as well as likelihood ratio approaches that assume independence of the old and new risk factors, i.e. “naive Bayes” methods, discussed in detail e.g. by [7] and used in [8] and [9]. We also assess performance of models updated based on a novel semiparametric conditional maximum likelihood approach that is more general than the likelihood ratio methods and also fully efficient [10]. We assume that a risk prediction model with an original set of predictors has been fit to a very large cohort and estimated parameters for that model are known without random error. We then assume that information on a new predictor (marker) is available in an independent dataset, that also contains all the predictors included in the existing risk model. We study updating when the new data arise from a cohort as well as from a case-control study. We assess the calibration of the new updated model and the variability of the predictions under various settings, including some that violate underlying assumptions. To create realistic correlations between predictors, we also simulate data based on the covariate distribution from a real dataset, the Viral Resistance to Antiviral Therapy of Chronic Hepatitis C (VIRAHEP-C) study, a multicenter clinical trial designed to test how African American patients respond to antiviral therapy for hepatitis C (HCV) compared to Caucasian patients.
2. Notation and set up
We let Y denote the binary outcome, where Y = 1 denotes diseased and Y = 0 denotes non-diseased individuals, X = X1,…, Xp)T is a vector of p standard covariates, and Z a covariate that we term “new marker”. We first let Z be a single marker, but extend methods to multivariate markers later. We assume that the true outcome-predictor relationship in the population is given by the logistic model
| (1) |
where βX = (β1,…, βp)′ are the log odds ratios for X and βZ is the log odds ratio for Z.
The original risk prediction model RX only included factors X, and we assume that it was estimated using a logistic regression model as
| (2) |
In our simulations we assume that the parameters with γ1=(γ11,…,γ1p)′ in RX were estimated based on large data and thus do not explicitly account for their variance.
Note, however, that in general if P(Y = 1|X, Z) is logistic then P(Y = 1|X) cannot have this form, as, after applying Bayes theorem,
| (3) |
where . Only when the outcome is rare and X and Z are independent can both models, RX and RX,Z, be logistic as discussed in Section 3.2.1. Thus RX is a “working model”, i.e. an approximation of the true probability P (Y|X). We study only methods based on (2) in simulations, but the methods described below apply to any functional form of RX.
We assume that a new study is available that has information on X and additional information on the marker, Z. Our goal is to update model RX with information on Z, while also utilizing information available from model RX in (2). That is we wish to fit model
| (4) |
to the new dataset.
3. Estimating an updated risk prediction model, RX,Z
In this section we summarize several approaches for combining information from an existing prediction model RX with information on the new marker Z to estimate a model RX,Z based on observations (Yi, Xi, Zi), i = 1,…, n. We first describe the approaches when observations (Y, X, Z) are available on members of a cohort, and then extend them for case-control data. Some of the approaches assume independence of Z and the original model predictors X, while others allow for dependence between Z and X.
3.1. Estimating RX,Zfrom new data only
A simple approach is to completely ignore information from the old model RX and to fit a logistic regression model
| (5) |
that includes the new marker Z and the original variables X as predictors, to the new data (Yi,Xi,Zi),i= 1,…,n. While this is not model “updating”, as the information from the original model RX is not used, we study this approach, called “logistic-new”, in Section 4 to quantify the gain in predictive performance and efficiency when including information on RX.
3.2. Incorporating information on RX into RX,Z via likelihood ratio (LR) updating
Several authors have proposed updating risk models using the likelihood ratio (LR) of Z|Y, X [e.g. 3,4,6]. We first outline this approach and then discuss various methods for estimation in detail.
From equation (3),
| (6) |
where
| (7) |
is the likelihood ratio for the new marker Z with respect to outcome Y conditional on covariates X. Although equation (6) is exact, the following estimate of the log(posterior odds),
| (8) |
is only approximate, because usually RX only approximates P(Y = 1 |X). Expression (8) can be applied to any functional form of the model RX. However, when RX is a logistic model, as in equation (2), then equation (8) reduces to
| (9) |
If we assume that RX,Z is a logistic model, (8) yields
| (10) |
which further simplifies if RX is a logistic model to
| (11) |
We studied the performance of (11) in our simulations. The variance of R̂X,Z can be calculated from the covariance matrices of the component models , using the delta method, which could be implemented e.g. via the deltamethod function in the R package msm, as suggested by [6] or alternatively the variance could be estimated using a parametric bootstrap.
3.2.1. Approaches to estimating LRY(Z|X) We now summarize and extend several approaches for estimating the LRY in equation (8)
Joint estimation of LRY(Z|X)
First, we show that if P(Z|X) is a distribution within the exponential family, i.e. P(Z|X) = exp(ζZ)h(z)c(ζ), where h and c are known functions and ζ = X′β, and the disease is rare, then P(Z|X, Y) also is in the exponential family. For controls (Y = 0) the result follows immediately, because the controls are representative of the general population for a rare disease,
| (12) |
For cases, equation (1) can be approximated by an exponential function for a rare disease, and
| (13) |
is in the exponential family with ζ̃ = ζ + βz and an appropriately adjusted normalizing constant c.
Special cases of interest in the exponential family are the logistic and normal distributions. When logit , in the general population, then in the cases, , with a new intercept α* and otherwise the same coefficients as in the logistic model for the controls, Y = 0. The different intercept terms in the models for cases and controls can be accommodated by fitting a single logistic model, , that also includes Y as a predictor in addition to X to the combined case-control data. The LRY model (7) for a binary marker Z is then given by
| (14) |
Similarly, for a marker Z that follows a normal distribution, , under the rare disease assumption , where the mean of Z has different intercept parameters for the Y = 0 and Y = 1 groups. The joint log-LR model for a normally distributed marker Z is
| (15) |
Note that only the means but not the variance terms differ for cases and controls, and thus equation (15) yields the same expression as one would obtain from linear discriminant analysis, see e.g. Chapter 6, [11].
Estimating LRY(Z|X) based on fitting separate models for cases (Y = 1) and non-cases (Y = 0)
For P(Z|X) in the exponential family, and assuming rare disease, equations (12) and (13) show that the same general exponential form holds for P(Z|X, Y), Y = 0,1. Thus we can separately estimate the numerator and the denominator of LRY(Z|X) in equation (7) by fitting two different models to the new dataset, one to cases (Y = 1) and one to controls (Y = 0). If Z is a binary marker, P(Z|Y, X) can be estimated e.g. using separate logistic regression models for cases and controls, yielding
| (16) |
where , Y = 0,1, indicates parameters in the models for controls and cases, respectively. For a normally distributed marker, , we estimate the parameters from two linear models fitted separately to cases and controls, yielding
| (17) |
In contrast to joint estimation, estimating the LRY separately in cases and controls also allows the variance to differ between the two groups, and thus corresponds to quadratic discriminant analysis, see e.g. Chapter 6, [11].
3.2.2. LR updating assuming independence of Z and X (independence Bayes)
A special case of the LR approach defined above, described e.g. in [7], and used by [12] to update a prostate cancer model with genetic information, is to assume that the new marker Z is independent of X in cases and non-cases, and therefore
| (18) |
When case-control data are used for updating, and the outcome is rare, then if X is independent of Z in the general population, X and Z are also independent in cases and controls, as shown e.g. in [13]. The assumption of independence of X and Z in the general population is somewhat weaker than assuming independence conditional on outcome.
Note that when the outcome is rare, and if X and Z are independent, then the parameter γ1 in equation (2) for model RX is approximately equal to the true population parameter β1 as , and the last integral corresponds to the moment generating function of Z. When additionally P(Z) is in the exponential family and the disease is rare, then using (12) and (13), we see that
| (19) |
Thus under independence of X and Z, for P(Z) in the exponential family and a rare outcome, the coefficients for X and Z in R̂X,Z in equation (10) are approximately unbiased.
We study two approaches to estimating LRY in the simulations. In the first approach, that we term “LR-indep” in the simulation section, we fit separate models to cases and controls.
Joint estimation, logistic model with offset
The linear dependency of log{LRY(Z)} on Z given in (19) was also noted by [8] for a marker with logistic or normal distribution. Thus [8] proposed to include the prior odds with parameters γ from the original risk model RX, as an offset term in a logistic regression model that is fit to the new dataset, including the new marker Z as the predictor to obtain RZ,X. Two new parameters (δ0, δ1) are estimated based on the model
| (20) |
Independence Bayes with shrinkage
A generalization of (18) that incorporates dependence between X and Z by fitting one additional parameter was proposed by [9]. Here, a shrinkage factor θ multiplies the likelihood ratio term log{LRY (Z)} in (6). [9] first estimated the LRY (Z) based on the new data and then obtained an estimate of θ by fitting a logistic regression model to the new data with the prior odds, , included as an offset term and LRY (Z) as the independent variable as
| (21) |
It can be seen that if θ is estimated to be zero, the new marker does not add any information to the prediction, and when θ=1, Z is independent of X. We refer to model (21) as “LR-shrink” in the presentation of the results, and also compare the two-step estimation approach to a single step approach that directly maximizes (21) as a function of θ and all parameters in LRY.
3.3. Adapting the above approaches to case-control data
If the new data arise from a case-control study, however, the disease prevalence in the case control data does not correspond to the true population value in model (1). To ensure that the intercept term in RX,Z yields the correct population prevalence or incidence of the outcome, we modify models (5), (20) and (21) assuming that the true disease prevalence P(Y = 1) is known from external data without error by solving the following equation for μ*:
| (22) |
For model (5), , and for model (20), .
To adjust the intercept for LR-shrink in (21), we first include an additional intercept θ0 in the model to absorb the case-control sampling ratio,
| (23) |
and after obtaining θ̂1 solve (22) for .
For a rare disease, the empirical distribution function in the controls in the case control study provides an estimate F̂(X, Z), if the controls constitute a random sample from the general population. If there is population information on F(X), e.g. from a large survey, it may be advantageous to utilize this information to obtain an estimate F̂(X) from these external data, and use that F̂(X, Z) = F̂(Z|X)F̂(X) and only estimate F(Z|X) from the controls in the case control study.
We show in the appendix (without stating all the regularity assumptions explicitly) that this two step approach leads to consistent, if not fully efficient, estimates of all parameters in the model.
3.4. Updating using constrained Maximum Likelihood Estimation (CML)
Similarly to earlier work by [14], [10] considered the problem of building regression models based on individual-level data from an “internal” study while utilizing information on parameters for a reduced model estimated from an “external” big-data source. They identified a set of general constraints that link internal and external models and used them to propose a semi-parametric maximum likelihood estimate for the new model that is equivalent to a form of empirical likelihood as pointed out by [15] in a very nice discussion of that work.
We briefly summarize the key idea following closely the presentation and notation in [10]. Let U(Y|X;γ) = ∂loggγ(Y|X)/∂γ denote the score function associated with the “external” reduced model RX in (2). The population parameter value γ for this model satisfies the equation
| (24) |
where P(Y, X) = P(Y|X)P(X) is the true underlying joint distribution of (Y, X). When the model (2) is misspecified, then RX ≠ P̂(Y = 1|X) but the above equation still holds true under mild conditions. Under the assumption that fβ(Y|Z,X) = RX,Z is correctly specified, we can write P(Y|X) = ∫fβo(Y|Z,X)P(Z|X)dZ, with β0 the true value of β. Thus, the constraint imposed by Equation (24) can be rewritten, after changing some ordering of integrals, as
The above equation converts the external information to a set of constraints, which is used in the analysis of internal data to improve efficiency of parameter estimates. The dimension of the constraints is the same as the number of parameters by which the external model has been summarized. We now give a specific example, following [15], when the internal sample is a simple random sample. In this case, letting pi = dF(Xi, Zi) denote the empirical version of F(X, Z) from the internal data sample {(Xi, Zi),i=1,…, N}, the CML estimate β = (βX, βZ) is defined through the constrained maximization
subject to
The authors in [10] derive MLEs under simple random sampling and under a case-control sampling design for the internal study.
The method does not require any parametric modeling assumption for the joint distribution of the risk-factors and produces consistent estimates of parameters of the updated model, assuming that one correctly specifies the probability distribution of the internal study, irrespective of whether the external model is correctly specified or not. The method can handle any type of regression models including logistic regressions and no assumption of rare disease is required. The authors showed that empirical-likelihood approach allows tractable computation of CML irrespective of the dimension of the risk-factors. Extensions for handling complex sampling designs, including case-control sampling, for the internal study are given. The distribution of covariates pi, can be estimated using either the internal sample or an external reference sample.
4. Simulations
We use several sets of simulations to assess bias and variability in predicted probabilities from models updated using the approaches in Section 3. For the first set we generate all covariates and outcome from known distributions. To obtain realistic correlations between predictor variables, we also base simulations on real data. For both settings, we assumed that the dataset used for updating is a cohort and then let the new marker be measured in a case-control study.
4.1. Data generation
As in Section 3, Y denotes the binary outcome variable, X = (X1, …, Xp)′ are p = 4 independent binary variables (predictors) in the original risk prediction model RX given in (2), with P(Xi = 1) = 0.2, i = 1,… 4. We study estimating RZ,X for a binary or a continuous marker Z. For binary Z we model its dependence on X using a logistic regression model
| (25) |
where α = (α1, …, αp)′. For a continuous marker Z we assume a normal distribution and model its dependence on X through the mean,
| (26) |
We let σ2 = 0.25 and study the impact of different values for the components of α. When Z and X are independent αj = 0 for j = 1,…, p, otherwise αj ≠ 0 for some j in{1,…,p}.
We also assessed the robustness of the methods to the assumption of normality of the new marker. We did that by simulating Z from a mixture distribution of two normals that had the same variance, σ2 = 1, and different means, with mixing proportion 10%, i.e. with α1 = (0.7,0.7, −0.7, −0.7)′and α20 = 0.5, α2 = (1,1,−1,−1)′.
The relationship between X, Z and the outcome Y was given by the logistic regression model in (1), namely
| (27) |
where βX = (β1,…, βp)′. We let βX = (0.5,0.5, −0.5, −0.5)′ and βZ = 1 for all simulations.
For each choice of parameters we created the population data by first generating X, then, given X, generating Z from model (25) or (26) and given X and Z, generating Y from model (27). We then split this dataset into three disjoint sets, A, B and C. Dataset A with nA = 1, 000,000 samples that only included predictors X was used to fit model RX in (2). Dataset B with information on (Y, X, Z) was used to estimate RZ,X based on all methods presented in Section 3. For a cohort, B with nB = 500 or nB = 1000 samples was used; for case-control data, dataset B was comprised of ncases = ncontrols = 250 or ncases = ncontrols = 500 cases and controls. The disease prevalence P(Y = 1) and the empirical distribution of X, F2(X), were estimated from dataset A, the empirical distribution F̂control(Z|X) was estimated from the controls in dataset B, and the joint distribution function was estimated as F̂(Z, X) = F̂control(Z|X)F̂A(X).
We used data from a third independent dataset, C, of size nC = 100,000 to evaluate the predictive performance of the models updated using the various methods. First we compute the predicted probability for each observation in dataset C based on models RZ,X constructed by all methods in Section 3. We then computed the bias of the predictions for each model RZ,X as the ratio of expected to observed cases, E/O = ΣP̂ii/ ΣYi overall, in subgroups defined by covariates Xi or Z, and in deciles of risk in the dataset C. For each setting we present means over 1000 simulations.
The variability of the prediction was assessed by first taking the mean of the predicted probabilities ΣP̂i/n in each simulation and then computing the standard deviation of the means over the simulation runs with the same setting.
4.2. Results
We focus here on results for case-control studies with complete risk factor information (Y, X, Z), as this setting is most relevant for molecular markers for rare outcomes. Qualitatively findings for model updating based on cohort data were similar, and thus the corresponding tables and figures are presented in Supplemental Material.
For case-control data for all settings that we simulated under independence of the predictors X and the new marker Z, i.e. α = (0, …, 0)′, RX,Z computed by all methods yielded unbiased estimates of P(Y|X,Z) with the exception of LR-offset, LR-shrink and Logistic-new, which produced estimates that were too high; E overestimated O by 3% to 10% (Supplemental Tables S6, S7, S8 and S9). The amount of overestimation decreased as P(Y = 1) decreased from 5% to 1%, and was not seen for the cohort setting (Supplemental Tables S2, S3, and S5). The results for case-control data with a = (0,…, 0) are thus presented in Supplemental Tables S6-S9 and Supplemental Figures S10, S13, S14, S15 and S17. We next describe settings where Z depends on X in detail.
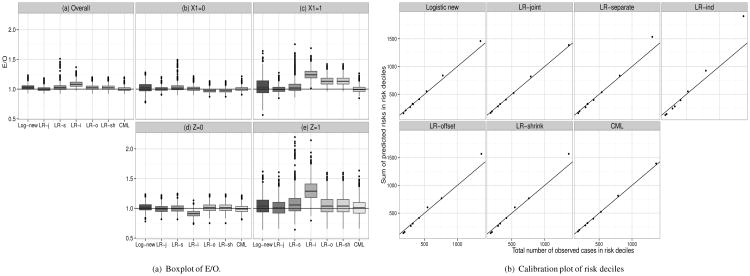
Figure 1(a) shows boxplots for E/O values from 1000 simulations for a binary marker Z that was dependent on X with coefficients α = (1,1, −1, −1)′ in model (25) (corresponding numbers are given in Supplemental Table S6). Overall, LR-indep, i.e. estimating the likelihood ratio assuming independence between X and Z, caused the largest bias in the predicted risks (panel (a)), and overestimated the observed risks by 8.6% (E/O = 1.086). LR-offset and LR-shrink had an overall bias of about 3%. The bias was even more pronounced in subsets of the population defined by covariate X1 or the new marker Z (Figure 1(a) panels (b)-(e)). The LR-indep method under-estimated true risks by about 9% in those with Z = 0 and over-estimated true risks by 30% in those with Z = 1, while all other methods had less than 8% bias. In those with X1 = 0, LR-shrink and LR-offset underestimated the true risks by about 3%, while in those with X1 = 1, LR-shrink and LR-offset overestimated risk by about 14%, and LR-indep overestimated by 25%. Calibration plots in figure 1(b) show that LR-indep strongly overestimates risk in the highest two risk deciles and LR-separate, LR-offset and LR-shrink overestimate in the highest risk decile, while Logistic-new shows only a slight lack of fit in the highest decile. The remaining methods resulted in well calibrated models. We note that for a binary Z, LR-offset and LR-shrink give the exact same predictions, as LR-offset fits two parameters to Z while LR-shrink fits two parameters to LRY which also takes only two values for binary Z.
Figure 1.
Observed number of events in risk deciles for case-control setting when models with p = 4 binary X were updated using one binary marker Z with P(X) = P(Z) = 0.2, P(Y) = 0.05, α0 = 0,α = (1, 1,−1,−1)′,βX = (0.5, 0.5, −0.5, −0.5)′, βZ = 1, ncases = ncontrols = 250. Log-new=Logistic new, LR-j=LR-joint, LR-s=LR-separate, LR-i=LR-ind, LR-o=LR-offset, LR-sh=LR-shrink. Compare with Supplemental Table S6.
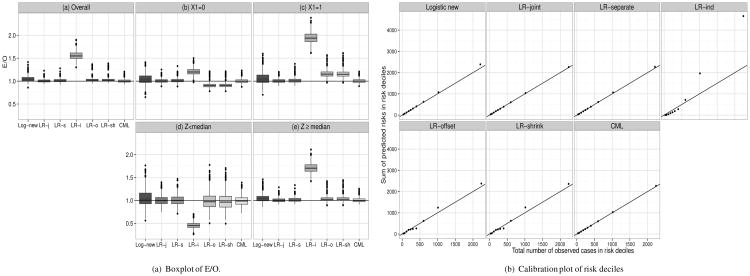
Figure 2(a) shows box plots for E/O ratios when models were updated using a normally distributed marker Z where the coefficients for the mean E(Z|X) = α′X were α = (1,1, −1, −1)′ in model (26) (with corresponding numbers in Supplemental Table S7). Here the biases are more pronounced than for a binary Z. In the entire population (panel (a)) E overestimated O for LR-shrink, LR-offset, Logistic-new, and LR-indep by 3%, 3%, 5% and 56%, respectively. Figure 2(a) panel (b)-(e) shows the bias in subsets defined by covariate X1 or the new marker Z ≥ median and Z < median. The LR-indep under-estimated true risks by about 54% in those with Z < median and overestimated them by 71% among those with Z ≥ median. Logistic-new somewhat overestimated in both those groups. LR-shrink and LR-offset overestimated among those with Z ≥ median by about 3%, while all other methods were nearly unbiased. In those with X1 = 0, LR-shrink and LR-offset underestimated by 10%, while model updating based on LR-indep and Logistic-new resulted in over-estimation. In those with X1 = 1, LR-shrink and LR-offset overestimated risk by 16% while LR-indep overestimated by 95%. When calibration was assessed in risk deciles (Figure 2(b)), those four methods overestimated risk in the highest two risk deciles, especially LR-indep; calibration was good for all other methods. Here LR-offset and LR-shrink had similar but not identical performance. CML and LR-joint resulted in unbiased estimates and had identical variability of the predictions.
Figure 2.
Observed number of events in risk deciles for case-control setting when models with p = 4 binary X were updated using one continuous marker Z with P(X) = 0.2, P(Y) = 0.05, α = (1, 1, −1, −1)′, βX = (0.5, 0.5, -0.5, -0.5)′, βZ = 1, ncases = ncontrols = 250. Log-new=Logistic new, LR-j=LR-joint, LR-s=LR-separate, LR-i=LR-ind, LR-o=LR-offset, LR-sh=LR-shrink. Compare with Supplemental Table S7.
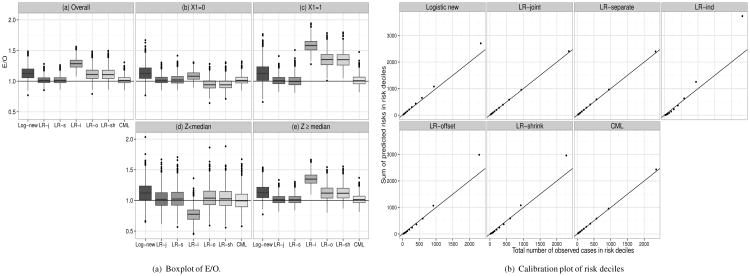
Figure 3(a) (with corresponding numbers in Supplemental Table S9) shows results from the robustness study, when Z was generated from a two component normal mixture model. Here LR-separate, LR-joint and CML were virtually unbiased overall and in subgroups defined by Z ≥ median and Z < median, and X1. Logistic-new, LR-offset, LR-shrink, LR-ind overestimated the true risks by 14%, 12%, 12% and 29% respectively overall (Figure 3, panel (a)), by 13%, 36%, 36% and 58% in those with X1 = 1 (panel (c)), and by 14%, 13%, 13% and 35% in those with Z ≥ median (Figure 3, panel (e)).
Figure 3.
Observed number of events in risk deciles for case-control setting when models with p = 4 binary X were updated using one continuous marker Z following a mixture distribution of normals. P(X) = 0.2, α01 = 0, αX1 = (0.7, 0.7,−0.7,−0.7)′, α02 = 0.5, αX2 = (1, 1,-1,-1)′, P(Y) = 0.05, βX = (0.5, 0.5, −0.5, −0.5)′, βZ = 1,ncases = ncontrols = 250. Log-new=Logistic new, LR-j=LR-joint, LR-s=LR-separate, LR-i=LR-ind, LR-o=LR-offset, LR-sh=LR-shrink. See also Supplemental Table S9.
When calibration was assessed in risk deciles (Figure 3(b)), there was evidence of lack of fit of the highest two risk deciles for Logistic-new, LR-shrink, LR-offset, LR-indep, while LR-separate, LR-joint and CML gave virtually unbiased estimates. Further results on Z arising from mixtures with different parameters are given in Supplemental Figures S17-S23, and Supplemental Tables S9-S11.
When LR-shrink was estimated in a single step that simultaneously estimated the parameters in the likelihood ratio and the shrinkage parameter, the results were very similar to the two-step, approach. For example, for the setting used in Table S7, third scenario, the E/O ratios for the single step approach were 1.034 overall, 0.913 for X1 = 0, 1.168 for X1 = 1, 0.982 for T < median and 1.041 for T ≥ median, and for the two step approach they were 1.027, 0.909, 1.159, 0.979 and 1.034 for the same subsets. In simulations with updating based on 1000 cases and controls, the two methods yielded E/O values that agreed to the third digit after the decimal point, and the variances of the estimates were virtually identically.
4.3. Simulations based on the covariate distribution from the Viral Resistance to Antiviral Therapy of Chronic Hepatitis C (VIRAHEP-C) study
4.3.1. Data and simulation setup
In the simulations presented in the previous section, we generated independent components of X and defined a specific relationship between X and Z. To obtain realistic correlations between predictors we also simulated data based on variables from the Viral Resistance to Antiviral Therapy of Chronic Hepatitis C (VIRAHEP-C) study. This study was conducted from 2002-2006 to investigate differences between African Americans and Caucasians in response to antiviral therapy for hepatitis virus C (HVC). The outcome was sustained virological response (SVR). We considered the following covariates X: race (white, non-white), sex (male, female), Ishak fibrosis score that assesses liver fibrosis stages ranging from normal to cirrhosis (regrouped into four categories) and AST/ALT enzyme ratio (in quartiles).
We updated the risk models by adding two new markers, Z1 and Z2, first separately and then jointly: interferon lambda 4 (IFNL4) genotype in two categories (∆G/∆G or ∆G/TT corresponding to Z1 = 0, and TT/TT corresponding to Z1 = 1), and continuous levels of pre-treatment HCV-RNA (log10(IU/ml); Z2). The marginal distributions of X and Z in the 350 patients with complete predictor information are in Table 2, together with the log odds ratio estimates from models that included only baseline predictors X, baseline predictors and each marker separately, and X, Z1 and Z2 jointly in the same model.
Table 2.
Distribution of the predictors in the N = 350 ViraHepC participants from which predictors were sampled for simulations. Log odds ratios β and standard errors for the baseline model and models updated with genetic and viral load information separately and combined. Parameter estimates from the baseline model were used as the values γ in equation (2). The baseline model was used Quartile cutoffs for AST/ALT ratio: 0.3165 (Min.), 0.6307 (25%), 0.7705 (50%), 0.9302 (75%); 2.275 (Max.).
| Variable | Categories | Distribution | Baseline model | Model with baseline covariates and additionally | |||
|---|---|---|---|---|---|---|---|
| IFNL4 genotype | HCV-RNA | IFNL4 genotype & HCV-RNA | IFNL4 & HCV-RNA & interaction HCV-RNA/Race | ||||
| β (std err) | β (std err) | β (std err) | β (std err) | β (std err) | |||
| Race | Caucasian | 52.7% | Ref | Ref | Ref | Ref | Ref |
| Non-white | 48.3% | -0.85 (0.241) | -0.58 (0.257) | -0.90 (0.244) | -0.62 (0.261) | 2.92 (2.110) | |
| Sex | Male | 65.4% | Ref | Ref | Ref | Ref | Ref |
| Female | 34.6% | 0.73 (0.262) | 0.74 (0.266) | 0.68 (0.264) | 0.68 (0.269) | 0.63 (0.270) | |
| Ishak fibrosis score | 0 | 10.6% | -0.29 (0.156) | -0.33 (0.159) | -0.29 (0.158) | -0.33 (0.161) | -0.33 (0.162) |
| (ordinal) | 1-2 3-4 5-6 | 52.9% | |||||
| 1-2 | 29.7% | ||||||
| 3-4 | 6.9% | ||||||
| AST/ALT ratio | per quartile | -0.39 (0.117) | -0.34 (0.119) | -0.37 (0.118) | -0.32 (0.121) | -0.31 (0.120) | |
| (ordinal) | |||||||
| IFNL4 | ∆G/(∆G or TT) | 72.0% | - | Ref | - | Ref | Ref |
| TT/TT | 28.0% | - | 0.90 (0.279) | - | 0.93 (0.282) | 0.92 (0.282) | |
| log10HCV-RNA level | - | 6.5(5.6,6.8) | - | - | -0.38 (0.158) | -0.41 (0.162) | -0.20 (0.196) |
| (median, IQRα) | |||||||
| HCV-RNA:Race interact. | -0.57 (0.340) | ||||||
|
| |||||||
| AUC* | 0.701 | 0.725 | 0.712 | 0.738 | 0.739 | ||
IQR - Intra-quartile range (25th percentile - 75th percentile);
AUC based on c-statistics from SAS PROC logistic
IFNL4, a novel gene associated with impaired clearance of HCV [16], illustrates dependence between the new marker and the original covariates. The strongest correlation between IFNL4 and the original variables is with race (Spearman rank correlation ρ = −0.40) and with the AST/ALT ratio (Spearman rank correlation ρ = −0.23). HCV-RNA levels however are only very weakly correlated with the original variables and therefore illustrate the independence case (strongest correlations with sex, Spearman rank correlation ρ = −0.10). See Supplemental Table S12 for all correlations.
To generate data, we first sampled covariate vectors (X, Z1,Z2) with replacement from the 350 study subjects to obtain data for n patients. We then used these covariate vectors to generate the outcome Y from a logistic regression model,
| (28) |
with β0 = 0.8, corresponding to an outcome prevalence of P(Y = 1) = 0.1. To obtain realistic estimates, the values βX and βZ were estimated by fitting model (28) to the 350 VirahepC patients (second from last column in Table 2). We additionally also generated outcomes from a model that included an interaction term of HCV-RNA with race,
| (29) |
with β0 = 1.2.
Similar to Section 4.1, we created three datasets that we used to assess performance of the updating methods. The original model RX was obtained by including the covariates X in a logistic regression model. We then updated the model first with Z1 and Z2 separately and then jointly with both markers to obtain three updated risk prediction models, Rx,Z1, Rx,Z2 and RX,Z1,Z2. To compute the LR for two markers, we used that
| (30) |
To estimate log{LRY (Z2 |Z1, X)} we simply included the marker Z1 among the predictors.
4.3.2. Performance assessment
We present the ratio of expected to observed cases, E/O = Σp̂i/ΣYi, results for the AUC, the area under the receiver operating characteristic (ROC) curve, that can be expressed as the probability that R̂x,Z for a randomly selected case exceeds that for a randomly selected control ([17], page 67). In addition, we present results for the mean squared error, MSE = n−1Σ(pi − p̂i)2 and the Brier score, also referred to as the mean squared error of prediction [18], estimated by BS = n−1 Σ(Yi − p̂i)2. The Brier score can be written as , the sum of the intrinsic binomial variability of Y and the MSE.
4.3.3. Results
Table 3 shows results when the model was updated only with the IFNL4 genotype (Z1). Overall, Logistic-new, LR-indep, LR-offset and LR-shrink all over-estimated true risks by 6% to 8%. Slightly more bias was seen for subsets defined by sex for these methods. In subsets defined by AST/ALT ratio, LR-indep overestimated true risks by 16% in the AST/ALT< median group and underestimated 6% in the ≥ median group, while LR-offset and LR-shrink overestimated true risks by 11% and under estimated them by 4% in these groups, respectively. In subsets defined by IFNL4 genotype, the LR-indep underestimated by 13% in the ∆G/∆G or ∆G/TT group and over-estimated by 27% in the TT/TT group. All other methods had less than 7% bias in subsets defined by genotype. When model updating was based on cohort data, a similar bias was seen for LR-indep (Supplemental Table S13).
Table 3.
Ratio of E=expected number of events over O=observed number of events (E/O) and standard deviations of Ē for simulations based on ViraHepC data with new marker IFNL4 with P(Y) = 0.1 based on ncases = ncontrols = 250.
| Overall | Sex | AST/ALT ratio | IFNL4 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||
| Methods | Male | Female | < median | ≥ median | ∆G/∆G or ∆G/TT | TT/TT | ||||||||
|
| ||||||||||||||
| E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | |
| Logistic new | 1.068 (0.001) | 0.0045 | 1.062 (0.003) | 0.0074 | 1.075 (0.004) | 0.0147 | 1.072 (0.002) | 0.0098 | 1.059 (0.004) | 0.0077 | 1.064 (0.003) | 0.0053 | 1.071 (0.004) | 0.0219 |
| LR-joint | 1.005 (0.001) | 0.0026 | 0.989 (0.001) | 0.0025 | 1.026 (0.001) | 0.0043 | 1.017 (0.001) | 0.0040 | 0.981 (0.001) | 0.0021 | 0.990 (0.002) | 0.0045 | 1.019 (0.003) | 0.0183 |
| LR-separate | 1.022 (0.001) | 0.0033 | 1.005 (0.001) | 0.0035 | 1.043 (0.002) | 0.0067 | 1.032 (0.001) | 0.0052 | 1.000 (0.002) | 0.0035 | 1.003 (0.002) | 0.0046 | 1.038 (0.003) | 0.0196 |
| LR-ind | 1.084 (0.001) | 0.0042 | 1.095 (0.002) | 0.0040 | 1.071 (0.001) | 0.0045 | 1.157 (0.002) | 0.0066 | 0.937 (0.001) | 0.0019 | 0.870 (0.002) | 0.0040 | 1.274 (0.004) | 0.0220 |
| LR-offset | 1.062 (0.001) | 0.0040 | 1.065 (0.001) | 0.0037 | 1.059 (0.001) | 0.0045 | 1.114 (0.001) | 0.0062 | 0.958 (0.001) | 0.0022 | 1.061 (0.003) | 0.0054 | 1.064 (0.003) | 0.0213 |
| LR-shrink | 1.062 (0.001) | 0.0040 | 1.065 (0.001) | 0.0037 | 1.059 (0.001) | 0.0045 | 1.114 (0.001) | 0.0062 | 0.958 (0.001) | 0.0022 | 1.061 (0.003) | 0.0054 | 1.064 (0.003) | 0.0213 |
| CML | 1.003 (0.001) | 0.0025 | 0.995 (0.001) | 0.0025 | 1.012 (0.001) | 0.0040 | 1.013 (0.001) | 0.0037 | 0.983 (0.001) | 0.0021 | 0.994 (0.002) | 0.0045 | 1.010 (0.003) | 0.0178 |
Not surprisingly, estimating Rx,Z from the new data alone, was associated with the largest variability in the estimates. This difference was most pronounced in subsets defined by AST/ALT ratio, where Logistic-new had up to four fold higher variability than most other methods. LR-separate often resulted in more variable predictions than all other likelihood ratio based methods. The variability in estimates from LR-joint was the same as that of CML in all subsets in Table 3.
There was little variation in the overall AUCs and the Brier scores, with values ranging from 0.721 to 0.726 for the AUC and from 0.086 to 0.087 for the Brier score, respectively (Table 4). However, the standard errors of the AUC were much larger for LR-separate and Logistic new than all other methods. The standard errors of the Brier score were largest for LR-ind, followed by LR-separate and Logistic new. The Brier score also did not vary much in the different subgroups. In contrast, the MSE estimates varied much more across the different methods, driven by the bias in the estimates. For example, the overall MSE ranged from 0.15 for CML and LR-joint to 0.28 for LR-ind.
Table 4.
AUC, MSE and Brier score for simulations based on ViraHepC data with new marker IFNL4 with P(Y ) = 0.1 based on ncases = ncontrols = 250.
| Overall | Sex | AST/ALT ratio | IFNL4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||||
| Methods | Male | Female | < median | ≥ median | ∆G/∆G or ∆G/TT | TT/TT | |||||||||
|
| |||||||||||||||
| AUC (se) | MSE (se) | BS(se) | MSE | BS | MSE | BS | MSE | BS | MSE | BS | MSE | BS | MSE | BS | |
| Logistic new | 0.723 (0.000142) | 0.0019 (0.000016) | 0.086 (0.000026) | 0.0015 | 0.076 | 0.0028 | 0.105 | 0.0025 | 0.112 | 0.0014 | 0.061 | 0.0009 | 0.061 | 0.0046 | 0.152 |
| LR-joint | 0.726 (0.000099) | 0.0015 (0.000007) | 0.086 (0.000023) | 0.0012 | 0.076 | 0.0020 | 0.104 | 0.0019 | 0.111 | 0.0011 | 0.060 | 0.0007 | 0.060 | 0.0036 | 0.151 |
| LR-separate | 0.721 (0.000164) | 0.0020 (0.000020) | 0.086 (0.000029) | 0.0016 | 0.076 | 0.0028 | 0.105 | 0.0025 | 0.112 | 0.0016 | 0.061 | 0.0008 | 0.061 | 0.0051 | 0.152 |
| LR-ind | 0.725 (0.000088) | 0.0028 (0.000029) | 0.087 (0.000036) | 0.0021 | 0.077 | 0.0040 | 0.106 | 0.0040 | 0.113 | 0.0015 | 0.061 | 0.0008 | 0.061 | 0.0077 | 0.155 |
| LR-offset | 0.724 (0.000110) | 0.0018 (0.000011) | 0.086 (0.000024) | 0.0015 | 0.076 | 0.0024 | 0.105 | 0.0024 | 0.112 | 0.0012 | 0.061 | 0.0009 | 0.061 | 0.0042 | 0.151 |
| LR-shrink | 0.724 (0.000110) | 0.0018 (0.000011) | 0.086 (0.000024) | 0.0015 | 0.076 | 0.0024 | 0.105 | 0.0024 | 0.112 | 0.0012 | 0.061 | 0.0009 | 0.061 | 0.0042 | 0.151 |
| CML | 0.726 (0.000100) | 0.0015 (0.000006) | 0.086 (0.000023) | 0.0012 | 0.076 | 0.0019 | 0.104 | 0.0018 | 0.111 | 0.0011 | 0.060 | 0.0007 | 0.060 | 0.0034 | 0.151 |
When the model was updated with HCV-RNA levels (Table 5), updating based on Logistic-new, LR-separate, LR-indep, LR-offset and LR-shrink all caused over-estimation of true risks by 4% to 7% overall and in subsets defined by sex. Similar patterns were seen in subsets defined by race, but LR-offset had higher bias, 9% for Non-whites, than all other methods. In the AST/ALT≥ median group, LR-indep and LR-separate had 11% and 12% upward bias, respectively. LR-indep and LR separate also overestimated by 16% and 15% in those with HCV-RNA< median and underestimated by 11% and 9% respectively in those with HCV-RNA ≥ median. LR-offset overestimated true risks overall by 6% and in all cells of the table, likely because of the disease prevalence adjustment. This bias was not seen for cohort data. When model updating was based on cohort data, there was generally less bias, and LR-shrink was nearly unbiased (Supplemental Table S14). As in Table 4, the AUC and Brier score values did not show much variation but the MSE varied appreciably (Table 6).
Table 5.
Ratio of E=expected number of events over O=observed number of events (E/O) and standard deviations of Ē for simulations based on ViraHepC data with new continuous marker HCV-RNA with P(Y) = 0.1 based on ncases = ncontrols = 250.
| Overall | Race | Sex | AST/ALT ratio | HCV-RNA | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||||||||
| Methods | Caucasian | Non-white | Male | Female | < median | > median | < median | > median | ||||||||||
|
| ||||||||||||||||||
| E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | |
| Logistic new | 1.063 (0.001) | 0.0038 | 1.061 (0.002) | 0.0092 | 1.068 (0.005) | 0.0080 | 1.067 (0.003) | 0.0071 | 1.057 (0.003) | 0.0143 | 1.067 (0.002) | 0.0092 | 1.054 (0.004) | 0.0079 | 1.103 (0.003) | 0.0102 | 1.011 (0.002) | 0.0061 |
| LR-joint | 0.995 (0.001) | 0.0017 | 0.995 (0.001) | 0.0028 | 0.997 (0.001) | 0.0012 | 0.993 (0.001) | 0.0018 | 0.999 (0.001) | 0.0028 | 1.006 (0.001) | 0.0024 | 0.975 (0.001) | 0.0017 | 1.029 (0.002) | 0.0078 | 0.952 (0.002) | 0.0059 |
| LR-separate | 1.049 (0.001) | 0.0043 | 1.069 (0.001) | 0.0068 | 0.993 (0.002) | 0.0026 | 1.065 (0.002) | 0.0048 | 1.029 (0.001) | 0.0047 | 1.014 (0.001) | 0.0053 | 1.122 (0.002) | 0.0051 | 1.155 (0.004) | 0.0135 | 0.914 (0.003) | 0.0071 |
| LR-ind | 1.044 (0.001) | 0.0040 | 1.044 (0.001) | 0.0054 | 1.043 (0.002) | 0.0026 | 1.046 (0.001) | 0.0039 | 1.041 (0.001) | 0.0044 | 1.010 (0.001) | 0.0041 | 1.113 (0.002) | 0.0047 | 1.162 (0.003) | 0.0126 | 0.892 (0.002) | 0.0061 |
| LR-offset | 1.061 (0.001) | 0.0036 | 1.051 (0.001) | 0.0047 | 1.092 (0.002) | 0.0025 | 1.050 (0.001) | 0.0031 | 1.075 (0.001) | 0.0045 | 1.073 (0.001) | 0.0045 | 1.037 (0.001) | 0.0028 | 1.100 (0.003) | 0.0100 | 1.011 (0.002) | 0.0059 |
| LR-shrink | 1.069 (0.001) | 0.0042 | 1.070 (0.001) | 0.0059 | 1.065 (0.002) | 0.0024 | 1.067 (0.001) | 0.0039 | 1.071 (0.001) | 0.0048 | 1.062 (0.001) | 0.0043 | 1.083 (0.002) | 0.0045 | 1.049 (0.003) | 0.0101 | 1.095 (0.002) | 0.0047 |
| CML | 1.002 (0.001) | 0.0020 | 1.003 (0.001) | 0.0033 | 0.998 (0.001) | 0.0013 | 0.995 (0.001) | 0.0020 | 1.010 | 0.0032 (0.001) | 1.008 | 0.0025 | 0.990 (0.001) | 0.0022 | 1.042 (0.002) | 0.0085 | 0.951 (0.002) | 0.0058 |
Table 6.
AUC, MSE and Brier score for simulations based on ViraHepC data with new continuous marker HCV-RNA with P(Y) = 0.1 based on ncases = ncontrols = 250.
| Overall | Race | Sex | AST/ALT ratio | HCV-RNA | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||||||||
| Methods | Caucasian | Non- white |
Male | Female | < median | ≥ median | <median | ≥median | |||||||||||
|
| |||||||||||||||||||
| AUC (se) | MSE (se) | BS (se) | MSE | BS | MSE | BS | MSE | BS | MSE | BS | MSE | BS | MSE | BS | MSE | BS | MSE | BS | |
| logistic new | 0.713 (0.000146) | 0.0025 (0.000015) | 0.087 (0.000027) | 0.0043 | 0.121 | 0.0006 | 0.050 | 0.0021 | 0.077 | 0.0033 | 0.105 | 0.0036 | 0.113 | 0.0014 | 0.061 | 0.0033 | 0.096 | 0.0018 | 0.078 |
| LR-joint | 0.717 (0.000097) | 0.0020 (0.000006) | 0.086 (0.000023) | 0.0035 | 0.120 | 0.0004 | 0.050 | 0.0018 | 0.076 | 0.0025 | 0.105 | 0.0029 | 0.112 | 0.0012 | 0.060 | 0.0025 | 0.095 | 0.0015 | 0.078 |
| LR-separate | 0.713 (0.000146) | 0.0070 (0.000088) | 0.091 (0.000091) | 0.0117 | 0.128 | 0.0019 | 0.052 | 0.0072 | 0.082 | 0.0064 | 0.109 | 0.0053 | 0.114 | 0.0086 | 0.068 | 0.0120 | 0.104 | 0.0019 | 0.078 |
| LR-ind | 0.716 (0.000122) | 0.0061 (0.000079) | 0.090 (0.000083) | 0.0092 | 0.126 | 0.0028 | 0.053 | 0.0055 | 0.080 | 0.0072 | 0.109 | 0.0044 | 0.114 | 0.0078 | 0.067 | 0.0104 | 0.103 | 0.0018 | 0.078 |
| LR-offset | 0.717 (0.000098) | 0.0021 (0.000009) | 0.086 (0.000023) | 0.0036 | 0.120 | 0.0005 | 0.050 | 0.0018 | 0.077 | 0.0027 | 0.105 | 0.0031 | 0.112 | 0.0012 | 0.060 | 0.0027 | 0.095 | 0.0015 | 0.078 |
| LR-shrink | 0.717 (0.000100) | 0.0029 (0.000035) | 0.087 (0.000042) | 0.0048 | 0.121 | 0.0009 | 0.051 | 0.0027 | 0.077 | 0.0034 | 0.106 | 0.0034 | 0.112 | 0.0025 | 0.062 | 0.0042 | 0.096 | 0.0017 | 0.078 |
| CML | 0.717 (0.000098) | 0.0020 (0.000007) | 0.086 (0.000023) | 0.0035 | 0.120 | 0.0004 | 0.050 | 0.0018 | 0.076 | 0.0025 | 0.105 | 0.0029 | 0.112 | 0.0012 | 0.060 | 0.0025 | 0.095 | 0.0015 | 0.078 |
When both, the binary genotype, Z1, and continuous HCV-RNA levels, Z2, were included to obtain RX,Z1 ,Z2, (Table 7), Logistic-new, LR-indep, LR-offset, LR-separate and LR-shrink overestimated risk on the entire population by 8 to 13%, with similar estimates for Caucasians. Models updated using LR-indep underestimated risks for the IFNL4 ∆G/∆G or ∆G/TT genotype by 6% and overestimated them for the TT/TT genotype group by 29%, while models updated using LR-separate overestimated in both genotype groups, by 4% and 10% respectively. LR-indep and LR-separate overestimated risk by 17 and 15%, respectively, in those with HCV-RNA< median, for whom LR-offset and Logistic-new, overestimated risk by 9%. Again, a similar bias for LR-indep was seen when the risk model was updated based on cohort data (Supplemental Table S15), while the bias was less pronounced for all other methods. In this setting the AUC values varied slightly more than in the previous scenarios, and ranged from 0.740 for CML and LR-joint to 0.729 for LR-separate, which also had a much larger MSE overall and in various subgroups than the other methods (Table 8).
Table 7.
Ratio of E=expected number of events over O=observed number of events (E/O) and standard deviations of Ē for simulations based on ViraHepC data with both markers IFNL4 and HCV-RNA with P(Y) = 0.1 based on ncases = ncontrols = 250.
| Overall | Race | IFNL4 | HCV-RNA | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods | Caucasian | Non-white | ∆G/∆G or ∆G/TT | TT/TT | <median | ≥median | ||||||||
| E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | E/O (se) | sd(Ē) | |
| Logistic new | 1.089 (0.002) | 0.0053 | 1.089 (0.002) | 0.0109 | 1.089 (0.005) | 0.0082 | 1.095 (0.003) | 0.0058 | 1.084 (0.004) | 0.0222 | 1.091 (0.003) | 0.0109 | 1.086 (0.003) | 0.0081 |
| LR-joint | 1.005 (0.001) | 0.0030 | 1.008 (0.001) | 0.0051 | 0.996 (0.001) | 0.0018 | 0.992 (0.002) | 0.0047 | 1.016 (0.003) | 0.0182 | 1.004 (0.002) | 0.0080 | 1.006 (0.003) | 0.0070 |
| LR-separate | 1.078 (0.002) | 0.0051 | 1.101 (0.002) | 0.0083 | 1.011 (0.002) | 0.0040 | 1.046 (0.003) | 0.0053 | 1.107 (0.003) | 0.0206 | 1.145 (0.004) | 0.0138 | 0.993 (0.004) | 0.0099 |
| LR-ind | 1.126 (0.002) | 0.0052 | 1.233 (0.002) | 0.0091 | 0.813 (0.002) | 0.0030 | 0.944 (0.002) | 0.0048 | 1.287 (0.004) | 0.0214 | 1.168 (0.003) | 0.0122 | 1.073 (0.003) | 0.0087 |
| LR-offset | 1.084 (0.002) | 0.0050 | 1.146 (0.002) | 0.0087 | 0.902 (0.002) | 0.0032 | 1.092 (0.003) | 0.0059 | 1.077 (0.004) | 0.0217 | 1.085 (0.003) | 0.0108 | 1.082 (0.003) | 0.0077 |
| LR-shrink | 1.089 (0.002) | 0.0053 | 1.159 (0.002) | 0.0093 | 0.884 (0.002) | 0.0032 | 1.106 (0.003) | 0.0061 | 1.075 (0.004) | 0.0218 | 1.019 (0.003) | 0.0106 | 1.180 (0.003) | 0.0071 |
| CML | 1.006 (0.001) | 0.0031 | 1.008 (0.001) | 0.0052 | 1.001 (0.001) | 0.0019 | 1.004 (0.002) | 0.0048 | 1.008 (0.003) | 0.0176 | 1.011 (0.002) | 0.0088 | 1.000 (0.002) | 0.0069 |
Table 8.
AUC, MSE and Brier score for simulations based on ViraHepC data with both markers IFNL4 and HCV-RNA with P(Y ) = 0.1 based on ncases = ncontrols = 250.
| Overall | Race | IFNL4 | HCV-RNA | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||||||||
| Methods | Caucasian | Non-white | ∆G/∆G or ∆G/TT | TT/TT | <median | ≥median | |||||||||
|
| |||||||||||||||
| AUC (se) | MSE (se) | BS (se) | MSE | BS | MSE | BS | MSE | BS | MSE | BS | MSE | BS | MSE | BS | |
| Logistic new | 0.736 (0.000141) | 0.0009 (0.000021) | 0.085 (0.000030) | 0.0015 | 0.118 | 0.0003 | 0.050 | 0.0005 | 0.060 | 0.0021 | 0.149 | 0.0012 | 0.094 | 0.0006 | 0.077 |
| LR-joint | 0.740 (0.000102) | 0.0003 (0.000010) | 0.085 (0.000024) | 0.0006 | 0.117 | 0.0001 | 0.050 | 0.0001 | 0.060 | 0.0008 | 0.148 | 0.0005 | 0.093 | 0.0002 | 0.076 |
| LR-separate | 0.729 (0.000171) | 0.0066 (0.000094) | 0.091 (0.000097) | 0.0110 | 0.127 | 0.0019 | 0.052 | 0.0041 | 0.064 | 0.0133 | 0.160 | 0.0120 | 0.104 | 0.0013 | 0.078 |
| LR-ind | 0.736 (0.000098) | 0.0059 (0.000092) | 0.090 (0.000095) | 0.0094 | 0.126 | 0.0022 | 0.052 | 0.0039 | 0.064 | 0.0112 | 0.158 | 0.0108 | 0.103 | 0.0010 | 0.077 |
| LR-offset | 0.738 (0.000111) | 0.0008 (0.000018) | 0.085 (0.000027) | 0.0014 | 0.118 | 0.0001 | 0.050 | 0.0005 | 0.060 | 0.0017 | 0.149 | 0.0011 | 0.093 | 0.0005 | 0.077 |
| LR-shrink | 0.735 (0.000108) | 0.0016 (0.000041) | 0.086 (0.000046) | 0.0026 | 0.119 | 0.0005 | 0.050 | 0.0013 | 0.061 | 0.0025 | 0.150 | 0.0023 | 0.095 | 0.0009 | 0.077 |
| CML | 0.740 (0.000104) | 0.0003 (0.000011) | 0.085 (0.000024) | 0.0006 | 0.117 | 0.0001 | 0.050 | 0.0002 | 0.060 | 0.0008 | 0.148 | 0.0005 | 0.093 | 0.0002 | 0.076 |
When data were generated from the model (29) that also included an interaction term between HCV-RNA and race, risk estimates from LR-joint and CML showed no bias overall, and had similar variability (Supplemental Table S17). For all other methods, however, the overall E/O ratios indicated that risks were overestimated, by amounts ranging from 7% for LR-separate to 21% for LR-independent. In groups defined by race, models updated using LR-indep also overestimated by 21% in Caucasians, while risks were unbiased in Non-whites. Models updated by LR-offset and LR-shrink had similar biases, with 11% overestimation in Caucasians, and 15% underestimation in Non-whites. LR-separate led to 34% overestimation in Non-whites. LR-joint and CML had a slight negative bias of 4% and 3% respectively in Non-whites, but negligible bias in those with HCV-RNA< median or with HCV-RNA ≥ median.
We also conducted a small robustness study based on the VIRAHEP-C data to assess the impact to violations of the assumption that the covariate distributions in the original cohort (A) that gave rise to the model Rx is the same as in the new study cohort (B) where Z is evaluated. As before, we generated data by first sampling covariate vectors (X, Z1,Z2) where Z1 denotes the IFNL4 genotype and Z2 continuous HCV-RNA levels, with replacement from the 350 study subjects to obtain data for n patients. However, to get data for dataset B, if Z1 = 0, we randomly computed a new variable Z1 by drawing a Bernoulli random variable with probability 0.3. This changes the marginal distribution of Z1 and also affects the correlation of the variables. We then used the covariate vectors (Xi, Z1i, Z2i) to generate outcomes Yi from the logistic regression model in equation (28), with all parameters, including the intercept unchanged from cohort A.
When the model was updated based on case-control data with 250 case sand 250 controls, CML and LR-joint showed the strongest bias overall, each underestimating the true number of events by 14% (Supplemental Tables S18 and S19). They also strongly under-estimated risk in cells defined by genotype, for which LR-ind also underestimated the true number of events appreciably. LR-offset and LR-shrink seemed to be most robust against violations of the assumption and showed the least bias of all methods overall and in subsets defined by covariates. The BS was the same for all methods, and the AUC values were not strongly affected by the bias (Table S19). The bias was similar when the model was updated using the various methods based on a cohort of 1000 subjects (Supplemental Tables S20 and S21).
5. Discussion
We assessed the performance of several methods for combining information from an available risk prediction model with data on a new predictor (marker), that is available jointly with the original model predictors in a new dataset, sometimes referred to as “model updating”. We studied both new cohort data and new case-control data with known disease prevalence. The methods included fitting the full model, including old and new predictors to new data, ignoring available information on the original prediction model, including the prior log odds as an offset term in a logistic regression model that also includes the new predictor [8], and various methods for updating based on Bayes theorem, which results in including the prior log odds and the likelihood ratio (LR) for the novel marker in the new model ((6) - (11)). We assessed using the LR assuming that the new marker is independent of the risk factors included in the original model, incorporating a shrinkage factor that captures the degree of dependence of the new and old risk factors [9], and by modeling the LR of the new marker as a function of the original risk factors. We extended the methods by [8] (LR-offset) and [9] (LR-shrink) to allow model updating based on case-control data, when the disease prevalence in the population is known from external sources. We studied bias in the predictions overall and in categories defined by risk factors and risk deciles, and the variability of the resulting estimates.
The rare disease setting is of special importance, as only under the rare disease assumption can both RX and RX,Z be logistic models. When the disease is not rare RX is mis-specified and only a “working model”. The rare disease assumption is thus needed to justify some of the implicit approximations for some of the methods. In simulations we found that when case-control data were used for updating, even when the new marker was independent of the original model predictors, LR-offset, LR-shrink and Logistic-new were sensitive to the disease prevalence, as the risk factor distribution in the controls was assumed to be the same as in the overall population. In the independence setting all other methods yielded unbiased results.
When the new marker was correlated with the original model predictors, estimating the LR assuming independence yielded biased risk estimates in all settings we studied while estimating the LR as a function of the original predictors X either separately for cases and controls (LR-separate) or jointly (LR-joint) resulted in largely unbiased predictions, with somewhat better performance by LR-joint. This likely is due to the fact that LR-joint behaves similarly to linear discriminant analysis, which captures differences in population means, while LR-separate corresponds to quadratic discriminant analysis, which also allows for population specific second order moments, but tends to lead to more extreme predictions in the tails of a distribution. Both these methods were also not sensitive to violations of the assumption of normality of a marker, as could be seen when we simulated the marker form a mixture of normals instead of a single normal distribution. The conditional maximum likelihood approach, a novel method for incorporating existing information into estimation [10] yielded unbiased predictions. This is not surprising as in contrast to the LR methods, which only approximate the true underlying model, CML also yields unbiased estimates of the true underlying model parameters.
Fitting a new model to the data with complete covariate information alone of course also provides unbiased predictions, but can be inefficient compared to other approaches. This was highlighted by results presented in Table S4, that show that even when the updating data set was increased to sample size nB = 3000, the standard deviation of the expected prediction was 0.0054 (Tables S4), much larger than that for CML = 0.002 with nB = 1000, (Table S3).
We also computed the AUC, the MSE and the Brier score for the models updated by the different methods. The Brier scores and the AUC values varied little across the different methods. This indicates that the Brier score, which is the sum of the MSE and the Bernoulli variation of the outcome, was dominated by Bernoulli variability. The AUC is generally not sensitive to bias, as it is a function of the ranks of the predicted probabilities. However, the standard errors for the AUC were noticeably larger for logistic new and LR-separate than the other methods and the standard error of the Brier score was largest for LR-ind. Only for the MSE did we observe noticeable differences for the various methods, driven by the bias in the estimates, which we emphasize in this paper. While the discriminatory ability of a model is very important, good calibration is needed in most applications and should be evaluated first.
Our simulations also highlight the need to assess calibration in subsets of the data, i.e. in cells defined by the predictors in the model, as checks of overall calibration can miss bias present in subsets of the population.
[19] also compared several methods to update pretest risk with information on a new test, independence Bayes, LR-offset and LR-shrink [8, 9]. However, the authors built the models in one real dataset comprised of 309 patients with chronic obstructive airway disease, and assessed performance in a second, independent validation study comprised of 161 individuals; they only assessed performance in quintiles of risk. They found that LR-offset had the best performance and recommended its use for updating risk models. In contrast, we extensively studied the methods in simulations, also based on real data, to obtain realistic correlations among old and new predictors. We also assessed the impact of various study designs (cohort and case-control studies) for the new marker study. While LR-offset was unbiased when cohort data were used as a source for updating the models, it had the same variability in the predictions as the ‘Logistic-new’ approach, which was larger than the variability of all other methods. When case-control data were used for updating, LR-offset had larger bias in the predictions than most methods, with the exception of the LR independent. Our conclusions are thus rather different from those in [19].
On the basis of these studies we recommend LR-joint or CML for updating. CML has theoretical appeal because it yields consistent estimates for model (1) and does not require specifying a distribution F(Z|X), which can be problematic if Z has many components. However, CML requires specialized programming to incorporate constraints. LR-joint is easily implemented with standard software and shares similar good calibration and precision of risk estimates as CML in our studies, even with disease prevalences as high as P(Y = 1) = 0.3. The good performance of LR-joint would seem to require (see equation (6)) both that: a) log{P(Y = 1|X)P(Y = 0|X)} is well approximated by and b) that LRY(Z|X) is correctly modeled by regression Z on X and Y in the new data. In Section 3.2. we showed that condition b) is satisfied for low prevalence outcomes with F(Z|X) in the exponential family. Under the rare disease assumption, . This is log-linear in X is , satisfying condition a). Condition a) is also satisfied if Z is independent of X (Section 3.2.2). However, LR-joint also performs well when the disease is not rare (Supplemental Tables S8 and S10). Taylor series expansion might offer further justification for the good performance of LR-joint with higher P(Y = 1).
An important limitation is that all methods assume that the distribution of covariates in the data that gave rise to the original risk model RX and the new data that include X and the novel marker Z are the same. We report simulations that revealed bias in CML and LR-joint when this assumption is violated. Further work is needed to assess the impact of violations to this assumption in practically relevant settings. Another limitation of our work is that we assumed parameter estimates are known without error as we estimated them from large data in our simulations. We provided theoretical approaches to accommodate the variance in the original model estimates for LR based methods, but future work should assess uncertainty in parameter estimates from the original risk model also for CML.
Supplementary Material
Table 1.
Summary of updating methods. is the prior odds from original risk model RX for X = (X1, …Xp)T. LRind = P(Z|Y = 1)/P(Z|Y = 0),LRdep = P(Z|Y=1,X)/P(Z|Y = 0,X), which is estimated separately (LR-separate) or jointly (LR-joint). Only “Logistic new” and CML, assuming that the covariate distributions in the population used to estimate RX and the population used to update the model are the same, estimate the parameters in equation (5) corresponding to the correct model.
| Method | Study type | log (posterior odds) = | Assumes independence of X and Z | Nr. of parameters estimated for | ||
|---|---|---|---|---|---|---|
|
| ||||||
| Z binary | Z continuous | |||||
|
| ||||||
| Logistic new | cohort |
|
No | p+2 | p+2 | |
| LR-joint |
|
No | p+2 | p+3 | ||
| LR-separate |
|
No | 2(p+1) | 2(p+1)+2 | ||
| LR-ind |
|
Yes | 2 | 4 | ||
| LR-offset |
|
Yes | 2 | 2 | ||
| LR-shrink |
|
No | 3 | 5 | ||
| Logistic new | case-control |
|
No | p+3 | p+3 | |
| LR-offset |
|
Yes | 3 | 3 | ||
| LR-shrink |
|
No | 5 | 7 | ||
| CML | No | p+2 | p+2 | |||
p: number of old risk factors
Acknowledgments
We thank Tom O'Brien for helpful comments on the ViraHepC data, and for access to the data and Yi-Hau Chen for access to the code for the CML method. The Virahep-C study was conducted by the Virahep-C Investigators and supported by the National Institute of Diabetes and Digestive and Kidney Diseases. The data and samples from the Virahep-C study reported here were supplied by the National Institute of Diabetes and Digestive and Kidney Diseases Central Repositories. This manuscript was not prepared in collaboration with the Virahep-C study group and does not necessarily reflect the opinions or views of the Virahep-C Trial, the National Institute of Diabetes and Digestive and Kidney Diseases Central Repositories or the National Institute of Diabetes and Digestive and Kidney Diseases. We thank Regina Riedl for access to R code, the reviewers for helpful suggestions and comments and the Technical University Munich Women in Science fund for sponsoring portions of this research.
References
- 1.Cox C, Rothwell S, Madans J, Finucane F, Freid V, Kleinman J, Barbano H, Feldman J. Plan and operation of the NHANES I Epidemiologic Followup Study, 1987. Vital Health Stat Ser 1. 1992;27:1–190. [PubMed] [Google Scholar]
- 2.Gail M, Brinton L, Byar D, Corle D, Green S, Schairer C, Mulvihill J. Projecting individualized probabilities of developing breast cancer for white females who are being examined annually. Journal of the National Cancer Institute. 1989;81(24):1879–1886. doi: 10.1093/jnci/81.24.1879. [DOI] [PubMed] [Google Scholar]
- 3.Janssens ACJW, Deng Y, Borsboom GJJM, Eijkemans MJC, Habbema JDF, Steyerberg EW. A new logistic regression approach for the evaluation of diagnostic test results. Medical Decision Making. 2005;25(2):168–177. doi: 10.1177/0272989X05275154. [DOI] [PubMed] [Google Scholar]
- 4.Ankerst DP, Groskopf J, Day JR, Blase A, Rittenhouse H, Pollock BH, Tangen C, Parekh D, Leach RJ, Thompson I. Predicting prostate cancer risk through incorporation of prostate cancer gene 3. The Journal of Urology. 2008;180(4):1303–1308. doi: 10.1016/j.juro.2008.06.038. [DOI] [PubMed] [Google Scholar]
- 5.Gu W, Pepe M. Estimating the capacity for improvement in risk prediction with a marker. Biostatistics. 2009;10(1):172–186. doi: 10.1093/biostatistics/kxn025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ankerst DP, Koniarski T, Liang Y, Leach RJ, Feng Z, Sanda MG, Partin AW, Chan DW, Kagan J, Sokoll L, et al. Updating risk prediction tools: A case study in prostate cancer. Biometrical Journal. 2012;54(1):127–142. doi: 10.1002/bimj.201100062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hand D, Yu K. Idiot's Bayes - not so stupid after all? International Statistical Review. 2001;69(3):385–398. [Google Scholar]
- 8.Albert A. On the use and computation of likelihood ratios in clinical chemistry. Clinical Chemistry. 1982;28(5):1113–1119. [PubMed] [Google Scholar]
- 9.Spiegelhalter DJ, Knill-Jones RP. Statistical and knowledge-based approaches to clinical decision-support systems, with an application in gastroenterology. Journal of the Royal Statistical Society Series A. 1984;147(1):35–77. [Google Scholar]
- 10.Chatterjee N, Chen YH, Maas P, Carroll RJ. Constrained maximum likelihood estimation for model calibration using summary-level information from external big data sources. Journal of the American Statistical Association. 2016;111(513):107–117. doi: 10.1080/01621459.2015.1123157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Anderson TW. An Introduction to Multivariate Statistical Analysis. 2nd. Wiley; New York: 1984. [Google Scholar]
- 12.Grill S, Fallah M, Leach R, Thompson I, Hemminki K, Ankerst D. A simple-to-use method incorporating genomic markers into prostate cancer risk prediction tools facilitated future validation. Journal of Clinical Epidemiology. 2015;68(5):563–573. doi: 10.1016/j.jclinepi.2015.01.006. [DOI] [PubMed] [Google Scholar]
- 13.Gail M, Pfeiffer R, Wheeler W, Pee D. Probability of detecting disease-associated single nucleotide polymorphisms in case-control genome-wide association studies. Biostatistics. 2008;9(2):201–215. doi: 10.1093/biostatistics/kxm032. [DOI] [PubMed] [Google Scholar]
- 14.Jing Q. Combining parametric and empirical likelihoods. Biometrika. 2000;87(2):484–490. [Google Scholar]
- 15.Han P, Lawless J. Comment. Journal of the American Statistical Association. 2016;111(513):118–121. doi: 10.1080/01621459.2016.1149399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Prokunina-Olsson L, Muchmore B, Tang W, Pfeiffer R, Park H, Dickensheets H, Hergott D, Porter-Gill P, Mumy A, Kohaar I, et al. A variant upstream of IFNL3 (IL28B) creating a new interferon gene IFNL4 is associated with impaired clearance of hepatitis c virus. Nature Genetics. 2013;45(2):164–171. doi: 10.1038/ng.2521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pepe MS. The statistical evaluation of medical tests for classification and prediction. Oxford University Press; 1994. [Google Scholar]
- 18.Brier GW. Verification of forecasts expressed in terms of probability. Monthly Weather Review. 1950;78:1–3. [Google Scholar]
- 19.Chan SF, Deeks JJ, Macaskill P, Irwig L. Three methods to construct predictive models using logistic regression and likelihood ratios to facilitate adjustment for pretest probability give similar results. Journal of Clinical Epidemiology. 2008;61(1):52–63. doi: 10.1016/j.jclinepi.2007.02.012. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.