Abstract
How prevalent is dyslexia? A definitive answer to this question has been elusive because of the continuous distribution of reading performance and predictors of dyslexia and because of the heterogeneous nature of samples of poor readers. Samples of poor readers are a mixture of individuals whose reading is consistent with or expected based on their performance in other academic areas and in language, and individuals with dyslexia whose reading is not consistent with or expected based on their other performance. In the present article, we replicate and extend a new approach for determining the prevalence of dyslexia. Using model-based meta-analysis and simulation, three main results were found. First, the prevalence of dyslexia is better represented as a distribution that varies as a function of severity as opposed to any single-point estimate. Second, samples of poor readers will contain more expected poor readers than unexpected or dyslexic readers. Third, individuals with dyslexia can be found across the reading spectrum as opposed to only at the lower tail of reading performance. These results have implications for screening and identification, and for recruiting participants for scientific studies of dyslexia.
Keywords: dyslexia, reading-disability, prevalence, diagnosis, Bayesian models
Dyslexia refers to a specific learning disability in reading. Perhaps the most widely used definition of dyslexia is a consensus definition developed from a partnership between the International Dyslexia Association, the National Center for Learning Disabilities, and the National Institute for Child Health and Human Development (Lyon, Shaywitz, & Shaywitz, 2003):
Dyslexia is a specific learning disability that is neurobiological in origin. It is characterized by difficulties with accurate and/or fluent word recognition and by poor spelling and decoding abilities. These difficulties typically result from a deficit in the phonological component of language that is often unexpected in relation to other cognitive abilities and the provision of effective classroom instruction. Secondary consequences may include problems in reading comprehension and reduced reading experience that can impede growth of vocabulary and background knowledge. (p. 2)
When dyslexia is characterized as a specific learning disability, two key characteristics emerge. First, individuals with specific learning disabilities have weaknesses in specific processes rather than having more generalized weakness in overall language or cognitive functioning (Grigorenko et al., 2019). For dyslexia, the most common processing weakness is a deficit in phonological processing, which refers to the use of speech-based coding when processing oral or written language (Wagner & Torgesen, 1987). Second, the reading problem is unexpected (Fletcher, Lyon, Fuchs, & Barnes, 2019). Different operational definitions of reading disability such as IQ-achievement discrepancy, inadequate response to instruction (RTI), and patterns of strengths and weaknesses (PASW) represent alternative approaches for operationalizing unexpected underachievement. Although the consensus definition was developed close to two decades ago, a recent survey of over 30 international dyslexia researchers and practitioners supported maintaining the definition without changes (Dickman, 2017).
Documented cases of individuals with dyslexia can be traced back to the 17th century (Grigorenko et al., 2019). The earliest cases involved acquired dyslexia, which refers typically to adults who learned how to read but could no longer read after a stroke or traumatic brain injury despite being otherwise intact. Subsequently, children with apparent cases of developmental dyslexia were described who were unable to learn to read despite being able to do mathematics and who did not suffer from obvious brain injury.
Prevalence
How prevalent is dyslexia? Knowing its prevalence is important for several reasons. For policy and practice, comparing existing rates of identification in school districts, states, or nations with known prevalence rates could be useful for determining whether under- or over-identification is occurring. Knowing prevalence can also be useful for identification in at least two ways. When inferences from test data and other sources of information that are not completely determinative are made, it is useful to know how common or rare a possible condition is. Less evidence may be required to support the existence of relatively common conditions whereas more evidence might be required to support the existence of a rare condition. The second way prevalence can be useful is in a mathematically more formal way in Bayesian diagnostic models that begin by using prevalence to determine a base-rate probability that is updated with additional information. Finally, it is confusing to individuals with dyslexia, their families, and professionals when disparate prevalence estimates are reported. Searching for what the prevalence of dyslexia is will turn up rates ranging from less than 5 percent to 1 in 5 or 20 percent.
A definitive answer to the question of how prevalent dyslexia is has been elusive for at least three reasons. First, indicators of dyslexia including reading difficulties tend to be continuously distributed in the population (Fletcher et al., 2019). This requires placing a cut-point on a continuous distribution for making the determination that a condition is present. Where the cut-point is placed can affect prevalence estimates. Second, different operational definitions are likely to yield different prevalence estimates. Of particular importance is whether the operational definition requires unexpected poor performance (i.e., poor performance relative to the individual’s performance in other academic areas and in language), absolute poor performance (i.e., poor performance relative to peers or state standards), or both. Finally, estimating prevalence is made difficult because of unreliability in commonly used identification procedures.
Effects of Cut Points used for Identification on Prevalence
How prevalent dyslexia is depends upon the severity or cut-off used for identification. Common estimates of the prevalence of dyslexia fall in the range of 3 to 7 percent when specifying a criterion of scoring 1.5 standard deviations or more below the mean on measures of reading (Fletcher et al., 2019, Peterson & Pennington, 2012; Snowling & Melby-Lervag, 2016). Similar estimates have been attained from cross-cultural studies (Moll, Kuntz, Neuhoff, Bruder, & Shulte-Korne, 2014; Snowling & Melby-Lervag, 2016). Prevalence estimates are higher when the cut-off used for identification is less stringent. For example, by applying a cut-off of scoring at the 25th percentile in reading (which corresponds to approximately two-thirds of a standard deviation) and/or an IQ-achievement regression-based definition of 1.5 standard deviations, prevalence was estimated to be 17.4 percent of the school-age population (Shaywitz et al., 1992). However, most estimates of prevalence fall below 10 percent (Hoeft, McCardle, & Pugh, 2015).
Effects on Prevalence of Whether Poor Absolute Performance, Relative Performance, or Both are Required
An issue that is not clarified by the consensus definition described previously is whether the “difficulties with accurate and/or fluent word recognition and by poor spelling and decoding abilities” are determined in relation to absolute poor performance (i.e., poor performance relative to peers or grade-level standards) or relative poor performance (i.e., poor performance relative to the individual’s performance in other areas), or both. In other words, is it necessary to perform more poorly than one’s peers or to fail to meet expected standards to be considered to have dyslexia, or is it sufficient to perform more poorly in reading than in other areas such as mathematics or spoken language?
This issue turns out to be relevant to public policy and practice (see Fletcher et al., 2019, pp. 17–21, for an informative discussion of this issue). In the United States, for example, dyslexia is mentioned in the current statutory definition of specific learning disability which came with the adoption of Public Law 94–142 (Education of All Handicapped Children Act in 1975).
The term “specific learning disability” means a disorder in one or more of the basic psychological processes involved in understanding or in using language, spoken or written, which may manifest itself in an imperfect ability to listen, speak, read, write, or to do mathematical calculations. The term includes conditions such as perceptual handicaps, brain injury, minimal brain dysfunction, dyslexia (italics added), and developmental aphasia. The term does not include children who have learning disabilities, which are primarily the result of visual, hearing, or motor handicaps, or mental retardation, or emotional disturbance, or of environmental, cultural, or economic disadvantage (U.S. Office of Education, 1968, p. 34).
This statutory definition mentions no requirement for absolute poor performance. To be implemented in policy and practice, regulations must be adopted to accompany statutory definitions. The initial regulatory definition was provided by the U.S. Office of Education in 1977.
[A child must exhibit] severe discrepancy between achievement and intellectual ability in one or more of the areas: (1) oral expression; (2) listening comprehension; (3) written expression; (4) basic reading skill; (5) reading comprehension; (6) mathematics calculation; or (7) mathematical reasoning. The child may not be identified as having a specific learning disability if the discrepancy between ability and achievement is primarily the result of: (1) a visual, hearing, or motor handicap; (2) mental retardation; (3) emotional disturbance; or (4) environmental, cultural, or economic disadvantage. (U.S. Office of Education, 1977, p. G1082)
This initial regulatory definition required relative poor performance (i.e., poor performance relative to intellectual ability) but not absolute poor performance (i.e., poor performance relative to one’s peers or grade-level standards). Public Law 94–242 was reauthorized in 2004 as the Individuals with Disabilities Education Act (IDEA), maintaining the original statutory definition provided earlier, but changing regulations to allow for alternative methods for identification. States were not prohibited from continuing to use discrepancy between achievement and intellectual ability but could not require use of this definition. They also were required to permit identification on the basis of response to scientific, research-based intervention, and were allowed but not required to permit the use of other alternative research-based definitions (U. S. Department of Education, 2006, p. 46786).
Finally, the Office of Special Education and Rehabilitation Services within the U.S. Department of Education issued revised regulations that included a requirement of absolute as opposed to relative poor performance. A child has a specific learning disability if:
The child does not achieve adequately for the child’s age or meet state-approved grade-level standards (italics added) in one or more of the following areas, when provided with learning experiences and instruction appropriate for the child’s age or State-approved grade-level standards: Oral expression, listening comprehension, written expression, basic reading skills, reading fluency skills, reading comprehension, mathematical calculation, mathematics problem-solving; or
The child does not make sufficient progress to meet age or state-approved to meet age or state-approved grade-level standards in one or more of the areas identified in 34 CFR 300.309(a) (1) when using a process based on the child’s response to scientific research-based intervention; or the child exhibits a pattern of strengths and weaknesses in performance, achievement, or both, relative to age, state-approved grade-level standards, or intellectual development, that is determined by the group to be relevant to the identification of a specific learning disability using appropriate assessments… (U.S. Department of Education, 2006, pp. 46786–46787).
How requiring relative versus absolute levels of poor performance affects prevalence is demonstrated by a study that reported one of the highest prevalence estimates of 17.4 percent. This estimate came from applying a cut-off of scoring at the 25th percentile in reading (which corresponds to approximately two-thirds of a standard deviation) and/or an IQ-achievement regression-based definition of 1.5 standard deviations (Shaywitz et al., 1992). Were it not for the limited range of the sample used, the expected prevalence rate of requiring either low absolute performance (25th percentile in reading) or low relative performance (1.5 standard deviation difference between IQ and achievement regardless of the level of achievement) would be over 30 percent (Fletcher et al., 2019).
The Problem of Poor Accuracy of Identification of Individuals with Dyslexia
Identification of individuals with dyslexia is difficult to do reliably (Wagner et al., 2011). Part of the reason for unreliability is measurement error, which affects identification particularly under three conditions. The first is when identification is a categorical decision but the underlying dimension is continuous rather than categorical. Identification then is based on which side of an arbitrary cut-point on a continuous distribution an individual’s score falls (Francis et al., 2005). The second condition is when the disorder has a relatively low prevalence or base-rate (e.g., under 10 percent). This is because the low prevalence means that the cut-point is near an end of the distribution, and individuals who are identified are necessarily close to the cut-point. Measurement error then can leave individuals on opposite sides of a nearby cut-point if measured on multiple occasions. This is why accuracy for the determination that a low-base rate condition is not present is usually higher than accuracy for determination that it is present. The third condition is when diagnosis relies primarily on a single criterion as opposed to multiple criteria. By combining multiple criteria, measurement error is reduced. Our understanding of some of the reasons for unreliability in identification can inform the development of more reliable models of identification. For example, models that combine multiple sources of information and that take into account prevalence should provide more reliable identification (Wagner, 2018).
Waesche, Schatschneider, Mane, Ahmed, and Wagner (2011) reported a study of agreement among alternative operational definitions of dyslexia applied to the same sample. The agreement between an aptitude-achievement discrepancy definition and a response to instruction or intervention (RTI) definition was only 31 percent. The agreement between an aptitude-achievement discrepancy definition and a low-achievement based definition was only 32 percent. In addition to poor agreement among alternative operational definitions, the longitudinal stability of all the definitions was poor: One-year stabilities for diagnosis based on the alternative operational definitions of dyslexia were 24, 34, and 41 percent for the discrepancy, RTI, and low-achievement operational definitions respectively. Schatschneider, Wagner, Hart, and Tighe (2016) used simulation to show that poor agreement and stability among alternative identification models occurred even when there was no true change in status across time (i.e., individuals did not change over time in whether they had a learning disability). Others have reported similarly poor levels of agreement and longitudinal stability (Barth et al., 2008; Fuchs, Fuchs & Compton, 2004; Wagner et al., 2011). All of these operational definitions primarily relied on a single criterion (e.g., poor decoding, IQ-achievement discrepancy, or inadequate response to instruction/intervention).
Approaches for Improved Identification
Hybrid Models.
One approach to reducing measurement error is to use hybrid models that incorporate multiple indicators or criteria (Fletcher, Lyon, Fuchs, & Barnes, 2019; Wagner et al., 2011). We have been investigating a version of a hybrid model we refer to as a constellation model because it incorporates a constellation of symptoms and indicators (Wagner, Spencer, Quinn, & Tighe, 2013). The constellation model differentiates causes, consequences, and correlates of dyslexia. The model includes three causes. The first is impaired phonological processing; the second is genetic risk; and the third is environmental influences that include quality and quantity of educational instruction and intervention. Beginning with phonological processing, impaired phonological processing predicts the development of dyslexia regardless of the written script to be learned (Branum-Martin et al., 2012; Song et al., 2016; Swanson et al., 2003). Genetic risk for dyslexia has been shown by behavioral genetic studies, and a meta-analysis has shown that a family history of reading problems increases the probability of having dyslexia by a factor of four (Snowling & Melby-Lervag, 2016). Finally, the importance of environmental influences is demonstrated by the fact that effective reading instruction and intervention, when required, reduces the incidence and severity of cases of dyslexia, although it does not eliminate the occurrence (VanDerHeydan, Witt, & Gilbertson, 2007).
Turning to potential correlates, ADHD co-occurs with reading disability from 30 to 50 percent of the time (Willcutt et al., 2003), and co-occurring math disability more than doubles the chances of having dyslexia (Joyner & Wagner, 2020). The prevalence of severe reading disability also is greater for males than females, with the ratio of males to females increasing with the severity of the reading problem (Quinn and Wagner, 2015).
The constellation model predicts four near-term consequences of dyslexia: poor decoding (e.g., nonword decoding accuracy and fluency) (Hermann, Matyas, & Pratt, 2006; Lyon, Shaywitz, & Shaywitz, 2003; Stanovich, 1988); impoverished sight-word vocabulary (e.g., real words that are decoded automatically) (Ehri, 1988); poor response to instruction and intervention (Fletcher et al., 2019; Fletcher & Vaughn, 2009); and listening comprehension better than reading comprehension (Badian, 1999; Stanovich, 1991a; Spencer et al., 2014).
Spencer et al. (2014) carried out a large-scale study (N = 31,339) of students who were followed longitudinally from first to second grade. They implemented a dimensional model and a categorical model based on the four consequences of dyslexia: limited sight-word vocabulary, poor decoding, minimal response to instruction, and listening comprehension better than reading comprehension. For the dimensional model, the four variables served as indicators of a single latent variable of reading ability/disability. Confirmatory factor analysis yielded an excellent model fit (χ2(2) = 263.4; Comparative Fit Index = .99; Tucker Lewis Index = .97; Root Mean Square Error of Approximation = .065 with a 95% confidence interval between .058 and .071). The one-year stability was 0.88 which was substantial. The categorical version of the model was based on the number of indicators that were present. Over the one-year time period, the stability of the model approached twice that of typical traditional models.
Bayesian Models.
Bayesian models are commonly used in medical diagnosis and policy (Spiegelhalter, Abrams, & Myles, 2004). Consider the case of mammography for detecting breast cancer, for which the test is not completely accurate. The probability that a woman with breast cancer will get a positive mammogram is .75. Conversely, the probability that a woman without breast cancer will get a positive mammogram is .1. What is the probability that a woman with a positive mammogram actually has breast cancer? It depends on her age. If she is in her 40s, breast cancer is rare with a prevalence of just over 1 percent (.014). Applying Bayes theorem to these data gives the answer that the probability that a woman in her 40s who has a positive mammogram actually has breast cancer is less than 10 percent (.096). For women in their 60s or 70s, the chances are higher because the prevalence is higher.
Bayesian models are flexible in that they can incorporate essentially any kind of predictive information. They can be more accurate than other models, especially when the data are not completely determinative, the condition is characterized by relatively low base rates or prevalence, and when informative priors (i.e., prevalence estimates) are available.
For an example of using a Bayesian model to estimate the probability of the presence of dyslexia, Wagner et al. (2019) operationally defined dyslexia as scoring at or below the 5th percentile on a factor score from the Spencer et al. (2014) study based on the four indicators of poor decoding, impoverished sight word vocabulary, poor response to instruction, and listening comprehension better than reading comprehension. Because they chose to define dyslexia as scoring at or below the 5th percentile, the prior probability of having dyslexia was 5 percent. They updated the prior probability based on additional data. For example, if the individual is female, the chance of having dyslexia goes down, from 5 to 3 percent; if male, the chance goes up, from 5 to 7 percent. Co-occurring ADHD increases the chances of having dyslexia fourfold, from 5 to 19 percent. Scoring at or below the 20th percentile on a battery of first-grade predictors triples the chances of having dyslexia, from 5 to 15 percent. Having an affected parent or sibling increases the chances fivefold, from 5 to 26 percent. Combinations of risk factors result in considerably more risk. For example, being male with ADHD increases the chances from 5 to 24 percent. Add in an affected parent or sibling and the chances increase to 76 percent. Finally, add in scoring low on the predictor battery and chances increase to 92 percent (Wagner et al., 2019)!
These probabilities were generated by applying Bayes’ theorem sequentially to data from Spencer et al. (2014). However, two simplifying assumptions were made. The first simplifying assumption, which only affects the probabilities from combinations of risk factors, was that the predictors were independent. This assumption is necessitated because Bayes theorem was applied sequentially without regard to possible correlations among the predictors. Fortunately, the assumption of independent predictors can be relaxed by using either Bayesian multiple regression for dyslexia as a continuous outcome or Bayesian logistic regression for dyslexia as a categorical outcome. For these models, Markov Chain Monte Carlo (MCMC) is used to generate parameter estimates and probabilities.
The second simplifying assumption is that the incidence rate of dyslexia is known, and that it is a discrete number. This assumption is likely to be incorrect based on the previously discussed information about the prevalence of dyslexia. Better estimates of the prevalence of dyslexia are required for developing useful Bayesian models of identification.
A New Approach to Estimating the Prevalence of Dyslexia
Although consensus suggests that prevalence depends upon severity of the reading problem—with lower rates for more severe problems—this consensus has not been incorporated in prevalence estimates; rather, it has been used to justify differences in proposed estimates. Wagner et al. (2019) proposed that no single prevalence estimate is correct, but rather that there is a distribution of prevalence as a function of severity. Creating this distribution required picking an operational definition that would be sufficient for determining prevalence.
As mentioned previously, there is consensus that a core feature of dyslexia is the concept of unexpectedness (Grigorenko et al., 2019), thereby distinguishing dyslexia from mere poor reading. On its face, the concept of unexpectedness implies a discrepancy-based definition (i.e., performance discrepant from predicted performance). Because of problems associated with an IQ-achievement discrepancy definition, a number of researchers have proposed replacing the IQ-achievement discrepancy with a difference between listening and reading comprehension levels (Aaron, 1991; Badian, 1999; Beford-Fuell, Geiger, Moyse, & Turner, 1995; Erbeli, Hart, Wagner, & Taylor, 2018; Spring & French, 1990; Stanovich, 1991b). Poor reading comprehension relative to listening comprehension would seem to have a functional use in the context of assistive technology. Assistive technology in the form of text to speech improves reading comprehension for individuals with reading disability or dyslexia (Wood, Moxley, Tighe, & Wagner, 2018). However, because text-to-speech essentially turns a reading-comprehension task into a listening-comprehension task, there is no reason to expect improvement for an individual whose listening comprehension is no better than his or her reading comprehension.
Wagner et al. (2019) did not propose using a discrepancy between listening comprehension and reading comprehension as a method for identifying individuals with dyslexia. Recall that no single-indicator model will have sufficient reliability. What they proposed was that a discrepancy between listening and reading comprehension could serve as a proxy for dyslexia to be useful for studying prevalence at population levels but not sufficient at for identification at the level of the individual. This distribution of prevalence had two potential uses. First, it could be used to estimate how many individuals with dyslexia would be expected at various levels of reading proficiency. Second, it could be used as a source of informative priors for a Bayesian model of identification.
They began by using model-based meta-analysis to estimate the population correlation between listening and reading comprehension. The meta-analysis they used was from Quinn and Wagner (2018). They then created a simulated dataset based on the meta-analytic results, and used the distribution of the discrepancy between listening comprehension and reading comprehension to examine the prevalence of dyslexia as a function of severity. They identified two kinds of readers: Unexpected poor readers (i.e., readers with dyslexia) were readers whose level of reading was substantially lower than their level of listening comprehension; expected poor readers were those whose level of reading was consistent with their level of listening comprehension.
There were three main conclusions from Wagner et al. (2019). First, prevalence is better conceptualized as a distribution that varies as a function of severity, and this distribution can be examined. Second, samples of poor readers will contain more expected poor readers than unexpected or dyslexic readers. Third, individuals with dyslexia occur across the reading spectrum as opposed to only existing at the lower tail of reading performance.
For the present study, we sought to replicate and extend the results of Wagner et al. (2019) by carrying out a meta-analysis of correlations obtained from nationally-normed standardized tests. Regarding replication, we carried out a new meta-analysis that was independent of the meta-analysis by Quinn and Wagner (2018) that was the basis of the previous study. Regarding extending the results Wagner et al. (2019), we examined prevalence at multiple levels of both poor reading, and discrepancy between listening comprehension and reading comprehension, instead of being limited to a single level. Finally, we sought to address a potential limitation of the previous study, namely that the results could have been affected by publication bias. Publication bias refers to the tendency for studies with statistically significant results to have a greater chance of being published than studies with non-significant results (Cooper, Hedges, & Valentine, 2019). A consequence of publication bias is inflated parameter estimates, which affects the results of studies.
We chose nationally normed tests for the following reasons. First, the reported correlations are not likely to be inflated by publication bias. Tests are not subject to the peer-review journal publication process that can lead to publication bias. Second, the results are based on large, nationally representative samples (total N was 82,242 for the included tests). Third, they provide an independent replication of the Wagner et al. (2019) study because standardized tests are not typically identified using common meta-analytic methods and databases. Indeed, no standardized tests were included in the Quinn and Wagner (2018) meta-analysis that was the basis of Wagner et al., 2019. Fourth and finally, they typically provide independent data for multiple ages or grades which facilitates testing for age or grade as moderators of the correlation between listening comprehension and reading comprehension.
Method
A model-based meta-analysis (Becker & Aloe, 2019) was carried out to calculate an average weighted correlation between listening and reading comprehension. An initial search was carried of the databases ProQuest, ERIC, Google Scholar and Pubmed. The search terms were “standardized measure(s)” and “norm referenced” and “reading” and English and intercorrelation, as well as search combinations with decoding, listening comprehension, reading comprehension and Phono*. These searches returned large numbers of articles that generally did not provide specific assessments meeting the search requirements. We altered our search strategy and carried out a Google search using the search string standardized measures of reading. Through this we found the Southwest Educational Development Laboratory (SEDL) reading assessment data base (www.sedl.org/reading/rad/list.html). We found additional assessments from an early reading assessment guiding tool on the Reading Rockets website (www.readingrockets.org) and from the Wrightslaw reading assessment list (www.wrightslaw.com/bks/aat/ch6.reading.pdf).
The search was completed in April, 2019, yielding 91 assessments. The following inclusionary criteria were then applied: (1) norm referenced; (2) nationally representative norming sample; (3) in English; (4) included subtests for measuring listening comprehension, reading comprehension, vocabulary, decoding, and phonological awareness; (5) correlation matrix of subtests and subtest reliability available; and (6) included data from multiple ages or grades. For the present analyses, only the correlation between listening comprehension and reading comprehension was of interest. The requirement of three additional subtests beyond listening comprehension and reading comprehension was because the present study is part of a larger effort that is directed at specific reading comprehension disability in addition to dyslexia.
Applying the inclusionary criteria yielded the following nine assessments: the Kaufman Test of Educational Achievement (KTEA III) (2014), the Woodcock Johnson IV (WJ IV) (2011), the Iowa Test of Basic Skills (ITBS) (2003), The Wechsler Individual Achievement Test III (WIAT III) (2009), The Woodcock Reading Mastery Test III (WRMT III) (2003), the Early Reading Diagnostic Test (ERDA) (2003), The Oral and Written Language Scales II (OWLS II) (2011), The Brigance Comprehensive Inventory of Basic Skills II (CIBS II) (2010) and the Stanford Achievement Test 10 (SAT10) (2004).
Results
The correlations obtained between reading comprehension and listening comprehension are presented in Table 1. The correlations were substantial with a median correlation of .61. The reliabilities were adequate with median reliabilities of .78 for listening comprehension and .87 for reading comprehension.
Table 1.
Obtained Correlations Between Reading Comprehension (RC) and Listening Comprehension (LC) and Reported Reliabilities
| Measure | N | RCLC | Rel. RC | Rel. LC |
|---|---|---|---|---|
| KTEA Grade 1 | 200 | .48 | .91 | .83 |
| KTEA Grade 2 | 200 | .54 | .89 | .84 |
| KTEA Grade 3 | 200 | .58 | .88 | .77 |
| KTEA Grade 4 | 200 | .66 | .91 | .89 |
| KTEA Grade 5 | 200 | .61 | .82 | .84 |
| KTEA Grade 6 | 199 | .71 | .88 | .82 |
| KTEA Grade 7 | 199 | .59 | .84 | .85 |
| KTEA Grade 8 | 200 | .69 | .85 | .83 |
| KTEA Grade 9 | 149 | .71 | .87 | .86 |
| KTEA Grade 10 | 150 | .65 | .91 | .82 |
| KTEA Grade 11 | 150 | .74 | .90 | .83 |
| KTEA Grade 12 | 150 | .76 | .91 | .90 |
| KTEA 17–18 | 120 | .71 | .92 | .83 |
| KTEA 19–20 | 75 | .48 | .90 | .82 |
| KTEA 21–25 | 75 | .72 | .92 | .88 |
| WJIV Ages 6–8 | 825 | .53 | . | . |
| WJIV Ages 9–13 | 1572 | .56 | . | . |
| WJIV Ages 14–19 | 1685 | .61 | . | . |
| WIAT III Grade 1 | 100 | .42 | .89 | .82 |
| WIAT III Grade 2 | 100 | .63 | .87 | .84 |
| WIAT III Grade 3 | 100 | .65 | .82 | .89 |
| WIAT III Grade 4 | 100 | .62 | .79 | .76 |
| WIAT III Grade 5 | 100 | .58 | .91 | .84 |
| WIAT III Grade 6 | 100 | .62 | .86 | .81 |
| WIAT III Grade 7 | 100 | .57 | .87 | .88 |
| WIAT III Grade 8 | 100 | .52 | .86 | .78 |
| WIAT III Grade 9 | 100 | .53 | .83 | .85 |
| WIAT III Grade 10 | 100 | .66 | .85 | .84 |
| WIAT III Grade 11 | 100 | .58 | .85 | .77 |
| WIAT III Grade 12 | 100 | .60 | .86 | .83 |
| WMRT III Pre K - Grade 2 | 300 | .43 | .74 | .70 |
| WMRT III Grade 3–8 | 600 | .61 | .71 | .75 |
| WMRT III Grade 9–12 | 400 | .61 | .69 | .62 |
| WMRT III Age 18–25 | 100 | .59 | . | . |
| WMRT III Age 26–40 | 200 | .72 | . | . |
| WMRT III Age 41–79 | 200 | .60 | . | . |
| ERDA II Grade 1 | 97 | .40 | .79 | .74 |
| ERDA II Grade 2 | 100 | .41 | .84 | .74 |
| ERDA II Grade 3 | 100 | .28 | .88 | .74 |
| OWLS II Age 5–6 | 404 | .47 | . | . |
| OWLS II Age 7–21 | 1497 | .65 | . | . |
| CIBS II | 1411 | .58 | .70 | .80 |
| SAT 10 Grade | 2189 | .52 | .91 | .86 |
| SAT 10 Grade | 2550 | .65 | .91 | .84 |
| SAT 10 Grade | 1680 | .69 | .92 | .82 |
| SAT 10 Grade | 2336 | .73 | .93 | .85 |
| SAT 10 Grade | 2224 | .68 | .92 | .81 |
| SAT 10 Grade | 2510 | .71 | .92 | .85 |
| SAT 10 Grade | 1468 | .72 | .92 | .86 |
| SAT 10 Grade | 1507 | .68 | .92 | .85 |
| SAT 10 Grade | 774 | .68 | .92 | .85 |
| ITBS Level 6 | 7128 | .50 | .89 | .76 |
| ITBS Level 7 | 14870 | .48 | .91 | .70 |
| ITBS Level 8 | 14870 | .54 | .90 | .72 |
| ITBS Level 9 | 14978 | .55 | .91 | .74 |
Note. From Technical & Interpretive Manual Kaufman Test of Educational Achievement, Third Edition (2014) and Technical Manual. Woodcock-Johnson IV Technical Manual (2014), Technical Manual Wechsler Individual Achievement Test – Third Edition (2009), Woodcock Reading Mastery Tests – Third Edition Manual (2011), Early Reading Diagnostic Assessment – Second Edition Technical Manual (2003), The Oral and Written Language – Second Edition Manual (2011), The Brigance Comprehensive Inventory of Basic Skills (CIBS II) Standardization and Validation Manual, The Stanford Achievement Test Series Tenth Edition Technical Data Report (2004) and The Iowa Test of Basic Skills Standardization and Validation Manual (2010).
The ‘metafor’ package in R (Viechtbauer, 2010) was used for all analyses. A random effects model yielded an average weighted correlation between listening comprehension and reading comprehension of .603, with a standard error of .012, and a 95% confidence interval from .580 to .627. The difference between this correlation and the correlation from Quinn and Wagner (2018) used in the Wagner et al. (2019) analyses was .1, which replicates their results using an independent set of studies for the meta-analysis. In contrast to fixed-effects models that assume all studies are providing estimates of a single population effect size, random effects models assume that studies provide estimates of a distribution of effect sizes in the population. The choice of a random effects model was supported by the tau-squared estimate of heterogeneity of population effect sizes of .007 (p < .001). The significant Q value of 1459 (df = 59, (p < .001) indicates the presence of significantly more variability in effect sizes across studies than would be expected on the basis of sampling error. The I-squared value of 95.51% indicates that 95 percent of the variability in effect sizes across studies was attributable to heterogeneity of effect sizes as opposed to sampling error.
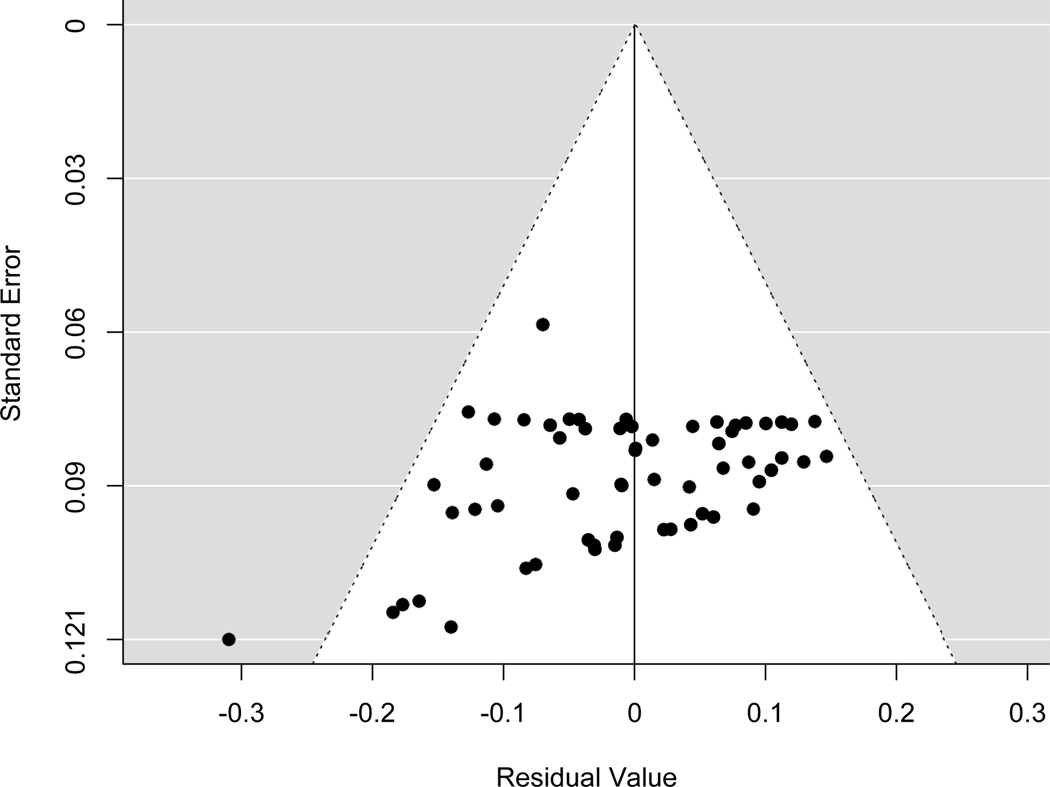
To determine whether grade or age moderated the correlation between listening and reading comprehension, we first converted grade to age to be able to analyze all of the studies together to maximize the sensitivity of the analysis. For the few samples that were multi-age, the median age was used. Age was a significant predictor of variability in effect sizes across studies with an estimate of .003 (p < .01), accounting for 9.81 percent of variability in effect sizes across studies. To determine whether the age effect was genuine or an artifact of age being correlated with third variables such as sample size or which assessments were used, two follow-up procedures were done.1 First, a funnel plot was created for residuals from the prediction of effect sizes by age and presented in Figure 1. The vertical orientation of the figure in the funnel plot and examining the pattern or points in the plot does not suggest that the age effect was a function of sample size. Second, for a more direct test, a second regression was run with age, sample size, and dummy variables representing assessments. The age effect remained at the same value of .003 but its significance level increased to p = .001. Sample size was not a significant predictor of effect size. Effect sizes did vary significantly across assessments.
Figure 1.
Funnel plot of residuals after regressing effect sizes on age.
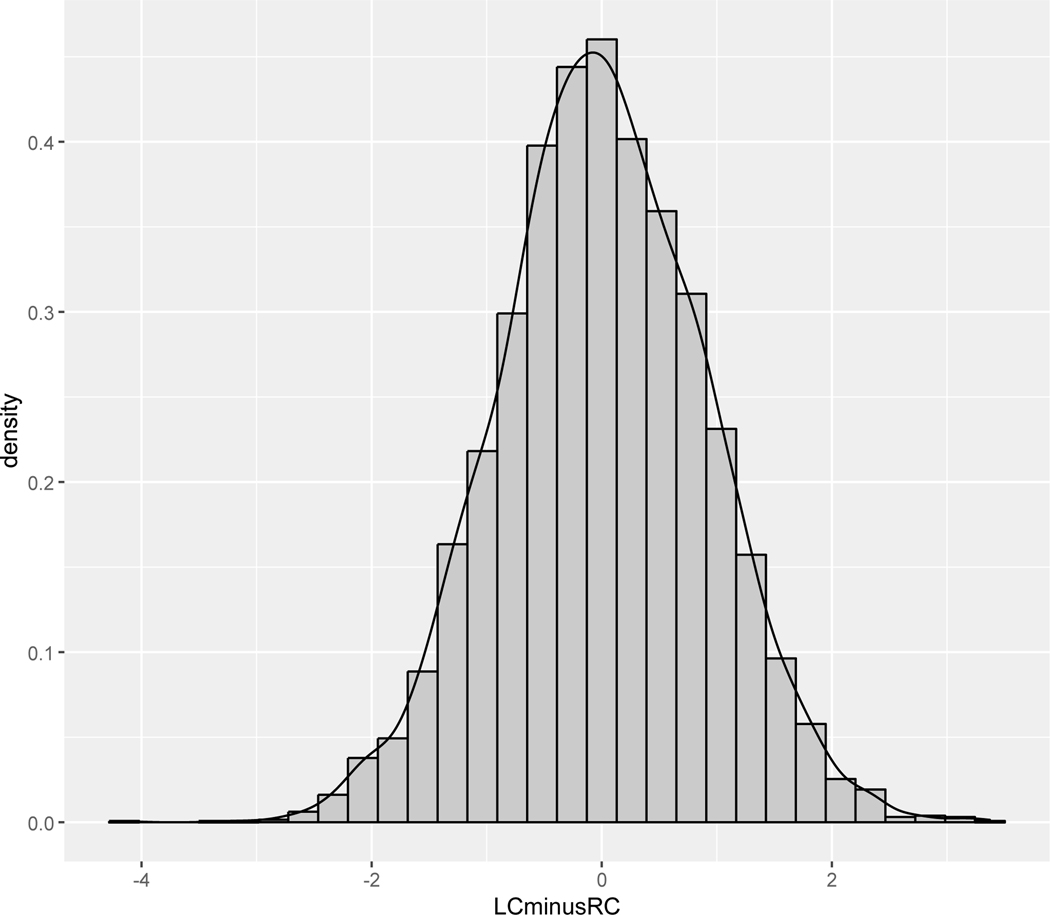
Next we created a simulated dataset with 5,000 observations using the mvrnorm function from the ‘MASS’ package in R (Venables & Ripley, 2002). The variables were listening comprehension and reading comprehension, and we created the variable of listening comprehension minus reading comprehension and included it in the dataset. The distribution of this listening comprehension minus reading comprehension is shown in Figure 2. Because both listening and reading comprehension were treated as standardized variables with means of 0, the overall mean of listening minus reading comprehension was also 0, and the standard deviation of the differences was 0.85.
Figure 2.
The distribution of the difference between listening comprehension and reading comprehension.
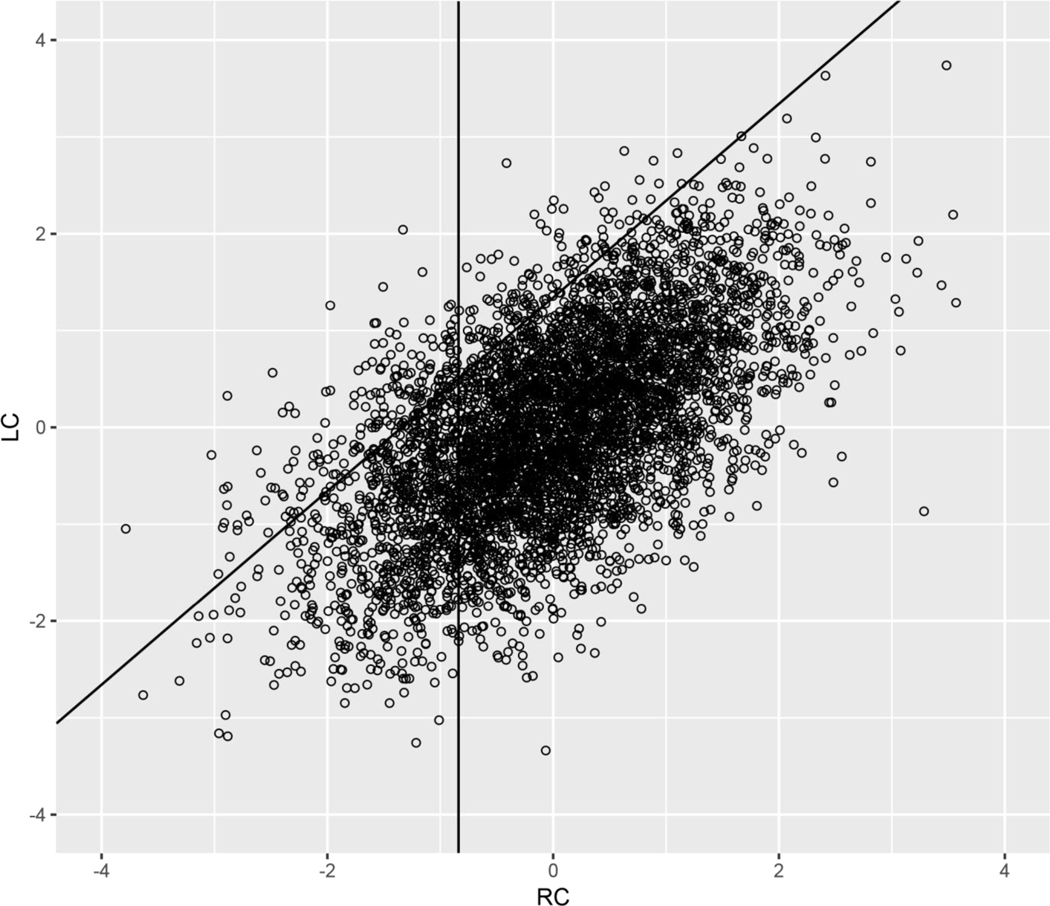
A scatterplot of reading comprehension by listening comprehension is presented in Figure 3. The distribution of the variable listening comprehension minus reading comprehension is represented as points on an imaginary vertical line drawn at any point of the reading comprehension distribution. The actual vertical line in Figure 3 demarcates the lowest 20 percent of readers. The normal distribution of listening comprehension minus reading comprehension can be seen by the concentration of points near the center of the vertical line relative to the fewer points in its tails. Turning to the diagonal line, points above this line represent unexpected poor reading as defined by a difference between listening and reading comprehension falling at or above 1.5 standard deviations (i.e., the 87th percentile or above size of the difference).
Figure 3.
Scatterplot of listening comprehension and reading comprehension. Points to the left of the vertical line represent scores of poor readers (i.e., the 20th %-ile in RC). Points above the diagonal line represent readers with listening comprehension better than reading comprehension (i.e., at or above 1.5 standard deviations above the mean in LC-RC discrepancy score).
Two main results are depicted in this scatterplot. First, among poor readers (i.e., the individuals represented by points to the left of the vertical line), more readers are expected (i.e., below the diagonal line) than unexpected (above the diagonal line). The second main point is that individuals whose reading comprehension is lower than their listening comprehension (i.e., individuals above the diagonal line) occur throughout the reading spectrum. They are not confined to the poor-reader segment.
Figure 3 represents arbitrarily chosen levels of poor reading (i.e., the 20th percentile cutoff) and of reading comprehension being worse than listening comprehension (i.e., 1.5 standard deviations above the mean or higher). We expand this analysis in Tables 2 and 4 by presenting results from three levels of poor reading (1, 1.5, and 2 standard deviations below the mean) and three levels of reading comprehension worse than listening comprehension (1, 1.5, and 2 standard deviations above the mean). Table 2 presents the percentages of poor readers who were unexpected (i.e., whose reading comprehension was worse than their listening comprehension). With only one exception, fewer than half of poor readers were unexpected. The rest had reading levels that were low but were consistent with their lower levels of listening comprehension. Table 3 presents the percentages of unexpected poor readers (i.e., individuals whose level of reading was worse than their level of listening comprehension) whose reading level nevertheless was above the poor reading cut-off. More discrepant individuals were found above rather than below the poor reader cut-offs examined for seven out of the nine comparisons that were done.
Table 2.
Percentage of Poor Readers whose Reading Comprehension is Discrepant from Listening Comprehension (i.e., Unexpected) at Three Levels of Poor Reading and Three Levels of Discrepancy
| Poor Reading Criterion Comprehension | Reading Comprehension Discrepant from Listening | ||
|---|---|---|---|
| 1 SD LC-RC | 1.5 SD LC-RC | 2.0 SD LC-RC | |
| −1 SD RC | 38% | 21% | 9% |
| −1.5 SD RC | 46% | 30% | 14% |
| −2.0 SD RC | 62% | 41% | 23% |
Table 3.
Percentage of Individuals whose Reading Comprehension is Discrepant from Listening Comprehension (i.e., Unexpected) but are Above the Poor Reader Cutoff at Three Levels of Poor Reading and Three Levels of Discrepancy
| Poor Reading Criterion Comprehension | Reading Comprehension Discrepant from Listening | ||
|---|---|---|---|
| 1 SD LC-RC | 1.5 SD LC-RC | 2.0 SD LC-RC | |
| −1 SD RC | 62% | 50% | 38% |
| −1.5 SD RC | 81% | 70% | 60% |
| −2.0 SD RC | 91% | 85% | 77% |
General Discussion
Our results replicate and extend those of Wagner et al. (2019). We used model-based meta-analysis and simulation to generate a distribution of the prevalence of dyslexia that varies as a function of severity. The results were highly similar to those of the previous study, as evidenced by comparing Figure 3 of the current study with Figure 2 of the previous one. In both studies, the difference between listening and reading comprehension was used as a proxy for unexpected reading difficulty or dyslexia. A discrepancy between listening and reading comprehension has been proposed as an operational definition of reading disability that is preferable to IQ-achievement discrepancy (Aaron, 1991; Badian, 1999; Beford-Fuell, Geiger, Moyse, & Turner, 1995; Spring & French, 1990; Stanovich, 1991). Although it indeed may be preferable to IQ-achievement discrepancy, it is clear that no approach to identification that relies primarily on any single criterion will be reliable at the level of the individual. However, our results and those of Wagner et al. (2019) support its use at the population level indicator to estimate the distribution of prevalence.
Results from the current study replicated two key results from Wagner et al. (2019). The first is that samples of poor readers will contain more expected poor readers (i.e., readers whose level of performance with print in on par with their level of performance in oral language) than unexpected poor readers (i.e., readers with dyslexia whose level of performance in reading is substantially lower than their level of performance in oral language). The second key result is that individuals whose level of performance in reading is substantially lower than their level of performance in oral language occur largely throughout the distribution of reading.
These results have implications for sample selection in scientific studies of dyslexia. Recruitment should target individuals whose reading is poor relative to their level of oral language instead of recruiting on the basis of poor reading relative to age or grade peers. They also have implications for screening for dyslexia. Approaches that rely on absolute rather than relative poor performance on predictors of reading, rudimentary aspects of reading such as letter knowledge, or reading itself will likely miss more individuals with dyslexia than it will correctly identify, and the majority of individuals identified will likely be expected rather than unexpected poor readers.
In addition to informing sample recruitment in studies of dyslexia and approaches to screening, an important potential use of a known distribution of the prevalence of dyslexia is as a distribution of informative priors for a Bayesian predictive model. Recall that expanding operational definitions of dyslexia to include multiple indicators should improve the reliability of diagnosis. Moving to Bayesian models with informative priors should result in additional improvement in diagnosis.
One issue that arises is that the conclusion that individuals with dyslexia occur throughout the reading spectrum is at odds with policy and practices that limit identification to individuals who are substantially behind their peers or state standards. We argue that science should inform public policy and practice rather than using public policy and practice to inform science. In the past, the definition of specific learning disability included the requirement that IQ needed to be equal or greater than 90. We now recognize that specific learning disabilities including dyslexia can occur throughout the range of cognitive and language abilities, which includes both lower than average and higher than average levels of functioning. Whether individuals with dyslexia whose level of reading performance is average or better than average relative to their peers should be eligible for special education services is an issue that reflects political and economic considerations in addition to scientific ones. At the very least, individuals with dyslexia and their families should know about their condition regardless of whether they are eligible for special education services at the present time. They might have better educational and occupational outcomes with access to accommodations and assistive technology such as text-to-speech (Wood et al., 2018).
Turning to limitations, it is important to validate our results with empirical datasets. Although an approach using model-based meta-analysis is likely to produce more stable results than would be obtained from individual empirical studies, it still is necessary to verify the distribution of dyslexia using ideally large-scale empirical datasets. A second limitation is that assumptions that were made need to be verified. For example, we assumed that both listening comprehension and reading comprehension are multivariate normally distributed variables. A consequence of this assumption is that the distribution of the difference between listening and reading comprehension is normally distributed and therefore symmetrical. These assumptions can be tested with empirical datasets.
Acknowledgments
The research described in this article was supported by Grant Number P50 HD52120 from the National Institute of Child Health and Human Development.
Footnotes
We thank an anonymous reviewer for raising the issue that the age effect might have been a result of its correlation with sample size or assessment and for suggesting the two strategies we adopted for examining this issue.
References
- Aaron PG (1991). Can reading disabilities be diagnosed without using intelligence tests? Journal of Learning Disabilities, 24(3), 178–186, 191. dx.DOI. 10.1177/002221949102400306 [DOI] [PubMed] [Google Scholar]
- Badian NA (1999). Reading disability defined as a discrepancy between listening and reading comprehension: A longitudinal study of stability, gender differences, and prevalence. Journal of Learning Disabilities, 32(2), 138–148. DOI. 10.1177/002221949903200204 [DOI] [PubMed] [Google Scholar]
- Barth AE, Stuebing KK, Anthony JL, Denton CA, Mathes PG, Fletcher JM, & Francis DJ (2008). Agreement among response to intervention criteria for identifying responder status. Learning and Individual Differences, 18, 296–307. DOI: 10.1016/j.lindif.2008.04.004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker BJ, & Aloe AM (2019). Model-based meta-analysis and related approaches. In Cooper HM, Hedges LV, & Valentine JC (Eds.), The handbook of research synthesis and meta-analysis (pp. 339–363). New York: Russell Sage. [Google Scholar]
- Beford-Fuell C, Geiger S, Moyse S, & Turner M. (1995). Use of listening comprehension in the identification and assessment of specific learning difficulties. Educational Psychology in Practice, 10(4), 207–214. https://DOI. 10.1080/0266736950100402 [DOI] [Google Scholar]
- Branum-Martin L, Tao S, Garnaat S, Bunta F, & Francis DJ (2012). Meta-analysis of bilingual phonological awareness: Language, age, and psycholinguistic grain size. Journal of Educational Psychology, 104(4), 932–944. dx. 10.1037/a0027755 [DOI] [Google Scholar]
- Breaux KC (2009). Wechsler Individual Achievement Tests III Technical Manual. San Antonio, TX: Pearson [Google Scholar]
- Carrow-Woolfolk E. (2011). Oral and written language scales, (2nd ed.). Torrance, CA: WPS. [Google Scholar]
- Cooper H, Hedges LV, & Valentine JC (2019). The handbook of research synthesis and meta-analysis (3d ed.). New York: Russell Sage Foundation. [Google Scholar]
- Dickman E. (2017). Do we need a new definition of dyslexia? The Examiner (International Dyslexia Association), 6(1). https://dyslexiaida.org/do-we-need-a-new-definition-of-dyslexia/ [Google Scholar]
- Ehri LC (1988). Grapheme-phoneme knowledge is essential for learning to read words in English. In Metsala JL & Ehri LC (eds.), Learning and teaching reading. London: British Journal of Educational Psychology Monograph Series II. [Google Scholar]
- Erbeli F, Hart SA, Wagner RK, & Taylor J. (2018). Examining the etiology of reading disability as conceptualized by the hybrid model. Scientific Studies of Reading, 22(2), 167–180. DOI: 10.1080/10888438.2017.1407321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher JM, Lyon GR, Fuchs LS, & Barnes MA (2019). Learning disabilities: From identification to intervention (2nd ed.). New York: Guilford. [Google Scholar]
- Fletcher JM & Vaughn S. (2009). Response to intervention: Preventing and remediating academic difficulties. Child Development Perspectives, 3, 30–37. DOI: 10.1111/j.1750-8606.2008.00072.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francis DJ, Fletcher JM, Stuebing KK, Lyon GR, Shaywitz BA, & Shaywitz SE (2005). Psychometric approaches to the identification of LD: IQ and achievement scores are not sufficient. Journal of Learning Disabilities, 38, 98–108. DOI: 10.1177/00222194050380020101 [DOI] [PubMed] [Google Scholar]
- French BF, & Glascoe FP (2010). Brigance comprehensive inventory of basic skills II standardization and validation manual. North Billerica, MA: Curriculum Associates. [Google Scholar]
- Fuchs D, Fuchs LS, & Compton D. (2004). Identifying reading disabilities by responsiveness-to-instruction: Specifying measures and criteria. Learning Disability Quarterly, 27, 216–227. dx.DOI. 10.2307/1593674 [DOI] [Google Scholar]
- Harcourt Educational Measurement (2004). Stanford technical data report. San Antonio, TX:Pearson. [Google Scholar]
- Grigorenko EL, Compton D, Fuchs L, Wagner RK, Willcutt E, & Fletcher JM (2019). Understanding, educating, and supporting children with specific learning disabilities: 50 years of science and practice. American Psychologist. Advance online publication. dx.doi. 10.1037/amp0000452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrmann JA, Matyas T, & Pratt C. (2006). Meta-analysis of the nonword reading deficit in specific reading disorder. Dyslexia: An International Journal of Research and Practice, 12(3), 195–221. DOI. 10.1002/dys.324 [DOI] [PubMed] [Google Scholar]
- Hoeft F, McCardle P, and Pugh K. (2015). The Myths and Truths of Dyslexia in Different Writing Systems. International Dyslexia Association. The Examiner. https://dyslexiaida.org/the-myths-and-truths-of-dyslexia/ [Google Scholar]
- Hoover HD, Dunbar SB, and Frisbie DA (2003). The Iowa tests: Guide to research and development. Chicago, IL: Riverside Publishing. [Google Scholar]
- Joyner RE, & Wagner RK (2020). Co-occurrence of Reading Disabilities and Math Disabilities: A Meta-Analysis. Scientific Studies of Reading, 1, 14–22. doi. 10.1080/10888438.2019.1593420 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaufman AS, & Kaufman NL (with Breaux KV) (2014). Technical and Interpretive Manual. Kaufman Test of Educational Achievement–Third Edition (KTEA-3). Bloomington, MN: NCS Pearson [Google Scholar]
- Lyon GR, Shaywitz SE, & Shaywitz BA (2003). A definition of dyslexia. Annals of Dyslexia, 53, 1–14. dx.DOI. 10.1007/s11881-003-0001-9 [DOI] [Google Scholar]
- McGrew KS, LaForte EM, & Schrank FA (2014). Technical Manual. Woodcock-Johnson IV. Rolling Meadows, IL: Riverside. [Google Scholar]
- Moll K, Kunze S, Neuhoff N, Bruder J, & Schulte-Korne(2014). Specific learning disorder: Prevalence and gender differences. PLoSOne. DOI: 10.1371/journal.pone.0103537 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen RL, & Pennington BF (2012). Developmental dyslexia. The Lancet, 379, 1997–2007. doi: 10.1016/S0140-6736(12)60198-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinn JM, and Wagner RK (2015). Gender Differences in Reading Impairment and the Identification of Impaired Readers: Results from a Large-Scale Study of At-Risk Readers. Journal of Learning Disabilities, 48(4):433–45. DOI: 10.1177/0022219413508323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Quinn JM, & Wagner RK (2018). Using meta-analytic structural equation modeling to study developmental change in relations between language and literacy. Child Development, 89, 1956–1969. Doi. 10.1111/cdev.13049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schatschneider C, Wagner RK, Hart SA, & Tighe EL (2016). Using simulations to investigate the longitudinal stability of alternative schemes for classifying and identifying children with reading disabilities, Scientific Studies of Reading, 20, 34–48. DOI: 10.1080/10888438.2015.1107072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaywitz SE, Escobar MD, Shaywitz BA, Fletcher JM, & Makuch R. (1992). Evidence that dyslexia may represent the lower tail of the normal distribution of reading ability. New England Journal of Medicine, 326, 145–150. DOI: 10.1056/NEJM199201163260301 [DOI] [PubMed] [Google Scholar]
- Snowling MJ, & Melby-Lervåg M. (2016). Oral language deficits in familial dyslexia: A meta-analysis and review. Psychological Bulletin, 142(5), 498–545. DOI: 10.1037/bul0000037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S, Georgiou GK, Su M, & Hua S. (2016). How well do phonological awareness and rapid automatized naming correlate with Chinese reading accuracy and fluency? A meta-analysis. Scientific Studies of Reading, 20(2), 99–123. dx. DOI. 10.1080/10888438.2015.1088543 [DOI] [Google Scholar]
- Spencer M, Wagner RK, Schatschneider C, Quinn JM, Lopez D, & Petscher Y. (2014). Incorporating RTI in a hybrid model of reading disability. Learning Disability Quarterly, 37, 161–171. DOI. 10.1177/0731948714530967 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiegelhalter DJ, Abrams KR, & Myles JP (2004). Bayesian approaches to clinical trials and health-care evaluation. West Sussex, England: John Wiley & Sons. [Google Scholar]
- Spring C, & French L. (1990). Identifying children with specific reading disabilities from listening and reading discrepancy scores. Journal of Learning Disabilities, 23(1), 53–58. 10.1177/002221949002300112 [DOI] [PubMed] [Google Scholar]
- Stanovich KE (1988). Explaining the differences between the dyslexia and the garden-variety poor reader: The phonological-core variable-difference model. Journal of Learning Disabilities, 21, 590–604. DOI: 10.1177/002221948802101003 [DOI] [PubMed] [Google Scholar]
- Stanovich KE (1991a). Discrepancy definitions of reading disability: Has intelligence led us astray? Reading Research Quarterly, 26(1), 7–29. [Google Scholar]
- Stanovich KE (1991b). Conceptual and empirical problems with discrepancy definitions of reading disability. Learning Disability Quarterly, 14(4), 269–280. dx.DOI. 10.2307/1510663 [DOI] [Google Scholar]
- Swanson HL, Trainin G, Necoechea DM, & Hammill DD (2003). Rapid naming, phonological awareness, and reading: A meta-analysis of the correlation evidence. Review of Educational Research, 73(4), 407–440. DOI. 10.3102/00346543073004407 [DOI] [Google Scholar]
- The Psychological Corporation. (2003). Early reading diagnostic assessment technical Manual (2nd ed.). San Antonio, TX: Pearson. [Google Scholar]
- U.S. Department of Education. (2006). 34 CFR Parts 300 and 301: Assistance to states for the education of children with disabilities and preschool grants for children with disabilities. Final rules. Federal Register, 71, 46540–46845. [Google Scholar]
- U.S. Office of Education. (1968). First annual report of the National Advisory Committee on Handicapped Children, Washington, DC: U.S. Department of Health, Education and Welfare. [Google Scholar]
- U.S. Office of Education. (1977). Assistance to states for education for handicapped children: Procedures for evaluating specific learning disabilities. Federal Register, 42, G1082-G1085. [Google Scholar]
- VanDerHeyden AM, Witt JC, & Gilbertson D. (2007). A multi-year evaluation of the effects of a response to intervention (RTI) model on identification of children for special education. Journal of School Psychology, 45(2), 225–256. dx.DOI. 10.1016/j.jsp.2006.11.004 [DOI] [Google Scholar]
- Venables WN & Ripley BD (2002) Modern Applied Statistics with S. Fourth Edition. Springer, New York. [Google Scholar]
- Viechtbauer W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1–48. DOI: 10.18637/jss.v036.i03 [DOI] [Google Scholar]
- Waesche JB, Schatschneider C, Maner JK, Ahmed Y, & Wagner RK, (2011). Examining agreement and longitudinal stability among traditional and RTI-based definitions of reading disability using the affected-status agreement statistic. Journal of Learning Disabilities, 44, 296–307. DOI: 10.1177/0022219410392048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner RK (2018). Why is it so difficult to diagnose dyslexia and how can we do it better? The Examiner, 7. Washington, DC: International Dyslexia Association. Retrieved from https://dyslexiaida.org/why-is-it-so-difficult-todiagnose-dyslexia-and-how-can-we-do-it-better/ [Google Scholar]
- Wagner RK, & Torgesen JK (1987). The nature of phonological processing and its causal role in the acquisition of reading skills. Psychological Bulletin, 101(2), 192–212. Doi. 10.1037/0033-2909.101.2.192 [DOI] [Google Scholar]
- Wagner RK, Edwards AA, Malkowski A, Schatschneider C, Joyner RE, Wood S, & Zirps FA (2019). Combining old and new for better understanding and predicting dyslexia. New Directions for Child & Adolescent Development, 165, 11–23. Doi. 10.1002/cad.20289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner RK, Spencer M, Quinn JM, & Tighe EL (2013, November). Towards a more stable phenotype of reading disability. Paper presented at the 8th Biennial Meeting of the Society for the Study of Human Development (SSHD), Fort Lauderdale, FL, USA. [Google Scholar]
- Wagner RK, Waesche JB, Schatschneider C, Maner JK, & Ahmed Y. (2011). Using response to intervention for identification and classification. In McCardle P, Lee JR, Miller B, & Tzeng O (Eds.), Dyslexia across languages: Orthography and the brain-gene-behavior link (pp. 202–213). Baltimore: Brookes Publishing. [Google Scholar]
- Willcutt EG, DeFries JC, Pennington BF, Smith SD, Cardon LR, & Olson RK (2003). Genetic etiology of comorbid reading difficulties and ADHD. In Plomin R, DeFries JC, Craig IW & McGuffin P (Eds.), Behavioral genetics in the postgenomic era (pp. 227–246) American Psychological Association, Washington, DC. DOI: 10.1037/10480-013 [DOI] [Google Scholar]
- Wood SG, Moxley JH, Tighe EL, Wagner RK (2018). Does use of text-to-speech and related read-aloud tools improve reading comprehension for students with reading disabilities? A meta-analysis. Journal of Learning Disabilities, 51, 73–84. DOI: 10.1177/0022219416688170 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodcock RW (2011). Woodcock reading mastery tests third edition manual (WRMT III).Bloomington, MN: NCS Pearson, Inc. [Google Scholar]