A toxicity cost function approach to optimal CPA equilibration in tissues.

Abstract

There is growing need for cryopreserved tissue samples that can be used in transplantation and regenerative medicine. While a number of specific tissue types have been successfully cryopreserved, this success is not general, and there is not a uniform approach to cryopreservation of arbitrary tissues. Additionally, while there are a number of long-established approaches towards optimizing cryoprotocols in single cell suspensions, and even plated cell monolayers, computational approaches in tissue cryopreservation have classically been limited to explanatory models. Here we develop a numerical approach to adapt cell-based CPA equilibration damage models for use in a classical tissue mass transport model. To implement this with real-world parameters, we measured CPA diffusivity in three human-sourced tissue types, skin, fibroid and myometrium, yielding propylene glycol diffusivities of 0.6 × 10⁻⁶ cm²/s, 1.2 × 10⁻⁶ cm²/s and 1.3 × 10⁻⁶ cm²/s, respectively. Based on these results, we numerically predict and compare optimal multistep equilibration protocols that minimize the cell-based cumulative toxicity cost function and the damage due to excessive osmotic gradients at the tissue boundary. Our numerical results show that there are fundamental differences between protocols designed to minimize total CPA exposure time in tissues and protocols designed to minimize accumulated CPA toxicity, and that “one size fits all” stepwise approaches are predicted to be more toxic and take considerably longer than needed.

Introduction

The ability to bank human tissues without compromising their viability is of paramount importance for transplantation and personalized medicine, translational research, biomarker discovery, and addressing the molecular basis of many diseases such as cancer. Tissue transplantation can be lifesaving (e.g., skin transplantation in severe burn cases) and/or life enhancing (e.g., replacing damaged ligaments) but suffers from a worldwide shortage of transplantable tissues according to the World Health Organization (WHO) [34]. Furthermore, the availability of diverse tissues cryobanked in a viable manner would enormously contribute to the emerging field of tissue engineering that also suffers from lack of a reliable cryopreservation method as identified by the Multi-Agency Tissue Engineering Science (MATES) [20]. Although some progress has been made in cryopreservation of certain tissues such as ovarian tissue and vein segments [33,36] preservation of many multicellular tissues and organs still remains challenging [15,21,35]. Typically, cryoprotective agents (CPAs) such as dimethylsulfoxide (DMSO), ethylene glycol (EG), and propylene glycol (PG) must be present both intra- and extracellularly to facilitate successful cryopreservation of tissues. However, addition and removal of such penetrating CPAs before and after cryopreservation, respectively, are challenging due to associated osmotic stresses and chemical toxicity of CPAs. In fact, mitigation of the CPA induced toxicity has been highlighted as one of the critical impediments of tissue and organ cryopreservation [28]. Consequently, innovative approaches are required to overcome such challenges. The objective of the present study was to develop an approach to optimize CPA addition toward minimizing osmotic stresses and chemical toxicity of CPAs.

Cryoprotectant equilibration and the response to ice concentrated media are the two facets of cellular cryobiological protocols most commonly covered by mathematical modeling. In these models, cells are typically assumed to have uniform, spatially independent extracellular concentrations and temperatures (see [3] for review). Spatial homogeneity and infinite bath media assumptions mean that ordinary differential equation models can be used to determine the intracellular state as a function of cryoprotocol. The transport equations typically used to describe the intracellular water volume W and moles of solute S as a function of time t:

$$\frac{dW}{dt}=-L_{\text{p}}ART\left(C_{\text{CPA}}^{\text{e}}+C_{\text{salt}}^{\text{e}}-C_{\text{CPA}}^{\text{i}}-C_{\text{salt}}^{\text{i}}\right),$$ (1)

$$\frac{dS}{dt}=P_{s}A\left(C_{\text{CPA}}^{\text{e}}-C_{\text{CPA}}^{\text{i}}\right),$$

are known as the two-parameter (or 2P) equations in contrast with the three parameter Kedem-Ketchalsky model which is now less used in cryobiological literature (see [26] for explanation). Here L_pRT and P_s are water and solute permeabilities respectively, A the cell surface area (assumed constant), C concentrations with superscript indicating extracellular or intracellular quantities (see Table 1 for a table of parameters). This model is coupled via a relationship between total cell volume and water volume known as the Boyle van’t Hoff relationship [6].

Table 1:

Table of Parameters

W,w	Intracellular water volume and its dimensionless form, respectively
S,s	Intracellular moles of CPA and its dimensionless form, respectively
t	Time
tf	Time at which desired concentration is reached
Lp	Hydraulic conductivity
Ps	Solute permeability
A	Cell surface area
R	Gas Constant
T	Temperature
$C_{\text{CPA}}^{\text{e}},C_{\text{salt}}^{\text{e}}$	Extracellular CPA and salt concentrations, respectively
$C_{\text{CPA}}^{\text{i}},C_{\text{salt}}^{\text{i}}$	Intracellular CPA and salt concentrations, respectively
Jtox	Toxicity cost functional
CCPA	Spatially dependent tissue CPA concentration
Cext, C0	Extra- and initial- tissue CPA concentration, respectively
Nt,, N∞	Moles CPA entering tissue during sorption period, and at equilibrium, respectively
Subscripts “ic”, “is”, and “sc”	Indicate the solution of the diffusion equation (2) under infinite cylinder, infinite slab, and short cylinder geometries.
ε	Tissue porosity parameter
Vt, Vd	Tissue volume and desorption bath volume, respectively
Cs ,Cd	Sorption bath PG concentration and desorption osmolarity, respectively
α	Cost functional parameter
D	CPA diffusivity
CD	Desired concentration
b	Dimensionless permeability parameter
$m_{\text{s}}^{\text{e}},m_{\text{n}}^{\text{e}}$	Dimensionless CPA and salt concentrations, respectively

Several modeling approaches have been used to predict optimal CPA equilibration strategies in single cells. Initially, it was observed that osmotically driven volume changes associated with CPA equilibration might be the cause of cell death in sensitive cells such as sperm [19]. To account for this, cell population specific osmotic tolerance limits were established that defined the limits to which cells could shrink and swell osmotically with no or little damage [17]. These limits are used in conjunction with the 2P model to determine CPA equilibration protocols that equilibrate cells with the desired amount of CPA with minimal osmotic damage. In many cell types, this is achieved with the default, single-step addition and removal protocols as cells are sufficiently permeable to CPA and/or have sufficient abilities to withstand large volume fluctuations with minimal damage [25].

The next step in development of CPA equilibration optimization was to choose among the remaining safe protocols. Levin suggested that one could avoid all osmotic challenges by using a transport equation such as Eq. 1 to determine extracellular concentration functions that facilitate the replacement of water with CPA in cells, effectively holding the cell volume constant [27]. These protocols, to our knowledge, were never put to practice, likely due to the difficulty of predicting the extracellular concentrations that could achieve this safely in one cell (e.g. an oocyte) or in a group of cells. Other investigators chose protocols with the minimal number of steps [18]. Along this vein, Benson described a cost-functional approach defining a protocol as optimal if it was achieved in minimal time [4,7], and this was implemented independently by Karlsson et al [24] in a stepwise approach. This cost functional approach has the benefit of formally acknowledging that CPA exposure is associated with cytotoxicity, and that the duration of exposure should be minimized in some way.

The cost functional approach to quantify non-osmotically induced CPA exposure damage was expanded by Higgins [23] and then Benson et al [9] where it was hypothesized that the rate of accumulation of damage during CPA exposure was proportional to a power function of the intracellular CPA concentration:

$$J_{\text{tox}}=\underset{0}{\overset{t_f}{\int }}{C}_{\text{CPA}}^{\alpha }dt,$$

where t_f is the time at which the cell reaches a desired intracellular concentration, C_CPA is the intracellular CPA concentration, modeled with the 2P equation, and α is a phenomenological rate parameter. Benson et al fit toxicity kinetics data in the literature and found α = 1.6 [9], a value that was confirmed in plated endothelial cells in a follow up study by Davidson et al [14]. In fact, the theoretically optimal step-wise CPA equilibration strategies determined by Davidson et al were implemented in plated endothelial cells [14]. Non-cost functional optimized equilibration strategies were compared with temperature dependent cost functional strategies and untreated controls, and while the classic non-cost-function approach showed dramatic cell death, no significant differences were found in the latter two [14].

To extend these toxicity minimization strategies to 3D tissues, a more complicated mass transfer model is necessary to account diffusion in the interstitial space, as well as transport across cell membranes. Until recently, tissue mass transport in cryobiology was modeled using classic spatially dependent transport models. In these models, some version of the diffusion equation is used to predict either the concentration of CPA or the temperature inside the tissue as a function of the external concentration or temperature field. For example, Han et al use radially symmetric diffusion model to find the diffusivity of CPA in rat ovaries [22], Abazari et al use a more sophisticated triphasic diffusion model that accounts for the biomechanics of articular cartilage as well as the movement of solutes and solvents [1], Manuchehrabadi et al use heat and mass transport modeling to predict thermal gradient induced stress inside tissues and organs [31]. At the heart of each of these models lies the basic diffusion model (see e.g. Anderson et al [3]):

$$\frac{\partial u}{\partial t}=\text{div}\cdot D\text{ grad }u,$$

where u is the quantity transported and D is a diffusion constant. This equation is coupled with initial and boundary conditions in the usual way, and evaluated over a relevant geometry.

In this study, we present a novel approach to quantify the damage due to the accumulation of toxicity as a function of cryoprotectant loading protocol in three tissues. We combine elements of individual cell cryoprotectant loading theory with the diffusion equation that allows the determination of concentration as a function of position. In particular, we expand the cost function J_tox to include spatial dependence while maintaining standard individual cell osmotic tolerance limit constraints as a proxy for the stresses that tissues undergo while equilibrating with high concentrations of cryoprotectants. The model in this study is informed by new diffusivity measurements on three human tissue types (skin, fibroid and myometrium), and existing permeability data from plated endothelial cells as a proxy for the cells on the exterior of the tissue. These tissue types were chosen because they are readily available and have diverse properties that will allow us to examine the versatility of our methods. In particular, fibroid tissue has a high density of extracellular matrix proteins and is relatively rigid compared with myometrium while skin contains both soft and tough connective tissues.

Methods and Models

Tissue collection and cryoprotectant permeability experiments

All myometrium and fibroid specimens were obtained from Augusta University Biorepository shortly after surgery. The Biorepository operates under institutional review board (IRB)-approved protocols and de-identifies samples before delivery. Similarly, skin samples that were obtained from patients undergoing plastic surgery procedures at the Medical College of Georgia were de-identified and acquired without any confidential information about patients. Our study was approved by the IRB at Augusta University (Protocol No. 668499–1 and 855935–1). Tissue samples were maintained in 90% Leibovitz’s 15 (L-15) medium (Gibco) containing 1X antibiotic-antimycotic mixture (Gibco) until processing. After washing in fresh 90% L-15 medium, myometrium and fibroid specimen were first sliced to 2 mm thickness using sterile tissue slicers (Zivic Instruments, Pittsburgh, PA). Next, tissue slices were cored to 2 mm diameter using sterile biopsy punches (Braintree Scientific, Braintree, MA). Skin samples were also cored to 2 mm diameter after dissection of subcutaneous fat. The cored tissue discs were washed in 90% L-15 and then exposed to 30% propylene glycol (PG) in 90% L-15 at ambient temperature for up to 60 minutes [note: all percentages are given in v/(v_total) and 30% propylene glycol (PG) in 90% L-15 was prepared by mixing 30 volumes of PG with 70 volumes of 90% L-15]. At 10-minute intervals, tissue samples were removed from 30% PG using fine tweezers and briefly placed on a kimwipe to remove the excess cryoprotectant solution on the tissue surface. Subsequently, tissue samples were individually transferred into microcentrifuge tubes containing 100 μL ultrapure water, where they were held for 3 hours to allow PG to diffuse out in ultrapure water. At the end of the holding period, 50 μL were taken from each microcentrifuge tube to measure the osmolality using a vapor pressure osmometer (Vapro 5520, Wescor, Logan, UT) and thus to determine the amount of PG diffused out into ultrapure water. The osmometer was calibrated using calibration standard of 100, 290, and 1000 mmol/kg.

Diffusion model

Here we assume an axially symmetric geometry, with spatial variables r and z. We use the linear diffusion equation and a constant, homogenous CPA diffusivity parameter, D. In the relevant cylindrical coordinates, this is modeled by the system

$$\frac{\partial C_{\text{CPA}}}{\partial t}=D\left(\frac{1}{r}\frac{\partial }{\partial r}r\frac{\partial C_{\text{CPA}}}{\partial r}+\frac{{\partial }^2{C}_{\text{CPA}}}{\partial z^2}\right),0<r<R,-l<z<l,t>0,$$

$$C_{\text{CPA}}=C_{\text{ext}}(t),r=R\text{ or }z=\pm l,t>0,$$ (2)

$$C_{\text{CPA}}=C_0(r,Z),t=0.$$

Here we define the extratissue concentration as a function of time C_ext(t) and the initial concentration as a function of space at time t = 0 as C₀(r, z). In small tissues, there is a potential for the variation of tissue volume during CPA loading and unloading. In these cases a careful mathematical consideration of the mass conservation and boundary conditions must be made (see. e.g. [3]). In the present case, we attempted to measure changes in tissue thickness as a function of PBS osmolality using calipers, but were unable to detect appreciable changes in tissue dimensions, possibly due to limitations of our approach (Table 2). In particular, the deformability of the skin tissue made it difficult to accurately measure the thickness. Nonetheless, the preliminary data in Table 2 indicate that any changes in tissue size are too small to be measurable. Therefore, we make the simplifying assumption that R and l are fixed throughout CPA equilibration. In fact, because the CPA will increase the intracellular volume appreciably, we expect that the equilibration volume to be approximately 15% higher. However, for the cylindrical biopsies we use (with diameter 2 mm and height 1.4 mm), this amounts to less than a 5% change in all dimensions, assuming uniformity. We believe this 5% is within tolerances given that we do not account for other potential errors such as concentration dependence of diffusion coefficients or the cell membrane water and solute permeabilities.

Table 2:

Skin tissue biopsy thickness as a function of extratissue nonpermeating osmolality after 20 min.

	Tissue thickness (cm)
PBS concentration	Before	After	% Difference
Control	0.145	0.145	0
0.5 x	0.123	0.129	4.7
1 x	0.136	0.138	1.4
2 x	0.142	0.143	0.7
4 x	0.154	0.156	1.3
8 x	0.145	0.149	2.8

Diffusion data collection

As described above the basic experimental approach is to expose a tissue sample to 30% PG solution for a range of time periods (the sorption period), then place the tissue in a microfuge tube containing 0.1 mL of pure water for 3 h (the desorption period). The amount of PG released during the desorption period was then estimated from the measured osmolality in the medium surrounding tissue. Note that at the low concentrations used here, osmolality (in units of osmoles/kg water) is equivalent to osmolarity (in units of osmoles/L of solution) because the volume occupied by solutes is negligible and the density of water is ~1 kg/L. Over the range of concentrations tested here, the osmolality and osmolarity are expected to differ by less than 3%. For consistency of units with the diffusion model, we use osmolarity units in the discussion below.

The resulting data were used to estimate the effective diffusion coefficient of PG as follows. During the sorption period we must account for transient diffusion into the tissue. To do so, we assume that initially there is no PG in the tissue, and that the concentration at the tissue surface is constant and equal to 4.084 mol/L (i.e., the molar concentration corresponding to a 30% v/v solution). This assumption is valid if the following conditions are met: PG transport to the tissue surface is much faster than diffusion into the tissue; and sorption of PG into the tissue has a negligible effect on the PG concentration in the bath. In all cases, our tissue geometry is that of a finite cylinder. The solution to the diffusion equation for the finite cylinder can be obtained by combining the solutions for an infinite slab and infinite cylinder.

For an infinite slab with half thickness L, the moles of PG entering the tissue during the sorption period (N_t) is can be expressed in terms of the diffusion coefficient D as follows (see [13], p. 48):

$${\left(\frac{N_{\text{t}}}{N_{\infty }}\right)}_{\text{is}}=1-\sum _{n=0}^{\infty }\frac{8}{{\left(2n+1\right)}^2{\pi }^2}\text{exp}\left[-\frac{D{\left(2n+1\right)}^2{\pi }^{2}t}{4L^2}\right],$$ (3)

where N_∞ is the total moles in the tissue at equilibrium and the subscript “is” denotes infinite slab.

For an infinite cylinder with radius R, the moles of PG entering the tissue during the sorption period is (see [13], p 73)

$${\left(\frac{N_{\text{t}}}{N_{\infty }}\right)}_{\text{ic}}=1-\sum _{n=1}^{\infty }\frac{4}{R^2{\alpha }_n^2}\text{exp}\left(-D{\alpha }_n^{2}t\right),$$ (4)

where the subscript “ic” denotes infinite cylinder and α_n is the nth root of

$$J_0\left(R{\alpha }_n\right)=0,$$

and where J₀(x) is the Bessel function of the first kind of order zero.

The solution for a short cylinder (sc) is obtained from the equations for the infinite slab and infinite cylinder as follows

$${\left(\frac{N_{\text{t}}}{N_{\infty }}\right)}_{\text{sc}}={\left(\frac{N_{\text{t}}}{N_{\infty }}\right)}_{\text{is}}+{\left(\frac{N_{\text{t}}}{N_{\infty }}\right)}_{\text{ic}}-{\left(\frac{N_{\text{t}}}{N_{\infty }}\right)}_{\text{is}}{\left(\frac{N_{\text{t}}}{N_{\infty }}\right)}_{\text{ic}}.$$ (5)

This equation was derived based on the expression for the concentration in a short cylinder that is commonly presented in mass transfer textbooks (e.g., [39]):

$$\frac{C_{\text{s}}-C_{\text{sc}}}{C_{\text{s}}-C_0}=\left(\frac{C_{\text{s}}-C_{\text{is}}}{C_{\text{s}}-C_0}\right)\left(\frac{C_{\text{s}}-C_{\text{ic}}}{C_{\text{s}}-C_0}\right),$$

where C_s is the PG concentration in the sorption bath, and the initial PG concentration is fixed at C₀ = 0. We can then solve for the concentration in the short cylinder and integrate this concentration over the volume of the short cylinder:

$$\underset{-l}{\overset{l}{\int }}\underset{0}{\overset{R}{\int }}2\pi r{C}_{\text{sc}} dr dz=\underset{-l}{\overset{l}{\int }}\underset{0}{\overset{R}{\int }}2\pi r{C}_{\text{is}} dr dz+\underset{-l}{\overset{l}{\int }}\underset{0}{\overset{R}{\int }}2\pi r{C}_{\text{ic}} dr dz-\underset{-l}{\overset{l}{\int }}\underset{0}{\overset{R}{\int }}2\pi r\frac{C_{\text{is}}{C}_{\text{ic}}}{C_{\text{s}}} dr dz,$$

which can be written in terms of the total amount of PG in the tissue at time t as

$${\left(N_t\right)}_{\text{sc}}={\left(N_t\right)}_{\text{is}}+{\left(N_t\right)}_{\text{ic}}-\frac{1}{C_{\text{s}}}\frac{{\left(N_t\right)}_{\text{is}}}{\pi R^2}\frac{{\left(N_t\right)}_{\text{ic}}}{2l}.$$

Given that the total amount of PG in the tissue at equilibrium N_∞ = C_s (πR²)(2l), we can rewrite the above equation as

$${\left(N_t\right)}_{\text{sc}}={\left(N_t\right)}_{\text{is}}+{\left(N_t\right)}_{\text{ic}}-\frac{{\left(N_t\right)}_{\text{is}}{\left(N_t\right)}_{\text{ic}}}{N_{\infty }}.$$

Finally, we arrive at Eq. 5 by dividing both sides of the above equation by N_∞.

Only the first 100 terms in Eqs. 3–4 were used to compute the solution, as increasing the number of terms had a negligible effect on the results.

The moles of PG in the tissue at equilibrium N_∞ can be expressed in terms of C_s as follows:

$$N_{\infty }=C_{\text{s}}\epsilon V_{\text{t}},$$

where ε is the tissue porosity (or void fraction) and V_t is the tissue volume.

The moles of PG in the tissue sample at time t, N_t, can be expressed in terms of the experimentally measured osmolarity in the desorption bath, C_d, as follows:

$$N_{\text{t}}=C_{\text{d}}\left(\epsilon V_{\text{t}}+V_{\text{d}}\right),$$

where V_d is the volume of the desorption bath. Because we are interested in modeling PG transport, C_d should include only the contribution of PG to the measured osmolarity. To account for the effects of the carrier solution (i.e., L15 medium) we used a control sample that was not exposed to PG. These control samples resulted in an osmolarity of about 20 mOsm/L in the desorption bath. The osmolarity for these control experiments was subtracted from the measured osmolarities for samples exposed to PG to account for release of components of L15 medium into the bath.

Combining these equations results in

$$C_{\text{d}}=\frac{{\left(\frac{N_{\text{t}}}{N_{\infty }}\right)}_{\text{sc}}{C}_{\text{s}}\epsilon V_{\text{t}}}{\epsilon V_{\text{t}}+V_{\text{d}}}.$$ (6)

The experimental data were fit using Eqs. 3–6 using the diffusivity D and porosity ε as variable parameters. Best-fit values of D and ε were determined by minimizing the sum of the error squared between the measured and predicted values of the osmolarity in the desorption bath. Tissue samples were obtained from 3, 2 and 2 sources for fibroid, myometrium and skin respectively. These samples were subdivided into small cylinders for testing PG sorption as a function of time. Fits were obtained separately for each tissue source.

Toxicity model

We wish to apply the toxicity cost functional approach previously used in single cell equilibration. The previous cost functional was defined on a cellular basis with no spatial concentration dependence. Therefore, we developed an extension of the model to account for spatial dependence; in particular, we implement the following new cost functional:

$$J_{\text{tox}}\left(C_{\text{ext}}\right)=\frac{1}{R^{2}l}\underset{0}{\overset{R}{\int }}\underset{-l}{\overset{l}{\int }}\underset{0}{\overset{t_f}{\int }}{C}_{\text{CPA}}^{\alpha } r dt dz dr,$$ (7)

where J_tox is a function that maps the function C_ext (evaluated on the interval 0 ≤ t ≤ t_f) to the real numbers. This form of cost function captures cumulative damage throughout the tissue and assumes that the concentration-dependent toxicity rate model is spatially homogenous. To compare real world protocols among multiple tissues, we normalize the toxicity cost by dividing by the tissue volume, effectively achieving a volume averaged cost function equivalent to the individual cell cost function described by Benson et al. [9]. During CPA addition, we define t_f as the first time such that

$$\underset{r,z}{\text{min }}{C}_{\text{CPA}}(t_{\text{f}})=C_D,$$ (8)

where C_D is the minimal concentration that we expect to vitrify at the minimal cooling rate in the tissue (see below).

Mechanical damage

Finally, to account for potential osmotic damage and act as a proxy for interstitial mechanical stress, we subject our control problem to a cell based osmotic tolerance state constraint. In particular the exterior cells of the tissue will experience the greatest osmotic challenges, and as such, if we design protocols that minimize their osmotic damage, this will minimize cell based osmotic damage in interior tissues. We assume that the cell volume on the exterior of the tissue is governed by the standard 2P model (Eq. 1). We nondimensionalize the model as in Davidson et al. [14] resulting in

$$\frac{dw}{d{t}^{\prime }}=\left(m_{\text{s}}^{\text{e}}+m_{\text{n}}^{\text{e}}-\frac{1+s}{w}\right),$$

$$\frac{ds}{d{t}^{\prime }}=b\left(m_{\text{s}}^{\text{e}}-\frac{s}{w}\right),$$

where s and w are the unitless moles of solute and intracellular volume of water, respectively, m^e are unitless extracellular concentrations, b is the lumped dimensionless permeability parameter, and t = t′τ, where τ is the time scaling parameter. We assume cells have osmotic tolerance limit state constraints defined by v_L ≤ w + γs ≤ v_H, where v_L and v_H are the lower and upper unitless osmotic tolerance limits, respectively (see [14]) and γ is an appropriately normalized partial molar volume. Because we don’t have explicit values for b, τ, v_L and v_H for the specific cells of our system, we use existing data from plated endothelial cells as a proxy [14,16] and set γ = 0.022035. A more refined model with tissue and cell specific parameters is in progress, and we explore the impacts of these parameters on predicted optimal protocol in the discussion.

To solve the above equations and apply the osmotic tolerance constraints, we used the following strategy. There are three fundamental time scales in this simulation. The first and longer one is the time scale of the CPA diffusion. This follows, in general the diffusion time defined by

$$t_{\text{diffusion}}=\frac{l^2}{2D},$$

where l is a characteristic length, and D the diffusivity. In our case the length is approximately l =0.075 cm, and diffusion constant approximately D = 10⁻⁶ cm²/s, yielding a diffusion time of approximately 2.8 × 10³ seconds, or 46 min. On the other hand, the exterior cells have a biphasic response to anisomotic permeating solute challenges. Upon exposure to high concentrations of CPA media, exposed cells rapidly lose water and slowly gain it back. In this study the time scales of these cellular events are the same as those shown in Davidson et al [14]. In particular, the rapid water loss happens on the scale of 10 s, and the re-equilibration happens on the scale of 100 seconds (at room temperature). Because of these three time scales, in our experience, standard Runge Kutta numerical integration techniques introduce significant error in the estimation of the minimal and maximal volumes achieved during equilibration. Therefore, we used the exact solution technique described by Benson et al [5] to estimate the minimal and maximal volumes achieved as well as the intracellular state at each time during the protocol.

Determination of goal CPA concentration C_D

Upon initial numerical analysis of CPA transport under the standard stepwise equilibration protocol used in the Eroglu laboratory and others [31], it is apparent that for general tissues of the size addressed in this manuscript, there is incomplete equilibration with this media (which would take several hours due to the asymptotic nature of the diffusion process). Therefore, our simulations suggested an “in practice” goal concentration of C_D = 34%. Ostensibly this is sufficient to achieve successful vitrification in the interior of the tissue, though explicit measurement of this has not been made to our knowledge. We note here and discuss below that this is a decision to facilitate the appropriate comparison with existing protocols and our approach can be easily extended to larger goal concentrations. Finally, note that for classical (e.g. monotonically increasing) CPA addition protocols, the concentration C_D and minimal cooling rate will be at the center of the tissue. However, it is possible to design protocols that have a high enough concentration in the center but not elsewhere.

To put this value into context, our cryopreservation protocol requires tissues to be equilibrated with CPA, placed in a cryovial in vitrification solution, and plunged into liquid nitrogen. The cooling rates in the tissue interior are thus determined by the system itself, and are fixed for fixed tissue geometries. Therefore, the minimal needed cooling rate for vitrification can be thought of as the minimal cooling rate at the tissue interior. To avoid overcomplicating our exploratory analysis, we use experimentally measured temperature as a function of time to estimate minimal cooling rates published by Teixeria et al [37], who found that achievable cooling and warming rates in media containing cryovials ranged between 200– 400 K/min.

Once the expected minimal interior cooling rate is established, we can use knowledge of the critical cooling rate—the minimal cooling rate at which the solution has an ice fraction less than 10⁻³, to predict the minimal required CPA concentration to ensure ice-free cryopreservation. In the case of the cryoprotectant PG used in our present study, 35% PG is associated with a critical cooling rate of approximately 200 K/min. This rate is needed to prevent more than 1% hexagonal ice formation, and at 40% PG, a rate of 40 K/min is required to vitrify the sample [11]. However, critical warming rates are much higher, and those rates feasible in the tissue require PG concentrations between 40% and 45%. In particular rates of more than 10⁴ K/min are required to completely avoid devitrification in 40% PG and more than 10² K/min to completely avoid devitrification in 45% PG [12]. However, the analysis of Boutron was in pure solutions devoid of myriad intra and intercellular solutes that will facilitate the reduction of the critical cooling rate.

This suggests that the achieved minimum of 34% may be insufficient for vitrification. However, this is a decision to facilitate the appropriate comparison with existing protocols and our approach can be easily extended to larger goal concentrations. Finally, note that for classical (e.g. monotonically increasing) CPA addition protocols, the concentration C_D and minimal cooling rate will be at the center of the tissue. However, it is possible to design protocols that have a high enough concentration in the center but not elsewhere.

Toxicity model optimization numerics

To calculate the cost J_tox(C_ext) defined in equation 7, we must spatially integrate the concentration function. One approach would be to use the known exact solution of the system described above. However, we note that we are not integrating the solution, approximated as a truncated infinite sum, but a non-integer power of the solution, and thus a power of an infinite sum. Infinite series product formulas exist but are challenging to calculate explicitly except in very specific cases. In particular, if we chose α = 2, the explicit formula for the product of C_CPA(r, z, t) with itself is the Cauchy product of the two infinite series, and can be thought of as the discrete convolution of the two series. The result is then integrated as defined in Equation (4). These terms however, are quite complex, requiring integrals of products of Bessel functions, and the rate of convergence of the product of two series is also not the same as the rate for them independently.

Another potential alternative approach is to use the analytic solution for diffusion in a finite cylinder to inform a numerical integration algorithm. We did not pursue this approach, as this and the above exact solution approach are limited solely to the specific geometry of these tissue plugs and the strictly linear diffusion equation. Additionally, it requires a large number of evaluations of terms of the infinite series truncation at each spatio-temporal location needed for the numeric integration of the two spatial and one temporal integrals.

Therefore, we chose to use a numerical integration approach to evaluate Equation (7). This approach can be optimized using standard matrix algebra techniques, is easily parallelized, and can be extended to nonlinear diffusion, non-homogenous systems, non-symmetric geometries, etc. In particular, the differential equation system defined in Eq. (2) was evaluated numerically using a n x m/2 rectangular grid of nodes in the r and z directions respectively. By symmetry in the z-direction we restrict our evaluation to z ≥ 0. System (2) was discretized spatially using 2^nd order centered difference formulas and a first order implicit time stepping scheme was implemented. At each time step exterior nodes were assigned extracellular concentrations defined by C_ext(t). Time stepping was performed until the minimal concentration requirement (Eq. 8) was met at step K, or a maximum step number threshold was exceeded, in which case a cost penalty equal to the difference between goal and minimum concentration was implemented. The integral of the cost was updated at each time-step by the simple explicit spatial and temporal integral formula

$$J_{k+1}=J_k+dt \sum _{j=1}^{m/2}\sum _{i=1}^n\left(i-1\right)dr C_{ijk}^{1.6},$$

where dr = R/(n − 1), and C_ijk = C(i dr, j dz, k dt).

For the external concentration function, we allowed classic piecewise constant, step-wise CPA concentrations easily implemented at the bench. We chose to use a four step approach for equilibration, allowing CPA concentration and step duration to be control parameters. For simplicity of modeling, we assumed a fixed isosmotic nonpermeating concentration. Therefore, we had four concentration parameters, and three time parameters with the last step continuing until the end criterion or the maximum integration time was reached. We limited minimal step durations to 10 seconds, though in practice, the minimal step durations were much longer for the toxicity optimal protocols. We also limited extracellular CPA concentrations to 0 ≤ C_ext ≤ C_max, where here we chose C_max =12 mol/L propylene glycol in 1 x PBS.

We implemented this code in Fortran programming language and minimized the cost J using a simulated annealing algorithm code DFSA [29].

Comparison with time-optimal and standard stepwise approaches

To facilitate comparison with more standard approaches to CPA equilibration in tissues, we defined two additional protocols. The first is a minimal time approach succinctly summarized by using the cost defined in Eq. 7 but with α = 0. In this case we define

$$J_{\text{time}}≔J_{\text{tox}}{|}_{\alpha =0} =t_{\text{f}}.$$

We determined the four-step protocol that minimized this cost using the same numerical approach defined above. The second approach is the standard three step protocol used for cryopreservation of tissue samples [31]. In particular, the standard protocol consists of the following concentrations and exposure times: (C₁, C₂, C₃, t₁, t₂, t₃) = (1.5,3,6, 10,25,25), where concentrations are in mol/kg and times are in minutes. As discussed above, this standard method does not necessarily end with intra-tissue concentrations consistent with the time- and toxicity methods, which were considered to be complete when the minimal concentration in the tissue was 4.5 mol/L. Therefore, to facilitate comparison with the time- and toxicity-optimized methods, we used numerical predictions to define a new exposure time in step 3 that resulted in a minimal concentration in the tissue of 4.5 mol/L.

Results

Diffusion parameters

Fig. 1 shows the measured osmolarity in the desportion bath after exposure of tissue samples to 30% PG for various times, along with predictions using the best-fit values of the diffusivity D and porosity ε. Table 3 summarizes the best-fit transport properties. The diffusivity of PG was similar for fibroid and myometrium, but about two-fold lower for skin. Fibroid tissue exhibited the lowest porosity.

Figure 1:

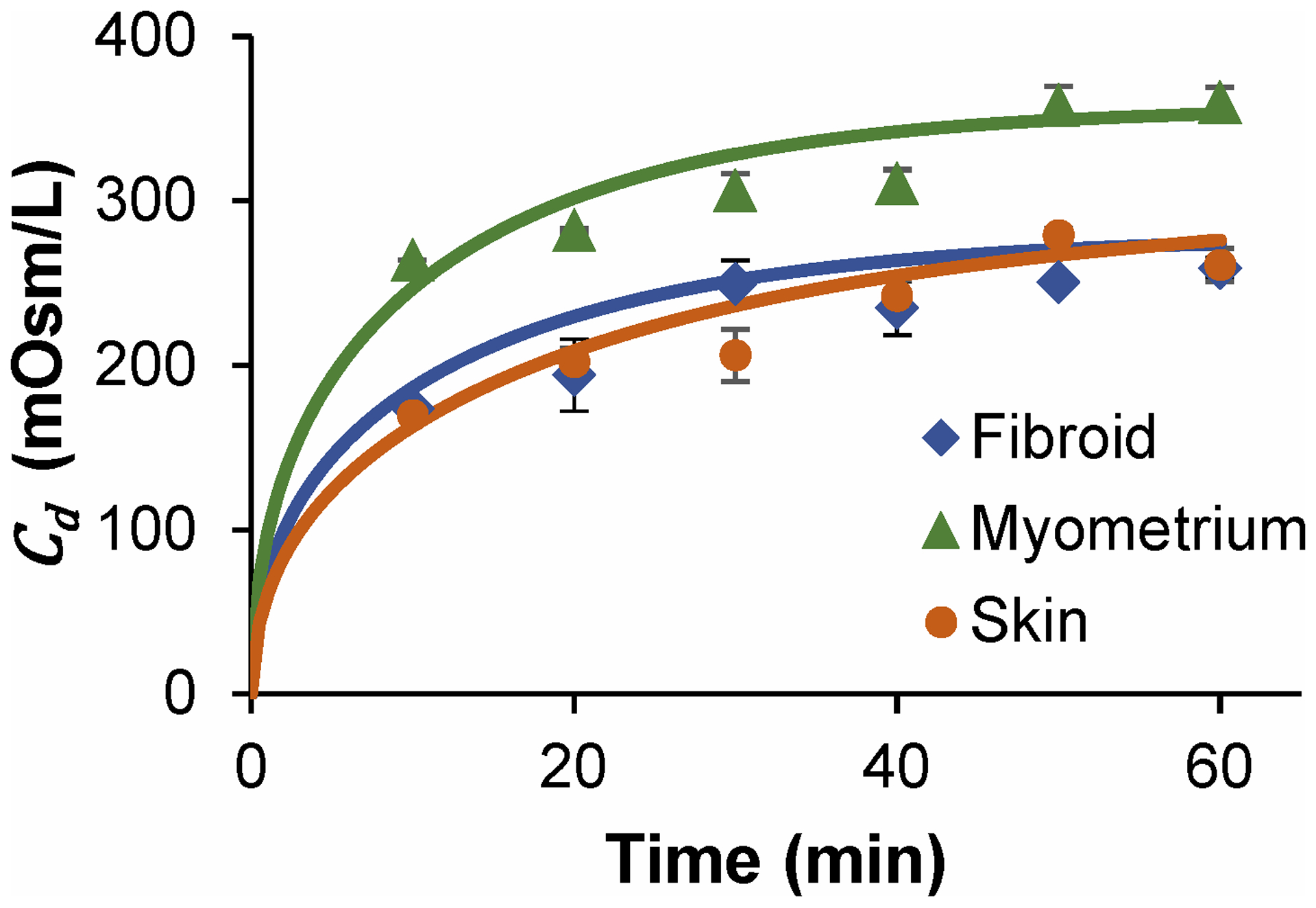
Desorption bath osmolality as a function of exposure time to 30% PG for three tissue types with best fit regressions according to equation 3, n=3 for fibroid, n=2 for skin and myometrium, and error bars indicate standard error of the mean.

Table 3:

Best fit (mean ± SEM; n=3) parameters for tissues..

Tissue type	D x 106 (cm2/s)	ε
Skin	0.6 ± 0.2	0.74 ± 0.09
Fibroid	1.2 ± 0.6	0.58 ± 0.04
Myometrium	1.3 ± 0.5	0.76 ± 0.06

Toxicity optimal vs time optimal vs standard protocols

Toxicity optimal, time optimal protocols, and standard protocols and their associated costs are given in Table 4. Representative plots of the intra-tissue concentration at the end time point for all three approaches are shown in Fig. 2, a plot of the minimal intratissue concentration as a function of tissue type and protocol is shown in Fig. 3. A representative plot of the exterior cell volumes as a function of the time, toxicity, and standard protocols are shown in Figs. 4–7.

Table 4: Optimal parameters for the addition phase of CPA equilibration for all three tissue types and associated time and toxicity costs.

C_tox, C_time, and C_std, represent protocols for the minimizer of the toxicity cost, the minimizer of the time cost, and the standard equilibration approach to the goal concentration. Concentrations are given in mol/L, and times in seconds and boldfaced concentrations are at the defined concentration limit. The parameter t_f is the total protocol time at which the minimal concentration in the tissue is predicted to be 4.5 mol/L, our arbitrary cutoff. For the standard protocols with only three steps, the defined third step of 25 min is replaced with a step of duration long enough that the t_f condition was met. Finally, note that these protocols are for the geometries and diffusivities used in the model explicitly and will not generalize to larger or smaller tissues.

	CPA Addition Parameters
	C1	C2	C3	C4	t1	t2	t3	tf	Jtox
Skin
Ctox	1.6	3.1	7.4	4.6	323	226	502	3712	1152
Ctime	3.4	5.1	7.5	12	4	4	5	1692	1666
Cstd	1.5	3.0	6.0	---	600	1500	---	4456	1304
Fibroid
Ctox	3.7	6.4	9.0	4.5	169	83	125	1502	574
Ctime	3.6	4.9	7.5	12	4	4	5	856	833
Cstd	1.5	3.0	6.0	---	600	1500	---	3094	762
Myometrium
Ctox	2.1	4.6	9.3	4.5	144	92	139	1486	526
Ctime	3.6	4.9	7.5	12	4	4	5	792	769
Cstd	1.5	3.0	6.0	---	600	1500	---	3000	726

Figure 2.

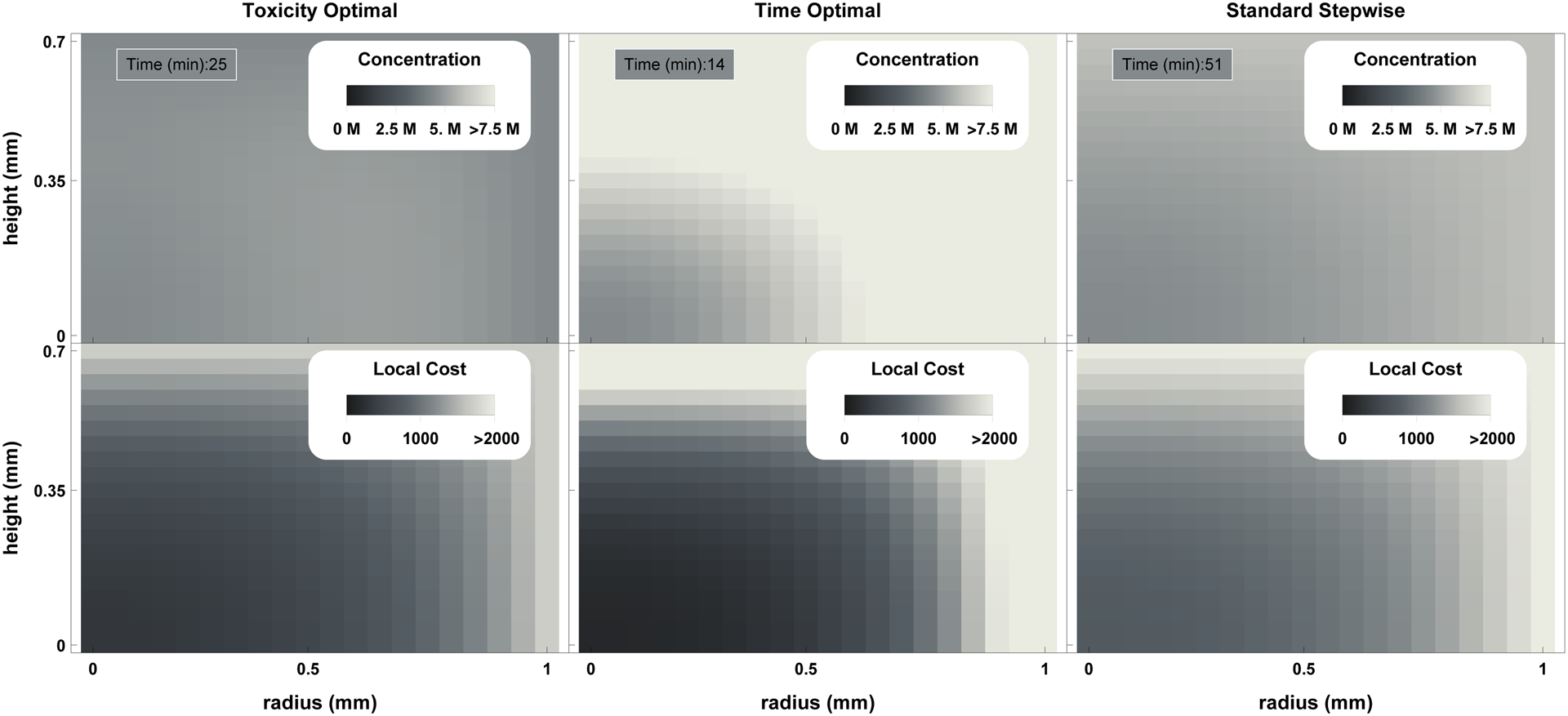
Plot of final concentration (top row) and accumulated toxicity (with α = 1.6) as a function of location under the toxicity optimal, time optimal, and standard stepwise protocols (left to right). It can be observed that while the toxicity optimal approach has both lower maximal local accumulated toxicity values and a lower mean accumulated toxicity value, more toxicity is accumulated at the center of the tissue. This approach allows the prediction of localized damage due to CPA exposure.

Figure 3:

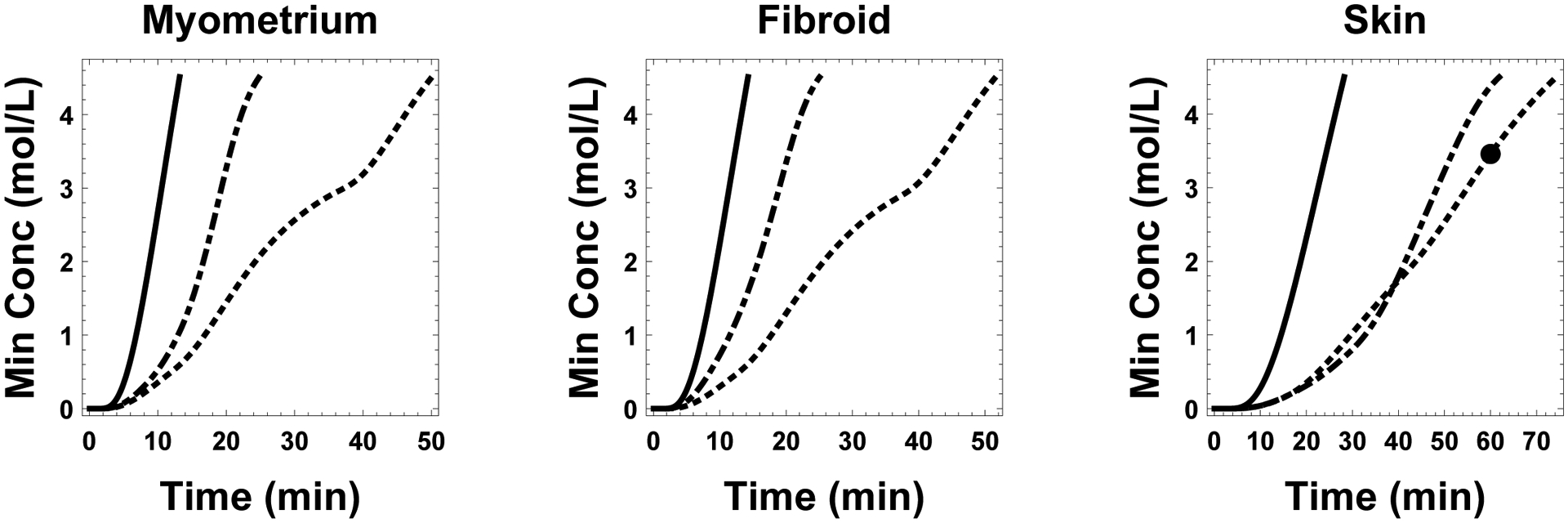
Plot of the minimal concentration in the tissue for all three tissue types and all three protocols. Concentrations associated with time-optimal, toxicity-optimal, and standard protocols are shown in solid, dash-dotted, and dotted lines, respectively. The solid dot placed on the standard protocol curve of the skin subplot indicates the concentration after the standard protocol would have been assumed complete (e.g. 10 min, 25 min, 25 min for the three steps).

Figure 4:

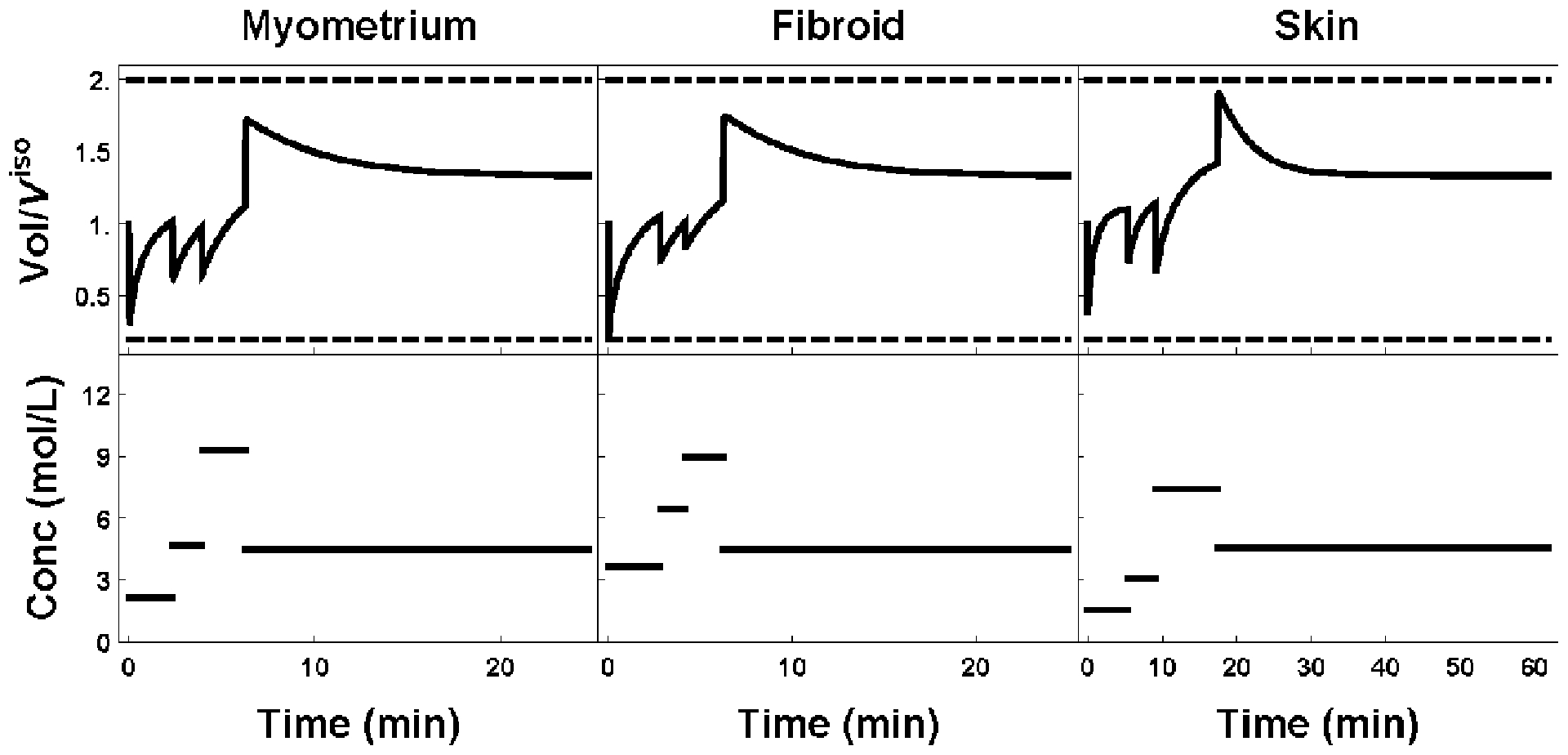
Plot of external cell volume (top row) as a function of the extratissue concentration (bottom row). Toxicity optimal protocols for myometrium, fibroid and skin are shown left to right, respectively.

Figure 7:

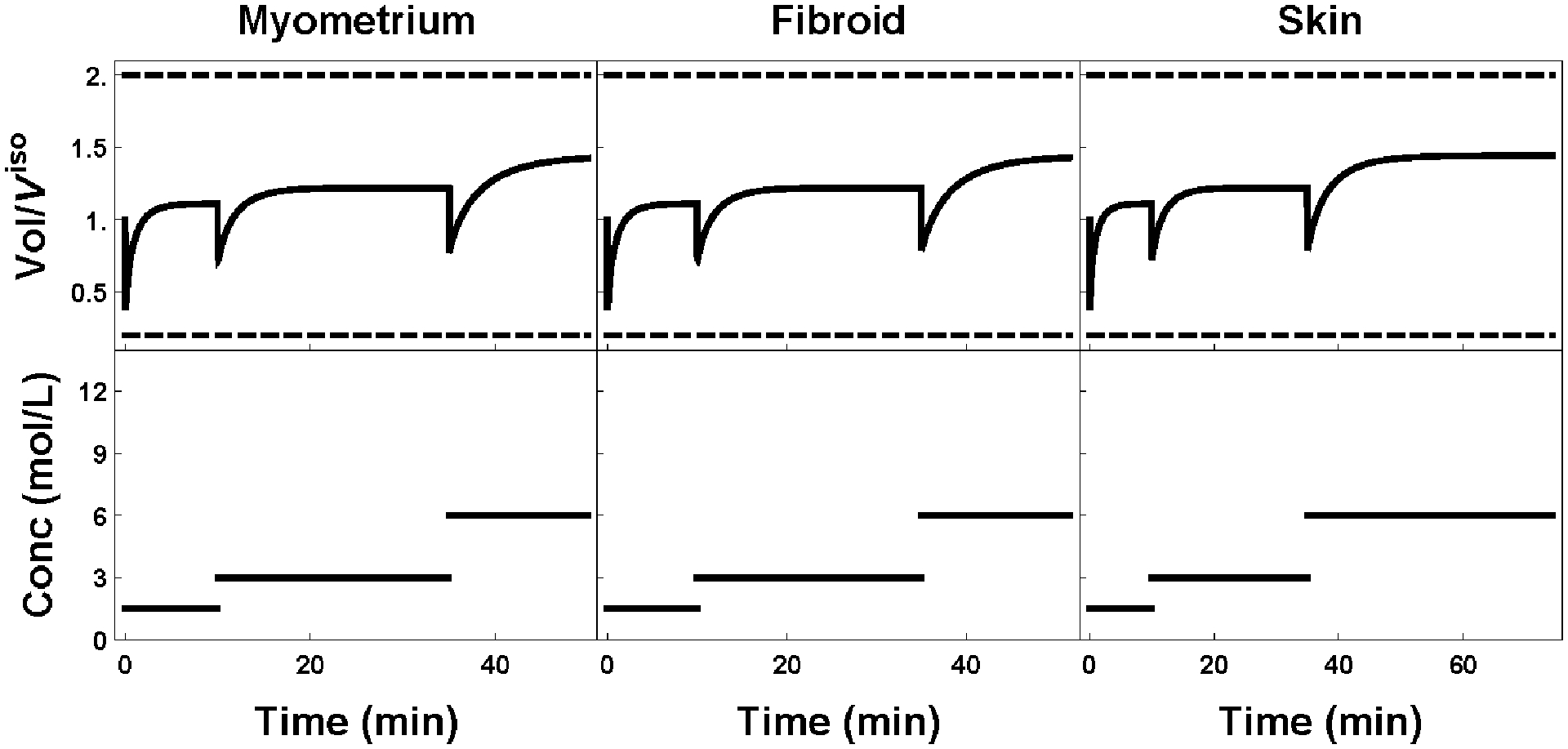
Plot of external cell volume (top row) as a function of the extratissue concentration (bottom row). Standard protocols for myometrium, fibroid, and skin are shown left to right respectively. All protocols are identical except for the last step, where the tissue is allowed to equilibrate until the minimal interior goal concentration criterion is reached.

Discussion

In this manuscript we describe a novel approach to optimization of cryoprotectant equilibration in tissues that accounts for the accumulation of concentration and time dependent exposure damage. In particular, we determined the relevant parameters of a mass transfer model that has wide applications in cryobiology, and adapted an existing model of damage to be applicable in tissues. This approach is a natural extension of our previous work in individual cell suspensions and then in plated cells.

Until this manuscript there has been little guiding theory for the equilibration of cryoprotectants in tissues. There have been many publications prescribing protocols to equilibrate vitrification solutions with minimal damage---many acknowledge that a step-wise approach is appropriate---but most protocols use somewhat arbitrary concentration steps and durations. There have been some approaches that use a mass transfer model to assure that the tissues are suitably equilibrated; for example in the recent publication by Manuchehrabadi et al [31], the intratissue concentration as a function of time in during exposure is measured using Computed Tomography and informs a similar mass transfer model to the one used in the present manuscript. However, in their approach, no effort is made to optimize the equilibration to and from high concentrations of cryoprotectant solutions.

This lack of modeling to minimize toxicity is surprising in some ways, because CPA toxicity has been highlighted as one of the chief impediments to successful cryopreservation of tissues and organs [28]. This, coupled with the fact that great gains have been made in the area of single cell suspension equilibration protocol optimization, including human and bovine oocytes [9,24,32], plated endothelial cells [14], sperm [18,19] and others, suggests that gains in CPA toxicity minimization may be made in tissues as well. This gain can be seen in Figure 8, where the accumulated toxicities as a function of protocol are shown for each tissue type. Here we can see that the standard stepwise approach is neither faster nor less toxic than the toxicity optimal protocol, and that, if CPA toxicity is not a concern, time optimal protocols can be 4–6 times shorter than the non-optimized standard stepwise approach and 2–3 times shorter than their respective toxicity optimal protocols.

Figure 8:

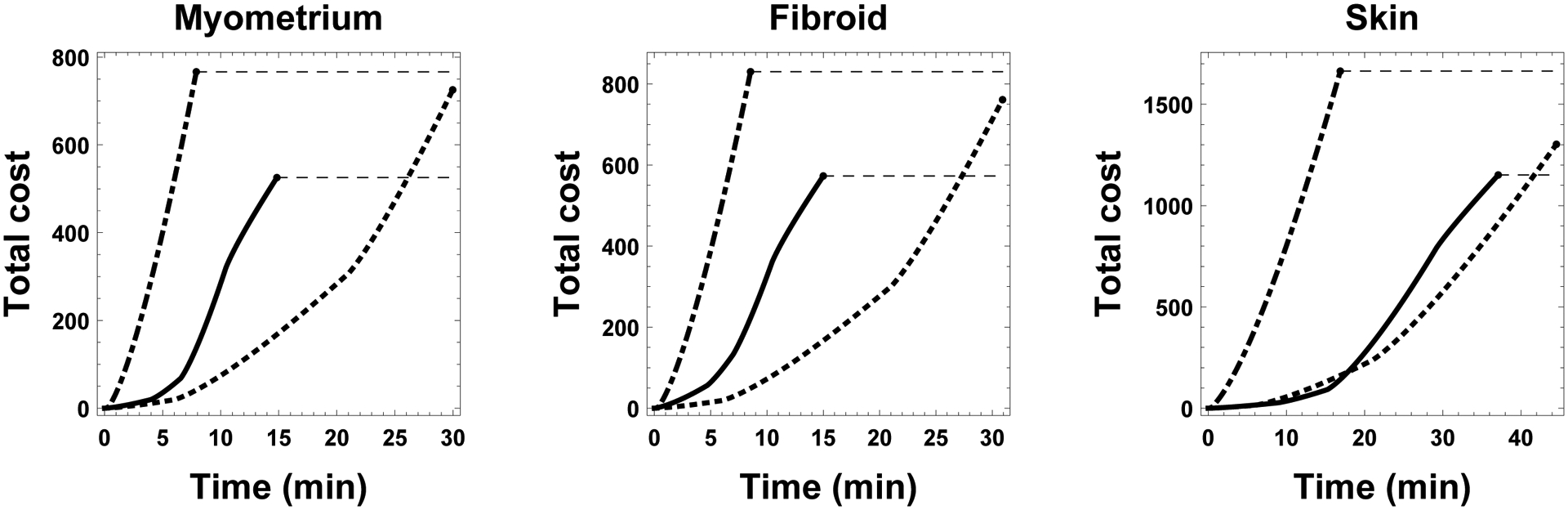
Comparison of accumulated toxicity as a function of three protocols for all three tissue types. Costs for time optimal, the stepwise, and toxicity optimal protocols are shown in dash-dot, dotted, and solid lines, respectively. Dashed lines allow for the comparison among protocols after completion.

The use of multistep protocols by other investigators suggests an awareness of the potential osmotic or mechanical damages encountered by placing tissues in high concentration solutions. Our approach to account for this damage was to assume that the principal osmotic damage would occur at the exterior of tissue, and that the cells on the exterior of the tissue would be beholden to similar osmotic tolerance limits as cultured adherent cells. We recognize that the actual mode of damage in this case is likely to be more complicated than our model can account for, and could foresee a model that accounts for intercellular stresses as a mechanism of osmotically caused mechanical damage. However, as a first pass, we feel that this damage modality is conservative in that our model catches the “easiest to damage” cells, perhaps at the expense of a less-than-optimal approach. Moreover, to our knowledge the damage mechanism of osmotic tolerance in general has not been studied in tissues and further exploration of this potential mode of damage is well warranted.

Our approach relied on measurement of bulk solute diffusivity in the three tissue types of interest. Our diffusivity values (Table 3) are on the order of 10⁻⁶ cm²/s and are comparable to the PG diffusion coefficient in water at infinite dilution, which is about 10⁻⁵ cm²/s at room temperature, as well as the diffusivity at a PG mole fraction of 0.2, which is about 5×10⁻⁶ cm²/s [38]. We also note that the skin tissue has a diffusivity value that is half that of the other tissues. This might be related to the dense packing of the epidermis layer in skin when compared with myometrial and fibroid tissues.

While our desorption curves were well-fit by our simple linear diffusion model, we note that, at the very least, diffusivity is typically considered a function of concentration [38] and that we do not model the interaction among the CPA and the base media nonpermeating solutes. It would be more appropriate to use a transport model that accounts for the salt, water, and CPA concentrations throughout. In fact, our approach neglecting the movement of salt and water is limiting in some ways because our previous work on CPA equilibration optimization [5,8,9,14] relied on media containing only CPA, instead of including standard nonpermeating solutes. By omitting the nonpermeating solute in these studies, an additional 300 mOsm of permeating solute could be used at each step, increasing the speed at which equilibration occurred. This more complete model is a subject of our future work.

In the present study we demonstrate that a clear choice exists between minimal time and minimal toxicity protocols. Minimal time protocols are simply constrained by the osmotic tolerance limit constraint: in their absence a minimal time optimal equilibration protocol would be to place the tissue in a media of concentration C_max until the mass transfer model predicts that the center of the tissue has concentration C_D. In fact, because of this, minimal time protocols can be predicted using the much simpler single cell dynamics. One could then use the minimal time optimal protocols that use continuous concentration controls instead of multistep protocols (see e.g. Benson et al [9]). Considerable gains in time-saving could be made in this case.

On the other hand, we have defined a concentration and time dependent tissue equilibration cost function dependent on a parameter α. In fact, in our previous work on endothelial cells [14], we showed that there is a clear delineation between protocols where α > 1 and α < 1. Optimal equilibration protocols based on this cost function are much different from those of time-optimal (α = 0) protocols. In particular, the time optimal approaches drive the exterior cells to their minimal volume at each step, and in so doing achieve the maximum extratissue concentration in minimal time. In contrast, the toxicity optimal approaches achieve a high extratissue concentration in a longer time, followed by backing off to the desired concentration near the end of the protocol. This approach reduces the exposure of the exterior cells to unnecessarily high concentrations. This is seen most clearly in figure 2, where the predicted toxicity accumulated is focused and considerably higher on the exterior of the tissue for the time-optimal method, whereas there is less localized damage in the toxicity optimal protocol.

Additionally, our results provide a rational explanation for the successful approach to cartilage cryopreservation developed by Jomha et al, who equilibrate the CPA in a “wave”, where successively increasing concentration steps are followed by a final lower step that allows the CPA to distribute throughout the tissue [2]. In future publications we will explore the effects of the value of α on the resultant optimal protocols. Moreover, considerable improvements in post-equilibration recovery were made in our previous work with plated endothelial cells when the use of more than one temperature was made available. Therefore, considerable work is needed to explore the temperature dependence of these parameters, as well as the effects of the relative magnitude of these parameters.

We note that there are slight qualitative differences among the similar time-optimal protocols. We attribute this to the challenging nature of our PDE and ODE state constrained optimization problem. While our optimization algorithm was able to converge to local optima in each case, it is likely that the global optimal solution was not found. Finding these global optima is a subject of future work, but as we see in Table 4, this approach reduced predicted tissue toxicities by 30% over the standard and time-optimal approaches.

Our present approach assumes that all cells accumulate damage according to the same model. This hypothesis is borne out of our previous work showing that the value of α = 1.6 is conserved among widely varying cell types [14]. However, the determination of these parameters is challenging, subject to considerable error, and it is likely that there are cell-specific toxicities to specific cryoprotectants that depend on the cell lineage, the cell state, and even the cell’s neighbors in the tissue. In some tissue types a continuum mass transfer model coupled to a spatially dependent cost function as described in Equation (7) could still be used to determine the total damage, where different cell types could be located in subregions of the tissue. However, most tissue structures have multiple cell types interspersed throughout all subregions. In this case, an individual cell-based or agent based model accounting for the specific location and concentration history of each individual cell in the tissue may be an ideal tool for this approach.

Towards this, we proposed and tested a cell-based ODE/PDE hybrid model of CPA equilibration in hamster islets of Langerhans [10], and work incorporating the damage modeling theory presented in this manuscript into that model is underway. In the future, more detailed cell-based models can be implemented using off-the-shelf computer packages such as PhysiCell [30].

Here we present only the equilibration to high concentrations of CPA, not equilibration from high concentrations of CPA for several reasons. First, we require further testing to determine the appropriate critical concentration for each tissue type. This critical concentration in turn will dictate the final CPA concentration distribution in the tissue, and will be defined by the optimal protocol plus the pre-quenching and post-warming handling times that will allow for further CPA concentration distribution throughout the tissues. Second, we have previously shown that the CPA equilibration to high concentrations is the critical part when it comes to toxicity accumulation [9]. This is in part because we exposed cells to concentrations that maximized their intracellular water volume, effectively diluting the intracellular CPA concentration and thus the integrand of equation 1. Finally, to remove CPA, we previously used media containing only nonpermeating solutes. This facilitates larger CPA gradients (transmembrane in our previous cases) and thus faster equilibration protocols. However, as discussed above, this feature was not included in our computational model for this study and is a subject of our present research.

Our approach used the total toxicity as our metric for comparison of protocols. This is not the only possibility. For example, if some regions of the tissue are known to be more robust, or are less critical for the end application, then protocols can be developed that minimize the toxicity in a particular region. Alternatively, one could design a protocol that minimizes the maximum accumulated toxicity at any point, instead of the average toxicity used in the present study. This flexibility opens the door to new approaches to rational CPA equilibration protocol design that will need to be informed by data on toxicity accumulation at a local level.

Finally, we note here that a number of decisions were arbitrary. For example, our goal concentration C_D was informed by phenomenological arguments. A better approach would be to establish actual measured critical concentrations as a spatial function inside the tissue given the cooling rate for the container. Our approach is equally valid whether C_D is set to 34% or 45%. In fact, it should have much higher payoffs in the prediction of reduced toxicity protocols when higher concentrations are desired. However, it is interesting to note that if C_D is in fact the correct value for this freezing rate, then our modeling indicates that for both myometrium and fibroid tissue, the standard protocol is overlong. This added unnecessary exposure at high concentrations would add dramatically to the accumulated toxicity, especially at the exterior region of the tissues. On the other hand for the skin tissue, Fig. 3 shows that the standard protocol (with total duration 60 min) would have ended too soon, and the tissue would have not been sufficiently equilibrated with CPA. In this case, the center of the tissue would have insufficient CPA to avoid significant ice formation. Therefore, even in the absence of toxicity cost function minimization, modeling CPA transport to develop equilibration protocols is essential to ensure appropriate tissue equilibration has taken place.

We also use an extremely high concentration as our maximum equilibration concentration,12 mol/L. The use of such a concentration is potentially feasible in tissues that can be submerged media contained in a dish or tube. However, the viscosity would likely prevent perfusing such high concentrations in vascularized tissues and organs. Moreover, the accuracy of our diffusion model is likely to be dramatically affected when the solute significantly outweighs the “solvent”. Nevertheless, this maximum concentration was only used in the time-optimal protocols; the maximum concentration used in the toxicity optimal protocol was 9.3 mol/L, or 71%. In either case, however, these constraints are simple to adjust.

Conclusions

Here we have presented a novel approach to cryoprotectant equilibration protocol design. This approach is the first to allow the quantification of the accumulation of cryoprotectant induced toxicity in tissues, and allows for the prediction of optimal equilibration protocols as well as the location of damages due to these protocols. While preliminary, we believe that this approach will allow for the development and testing of protocols that may overcome the CPA toxicity barrier to regular and facile small tissue vitrification.

Figure 5:

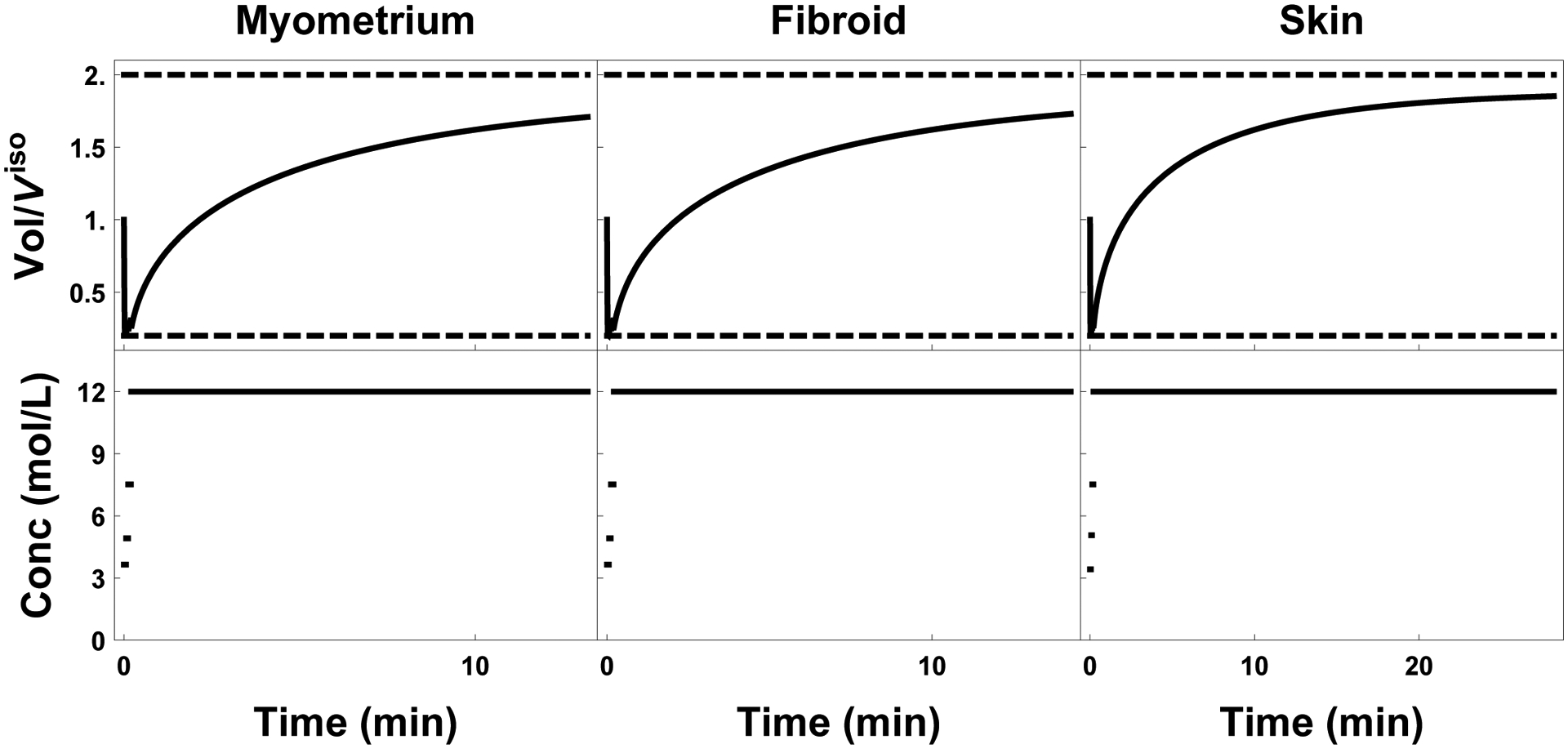
Plot of external cell volume (top row) as a function of the extratissue concentration (bottom row). Time optimal protocols for myometrium, fibroid, and skin are shown left to right respectively.

Figure 6:

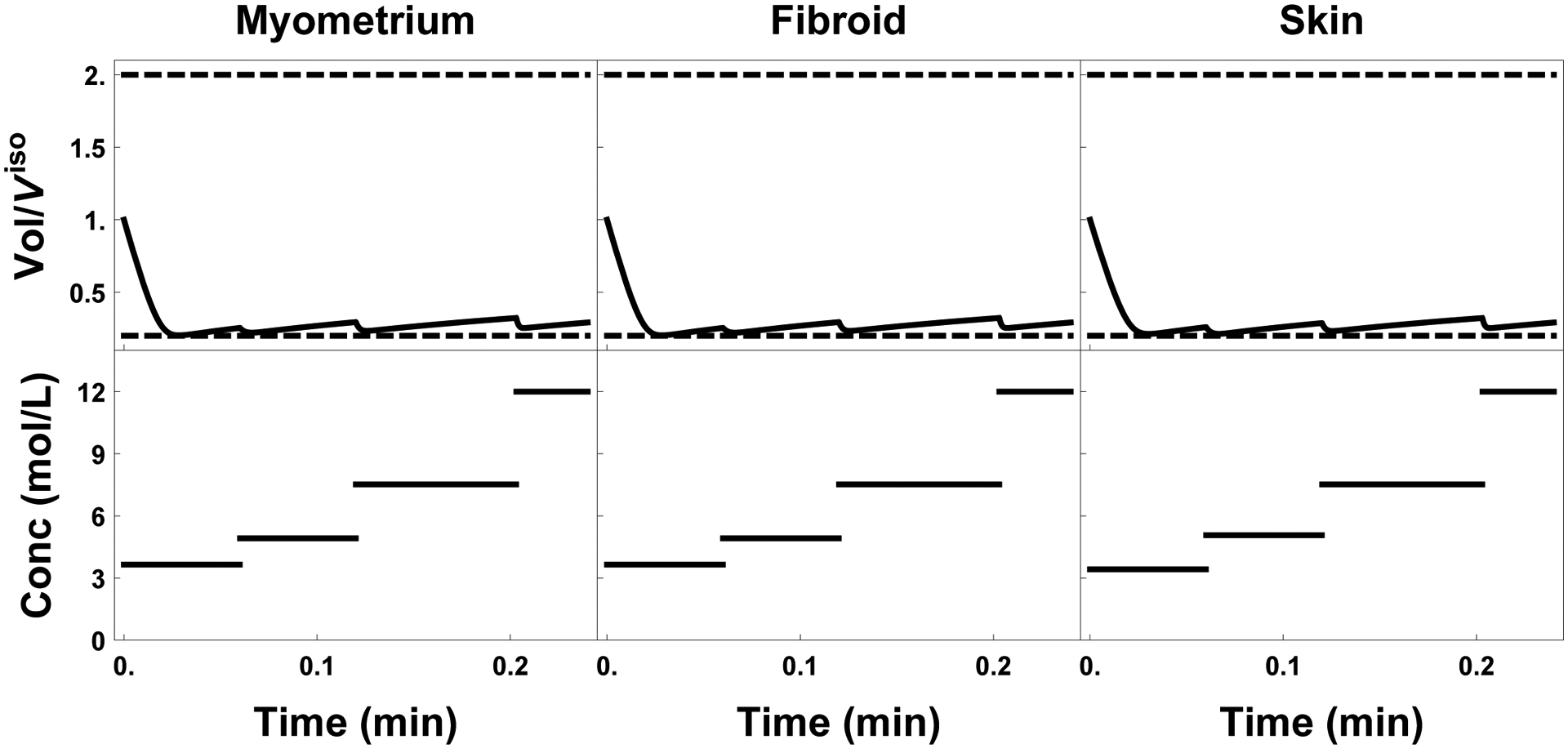
Initial 15 seconds of the time optimal protocols for all three tissues. The top portion of each subfigure shows the exterior cell volume response, and the bottom the extratissue concentration in mol/L.