Emerging neurodevelopmental perspectives on mathematical learning

Abstract

Strong foundational skills in mathematical problem solving, acquired in early childhood, are critical not only for success in the science, technology, engineering, and mathematical (STEM) fields but also for quantitative reasoning in everyday life. The acquisition of mathematical skills relies on protracted interactive specialization of functional brain networks across development. Using a systems neuroscience approach, this review synthesizes emerging perspectives on neurodevelopmental pathways of mathematical learning, highlighting the functional brain architecture that supports these processes and sources of heterogeneity in mathematical skill acquisition. We identify the core neural building blocks of numerical cognition, anchored in the posterior parietal and ventral temporal-occipital cortices, and describe how memory and cognitive control systems, anchored in the medial temporal lobe and prefrontal cortex, help scaffold mathematical skill development. We highlight how interactive specialization of functional circuits influences mathematical learning across different stages of development. Functional and structural brain integrity and plasticity associated with math learning can be examined using an individual differences approach to better understand sources of heterogeneity in learning, including cognitive, affective, motivational, and sociocultural factors. Our review emphasizes the dynamic role of neurodevelopmental processes in mathematical learning and cognitive development more generally.

Introduction

Mathematical knowledge is essential for academic and professional success in the 21^st century (Butterworth, Varma, & Laurillard, 2011; Geary, 1994; Iuculano & Menon, 2018; National Mathematics Advisory Panel, 2008; Parsons & Bynner, 2005; Richland, Zur, & Holyoak, 2007). Strong foundational skills in mathematical problem solving, acquired in early childhood, are critical not only for success in the science, technology, engineering, and mathematical (STEM) fields but also for quantitative reasoning in everyday life (Butterworth & Walsh, 2011; Geary, 2013; Geary, Berch, Ochsendorf, & Koepke, 2017; Geary, Nugent, & Bailey, 2013; National Mathematics Advisory Panel, 2008; PISA, 2017). More than ever, the use of mathematics is ubiquitous in all aspects of human cognition in our technologically-driven society (Butterworth et al., 2011; Nelson & Reyna, 2007; Peters, 2007; Peters et al., 2006; Reyna & Brainerd, 2007).

Current theories of brain development emphasize the role of learning, experience, and education in shaping brain function and structure (Posner & Rothbart, 2007). The emergence of regional functional specialization and fine-tuning of neuronal response properties is influenced by interactions and communications with other brain regions (Menon, 2013; Passingham, Stephan, & Kotter, 2002). This process of interactive specialization and reorganization of functional circuits is thought to play a prominent role in children’s cognitive development (Johnson, 2001, 2011; Menon, 2013). Repeated co-activation strengthens intrinsic functional connections between brain regions, resulting in increased differentiation between functional brain networks that subserve distinct cognitive processes (Fair, Dosenbach, et al., 2007; Fox & Raichle, 2007; Jolles, van Buchem, Crone, & Rombouts, 2013; Kelly et al., 2009; Mackey, Singley, & Bunge, 2013; Supekar, Menon, Rubin, Musen, & Greicius, 2008).

These interactive neurocognitive processes are particularly relevant for complex cognitive skills such as numerical problem solving that rely on coordinated interactions between distributed brain structures. Thus, the development of core brain systems for mathematical learning is supported by multiple distributed neural processes involved in quantity representations, symbolic number form, as well as memory and cognitive control (Arsalidou & Taylor, 2011; Cho et al., 2012; Fias, Menon, & Szucs, 2013; Qin et al., 2014; Rosenberg-Lee, Barth, & Menon, 2011; Supekar & Menon, 2012) (Figure 1; Table 1). The manner in which distributed brain regions are engaged may depend on task complexity, individual’s level of expertise, or individual differences in domain-general cognitive abilities such as working memory associated with mathematical learning.

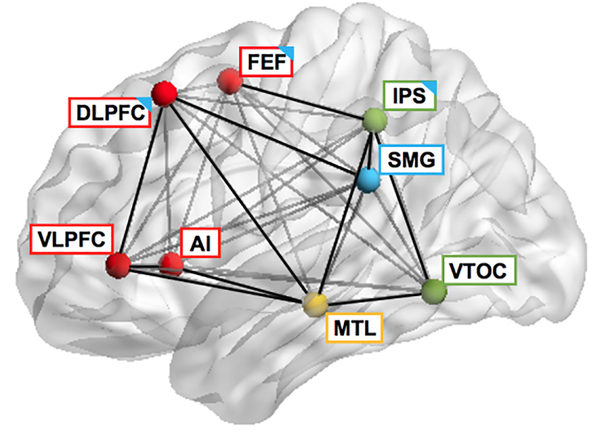
Figure 1. Brain network model of mathematical learning.

Schematic diagram of neurocognitive systems involved in mathematical skill development. The visual number form processing system, anchored in the VTOC, and the quantity representation system, anchored the IPS, build semantic representations of numerical quantity, which form core building blocks for higher-level mathematical cognition (light green). The declarative memory system, anchored in the MTL, plays an important role in long-term memory formation of number and math knowledge and generalization of learning (orange yellow). Parietal and frontal systems, including the IPS, SMG, FEF, and DLPFC, support visuospatial attention for objects and short-term representations and manipulations of quantities (light blue). Finally, prefrontal control circuits, anchored in the DLPFC, VLPFC, and AI, serve as flexible hubs for integrating information across multiple brain systems, thereby facilitating numerical problem-solving skill acquisition (red). AI: anterior insula; DLPFC: dorsolateral prefrontal cortex; IPS: intraparietal sulcus; FEF: frontal eye field; MTL: medial temporal lobe; SMG: supramarginal gyrus; VLPFC: ventrolateral prefrontal cortex; VTOC: ventral temporal-occipital cortex. Adapted from Menon (2016a).

Table 1.

Overview of neurocognitive systems involved in mathematical skill development.

Neurocognitive systems	Brain regions	Functional roles
Visual number form processing	Ventral temporal-occipital cortex (VTOC)  • fusiform gyrus  • inferior temporal gyrus	• symbolic number processing • semantic representations of numerical quantity
Quantity representation	Posterior parietal cortex (PPC)  • intraparietal sulcus (IPS)
Declarative memory	Medial temporal lobe (MTL)  • hippocampus  • parahippocampal gyrus	• long-term memory formation of number and math knowledge • generalization of learning
Parietal and prefrontal cortices	Posterior parietal cortex (PPC)  • IPS  • supramarginal gyrus (SMG) Prefrontal cortex  • dorsolateral prefrontal cortex (DLPFC)  • frontal eye field (FEF)	• visuospatial attention for objects • short-term representations and manipulations of quantities
Prefrontal control	Prefrontal cortex  • anterior insula (AI)  • DLPFC  • ventrolateral prefrontal cortex (VLPFC)	• cognitive control • flexible hubs for integrating information across multiple brain systems

Here we synthesize emerging findings on the neurodevelopmental basis of mathematical learning. We use a systems neuroscience approach to characterize the development of distributed brain networks that support multiple aspects of math learning. We review core neural building blocks of numerical cognition, interactive functional brain circuits associated with math learning, functional and structural brain plasticity that underlie math learning, as well as sources of individual differences in math learning in children. We discuss distributed brain systems involved in math learning, with a particular focus on emerging evidence for the role of the medial temporal lobe (MTL) in the acquisition of mathematical problem-solving skills (Cho et al., 2012; Qin et al., 2014; Rosenberg-Lee et al., 2018; Supekar, Chang, Mistry, Iuculano, & Menon, 2021). We conclude by highlighting directions for future research.

Core building blocks of mathematical learning

The development of mathematical skills relies on distinct yet interacting neurocognitive processing systems, including those subserving perception of symbolic numbers, as well as declarative memory, working memory, and cognitive control processes used to manipulate representations of quantity (Arsalidou, Pawliw-Levac, Sadeghi, & Pascual-Leone, 2018; Fias et al., 2013) (Figure 1). Brain systems for representing non-symbolic (e.g., array of dots) and symbolic (e.g., Arabic numerals) numerical quantities may contribute to critical building blocks from which higher-level mathematical knowledge is constructed. Core functional systems of numerical cognition include quantity representation system, anchored in the intraparietal sulcus (IPS) in the posterior parietal cortex (PPC), and visual number form processing system, anchored in the ventral temporal-occipital cortex (VTOC). Quantity-selective neurons have been found in non-human primate IPS (Nieder, 2016; Nieder & Dehaene, 2009) and functional magnetic resonance imaging (fMRI) adaptation paradigms have suggested that the human IPS is sensitive to quantity across stimulus formats (Bulthé, De Smedt, & Op de Beeck, 2014; Cohen Kadosh, Cohen Kadosh, Kaas, Henik, & Goebel, 2007; Piazza, Pinel, Le Bihan, & Dehaene, 2007). Similarly, specialization for visually-presented symbolic numbers has been detected in the VTOC (Abboud, Maidenbaum, Dehaene, & Amedi, 2015; Hannagan, Amedi, Cohen, Dehaene-Lambertz, & Dehaene, 2015; Piazza & Eger, 2016; Shum et al., 2013; Yeo, Wilkey, & Price, 2017). Together, the IPS and the VTOC build semantic representations of quantity (Ansari, 2008) and facilitate efficient manipulation of numerical quantity necessary for numerical problem solving (Menon, 2015).

In addition to brain regions important for non-symbolic and symbolic representations of quantity, working memory and declarative memory systems facilitate mathematical learning and skill acquisition. Performance and learning in multiple mathematical domains, including numerical magnitude processing, arithmetic problem solving, and logical reasoning, involve maintenance and manipulation of quantity representations in working memory (Alloway & Alloway, 2010; Ashkenazi, Rosenberg-Lee, Metcalfe, Swigart, & Menon, 2013; Bugden & Ansari, 2016; De Visscher & Noël, 2014; De Visscher, Szmalec, Van Der Linden, & Noël, 2015; Friso-Van Den Bos, Van Der Ven, Kroesbergen, & Van Luit, 2013; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Gilmore et al., 2013; Menon, 2016b; Metcalfe, Ashkenazi, Rosenberg-Lee, & Menon, 2013; Morsanyi, Devine, Nobes, & Szűcs, 2013; Raghubar, Barnes, & Hecht, 2010). Working memory is regulated by the visuospatial attention system, anchored in the IPS, supramarginal gyrus, frontal eye field, and dorsolateral prefrontal cortex (PFC) regions, and the cognitive control system, anchored in the insula, dorsolateral and ventrolateral PFC, which serves as a flexible hub for integrating functional circuits engaged in numerical problem solving (Menon, 2016a).

It is important to note that multiple parietal and prefrontal cortical regions play a scaffolding role in mathematical skill acquisition during development (Arsalidou et al., 2018), and this is true even for basic magnitude processing tasks (Ansari, Garcia, Lucas, Hamon, & Dhital, 2005). In the case of arithmetic problem solving, greater PFC activation has been observed in younger children (Rivera, Reiss, Eckert, & Menon, 2005). Together, these findings point to greater cognitive and working memory demands in children during the early stages of skill acquisition. In addition, growing evidence suggests that the declarative memory system, anchored in the MTL, also plays an important role in associative learning and the acquisition of math facts in children, a topic to which we return at some length in the following sections.

Mechanisms of interactive specialization in mathematical skill development

Developmental studies have shown age-related decreases in neural activity in the MTL and PFC and increases in IPS and VTOC activity during quantity judgment and mental arithmetic tasks (Arsalidou & Taylor, 2011; Houde, Rossi, Lubin, & Joliot, 2010; Rivera et al., 2005). Such a developmental shift reflects decreasing demands on declarative memory and cognitive control systems, accompanied by increased reliance on specialized functional networks (modules) along the dorsal and ventral visual pathways linking the IPS and VTOC. These neurodevelopmental changes are consistent with the theoretical framework of interactive specialization (IS) model, which posits that cognitive development depends on selective strengthening of some brain circuits and weakening of others, giving rise to the formation of specialized and inter-connected functional modules over time (Johnson, 2000, 2001, 2011; Menon, 2013; Supekar, Musen, & Menon, 2009). The IS framework is especially relevant for understanding the mechanisms of acquisition of numerical problem-solving skills in children, which involves engagement of distributed brain areas that changes dynamically with skill acquisition (Menon, 2016a).

To date, the majority of brain imaging studies applying the IS model has been based on observations of changes in regional brain responses, rather than changes in inter-regional interactions or functional brain circuits (Cohen Kadosh, Cohen Kadosh, Dick, & Johnson, 2011; Cohen Kadosh, Bahrami, et al., 2011; He, Garrido, Sowman, Brock, & Johnson, 2015; Joseph, Gathers, & Bhatt, 2011). Moreover, although longitudinal studies are essential for investigating individual trajectories of learning and development in children (Bjorklund & Causey, 2018; Kraemer, Yesavage, Taylor, & Kupfer, 2000; Weinert & Schneider, 1999), much of the studies testing hypotheses arising from the IS model has used cross-sectional designs, which are less desirable for this purpose. Longitudinal designs examining plasticity of functional circuits over time are necessary for understanding how coordination of multiple functional circuits lead to specialized functional modules across development and contribute to mathematical learning and cognitive development more generally.

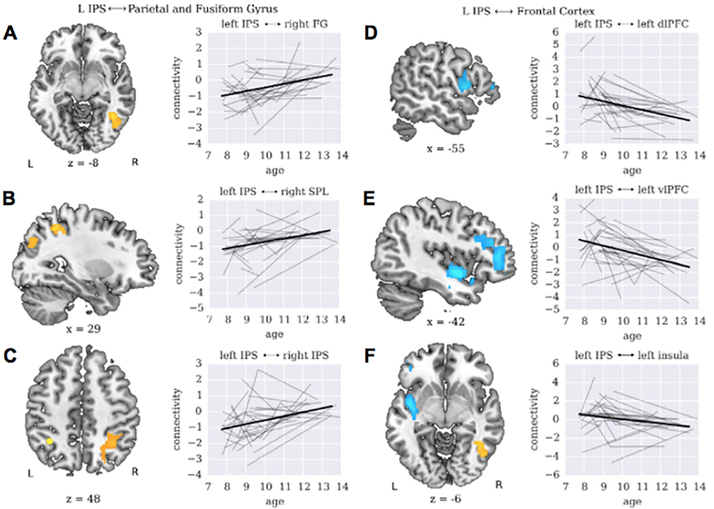
Using a longitudinal cohort of children sampled at multiple time points over a 6-year period spanning from childhood to early adolescence, Battista et al. (2018) characterized developmental trajectories associated with plasticity of functional connectivity of the IPS, known to play a critical role in numerical problem solving. In line with the IS model, the developmental changes in numerical task-related IPS functional circuits were characterized by both increases and decreases over time. The left IPS connectivity with other posterior brain regions, including the right fusiform gyrus (FG) in the VTOC, the right superior parietal lobule (SPL) in the PPC, and the right IPS increased, while connectivity between the left IPS and PFC regions decreased across development (Figure 2). These changes in connectivity were accompanied by improvements in arithmetic task performance: from ages 7 to 14, children improved their performance at a rate of 2%/yr increase in accuracy and 179.8ms/yr decrease in reaction time (Battista et al., 2018). Consistent with these behavioral findings, significant age-related decreases in engagement of frontoparietal circuits point to reduced reliance on the cognitive control and working memory system (PFC) during numerical problem solving.

Figure 2. Interactive specialization of IPS circuitry.

The left IPS connectivity with the (A) right fusiform gyrus (FG) in the VTOC and (B) right SPL, and (C) right IPS increases with age, while the left IPS connectivity with the (D) left DLPFC, (E) left VLPFC, and (F) left insula decreases with age during arithmetic problem solving. Target brain regions of left IPS circuits positively and negatively associated with age are shown in orange-yellow and light blue, respectively. Line plots show hierarchical linear modeling (HLM) fits for target brain regions from the left IPS to whole-brain connectivity analysis. Model fits and individual trajectories are shown in thick black and light gray lines, respectively. L: Left; R: Right. Other abbreviations are the same as in Figure 1. Adapted from Battista et al. (2018).

Stronger interactions between dorsal and ventral visual pathways, linking the parietal quantity representation system (IPS) with the visual number form processing system (VTOC), reflect tighter functional integration of key components of numerical processing at later developmental stages. Greater functional connectivity between the IPS and SPL may represent enhanced visuospatial attention to support arithmetic problem solving (Hubbard, Piazza, Pinel, & Dehaene, 2005; Knops, Thirion, Hubbard, Michel, & Dehaene, 2009). In line with this argument, in addition to the IPS, the SPL has also been reported to be involved in numerical processing (Ansari et al., 2005; Sokolowski, Fias, Mousa, & Ansari, 2017), arithmetic (Rosenberg-Lee, Barth, et al., 2011; Rosenberg-Lee, Chang, Young, Wu, & Menon, 2011), and abacus-based mental calculation (Chen et al., 2006). Together, these longitudinal findings provide direct evidence for age-related refinement of IPS functional circuits, with increased functional coupling between posterior brain systems and decreased frontoparietal interactions over time, that support neurocognitive development of mathematical skills.

These findings emphasize an important strength of the IS model that can incorporate multiple cognitive functions of a specific brain region, which depend on its context-dependent interactions with task-relevant brain regions, rather than isolated, regional specialization of domain-specific functions (Johnson, 2001, 2011; McIntosh, 2000; Menon, 2015). The IS model highlights an important perspective that specialization of functional modules emerges from dynamic changes in inter-regional connectivity with both increases and decreases in specific functional circuits, contributing to the development of cognitive skills over time. Consistent with this view, the IPS is not only important for quantity processing and manipulation, but also subserves other cognitive functions such as visuospatial representations and short-term memory that contribute to numerical problem solving (Hubbard et al., 2005; Knops, Piazza, Sengupta, Eger, & Melcher, 2014). In this context, selective strengthening of dorsal-ventral visual pathways and weakening of frontoparietal circuits over time in Battista et al. (2018) may reflect different cognitive mechanisms of numerical problem solving across development. Precisely how changes in functional circuits contribute to the development of fine-tuned regional representations (and vice versa) remains an important topic for future studies.

Finally, it should be noted that the extent to which specialization of brain circuits that support mathematical skill acquisition depends on educational experience versus normative brain maturation remains to be determined. We suggest that short-term training studies can provide a way to examine the influence of learning experience, by minimizing the effects of ongoing brain maturation, a topic that is discussed below in Disentangling the effects of experience and brain maturation on mathematical learning section.

Role of medial temporal lobe declarative memory system in mathematical learning

In addition to IPS and VTOC regions which play important roles for representing non-symbolic and symbolic representations of quantity and PFC regions important for working memory and cognitive control, the MTL declarative memory system helps scaffold mathematical learning and skill acquisition. Evidence for this comes from cross-sectional and longitudinal investigations of changes in arithmetic problem-solving strategies used by children at different stages of development. Children’s gains in arithmetic problem-solving skills during early school years are characterized by the gradual reduction of inefficient procedural strategies (e.g., counting) and increase in direct retrieval of math facts (Barrouillet & Fayol, 1998; Butterworth, 1999; Chen & Siegler, 2000; Cho, Ryali, Geary, & Menon, 2011; Geary, 1994, 2011; Geary & Brown, 1991; Geary & Hoard, 2003; Imbo & Vandierendonck, 2007; Qin et al., 2014; Siegler & Shipley, 1995; Siegler & Shrager, 1984). Over the past decade, evidence has been accumulating for a developmentally-specific role of the MTL declarative memory system in this gradual transition between arithmetic problem-solving strategies. Specifically, converging evidence from multiple experiments points to the importance of the MTL during the development of arithmetic fact retrieval in elementary school children (Chang, Rosenberg-Lee, Qin, & Menon, 2019; Cho et al., 2012; Cho et al., 2011; De Smedt, Holloway, & Ansari, 2011; Qin et al., 2014; Rosenberg-Lee et al., 2015; Rosenberg-Lee et al., 2018; Supekar, Swigart, et al., 2013).

The role of the MTL, particularly its hippocampal subdivision, in learning and memory consolidation for events in space and time is well known (Davachi, 2006; Davachi, Mitchell, & Wagner, 2003; Diana, Yonelinas, & Ranganath, 2007; Eichenbaum, Yonelinas, & Ranganath, 2007; Squire, 1992; Squire, Genzel, Wixted, & Morris, 2015; Squire, Stark, & Clark, 2004; Tulving, 1983). Importantly, the hippocampus plays an essential role in binding or integrating information together (Davachi, 2006; Eichenbaum, 2004; Giovanello, Schnyer, & Verfaellie, 2004; McClelland, McNaughton, & O’Reilly, 1995; Olsen, Moses, Riggs, & Ryan, 2012; Ranganath, 2010; Staresina & Davachi, 2009; Zeithamova & Bowman, 2020), which may support multiple complements of mathematical learning at different developmental stages of cognitive skill acquisition. For example, in the context of arithmetic fact learning, the hippocampus may be involved in binding operands (e.g., “3 + 5”) to answers (e.g., “8”). In early childhood, the hippocampus may contribute to the binding of neural representations across non-symbolic and symbolic quantities when children understand the magnitude of symbolic numbers (e.g., numeral “3” or number word “three”) by linking them to concrete non-symbolic representations of quantities (e.g., three objects), which is thought to facilitate numerical problem-solving skill acquisition (Brankaer, Ghesquiere, & De Smedt, 2014; Carey, 2004; Dehaene, 2011; Feigenson, Dehaene, & Spelke, 2004; Lipton & Spelke, 2005; Malone, Heron-Delaney, Burgoyne, & Hulme, 2019; Mundy & Gilmore, 2009; Szkudlarek & Brannon, 2017). Similarly, the hippocampus may also facilitate formation of structural mapping between “ordered set of numerals” (i.e., count list) and magnitude representations for larger quantities (Sullivan & Barner, 2013), allowing individuals to use knowledge about smaller numbers to guide estimation of larger numbers (Sullivan & Barner, 2014).

It has been proposed that the hippocampal engagement is required during the early stages of learning (McClelland et al., 1995; Smith & Squire, 2009) and for building schematic knowledge – i.e., frameworks of associative knowledge (Wang & Morris, 2010). For example, when learning arithmetic, children, who are still in the process of developing schematic knowledge, may rely more on the hippocampus, compared to adults. This proposal may help explain the lack of reliable hippocampal engagement reported in adults, when solving overlearned arithmetic or multiplication problems likely solved by fact retrieval (Delazer et al., 2003; Delazer et al., 2005; Grabner, Ischebeck, et al., 2009; Hayashi, Ishii, Kitagaki, & Kazui, 2000; Ischebeck, Zamarian, Egger, Schocke, & Delazer, 2007; Ischebeck et al., 2006; Lee, 2000; Rosenberg-Lee, Chang, et al., 2011; Zamarian, Ischebeck, & Delazer, 2009) or problems self-reported as solved by retrieval strategy (Grabner, Ansari, et al., 2009). Adults in later stages of learning may have a well-established schema for arithmetic problem solving, which no longer require hippocampal engagement. Further, decreased MTL involvement may be accompanied by concomitant increases in the reliance on neocortical systems in later stages of learning (McClelland et al., 1995). Indeed, adults frequently show a relative increase in engagement of the angular gyrus (AG) in the inferior parietal lobe during arithmetic fact retrieval (Delazer et al., 2003; Delazer et al., 2005; Fresnoza et al., 2020; Grabner, Ansari, et al., 2009; Grabner et al., 2007; Grabner, Ischebeck, et al., 2009; Ischebeck et al., 2007; Ischebeck et al., 2006; Jost, Khader, Burke, Bien, & Rösler, 2011; Klein et al., 2016; Lee, 2000), processing symbolic numbers (Price & Ansari, 2011; Van Der Ven, Takashima, Segers, Fernández, & Verhoeven, 2016), metacognitive functioning (Anderson, Betts, Ferris, & Fincham, 2011), schematic memory (Thakral, Madore, & Schacter, 2017; van der Linden, Berkers, Morris, & Fernández, 2017; Wagner et al., 2015), and multimodal integration (Cabeza, Ciaramelli, & Moscovitch, 2012; Ramanan & Bellana, 2019; Ramanan, Piguet, & Irish, 2017; Seghier, 2013). Although AG activity has been also observed during arithmetic fact retrieval in children (Polspoel, Peters, Vandermosten, & De Smedt, 2017), the findings in adults are much more robust across multiple studies. Thus, despite its critical role in learning and memory formation, hippocampal contributions to mathematical learning, and cognitive development more broadly, have received little attention until recent evidence in children.

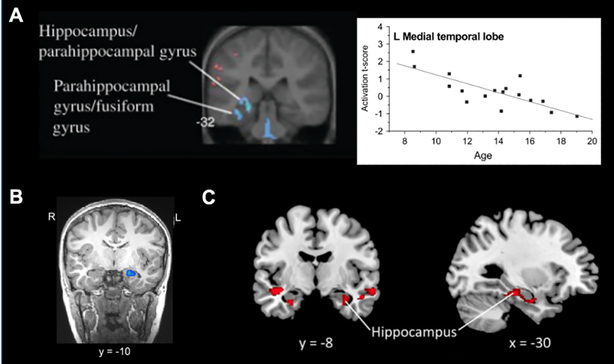
The first evidence for the differential engagement of the hippocampal memory system in mathematical cognition over development came from a cross-sectional study in children, adolescents, and young adults spanning the ages between 8 to 19 (Rivera et al., 2005). Younger children exhibited significantly greater engagement of MTL regions, including the hippocampus, when solving small single-digit addition and subtraction problems with sums and minuends less than 10 (Figure 3A). Similarly, De Smedt and colleagues (2011) demonstrated greater hippocampal response when solving smaller, compared to larger, arithmetic problems and during addition, compared to subtraction, problem solving in 10–12-year old children (Figure 3B). Rosenberg-Lee et al. (2015) further observed greater hippocampal activity during addition compared to subtraction in 7–9-year-old children (Figure 3C). As memory-based problem-solving strategies are more often observed in smaller, compared to larger, arithmetic problems, and addition, compared to subtraction, problems (Barrouillet, Mignon, & Thevenot, 2008; Imbo & Vandierendonck, 2008), these findings suggest a role of the hippocampus in arithmetic fact retrieval.

Figure 3. The role of the hippocampus in memory-based numerical problem-solving in children.

A. Children show significant hippocampal engagement during single-digit arithmetic problem solving, which decreases with age between childhood and adulthood. Areas of activation that are positively and negatively associated with age are shown in red and blue, respectively. B. The left hippocampus shows greater activation during addition than subtraction problem solving (shown in blue) in 10–12-year-old children. C. Greater brain activation for addition than subtraction problem solving (shown in red) is observed in the bilateral hippocampus in 7–9-year-old children. L: Left; R: Right. Adapted from Rivera et al. (2005) [A], De Smedt et al. (2011) [B], and Rosenberg-Lee et al. (2015) [C].

Many previous studies on arithmetic problem solving rely on the assumption that certain amount of practice, problem size, and arithmetic operations elicit a particular strategy. Highly practiced problems, smaller problems, and addition and multiplication, relative to subtraction and division, have been shown to be more often solved by retrieval than procedural strategy (Barrouillet & Lepine, 2005; Barrouillet et al., 2008; Campbell & Xue, 2001; Grabner, Ansari, et al., 2009; Imbo & Vandierendonck, 2008; LeFevre et al., 1996; LeFevre, DeStefano, Penner-Wilger, & Daley, 2006; Rosenberg-Lee, Chang, et al., 2011; Siegler & Shipley, 1995). However, variations in strategy use can occur between individuals as well across trials within an individual (Dowker, 2019; Siegler, 1987). Thus, an alternate, more direct approach is to assess strategy use in each individual on a trial-by-trial basis. In a trial-by-trial strategy assessment, participants are first asked to solve an arithmetic problem, and then are probed on how they solved the problem. This approach has been demonstrated to have strong construct validity (e.g., children who report using retrieval more often than counting strategies show faster reaction times than children who report to rely more on counting; Wu et al., 2008), and has been successfully used in adults (Campbell & Xue, 2001; Campbell & Timm, 2000) and children (Barrouillet & Lepine, 2005; Barrouillet et al., 2008; Ramirez, Chang, Maloney, Levine, & Beilock, 2016).

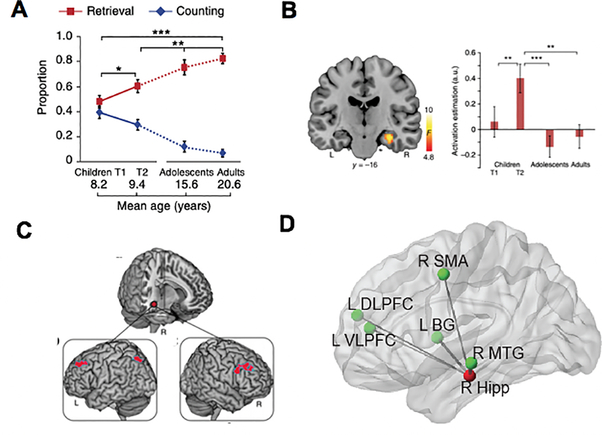
Utilizing strategy assessments, Cho and colleagues (2011) divided a sample of 7–9 year old children into ‘Retrievers’ and ‘Counters’ (children who retrieved and counted more than 60% of correctly solved trials, respectively). In this study, ‘Retrievers’ showed greater activation in the left ventrolateral PFC, compared to ‘Counters’ during addition problem solving, which suggests that the use of memory retrieval strategy (or shifting from counting to retrieval strategy) relies on PFC cognitive control resources in children. Additionally, multivariate activation pattern analysis revealed that these groups could be significantly discriminated by differences in spatial activity patterns in multiple brain regions, including the MTL, ventrolateral PFC, and PPC. Notably, high classification accuracy was observed in the bilateral hippocampus (86% accuracy). The existence of decodable, fine scale differences in the spatial pattern of fMRI signals suggests that the underlying neural activity in distributed brain regions, including the hippocampus, are accessed and used differently during each strategy. A follow-up study revealed that higher activity levels in the right hippocampus are associated with an increased use of retrieval strategy and faster reaction time to solve addition problems (Cho et al., 2012). Furthermore, dynamic bidirectional interactions were observed between the right hippocampus and dorsolateral and ventrolateral PFC during addition problem solving. Taken together, these findings suggest that hippocampal activity and connectivity contribute to children’s use of efficient retrieval strategy during arithmetic problem solving.

To better understand neurodevelopmental changes associated with shifts in strategy use during arithmetic problem solving, Qin and colleagues (2014) used a longitudinal design with two time points for strategy assessment and fMRI session (Time 1 at ages between 7 to 9 years and Time 2 at 1.2 years later). After 1.2 years, children reported using retrieval strategy during addition problem solving more frequently than before (Figure 4A). Crucially, task-related activity in the hippocampus increased over this time interval (Figure 4B). These changes in brain activity were not correlated with changes in retrieval strategy use. Additional cross-sectional data analysis comparing strategy use and brain activity between children from two time points, adolescents, and adults provided evidence that while adolescents and adults use retrieval strategy more frequently than children, their hippocampal engagement was significantly lower than children at Time 2, and not distinguishable from children at Time 1. This pattern of initial increase and subsequent decrease in hippocampal activation supports the models of long-term memory consolidation, which posit that the hippocampus plays a time-limited role in the early phases of knowledge acquisition (McClelland et al., 1995; Smith & Squire, 2009; Tse et al., 2007).

Figure 4. Hippocampal-neocortical circuits support mathematical learning.

A. The use of memory-based problem-solving strategy increases while counting strategy use decreases during addition problem solving across development. Solid and dotted lines represent longitudinal data from children at Time 1 (T1) and Time 2 (T2; ~1.2 years apart) and cross-sectional data from adolescents and adults, respectively. B. The right hippocampus shows longitudinal changes associated with arithmetic problem-solving skill development, with a greater engagement at T2 relative to T1. C. Plasticity of functional connectivity of the right hippocampus with the bilateral DLPFC and left IPS is associated with longitudinal improvements in retrieval fluency from T1 to T2. D. Pre-training functional connectivity of the right hippocampus (Hipp) with the left DLPFC, left VLPFC, right supplementary motor area (SMA), left basal ganglia (BG), and right middle temporal gyrus (MTG) is positively correlated with training-related performance gains in arithmetic problem solving. *p < .05, **p < .01, ***p < .001. L: Left; R: Right. Other abbreviations are the same as in Figure 1. Adapted from Qin et al. (2014) [A–C] and Supekar et al. (2013) [D].

Interestingly, although Qin et al. (2014) showed that regional changes in hippocampal activity were not associated with changes in retrieval strategy use, changes in hippocampal connectivity with dorsolateral PFC and IPS were positively correlated with changes in retrieval strategy use in this study (Figure 4C). Similarly, in a training study designed to facilitate rapid retrieval of arithmetic facts, hippocampal functional circuits predicted training-related performance gains (Figure 4D). Specifically, children who exhibited higher intrinsic functional connectivity of the hippocampus with dorsolateral and ventrolateral PFC, basal ganglia, supplementary motor area, and middle temporal gyrus prior to training showed greater performance improvements in arithmetic problem solving (Supekar, Swigart, et al., 2013). Together, these findings suggest that hippocampal-neocortical circuit reorganization, rather than changes in activation in isolated brain regions, plays an important role in children’s shift from effortful procedural strategy to more efficient memory-based problem-solving strategy (Barrouillet & Fayol, 1998; Imbo & Vandierendonck, 2007; Siegler & Shipley, 1995; Siegler & Shrager, 1984).

It is noteworthy that several recent findings have begun to demonstrate hippocampus-dependent math learning in adults as well. Qin and colleagues (2014) found refinements in multivariate patterns of activity in the hippocampus in adolescence and adulthood, even without significant hippocampal activity relative to baseline. In addition, Bloechle and colleagues (2016) have recently found greater hippocampal activity for trained relative to untrained problems after training as well as trained (after training) relative to to-be-trained (before training) problems in adults, using repeated fMRI measures before and after training. Furthermore, Klein and colleagues (2016) found hippocampal activity associated with arithmetic fact retrieval during number bisection and mental addition tasks in adults. These results suggest that the hippocampus may continue to be involved in retrieval of math facts across development. However, earlier arithmetic training studies in adults have not reported changes in hippocampal activity associated with learning (Delazer et al., 2003; Delazer et al., 2005; Grabner, Ischebeck, et al., 2009; Ischebeck et al., 2007; Ischebeck et al., 2006; Zamarian et al., 2009). Inconsistent findings of MTL engagement in studies of adults may in part be due to different levels of math proficiency or different educational backgrounds that vary in emphasis on retrieval-based learning (Geary, Chen, Salthouse, & Fan, 1996; Geary & Wiley, 1991; Imbo & LeFevre, 2009) across participants. Further work with larger samples with different educational backgrounds and more comprehensive assessments of math and other cognitive abilities combined with multivariate neuroimaging analysis, which provides more sensitive measures of distributed patterns of brain activity (Kragel, Koban, Barrett, & Wager, 2018; Popal, Wang, & Olson, 2019), is needed to understand sources of variability across studies.

Taken together, emerging evidence highlights the developmentally-specific role of the hippocampus in the acquisition of memory-based numerical problem solving, with greater engagement during a key developmental stage for acquisition of arithmetic skills in childhood. Findings also suggest that interactions between the MTL and the PFC and parietal cortex, contribute to mathematical learning, consistent with the view that coordination of multiple functional circuits leads to specialized cognitive functions (Johnson, 2011; Menon, 2013). Future studies will need to further examine the role of the MTL and other brain areas in learning mathematical concepts such as cardinality or associativity as well as skill acquisition in more complex domains of mathematical cognition.

Disentangling the effects of experience and brain maturation on mathematical learning

A fundamental goal of developmental cognitive neuroscience is to distinguish brain mechanisms associated with different aspects of cognitive skill acquisition from normative brain development. Although longitudinal studies provide essential knowledge about individual trajectories of learning, changes observed over an extended time period cannot be solely attributed to learning experiences, due to the ongoing brain maturation during childhood and adolescence. Training studies are uniquely positioned to assess trajectories of learning-related cognitive and brain plasticity in a more precise manner. For example, learning from effective, targeted training programs can be achieved in a relatively short time period in training studies, thus minimizing the effects of ongoing brain maturation. Moreover, training studies with systematic experimental manipulations enable direct links between specific learning experiences and changes in brain and behavior across individuals. Tightly constrained short-term training studies with appropriate control groups or conditions can evaluate the causal role of training on behavioral changes and specialization of brain circuits that support math learning, thereby disentangling the effects of experience and brain maturation on cognitive skill development, which has broader implications for educational practices and learning interventions.

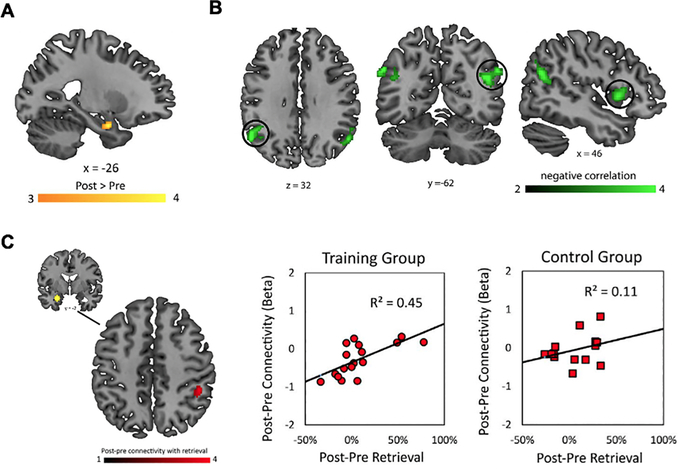
To address whether longitudinal changes in the hippocampal recruitment in children are results of maturational changes in the brain or experience-dependent effects of mathematical learning, Rosenberg-Lee et al. (2018) examined whether eight weeks of short-term training in arithmetic alters brain responses and connectivity in a similar way as longitudinal developmental changes do over the course of a year in children, as shown in Qin et al. (2014). This study found that training leads to increased activity in the anterior hippocampus during numerical problem solving. Additionally, decreased frontoparietal activity and increased hippocampal-parietal connectivity were associated with greater use of memory-based strategies with training (Figure 5). These changes were not observed in the control group. These results demonstrate that similar to long-term cognitive skill development, short-term training-induced learning is accompanied by the plasticity of hippocampal activation and connectivity in children. Convergent findings of hippocampal engagement in math learning across longitudinal and training study designs suggest that it is the learning experience, through formal education or short-term intervention, that drives brain plasticity, rather than maturational changes in the brain. These findings further advance our understanding of the neurobiological mechanisms of learning and provide insights into designing interventions that induce learning and brain plasticity more effectively.

Figure 5. Effects of math training on hippocampal response and connectivity.

A. The left anterior hippocampus shows greater activation after training, compared to before training, in children. B. Changes in brain activity in the bilateral angular gyrus and right inferior frontal gyrus are negatively correlated with training-induced changes in retrieval strategy use. C. Plasticity of functional connectivity of the left anterior hippocampus with the right intraparietal sulcus is associated with training-related increase in retrieval strategy use. Adapted from Rosenberg-Lee et al. (2018).

It should be noted that the changes in hippocampal-cortical connectivity were less distributed after short-term training in Rosenberg-Lee et al. (2018), compared to after a year of longitudinal change in Qin et al. (2014). In Qin et al., changes in hippocampal-parietal and hippocampal-prefrontal circuits were related to changes in retrieval strategy use. In contrast, Rosenberg-Lee et al. showed plasticity of hippocampal-parietal connectivity but no changes in the hippocampal-prefrontal circuits associated with training-related gains in retrieval strategy use. These results suggest that learning-related reorganization of hippocampal-prefrontal connectivity might be better characterized over longer time periods. In fact, the prefrontal cortex is known to mature more slowly than the parietal cortex (Giedd et al., 1996; Tamnes et al., 2017; Ziegler, Ridgway, Blakemore, Ashburner, & Penny, 2017). Follow-up experiments with multiple brain and behavioral measures at different time intervals may provide a better understanding of when and how different functional circuits contribute to various aspects of mathematical learning.

Functional and structural brain plasticity in response to intervention

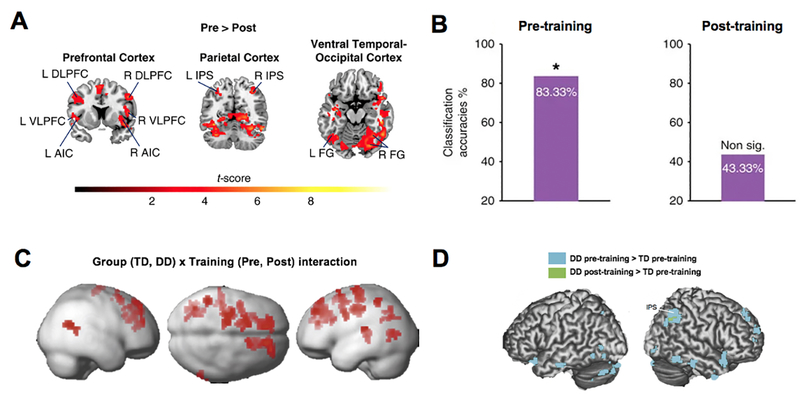
Recent research has identified remarkable plasticity in brain systems underlying mathematical skill development. Several fMRI studies have now begun to examine the extent to which interventions alter aberrant functional activity and connectivity in relevant neurocognitive systems in children with learning disabilities. Utilizing a similar intervention shown to significantly improve mathematical skills in children with different levels of math abilities (Christensen & Gerber, 1990; Fuchs, Fuchs, Hamlet, et al., 2006; Fuchs, Fuchs, & Compton, 2013; Fuchs, Fuchs, Compton, et al., 2006; Fuchs, 2007a, 2007b, 2004, 2002; Okolo, 1992), Iuculano et al. (2015) found that math intervention leads to marked reductions in brain responses in children with mathematical learning disabilities (MLD), resulting in normalization of brain activity to levels similar to those seen in typically developing (TD) children. Brain plasticity in children with MLD was evident in a distributed network of parietal, VTOC, and prefrontal regions important for numerical problem solving (Arsalidou et al., 2018; Fias et al., 2013; Peters & De Smedt, 2017) (Figure 6A). Remarkably, machine learning algorithms revealed that brain activity patterns in children with MLD were significantly different from TD peers before training, but statistically indistinguishable after training (Figure 6B). Similarly, a mental number line training has been shown to induce greater decrease in recruitment of frontal and parietal regions in children with developmental dyscalculia (DD), compared to TD children (Kucian et al., 2011) (Figure 6C). Moreover, this type of training has been associated with normalization of brain hyperconnectivity between the IPS and parietal, temporal, occipital, and frontal areas in children with DD to levels seen in TD controls (Michels, O’Gorman, & Kucian, 2018) (Figure 6D).

Figure 6. Brain plasticity in distributed functional networks in response to math training.

A. Math training induces functional brain plasticity in children with mathematical learning disabilities (MLD). Before training, compared with post-training, children with MLD exhibit hyper-activation during arithmetic problem solving in the bilateral DLPFC, VLPFC, AI, IPS, and fusiform gyrus (FG) in the VTOC. No brain areas show greater activation post-training, compared to pre-training. B. A linear classifier built using a support vector machine with leave-one-out cross validation reveals that brain activation patterns between MLD and typically developing (TD) groups are highly discriminable before training, but no longer discriminable after training. C. Training in mental number line results in greater reduction in brain activation during numerical task performance in children with developmental dyscalculia (DD), compared to TD children. D. Before training, greater bilateral IPS functional connectivity with parietal, temporal, occipital, and frontal regions is evident in the DD group relative to TD group. After training, IPS hyperconnectivity in the DD group only remains in a small parietal region. *p < .05. L: Left; R: Right. Other abbreviations are the same as in Figure 1. Adapted from Iuculano et al. (2015) [A–B], Kucian et al. (2011) [C], and Michels et al. (2018) [D].

Observations of pre-training hyperactivation and hyperconnectivity in regions typically involved in mathematical processing (Iuculano et al., 2015; Kucian et al., 2011; Michels et al., 2018) are consistent with cross-sectional studies in children with mathematical difficulties (Cappelletti & Price, 2013; Davis et al., 2009; Kaufmann et al., 2009; Rosenberg-Lee et al., 2015) and likely reflect the need for additional neural resources rather than inability to engage task-relevant brain areas. Findings of normalization of brain activity and connectivity indicate that intervention increases automaticity and decreases reliance on working memory resources during numerical task performance in children with learning disabilities. Taken together, these studies suggest that mathematical training more likely leads to normalization of brain activity and connectivity in children with learning disabilities, rather than engagement of compensatory mechanisms of plasticity (which would posit that after training, children with learning disabilities would recruit additional or distinct brain systems compared to controls). The extent to which these effects persist or “fade out” (Bailey, Duncan, Cunha, Foorman, & Yeager, 2020) after months or years post-intervention remain to be investigated in follow-up studies.

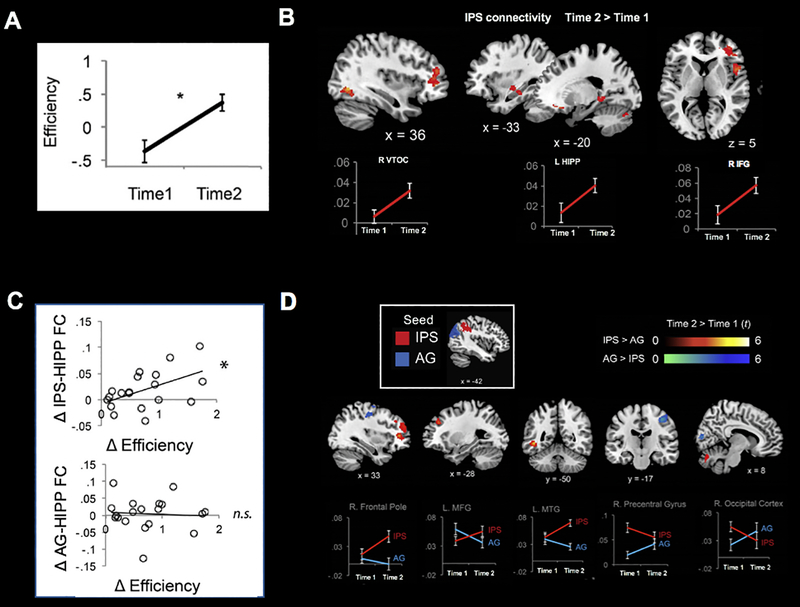
In addition to determining task-dependent functional brain plasticity, it is important to understand whether interventions also alter brain circuits in a context-independent manner. To address such question, researchers have used resting-state fMRI to examine intrinsic functional connectivity, which is less likely to be influenced by task engagement or individual differences in performance or strategy use (Church et al., 2009; Fair, Schlaggar, et al., 2007; Finn et al., 2014; Koyama et al., 2011; Supekar, Uddin, et al., 2013; Uddin, Supekar, & Menon, 2013). Using this approach, Jolles et al. (2016) characterized plasticity of intrinsic connectivity of parietal circuits in response to math intervention in children, incorporating the emerging view that higher-level cognition requires inter-regional interactions between multiple brain areas (Bressler & Menon, 2010; McIntosh, 2000). Several key findings from this study provide evidence for experience-dependent brain plasticity and differentiation of parietal networks underlying math learning. First, training in arithmetic problem-solving improved performance and strengthened IPS connectivity with VTOC, MTL, and PFC regions. Second, changes in IPS connectivity were correlated with individual differences in training-induced performance gains. Finally, training-related changes in IPS connectivity patterns were remarkably distinct from those of an adjacent parietal region, AG (Figure 7).

Figure 7. Interactive specialization of parietal circuits in response to math training.

A. Math training increases performance efficiency in arithmetic problem solving in third grade children. B. Training increases functional connectivity of the IPS with the right VTOC, left hippocampus (HIPP), and right inferior frontal gyrus (IFG). C. Training-related performance gains are associated with increased connectivity between the IPS (but not angular gyrus [AG]) and right hippocampus. D. Training leads to differential functional connectivity patterns of IPS vs. AG. Post-training, compared to pre-training, IPS shows greater functional connectivity with the right frontal pole, left middle frontal gyrus (MFG), and left middle temporal gyrus (MTG), while AG shows greater connectivity with the right precentral gyrus and right occipital cortex. *p < .05. L: Left; R: Right. Other abbreviations are the same as in Figure 1. Adapted from Jolles et al. (2016).

While studies of functional brain circuits provide rich information about task-related and context-independent brain plasticity associated with behavioral changes, neuroanatomical investigations of gray and white matter allow researchers to more directly examine how cognitive functions emerge from brain structures (Kucian et al., 2014; Matejko & Ansari, 2015; Rotzer et al., 2008; Rykhlevskaia, Uddin, Kondos, & Menon, 2009; Wilkey, Cutting, & Price, 2018). Moreover, systematic identification of anatomical deficits can provide concrete and convergent evidence for neurodevelopmental disorders and individual differences in mathematical performance and learning. Decreased gray matter volume in multiple PPC, VTOC, and MTL areas implicated in numerical problem solving has been consistently reported in children and adolescents with mathematical difficulties (Ranpura et al., 2013; Rotzer et al., 2008; Rykhlevskaia et al., 2009) (Figure 8A). Structural abnormalities in children with MLD have been shown to persist across 4 years of development from 8 to 10 years of age (McCaskey, von Aster, O’Gorman, & Kucian, 2020). Increased gray matter volume of the left IPS (Li, Hu, Wang, Weng, & Chen, 2013; Price, Wilkey, Yeo, & Cutting, 2016), bilateral hippocampus, and right inferior frontal gyrus (Wilkey et al., 2018) have been reported to be associated with higher math achievement. Further, plasticity in cortical surface measures (cortical thickness, folding regularity) in parietal, temporal, and frontal regions from 5 to 8 years of age have been associated with individual differences in math skills (Kuhl, Friederici, & Skeide, 2020). Finally, it has been shown that gray matter volume in the left PPC, VTOC, and PFC areas predict long-term gains in math ability from 8 to 14 years of age (Evans et al., 2015), whereas gray matter volume in the right hippocampus predicts learning in response to short-term math training (Supekar, Swigart, et al., 2013), consistent with the view that the hippocampus plays time-limited role during the early stages of learning (McClelland et al., 1995). Remarkably, both neuroanatomical and functional circuit measures are shown to be more sensitive predictors of learning than behavioral measures alone in children (Evans et al., 2015; Supekar, Swigart, et al., 2013).

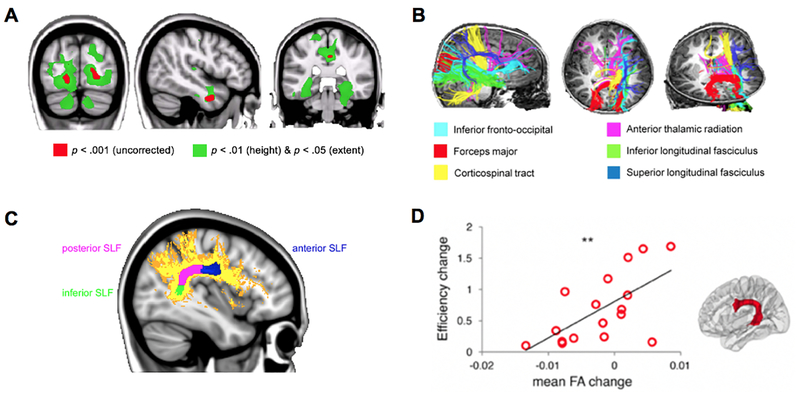
Figure 8. Structural integrity and plasticity associated with individual differences in mathematical learning.

A. Children with developmental dyscalculia (DD) show reduced gray matter volume in the PPC, VTOC, and MTL regions, compared to typically developing (TD) children. B. Children with DD show aberrant white matter pathways passing through the right temporal-parietal regions, compared to TD children. C. Children with DD, compared to TD children, showed significantly lower fractional anisotropy (FA), a quantitative measure of white matter integrity (Le Bihan et al., 2001), in the posterior part of superior longitudinal fasciculus (SLF), shown in pink. D. Changes in FA in the left SLF linking frontal and temporal cortices are positively associated with individual differences in training-related performance gains in numerical problem solving. **p < 0.01. Adapted from Rykhlevskaia et al. (2009) [A–B], Kucian et al. (2014) [C], and Jolles et al. (2016) [D].

In addition to differences in gray matter, children with MLD show deficits in white matter pathways linking parietal, temporal, and frontal regions, compared to TD children (Kucian et al., 2014; Rykhlevskaia et al., 2009) (Figures 8B–C). In TD children and young adults, these white matter pathways have been linked to individual differences in mathematical abilities (Li, Hu, Wang, Weng, & Chen, 2013; Matejko, Price, Mazzocco, & Ansari, 2013; Tsang, Dougherty, Deutsch, Wandell, & Ben-Shachar, 2009). Notably, a training study demonstrated that experience-dependent plasticity of white matter tracts is associated with individual differences in mathematical learning. Using novel fiber tracking algorithms, Jolles et al. (2016) identified sections of the superior longitudinal fasciculus linking frontal and parietal, parietal and temporal, and frontal and temporal cortices. They found that training-related changes in white matter integrity in the left frontotemporal tract that connects posterior temporal and lateral prefrontal cortices is positively correlated with individual differences in math performance gains (Figure 8D). This tract is well positioned to integrate symbolic number form and cognitive control processing systems (Arsalidou & Taylor, 2011).

Taken together, findings to date suggest that structural integrity and plasticity of multiple parietal, temporal, and prefrontal cortical regions contribute to mathematical learning and skill development. Further validation and advances in developmental systems neuroscience research will allow researchers to develop brain-based biomarkers for early identification of individual differences in mathematical learning as well as special needs for individualized instructions in children (Hale et al., 2010).

Brain network plasticity associated with math learning

Moving beyond properties of individual brain regions, there is now growing evidence that learning involves changes in large-scale brain network organization (Bassett & Mattar, 2017; Bassett, Zurn, & Gold, 2018). For example, global and regional network organization (Stanley, Dagenbach, Lyday, Burdette, & Laurienti, 2014; Stevens, Tappon, Garg, & Fair, 2012; Wang, Hu, Weng, Chen, & Liu, 2020) and dynamic changes in brain networks (Bassett et al., 2011; Bassett, Yang, Wymbs, & Grafton, 2015; Braun et al., 2015; Finc et al., 2020; Yin et al., 2020) are shown to be related to individual differences in cognitive abilities or learning. By providing rich, quantitative, and mechanistic information about interactions between distributed brain systems linked to behavior (Bassett & Sporns, 2017; Bullmore & Sporns, 2009; Cohen & D’Esposito, 2016; Grayson & Fair, 2017; Petersen & Sporns, 2015; Rubinov & Sporns, 2010; Sporns, 2014; Supekar et al., 2009; Uddin, Supekar, & Menon, 2010), functional and structural network organizations are emerging as reliable biomarkers for clinical symptoms (Collin et al., 2018), learning difficulties (Astle, Bathelt, Team, & Holmes, 2019; Siugzdaite, Bathelt, Holmes, & Astle, 2020), and intervention-related gains (Gallen & D’Esposito, 2019).

Given that mathematical cognition and learning involve distributed brain systems (Arsalidou et al., 2018; Fias et al., 2013; Peters & De Smedt, 2017), research incorporating brain network analysis approaches can provide valuable insights into understanding the emergence of specialized functional brain networks. For example, analysis of global and regional functional network organization for symbolic and non-symbolic number processing has revealed that overlapping and distinct characteristics of brain network architecture support quantity processing in the two number formats (Conrad, Wilkey, Yeo, & Price, 2020). In Conrad et al. (2020), the community membership (i.e., the extent to which two regions belong to the same network) of the left IPS and the right inferior temporal gyrus in the VTOC was significantly different between the number formats, which demonstrates distinguishable patterns of functional connectivity of quantity processing systems between number formats in the context of large-scale brain network organization. This study also showed that the global modularity (i.e., the degree of functional segregation relative to integration across brain networks) is similar between the number formats, which points to common neural mechanisms between symbolic and non-symbolic number processing and suggests that global and regional network properties may support different aspects of cognition (Stanley et al., 2014).

In the context of math learning in children, Supekar et al. (2021) examined how plasticity of brain networks supports efficient math learning in children. Using quantitative network analysis and neurocognitive process modeling of latent memory processes, this study demonstrated that training designed to improve children’s arithmetic problem solving skills induces changes in global modular organization and regional network reorganization of hippocampal-cortical circuits, as well as increase in use and efficiency of latent measures of memory retrieval-based strategies during addition problem solving. Notably, training-related changes in inter-modular functional connections of the right rostral hippocampus predicted learning gains and changes in efficiency of memory retrieval-based strategies. Interestingly, these effects were specific to the hippocampus and no other brain regions typically associated with numerical processing (e.g., IPS) showed changes in inter-modular functional connections that relate to learning gains. Taken together, these findings provide novel evidence that the emergence of brain network modules support the development of mathematical skills. Further understanding of individual differences in integrity and plasticity of brain networks associated with math learning may provide a more comprehensive understanding of the neurobiology of mathematical learning and skill development.

Mechanisms of individual differences in transfer of mathematical learning

Successful learning not only involves acquiring knowledge efficiently but also entails transferring the newly acquired knowledge beyond specific instances and contexts. Transfer is an essential mechanism for discovering and applying the regularities of learnt knowledge by linking individual events or knowledge to more complex structural knowledge (Zeithamova & Bowman, 2020). For example, in early childhood, transfer occurs when children understand that the number word, “three,” represents three objects after learning that “two” represents two objects and subsequently infer this knowledge across the count list (Spelke, 2000). Yet, how and to what extent individuals transfer their knowledge from one problem, context, or domain to others has been one of unresolved challenges across various cognitive domains (Melby-Lervag & Hulme, 2013; Simons et al., 2016). Moreover, few studies have considered individual differences in learning that may influence one’s ability to generalize newly acquired knowledge and skills (Jaeggi, Buschkuehl, Jonides, & Shah, 2011; Jaeggi, Buschkuehl, Shah, & Jonides, 2014). Understanding the neurocognitive mechanisms underlying learning and transfer is crucial for determining why some children learn and transfer their knowledge better than others.

Using an individual differences approach, a recent study addressed critical gaps in our understanding of brain mechanisms that support mathematical learning and transfer in elementary school children. Chang et al. (2019) showed that the two aspects of learning – speed of learning and depth of learning (transfer) – are related. Using multivoxel representational similarity and large-scale functional network analysis, this study demonstrated that distinct, complementary neural processes occur in parallel to support learning and transfer: overlap in neural representations at the level of regional circuitry and differentiation of functional brain circuits between highly practiced and novel problems in 8–10-year-old children. Notably, these patterns of results were learning-rate dependent: faster learners drew on common neural representations across practiced and novel problems in multiple brain areas including the MTL, while efficiently recruiting specialized brain networks for practiced problems (Figure 9). These results are in line with behavioral findings: faster learners performed better on both practiced and novel problems and demonstrated greater ability to differentiate between practiced and novel problems post-training. Importantly, these findings suggest that learning and transfer are interrelated and can occur at the same time through shared and distinct neural mechanisms. Similar findings have been observed in other domains, where segregation and integration of functional circuits promote efficient learning (Bassett et al., 2015; Finc et al., 2020; Salmi et al., 2020) and transfer or generalization (Dahlin, Neely, Larsson, Backman, & Nyberg, 2008; Schlichting, Mumford, & Preston, 2015), respectively. While these studies are promising, much more work is needed to advance our understanding of transfer and generalization associated with mathematical skill acquisition.

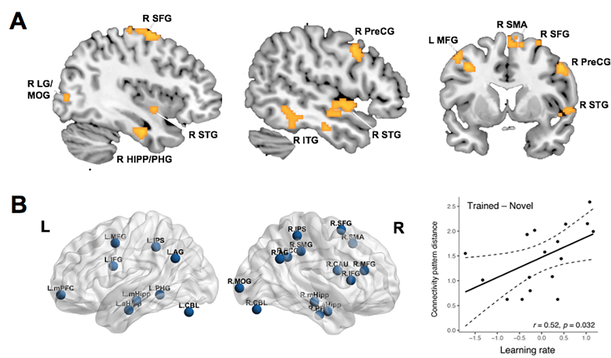
Figure 9. Distinct neurocognitive processes support mathematical learning and transfer.

A. Learning rate over five days of training in arithmetic problem solving is correlated with neural representational similarity between trained and novel problems in multiple brain regions, including the MTL and frontal, temporal, and occipital regions after training. B. Learning rate predicts greater differentiation of large-scale brain networks between trained and novel problems, measured by connectivity pattern distance. Functional brain network was constructed from arithmetic task-related brain activation. Links significantly different between trained and novel problems were used as input features in a linear support vector machine (SVM) classifier with leave-one-out cross validation. Connectivity pattern distance was computed using sum of absolute distance to each condition from the SVM hyperplane that separated connectivity between trained and novel conditions. L: Left; R: Right. AG: angular gyrus; aHipp: anterior hippocampus; CAU: caudate; CBL: cerebellum; HIPP: hippocampus; IFG: inferior frontal gyrus; ITG: inferior temporal gyrus; IPS: intraparietal sulcus; LG: lingual gyrus; MFG: middle frontal gyrus; MOG: middle occipital gyrus; mHipp: medial hippocampus; mPFC: medial prefrontal cortex; PCC: posterior cingulate cortex; PHG: parahippocampal gyrus; PreCG: precentral gyrus; SFG: superior frontal gyrus; SMG: supramarginal gyrus; SMA: supplementary motor area; STG: superior temporal gyrus. Adapted from Chang et al. (2019).

The level of mathematical problem-solving skills studied in Chang et al. (2019) was more complex than simple arithmetic used in most neuroimaging studies with children of similar age. Across 5 days of intensive tutoring sessions, children learned how to solve a set of double-digit plus single-digit addition (“practiced problems”), which are complex arithmetic problems that are not typically solved by memory retrieval strategy without deliberate practice in early elementary school children. In this context, transfer between practiced and novel problems would likely have occurred by applying generalizable knowledge and skills related to arithmetic problem solving. More broadly, transfer of procedural knowledge and skills may be the mechanism by which children acquire proficiency in solving a wide range of different mathematical problems. Future studies will need to address neurodevelopmental changes accompanying transfer that facilitate more complex math problem solving. This topic may be best addressed by integrating neuroscience research with computational models that dissociate multiple processing stages (Anderson, Betts, Ferris, & Fincham, 2012; Qin et al., 2004).

The role of affective, motivational, and sociocultural factors in mathematical learning

In addition to cognitive abilities, multiple lines of evidence suggest that affective, motivational, and sociocultural factors (Aiken, 1976; Duckworth et al., 2019; Halpern et al., 2007) contribute to individual differences in mathematical learning. For instance, math anxiety, which involves feelings of tension or apprehension in a wide variety of math-related academic and life situations (Richardson & Suinn, 1972), is a prominent affective factor generally associated with poor math performance and learning (Aiken, 1976; Chang & Beilock, 2016). The neural correlates of math anxiety have been investigated in various fMRI, event-related brain potential (ERP), and transcranial direct current stimulation (tDCS) studies in adults (Chang, Sprute, Maloney, Beilock, & Berman, 2017; Lyons & Beilock, 2012a, 2012b; Núñez-Peña & Suárez-Pellicioni, 2014; Pletzer, Kronbichler, Nuerk, & Kerschbaum, 2015; Sarkar, Dowker, & Cohen Kadosh, 2014; Suarez-Pellicioni, Nunez-Pena, & Colome, 2014; Suaŕez-Pellicioni, Nú̃nez-P̃ena, & Colomé, 2013; Suárez-Pellicioni, Núñez-Peña, & Colomé, 2013). In children, several studies have begun to provide some insights into the neurodevelopmental basis of math anxiety (Hartwright et al., 2017; Kucian, McCaskey, O’Gorman Tuura, & von Aster, 2018; Supekar, Iuculano, Chen, & Menon, 2015; Young, Wu, & Menon, 2012). Young et al. (2012) observed increased activity in the right amygdala, a brain region associated with processing negative emotion, and decreased activity in fronto-parietal regions that support numerical problem solving in highly math anxious children. Moreover, reduced gray matter volume in the right amygdala and left IPS has been reported in children with higher levels of math anxiety (Hartwright et al., 2017; Kucian et al., 2018). Finally, it is noteworthy that training designed to improve numerical problem solving skills reduces math anxiety and amygdala activity in children (Supekar et al., 2015) (Figure 10A), suggesting that math interventions can be beneficial for both reducing math anxiety and enhancing math learning, converging with behavioral findings from a randomized controlled study in children (Berkowitz et al., 2015). The direction of the relation between math anxiety and math learning (Carey, Hill, Devine, & Szucs, 2015; Geary et al., 2019) remains to be elucidated.

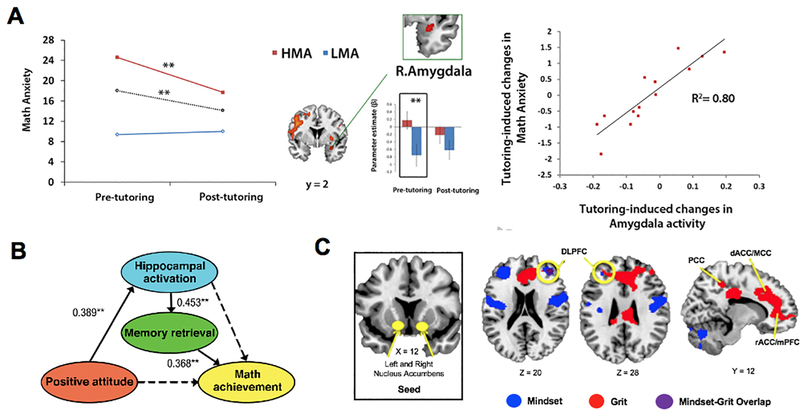
Figure 10. Neural mechanisms of affective and motivational factors in mathematical learning.

A. Math anxiety decreases with training in arithmetic problem solving, with greater reductions for high math anxious (HMA) group, compared to low math anxious (LMA) group. Before training, the HMA relative to LMA group shows greater activation in the right amygdala. After training, there is no group difference in brain responses. Remediation of aberrant amygdala reactivity is correlated with training-induced reductions in math anxiety. B. Structural equation model illustrates that the relation between positive attitudes toward math and math achievement is mediated by hippocampal activation and memory retrieval. Values represent standardized estimates of path coefficients; solid and dashed lines indicate significant and nonsignificant paths, respectively. C. Functional connectivity of the ventral striatum (nucleus accumbens) with the dorsolateral prefrontal cortex (DLPFC) correlates with both growth mindset and grit. **p < .01. L: Left; R: Right. dACC: dorsal anterior cingulate cortex; MCC: midcingulate cortex; mPFC; medial prefrontal cortex; PCC: posterior cingulate cortex; rACC: rostral anterior cingulate cortex. Adapted from Supekar et al. (2015) [A], Chen et al. (2018) [B], and Myers et al. (2016) [C].

Math anxiety has also been related to gender-biased beliefs and expectations (stereotypes) about who is better at math, which can be transmitted from teachers or parents to students. For example, female teachers’ math anxiety has been associated with first- and second-grade female students’ belief that “boys are good at math, and girls are good at reading” (Beilock, Gunderson, Ramirez, & Levine, 2010). Such stereotypes can result in higher math anxiety in female than male students (Baloglu & Koçak, 2006; Betz, 1978; Devine, Fawcett, Szucs, & Dowker, 2012; Else-Quest, Hyde, & Linn, 2010; Hembree, 1990; Ma & Cartwright, 2003; Wigfield & Meece, 1988) and negatively influence math performance in female students, compared to male students with equivalent math backgrounds (Spencer, Steele, & Quinn, 1999). Although societal stereotypes could be one mechanism that relates to negative math attitudes in female students (Cvencek, Brečić, Gaćeša, & Meltzoff, 2021), it remains to be determined whether other factors such as interests in math or spatial skills (Ganley et al., 2013) also play a role in gender differences in math performance.

While negative math attitudes have been associated with poor math performance and learning, positive attitudes toward math (e.g., the degree to which a child likes math or considers themselves good at math) have been associated with higher math achievement (Aiken, 1976; Aiken & Dreger, 1961; Lee, Ning, & Goh, 2014; Marsh & Yeung, 1997; Pinxten, Marsh, De Fraine, Van Den Noortgate, & Van Damme, 2014; Seaton, Parker, Marsh, Craven, & Yeung, 2013; Stankov & Lee, 2014; Zimmerman, Bandura, & Martinez-Pons, 1992). Chen et al. (2018) examined the neurocognitive mechanisms by which positive attitudes toward math enhance math achievement in children. In this fMRI study, positive attitudes toward math were associated with brain activity in the hippocampus during arithmetic problem solving. Notably, hippocampal activity and the use of retrieval strategy mediated the relation between positive attitudes toward math and math achievement (Figure 10B). These findings suggest that positive attitudes facilitate math achievement through greater engagement of the hippocampus involved in learning and memory formation (Gruber, Gelman, & Ranganath, 2014; Kao, Davis, & Gabrieli, 2005).

Other non-cognitive, motivational factors linked to academic learning and achievement include grit and growth mindset (Blackwell, Trzesniewski, & Dweck, 2007; Duckworth, Peterson, Matthews, & Kelly, 2007; Duckworth et al., 2019; Dweck, 2008; Park, Tsukayama, Yu, & Duckworth, 2020; Parker, Marsh, Ciarrochi, Marshall, & Abduljabbar, 2013; Yeager et al., 2019; Yeager et al., 2016). One fMRI study examined neural correlates of grit (perseverance of one’s long-term goals) and growth mindset (belief about malleability of one’s ability) in adolescents (Myers, Wang, Black, Bugescu, & Hoeft, 2016). Myers et al. (2016) found that these measures are associated with greater functional connectivity of the striatum, a region important for reward-based learning (Cardinal, Parkinson, Hall, & Everitt, 2002; Clithero, Reeck, Carter, Smith, & Huettel, 2011; Liljeholm & O’Doherty, 2012; Pauli, O’Reilly, Yarkoni, & Wager, 2016; Shohamy, 2011), with the dorsolateral PFC, a region associated with cognitive control (Menon, 2016a) (Figure 10C). In addition, when controlling for grit, growth mindset was uniquely associated with connectivity of the striatum with the dorsolateral PFC and dorsal anterior cingulate cortex (ACC). Converging evidence from ERP studies in adults also suggests an important role of the ACC in efficient error monitoring in individuals who endorse higher growth mindset (Mangels, 2006; Moser, Schroder, Heeter, Moran, & Lee, 2011). Taken together, these findings suggest cortico-striatal networks are involved in motivational factors associated with mathematical learning.

To date, the majority of investigations on the neurodevelopmental basis of affective and motivational factors that contribute to mathematical learning have been based on cross-sectional studies. To establish causal links between these constructs and brain systems involved, particularly in regard to brain plasticity associated with changes in affect, attitude, or motivation that underlie individual differences in mathematical learning, future studies will need to use longitudinal or training designs that incorporate multiple brain and behavioral measures across time. Finally, investigations of complex interactions between affective, motivational, and sociocultural factors (Cargnelutti, Tomasetto, & Passolunghi, 2017; Halpern et al., 2007; Wang et al., 2015), and their underlying neurocognitive processes that contribute to mathematical skill acquisition remain important areas for future research. More generally, a better understanding of neural mechanisms of the development of these non-cognitive characteristics will complement and refine neurodevelopmental models of mathematical learning, which could serve as an important step for tailoring various interventions.

Conclusions and future directions

Children show a wide range of individual differences in their learning and developmental trajectories of mathematical problem-solving skills (Geary, 1994; Menon, 2015; Siegler, 1996). Understanding neurocognitive processes underlying heterogeneity of mathematical development can provide important insights into optimizing math education (Hyde & Ansari, 2018). Converging evidence from neuroimaging studies suggests that distributed, interactive brain circuits encompassing the PPC, VTOC, MTL, and PFC (Figure 1) support multiple aspects of numerical problem-solving skill acquisition during development, consistent with the theoretical framework that interactions between multiple brain circuits dynamically change with skill acquisition and give rise to specialized cognitive functions (Johnson, 2011; Menon, 2013). Of particular relevance to this perspective is the pivotal role of emergent hippocampal-cortical circuitries in mathematical learning (Supekar et al., 2021).

Further work is needed to determine neurodevelopmental changes associated with learning in other mathematical domains beyond arithmetic problem solving as well as neurocognitive biomarkers important for early identification and remediation of mathematical learning difficulties Advances in combined modeling of cognitive and neural processes, from a systems neuroscience perspective, may distinguish latent neurocognitive processes associated with different aspects of mathematical learning. The efficacy of training programs that enhance or remediate children’s mathematical skills will need to be assessed on multiple dimensions of cognitive, affective, and motivational factors that collectively contribute to mathematical learning (Cargnelutti et al., 2017; Duckworth et al., 2019; Geary, 2011; Geary, Nicholas, Li, & Sun, 2017; Lyons, Price, Vaessen, Blomert, & Ansari, 2014; Vukovic, Kieffer, Bailey, & Harari, 2013; Wang et al., 2015; Wu et al., 2017). Further studies are also needed to determine the extent of transfer and generalization as well as long-term effects of training on brain function and behavioral outcomes.

Recent advances in brain network analysis approaches to investigate large-scale brain network organization associated with numerical processing and learning are promising (Conrad et al., 2020; Supekar et al., 2021). Future studies will need to determine whether observed patterns of network organization remain stable or change across development. Further advances in multivariate predictive models (Woo, Chang, Lindquist, & Wager, 2017) may provide greater insights into how functional and structural brain network organizations predict individual differences in math learning and whether these findings are generalizable beyond study contexts and populations.

Finally, while it has been reported that gender differences in math performance have decreased or even diminished (Hyde, 2005; Hyde, Lindberg, Linn, Ellis, & Williams, 2008; Lindberg, Hyde, Petersen, & Linn, 2010; Stoet & Geary, 2018), implicit stereotypes that associate males with math and science are still prevalent (Kiefer & Sekaquaptewa, 2007; Nosek, Banaji, & Greenwald, 2002; Nosek et al., 2009), persistently contributing to underrepresentation of female students and women in the STEM fields. Future research investigating the neural mechanisms of sociocultural influences on math attitudes, performance, and learning may provide important insights into the development of effective interventions that reduce the gender gap and promote both female and male students’ engagement in math and science.

Successful progress on these fronts will need an integrative approach, bringing in expertise from neuroscience, psychology, and education, as well as advanced analytical tools including computational modeling and machine learning. Such a multidisciplinary approach will not only enrich our understanding of brain mechanisms underlying individual differences in mathematical learning across development, but also inform evidence-based decisions in educational practice and policy (Carew & Magsamen, 2010; De Smedt, Ansari, et al., 2011; Goswami, 2006; Sigman, Pena, Goldin, & Ribeiro, 2014; Thomas, Ansari, & Knowland, 2019), eventually enabling all individuals to reach their highest potential.

Highlights.

• Cognitive development emerges from interactions between functional brain circuits.

• Distributed brain networks support mathematical learning.

• Emerging evidence for hippocampus-dependent math learning in children.

• Math interventions induce functional and structural brain plasticity in children.

• Multiple cognitive and noncognitive factors contribute to mathematical learning.