Modelling the spread of SARS-CoV-2 pandemic - Impact of lockdowns & interventions

Abstract

Background & objectives:

To handle the current COVID-19 pandemic in India, multiple strategies have been applied and implemented to slow down the virus transmission. These included clinical management of active cases, rapid development of treatment strategies, vaccines computational modelling and statistical tools to name a few. This article presents a mathematical model for a time series prediction and analyzes the impact of the lockdown.

Methods:

Several existing mathematical models were not able to account for asymptomatic patients, with limited testing capability at onset and no data on serosurveillance. In this study, a new model was used which was developed on lines of susceptible-asymptomatic-infected-recovered (SAIR) to assess the impact of the lockdown and make predictions on its future course. Four parameters were used, namely β, γ, η and ε. β measures the likelihood of the susceptible person getting infected, and γ denotes recovery rate of patients. The ratio β/γ is denoted by R₀ (basic reproduction number).

Results:

The disease spread was reduced due to initial lockdown. An increase in γ reflects healthcare and hospital services, medications and protocols put in place. In Delhi, the predictions from the model were corroborated with July and September serosurveys, which showed antibodies in 23.5 and 33 per cent population, respectively.

Interpretation & conclusions:

The SAIR model has helped understand the disease better. If the model is correct, we may have reached herd immunity with about 380 million people already infected. However, personal protective measures remain crucial. If there was no lockdown, the number of active infections would have peaked at close to 14.7 million, resulted in more than 2.6 million deaths, and the peak would have arrived by June 2020. The number of deaths with the current trends may be less than 0.2 million.

COVID-19 pandemic has affected India as much as it has the rest of the world and the updated data for India are available in the public domain1,2,3. India, in spite of being the second most populated country in the world with less than ideal healthcare infrastructure, has been fortunate to have had a fairly low case-fatality rate until now4,5. The role of various measures to reduce transmission is now better defined6,7,8,9,10. The exact reasons for the outcome in India are possibly multidimensional, but the various steps implemented by the Policy makers to slow down transmission of the virus have also been important11,12,13. Besides aiding in flattening the curve, these have given the scientific community an opportunity to better understand the vector host environment dynamics14,15. These actions have also provided time for the existing healthcare organizations to plan, activate and reallocate resources to help prepare for the surge. There was an urgent need to be ready to cater to a large number of patients over a short period of time. The time gained through various government policies has also helped nurture individual innovators and industry partnerships to achieve self-sufficiency in resources, such as the personal protective equipment, sanitizers and hospital beds16, at a time when the world grappled with the crises17,18. We have presented a mathematical model for a time series prediction and to analyze the impact of a lockdown in the country.

Material & Methods

A consultative committee was constituted by the Department of Science and Technology under the Ministry of Science and Technology, Government of India, to develop a supermodel consisting of mathematical predictions as related to the COVID-19 pandemic in India19. During the deliberations of the committee, there were extensive discussions and literature review of the evolving pandemic and experience from other countries20,21,22,23,24. Several mathematical models submitted to the committee, for the spread of a pandemic were analyzed in detail and the gaps identified, namely the inability of the standard susceptible-infected-recovered (SIR)/susceptible-exposed-infected-recovered (SEIR) models to account for asymptomatic patients, which were a novel feature of COVID-1921. There is a paucity of data on the behaviour of the virus among Indian population14,15,23. Limited testing capability in India at the time of onset of the pandemic25,26, non-availability of standardized tests for serosurveillance27 and non-availability of data on asymptomatic cases were other limitations. In the current COVID-19 pandemic, a large fraction of population showed little or no symptoms. The standard mathematical models could not explain the role of asymptomatic cases in unfolding of the pandemics.

A new susceptible-asymptomatic-infected-recovered (SAIR) model: Based on an in-depth analysis, a mathematical model was proposed, which built on an earlier model27,28. Before this, another mathematical model provided estimates of the inventories of vital equipment required to cope with the pandemic29. This model developed on lines of susceptible-asymptomatic-infected-recovered (SAIR) was used to assess the magnitude of the impact of the lockdown on the disease burden. In addition, predictions on the future course of the pandemic were also made.

The standard model for pandemic dynamics called SIR classifies the population in three categories: susceptible (S), infected (I) and removed (R). A subcategory of removed is deceased (D). To differentiate between asymptomatic and symptomatic patients, a new category of asymptomatic (A) was introduced with the population in category I of SIR model divided into A (asymptomatic patients) and I (symptomatic patients). Further, it has been assumed that whether a person is categorized in A or I upon infection solely depends on the physiology of the person (immunity level, genetic disposition, comorbidities, etc.). This splits category S into two: S_A (asymptomatic upon getting infected) and S_I (infection and manifesting disease upon getting infected).

Parameter estimation was based on four parameters in this model, namely β, γ, η and ε. In brief, β measures the likelihood that contacts between a susceptible person on the one hand, and an asymptomatic or an infected person on the other hand, leads to the susceptible person getting infected. The parameter γ corresponds to the rate at which asymptomatic or infected patients recover. The parameter η measures the rate at which infected patients die (the presumption is that all asymptomatic patients recover). Finally, the parameter ε measures the ratio between infected symptomatic and asymptomatic patient populations.

Results

The ratio β/γ is known as the basic reproduction ratio and is denoted by R₀. If R₀ <1, then the pandemic does not take off because it means that asymptomatic/infected patients recover faster than they can infect the susceptible population. However, if R₀ >1, then the number of infections increases at first before decreasing to a steady state value. Therefore, to make predictions using the model, it is essential to form reliable estimates of these parameters based on the available data.

For data, the model used three daily time series reported: active infections, cumulative recovered and cumulative deaths1. We took these three as the daily values of I, R_I and D, respectively. This may not be exactly true since many asymptomatic patients are also reported and some deaths are not reported. Four parameters were used in this model, namely β, γ, η, ε and these four parameters change with time. The parameter β is a function of interactions between people and so, lockdowns directly impact it by reducing it. The parameters γ denotes recovery rate and η the deaths which depend on the medical care available. Improvements in medical care increases γ and reduces η. Parameter ε is the ratio of infected with disease and asymptomatic cases.

In principle, the parameter ε should not change as the ratio of infected and asymptomatic remains constant in the model. However, its measurement is not exact for two reasons. First, initially, the infection is limited to a small section of population in the region under study, and it takes time for it to spread to the entire region. Since we do not know the exact size of initial infected population, we get a significant underestimate of ε initially as we use total population of the region to compute it. The measured value slowly increases to eventually stabilize once the entire region is covered - this makes ε also dependent on lockdown. Second, measured values of active infections and cumulative removed (recovered plus deceased) also include parts of A and R_A, respectively. Hence, actual values of I and R_I are smaller than calculated by parameter estimation. This causes the value of ε to be overestimated. Adjustments can be made to get a better estimate of ε by estimating how the infection is spreading in the region and recording the fraction of asymptomatic cases in reported positive ones.

The details of these equations and calculations as developed by the authors and part of the mandate for the Committee are as follows:

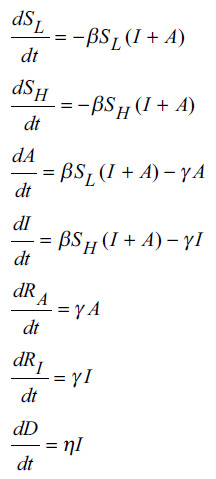
Susceptible (S) is the uninfected fraction of population. It is divided in two: S_H and S_L fractions that transition to I and A, respectively, on infection. Asymptomatic (A) is the fraction of population who is infected but goes undetected. Infected (I) is the fraction of population who is infected and detected. Removed (R) is the fraction of population who had infection but no longer infected (either through recovery or by demise). It is also divided in two: I and A transition to R_I and R_A, respectively. The denominator dt is over a continuous timeframe.

Pandemic progression in India: The estimated parameters for the five phases are depicted in Table I. The mathematical model and predictions are further depicted in Figure 1, which depicts that the actual data suggest a peak on September 17, 2020. The model overestimates the actual growth by around 1.5 per cent and the peak arrives four days later. Cumulative deaths are predicted to be around 0.2 million. The β and γ values for the last phase imply R₀ value around 1.39, and the herd immunity for this value of R₀ at around 28 per cent of population in A, I and R categories. This translates to around 3.9 million population infected or with antibodies at the peak. On September 17, the numbers in I and R_I categories were around 5.2 million. Using the 1/ε value (=67) of phase 6, the model predicts total population with infection or antibodies to be around 3.5 million.

Table I.

Predicted parameters for phases of the pandemic in India

Pandemic phase	1/ε	1/β	γ	η
1	475,400	4.6	0.020	0.005
2	20,850	7.4	0.030	0.003
3	1108	9.9	0.048	0.002
4	773	6.8	0.065	0.002
5	151	8.2	0.076	0.002
6	67	8.2	0.087	0.001

Fig. 1.

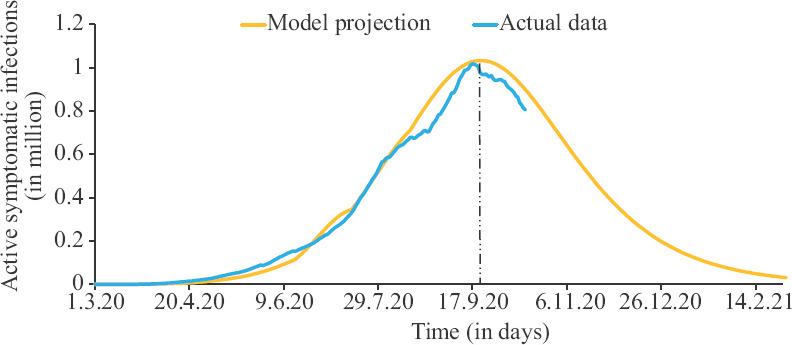
Progression of the pandemic in India. Source: Ref. 1 for actual data.

Analysis of disease progression in Delhi: The estimated parameters for the phases 1-6 for Delhi are depicted in Table II. For Delhi, first phase starts from April 1, as data were available in the open domain only from March and a window of 14 days is required for calculations by the model. The Delhi plot of projections are of special interest since the data from two serosurveys can be used to validate the calculations made by this model. The mathematical model and predictions are further depicted in Figure 2, which depicts that the projected trajectory follows the actual line closely, except that the second wave starts about a week early, first peak is about 20 per cent higher, and second is about 10 per cent higher. Cumulative deaths are to be around 6500. July serosurvey showed antibodies in 23.5 per cent of population30, and R_I at the start of survey was around 55000. The model predicts R (=1/ɛ×R_I) to be around 5.4 million (1/ɛ=104 for phase 3 assuming the population of Delhi to be around 20 million. This is close to 27.5 per cent of population which is 4 per cent higher than actual data. September serosurvey showed antibodies in 33 per cent of population31 and R_I at the start of the survey was around 0.16 million. The model predicts R (=1/ɛ×R_I) to be around 6.5 million (1/ɛ= 41 for phase 5). This amounts to 33.7 per cent which is 0.76 per cent higher than actual data. As evident by the calculations in this model, there was a good association between the predicted numbers and the actual data obtained in the serosurvey.

Table II.

Predicted parameters for phases of the pandemic in Delhi

Pandemic phase	1/ε	1/β	γ	η
1	1356	7.1	0.032	0.001
2	243	7.5	0.034	0.003
3	104	5.6	0.102	0.003
4	80	5.7	0.116	0.002
5	41	4	0.110	0.001
6	36	4.2	0.133	0.001

Fig. 2.

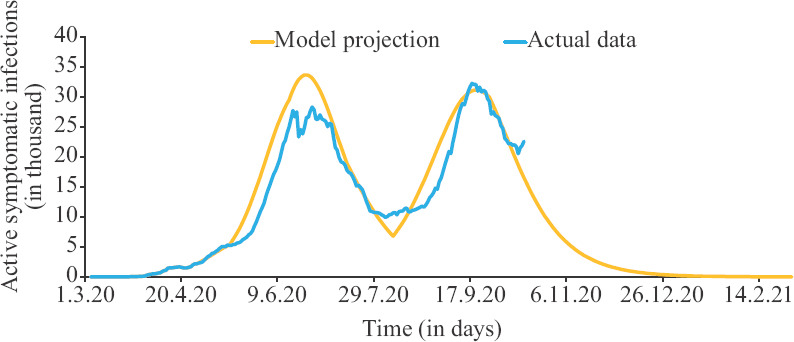
Progression of the infection in Delhi. Source: Ref. 1 for actual data.

The effect of lockdown and the spread in active infections and hypothetical effects of timing of lockdown are depicted in Figure 3. It revealed that if there was no lockdown, the number of active infections would have peaked at 14+ million and the peak would have arrived by mid-May. This would have resulted in overwhelming our hospitals. The impact of delay in lockdown is starkly reflected in projected mortality and the same is depicted in Figure 4. If there was no lockdown, it would have resulted in more than two million deaths. The number of deaths with current trends is projected to be less than 0.2 million.

Fig. 3.

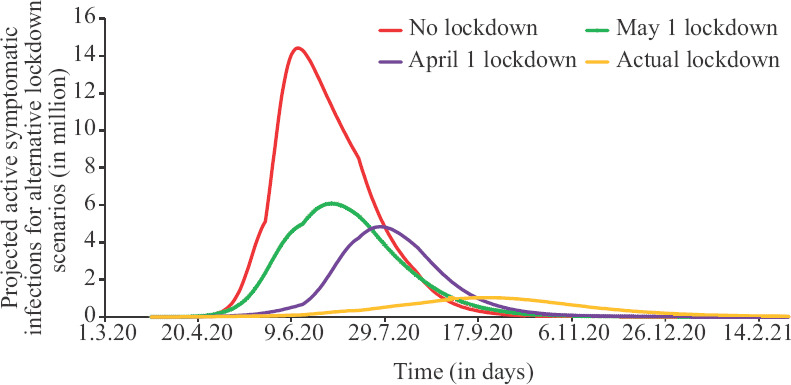
Effects of timing of lockdown on the number of active cases.

Fig. 4.

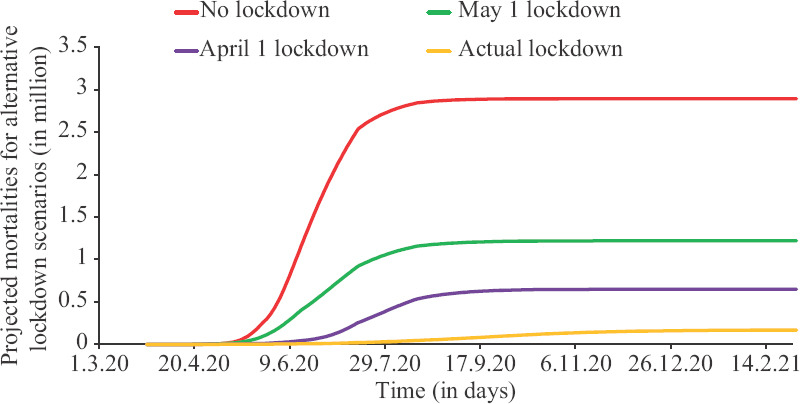
Impact of timing of lockdown on mortality.

Discussion

The presence of asymptomatic patients, who can infect the susceptible population when they come in contact with, changes the dynamics of disease21. Among the total population who test positive, only the symptomatic and sick patients (which is a small fraction), require major medical intervention. Thus, the estimates for medical inventory, including oxygen, ventilators and intensive care unit beds, needs to be planned based on projections of this number and not the total infected persons. At the same time, asymptomatic patients need to be advised isolation so that they do not spread the infection. In the present model, time period of the disease progression in the country was divided in six phases. These were obtained by identifying the dates on which the value of ε increased significantly: phase 1: period up to April 5; phase 2: period from April 5 to 30; phase 3: period from May 1 to June 15; phase 4: period from June 16 to July 15; phase 5: period from July 16 to August 15; and phase 6: period from August 15 to date.

These phases correspond to different levels of lockdown introduced in the country with some delay. For each of these phases, parameters were estimated for India as a whole and specifically for the city of Delhi (due to lack of early data, for Delhi, the phases began from April 1 and there were slight changes in phase boundaries).

The progression of the pandemic in India revealed that there was a significant reduction in β due to initial lockdown. It was more or less stabilized despite relaxations in lockdown. This possibly reflects the protective measures being ensured by the susceptible population all over the country such as use of mask and social distancing. An increase in γ was observed following initial lockdown. This reflects healthcare and hospital services, medications and protocols put in place. η remained stationary in the first three phases and then started reducing. This possibly reflects improved medical interventions and increasing number of asymptomatic patients being diagnosed and counted towards total cases.

The progression of the disease in Delhi revealed that the value of 1/ɛ dropped and more so from phase 1 to 3. This suggested that the virus did not initially spread over the entire population uniformly. The value of β increased significantly from phase 2 to 3 and again from phase 4 to 5. This reflected relaxation of lockdown leading to increased human interactions and increasing cases. γ increased significantly from phase 2 to 3 reflecting the major improvements in medical care in June. Decreasing η reflected improvements in medical care provided, thus reducing mortality.

The pandemic progression actual data showed a peak on September 1730. Our model predicted a slightly higher peak (by ~1.5%) four days later. Cumulative deaths are predicted to be slightly less than 0.2 million. The β and γ values for phase 6 imply R₀ value around 1.39 and the herd immunity for this value of R₀ is at around 28 per cent of population in A, I and R categories. This translates to around 3.85 million population with infection or with antibodies at peak. On September 17, the numbers in I and R_I categories were around 5.2 million. Using the 1/ε value (=67) of phase 6, the model predicts total population with either infection or antibodies to be around 350 million. If the model is correct and there is no significant increase in R₀ value, we perhaps have reached herd immunity. However, to ensure that R₀ stays small, it is important to continue the use of personal protective measures such as mask, hand hygiene and physical distancing.

The mathematical model used in this study was developed to analyze the spread of the disease under three different hypothetical scenarios, namely no lockdown, lockdown starting April 1, 2020 and lockdown starting May 1, 2020. To simulate the trajectories, the assumptions made are that no lockdown on March 26 allows migrants and others to travel back home. Due to this, a small number of infected people reach many parts of the country. We incorporated this by reducing the value of 1/ε, the parameter that captures reach of the disease to different regions, to phase 3 value (1108) on April 5 instead of phase 2 value (20,850). There appeared a sharp reduction; however, even with strict lockdown, this reduction happened within a month. Hence, it is reasonable to assume that with no lockdown and significant travel all over, the reduction would have happened much faster.

For no lockdown, the value of 1/ε continues to reduce sharply, the value of 1/β remains as in phase 1 and γ and η improve slowly. Lockdown from April 1 changes the value of 1/β to phase 2 value. However, the value of γ improves slowly. This is because, with rapid spread of infection, hospitals start getting overwhelmed (as would be evident from plots below) and so are unable to ramp up and put in place a proper setup. Lockdown from May 1 reduces values of 1/ε further and values of 1/β; γ and η improve but slowly.

If there was no lockdown, the number of active infections would have peaked at 14+ million and the peak would have arrived by mid-May. This would have resulted in overwhelming our hospitals and widespread panic. There was little qualitative difference between two lockdown timings of April 1 and May 1, 2020. These would have resulted in a peak between 0 and 5 million active infections by mid-June. If there was no lockdown, it would have resulted in more than 2 million deaths. The two lockdowns (April 1 and May 1, 2020) would have resulted in between 0.5-1 million deaths. The number of deaths with current trends is projected to be less than 0.2 million.

The major limitation of our model was the non-availability of accurate data. While our modelling efforts have tried to match the available data, the utility of our projections is limited by the accuracy and reliability of the available data. Hence, more accurate and reliable input data to the model would result in more reliable projections.

In conclusions the new model is useful to calculate the possible disease burden in a realistic manner and may help plan for the resources. The impact of lockdown and interventions undertaken in a timely manner has been highlighted. The continuing importance of interventions such as use of mask, hand hygiene and physical distance is reinforced.