Abstract
The structure-function coupling in brain networks has emerged as an important research topic in modern neuroscience. The structural network could provide the backbone of the functional network. The integration of the functional network with structural information can help us better understand functional communication in the brain. This paper proposed a method to accurately estimate the brain functional network enriched by the structural network from diffusion magnetic resonance imaging. First, we adopted a simplex regression model with graph-constrained Elastic Net to construct the functional networks enriched by the structural network. Then, we compared the constructed network characteristics of this approach with several state-of-the-art competing functional network models. Furthermore, we evaluated whether the structural enriched functional network model improves the performance for predicting the cognitive-behavioral outcomes. The experiments have been performed on 218 participants from the Human Connectome Project database. The results demonstrated that our network model improves network consistency and its predictive performance compared with several state-of-the-art competing functional network models.
Keywords: Functional network, structure-function coupling, simplex regression, graph-constrained elastic net
Graphical Abstract
1. Introduction
Brain network analysis is a powerful technique for investigating a hard-wired brain architecture and its functions (Rubinov and Sporns, 2010). Typically, the functional network, reflecting brain activation patterns, is defined as the temporal coherence of resting-state functional magnetic resonance imaging (rs-fMRI) between different brain regions (Rubinov and Sporns, 2010). Structural network is defined as structural wiring in the white matter, approximated by tractography algorithm using diffusion-weighted magnetic resonance imaging (dMRI) between the brain regions (Hagmann et al., 2008). Other studies have explored covariance patterns of morphometry, such as volume and cortical thickness, between different brain regions (He et al., 2007; Mechelli et al., 2005) as a surrogate of the structural network.
The rapid growth of the public database on neuroimaging allowed the researcher investigating the relationship between an individual’s brain network properties and behavior differences. For example, many researchers demonstrated that functional network property was related to cognition and behavior. Finn et al. proposed a unique connectome fingerprinting used to predict an individual’s human intelligence (Finn et al., 2015; Miranda-Dominguez et al., 2014). Baum et al. demonstrated that the structural-functional network coupling was associated with higher-order cognitive processes during youth (Baum et al., 2020). Some studies demonstrated that functional network patterns could predict cognitive abilities, behavior outcomes, and personality traits, as well as could distinguish healthy and diseased brains (Beaty et al., 2018; Damaraju et al., 2014; Hsu et al., 2018; Nostro et al., 2018; Park et al., 2016; Rosenberg et al., 2016; Stam et al., 2007).
Recently, identifying structure-function coupling in brain network has been an important research topic in modern neuroscience. The structural network could provide the backbone of the functional network. The integration of the functional network with structural information can help us better understand functional communication in the brain. For example, the researchers demonstrated that the structural network provides cortico-cortical and cortico-subcortical connectivity information that reflects spatial proximity and long-range structural wiring and governs ongoing repertoire of cognitive function (Batista-Garc\’\ia-Ramó and Fernández-Verdecia, 2018; Baum et al., 2020; Mišić and Sporns, 2016; Park and Friston, 2013; Rubinov and Sporns, 2010; Snyder and Bauer, 2019). However, most of the functional network studies did not consider structural information; the functional network based on the statistical association, such as Pearson’s correlation, partial correlation, and sparse inverse covariance (Friedman et al., 2008). Hence, the integration of multi-modal brain networks (i.e., coupling structural network with the functional network) may lead to the construction of more sensitive brain network than using a single modality.
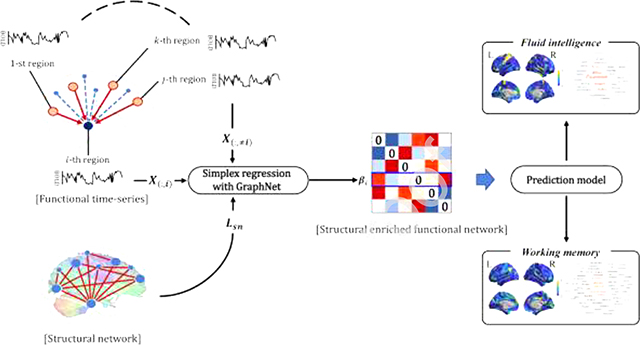
In this sense, we proposed a method to estimate the brain functional network enriched by structural network accurately. A simplex regression model with graph-constrained Elastic Net (GraphNet) was adopted to estimate the functional networks enriched by the structural network (Grosenick et al., 2013; Kim et al., 2020). Our main scientific contributions were described as follows. First, we incorporated GraphNet and simplex constraints to estimate the interpretable functional network enriched by the structural network. Second, we proposed an efficient optimization algorithm using the projected gradient descent method. Third, we applied and compared several state-of-the-art network models with our method to provide insights into the clinical benefits of our model.
The rest of the study is organized as follows: In Section 2, we briefly described the data, the related pre-processing procedure, and how we estimated the SFN. In Section 3, we described the experimental setups and results. We evaluated our network approach and compared it with the competing network models. In Section 4, a summary of this study and discussion for potential implications were included.
2. Material and Methods
2.1. Data collection and pre-processing
2.1.1. Datasets
In this study, we collected neuroimaging data (i.e., rs-fMRI and dMRI) for 218 participants from the Human Connectome Project (HCP) database (Van Essen et al., 2013). The participants who are genetically unrelated, non-twins, non-Hispanic with full demographic information were considered. The average age was 29.11 years (standard deviation = 3.74 years, range 22–36 years). Further details were shown in Table 1.
Table 1. Demographic information.
Values are reported as mean ± standard deviation (SD) format.
| Demographic information | |
|---|---|
| Age | 29.11 ± 3.74 |
| Sex | M: 118, F:100 |
| Fluid intelligence | 17.66 ± 4.58 |
| Working memory 2-back accuracy [%] | 84.44 ± 9.90 |
2.1.2. fMRI pre-processing
The HCP database provided the pre-processed rs-fMRI data following “minimal preprocessing pipeline” (Glasser et al., 2013). The rs-fMRI data were provided as the Connectivity Informatics Technology Initiative (CIFTI) dense time-series format which was defined in standard grayordinate space. The pre-processing procedures included skull removal, intensity normalization, distortion correction, and head motion correction, and registration to the Montreal Neurological Institute’s standard space. The artifacts (e.g., head movement, cardiac pulsation, arterial, and large vein related noise) were removed using FMRIB’s ICA-based X-noisifier (FIX) (Salimi-Khorshidi et al., 2014). Finally, we computed the functional network using the averaged vertex-wise time courses (filename “dt-series”) for brain regions. We concatenated the time series of each left-to-right/right-to-left phase-encoded data into form a single time series data.
The Human Connectome Project multi-modal parcellation atlas (HCP-MMP) was used to determine the nodes of the network (Glasser et al., 2016). The HCP-MMP atlas is one of the most detailed cortical in-vivo parcellations, which divided the cortical area into 360 regions considering cortical architecture, function, connectivity, and topography in a precisely aligned group average of 210 healthy young adults. To compute edges of the functional network, we adopted different similarity measurements, as described in Section 2.2 and 3.1., between each pair of the brain regions.
2.1.3. dMRI pre-processing
For dMRI data, HCP released the estimated fiber orientation data processed with FSL’s multishell spherical deconvolution toolbox (bedpostx) (Jbabdi et al., 2012). In detail, the following steps were performed; intensity normalization, distortion correction, eddy current correction, head motion correction, and gradient nonlinearity correction (Andersson et al., 2012). Then, fiber orientation for each voxel was estimated from dMRI. We then added tractography steps to construct the structural network (SN). In detail, the probabilistic tractography algorithm, implemented in FSL (probtrackX), was performed to estimate fiber streamlines for every voxel (Behrens et al., 2003). Output streamlines of the probtrackX were mapped onto the 360 brain regions of HCP-MMP to build the structural connectivity matrix. Finally, the constructed matrix was used as the SN that was used as the constraint in our proposed approach described later.
2.2. Estimation of structural enriched functional network
Herein, we used the boldface lowercase letter to denote a vector, and the boldface uppercase letter to denote a matrix. Specifically, given the datasets , where X corresponded to the rs-fMRI data as described in Section 2.1.2., n denoted the number of time-points of the rs-fMRI, and p denoted the number of brain regions.
2.2.1. Functional network based on simplex regression framework
In this section, we calculated the functional network based on the simplex regression framework (FNsimplex). The simplex regression framework has advantages for interpretation and low model complexity due to simplex constraint (Huang et al., 2013, 2015). The model is defined as follows.
| (1) |
where, X(:,≠i) is the matrix X with the i-th column (i.e., region) removed, X(:,i) is the i-th column vector from matrix X, and is the estimated coefficient vector for the i-th brain region. We constructed the functional network by solving the Eq. (1) p times for every brain region. The is a p-dimensional vector, where zero value is inserted for the i-th coefficient of estimated coefficients vector . The symmetric functional network based on the simplex regression framework (FNsimplex) was computed by the elementwise average between S and its transpose.
2.2.2. Structural enriched functional network based on simplex regression with GraphNet penalization
In this section, we expanded the FNsimplex by adding the GraphNet constraint for integrating the functional network with the structural network. This approach has the advantage of integrating prior information of structural network into the functional network (Du et al., 2016; Grosenick et al., 2013; Kim et al., 2020). The model is defined as follows:
| (2) |
where, Lsn is the Laplacian matrix of the SN, and λG is the regularization parameter. The Laplacian matrix is defined as Lsn = D − A, where D is the degree of structural network matrix A. Eq. (2) was optimized using the accelerated projected gradient method (Huang et al., 2015).
The enriched functional network was constructed by repeating the Eq. (2) p times for every brain region. The denoted a p-dimensional vector and zero was inserted for the i-th element of estimated coefficients vector . Finally, we obtained the symmetric SFN based on the simplex regression with GraphNet (SFNsimplex) by the elementwise average between S and its transpose. Detailed description for constructing the SFNsimplex is described in the next section and open-source implementation of the model including documentation and examples is publicly available on GitHub (https://github.com/lshen/sfn).
The regularization parameter λG of SFNsimplex was tuned using the nested 5-fold cross-validation strategy. Blind grid search of the parameters is very time-consuming and thus we tuned the parameter from the following finite set: [10−3, 10−2, 10−1, 100, 101, 102, 103]. The optimized ‘s varied across different nodes and different subjects; see Figure S1 in Supplementary Material for their distributions.
2.2.3. Efficient optimization algorithm for constructing SFNsimplex
In this section, we describe how to efficiently optimize Eq. (2) using the accelerated projected gradient descent method and construct the SFNsimplex. Let be the estimate of βi at the previous iteration k − 1, the update rules for estimating βi at the current iteration k is defined as follows:
| (3) |
| (4) |
| (5) |
where t is the step size, is the derivative of the Eq. (2) with respect to βi, and C(k) is the acceleration coefficient as follows:
| (6) |
| (7) |
Algorithm 1.
Efficient algorithm for constructing SFNsimplex
| Input: Normalized data , and parameter λG. | |
| Output : | |
| 1: | Initialize c(0), |
| 2: | for each region i (i = 1, ..., p) do |
| 3: | Set k = 0 |
| 4: | While no convergence do |
| 5: | k = k + 1 |
| 6: | , |
| 7: | , |
| 8: | |
| 9: | |
| 10: | end |
| 11: | |
| 12: | end for |
| 13: | |
| 14: | |
The unconstrained formulation of the Eq. (3) can be written as
| (8) |
where γ and λ are a Lagrangian multiplier and Lagrangian multiplier vector, respectively and both of them are to be determined. Since the problem of Eq. (3) is a convex optimization problem with differentiable objective and constraint functions and is strictly feasible (Slater’s condition holds), the Karush–Kuhn–Tucker conditions provide necessary and sufficient conditions for optimality (Boyd et al., 2004). The detailed optimization procedure for Eq. (8) is described in Supplementary Section 1.
The pseudocode of algorithm was described in Algorithm 1.
2.3. Model evaluation using prediction task
2.3.1. Behavioral outcome prediction
The constructed networks were used to predict two different behavioral outcomes (i.e., fluid intelligence [gF] and working memory 2-back recall accuracy [WM-2bk-acc]) to assess the association between higher-order cognitive ability and network measures. We chose seven different functional network models (as described in Section 3.1) and compared their predictive performances. In the prediction model, we used the degree centrality of the constructed networks as predictors and each behavior outcome as the response variable. The elastic-net regression model was adopted to build the prediction model for predicting the behavioral outcome. The model was trained on 90% of data and tested on the remaining 10% of data, which was repeated 1,000 times to evaluate the stability of the model in a bootstrapping framework. The performance of the prediction model was measured using correlation coefficient and root-mean-square-error (RMSE) between the actual and predicted behavior scores.
2.3.2. Neurosynth meta-analysis
To interpret prediction results from a biological perspective, we adopted the Neurosynth meta-analysis platform (Gorgolewski et al., 2015; Yarkoni et al., 2011) (http://neurosynth.org, http://neurovault.org). Neurosynth is a platform to characterize the neural systems associated with the topics (e.g., cognitive, movement, or decision) by identifying the relationship and mapping between the brain activation map and the topic loading. We uploaded 14 sets of the averaged standardized regression coefficients (7 for gF prediction, and 7 for WM-2bk-acc prediction) to the Neurosynth and Neurovalt websites to decode our results. The cognition-related topics (78 topics) were selected by the intersection of the list of cognitive topics (250 topics) in Table S1 of (Poldrack et al., 2012) and the list of all topics (1,308 topics) provided by the Neurosynth website. The decoded topics were visualized in the word-cloud function in Matlab. The Neurosynth decoding results of our 14 sets of the averaged standardized regression coefficients are available on Neurovault at https://neurovault.org/collections/8470/.
3. Experiments and Results
3.1. Experimental setups
The proposed network models based on the simplex framework (i.e., FNsimplex and SFNsimplex) were compared with other competing network models using the same dataset: Pearson’s correlation functional network (FNPearson), partial correlation functional network (FNPartial), graphical LASSO functional network (FNgl), structural network (SN), and adaptive graphical LASSO network (SFNagl). In detail, the FNPearson and FNPartial were calculated using MATLAB (i.e., command corr and parcorr, respectively), and the FNgl and SFNagl were computed using a library implemented Python (Hsieh et al., 2014).
We used graph theory for comparing networks and the comparison is heavily influenced by the number of nodes and the average degree of the network. Direct comparisons of graph measures between the networks with different numbers of nodes or average degree can yield spurious results (Drakesmith et al., 2015). To make fair comparison among various networks, we controlled all the networks to be at the same sparsity level (i.e., the ratio between the number of connected nodes and the number of all possible connections) according to the existing literature (Margulies et al., 2016; Toussaint et al., 2014; van Wijk et al., 2010; Wang et al., 2009). Specifically, we retained the top 10% connections in actual values of a given network for each subject.
3.2. Whole-brain network characteristics
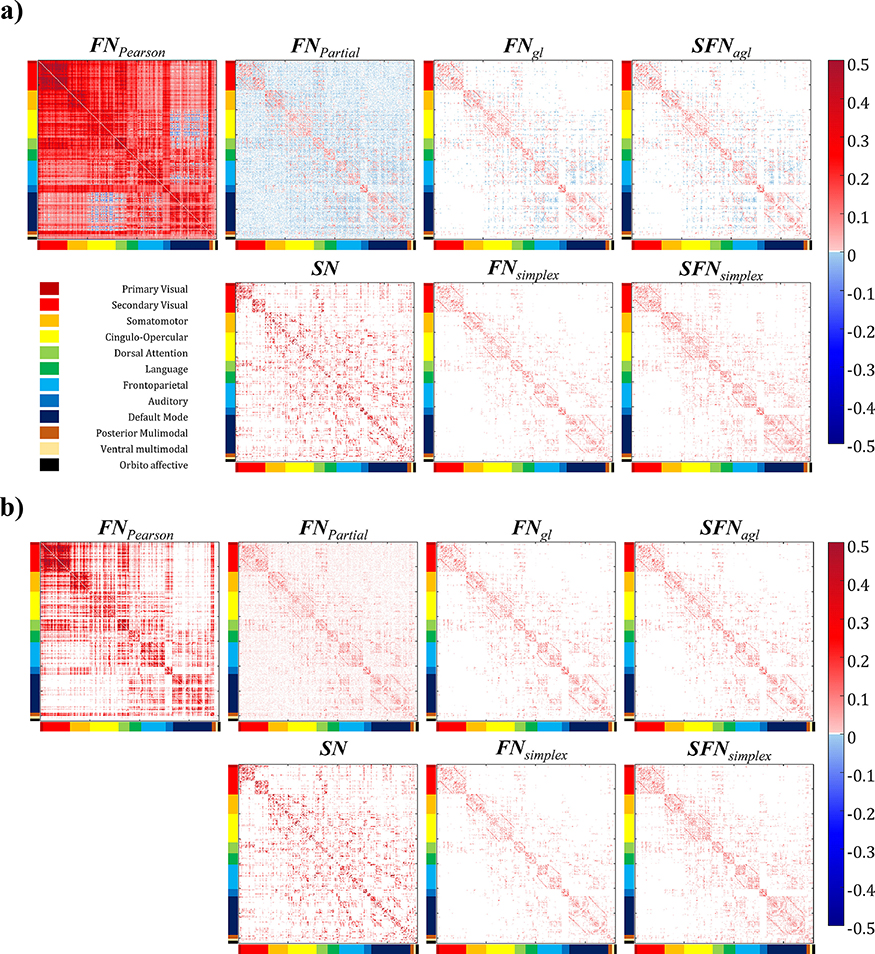
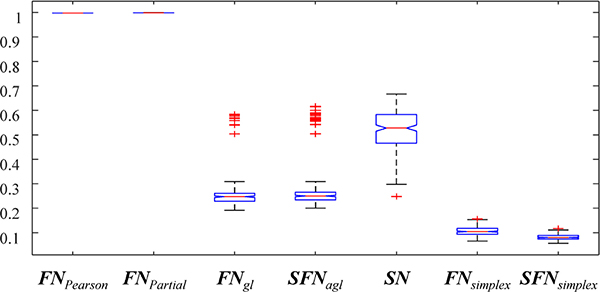
The average connectivity matrices constructed with eight different network models (i.e., FNPearson, FNPartial, FNgl, SFNagl, SN, FNsimplex, and SFNsimplex) were shown in Figure 1. Before any thresholding, the average network density (the ratio of non-zero elements in the connectivity matrix) across subjects is shown in Figure 2. We found that FNPearson and FNPartial were almost fully connected, (mean density of 99.72%, SD of 0.007%, and mean density of 99.86%, SD of < 0.001% respectively), SN showed 52.04% of mean density, and FNgl, SFNagl, FNsimplex, and SFNsimplex showed 8.10% ~ 27.41% of mean density, as shown in Figure 2. The results were as expected because sparse models led to lowered mean density of connectivity.
Figure 1. Visualizing the average network pattern across subjects.
Sub-figures (a) and (b) visualized the average network pattern before thresholding and after thresholding, respectively. The brain regions were ordered according to the Cole-Anticevic Brain-side Network (Ji et al., 2019).
Figure 2. Boxplots of density values for seven different brain network approaches.
Boxplots of density values for seven different brain network approaches.
3.3. Structural-functional correlation
To explore the network-level structural-functional relationship, we performed correlation analyses between proposed networks (i.e., FNsimplex, and SFNsimplex) and SN/FNPearson. Overall, the SFNsimplex showed a higher correlation coefficient with SN (0.401 for SFNsimplex and 0.390 for FNsimplex) and a lower correlation with FNPearson (0.394 for SFNsimplex and 0.400 for FNsimplex) compared with the FNsimplex. Specifically, we found that both FNsimplex and SFNsimplex showed a high correlation with FNPearson in the primary visual, dorsal attention, language, frontoparietal, and posterior multimodal networks. Both FNsimplex and SFNsimplex showed a high correlation with SN in the secondary visual, auditory, ventral multimodal, and orbito affective networks. The detailed network-level correlation results were shown in Table 2.
Table 2. Network-level structural-functional correlation for the simplex based networks.
The correlation coefficients were reported in terms of twelve subnetworks. The sub-network acronyms were reported as follows: V1=Primary visual network, V2=Secondary visual network, SM=Somatomotor network, CO= Cingulo-opercular network, DA=Dorsal attention network, L=Language network, FP=Frontoparietal network, A=Auditory network, DMN=Default mode network, PM=Posterior multimodal network, VM=Ventral multimodal network, and OA=Orbito affective network
| Overall | V1 | V2 | SM | CO | DA | L | FP | A | DMN | PM | VM | OA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SN vs. FNsimplex | 0.390 | 0.018 | 0.456 | 0.394 | 0.416 | 0.331 | 0.459 | 0.284 | 0.681 | 0.437 | 0.434 | 0.482 | 0.649 |
| SN vs. SFNsimplex | 0.401 | 0.041 | 0.474 | 0.417 | 0.437 | 0.332 | 0.465 | 0.283 | 0.704 | 0.451 | 0.443 | 0.541 | 0.676 |
| FNPearson vs. FNsimplex | 0.400 | 0.537 | 0.34 | 0.39 | 0.438 | 0.475 | 0.596 | 0.508 | 0.529 | 0.462 | 0.544 | 0.215 | 0.289 |
| FNPearson vs. SFNsimplex | 0.394 | 0.546 | 0.337 | 0.387 | 0.435 | 0.474 | 0.598 | 0.504 | 0.528 | 0.458 | 0.548 | 0.171 | 0.288 |
3.4. Consistency of networks across subjects
We compared the consistency of the networks across subjects by calculating the proportion of the common edges across subjects (POC) and the coefficient of variation (COV). Given a specific edge (i, j), its POC(i, j) is the proportion of the subjects with nonzero edge weights, and is defined as follows: POC(i, j) = |x: x ≠ 0, x ∈ xε(i, j)|/N, where FN(i, j) denotes a set of all functional network edges between i-th and j-th regions across all samples, and N denotes the number of samples. The COV is the ratio of the standard deviation to the mean edge weight across subjects, and is defined as follows:, where FN(n)(i, j) denotes network edge value between i-th and j-th regions for n-th sample. The COV and POC were computed before and after thresholding the networks to measure inter-subject variability.
We found that the FNPearson showed the lowest inter-subject variability (2.322 mean COV). The proposed networks (i.e., FNsimplex, and SFNsimplex) showed low inter-subject variability (5.423 and 6.111 mean COV, respectively). However, the FNPartial, FNgl, and SFNagl showed high inter-subject variability (mean COV > 10). The full details were shown in Table 3.
Table 3. The comparison of mean coefficients of variation (COV) for seven different approaches for building the networks.
The mean COV across the edges were reported. The low COV denoted that the constructed network showed lower inter-subject variability.
| FNPearson | FNPartial | FNgl | SFNagl | SN | FNsimplex | SFNsimplex | |
|---|---|---|---|---|---|---|---|
| COV | 2.322 | 151.660 | 53.349 | 54.880 | 3.167 | 5.423 | 6.110 |
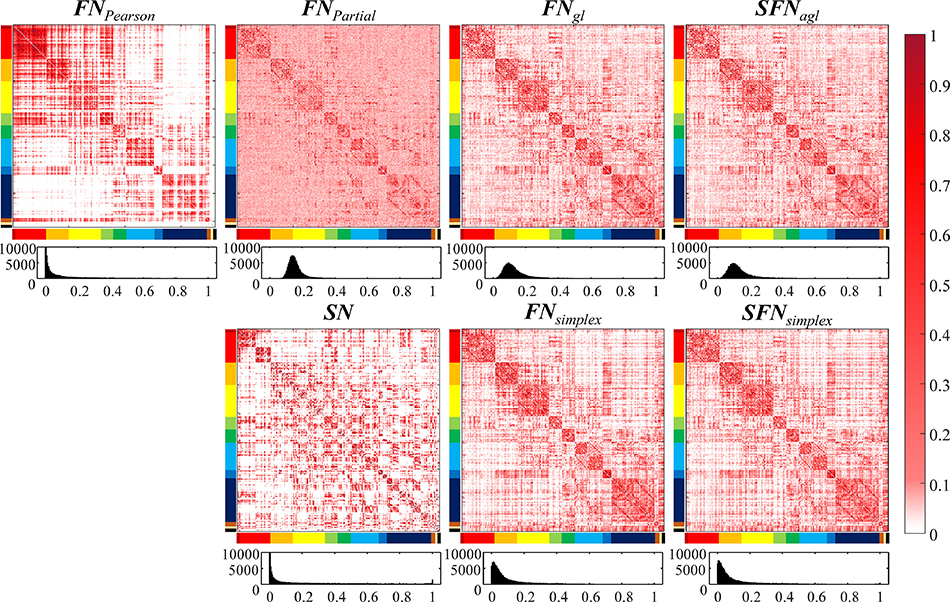
Figure 3 showed the heatmap and the histograms of the POC for after thresholding the network. Specifically, we observed high POC within sub-network module and low POC between sub-network modules for all approaches, as shown the heatmap in Figure 3. Furthermore, we found that the distributions of POC in the FNPearson, SN, FNsimplex, and SFNsimplex approximately followed the power law. However, those of the FNPartial, FNgl, and SFNagl followed approximately normal distributions.
Figure 3. The comparison of proportion of common connection (POC) for seven different approaches for building the networks.
The POC was computed after thresholding the networks. Each subfigure has two rows, where the first row visualized the heatmap of the POC, and the second row visualized the histogram of the POC. The histogram distribution following the power law denoted lower inter-subject variability.
3.5. Model evaluation for prediction tasks
We compared the performance of prediction models based on an elastic-net regression framework using the degree centrality from the constructed networks including features from single-modality networks, either dMRI or rs-fMRI, (i.e., FNPearson, FNPartial, FNgl, FNsimplex, and SN), features from the network fusing dMRI and rs-fMRI (i.e., SFNagl, and SFNsimplex), and features from two different the single modality networks in a concatenated fashion (i.e., FNPearson + SN, FNPartial + SN, and FNgl + SN).
3.5.1. Predicting working memory 2-back recall accuracy
We compared the models to predict a working memory 2-back recall accuracy (WM-2bk-acc) in a format of mean ± SD over 1,000 bootstrap samples. The prediction model using features from SFNsimplex yielded the highest correlation coefficient of 0.304 ± 0.098 and a relatively low RMSE of 10.47 ± 1.39 between the actual and predicted WM-2bk-acc scores. The model of SFNagl yielded the second-highest correlation coefficient of 0.299 ± 0.114 with a low RMSE 10.60 ± 1.53, and model of SN was the third place (i.e., the correlation coefficient of 0.281 ± 0.099, and RMSE of 10.60 ± 1.40). The full details were shown in Table 4.
Table 4. Comparison of the prediction models to predict a WM-2bk-acc score.
The prediction performance was reported in terms of RMSE and correlation coefficient (r) between actual and predicted scores. The values were reported as format of mean ± standard deviation. The performance measurements were computed from 1,000 bootstrap samples.
| Functional Network | FNPearson | FNPartial | FNgl | FNsimplex | ||
| r | 0.059 ± 0.155 | 0.142 ± 0.116 | 0.257 ± 0.113 | 0.263 ± 0.090 | ||
| RMSE | 11.85 ± 4.59 | 10.40 ± 1.12 | 10.40 ± 1.33 | 10.95 ± 1.58 | ||
| Functional + Structural | SN + FNPearson | SN + FNPartial | SN + FNgl | SFNagl | SFNsimplex | |
| r | 0.255 ± 0.131 | 0.195 ± 0.151 | 0.241 ± 0.168 | 0.299 ± 0.114 | 0.304 ± 0.098 | |
| RMSE | 4.98 ± 1.88 | 9.52 ± 1.89 | 9..45 ± 1.85 | 10.60 ± 1.53 | 10.47 ± 1.39 | |
| Structural Network | SN | |||||
| r | 0.281 ± 0.099 | |||||
| RMSE | 10.60 ± 1.40 | |||||
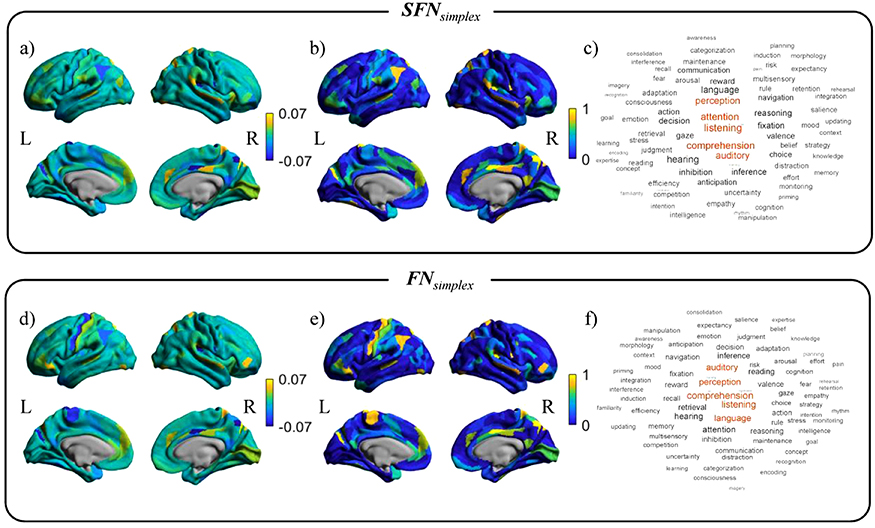
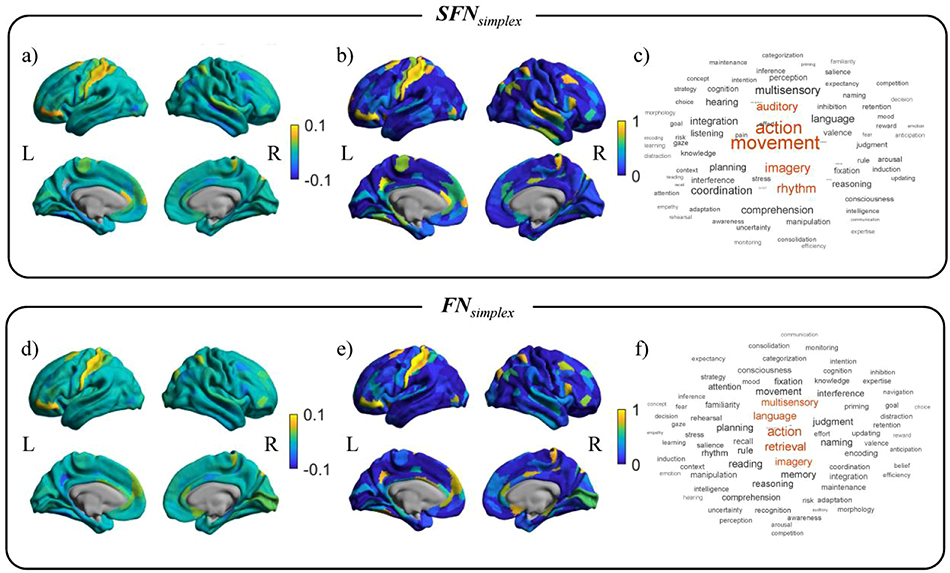
The averaged standardized regression coefficients of the prediction model over 1,000 bootstrap samples for SFNsimplex and FNsimplex were shown in Figures 4-(a) and (d). The yellow or blue regions showed positive or negative contributions to predict the WM-2bk-acc, respectively. The selection probability values over 1,000 bootstrap samples for SFNsimplex and FNsimplex were shown in Figure 4-(b) and (e). The yellow regions were consistently selected regions over 1,000 bootstraps. We mapped the regression coefficients map with 78 cognitive-related topics extracted from Poldrack et al. (Poldrack et al., 2012), as shown in Figure 4-(c) and (f). The detailed results for other networks were shown in Supplementary Figure S2.
Figure 4. The activation pattern maps and the related cognitive topics for predicting WM-2bk-acc score.
Top row: the mean standardized regression coefficients from the prediction model and their decoding results using SFNsimplex. Bottom row: the mean standardized regression coefficients from the prediction model and their decoding results using FNsimplex. For each sub-figure, left column: mean standardized regression coefficients map. Center column: selection probability map. Right column: word clouds plot related to cognitive function in the Neurosynth database.
For the SFNsimplex, we observed that the parietal lobe, prefrontal cortex, precuneus gyrus, and cingulum cortex contributed to predicting WM-2bk-acc scores. We found that listening, comprehension, attention, auditory, and perception were highly associated with the regression coefficients map, as shown in Figure 4-(c). For the FNsimplex, we observed that the somatosensory cortex, parietal lobe, prefrontal cortex, para-central lobe, and cingulum cortex contributed to predicting WM-2bk-acc scores. We found that comprehension, listening, perception, language, auditory, and attention, were highly associated with the regression coefficients map, as shown in Figure 4-(f). We found that twelve topics commonly contributed to the prediction for WM-2bk-acc between SFNsimplex and FNsimplex. The full details were shown in Table S1 and Figure S3 in Supplementary Material.
3.5.2. Predicting fluid intelligence
For gF score prediction, the prediction model using features from the SN yielded the highest correlation coefficient of 0.331 ± 0.109 and the lowest root-mean-square-error (RMSE) of 4.48 ± 0.38 between the actual and predicted gF scores. The models of SFNsimplex yielded the second-highest correlation coefficient of 0.287 ± 0.090 with the RMSE of 4.54 ± 0.37, and model of the FNsimplex took the third place (the correlation coefficient of 0.271 ± 0.054, and RMSE of 4.53 ± 0.35). The full details were shown in Table 5.
Table 5. Comparison of the prediction models to predict a gF score.
The prediction performance was reported in terms of RMSE and correlation coefficients between actual and predicted scores. The values were reported as format of mean ± standard deviation. The performance measurements were computed from 1,000 bootstrap samples.
| Functional Network | FNPearson | FNPartial | FNgl | FNsimplex | ||
| r | 0.062 ± 0.109 | 0.103 ± 0.110 | 0.080 ± 0.104 | 0.271 ± 0.054 | ||
| RMSE | 5.28 ± 2.06 | 4.79 ± 0.44 | 4.77 ± 0.40 | 4.53 ± 0.35 | ||
| Functional + Structural | SN + FNPearson | SN + FNPartial | SN + FNgl | SFNagl | SFNsimplex | |
| r | 0.255±0.131 | 0.110 ± 0.080 | 0.112 ± 0.089 | 0.105 ± 0.107 | 0.287 ± 0.090 | |
| RMSE | 4.98±1.88 | 4.61 ± 0.51 | 4.61 ± 0.40 | 4.73 ± 0.39 | 4.54 ± 0.37 | |
The averaged standardized regression coefficients of the prediction model over 1,000 bootstrap samples for SFNsimplex and FNsimplex were shown in Figures 5-(a) and (d). The yellow or blue regions showed positive or negative contributions to predict the gF score, respectively. The selection probability values over 1,000 bootstrap samples for SFNsimplex and FNsimplex were shown in Figures 5-(b) and (e). The yellow regions were consistently selected regions over 1,000 bootstraps. We mapped the regression coefficients map with 78 cognitive-related topics extracted from Poldrack et al. (Poldrack et al., 2012), as shown in Figure 5-(c) and (f). The detailed results for competing networks were shown in Supplementary Figure S4.
Figure 5. The activation pattern maps and the related cognitive topics for predicting the gF score.
Top row: the mean standardized regression coefficients from the prediction model and their decoding results using SFNsimplex. Bottom row: the mean standardized regression coefficients from the prediction model and their decoding results using FNsimplex. For each sub-figure, left column: mean standardized regression coefficients map. Center column: selection probability map. Right column: word clouds plot related to cognitive function in the Neurosynth database.
For the SFNsimplex, we observed that the sensorimotor cortex, medial prefrontal cortex, ventrolateral prefrontal cortex, and precuneus gyrus were highly contributing to predicting gF score. We found movement, action, imagery, rhythm, and auditory were highly associated with the regression coefficients map, as shown in Figure 5-(c). For the FNsimplex, we observed that the somatosensory cortex, prefrontal cortex, mid temporal gyrus, and cingulum cortex contributed to predicting gF scores. We observed action, retrieval, imagery, language, and multisensory were highly associated with the regression coefficient map, as shown in Figure 5-(f). We found that seven topics commonly contributed to the prediction for gF between SFNsimplex and FNsimplex. The full details were shown in Supplementary Table S1 and Figure S3.
4. Discussion
In this study, we used seven different techniques, including Pearson’s correlation, partial correlation, graphical LASSO, adaptive graphical LASSO, structural connectivity, simplex regression, and simplex regression with GraphNet, to model brain connectivity. We compared the network characteristics in terms of the network density, consistency, and network measurements and performances of the prediction task for cognitive-behavioral outcomes: working memory 2-back accuracy and fluid intelligence. We choose node-based degree centrality (DC) measures to predict the clinical outcomes due to its relative simplicity, neurobiological interpretability, and wide usage compared with four other regional measures, including betweenness centrality, eigenvector centrality, clustering coefficients, and local efficiency, as shown in Supplementary Section 2 and Table S2.
Many studies demonstrated that functional communication in the brain was highly associated with the structural connection (Baum et al., 2020; Greicius et al., 2009; Rykhlevskaia et al., 2008; Van Den Heuvel et al., 2009). We confirmed that the constructed networks showed similar functional-structural correlation patterns as shown in Section 3.3 and Table 2. We found that SN outperformed all four kinds of FNs, including FNPearson, FNPartial, FNgl, and FNsimplex, in terms of correlation in Tables 4 and 5. A previous study reported that the correlation between FA values and working memory score was higher than that of blood-oxygen-level-dependent response (Olesen et al., 2003). Several studies showed that working memory score was associated with the white matter integrity in the parietal lobe and lateral prefrontal cortex, which supports our findings (Baddeley, 2003; Klingberg, 2006; Takeuchi et al., 2010). Previous studies demonstrated that complex brain structure information, including brain network organization of white matter, total brain volume, and cortical thickness, was linked with human intelligence (Chiang et al., 2009; Choi et al., 2008; Park et al., 2014; Thompson et al., 2001). These studies collectively supported and suggested that SN could have a stronger association with the working memory score than FNs.
We demonstrated that the multimodal integration network models (i.e., SFNsimplex and SFNagl) offer advantages over single modal network models (i.e., FNPearson, FNPartial, FNgl, FNsimplex, and SN). Specifically, we observed that only the proposed model (i.e., SFNsimplex) outperformed SN in the WM-2bk-acc prediction task and it was also ranked the second place in gF prediction task. Furthermore, the prediction performance using SFNsimplex was better than those of the FNsimplex: up to 15.58 % for predicting WM score, 5.90% for predicting the gF score. Here, we identified several brain regions predictive of cognitive functions for working memory and fluid intelligence. These regions included frontoparietal and limbic regions, as well as somatosensory areas. The frontoparietal and limbic cortices are located at the higher end of the cortical hierarchy, which controls human cognition (Margulies et al., 2016; Mesulam, 1998). Our findings are supported by earlier studies that associated connectomics in higher-order brain regions and an individual’s cognitive performance (Dryburgh et al., 2019; Greene et al., 2018; Jiang et al., 2020). Somatosensory regions are located at the other end of the cortical hierarchy from frontoparietal and limbic networks, which regulates an individual’s primary sensory processing such as motor, vision, and audition (Margulies et al., 2016; Mesulam, 1998). The development of sensory regions is highly associated with the development of executive controls. Indeed, the sensory-first theory supports that the abnormal maturation of sensory circuits during early age yield higher-order functions in adults, such as communication and social cognition (Hong et al., 2019; Robertson and Baron-Cohen, 2017). These studies collectively support our findings that the identified brain regions are associated with executive functions and further provide the rationale for constructing structural-enriched functional networks.
This study has several limitations. First, we performed the multimodal network integration by regularizing the regression model with the GraphNet penalty focusing on the squared loss between signals from one region and estimated signals from the other regions. This was equivalent to optimization at the column level of the raw data. Still, the same network can be generated by solving the simplex regression at the node level equivalent to the optimization of each element in the raw data (i.e., element level), which is left for future research. Another issue is that we employed the same parcellation to integrate functional and structural networks, where the performance could be suboptimal. The different imaging modalities (e.g., rs-fMRI and dMRI) require different parcellations (e.g., automated anatomical label and Power templates) optimized for the given modality. Applying different templates to the model may vary the performance for integrating functional and structural networks, which is an interesting future research topic. Another issue is sample size. We evaluated clinical benefits of networks by measuring predictive performance. We collected neuroimaging data from the HCP database with limited samples. The relatively small sample size might lead to an overfitting problem. Specifically, the predictive performances of three kinds of Structural+Functional methods (i.e., SN + FNPearson, SN + FNPartial, and SN + FNgl) were lower than that of SN. This could be partly attributed to the fact that the number of features (i.e., 720 features) was larger than the sample size (i.e., 218 samples), leading to an overfitting risk. Hence, our algorithm’s results should be further confirmed with independent replications and possibly with additional biological evidence.
5. Conclusion
In this study, we applied a simplex regression model with GraphNet to estimate SFN better. Specifically, the SFNsimplex approach improved the predictive performance for cognitive-behavioral outcomes compared to seven different network models. Furthermore, the SFNsimplex showed robust performance in network consistency across subjects. We hope to apply our algorithm to disease cohorts to see if our algorithm generalizes to other cases.
Supplementary Material
Highlights.
A new method incorporating GraphNet and simplex constraints is proposed to estimate interpretable and structural enriched functional brain networks.
An efficient optimization algorithm using the projected gradient descent method is proposed for the construction of structural enriched functional brain networks.
Extensive experiments demonstrate the promise of the proposed structural enriched functional brain networks on predicting interesting behavioral outcomes.
Acknowledgments
This work was supported in part by the National Institutes of Health [R01 EB022574, R01 LM013463, U01 AG068057] and National Science Foundation [IIS 1837964]. This work was also supported in part by the National Research Foundation of Korea (NRF-2020R1A6A3A03038525). Data were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research; and by the McDonnell Center for Systems Neuroscience at Washington University.
Footnotes
Conflict of Interest: All Authors declare that we have no conflicts of interest.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional Information
Financial Disclosure of all authors: None
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Andersson JLR, Xu J, Yacoub E, Auerbach E, Moeller S, Ugurbil K, 2012. A comprehensive Gaussian process framework for correcting distortions and movements in diffusion images, in: Proceedings of the 20th Annual Meeting of ISMRM. p. 2426. [Google Scholar]
- Baddeley A, 2003. Working memory: looking back and looking forward. Nat. Rev. Neurosci 4, 829–839. [DOI] [PubMed] [Google Scholar]
- Batista-Garc\’\ia-Ramó K, Fernández-Verdecia CI, 2018. What we know about the brain structure--function relationship. Behav. Sci. (Basel) 8, 39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baum GL, Cui Z, Roalf DR, Ciric R, Betzel RF, Larsen B, Cieslak M, Cook PA, Xia CH, Moore TM, others, 2020. Development of structure--function coupling in human brain networks during youth. Proc. Natl. Acad. Sci 117, 771–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beaty RE, Kenett YN, Christensen AP, Rosenberg MD, Benedek M, Chen Q, Fink A, Qiu J, Kwapil TR, Kane MJ, others, 2018. Robust prediction of individual creative ability from brain functional connectivity. Proc. Natl. Acad. Sci 115, 1087–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens TEJ, Woolrich MW, Jenkinson M, Johansen-Berg H, Nunes RG, Clare S, Matthews PM, Brady JM, Smith SM, 2003. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn. Reson. Med. An Off. J. Int. Soc. Magn. Reson. Med 50, 1077–1088. [DOI] [PubMed] [Google Scholar]
- Boyd S, Boyd SP, Vandenberghe L, 2004. Convex optimization. Cambridge university press. [Google Scholar]
- Chiang M-C, Barysheva M, Shattuck DW, Lee AD, Madsen SK, Avedissian C, Klunder AD, Toga AW, McMahon KL, De Zubicaray GI, others, 2009. Genetics of brain fiber architecture and intellectual performance. J. Neurosci 29, 2212–2224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi YY, Shamosh NA, Cho SH, DeYoung CG, Lee MJ, Lee J-M, Kim SI, Cho Z-H, Kim K, Gray JR, others, 2008. Multiple bases of human intelligence revealed by cortical thickness and neural activation. J. Neurosci 28, 10323–10329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damaraju E, Allen EA, Belger A, Ford JM, McEwen S, Mathalon DH, Mueller BA, Pearlson GD, Potkin SG, Preda A, others, 2014. Dynamic functional connectivity analysis reveals transient states of dysconnectivity in schizophrenia. NeuroImage Clin. 5, 298–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drakesmith M, Caeyenberghs K, Dutt A, Lewis G, David AS, Jones DK, 2015. Overcoming the effects of false positives and threshold bias in graph theoretical analyses of neuroimaging data. Neuroimage 118, 313–333. 10.1016/j.neuroimage.2015.05.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dryburgh E, McKenna S, Rekik I, 2019. Predicting full-scale and verbal intelligence scores from functional Connectomic data in individuals with autism Spectrum disorder. Brain Imaging Behav. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du L, Huang H, Yan J, Kim S, Risacher SL, Inlow M, Moore JH, Saykin AJ, Shen L, 2016. Structured sparse canonical correlation analysis for brain imaging genetics: An improved GraphNet method. Bioinformatics 32, 1544–1551. 10.1093/bioinformatics/btw033 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn ES, Shen X, Scheinost D, Rosenberg MD, Huang J, Chun MM, Papademetris X, Constable RT, 2015. Functional connectome fingerprinting: identifying individuals using patterns of brain connectivity. Nat. Neurosci. 18, 1664–1671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedman J, Hastie T, Tibshirani R, 2008. Sparse inverse covariance estimation with the graphical lasso. Biostatistics 9, 432–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Coalson TS, Robinson EC, Hacker CD, Harwell J, Yacoub E, Ugurbil K, Andersson J, Beckmann CF, Jenkinson M, Smith SM, Van Essen DC, 2016. A multi-modal parcellation of human cerebral cortex. Nature 536, 171–178. 10.1038/nature18933 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser MF, Sotiropoulos SN, Wilson JA, Coalson TS, Fischl B, Andersson JL, Xu J, Jbabdi S, Webster M, Polimeni JR, others, 2013. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorgolewski KJ, Varoquaux G, Rivera G, Schwarz Y, Ghosh SS, Maumet C, Sochat VV, Nichols TE, Poldrack RA, Poline J-B, others, 2015. NeuroVault. org: a web-based repository for collecting and sharing unthresholded statistical maps of the human brain. Front. Neuroinform. 9, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greene AS, Gao S, Scheinost D, Constable RT, 2018. Task-induced brain state manipulation improves prediction of individual traits. Nat. Commun 9, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greicius MD, Supekar K, Menon V, Dougherty RF, 2009. Resting-state functional connectivity reflects structural connectivity in the default mode network. Cereb. cortex 19, 72–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosenick L, Klingenberg B, Katovich K, Knutson B, Taylor JE, 2013. Interpretable whole-brain prediction analysis with GraphNet. Neuroimage 72, 304–321. 10.1016/j.neuroimage.2012.12.062 [DOI] [PubMed] [Google Scholar]
- Hagmann P, Cammoun L, Gigandet X, Meuli R, Honey CJ, Wedeen VJ, Sporns O, 2008. Mapping the structural core of human cerebral cortex. PLoS Biol. 6, e159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y, Chen ZJ, Evans AC, 2007. Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb. cortex 17, 2407–2419. [DOI] [PubMed] [Google Scholar]
- Hong S-J, De Wael RV, Bethlehem RAI, Lariviere S, Paquola C, Valk SL, Milham MP, Di Martino A, Margulies DS, Smallwood J, others, 2019. Atypical functional connectome hierarchy in autism. Nat. Commun 10, 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsieh C-J, Sustik MA, Dhillon IS, Ravikumar P, 2014. QUIC: quadratic approximation for sparse inverse covariance estimation. J. Mach. Learn. Res 15, 2911–2947. [Google Scholar]
- Hsu W-T, Rosenberg MD, Scheinost D, Constable RT, Chun MM, 2018. Resting-state functional connectivity predicts neuroticism and extraversion in novel individuals. Soc. Cogn. Affect. Neurosci 13, 224–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H, Yan J, Nie F, Huang J, Cai W, Saykin AJ, Shen L, 2013. A new sparse simplex model for brain anatomical and genetic network analysis, in: International Conference on Medical Image Computing and Computer-Assisted Intervention. pp. 625–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang J, Nie F, Huang H, 2015. A new simplex sparse learning model to measure data similarity for clustering, in: Twenty-Fourth International Joint Conference on Artificial Intelligence. [Google Scholar]
- Jbabdi S, Sotiropoulos SN, Savio AM, Graña M, Behrens TEJ, 2012. Model-based analysis of multishell diffusion MR data for tractography: how to get over fitting problems. Magn. Reson. Med 68, 1846–1855. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ji JL, Spronk M, Kulkarni K, Repovš G, Anticevic A, Cole MW, 2019. Mapping the human brain’s cortical-subcortical functional network organization. Neuroimage 185, 35–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang R, Zuo N, Ford JM, Qi S, Zhi D, Zhuo C, Xu Y, Fu Z, Bustillo J, Turner JA, others, 2020. Task-induced brain connectivity promotes the detection of individual differences in brain-behavior relationships. Neuroimage 207, 116370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim M, Won JH, Youn J, Park H, 2020. Joint-Connectivity-Based Sparse Canonical Correlation Analysis of Imaging Genetics for Detecting Biomarkers of Parkinson’s Disease. IEEE Trans. Med. Imaging 39, 23–34. 10.1109/TMI.2019.2918839 [DOI] [PubMed] [Google Scholar]
- Klingberg T, 2006. Development of a superior frontal--intraparietal network for visuo-spatial working memory. Neuropsychologia 44, 2171–2177. [DOI] [PubMed] [Google Scholar]
- Margulies DS, Ghosh SS, Goulas A, Falkiewicz M, Huntenburg JM, Langs G, Bezgin G, Eickhoff SB, Castellanos FX, Petrides M, others, 2016. Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc. Natl. Acad. Sci 113, 12574–12579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mechelli A, Friston KJ, Frackowiak RS, Price CJ, 2005. Structural covariance in the human cortex. J. Neurosci 25, 8303–8310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mesulam M-M, 1998. From sensation to cognition. Brain a J. Neurol 121, 1013–1052. [DOI] [PubMed] [Google Scholar]
- Miranda-Dominguez O, Mills BD, Carpenter SD, Grant KA, Kroenke CD, Nigg JT, Fair DA, 2014. Connectotyping: model based fingerprinting of the functional connectome. PLoS One 9, e111048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mišić B, Sporns O, 2016. From regions to connections and networks: new bridges between brain and behavior. Curr. Opin. Neurobiol 40, 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nostro AD, Müller VI, Varikuti DP, Pläschke RN, Hoffstaedter F, Langner R, Patil KR, Eickhoff SB, 2018. Predicting personality from network-based resting-state functional connectivity. Brain Struct. Funct 223, 2699–2719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olesen PJ, Nagy Z, Westerberg H, Klingberg T, 2003. Combined analysis of DTI and fMRI data reveals a joint maturation of white and grey matter in a fronto-parietal network. Cogn. Brain Res 18, 48–57. [DOI] [PubMed] [Google Scholar]
- Park B, Seo J, Park H, 2016. Functional brain networks associated with eating behaviors in obesity. Sci. Rep 6, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park H-J, Friston K, 2013. Structural and functional brain networks: from connections to cognition. Science (80-.) 342. [DOI] [PubMed] [Google Scholar]
- Park H, Yang J, Seo J, Choi Y, Lee K, Lee J, 2014. Improved explanation of human intelligence using cortical features with second order moments and regression. Comput. Biol. Med 47, 139–146. [DOI] [PubMed] [Google Scholar]
- Poldrack RA, Mumford JA, Schonberg T, Kalar D, Barman B, Yarkoni T, 2012. Discovering relations between mind, brain, and mental disorders using topic mapping. PLoS Comput Biol 8, e1002707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robertson CE, Baron-Cohen S, 2017. Sensory perception in autism. Nat. Rev. Neurosci 18, 671. [DOI] [PubMed] [Google Scholar]
- Rosenberg MD, Finn ES, Scheinost D, Papademetris X, Shen X, Constable RT, Chun MM, 2016. A neuromarker of sustained attention from whole-brain functional connectivity. Nat. Neurosci 19, 165–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M, Sporns O, 2010. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069. [DOI] [PubMed] [Google Scholar]
- Rykhlevskaia E, Gratton G, Fabiani M, 2008. Combining structural and functional neuroimaging data for studying brain connectivity: a review. Psychophysiology 45, 173–187. [DOI] [PubMed] [Google Scholar]
- Salimi-Khorshidi G, Douaud G, Beckmann CF, Glasser MF, Griffanti L, Smith SM, 2014. Automatic denoising of functional MRI data: combining independent component analysis and hierarchical fusion of classifiers. Neuroimage 90, 449–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder AZ, Bauer AQ, 2019. Mapping structure-function relationships in the brain. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 4, 510–521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P, 2007. Small-world networks and functional connectivity in Alzheimer’s disease. Cereb. cortex 17, 92–99. [DOI] [PubMed] [Google Scholar]
- Takeuchi H, Sekiguchi A, Taki Y, Yokoyama S, Yomogida Y, Komuro N, Yamanouchi T, Suzuki S, Kawashima R, 2010. Training of working memory impacts structural connectivity. J. Neurosci 30, 3297–3303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson PM, Cannon TD, Narr KL, Van Erp T, Poutanen V-P, Huttunen M, Lönnqvist J, Standertskjöld-Nordenstam C-G, Kaprio J, Khaledy M, others, 2001. Genetic influences on brain structure. Nat. Neurosci 4, 1253–1258. [DOI] [PubMed] [Google Scholar]
- Toussaint P-J, Maiz S, Coynel D, Doyon J, Messé A, de Souza LC, Sarazin M, Perlbarg V, Habert M-O, Benali H, 2014. Characteristics of the default mode functional connectivity in normal ageing and Alzheimer’s disease using resting state fMRI with a combined approach of entropy-based and graph theoretical measurements. Neuroimage 101, 778–786. [DOI] [PubMed] [Google Scholar]
- Van Den Heuvel MP, Mandl RCW, Kahn RS, Hulshoff Pol HE, 2009. Functionally linked resting-state networks reflect the underlying structural connectivity architecture of the human brain. Hum. Brain Mapp 30, 3127–3141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Smith SM, Barch DM, Behrens TEJ, Yacoub E, Ugurbil K, Consortium W-MHCP, 2013. The WU-Minn human connectome project: an overview. Neuroimage 80, 62–79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Wijk BCM, Stam CJ, Daffertshofer A, 2010. Comparing Brain Networks of Different Size and Connectivity Density Using Graph Theory. PLoS One 5, 1–13. 10.1371/journal.pone.0013701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J, Wang L, Zang Y, Yang H, Tang H, Gong Q, Chen Z, Zhu C, He Y, 2009. Parcellation-dependent small-world brain functional networks: A resting-state fMRI study. Hum. Brain Mapp 30, 1511–1523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC, Wager TD, 2011. Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods 8, 665–670. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.