A self-decoupled 32-channel receive array for human-brain MRI at 10.5 T

Abstract

Purpose:

Receive array layout, noise mitigation, and B₀ field strength are crucial contributors to SNR and parallel-imaging performance. Here, we investigate SNR and parallel-imaging gains at 10.5 T compared with 7 T using 32-channel receive arrays at both fields.

Methods:

A self-decoupled 32-channel receive array for human brain imaging at 10.5 T (10.5T-32Rx), consisting of 31 loops and one cloverleaf element, was co-designed and built in tandem with a 16-channel dual-row loop transmitter. Novel receive array design and self-decoupling techniques were implemented. Parallel imaging performance, in terms of SNR and noise amplification (g-factor), of the 10.5T-32Rx was compared with the performance of an industry- standard 32- channel receiver at 7 T (7T-32Rx) through experimental phantom measurements.

Results:

Compared with the 7T-32Rx, the 10.5T-32Rx provided 1.46 times the central SNR and 2.08 times the peripheral SNR. Minimum inverse g-factor value of the 10.5T-32Rx (min[1/g] = 0.56) was 51% higher than that of the 7T-32Rx (min[1/g] = 0.37) with R = 4 × 4 2D acceleration, resulting in significantly enhanced parallel-imaging performance at 10.5 T compared with 7 T. The g-factor values of 10.5 T-32 Rx were on par with those of a 64-channel receiver at 7 T (eg, 1.8 vs 1.9, respectively, with R = 4 × 4 axial acceleration).

Conclusion:

Experimental measurements demonstrated effective self-decoupling of the receive array as well as substantial gains in SNR and parallel-imaging performance at 10.5 T compared with 7 T.

1 |. INTRODUCTION

Ultrahigh-field (UHF) MRI advantages, including higher image resolution, reduced acquisition time, and better SNR, have opened new opportunities for advancement of various clinical and basic research projects (eg, Refs. 1–4). Applications of primary interest that rely on exploiting these UHF advantages include functional MRI studies (eg, Refs. 2,4–7), brain connectivity mapping using diffusion-weighted MRI (eg, Refs. 8–11), and anatomical imaging (eg, Refs. 12–15).

The push for UHF MRI is predicated primarily on the premise of significant ultimate intrinsic SNR^16–19 gains and less SNR penalty with parallel-imaging acceleration^13,20–23 at higher B₀ field strengths. Acceleration through parallel imaging comes with a penalty in SNR quantified in terms of noise amplification or g-factor.²⁴ Increasing the B₀ field strength has been shown to mitigate the SNR penalty attributed to acceleration,^22,25,26 hence affording better parallel-imaging performance. However, parallel-imaging performance depends significantly on receiver array noise correlation^27,28 as well, which needs to be addressed with careful decoupling strategies.

Various RF array decoupling strategies have been proposed and implemented in the past. Overlap and preamplifier decoupling proposed by Roemer et al²⁹ have been improved and used extensively in designs of high-density receive arrays.^30–35 Noise matching the preamplifiers^35,36 and inductive decoupling³¹ were also heavily relied upon in previous works. Furthermore, self-decoupling techniques for low-density (up to eight channels) transmit arrays using intentionally unbalanced capacitive distribution were introduced.^37,38 Lakshmanan et al³⁸ proposed the “loopole antenna,” in which segmenting capacitors inside transceiver loops were distributed unevenly to cause an unbalanced current distribution in the loop with electromagnetic (EM) field patterns resembling that of a dipole antenna. Yan et al³⁷ proposed a transceiver self-decoupling scheme for 7 T/298 MHz, in which a relatively small RF impedance (eg, 8.5-pF capacitance) is placed opposite a relatively large RF impedance (eg, 0.4 pF), which approaches an open circuit at the RF frequency. This results in the current distribution being unbalanced so that the coil resembles a dipole antenna. In this work, we build on Yan et al’s work to present a strategy for receiver-coil self-decoupling at 447 MHz, based on our observation that higher frequencies allow for a more balanced capacitive segmentation of receive elements while maintaining acceptable decoupling. We compare the performance of self-decoupled receivers, in terms of SNR, with overlap-decoupled loops. Receiver-coil self-decoupling provides interelement isolation comparable to overlap decoupling, while not requiring geometric overlap or interelement transformers or decoupling networks, and therefore is much more practical to implement in high-density receive arrays. Furthermore, we show that receiver-coil self-decoupling presented here provides higher SNR compared with overlap decoupling.

The primary contributions of this work are (1) building a high-density, self-decoupled 32-channel receive array for 10.5 T/447 MHz for the first time, and (2) demonstrating SNR and parallel-imaging gains at 10.5 T compared with 7 T, with preliminary results reported in an ISMRM abstract.³⁹ The self-decoupled 32-channel receive array (10.5T-32Rx) provided substantial experimental peripheral (corresponding to cortical regions in a human head) and central SNR gains compared with an industry-standard 32-channel receive array at 7 T. Furthermore, parallel-imaging performance at 10.5 T was superior to that of 7 T, with 10.5T-32Rx providing acceleration performance comparable to a 64-channel array coil at 7 T. Our results also confirm the clear advantages of higher B₀ field in terms of SNR and parallel-imaging performance.

2 |. METHODS

2.1 |. Sixteen-channel transmitter

The primary focus of this paper is on the contribution of receiver-coil self-decoupling and B₀ field strength to SNR and parallel-imaging performance. Therefore, the transmitter design is covered here only briefly, with its detailed characterization published separately.⁴⁰ A 16-channel transmitter consisting of two rows of eight inductively decoupled rectangular loops was used.^32,40 The two-row design of the transmitter array^32,41,42 has the potential of increasing degrees of freedom in parallel-transmit RF pulse design, especially for specific absorption rate control.^43–45 In order to minimize transmit–receive interaction, the transmitter was actively tuned (ie, a PIN diode circuitry was used to tune the transmitter during signal transmission, leaving it off-resonance during reception). The 10.5T MR scanner is currently operated under a Food and Drug Administration investigational device exemption, which requires that all RF coils planned for human use are approved by the Food and Drug Administration. The procedure to obtain necessary approvals for in vivo human brain imaging using this transmitter, together with a receive coil inserted in it, is currently ongoing.

The receiver design and construction involved several steps: (1) two-loop simulations with the primary purpose of verifying and characterizing the self-decoupling concept at 10.5 T, (2) prototyping an eight-channel subset of the 32-channel receiver with the primary purpose of assessing noise correlation, and (3) building and characterizing the final 32-channel receiver. These steps are discussed in the following sections.

2.2 |. Receiver coil self-decoupling

Rectangular loops similar in size to those used in the array were modeled in several scenarios. First, two 5 × 5 cm² loops and then two 2.5 × 5 cm² loops were positioned (in simulations) on a flat surface in proximity to a cubic phantom (permittivity ε_r = 50, conductivity σ = 0.6 S/m, to approximate human brain-tissue properties⁴⁶ across all simulations). These loops were constructed using 18 AWG (American Wire Gauge) copper wire (diameter = 1.02 mm) and were divided into four segments using three capacitors and the feed point. Two fixed capacitors and a trimmer capacitor (X_tr), with values in the same range as fixed capacitors, were used inside each loop. The feed circuitry, presented in Figure 1A, consisted of a detune trap as well as tune (X_t) and match (X_m) adjustable capacitors. Furthermore, similar principles were used to construct non-overlapped 10 × 10 cm² loops using balanced capacitive distribution on a cylindrical surface at a constant distance from a cylindrical sample (ε_r = 50, σ = 0.6 S/m).

FIGURE 1.

The 10.5T 32-channel receive array. A, schematic of the feed circuit and loop element, showing the tune (X_t) and match (X_m) capacitors, the detuning trap (L_dt and C_dt), the loop element (fixed C₁ and C₂ capacitors and trimmer capacitor X_tr), and an RF choke (L_RFC). B, Flattened layout of the coil (approximate dimensions in millimeters). C, Photograph of the coil as built (with the blue box marking the preamplifier boards and the red box marking the input cable traps)

Electromagnetic/circuit co-simulations were performed using CST Studio (Dassault Systèmes Simulia, Johnston, RI). Coil elements were modeled in SolidWorks (SolidWorks, Waltham, MA) and imported into CST. Simulations were performed over a frequency range of 2 GHz using the finite-difference time-domain method to solve Maxwell’s equations and were partially accelerated using one GPU. The loops were tuned to 447 MHz (proton resonance at 10.5 T) and matched to 50 Ohm. The simulation pipeline has been discussed in more detail in previous works.⁴⁰

Several EM/circuit optimization problems were set up with the goal of finding X_tr, X_t, X_m to minimize S_21,f conditioned on S_11,f ≤ −12dB and S_22,f ≤ −12dB, where f = 447 MHz is the resonant frequency. Values of X_tr, X_t, X_m were limited to practical ranges guided by bench experiments. Other 3D EM model parameters, including the distance between loop elements and the gap between the coils and the phantom, were kept constant and equal to practical receive-array values during optimization. Note that the objective function and the cost (loss) function for these optimizations can be defined in various ways. In our experience, incorporating the objective (S_21,f) into the loss function to form a weighted linear combination of individual L1 norms in the linear (as opposed to dB) scale of real and imaginary parts of the S-parameters resulted in faster convergence. The trust region method and the Nelder Mead simplex algorithm were used to solve for optimums. It should be noted that, in practice (on the bench), such an optimization is straight-forward and is substantially less time-consuming compared with the numerical simulations because, on the bench, the results of parameter modifications can be monitored immediately in an analogue manner using a vector network analyzer. Nevertheless, the simulations were useful in validating our bench implementation of self-decoupling (in terms of component values and s-parameters) and comparing self-decoupling with overlap decoupling (in terms of field pattern and SNR). For the 25 × 50 mm² self-decoupled loops, the simulation resulted in X_tr = 8pF, X_t = 1.4pF, X_m = 8pF, which were consistent with the on-the-bench implementation using X_tr = 8.2pF, X_t = 1.5pF, X_m = 8.8pF. For the 50 × 50 mm² loops, simulation results were X_tr = 6.5pF, X_t = 2.5pF, X_m = 3.5pF, while bench measurements were X_tr = 7pF, X_t = 2.5pF, X_m = 4pF.

Numerical results for S-parameters and per-port, complex-valued H-fields at 447 MHz were exported to ASCII files. Postprocessing and analysis of magnetic field results were performed using customized Python scripts. Complex-valued receive magnetic fields were calculated for each coil element using $B_1^{-}={\mu }_0\left(H_x^{*}+j{H}_y^{*}\right)/2$, where μ₀ is the permeability of free space, and x, y are Cartesian coordinates orthogonal to the static magnetic field (B₀). To compare the receive field between overlap and self-decoupling methods, two metrics were calculated: sum of magnitude of the complex combined magnetic fields, $SOM={\sum }_{\mathit{\text{sample}}}{\sum }_{\mathit{\text{channels}}}|{\text{B}}_1^{-}|$, and the root sum of squares (RSOS) of magnitudes of each channel’s magnetic field $\mathit{\text{RSOS}}={\sum }_{\mathit{\text{sample}}}\sqrt{({\sum }_{\mathit{\text{channels}}}{|{\text{B}}_1^{-}|}^2)}$ (ie, $\mathit{\text{RSOS}}={\sum }_{\mathit{\text{sample}}}\sqrt{B^{H}B}$, where B is a vector consisting of complex magnetic receive fields of each individual channel, and H is Hermitian transpose). Furthermore, RSOS was corrected for noise correlation, to calculate noise correlation–weighted SNR as given by $SNR={\sum }_{\mathit{\text{sample}}}\sqrt{B^H{\psi }^{-1}B}$, where ψ is the normalized noise-correlation matrix calculated using the simulated complex-valued scatter matrix.^{19,36,47–49} The summation over sample is intended to collapse spatial maps into a single numeric metric for comparison purposes. These metrics are particularly appropriate here, as we are considering receive-only coils; so we are interested in SNR, not transmit efficiency.

2.3 |. Eight-channel prototype

A prototype consisting of eight channels, arranged in four rows, to be representative of the final layout of the 32-channel receiver, was initially built and tested both on the bench and in the 10.5T scanner with the primary purpose of assessing the noise correlation. A 16 AWG silver-coated wire was used to construct the loops. Lumped capacitor values used in the loops were 3.3 pF, 4.7 pF, and 6.8 pF. One trimmer capacitor with a value range of 8–20 pF or 2–6 pF (SGC3S300NM or SGC3S060NM; Sprague-Goodman, Westbury, NY), included inside each loop, was carefully adjusted to decouple the loops in each row based on their scatter matrix parameters. The values of the larger trimmers were measured to be in the range of 8.5–15 pF after adjustment. The feed board, including the active detuning circuitry, and the preamplifier board were similar to those presented in a previous ISMRM abstract.⁵⁰

Using the eight-channel prototype, preamplifier interactions and coaxial cable interactions were investigated to characterize the effects of stacking preamps/coaxial cables close to each other as well as cable routing. Noise-correlation matrices for various cabling, preamplifier configurations, and cable trap locations were measured inside the 10.5T MR scanner with the eight-channel prototype. Although we did not observe any improvement in noise correlation by distancing the preamplifier boards from each other, having a single cable trap at the center of each input coaxial cable improved noise correlation. Furthermore, routing the preamplifier input coaxials along the center of transmit loops reduced transmit/receive interaction. Methods of characterization of the receiver array noise correlation and transmitter/receiver interaction are discussed in more detail subsequently.

2.4 |. Thirty-two-channel receiver array

A close-fitting receive former (helmet) was designed while considering physical constraints imposed by the transmitter (inner diameter of transmitter = 28.5 cm). The shape of the former was optimized based on previous helmet designs, numerical model of a human head, and consideration of average range of head sizes. A structure for mechanical support of the preamplifiers and cables was designed to be mounted as an additional part on top of the head former. A visual channel at the level of the eyes was designed to accommodate the needs of future functional MRI studies, which often involve visual stimulus presentation or eye tracking. The distribution of preamplifier substrates was driven by cable routing design, which will be discussed subsequently, as well as preamplifier interactions and directional sensitivity relative to the B₀ direction.

The 32Rx receive array consists of 31 loops, divided into four rows along the z-axis, and one cloverleaf element covering the top. The layout of the loops, presented in Figure 1B, allowed for partial overlap among elements of the different rows (8–10 mm) and gaps between neighboring loops within each row (5–8 mm); the self-decoupled loops with gaps in the axial (x-y) plane are included here to provide an SNR advantage compared with overlapped loops. Each row of loop elements was shifted (by a half loop), compared with the neighboring rows (ie, rotated azimuthally in the real coil). Overlap along the z-axis (along the center of the MR scanner bore) was maintained to further improve SNR through increased channel density. A key consideration in designing the layout was a primary focus on the visual cortex, driven by a large array of vision neuroscience projects conducted at the Center for Magnetic Resonance Research that can greatly benefit from higher field strength; this, in turn, motivated an increase in density in the posterior array for the rows that will be facing the occipital lobe, at the expense of a reduced density at the top (six loops) and bottom (three loops) rows. Loop elements with the plane of the loop aligned perpendicularly to the z-axis would have compromised sensitivity; therefore, a cloverleaf element, rather than loop elements, was placed at the top of the coil, resulting in a Poynting vector perpendicular to the z-axis.⁵¹ The cloverleaf element consisted of two figure-8 loops placed perpendicular to each other; the outputs of the figure-8 elements were combined in hardware as a quadrature pair to form a single receive channel. The as-built photograph of the receive array is presented in Figure 1C.

2.5 |. Receiver noise-correlation mitigation

On the bench, the scatter matrix (S_ij) was measured using a calibrated 16-port vector network analyzer (VNA, ZNBT8; Rohde & Schwarz, Munich, Germany). Bench measurements between all coil pairs using the eight-channel prototype showed little interaction between elements far from each other. Therefore, similar S_ij bench measurements for the completed 32-channel array were limited to adjacent coils in the same row or overlapping coils from different rows, considered to represent worst-case scenarios based on the prototype measurements. Later, the full noise correlation matrix for the 32-channel receiver was measured in the scanner. Measurements were done after tuning, matching, and self-decoupling the coils, and both before and after adding preamplifiers. Self-decoupling of adjacent loops within each row provided robust interelement isolation. Low-noise preamplifiers (WMA447A; WanTcom, Minneapolis, MN) with input impedance of 1.5Ω and noise figure of 0.45 dB were used for preamplifier decoupling. Preamplifiers were mounted on a ground plane, which helped minimize interactions with transmitter/receiver elements and preamp oscillations. To reflect the actual use case, S_ij measurements were done with all receive elements in the tuned state.

Coaxial cables were isolated using self-shielded input cable traps to suppress shield current–induced noise.^52,53 Traps were carefully tuned after being installed on preamplifier input coaxial cables; however, several cable traps were intentionally tuned slightly off-resonance to mitigate their interaction with resonant loops of the receiver or transmitter.³² These input cable traps are resonant structures constructed using a trimmer capacitor (8–30 pF; SGC3S300NM; Sprague-Goodman) soldered to copper tape wrapped around a dielectric cylinder mounted on the outer conductor of preamplifier input coaxials (with the copper tape soldered to the outer conductor). One further s-matrix measurement was made with output cable traps detuned to investigate potential crosstalk between those resonant structures as well.

2.6 |. Transmit–receive interaction

Design of routing paths for preamplifier input coaxial cables was driven by noise correlation and receive–transmit interaction considerations. Coaxial cables may present a significant conductor barrier to the transmitter. Based on previous experience with loop transmitter designs,³¹ knowledge of transmit field patterns,⁴⁰ and prototype experiments explained previously, we observed that collecting coaxial cables in five paths along the z-axis parallel to the center of the transmit loops would result in minimum transmit/receive (Tx/Rx) interaction.

Measurements of the receive–transmit interaction were performed both on the bench and in the scanner. On the bench, scatter matrix parameters of the transmitter were monitored before, during, and after insertion of the receive array, while the receiver was actively detuned using DC supply to PIN diodes⁵⁰ and loaded with a human head–shaped phantom. In the scanner, transmit field maps were acquired in two configurations: first, with the 16-channel transmitter and 32-channel receiver as an ensemble of transmit-only and receive-only arrays; and second, with the 16-channel transmitter used as a transceiver in the absence of the 32-channel receiver. Relative transmit ${\text{B}}_1^{+}$ maps were acquired using a small flip-angle multislice gradient-echo (GRE) sequence with magnitude images from sequential single-channel transmissions normalized by their sum.⁵⁴ Absolute transmit ${\text{B}}_1^{+}$ maps were then generated by normalizing relative transmit maps by $\mathrm{sin }(\mathrm{\alpha }(\overrightarrow{r}))$, where $\mathrm{\alpha }(\overrightarrow{r})$ is the actual flip angle as a function of spatial coordinate $(\overrightarrow{r})$ obtained through 3D-GRE actual flip-angle (AFI) acquisitions obtained with all channels transmitting.^54–56 Absolute transmit field maps were acquired both with and without the receive array in place, with the transmitter used as a 16-channel transceiver when the 32-channel receive array was not inserted.

2.7 |. Signal-to-noise ratio and g-factor

2.7.1 |. Data acquisition

Data were acquired on a 10.5T MRI (Siemens Healthcare, Erlangen, Germany) system using a phantom with permittivity ε_r ≃ 47.25 and conductivity σ ≃ 0.65 S/m at 447 MHz, as measured with a DAKS-12 (SPEAG, Zürich, Switzerland) to approximate human brain-tissue properties.⁴⁶ All SNR measurements were replicated two times: once with the 16Tx/32Rx coil described previously at 10.5 T, then with an industry-standard 1Tx/32Rx coil (Nova Medical, Wilmington, MA) at 7 T using protocols, acquisition parameters, setups, and data-analysis pipelines similar to those at 10.5 T.

Relative transmit field maps were obtained using a series of small flip-angle multislice GRE (2D-GRE) sequences, pulsing on one transmit channel at a time.^57,58 Typical sequence parameters were seven 5-mm-thick axial slices (with center slice being isocenter), TR = 100 ms, TE = 3.5 ms, flip angle (FA) = 10°, and pixel bandwidth = 300 Hz/pixel. The AFI⁵⁶ maps were acquired (3D, TR = 75 ms, TE = 2.0 ms, nominal FA = 50°) with all channels transmitting together. The SNR data were acquired at approximately fully relaxed longitudinal magnetization, with a multislice GRE sequence, with TR = 7000 ms-10 000 ms, TE = 3.5 ms, FA = 80°, and pixel bandwidth = 300 Hz/pixel. This was followed by a noise scan that was identical to the SNR sequence except for FA = 0° (no RF pulse) and TR = 70–100 ms.⁵⁹ When measuring AFI maps for SNR normalization at 10.5 T, a 16Tx, circularly polarized transmit-field ${\text{B}}_1^{+}$ phase shim setting was calculated for the 16 transmit channels, allowing for acceptable ${\text{B}}_1^{+}$ efficiency over a large fraction of the phantom.^60,61

2.7.2 |. Calculations

The noise-correlation matrix was calculated based on complex noise data (obtained in the absence of RF pulsing) and used to decorrelate the SNR data before they were combined using the RSOS method.^29,48 In the steady state, signal intensity in a GRE sequence is proportional to ρ(1 − E₁)(sinθ) / (1 − E₁cosθ)E₂, where ρ represents proton density; E₁ = exp(−T_R/T₁);$E_2=\exp \left(-T_E/T_2^{*}\right)$; and θ is the spatially varying, voltage-normalized actual flip angle. With T_R ≫ T₁, it follows that E₁ ≪ 1, which results in SNR ∝ ρsin(θ)E₂. The SNR maps were normalized by sin(θ) derived from AFI maps, voxel size, number of acquisitions, number of samples along the read-out and phase-encoding directions, and bandwidth, to make SNR calculations comparable across experiments.⁵⁵ The SNR ratios were further normalized by $T_2^{*}$ values, which were measured at 34 ms and 28 ms at 7 T and 10.5 T, respectively. The noise figure from receiver chain of the MR scanners (excluding RF coil and preamplifiers) was not reflected in these calculations. Noise amplification in accelerated images was quantified in terms of g-factor²⁴ and calculated as $g=SNR/\left(SN{R}_R\times \sqrt{R}\right)$, where R is the acceleration factor and SNR_R is the accelerated SNR calculated based on fully sampled acquisitions that were retrospectively undersampled. To be able to compare g-factor numbers of the 10.5–32Rx presented here with previously published²³ g-factors of 7T-32Rx and 7T-64 Rx, the same acquisition and postprocessing pipeline used for 7T-32Rx and 7T-64Rx were maintained in our experiments with the 10.5T-32Rx.

3 |. RESULTS

3.1 |. Receiver coil self-decoupling

Figure 2 presents self-decoupling results for two 10 × 10 cm² receive loops. The resulting simulated crosstalk between receive elements is S₂₁ = −12 dB. Figure 2C shows the magnetic field B₁ of a single excited loop that is consistent with the classic field pattern of a loop at this frequency. The surface current distribution is almost symmetric with strong current distributed on all segments of the excited loop (and limited current induced on the second loop) (Figure 2D).

FIGURE 2.

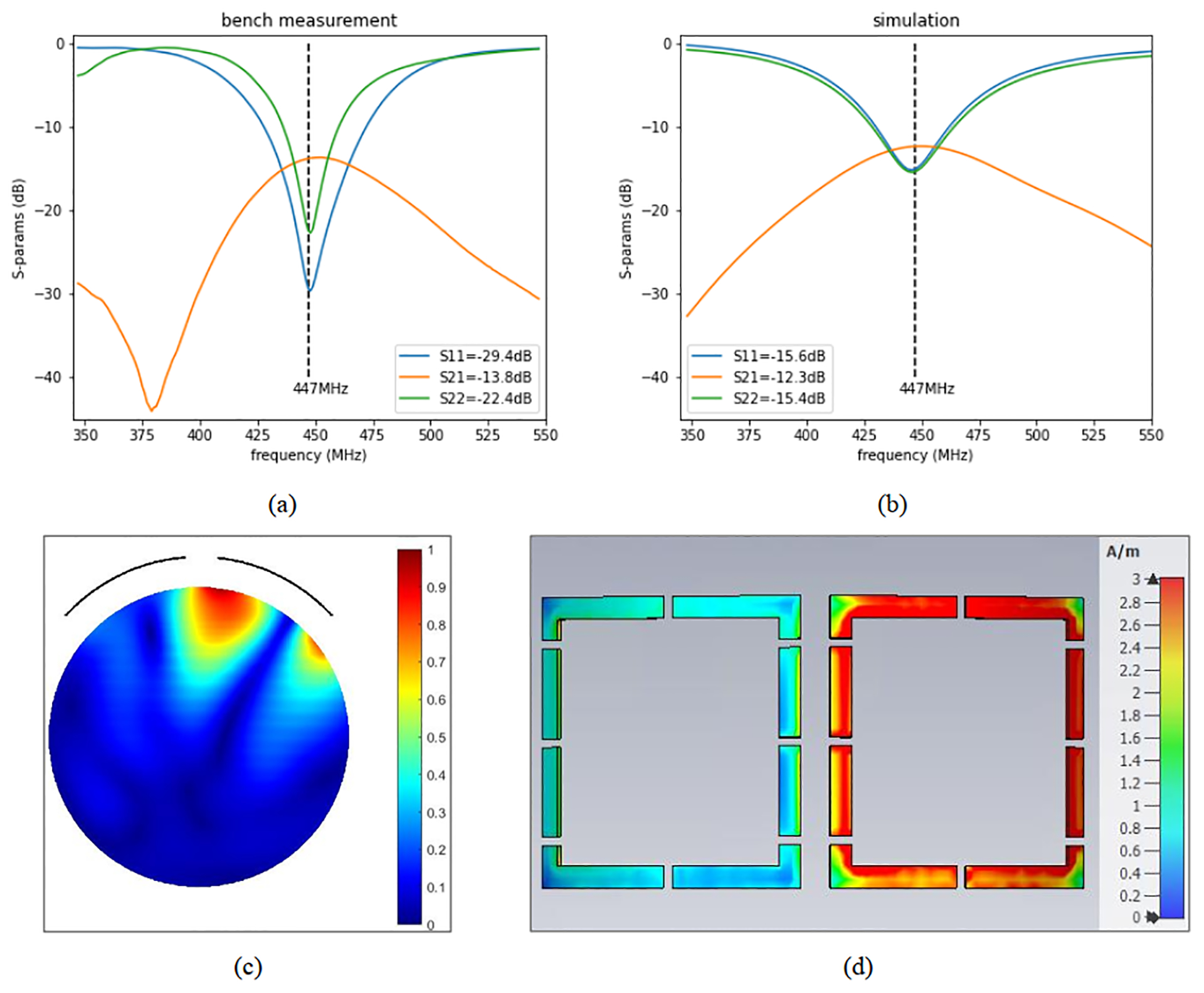
Experimental S-parameters (measured on the bench) demonstrating self-decoupling of adjacent loops (A), simulated S-parameters (B), magnitude B₁ field of one loop (axial, center slice, normalized to 1, showing the location of the loops as arcs) (C), and average magnitude surface current distribution (when only the right loop is excited) (D). The S_ij values included in (A) and (B) are at 447 MHz

Simulation results for 25 × 50 mm² receive loops demonstrated −11.2 dB isolation using the self-decoupling method (compared with −13.8 dB using overlap) at 447 MHz. In the case of 50 × 50 mm² loops, self-decoupling provided S₂₁ = −12.9 dB interelement isolation (compared with −16.8 dB using overlap). These results indicate that the proposed self-decoupling method achieves better than −11 dB isolation (in the worst-case scenario). Preamplifier decoupling will further improve the isolation.

Figure 3 depicts the ${\text{B}}_1^{-}$ resulting from two self-decoupled loops and provides a qualitative comparison with ${\text{B}}_1^{-}$ from two loops of the same size but overlapped. The RSOS combination of receive signals from the two self-decoupled loops shows strong receive signal despite the gap between the two loops (Figure 3A); a hint of the separation between the two loops is present in the form of two overlapping distributions of ${\text{B}}_1^{-}$, with two distinct maximal penetration peaks. The two overlapping loops, as expected, show more of an overlapping ${\text{B}}_1^{-}$ distribution. Table 1 presents a quantitative comparison between sum of magnitude and RSOS of ${\text{B}}_1^{-}$ and SNR integrated over the sample of self-decoupled and overlapped loops for two sets of loop sizes. Compared with overlapped loops, the proposed self-decoupling method provides 17% more RSOS ${\text{B}}_1^{-}$ for the 25 × 50 mm² loops and 32% more RSOS ${\text{B}}_1^{-}$ for the 50 × 50 mm² loops. Furthermore, self-decoupling results in 10% and 26% higher noise correlation–weighted SNR for 25 × 50 mm² and 50 × 50 mm² loops, respectively.

FIGURE 3.

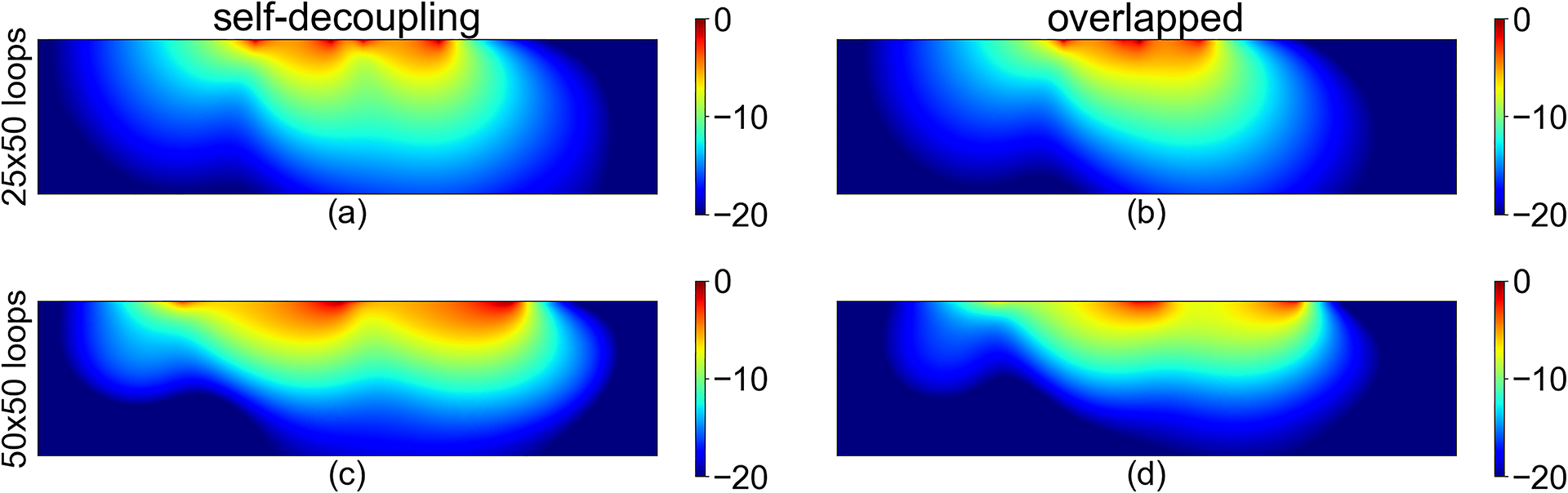
Normalized root sum of squares (RSOS) combined B₁ receive fields of two 25 × 50 mm², self-decoupled loops (A), two 25 × 50 mm², overlap decoupled loops (B), two 50 × 50 mm², self-decoupled loops (C), and two 50 × 50 mm², overlap decoupled loops (D). Numbers are in decibels. Phantom size is 50 × 200 mm² in all cases

TABLE 1.

Percentage gain in sum of magnitude, RSOS, and SNR obtained using self-decoupled loops instead of overlap-decoupled loops (calculated as [self_decoupling_snr − overlap_snr]/overlap_snr * 100) at 10.5 T/447 MHz

Loop size	SOM	RSOS	SNR
25 × 50 mm2	19	17	10
50 × 50 mm2	47	32	26

Abbreviation: SOM, sum of magnitude.

3.2 |. Receiver noise correlation and interaction with transmit field

The interelement isolation was measured before preamplifier decoupling as S₂₁ at the resonance frequency of 447 MHz; these values were, on average, in the range of 11–12 dB for self-decoupled adjacent coils in the same row, 12–15 dB for partially overlapped coils from different rows, and in the range of 20–30 dB for distant neighbors, demonstrating self-decoupling of the 32-channel receive array. Preamplifier decoupling further reduced crosstalk between receive array elements to negative 35–40 dB.

The noise-correlation matrix measured inside the 10.5T MR scanner resulted in maximum noise correlation of 0.37 (Figure 4), which is a significant improvement compared with previous works.²³ We attribute this to the novel self-decoupling technique, experimentally optimized cable routing (relative to transmit elements to minimize shield current–induced noise and transmit field distortion), and cable trap locations (to minimize trap interference with receive element resonances).

FIGURE 4.

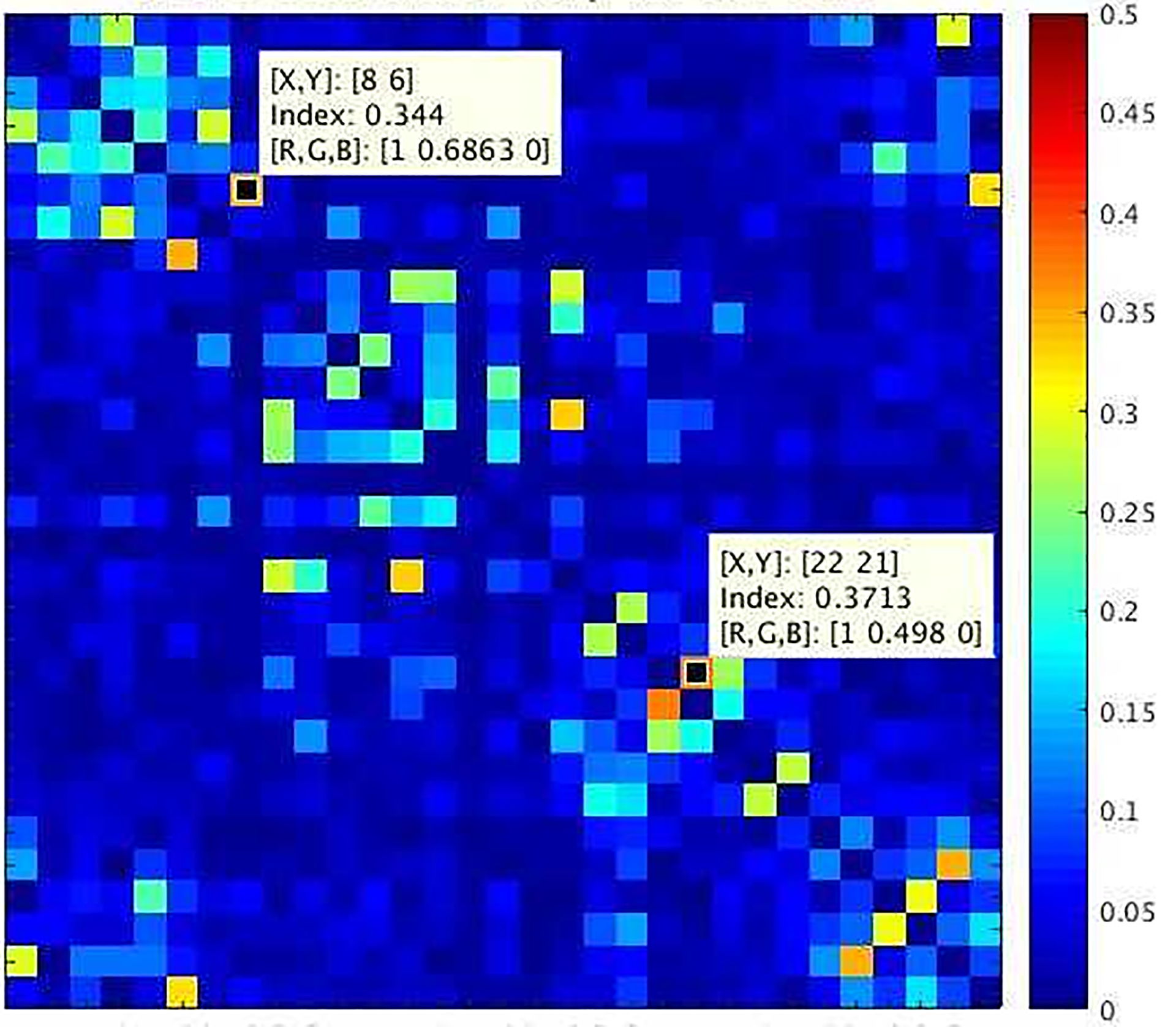
Experimental noise-correlation map for the 32-channel receiver at 10.5 T (10.5T-32Rx) demonstrating effective decoupling of receive elements (maximum noise correlation is 0.37)

Figure 5 shows power-normalized transmit field maps (in $\mu T/\sqrt{W}$) measured in the 10.5T scanner using the 16-channel transmitter with and without insertion of the 32Rx receive array, with the phases of the different channels on the transmitter set so as to generate a circularly polarized ${\text{B}}_1^{+}$ field, which results in the center bright ${\text{B}}_1^{+}$ maps.⁶⁰ These maps demonstrated less than 10% distortion of the transmit field after inserting the receive array, as such, characterizing the limited transmit field change following the insertion of the receive array. This characterization allows for streamlining safety validation studies by obviating the need for inclusion of the receive array in EM simulations of specific absorption rate.

FIGURE 5.

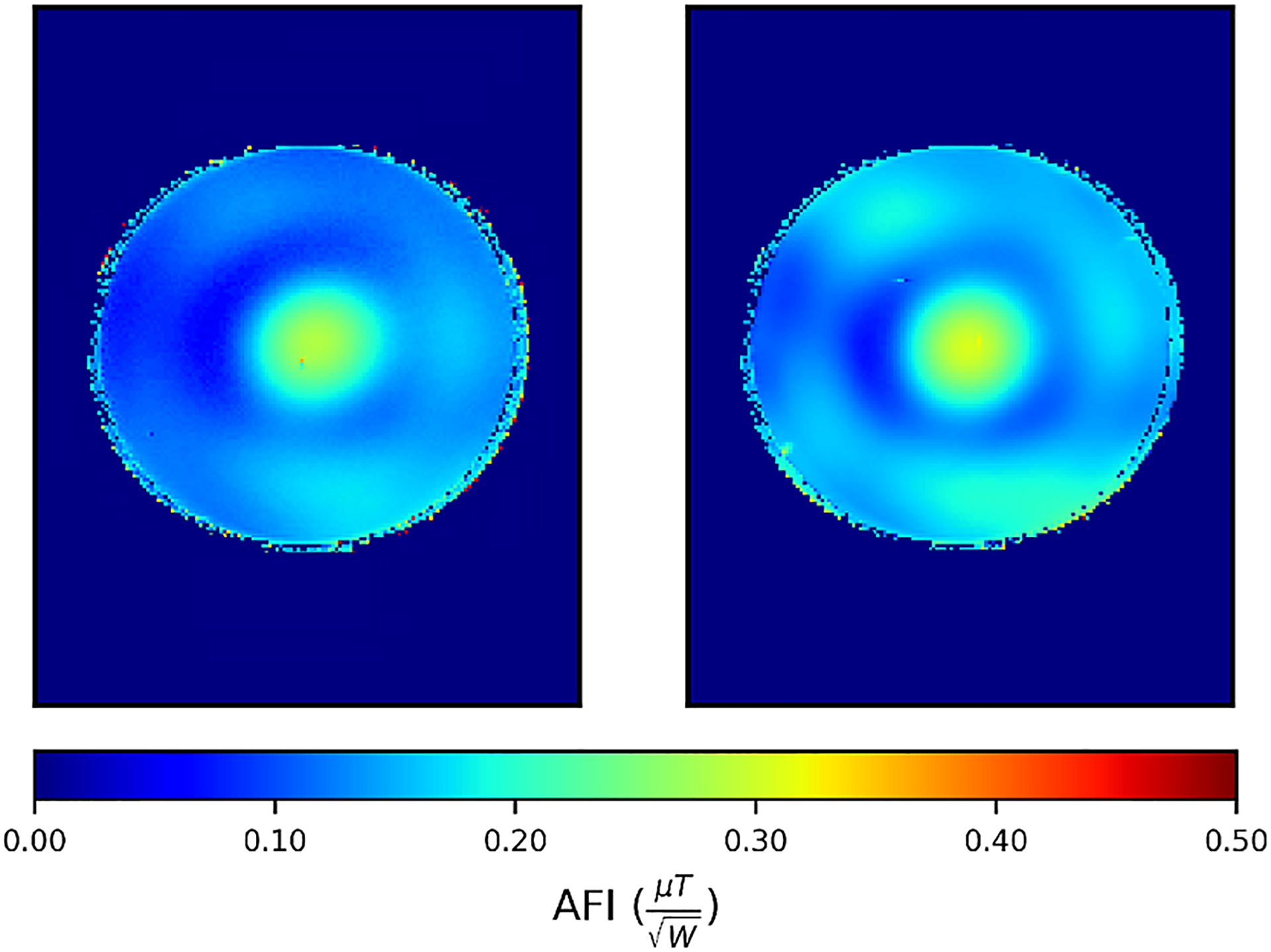
Comparing experimental normalized transmit-field maps of 10.5T-16Tx used as transceiver without the presence of 32Rx (left) versus 10.5T-16Tx/32Rx (right), demonstrating the effect of Rx insertion to be limited to 10%, where signal intensity is reliable. Abbreviation: AFI, actual flip angle

3.3 |. Signal-to-noise ratio and g-factor

Figure 6 illustrates the experimental, unaccelerated SNR comparisons in axial slices obtained with identical protocol, experimental setups, and analysis pipeline using a 32-channel receiver at 7 T (7T-32Rx) and a 32-channel receiver at 10.5 T (10.5T-32Rx). The phantom and regions of interest used for SNR comparison are depicted in Figure 7A,B. The SNR comparisons were made by averaging over a central region and a peripheral region defined by a circular boundary at depth “d” into the phantom (Figure 7B). Table 2 presents the SNR ratios for various peripheral versus central segmentations parametrized by the depth “d” of the central/peripheral boundary. The SNR comparison demonstrated 1.46-times central and 2.08-times peripheral SNR gains at 10.5 T with d = 20 mm. Figure 7C provides unaccelerated 3D (axial, coronal, sagittal) SNR comparisons between 10.5T-32Rx and 7T-32Rx in the central slices.

FIGURE 6.

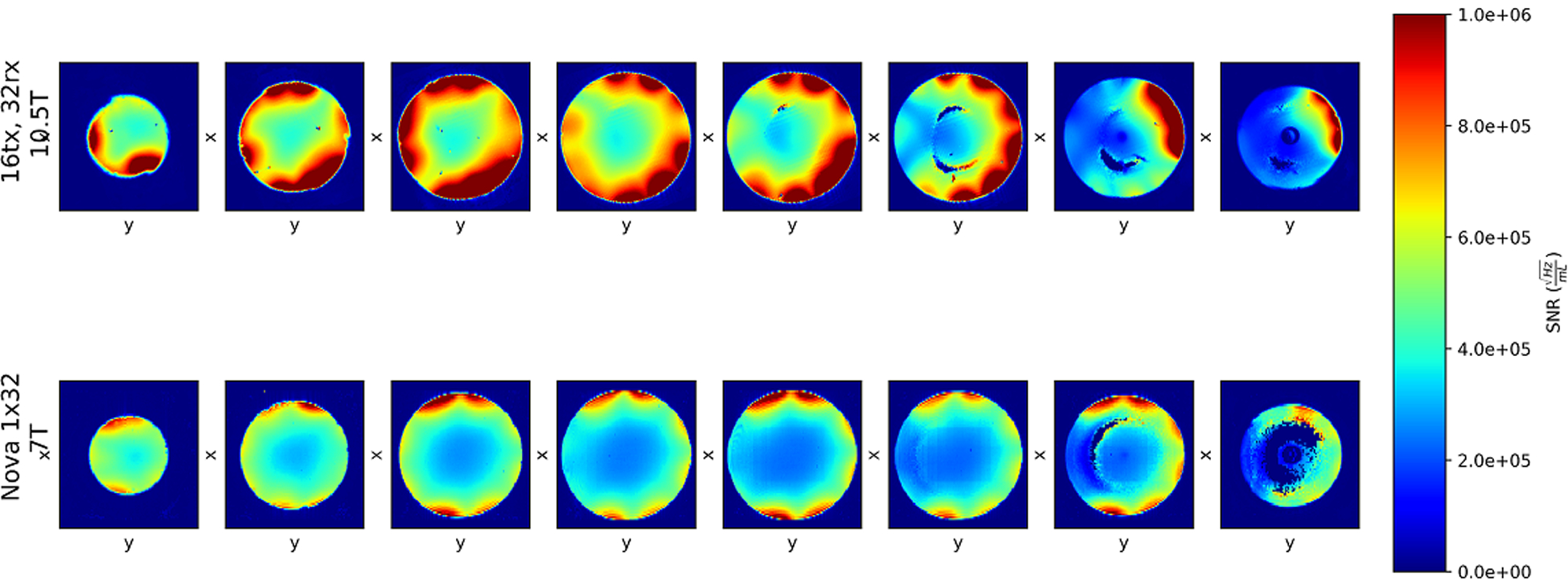
Comparing normalized SNR of the 10.5T-32Rx (top row) and industry-standard 7T-32Rx (bottom row) on eight axial slices. Local defects (the crescent-shaped signal loss in first three slices from right) are due to specific transmit B₁ shim. The dark center (in the first two slices from right) is an oil reference. Numbers are presented in $\sqrt{\text{Hz}}/\text{ml}$

FIGURE 7.

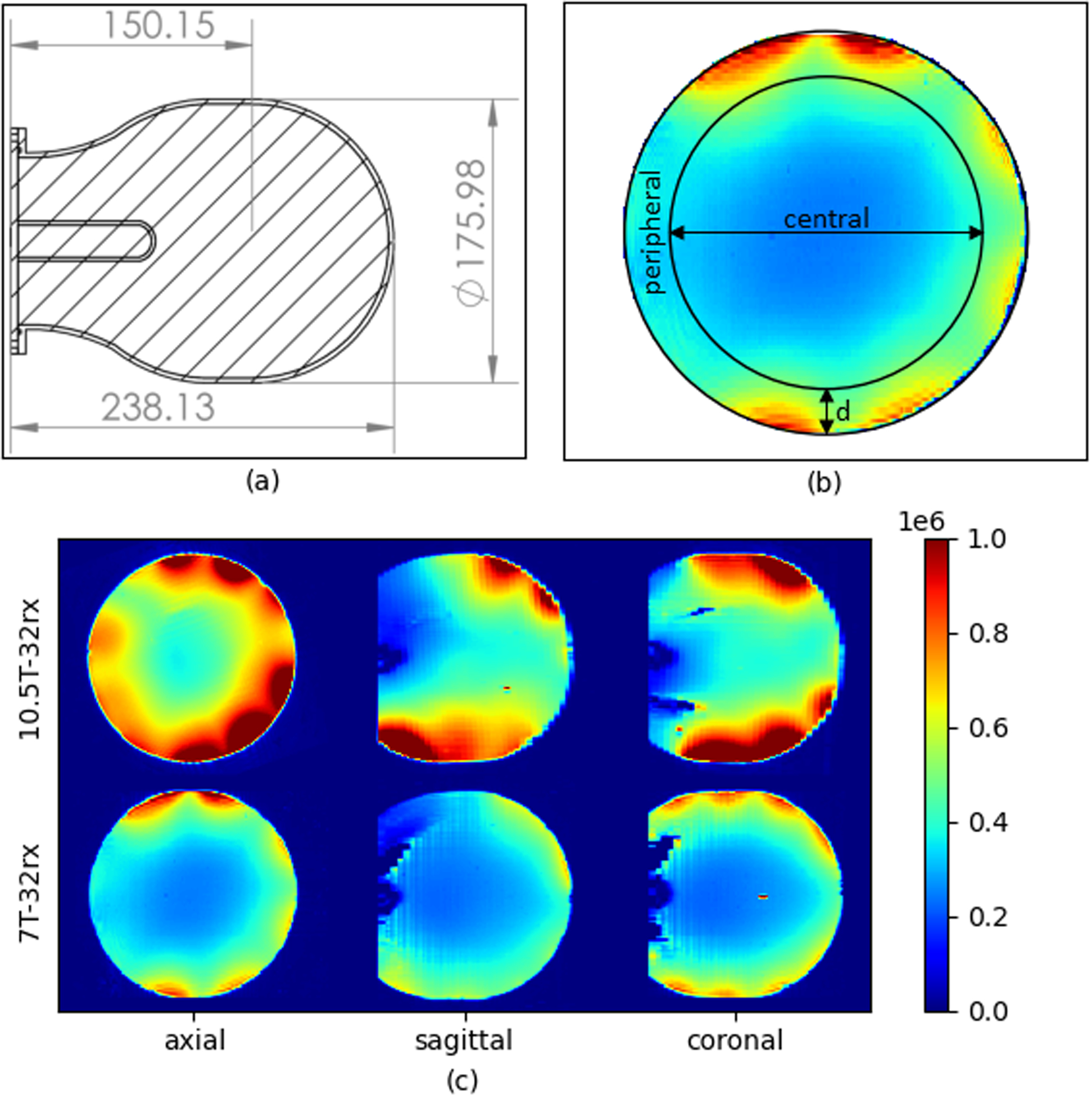
A, Phantom cross section; the cylindrical tube is an oil reference. B, Axial cross section showing the central versus peripheral regions demarcated by depth (d) into the sample. C, Comparing SNR from the 10.5T-32Rx (top row) with SNR from the 7T-32Rx (bottom row) in three orthogonal planes (SNR in $\sqrt{\text{Hz}}/\text{ml}$)

TABLE 2.

Ratio of the average 10.5T-32Rx SNR divided by average 7T-32Rx SNR for various values of d (peripheral vs central boundary, delineated in Figure 7B)

Depth (d, mm)	Peripheral SNR ratio	Central SNR ratio	Overall average SNR ratio
30	1.95	1.44	1.81
25	2.00	1.46	1.81
20	2.08	1.46	1.81
15	2.25	1.47	1.81
10	2.58	1.47	1.81

The overall average SNR gain using the 10.5T-32Rx was 81%. Expressed as an exponent n of the static magnetic field strength (ie, as $B_0^n$), the overall average n ≃ 1.5, and in the periphery n ≃ 1.8 (using SNR ratios for d = 20 mm). This enhanced SNR is primarily attributed to higher static magnetic field B₀ strength as well as noise mitigation and SNR advantages provided by the self-decoupling method. The less-than-expected SNR gains at the center are probably due to smaller loop sizes and non-overlapping loops used in self-decoupling, resulting in lower density of azimuthally distributed coverage. For a given row of azimuthally distributed loops, overlapping the loops would lead to either a larger number of loops (when loop size is equal to the self-decoupled design), or radially larger loops (when loop count is equal to the self-decoupled design). Both cases may produce a stronger receive B₁ field in the central regions.

The performance of the 10.5T-32Rx in 2D accelerated acquisitions can be compared with the 7T-32Rx in terms of g-factors (presented in Table 3). The mean inverse g-factor of the 10.5T-32Rx (1/g = 0.69) is 18% more than mean inverse g-factor of the 7T-32Rx (1/g = 0.59) for 4 × 4 acceleration.

TABLE 3.

Comparing g-factor values for 4 × 4 2D accelerated acquisitions using 10.5T-32Rx with g-factor values for 7T-64Rx²³ and 7T-32Rx²³

	g-factor		Inverse g-factor
10.5T-32Rx	Mean	1.44	Mean	0.69
	Max	1.8	Min	0.56
7T-64Rx	Mean	1.3	Mean	0.77
	Max	1.9	Min	0.53
7T-32Rx	Mean	1.7	Mean	0.59
	Max	2.7	Min	0.37

Abbreviations: Max, maximum; Min, minimum.

4 |. DISCUSSION

Previous studies have shown that ultimate intrinsic SNR increases with the magnetic field magnitude^16,18,25; the use of high-density receive arrays is necessary at UHF to approach ultimate intrinsic SNR⁶² available at UHF, and capitalize on the acceleration potential of UHF MRI. However, capturing these potential gains experimentally with increasing number of channels in UHF also depends on the execution of the RF coil array, both in accelerated and unaccelerated imaging. As such, strategies for mitigating interelement coupling and receiver noise play a critical role.

Here, we improved upon a novel self-decoupling approach³⁷ to build a 10.5T 32-channel receive array. The self-decoupling method presented by Yan et al³⁷ introduced a promising new method for decoupling of high-density receiver arrays. However, the method at 3T and 7T operating frequencies requires significantly unbalanced distributed capacitors or introduction of inductive circuit elements to achieve the desirable unbalanced current distributions. Primarily because of the higher operating frequency, the same self-decoupling effect was achieved at 10.5 T with a more uniform capacitive distribution for the loop sizes appropriate for a 32-channel receive array targeting coverage over the human brain. In RF coil validation efforts, achieving a match between the simulated and experimental field maps can be easier when current distribution on the loop is more uniform.

The effort presented here is the first implementation of the self-decoupling method in a 3D conformal, high-density, 32-channel receive-only array for human-brain imaging, albeit in this case it was done for the very high frequency of 447 MHz. Our data confirm Yan et al’s suggestion that in high-density, 3D conformal receive arrays, self-decoupling can be paired with preamplifier decoupling to improve interelement isolation. Importantly, we demonstrate that the combination of higher frequency (447 MHz), smaller loop sizes appropriate for a 32-channel receiver, and distributed inductance of such loops being in the range required for self-decoupling can be exploited to achieve acceptable interelement isolation with a more uniform capacitive distribution at 447 MHz. The resulting approach improves the RSOS of magnitudes of receive fields substantially, and results in better noise correlation–weighted SNR compared with overlapped decoupling.

Experimental noise-correlation matrix demonstrated effective interelement receiver decoupling, which is indicative of promising potential for parallel imaging. Indeed, the array provided substantially improved parallel-imaging performance at 10.5 T compared with a 32-channel industry-standard RF coil operating at 7 T, and comparable to a 64-channel array at 7 T (Table 3). It is not possible to distinguish whether the gains are primarily because of the coil design and interelement decoupling approach used, or reflect the gains expected from going to a very high magnetic field.^19,22,25 Nevertheless, the approach used has enabled the realization of the anticipated gains in parallel-imaging performance at UHF that push the EM operating regime toward the far field domain.

We anticipate that at ultrahigh frequencies (447 MHz and higher), the self-decoupling strategy will significantly simplify future high-density receive array design and construction, as it obviates practical complexities of common decoupling techniques. In addition, the receive array as constructed was shown to result in limited transmit-field distortion following insertion into a complex, 16-channel transmitter. This will facilitate the EM simulation effort for specific absorption rate and regulatory validation by accounting for the small effect of the receive array by including it in a safety margin when calculating the maximal allowable power use. Furthermore, limited receiver–transmitter interaction should enable an interchangeable coil setup, in which a single transmitter can be used with 32-channel, 64-channel, and 128-channel receivers.

Peripheral and central SNR gains presented here in comparison to 7 T confirm the expected gains for UHF imaging targeting the human head^{18,19,63–65}; however, consistent quantitative comparisons are difficult to make. In EM simulations, it is generally reported that the gains in ultimate intrinsic SNR are supralinear with field magnitude in the center of the head,^18,19,64 all suggesting approximately quadratic increases with field magnitude. In the periphery, however, findings are not so consistent: Wiesinger et al¹⁹ predict supralinear gains in the periphery, but other studies predict linear¹⁸ or even less.⁶⁴ In part, the discrepancies may emerge from the particular human head model,^18,64 or approximations of the human head⁶⁴ used, physical locations of the current distribution relative to the model, and the regions of interest over which the ultimate intrinsic SNR was averaged. Regardless of the quantitative differences, however, the aforementioned studies predict supralinear gains with field magnitude averaged over the brain, approximately in agreement with $B_0^{165}$ dependence experimentally reported by Pohmann et al.⁶³ The results from our 7T and 10.5T comparison agree with this general conclusion. However, the gains we measured were less than quadratic overall, although they were quadratic in the peripheral region of interest. In interpreting these results, it must be realized that different receive array designs can lead to different SNR gain distributions and may have different degree of success in capturing the ultimate intrinsic SNR in different regions of the object being imaged; this will affect comparisons between two different coils at two different field strengths. Moreover, the implementation of a real coil can deviate significantly from the modeling efforts, especially from ultimate intrinsic SNR. Compared with simulations of ultimate intrinsic SNR, the proximity of the coil elements to the object is not uniform, nor is the size of the coils used. Although we demonstrate that the self-decoupling approach is an improvement in capturing SNR compared with the overlapped-decoupling method when both methods use equal numbers of geometrically identical loops, an overlapped design that allows for larger loops covering the same surface area may potentially improve central SNR. There are also other potential noise sources, such as imperfect preamplifier decoupling, that can lead to the preamplifier noise being propagated back into receive loops.

This work is also a significant milestone also toward building 64-channel and 128-channel receiver arrays for human-brain imaging at 10.5 T. It is fully anticipated that scaling up to a 128-channel design will pose additional challenges in noise mitigation, preamplifier design, and receiver–transmitter interactions. However, expected SNR and parallel-imaging gains provide strong rationale and impetus to address such challenges.

5 |. CONCLUSIONS

There is significant clinical and research interest in capitalizing on the acceleration and SNR potential of UHF MRI. Here, we present the first self-decoupled 32-channel receive array and capture substantially superior SNR and parallel-imaging performance using a 10.5T MRI system compared with a 7T MRI system. The 10.5T-32Rx provided significant peripheral and central SNR gains compared with an industry-standard 7T-32Rx, both in unaccelerated and 2D accelerated acquisitions. This achievement delivers the much-anticipated SNR boost in highly accelerated UHF imaging required for further understanding of human brain function and connectivity.