Platelet heterogeneity enhances blood clot volumetric contraction: an example of asynchrono-mechanical amplification

Abstract

Physiological processes such as blood clotting and wound healing as well as pathologies such as fibroses and musculoskeletal contractures, all involve biological materials composed of contracting cellular population within a fibrous matrix, yet how the microscale interactions among the cells and the matrix lead to the resultant emergent behavior at the macroscale tissue level remains poorly understood. Platelets, the anucleate cell fragments that do not divide nor synthesize extracellular matrix, represent an ideal model to study such systems. During blood clot contraction, microscopic platelets actively pull fibers to shrink the macroscale clot to less than 10% of its initial volume. We discovered that platelets utilize a new emergent behavior, asynchrono-mechanical amplification, to enhanced volumetric material contraction and to magnify contractile forces. This behavior is triggered by the heterogeneity in the timing of a population of actuators. This result indicates that cell heterogeneity, often attributed to stochastic cell-to-cell variability, can carry an essential biophysical function, thereby highlighting the importance of considering 4 dimensions (space + time) in cell-matrix biomaterials. This concept of amplification via heterogeneity can be harnessed to increase mechanical efficiency in diverse systems including implantable biomaterials, swarm robotics, and active polymer composites.

Introduction

Upon vascular injury, a cascade of signaling events leads to the aggregation of platelets that undergo acto-myosin-based contraction with nascent fibrin fibers to stem hemorrhage and restore hemostasis. Understanding the contraction of this self-assembled biological material has long been a source of scientific inquiry [1-4], owing to the dramatic decrease in clot size and increase in clot stiffness, which can both change by an order of magnitude [5, 6] (Fig. 1a). Clot biomechanics has clinical relevance as poor clot contraction and altered clot mechanical properties have been associated with numerous pathologies [7, 8]. For example, various studies have shown that patients with bleeding disorders can have clots that are seven times softer than healthy controls [9] or have low single platelet force [6]. Patients that have had an infarct event can have clots that are 50% stiffer than healthy controls [11]. An increased clot force has been observed in patients with chest pain [9] and severe coronary artery disease[10]. Impaired clot contraction has also been observed in patients with acute ischemic stroke [12], asthma [11-13], sickle cell disease [14], systemic lupus erythematosus [15], and trauma [16]. However, as the clot contraction process and associated biophysics remain poorly understood, probing the underlying mechanisms for these changes has been difficult. With thrombosis being a common reason for failure in implanted biomaterials [17] and clot contraction being a major aspect of thrombosis, better understanding of clot contraction process could render it to be a therapeutic target to thereby increase efficacy and longevity of implanted biomaterials. Furthermore, there is a recent explosion of platelet-rich plasma (PRP) for therapeutic use in musculoskeletal medicine, with a wide variability in the preparation, composition, and concentrations of these products [18, 19]. However, the specific characteristics of the optimal PRP formulations for use in treating different musculoskeletal pathologies remain unknown [20]. This is in part due to our poor understating of the platelet biophysics and the interaction with fibrin matrix.

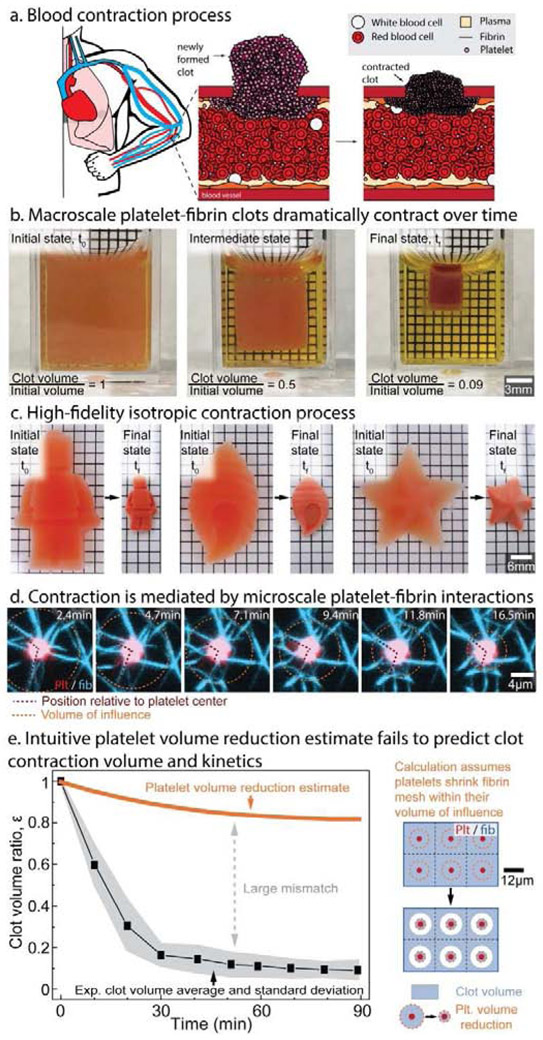
Figure 1: Blood clot contraction is an emergent behavior that arises from platelets interacting with a fibrin scaffold that cannot be extrapolated or predicted from those individual events alone.

a, At the site of vascular injury, activated platelets aggregate and bind to the nascent fibrin network and undergo muscle-like contraction, which significantly decreases the overall clot size. b, Experimentally, clots contract by over an order of magnitude and is a c, high fidelity, isotropic process. d, This dramatic phenomenon is driven by the microscale movements of contractile platelets pulling against a fibrin scaffold within a sphere of influence. e, However, calculations treating the clot as a series of independent platelets contracting within their sphere of influence significantly underestimate experimental clot volume change, which therefore suggests the presence of a more complex emergent behavior.

During our initial experiments, we observed that clots in cubic containers remained cubic upon completion of contraction, suggesting an isotropic process (Fig. 1b, Supplementary Video 1). We further tested this concept by creating in vitro clots of various complex shapes and found that contraction is a high fidelity process that preserves all key aspects of the original shape (Fig. 1c, Supplementary Video 2). Remarkably, the collective microscopic movements of 2 um-sized platelets interacting with a fibrin scaffold (Fig. 1d) mediate this significant macroscopic change, although the detailed biophysical mechanisms of this process remain entirely unclear. All experimental tools measure either microscopic platelet interactions with fibrin at the single cell scale [21] or bulk biomaterial contraction [4], and no tools are capable of linking the microscopic platelet movements to bulk contraction. Although multiple hypotheses of how platelet-based actomyosin leads to contraction of the clot macroscopically have been proposed [1, 22, 23], testing their validity has been exceedingly difficult. To circumvent this issue, we created the first mesoscale model capable of predicting bulk contraction extent from the fundamental behavior of a single platelet contracting a fibrin scaffold. Such a model has only been possible due to the collection of work that defines both the biophysical properties of fibrin [24-29] and single platelet behavior [6, 21, 30, 31].

Results

Clot contraction cannot be rationalized by a model disregarding platelet-fibrin interaction

Our initial investigation into platelet contraction using an intuitive estimate that links single platelet behavior to bulk biomaterial contraction revealed that dependent phenomenon likely play a key role in clot contraction. At the single platelet level, platelets extend filopodia to adhere onto fibrin fibers or other platelets and then pull inward. To estimate the typical number and length of filopodia, we fixed freshly formed clots, stained the platelets and fibrin, and acquired 3d stacks of over 45 platelets using confocal microscopy. A methodical analysis revealed that platelets extend up to 12 filopodia, each up to 6 micrometers in length (Supplementary Fig. 1), which agrees with other published work [21, 23]. Separately, previous studies had also shown that platelets contract for approximately 20-30 minutes [6]. Our intuitive estimate used these experimental measurements of single platelets to estimate bulk clot contraction by assuming that platelets can shrink all the fibrin contained in a spherical region with a radius equal to the maximum filopodia length. We compared the estimate with the contraction of platelet-fibrin clots in cuvettes over time (Fig. 1b). Each cuvette was prepared as described previously [4], and clots were imaged every 10 minutes for 120 minutes. Completion of clot contraction occurred at 90 minutes, when clots had a less than 1% change in volume in 10 minutes. To ease comparisons of the experimental data and the calculation, we defined a clot volume ratio of ε = V(t)/V₀, where V is the clot volume at time t and V₀ is the initial clot volume at time t = 0 when thrombin is added. The volume contraction in the experiments in Fig. 1b yields ε = 0.1. Despite our initial assumption exaggerating the ability of platelets to contract surrounding fibrin, we found that this simplistic calculation significantly underestimates the experimental clot contraction with a final clot volume ratio of ε = 0.82. This initial calculation implicitly assumed that the volumetric contraction of each single platelet is independent of one another and does not depend on neighboring platelet-fibrin interactions. The poor agreement of this calculation with experimental data suggests that including dependent phenomenon is essential for developing a predictive model.

iClot model incorporates the essential elements of blood clots

To gain insight into the biophysical underpinnings of platelet fibrin interactions and their effects on clot biomaterial contraction, we created the first fully digitized 3D model of a contracting clot, an in silico clot (iClot) containing iPlatelets and iFibrin scaffold. iPlatelets were modeled as 2 μm discoids and filopodia were represented as elastic bonds that randomly attach to an iFibrin upon iPlatelet contraction onset (Fig.2a), similar to the extension of filopodia that occurs after platelet activation in experiments. Each iPlatelet fully contracts its filopodia within 20 minutes. Based on the experimental data (Fig. S1), each iPlatelet had 12 filopodia that were able to randomly grab any iFibrin surrounding the iPlatelet, provided that the filopodia maximum length is 6 μm or less. After creating a model for a single iPlatelet, we digitized an intact experimental fibrin scaffold from a confocal microscopy 3D image of a newly formed and fixed platelet-fibrin clot (Fig. 2b). As iPlatelet retracts filopodia, the iFibrin scaffold wraps around the iPlatelet, recapitulating the morphology observed in experiments (Fig. 2a, Supplementary Video 3). As our own observations and those of others [21] determined that single platelets typically complete microscale contractions in 20 minutes, all iPlatelets were set to have an active time of 20 minutes. Additional details can be found in Methodology Section.

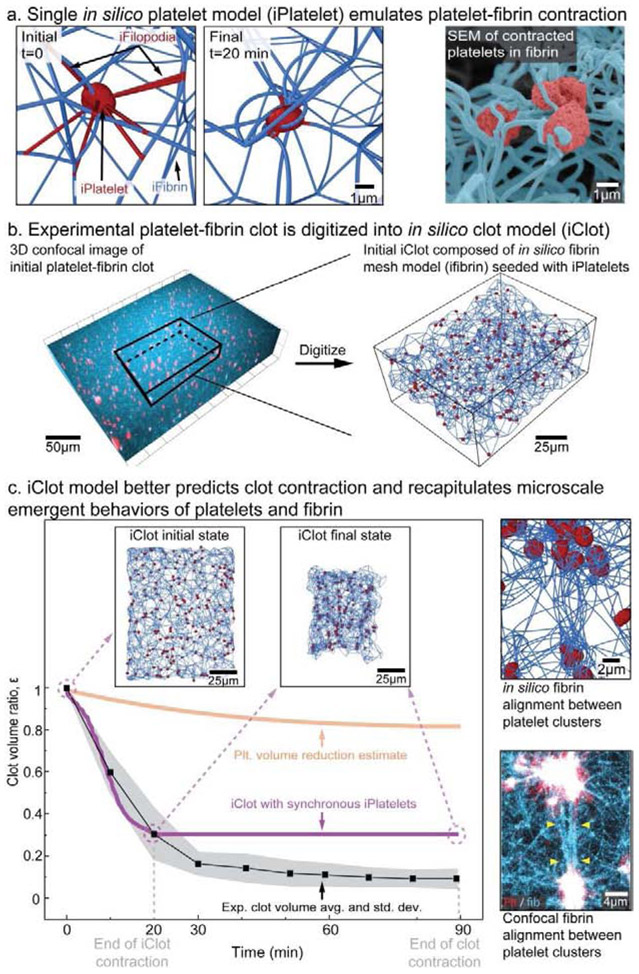
Figure 2: Our in silico model of clot contraction accurately predicts volumetric contraction and recapitulates key microscale behaviors.

a, Based on measurements of platelet filopodia length, number, and direction, a contracted iPlatelet (in silico platelet) resembles high-resolution images of platelets in contracted clots. b, Fibrin scaffolds are digitized and populated with iPlatelets to create an iClot. c, The iClot model with synchronous iPlatelets significantly improves the predicted volumetric clot contraction but not the kinetics. By modeling single platelet contraction within an iFibrin scaffold, the iClot recapitulates key microscale behaviors such as fibrin alignment and platelet clustering that are observed experimentally.

Homogeneous iClot contraction significantly underestimates experimental data

When we assume all iPlatelets contract simultaneously at t = 0, iClots contract to a final volume of ε_iClot = 0.3, which is much closer to the experimental value of ε_exp = 0.1 than our initial calculation. Furthermore, iClots exhibit unique microscale behaviors characteristic of clot contraction. iPlatelets cluster together, a phenomenon that has long been observed in experiments [22-24], and recently shown to be related to close platelet spatial location [21]. Our experimental data confirms this observation and found that as multiple iPlatelets pull on the same iFibrin, they are moved closer together producing a cluster (Fig. 2c). Importantly, the iClot allows for the tracking of iPlatelets over large displacements in isotropic, free boundary conditions. The clustering leads to alignment and densification of iFibrin scaffold resulting in the formation of fibrin bundles, that has been observed previously [22-24] and in our own experiments (Fig. 2c, Supplementary Video 4). Although some experimental biomaterial scaffold densification may be expected from continued polymerization of fibrinogen over time, our results highlight that mechanics alone can lead to this alignment and densification. Mechanistically, increased clot biomaterial contraction occurs due to the coupling of iPlatelet movements with iFibrin. Nevertheless, an iClot with simultaneously contracting iPlatelets significantly underestimates both the experimental clot contraction (by 300%) and the time needed for a clot to complete contraction (t_iClot = 20 min vs. t_exp = 90 min). Given that a single platelet contracts in 15 – 20 minutes (Fig. 1c) [6, 21, 31], whereas a bulk clot takes 90 minutes to contract (Fig. 1a, Supplementary Video 1 & 2), it is reasonable to assume that some asynchronous platelet activity must be occurring over the entire 90 minute time period in which bulk contraction occurs.

Platelets exhibit asynchronous contraction

Our data suggest that asynchronous platelet contraction occurs across the population of platelets as well as within an individual platelet. Platelets themselves are known to be intrinsically heterogeneous in terms of size [32] and contractile force [6, 30] and biologically when exposed to the same initial conditions, as shown by markers of activation such as P-selectin expression [33], phosphatidylserine (PS) exposure [34], and integrin α_IIbβ₃ activation [35]. To test whether platelets also display heterogeneous behavior in a clotting environment, we examined the times at which platelets express the activation marker PS in a fibrin scaffold. Initially, only a minority of platelets express this marker, and over the course of 120 minutes, there is a steady increase in the number of platelets that become PS positive, supporting the premise that because platelets finish (and start) activation at different time points, platelet contraction occurs asynchronously over similar timescales (Fig 3a, Supplementary Video 5). Our data is in agreement with other reports showing that fibrin clot contraction continues for at least 50 minutes and is abrogated by platelet inhibitors [21]. Our study of the real-time movement of single filopodia indicates that the extension and retraction of filopodia occurs at different time points is an additional source of asynchronous contraction (Supplementary Fig. 2, Supplementary Video 6). The concept of asynchronous filopodia retraction is also supported by other studies showing that filopodia are able to kink fibrin fibers [21], since kinking only occurs if retraction happens at different times. Furthermore, other studies in non-physiological systems have suggested that platelets may experience a late (>1 hour) second wave of filopodia extension and retraction [36].

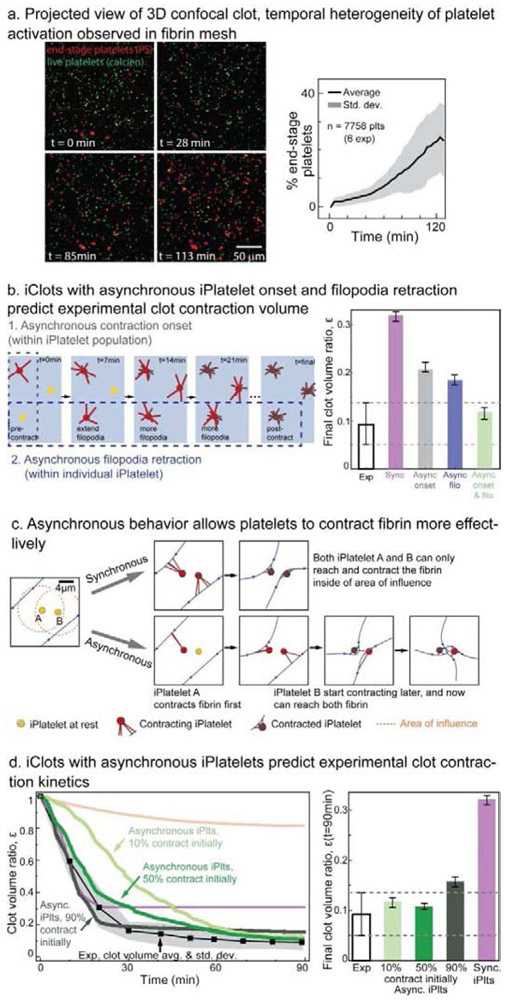
Figure 3: Asynchrono-mechanical amplification emerges from asynchronous platelet contraction and confers close agreement with experimental volume contraction kinetics.

a, Within a clot, platelets reach their physiologic end-stage, as measured by phosphatidylserine exposure, at different times suggesting asynchronous behavior. b, Similarly, platelet asynchronous contraction may be modeled by changing the timing of filopodia retraction or the timing of platelet contraction onset, yet both are needed for agreement with experimental data. c, Asynchronous contraction effectively enables platelets to enlarge their influence area. Therefore, this temporal heterogeneity enables platelets to contract fibrin more effectively. d, The kinetics of bulk clot contraction may be tuned by changing the proportion of initially contracting platelets. When the proportion of initially contracting iPlatelets is below 50%, there is poor agreement with experimental clot kinetics. When the proportion of initially contracting iPlatelets is above 80%, there is poor agreement with experimental clot final volume.

iPlatelet temporal heterogeneity enhances clot contraction

Remarkably, incorporating asynchronous iPlatelet contraction both resolves the timing discrepancy and increases the amount of iClot contraction to match our experimental data (Fig. 3b). We extensively explored multiple manners of modeling asynchronous contraction, as discussed in Materials and Methods, but found that both asynchronous contraction onset in the platelet population and asynchronous filopodia retraction in each platelet are essential for predicting experimentally measured final clot volume (Fig. 3b, Supplementary Fig. 3). Effectively, asynchronous contraction allows platelets to trade time for enhanced mechanical function to shrink the clot (Fig. 3d), an emergent behavior we termed asynchrono-mechanical amplification. Asynchrono-mechanical amplification occurs when one platelet pulls in the fibrin scaffold and enables a second platelet that extends filopodia at later time to pull on a portion of the scaffold that it was unreachable initially. Asynchrono-mechanical amplification also occurs in each platelet when the filopodia are extended sequentially to enable the platelet to reach and contract fibrin that is more than a single filopodia length away.

Asynchronous iClot contraction kinetics matches experimental data

Experimentally, the rate of clot biomaterial contraction can be separated into two phases. First the clot contracts rapidly, and then transitions to a more gradual contraction rate (Fig. 1e) (see also [21]). This suggests that there is a first subpopulation of platelets that drives the rapid initial biomaterial contraction, whereas a second subpopulation acts over an extended time to set the final clot shape. Indeed, when iPlatelets have contraction onset spaced uniformly over the entire period of clot contraction, the iClot volume kinetics poorly match the experiments. However, when we introduced a larger group of iPlatelets that start contracting at t = 0, we find a significantly improved match with the experimental kinetics. The strongest agreement with experimental clot kinetics occurs when at least 50% of iPlatelets start contracting at t = 0. The strongest agreement with experimental clot final volume occurs when the second group of iPlatelets contract evenly over time is larger than 20% (Fig 3d, Supplementary Fig. 4). Increasing the proportion of initially contracting iPlatelets over 50% mildly accelerates the initial contraction, but negatively affects the final contraction ratio (Fig. 3d, Supplementary Fig. 4). Therefore, in all subsequent simulations, we set the proportion of initially contracting iPlatelet to be 50%. The expectation that 50% – 80% of platelets are initially contractile is in good agreement with previous atomic force microscopy data, which found that the majority of platelets contract upon contact with a fibrinogen coated surface [30]. This also explains part of the origin of the differing contraction kinetics or phases of contraction seen in whole blood clots [4].

iClot correctly predicts clot contraction for a wide range of platelet concentrations

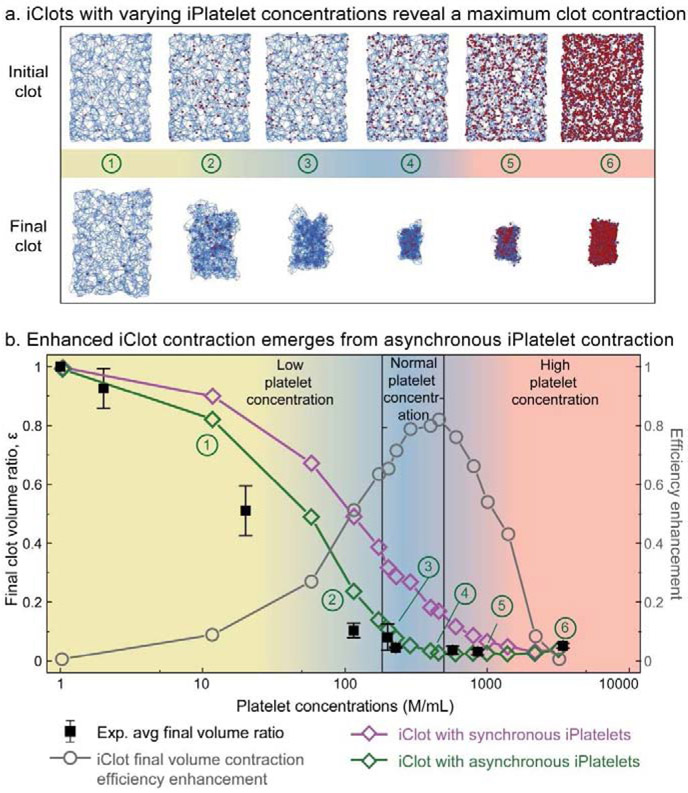
After demonstrating that emergent asynchronous contraction enables the iClot to match experimental data for a single concentration of iPlatelets, we applied our model to examine the dependence of clot material contraction on platelet concentrations (Fig. 4). Physiologically, it is well established that the concentration of platelets can vary depending on the location of the clot, as seen in platelet rich arterial thrombi or platelet poor venous thrombi. As such, a robust model that is capable of predicting clot biomaterial behavior over a wide range of platelet concentrations would be of significant value to hemostasis and thrombosis research since abnormal platelet concentration is associated with various blood disorders [37, 38]. Here, predictions were generated by populating the same iFibrin scaffold with different numbers of iPlatelets (Fig. 4a). Remarkably, experimental measurements of clot biomaterial contraction had excellent agreement with iClots for platelet concentrations spanning three orders of magnitude, from 1 × 10⁶ plts/mL to 3500 × 10⁶ plts/mL (Fig. 4b). The agreement is especially high for the physiologically normal to high platelet concentrations and the model even successfully predicted a local nadir in final clot volume at 600 × 10⁶ plts/mL. At concentrations above this point, the packing density of platelets drives the final size of the clot rather than the contraction of the scaffold. Furthermore, iClots with asynchronous platelets contract more efficiently than iClots with synchronous contraction over the entire concentration range that we studied. Specifically, the volume contraction efficiency enhancement, defined as (ε_iClot,homo – ε_iClot,hetero)/ε_iClot,homo , approaches 80% when the concentration of iPlatelets is in physiological platelet concentration in human blood. We note that whereas the contraction of macroscopic clots is isotropic (Fig. 1c), iClot final shape does not fully replicate the initial geometry ((Supplementary Fig. 6). This can be related to a relatively small size of iClot and, therefore, points to potential anisotropy of microclots. The ability to predict the final clot volume based on the platelet concentration is valuable for identifying diseases associated with low platelet count, as there is a significant variation of the final clot volume with platelet concentration. When platelets are used in biomaterials, their concentration can depart from the physiological concentration range and can be based on the functional requirements. Thus, the concentration can be used to regulate mechanical properties, porosity, and size of biomaterials.

Figure 4: Emergent asynchrono-mechanical amplification increases the volumetric contraction of iClots and reconciles experimental data for platelet concentrations spanning three orders of magnitude.

a, Here, only the concentration of platelets was changed, all other parameters were kept constant. Interestingly, the iClot predicts the platelet concentration that results in maximum clot contraction. At concentrations above this point, the packing density of platelets drives the final size of the clot rather than the contraction of the scaffold. b, Experimental data (black squares) agree with the iClot predictions that incorporate asynchronous platelet contraction (green), especially when the concentration is above 200 × 10⁶ platelets/mL, whereas the iClot with synchronous platelets (purple) significantly underestimate the clot contraction. Hence, emergent asynchrono-mechanical amplification is concentration dependent and confers an efficiency advantage that is most significant at physiological platelet concentrations.

Asynchronous platelet contraction enhances forces generated by clot

Pathophysiological changes in isometric clot biomaterial forces have long been tied to various diseases including bleeding, heart attack, stroke, and trauma among others [7, 8], but understanding of the mechanistic underpinnings of these alterations has remained difficult. Given the portability of our iClot framework, we extended the system to study the link between single platelet force and bulk clot biomaterial forces (Fig 5). We found that asynchrono-mechanical amplification also enhances the applied bulk forces.

Figure 5: Emergent asynchrono-mechanical amplification increases the iClot force to match experimental data.

a, By constraining the iClots between fixed parallel walls, wall constrained contraction can be modeled and used to estimate force generated by clots. b, Within the contracted iClot, iPlatelets apply a distribution of forces, similar to a population of single contracting platelets as measured experimentally with a contraction cytometer. In the iClots incorporating asynchronous contraction, the total force generated agrees with bulk experimental force data, unlike the iClot with synchronized iPlatelet contraction. Therefore, emergent asynchrono-mechanical amplification enhances the force efficiency of the clot by 70% and comes with no added energetic cost.

To explore this effect, we probed contraction of an iClot attached between two fixed walls (Fig. 5a). We set each iPlatelet filopodia to pull with a linear force up to 10nN, which allowed iPlatelet force to match experimental values of isolated single platelet contraction forces [6, 30] (Supplementary Fig. 5). We then evaluated the forces and stresses generated in the contracting iClot. Constrained iClot contraction results in hour-glass shape with small iPlatelet clusters at the intersections of vertically aligned fibrin bundles (Fig. 5a). We extracted the total force, in the direction of contraction, that each iPlatelet exerts on its surrounding iFibrin scaffold. Although it is not an exact like-for-like comparison, it is interesting to note that the distribution of iPlatelet forces within the iClot is similar to experimental measurements of isolated platelets [6] (Fig. 5b). Furthermore, the stress applied on the wall of the contracted constrained iClot with asynchrono-mechanical amplification is not significantly different from experimental bulk clot stress values. However, the iClot with synchronous platelet contraction and, therefore, no asynchrono-mechanical amplification, had forces that were significantly lower than experimental values (p < 0.05). Remarkably, asynchrono-mechanical amplification enhanced the stress by 70%, yet only comes at the expense of time and does not introduce an energetic penalty.

Discussion

Since our iClot model has high agreement with experimental biomaterial data and is based only on biophysical measurements of single platelets and fibrin networks, this suggests that our model has adequately captured all the essential major physical components of clot contraction. Previously published observations support our asynchronous contraction framework by providing qualitative evidence that platelet mediated contraction is a continuous process. This includes interesting time-lapse confocal microscopy of single platelet “hand-over-hand” motion [21], monotonically increasing force generation over time [23], and ultrastructure observations of long filopodia late in the clot contraction process [23]. Within the context of hemostasis, our iClot is the first to quantitatively estimate the magnitude of importance of heterogenous platelet timing and heterogeneous filopodia timing. Moreover, as some diseases may influence filopodia behavior [39], this also points to the possibility that pathological changes to the number or length of filopodia could have implications in hemostasis, although it was previously impossible to assess exactly how this would affect the process.

Our iClots allow us to obtain highly detailed information at different spatial and temporal scales about the kinetics and dynamics of the biomaterial contraction process that currently cannot be achieved experimentally. Atomistic methods capture more detailed features (receptor-ligand binding, protein-protein interactions, crowding, and confinement), but cannot model the contraction of a clot. Our mesoscale approach provides flexibility in choosing length scales that model larger physical systems while capturing the essential features of the microscale structures and interactions. In our model, iPlatelets and iFibrin match the physical properties of platelets and fibrin, while the interactions among them recapitulate the morphology observed in experiments. At the same time, bulk iClot contraction, force, and configuration can be directly related to experimental measurements. Such balance between microscopic details and macroscopic responses is the major advantage of mesoscopic modeling. Continuum modeling effectively predicts macroscopic clot properties[3], but disregards the important events among individual clot components that influence bulk contraction. By linking scales, we can directly modulate the properties of iPlatelets and iFibrin to examine how each influences bulk clot kinetics and mechanics. Despite these advances, our model has some limitations that will be addressed in subsequent work. First, our model does not consider platelet adhesion to the vessel wall via collagen or von Willebrand Factor (VWF), although these are typically 2D interactions occurring during the initial phase of hemostasis. Second, our current iClot implementation does not incorporate the effects of fluid flow and shear stress, although our framework can be extended to include these important effects now that we have verified the functionality. Finally, our simulations only examine the fibrin structure produced from one fibrinogen and thrombin concentration. While this was key to creating a robust model and elucidating asynchrono-mechanical amplification, our future work will incorporate fibrinogen and thrombin concentration changes.

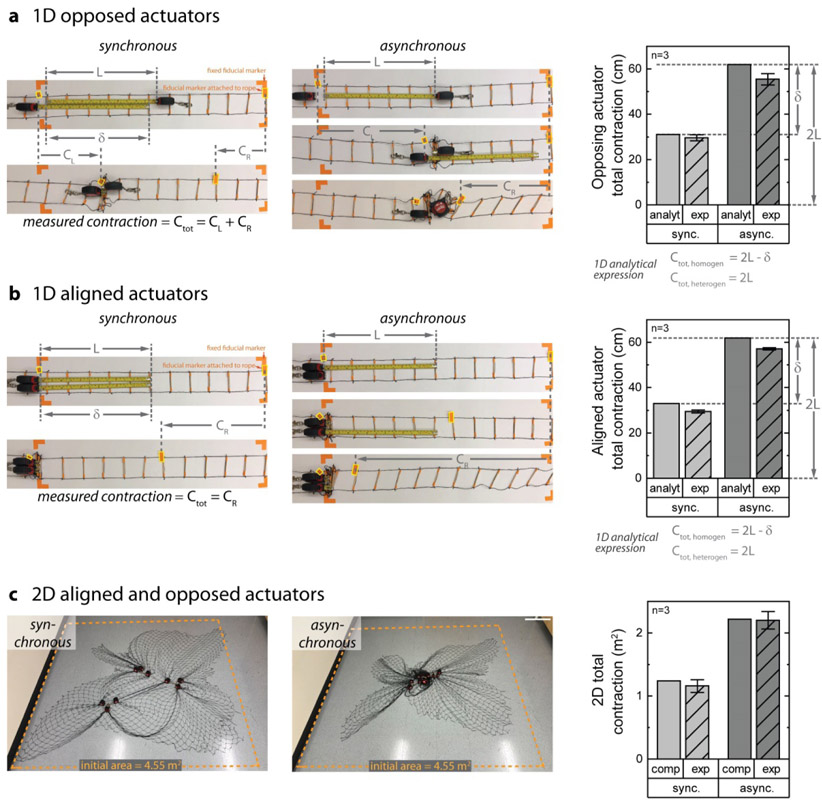
More broadly, asynchrono-mechanical amplification can be extended to other physical systems and may find use in designing novel active synthetic and hybrid polymeric materials and distributed robotic systems. To illustrate this generalizability, we constructed a simple 1D paired actuator system and more complex 2D multi-actuator system from tape measures and a scaffold to test how asynchronous actuation enhances packing efficiency. Defining the actuator length, L, and actuator overlap, δ, the total theoretical contraction may be analytically derived for both opposed (Fig 6a) and aligned (Fig 6b) 1D actuators. Kinematic experimental results on the motion of the actuators confirmed the validity of the analytical analysis, which can be formalized for any number of actuators. Interestingly, our calculations show that imposing synchronous contraction on a system has the effect of creating a penalty on the maximum contraction length (δ). Kinematic results of a 2D multi-actuator system with aligned and opposed actuators demonstrate that asynchronous actuation also improves packing in planar systems (Fig 6c). Although deriving an analytical expression for a 2D system would be non-trivial, computational results (see methods) have excellent agreement with experimental data. Hence, our investigations into the mechanisms for the dramatic reduction in volumes of an active material, cells in a fibrin scaffold, revealed a broadly applicable strategy that can be used to improve the mechanical efficiency of a system through sequential motion of mechanically linked actuators.

Figure 6: Asynchrono-mechanical amplification generalizes to non-biological, physical systems and enhances packing efficiency without an additional energetic cost.

a-b, To demonstrate this concept experimentally, a simple 1D physical system was created using tape measures as simple actuators and a rope ladder as a scaffold. Asynchronous actuators contract the scaffold more efficiently than synchronized contraction, regardless of opposed or aligned orientation. Analytical estimates for this 1D system strongly agree with experimental data, and show that synchronous actuation incurs a penalty in contraction due to actuator overlap as compared with asynchronous contraction. c, To demonstrate this concept experimentally in 2D, a physical system was created using tape measures as simple actuators and a nylon net as a scaffold. With 18 actuators (3 sets of 6), this system incorporates both opposed and aligned actuation and also exhibited enhanced packing with asynchronous contraction. Although the enhanced complexity in the 2D case precludes simple analytical expressions, computational estimates strongly agree with experimental data.

Conclusions

Overall, there are three classes of contractile cells: those that have synchronized movements, such as myoctes, which actuate structures such as the heart and limbs; those that work independently, such as pericytes, which contract to regulate capillary blood flow; and those that are embedded in and contract against a scaffold, such as platelets or myofibroblasts, as described in this work. Here, we show that heterogeneity of cells in scaffolds is not simply an artifact, but an effective biological strategy to trade speed for increased contraction and force. More broadly, our iClot model helps solve a central challenge in the field of mechanobiology, namely, linking microscale single cell biophysical behavior to macroscale biomaterial behavior and tissue mechanics. From a hematological perspective, this work could help explain why blood clots from patients with bleeding disorders are seven times softer than healthy controls [40] whereas clots from patients with thrombotic disorders can be up to twice as stiff [41]. Alternatively, many disorders involve myofibroblast mediated shortening of tissue, as seen in Dupuytren’s contracture [42] and Peyrionie’s disease [43], or increases in tissue stiffness, as seen in pulmonary fibrosis, hepatic fibrosis, and non-alcoholic fatty liver disease (NASH), and tumor stiffening. As myofibroblasts exhibit short individual contraction times [44] relative to the contraction of a cell-laden fibrous collagen matrix [45, 46], our iClot model can be modified to mechanistically reveal how single cell alterations in myofibroblast biophysical behavior leads to macroscale biomaterial contracture or stiffness in those diseases. As such, our work suggests that ECM synthesis and deposition are not needed to “shield” cells from tissue forces and enable significant contracture for wound healing, as previously theorized [47]. A better understanding of the link between single cell behavior and bulk tissue behavior would also lead to improvements in the material properties of the many modern regenerative medicine strategies that encapsulate cells with fibrin and collagen constructs. Thus, our work highlights how mechanobiological processes should be considered from a 4D (spatial + time) rather than 3D coordinate system.

Furthermore, the work findings point into a new direction of developing 4D synthetic and hybrid biomaterials where engineered heterogeneity can be harnessed to enhance their mechanical properties and to mediate complex shape transformations. The novel mechanism, which cells use to modulate material size, stiffness, and porosity, implies a novel method to regulate biomaterial cell encapsulation. Our work could serve as platform to characterize the optimal composition of natural platelet-based products such as platelet-rich plasma (PRP), platelet gel, and platelet eye drops, which are becoming preclinically evaluated and clinically attractive technologies to promote wound healing and tissue regeneration [48-51]. Furthermore, our results provide valuable guidelines for and inform the design of platelet-inspired biomaterials, such as synthetic platelet mimics and platelet-relevant biomolecule releasing delivery platforms [52, 53]. Our work shows a novel functionality of platelet heterogeneity which may find use in biomaterials if recapitulated in synthetic cells. In this fashion, our work points to a new direction of modifying, designing and regulating biomaterials and platforms based on functional requirements through the introduction of nature or synthetic cells capable of asynchrono-mechanical amplification.

Materials and Methods

EXPERIMENTAL

Sample collection

Healthy blood donors and patient donors had abstained from aspirin in the last two weeks, and consent was obtained according to GT IRB H15258. Blood was drawn by median venipuncture into acid-citrate-dextrose (ACD) solution 2. The sample was subsequently centrifuged at 150 G for 15 min, and the resulting platelet rich plasma above the packed red blood cells was carefully pipetted off for use in experiments or further processing. Washed platelets were isolated from platelet rich plasma by centrifuging with an addition 10% ACD by volume at 900G for 5 min. The supernatant, platelet poor plasma, was discarded or saved for other experiments and the platelets were re-suspended into HEPES modified Tyrodes buffer [54].

Bulk clot contraction

Cubic clots:

Polystyrene fluorimeter cuvettes (Sigma-Aldrich) with attached grids of 1 mm spacing were incubated with 1% F-127 pluronic (Sigma) at room temperature for 1 hour. A solution consisting of 2 mg/mL of purified human fibrinogen (FIB 3, Enzyme Research Laboratories), and washed platelets was prepared. The final concentration of platelets varied depending on experiment and ranged from 2×10⁶/mL to 0.571×10⁹/mL. This platelet-fibrin solution (1000 μL) was then combined with 1U/mL of human α-thrombin (haematological technologies) and 5mM CaCl₂ in the cuvette and kept at 37°C. Experiments were also performed at room temperature (22°C) and similar final contraction volumes were observed, although clot contraction times were longer and not as consistent. Pictures (or videos) of clot contraction were taken every 10 minutes, and clot dimensions were estimated using the attached grid. Volume was calculated from the clot dimensions. Clots were formed in triplicate and clots with 200×10⁶ platelets/mL performed for three different healthy volunteers.

Geometrically complex clots:

To determine the extent of contraction fidelity, platelet rich plasma was combined with 1U/mL of α-thrombin and 10mM CaCl₂ and placed into a silicone candy mold that was pretreated with 1% F-127 pluronic (Sigma) at room temperature for 1 hour. The filled molds were placed in an incubator for 10 minutes as the clot formed. The molds were then gently stretched to release the clot and the clot was either placed into HEPES modified Tyrodes buffer with 2% paraformaldehyde to determine the initial shape or allowed to contract 37°C for 90 mins in donor matched serum with 1U/mL of α-thrombin and 10mM CaCl₂, and then fixed in 2% PFA/Tyrodes. Serum was created from adding 1U/mL of α-thrombin and 2mM CaCl₂ to donor matched platelet poor plasma, allowing to clot for 1 hour, removing polymerized fibrin, collecting the supernatant, and storing at 4C for 24 hours before use. Videos of geometrically complex contracting clots were taken at room temperature conditions given the added complexity of providing adequate lighting for visualization.

High platelet count clots:

For clots with platelet counts of 0.857×10⁹/mL to 3.4×10⁹/mL, the high platelet count necessitated the use of smaller clot volumes to limit total blood volume withdrawl from donors. Here, smaller 200μL clots were placed in 500μL centrifuge tubes that were pretreated with 1% F-127 pluronic as above. Once formed, clots were conical frustums and remained in this shape for the duration of the experiment. Volumes were calculated from measurements of the top diameter of the frustum, the bottom diameter, and the height, and clots were formed in triplicate. To validate this approach, cubic clots were also prepared with platelet concentrations of 0.86×10⁹/mL in cuvettes as above, and the final clot contraction volume of the 1000μL clots were within 1% of the 200μL clots.

Bulk clot force:

Force measurements were performed with a stress-controlled rheometer (Anton Paar MCR 501) using cone-plate geometry. The clot was formed in situ and the normal force were measured as the clot formed. Final clots composition consisted of: 2mg/mL of purified human fibrinogen (FIB 3, Enzyme Research Laboratories), 250×10⁶ washed platelets/mL, 1U/mL of thrombin, and 1 mM CaCl₂.

Single platelet studies

Fibrin structure, filopodia number, filopodia direction, and filopodia dynamics:

To image platelet filipodia number and direction, small 200μL half-sphere clots were formed in glass coverslip bottom petri dishes (Matek P35GC-1.5-14-C). Suspended in Tyode’s buffer, the final concentration of each clot was 200×10⁶ platelets/mL, 2mg/mL of fibrin with 2% Alexa Fluor 488 tagged fibrinogen (ThermoFisher F13191), 1U/mL α-thrombin, 1μL/mL CellMask Orange (ThermoFisher, C10045), 10 mM CaCl₂. This preparation maximized optical clarity to enable visualization of fine fibrin details and platelet filopodia.

To measure the fibrin structure, filopodia number, and filipodia direction, the clot was allowed to form in the glass bottomed petri dish for 5mins, and then submerged in Tyrodes buffer with 2% PFA. After fixation overnight, the clot was imaged using a Perkin Elmer UltraVIEW VoX spinning disk confocal microscope. To measure the fibrin structure, a 40× / 1.3 NA was used to capture an image that was approximately 190μm×255μm×50μm (0.25μm increments in vertical plane). To measure the filipodia number and direction, 3d image stacks of clots were aquired with a 100× / 1.45NA objective. Volocity (Quorum Technologies) was used to manually identify in 3D space the centroid and filopodia tips of 47 platelets. Filopodia lengths and directionality were reported from the centroid.

To measure filopodia dynamics, clots were formed in the glass coverslip bottom petri dish at the confocal and immediately imaged. To reduce the movements of single platelets and enable the imaging of filopodia dynamics, the platelet concentration was reduced to 20×10⁶ /mL. Three-dimensional image stacks were acquired with a Carl Zeiss LSM 780 using a 63× / 1.4NA and captured at 180s intervals.

PS activation:

To better understand the heterogeneity in platelet timing, we measured the time at which single platelets in a 3D clotting environment exposed phosphatidylserine on their outer surface. Phosphatidylserine is a commonly used marker of platelet activation and more broadly of cellular apoptosis. Starting from isolated platelet rich plasma, live platelets were stained with a 1μM Calcien AM (ThermoFisher, L3224) at room temperature for 15 mins. Phosphatidylserine was measured with Annexin V-AF568 (1:20) (ThermoFisher, A13202) and 3d image stacks were collected using a Perkin Elmer UltraVIEW VoX spinning disk confocal with a 20× / 0.75NA objective.

The percentage of PS positive platelets was measured using Volocity 3D imaging software. Platelets stained with calcien were counted at the beginning and end of the experiment with the Volocity built in function, “find objects”, which allowed for consistent tracking of platelet count ensuring experimental platelet count did not change over the course of the experiment. The “find objects” feature was then used to track PS exposed platelets stained with Annexin V-AF568 at each time point. PS exposure data was reported as the percentage of platelets that were PS exposed.

Single platelet force measurements:

Single platelet force measurements were performed as described previously using a contraction cytometer [6]. Our contraction cytometer utilizes an array of fibrinogen microdot pairs patterned on 4 parallel microstrips of a polyacrylamide (PAA) hydrogel with a stiffness of 75 kPa. In brief, fluorescently tagged fibrinogen (Thermo Fisher Scientific) was incubated on 10 mm × 10 mm × 3 mm PDMS squares at a concentration of 30 μg/mL for 1 hour, rinsed, and blown dry with compressed air. The PDMS squares were then brought in contact with O₂ plasma treated silicon molds and then pulled away to create a microdot pattern which was then transferred to an O₂ plasma treated 18 mm × 18 mm coverslip. This was subsequently transferred to the gel microstrips, which had a stiffness of 75 kPa, which were then covered with a microfluidic. The fibrinogen concentration represents an optimal that is sufficient for platelet adhesion, but not so high as to reduce the patterning fidelity. Detailed calculations show that gel stiffnesses ranging from 25-100 kPa approximate the mechanical stiffnesses of different platelet/fibrin geometric arrangements that occur within a clot [6].

Washed platelets are isolated as described previously and additionally gel filtered through a Sepharose-2B (GE) column to remove free fibrinogen. Immediately prior to loading platelets in the microfluidic (4 × 10⁶/mL), the following is added: 5 mM of CaCl₂, 5 mM of MgCl₂, 3 μg/mL of fibrinogen, and1U/mL of human α-thrombin (Haematologic Technologies, Inc). After 15 minutes, 60 μL of a wash solution consisting of 5 mM of CaCl₂, 5 mM of MgCl₂, and 1 U/mL of human α-thrombin is added, and the adhered platelets are incubated for 90 minutes at room temperature. During this time period, activated platelets adhere to a single fibrinogen microdot, spread to the neighboring microdot, and contract, pulling the pair of microdots closer together. As the stiffness of the gel is set, the applied force is proportional to the microdot displacement, akin to a Hookean spring configuration. Importantly, since platelet force is directly proportional to the microdot displacement, only a single microscopy measurement is needed to determine the force applied by each single platelet. Platelets are then fixed with 4% paraformaldehyde in Tyrode’s buffer, stained with a plasma membrane dye (Cell Mask Orange, Life Technologies), and imaged using a Zeiss LSM 700-405 confocal microscope with a 20× 0.8 NA lens.

Scanning electron microscopy images:

Contracted cubic clots prepared as described in cubic clots section. Clots were washed in 0.05M sodium cacodylate (pH 7.4), 0.10 M NaCl for at least 2 hours and then rinsed with 0.05M sodium cacodylate (pH 7.4), 0.1M NaCl. Clots were dehydrated in solutions with progressively increasing amounts of EtOH, from 30% to 100%, and then 50%HMDS/50%EtOH, and finally 100% HMDS, which was evaporated off overnight. Samples were then sputter coated with gold-palladium and imaged with a Hitachi SU8230 scanning electron microscope. False coloring was performed using Illustrator (Adobe, Inc).

Platelet volume reduction calculation

In experimental clots, platelets extend filopodia, which attach to fibrin fibers or other platelets, and then pull inward. Here, we sought to understand how much this volumetric contraction, in the absence of any other phenomenon, influenced bulk clot contraction. We assumed that each individual platelet can shrink all the fibrin contained in an initial spherical region with a radius equal to the maximum filopodia length. When platelets finish the filopodia retraction, all fibrin in the initial spherical region are contracted to a more compacted final spherical region. The final spherical region has a radius equal to the platelet size. The reduction of this spherical region for each platelet sums together to cause the volume reduction in the bulk clot.

$$\begin{gathered} V_{clot}(t)=V_{i,clot}-{\sum }_N\Delta V_{plt}(t) \\ \Delta V_{plt}=(3∕4\pi r_i^2)-(3∕4\pi r(t{)}^2) \end{gathered}$$

Here, V_i,clot is initial clot volume, V_f,clot is final clot volume, N is total number of platelets, ΔV_plt is the volume reduction of a platelet, r_i = 6μm is the radius of the spherical region a platelet can contract, r_f = 1μm is the radius of the spherical region after a platelet contracts. With platelet concentration 200 × 10⁶ plts/mL, assuming filopodia contracts at constant speed in 20 minutes, the clot volume ratio ε = V_clot(t)/V_i,clot is evaluated (Table 1). The final clot volume ratio ε_f = V_f,clot/V_i,clot = 0.82.

Table 1:

Clot volume reduction estimate based on platelet volume change.

Initial clot volume (mL)	1
Platelet concentration (M/mL)	200
Initial platelet radius r (μm)	6
Final platelet radius r (μm)	1
Initial platelet population volume (μm3)	1.810E+11
Final platelet population volume (μm3)	3.879E+06
Platelet volume reduction (mL)	0.18
Final clot volume (mL)	0.82
Final clot volume ratio	0.82

1D and 2D actuator system

A simple 1D physical system was created using tape measures as simple actuators and a rope ladder as a scaffold. To construct the ladder, wooden sticks were attached to a nylon net material, which was cut to size, using tape. The stiff ladder rungs prevent the nylon mesh from collapsing, and therefore, confine all motion to be one dimensional. Four conditions were tested; heterogeneous contraction with tape measures facing opposite to each other (het-op), heterogeneous contraction with tape measures facing the same direction (het-same), homogeneous contraction with tape measures facing opposite to each other (hom-op), and homogeneous contraction with tape measures facing the same direction (hom-same). Tape measures were set to reach to an arbitrary distance of L = 12.5in (31.75cm) and were fastened to the closest rung on the ladder for contraction. As this was a kinematic (motion) study, tape measures were manually contracted if they did not have sufficient spring force to contract the scaffold. Two fiducial marks were placed on the ladder to demarcate a length of 2L, or 25in (63.5cm), and the corners of the experimental area were marked using masking tape. One tape measure was placed at the first fiducial mark and the second tape measure was placed at the second fiducial mark. For the heterogeneous experiment, one tape measure was extended to 12.5cm and then retracted completely along with the rung closest to the extended position. The second tape measure was then extended to 12.5cm, fastened in place, and then retracted completely. For the homogenous experiments, both tape measures were extended and contracted at the same time.

For the 2D experiment, a physical system was created using 18 tape measures as simple actuators and a nylon net as a scaffold that was approximately 84×84 in (213.36×213.36 cm). There were three clusters of six tape measures, with three clusters of two adjacent tape measures per cluster of six. The tape measured were fastened to the net to begin the experiment using an integrated keychain clip. To perform the heterogeneous experiment, each tape measure was assigned a number from 1-18. A random number generator was used to select each tape measure in turn. This tape measure was extended outward to L = 15in (38.1cm) and then retracted. For homogeneous contraction, the same procedure was repeated, except the two adjacent tape measures were extended and contracted at the same time. Clusters of two were assigned numbers from 1-9, and the random number generator was used to select each pair in turn. As this was a kinematic (motion) study, tape measures were manually contracted if they did not have sufficient spring force to actuate the structure.

COMPUTATIONAL

Digitization of clots

We digitized confocal 3d image stacks of an experimental platelet fibrin clot (size 190μm × 255μm × 50μm) that was fixed shortly after formation. Only the center portion of the clot in the x and y directions (size 115 μm × 150 μm × 50 μm) was used since it had more consistent fluorescent intensity and lower background noise. A MATLAB script (publicly available at Github) identified the 3D locations of each platelet and all fibrin fiber intersections in the experimental clot based on the color intensity profiles of all images at all clot heights. This information was combined with the biophysical properties of fibrin [25, 26, 29] to create a replicate 3D iFibrin mesh that was then populated with iPlatelets in the same locations as the experimental clot.

Computational model of in-silico clot (iClot)

We constructed the three-dimensional model of a contracting platelet fibrin clot with a mesoscale approach, in which iPlatelets and iFibrin mesh were modeled as combinations of beads tied with harmonic bonds. Nonbonded interaction forces between beads follow the dissipative particle dynamics potentials including repulsive, dissipative and random forces that conserve local momentum [55]. We modeled platelets contracting fibrin through filopodia retraction by creating bonds between iPlatelets and iFibrin and then contracting these bonds. We prevented polymers from crossing each other by applying repulsion forces between bonds that are closer than a minimum distance [56]. To include the effect of a viscous solvent, we imposed viscous and random forces evaluated from the Langevin thermostat to represent an implicit solvent. Forces and velocities of all beads are integrated between each time step using the velocity Verlet algorithm.

iFibrin mesh

We modeled fibrin mesh as semi-flexible polymer chains randomly interconnected at branching points obtained from the confocal image analysis of an experimental platelet fibrin clot [57]. By allowing each branching node randomly connects to 5 neighbors, we obtained iFibrin mesh with an average fibrin filament length 10μm. Each fibrin filament is a polymer chain with n beads (monomers) that connects two branching points. The number of monomers depends on the length of each fibrin filament. With a selected force scale, we set the bond stiffness K_bond and the bending stiffness K_bend of the harmonic bonds such that elastic modulus of modeled iFibrin matches experimental measurements. We performed bending tests with a 15μm filament to tune K_bond and K_bend such that the chain elastic modulus is 14MPa [25]. To this end, with two end monomers fixed, we applied small incremental forces to the center bead to measure the filament deflection and then calculated the elastic modulus using theory of deflection of a simple beam.

iPlatelet

We modeled iPlatelets as clusters of interconnected beads. iPlatelets at rest remain disk-like shape with a 2μm diameter and do not actively interact with other clot elements. When an iPlatelet becomes active, it extends up to 12 filopodia that connect the iPlatelet with random fibrin filaments located within 6μm from the platelet center. The retraction of filopodia is modeled by gradually reducing the total bond length to 1μm using a series of small increments. After each step the system is equilibrated. Filopodia properties were chosen such that the contractile force exerted by a single filopod is limited to 10nN. iPlatelets are set to have an active time of 20 minutes.

We placed iPlatelets at rest into uncontracted iFibrin mesh to create the initial iClot. iPlatelet locations were obtained from confocal image analysis. In this case, the single platelet concentration was 200 M/mL. We also generated iClots with different platelet concentrations by randomly distributing required number of iPlatelets in iFibrin mesh. We investigated the asynchronous platelet contraction activities involved in clot contraction by controlling when individual iPlatelets start contraction.

iClots with synchronous iPlatelet contraction assumes all iPlatelets within iClot start contraction at the initial time t = 0 and each iPlatelet extends all filopodia once contraction begins, mimicking the condition where all platelets inside the clot reacts to thrombin immediately. iClot volume reduction ceases when all filopodia are fully retracted.

iClots with asynchronous iPlatelet contraction incorporated asynchronous contraction onset within iPlatelet population and asynchronous filopodia retraction by individual iPlatelets. When an iPlatelet starts contracting, it extends filopodia in three waves that are evenly spaced in time such that all filopodia are extended and fully retracted within 20 minutes. We split the total N_p of iPlatelets within an iClot into two unequal groups: the first group with N₁ iPlatelets that start contraction at t = 0, and the second group with N₂ iPlatelets that are further divided into 9 sub-groups that start contraction at nine equally spaced time intervals, such that all iPlatelets complete contraction at t = 90 minutes. We vary N₁ from 0.1N_p to N_p, where N₁ = 0.1N_p represents the scenario where the onset of all iPlatelets is evenly distributed over the clot contraction time, and N₁ = N_p represents the scenario where all iPlatelets start contraction at time t = 0.

Wall constrained iClot contraction

We examined contraction of iClot attached to two parallel riding walls. The force required to keep each wall stationary is obtained once the clot contraction is completed. iClot stress is calculated as iClot force divided by the initial iClot cross-sectional area. To examine forces of individual iPlatelets within a contracting iClot, we summed the magnitudes of all filopodia forces in the direction of contraction for each iPlatelet.

Since the force generated by iClot and applied to the wall may be influenced by the fibrin mesh structure, we modeled different iFibrin mesh compositions and changed iPlatelet locations. Additional iFibrin meshes were generated using a random set of fibrin-fibrin branching points that were spaced in a manner such that the distribution of spaces between these points matched those of the initial digitized iFibrin mesh.

Analytical 1D and 2D contraction

We developed a model to analyze the contraction of a 1D clot with two platelets contracting a 1D fibrin mesh. The contraction C_tot of the 1D fibrin mesh is the difference between its initial and final length. Each platelet extends one filopod of length l and then fully retracts it. The distance δ is the overlap between the filopodia from the two platelets. The synchronous case is represented by two platelets contracting at same time, yielding maximum contraction C_tot = 2L – δ. When the two platelets are located closer than l, δ is larger than zero leading to reduced contraction. In the case of asynchronous contradiction, the two platelets contract one after another yielding the maximum contraction C_tot = 2L independently of the initial distance between the platelets.

We developed a model to analyze the contraction of a 2D clot with platelets contracting a 2D fibrin mesh. Fibrin mesh contraction is defined as the difference between the initial and final sizes. Platelets are placed randomly in the fibrin mesh and move with it. Platelet contraction results in the radial motion of the fibrin towards the platelet. The displacement magnitude Δd_i of fibrin mesh point i caused by platelet contraction is given by Δd_i = r_i when r_i ≤ r_filo, and Δd_i = r_filo · r_filo/r_i when r_i > r_filo. Here, r_i is the original distance between fibrin mesh point i and this platelet, and r_filo is the maximum filopodia length. For synchronous platelets, all platelets contract simultaneously, and the effects of different platelets are combined. For asynchronous platelets, fibrin mesh is moved by each consecutively contracting platelet until all platelets contract.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.