Color, Pattern, and the Retinal Cone Mosaic

Abstract

Textbook trichromacy accounts for human color vision in terms of spectral sampling by three classes of cone photoreceptors. This account neglects entangling of color and pattern information created by wavelength-dependent optical blur (chromatic aberrations) and interleaved spatial sampling of the retinal image by the three classes of cones. Recent experimental, computational, and neurophysiological work is now considering color and pattern vision at the elementary scale of daylight vison, that is at the scale of individual cones. The results provide insight about rich interactions between color and pattern vision as well as the role of the statistical structure of natural scenes in shaping visual processing.

Introduction

Trichromacy provides the foundation for understanding of human color vision, and the standard textbook treatment may be easily summarized. Light entering the eye is encoded by the excitations of three classes of cone photoreceptors, each with its characteristic spectral sensitivity (Figure 1A). The nature of this encoding places strong constraints on our color experience, since any information about spectra not encoded by the cone excitations will not be available to human experience. Indeed, two physically-different spectra can produce the same cone excitations, and these two lights must then necessarily appear the same to us – no subsequent processing can restore spectral distinctions that are not available at the first stage of light encoding [1]. This observation underlies our theoretical and practical understanding of color mixing, where mixtures of three primary lights may be used to elicit essentially the full gamut of color sensations. Indeed, this understanding is the basis of color recording and color reproduction technologies [e.g., the colors on televisions and computer displays are produced by mixtures of red, green and blue primaries, rather than be recreating the actual spectra we encounter in daily viewing; 2].

Figure 1. Trichromacy and the Interleaved Cone Mosaic.

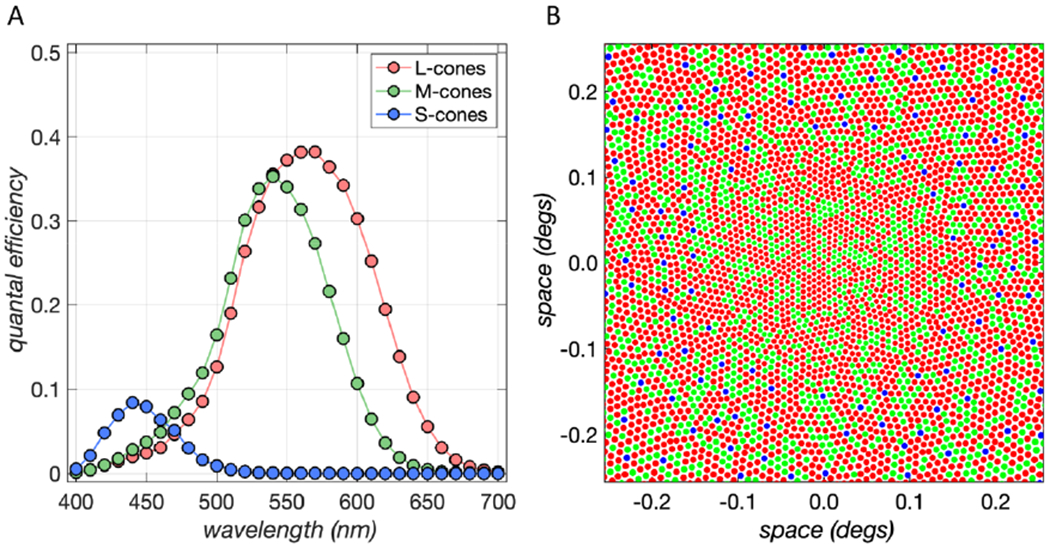
A) The human retina contains three classes of cone photoreceptors, referred to as the long-wavelength-sensitive (L), middle-wavelength-sensitive (M) and short-wavelength-sensitive (S) cones. Each class of cones has a distinct spectral sensitivity, so that the relative excitations of the three classes depends on the spectrum of the incident light. B) Schematic of human foveal cone mosaic. There are approximately 2 L cones (red) for every M cone (green), while S cones make up only a small fraction of the mosaic (about 5%). The arrangement of S cones depicted is semi-regular; the actual S-cone mosaic may be less regular than shown. There are no S cones in the central portion (here 0.3 deg) of the fovea. The algorithm used to generate this model mosaic is described in [37]. Figure courtesy of Nicolas Cottaris.

Although the textbook account is deep and correct, it also embodies an important simplification. In particular, it encourages the view that color vision may be understood without consideration of the spatial pattern of the images that reach the retina, that is that color vision and pattern vision are in some sense independent processes. Under this view, it would be appropriate to study color vision for spatially uniform patches and pattern vision for grayscale (luminance) images, with any interactions between the two relegated as effects of interest only to specialists. Although there is no denying that we have learned much about both color and pattern vision through separate consideration of the two, there is also no doubt that there can be large and striking interactions between color and pattern vision (Figure 2).

Figure 2. Interactions between space and color.

A) The panel shows an example of color assimilation. The two reddish bars have the same RGB values, but appear quite different. This difference is a consequence of where the reddish bars are inserted into the blue-yellow grating. B) Color assimilation depends on spatial pattern. The reddish bars again have the same RGB values as each other (and the same RGB values as the reddish bars in A), and the RGB values of the blue-yellow grating are also matched those in A. The effect of assimilation is reduced in B, as compared to A. See [48] for discussion of possible mechanisms underlying color assimilation. Comparison of the panels also reveals a difference in the color appearance of the blue and yellow bars.

This short review argues that there are fundamental reasons for interactions between color and pattern vision; that is, these interactions begin with a confounding of color and pattern information that occurs at the initial stage of visual encoding that unavoidably leads to tradeoffs between the acuity of color and pattern vision. Consideration of the implications of color-pattern encoding may yield important general insights about color vision and its evolution.

The Interleaved Cone Mosaic and Color-Pattern Information Loss

Figure 1B illustrates the arrangement of cones in a patch of retinal mosaic typical of the high-resolution human fovea. Several observations are noteworthy. First, although the mosaic as a whole is trichromatic, at each retinal location there is only one cone. That is, at its elementary spatial scale the retina is locally monochromatic rather than trichromatic: the trichromacy we experience for spatially-coarse stimuli must arise by neural comparisons that operate not only across cones of different classes but also across cones at different spatial locations.

Second, the L and M cones vastly outnumber the S cones; in a typical retina over 90% of cones will be L or M, with only a small fraction of S cones [3–6]. The small fraction of S cones is likely related to chromatic aberration in the eye’s optics, which lead to a much blurrier short wavelength retinal image relative to that at longer wavelengths [7]. Chromatic aberration is another form of color-pattern interaction in early vision, which we do not expand on in detail here. There are also typically more L cones than M cones (about 2:1 L to M), but this varies considerably across individuals [4].

Third, the arrangement of the L and M cones is quite irregular, close to random [4]. This leads to a retinal patchiness, with some local regions L dominated and others M dominated. This patchiness is not readily apparent in our everyday experience of color. This, as well as the variation across individuals in L:M cone ratio, suggests that neural processing must be tailored to the local arrangement of the cone mosaic to account for the local pattern of spatial sampling [8–10, see also 11].

It is worth emphasizing that although the interleaving of cones in the retina occurs at a fine spatial scale, the consequences of such interleaving can propagate to coarser scales. One way to appreciate this is to consider artifacts that occur in digital imaging, as digital cameras also generally employ a sensor design that interleaves elements with three distinct (R, G and B) spectral sensitivities. Figure 3A shows salient chromatic fringing artifacts that can occur in images acquired with such sensors. The reason is that interleaved sampling loses the distinction between fine grayscale patterns (e.g. the herringbone pattern of the jacket) and coarse color patterns (e.g. the artifactual red-green pattern seen over portions of the jacket). The information loss can be understood by considering a simple example with just two sensor elements, one R and one G (Figure 3B,C top). A fine dark to light pattern across these two elements will produce a low response in the R sensor and a high response in the G element. The same low-to-high response pair will also be produced by a spatially-uniform green pattern, which will excite the G element more than its neighboring R 3B, bottom). Similarly, a light-to-dark grayscale pattern produces the same pair of sensor responses as a spatially-uniform red pattern (3C, bottom). Thus, fine grayscale patterns can be indistinguishable from coarse color patterns in the encoding of images by interleaved mosaics. In the image shown, this effect plays out as the jacket is imaged by the camera’s interleaved mosaic and the image is rendered by the camera’s software. Although a different camera image-rendering algorithm might have avoided the artifact shown, such an algorithm would then have been subject to rendering actual coarse color patterns as fine grayscale patterns, an equally salient error.

Figure 3. Color-pattern artifacts.

A) A digital color image taken with a camera that employed an interleaved RGB sensor design. Note the green-red color artifacts on the jacket. The subject’s face has been intentionally distorted to protect identity; that distortion is not what is being illustrated here. [Panel A reproduced with permission from 9.] B) A high-spatial-frequency grayscale pattern can produce the same low/high alternation of sensor responses as a low-spatial-frequency green pattern, for a simple two-pixel RG interleaved sensor. C) When the phase of the high-spatial-frequency pattern is shifted relative to the sensor, the grayscale pattern produces the same high/low alternation of sensor responses as a low-spatial-frequency red pattern. The type of effects illustrated in panels B and C lead to the red-green artifacts shown in A. [Panels B and C reproduced with permission from 38.]

Implications for Perception

When we look at the world, we do not typically experience salient artifacts of the sort illustrated in Figure 3, even though our retinas consist of an interleaved cone mosaic. That said, there is a perceptual phenomenon known as Brewster’s colors [12], in which subtle colored splotches are sometimes seen when we look at fine black and white stripes. Experiments that explore Brewster’s colors suggest that they indeed have their origin in interleaved sampling by the cone mosaic, and that their subtlety is a consequence of sophisticated neural processing that minimizes our exposure to the information lost to us through interleaved sampling [13]. The exact nature of this processing remains mysterious, but recent theoretical and experimental approaches are now advancing our understanding and promise to inform us about the degree to which some color-pattern interactions may be ascribed to such processing.

Bayesian approach to reconstruction from samples.

At a broad level, an interleaved cone mosaic collects less information about the retinal image than a hypothetical “ideal” mosaic where all cone classes sample the retinal image at each location. The consequences of this depend strongly on the nature of the images that the visual system will view. If it were known, for example, that all environmental images were spatially uniform and varied only in color then the consequences of interleaved sampling would be negligible. Similarly, if it were known that there was no variation in image color so that all environmental images were grayscale, again there would be little consequence of interleaved sampling (and indeed, little need for more than one type of cone). In the actual case, where images vary in both color and pattern, the consequences of interleaved sampling depend on the spatio-chromatic regularities in natural images. These may be examined by using Bayesian methods [14], together with explicit models of natural image statistics and retinal image formation, to reconstruct the external image from the cone excitations [15]. Distortions in the reconstructions then provide hypotheses about the sorts of color-pattern interactions we might expect to find in human vision.

An analysis along these lines [9] incorporated the known strong correlations between natural image values at nearby locations [16] and between the excitations of cones of different classes [17]. The results indicated, among other observations, that the human visual system’s well-known [18, 19] lack of sensitivity to high-spatial frequency chromatic patterns (both blue-yellow and red-green) may have its origins in the combined effect of optical chromatic aberrations and interleaved cone sampling.

Experiments with small spots.

Studying directly consequences of interleaved cone sampling has historically been difficult. The primary reason is that under normal circumstances, blurring of the retinal image as well as fixational eye movements prevent precise experimental control of the excitations of individual cones. It has also historically been difficult to determine the spectral class of any individual cone in the living retina.

Early insights were gained by study of the S-cone submosaic, whose distinct spectral sensitivity and spatial sparseness within the mosaic (Figure 1) make it more amenable to cone-specific selective stimulation [20, 21]. Another fruitful approach was the use of interferometric stimuli, which allowed presentation of high-contrast high-spatial frequency sinusoidal gratings on the retina. Resulting distortions of perceived spatial patterns revealed consequences of spatial sampling by the mosaic as a whole [22], but interactions between color and pattern remained difficult to assess [but see 19, 23].

Recently, however, techniques have been developed that promise much richer experimental understanding. Adaptive compensation of aberrations in the eye [24, 25], combined in some cases with real-time tracking of fixational eye movements [26, 27], now allow targeted stimulation of individual cones and groups of cones for psychophysical study [28, 29]. Wavelength-selective imaging using adaptive optics also enables determining the spectral class of individual cones in an individual’s eye [3–6].

Experiments using these techniques are now providing a wealth of fundamental information about color and spatial vision at the elementary spatial scale of the visual system. We now know that signals from individual cones can result in a reliable perceptual signal [28, 30], at least in the central visual field; that signals from multiple cones can be combined by neural processes to improve detection performance of small spots [31, see also 32]; and that there is variation in the color percept associated with stimulating different single cones of the same class [30]. For example, stimulation of one L cone in an observer’s retina results in reliable reports of perceived red, while stimulation of a different L cone leads to reliable reports of perceived white [33, see also 34].

This latter effect, which at first seems counter-intuitive, may be understood as a rather direct characterization of color-pattern interactions at the finest spatial scale available to the visual system, that of the cone mosaic. The general form of the interaction is consistent with the Bayesian image reconstruction analyses described above [9]. To provide intuition, Figure 4 shows Bayesian reconstructions obtained from two model cone mosaics where incremental stimulation was provided to a single L cone. The figure shows an expanded view of two model mosaics, each with an L cone near its center. For each mosaic, we simulated the cone excitations that would have occurred with incremental stimulation of the central L cone using adaptive optics, against an otherwise spatially uniform gray background. The cone excitations were then processed using a Bayesian image reconstruction algorithm that learned its prior from a dataset of natural images. Note that although the central L cone is excited in the same way in each case, the resulting reconstructions differ, particularly in their color appearance. The intuition for this is that different information about the stimulus is provided by the cones surrounding the single stimulated cone, and this information differs depending on the type of the cones in the local neighborhood of the stimulated cone. In one case, there are only L cones in the immediate neighborhood, and little direct information is available about stimulus color. In the other, the mix of L and M cones provides different information, leading the algorithm to a redder reconstruction, based on the low response of the nearby M cones. To implement the Bayesian reconstructions shown here, the prior was based on an independent-components analysis [35] of the CIFAR image dataset (https://www.cs.toronto.edu/~kriz/cifar.html), and the distribution of the coefficients for each independent component was assumed to be exponential. The computation was implemented using cross-validated lasso regression [36] and by taking advantage of the ISETBio [37] software to determine the relation between training image data and the mosaic’s cone excitations; it will be described in detail in a future publication. See also Figures 7 and 8 in [9] and associated discussion. It is not yet clear the extent to which a Bayesian computational model is consistent in detail with current experimental results [see also 38]; this remains an exciting direction for future experimental and modeling work.

Figure 4. Bayesian small spot reconstructions.

Expanded view of two cone mosaics with an L cone near the center (left column). Corresponding Bayesian image reconstructions based on the cone excitations of each mosaic. The reconstructions for incremental stimulation of a single L cone (circled in black in each case) are quite different, as they depend on the responses of the whole mosaic and the information carried by the two mosaics differ. See main text for additional description. Figure courtesy Lingqi Zhang.

Mechanisms.

In work that parallels targeted single-cone psychophysics, it is now possible to measure individual cone inputs to single neurons in the visual pathways [39–41, see also 42]. This work seems likely to enable strong links between psychophysical results obtained with single cone stimulation and the neural mechanisms that mediate those results [see 43].

Evolution.

The selective advantages conveyed by color vision have received considerable treatment in the literature, particularly in the context of how color vision evolved and why it differs across species [44–46]. Less considered in this literature are the tradeoffs between color and pattern vision mandated when cones of different classes sample the retinal image in an interleaved fashion. As we understand more about how visual systems can and do optimize post-receptoral processing to handle the information loss imposed by interleaved sampling, and how this processing depends on the statistical structure of any given species’ visual ecology (both in terms of the statistical structure of scenes and in terms of what features of those scenes are behaviorally relevant), there should be an opportunity to bring consideration of interleaved sampling into the discussion. Such consideration may clarify when increased dimensionality of the color sensory apparatus (i.e. number of distinct receptor classes) is beneficial and when it is not [see 38, 47].

Highlights.

1. Color and pattern information are entangled by the initial stages of visual encoding.

2. Experiments at vision’s elementary spatial scale can now probe color-pattern interactions.

3. Computational models predict limits of vision imposed by optics and the interleaved cone mosaic.