Statistical methods for mediation analysis in the era of high-throughput genomics: Current successes and future challenges

Graphical abstract

Abstract

Mediation analysis investigates the intermediate mechanism through which an exposure exerts its influence on the outcome of interest. Mediation analysis is becoming increasingly popular in high-throughput genomics studies where a common goal is to identify molecular-level traits, such as gene expression or methylation, which actively mediate the genetic or environmental effects on the outcome. Mediation analysis in genomics studies is particularly challenging, however, thanks to the large number of potential mediators measured in these studies as well as the composite null nature of the mediation effect hypothesis. Indeed, while the standard univariate and multivariate mediation methods have been well-established for analyzing one or multiple mediators, they are not well-suited for genomics studies with a large number of mediators and often yield conservative p-values and limited power. Consequently, over the past few years many new high-dimensional mediation methods have been developed for analyzing the large number of potential mediators collected in high-throughput genomics studies. In this work, we present a thorough review of these important recent methodological advances in high-dimensional mediation analysis. Specifically, we describe in detail more than ten high-dimensional mediation methods, focusing on their motivations, basic modeling ideas, specific modeling assumptions, practical successes, methodological limitations, as well as future directions. We hope our review will serve as a useful guidance for statisticians and computational biologists who develop methods of high-dimensional mediation analysis as well as for analysts who apply mediation methods to high-throughput genomics studies.

1. Introduction

Advances of various high-throughput biological technologies have revolutionized the field of genomics. In particular, both array-based and sequencing-based techniques have enabled genomics studies to be performed at the genome-wide scale [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], providing unprecedented insights into many fundamental biological questions that are previously impossible to address [7], [12], [13], [14], [15], [16], [17], [18]. These genomics studies produce various molecular-level traits by measuring gene expression profiles and characterizing different covalent modifications of DNA and histone proteins. The molecular-level traits, including both expression and methylation, have been revealed to mediate the effects of DNA, environments and/or behaviors on many diseases and traits [5], [19], [20], [21], [22], [23], [24], [25], [26], [27], [28], [29], [30], [31], and hold the key to understanding the genetic and environmental foundations of disease susceptibility and phenotypic variation.

As one example, genome-wide association studies (GWASs) have recently identified hundreds of thousands of genetic loci associated with complex diseases and traits, but most of the discovered genetic variants are located outside protein-coding regions and are of unknown functions [7], [13], [14], [32]. It has been hypothesized that genetic associations with diseases in many cases might be mediated at the epigenomic level through molecular-level traits [33], [34]. Evidence that supports the mediating role of molecular-level traits includes differential gene expression analyses which have detected plentiful associations between expressions and disease status [35], [36], [37], and expression quantitative trait loci (eQTL) mapping studies, as well as allelic specific expression analyses which have detected associations between expressions of specific transcripts with individual genetic alleles [38], [39]. Evidence also includes other genomics studies which have identified differentially methylated GpG sites or regions with respect to disease statuses [35], [40] and have linked differences in methylation to specific genetic alleles [41]. Therefore, mounting evidence suggests that the molecular-level traits such as expression and methylation can mediate the genetic effects on disease susceptibility.

As another example, many epidemiological studies have also been performed to elaborate the environmental and socioeconomic basis of disease susceptibility. It has been well established that socioeconomic indicators (such as education, income, wealth, and occupation) and overall socioeconomic status (SES)/position (SEP) are associated with cardiovascular disease (CVD) risk [42], [43], [44], [45], [46], [47]; such that CVD incidence, prevalence and mortality are all higher in persons with lower socioeconomic status. The effects of these socioeconomic factors are also confirmed to be mediated, as least in part, through molecular-level traits including methylation, as socioeconomic status/position are associated with changes in DNA methylations [26], [48], [49], [50], [51], [52], which in turn are also related to CVD risk [53], [54]. Therefore, integrating various molecular-level traits from omics studies with data from either GWASs or epidemiological studies has become an important topic in the genomics era. Such integrative analysis can improve our understanding of the molecular basis of complex diseases and traits. Indeed, treating molecular-level traits as mediators and evaluating how they mediate the genetic or socioeconomic effects on disease susceptibility or phenotypic variation has become an important first step towards better characterization of disease etiology and phenotypic distinction [55], [56], [57], [58], [59], [60], [61], [62], [63].

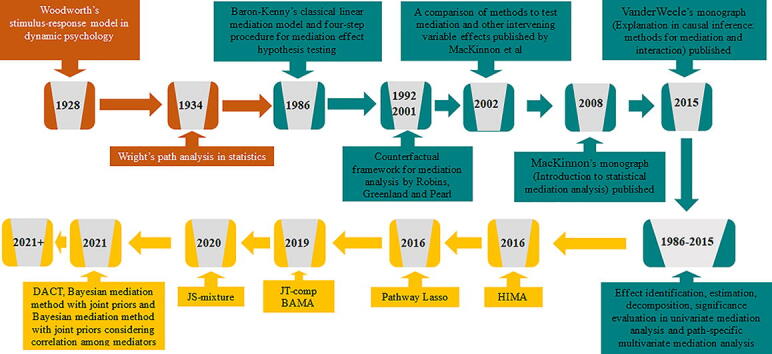
Mediation analysis is a contemporary statistical method that can be employed to elucidate the mediating role of various molecular-level traits in genomics. Conceptually, mediation analysis aims to investigate how an intermediate variable, commonly referred to as a mediator, explains the mechanism or pathway through which an exposure affects an outcome [64], [65]. The rudimentary idea of mediation analysis can be at least dated back to Woodworth’s stimulus–response model in dynamic psychology in 1928 [66] and Wright’s path analysis in statistics in 1934 [67]. Since Baron and Kenny (1986) [68] established the classical statistical formula for mediation analysis, there is a tremendous growth in both methodological development and applications of mediation methods over the past two decades (Fig. 1A), across a wide variety of research areas (Fig. 1B). Mediation analysis is now being routinely carried out in the fields of psychology [69], [70], [71], sociology [65], [72], [73], epidemiology [74], [75], [76], [77], environmental science [19], genetics [78], [79], [80], [81], [82], [83], [84], and appears in a substantial proportion, sometimes more than a third, of research articles published in many disciplines [69], [85]. Various mediation analyses performed thus far have helped establish the foundation of many important psychological and sociological theories. Overall, mediation analysis has become an effective statistical tool for understanding the causal and mediating mechanism underlying the exposure effect on the outcome across a wide range of applications [64], [65].

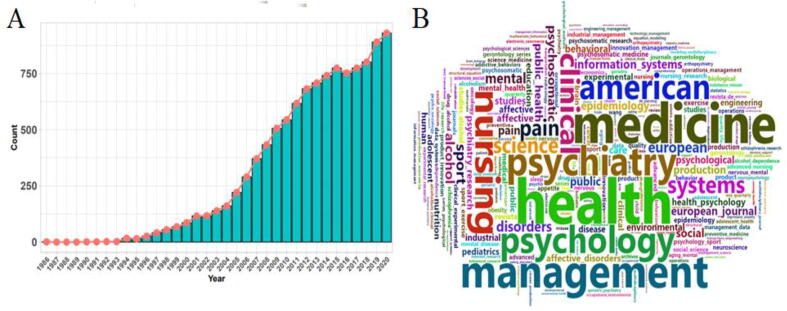
Fig. 1.

(A) Citations of the Baron-Kenny’s 1986 classical mediation analysis article in terms of PubMed retrieval, which reflects the popularity of mediation analysis in biomedical research areas. (B) Word cloud shows the key words of the names of journals that published articles citing the Baron-Kenny’s work, reflecing the diversity of biomedical research displines which employ various mediation methods.

Detailed statistical methodology for mediation analysis is generally constructed under the counterfactual framework, which is also known as the potential outcome framework or Rubin’s model [64], [65], [86], [87], [88], [89], [90], [91], [92], developed in the field of causal statistical inference. The counterfactual framework facilitates methodological establishment for mediation analysis to accommodate different outcome types that include continuous [64], [65], [69], [70], binary [76], [88], [93] and survival outcomes with censoring [74], [80], [92], [94], [95], [96], as well as to account for possible interactions between exposure and mediator [64], [88]. Under the counterfactual framework, mediation analysis makes further modeling assumptions to effectively represent the relationship among the exposure, mediator, and outcome through a directed acyclic graph that links the exposure to the outcome through the mediator (see below) [97], [98]. Mediation analysis then proceeds by decomposing the total effect of the exposure on the outcome into two parts: a direct effect, which represents the exposure on outcome effect not mediated through the mediator; and an indirect effect, which represents the exposure on outcome effect mediated through the mediator. Decomposition of the total effect allows for a mechanistic characterization of the exposure effect on the outcome, facilitating the investigation of causal mediating role of the mediator.

Methodological development for mediation analysis in the past three decades has been primarily focused on univariate mediation analysis where only one mediator is present or multivariate mediation analysis where a few mediators are present [64], [65], [69], [70]. Methods for univariate and multivariate mediation analyses have been thoroughly reviewed by multiple excellent review articles [64], [75], [85], [87], [69], [70], [71], [72], [99], [100], [101], [102], [103], [104], [105], [106], which describe at length the identification, estimation, inference, decomposition and explanation of causal effects in various application fields [65], [68], [70], [85], [86], [107], [108]. Unfortunately, it has become increasingly challenging and often infeasible to directly apply them towards the large and complex data collected in genomics due to several reasons listed as follows [78], [79], [81], [109]. First, the number of potential mediators in the form of molecular-level traits collected in high-throughput genomics studies is in general large, often in the order of thousands to hundreds of thousands, exceeding the collected sample size and thus the capacity accommodated by the univariate and multivariate mediation analyses. For example, the Illumina Infinium HumanMethylation450 BeadChip can array approximately half a million GpG sites but the sample size in methylation studies is typically restricted to be at most a few hundreds or thousands due to heavy experimental costs [78], [79], [81], [109]. Second, genome-wide genomics studies are generally interested in identifying among a large number of potential mediators the ones which exhibit non-zero mediation effects. While univariate mediation methods can perform hypothesis test to examine one potential mediator at a time [70], these methods are often overly conservative and do not fare well for large-scale multiple testing tasks [78], [79], [81], [109]. In particular, the univariate mediation methods rely on asymptotics for hypothesis testing and do not directly accommodate for the composite nature of the null hypothesis as will be detailed below. Third, the potential mediators in genomics are often correlated with each other, sometimes quite strongly. For example, methylation measurements on proximal CpG sites are generally similar to each other and genes in the same pathway also show coordinated co-expression pattern [110]. However, existing univariate and multivariate mediation methods do not explicitly model correlation among potential mediators. Altogether, the above new challenges brought by high-throughput genomics have motivated the intense recent development of high-dimensional mediation methods that aim to accommodate a large number of potentially correlated mediators [78], [79], [81], [82], [96], [109], [111], [112], [113], [114], [115].

Here, we present a thorough literature review on statistical methods that have been developed in recent years for performing high-dimensional mediation analysis in high-throughput genomics studies. A timeline of these methods is shown in Fig. 2. In the review, we begin with the classical univariate and multivariate mediation methods to setup notations and basic statistical formula for mediation analysis. These classical methods include the univariate Baron-Kenny linear mediation model and its extensions to multiple mediators. There, we will introduce the basic concepts, modeling assumptions, effect estimation and decomposition, inference, and significance test for mediation analysis. We will then review recently developed high-dimensional mediation methods for genomics studies that can model thousands of correlated mediations jointly or perform hypothesis tests that can account for the composite nature of the null hypothesis. We discuss their detailed modeling assumptions, important methodological benefits, as well as potential practical drawbacks. We finally conclude our review with future directions for high-dimensional mediation analysis.

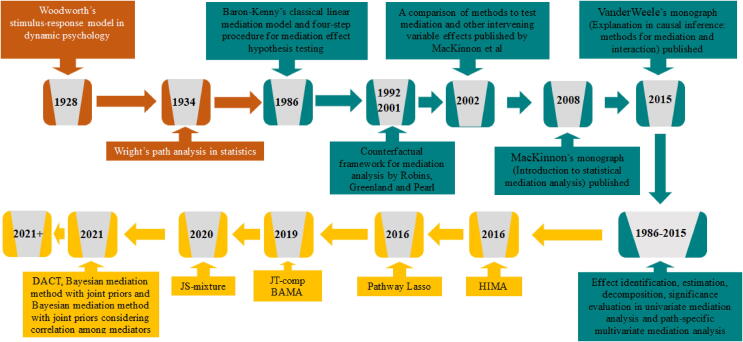
Fig. 2.

Timeline of several key mediation methods developed over the years. Orange color represents initial methods with rudimentary ideas for mediation analysis. Green color represents classical mediation methods developed for univariate and multivariate mediation analysis. Yellow color represents high-dimensional mediation methods targeted for a large number of potential mediators. HIMA: high-dimensional mediation analysis, BAMA: Bayesian mediation method, DACT: divide-aggregate composite-null test. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2. Modeling framework for univariate mediation analysis

We first describe the classical univariate mediation analysis framework [64], [65], [68], [86], [101], [116], also known as Baron-Kenny mediation model [68]. This classical mediation model describes the relationship among a triplet that includes an exposure variable (X), a continuous mediator variable (M), and a continuous outcome variable (Y) (Fig. 3A and 3B)

$$\left\{\begin{array}{c}exposure-outcomemodelY=X\times c+U_X+e_X\\ exposure-mediatormodelM=X\times a+U_M+e_M\\ mediator-outcomemodelY=X\times c^{\prime }+M\times b+U_{\mathit{XM}}+e_{\mathit{XM}}\end{array}\right)$$

Fig. 3.

Directed acyclic graph depicting the relationship among an exposure (X), a mediator (M) or multiple mediators (M = (M₁, …, M_m)), and an outcome (Y) in the classical mediation analysis. (A) Relationship between the exposure and the outcome, without considering the mediator. Here, c is the total exposure effect on outcome. (B) Relationship between the exposure, the mediator, and the outcome. Here, c′ is the direct effect of exposure on outcome, a is the exposure effect on the mediator, and b is the mediator effect on the outcome. The product of a and b (i.e., ab) represents the indirect/mediation effect. (C) Relationship between the exposure and the outcome with multiple mediators M = (M₁, …, M_m). Here, m is the total number of potential mediators; a = (a₁, …, a_m) is a vector of exposure effects on the mediators; and b = (b₁, …, b_m) is a vector of mediator effects on the outcome. The product of a and b (i.e., a^Tb) represents the indirect/mediation effects.

where c is the total exposure effect on the outcome; a is the exposure effect on the mediator; c′ is the direct exposure effect on the outcome after controlling for the mediator; b is the mediator effect on the outcome; U_X, U_M and U_XM are confounding effects from known covariates; and e_X, e_M and e_XM are residual errors that are mutually independent of each other. For simplicity of presentation, we assume that the mediator and the outcome are standardized to have mean zero, thus ignoring the intercept terms in the above models.

These effects (i.e., a, b, c and c′) in model can be interpreted in a causal way when the mediation model is correctly specified and certain identifiability assumptions are satisfied [75], [85], [86]. The required identifiability assumptions are known as the sequential ignorability assumptions and are sometimes also referred to as the no unmeasured confounding assumptions. In particular, besides the implicit assumption of temporal ordering between the exposure, mediator and outcome, we assume that all confounders in the three equations are correctly controlled for and that no confounders affecting both the mediator and the outcome are affected by the exposure [72], [78], [101], [103], [104]. While some of these assumptions can be enforced in observational studies, some of them cannot [72], [117], [118], [119]. For example, it is sometimes feasible to control for unmeasured confounders in the exposure-mediator model and in the exposure-outcome model through randomizing the exposure. However, it is challenging to randomize the mediator to control for confounders in the mediator-outcome model. Nevertheless, mediation analysis methods can still be applied for screening purposes, identifying potential biomarkers and genetic regions for further exploration, even when the above causality conditions are not completely satisfied.

3. Extensions of the univariate mediation analysis

The univariate mediation model in has been extended to accommodate a binary mediator and/or a binary outcome [76], [88], [93]. In this case, a logistic regression model is applied in place of the corresponding linear regression to model the exposure-mediator and/or the mediator-outcome relationship. The univariate mediation model has also been extended to accommodate interactions between the exposure and the mediator by adding an interaction term to the mediator-outcome model [75], [88]. In addition, the univariate mediation model has been generalized to accommodate multiple mediators [77], [111], [120], [121], [122]. With m continuous mediators M = (M₁, …, M_m) (Fig. 3C), the relationship among the exposure, mediators and outcome can be characterized by the following equations

$$\left\{\begin{array}{c}exposure-outcomemodelY=X\times c+U_X+e_X\\ exposure-mediatormodels{M}_k=X\times a_k+U_M+e_M,k=1,...,m\\ mediator-outcomemodelY=X\times c^{\prime }+Mb+U_{\mathit{XM}}+e_{\mathit{XM}}\end{array}\right)$$

where a = (a₁, …, a_m) is the m-vector of the exposure on mediator effects; and b = (b₁, …, b_m) is the m-vector of the mediator on outcome effects. The multivariate mediation model defined in equation can easily accommodate binary mediators and/or binary outcome through logistic regressions. The model effectively treats all mediators en bloc, where the indirect effect is defined as the exposure on outcome effect mediated through at least one of the mediators while the direct effect is defined as the exposure on outcome effect acting around all mediators [64], [65].

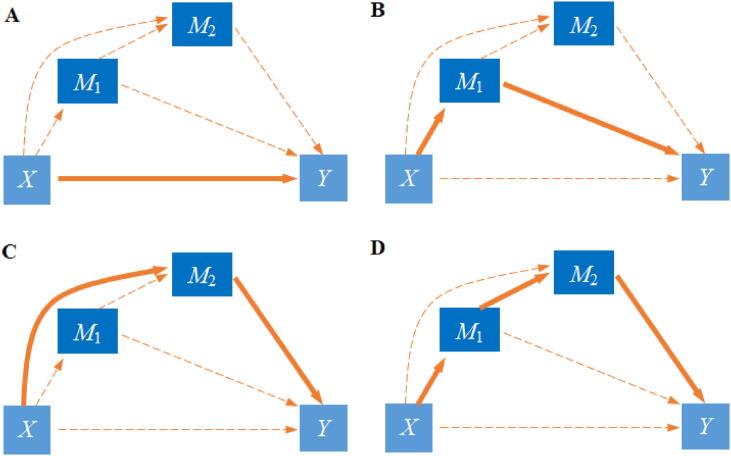
The model is not the only multivariate mediation extension. Indeed, other than treating all mediators en bloc, one can also attempt to incorporate the ordering of mediators into consideration and decompose the total exposure on outcome effect as the sum of separate effects along each possible pathway that consists of a set of ordered mediators [77], [121]. An example of the relationship among the exposure, outcome and two ordered mediators is displayed in Fig. 4. If the detailed ordering of the mediators and their relationship with respect to the exposure and outcome is known, one can perform proper decomposition of mediation effect and potentially interpret the causal mediation effect under the counterfactual framework. Certainly, the ordering of potential mediators is generally unknown in most genomics studies, making the causal interpretation of the mediation estimation challenging. In addition, exploring the exponential number of possible orderings among mediators can quickly become computationally infeasible in high-dimensional settings.

Fig. 4.

Possible relationships among the exposure (X), outcome (Y), and two ordered mediators (M₁ and M₂). (A) Only the direct effect from the exposure to the outcome is present; neither M₁ nor M₂ has a mediating role. (B) The indirect effect of the exposure is mediated by M₁ only. (C) The indirect effect of the exposure is mediated by M₂ only. (D) The indirect effect of the exposure is mediated by M₁, followed by M₂. The case where the indirect effect of the exposure is mediated by M₂ followed by M₁ is not displayed. In all panels, the solid line stands for the presence of a relationship while the dot line stands for the absence of a relationship. Here, we ignore the residual terms that are shown in Fig. 3.

Fig. 1. (A) Citations of the Baron-Kenny’s 1986 classical mediation analysis article in terms of PubMed retrieval, which reflects the popularity of mediation analysis in biomedical research areas. (B) Word cloud shows the key words of the names of journals that published articles citing the Baron-Kenny’s work, reflecing the diversity of biomedical research displines which employ various mediation methods.

Fig. 2. Timeline of several key mediation methods developed over the years. Orange color represents initial methods with rudimentary ideas for mediation analysis. Green color represents classical mediation methods developed for univariate and multivariate mediation analysis. Yellow color represents high-dimensional mediation methods targeted for a large number of potential mediators. HIMA: high-dimensional mediation analysis, BAMA: Bayesian mediation method, DACT: divide-aggregate composite-null test.

Fig. 3. Directed acyclic graph depicting the relationship among an exposure (X), a mediator (M) or multiple mediators (M = (M₁, …, M_m)), and an outcome (Y) in the classical mediation analysis. (A) Relationship between the exposure and the outcome, without considering the mediator. Here, c is the total exposure effect on outcome. (B) Relationship between the exposure, the mediator, and the outcome. Here, c′ is the direct effect of exposure on outcome, a is the exposure effect on the mediator, and b is the mediator effect on the outcome. The product of a and b (i.e., ab) represents the indirect/mediation effect. (C) Relationship between the exposure and the outcome with multiple mediators M = (M₁, …, M_m). Here, m is the total number of potential mediators; a = (a₁, …, a_m) is a vector of exposure effects on the mediators; and b = (b₁, …, b_m) is a vector of mediator effects on the outcome. The product of a and b (i.e., a^Tb) represents the indirect/mediation effects.

4. Partition of total effect: Natural direct effect and natural indirect effect

As brought up earlier, the total effect (TE) of the exposure on the outcome can be partitioned into two parts: the natural direct effect (NDE) and the natural indirect effect (NIE); the latter is also known as the mediation effect. The partition of total effect is formally derived under the counterfactual framework [64], [65], [86], [87], [88], [89], [90], [91], [92]. Conceptually, NDE quantifies how much the outcome will change on average when the exposure changes from x₀ to x₁ but the mediator is fixed at the level it would be in the absence of the exposure. NIE measures how much the outcome will change on average when the exposure is controlled at the level of x₁, but the mediator changes from the level it would be at the exposure level of x₀ to the level it would be at the exposure level of x₁. TE quantifies how much the outcome will change overall for a change of the exposure varying from x₀ to x₁. In the univariate mediation model with the absence of the interaction effect, NDE equals to c′ while NIE equals ab if assuming x₁ = 1 and x₀ = 0, which are exactly the same direct and indirect effects obtained through the classical Baron-Kenny mediation analysis [68].

One advantage of partitioning the total effect within the counterfactual framework is that the equation of TE = NDE + NIE holds regardless whether the relationship among exposure, mediator and outcome is linear or non-linear, and regardless whether there is a presence or absence of exposure-mediator interactions. The definition of NDE and NIE in non-linear mediation models for a binary mediator/outcome is also well studied in the literature [72], [75], [76], [88], [100], [103]. There, the mediation effect is no longer in a simple product form when the outcome is binary as the exposure-outcome model and the mediator-outcome model are both expressed as logistic regressions [93], [123], [124], [125]. However, an approximation exists. That is, in the mediation analysis with a binary outcome, in the absence of the interaction effect, one can adopt the approximate log-scale formula to express the log transformed NIE as log(NIE)≈ab, which is an effective approximation when the binary outcome is rare in the population [75], [76], [81].

During the partitioning of the total effect, one can also calculate two ratio quantities: the ratio of the mediation effect to the total effect, P_M = θ/c = ab/(ab + c′), which quantifies the proportion of the exposure effect on the outcome mediated by the mediator; and the ratio of the mediation effect to the direct effect, P_D = θ/c′=ab/c′, which quantifies the relative strength of the direct and indirect effects [101], [126]. These ratio quantities are defined on the latent variable scale when the outcome is binary [127], [128], [129], [130]. A potential drawback of the two quantities is that they can only be estimated accurately when the sample size is large (e.g., >5000 as demonstrated by simulations in [126]) and are only meaningful when ab and c (or c′) have the same sign. When ab and c (or c′) have the opposite signs, the two ratio quantities may exceed 100% or become negative, making interpretation challenging [126]. Therefore, P_M and P_D are only recommended to be reported in practical mediation analysis when the calculated values are reasonable [71], [85], [131].

5. Methods for testing mediation effect in univariate mediation analysis

5.1. Testing for mediation effect and the composite nature of the null hypothesis

The significance test of the mediation effect, commonly referred to as the mediation test, is of great scientific interest in many application areas. Baron and Kenny (1986) [68] initially advocated on carrying out the mediation test in a four-step procedure, where the next test step is proceeded only when the test in the previous step is significant. The four steps include: (i) test whether there is a presence of a non-zero total effect (H₀: c = 0) in the exposure-outcome model; (ii) test whether the exposure is associated with the mediator (H₀: a = 0) in the exposure-mediator model; (iii) test whether the mediator is associated with the outcome after controlling for the direct effect of the exposure (H₀: b = 0) in the mediator-outcome model; and (iv) test whether the mediator fully mediates the exposure on outcome effect (H₀: c′=0).

Because the four-step procedure requires a series of statistical tests that each has a different statistical power, its results from different steps are not always consistent with each other [69], [70]. For example, when the direct effect c′ is in the opposite sign of the indirect effect ab and both effects are comparable to each other in magnitude, it is possible that the total effect c is not significantly different from zero but the direct effect c′ is, resulting in suppression or inconsistent mediation [70], [71], [88], [132], [133]. To avoid results inconsistency, most studies have recommended on testing the mediation effect directly through the null hypothesis H₀: ab = 0, based on steps (ii) and (iii) [71], [88]. The last step of testing c′ can sometimes also be beneficial as it facilitates the further interpretation of the mediation test results: complete or perfect mediation occurs when c′=0 [68] while partial mediation occurs when c′≠0 [68], [70], [88].

Direct hypothesis test on the mediation effect based on H₀: ab = 0, however, turns out to be challenging [70], [78], [81], [109], [112]. In particular, such test is complicated by the composite nature of the null hypothesis, which corresponds to three sub-null scenarios

$$H_0=\left\{\begin{array}{c}{H}_{01}:a=0andb\ne 0\\ H_{10}:a\ne 0andb=0\\ H_{00}:a=0andb=0\end{array}\right)$$

where H₀₁ represents an absence of the exposure on mediator effect but a presence of the mediator on outcome effect; H₁₀ represents a presence of the exposure on mediator effect but an absence of the mediator on outcome effect; and H₀₀ represents an absence of both the exposure on mediator effect and the mediator on outcome effect. Ignoring the composite nature of the null hypothesis testing can lead to uncalibrated test statistics [70], [78], [81], [109], [112].

5.2. Sobel test

Many methods have been previously developed to evaluate the mediation effect based on H₀: ab = 0 [70], [81], [126]. Among them, the Sobel test and the joint significance test (JST) are two most common ones, though both yield conservative p-values (more details in Section 5.4). The Sobel test, also known as the product method, assesses the mediation effect ab directly as a product of the exposure on mediator effect and the mediator on outcome effect [68], [134]. The Sobel test depends on the following statistic

$$z=\frac{\widehat{a}\widehat{b}}{S_{\widehat{a}\widehat{b}}},S_{\widehat{a}\widehat{b}}=\sqrt{{\widehat{b}}^2{S}_{\widehat{a}}^2+{\widehat{a}}^2{S}_{\widehat{b}}^2}$$

where $\widehat{a}$ and $\widehat{b}$ are the estimates of a and b obtained in the exposure-mediator model and mediator-outcome model, respectively; $S_{\widehat{a}}$ and $S_{\widehat{b}}$ are the corresponding standard errors; $\widehat{a}\widehat{b}$ is the point estimate of mediation effect ab; $S_{\widehat{a}\widehat{b}}$ is the corresponding standard error obtained through the multivariate delta method [68], [123], [134]; and z is the resulting Sobel test statistic. The Sobel test assumes that the test statistics z follows a standard normal distribution and obtains a p-value from the z statistics accordingly. However, the standard normal distribution is invalid even under H₀₀ as the multivariate delta method to arrive at equation does not hold, implying that the Sobel test is not appropriate under all null scenarios listed in (more details in Section 5.4). Other alternative formulas for computing $S_{\widehat{a}\widehat{b}}$ also exist [126] and these include the second-order exact solution [68], [134], [135] as well as the Goodman estimator [136].

It assumes that the Sobel z-statistic in asymptotically follows a standard normal distribution and thus can be further converted to a P value [68], [134], [137]. Confidence intervals for the mediation effect estimate $\widehat{a}\widehat{b}$ can also be constructed under the same asymptotic normality assumption in the form of ($\widehat{a}\widehat{b}\text{-}1.96S_{\widehat{a}\widehat{b}}$, $\widehat{a}\widehat{b}+1.96S_{\widehat{a}\widehat{b}}$). Because of the composite nature of the null, however, the asymptotic normality of the Sobel z-statistic is not guaranteed even when both $\widehat{a}$ and $\widehat{b}$ respectively follow a normal distribution. Indeed, simulations have shown that the symmetric confidence intervals often generate asymmetric error rates and are generally conservative, especially when the sample size and mediation effect are small, resulting in uncalibrated type I error control and reduced power [70], [71], [123].

5.3. Joint significance test

JST, also known as the causal path method or the maximum P-value method, is another popular traditional mediation test [138]. JST proceeds by performing two separate tests: one for a in the exposure-mediator model and the other for b in the mediator-outcome model. Through the two tests, JST obtains two z-statistics ($z_a=\widehat{a}/S_{\widehat{a}}$ and $z_b=\widehat{b}/S_{\widehat{b}}$) and converts them into two P values (P_a and P_b) based on an asymptotic standard normal null distribution. Afterwards, JST obtains the maximum value among the two P values, P_max = max(P_a, P_b), to serve as the mediation effect test statistic [70]; then it deems the mediation effect to be significant at a level α if and only if P_max is significant at the level α (i.e., P_max < α) [70], [139], [140]. JST is essentially an intersection–union test (IUT) and a level-α test with type I error guaranteed to be at most α. Due to the composite nature of the null, however, type I error generated from JST is also conservative and equals α only under certain regularity conditions [141], [142], [143].

5.4. Conservativeness of the Sobel test and the joint significance test

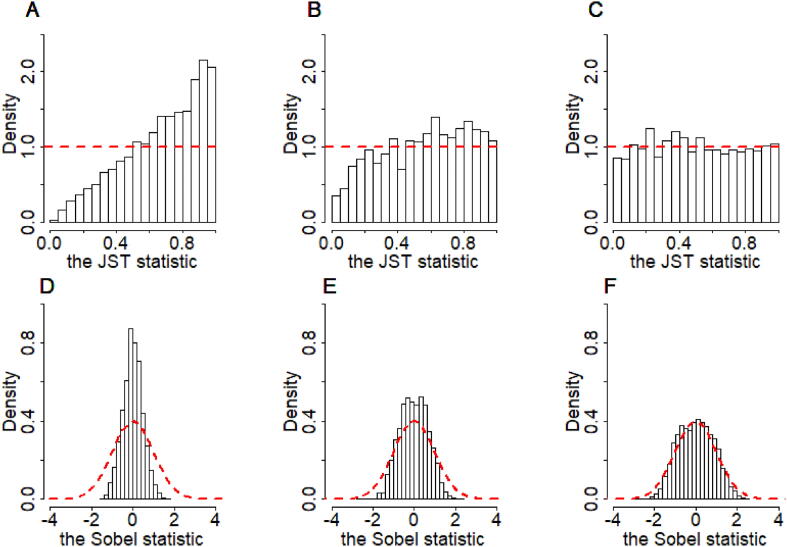
Extensive simulations have been previously conducted to assess the performance of the Sobel test and JST under different sub-null scenarios [70], [81]. For JST, it has been shown that it is extremely conservative under H₀₀ as the true null distribution for P_max is no longer a uniform distribution there but skewed towards to one (Fig. 5A). Indeed, P_max follows Beta(2,1) under H₀₀ [109]. In addition, the uniform distribution of P_max under H₀₁ or H₁₀ holds only under some regularity conditions (Fig. 5B-C). For example, the uniform distribution of P_max holds under H₁₀ only when the null hypothesis testing of a = 0 against a ≠ 0 is dominantly more powerful as compared to the test of b = 0, which guarantees a P_a consistently smaller than P_b [81], [109], [112]. For the Sobel test, it has also been demonstrated that it is underpowered under H₀₀ because the null distribution of the Sobel test statistic does not follow a standard normal distribution even with large sample sizes (Fig. 5D) [70], [78], [81], [126]. In addition, the Sobel test statistic follows a standard normal distribution under H₀₁ or H₁₀ only when the exposure on mediator effect size or the mediator on outcome effect size is far from zero, respectively (Fig. 5E-F).

Fig. 5.

Distribution of the JST statistic (top: A-C) and the Sobel test statistic (bottom: D-F) under three sub-null scenarios. Simulations were performed based on model under H₀₀: a = 0 and b = 0 (A and D); under H₁₀: b = 0, with a relatively weak exposure-to-mediator effect a = 0.05 (B and E); or under H₁₀: b = 0, with a relatively strong exposure-to-mediator effect a = 0.10 (C and F). In all scenarios, we set c′=0.50 and draw the exposure X and the residuals for the exposure-mediator model and the mediator-outcome model from independent standard normal distributions. The sample size was set to 10³. For each dataset consisting of simulated exposure, mediator, and outcome, we separately estimated and inferred a or b in the exposure-mediator model or in the mediator-outcome model using the ordinary least squares estimation procedure. Afterwards, we obtained $\widehat{a}$, $S_{\widehat{a}}$ and P_a as well as $\widehat{b}$, $S_{\widehat{b}}$ and P_b, based on which we obtained the Sobel test statistic and the JST statistic. In each simulation scenario we ran 10⁴ replicates. The red dashed line in each panel represents the asymptotic distribution: uniform for A-C and standard normal for D-F. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Because the asymptotic distribution for the Sobel test statistic or JST statistic is challenging to obtain accurately in an analytic form, various bootstrap sampling approaches, including parametric, nonparametric, and bias-corrected versions, have been proposed to obtain their empirical null distributions [71], [140], [144], [145], [146], [147], [148], [149], [150]. Constructing an empirical null distribution through sampling has been shown to lead to accurate confidence intervals and P value in certain settings but not all settings [81]. In addition, constructing the empirical null distribution remains difficult if one does not know the accurate proportions of the three sub-null scenarios [78], [109]. We will discuss these details in the high-dimensional mediation analysis section.

6. Mediation analysis approaches in the presence of high-dimensional mediators

The univariate and multivariate mediation methods described in the previous sections, unfortunately, are not directly applicable for performing mediation effect test in the presence of high-dimensional mediators collected from high-throughput genomics studies. In particular, when the number of mediators exceeds the sample size (i.e., m≫n), the multivariate mediation model defined in becomes unidentifiable, making it infeasible to detect active mediators through joint mediator modeling. In addition, examining one mediator at a time using the traditional univariate mediation model is not feasible either, as the P values from the univariate methods are not calibrated due to the composite nature of the null hypothesis. Because of these drawbacks of univariate and multivariate methods, many high-dimensional mediation methods have been recently developed to model high-dimensional mediators (Table 1). These recent mediation methods can be generally classified into three methodological categories. The first category of mediation methods performs dimension reduction or mediator screening on the high-dimensional mediators to extract a set of low-dimensional variables. Afterwards, they directly apply standard univariate or multivariate mediation methods to these extracted low-dimensional variables to detect active ones that are involved in mediation. The second category of mediation methods examines either one or a few mediators that are within a genomic testing unit (e.g., a gene) one at a time. However, different from standard testing approaches, these new methods explicitly account for the composite nature of the null mediation effect hypothesis to obtain calibrated test statistics. The third category of mediation methods models all potentially mediators jointly in the mediation model by specifying additional modeling assumptions on the mediator on outcome effects as well as on the exposure on mediator effects to ensure model identifiability. We describe the three categories of high-dimensional mediation methods in the following sections.

Table 1.

Summary of statistical methods for mediation analysis in the presence of multiple or high-dimensional mediators.

First category: Mediation methods based on dimension reduction or mediator screening
Methods	Test Statistics	Null Distribution	References
correlation-based method	Pmax	permutation	[120]
Huang-Pan method	marginal and component-wise ME based on PCA	Monte Carlo (normal-based or bootstrapping)	[122]
causal inference test (CIT)	Pmax	permutation	[157]
direction of mediation	PCA-based	bootstrapping	[158]
MCP-subset	Pmax	screening followed by multiple comparison procedure	[106]
MCP-subset based on Westfall-Young	Pmax	screening followed by multiple comparison procedure	[106]
MCP-subset based on multivariate	Pmax	screening followed by multiple comparison procedure	[106]
HDMA	Pmax	screening followed by debiased estimation	[159]
gHMA#	ACAT combining gHMA-L and gHMA-NL	screening followed by multiple comparison procedure	[160]
global test + ScreenMin#	Pmin followed by Pmax	screening followed by multiple comparison procedure	[161]
Second category: Mediation methods accounting for the composite nature of the null
Methods	Test Statistics	Null Distribution	References
JTV-comp#	mixture of multiple-mediator based P value without estimating the proportions	composite null	[79]
JT-comp	mixture of single-mediator based P value without estimating the proportions	composite null	[78]
DACT	mixture of single-mediator based P value with estimated proportion	composite null	[109]
JS-mixture	mixture of single-mediator based P value with estimated proportion	composite null	[112]
Third category: Penalization-based mediation regression methods and Bayesian mediation methods
Methods	Prior Effects Assumptions	Optimization Procedure	References
pathway Lasso	penalization based method	ADMM	[162]
HIMA	Pmax	screening followed by minimax concave penalty estimation	[111]
BAMA	spike-and-slab prior	MCMC	[163]
BAMA with joint priors	Gaussian mixture prior and, product threshold Gaussian prior	MCMC	[164]
BAMA with joint priors considering correlation among mediators	the Potts prior and logistic normal prior	MCMC	[165]

Note: we focus primarily on methodological papers and have not listed applied work that employs mediation methods similar to these listed above (e.g., Wu et al. (2018) [166], Luo et al. (2020) [96]). In addition, we only focus on methods that aim to detect active mediators and have not listed mediation methods for effect estimation and decomposition (e.g., VanderWeele and Vansteelandt (2014) [77], Daniel et al. (2015) [121], Huang and Yang (2017) [92], Steen et al. (2017) [167], Taguri et al. (2018) [168], Zhou et al. (2020) [115], and Zhao et al. (2020) [114]. ADMM: alternating direction method of multipliers; MCMC: Markov chain Monte Carlo; BAMA: Bayesian medaition analysis method; gHMA: gene based high-dimensional mediation analysis; PCA: principal component analysis; MCP: multiple comparison procedure; DACT: divide-aggregate composite-null test; HDMA: high-dimensional mediation analysis; ACAT: aggregated Cauchy association test. Above, # denotes a gene-centric mediation method.

Certainly, one common challenge for all high-dimensional mediation analysis methods is on establishing the causal interpretation of mediation effect. Mediation effects in high-dimensional mediation analysis can be causally interpreted when the required sequential ignorability assumptions hold [78], [79]. However, these sequential ignitability assumptions can be generally challenging to establish in practice as they require additional biological knowledge. For example, to investigate the role of DNA methylations in mediating the effect of smoking behavior on gene expression [79], one needs to assume a priori that smoking can lead to methylation alterations, which in turn can regulate gene expression [151], [152], [153], [154]. Such assumption may be violated as the expression of certain genes can sometimes influence methylation, thus potentially reversing the order of mediator and outcome. In addition, due to the consequence of global epigenetic remodeling mechanism [155], [156], altered DNA methylation may simply represent a passenger event rather than a mediation event. In particular, the expression of key genes may influence the outcome directly while at the same time affects DNA methylation at multiple CpG sites as a by-product. Therefore, when studying the role of gene expression in mediating the impact of DNA methylation on an outcome, it is important to distinguish passenger methylation events from mediation methylation events that likely exert a direct or indirect effect on the outcome. Distinguishing between passenger events and mediation events will also require additional domain knowledge.

6.1. High-dimensional mediation methods based on dimension reduction or mediator screening

The first category of methods attempts to apply multivariate mediation methods directly on a suitable set of potential mediators or a transformed version of mediators that have a dimensionality below the sample size (Table 1). This category primarily includes gene-centric methods such as gene high-dimensional mediation analysis (gHMA) [160], principal component analysis (PCA) based methods [122] as well as several mediator-screening based methods [111]. In brief, gHMA examines one gene at a time and perform mediation analysis on the potential mediators that reside within the examined gene together. Such gene-centric analysis limits the number of analyzed potential mediators to be those within the gene, thus making the standard multivariate mediation methods applicable. Alternatively, the PCA-based mediation method aims to transform the original set of high-dimensional mediators into a low-dimensional space and then analyzes the resulting low-dimensional components using standard multivariate mediation analysis. Finally, a group of mediation methods perform variable screening on mediators to select a subset of potentially active mediator candidates. These methods then apply multivariate mediation methods to analyze these mediator candidates. We describe all these methods in detail below.

6.1.1. Gene-centric mediation methods

The gHMA method adapts linear or non-linear kernels to characterize the relationship between multiple mediators and the outcome [160]. Specifically, the linear-version of gHMA (gHMA-L) examines one gene at a time and focuses on potential mediators that reside in the gene. For the gene of interest, gHMA tests the significance of the exposure on mediator effect (i.e., a in Equation) for each mediator using a univarate mediation model and obtain a corresponding P value; then it combines the P values aross all mediators in that gene using a new Fisher’s combination method that accounts for correlation among P values [169]. Afterwards, gHMA evaluates the significance of multiple mediator on outcome effects (i.e., b in Equation) through the likelihood ratio test, and further integrates the evidience of testing a and b through the same principle of JST. Besides the linear version gHMA-L, gHMA also provides an alternative version gHMA-NL that accommodates non-linear relationship between the mediators and the outcome using kernel principal components (KPC) [160]. The P values from the linear and non-linear versions of gHMA can be further combined through the ACAT (aggregated Cauchy association test) procedur to achieve robust power across various application scenarios while accounting for positive dependence among test statistics of gHMA-L and gHMA-NL [170], [171].

6.1.2. PCA-based mediation methods

Huang and Pan (2016) [122] proposed to first transform the potentially correlated mediators into independent ones based on PCA. Afterwards, Huang-Pan’s method performs multivariate mediation analysis on the resulting principal components using Monte-Carlo resampling. Huang-Pan’s method of testing for marginal mediation effects is equivalent to the integrative statistical framework proposed in Zhao et al (2014) [172]. A similar PCA-based dimension reduction strategy was also applied for mediation analysis in neuroimaging datasets [66]. While the dimension reduction-based mediation analysis effectively addresses the high number of potential mediators and the correlation among them, it is not always easy to interpret the results from the subsequent mediation analysis — after all, the transformed variables are a linear combination of the original mediators and may not have direct biological interpretation. Subsequently, the PCA-based mediation analysis [114] is recently extended to rely on sparse PCA [173] for dimension reduction, which improves the interpretability of the obtained principle components and subsequent mediation analysis results.

6.1.3. Screening-based mediation methods

Finally, several mediation methods perform mediator screening and include only potentially active mediators to the multivariate mediation model for final analysis (Table 1). For example, borrowing ideas in replicability analysis [174], Sampson et al. (2018) first selected mediators that had potential mediating effects based on the marginal mediator-outcome model [106]. The selected mediators were then analyzed in a multiple comparison procedure to ensure correct control of familywise error rate (FWER) or false discovery rate (FDR). Similar screening strategy is also employed by the penalization-based mediation analysis in the third category of high dimensional mediation methods discussed below.

6.2. High-dimensional mediation methods accounting for the composite nature of the null hypothesis

The second category of high-dimensional mediation methods perform hypothesis testing by examining one potential mediator at a time (or a set of potential mediators within a testing unit, one unit at a time) (Table 1). Different from standard univariate methods such as the Sobel test or JST, however, these methods borrow information across all potential mediators to infer key parameters of the three sub-null scenarios as shown in , thus allowing for the computation of calibrated P values. Calibrated P values from these methods lead to correct type I error control across all potential mediators and are essential for detecting promising mediators at the genome-wide significance threshold. Four methods belong to this category, including JT-comp [78], DACT (divide-aggregate composite-null test) [109], JS-mixture [112], and JTV-comp [79]. The first three examine potential mediators one at a time, while the last one is a gene-centric method.

6.2.1. JT-comp

JT-comp is the first method that attempts to accomodate the composite nature of the null hypothesis for testing mediation effect in high-dimensional setting [78]. JT-comp examines one mediator at a time. For each mediator in turn, JT-comp calculates two z-statistics ($z_a=\widehat{a}/S_{\widehat{a}}$ and $z_b=\widehat{b}/S_{\widehat{b}}$) by performing two separate tests: one for a in the exposure-mediator model and the other for b in the mediator-outcome model. Afterwards, it derives the null distribution of the product of z_a and z_b by carefully examining the two z-statistics under the three sub-null scenarios. Specifically, under H₀₁, z_a follows a standard normal distribution while z_b follows a normal distribution N(μ_b,1) with the mean parameter μ_b characterized by the mediator on outcome effect b. Under H₁₀, z_b follows a standard normal distribution while z_a follows a normal distribution N(μ_a,1) with the mean parameter μ_a characterized by the exposure on mediator effect a. Under H₀₀, both z_a and z_b asymptotically follow the standard normal distribution. Therefore, one can compute the P value for the product of z_a and z_b under H₀₀ directly, though computing the P value under either H₀₁ or H₁₀ would require knowing μ_a and μ_b which rely on the true effects a and b. JT-comp overcomes the difficulty of unknown μ_a and μ_b by making additional assumptions on how they distribute across all potential mediators. In particular, it assumes that μ_a follows a normal distribution N(0,τ_a) and μ_b follows another normal distribution N(0,τ_b). Consequently, if τ_a and τ_b are known, then $z_a{z}_b/\sqrt{\text{1}+{\tau }_b}$ becomes a product of two independent standard normal distributions under H₀₁ and $z_a{z}_b/\sqrt{\text{1}+{\tau }_a}$ becomes a product of two independent standard normal distributions under H₁₀. As a result, one can obtain a P value under each of the three sub-null hypotheses if τ_a and τ_b are given. If one knows further the probability of each sub-null hypothesis, then one can compute a final P value for testing H₀: ab = 0 as [78]

$$P_{\mathit{ab}}={\pi }_{00}F\left(z_a{z}_b\right)+{\pi }_{01}F\left(z_a\frac{z_b}{\sqrt{1+{\tau }_b}}\right)+{\pi }_{10}F\left(\frac{z_a}{\sqrt{1+{\tau }_a}}{z}_b\right)$$

where π₀₁, π₁₀, and π₀₀ represent the probabilities of H₀₁, H₁₀, and H₀₀, respectively; $F(z)={\int }_{|z|}^{\infty }f(x)dx$ is the right-sided tail probability of a normal product distribution evaluated at point z, with f(x) = K₀(x)/π (-∞<x<∞) being the probability density function of the normal product distribution and K₀(x) being the modified Bessel function of the second kind with order 0. Note that, computing the P value based on requires estimating the two variance parameters (τ_a and τ_b) and the three probability parameters (π₀₁, π₁₀, and π₀₀). Estimating these parameters individually through, for example mixture modeling, may not be accurate. To circumvent the difficulty of estimating each of these parameters individually, JT-comp makes further modeling assumptions. In particular, it assumes that τ_a and τ_b are relatively small and that the mediation signals are sparse [78], so that the sample variance of z_a and z_b across mediators, var(z_a) and var(z_b), are related to the individual parameters through var(z_a) = 1 + π₁₀τ_a and var(z_b) = 1 + π₀₁τ_b. With these additional assumptions, JT-comp can now approximately compute the final P value for each mediator through

$$P_{\text{JT - comp}}\approx F\left(z_a\frac{z_b}{\sqrt{var(z_b)}}\right)+F\left(\frac{z_a}{\sqrt{var(z_a)}}{z}_b\right)\text{-}F\left(z_a{z}_b\right)$$

Extensive simulations have shown that the JT-comp testing procedure described above is more powerful than JST and maintains calibrated type I error control when the JT-comp approximation assumptions hold [78]. A drawback of JT-comp, however, is that it may fail to control for type I error well when the sample size is large (e.g., n > 500) and var(z_a) or var(z_b) is>1.5 [78], [109]. A large sample size makes the two assumptions of JT-comp — small effect sizes of a and b characterized by small τ_a and τ_b as well as the sparse mediation effects — harder to satisfy in practice.

6.2.2. DACt

DACT is another mediation method that attempts to borrow information across mediators to produce calibrated P values [109]. Different from JT-comp, DACT relies on a modified test statistic and directly estimates the proportions of the three sub-null hypotheses across whole genome mediators. Like JT-comp, DACT examines one potential mediator at a time and performs the same two tests explained before: one for a in the mediator-exposure model and the other for b in the outcome-mediator model. Afterwards, DACT calculates two P values, P_a and P_b, from these two tests based on asymptotic normality. Intuitively, Under H₀₁, if the mediator-to-outcome effect is non-zero (i.e., b ≠ 0), then one only needs to test H₀₁: a = 0 and uses P_a for assessing the significance of meditation effect. Under H₁₀, if the exposure-to-mediator effect is non-zero (i.e., a ≠ 0), then one only needs to evaluate test H₁₀: b = 0 and uses P_b for evaluating meditation effect. Under H₀₀, the maximum P value of the two, P_max, follows Beta(2,1); thus $P_{\text{max}}^2$ follows a uniform distribution [109]. Taking these together, DACT generates the P value for testing H₀: ab = 0 as a weighted summation of P values under the three sub-null hypotheses

$$P_{\mathit{DACT}}=w_{01}{P}_a+w_{10}{P}_b+w_{00}{P}_{max}^2$$

where the weights are given as

$$\begin{array}{c}{w}_{01}=(1-{\pi }_{b0}){\pi }_{a0}/\varpi \\ w_{10}=(1-{\pi }_{a0}){\pi }_{b0}/\varpi \\ w_{00}=(1-{\pi }_{a0})(1-{\pi }_{b0})/\varpi \\ \varpi ={\pi }_{a0}(1-{\pi }_{b0})+(1-{\pi }_{a0}){\pi }_{b0}+(1-{\pi }_{a0})(1-{\pi }_{b0})\end{array}$$

with π_a0 and π_b0 being the probabilities of H₀₁ and H₁₀, respectively. The equation makes an implicit assumption that the effects of a and b are independent of each other, such that the probability of a = 0 is not influenced by b, and vice versa. Such independence is guaranteed by the sequential ignorability assumptions described before. DACT estimates π_a0 and π_b0 using novel methods that have been well-established in prior FDR work [111], [122], [175], [176], [177], [178], [179], [180], [181], [182], such as Efron’s approach [183] using either the central matching method [177] or the empirical characteristic function and Fourier analysis [175]. DACT has been shown to be comparable to or more powerful than JT-comp across various simulation scenarios [109] and, in contrast to JT-comp, is not sensitive to sample size.

6.2.3. JS-mixture

JS-mixture is also a recent mediation method that is designed to produce calibrated P values and bares some conceptual similarity with JT-comp and DACT. JS-mixture aims to directly construct the null distribution for the JST statistic, P_max, to correct for its conservative type I error control [112]. Specifically, JS-mixture applies JST to examine one potential mediator at a time and obtains the maximum P value for the j^th mediator as P_{max, j} (j = 1, …, m); then it estimates the proportions of the three sub-null hypotheses and constructs a null distribution for P_{max, j} through

$$\begin{array}{c}Pr(P_{max,j}⩽u|H_{0j})=Pr(P_{a,j}⩽u|H_{01,j})Pr(P_{b,j}⩽u|H_{01,j})Pr(H_{01,j})\\ +Pr(P_{a,j}⩽u|H_{10,j})Pr(P_{b,j}⩽u|H_{10,j})Pr(H_{10,j})\\ +Pr(P_{a,j}⩽u|H_{00,j})Pr(P_{b,j}⩽u|H_{00,j})Pr(H_{00,j})\\ ={\pi }_{01}{u}_{01}{p}_{01}+{\pi }_{10}{u}_{10}{p}_{10}+{\pi }_{00}{u}_{01}{u}_{10}\\ u_{01}=Pr(P_{a,j}⩽u|H_{01,j})=u\\ u_{10}=Pr(P_{b,j}⩽u|H_{10,j})=u\end{array}$$

where π₀₁, π₁₀ and π₀₀ are the proportions of the three sub-null scenarios; u is a given cut-off value for significance evaluation; p₀₁ is the probability/power of rejecting b = 0 under H_{01, j}; and p₁₀ is the probability/power of rejecting a = 0 under H_{10, j}. Both p₀₁ and p₁₀ can be estimated via the Grenander method [184]. When sample size is large, equation can be further approximated by

$$\begin{array}{c}Pr(P_{max,j}⩽u|H_0)={\pi }_{01}u+{\pi }_{10}u+{\pi }_{00}{u}^2=({\pi }_{01}+{\pi }_{10})F_1+{\pi }_{00}{F}_2\\ p_{01}=Pr{(P_{b,j}⩽u|H_{01,j})}_{n\to \infty }=1\\ p_{10}=Pr{(P_{a,j}⩽u|H_{10,j})}_{n\to \infty }=1\end{array}$$

where F₁ is the standard uniform distribution U(0,1); and F₂ is a right skewed distribution for the maximum of two independent random variables drawn from the standard uniform distribution, with a cumulative distribution function Pr(P_max ≤ u) = u². It is easy to see that JS-mixture given in becomes very similar to DACT shown in under the case of large sample sizes, with the only difference being that JS-mixture controls FWER or FDR based on a newly estimated significance rule while DACT directly controls FWER or FDR based on the final weighted P values. The additional estimation of power functions p₀₁ and p₁₀ in JS-mixture might lead to higher statistical power compared to DACT which instead fixes them to be one. The proportion parameters required in JS-mixture can be also estimated with the same methods as used in DACT [111], [122], [175], [176], [177], [178], [179], [180], [181], [182].

6.2.4. JTV-comp

Unlike the three methods discussed above, JTV-comp [79] performs the gene-centric mediation analysis by examining one gene at a time and analyizng the mutiple mediators located within a gene together. JTV-comp accounts for the composite nature of the null hypothesis by making additional assumptions. Specifically, JTV-comp treats the mediator effects as random effects and assumes the exposure on mediator effect (i.e., a) and mediator on outcome effect (i.e., b) for the k^th mediator in a given gene follow arbitrary dsitributions with mean zero and a variance being either κ_a and κ_b, respectively [79]. That is

$$a_k\sim F_a(0,{\kappa }_a),b_k\sim F_b(0,{\kappa }_b),k=1,...,p$$

Because κ_a = 0 implies a = 0 and κ_b = 0 implies b = 0, testing a = 0 and b = 0 can be translated into testing κ_a and κ_b, respectively. By this way, JTV-comp therefore translates testing H₀: a = 0 or b = 0 into two variance component tests: a multivariate variance component test on κ_a and a univariate variance component test on κ_b. JTV-comp performs the variance component tests based on score statistics [185], [186], [187], [188], [189] within the framework of kernel machine learning [79], [187], [189]. Alternatively, JTV-comp can also perform the variance component test on κ_a = 0 based on the inverse regression framework [161]. With the variance component tests, JTV-comp obtains two P values on testing κ_a and κ_b and converts them into two z-statistics (z′_a and z′_b) using the probit function. With the transformed statistics z′_a and z′_b, JTV-comp proceeds with the same procedure of JT-comp to perform hypothesis tests [79]. Because JTV-comp relies on the same procedure of JT-comp to account for the composite nature of the null, it has similar advantages and limitations of JT-comp as mentioned in the previous subsection.

6.3. High-dimensional mediation methods jointly modeling exposure on mediator effects and mediator on outcome effects

The last category of high-dimensional mediation methods directly models all mediators jointly. To account for the large number of mediators, these methods either penalize mediation effects or specify particular priors on them to make the mediation model identifiable. Two types of methods belong to this category: penalization-based regression methods such as HIMA (high-dimensional mediation analysis) [190] and pathway Lasso [162]; and Bayesian methods such as BAMA (Bayesian variable selection mediation method) [163] and its extensions (Table 1). Both types of methods can also rely on an initial screening procedure in the mediator-outcome model to reduce the number of mediators to a reasonable size before analyzing them collectively.

6.3.1. Penalization-based high-dimensional mediation methods

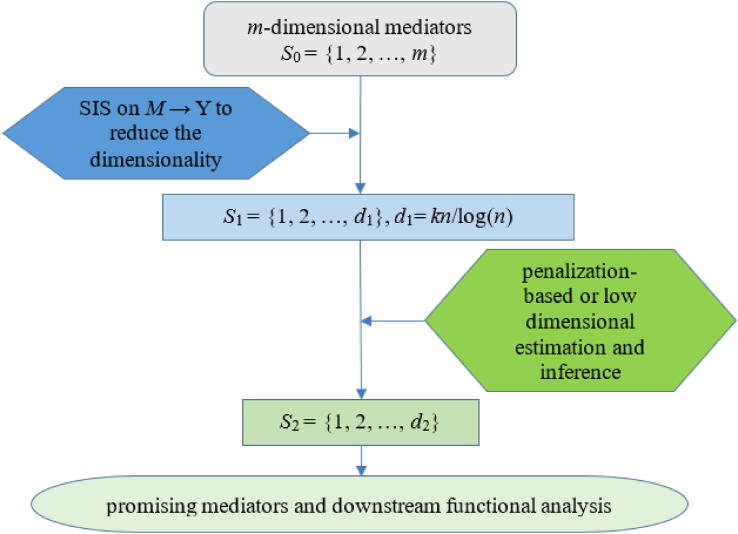
HIMA is one of the first penalization-based regression methods for high-dimensional mediation analysis [111] and includes the following three steps (Fig. 6). First, HIMA applies the sure independence screening (SIS) [191], [192] in the mediator-outcome model to reduce the dimensionality of mediators from ultra-high to high. This first step of HIMA can reduce the number of mediators from m to d₁ = [kn/log(n)], where k is assigned by the user. Second, HIMA applies the multivariate mediator-outcome model to model the selected candidate mediators together and relies on the minimax concave penalty (MCP) [190] to shrink the mediator on outcome effects towards zero

$$\begin{array}{c}{Q}_{\mathit{MCP}}=\frac{1}{2n}{(Y-X{c}^{\prime }-\sum _{j=1}^{d_1}{M}_j{b}_j-U_{\mathit{XM}})}^T(Y-X{c}^{\prime }-\sum _{j=1}^{d_1}{M}_j{b}_j-U_{\mathit{XM}})\\ +\sum _{j=1}^{d_1}\left\{\lambda \left[|b_j|-\frac{|b_j^2|}{2\delta \lambda }\right]I(0⩽|b_j|⩽\delta \lambda )+\frac{{\lambda }^2\delta }{2}I(|b_j|>\delta \lambda )\right\}\end{array}$$

where λ > 0 is the tuning parameter that controls the shrinkage and δ > 0 determines the concavity of MCP. By optimizing , HIMA can select mediators that have non-zero mediator on outcome effects. In particular, the P values of testing for b for mediators with non-zero effects can be calculated as

$$P_{\mathit{bs}}=2\left\{1-\mathrm{\Phi }(\frac{|{\widehat{b}}_s\}}{\mathit{se}({\widehat{b}}_s)})\right\},s\in S_2=\{s:{\widehat{b}}_s\ne 0\}$$

where ${\widehat{b}}_s$ is the MCP estimate of b_s and $\mathit{se}({\widehat{b}}_s)$ is the corresponding standard error obtained based on the oracle property of MCP [190]. Besides b, HIMA also examines the mediator on outcome effects a in the exposure-mediator model and obtains the corresponding P values, P_as (s = 1, …, S₂), based on the linear regression. Finally, HIMA evaluates the significance of the mediation effect using P_{max, s} = max($P_{\mathit{bs}}$, P_as) and adjusts for multiple comparisons through Bonferroni correction. HIMA has been recently extended to survival outcomes [96] and to yield unbiased mediator on outcome effects with debiased Lasso [159].

Fig. 6.

Overall workflow for HIMA with screening and penalization-based selection on mediators. HIMA includes the three main processes: (i) applying variable selection techniques for preliminary screening to reduce the high-dimensionality of mediators to tractable level (from m to d₁); (ii) conducting penalization-based variable selection and estimation for the remaining mediators to reduce dimensionality further (from d₁ to d₂); (iii) performing the joint significance test for mediation effects. In the screening procedure, k is a tuning parameter determined by users.

The pathway Lasso is another penalization-based mediation method [162], which imposes a convex Lasso-type penalty on the mediation effects. In particular, the pathway Lasso attempts to minimize the following penalized likelihood function

$$\begin{array}{c}{Q}_{\mathit{pL}}=\left\{\sum _{j=1}^m{(M_j-X{a}_j)}^2+{(Y-X{c}^{\prime }-\sum _{j=1}^m{M}_j{b}_j)}^T(Y-X{c}^{\prime }-\sum _{j=1}^m{M}_j{b}_j)\right\}\\ +{\lambda }_1\sum _{j=1}^m\left\{|a_j{b}_j|+\varphi (a_j^2+b_j^2)+|a_j|+|b_j|\right\}\end{array}$$

where $\varphi$, λ₁ and λ₂ are tunning parameters. In the pathway Lasso, the first penalty aims to shrink the mediation effect as the product of a_j and b_j, while the second term penalizes individual a_j and b_j. The pathway Lasso applies the alternating direction method of multipliers (ADMM) for parameter estimation [193]. By optimizing , pathway Lasso can select active mediators with non-zero a_jb_j.

6.3.2. Bayesian high-dimensional mediation methods

BAMA is a Bayesian mediation method for selecting active mediators [163]. BAMA specifies a Bayesian sparse linear mixed model (BSLMM) prior [194], also known as the two-component spike-and-slab prior [195], on both the exposure on mediator effects and the mediator on outcome effects. The BSLMM prior assumes that each effect for the j^th mediator, a_j or b_j, follows a mixture of two normal distributrions, one with a large variance and the other with a small variance

$$\left\{\begin{array}{c}{a}_j\sim {\pi }_{a}N(0,{\kappa }_{a1})+(1-{\pi }_a)N(0,{\kappa }_{a0})\\ b_j\sim {\pi }_{b}N(0,{\kappa }_{b1})+(1-{\pi }_b)N(0,{\kappa }_{b0})\end{array}\right),j=1,...,m$$

where κ_a1 > κ_a0 and κ_b1 > κ_b0, and π_a (or π_b) denote the probability that the effect belongs to the normal distribution with a larger variance. BAMA applies a Markov chain Monte Carlo (MCMC) sampling algorithm to obtain posterior samples [163] and uses the posterior inclusion probability (PIP) to select active mediators with both a and b belonging to the large normal components.

Song et al (2020) [164] extended the separate priors on a_j and b_j in BAMA towards joint modeling of both sets of effects. In particular, the authors depended on the four-component Gaussian mixture model (GMM) developed in genome-wide association studies [196] to decompose the exposure on mediator and mediator on outcome effects into four components

$$\left[a_j,b_j\right]\sim {\pi }_{00}{\delta }_0+{\pi }_{10}N\left(0,\left[\begin{array}{cc}{\sigma }_{\alpha }^2& 0\\ 0& 0\end{array}\right]\right)+{\pi }_{01}N\left(0,\left[\begin{array}{cc}0& 0\\ 0& {\sigma }_b^2\end{array}\right]\right)+{\pi }_{11}N\left(0,\left[\begin{array}{cc}{\sigma }_{\alpha }^2& \rho {\sigma }_{\alpha }{\sigma }_b\\ \rho {\sigma }_{\alpha }{\sigma }_b& {\sigma }_b^2\end{array}\right]\right),j=1,...,m$$

where δ₀ is a point mass at zero; ${\sigma }_{\alpha }^2$ is the prior variance for the exposure on mediator effect; ${\sigma }_b^2$ is the prior variance for the mediator on outcome effect; ρ is the correlation between the two sets of effects; and π₀₀, π₁₀, π₀₁, and π₁₁ are the probabilities of the four components, respectively. The components in capture all possible relationship among the exposure, mediator and outcome: the first three components directly correspond to the three sub-null hypotheses while the last component representing the alternative. The GMM-based mediation method has been shown to enjoy excellent and robust performance for mediator selection and mediation effect estimation [164]. A potential drawback of the GMM prior, however, is that it does not directly impose sparsity on the mediation effects for mediator selection. Therefore, Song et al (2020) [164] provided a second method, based on a product threshold Gaussian (PTG) prior, to directly sparsity on the mediation effects. Song et al (2020) [164] relied on a latent variable-based MCMC algorithm for parameter estimation in both these two models.

Song et al. (2020) [165] further extended the above Bayesian approaches towards direct modeling of the correlation structure among active mediators. Intuitively, if the active mediators are correlated with each other, then accounting for such correlation would improve power to detect them. Song et al (2020) [165] developed two methods to account for such correlation among active mediators under the GMM-based Bayesian joint mediation model. The first is to use the Potts distribution [197], which is a generalization of the Ising distribution and accounts for the complex dependency structures among multiple groups. The second is based on joint modeling of the mediator-specific mixing probabilities via a logistic normal distribution [198] similar to that used in Zeng et al (2018) [196], where the group probabilities reflect the underlying correlation structure. Therefore, this newly developed joint mediatin method allows for identifying correlated active mediators that could be missed by other methods [165].

7. Conclusions

We have presented a systematacial review of statistical methods for mediation analysis, with a special emphasis on recent methods developed for high-dimensional mediators commonly encountered in high-throughput genomics studies. In spite of current successes of these newly developed high-dimensional mediation methods, many challenges remain. For example, accurately estimating the proportion parameters of different sub-null hypotheses is critical for generating calibrated P values from both DACT [109] and JS-mixture [112], but accurate estimation of these parameters may be hard to achieve. As another example, the empirical null distribution of JS-mixture is currently constructed in a nonparametric manner [112], and it remains important to explore whether parametric mixture distributions such as Beta mixture can help improve power further. For Bayesian mediation methods [163], [164], [165], the current sampling-based algorithms are not computationally efficent. Future algorithmic development is needed to adapt them for truly genome-wide mediation studies with large sample sizes. In addition, various extensions of these high-dimensional mediation methods towards modeling non-linear relationship between mediators and outcomes, accomodating missing data [199], [200] and exposure-mediator interaction, performing sensitivity analysis under model misspecifications [72], [117], [119], accounting for multilevel or longitudinal outcomes [201], [202], [203], could all yield fruitful results. Finally, a comprehensive comparison among methods for high-dimensional mediation analysis is warrented for evaluating their relative performance and understanding their practical advantages and drawbacks in high-throughput genomics applications.

CRediT authorship contribution statement

Ping Zeng: Conceptualization, Methodology, Writing - original draft, Writing - review & editing, Project administration. Zhonghe Shao: Writing - original draft, Visualization. Xiang Zhou: Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.