covNorm: An R package for coverage based normalization of Hi-C and capture Hi-C data

Graphical abstract

Abstract

Hi-C and capture Hi-C have greatly advanced our understanding of the principles of higher-order chromatin structure. In line with the evolution of the Hi-C protocols, there is a demand for an advanced computational method that can be applied to the various forms of Hi-C protocols and effectively remove innate biases. To resolve this issue, we developed an implicit normalization method named “covNorm” and implemented it as an R package. The proposed method can perform a complete procedure of data processing for Hi-C and its variants. Starting from the negative binomial model-based normalization for DNA fragment coverages, removal of genomic distance-dependent background and calling of the significant interactions can be applied sequentially. The performance evaluation of covNorm showed enhanced or similar reproducibility in terms of HiC-spector score, correlation of compartment A/B profiles, and detection of reproducible significant long-range chromatin contacts compared to baseline methods in the benchmark datasets. The developed method is powerful in terms of effective normalization of Hi-C and capture Hi-C data, detection of long-range chromatin contacts, and readily extendibility to the other derivative Hi-C protocols. The covNorm R package is freely available at GitHub: https://github.com/kaistcbfg/covNormRpkg.

1. Introduction

The combination of chromosome conformation capture–based “C” technologies with high-throughput sequencing has revolutionized the study on the 3D chromatin structure, revealing its hierarchical organization at various scales and functional implications [1], [2], [3], [4], [5]. In these “C” technologies, each crosslinked protein-DNA complex is digested by restriction enzymes and ligated back to a single molecule to capture and sequence spatially proximal DNA fragments. The spatial proximity between two genomic regions can be represented by the number of ligated reads.

However, many experimental and intrinsic sequence-oriented biases such as the number of restriction sites, digestion efficiency, ligation efficiency, and genome mappability have been reported [6]. These biases affect the probability that certain DNA fragments are recognized, hindering precise quantification of spatial proximity based on the number of ligated reads.

Several computational methods have been proposed to eliminate such biases. These methods mainly target Hi-C, which is the most widely used “C” method as it can detect chromatin contacts in a genome-wide unbiased manner. The method “HiCNorm” used a parametric model to estimate biases caused by the GC content, effective fragment length, and mappability [6], [7]. In the case of “iterative correction of Hi-C data” (ICE), an iterative correction approach was applied based on the assumption that all loci should have equal visibility when biases are eliminated [8]. However, there is ample room for improving these methods since not all bias factors cannot be explicitly considered or operations under strong assumptions cannot be easily applicable to various “C” technologies.

Here, we propose “covNorm”, a negative binomial model-based implicit normalization approach that consists of bias removing step and genomic distance-dependent background normalization step. We hypothesized that the experimental and intrinsic biases can be combined in the form of coverage, computed by the number of ligated reads aligned to a given DNA fragment. Using generalized linear model (GLM) fitting, we can estimate expected ligation frequencies at given coverages of two DNA fragments, which can be used to adjust the number of ligated reads to remove biases effectively. The usage of weak assumptions and adaptation of flexible and simple fitting process may allow the expanded application of our method to many derivative Hi-C protocols such as DNase Hi-C [9], [10] and a modified Hi-C protocol combined with multiple restriction enzymes [11]. In addition, targeted Hi-C methods including capture-C [12], capture Hi-C [13], and HiChIP [14] are allowed as inputs with minor modifications. We have successfully applied the preliminary forms of the proposed method in our previous studies [15], [16], [17] and the optimized code is arranged in the form of an R package.

2. Materials and methods

2.1. Data collection and preparation of input data

We obtained published Hi-C experimental data of two lymphoblastoid cell lines (GM19204 and GM19240) [18] for the performance measurement of covNorm (Table 1). The fastq files were downloaded from Short Read Archive (SRA) using sra-toolkit. Using BWA-mem [19] with default parameters, the fastq files were aligned to the human reference genome 38 (hg38). The generated SAM files for each fastq file were merged into a paired-end BAM file after removing low-quality reads (MAPQ < 10). Putative self-ligation reads were removed by deleting ligated reads within a distance shorter than 15 kb. As we focus on the cis-interactions (or intra-chromosomal interactions) only, inter-chromosomal interactions were also filtered. A filtered BAM file was processed by Picard MarkDuplicates software to remove PCR duplicates. Coverage profiles of individual chromosomes at 40 kb resolution were obtained by using BEDTools coverage [20]. Interaction frequencies and coverage values between DNA fragments were summarized into a desired input table format of the developed package (Table 2).

Table 1.

Details of used Hi-C dataset for reproducibility measurement.

Cell line	# of reads	SRA id
GM19204	143,123,334	SRR11935528
	203,469,737	SRR11935527
	19,765,759	SRR11935526
GM19240	294,731,559	SRR11935549
	126,469,899	SRR11935548

Table 2.

Example of required input format.

frag1	frag2	cov_frag1	cov_frag2	freq	dist
chr17.140000.160000	chr17.83160000.83180000	2296	2304	1	83020000
chr17.140000.160000	chr17.83180000.83200000	2296	2072	2	83040000
chr17.140000.160000	chr17.83200000.83220000	2296	778	2	83060000
…	…	…	…	…	…
chr17.160000.180000	chr17.200000.220000	2119	2253	12	40000

Note: ‘frag1’ and ‘frag2’: dot (‘.’) spliced chromosome, start coordinate, end coordinate of the first/second DNA fragment. ‘cov_frag1’ and ‘cov_frag2’: coverage values of frag1/2 bins. ‘freq’: raw interaction frequency between two bins. ‘dist’: the genomic distance between two bins.

To demonstrate the application of the developed method to Hi-C protocol variants, the normalization of promoter capture Hi-C was also included in the benchmark. In the case of promoter capture Hi-C (pcHi-C), preprocessed input data of published GM12878 and GM19240 pcHi-C results [16] were offered by the author and used for the normalization.

2.2. Preprocessing of Hi-C input data

Hi-C contact map is a sparse matrix, and frequent zero-valued bins can lead to incorrect results in the generalized linear model fitting. Thus, the zero-valued DNA fragment pairs were removed from the demonstrated input data in this study. We further filtered the DNA fragments with low coverage, which mostly reside in repeat regions, centromeres, or telomeres. The default coverage cut-off threshold was selected as 200 at 40 kb resolution, but the user can define this threshold according to the resolution and sequencing depth of user input. Before the normalization process, 50% of the fragment 1 and 2′s coverage values were shuffled to prevent potential biases caused by the sorted order of the input data during the fitting.

2.3. Preprocessing of promoter capture Hi-C input data

For the pcHi-C data normalization, we added three different preprocessing steps to the Hi-C data: (1) separated processing and filtration of promoter-promoter (P-P) and promoter-other (P-O) interactions, (2) no coverage shuffling used, and (3) selecting promoter-centered long-range interactions over 15 kb and within 2 Mb (default 2 Mb, user-adjustable). As capture probes were designed to target promoter regions in pcHi-C, the captured promoter regions are expected to have higher coverage values than the “other” regions, thus separated analysis and filtering threshold are required to avoid capture-dependent biased results. The provided example used 200 as a promoter side threshold but a value of 50 was used to filter the “other” side coverage. The first fragment is fixed as promoter side in P-O interaction normalization, so no shuffling of coverage values between the fragment 1 and 2 was performed.

2.4. Removing biases based on coverage values of DNA fragments

Let raw ligation frequency between two DNA fragments i and j as Y_ij, which is assumed to follow the negative binomial distribution (Y_ij ~ NB) with mean of µ and variance µ + αµ² (α > 0, over-dispersion parameter). The expected frequency of two DNA fragments based on the coverage C_i and C_j were obtained by fitting a generalized linear model log(u_ij) = β₀ + β₁C_i + β₂C_j. Here β₀ is the intercept term. β₁ and β₂ represent the fragment i coverage bias and fragment j coverage bias, respectively. We fit this negative binomial model, estimating corresponding parameters β̂₀, β̂₁, and β̂₂. The residual R_ij = Y_ij / exp(β̂₀ + β̂₁C_i + β̂₂C_j) was defined as a bias-removed ligation frequency. The fitting was implemented by using the R “MASS::glm.nb” function.

2.5. Normalization against genomic distance-dependent background signal

The Hi-C contact probability decreases along with the genomic distance between DNA fragments due to the polymer nature of chromatin. Thus, another normalization step against genomic distance-dependent background signal is required to precisely identify biologically meaningful chromatin contacts such as enhancer-promoter interactions. To this end, similar to the coverage normalization, the model log(u_ij) = β₀ + β₁D_ij was used to estimate E_d which is the expected ligation frequency at distance d. The D_ij is the genomic distance between two DNA fragments. Given the residual R_ij, the final distance-dependent background removed signal was obtained by computing (R_ij + avg(R_ij) / (E_d + avg(R_ij)) where avg(R_ij) is a pseudocount parameter.

2.6. Identification of significant long-range chromatin contacts

Next, the significance of the chromatin contact was measured by fitting distance-normalized interaction frequencies to the three-parameter (3P-) Weibull distribution. The preliminary forms of covNorm used all distance-dependent background normalized data for the fitting process. In this version, only normalized values within 2-fold of the expected values were used as background distribution to properly calculate the statistical significance of extraordinarily high interaction frequencies. This was inspired by a two-step spline strategy used in the “Fit-Hi-C” method [21] to calculate proper p-values of outliers. The three parameters (location, shape, and scale) were obtained by using the R “propagate::fitDistr” function. The p-value of each chromatin contact was computed by the R “FAdist::pweibull3” function, using the obtained three parameters. The false discovery rate (FDR) was also obtained by the R “p.adjust” function with the “fdr” method option.

2.7. Performance evaluation metrics and baseline methods

In the case of Hi-C, the performance was evaluated by the reproducibility between two biological replicates after normalization, which was measured by the Hi-C contact map reproducibility, correlations of compartment A/B profiles, and identification of the reproducible significant interactions. For the contact map reproducibility measurement, HiC-spector [22] was used. The “run_reproducibility_v2.py” script was downloaded from the software repository (https://github.com/gersteinlab/HiC-spector) and applied to each chromosome pair from chromosome 1 to chromosome X. The “get_reproducibility” function with the “num_evec” parameter of 20 (default) was used to obtain the HiC-spector score. For the compartment A/B calling, in-house scripts were used to apply Principal Component Analysis (PCA) to the distance-normalized Hi-C contact maps. The sign of the first principal component (PC1) was corrected based on gene density where bins with higher gene density were assigned to compartment A. The compartment A/B profiles of chromosome 1 to X in 40 kb resolution were obtained, and the Pearson correlation coefficient and Spearman’s rank correlation (ρ) were computed between the biological replicates.

The results of HiC-spector and compartment A/B correlation were compared with ICE, Knight-Ruiz (KR) [23] sequential component normalization (SCN) [24] and raw Hi-C contact maps. Python “iced” package (https://github.com/hiclib/iced) was used to run ICE and SCN normalization on the prepared Hi-C contact maps. In the case of KR, “HiCcompare::KRnorm” function of “HiCcompare” R package was used [25].

To evaluate the significant interaction calls of covNorm, the ability to identifying reproducible significant interactions from the biological replicates were examined. In the case of Hi-C data, Fit-Hi-C was used as the baseline method. The Hi-C data was processed by the Fit-Hi-C using 40 kb resolution/2Mb distance as the running parameters. The q-value output from Fit-Hi-C was used as a significance threshold.

The reproducibility of significant interactions between two biological replicates was also used to evaluate the performance of covNorm in pcHi-C data, which was compared with “CHiCAGO” [26]. The P-O cis-interactions within 2 Mb distance were collected from CHiCAGO output, and "score" was used as a significance threshold. The statistical significance of the overlapping ratio between two replicates or methods was measured by using R “phyper” function.

3. Results and discussion

3.1. Effective elimination of various sources of bias

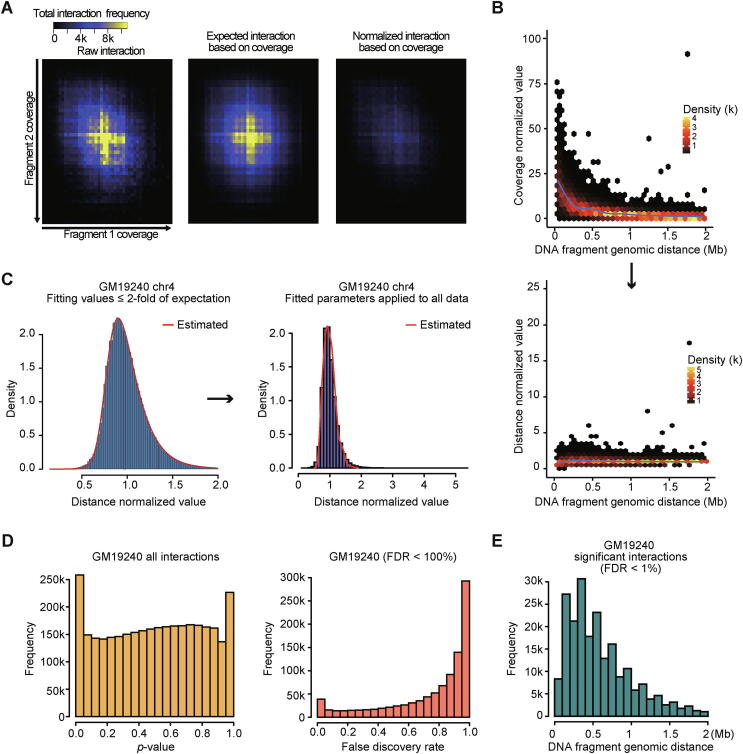
The step-by-step normalization results of the developed package are shown in Fig. 1. The two-dimensional density plot demonstrates that raw interaction frequencies are strongly proportional to the coverages of aligned ligated-reads (Fig. 1A left). The negative binomial regression model well estimated the expected interaction frequencies for given coverages (Fig. 1A middle). The final normalization result demonstrates the elimination of such dependencies (Fig. 1A right), validating the removal of experimental and intrinsic biases. Next, we applied the distance-dependent background normalization step, which mitigates the skewed ligation frequencies at shorter genomic distances as a result of the polymer nature of chromatin (Fig. 1B).

Fig. 1.

Visualization of normalization results A. Heatmaps showing correlations between fragment 1 (x-axis) and 2 (y-axis) coverages and interaction frequencies (color scale). Before normalization (left), computed expectation (middle), and after normalization (right) are shown. The coverage-dependent biased ligation frequencies were removed after normalization. B. Scatter plots showing distant-dependent intensity (color scale) before the distance normalization (top) and after the distance normalization (bottom). Concentrated interactions at shorter distances decreased after distance normalization. Blue lines indicate the loess regression result of each scatter plot. C. Examples from GM19240 chromosome 4 showing the fitting of the normalized values to three-parameter Weibull distribution. Left blue histogram indicates fitting with values ≤2-fold of expectation, and right purple histogram indicates the application of fitted parameters to all data points. D. Histograms showing the distribution of raw p-values (left) and false discovery rate (FDR) < 100% (right) in GM19240 Hi-C data. E. A histogram showing the distribution of the genomic distance between fragments in identified significant interactions (FDR < 1%) in GM19240. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Unlike other Hi-C normalization methods, covNorm also provides a list of significant interactions. An example of significant interaction calling process based on the 3P-Weibull distribution is shown in Fig. 1C. Regression parameters of background distribution using normalized values < 2-fold of expected values were obtained (Fig. 1C, left). After that, the parameters were applied to fit all values to the distribution and calculate the statistical significance (Fig. 1C right). As exemplified for the GM19240 Hi-C result, the proposed procedure generates a uniform-like distribution of p-values (Fig. 1D left), which leads to the acquisition of a proper FDR value profile (Fig. 1D right). The median distance of identified significant interactions (FDR < 1%) was 400 kb and the frequency of significant interactions gradually decrease along with the genomic distances as expected (Fig. 1E).

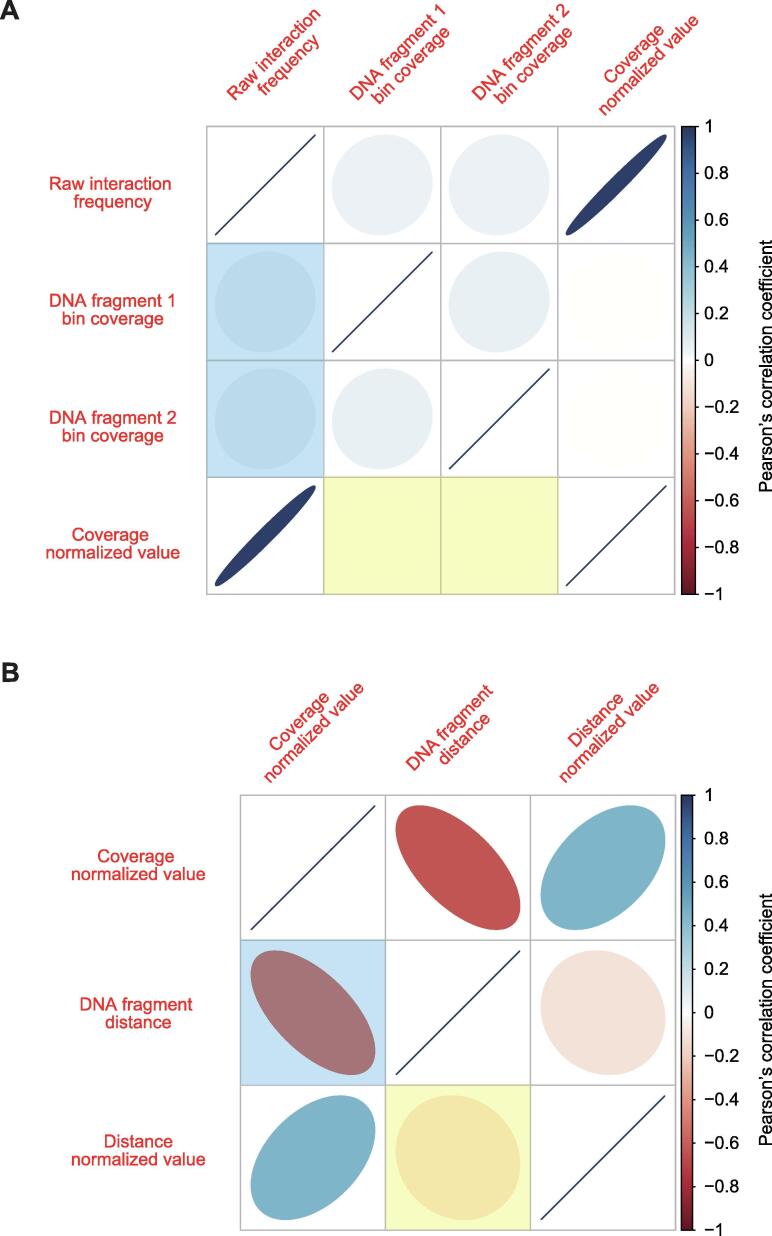
The efficiency of the coverage and distance normalization can be quantified by measuring the Pearson’s correlation coefficient between the ligation frequency and coverage/distance, which should decrease after normalization. The developed package provides visualization functions that can plot the correlation between the normalization factors (Fig. 2) for easier quality control, including coverage sorted heatmaps and distance-interaction frequency plots on Fig. 1A and B.

Fig. 2.

Correlation matrices between interaction frequencies and normalization factors. The color indicates the correlation value (Pearson’s correlation coefficient) where the eccentricity of the ellipse shows absolute magnitude and direction corresponds to positive/negative correlation (tilted right: positive correlation, tilted left: negative correlation). A. Correlation between interaction frequencies and coverages before and after normalization. Before coverage normalization, a weak positive correlation between the interaction frequencies and coverages exists (translucent blue) but dropped to near zero after normalization (translucent yellow). B. Correlation between interaction frequencies and fragment distance before and after normalization. There is a negative correlation between the interaction frequencies and distance (translucent blue) but weakened after normalization (translucent yellow). The reduced correlation for the factor to be normalized illustrates that normalization processes were properly performed. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In the case of tumor or cancer cell line Hi-C data which is expected to have a highly rearranged genome, it is not appropriate to apply the distance normalization and significant interaction calling since covNorm uses the genomic distance based on the reference genome. However, the effect of copy number alterations is theoretically neglectable in covNorm through coverage normalization. Inter-chromosomal or trans-interactions cannot be used for distance normalization as the genomic distance between DNA fragments is undefinable.

3.2. Performance evaluation of covNorm normalization

We tested reproducibility between the biological replicates as a performance evaluation of covNorm normalization. Using published in situ Hi-C data of lymphoblastoid cell lines GM19204 and GM19240 [16], [18], the reproducibility of 40 kb-resolution Hi-C contact maps and compartment A/B profiles derived from the contact maps were compared.

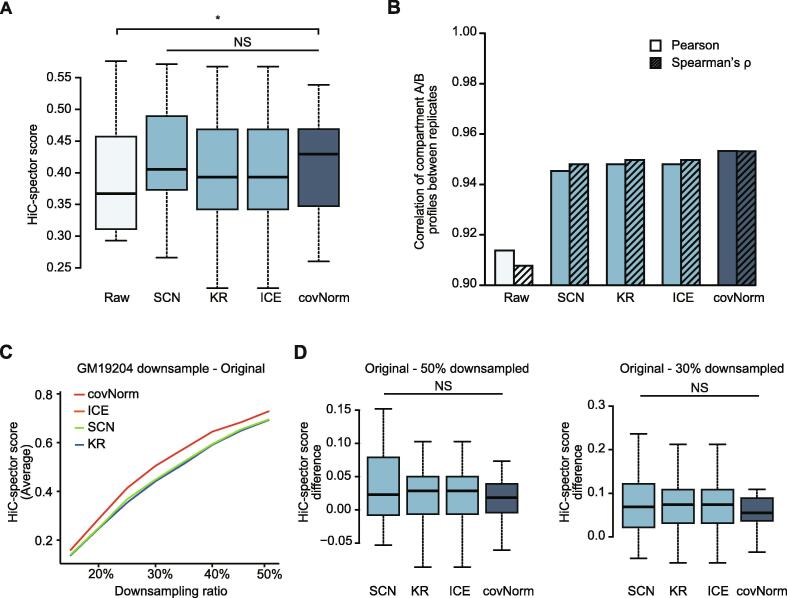
In terms of the contact map reproducibility between two tested lymphoblastoid cell lines, the baseline methods and covNorm's median HiC-spector score increased compared to the raw Hi-C contact maps (Fig. 3A). The HiC-spector score sets of covNorm significantly changed against the raw data’s score set (paired t-test, p-value = 0.019). High similarity between the KR and ICE's HiC-spector scores were observed, and SCN recorded the highest upper quartile (75th percentile or Q3) value in the benchmark datasets. While none of the examined methods showed significantly high HiC-spector scores than the other methods (paired t-test, p-values > 0.05), covNorm recorded the highest median value.

Fig. 3.

Evaluation of Hi-C contact map normalization. (Light cyan: raw Hi-C contact maps, Light blue: baseline methods, Dark blue: covNorm) A. Boxplots showing HiC-spector measured reproducibility scores of Hi-C contact maps between two biological replicates (GM19204 and GM19240) . The proposed method showed significantly higher HiC-spector score compared to the raw data (paired t-test, p-value = 0.019). Normalization methods did not show significant differences (paired t-test, p-value > 0.05, NS). B. Bar plots showing Pearson’s correlation coefficient (left bars, no face pattern) and Spearman’s rank correlation (right bars, dashed face pattern) between GM19204 and GM19240 40 kb compartment A/B profile before and after normalization. The proposed method showed the highest correlation between two biological replicates. C. A line plot showing reproducibility (average of 23 chromosome pairs’ HiC-spector score) between the original and downsampled Hi-C data of GM19204. Line colors indicate each method. The sampling ratio is at 5% intervals from 15% to 50%. The results of ICE and KR overlapped. D. Boxplots showing the chromosome-wise contact map HiC-spector score difference between the original-50% downsampled (left) and original-30% downsampled (right) GM19204 Hi-C data (paired t-test, p-value > 0.05, NS). For the boxplots, the box represents the interquartile range (IQR) and the whiskers correspond to the highest and lowest points within 1.5 × IQR. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The preservation of inferred information can be more meaningful than the simple resemblance of the Hi-C contact matrices. In the correlation measurement of compartment A/B profile, covNorm recorded the best correlation coefficient values in both Pearson’s correlation coefficient and Spearman’s ρ. Again, highly similar compartment A/B score correlation values between KR and ICE were observed. However, SCN which showed the best Q3 score at the contact map reproducibility measurement demonstrated the lowest correlation. The raw Hi-C contact map presented a remarkably low correlation compared to the normalized data even though such trend was not observed in HiC-spector score.

We also tested the methods’ robustness by measuring contact map reproducibility after applying the random downsampling (use sampled data only) to the Hi-C data and comparing the normalization result with that of original data. The sampling ratios from 15% to 50% at 5% intervals were applied to the GM19204 (~100 M usable cis reads) and used as an input for each method. All methods' HiC-spector score decreased in proportion to the sampling ratio, but covNorm maintained the highest average HiC-spector score at all sampling ratios (Fig. 3C). In the comparison of HiC-spector score to the normalization result after 50% (Fig. 3D left) and 30% downsampling (Fig. 3D right), covNorm showed the lowest reduction rate of HiC-spector score (paired t-test, p-values > 0.05) than the baseline methods.

Collectively, we examined the normalization efficiency of covNorm in various metrics, demonstrating that covNorm has comparable or enhanced performance than the other baseline methods.

3.3. Identification of significant long-range chromatin contacts

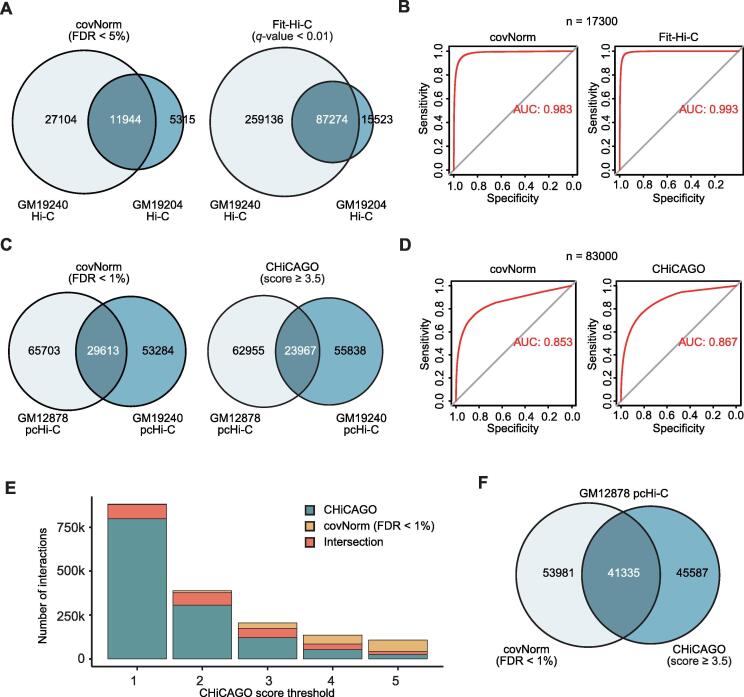
Unlike previously developed Hi-C normalization methods, covNorm provides a unique integrative analysis pipeline for computing long-range significant chromatin contacts after the normalization of biases. The identification of reproducible significant interactions between the biological replicates was measured and compared with the results of Fit-Hi-C (Hi-C data) and CHiCAGO (pcHi-C data). For the comparison between covNorm and the baseline methods, (1) the fraction of reproducible long-range significant chromatin contacts between replicates, (2) ROC curve assuming that the replicate with a smaller number of significant interactions as a true set, and (3) difference of called interactions between covNorm and baseline method for the same replicate were measured.

Both covNorm and Fit-Hi-C showed a high fraction of reproducible long-range significant chromatin contacts between replicates (over 65%, Fig. 4A). Both methods also presented the high area under curve (AUC) value in the ROC plots which were less than 1% difference (Fig. 4B), indicating that the uniquely identified interactions in one replicate actually present strong chromatin contacts in other replicates. Under the various adjusted p-value threshold conditions, Fit-Hi-C generated more interaction calls than covNorm; however, the called significant interactions showed a high consensus between the two methods. When the FDR < 1% threshold was used for covNorm, the ratio of two methods’ intersection maintained more than 80% even if the q-value of Fit-Hi-C was adjusted from 10% to 0.0001% (data not shown).

Fig. 4.

Evaluation of significant interaction calling from Hi-C and pcHi-C. A. Venn diagrams showing the fraction of reproducible significant interactions between GM19204 and GM19240 Hi-C data (Hypergeometric p-values ~0). B. ROC plots showing the accuracy of the covNorm and Fit-Hi-C for discovering GM19204′s significant interactions (n = 17300, nearest integer to the actual value) in the GM19240. C. Venn diagrams showing the fraction of reproducible significant interactions between GM12878 and GM19240 pcHi-C data (Hypergeometric p-values ~0). D. ROC plots showing the accuracy of the covNorm and CHiCAGO for discovering GM19240′s significant interactions (n = 83000, nearest integer to the actual value) in the GM12878. E. A stacked barplot showing the number of called interactions between covNorm (fixed threshold: FDR < 1%) and CHiCAGO (score ≥ 1 to 5, x-axis). Intersections between the two methods are marked with orange. F. A Venn diagram showing similar number of significance interaction call of covNorm (FDR < 1%) and CHiCAGO (score ≥ 3.5) in GM12878 pcHi-C data (Hypergeometric p-value ~0). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

In the case of pcHi-C data, the difference between replicates was more significant than that of Hi-C. The fraction of reproducible long-range significant chromatin contacts between replicates was lower (~30%) in both covNorm and CHiCAGO (Fig. 4C). The AUC value of the ROC curve were about 85% for both methods (Fig. 4D). Unlike Fit-Hi-C, which consistently made more interaction calls than covNorm under various cutoffs, CHiCAGO called a smaller number of interactions when the “score” threshold of ≥4 was used (Fig. 4E). Also, the portion of method-specific results increased as the CHiCAGO’s score threshold increases (covNorm FDR threshold fixed to < 1%). Both methods report a similar number of significant interactions when we use CHiCAGO score over 3.5, but 56% and 52% of significant interactions were uniquely reported by covNorm and CHiCAGO, respectively (Fig. 4F).

3.4. Enriched chromatin signatures of covNorm-specific significant long-range chromatin contacts

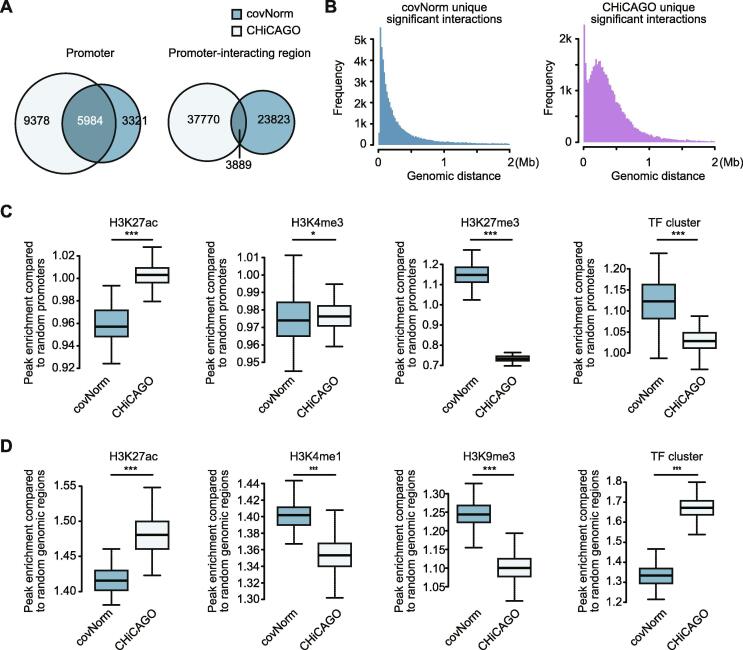
Further analysis was conducted to find out the cause of different results between covNorm and CHiCAGO. We firstly investigated the uniqueness of the promoters and promoter-interacting other genomic regions. The results shown in Fig. 5 illustrate the overlapping ratio of interacting elements associated with the unique significant interactions between the two methods. The promoters involved in the interactions showed moderate consensus as 64% of the two sets matched in terms of the smaller number set (Fig. 5A left). The promoter-interacting regions (Fig. 5A right) presented a greater difference as the overlap ratio decreased to 14%, indicating that many of covNorm-specific significant interactions are originated from the unique promoter-interacting regions regions rather than promoters.

Fig. 5.

Different properties of method-specific significant interactions. A. Venn diagrams showing the fraction of overlaps of the unique promoter (left) and promoter-interacting region (right) between two methods’ specific significant interaction sets (Hypergeometric p-values > 0.05 for the promoter and < 9.56e-231 for the other regions). B. Histograms showing genomic distance distribution of method-specific significant interactions (Left: covNorm, right: CHiCAGO). C. Boxplots showing enriched chromatin signatures (H3K27ac, H3K4me3, H3K27me3, and TF cluster in series) at the promoter regions specifically associated with method-specific significant long-range chromatin contacts. The y-axis indicates the peak inclusion ratio compared to the promoter side fragment of random non-significant interactions. (Asterisks indicate significance, two-sided Komologv-Sminorv test, p-values of 4.807e-14, 0.01581, < 2.2e-16, and 1.071e-06 in series) D. Boxplots showing enriched chromatin signatures (H3K27ac, H3K4me1, H3K9me3, and TF cluster in series) of method-specific promoter-interacting region sets. The y-axis indicates the peak inclusion ratio compared to the promoter-interacting region side fragment of random non-significant interactions (Asterisks indicate significance, two-sided KS-test, p-value < 2.2e-16 for all boxplots). For the boxplots, the box represents the interquartile range (IQR) and the whiskers correspond to the highest and lowest points within 1.5 × IQR.

The distance distribution profiles of unique significant interactions were also investigated. While covNorm’s unique significant interactions followed an expected profile that exponentially decreases as genomic distance increases (Fig. 5B right), CHiCAGO’s unique significant interactions showed another peak at 250 kb regions (Fig. 5B left). This suggests that the ways to incorporate genomic distance dependent background model may cause the method-specific preference.

We further hypothesized that the different chromatin states of the interacting loci resulted in method-specific results since the higher-order chromatin structure is lhighly correlates with the chromatin states. To this end, we tested the enrichment of chromatin signatures at the loci of the method-specific promoter or promoter-interacting regions. The lists of peaked regions for individual ChIP-seq results of GM12878 cell line were downloaded from the ENCODE data portal [27]. The H3K27ac (active enhancer), H3K4me3 (active promoter), H3K4me1 (poised enhancer), H3K9me3 (constitutive heterochromatin), and H3K27me3 (silencer, bivalent promoter, and facultative heterochromatin) ChIP-seq results were selected as these histone modifications are well-known markers of the chromatin state. We also included a list of transcription factor (TF) clusters, which were highly involved in long-range chromatin interactions [16]. The ratios of ChIP-seq peak/TF cluster inclusion (whether each fragment contains the ChIP-seq peak or not) compare to the 100 control sets (promoter from the random promoter regions and promoter-interacting region from the random non-significant interactions) were measured.

The enrichment test results of the promoter side (Fig. 5C) showed that all ChIP-seq peaks and TF clusters were enriched below compared to the random promoter regions (1 equals the expected enrichment at the promoter regions). This result indicates that the promoters uniquely associated with method-specific significant chromatin contacts tend to possess weak promoter signatures. Despite such weak promoter signals, we observed that the significantly higher enrichment of H3K27ac in CHiCAGO (two-sided Kolomogov-Smirnov test, p-value = 4.807e-14) while covNorm showed significant enrichment of H3K27me3 and TF cluster (two-sided KS-test, p-values < 2.2e-16 and 1.1e-06, respectively). In the case of H3K4me3, covNorm has higher dispersion and maximum values while CHiCAGO has a slightly higher median value (two-sided KS-test, p-value = 0.016).

Unlike the promoter regions, the promoter-interacting region side (Fig. 5D) had significant enrichment of covNorm in H3K4me1 and H3K9me3 (two-sided KS-test, p-values < 2.2e-16) while CHiCAGO had higher enrichment at H3K27ac and TF cluster (two-sided KS-test, p-values < 2.2e-16) compared to the random expectation. The distinct enrichments of ChIP-seq peaks demonstrate that the unique interactions of the covNorm were more associated with the genomic regions corresponding to silencer or poised enhancer signatures, while CHiCAGO’s interactions were highly related with the active enhancers. The H3K27me3 was also tested; however, the data was excluded as the enrichment level results of both methods showed no difference compared to the random control.

Interaction frequencies are expected to be different depending on the loci’s chromatin state. For example, chromatins in the different compartment are expected to have distinct characteristics in the established long-range chromatin interactions. Such features might be differently processed by the covNorm and CHiCAGO and contribute to the differences of the results. Also, the results indicate that there is still ample room for the advancing significant interaction calling techniques. Different significant interactions are called depending on the genome feature; however, none of the methods currently considers chromatin state for calling significant interactions.

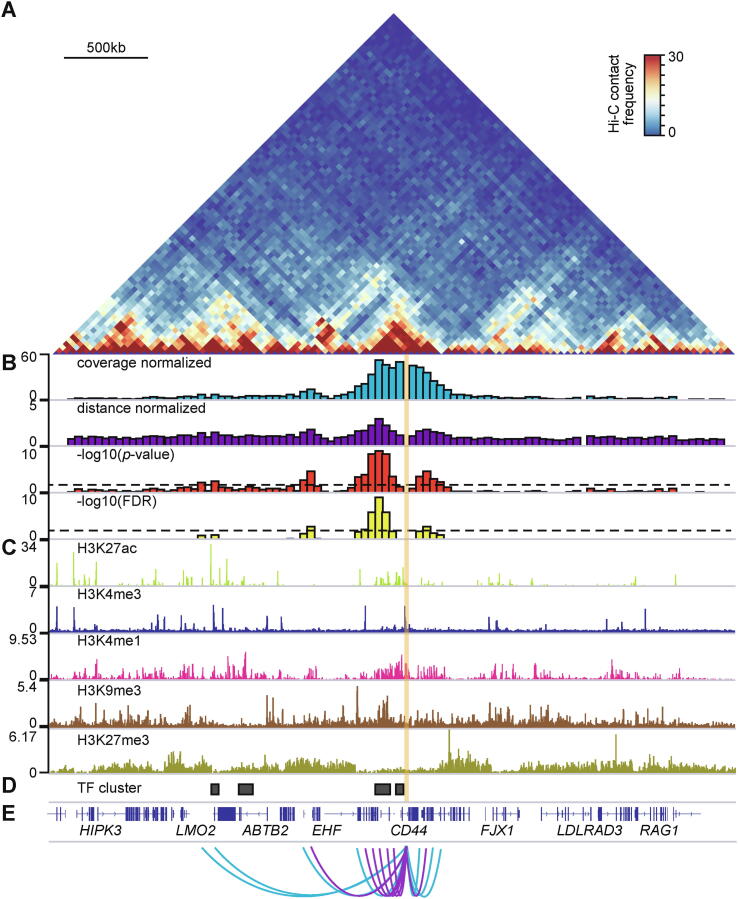
Even though covNorm was not made only for significant interaction calling, it showed similar or enhanced performance to other dedicated software in some criteria. An example of promoter-centered significant interactions from the GM19204 Hi-C data which shows the interactions between the TF clusters and loci with multiple chromatin signatures is provided in Fig. 6.

Fig. 6.

Visualization of CD44 gene-centered significant long-range interactions in GM19240 Hi-C data A. Normalized Hi-C contact map (chr11:33,120,000–37,120,000) of GM19240 cell line and CD44 gene loci (translucent orange box). Scale bar indicates 500 kb distance. B. Genome tracks showing coverage normalized, distance-dependent signal normalized, interaction p-value, and false discovery rate (FDR) of CD44 gene-centered Hi-C interactions. Dashed lines indicate -log10(p-value) > 2 and -log10(FDR) > 2 threshold. C. Genome tracks showing H3K27ac, H3K4me3, H3K4me1, H3K9me3, and H3K27me3 level. D. Genome track showing location of GM12878 transcription factor clusters. E. Arcs indicating the significant interactions under different thresholds (blue: -log10(p-value) > 2 and purple: -log10(FDR) > 2). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.5. Fitting parameter acquisition by subsampled data for scalability

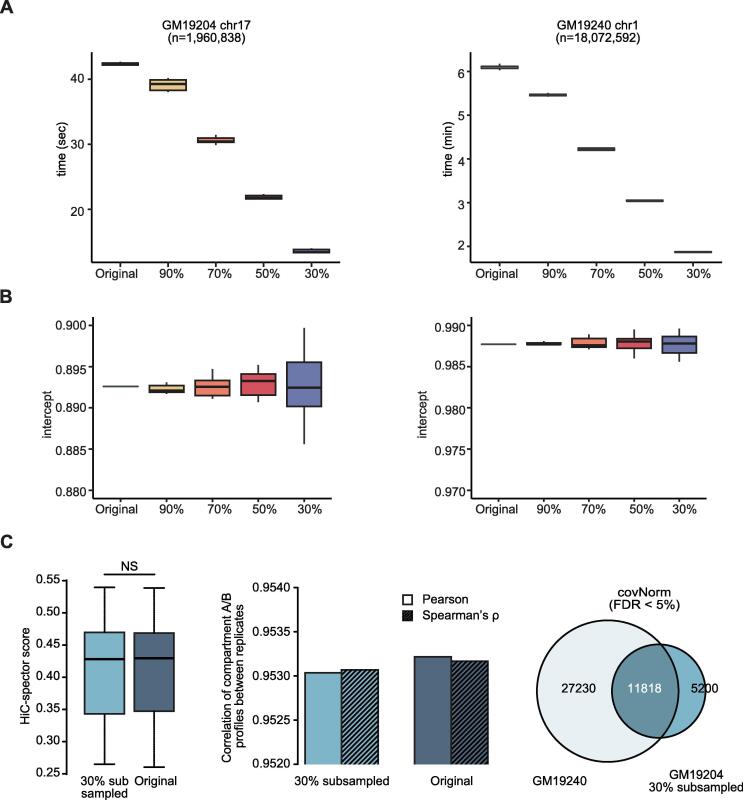
The advance of cost-effective high-throughput sequencing technologies allows the rapid increase of the high sequencing depth Hi-C data. In this aspect, the scalability of the method to keep up with increasing data volumes is critical. The fitting-based normalization provides many advantages such as handling data from the variant protocol or simplicity of implementation; however, computational and time burden for the fitting increase as input data size increases. To address this issue in covNorm, we hypothesized that if the data size is large enough, the parameters obtained by fitting the sampled data will remain unaffected. The functions for “fitting by subsampled data” with user-adjustable sampling ratio were implemented in covNorm. Note that this procedure differs from the “downsampling” mentioned in the previous section. In this procedure, the GLM fitting uses sampled data only, but all input data are processed by the obtained parameters after fitting instead of discarding the unsampled data. By doing so, we expected that the time and resources required for fitting are reduced, but the regression model of subsampled data remains similar to the original model.

For the evaluation of the proposed idea, we measured the time/parameter changes at the various sampling ratio conditions (90%, 70%, 50%, and 30%) when fitting small (GM19204 chr17, ~2M usable cis- reads) and large (GM19240 chr1, ~18 M usable cis- reads) data. The time required for the fitting linearly decreases as the data used for the fitting decrease by subsampling (Fig. 7A). The obtained parameter after fitting (intercept in this case) showed a larger variance as less portion of the original data used (Fig. 7B). As expected, the sample with the low depth had a higher variance of estimated parameters as the sampling ratio decreases. Despite such variations, surprisingly, the Hi-C contact map similarity (Fig. 7C left), compartment A/B correlation (Fig. 7C middle), and reproducible significant interactions between replicates (Fig. 7C right) showed almost the same results or non-significant changes (paired t-test, p-value = 0.18) with the original analysis even though only 30% of the GM19240 (~222 M usable cis reads in total) data were used. The scalable architecture of covNorm enabled users to efficiently normalize and identify significant interactions with high-depth Hi-C data.

Fig. 7.

Performance evaluation by parameter fitting with subsampled data A. Boxplots showing computation time for coverage-normalization of GM19204 chr17 (left) and GM19240 chr1 (right) Hi-C data at the multiple sampling ratio (n = 10). B. Boxplots showing changes of the fitting parameter (intercept) of GM19204 chr17 (left) and GM19240 chr1 (right) Hi-C data at the multiple sampling ratio (n = 10). C. Hi-C contact map reproducibility boxplot (left), compartment A/B correlation barplot (middle), and replicate-consensus significant interaction Venn diagram (right) generated by the subsampled GM19240 Hi-C (sampling ratio of 30%) data and the original data. The boxplots showed no significant differences (paired t-test, p-value = 0.18, NS). Hypergeometric test on the Venn diagram showed p-value ~0. For the boxplots, the box represents the interquartile range (IQR) and the whiskers correspond to the highest and lowest points within 1.5 × IQR.

4. Conclusion

In summary, we developed covNorm, an accurate method that is applicable to the normalization of Hi-C and capture Hi-C. Unlike previously developed methods that focus on either normalization of Hi-C contact map [6], [7], [8] or detection of long-range chromatin contacts [21] covNorm supports both functions together. covNorm, featured by flexible architecture and simple prerequisites, is expected to be highly useful for analyzing various Hi-C protocols.

Declaration of Competing Interest

The developed software is registered at the Korea Copyright Commission through KAIST Intellectual Property and Technology Transfer Center.