Predictive performance of machine and statistical learning methods: Impact of data-generating processes on external validity in the “large N, small p” setting

Abstract

Machine learning approaches are increasingly suggested as tools to improve prediction of clinical outcomes. We aimed to identify when machine learning methods perform better than a classical learning method. We hereto examined the impact of the data-generating process on the relative predictive accuracy of six machine and statistical learning methods: bagged classification trees, stochastic gradient boosting machines using trees as the base learners, random forests, the lasso, ridge regression, and unpenalized logistic regression. We performed simulations in two large cardiovascular datasets which each comprised an independent derivation and validation sample collected from temporally distinct periods: patients hospitalized with acute myocardial infarction (AMI, n = 9484 vs. n = 7000) and patients hospitalized with congestive heart failure (CHF, n = 8240 vs. n = 7608). We used six data-generating processes based on each of the six learning methods to simulate outcomes in the derivation and validation samples based on 33 and 28 predictors in the AMI and CHF data sets, respectively. We applied six prediction methods in each of the simulated derivation samples and evaluated performance in the simulated validation samples according to c-statistic, generalized R², Brier score, and calibration. While no method had uniformly superior performance across all six data-generating process and eight performance metrics, (un)penalized logistic regression and boosted trees tended to have superior performance to the other methods across a range of data-generating processes and performance metrics. This study confirms that classical statistical learning methods perform well in low-dimensional settings with large data sets.

1 Introduction

Predicting the probability of the occurrence of a binary outcome or event is of key importance in clinical medicine. Accurate prediction of the probability of adverse outcomes, such as mortality, allows for effective risk prediction to inform clinical decision making. There is increasing interest in the use of machine learning methods to estimate patient prognosis.

Hastie and colleagues use the term ‘learning’ to describe the process of making predictions about outcomes using empirical data. ¹ Breiman suggested that there are two cultures in the use of statistical models. ² The first assumes underlying stochastic models through which the data were generated, while the second treats the data mechanism as unknown and is based on the use of algorithms for prediction. For the purposes of the current paper, we use the term ‘statistical learning’ to describe the use of parametric models for prediction. We use the term ‘machine learning’ to describe the use of algorithms for prediction. Thus, bagged classification trees, random forests, and boosted trees would be examples of machine learning methods, while unpenalized logistic regression would be an example of a statistical learning method. Penalized regression, such as the lasso, is embraced by both cultures although these are highly parametric statistical models in the purest sense.

Several studies have compared the relative performance of methods from the machine learning literature with that of conventional statistical methods for predicting patient outcomes. Christodoulou and colleagues reviewed 71 studies that employed both types of methods for predicting binary outcomes. ³ They found that, in those comparisons that were at low risk for bias, the mean difference in c-statistic between the two types of approaches was 0. However, for those comparisons at high risk of bias, the mean logit of the c-statistic was 0.34 higher for machine learning than for logistic regression. Similarly, Couronné and colleagues applied random forests and logistic regression to 243 real datasets and found that, on average, the c-statistic for random forests was 0.041 higher than for logistic regression. ⁴ However, they also found that the results were dependent on the criteria to select datasets for inclusion in the analyses.

Our objective was to identify when machine learning methods perform better than a classical learning method. We hereto compare the relative predictive accuracy of five common machine learning and statistical methods with that of conventional unpenalized logistic regression. We considered six different data-generating processes, each based on a different machine or statistical learning method, and focused on external validation. The paper is structured as follows: In Section 2, we introduce the data on which the simulations will be based, describe six different machine and statistical learning methods, and describe the design of our simulations. In Section 3, we report the results of these simulations. Finally, in Section 4, we summarize our findings and place them in the context of the existing literature.

2 Methods

We performed simulations in two cohorts of patients hospitalized with cardiovascular disease. Within each cohort, six different data-generating processes were used, each based on fitting a different statistical or machine learning method to a derivation sample. Simulated binary outcomes were then generated in both the derivation sample and in an independent validation sample using the fitted model. In this section, we describe the data, the models and algorithms used, the data-generating processes and the statistical analyses that were conducted.

2.1 Data sources

We used data from The Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study, ⁵ which collected data on patients hospitalized with heart disease during two distinct temporal periods. During the first phase (referred to as EFFECT Phase 1), detailed clinical data were collected on patients hospitalized with acute myocardial infarction (AMI) and congestive heart failure (CHF) between April 1, 1999 and March 31, 2001 at 86 hospital corporations in Ontario, Canada, by retrospective chart review. During the second phase (referred to as EFFECT Phase 2), data were abstracted on patients hospitalized with these two conditions between 1 April 2004 and 31 March 2005 at 81 Ontario hospital corporations. Data on patient demographics, vital signs and physical examination at presentation, medical history, and results of laboratory tests were collected for these samples. In our simulations, we consider external validation. We used the two EFFECT Phase 1 samples (AMI and CHF) as derivation samples and the two EFFECT Phase 2 samples (AMI and CHF) as validation samples.

For the current study, data were available on 9484 and 7000 patients hospitalized with a diagnosis of AMI during the first and second phases of the study, respectively (8240 and 7608 for CHF, respectively).

The outcome was a binary variable denoting whether the patient died within 30 days of hospital admission (including out-of-hospital deaths). In each of the Phase 1 and Phase 2 AMI samples, 19.6% of patients died within 30 days of hospital admission. In the Phase 1 CHF sample, 32.7% of patients died within 30 days of hospital admission, while in the Phase 2 CHF sample, 31.2% of patients died within 30 days of hospital admission. Outcomes were ascertained through linkage with provincial death registries. Thus, loss to follow-up was not an issue in ascertaining mortality.

We considered 33 candidate predictor variables in the AMI sample. These consisted of demographic characteristics (age, sex); presentation characteristics (cardiogenic shock, acute congestive heart failure/pulmonary edema); vital signs on presentation (systolic blood pressure, diastolic blood pressure, heart rate, respiratory rate); classic cardiac risk factors (diabetes, hypertension, current smoker, dyslipidemia, family history of coronary artery disease); comorbid conditions (cerebrovascular disease/transient ischemic attack, angina, cancer, dementia, peptic ulcer disease, previous AMI, asthma, depression, peripheral vascular disease, previous revascularization, congestive heart failure, hyperthyroidism, aortic stenosis); and laboratory tests (hemoglobin, white blood count, sodium, potassium, glucose, urea, creatinine). The variance inflation factors (VIFs) for these 33 variables in the Phase 1 AMI sample ranged from 1.0 to 2.2, while the VIFs ranged from 1.0 to 2.1 in the Phase 2 AMI sample, suggesting limited collinearity.

We considered 28 candidate predictor variables in the CHF sample. These consisted of demographic characteristics (age, sex); vital signs on admission (systolic blood pressure, heart rate, respiratory rate); signs and symptoms (neck vein distension, S3, S4, rales > 50% of lung field, pulmonary edema, cardiomegaly); comorbid conditions (diabetes, cerebrovascular disease/transient ischemic attack, previous AMI, atrial fibrillation, peripheral vascular disease, chronic obstructive pulmonary disease, dementia, cirrhosis, cancer); left bundle branch block; and laboratory tests (hemoglobin, white blood count, sodium, potassium, glucose, urea, creatinine). The VIFs for these 28 variables in the Phase 1 CHF sample ranged from 1.0 to 1.9, while the VIFs ranged from 1.0 to 2.0 in the Phase 2 CHF sample. Thus, multicollinearity was limited in both the AMI and CHF samples.

It is important to note that the multivariate distribution of these covariates (including correlation between covariates) reflect those observed in two distinct populations of patients with cardiovascular disease (patients hospitalized with AMI and patients hospitalized with CHF).

2.2 Statistical and machine learning methods for predicting mortality

We considered six different methods for predicting the probability of 30-day mortality for patients hospitalized with cardiovascular disease: unpenalized (or conventional) logistic regression, bootstrap aggregated (bagged) classification trees, random forests of classification trees, boosted trees, ridge regression, and the lasso. Readers are referred elsewhere for details on these methods.^1,6–10

For bagged classification trees, a classification tree was grown in each of 500 bootstrap samples. A hyper-parameter was the minimum size of the terminal nodes. Selection of the hyper-parameters for all six methods is described in the following section. For random forests, 500 classification trees were grown. For random forests, there were two hyper-parameters: the minimum size of terminal nodes and the number of variables randomly sampled as candidates for defining each binary split. For boosted trees we applied Friedman's stochastic gradient boosting machines using trees as the base learners (we refer to hereafter as boosted trees).^9,11,12 For boosted trees, we considered sequences of 100 trees. There were two hyper-parameters: the interaction depth (specifying the maximum depth of each tree) and the shrinkage or learning rate parameter. When using unpenalized logistic regression to predict the probability of 30-day mortality, the regression model included as main effects all the variables listed above. The relationship between the log-odds of death and each continuous variable was modeled used restricted cubic smoothing splines. ¹³ For unpenalized logistic regression, there was one hyper-parameter: the number of knots used when constructing restricted cubic splines. Both ridge regression and the lasso considered the variables included in the unpenalized logistic regression model (however, for continuous variables, only linear terms were considered).

For all methods, we used implementations available in the R statistical programming language (R version 3.6.1, R Foundation for Statistical Computing, Vienna, Austria). For bagging and random forests, we used the randomForest function from the randomForest package (version 4.6–14). When fitting bagged classification trees, the mtry parameter was set to 33 (AMI sample) or 28 (CHF sample), so that all variables were considered at each split. The number of trees (500) was the default in this implementation. For boosted trees, we used the gbm function from the gbm package (version 2.5.1)). The number of trees (100) was the default in this implementation. We used the lrm and rcs functions from the rms package (version 5.1–3.1) to estimate the unpenalized logistic regression model incorporating restricted cubic regression splines with standard maximum likelihood for model estimation. Ridge regression and the lasso were implemented using the functions cv.glmnet (for estimating the λ parameter using 10-fold cross-validation) and glmnet from the glmnet package (version 2.0–18).

Bagged classification trees and random forests of classification are classifiers. In the current paper, we are focused on estimating probabilities rather than on classification. A predicted probability of the occurrence of the outcome was extracted from each of these two methods using the estimated class probabilities provided by the randomForest function.

2.3 Hyper-parameter tuning

Hyper-parameter tuning was performed in the EFFECT Phase 1 sample. A user-derived grid search was used for bagged classification trees, boosted trees, random forests and unpenalized logistic regression. The grid had one dimension for bagged classification trees (minimum size of terminal nodes) and unpenalized logistic regression (number of knots for the restricted cubic splines) and two dimensions for boosted trees (interaction depth and shrinkage or learning rate) and random forests (number of sampled candidate variables and minimum size of terminal nodes). For a given point on this grid (e.g. for a given number of sampled candidate variables and minimum size of terminal nodes for random forests), the EFFECT Phase 1 sample was randomly divided into 10 approximately equally sized groups. The given model, with the parameters set to those of the grid point, was fit in nine of the groups. The fitted model was then applied to the remaining group and predicted probabilities of the outcome were obtained for each subject in this remaining group. The accuracy of predictions was quantified using the Brier score (defined in a subsequent section). This process was conducted 10 times, so that each of the 10 groups was used once for validating predictions. The Brier score was then averaged across all 10 iterations of this procedure. The grid point that resulted in the lowest value of the Brier score was selected for all subsequent applications of that method. For both ridge regression and the lasso, the tuning parameter λ was estimated using ten-fold cross-validation in the derivation sample using the cv.glmnet function from the glmnet package.

In the AMI sample, the grid searches resulted in the following values for the hyper-parameters: bagged classification trees (minimum terminal node size: 19), boosted trees (interaction depth: 3; shrinkage/learning rate: 0.075), random forests (number of randomly sampled variables: 4; minimum terminal node size: 10), unpenalized logistic regression (number of knots: 4), lasso (λ = 0.000877), and ridge regression (λ = 0.0146).

In the CHF sample, the grid searches resulted in the following values for the hyper-parameters: bagged classification trees (minimum terminal node size: 19), boosted trees (interaction depth: 3; shrinkage/learning rate: 0.095), random forests (number of randomly sampled variables: 4; minimum terminal node size: 20), unpenalized logistic regression (number of knots: 4), lasso (λ = 0.00139), and ridge regression (λ = 0.0121).

2.4 Six data-generating processes for simulating outcomes

We considered six different data-generating processes for each of the two diseases (AMI and CHF). We describe the approach in detail for the AMI sample. An identical approach was used with the CHF sample. We used the EFFECT Phase 1 sample as the derivation sample and the EFFECT Phase 2 sample as the validation sample. For a given learning method (e.g. random forests), the method was fit in the EFFECT Phase 1. The fitted model was then applied to both the derivation sample (EFFECT Phase 1) and the validation sample (EFFECT Phase 2). Using the model/algorithm fit in the derivation sample, a predicted probability of the outcome (death within 30 days of hospital admission) was obtained for each subject in each of the two datasets (Phase 1 (derivation sample) and Phase 2 (validation sample)). Using these predicted probabilities, a binary outcome was simulated for each subject using a Bernoulli distribution with the given subject-specific probability. Thus, the simulated outcomes reflected the multivariable relationship between the baseline covariates and the outcome that were implied by the fitted algorithm (e.g. random forests). This process was repeated 1000 times, resulting in 1000 pairs of derivation and test samples. This process was repeated for each of the six different statistical/machine learning methods. Thus, we had a data-generating process based on bagged classification trees, boosted trees, random forests, ridge regression, the lasso, and unpenalized logistic regression. This approach to simulating outcomes is similar to that which was used in a previous study that examined the ‘data-hungriness’ of different statistical and machine learning methods. ¹⁴

2.5 Determining the performance of different predictive methods under different data-generating processes

For a given pair of derivation and validation samples, we fit each of the six statistical/machine learning methods (bagged classification trees, boosted trees, random forests, the lasso, ridge regression, and unpenalized logistic regression) in the derivation sample and then applied the fitted model to the test or validation sample. In the test or validation sample, we obtained, for each subject, a predicted probability of the outcome for each of the six prediction methods. The performance of the predictions obtained using each method was assessed using eight measures. The c-statistic (equivalent to the area under the receiver operating characteristic (ROC) curve) indicates discriminative ability. The c-statistic is defined as the proportion of all possible pairs of subjects, one of whom experienced the outcome of interest and one of whom did not, in which the subject who experienced the outcome of interest had a higher predicted probability of the outcome occurring than does the subject who did not experience the outcome. Nagelkerke’s generalized R² statistic, the Brier score, the integrated calibration index (ICI), E90, the calibration intercept and the calibration slope were used to assess calibration of predictions (i.e. correspondence between observed outcome proportions to predicted risks).^13,15,16 Nagelkerke’s generalized R² statistic is defined as $\frac{1-\exp (-LR/N)}{1-\exp (-L^0/N)}$ , where LR is the global likelihood ratio test statistic for comparing the model with p predictors to the null model, L⁰ is the -2 log likelihood for the null model, and N is the sample size. ¹³ Brier’s score is defined as $\frac{1}{N}{\displaystyle {\sum }_{i=1}^N{({\widehat{P}}_i-Y_i)}^2}$ , where $Y_i$ and ${\widehat{P}}_i$ denote the observed outcome and predicted probability for the ith subject, respectively. Lower values of the Brier score indicate greater predictive accuracy. The ICI is a calibration metric that denotes the mean differences between observed proportions and the predicted probability of the outcome. It is equivalent to the weighted difference between a smoothed calibration curve and the diagonal line denoting perfect calibration, averaged across the distribution of predicted risk.^16,17 E90 is a calibration metrics that denote the 90th percentile of the absolute differences between observed proportion and predicted probability of the outcome.^13,16 The calibration slope on the logit scale assesses deviation between observed and expected probabilities of mortality across the range of predicted risk. Deviation of the calibration slope from unity denotes miscalibration and indicates whether there was a need to shrink predicted probabilities at model development. The calibration intercept and slope are obtained by using logistic regression to regress the binary outcome on the linear predictor (log-odds) derived from the predicted probability. These seven performance measures were computed using the val.prob function from the rms package (version 5.1–3.1). Finally, we computed the negative of the out-of-sample binomial log-likelihood of the estimated probabilities in the validation sample.

Thus, when outcomes were simulated in the derivation and validation samples using random forests, we assessed the predictive accuracy of bagged classification trees, boosted trees, random forests, the lasso and ridge regression, and unpenalized logistic regression. This process was repeated using the datasets in which outcomes were simulated using the five other data-generating processes. The steps in the simulations are described in Box 1 for the random forests data-generating process (a similar process is used for each of the other five data-generating processes).

3 Results

We present the simulations results for the AMI and CHF samples separately. For each performance metric, we summarize the results across the 1000 simulation replicates using boxplots, with one boxplot for each combination of data-generating process and analytic method.

3.1 AMI sample

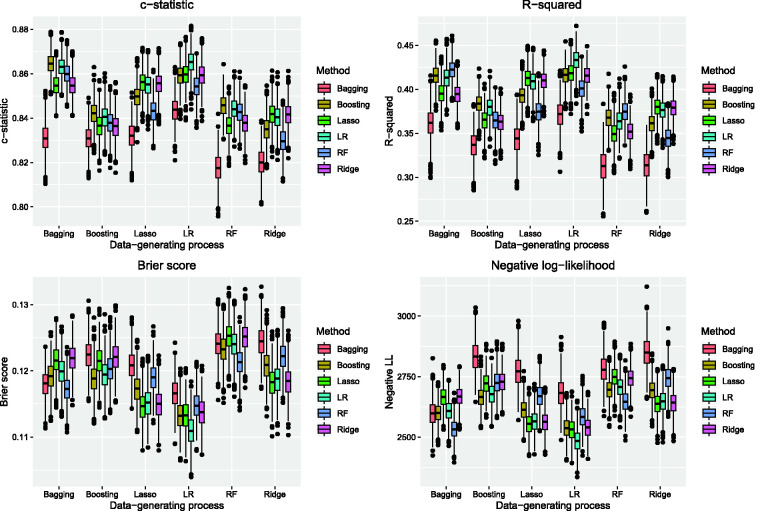
The performance of the six prediction methods under the six different data-generating processes is reported in Figures 1 and 2. Under the three tree-based data-generating processes, the use of boosted trees and unpenalized logistic regression tended to result in predictions with the highest c-statistics in the test samples (top-left panel in Figure 1). Under the three logistic regression-based data-generating processes, the use of unpenalized logistic regression tended to result in predictions with the highest c-statistics. When the data-generating process was based on either the lasso or ridge regression, the use of the three logistic regression-based approaches tended to result in estimates with similar c-statistics. Across all six data-generating processes, the use of bagged classification trees tended to result in estimates with the lowest c-statistic.

Figure 1.

AMI sample: model performance assessed using c-statistic, R-squared, Brier score, and negative log-likelihood. (There are eight panels across each pair of figures, one panel for each of the eight metrics of model performance. Each panel consists of six sets of six box plots. Each box plot describes the variation in the given performance metric across the 1,000 simulation replicates when a particular data-generating process and analytic method were used.)

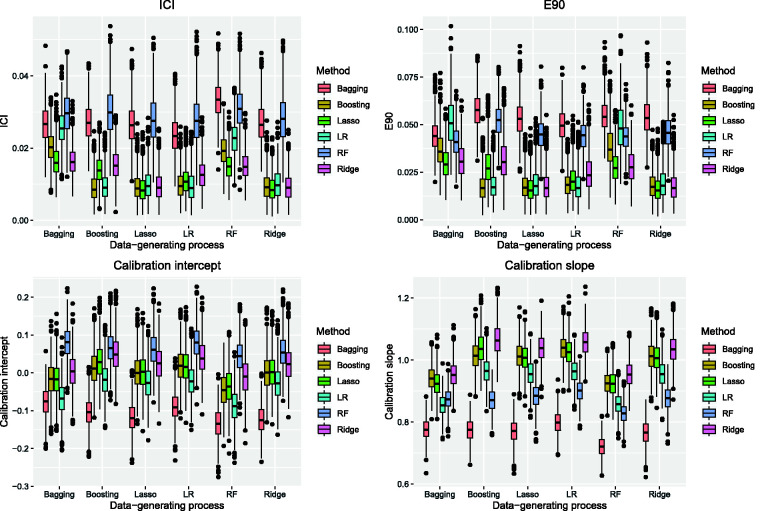
Figure 2.

AMI sample: model performance assessed using ICI, E90, calibration intercept, and calibration slope.

Boosted trees and unpenalized logistic regression tended to result in estimates with high R², regardless of the data-generating process (top-right panel in Figure 1). Random forests resulted in the highest R² when the outcomes were generated using either bagged classification trees or random forests. Under the four other data-generating processes, the use of boosted trees and unpenalized logistic regression tended to result in predictions with the highest generalized R² statistic in the test samples. The lasso and ridge regression had performance comparable to that of unpenalized logistic regression when outcomes were generated using either the lasso or ridge regression. Bagged classification trees resulted in the lowest R² across all six data-generating processes.

Unpenalized logistic regression tended to result in estimates with the lowest Brier score when outcomes were generated using one of the three logistic regression-based data-generating processes (bottom-left panel of Figure 1). When outcomes were generated using either the lasso or ridge regression, then these two methods tended to result in estimates with a Brier score comparable to that of unpenalized logistic regression. When outcomes were generated using either bagged classification trees or random forests, then the use of random forests tended to result in estimates with the lowest Brier score. When outcomes were generated using boosted trees, then both boosted trees and unpenalized logistic regression tended to result in estimates with the lowest Brier score.

When outcomes were generated using a logistic regression-based approach, then unpenalized logistic regression tended to result in estimates with among lowest the out-of-sample negative log-likelihood (bottom-right panel in Figure 1). The lasso and ridge regression had performance comparable to that of unpenalized logistic regression when outcomes were simulated under either the lasso or ridge regression. The use of random forests resulted in estimates with the lowest negative log-likelihood when outcomes were generated using either bagged classification trees or random forests. Boosted trees resulted in estimates with the lowest negative log-likelihood when outcomes were generated using boosted trees; however, unpenalized logistic regression had performance that approached that of boosted trees in this scenario.

When a logistic regression-based approach was used to simulated outcomes, the lasso and unpenalized logistic regression tended to result in estimates with the lowest ICI (top-left panel in Figure 2) and E90 (top-right panel in Figure 2), with the lasso tending to be slightly preferable to unpenalized logistic regression. Random forests tended to result in estimates with the lowest ICI and E90 when outcomes were generated using bagged classification trees or random forests. Unpenalized logistic regression tended to result in estimates with the lowest ICI and E90 when outcomes were generated using boosted trees (although boosted trees tended to be a close competitor).

Boosted trees tended to result in calibration intercepts very close to zero across five of the six data-generating processes (bottom-left panel in Figure 2). The one exception was when outcomes were generated using a random forest. Across five of the six data-generating processes, bagged classification trees resulted in estimates with a calibration intercept furthest from zero. The lasso resulted in estimates with calibration intercepts closer to zero than did unpenalized logistic regression across all six data-generating processes. Across five of the six data-generating processes, the use of the lasso and unpenalized logistic regression tended to result in estimates with a calibration intercept closer to zero than did the use of random forests (the one exception being when outcomes were generated using a random forest).

The use of bagged classification trees resulted in calibration slopes further from unity than the other five methods across all six data-generating processes (bottom-right panel in Figure 2). When using a logistic regression-based data-generating process, the use of the lasso resulted in estimates with calibration slope closer to unity than did the other five methods. When using a tree-based data-generating process, the use of boosted trees tended to result in calibration slopes close to unity.

3.2 CHF sample

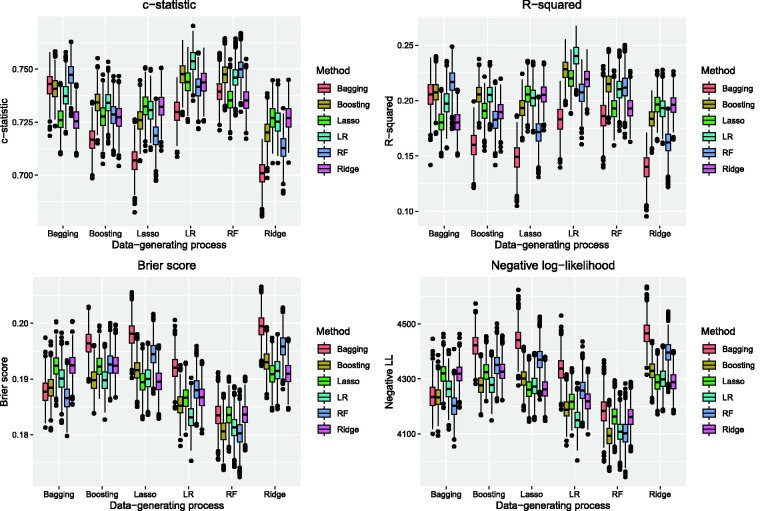
The performance of the six different prediction methods under the six data-generating processes is reported in Figures 3 and 4. Under the three tree-based data-generating processes, the use of boosted trees, random forests and unpenalized logistic regression tended to result in predictions with the highest c-statistics in the test samples (top-left panel in Figure 3). Under the three logistic regression-based data-generating processes, the use of unpenalized logistic regression tended to result in predictions with the highest c-statistics. When the data-generating process was based on either the lasso or ridge regression, the use of the three logistic regression-based approaches tended to result in estimates with comparable c-statistics. Across four of the six data-generating processes, the use of bagged classification trees tended to result in estimates with the lowest c-statistic.

Figure 3.

CHF sample: model performance assessed using c-statistic, R-squared, Brier score, and negative log-likelihood.

Figure 4.

CHF sample: model performance assessed using ICI, E90, calibration intercept, and calibration slope.

Boosted trees and unpenalized logistic regression tended to result in estimates with high R², regardless of the data-generating process (top-right panel in Figure 3). Random forests only resulted in estimates with the highest R² when outcomes were generated using bagged classification trees. The lasso and ridge regression had performance comparable to that of unpenalized logistic regression when outcomes were generated using either the lasso or ridge regression. Bagged classification trees resulted in the lowest R² across five of the six data-generating processes.

Unpenalized logistic regression tended to result in estimates with the lowest Brier score when outcomes were generated using one of the three logistic regression-based data-generating processes (bottom-left panel of Figure 3). When outcomes were generated using either the lasso or ridge regression, then these two methods tended to result in estimates with a Brier score comparable to that of unpenalized logistic regression. When outcomes were generated using either bagged classification trees or random forests, then the use of random forests tended to result in estimates with the lowest Brier score. When outcomes were generated using boosted trees, then both boosted trees and unpenalized logistic regression tended to result in estimates with the lowest Brier score.

When outcomes were generated using a logistic regression-based approach, then unpenalized logistic regression tended to result in estimates with among the lowest negative log-likelihood (bottom-right panel in Figure 3). The lasso and ridge regression had performance comparable to that of unpenalized logistic regression when outcomes were simulated under either the lasso or ridge regression. The use of random forests resulted in estimates with amongst the lowest negative log-likelihood when outcomes were generated using either bagged classification trees or random forests. Boosted trees and unpenalized logistic regression resulted in estimates with the lowest negative log-likelihood when outcomes were generated using boosted trees.

When a logistic regression-based approach was used to simulated outcomes, boosted trees, the lasso and unpenalized logistic regression tended to result in estimates with the lowest ICI (top-left panel in Figure 4) and E90 (top-right panel in Figure 4). The lasso and ridge regression tended to result in estimates with the lowest ICI and E90 when outcomes were generated using bagged classification trees or random forests. Boosted trees and unpenalized logistic regression tended to result in estimates with the lowest ICI and E90 when outcomes were generated using boosted trees.

Boosted trees tended to result in calibration intercepts very close to zero across five of the six data-generating processes (bottom-left panel in Figure 4). The one exception was when outcomes were generated using a random forest. Across five of the six data-generating processes, bagged classification trees resulted in estimates with a calibration intercept furthest from zero. The lasso resulted in estimates with calibration intercepts closer to zero than did unpenalized logistic regression across five of the six data-generating processes. Across five of the six data-generating processes, the use of the lasso and unpenalized logistic regression tended to result in estimates with a calibration intercept closer to zero than did the use of random forests (the one exception being when outcomes were generated using a random forest). Even when outcomes were generated using random forests, the use of the lasso resulted in estimates with a calibration intercept closer to zero than did the use of random forests.

The use of bagged classification trees resulted in calibration slopes further from unity than the other five methods across all six data-generating processes (bottom-right panel in Figure 4). When using a logistic regression-based data-generating process, the use of the lasso resulted in estimates with calibration slope closer to unity than did the other five methods. When using a tree-based data-generating process, the use of boosted trees tended to result in calibration slopes close to unity.

4 Discussion

There is a growing interest in comparing the relative performance of different machine and statistical learning methods for predicting patient outcomes. In order to better understand differences in the relative performance of competing learning methods, we used six different data-generating processes, each based upon a different learning method. This enabled us to examine the performance of methods different from those under which the data were generated compared to the method that was used to generate the data.

None of the six estimation methods had consistently superior performance across all eight performance metrics and across both samples. However, unpenalized logistic regression and boosted trees tended to have superior performance compared to the other six methods across a range of performance metrics. Furthermore, even when outcomes were generated using bagged classification trees, the use of bagging resulted in poorer performance compared to that of the competing methods. A potential explanation for the poor performance is that, in the presence of strong predictors, the grown regression trees may be correlated with one another. Random forests attempt to solve this problem by only considering a random sample of the predictors at each split.

When an algorithm (i.e. bagging, boosting or random forests) was used to generate the outcomes, the estimation of a prediction model with this algorithm tended to result in estimates with the best performance across the difference metrics; as might be expected. Some exceptions occurred. For instance, when outcomes were generated using bagged classification trees, random forests or boosted trees often resulted in estimates with the best performance. Furthermore, unpenalized logistic regression often had performance similar to that of the best-performing algorithm when outcomes were simulated using an algorithm.

We considered eight different metrics for assessing the performance of prognostic models. All eight were included in the current study to allow for a comprehensive assessment of the relative performance of different methods. However, in practice, greater emphasis is often placed on a small subset of these eight metrics. In practice, the c-statistic is often used as a measure of overall performance. Calibration is a second key component of model validation. In specific applied studies, the focus would often be on assessing calibration visually used smoothed calibration curves. As this is not feasible in studies using Monte Carlo simulations, we use the ICI as a summary measure of calibration as it represents the weighted average distance from the smoothed calibration curve and the diagonal line denoting perfect calibration. When focusing on the c-statistic, one would conclude that unpenalized logistic regression and boosted trees performed well across a wide variety of scenarios. When focusing on the ICI, the lasso performed well across a variety of scenarios. When outcomes were generated using a logistic regression-based method, then the use of the lasso often resulted in estimates the lowest ICI.

A strength of the current study was that our simulations were based on two real data sets, each with a realistic correlation structure between predictors and with realistic associations between predictors and outcomes. This is in contrast to many simulation studies, in which both the correlation structure between predictors and the strength of prognostic associations is chosen rather arbitrarily. Admittedly, other types of prediction problems may have stronger correlation structures, which might favor other methods than in our case studies. A second strength of the current study was our assessment of external validity. Due to the availability of independent derivation and validation samples that were obtained in temporally distinct eras, we were able examine the performance of each method in more recent independent validation samples.

Limitations to the current study included that both real datasets were of approximately the same size and both had approximately the same number of predictor variables (33 and 28 in the AMI and CHF samples, respectively). It is conceivable that different results could be observed with datasets of substantially different sizes (small n) or with a much larger number of predictor variables (large p). Moreover, the derivation and validation samples (Phase I versus II) were relatively similar. Differences in case-mix may be larger in independent validation studies from different regions. ¹⁸ Given that both our samples were of moderate to large size and contained a relatively small number of candidate predictor variables, the results of our simulations may not hold in other settings. In particular, the relative performance of the different prediction methods may differ in small n, large p scenarios. However, our sample sizes and number of candidate predictor variables are reflective of those in many clinical studies in which there is an interest in applying machine learning methods for predicting patient outcomes. Another limitation of the current study is its focus on predicting the probability of binary outcomes. Due to space constraints, we were unable to consider continuous and time-to-event (or survival) outcomes. However, predicting the occurrence of binary outcomes is an important issue in biomedical research, and many authors are interested in using machine learning methods for this purpose. The relative performance of these methods for predicting continuous and time-to-event outcomes merits examination in a subsequent study. A final limitation is that while the correlation structures for the candidate predictor variables reflected those observed for patients hospitalized with cardiovascular disease, it is conceivable that different results would be observed in settings with substantially different correlation structures. However, the fact that our simulations are based on empirical data on patients with cardiovascular disease, strengthens the generalizability of our findings when considering future application of statistical and machine learning methods in similar clinical contexts.

The focus of the current study was on the relative predictive accuracy of different learning methods when outcomes were simulated using different methods. While our focus was on using different performance metrics for assessing predictive accuracy, it should be highlighted that logistic regression-based approaches offer an interpretative advantage compared to tree-based ensemble methods. Logistic regression-based approaches produce odds ratios that allow one to quantify the relative contribution of each covariate to the outcome. In scenarios in which logistic regression-based approaches had comparable performance to that of machine learning methods, this would suggest that the logistic regression-based approaches should be preferred.

Many studies have compared the performance of logistic regression with that of machine learning methods using empirical datasets. As noted in section 1, Christodoulou and colleagues reviewed 71 studies that employed both types of methods for predicting binary outcomes. ³ For those comparisons at low risk of bias, the difference in the logit of the c-statistic between logistic regression and machine learning methods was 0 (95% CI: −0.18 to 0.18), while for those comparisons at high risk of bias, the logit of the c-statistic was, on average, 0.34 higher (95% CI: 0.20 to 0.47) for machine learning methods. Calibration was not assessed in the majority of studies. Similarly, Couronné and colleagues applied both random forests and logistic regression to 243 real datasets. ⁴ The mean difference between the c-statistic between random forests and logistic regression was 0.041 (95% CI: 0.031–0.053), with random forests having, on average, higher c-statistics than logistic regression. They observed that their results were dependent on the criteria used to select datasets for inclusion in their analyses. Shin and colleagues conducted a review of 20 published studies that compared the performance of conventional statistical methods with that of machine learning methods for predicting mortality and readmission in patients hospitalized with heart failure. ¹⁹ In general, machine learning methods tended to result in estimates with higher c-statistics than did conventional statistical methods. Finally, Hassanipour and colleagues conducted a systematic review incorporating 10 studies that compared artificial neural networks to logistic regression for predicting outcomes in trauma patients. ²⁰ The pooled estimate of the c-statistic for neural networks was 0.91, while it was 0.89 for logistic regression. Common to all the comparisons summarized in the above four studies is that they were all conducted using actual (or empirical) datasets. There is a paucity of studies that have used simulations to compare the performance of logistic regression with that of machine learning methods for prediction. An advantage to the use of simulations is that the investigator knows what the ‘truth’ is, and can compare the estimates obtained using different methods to those obtained when using the ‘true’ model. Van der Ploeg used simulations similar to our simulations, when assessing the relative ‘data hungriness’ of different learning methods. ¹⁴ We are unaware of any studies that used simulations to compare the performance of logistic regression with that of machine learning methods for prediction in a new, external setting. There are a small number of studies that used simulations to compare different methods for classification. Kirasich et al. used simulations to compare the performance of logistic regression with that of random forests for binary classification (as opposed to binary prediction, as was done in the current study). ²¹ They found that logistic regression performed with a higher overall accuracy compared to random forests. Similarly, Vafeiadas and colleagues used simulations to compare a set of classification methods (including logistic regression) to the boosted version of each classifier. ²² They found that the boosted version of each classifier had superior performance to the unboosted version of each classifier. A strength of the current study is that we considered six different data-generating processes, each based on a different machine or statistical learning method. In particular, we compared the predictive performance of the method under which outcomes were simulated with that of other methods. Furthermore, as noted above, our simulations were informed by analyses of empirical datasets, so that the correlation structure and prognostic associations reflected those observed in practice.

In conclusion, we found that when assessing internal validity, boosted trees, the lasso, ridge regression and unpenalized logistic regression tended to have superior performance to other learning methods across a wide range of data generating processes. Random forests tended to have poor performance when outcomes were generated under a method other than random forests. When assessing external validity, boosted trees, lasso, ridge regression and unpenalized logistic regression tended to have superior performance to other learning methods across a wide range of data generating processes. Importantly, conventional unpenalized logistic regression without any shrinkage or feature selection tended to have good performance, often exceeding that of competing machine learning methods. Given the importance of external validation when assessing clinical prediction models, we suggest that greater attention should be placed on the second set of findings.

Appendix 1. R code for a data-generating process based on random forests

This code is available at https://github.com/peter-austin/SMMR-Machine-Learning-data-generating-processes.

# THIS CODE IS PROVIDED FOR ILLUSTRATIVE PURPOSES AND COMES WITH

# ABSOLUTELY NO WARRANTY.

# 1) Applies a random forest to the EFFECT1 dataset.

# 2) Determines the predicted probability of the event in EFFECT1 and EFFECT2

# data using the model fit to the EFFECT1 data.

# 3) For each subject in each of the two phases of EFFECT, a binary outcome is

# simulated using this predicted probability.

# 4) The other models are then applied to the EFFECT data with these simulated

# outcomes:

# 5) Each model is developed in the EFFECT1 sample (with simulated outcome).

# 6) Each model is then applied to the EFFECT2 sample

# (with the simulated outcome).

library(rms)

library(randomForest)

library(gbm)

library(glmnet)

################################################################################

# Fix number of trees for different methods

################################################################################

n.tree.rf <- 500

n.tree.bagg <- 500

# Default number of trees for RF/Bagging

n.tree.gbm <- 100

# Default number of trees for GBM.

################################################################################

# Read in parameter values from grid search for tuning ML parameters.

################################################################################

tune.bagg.list <- list(bagg.nodesize = 0)

tune.bagg <- scan("TUNE/BAGG/bagg.optimal",tune.bagg.list)

tune.gbm.list <- list(gbm.interaction.depth = 0,gbm.shrinkage = 0)

tune.gbm <- scan("TUNE/GBM/gbm.optimal",tune.gbm.list)

tune.lrm.list <- list(lrm.knot = 0)

tune.lrm <- scan("TUNE/LRM/lrm.optimal",tune.lrm.list)

tune.rf.list <- list(rf.mtry = 0,rf.nodesize = 0)

tune.rf <- scan("TUNE/RF/rf.optimal",tune.rf.list)

tune.lasso.list <- list(lasso.lambda = 0)

tune.lasso <- scan("TUNE/LASSO2/lasso.optimal",tune.lasso.list)

tune.ridge.list <- list(ridge.lambda = 0)

tune.ridge <- scan("TUNE/RIDGE2/ridge.optimal",tune.ridge.list)

remove(tune.bagg.list,tune.gbm.list,tune.lrm.list,tune.rf.list,

tune.lasso.list,tune.ridge.list)

################################################################################

# Reads in EFFECT1 and EFFECT2 data from datasets created in SAS.

################################################################################

effect1.df <- read.table("ami_1.txt",header=T)

effect2.df <- read.table("ami_2.txt",header=T)

################################################################################

# Create matrices for use with LASSO and ridge regression

################################################################################

attach(effect1.df)

X.derive <- cbind(age,female,cshock,acpulmed,sysbp,

diasbp,hrtrate,resp,diabetes,highbp,smokhx,dyslip,famhxcad,cvatia,

angina,cancer,dementia,pud,prevmi,asthma,depres,perartdis,prevrevasc,

chf,hyprthyr,as,hgb,wbc,sod,pot,glucose,urea,cr)

detach(effect1.df)

attach(effect2.df)

X.valid <- cbind(age,female,cshock,acpulmed,sysbp,

diasbp,hrtrate,resp,diabetes,highbp,smokhx,dyslip,famhxcad,cvatia,

angina,cancer,dementia,pud,prevmi,asthma,depres,perartdis,prevrevasc,

chf,hyprthyr,as,hgb,wbc,sod,pot,glucose,urea,cr)

detach(effect2.df)

################################################################################

# Fits random forest to the EFFECT1 sample.

# Apply fitted model to EFFECT1 and EFFECT2 samples to get predicted probabilities

# to be used to generate outcomes.

# For different data-generating processes, code for the appropriate model

# replaces the random forest code in this block of code.

################################################################################

set.seed(28042020)

rf.effect1 <- randomForest(as.factor(mort1yr) ∼ age + female + cshock +

acpulmed + sysbp +

diasbp + hrtrate + resp + diabetes + highbp + smokhx + dyslip + famhxcad +

cvatia + angina + cancer + dementia + pud + prevmi + asthma + depres +

perartdis + prevrevasc + chf + hyprthyr + as + hgb + wbc + sod + pot +

glucose + urea + cr,

mtry=tune.rf$rf.mtry,nodesize=tune.rf$rf.nodesize,

ntree=n.tree.rf,replace=T,importance=T,

data=effect1.df)

prob.rf1 <- predict(rf.effect1,type="prob",newdata=effect1.df)[,2]

prob.rf2 <- predict(rf.effect1,type="prob",newdata=effect2.df)[,2]

effect1.df$prob.rf1 <- prob.rf1

effect2.df$prob.rf2 <- prob.rf2

################################################################################

# Main body of simulations.

################################################################################

for (iter in 1:1000){

set.seed(iter)

################################################################################

# Random forests data-generating process

# Generate outcomes in EFFECT1 and EFFECT2 using probabilities from RF.

################################################################################

effect1.df$Y <- rbinom(nrow(effect1.df),1,effect1.df$prob.rf1)

effect2.df$Y <- rbinom(nrow(effect2.df),1,effect2.df$prob.rf2)

################################################################################

# Apply logistic regression to simulated data.

################################################################################

lrm.1 <- lrm(Y ∼ rcs(age,tune.lrm$lrm.knot) + female + cshock + acpulmed +

rcs(sysbp,tune.lrm$lrm.knot) + rcs(diasbp,tune.lrm$lrm.knot) +

rcs(hrtrate,tune.lrm$lrm.knot) + rcs(resp,tune.lrm$lrm.knot) + diabetes +

highbp + smokhx + dyslip + famhxcad + cvatia + angina + cancer + dementia +

pud + prevmi + asthma + depres + perartdis + prevrevasc + chf + hyprthyr +

as + rcs(hgb,tune.lrm$lrm.knot) + rcs(wbc,tune.lrm$lrm.knot) +

rcs(sod,tune.lrm$lrm.knot) + rcs(pot,tune.lrm$lrm.knot) +

rcs(glucose,tune.lrm$lrm.knot) + rcs(urea,tune.lrm$lrm.knot) +

rcs(cr,tune.lrm$lrm.knot),

data=effect1.df)

pred.valid.lrm.xbeta <- predict(lrm.1,newdata=effect2.df)

pred.valid.lrm <- exp(pred.valid.lrm.xbeta)/(1 + exp(pred.valid.lrm.xbeta))

val.lrm <- val.prob(pred.valid.lrm,effect2.df$Y,pl=F)

roc.valid.lrm <- val.lrm["C (ROC)"]

r2.valid.lrm <- val.lrm["R2"]

brier.valid.lrm <- val.lrm["Brier"]

ici.valid.lrm <- val.lrm["Eavg"]

E90.valid.lrm <- val.lrm["E90"]

Emax.valid.lrm <- val.lrm["Emax"]

intercept.valid.lrm <- val.lrm["Intercept"]

slope.valid.lrm <- val.lrm["Slope"]

p.valid <- mean(effect2.df$Y)

brier.max.valid <- p.valid*((1-p.valid)^2) + (1-p.valid)*(p.valid^2)

brier.max.valid.lrm <- 1 - (brier.valid.lrm/brier.max.valid)

pred.valid.lrm <- ifelse(pred.valid.lrm==0,0.00001,pred.valid.lrm)

negLL <- -sum((effect2.df$Y)*log(pred.valid.lrm) +

(1-effect2.df$Y)*log(1-pred.valid.lrm))

cat(iter,roc.valid.lrm,r2.valid.lrm,brier.valid.lrm,brier.max.valid.lrm,

ici.valid.lrm,E90.valid.lrm,Emax.valid.lrm,intercept.valid.lrm,

slope.valid.lrm,negLL,

file="dgp.rf.lrm.out",fill=T,append=T)

remove(lrm.1,pred.valid.lrm.xbeta,pred.valid.lrm,val.lrm)

################################################################################

# Apply random forests to the simulated data.

################################################################################

rf.1 <- randomForest(as.factor(Y) ∼ age + female + cshock + acpulmed + sysbp +

diasbp + hrtrate + resp + diabetes + highbp + smokhx + dyslip + famhxcad +

cvatia + angina + cancer + dementia + pud + prevmi + asthma + depres +

perartdis + prevrevasc + chf + hyprthyr + as + hgb + wbc + sod + pot +

glucose + urea + cr,

mtry=tune.rf$rf.mtry,nodesize=tune.rf$rf.nodesize,

ntree=n.tree.rf,replace=T,importance=T,

data=effect1.df)

pred.valid.rf <- predict(rf.1,newdata=effect2.df,type="prob")[,2]

val.rf <- val.prob(pred.valid.rf,effect2.df$Y,pl=F)

roc.valid.rf <- val.rf["C (ROC)"]

r2.valid.rf <- val.rf["R2"]

brier.valid.rf <- val.rf["Brier"]

ici.valid.rf <- val.rf["Eavg"]

E90.valid.rf <- val.rf["E90"]

Emax.valid.rf <- val.rf["Emax"]

brier.max.valid.rf <- 1 - (brier.valid.rf/brier.max.valid)

intercept.valid.rf <- val.rf["Intercept"]

slope.valid.rf <- val.rf["Slope"]

pred.valid.rf <- ifelse(pred.valid.rf==0,0.00001,pred.valid.rf)

negLL <- -sum((effect2.df$Y)*log(pred.valid.rf) +

(1-effect2.df$Y)*log(1-pred.valid.rf))

cat(iter,roc.valid.rf,r2.valid.rf,brier.valid.rf,brier.max.valid.rf,

ici.valid.rf,E90.valid.rf,Emax.valid.rf,intercept.valid.rf,slope.valid.rf,

negLL,

file="dgp.rf.rf.out",fill=T,append=T)

remove(rf.1,pred.valid.rf,val.rf,negLL)

################################################################################

# Apply bagged classification trees to the simulated data.

################################################################################

bagg.1 <- randomForest(as.factor(Y) ∼ age + female + cshock + acpulmed + sysbp +

diasbp + hrtrate + resp + diabetes + highbp + smokhx + dyslip + famhxcad +

cvatia + angina + cancer + dementia + pud + prevmi + asthma + depres +

perartdis + prevrevasc + chf + hyprthyr + as + hgb + wbc + sod + pot +

glucose + urea + cr,

mtry = 33,ntree=n.tree.bagg,

nodesize=tune.bagg$bagg.nodesize,

replace=T,importance=T,

data=effect1.df)

pred.valid.bagg <- predict(bagg.1,newdata=effect2.df,type="prob")[,2]

val.bagg <- val.prob(pred.valid.bagg,effect2.df$Y,pl=F)

roc.valid.bagg <- val.bagg["C (ROC)"]

r2.valid.bagg <- val.bagg["R2"]

brier.valid.bagg <- val.bagg["Brier"]

ici.valid.bagg <- val.bagg["Eavg"]

E90.valid.bagg <- val.bagg["E90"]

Emax.valid.bagg <- val.bagg["Emax"]

brier.max.valid.bagg <- 1 - (brier.valid.bagg/brier.max.valid)

intercept.valid.bagg <- val.bagg["Intercept"]

slope.valid.bagg <- val.bagg["Slope"]

pred.valid.bagg <- ifelse(pred.valid.bagg==0,0.00001,pred.valid.bagg)

negLL <- -sum((effect2.df$Y)*log(pred.valid.bagg) +

(1-effect2.df$Y)*log(1-pred.valid.bagg))

cat(iter,roc.valid.bagg,r2.valid.bagg,brier.valid.bagg,brier.max.valid.bagg,

ici.valid.bagg,E90.valid.bagg,Emax.valid.bagg,intercept.valid.bagg,

slope.valid.bagg,negLL,

file="dgp.rf.bagg.out",fill=T,append=T)

remove(bagg.1,pred.valid.bagg,val.bagg,negLL)

################################################################################

# Apply GBM to the simulated data.

################################################################################

gbm.1 <- gbm(Y ∼ age + female + cshock + acpulmed + sysbp +

diasbp + hrtrate + resp + diabetes + highbp + smokhx + dyslip + famhxcad +

cvatia + angina + cancer + dementia + pud + prevmi + asthma + depres +

perartdis + prevrevasc + chf + hyprthyr + as + hgb + wbc + sod + pot +

glucose + urea + cr,

data = effect1.df,

distribution = "bernoulli",

n.trees = n.tree.gbm,

interaction.depth = tune.gbm$gbm.interaction.depth,

shrinkage = tune.gbm$gbm.shrinkage,

bag.fraction = 0.5,

train.fraction = 1.0,

cv.folds = 0,

keep.data = TRUE)

pred.valid.gbm <- predict(gbm.1,newdata=effect2.df,n.trees=n.tree.gbm,

type="response")

val.gbm <- val.prob(pred.valid.gbm,effect2.df$Y,pl=F)

roc.valid.gbm <- val.gbm["C (ROC)"]

r2.valid.gbm <- val.gbm["R2"]

brier.valid.gbm <- val.gbm["Brier"]

ici.valid.gbm <- val.gbm["Eavg"]

E90.valid.gbm <- val.gbm["E90"]

Emax.valid.gbm <- val.gbm["Emax"]

brier.max.valid.gbm <- 1 - (brier.valid.gbm/brier.max.valid)

intercept.valid.gbm <- val.gbm["Intercept"]

slope.valid.gbm <- val.gbm["Slope"]

pred.valid.gbm <- ifelse(pred.valid.gbm==0,0.00001,pred.valid.gbm)

negLL <- -sum((effect2.df$Y)*log(pred.valid.gbm) +

(1-effect2.df$Y)*log(1-pred.valid.gbm))

cat(iter,roc.valid.gbm,r2.valid.gbm,brier.valid.gbm,brier.max.valid.gbm,

ici.valid.gbm,E90.valid.gbm,Emax.valid.gbm,intercept.valid.gbm,

slope.valid.gbm,negLL,

file="dgp.rf.gbm.out",fill=T,append=T)

remove(gbm.1,pred.valid.gbm,val.gbm,negLL)

################################################################################

# Apply Lasso to the simulated data.

################################################################################

lasso.1 <- glmnet(X.derive,effect1.df$Y,alpha = 1,family="binomial",

lambda=tune.lasso$lasso.lambda)

pred.valid.lasso <- predict(lasso.1,X.valid,s=tune.lasso$lasso.lambda,

type="response")

val.lasso <- val.prob(pred.valid.lasso,effect2.df$Y,pl=F)

roc.valid.lasso <- val.lasso["C (ROC)"]

r2.valid.lasso <- val.lasso["R2"]

brier.valid.lasso <- val.lasso["Brier"]

ici.valid.lasso <- val.lasso["Eavg"]

E90.valid.lasso <- val.lasso["E90"]

Emax.valid.lasso <- val.lasso["Emax"]

brier.max.valid.lasso <- 1 - (brier.valid.lasso/brier.max.valid)

intercept.valid.lasso <- val.lasso["Intercept"]

slope.valid.lasso <- val.lasso["Slope"]

pred.valid.lasso <- ifelse(pred.valid.lasso==0,0.00001,pred.valid.lasso)

negLL <- -sum((effect2.df$Y)*log(pred.valid.lasso) +

(1-effect2.df$Y)*log(1-pred.valid.lasso))

cat(iter,roc.valid.lasso,r2.valid.lasso,brier.valid.lasso,brier.max.valid.lasso,

ici.valid.lasso,E90.valid.lasso,Emax.valid.lasso,intercept.valid.lasso,

slope.valid.lasso,negLL,

file="dgp.rf.lasso.out",fill=T,append=T)

remove(lasso.1,pred.valid.lasso,val.lasso,negLL)

################################################################################

# Apply ridge regression to the simulated data.

################################################################################

ridge.1 <- glmnet(X.derive,effect1.df$Y,alpha = 0,family="binomial",

lambda=tune.ridge$ridge.lambda)

pred.valid.ridge <- predict(ridge.1,X.valid,s=tune.ridge$ridge.lambda,

type="response")

val.ridge <- val.prob(pred.valid.ridge,effect2.df$Y,pl=F)

roc.valid.ridge <- val.ridge["C (ROC)"]

r2.valid.ridge <- val.ridge["R2"]

brier.valid.ridge <- val.ridge["Brier"]

ici.valid.ridge <- val.ridge["Eavg"]

E90.valid.ridge <- val.ridge["E90"]

Emax.valid.ridge <- val.ridge["Emax"]

brier.max.valid.ridge <- 1 - (brier.valid.ridge/brier.max.valid)

intercept.valid.ridge <- val.ridge["Intercept"]

slope.valid.ridge <- val.ridge["Slope"]

pred.valid.ridge <- ifelse(pred.valid.ridge==0,0.00001,pred.valid.ridge)

negLL <- -sum((effect2.df$Y)*log(pred.valid.ridge) +

(1-effect2.df$Y)*log(1-pred.valid.ridge))

cat(iter,roc.valid.ridge,r2.valid.ridge,brier.valid.ridge,brier.max.valid.ridge,

ici.valid.ridge,E90.valid.ridge,Emax.valid.ridge,intercept.valid.ridge,

slope.valid.ridge,negLL,

file="dgp.rf.ridge.out",fill=T,append=T)

remove(ridge.1,pred.valid.ridge,val.ridge,negLL)

}

Box 1.

Design of Monte Carlo simulations, starting with a random forest model.

1. Fit a random forest to the EFFECT1 sample using the observed outcomes. The observed outcomes are no longer used after this step.

2. Apply the random forest fit in Step 1 to both the EFFECT1 and EFFECT2 samples. Obtain a predicted probability of the outcome for each subject in the EFFECT1 and EFFECT2 samples using the fitted model.

3. Generate a binary outcome for each subject in the EFFECT1 and EFFECT2 samples using a Bernoulli random variable with subject-specific probability equal to the predicted probability obtained in Step 2. These are the simulated outcomes that will be used in all subsequent steps.

4. Apply a given analysis method (e.g. unpenalized logistic regression) by fitting that model to the EFFECT1 sample with the simulated outcomes generated in Step 3.

5. Apply the fitted model from Step 4 to the EFFECT2 sample.

6. For each subject in the EFFECT2 sample, obtain a predicted probability of the outcome based on the fitted analysis model that was applied to the EFFECT2 sample in Step 5.

7. Use the eight performance metrics to compare the predicted probability of the outcome obtained in Step 6 with the simulated binary outcome generated in Step 3.

8. Repeat Steps 3 to 7 1000 times. Summarize the performance metrics across the 1000 simulation replicates.

9. Repeat Steps 3 to 8 for a total of six analysis methods (lasso, ridge regression and unpenalized logistic regression; random forest, bagged classification trees, boosted trees).

10. Repeat Steps 1 to 9 with the five other data-generating processes (bagged classification trees, boosted trees, the lasso, ridge regression, and unpenalized logistic regression).