Abstract
Biosensor data have the potential to improve disease control and detection. However, the analysis of these data under free-living conditions is not feasible with current statistical techniques. To address this challenge, we introduce a new functional representation of biosensor data, termed the glucodensity, together with a data analysis framework based on distances between them. The new data analysis procedure is illustrated through an application in diabetes with continuous-time glucose monitoring (CGM) data. In this domain, we show marked improvement with respect to state-of-the-art analysis methods. In particular, our findings demonstrate that (i) the glucodensity possesses an extraordinary clinical sensitivity to capture the typical biomarkers used in the standard clinical practice in diabetes; (ii) previous biomarkers cannot accurately predict glucodensity, so that the latter is a richer source of information and; (iii) the glucodensity is a natural generalization of the time in range metric, this being the gold standard in the handling of CGM data. Furthermore, the new method overcomes many of the drawbacks of time in range metrics and provides more in-depth insight into assessing glucose metabolism.
Keywords: CGM technology, diabetes, biosensor data, distributional data analysis
1 Introduction
The steadily increasing availability and prominence of biosensor data have given rise to new methodological challenges for their statistical analysis. A primary feature of these data is that the monitored individuals are in free-living conditions, making a direct analysis of the recorded time series between groups of patients problematic if not infeasible. A clear example of such data is found in the study of diabetes, where continuous glucose monitoring (CGM) is increasingly used. The elevation of glucose is distinct between individuals and is influenced by factors such as mealtimes, diet composition, or physical exercise. 1 Consequently, an exciting topic of debate is how to exploit the enormous wealth of information recorded by CGM to draw more reliable conclusions about glucose homeostasis rather than the cursory summary measures such as fasting plasma glucose (FPG) or glycated hemoglobin (A1c). 2
Since 2010, the American Diabetes Association (ADA) has included measurement of A1c levels to both diagnosis and diabetes control. 3 A1c levels reflect underlying glucose levels over the preceding three months, testing is convenient because blood samples can be obtained at any time of day, overnight fasting is not required, and A1c within patient reproducibility is superior to that of fasting plasma glucose and oral glucose tolerance tests (OGTTs). 4 However, recent articles have provided evidence for the need to go beyond A1c and use new measures for glycemic control,5,6 in order to capture more diverse aspects of the temporally evolving glucose levels beyond the average, for example, glucose variability and time in range metrics. The time in range metric measures the proportion of time an individual’s glucose levels are maintained in different target zones. In the case of diabetes, these can include ranges corresponding to hypoglycemia and hyperglycemia. An innovative article 7 validated the time in range metric, showing that it is a good predictor of long-term microvascular complications despite just measuring glucose values seven times per day. Lu et al. 8 reached similar conclusions but using CGM technology only for 24 h in each patient. At the same time, it is well known that two patients may have the same glycosylated hemoglobin and a completely different glycemic profile. 9 These new approaches and findings have led clinical specialists to consider that continuous glucose measurement during long monitoring periods can lead to more accurate research and clinical practice results than standard methods. 10 In fact, since 2012, the European Medicine Agency 11 recommends the use of CGM to validate the effect of drugs for treatment or prevention of diabetes mellitus.
Traditionally, CGM was designed for risk management in real-time for type 1 diabetes, and control of glucose values with insulin pumps.12–14 Notwithstanding, more recent applications of CGM have been more general. For example, they involve screening patients, optimizing diet, epidemiological studies, assessing patient prognosis, supporting treatment prescriptions, and have even been used in healthy populations.15–17 In addition to the increasing utility of CGM data, the technology is gradually becoming cheaper, and new devices capable of measuring glucose in a non-invasive way are quickly emerging. 18 All of these advances are facilitating the adoption of CGM in standard clinical practice.
In 2012, a panel of experts discussed how to represent CGM data in an “easy to view format”. 19 They also analyzed the convenience of using glycemic variability measures and other summary measures such as time in range to extract the CGM’s recorded information. In 2019, 20 ADA launched an updated consensus guide for promoting the correct and standardized use of time in range metrics in standard clinical practice, defining several practitioners’ target zones. A more recent review about the CGM metric establishes time in range as a gold standard measure. 21
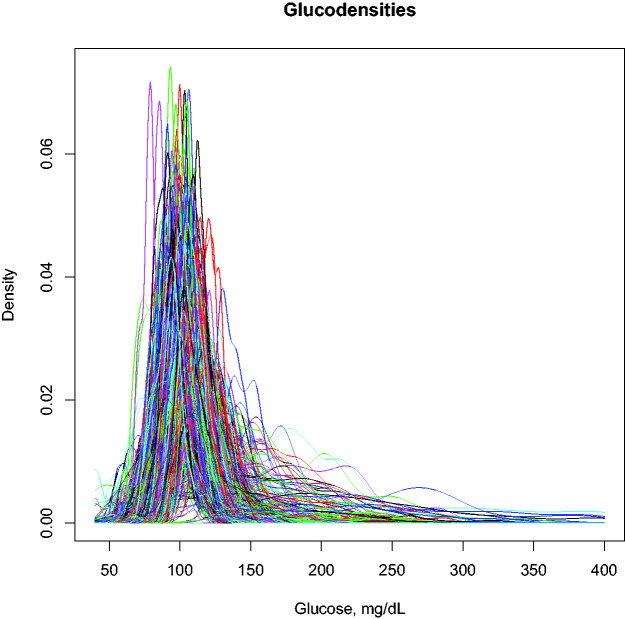
Motivated by the problem of analyzing data gathered via CGM more precisely while still leveraging the advantages possessed by time in range metrics, we propose an approach based on the construction of a functional profile of glucose values for each subject. Conceptually, the approach is a natural extension of time in range metrics in which the intervals simultaneously shrink in size and increase in number so that the new profile effectively measures the proportion of time each patient spends at each specific glucose concentration rather than a coarsely defined range. As a result, the new functional profile, which we refer to as a glucodensity, automatically and simultaneously captures all parameters arising from individual glucose distributions. To illustrate our new glucose representation graphically, Figure 1 shows a set of constructed glucodensities that represent the data objects for which we will propose using a tailored set of statistical methods. The glucose profile patterns are clearly heterogeneous between individuals, both in mean, variability, or any other distributional characteristics including the hypo and hyperglycemia range, where glucodensities have different support depending on patient condition. For example, in normoglycemic patients, glucose generally oscillates between 75 and 150 mg/dL, while in some patients with diabetes, glucose can reach concentrations of 400 mg/dL in the range of severe hyperglycemia. Moreover, the shape of the glucodensities is entirely different, with existing variability patterns along all glucose concentrations between normoglycemic and diabetes patients.
Figure 1.
Glucodensities are estimated from a random sample of the AEGIS study including normoglycemic and patients with diabetes. For each patient, our glucose representation estimates the proportion of time spent at each glucose concentration over a continuum, representing a more sophisticated approach to assess glucose metabolism. Currently, the time in range metrics that are the gold standard CGM data representation in diabetes only quantify glycemic distributional differences along the previously predefined target zones that correspond to coarsely defined intervals, resulting in information loss.
Mathematically, glucodensities constitute functional-distributional data since each glucodensity represents a distribution of glucose concentrations. As such, these complex and constrained curves cannot be directly analyzed with the usual techniques. To overcome this, we introduce a framework for the analysis of glucodensities by compiling suitable methods based on the calculation of distances between them. We also reveal our representation’s superior clinical capacity compared to classical measures of diabetes control and diagnostics. Finally, we demonstrate that our representation has a higher sensitivity than the standard time in range metric to explain the glycemic differences between patients in various settings, including regression analysis. A new shiny interface to use the methods outlined in this paper is available at https://tec.citius.usc.es/diabetes.
1.1 Outline
The structure of this paper is as follows. First, we briefly describe the AEGIS study. We then formally introduce the concept of glucodensity, the estimation methods, and some essential statistical background to understand the statistical procedures introduced in the paper. Subsequently, we explain the regression models used in the validation of the representation. Afterward, we show the results that demonstrate the superiority of glucodensity over glucose representations that are currently in use. Then, we illustrate the use with real data of the glucodensities methodology in two-sample testing and cluster analysis. Finally, we discuss the clinical implications of these results, their limitations, and new perspectives of the glucodensities method in medicine and device technology.
2 Sample and procedures
2.1 Study design
A subset of the subjects in the A Estrada Glycation and Inflammation Study (AEGIS; trial NCT01796184 at www.clinicaltrials.gov) provided the sample for the present work. In the latter cross-sectional study, an age-stratified random sample of the population (aged ≥18) was drawn from Spain’s National Health System Registry. A detailed description has been published elsewhere. 22 For a one-year period beginning in March, subjects were periodically examined at their primary care center where they (i) completed an interviewer-administered structured questionnaire; (ii) provided a lifestyle description; (iii) were subjected to biochemical measurements, and (iv) were prepared for CGM (lasting six days). The subjects who made up the present sample were the 581 (361 women, 220 men) who completed at least two days of monitoring, out of an original 622 persons who consented to undergo a six-day period of CGM. Another 41 original subjects were withdrawn from the study due to non-compliance with protocol demands (n = 4) or difficulties in handling the device (n = 37). The characteristics of the participants are shown in the Table 1.
Table 1.
Characteristics of AEGIS study participants by sex. Mean and standard deviation are shown.
| Men (n = 220) | Women (n = 361) | |
|---|---|---|
| Age, years | 47.8 ± 14.8 | 48.2 ± 14.5 |
| A1c, % | 5.6 ± 0.9 | 5.5 ± 0.7 |
| FPG mg/dL | 97 ± 23 | 91 ± 21 |
| HOMA-IR mg/dL.µUI/m | 3.97 ± 5.56 | 2.74 ± 2.47 |
| BMI kg/m2 | 28.9 ± 4.7 | 27.7 ± 5.3 |
| CONGA mg/dL | 0.88 ± 0.40 | 0.86 ± 0.36 |
| MAGE mg/dL | 33.6 ± 22.3 | 31.2 ± 14.6 |
| MODD | 0.84 ± 0.58 | 0.77 ± 0.33 |
BMI: body mass index; FPG: fasting plasma glucose; : glycated hemoglobin; HOMA: IR: homeostasis model assessment-insulin resistance; CONGA: glycemic variability in terms of continuous overall net glycemic action; MODD: mean of daily differences; MAGE: mean amplitude of glycemic excursions.
2.2 Ethical approval and informed consent
The present study was reviewed and approved by the Clinical Research Ethics Committee from Galicia, Spain (CEIC2012-025). Written informed consent was obtained from each participant in the study, which conformed to the current Helsinki Declaration.
2.3 Laboratory determinations
Glucose was determined in plasma samples from fasting participants by the glucose oxidase peroxidase method. A1c was determined by high-performance liquid chromatography in a Menarini Diagnostics HA-8160 analyzer; all A1c values were converted to DCCT-aligned values. 23 Insulin resistance was estimated using the homeostasis model assessment method (HOMA-IR) as the fasting concentration of plasma insulin (μ units/mL) × plasma glucose (mg/dL)/405. 24
2.4 Glycemic variability
Glycaemic variability was measured in terms of continuous overall net glycemic action (CONGA), 25 the mean amplitude of glycemic excursions (MAGE), 26 and the mean of the daily differences (MODD) 27 in glucose concentration.
2.5 CGM procedures
At the start of each monitoring period, a research nurse inserted a sensor (Enlite™, Medtronic, Inc., Northridge, CA, USA) subcutaneously into the subject’s abdomen and instructed him/her in the use of the iPro™ CGM device (Medtronic, Inc., Northridge, CA, USA). The sensor continuously measures the interstitial glucose level 40–400 (range mg/dL) of the subcutaneous tissue, recording values every 5 min. Participants were also provided with a conventional OneTouchR VerioR Pro glucometer (LifeScan, Milpitas, CA, USA) as well as compatible lancets and test strips for calibrating the CGM. All subjects were asked to make at least three capillary blood glucose measurements (usually before the main meals). These readings were taken without checking the current CGM reading. The sensor was removed on the seventh day, and the data downloaded and stored for further analysis. If the number of data-acquisition “skips” per day totaled more than 2 h, the entire day’s data were discarded.
2.6 Time-in-range metric
The time in range metric was calculated with two different methods. In the first, through the CGM records of the AEGIS study, we estimate the deciles of CGM records with normoglycemic patients and use these deciles as cut-offs that define the relevant ranges (Table 2). In the second, we use cut-off points established by the ADA in the 2019 Medical guideline 20 (Table 3).
Table 2.
Cut-offs for metric time in range using own estimations through normoglycemic individuals of AEGIS study.
| Range 1 | <85 |
| Range 2 | |
| Range 3 | |
| Range 4 | |
| Range 5 | |
| Range 6 | |
| Range 7 | |
| Range 8 | |
| Range 9 | |
| Range 10 | >125 |
Table 3.
Cut-offs for metric time in range following ADA guidelines 20 .
| Range 1 | <54 |
| Range 2 | |
| Range 3 | |
| Range 4 | |
| Range 5 | >250 |
3 Definition and estimation of the glucodensity
For patient i, denote the gathered glucose monitoring data by pairs where the tij represent recording times that are typically equally spaced across the observation interval, and Xij is the glucose level at time Note that the number of records mi, the spacing between them, and the overall observation length Ti can vary by patient. One can think of these data as discrete observations of a continuous latent processes with The glucodensity for this patient is defined in terms of this latent process as where
| (1) |
| (2) |
is the proportion of the observation interval in which the glucose levels remain below x. Since Fi are increasing from 0 to 1, the data to be modeled are a set of probability density functions
Of course, neither Fi nor the glucodensity fi is observed in practice, but one can construct an approximation through a density estimate obtained from the observed sample. In this case of CGM data, the glucodensities may have different support and shape. Therefore, we suggest using a non-parametric approach to estimate each density function. For example, using a kernel-type estimator, we have
where hi > 0 is the smoothing parameter and . The choice of K does not have a big impact on the efficiency of the estimator, but the value of hi is crucial. 28
In the standard setting of independent random samples, a vast number of approaches for selecting the smoothing parameter are available in the literature. Common strategies include cross-validation, minimizing the estimated mean integrated squared error (MISE), or a “rule of thumb” derived from the assumption that the density is Gaussian. In this last case, the choice can be explicitly written as , where is the sample standard deviation of the Xij. 29
Nevertheless, in our particular setup, we are estimating the density function of a stochastic process/time series, which is more difficult in theory. However, in a seminal work in this area, Hall et al. 30 showed that the rule of thumb and other traditional smoothing parameter selection strategies behave well. Additionally, the number of density function estimators that exist are considerable, and we can also employ other approaches as the use of orthogonal expansions (e.g. Fourier or Wavelet basis), splines, and histograms. For further details, the reader is referred to the relevant literature.28,31,32
3.1 Distance-based descriptive statistics
Let be an interval of the real line, which may be unbounded, and suppose that each glucodensity fi has support contained in . From a statistical point of view, the sample may be modeled and analyzed using methods of functional data analysis.33,34 However, since the fi must be positive and satisfy classical methods have in recent years been adapted to account for the nonlinear, distributional structure of density samples.35,36 The general approach is to define a metric or distance between densities that, in turn, leads to descriptive statistics that respect the unique density properties. For example, define the data space of glucodensities as . Given two arbitrary glucodensities , the 2-Wasserstein distance 37 between f and g is
| (3) |
where F and G are the cumulative distribution functions (cdfs) of the density functions f and g.
The 2-Wasserstein distance is a natural distance to measure the similarity between density functions through its representation in the space of the quantile (inverse cdf) functions, and it has already been successfully applied in biological problems. Furthermore, it has computational and modeling advantages compared to the usual metric when glucodensities have different support within . Finally, it has a physical interpretation in the theory of optimal transport.
As glucodensities are distributional data, the subsequent application of the usual techniques for functional data, such as estimation of mean, covariance, and regression models, may lead to misleading results. Hence, we have chosen to use models based on the 2-Wasserstein distance, although other choices are possible. As a starting point, based on the notion of distance, we can generalise the mean and variance of a random variable that takes values in an abstract space with metric structure. 38 As we will see, similar adaptations can be developed for regression, hypothesis testing, or to perform cluster analysis. Given a distance between density functions, of which is one example, and a random variable f defined on A, the Fréchet mean of f is
The Fréchet variance of f is then
If the choice of distance is the Wasserstein metric these are given the names of Wasserstein mean and variance, respectively. In this particular case, equation (3) implies that μf is the density whose quantile function is the pointwise mean of the random quantile function . Moreover, is interpreted as the integral of the pointwise variance of . In general, calculation of the Fréchet mean is not easy, and we must resort to computational approximations. 39
In the following subsections, we will extend these concepts of Frèchet to statistical methodologies of regression, clustering, and hypothesis testing based on the notion of distance.
4 Regression models with glucodensities
4.1 Non-parametric regression model with glucodensity as the predictor
Let f be a functional random variable taking values in and Y a random variable that takes values in the real line. We assume the following regression relationship between f and Y, which represent the predictor and response variables, respectively:
| (4) |
where is an unknown smooth function, and the random error ϵ satisfies .
Given a sample , most non-parametric estimators have the form of a weighted average of the responses,
| (5) |
In general, the weights depend on the distance selected to measure the similarities between the density functions fi and x, with larger distances receiving lower weights, and satisfy . 40 A typical choice would be the Nadaraya-Watson weights
| (6) |
where h is a smoothing parameter and is a known univariate probability density function called the kernel. For more details about this procedure, see Ferraty and Vieu. 40 As an alternative for the above method, we can use the kernel methods in Reproductive Kernel Hilbert Spaces (RKHS).41,42
4.2 Regression model with glucodensity as the response
In the case of regression models with a density function as response, the literature is not very extensive to the current date.43–47 In this article, we use the model proposed in Petersen and Müller 45 which allows us to incorporate the desired metric and is a direct generalization of classical linear regression. The primary rationale for the use of this model is that, unlike the other approaches cited above, there is a methodology developed to perform inferential procedures such as confidence bands and hypothesis testing in order to establish the significance of the input variables in the model. 48
Let f be a random variable (e.g. a glucodensity) that take values in the space of defined above. Consider a random vector that contains the set of predictors. Our interest is in the Frèchet regression function, or function of conditional Frèchet means,
| (7) |
Petersen and Müller 45 impose a particular model for that, in direct analogy to classical linear regression, takes the form of a weighted Frèchet mean
| (8) |
Here, the weight function is
| (9) |
and Σ is assumed to be positive definite.
Given a sample of independent pairs each distributed as one can proceed to estimate for any desired input u. Due to the intimate connection between the Wasserstein metric and quantile functions as in equation (3), for most inferential procedures it is sufficient to estimate the conditional Wasserstein mean quantile function corresponding to Let D be the set of quantile functions, Qi the quantile function corresponding to the random density and define empirical weights where and are the sample mean and variance of the respectively. The natural estimator under is the weighted empirical mean quantile function
| (10) |
where denotes the norm on D.
A straightforward algorithm for computing is shown in Supplementary Material of the original reference. 48 In addition, two algorithms are given to estimate the confidence bands at a given significance level α for both the quantile functional parameter and the density parameter .
4.3 Outline tuning parameters in statistical analysis and software details
The density function of each individual was estimated with a non-parametric Nadaraya-Watson procedure. For this purpose, we used a Gaussian kernel and rule of thumb as a smoothing parameter. As some computations involving the 2-Wasserstein metric only require a quantile function as input, these were estimated using the empirical quantile function of the observations.
Concerning prediction, the two regression models previously described were used in glucodensity validation: (i) the non-parametric kernel functional regression model with the 2-Wasserstein distance having the glucodensity as predictor 40 and (ii) a global 2-Wasserstein regression model where the glucodensity is the response. 45 In addition, with standard vector-valued time in range metrics, k-nearest neighbor algorithms were employed with k = 10 neighbors. These time in range metrics we first transformed using the isometric log-ratio (ilr) transformation for compositional data prior to fitting the model. 49 In order to avoid problems associated with zero values in any of these predefined ranges, a fixed positive constant was added to each range, which were then normalized to add to 1.
All analyses were carried out using R software. Functional data analysis was performed using the fda.usc package, 50 which is freely available at https://cran.r-project.org/, and our own implementations of the ANOVA test of Dubey and Müller 51 or Fréchet regression in Petersen and Müller 45 using the 2-Wasserstein distance. The glucodensities and their quantile representation were estimated using the R basis functions.
5 Clinical validation of the glucodensity
To validate the glucodensity representation, we use the database from the AEGIS study. 22 The database contains the continuous glucose monitoring data between two and six days of 581 patients from a general population’s random sample. To develop the validation task, we use two different regression models: (i) a non-parametric regression model where the unique predictor is glucodensity and (ii) a linear regression model where the response is a glucodensity. The first model was used to predict glycated hemoglobin (A1c), 52 homeostatic model assessment (HOMA-IR), 53 and the following measures of glycemic variability22,54,55: continuous overall net glycemic action (CONGA), mean amplitude of glycemic excursions (MAGE) and mean of daily differences (MODD), through glucodensity representation. In contrast, the second was used to predict the glucodensity with the five variables above. Figure 1 gives a visualization of the sample of glucodensities used in these models. Biological significance in variables under consideration is described in Table 4.
Table 4.
Clinical importance of biomarkers used in the statistical analysis.
| Biomarker | Clinical significance |
|---|---|
| A1c | Gold standard marker in diabetes diagnosis and control |
| HOMA-IR | Measurements to quantify insulin resistance and β-cell function |
| CONGA | |
| MODD | Summary indices of glucose variability |
| MAGE |
5.1 Prediction of biomarkers using the glucodensity
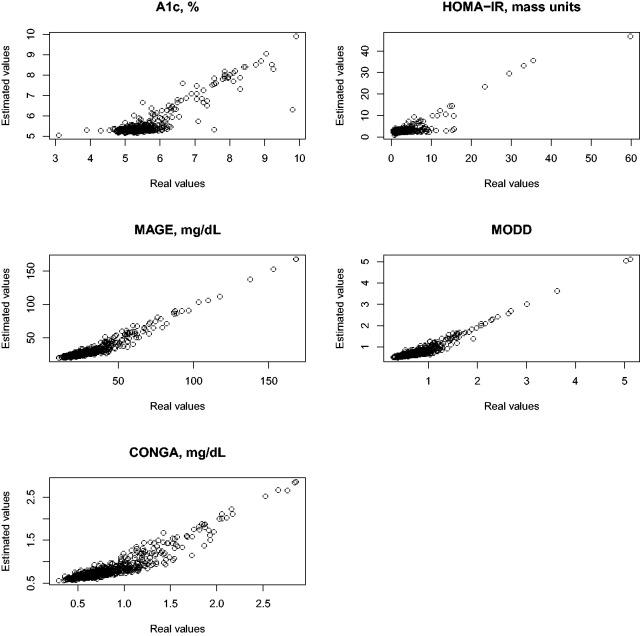
The aim of the first set of regression analyses is to demonstrate that the glucodensity is sufficiently rich in its information content to recover the biomarkers mentioned above with high precision. To quantify this precision, we estimated the R2 after fitting a non-parametric model for each biomarker as the outcome variable, using the glucodensity as the sole predictor (i.e. independent variable). The R2 estimates for A1c, HOMA-IR, MAGE, MODD, CONGA were 0.79, 0.79, 0.92, 0.86, and 0.92, respectively. To supplement the results, Figure 2 shows the predicted values against the observed values, where the outstanding predictive capacity of the glucodensity can be seen independently of high or low response values.
Figure 2.
Real values vs. estimated values when glucodensity is predictor.
5.2 Prediction of the glucodensity using biomarkers
In the second regression analysis with the glucodensity as the outcome variable, we aim to show that the previous measurements commonly used in the clinical practice cannot capture the glucodensity with high accuracy. This fact is not completely surprising because, as noted by some authors, 2 the information provided by a CGM is more precise than that contained in summary measures. To accomplish this, we computed a suitable version of R2 for this task after fitting a regression model where the response is a glucodensity, and the previous variables are the predictors. In this case, the R2 estimate was 0.74. As predicted, compared to the previous section’s results, we could not accurately capture the complex nature of glucodensities, even while using the combined predictive power of several commonly used summary measures. Moreover, in some cases, the prediction differences can be significant (see Figure 3).
Figure 3.
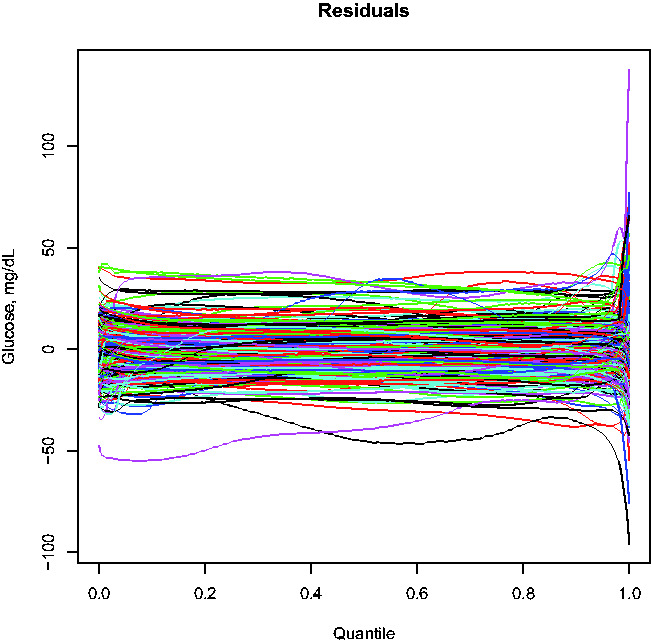
Residuals in quantile space when predicting glucodensities.
5.3 Comparison of time in range metrics with glucodensities
To illustrate the higher clinical sensitivity of glucodensities compared to time in range metrics, we compared each representation’s ability to predict A1c, HOMA-IR, and glycemic variability metrics MODD, MAGE, and CONGA, using the data from the AEGIS study. The predictive capacity of the glucodensity representation was illustrated above, and this section gives the corresponding results for time in range metrics, where these were calculated according to two sets of cut-offs. In the first, the normoglycemic individuals’ deciles from the AEGIS study were used, while those proposed by the ADA were used in the second. Tables 2 and 3 show the exact cut-off values for both cases. Since the time in range metrics constitute a sample of compositional data, 49 the isometric log-ratio (ilr) transformation was employed in combination with a k-nearest neighbor algorithm as a regression model for predicting the scalar variables.
5.4 Prediction of A1c, HOMA-IR, and glycemic variability measures using time in range metrics
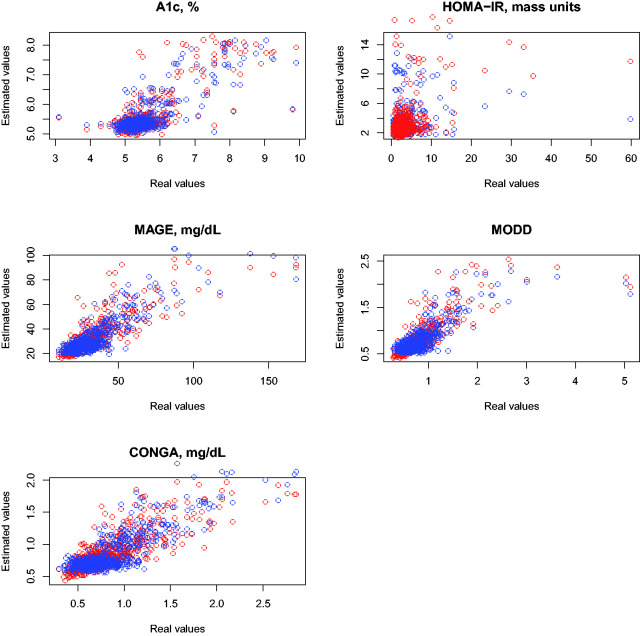
Figure 4 compares the real and estimated values of the previous five variables under the two time in range metrics under consideration with. Table 5 provides the estimates of R2 for each variable and metric.
Figure 4.
Real values vs. estimated values when time in range metric is the predictor. Blue, time in range metric with cut-offs calculated with normoglycemics from the AEGIS database. Red, time in range metric using of cut-offs suggested by ADA.
Table 5.
R2 estimated with time in range metrics under consideration and glucodensity.
| A1c | HOMA-IR | CONGA | MAGE | MODD | |
|---|---|---|---|---|---|
| Normoglycemic cut-off | 0.63 | 0.22 | 0.68 | 0.65 | 0.65 |
| ADA cut-off | 0.61 | 0.08 | 0.73 | 0.69 | 0.60 |
| Glucodensity | 0.79 | 0.79 | 0.92 | 0.92 | 0.86 |
The predictive capacity is significantly worse than that attained by the glucodensity methodology. The superiority of the glucodensity is particularly noteworthy in the case of the HOMA-IR variable, where the association is relatively weak for time in range metrics. Even for the other variables where the values of R2 are moderate, the larger residuals seen in patients with diabetes with more severe alterations of glucose metabolism indicate that time in range metrics are particularly poorly suited for such patients. Interestingly, we do not observe substantial or consistent differences between the two time in range metrics used, as deciles perform better than ADA criteria for two of the variables, while the ordering was reversed in other instances.
6 Hypothesis testing and clustering analysis with glucodensities
6.1 Analysis of variance with glucodensities
As a special case of regression, suppose we have a sample f1, fn of glucodensities defined on belonging to k different groups that partition and are of size nj , so that . If the goal is to simply test whether the Wasserstein means are equal for each group, Petersen et al. 48 developed testing procedures based on model (8) for this purpose. An advantage of this model is its flexibility, which allows for multiple factor layouts as well as tests for interactions. However, the theoretical properties of these tests require a type of equal variance assumption that may be restrictive for some data sets.
More generally, one may wish to test the null hypothesis that the population distributions of the k groups share common Wasserstein means and variances, against the alternative that at least one of the groups has a different population distribution compared to the others in terms of either its Wasserstein mean or variance. In this scenario, Dubey and Müller 51 investigated a test statistic based on the group proportions , the groupwise sample Wasserstein means and variances the pooled Wasserstein mean and variance and finally the quantities
as estimates of the variance of Then, with
the proposed test statistic is
| (11) |
Dubey and Müller 51 demonstrated that the corresponding test is distribution-free, in that the limiting distribution of Tn does not depend on the underlying distribution under some assumptions. In practice, it was also demonstrated that it could be useful to calibrate the test under the null hypothesis via a simple empirical bootstrap over the preceding statistics. For more details, we refer the reader to the supplementary material of the original reference.
6.2 Energy distance methods with glucodensities
The energy distance is a statistical distance between two distribution functions proposed in 1984 by Gábor J. Székely. 56 This distance is inspired by the concept of gravitational energy between two bodies and has experienced a rise in appeal for modern statistical applications due to its applicability to data of a complex nature such as functions, graphs, or objects that live in negative type space. 57
Consider independent random variables and that are defined on a (semi)metric space of negative type, where is the semi-metric. Although the notation in this section is quite general, in particular, we have in mind the case corresponding to glucodensities. The energy distance associated with ρ between the distribution F and G is
Given random samples and , the sample energy distance is
The asymptotic distribution of the above statistic for a null hypothesis as well as for the alternative is dependent on the chosen semi-metric ρ. Besides, its expression is difficult to calculate and to implement in practice. Hence, when using the energy distance based methods, the distribution under the null hypothesis is usually calibrated with a permutation method. Alternatives to calibrate the distribution under the null hypothesis include the wild or a weighted bootstrap, as described in literature.58,59 The energy distance can also be extended to handle samples from more than two populations. Given k independent samples the energy distance statistic is
where
We now explain how this statistic can be adapted to perform clustering. Consider random pairs where Yi is observed and takes values in while is an unobserved label of cluster membership. The task is to recover the true clusters Let be a generic partition of , and denote the size of each cluster by . Then, a clustering may be chosen by optimizing the statistic
| (12) |
| (13) |
over all possible clusters At first view, this seems computationally intractable due to the appearance of distances between the elements of each cluster. However, defining
| (14) |
it can be proven that is constant. This implies that maximizing is equivalent to minimizing .
In Franca et al., 60 the authors show the equivalence between the previous optimization problem with the clustering procedure kernel k-means. The latter relationship allows the solving of kernel k-group clustering procedure through the popular heuristics algorithms as Hartigan and Lloyd allow finding the optimal solution with the k-means algorithm.
6.3 Example of hypothesis testing and clustering analysis with glucodensity methodology
Below, we illustrate the methodology of glucodensities in hypothesis testing and cluster analysis with the 2-Wasserstein distance. We use the ANOVA test 51 and the k-groups algorithm. 60
6.4 Hypothesis testing
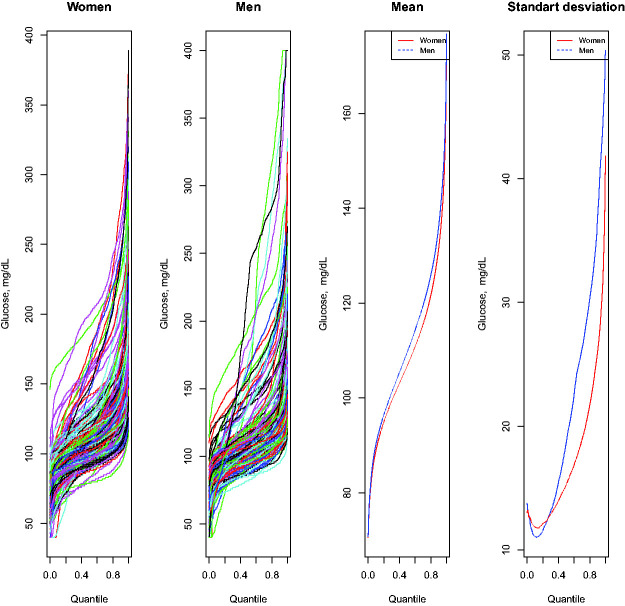
An interesting question to address in an epidemiological study is whether there are differences between men and women in the glycemic profile. The ANOVA test is an important instrument to establish whether there are statistically significant differences in mean and variance with glucodensities, where there are two or more patient groups. After applying this method with AEGIS data, the test yields a p-value equal to 0.10. Therefore, there is no statistically significant difference between men and women at the significance level of 5 percent.
Figure 5 shows the glucodensity samples for each gender using their quantile representations. The pointwise means of these quantile functions constitute the quantile function of the sample Wasserstein mean glucodensities. These, together with pointwise standard deviation curves, are also shown in Figure 5. On average, the groups are quite similar. However, certain discrepancies are observed between both groups in terms of their variance, although not large enough for the test to show statistically significant differences.
Figure 5.
(Left two panels) Glucodensities for men and women of the AEGIS study, plotted as quantile functions; (Third panel) 2-Wasserstein mean quantile functions for each group (Fourth Panel). Cross-sectional standard deviation curves for quantile functions in each group.
6.5 Clustering analysis
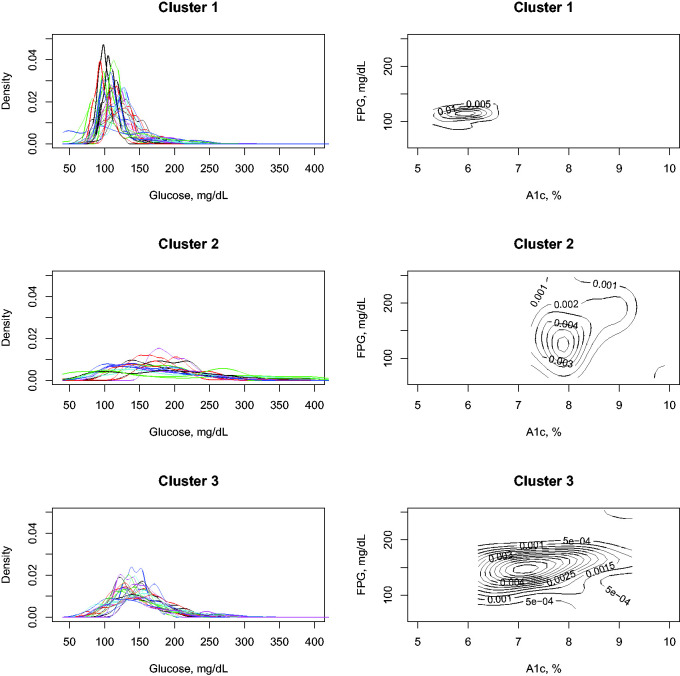
Cluster analysis is an essential tool for identifying subgroups of patients with similar characteristics. As an example, with the diabetes patients’ data from the AEGIS study, we perform a cluster analysis using three clusters. To establish when a patient has diabetes, we use the doctor’s previous diagnostic criteria, or if individuals currently have their glucose values measured with A1c and FPG in the ADA ranges to be classified in that category.
Figure 6 contains the results of applying the cluster analysis in diabetes patients. The algorithm has identified three differentiated groups of patients. The first group is patients with normal glucose values, probably because they are on medication, and the diagnosis of diabetes was made in the past. The second group is patients with severely altered glucose values, and as can be seen in the glucodensities, their glucose is continuously fluctuating. Finally, the last group is patients with slightly altered diabetes metabolism. The two-dimensional graphical representation of the density function of A1c and FPG helps to validate these findings.
Figure 6.
Clustering analysis of diabetes patients in AEGIS study.
7 Discussion
The primary contribution of this article is to propose a new representation of CGM data called glucodensity. We have validated this representation from a clinical point of view, proving that it is more accurate than time in range metrics.
7.1 Diabetes etiology and biological components to capture in a mathematical representation
Diabetes encompasses a heterogeneous group of impaired glucose metabolism, such as the frequent presence of hyperglycemias or hypoglycemias. 3 Anomalous glucose fluctuations are another essential trait of dysglycemic regulation.55,61 The use of glycemic control measures that go beyond the average glucose values such as A1c and also capture (i) the impact of time spent at each glucose concentration on the glucose deregulation process, (ii) the oscillations of glucose associated with cellular damage, 61 is crucial in the management of patients with diabetes as in the assessment of glucose metabolism with a high degree of precision.
7.2 Clinical validation of glucodensity
Our proposal accurately captures the components of diabetes mentioned above. Using clinical data, we evaluated the clinical sensitivity against established biomarkers in diabetes. We found a high association between A1c, HOMA-IR, CONGA, MODD, MAGE, and glucodensity. In the case of the HOMA-IR variable, the predictive ability does not seem excellent, although, to the best of our knowledge, no known marker shows a predictive ability against that variable. However, our model can provide consistent values in moderate and large HOMA-IR values. While the fit for the variable A1c was not perfect, we must consider that the time scale for the A1c and the glucodensities were quite different. A1c is a measure that reflects the average glucose over 2--3 months while monitoring patients for less than one week to compute the glucodensity. Our R2 of 0.79 is better than the average glucose recorded by the monitoring period ( ), which indicates that an individual’s glucose distributional values may give extra information to the long-term glucose averages.
In the prediction of glucodensity from A1c, HOMA-IR, and glycemic variability measures, the estimated R2 shows a moderate relationship between those variables. However, we are introducing the essential variables of the glucose deregulation process. A possible explanation of this is that the use of the summary measures commonly used in diabetes can hardly capture an individual’s glycemic profile.
Glucose metabolism is very complex and highly dependent on the patient’s conditions. For example, the cellular mechanism between patients with diabetes type I and type II are significantly different. Diabetes type II is characterized primarily by insulin resistance, while diabetes type I is caused by the selective autoimmune destruction of pancreatic β-cells and consequent non-insulin production. 62 In this context, the introduction of the concept of glucodensity provides greater clinical accuracy to the possible decisions derived from such representation compared to traditional methods because we utilize the entire distribution of glucose concentrations of an individual over time.
7.3 Time in range metrics vs. glucodensity
While time in range metrics may also achieve the previous aim, they do so to a clearly lesser extent than the glucodensity. Our proposal can capture the differences between individuals in each glucose concentration. In contrast, time in range only measures glucose differences along intervals, with a subsequent loss of information. Also, time in range metrics are substantially limited since the target zones must be defined previously, and these may also depend on the study population or the aim of the analysis.
Empirical results demonstrate the advantages of our proposal apart from the theoretical framework. The ability of glucodensity to predict A1c, HOMA-IR, and the CONGA, MAGE, and MODD variability measures is surprisingly high, much higher than that achieved with the range metric despite using two different target zones: the deciles of normoglycemic patients glucose values and the target zones prescribed by the ADA.
The estimated R2 between glucodensities and A1c is similar to that reported by other authors between A1c and average glucose values. 63 However, in this study, patients are monitored only for two to six days and not for weeks. Two possible factors must be considered in the analysis of the results. First, there are people with and without diabetes, and, second, the glucodensity captures A1c better because it represents the entire distribution of glucose concentration values, while glycation rates are known to increase with glucose concentrations. 64 In particular, the estimated R2 between A1c and the mean glucose in our database is only 0.61.
7.4 Statistical considerations
From a statistical standpoint, glucodensities are a special constrained type of functional data known as distributional data; therefore, we cannot use the usual statistical techniques directly. To alleviate this limitation, this paper proposes a framework for the analysis of these distributional data based on distances with existing techniques for hypothesis testing, cluster analysis, and regression models. However, it is important to point out that alternative approaches are available, including functional transformations35,65 that embed the densities in an unconstrained Hilbert Space, after which standard functional analysis techniques can be applied. Nevertheless, these particular transformations cannot be applied directly in our setting due to differences in the supports of the glucodensities. Moreover, these functional transformations have the significant disadvantage that methodology for standard inferential tasks, such as building a theoretically justified confidence band, is lacking. However, utilizing the regression model based on the 2-Wasserstein geometry, asymptotic results and resampling techniques can be used in an intuitive way to build confidence bands. 48 Additionally, the application of these transformations can be difficult to interpret. For example, the functional mean in the transformed space lacks a clear meaning, so that the results of an functional ANOVA test, say, may not yield a completely incisive analysis. Finally, distributional data analysis is an exciting research area where new methodological contributions to address different real problems are needed. Examples of such problems include a mixed models or causal inference methods.
7.5 Limitations
A potential limitation of our representation is that it ignores the order of events. Instead, it analyzes only the distribution of glucose values. Nevertheless, following different animal models in diabetes, the event sequence may not be a critical component in diabetes modeling. The main factor of microvascular and macrovascular complications is chronic hyperglycemia,66,67 and this is captured with high accuracy by our models. Moreover, an essential aspect of managing diabetes patients is hypoglycemia control, and our proposal also captures this. Finally, the third component of dysglycemia, 55 glucose variability, can be accurately predicted by our representations, at least through metrics CONGA, MAGE, and MODD.
From another point of view, for other authors as Zaccardi and Khunti, 2 it is expected that different glucose fluctuations on different time scales may provide extra information on glucose homeostasis. Two extensions of our models could potentially take into account this variability. The first one is to utilize functional multilevel models68,69 applied to transformed glucodensities, using the distributional transformations discussed above. A second approach would be to build similar densities of glucose speed and acceleration values, both marginally and as multivariate functions in the statistical models.
The sample size used may also be a limitation from a statistical point of view. Nevertheless, in the field of diabetes, the AEGIS study is one the world’s largest databases and, unlike other studies, is composed of randomly selected individuals from a general population. 70 Finally, for study validation, perhaps the most reliable way of validating the new representation is in terms of the patients’ long-term prognosis. However, to the best of our knowledge, no study with a reasonable sample size has this information from CGM technology’s intensive use. Moreover, the clinical validation was based on performance with variables associated with the biological and molecular mechanisms of diabetes development, diabetes status, and future diabetes patients’ prognosis, as we can see in the literature.
7.6 Potential applications
Adopting the concept of glucodensity in clinical practice and biomedical research could be very promising in the following ways.
To have a simple and more accurate representation of the glycemic profile of an individual. This representation is especially useful in managing diabetic patients and assessing the effects of an intervention.
To establish if there are statistically significant differences between patients subjected to different interventions, for example, in a clinical trial.
To identify different subtypes of patients based on their glycemic condition and other variables. Cluster analysis of glucodensities can create new patient subtypes based on the risk of diabetes or other complications. Furthermore, it allows us to better describe the disease’s etiology by creating groups of subjects whose glucose profiles and other clinical characteristics are similar.
To establish the prognosis or risk of a patient or analyze the relationship of an individual’s glycemic profile with different clinical variables in epidemiological studies.
To predict changes in the glycemic profile based on the individuals’ characteristics and the intervention performed. For example: how does the glucodensity vary according to the diet?
To recommend the most advantageous treatments for a patient. Following the previous idea, a causal inference model could be fitted where the response is glucodensity, for example, to establish which diet is the most beneficial for the individual to achieve suitable glucose levels.
7.7 Future work
We introduce glucodensity methodology with CGM data. However, our methodology is also valid for data from other biosensors such as accelerometers to measure physical activity levels. In this domain, the time in range metric is one of the most used representations, and perhaps the adoption of our approach can lead to better results.71,72 The adoption of new methodology with other biosensors may be an essential research issue to be addressed in the future.
From a statistical point of view, and with biosensor data in different domains, it would be exciting to do an extensive comparison to establish differences in performance between distributional transformations,35,65 perhaps with less complex functional models than some we have considered. In general, the statistical models employed in this paper are non-parametric, and a considerable sample size is necessary, a requirement that is always not satisfied in many studies. In such cases, with a proper transformation, it may be possible to utilize simpler models, for example functional linear regression, for some analytic tasks.
In the diabetes field, two different directions of future work are essential. First, from a more clinical point of view, it will be necessary to evaluate the predictive capacity of the glucodensity in the long-term prognosis of patients. In addition, it would be interesting to assess, in more extended monitoring periods, the reproducibility between days and weeks with the representation constructed. One way to accomplish this is to compute the intraclass correlation coefficient (ICC) using, for example, the methodology proposed recently in Xu et al. 73 and based on distances between functions. Second, we need to explore the possibility of incorporating more information about glucose fluctuations with multidimensional glucodensities or multilevel models, although this increases model complexity and hence demands higher volumes of data.
Acknowledgements
We would like to thanks Russell Lyons for his discussions on the use of energy-distance-based methods with glucodensities.
Footnotes
Declaration of conflicting interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work has received financial support from Instituto de Salud Carlos III (ISCIII), Grant/Award Number: PI16/01395; Ministry of Economy and Competitiveness (SPAIN) European Regional Development Fund (FEDER); the Axencia Galega de Innovación, Consellería de Economía, Emprego e Industria, Xunta de Galicia, Spain, Grant/Award Number: GPC IN607B 2018/01; National Science Foundation, Grant/Award Number: DMS-1811888; the Spanish Ministry of Economy and Competitiveness Grant/Award Number: TIN2015-73566-JIN and TIN2017-84796-C21-R; the Spanish Ministry of Science, Innovation and Universities under Grant RTI2018-099646-B-I00, the Consellería de Educación, Universidade e Formación Profesional and the European Regional Development Fund under Grant ED431G-2019/04.
ORCID iDs: Marcos Matabuena https://orcid.org/0000-0003-3841-4447
Francisco Gude https://orcid.org/0000-0002-9681-1662
Supplemental material: Supplemental material for this article is available online.
References
- 1.Ewings SM, Sahu SK, Valletta JJ, et al. A Bayesian network for modelling blood glucose concentration and exercise in type 1 diabetes. Stat Meth Med Res 2015; 24: 342–372. [DOI] [PubMed] [Google Scholar]
- 2.Zaccardi F, Khunti K. Glucose dysregulation phenotypes – time to improve outcomes. Nature Rev Endocrinol 2018; 14: 632–633. [DOI] [PubMed] [Google Scholar]
- 3.Association AD, et al. Glycemic targets: standards of medical care in diabetes-2018. Diabetes Care 2018; 41(Supplement 1): S55–S64. [DOI] [PubMed] [Google Scholar]
- 4.Selvin E, Crainiceanu CM, Brancati FL, et al. Short-term variability in measures of glycemia and implications for the classification of diabetes. Arch Intern Med 2007; 167: 1545–1551. [DOI] [PubMed] [Google Scholar]
- 5.Group BAW. Need for regulatory change to incorporate beyond A1c glycemic metrics. Diabetes Care 2018; 41: e92–e94. [DOI] [PubMed] [Google Scholar]
- 6.Bergenstal RM. Glycemic variability and diabetes complications: does it matter? simply put, there are better glycemic markers! Diabetes Care 2015; 38: 1615–1621. [DOI] [PubMed] [Google Scholar]
- 7.Beck RW, Bergenstal RM, Riddlesworth TD, et al. Validation of time in range as an outcome measure for diabetes clinical trials. Diabetes Care 2019; 42: 400–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lu J, Ma X, Zhou J, et al. Association of time in range, as assessed by continuous glucose monitoring, with diabetic retinopathy in type 2 diabetes. Diabetes Care 2018; 41: 2370–2376. [DOI] [PubMed] [Google Scholar]
- 9.Beck RW, Connor CG, Mullen DM, et al. The fallacy of average: how using hba1c alone to assess glycemic control can be misleading. Diabetes Care 2017; 40: 994–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hirsch IB, Sherr JL, Hood KK. Connecting the dots: validation of time in range metrics with microvascular outcomes. Diabetes Care 2019; 42(3): 345–348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.For Medicinal Products for Human Use C, et al. Guideline on clinical investigation of medicinal products in the treatment or prevention of diabetes mellitus. London: European Medicines Society, 2012. [Google Scholar]
- 12.Kovatchev BP, Breton M, Man CD, et al. In silico preclinical trials: a proof of concept in closed-loop control of type 1 diabetes. J Diabetes Sci Technol 2009; 3: 44–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Feig DS, Donovan LE, Corcoy R, et al. Continuous glucose monitoring in pregnant women with type 1 diabetes (conceptt): a multicentre international randomised controlled trial. Lancet 2017; 390: 2347–2359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.DiMeglio LA, Evans-Molina C, Oram RA. Type 1 diabetes. Lancet 2018; 391: 2449–2462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Freeman J, Lyons L. The use of continuous glucose monitoring to evaluate the glycemic response to food. Diabetes Spect 2008; 21: 134–137. [Google Scholar]
- 16.Hall H, Perelman D, Breschi A, et al. Glucotypes reveal new patterns of glucose dysregulation. PLOS Biol 2018; 16: 1–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lu J, Wang C, Shen Y, et al. Time in range in relation to all-cause and cardiovascular mortality in patients with type 2 diabetes: a prospective cohort study. Diabetes Care 2021; 44: 549–555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nichols SP, Koh A, Storm WL, et al. Biocompatible materials for continuous glucose monitoring devices. Chem Rev 2013; 113: 2528–2549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bergenstal RM, Ahmann AJ, Bailey T, et al. Recommendations for standardizing glucose reporting and analysis to optimize clinical decision making in diabetes: the ambulatory glucose profile (AGP). Diabetes Technol Ther 2013; 15: 198–211. [DOI] [PubMed] [Google Scholar]
- 20.Battelino T, Danne T, Bergenstal RM, et al. Clinical targets for continuous glucose monitoring data interpretation: recommendations from the international consensus on time in range. Diabetes Care. Epub ahead of print 8 June 2019. DOI:10.2337/dci19-0028. [DOI] [PMC free article] [PubMed]
- 21.Nguyen M, Han J, Spanakis EK, et al. A review of continuous glucose monitoring-based composite metrics for glycemic control. Diabetes Technol Ther 2020; 44: 613–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gude F, Díaz-Vidal P, Rúa-Pérez C, et al. Glycemic variability and its association with demographics and lifestyles in a general adult population. J Diabetes Sci Technol 2017; 11: 780–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hoelzel W, Weykamp C, Jeppsson JO, et al. IFCC reference system for measurement of hemoglobin A1c in human blood and the national standardization schemes in the united states, japan, and Sweden: a method-comparison study. Clin Chem 2004; 50: 166–174. [DOI] [PubMed] [Google Scholar]
- 24.Matthews D, Hosker J, Rudenski A, et al. Homeostasis model assessment: insulin resistance and β-cell function from fasting plasma glucose and insulin concentrations in man. Diabetologia 1985; 28: 412–419. [DOI] [PubMed] [Google Scholar]
- 25.McDonnell C, Donath S, Vidmar S, et al. A novel approach to continuous glucose analysis utilizing glycemic variation. Diabetes Technol Ther 2005; 7: 253–263. [DOI] [PubMed] [Google Scholar]
- 26.Service FJ, Molnar GD, Rosevear JW, et al. Mean amplitude of glycemic excursions, a measure of diabetic instability. Diabetes 1970; 19: 644–655. [DOI] [PubMed] [Google Scholar]
- 27.Molnar G, Taylor W, Ho M. Day-to-day variation of continuously monitored glycaemia: a further measure of diabetic instability. Diabetologia 1972; 8: 342–348. [DOI] [PubMed] [Google Scholar]
- 28.Müller HG, Petersen A. Density estimation including examples. Wiley StatsRef: Statistics Reference Online, https://onlinelibrary.wiley.com/doi/10.1002/9781118445112.stat02808.pub2 (2014, accessed 24 February 2021). [Google Scholar]
- 29.Silverman BW. Density estimation for statistics and data analysis. London: Chapman & Hall, 1986. [Google Scholar]
- 30.Hall P, Lahiri SN, Truong YK, et al. On bandwidth choice for density estimation with dependent data. Ann Stat 1995; 23: 2241–2263. [Google Scholar]
- 31.Antoniadis A. Wavelets in statistics: a review. J Ital Stat Soc 1997; 6: 97. [Google Scholar]
- 32.Izenman AJ. Review papers: recent developments in nonparametric density estimation. J Am Stat Assoc 1991; 86: 205–224. [Google Scholar]
- 33.Ramsay J, Ramsay J, Silverman B. Functional data analysis. Berlin: Springer Series in Statistics, Springer, 2005. [Google Scholar]
- 34.Wang JL, Chiou JM, Müller HG. Functional data analysis. Annu Rev Stat Applic 2016; 3: 257–295. [Google Scholar]
- 35.Petersen A, Müller HG. Functional data analysis for density functions by transformation to a Hilbert space. Ann Statist 2016; 44: 183–218. [Google Scholar]
- 36.Hron K, Menafoglio A, Templ M, et al. Simplicial principal component analysis for density functions in Bayes spaces. Comput Stat Data Anal 2016; 94: 330–350. [Google Scholar]
- 37.Villani C. Optimal transport: old and new. volume 338. Berlin: Springer Science & Business Media, 2008.
- 38.Fréchet MR. Les éléments aléatoires de nature quelconque dans un espace distancié. Ann l’institut Henri Poincaré 1948; 10: 215–310. [Google Scholar]
- 39.Panaretos VM, Zemel Y. Statistical aspects of Wasserstein distances. Annu Rev Stat Applic 2019; 6: 405–431. [Google Scholar]
- 40.Ferraty F, Vieu P. Nonparametric functional data analysis: theory and practice (Springer Series in Statistics). Berlin, Heidelberg: Springer-Verlag, 2006. [Google Scholar]
- 41.Preda C. Regression models for functional data by reproducing kernel Hilbert spaces methods. J Stat Plann Inference 2007; 137: 829–840. [Google Scholar]
- 42.Szabó Z, Sriperumbudur BK, Póczos B, et al. Learning theory for distribution regression. J Mach Learn Res 2016; 17: 5272–5311. [Google Scholar]
- 43.Nerini D, Ghattas B. Classifying densities using functional regression trees: applications in oceanology. Comput Stat Data Anal 2007; 51: 4984–4993. [Google Scholar]
- 44.Han K, Müller HG, Park BU. Additive functional regression for densities as responses. J Am Stat Assoc 2020; 115: 997–1010. [Google Scholar]
- 45.Petersen A, Müller HG. Fréchet regression for random objects with Euclidean predictors. Ann Statist 2019; 47: 691–719. [Google Scholar]
- 46.Capitaine L, Bigot J, Thiébaut R, et al. Fréchet random forests for metric space valued regression with non euclidean predictors, 2020, https://arxiv.org/abs/1906.01741. 1906.01741.
- 47.Talská R, Menafoglio A, Machalová J, et al. Compositional regression with functional response. Comput Stat Data Anal 2018; 123: 66–85. [Google Scholar]
- 48.Petersen A, Liu X, Divani AA. Wasserstein f-tests and confidence bands for the Frèchet regression of density response curves. Ann Statist 2021; 49: 590–661.
- 49.Pawlowsky-Glahn V, Egozcue JJ, Tolosana-Delgado R. Modeling and analysis of compositional data. New Jersey: John Wiley & Sons, 2015. [Google Scholar]
- 50.Febrero-Bande M, de la Fuente M. Statistical computing in functional data analysis: The R package fda.usc. J Stat Software 2012; 51: 1–28. [Google Scholar]
- 51.Dubey P, Müller HG. Fréchet analysis of variance for random objects. Biometrika 2019; 106(4): 803–821. [Google Scholar]
- 52.Kilpatrick ES. Glycated haemoglobin in the year 2000. J Clin Pathol 2000; 53: 335–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ausk KJ, Boyko EJ, Ioannou GN. Insulin resistance predicts mortality in nondiabetic individuals in the U.S. Diabetes Care 2010; 33: 1179–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Service FJ. Glucose variability. Diabetes 2013; 62: 1398–1404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Monnier L, Colette C, Owens DR. Glycemic variability: the third component of the dysglycemia in diabetes. Is it important? How to measure it? J Diabetes Sci Technol 2008; 2: 1094–1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Székely GJ, Rizzo ML. The energy of data. Annu Rev Stat Applic 2017; 4: 447–479. [Google Scholar]
- 57.Lyons R. Distance covariance in metric spaces. Ann Probab 2013; 41: 3284–3305. [Google Scholar]
- 58.Leucht A, Neumann MH. Dependent wild bootstrap for degenerate u- and v-statistics. J Multivariate Anal 2013; 117: 257–280. [Google Scholar]
- 59.Jiménez-Gamero M, Alba-Fernández M, Ariza-López F. Approximating the null distribution of a class of statistics for testing independence. J Comput Appl Math 2019; 354: 131–143. [Google Scholar]
- 60.Franca G, Vogelstein JT, Rizzo M. Kernel k-groups via Hartigan’s method. IEEE Trans Pattern Anal Machine Intell . Epub ahead of print 28 May 2020. DOI: 10.1109/TPAMI.2020.2998120 [DOI] [PMC free article] [PubMed]
- 61.Monnier L, Colette C. Glycemic variability: can we bridge the divide between controversies? Diabetes Care 2011; 34: 1058–1059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Taylor R. Type 2 diabetes. Diabetes Care 2013; 36(4): 1047–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Nathan D, Turgeon H, Regan S. Relationship between glycated haemoglobin levels and mean glucose levels over time. Diabetologia 2007; 50: 2239–2244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Singh R, Barden A, Mori T, et al. Advanced glycation end-products: a review. Diabetologia 2001; 44: 129–146. [DOI] [PubMed] [Google Scholar]
- 65.Van den Boogaart KG, Egozcue JJ, Pawlowsky-Glahn V. Bayes Hilbert spaces. Austral New Zealand J Stat 2014; 56: 171–194. [Google Scholar]
- 66.Cryer PE. Glycemic goals in diabetes: trade-off between glycemic control and iatrogenic hypoglycemia. Diabetes 2014; 63: 2188–2195. [DOI] [PubMed] [Google Scholar]
- 67.Škrha J, Šoupal J, Práznỳ M. Glucose variability, HBA1c and microvascular complications. Rev Endocrine Metab Disorders 2016; 17: 103–110. [DOI] [PubMed] [Google Scholar]
- 68.Di CZ, Crainiceanu CM, Caffo BS, et al. Multilevel functional principal component analysis. Ann Appl Stat 2009; 3: 458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Gaynanova I, Punjabi N, Crainiceanu C. Modeling continuous glucose monitoring (CGM) data during sleep. Biostatistics. Epub ahead of print 22 May 2020. DOI:10.1093/biostatistics/kxaa023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Zeevi D, Korem T, Zmora N, et al. Personalized nutrition by prediction of glycemic responses. Cell 2015; 163: 1079–1094. [DOI] [PubMed] [Google Scholar]
- 71.Dumuid D, Stanford TE, Martin-Fernández JA, et al. Compositional data analysis for physical activity, sedentary time and sleep research. Stat Meth Med Res 2018; 27: 3726–3738. [DOI] [PubMed] [Google Scholar]
- 72.Dumuid D, Pedišić Ž, Palarea-Albaladejo J, et al. Compositional data analysis in time-use epidemiology: what, why, how. Int J Environ Res Public Health 2020; 17: 2220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Xu M, Reiss PT, Cribben I. Generalized reliability based on distances. Biometrics 2021; 77: 258–270. [DOI] [PMC free article] [PubMed]