Abstract
Everyday tasks in social settings require humans to encode neural representations of not only their own spatial location, but also the location of other individuals within an environment. At present, the vast majority of what is known about neural representations of space for self and others stems from research in rodents and other non-human animals1–3. However, it is largely unknown how the human brain represents the location of others, and how aspects of human cognition may affect these location-encoding mechanisms. To address these questions, we examined individuals with chronically implanted electrodes while they carried out real-world spatial navigation and observation tasks. We report boundary-anchored neural representations in the medial temporal lobe that are modulated by one’s own as well as another individual’s spatial location. These representations depend on one’s momentary cognitive state, and are strengthened when encoding of location is of higher behavioural relevance. Together, these results provide evidence for a common encoding mechanism in the human brain that represents the location of oneself and others in shared environments, and shed new light on the neural mechanisms that underlie spatial navigation and awareness of others in real-world scenarios.
Environmental boundaries play a crucial part in the formation of cognitive representations of space, as they are essential for reorientation4, to correct noisy position estimates during spatial navigation5,6, and for spatial memory functions6–9. Moreover, electrophysiological studies in rodents have shown that boundaries have a strong influence on spatial representations at a single-cell level5,10–16. In humans, boundary-related neural signatures have been observed at the level of cell populations, using functional magnetic resonance imaging and intracranial electroencephalographic (iEEG) recordings17,18. Crucially, however, participants in these studies did not physically move, but instead navigated a virtual environment displayed on a computer screen. Furthermore, none of these studies involved tasks that required the encoding of another person’s location.
Here, we investigated whether boundary-related neural representation mechanisms are present during real-world spatial navigation in walking participants, and can encode not only one’s own location, but also the location of another person in a shared environment.
We recorded iEEG activity from the medial temporal lobe (MTL) of five individuals, in whom the RNS® System (NeuroPace Inc.) had been chronically implanted for the treatment of epilepsy19 (Fig. 1), while they performed spatial self-navigation and observation tasks (Fig. 2). During the self-navigation task, participants alternated between periods of navigating to a wall-mounted sign and searching for a hidden target location (Extended Data Fig. 1a). During the observation task, participants sat on a chair in a corner of the room and were asked to keep track of the experimenter’s location as they walked around, and to press a button whenever the experimenter crossed a previously learned self-navigated target location (see Methods for details).
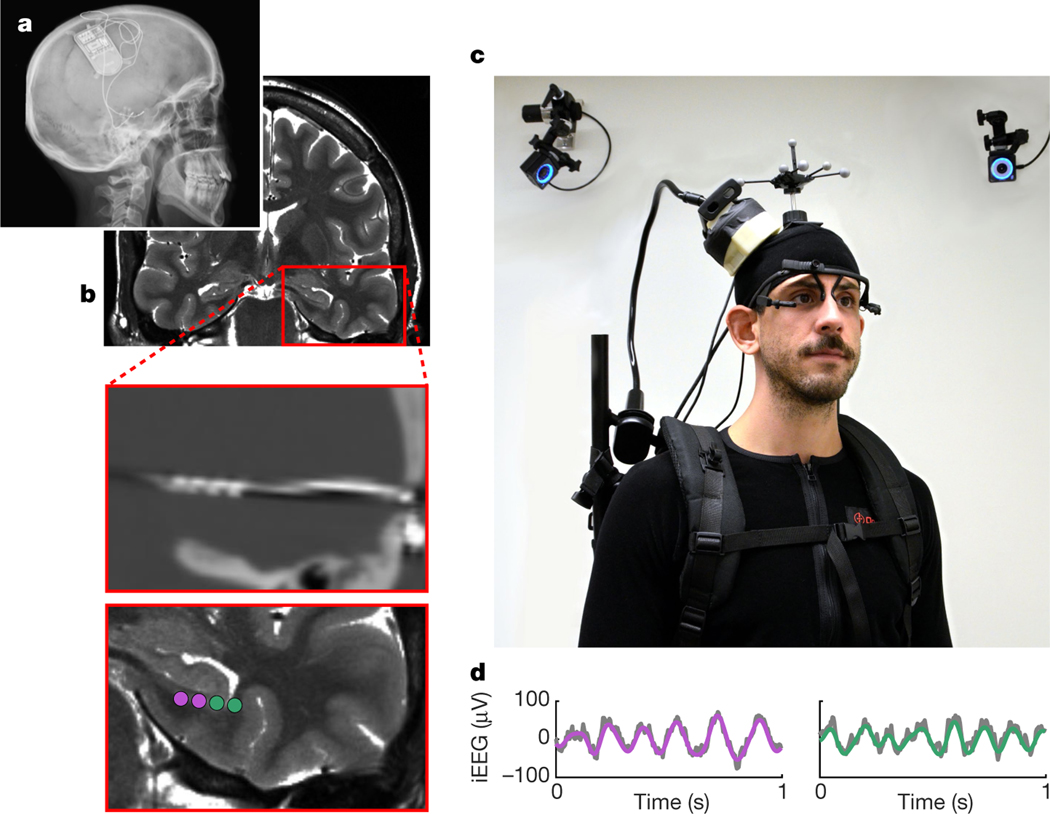
Fig. 1 |. RNS System and experimental setup.
a, X-ray image of a participant with a chronically implanted RNS System (NeuroPace Inc.). b, Preoperative magnetic resonance image (top), co-registered with a postoperative computed tomography image showing an implanted depth electrode (middle), and contact locations of two bipolar recording channels (bottom). c, iEEG data were continuously recorded with a NeuroPace Wand that was secured on a participant’s head, allowing the participant to freely walk around during recordings. Their position was tracked via motion-tracking cameras and reflective markers on the participant’s head. Eye movements were tracked with a mobile eye-tracking headset. Shown is an experimenter, rather than an actual participant, wearing the full setup for illustrative purposes. d, Example raw iEEG signal (grey) from two recording channels, overlaid with bandpass-filtered low-frequency oscillations (purple and green; 3–12 Hz).
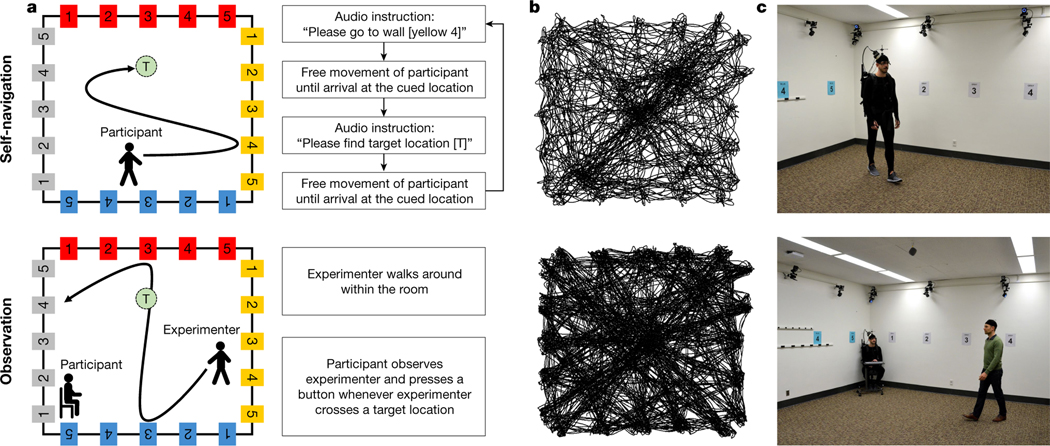
Fig. 2 |. Self-navigation and observation tasks.
a, Twenty unique signs (with different combinations of colours and numbers) were mounted along the room walls, and target locations (each named with a letter) were distributed around the room but not visible to participants. In the self-navigation task, participants were repeatedly asked to first walk to a wall-mounted sign (for example, ‘yellow 4’) before searching for a target location (for example, target location ‘T’). During the observation task, the experimenter walked around the room, while participants sat on a chair and observed the experimenter’s movements from a corner of the room. Participants were asked to press a button whenever the experimenter crossed one of the target locations. b, Example movement patterns from a top-down perspective for one participant in the self-navigation task and the experimenter in the observation task. c, Illustration of the task setup.
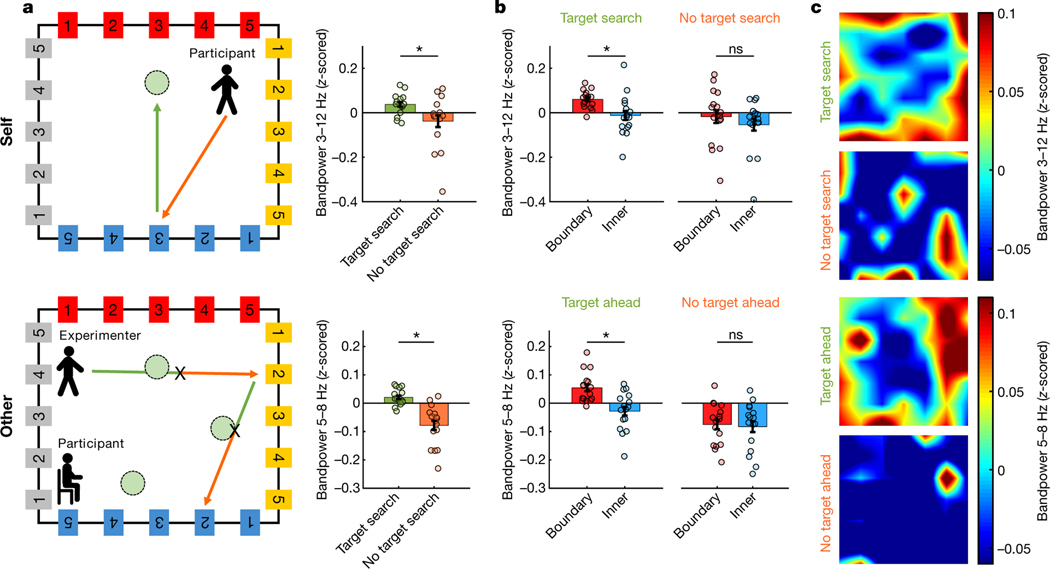
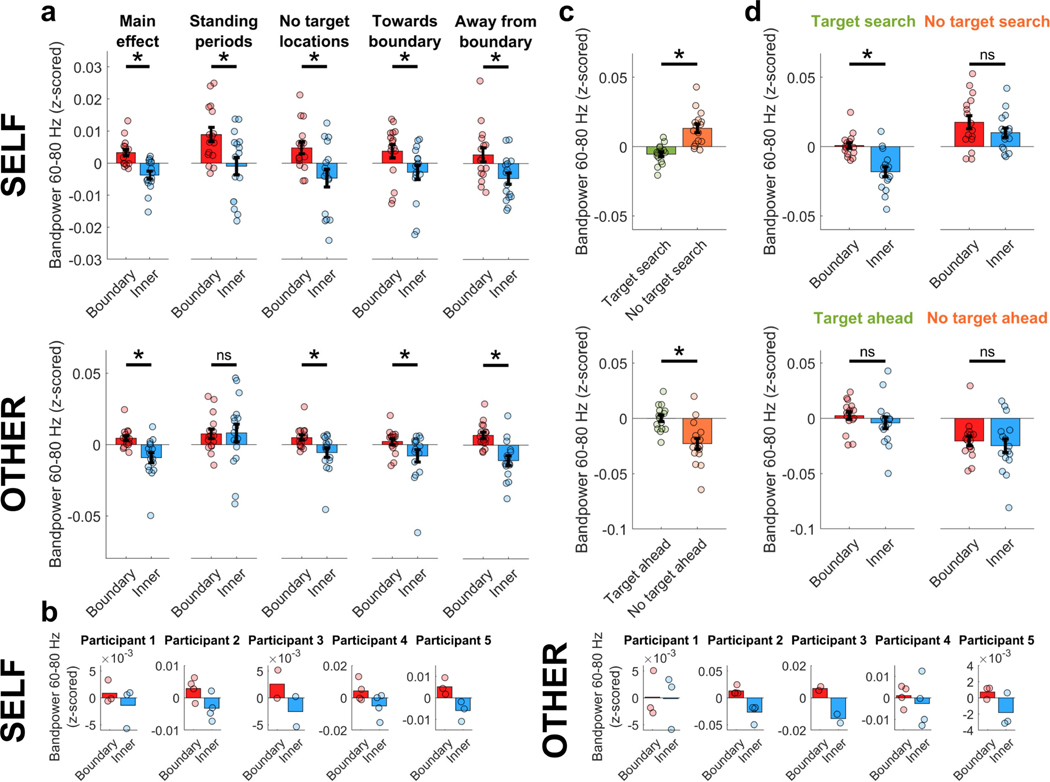
We found that, during self-navigation, oscillatory activity in the MTL was modulated by the participants’ proximity to the boundaries of the room (Fig. 3a–c). Specifically, low-frequency oscillatory power was significantly higher when participants were close to a boundary (defined as less than 1.2 m away from the wall; see Extended Data Fig. 1b for other distance definitions), compared with periods when they were in the inner room area. Interestingly, a similar effect was found during the observation task: while participants were sitting, their MTL activity was modulated by the experimenter’s location, with significantly stronger oscillatory power seen during periods when the experimenter was close to a boundary compared with the inner room area. During both self-navigation and observation, the effect was most prominent in the theta frequency band (Fig. 3b), with the strongest ‘boundary’ versus ‘inner’ power differences seen around 5–8 Hz for the observation task, and a slightly wider frequency band (around 3–12 Hz) seen during self-navigation (observation, P < 0.001; self-navigation, P < 0.001; number of recording channels (nCh) = 16). Boundary-related oscillatory effects could not be explained by differences in time spent in the ‘boundary’ versus ‘inner’ room areas, as the amount of data within each condition was accounted for throughout all analyses, by iteratively selecting random subsets of size-matched data (see Methods).
Fig. 3 |. Oscillatory power is modulated by one’s own and another individual’s location.
a, Normalized ‘boundary’–’inner’ power difference during self-navigation (‘self’) and observation (‘other’). Data show mean values ± s.e.m. from nCh = 16. Horizontal bars indicate significant differences in one-sided permutation tests for individual frequencies (P < 0.05; green, uncorrected; red, false discovery rate (FDR) corrected). b, Higher bandpower at ‘boundary’ versus ‘inner’ locations in 3–12 Hz (self, P < 0.001) and 5–8 Hz (other, P < 0.001) frequency bands. Data show mean values ± s.e.m. from nCh = 16. Asterisks denote a significant difference (P < 0.05, uncorrected) in a one-sided permutation test. c, Bandpower across room locations (top-down perspective), averaged across one channel per participant. White rectangle illustrates the ‘boundary’ versus ‘inner’ division. d, Numerically higher bandpower at ‘boundary’ versus ‘inner’ locations, shown for each participant separately. Data show mean values across channels per participant (participants 1 and 5, nCh = 3; participants 2 and 4, nCh = 4; participant 3, nCh = 2).
In order to ensure that results were not driven by a subset of individuals, we analysed boundary-related oscillatory power changes for each participant separately, finding that effects were consistent across participants, with each showing the expected pattern of results (Fig. 3d).
In line with our previous work20, theta oscillations were not continuous but occurred in bouts (roughly 10–20% of the time). The prevalence of these bouts, however, was not significantly higher near boundaries (Extended Data Fig. 1c), suggesting that boundary-related theta power increases were driven predominantly by an increase in oscillatory amplitude rather than by the prevalence of bouts.
Next, we tested whether changes in momentary cognitive state had an impact on the observed findings. We found that during self-navigation (Fig. 4, upper panels), theta power was higher when participants searched for target locations (‘target search’ periods), compared with ‘no target search’ periods when they navigated towards a wall-mounted sign (P = 0.009; nCh = 16). Moreover, ‘boundary’ versus ‘inner’ theta power differed only during ‘target search’ and not during ‘no target search’ periods (‘target search’, P = 0.003; ‘no target search’, P = 0.212; nCh = 16).
Fig. 4 |. Impact of cognitive state.
a, Higher theta power during ‘target search’ versus ‘no target search’ periods (self, P = 0.009), and ‘target ahead’ versus ‘no target ahead’ periods (other, P < 0.001). The diagrams at the left illustrate ‘target search/ahead’ periods (green arrows) and ‘no target search/ahead’ periods (orange arrows); ‘X’ denotes button presses during observation. Data show mean values ± s.e.m. from nCh = 16. Asterisks denote a significant difference (P < 0.05, uncorrected) in a one-sided permutation test. b, ‘Boundary’ versus ‘inner’ theta power was significantly different only during ‘target search/ahead’ periods (self, P = 0.003; other, P < 0.001) and not during ‘no target search/ahead’ periods (self, P = 0.212; other, P = 0.398). In addition, the ‘boundary’–’inner’ power difference was significantly larger for ‘target search/ahead’ than ‘no target search/ahead’ periods ([BoundaryTargetSearch/Ahead – InnerTargetSearch/Ahead] versus [BoundaryNoTargetSearch/Ahead – InnerNoTargetSearch/Ahead]; self, P = 0.012; other, P = 0.005). Data show mean values ± s.e.m. from nCh = 16. Asterisks denote a significant difference (P < 0.05, uncorrected) in a one-sided permutation test; ns, non-significant. c, Bandpower across room locations (top-down perspective), averaged across all channels (nCh = 16).
Interestingly, we observed a similar effect of cognitive state during the observation task (Fig. 4, lower panels). As the experimenter walked in straight lines, their translational movements could be divided into two phases that differed in behavioural relevance to the participant: first, ‘target ahead’ periods when the experimenter walked towards a presumed target location (when encoding the experimenter’s momentary location was crucial for task completion, that is, to know when to press the button); and second, ‘no target ahead’ periods after the experimenter passed a presumed target location (when their momentary location was less important). We found that participants’ theta power was significantly higher before the experimenter hit a presumed target location, compared with afterwards when no presumed target was ahead (P < 0.001; nCh = 16). Further, ‘boundary’ versus ‘inner’ theta power differed before but not after a presumed target location (‘target ahead’, P < 0.001; ‘no target ahead’, P = 0.398; nCh = 16).
It is thus plausible that boundary-related oscillatory representations of location for self and others are stronger during periods when encoding one’s momentary location is of higher behavioural relevance: to correctly perform the task, ‘target search’ and ‘target ahead’ periods require continuous updating/encoding of one’s positional estimate (relative to boundaries or other positional cues), as compared with a cognitively less-demanding task of walking towards a wall-mounted sign. Moreover, given previous work showing that theta power is associated with task demands21–25, it is possible that elevated theta power during ‘target search/ahead’ periods is related to increased demands on more-general cognitive processes, such as attention, short-term memory, or cognitive control (see Supplementary Discussion 1 for more details).
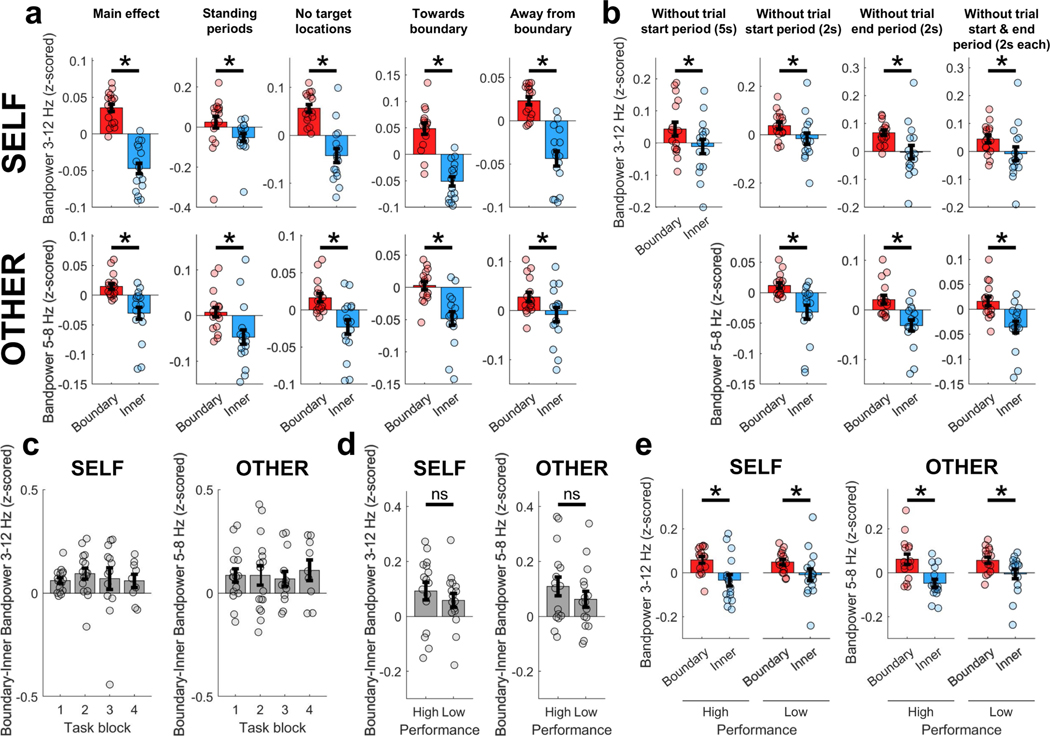
To further characterize effects and exclude confounding variables (for example, differences in behaviour between room areas), we reanalysed the data under different conditions. First, we observed that theta power was significantly increased near boundaries when the participant or experimenter was standing still (Extended Data Fig. 2a), showing that differences in movement behaviour cannot explain boundary-related effects. Second, we found a boundary-related increase in theta power when the participant or experimenter walked both towards and away from a boundary (Extended Data Fig. 2a), suggesting that the effects are not driven by orientation relative to boundaries. Third, we excluded data from positions within a one-metre diameter around targets, and found that theta power was still significantly increased near boundaries, suggesting that the observed effects are not driven by oscillatory changes that occur around target locations (Extended Data Fig. 2a). Fourth, we investigated whether the effect of increased theta power near boundaries was modulated by the learning of target locations. The strength of boundary-related effects did not vary significantly over learning blocks, nor was it significantly different between trials with high versus low memory performance (Extended Data Fig. 2c–e), suggesting that boundary-related effects are independent of learning over time. Finally, it is unlikely that increased theta power near boundaries solely reflected neural or behavioural processes that are specific to the beginning or end of a behavioural episode (such as initial planning or prediction of the next trajectory), as theta power was increased near boundaries even after excluding data from the beginning and end of behavioural episodes (Extended Data Fig. 2b).
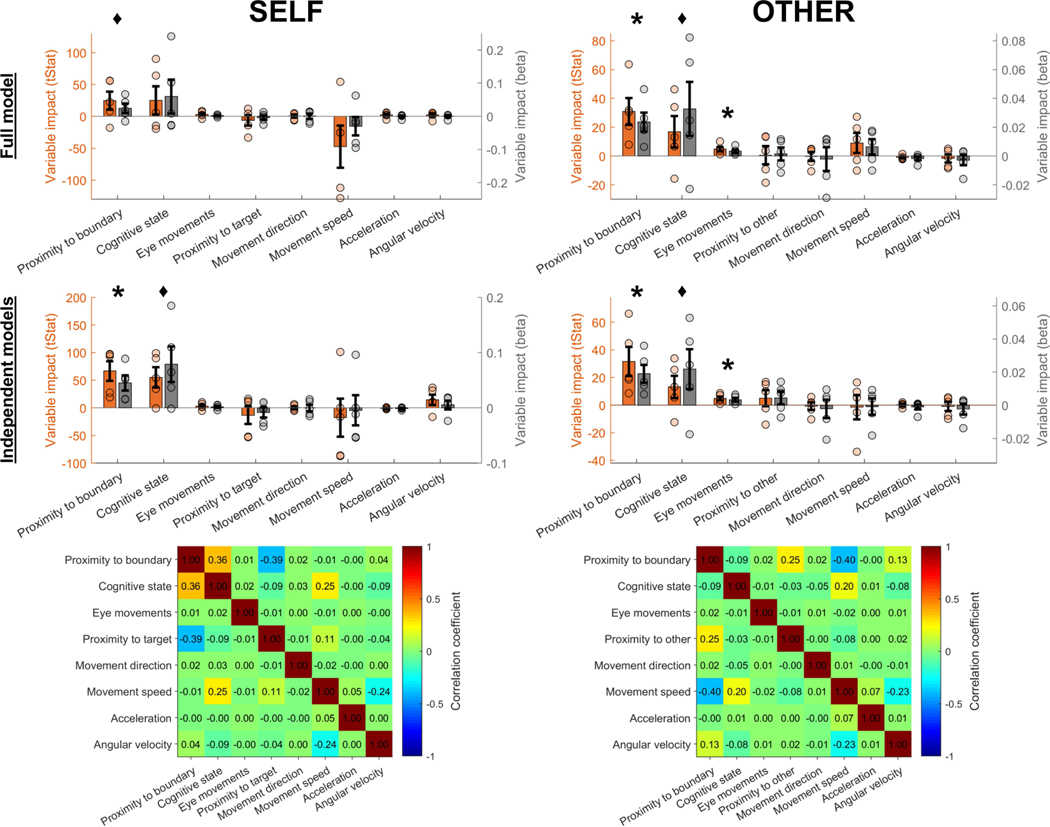
Several other variables, in addition to proximity to boundaries and momentary cognitive state, could contribute to changes in theta power during self-navigation and observation. Therefore, we also considered movement direction, magnitude of eye movements, proximity to target locations during ‘target search’ periods, distance between the participant and experimenter during the observation task, and velocity-related variables (movement speed, acceleration and angular velocity) as continuous predictors of theta power. Quantifying the impact of each variable in a linear mixed-effect model confirmed that proximity to boundary and momentary cognitive state had the strongest impact on theta power, while other variables contributed not at all or weakly by comparison (Extended Data Fig. 3).
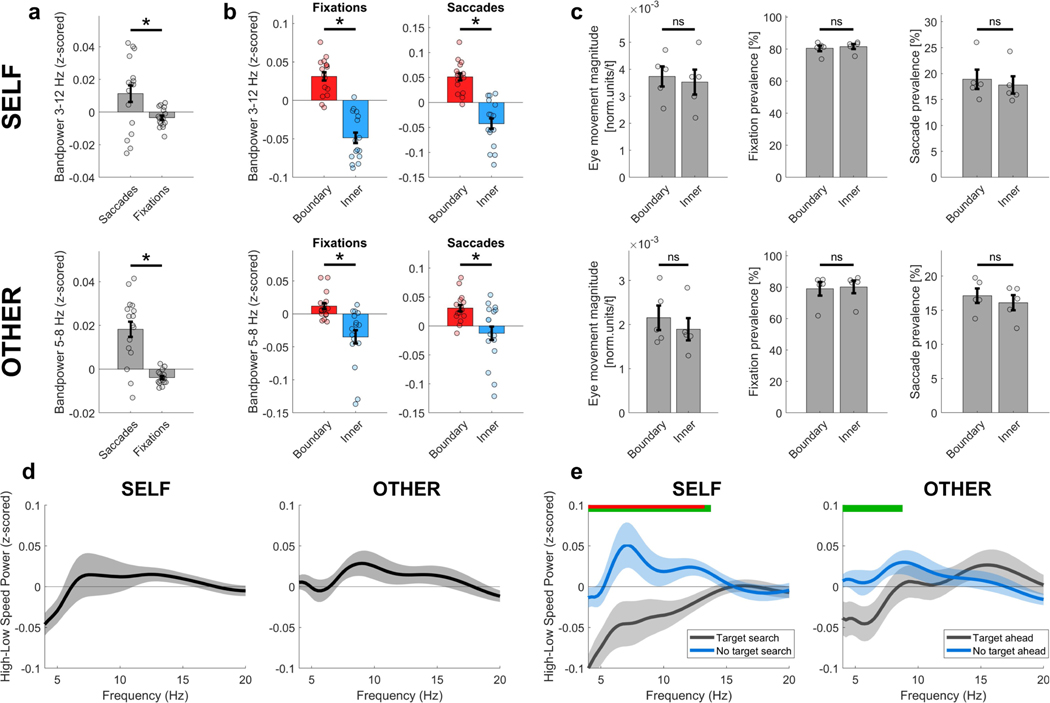
Interestingly, the mixed model analysis revealed that eye movements during observation significantly modulated theta power, consistent with findings from non-human primates26. Further, theta power was significantly increased during saccadic compared with fixation periods (Extended Data Fig. 4a). It is unlikely, however, that eye movements account for boundary-related theta changes: we found no differences in the magnitude of eye movements, the prevalence of fixations or the prevalence of saccades between ‘boundary’ versus ‘inner’ room areas, and boundary-related effects on theta power were present during both saccade and fixation periods (Extended Data Fig. 4b, c).
Previous work has shown that theta oscillations are modulated by movement speed20,27,28. Our mixed model results suggest that overall movement speed does not have a substantial impact on theta power. However, a closer look shows that the relationship between movement speed and theta power depends on cognitive state (Extended Data Fig. 4d, e): during self-navigation, speed was positively associated with theta power (roughly 8 Hz peak) when participants walked towards a wall-mounted sign (‘no target search’) but not when they searched for a hidden target location (‘target search’). For the observation task, a similar pattern of results emerged, although not statistically significant.
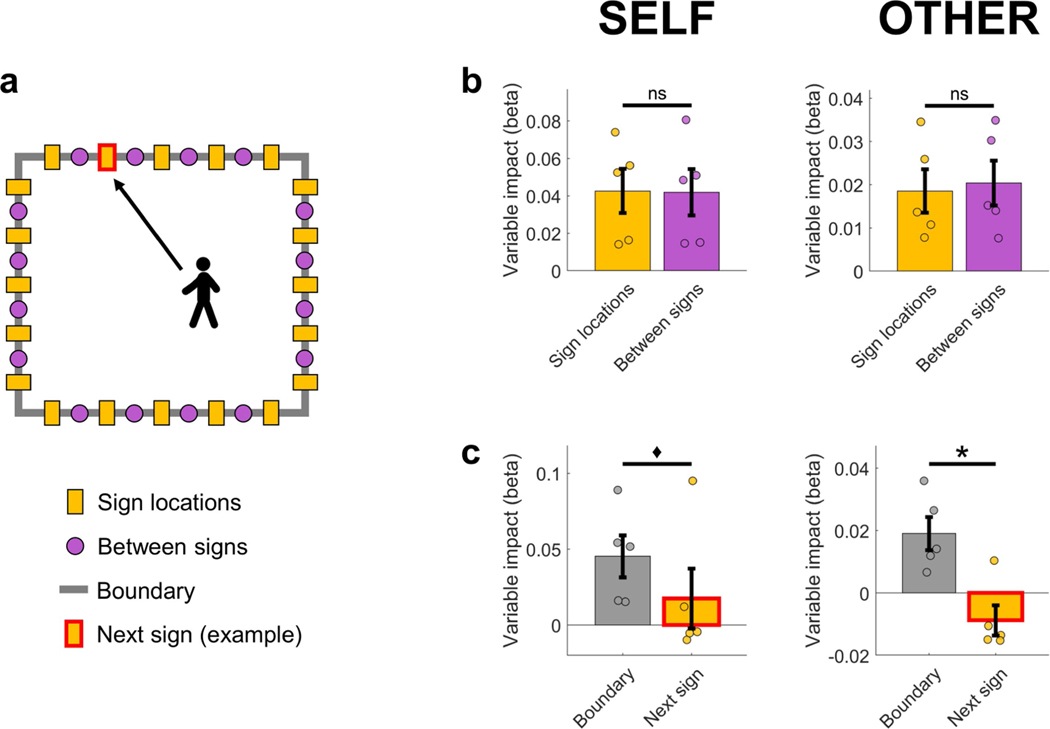
Next, we considered the possibility that wall-mounted signs, which provide strong salient cues for orientation, could be encoded as objects, and that proximity to these cues (rather than to boundaries per se) could contribute to boundary-related effects. We estimated the impact of wall-mounted signs using linear mixed-effect models, and found no difference between the predictive power of the proximity to the nearest wall-mounted sign versus the nearest location in between signs, and that proximity to boundary had a higher impact on theta power than the proximity to the next wall-mounted sign that was approached (Extended Data Fig. 5). Moreover, boundary-related theta power increased during movement both towards and away from boundaries (Extended Data Fig. 2a), suggesting that boundary-related effects are not solely driven by object representations, given that neuronal responses to objects show increased activity mainly during approach from specific orientations29 (for example, walking towards but not away). We note, however, that these findings do not exclude the possibility that object representations or other similar neural mechanisms, such as a reorganization of place-cell firing fields in relation to object or goal locations30–33, may contribute to the observed findings.
In addition to effects in the theta frequency band, we found boundary-related oscillatory power increases within the gamma frequency band around 60–80 Hz (Fig. 3a and Extended Data Fig. 6a). Although the general pattern of results for gamma power was largely similar to the results for the theta frequency band, including consistency across participants, gamma effects tended to be smaller and more variable across analyses under different behavioural conditions (Extended Data Fig. 6).
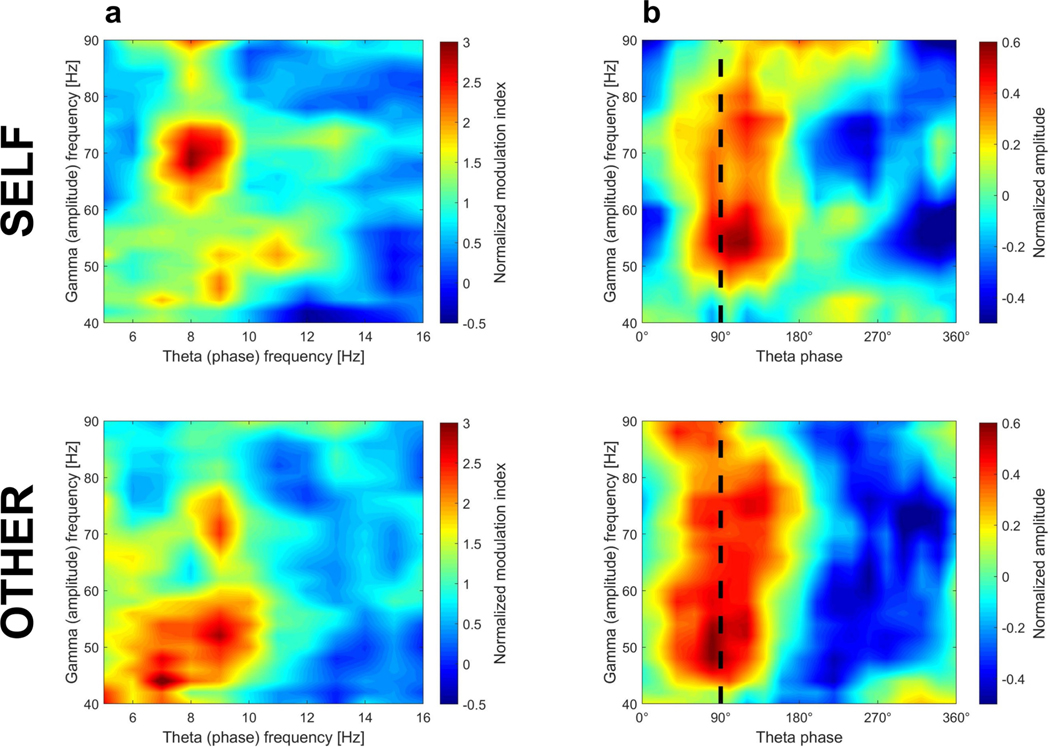
Given the effects in both theta and gamma frequency bands, we explored whether gamma oscillations were coupled with specific theta phases, as found in previous work34,35. During self-navigation, theta– gamma coupling was strongest for the 6–10 Hz theta phase coupled to the 60–80 Hz gamma amplitude (Extended Data Fig. 7). A similar pattern was evident during observed navigation; however, theta oscillations appeared to be coupled with lower-frequency (40–60 Hz) gamma amplitudes. Moreover, gamma amplitude was most strongly coupled to a theta phase of approximately 90 degrees, and this ‘preferred’ theta phase was similar between self-navigation and observation.
In summary, our results show that oscillatory activity in the human MTL is modulated by one’s own and another individual’s spatial location. Specifically, a person’s theta and gamma oscillatory power increases when observing another individual in close proximity to a boundary, even when the observer’s own location remains unchanged. These findings provide, to our knowledge, the first evidence for a mechanism in the human brain that encodes another person’s spatial location — essential, for example, in social situations in a shared environment where keeping track of another’s location is necessary. Moreover, boundary-anchored neural representations of location for both self and other are modulated by cognitive state, and strengthened when the encoding of location is of higher behavioural relevance.
We found that boundary-related oscillatory changes were strikingly similar between tasks that required self-navigation versus observation of another person. Together with recent findings in rats and bats, showing that a subpopulation of hippocampal place cells codes for both the animal’s own location as well as the location of conspecifics2,3, our results suggest that the mammalian brain uses common coding mechanisms to represent the location of self and others.
Given that the oscillatory brain signals measured here probably reflect the summed activity of populations of neurons, it is possible that our effects reflect a combined contribution of several spatially tuned cell populations, including border cells10, boundary-vector cells11, object-vector cells29, and increased place-cell activity near boundaries, goals or objects30–33. Future studies should examine the contributions of specific cell types, for example through single-cell recordings and experimental manipulation of boundaries and other spatial cues. Furthermore, while we are unable to determine whether signals are driven by specific MTL subregions, future work will be able to examine the precise localization of the cell populations responsible for these oscillations in the human brain (see also Supplementary Discussion 2).
Findings from a recent self-navigation study showing increased boundary-related theta power during navigation in a two-dimensional view-based virtual environment17 are consistent with our results, and suggest that similar boundary-related neural mechanisms support location-encoding during stationary virtual and ambulatory real-world navigation. However, our results further highlight the importance of gamma oscillations (around 60–80 Hz) and theta–gamma coupling mechanisms in location-encoding for oneself as well as for another. It is possible that these additional effects reflect oscillatory processes specific to natural walking in real-world environments that are undetectable in stationary view-based spatial navigation studies.
Our findings open up a number of exciting research questions to be addressed in follow-up studies. First, future work should investigate whether similar effects are present in more-complex scenarios, for example when the location of two or more people is encoded. Second, it is likely that boundary-related oscillatory changes are part of a larger set of spatial representations that encode another person’s location. For example, firing of place and grid cells, or their mesoscopic representations on the level of cell populations36, may provide complementary mechanisms to encode the location and movement of others. Third, it should be investigated whether similar oscillatory representations also encode the location of inanimate objects, or reflect processes independent of physical movement, such as the dimensional coding of one’s attentional focus or locations in higher-order cognitive space37. Ultimately, these are some of the key remaining questions that will elucidate the precise neural mechanisms that underlie spatial navigation, spatial awareness of others, and memory functions in complex real-world scenarios.
Online content
Any methods, additional references, Nature Research reporting summaries, source data, extended data, supplementary information, acknowledgements, peer review information; details of author contributions and competing interests; and statements of data and code availability are available at https://doi.org/10.1038/s41586–020-03073-y.
Methods
Participants
Five participants (31–52 years old; three males and two females) with pharmaco-resistant focal epilepsy took part in this study (Extended Data Table 1); they had previously been implanted with the FDA-approved RNS System (NeuroPace Inc.) for treatment of epilepsy19. Electrode placements were determined solely on the basis of clinical treatment criteria. All participants volunteered for the study by providing informed consent according to a protocol approved by the UCLA Medical Institutional Review Board (IRB).
Self-navigation and observation tasks
All participants took part in several experimental blocks, each of which started with about 15 min of a self-navigation task, followed by about 15 min of an observation task. The exact number of blocks per participant is shown in Extended Data Table 1. Both the self-navigation and the observation task took place within a rectangular room (about 5.9 m × 5.2 m, or 19.4 feet × 17.1 feet), in which 20 signs (a single colour per wall, with numbers 1 to 5) were mounted along the 4 walls (Fig. 2). In addition, three predefined target locations (each named with a letter) were randomly distributed throughout the room, but not visible to participants (Extended Data Fig. 1a). Target locations were circular with a diameter of 0.7 m.
In the self-navigation task, participants performed multiple trials in which they were asked to find and learn hidden target locations within the room. Each trial had the following structure. First, a computerized voice asked them to walk to one specific sign along the wall (for example, ‘yellow 4’). Second, after arriving at this sign, they were instructed to find one of the target locations (for example, target location ‘T’). Participants could either freely walk around searching for the cued target location, or walk directly to the target location if they remembered it from a previous trial. A new trial began after the participant arrived at the target location. The experimenter observed the participants’ movements in real-time via video; neither the experimenter nor any others were visible to participants during the self-navigation task.
During the observation task, participants sat on a chair in a corner of the room (the specific corner varied across task blocks; see Extended Data Fig. 1a), while the experimenter walked around the room. Participants were asked to continuously keep track of the experimenter’s location, and to press a button whenever the experimenter crossed one of the hidden target locations. The experimenter’s walking trajectory within the room was predefined by a pseudo-randomized sequence of translations between the signs on the wall and the room centre. The experimenter received auditory instructions on where to go next from a computerized voice via an in-ear Bluetooth headset; instructions were inaudible to participants.
Participant 1 performed a slightly modified version of the task, in which there were 4 (instead of 3) different target locations, and these were named with numbers 1–4 (instead of letters).
Unity application for experimental control
The Unity game engine (version 2018.1.9f2) was used for experimental control. Participants’ and the experimenter’s momentary position and orientation per time point were recorded with a motion-tracking system (see below). The Unity application was programmed to read the motion-tracking data in real-time during the experiment, in order to trigger auditory events that depended on the participant’s momentary location. For instance, the Unity application was programmed to automatically detect when a participant arrived at a hidden target location during a ‘target search’ trial, and then to trigger the next auditory instruction. Next, the Unity application was programmed to detect when a participant arrived at the cued wall-mounted sign, at which point another auditory instruction was triggered to direct participants to find the next target location, and so on.
Moreover, the Unity application was programmed to trigger iEEG data storage automatically, and to insert a mark at specific time points in the iEEG data. These synchronization marks were sent at the beginning and end of each 3.5–4-min recording interval, allowing for synchronization of iEEG data with data from other recording modalities (for example, motion tracking and eye tracking). See ref. 38 for further technical details and specifications of this setup.
Motion tracking
The location and orientation of participants (throughout the experiment) and the experimenter (during the observation task) were tracked with submillimetre resolution using the OptiTrack system (Natural Point Inc.) and the OptiTrack MOTIVE application (version 2.2.0). Twenty-two high-resolution infrared cameras were mounted on the ceiling, in order to track, with a sampling frequency of 120 Hz, the location of a rigid body-position marker that comprised several reflective markers mounted on the participant’s and experimenter’s heads (Fig. 1c). Example movement patterns in Fig. 2b show raw (non-interpolated) x/y position coordinates across all task blocks (one black dot per sampling point) of one participant during the self-navigation task and the experimenter during the observation task. One additional camera from the motion-tracking system recorded a wide-angle video of the room during the experiment.
On the basis of the motion-tracking data, movement speed was quantified as positional change in the horizontal plane (x/y coordinates) between two sampling points. Angular velocity was quantified as angular displacement in the horizontal plane (yaw) between two sampling points. Acceleration was quantified as the change in movement speed between two sampling points.
To distinguish movement from non-movement (standing) periods, we classified periods with movement speeds of 0.2 m s−1 or more as movement periods, and movement speeds of less than 0.2 m s−1 as periods of no movement, in order to account for residual head movements that do not reflect positional change. Movement-onset time points indicate periods when movement speed changes from ‘no movement’ (speeds of less than 0.2 m s−1) to ‘movement’ (speeds of 0.2 m s−1 or more) and then remains above 0.2 m s−1 for at least one second.
To distinguish movements towards versus away from boundaries, we first measured the distance to the nearest boundary for each sampling point, and then calculated whether this distance decreased (categorized as ‘towards boundary’) or increased (categorized as ‘away from boundary’) between two sampling points.
Eye tracking
Eye-tracking data were acquired with the Pupil Core headset for mobile eye tracking (Pupil Labs GmbH). Pupil movements were captured with a frequency of about 200 Hz (accuracy 0.6°), allowing the calculation of the pupil’s position per time point within a normalized two-dimensional reference frame of 192 pixels by 192 pixels (video of the eye). Data were recorded with the Pupil Capture application (v1.11) and exported with Pupil Player (v1.11).
The magnitude of eye movements was quantified using the distance of pupil movement within the reference frame by , where Δx and Δy are the distances of pupil movement in x and y dimensions.
To classify eye movements per time point as saccades or fixations, we applied the Cluster Fix toolbox for MATLAB, which detects fixations and saccades on the basis of a k-means cluster analysis of distance, velocity, acceleration and angular velocity of eye movements39. Fixation and saccade prevalence were defined as the percentage of time when fixations/saccades could be observed, relative to the total duration of the experiment.
iEEG data acquisition
The US Food and Drug Administration (FDA)-approved RNS System is designed to detect abnormal electrical activity in the brain and to respond in a closed-loop manner by delivering imperceptible levels of electrical stimulation intended to normalize brain activity before an individual experiences seizures. To avoid stimulation artefacts in the recorded brain activity for the duration of the experiment, stimulation was temporarily turned off with the participant’s informed consent, and the RNS System was used only to record iEEG activity.
Each participant had two implanted depth electrode leads with four electrode contacts per lead, and a spacing of either 3.5 mm or 10 mm between contacts (Extended Data Table 1). This setup allowed for continuous recording of bipolar iEEG activity (where the signal reflects differential activity between two neighbouring contacts) from up to 4 channels per participant, with a sampling frequency of 250 Hz.
Participants had the RNS Neurostimulator model RNS-300M or the model RNS-320 implanted. The amplifier settings were changed from clinical default settings to a 4 Hz high-pass and 120 Hz low-pass filter for model RNS-300M, and a 1 Hz high-pass and 90 Hz low-pass filter for model RNS-320. We note that, despite the 4 Hz cut-off frequency of the high-pass filter in the RNS-300M model, data for a frequency window between 3 Hz and 4 Hz were included in some analyses. A quantification of the filter’s attenuation showed that amplitudes are attenuated by only about 20% between 3 Hz and 4 Hz (see also ref. 20). Moreover, in all plots and analyses that show time–frequency power for individual frequency steps (for instance, power shown separately for 3 Hz, 3.25 Hz and so on; see, for example, Fig. 3a), power timeseries were normalized individually for each frequency step (for example, 3 Hz power at any given time point was z-scored relative to all power values of the 3 Hz timeseries), which further accounts for the bandpass filter’s attenuation of amplitudes below 3 Hz in model RNS-300M, and allows for a comparison of frequencies independently of their overall level of amplitude.
During the experiment, iEEG data were continuously monitored and recorded using near-field telemetry with a NeuroPace Wand that was secured on the participant’s head over the RNS Neurostimulator implant site. Via a custom-made wand-holder, the NeuroPace Wand was mounted on a backpack worn by participants, allowing them to freely walk around during recordings (see ref. 38 for more details). Data were stored automatically (without any interaction between participants and the experimenter) in intervals (roughly 3.5–4 min), separated by short task breaks (roughly 10 s). During these breaks, participants were asked by a computerized voice to avoid any movements.
Note that the experimental setup did not involve a wired connection between the recording device (the implanted RNS Neurostimulator) and an external power source; hence it is highly unlikely that the oscillatory changes observed here could be attributed to resonances from the system, such as noise from power-line frequency. In particular, line frequency noise could not explain ‘boundary’ versus ‘inner’ power differences during the observation task, as the participants’ location did not change throughout a task block, and therefore any system-inherent influences would be identical between periods when the experimenter was near or far from room boundaries.
Electrode localization
High-resolution postoperative head computed tomography was obtained in all participants. The precise anatomical location of each electrode contact was determined by co-registering this computed tomography image to a preoperative high-resolution structural magnetic resonance image (T1- and/or T2-weighted sequences) for each participant (Fig. 1). Recording contacts were located in a variety of MTL regions, including the hippocampus, subiculum, entorhinal cortex, parahippocampal cortex and perirhinal cortex (Extended Data Table 1). No recording contacts were located in the amygdala. Recording channels outside the MTL were excluded from further analyses.
Detection of epileptic events
To detect epileptic events such as interictal epileptiform discharges (IEDs) individually for each recording channel, we applied a method described previously40, which we have used in previous studies with the RNS System20,41. This method uses a double thresholding algorithm with two criteria. iEEG data samples for which one of the following two criteria was met were marked as ‘IED samples’, and were excluded from further analyses: first, the envelope of the unfiltered signal was six standard deviations above baseline; or second, the envelope of the filtered signal (15–80 Hz bandpass filter after signal rectification) was six standard deviations above baseline. In addition, the vector of identified IED samples (a logical array of zeros and ones that has the same length as the number of iEEG samples for a given channel, with value ‘1’ marking IED samples and value ‘0’ marking all remaining samples) was smoothed by a one-dimensional gaussian filter with a ‘moving average’ window length of 0.05 s, and all samples with values of above 0.01 after smoothing were also marked as IED samples, to capture residual epileptic activity before or after an epileptic event. This procedure adds a time window of about 250 ms around each detected IED sample, which was then excluded from all subsequent analyses. Using this method, we identified an average of 1–2% of data in each participant as IED events (minimum amount, 1.1% for participant 2; maximum amount, 2.0% for participant 1), similar to previous results20.
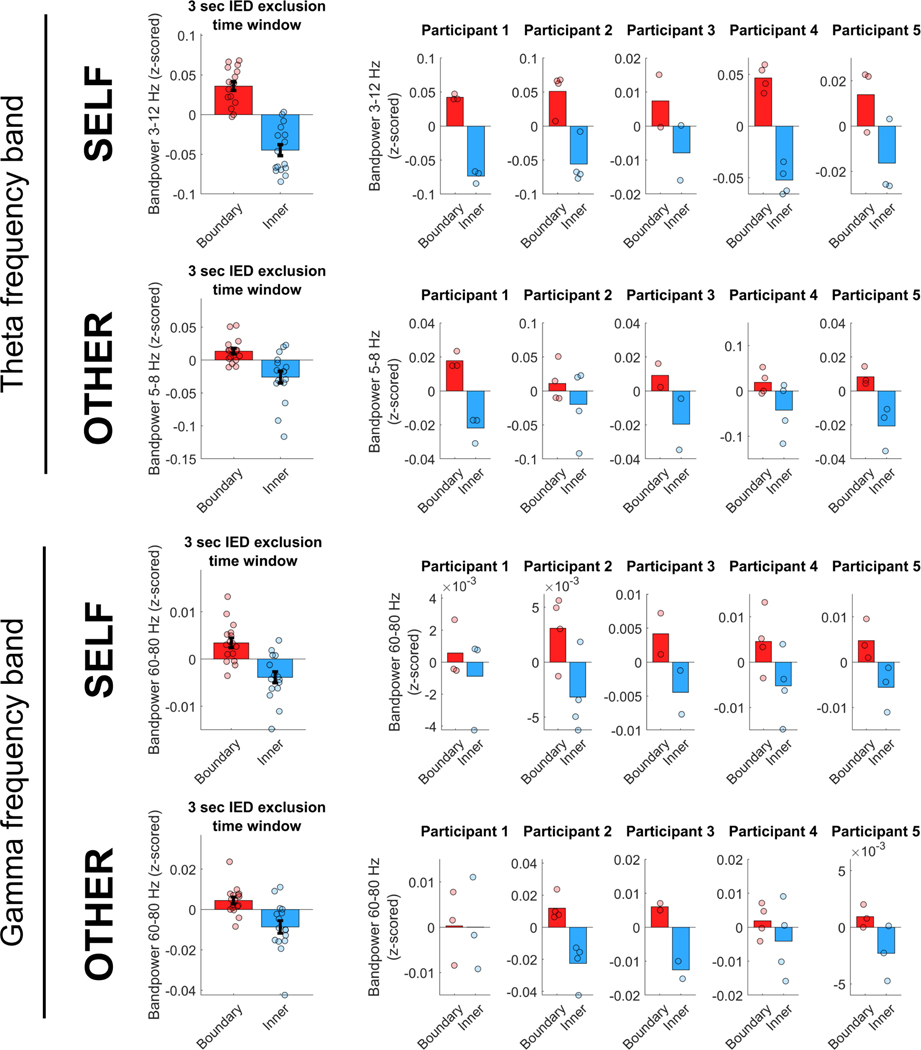
Moreover, in order to confirm that our results are not due to an insufficient time window added around epileptic events, we performed a control analysis in which we excluded data within a larger time window of 3 s around each epileptic event (1.5 s before and after each detected IED sample). The results using this larger time window (Extended Data Fig. 8) are consistent with the main results, on average across all recording channels as well as for each participant individually, suggesting that the presented results are not substantially affected by the length of the time window around epileptic events.
It is also worth noting that we deliberately recruited participants with relatively low IED activity (epileptic events). The RNS System allows for the viewing of a past number of epileptic events per day, which we used to approximate the average number of daily epileptic events over the prior three months. We invited participants with a low average number of daily events (roughly 500–800).
We further note that all participants gave informed consent to turn off the detection of epileptic events and consequent stimulation during the study in order to prevent stimulation artefacts in the iEEG recordings.
iEEG data analysis
A general overview of the main analysis pipeline for iEEG data, and how it is combined with behavioural data, is illustrated in Extended Data Fig. 9.
Time–frequency analyses of iEEG data were carried out using the BOSC toolbox42,43 to calculate oscillatory power at individual frequencies with sixth-order wavelets for individual frequency steps between 3 Hz and 90 Hz, with a step width of 0.25 Hz for low-frequency oscillations (less than 30 Hz) and a step width of 1 Hz for high-frequency oscillations (30 Hz or more). After calculating power timeseries for each frequency step, bandpower was calculated across multiple steps for specific frequency bands (for example, 5–8 Hz theta oscillations). Power timeseries were normalized before further analyses, by z-scoring each timeseries for a specific frequency or frequency band over the entire timeseries data, separately for each recording channel.
To detect significant oscillations (the prevalence of theta oscillations, as reported in Extended Data Fig. 1c), we used the BOSC toolbox to detect bouts of at least 2 cycles and above 95% chance level for individual frequency steps between 3 Hz and 20 Hz with a step width of 0.25 Hz. Prevalence of an oscillation was defined as the percentage of time (relative to the total duration of the experiment) when such oscillations could be observed at a given frequency.
To detect phase–amplitude coupling between the phase of low-frequency (theta) oscillations and the amplitude of high-frequency (gamma) oscillations, we calculated the ‘modulation index’, as described previously34. To explore the specific range of theta and gamma frequencies most strongly coupled to each other, we computed the modulation index for each theta–gamma frequency pair. We included low frequencies between 4 Hz and 16 Hz (1 Hz steps with a frequency window of ±1 Hz; that is, 3–5 Hz, 4–6 Hz, and so on) and high frequencies between 40 Hz and 90 Hz (2 Hz steps with a frequency window of ±2 Hz; that is, 38–42 Hz, 40–44 Hz and so on). The resulting modulation index for a theta–gamma frequency pair was then normalized relative to a surrogate distribution (determined for each frequency pair by 100 iterations of calculating the coupling of gamma amplitudes with randomly shuffled 1-second theta phase segments), as suggested previously34. As an example, a normalized modulation index of 3 indicates that the observed modulation index for this phase–amplitude pair is 3 standard deviations higher than what would be expected by chance (that is, the random surrogate distribution). To determine the specific low-frequency phase to which high-frequency amplitudes are coupled, we quantified the height of high-frequency amplitudes (using the Hilbert transform) for different segments of the 0 degrees to 360 degrees low-frequency phase range (segmented into 18 phase bins of 20 degrees each). For display purposes, heat maps illustrating phase–amplitude coupling results (Extended Data Fig. 7) were smoothed using MATLAB’s ‘interp2’ function with a ‘smoothing factor’ of k = 7, which performs an interpolation for two-dimensional gridded data by calculating interpolated values on a refined grid formed by repeatedly halving the intervals k times in each dimension.
Calculation of behavioural task performance
In order to calculate a participant’s performance in the self-navigation task, we calculated a participant’s ‘detour’ for each ‘target search’ period (that is, their walked distance between presentation of the target cue and arrival at the target, relative to the direct distance between these two locations). For the observation task, performance was quantified for every ‘target ahead’ period, by the distance between the experimenter’s location in the moment of a participant’s keypress, relative to the distance between the experimenter and the nearest target location. Individual trials (that is, each ‘target search’ period during self-navigation, and each of the experimenter’s individual straight trajectories during the observation task) were then classified as either ‘high’ or ‘low’ performance trials, based on a median split of performance during all trials (separately for the self-navigation and the observation task, respectively).
‘Boundary’ versus ‘inner’ distance threshold
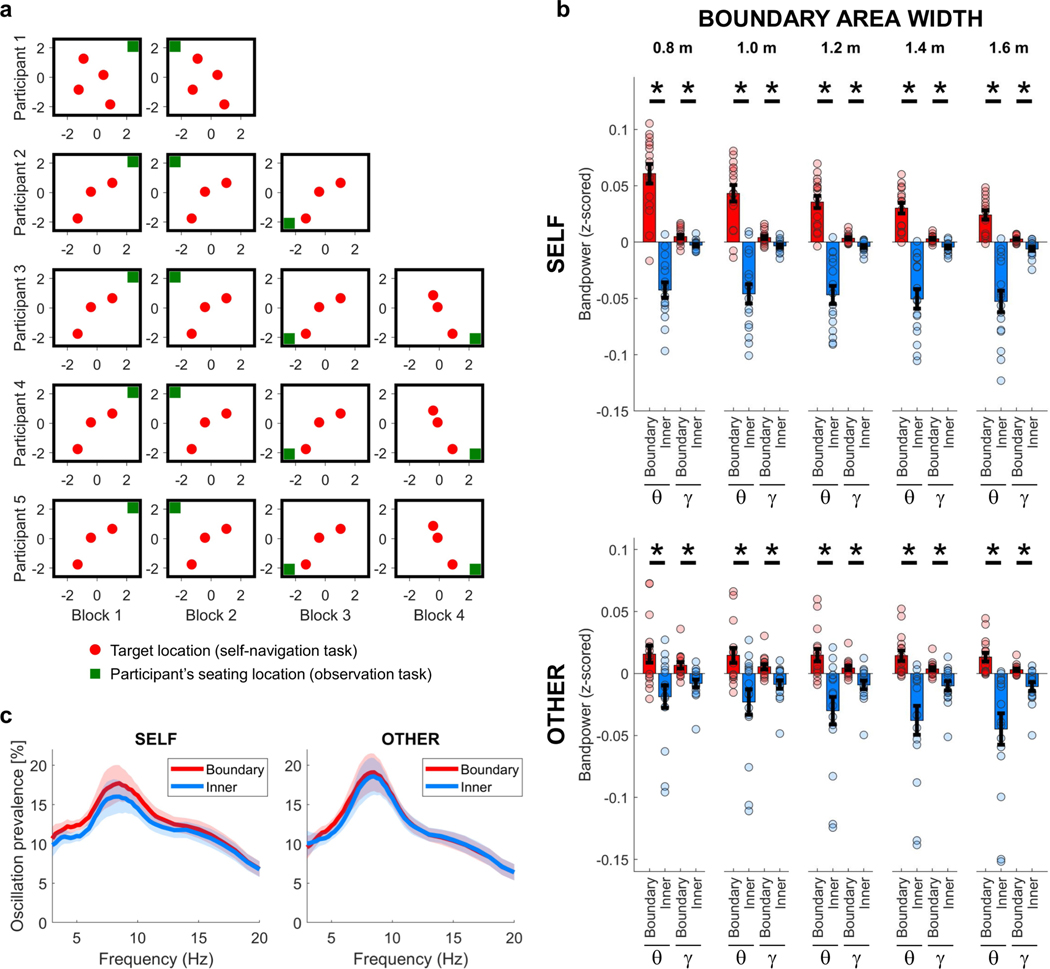
The selection of an appropriate threshold for the distinction between the ‘boundary’ and ‘inner’ areas of the room was based on an exploratory analysis, in which location-dependent bandpower changes were analysed using a range of thresholds (Extended Data Fig. 1b). The results of this analysis were used, together with illustrations of average bandpower differences across the room (such as heat maps, as shown for example in Fig. 3c), to identify an appropriate threshold for statistical analysis. Upon visual investigation of the data, we found that a threshold of 1.2 m captured oscillatory differences for several conditions of interest, that is, during both self-navigation and observation, for both theta and gamma, and with an amount of data (room coverage) in both room areas that allows a statistical comparison of ‘boundary’ versus ‘inner’ bandpower.
We note, however, that the reported effects do not depend on the selection of this threshold, as the exploratory analysis showed that the size of the effect is largely similar across alternative thresholds, and that the effects remain significant at each threshold throughout all tested alternatives (Extended Data Fig. 1b).
Moreover, in our linear mixed-effect model analysis that compares the impact of different variables on theta power, proximity to boundaries was used not as a categorical but as a continuous variable. The results of this analysis confirm that proximity to boundaries was a significant predictor of theta power, clearly stronger than other variables included in the model, and independent of the selected ‘boundary’ versus ‘inner’ threshold (Extended Data Fig. 3).
Linear mixed-effect model analysis
Linear mixed-effect models were calculated using each participant’s normalized theta bandpower timeseries as a ‘response variable’ and a range of ‘predictor variables’ (for example, proximity to boundary or movement speed at any point in time) to predict theta power variability over time.
All predictor variables were specified as fixed effects. Recording channel numbers were used as random-effect variables (‘blocking variables’), in order to control for the variation coming from different channels and to account for different numbers of recording channels between participants. Note that proximity to boundaries was specified as a continuous numerical variable (instead of a threshold-based ‘boundary’ versus ‘inner’ categorization); the model thus tests for a linear relationship between proximity to boundary and theta power, rather than evaluating power differences between the two room areas. Cognitive state was specified as a categorical variable with two states (‘target search’ versus ‘no target search’ for self-navigation, and ‘target ahead’ versus ‘no target ahead’ during observation). ‘Proximity to other’ indicates the distance between the participant and the experimenter during the observation task. Movement direction was quantified as a categorical variable in 12 equally sized directional bins (30 degrees each), and resulting beta estimates were averaged over bins, because movement direction as a numeric variable (due to its circular nature) is not expected to have a linear relationship with theta power (for example, minimum and maximum movement direction values of 1 and 359 degrees should evoke similar responses). Eye movements were specified as the magnitude of eye movement per time point. See Methods sections on ‘Eye tracking’ and ‘Motion tracking’ for more details about the calculation of predictor variables related to eye movement and movement speed. All non-categorical predictor variables were standardized (z-scored) before model fitting, in order to enable a direct comparison of the impact of each variable on theta power against each other. The frequency range for theta was identical to the main ‘boundary’ versus ‘inner’ analyses (3–12 Hz for self-navigation, 5–8 Hz for observation). Each of the predictor variables’ impact on the response variable is reflected by the variable’s beta weight (standardized effect size) and corresponding t-statistic (tStat).
The ‘full model’ in Extended Data Fig. 3 indicates a single model that includes all predictor variables. In the full model, however, some variables’ beta estimates may become suppressed or enhanced because of interactions and correlations between the different variables in the model. We therefore calculated also ‘independent models’ (separate models for each predictor variable) to provide a largely unbiased estimate of each variable’s impact that is independent of interactions and correlations with the other variables in the model.
Separate models were also used for analyses shown in Extended Data Fig. 5, comparing the impact of proximity to the nearest wall-mounted sign versus proximity to the nearest location in between the signs, and the proximity to the next wall-mounted sign (the specific sign that the participant or experimenter are walking towards) versus the proximity to the nearest boundary.
Data subsampling for statistical analysis
Because participants and the experimenter walked freely around the environment during the experimental tasks, it is possible that they spent more time close to a boundary than in the inner room area, or vice versa, which would affect statistical comparisons (for example, comparisons of bandpower) between these different areas. In order to enable a reliable statistical comparison between the two room areas (‘boundary’ versus ‘inner’), we corrected for potential differences in data amount by performing calculations on 500 iteratively generated, equally sized subsets of data. For each participant individually, this correction method included the following steps. First, we calculated the amount of time (quantified by the number of data samples) spent in each room area. Second, from the room area in which more time was spent, we randomly selected a subset of data that matched the amount of data from the other room area. For this random data subset selection, we used MATLAB’s ‘datasample’ function, which selects data uniformly at random, with replacement, from all available samples. Third, we used the selected subset of data to calculate parameters of interest (such as bandpower within that room area); hence calculations were carried out in equal data amounts for both room areas. Fourth, we ran 500 iterations of the random data subset selection and parameter calculation, averaged the resulting parameters across iterations, and used the averaged parameters for statistical comparisons and plotting.
We used the same logic and approach to account for differences in data amount between other conditions, such as for statistical comparisons and plotting of bandpower during ‘target search’ versus ‘no target search’, as well as ‘target ahead’ versus ‘no target ahead’ conditions.
Statistical comparisons and illustrations
Statistical comparisons were carried out using one-sided permutation tests with 10,000 permutations, unless otherwise noted.
To compare two paired arrays of values (for example, bandpower) between conditions, the permutation test calculates whether the mean difference between value pairs is significantly different from zero. It estimates the sampling distribution of the mean difference under the null hypothesis, which assumes that the mean difference between the two conditions is zero, by shuffling the condition assignments and recalculating the mean difference many times. The observed mean difference is then compared to this null distribution as a test of significance. The key steps of this procedure are described in more detail below.
Step 1: the observed difference between conditions is calculated, by first calculating the difference between conditions for each value pair (condition 1 value minus condition 2 value), and then calculating the average difference across pairs.
Step 2: condition labels are randomly shuffled within each value pair, and the difference between ‘shuffled conditions’ is calculated, by first calculating the difference between randomly labelled conditions for each value pair (value randomly labelled with condition 1 minus value randomly labelled with condition 2), and then calculating the average difference across pairs. This step is repeated nPerm times (in nPerm permutations), to generate a distribution of nPerm ‘random differences’ between conditions.
Step 3: the observed difference between conditions (calculated in step 1) is compared with the distribution of random differences from shuffling condition labels (calculated in step 2). The P value is calculated by the number of random differences that are larger than the observed difference, divided by the total number of samples in the distribution.
To determine whether the mean of an array of values is significantly different from zero, the permutation test uses a similar procedure to that described above. However, instead of randomly shuffling labels in each permutation step, the sign of each value is randomly assigned (as positive or negative). Repeating these steps nPerm times estimates the distribution of the mean under the null hypothesis, which if true would generate data values half of which are above zero and half of which are below. The observed mean is then compared with the null distribution of means as a test of significance.
When a multiple comparisons correction was performed, P values were adjusted using the false discovery rate (FDR44,45).
For display purposes, heat maps illustrating bandpower differences across the room area from a top-down perspective (for example, Figs. 3c, 4c) were smoothed as follows. The walkable room area was divided into a 7 × 7 grid tiling the environment, and the average bandpower was calculated for each tile. The resulting map was smoothed using MATLAB’s ‘interp2’ function with a smoothing factor of k = 7, which performs an interpolation for two-dimensional gridded data, by calculating interpolated values on a refined grid formed by repeatedly halving the intervals k times in each dimension. Heat maps in Fig. 3c show mean values across all participants (n = 5), using data from each participant’s channel with the highest difference between ‘boundary’ and ‘inner’ bandpower (in order to reduce noise from channels with a low response to boundary proximity). Heat maps in Fig. 4c show mean values across all recording channels (nCh = 16).
Analysis software
Data were analysed with MATLAB 2019a (The MathWorks, Natick, MA, USA), using its built-in functions as well as the Curve Fitting Toolbox, Statistics and Machine Learning Toolbox, and Optimization Toolbox.
Statistics and reproducibility
The experiment was carried out once per participant, and was not replicated. No statistical methods were used to predetermine sample size. The experiment was not randomized and the investigators were not blinded to allocation during the experiment and outcome assessment.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this paper.
Extended Data
Extended Data Fig. 1 |. Target locations, participants’ seating location, ‘boundary’ versus ‘inner’ distance thresholds, and prevalence of theta bouts.
a, Target locations (red dots) during the self-navigation task and the participants’ seating location (green squares) during the observation task. There were three target locations in each task block, except in the case of participant 1, who performed a slightly modified version of the task with four target locations. Target locations remained unchanged throughout the first three task blocks. For those participants who took part in more than three task blocks, new target locations were introduced in task block four. All units are in metres. b, Distance thresholds for ‘boundary’ versus ‘inner’ room area. Tested thresholds range between 0.8 m and 1.6 m. Both theta (θ) and gamma (γ) bandpowers were significantly increased near boundaries, independent of the selected boundary width threshold to distinguish ‘boundary’ versus ‘inner’ room areas (self, P < 0.001 for all thresholds and both frequency bands; other, P = 0.001 for theta at thresholds 0.8 m and 1.0 m, P < 0.001 for all other boundary widths and both frequency bands). θ denotes the theta frequency band (self, 3–12 Hz; other, 5–8 Hz); γ denotes the gamma frequency band (self/other, 60–80 Hz). Data show means ± s.e.m. from nCh = 16. Asterisks denote significant differences (P < 0.05, uncorrected) in a one-sided permutation test. ‘Boundary’ versus ‘inner’ comparisons and plots were corrected for differences in data amount between room areas (see Methods). c, Prevalence of theta bouts. Episodes of significant theta oscillations were detected using the BOSC toolbox42,43 for individual frequency steps between 3 Hz and 20 Hz with a step width of 0.25 Hz, separately for self-navigation (self) and observation (other). The prevalence of an oscillation was defined as the percentage of time (relative to the total duration of the experiment) when such oscillations could be observed at a given frequency (see Methods). Data show means ± s.e.m. from nCh = 16. Oscillation prevalence was not significantly different between ‘boundary’ and ‘inner’ room area for any of the tested frequencies in a one-sided permutation test for nCh = 16 (all P > 0.05, uncorrected).
Extended Data Fig. 2 |. Main effect and control analyses for the theta frequency band.
a, Theta bandpower was significantly higher for ‘boundary’ versus ‘inner’ locations (‘Main effect’; self, P < 0.001; other, P < 0.001), shown also during periods of immobility (when movement periods were excluded from data analysis; ‘Standing periods’; self, P = 0.021; other, P = 0.008), when circular areas with a diameter of 1 m around target locations were excluded from data analysis (‘No target locations’; self, P < 0.001; other, P < 0.001), for movements towards a boundary (‘Towards boundary’; self, P < 0.001; other, P < 0.001), and for movements away from a boundary (‘Away from boundary’; self, P < 0.001; other, P = 0.019). b, Theta bandpower was significantly higher for ‘boundary’ versus ‘inner’ locations, after excluding start and end periods per trial (where each trial is a ‘target search’ period during self-navigation or an individual trajectory of the experimenter during the observation task) from analysis. Time windows of 2 s and 5 s were excluded for self-navigation (‘Without trial start period (5s)’, P = 0.008; ‘Without trial start period (2s)’, P = 0.003; ‘Without trial end period (2s), P = 0.012; ‘Without trial start & end period (2s each)’, P = 0.020). For observation task trials, which were considerably shorter and did not have long breaks in between individual trajectories, only 2-s windows were excluded (‘Without trial start period’, P < 0.001; ‘Without trial end period’, P < 0.001; ‘Without trial start & end period’, P < 0.001). c, The strength of the main effect, quantified as each channel’s average ‘boundary’ minus ‘inner’ bandpower, did not significantly differ between different task blocks (P > 0.05 for all pairwise comparisons, separately for ‘self’ and ‘other’ task blocks). d, The strength of the main effect did not significantly differ between trials with high versus low performance (self, P = 0.210; other, P = 0.151). Performance was classified as ‘high’ or ‘low’ on the basis of a median split of performance during all trials (see Methods). e, Theta power was significantly increased near boundaries during high-performance as well as low-performance trials, both for self-navigation (self, high performance P = 0.003; low performance P = 0.021) and during observation (other, high performance P < 0.001; low performance P = 0.012). All plots (a–e) show means ± s.e.m. from nCh = 16. Asterisks denote a significant difference (P < 0.05, uncorrected) in a one-sided permutation test; ns, non-significant. ‘Boundary’ versus ‘inner’ comparisons and plots were corrected for differences in data amount between room areas (see Methods).
Extended Data Fig. 3 |. Simultaneous impact of multiple variables on theta power.
Linear mixed-effects models were calculated to predict each participant’s normalized theta power timeseries (response variable) by a range of predictor variables (fixed effects) that can simultaneously affect theta power variability over time. Proximity to boundary was specified as a continuous numerical variable (instead of a threshold-based ‘boundary’ versus ‘inner’ categorization). Cognitive state was specified as a categorical variable with two states (‘target search’ versus ‘no target search’ for self-navigation, and ‘target ahead’ versus ‘no target ahead’ during observation). Movement direction was quantified as a categorical variable in 12 equally sized directional bins. Eye movements were specified as the magnitude of eye movement per time point. ‘Proximity to other’ indicates the distance between the participant and the experimenter during the observation task. See Methods section ‘Linear mixed-effect model analysis’ for more details on how predictor variables were specified. All non-categorical predictor variables were standardized (z-scored) before model fitting. Each variable’s impact on theta power is reflected by the variable’s beta weight (standardized effect size; grey bars) and corresponding t-statistic (tStat; orange bars). The frequency range for theta was identical to the range in the main ‘boundary’ versus ‘inner’ analyses (3–12 Hz for self-navigation, 5–8 Hz for observation). The upper panels show results from a ‘full model’ including all predictor variables. Interactions and correlations between predictor variables (see also correlation matrices in bottom panels) can lead to enhancement or suppression of some variables’ beta weights (that is, overestimation or underestimation of the variables’ impact). Therefore, each variable’s impact was also calculated in ‘independent models’ (separate models for each of the predictor variables, thus showing each variable’s impact independently of interactions and correlations with the other variables). Asterisks denote a significant impact of a variable on theta power (P < 0.05, uncorrected). Significance was determined for each variable by testing whether the variable’s beta weight was significantly different from zero in a one-sided permutation test across participants. Diamonds denote P < 0.1 (non-significant). Data are mean beta/tStat values ± s.e.m. across n = 5 participants.
Extended Data Fig. 4 |. Impact of eye movements, and relationship between movement speed and theta power.
a, Participants’ eye movements were quantified throughout the experiment by measuring the pupil position on a normalized two-dimensional recording plane. Epochs of saccades and fixations were classified through algorithms based on a k-means cluster analysis39. Reported data for fixations and saccades indicate their prevalence over time (percentage of time throughout all task blocks). Theta power was higher during saccadic compared with fixation periods, for both self-navigation (P = 0.029) and observation (P < 0.001). b, Theta power was increased significantly near boundaries during both saccadic and fixation periods, for both self-navigation (saccades, P < 0.001; fixations, P < 0.001) and observation (saccades, P = 0.007; fixations, P = 0.002). c, The magnitude of eye movements (in normalized units per time point), fixation prevalence and saccade prevalence were not significantly different between ‘boundary’ and ‘inner’ room areas, neither during self-navigation (eye movement magnitude, P = 0.190; fixations, P = 0.189; saccades, P = 0.191) nor during observation (eye movement magnitude, P = 0.183; fixations, P = 0.372; saccades, P = 0.502). d, Theta power during epochs of high movement speed and low movement speed, based on a median split of movement speed values across all data from the self-navigation (self) or observation (other) tasks. Plots show the average power during movements with low speed (below median) subtracted from high speed (above median); thus, positive values indicate higher power for fast compared with slow movements. High–low speed power was not significantly different after multiple comparisons correction (FDR44,45) for any of the tested frequencies, in a one-sided permutation test for nCh = 16 (all P > 0.05, uncorrected). e, Theta power during epochs of high movement speed versus low movement speed, separately for ‘target search’ versus ‘no target search’ periods during self-navigation, and for ‘target ahead’ versus ‘no target ahead’ periods during the observation task. Green horizontal bars indicate significant high–low speed power differences (uncorrected) between ‘target search’ versus ‘no target search’ periods (self) or ‘target ahead’ versus ‘no target ahead’ (other) periods, and the inset red bars indicate significance after multiple comparisons correction (FDR44,45), in a one-sided permutation test for nCh = 16. The power difference between ‘target search/ahead’ and ‘no target search/ ahead’ was not significantly different between self-navigation and observation ([NoTargetSearchself – TargetSearchself] versus [NoTargetAheadother – TargetAheadother]; P > 0.05 for all frequencies; P < 0.1 for frequencies between 7 Hz and 14 Hz; FDR-corrected44,45; one-sided permutation test for each frequency in steps of 1 Hz; nCh = 16). Data in all plots show means ± s.e.m. from nCh = 16 (a, b, d, e) or n = 5 participants (c). Asterisks denote a significant difference (P < 0.05, uncorrected) in a one-sided permutation test; ns, non-significant. Analyses and plots of bandpower differences were corrected for differences in data amount between conditions (see Methods).
Extended Data Fig. 5 |. Impact of wall-mounted signs on theta power.
Linear mixed-effect models were used to quantify the impact of wall-mounted signs and proximity to the boundary on theta power during self-navigation (self) and observation (other). The theta frequency range was identical to the main ‘boundary’ versus ‘inner’ analyses (self, 3–12 Hz; other, 5–8 Hz). a, Diagram of the room from the top-down perspective, with yellow rectangles indicating wall-mounted signs (which provided strong visual cues for the participants), purple dots indicating locations in between signs (which did not correspond to visible landmarks but were defined for post hoc analysis only), and the grey rectangle indicating the room boundary. The red rectangle frame indicates the next wall-mounted sign that the participant (during self-navigation) or the experimenter (during observation) was walking towards (shown here is one example; the specific sign changed between trials). b, Comparison between the impact of proximity to sign locations versus proximity to locations in between signs. The impact of proximity to sign locations on theta power was not significantly different from the impact of locations in between signs, either during self-navigation (self, P = 0.815) or during observation (other, P = 0.176). c, Comparison between the impact of proximity to boundary versus the next wall-mounted sign that the participant or experimenter was walking towards. The impact of proximity to boundary was numerically higher in both conditions, but the difference between the variables’ impact was statistically significant only during observation (other, P = 0.028) and not during self-navigation (self, P = 0.059). Note that periods of walking towards the next wall-mounted sign during self-navigation are equivalent to ‘no target search’ periods, and that the proximity of the experimenter to the next wall-mounted sign during the observation task is generally highest during ‘no target ahead’ periods. This explains the low or negative relationship between theta power and proximity to the next wall sign, as theta power is generally decreased and there is no significant effect of boundaries on theta power during these periods (Fig. 4). The difference between the impact of ‘boundary’ and ‘next sign’ was not significantly different between self-navigation and observation ([Boundaryself – NextSignself] versus [Boundaryother – NextSignother], P = 0.493). Data in all plots (b, c) show mean beta values ± s.e.m. from n = 5 participants. The asterisk denotes a significant difference (P < 0.05, uncorrected) in a one-sided permutation test; the diamond denotes P < 0.1 (non-significant); ns, P > 0.1 (non-significant).
Extended Data Fig. 6 |. Effects in the gamma frequency band.
a, Gamma (60–80 Hz) bandpower at ‘boundary’ versus ‘inner’ locations (‘Main effect’; self, P < 0.001; other, P < 0.001), shown also during periods of immobility (when movement periods were excluded from data analysis; ‘Standing periods’; self, P = 0.004; other, P = 0.464), when circular areas with a diameter of 1 m around target locations were excluded from data analysis (‘No target locations’; self, P = 0.003; other, P = 0.001), for movements towards a boundary (‘Towards boundary’; self, P = 0.031; other, P = 0.010), and for movements away from a boundary (‘Away from boundary’; self, P = 0.022; other, P < 0.001). b, Numerically higher gamma bandpower at ‘boundary’ versus ‘inner’ locations, shown for each participant separately. Plots show mean values across channels per participant (participants 1 and 5, nCh = 3; participants 2 and 4, nCh = 4; participant 3: nCh = 2). c, During self-navigation (self), gamma bandpower was significantly lower for ‘target search’ versus ‘no target search’ periods (P < 0.001). During the observation task (other), gamma power was significantly higher for ‘target ahead’ versus ‘no target ahead’ periods (P < 0.001). d, For self-navigation, gamma bandpower was significantly different between ‘boundary’ versus ‘inner’ areas during ‘target search’ (P < 0.001) but not during ‘no target search’ periods (P = 0.113). During the observation task, gamma bandpower was not significantly different between ‘boundary’ versus ‘inner’ areas of the room, both for ‘target ahead’ (P = 0.137) and for ‘no target ahead’ (P = 0.255) periods. The difference between ‘boundary’ and ‘inner’ bandpower was not significantly different between ‘target search/ahead’ and ‘no target search/ahead’ periods ([BoundaryTargetSearch/Ahead – InnerTargetSearch/Ahead] versus [BoundaryNoTargetSearch/Ahead – InnerNoTargetSearch/Ahead]; self, P = 0.087; other, P = 0.347). Data in a, c, d show means ± s.e.m. from nCh = 16. Asterisks denote a significant difference (P < 0.05, uncorrected) in a one-sided permutation test; ns, non-significant. Statistical comparisons and plots were corrected for differences in data amount between conditions (see Methods).
Extended Data Fig. 7 |. Phase–amplitude coupling.
a, Phase–amplitude coupling was calculated between the phase of low-frequency (theta) oscillations and the amplitude of high-frequency (gamma) oscillations, following a procedure used previously34. The intensity of phase–amplitude coupling was quantified by the ‘modulation index’, calculated for each theta–gamma frequency pair individually. The low-frequency (theta) range was between 4 Hz and 16 Hz (in 1 Hz steps, with a frequency window of ±1 Hz; that is, 3–5 Hz, 4–6 Hz, and so on), and the high-frequency (gamma) range was between 40 Hz and 90 Hz (in 2 Hz steps, with a frequency window of ±2 Hz; that is, 38–42 Hz, 40–44 Hz, and so on). The modulation index was normalized relative to a surrogate distribution (determined for each frequency pair by 100 iterations of calculating the coupling of gamma amplitudes with randomly shuffled 1-s theta-phase segments). Warmer colours indicate stronger coupling of high-frequency amplitudes to a specific low-frequency phase. Strong phase–amplitude coupling is evident at a low-frequency (phase) peak between 6 Hz and 10 Hz. b, Illustration of average gamma amplitude height for different segments of the 0 to 360 degrees theta-phase range (segmented into 18 phase bins of 20 degrees each). Theta frequency was defined as 6–10 Hz. Warmer colours indicate higher (normalized) high-frequency amplitude. Strong coupling of gamma amplitude to theta oscillations is evident at a theta phase of about 90 degrees (indicated by the black dashed line, for visualization purpose only), during both self-navigation (self) and observation (other). Heat maps (a, b) were smoothed for display purposes.
Extended Data Fig. 8 |. Main effects after exclusion of an extended 3-s time window around epileptic events.
Control analysis confirming the main effects of increased theta (top two rows) and gamma (bottom two rows) bandpower near boundaries, as compared with the inner area of the room, during both self-navigation (self) and observation (other), after excluding data within a time window of 3 s around each epileptic event (1.5 s before and after each detected IED sample, respectively). Data in the left panel show means ± s.e.m. from nCh = 16. Data in the right panels show mean values across channels per participant (participants 1 and 5, nCh = 3; participants 2 and 4, nCh = 4; participant 3, nCh = 2).
Extended Data Fig. 9 |. Main analysis pipeline.
First, interictal epileptiform discharges were identified in the iEEG raw data and excluded from further analyses. Then, time–frequency analyses of the iEEG data were performed. Resulting power and bandpower timeseries were analysed and compared for different conditions, which were derived from behavioural data (motion- tracking data, eye-tracking data, or task-related events). See Methods for more details.
Extended Data Table 1 |.
Participant and RNS System details
| Participant number | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| Age | 49 | 52 | 34 | 33 | 31 | |
| Gender | female | female | male | male | male | |
| Number of performed task blocks(1) | 2 | 3 | 4 | 4 | 4 | |
| RNS Neurostimulator model | RNS-300M | RNS-300M | RNS-320 | RNS-300M | RNS-300M | |
| Electrode 1 | Hemisphere | left | left | left | left | left |
| Implant orientation(2) | 0 | 0 | 0 | L | L | |
| Contact spacing | 3.5 mm | 3.5 mm | 10 mm | 10 mm | 10 mm | |
| Number of MTL channels | 2 | 2 | 1 | 2 | 2 | |
| Channel 1 localization(3) | Sub/Sub | Sub/Sub | ERC/PRC | HPP/Sub | HPP/HPP | |
| Channel 2 localization(3) | HPP/PWM | HPP/PRC | Sub/Sub | HPP/Sub | ||
| Electrode 2 | Hemisphere | right | left | right | right | right |
| Implant orientation(2) | 0 | L | 0 | L | O | |
| Contact spacing | 10 mm | 10 mm | 10 mm | 10 mm | 10 mm | |
| Number of MTL channels | 1 | 2 | 1 | 2 | 1 | |
| Channel 1 localization(3) | HPP/PRC | HPP/HPP | Sub/PRC | HPP/Sub | Sub/PWM | |
| Channel 2 localization(3) | HPP/HPP | Sub/Sub | ||||
Each block comprised about 15 min of the self-navigation task, followed by about 15 min of the observation task.
L, along the longitudinal axis of the hippocampus; O, orthogonally to the long axis of the hippocampus.
Localization of two electrode contacts (+/−) per bipolar recording channel. ERC, entorhinal cortex; HPP, hippocampus (CA1/CA2/CA3/DG); PRC, perirhinal cortex; PWM, parahippocampal white matter; Sub, subiculum.
Supplementary Material
Acknowledgements
This work was supported by the National Institutes of Health (NIH) National Institute of Neurological Disorders and Stroke (NINDS; grant NS103802), the McKnight Foundation (Technological Innovations Award in Neuroscience to N.S.) and a Keck Junior Faculty Award (to N.S.). We thank all participants for taking part in the study, and all members of the Suthana laboratory for discussions. We also thank A. Lin for support with statistical analyses, J. Schneiders and T. Wishard for help with illustrations and manuscript preparation, and J. Gill for methodological support.
Footnotes
Competing interests N.R.H. is an employee of NeuroPace Inc., Mountain View, CA, USA.
Additional information
Supplementary information is available for this paper at https://doi.org/10.1038/s41586–020-03073-y.
Peer review information Nature thanks Jack Lin, Hugo Spiers and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The custom computer code and algorithms used to generate our results are available from the corresponding authors upon reasonable request.
References
- 1.Moser M-B, Rowland DC & Moser EI Place cells, grid cells, and memory. Cold Spring Harb. Perspect. Biol 7, a021808 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Omer DB, Maimon SR, Las L & Ulanovsky N. Social place-cells in the bat hippocampus. Science 359, 218–224 (2018). [DOI] [PubMed] [Google Scholar]
- 3.Danjo T, Toyoizumi T & Fujisawa S. Spatial representations of self and other in the hippocampus. Science 359, 213–218 (2018). [DOI] [PubMed] [Google Scholar]
- 4.Julian JB, Keinath AT, Marchette SA & Epstein RA The neurocognitive basis of spatial reorientation. Curr. Biol 28, R1059–R1073 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hardcastle K, Ganguli S & Giocomo LM Environmental boundaries as an error correction mechanism for grid cells. Neuron 86, 827–839 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Doeller CF & Burgess N. Distinct error-correcting and incidental learning of location relative to landmarks and boundaries. Proc. Natl Acad. Sci. USA 105, 5909–5914 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Horner AJ, Bisby JA, Wang A, Bogus K & Burgess N. The role of spatial boundaries in shaping long-term event representations. Cognition 154, 151–164 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Meilinger T, Strickrodt M & Bülthoff HH Qualitative differences in memory for vista and environmental spaces are caused by opaque borders, not movement or successive presentation. Cognition 155, 77–95 (2016). [DOI] [PubMed] [Google Scholar]
- 9.Bellmund JLS et al. Deforming the metric of cognitive maps distorts memory. Nat. Hum. Behav 4, 177–188 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Solstad T, Boccara CN, Kropff E, Moser M-B & Moser EI Representation of geometric borders in the entorhinal cortex. Science 322, 1865–1868 (2008). [DOI] [PubMed] [Google Scholar]
- 11.Lever C, Burton S, Jeewajee A, O’Keefe J & Burgess N. Boundary vector cells in the subiculum of the hippocampal formation. J. Neurosci 29, 9771–9777 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Savelli F, Yoganarasimha D & Knierim JJ Influence of boundary removal on the spatial representations of the medial entorhinal cortex. Hippocampus 18, 1270–1282 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.O’Keefe J & Burgess N. Geometric determinants of the place fields of hippocampal neurons. Nature 381, 425–428 (1996). [DOI] [PubMed] [Google Scholar]
- 14.Lever C, Wills T, Cacucci F, Burgess N & O’Keefe J. Long-term plasticity in hippocampal place-cell representation of environmental geometry. Nature 416, 90–94 (2002). [DOI] [PubMed] [Google Scholar]
- 15.Krupic J, Bauza M, Burton S, Barry C & O’Keefe J. Grid cell symmetry is shaped by environmental geometry. Nature 518, 232–235 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stensola T, Stensola H, Moser M-B & Moser EI Shearing-induced asymmetry in entorhinal grid cells. Nature 518, 207–212 (2015). [DOI] [PubMed] [Google Scholar]
- 17.Lee SA et al. Electrophysiological signatures of spatial boundaries in the human subiculum. J. Neurosci 38, 3265–3272 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Shine JP, Valdés-Herrera JP, Tempelmann C & Wolbers T. Evidence for allocentric boundary and goal direction information in the human entorhinal cortex and subiculum. Nat. Commun 10, 4004 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Morrell MJ & RNS System in Epilepsy Study Group. Responsive cortical stimulation for the treatment of medically intractable partial epilepsy. Neurology 77, 1295–1304 (2011). [DOI] [PubMed] [Google Scholar]
- 20.Aghajan ZM et al. Theta oscillations in the human medial temporal lobe during real-world ambulatory movement. Curr. Biol 27, 3743–3751 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Caplan JB, Madsen JR, Raghavachari S & Kahana MJ Distinct patterns of brain oscillations underlie two basic parameters of human maze learning. J. Neurophysiol 86, 368–380 (2001). [DOI] [PubMed] [Google Scholar]
- 22.Caplan JB et al. Human θ oscillations related to sensorimotor integration and spatial learning. J. Neurosci 23, 4726–4736 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ekstrom AD et al. Human hippocampal theta activity during virtual navigation. Hippocampus 15, 881–889 (2005). [DOI] [PubMed] [Google Scholar]
- 24.Kahana MJ, Sekuler R, Caplan JB, Kirschen M & Madsen JR Human theta oscillations exhibit task dependence during virtual maze navigation. Nature 399, 781–784 (1999). [DOI] [PubMed] [Google Scholar]
- 25.Mizuhara H, Wang L-Q, Kobayashi K & Yamaguchi Y. A long-range cortical network emerging with theta oscillation in a mental task. Neuroreport 15, 1233–1238 (2004). [DOI] [PubMed] [Google Scholar]
- 26.Jutras MJ, Fries P & Buffalo EA Oscillatory activity in the monkey hippocampus during visual exploration and memory formation. Proc. Natl Acad. Sci. USA 110, 13144–13149 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Jeewajee A, Barry C, O’Keefe J & Burgess N. Grid cells and theta as oscillatory interference: electrophysiological data from freely moving rats. Hippocampus 18, 1175–1185 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McFarland WL, Teitelbaum H & Hedges EK Relationship between hippocampal theta activity and running speed in the rat. J. Comp. Physiol. Psychol 88, 324–328 (1975). [DOI] [PubMed] [Google Scholar]
- 29.Høydal ØA, Skytøen ER, Andersson SO, Moser M-B & Moser EI Object-vector coding in the medial entorhinal cortex. Nature 568, 400–404 (2019). [DOI] [PubMed] [Google Scholar]
- 30.Barry C. et al. The boundary vector cell model of place cell firing and spatial memory. Rev. Neurosci 17, 71–97 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hollup SA, Molden S, Donnett JG, Moser M-B & Moser EI Accumulation of hippocampal place fields at the goal location in an annular watermaze task. J. Neurosci 21, 1635–1644 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dupret D, O’Neill J, Pleydell-Bouverie B & Csicsvari J. The reorganization and reactivation of hippocampal maps predict spatial memory performance. Nat. Neurosci 13, 995–1002 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bourboulou R. et al. Dynamic control of hippocampal spatial coding resolution by local visual cues. eLife 8, e44487 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tort ABL, Komorowski R, Eichenbaum H & Kopell N. Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. J. Neurophysiol 104, 1195–1210 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Canolty RT & Knight RT The functional role of cross-frequency coupling. Trends Cogn. Sci 14, 506–515 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kunz L. et al. Mesoscopic neural representations in spatial navigation. Trends Cogn. Sci 23, 615–630 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bellmund JLS, Gärdenfors P, Moser EI & Doeller CF Navigating cognition: spatial codes for human thinking. Science 362, eaat6766 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Topalovic U. et al. Wireless programmable recording and stimulation of deep brain activity in freely moving humans. Neuron 108, 322–334 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.König SD & Buffalo EA A nonparametric method for detecting fixations and saccades using cluster analysis: removing the need for arbitrary thresholds. J. Neurosci. Methods 227, 121–131 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gelinas JN, Khodagholy D, Thesen T, Devinsky O & Buzsáki G. Interictal epileptiform discharges induce hippocampal-cortical coupling in temporal lobe epilepsy. Nat. Med 22, 641–648 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Aghajan ZM et al. Modulation of human intracranial theta oscillations during freely moving spatial navigation and memory Preprint at 10.1101/738807 (2019). [DOI] [Google Scholar]
- 42.Whitten TA, Hughes AM, Dickson CT & Caplan JB A better oscillation detection method robustly extracts EEG rhythms across brain state changes: the human alpha rhythm as a test case. Neuroimage 54, 860–874 (2011). [DOI] [PubMed] [Google Scholar]
- 43.Seager MA, Johnson LD, Chabot ES, Asaka Y & Berry SD Oscillatory brain states and learning: impact of hippocampal theta-contingent training. Proc. Natl Acad. Sci. USA 99, 1616–1620 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Benjamini Y & Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Stat. Soc. B 57, 289–300 (1995). [Google Scholar]
- 45.Benjamini Y & Yekutieli D. The control of the false discovery rate in multiple testing under dependency. Ann. Stat 29, 1165–1188 (2001). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.