Non-Invasive Wearable Patch Utilizing Seismocardiography for Peri-Operative Use in Surgical Patients

Abstract

Objective:

Optimizing peri-operative fluid management has been shown to improve patient outcomes and the use of stroke volume (SV) measurement has become an accepted tool to guide fluid therapy. The Transesophageal Doppler (TED) is a validated, minimally invasive device that allows clinical assessment of SV. Unfortunately, the use of the TED is restricted to the intra-operative setting in anesthetized patients and requires constant supervision and periodic adjustment for accurate signal quality. However, post-operative fluid management is also vital for improved outcomes. Currently, there is no device regularly used in clinics that can track patient’s SV continuously and non-invasively both during and after surgery.

Methods:

In this paper, we propose the use of a wearable patch mounted on the mid-sternum, which captures the seismocardiogram (SCG) and electrocardiogram (ECG) signals continuously to predict SV in patients undergoing major surgery. In a study of 12 patients, hemodynamic data was recorded simultaneously using the TED and wearable patch. Signal processing and regression techniques were used to derive SV from the signals (SCG and ECG) captured by the wearable patch and compare it to values obtained by the TED.

Results:

The results showed that the combination of SCG and ECG contains substantial information regarding SV, resulting in a correlation and median absolute error between the predicted and reference SV values of 0.81 and 7.56 mL, respectively.

Significance:

This work shows promise for the proposed wearable-based methodology to be used as an alternative to TED for continuous patient monitoring and guiding peri-operative fluid management.

I. INTRODUCTION

Peri-operative fluid management has been shown to impact clinical outcomes including reducing the duration of hospital and/or intensive care unit (ICU) stays. Achieving and maintaining optimum fluid status is clinically challenging, especially since physiologic alterations associated with surgery may complicate interpretation of routine parameters. Clinicians often rely on additional hemodynamic parameters, such as stroke volume (SV), to guide peri-operative fluid management [1–8]. Several studies have demonstrated the advantages of fluid management by administering crystalloids or colloids to maintain SV within 10% of baseline [9–11].

In the last decade, hemodynamic monitoring at the bedside has been evolved remarkably both in the operating room and ICU. The most significant progression has been the declining use of the pulmonary artery catheter and increasing adoption of continuous, real time and less invasive monitoring techniques [12]. Today, a commonly used tool for SV estimation in the operating room is the Transesophageal Doppler (TED) which measures blood flow velocity in the descending thoracic aorta [9, 11]. Although the TED is generally considered to be sufficiently accurate for fluid management intra-operatively, it has some disadvantages. It requires general anesthesia or deep sedation and therefore must be removed on emergence. In addition, it requires periodic repositioning and constant supervision by an experienced professional. Surgical patients often experience significant alterations in volume status post-operatively, however the TED is not a valid monitor in those situations for these reasons [1, 13]. There is therefore a clinical need for a non-invasive alternative to the TED, that could be used for monitoring SV in patients during the entire peri-operative period.

Although multiple technologies for non-invasive SV prediction have been described in the literature, none is suitable for use in the pre-, intra- and post-operative settings. Impedance cardiography (ICG) involves placing 4–8 electrodes on the thorax, sending a small electrical current into the body and measuring the subsequent voltage drop to compute thoracic impedance changes resulting from aortic ejection of blood. While ICG has been demonstrated to be accurate for SV estimation in some settings, the accuracy is limited in patients with low cardiac output, subjects with high body mass index, and can be confounded by other fluids in the thoracic cavity (e.g., edema) [14–17]. Volume-clamping based continuous blood pressure measurement technologies have also been implemented with empirical algorithms for estimating SV, however their accuracy has typically been shown to be low in large studies [18–21]. Ballistocardiography (BCG) based techniques, quantifying whole-body movements in response to the blood movement in the vascular tree, have been investigated as well for SV estimation; however, such techniques require cumbersome beds or tables and are thus not well-suited to clinical settings and cannot be applied readily to ambulatory settings [22, 23].

In this study, our primary aim was to develop an alternative to TED, which can track a patient’s SV continuously and non-invasively both during and after surgery. Our group has previously developed [24] and studied a wearable patch for ambulatory monitoring in heart failure patients and found that it accurately reflects changes in clinical status [25, 26]. In this proof of concept study, we investigated the feasibility of estimating SV with our wearable patch that measures the seismocardiogram (SCG) and electrocardiogram (ECG) signals in patients undergoing major gynecologic oncology surgery. To achieve this, an end-to-end signal processing and regression-based prediction algorithm using the features extracted from the patch signals was presented. The TED was used as a reference standard against which the estimates from the wearable patch could be compared. With such a mapping function, the wearable patch is expected to enable non-invasive and continuous hemodynamic monitoring and guide fluid management throughout the entire peri-operative phase.

II. STUDY DESIGN AND SUBJECT DEMOGRAPHICS

This project was conducted under a protocol approved by the Northwestern University Institutional Review Board (STU00204403, approved on 1/18/2017) and all subjects provided written consent. A total of 12 female subjects (Age: 52.0±10.1, Weight: 79.2±23.2kg, Height: 162.6±5.4 cm) undergoing major intra-abdominal gynecological oncology surgery participated in the study. The peri-operative care of all subjects was based on the Institutional Enhanced Recovery (ERAS) Protocol for Gynecologic Oncology patients. The protocol included pre-operative hydration and multimodal analgesia. The wearable patch was applied pre-operatively, to the anterior chest of the subject at the mid-sternal level. All patients received an opioid sparing total intravenous anesthetic. The TED was inserted following tracheal intubation. The intravenous fluid therapy protocol was based on the ERAS protocol, guided by the Doppler parameters to maintain an SV greater than 70 mL/beat. Upon emergence from anesthesia, the endotracheal tube and the TED were removed in all subjects. Additionally, post-operative analgesia, intravenous fluid therapy, oral intake and physical activity were based on the ERAS protocol in all subjects.

A. Transesophageal Doppler (TED)

Following endotracheal intubation, the TED (CardioQ-ODM, Deltex Medical, Greenville, SC) was inserted into the esophagus of the subject by an experienced practitioner. Once the appropriate Doppler signal and waveform were obtained, monitoring commenced [9, 27]. Windows (30 second length) of the resulting velocity-time waveform were used to calculate various parameters such as mean acceleration, peak velocity, and stroke distance. SV was calculated from the TED waveform by multiplying the distance a column of blood moves along the aorta at each left ventricular contraction (stroke distance) with a calibration constant (the approximate area of the aorta based on patient age, weight and height).

B. Wearable Patch

The custom wearable patch, which is shown in Fig. 1(a), was applied to the anterior chest of the subject at the mid-sternal level using three Ag/AgCl ECG adhesive-backed gel electrodes (Red Dot 2560, 3M, Maplewood, MN). It weighs 65 grams and has a diameter of 10 cm, which does not make the subjects uncomfortable during data collection. To capture the ECG, an analog-front-end (AFE) integrated circuit (IC) with on board analog-to-digital converter, ADC, (ADS1292 Texas Instruments, Dallas, TX), which connects to these three electrodes, was used. Each electrode corresponds to either the positive reference, negative reference, or right-leg drive.

Fig. 1.

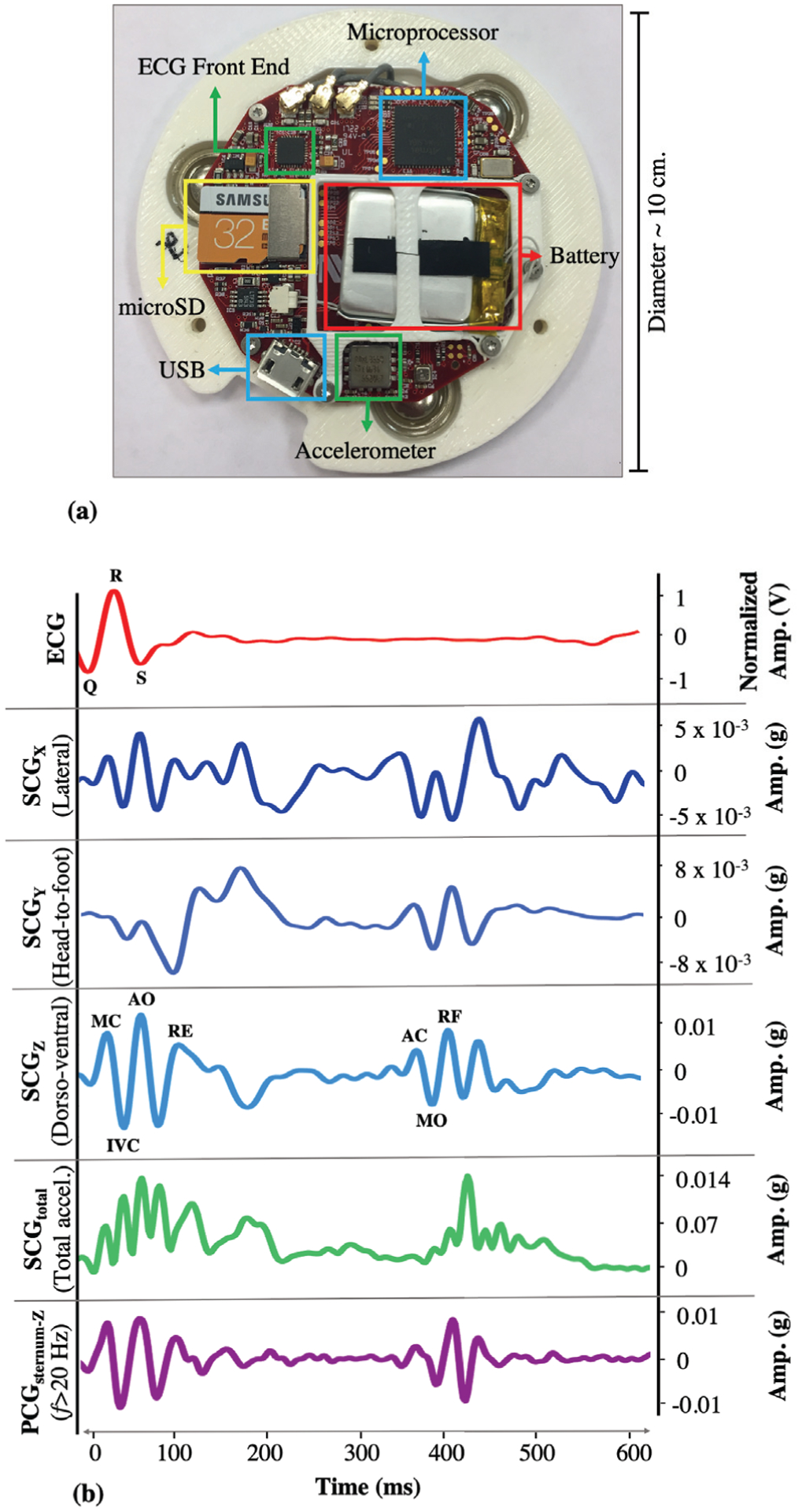
(a) Custom-made patch hardware. (b) A representative beat from the ECG, SCG_x,y,z,total and PCG_sternum signals (for PCG, only Z-axis is shown as the other axes are less commonly used). The portion within each R-R interval is called a beat, which is usually around ~ 600 – 1000 ms. The R-peak locations on the ECG signal are used to split the SCG into individual beats. The peaks and valleys on the SCG signals correspond to specific cardiac events.

While the ECG waveform measures the electrical activity of the heart, the SCG waveform assesses the mechanical motions and corresponds to the local thoracic vibrations originating from the contraction of the heart and ejection of blood from the ventricles. An SCG waveform is generated for each contraction, which is characterized by several peaks and valleys. A tri-axial ultralow noise accelerometer (ADXL355, Analog Devices, Norwood, MA) is used to capture the SCG signals in lateral (X-axis), head-to-foot (Y-axis) and dorso-ventral (Z-axis) directions. SCG components each having a specific morphology, can be observed in all three axes as shown in Fig. 1(b), [23, 28].

The patch includes an ATSAM4LS8B (Microchip Technology, Chandler, AZ) to sample all sensors (ECG at 1kHz and the accelerometer at 500 Hz) and to save the data to an on-board microSD card. When interfaced with a computer through a microUSB port, HeartPulse App (Department of Anesthesiology, Northwestern University, Chicago, IL) communicates with the microcontroller to download and subsequently delete the data on the microSD card. Additionally, the inserted microUSB interfaces with the battery charger (BQ24232RGTR, Texas Instruments) to charge the 150 mAh battery. The battery life of the patch is approximately 48 hours, which is more than adequate to record the data for the entirety of most surgeries and the first post-operative day.

C. Pre-processing and Signal Segmentation

The SCG_x,y,z and ECG signals were filtered using finite impulse response (FIR) Kaiser-window band-pass filters (1–45 Hz and 0.5–40 Hz, respectively) to reduce the motion artifacts while preserving the shape of the signals. These cut-off frequencies were determined based on the existing literature [29, 30]. With these cut-off values, low frequency noise caused by respiratory chest wall movements was also attenuated as these movements are usually observed below 0.5 Hz [31, 32]. In addition to the SCG_x,y,z signals, the total acceleration magnitude, SCG_total, was calculated using the formula $\sqrt{{\text{SCG}}_{\text{x}}^2\left(t\right)+{\text{SCG}}_{\text{y}}^2\left(t\right)+{\text{SCG}}_{\text{z}}^2\left(t\right)}$, where SCG_x(t), SCG_y(t) and SCG_z(t) represent the acceleration measured in the X, Y, Z directions at time instant t (Fig. 1(b)). This new signal represents the total physical activity of the heart by assessing the spatial curve of the displacement vector instead of separating the vector space into individual axis components [30, 33]. The TED and patch clocks were aligned using the corresponding timestamps in the stored data. The heart rate (HR) and SV values were obtained from the TED as the reference values. Since the TED averages and updates the HR and SV every 30 seconds, the SCG_x,y,z,total and ECG signals obtained from the wearable patch were processed in a similar manner. The ECG and SCG_x,y,z,total signals were split into 30 seconds long segments to ensure coherence with the TED measurements (Fig. 2).

Fig. 2.

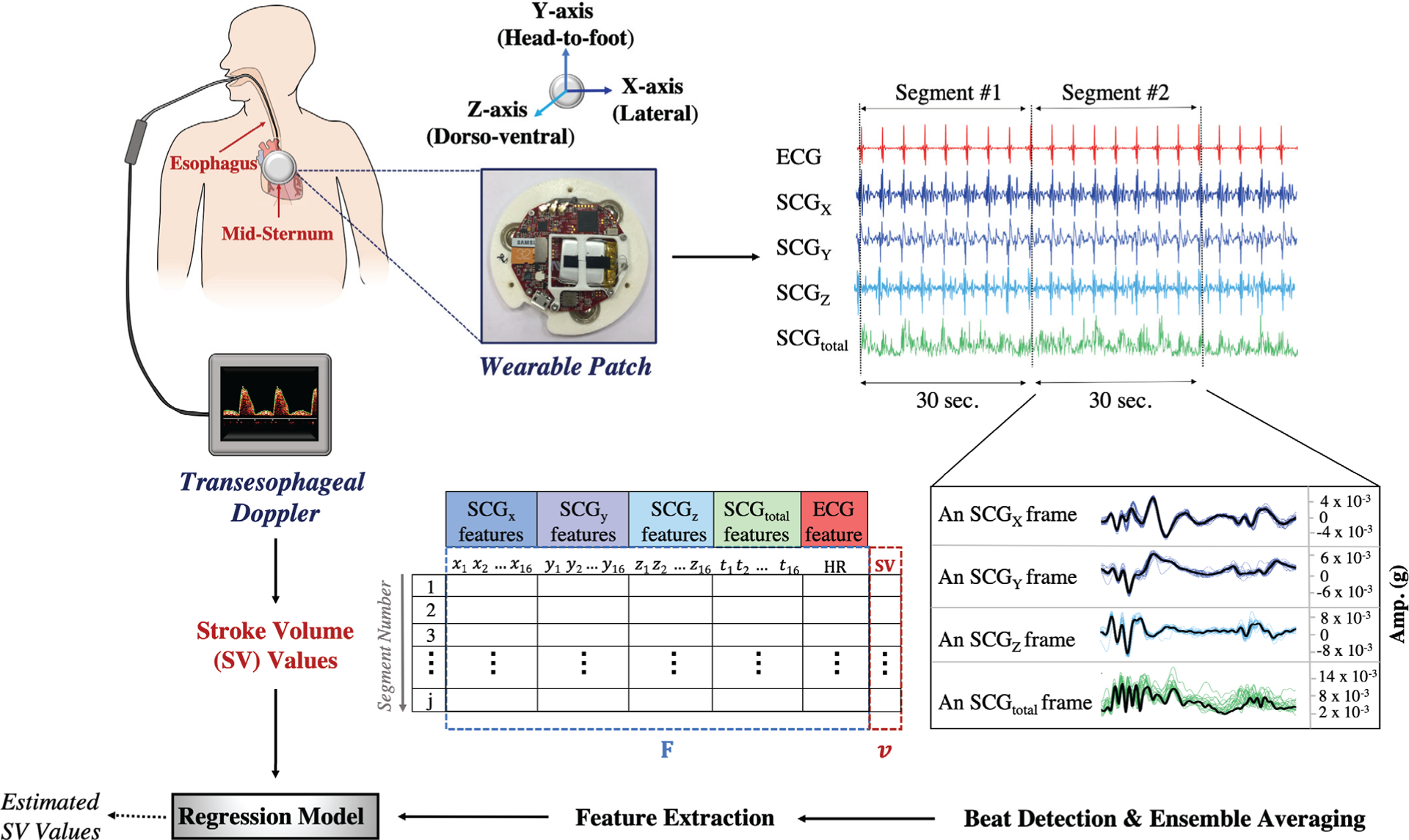
The block diagram for the data acquisition and signal processing. The wearable patch was mounted on the mid-sternum while the patient was undergoing a surgery. The ECG and SCG_x,y,z signals were recorded throughout the surgery while the SV values were being acquired with the TED. In addition to the SCG_x,y,z signals, the total acceleration magnitude, SCG_total, was calculated. As the TED was averaging and storing the SV values every 30 seconds, the ECG and SCG_x,y,z,total signals were split into 30 seconds-long segments. Within each segment, the R-peak locations were found on the ECG and used to detect the individual beats on the SCG_x,y,z,total. The ensemble average of the detected beats was calculated, so per segment there was one single ensemble averaged frame for each axis. In total 65 features were extracted for the analysis. Then a random forest regression model was trained to predict the corresponding SV values.

The first 20 minutes (data recorded during pre-incision) was considered as baseline or pre-incision data. For the intra-operative data, the patch signals were segmented into non-overlapping segments in accordance with the TED clock as previously explained (Fig. 2). The average number of intra-operative data points was 228±128 (min:62, max:418). The differences between the number of data points were due to either the varying length of the surgeries or loss in TED/patch signals. For the pre-incision data, a different signal segmentation method was employed to increase the number of instances. As the TED updates the SV and HR values every 30 seconds, there were 40 data points in each of the pre-incision SV and HR vectors. Cubic spline interpolation was applied on these SV and HR vectors in order to artificially increase the number of data points. Cubic spline interpolation was chosen as it has been found to be an effective and computationally efficient method in the literature [34, 35]. It fits a series of unique cubic polynomials between adjacent pairs of points, so that a smooth and continuous curve is obtained [36]. From the interpolated SV and HR curves, equally spaced data points were obtained to increase the frequency of the SV and HR readings. The interval was selected as 3 seconds, so that the reference SV and HR values could be updated every 3 seconds, rather than every 30 seconds. The pre-incision SCG_x,y,z,total and ECG signals were segmented in accordance with these interpolated SV and HR values. A moving 30 seconds long window with 90% overlap (i.e. step size of 3 seconds for coherence with the interpolated SV and HR values) was applied on the SCG_x,y,z,total and ECG signals to obtain the segments (Fig. 3).

Fig. 3.

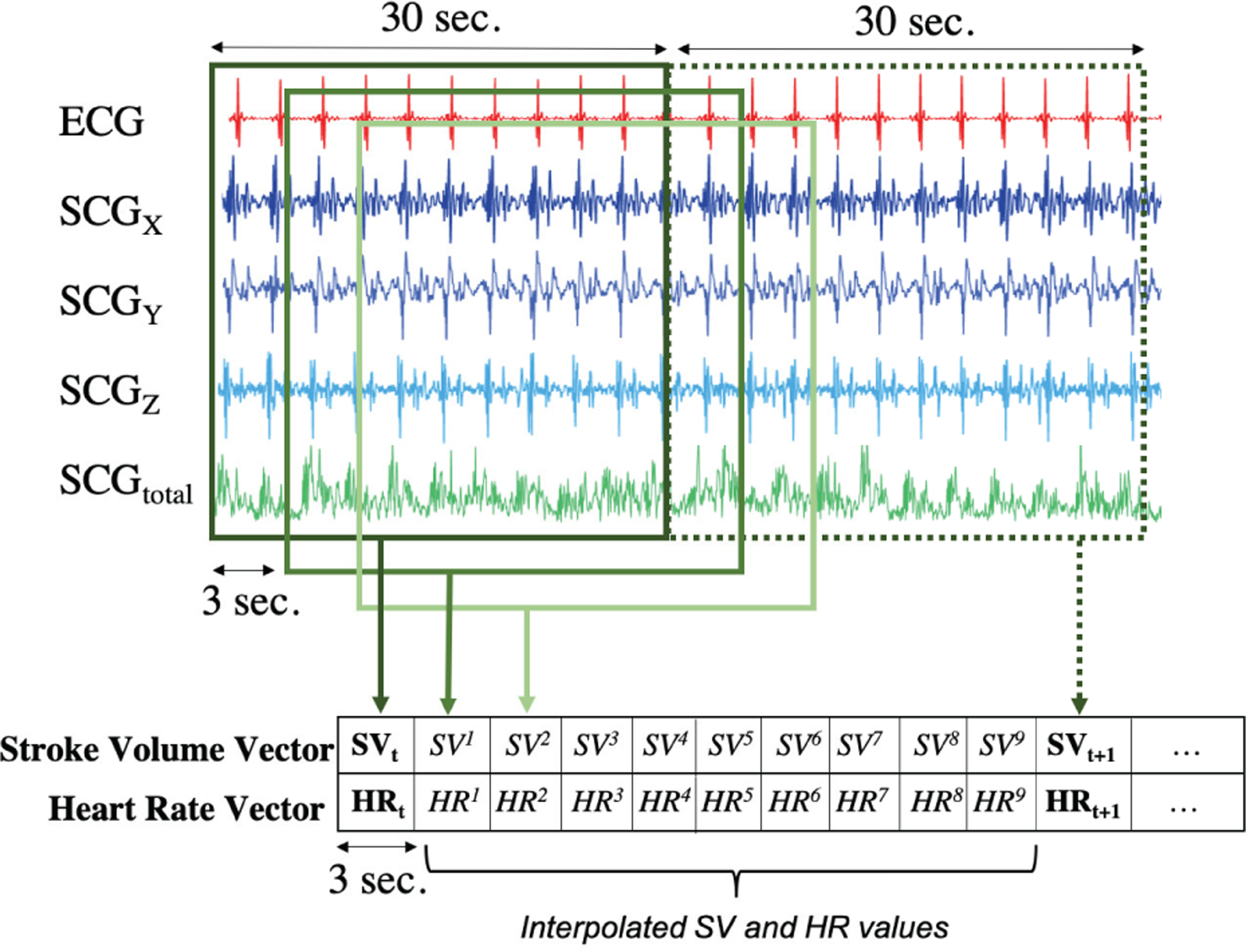
Cubic spline interpolation was performed on the pre-incision SV and HR vectors to increase the number of instances. From the interpolated SV and HR curves, equally spaced (3 seconds) data points were obtained to increase the frequency of the SV and HR readings. Similarly, the patch signals were segmented using a 30 seconds long moving window with 90% overlap (step size = 3 seconds).

D. Feature Extraction

The R-peaks of the ECG were detected using a simple peak detection algorithm within each segment. The peaks were used to extract individual beats of the SCG in each of the three axes. These beats were then truncated to a length of 600 ms and ensemble averaged to produce a single averaged beat, or frame, per each segment for all three directions [37]. Additionally, for each segment, the average R-R interval duration (t_RR) was calculated using the ratio 60 / t_RR to obtain the average HR in beats per minute (bpm). These HR values were compared with the reference HR values obtained from the TED, and any 30 seconds-long segment was discarded from the analysis unless the reference and calculated average HR values were in 10% agreement.

SCG signals are characterized by several peaks and valleys, which are labeled in Fig. 1(b) based on their corresponding physiological events: MC (mitral valve closure), IVC (isovolumetric contraction), AO (aortic valve opening), RE (rapid ejection), AC (aortic valve closure), MO (mitral valve opening), and RF (rapid filling) [23]. In the current analysis, the peaks or valleys were not matched with specific cardiac events as the cardiac events points are subject specific and prone to instability. Such instability may occur because, 1) SCG signals have high inter-subject variability and it is not always possible to detect these points accurately, 2) SCG signal morphology may change depending on the position of the subject or the location of the patch, 3) The current data set consists of subjects undergoing surgery rather than healthy subjects, and thus the subjects’ physiological state is not as stable as for healthy subjects. Thus, there was a need to account for instability of the signal morphology in the proposed methodology [28, 38]. Accordingly, rather than putting emphasis on specific physiological points (AO, MC, etc.), the methods in the literature were followed [37, 39] and a new feature set was defined consisting of maxima and minima points of the signal (instead of matching the peaks or valleys with underlying physiological events).

A total of 65 features were extracted for the analysis (Table I): 64 of these features were from the SCG_x,y,z,total frames, i.e. 16 features were extracted from each SCG signal. These features included maxima-minima amplitudes and locations, powers, and peak-to-peak amplitudes. As the final feature, calculated average HR values were used. All features were stored in a matrix, and the same feature extraction procedure was repeated for each subject. For n^th subject, we denote the feature matrices obtained from the pre-incision and intra-operative data by B_n and S_n, respectively. A sample feature matrix is shown in Fig. 2. In these feature matrices, each row corresponds to a 30 seconds-long segment, and is of the form: (F_j, v_j), where F_j = (x_j,1, x_j,2, …, y_j,1, y_j,2, …, z_j,1, z_j,2, …, t_j,1, t_j,2, …, HR) are the 65 features extracted as described in the previous section, and v_j is the SV values we obtained from the TED.

Table I.

Features extracted from the signals

	Feature Names	Number of Features
SCGx,y,z,total 0–250ms	First and second largest maxima (amp. and loc.) First and second largest minima (amp. and loc.) RMS power Peak-to-peak amplitude	10 (4 signals=40)
SCGx,y,z,total 250–500ms	Largest maximum (amp. and loc.) Largest minimum (amp. and loc.) RMS power Peak-to-peak amplitude	6 (4 signals=24)
ECG	Average HR derived from R-R interval length	1
Total		65 features

E. Regression Model and Validation

Random forest-based regression was used to estimate SV values as it can achieve high accuracy without overfitting. In this method, rather than relying on a single tree, multiple trees are bootstrapped by using randomized subsets drawn from the original dataset. The trees are trained in parallel independently and their final predictions are averaged to obtain the predicted target value [40, 41]. During the training phase, the model learned the relationship between the reference SV values and extracted features. This trained model was then used to predict the SV values for the incoming unseen segments.

The model was validated using leave-one-subject-out cross-validation (LOSO-CV). The feature matrices obtained from each subject from the pre-incision and intra-operative data were called as B_n and S_n, respectively. In each fold i, we left the intra-operative data (S_i) from the i^th subject out and trained our model using the remaining S_n, where n ≠ i, and all pre-incision data (B_n). This effectively simulates the clinical scenario of requiring a calibration period with TED B_i after which time the TED would no longer be required intra- or post-operatively. The combination of these matrices and the corresponding SV values were the training data and training targets, respectively. The model was then tested on S_i and the predicted SV values were stored. A simplified representation of the proposed LOSO-CV framework is presented in Fig. 4. The same procedure was repeated for each subject.

Fig. 4.

A simplified representation of how leave-one-subject-out cross-validation (LOSO-CV) was performed. In each fold, intra-operative data from one subject was left out (S_i). The model was trained using the remaining S_n where n≠i and all B_n. The model was then tested on S_i and the predicted SV values were stored. This step was repeated for each subject.

The correlation coefficient (r-value) and the median absolute error (MedAE) between the reference and predicted SV were computed to assess the performance of the model. Beyond correlation, Bland-Altman methods were used to quantify the agreement between the SCG-based SV values and the reference standard values from TED [42]. Although a Bland-Altman plot presents the bias and limits of agreement, it does not provide direct information on whether the difference between the reference and predicted values is clinically acceptable. The most important reason is inter-subject variability, i.e. one limit of agreement might be acceptable for a subject with high SV, but it may be too high for a subject with low SV [43]. One of the methods to overcome this problem is to calculate the percent error (PE) for each subject, i.e. dividing the limits of agreement by the mean reference SV value [43, 44]. This error should be within ±30% to consider the new method as “interchangeable” with the reference method. It should be noted that in this study, rather than using the limits of agreement across all subjects, each subject’s own limits of agreement and mean reference SV value were used to remove the effect of inter-subject variability. In the MedAE calculation, first the prediction error, i.e. the difference between the reference and predicted SV values of all segments from all subjects, was calculated. Then the absolute value of the errors was computed, and their median was calculated. This yielded the MedAE of the model. MedAE was selected rather than mean error to reduce sensitivity of the assessment to outliers.

F. Elucidating Mechanistic Insight Regarding Stroke Volume Correlations to SCG

The analysis pipeline was built using the features from both SCG and ECG signals as explained in the previous section. To show that SV prediction would benefit from an electro-mechanical approach rather than relying only on electrical or mechanical schemes, different models were trained using: (i) features from SCG axes (only mechanical), (ii) features from ECG, i.e. HR (only electrical), and (iii) features from SCG axes and ECG together (the electro-mechanical approach presented in the previous section). Then the performance metrics described above (correlation coefficient and MedAE) were calculated.

In addition, the importance of using multiple directions of acceleration (dorso-ventral, lateral, and head-to-foot), and their effect on the regression result were examined to investigate which acceleration direction(s) provide(s) better mechanistic insight into the physiological underpinnings of the signal. Different models were trained using the features derived from each direction (or their combinations) and the correlation coefficient and MedAE value were calculated.

After investigating the effect of acceleration direction, each feature’s individual contribution to SV prediction was calculated by obtaining the feature importance scores from the random forest model. In each tree, every node splits the values of a feature based on impurity (variance) criteria, so that the similar feature values are grouped under the same set. Therefore, feature importance scores can easily be obtained by calculating each feature’s contribution to decreasing the weighted impurity [45]. Leveraging this fact, the feature importance scores were obtained from the model and ranked in descending order. While calculating the feature importance scores, two different approaches were employed to investigate the bias and outlier effects on the model: (i) obtaining the feature scores in each fold and averaging them across all folds, (ii) re-training the random forest model on the whole dataset and computing the feature importance scores.

Finally, to investigate feature contributions further, the Pearson correlation coefficients between feature pairs were calculated. Pearson correlation analysis measures the strength and direction of the relationship between two variables [46]. If any feature pair has an absolute correlation coefficient close to 1 (high correlation), this means that these two features are linearly dependent and have almost the same effect on the dependent variable, in this case: SV. On the other hand, having lower absolute correlation coefficient means that these two features have distinguishable effect on the dependent variable. Thus, having less correlated features, and therefore diversification within a feature set, is actually better for information gain, thus model training.

G. Comparison with State-of-the-Art

1). Contribution of the Acoustic and Vibration Components:

In the literature, it was shown that the SCG signal is composed of two main components: low frequency (i.e. vibration, 1 < f < 20Hz) component emerging from the cardiac output and high frequency (i.e. acoustic, f > 20Hz) component originating from the heart sounds [47, 48]. The latter is also known as the phonocardiogram (PCG) waveform (Fig. 1(b)). In this paper, in addition to investigating the SCG signal as a whole, the individual contributions of the PCG and vibration components were also investigated. However, it should be noted that the sensor placement was not optimized for PCG and thus it is not quite a fair head to head comparison.

In accordance with the frequency cut-off presented in the literature, the SCG signals were split into PCG and vibration segments: f > 20Hz (PCG_sternum) and 1 < f < 20Hz (SCG_vib). Again, the lower frequency cut-off was selected as 1 Hz to remove any chest movements originated from respiration (generally f < 0.5Hz) [31]. After segmenting the SCG_x,y,z,total signals into PCG and vibration segments, the whole analysis pipeline was run with the same features and same ML model (random forest including 20-min of calibration) for PCG_sternum, SCG_vib, and the combination of PCG_sternum and SCG_vib cases.

2). Comparison with the Existing Literature:

Previously the relationship between SCG and SV was investigated in 8 individuals by recording their uni-axial SCG signals (using 393C, PCB Piezotronics) in two separate sessions at least a day apart [49]. In that study, the following features were extracted from each beat: the time between the ECG R-wave and the opening of mitral valve (t_MO), the maximum of rapid ejection (RE_max) and the slope of its increase (m_RE), the area under curve during rapid systolic ejection (AUC_RE), isovolumic contraction time (t_MC–AO) and its slope (m_MC–AO), systolic ejection time (t_AO–AC) and isovolumic relaxation time (t_AC–MO). For each subject, a linear regression model was trained on the first recording session and the second session was used for testing.

To provide a fair comparison with [49], the points corresponding to the cardiac events (the features above) were extracted from each of the SCG_x,y,z,total signals. Then for each subject, the first half of the SCG signal was used to train a linear regression model and the second half was used for testing the model. It should be noted that there were several differences in the experimental setups of this study and the one being compared. In this study, (i) the recordings were taken at a single session where the subjects were undergoing surgery (i.e. their hemodynamic state was varying), (ii) instead of a uni-axial accelerometer, a 3-axis accelerometer was used, (iii) the features were extracted from the ensemble averaged frames derived from 30-sec long segments as the TED was updating the SV every 30 seconds.

III. RESULTS AND DISCUSSION

A. Machine Learning Based Estimation of Stroke Volume

The regression model trained on the combination of the SCG and ECG features was correlated to the TED reference standard (r = 0.81) with a relatively low MedAE (7.56 mL) across all subjects. Using the cardio-mechanical information only (i.e., SCG signal features alone) resulted in a correlation value of 0.67 and a MedAE of 9.51 mL, whereas using only the electrical (ECG) information resulted in a correlation value of 0.31 and a MedAE of 14.75 mL. Fig. 5(a) provides the regression plot for the electro-mechanical approach, with each subject represented by a different color for ease of visualization.

Fig. 5.

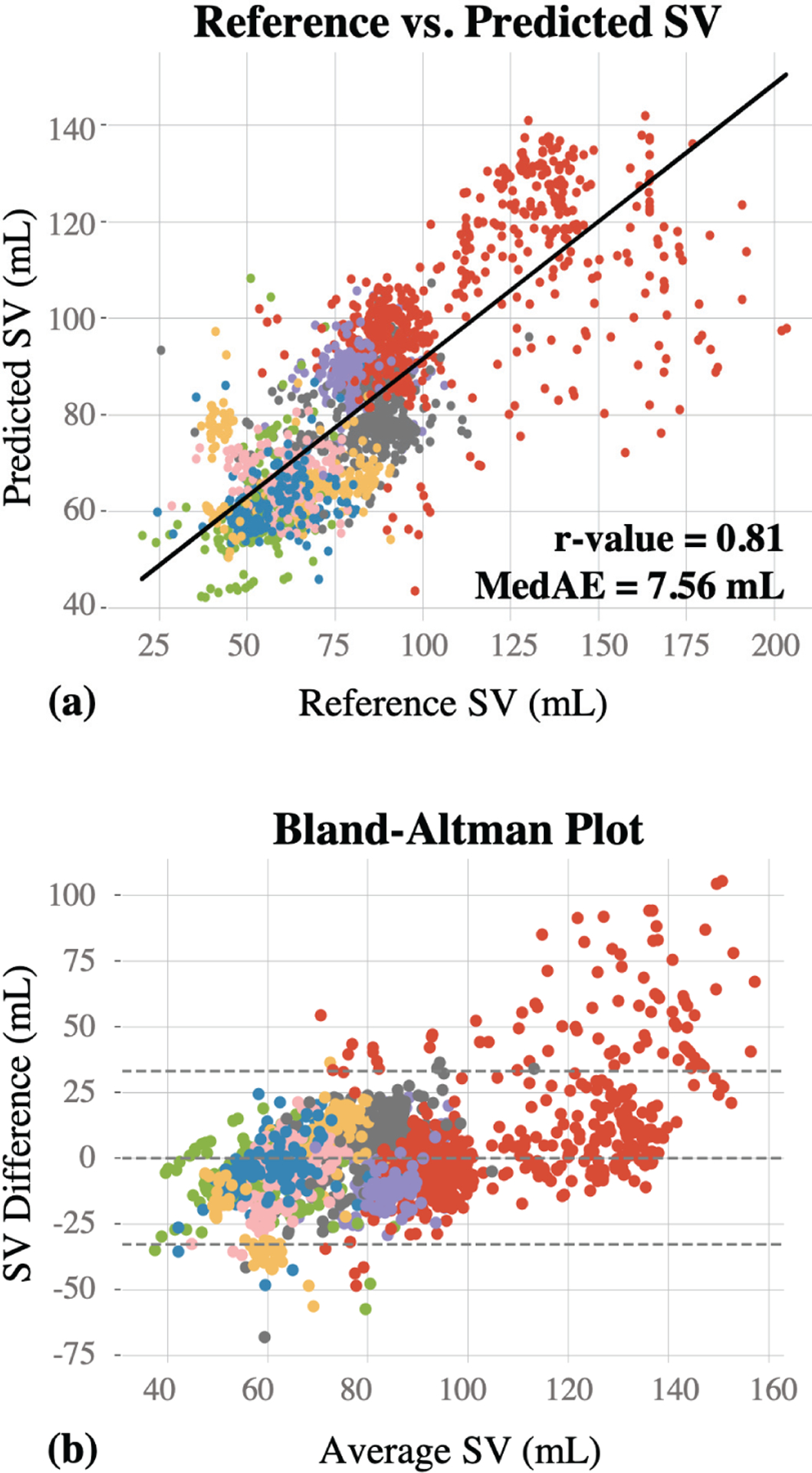
(a) The reference vs. predicted SV values are presented. 65 features were extracted and used to train a random forest regression model. This resulted in a correlation coefficient (r-value) of 0.81 and MedAE of 7.56 mL. (b) The Bland-Altman graph for the reference and predicted SV values. Horizontal line in the middle represents the bias line, whereas the area between the upper and lower horizontal lines represent the 95% confidence interval, (mean ± 2*standard deviation).

The results of this study demonstrated that the combination of the SCG and ECG features contains salient information for enabling estimation of SV with sufficiently high correlation and low MedAE across all subjects. The error is higher in SV values greater than 100 mL, and in particular quite high for SV values above 150 mL. According to the Bland-Altman results (Fig. 5(b)), the differences between the reference and predicted SV values are closer to zero within the 60–100mL range, which justifies that the model achieves higher prediction performance within this range. Most of the data points are within the 95% confidence interval (limits of agreement: +33.08mL and −32.86mL), and the scatter around the bias line (mean difference: 0.11mL) increases as the average SV increases, demonstrating that the variability is not consistent throughout the graph. One reason for the greater error at higher values of SV is the high inter-subject variability in the dataset, as shown with different colors in Fig. 5(a,b); since most of the datapoints at these higher values of SV were from one subject, the model trained on other subjects with lower SV values did not perform as well for this case. In addition to the Bland-Altman plot, PE for each subject was calculated to investigate whether the proposed algorithm could be considered as “interchangeable” with the reference method. This analysis resulted in average PE of 37.5±22.45 for the lower limit (6 subjects being <%30), and 25.6±16.7 for the upper limit (9 subjects being <%30).

B. Interpretation of Acceleration Directions and Features

In contrast to the ECG signal which has been studied for more than a century and is well understood regarding its mechanistic underpinnings, the SCG signal is not as well characterized. The literature reports that the dorso-ventral component of the signal represents a combination of body acceleration responses to both heart and blood movement in the thoracic cavity [23]. Our group has previously reported that the head-to-foot component may better reflect blood movement [25]– due to the anatomical alignment of the aorta and the large component of the body acceleration that is originated from the change of direction of blood through the aortic arch – and thus a sub-hypothesis of this work aimed at elucidating physiological mechanistic insight was that the head-to-foot SCG components would better reflect hemodynamic forces (e.g., stroke volume). In the current study similarly, a relatively higher correlation was obtained between the predicted and reference SV values when the features from the head-to-foot axis were used to train the model (r=0.65) compared to the dorso-ventral (r=0.50) or lateral (r=0.22) axes. In contrast, the dorso-ventral axis, which represents a combination of body acceleration responses to both heart and blood movement in the thoracic cavity, resulted in smaller MedAE (10.86 mL) compared to other axes. When the total heart activity signal was used, the correlation and MedAE values were calculated as 0.56 and 10.49mL, respectively. The regression results of the models trained using features from each SCG axis and their combinations are presented in Table II.

Table II.

Experiments with axis-combinations

	Correlation (r-value)	MedAE (mL)
SCGx	0.22	13.76
SCGy	0.65	12.46
SCGz	0.50	10.86
SCGtotal	0.56	10.49
ECG (HR)	0.31	14.75
SCGx and ECG	0.58	9.64
SCGy and ECG	0.74	8.44
SCGz and ECG	0.67	9.29
SCGtotal and ECG	0.71	9.65
SCGx,y	0.48	10.81
SCGx,z	0.53	11.80
SCGy,z	0.61	10.94
SCGx,y and ECG	0.77	7.93
SCGx,z and ECG	0.74	8.73
SCGy,z and ECG	0.73	8.86
SCGx,y,z	0.64	10.63
SCGx,y,z,total	0.67	9.51
SCGx,y,z and ECG	0.80	7.61
SCGx,y,z,total and ECG	0.81	7.56

Each feature’s contribution to SV prediction was investigated by analyzing the feature importance scores obtained from the random forest models. Regardless of the method used (averaging across folds vs. re-training on the whole dataset), the same features were obtained as the top 15 most important features. In Table III, the importance scores from the first method (averaging across all folds) are presented. The feature which has the highest importance is heart rate obtained from the patch ECG. This is followed by the amplitude of the minimum point within the first 250 ms of the dorso-ventral signal. From a physiological perspective, this point corresponds to the start of isovolumetric contraction, which occurs immediately before systolic ejection. Since stroke volume is defined as the difference between the end diastolic and end systolic volumes, finding isovolumetric contraction as one of the most prominent features is consisted with the underlying physiological events.

Table III.

Random Forest Feature Importance Ranking

Feature Names	Normalized Feature Scores
Wearable Heart Rate (HR)	0.314
0–250ms, First Min. Amp, Z	0.125
0–250ms, First Max. Amp, X	0.079
0–250ms, Peak-to-Peak, Y	0.050
0–250ms, First Min. Loc, X	0.048
0–250ms, First Min. Loc, Z	0.041
0–250ms, First Min. Loc, Y	0.035
0–250ms, Second Max. Amp, Z	0.026
0–250ms, First Max. Loc, Z	0.024
0–250ms, First Max. Amp, Z	0.020
250–500ms, Peak-to-Peak, Y	0.017
0–250ms, RMS Power, Y	0.014
250–500ms, First Min. Amp, Z	0.013
250–500ms, First Min. Amp, Y	0.013
0–250ms, Second Min. Amp, Y	0.012

Secondly, amplitude values of the maxima and minima points are dominating the location (timing) values of these points. As SV is directly related to the contraction and strength of the heart, it was expected to have mostly the amplitude-related features in the top features. Lastly, most of the top features belong to either the head-to-foot or dorso-ventral axes. These scores are consisted with the findings of the proposed regression analysis, and explain why dorso-ventral and head-to-foot axes resulted in relatively higher performance compared to the lateral axis. In contrast, none of the total heart activity features appeared in the top 15 list.

Finally, the heatmaps showing the Pearson correlation coefficients between the feature pairs are presented in Fig. 6. Based on these heatmaps, most of the feature pairs have correlation coefficients ranging between −0.25 and 0.50. In the literature, especially in medical research, this range falls under negligible-low correlation group (0–0.3 negligible correlation, 0.3–0.5 low correlation) [50–52]. Therefore, it can be inferred that the features are not linearly dependent and each feature has a unique contribution to the analysis.

Fig. 6.

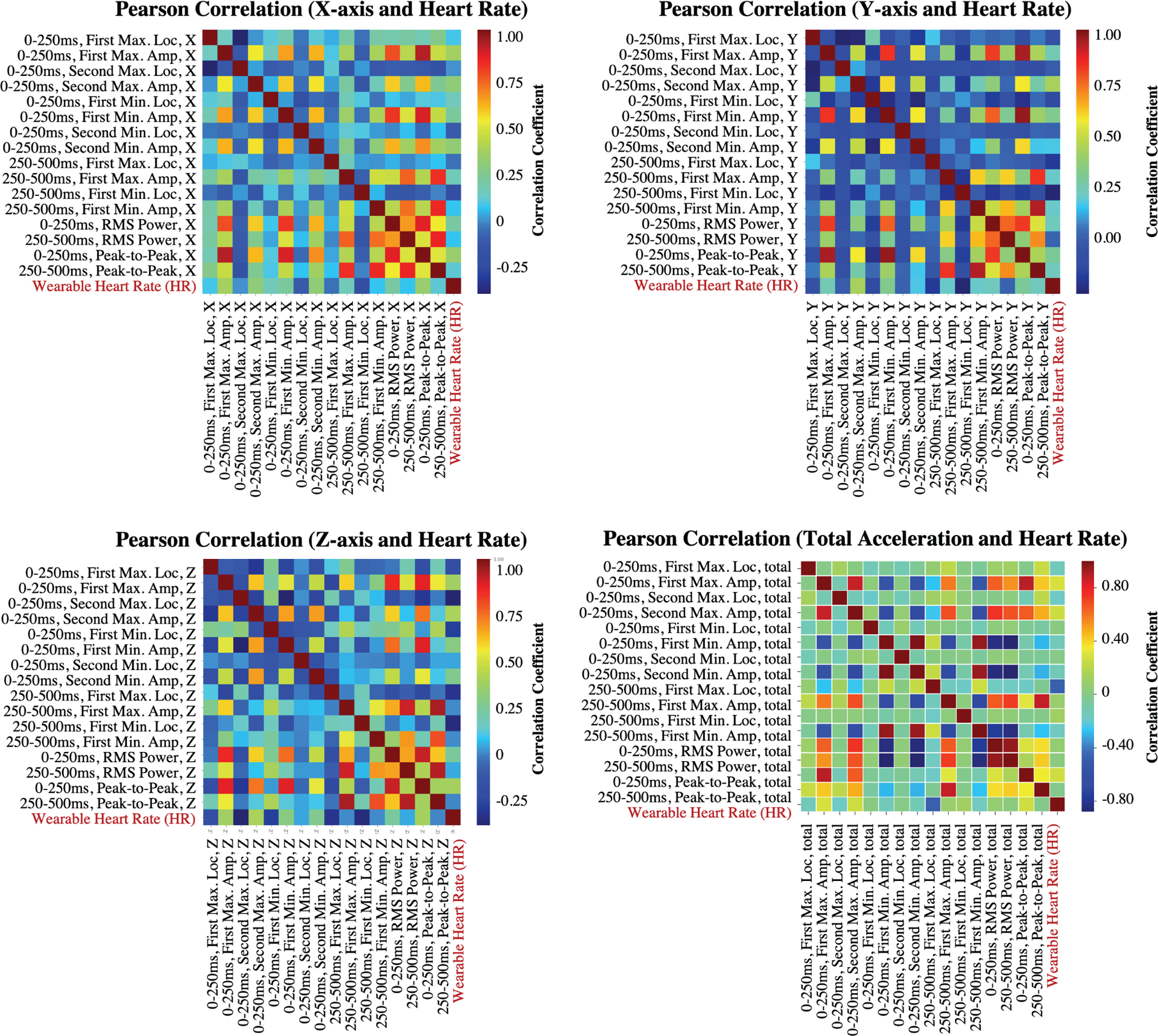
Pearson correlation coefficients between different feature pairs from SCG_x,y,z,total signals.

C. Comparison with State-of-the-Art

1). Contribution of the Acoustic and Vibration Components:

After segmenting the SCG_x,y,z,total signals into PCG and vibration segments, the whole analysis pipeline was run with the same features and same ML model (random forest including 20-min of calibration) for PCG_sternum, SCG_vib, and the combination of PCG_sternum and SCG_vib cases. Results in Table IV show that the combination of PCG_sternum and SCG_vib segments has superior performance (r=0.76, MedAE=9.87 mL) compared to using only-PCG_sternum (r=0.69, MedAE=11.67 mL) or only-SCG_vib (r=0.35, MedAE=12.67 mL) segments. Moreover, using the ECG features, i.e. HR, increases the estimation performance. Indeed, the combination of PCG_sternum, SCG_vib and ECG resulted in similar correlation (r=0.81) and MedAE (7.99 mL) values to the method presented in this paper (r=0.81, MedAE=7.56 mL). Therefore, SV estimation benefits from both the acoustic and vibrational characteristics of the cardiovascular system. In addition, although the most important feature was heart rate in our proposed algorithm, when PCG_sternum and SCG_vib components were separated from each other, the first and second minima of the total acceleration magnitude (0–250ms) and the peak-to-peak amplitude of the head-to-foot direction (0–250ms) outperformed heart rate. In a typical PCG, the first oscillation (S1 heart sound) corresponds to the closing of the mitral valve. Thus, having features related to S1 heart sounds as the key features is indeed consistent with the underlying physiological events as stroke volume is defined as the difference between the end diastolic and end systolic volumes [53].

Table IV.

Comparison with State-of-the-art

Contribution of the Acoustic and Vibration Components (SCGx,y,z,total and ECG)
	Correlation (r-value)				MedAE (mL)
PCGsternum	0.69				11.67
PCGsternum + ECG	0.75				10.39
SCGvib	0.35				12.67
SCGvib + ECG	0.64				10.16
PCGsternum + SCGvib	0.76				9.87
PCGsternum + SCGvib + ECG	0.81				7.99
THIS WORK	0.81				7.56
Comparison with the Existing Literature
	SCGx		SCGy		SCGz		SCGtotal
	Corr (r-value)	MedAE (mL)	Corr (r-value)	MedAE (mL)	Corr (r-value)	MedAE (mL)	Corr (r-value)	MedAE (mL)
Tavakolian et al. [49] (mean ± std)	0.15±0.21	13.29±10.98	0.09±0.13	13.54±10.68	0.11±0.26	13.21±10.75	0.13±0.21	12.96±10.91
THIS WORK	0.22	13.76	0.65	12.46	0.50	10.86	0.56	10.49

2). Comparison with the Existing Literature:

Finally, the analysis pipeline offered by Tavakolian et al. was applied on the current dataset to provide a quantitative comparison. It should be noted that the comparison was not head to head as there were differences in the experimental setups of the two studies (mentioned in Section II-G2). In addition, the analysis pipeline presented in this study was based on training a global model and validating with LOSO-CV, whereas in [49] subject-specific models were used. Thus, the correlation and MedAE values were calculated for each subject separately and presented as mean±std in Table IV. Overall, the MedAE results of the two studies were close to each other, however there was a great difference between the correlation values. In addition, there was a great variance among the correlation and MedAE values of the subjects, e.g. one subject had a correlation value of 0.71, whereas another one had a correlation value of 0.01. One reason might be the insufficiency of linear regression as it assumes a linear relationship between both the dependent and independent variables. Another reason might be the errors during the detection of the cardiac event points (AC, AO, etc.). As the subjects in the current dataset were undergoing surgery, it was challenging to locate and detect these fiducial points accurately. Therefore, it can be deduced that detecting the maxima and minima amplitudes and locations instead of the actual cardiac event points indeed contributes to such frameworks by providing a more representative feature set.

D. Limitations and Future Work

The limitations of this study are the relatively small sample size, and that the study was conducted at a single clinical site. Future studies will be necessary to assess the reproducibility of the methods including larger and more diverse datasets in patients having various diseases, and undergoing a variety of surgical procedures or different anesthetics techniques. For example, more extensive studies with serial measurements under various surgical conditions (such as fluid loading etc.) needs to be done to ensure accurate stroke volume prediction. Similarly, an increase in the number of subjects in the training set will improve the generalizability of the algorithm as well as the determination of key SCG features associated with SV prediction. Once the generalizability is achieved through validation in larger datasets, potential ways to achieve real-time monitoring will also be studied. Future versions of the wearable patch will attempt to minimize form factor and improve comfort as well.

Another drawback of this study is the additional prediction error introduced by inter-subject variability. The current problem was framed as monitoring the changes in SV throughout and after the surgery relative to the reference SV values taken in pre-incision period, therefore some baseline data was included in the training set for each subject. This reduced the added inter-subject variability error in SV prediction, but requires a brief calibration period (pre-incision) during which both the wearable device and TED were being used. To adapt the wearable patch as an alternative to the TED, the ideal scenario would be having a model without any baseline data. Therefore, future work will also focus on methods to eliminate the effects of inter-subject variability, and the need for a baseline set to enhance the prediction performance of the trained model.

IV. CONCLUSION

The results of this study demonstrate the feasibility of a wearable patch system to monitor the SV continuously and non-invasively that is applicable to pre-, intra- and post-operative periods. With this proposed technology, the wearable sensor could be applied to conscious, ambulatory patients and used to monitor SV without requiring anesthesia or any invasive intervention. There are obvious benefits of this technology from a patients’ perspective. It eliminates the discomfort and risks associated with other techniques for hemodynamic monitoring. Additionally, this technology also has several benefits for healthcare providers. The rapidity and ease with which the device is applied to the patient and the lack of the risks associated with inadvertent needlesticks and exposure to bloodborne infections cannot be underestimated.

In conclusion, the proposed wearable patch system could be a viable alternative for peri-operative hemodynamic monitoring of surgical patients throughout the entire encounter. Combined with appropriate remote capabilities, it could facilitate monitoring the patients remotely after discharge to their homes as well. In addition, as the success of fluid management protocols based on monitoring intra-operative SV has been recently shown, this wearable technology can also be used in the future to potentially guide peri-operative fluid management.