Subtle changes in crosslinking drive diverse anomalous transport characteristics in actin-microtubule networks

Abstract

Anomalous diffusion in crowded and complex environments is widely studied due to its importance in intracellular transport, fluid rheology and materials engineering. Specifically, diffusion through the cytoskeleton, a network comprised of semiflexible actin filaments and rigid microtubules that interact both sterically and via crosslinking, plays a principal role in viral infection, vesicle transport and targeted drug delivery. Here, we elucidate the impact of crosslinking on particle diffusion in composites of actin and microtubules with actin-actin, microtubule-microtubule and actin-microtubule crosslinking. We analyze a suite of transport metrics by coupling single-particle tracking and differential dynamic microscopy. Using these complementary techniques, we find that particles display non-Gaussian and non-ergodic subdiffusion that is markedly enhanced by cytoskeletal crosslinking, which we attribute to suppressed microtubule mobility. However, the extent to which transport deviates from normal Brownian diffusion depends strongly on the crosslinking motif – with actin-microtubule crosslinking inducing the most pronounced anomalous characteristics. Our results reveal that subtle changes to actin-microtubule interactions can have complex impacts on particle diffusion in cytoskeleton composites, and suggest that a combination of reduced filament mobility and more variance in actin mobilities leads to more strongly anomalous particle transport.

Introduction

The cytoskeleton is a complex network of filamentous proteins, including semiflexible actin filaments and rigid microtubules^1–3. Numerous crosslinking proteins that can link actin to actin^4–7, microtubules to microtubules^8–10, and actin to microtubules^11–15 enable the cytoskeleton to adopt diverse architectures and stiffnesses to drive key processes such as cell motility, meiosis and apoptosis^10,16–20. These varying structural and rheological properties, in turn, directly impact the intracellular transport of vesicles and macromolecules traversing the cytoplasm^{14,15,21–23}. More generally, thermal transport of particles in biomimetic, cell-like and crowded environments continues to be intensely investigated due to the intriguing anomalous properties, i.e. properties not found in normal Brownian motion^{14,15,21,22,24–27}, that have been reported in these systems.

Single-particle tracking (SPT), often used to characterize particle diffusion in complex environments, can determine anomalous transport characteristics such as: subdiffusion, in which the mean-squared displacement (MSD) scales as ${~\mathrm{\Delta }t}^{\alpha }$ where $a<1$^26,28–31; ergodicity-breaking, in which the time-averaged MSD differs from the ensemble-averaged MSD^32–34; and non-Gaussianity, in which the distribution of particle displacements deviates from the normal distribution consistent with Brownian motion^35–40. While with single particle tracking, we can measure the motion of individual particles to measure transport properties, differential dynamic microscopy (DDM) extracts complementary information by probing density fluctuations in Fourier space. Anomalous transport dynamics manifest in DDM measurements in the form of intermediate scattering functions (ISF) fit by stretched exponentials^41–43 or ISFs that do not decay to zero, but have a non-zero plateau^43–45 – hallmarks of heterogeneity and nonergodicity, respectively. We use SPT and DDM on similarly acquired images, but as SPT and DDM rely on separate assumptions and user-defined inputs we can take the fact that both techniques reveal similar anomalous transport trends as an indicator of the robustness of our results.

We previously showed that varying the relative concentrations of actin and microtubules in entangled actin-microtubule composites (without crosslinkers) led to surprising and complex effects on particle transport in these networks¹⁵. Namely, as the ratio of actin to microtubules increased, transport became more subdiffusive, less ergodic and exhibited more pronounced non-Gaussianity. We attribute these results to the smaller mesh size of actin-rich networks compared to microtubule-rich networks. However, the ~100-fold higher rigidity of microtubules compared to actin filaments also affected the dynamics, leading to non-monotonic dependences of multiple transport metrics with respect to the ratio of actin to microtubules. These intriguing results beg the question as to the role that filament crosslinking, which directly impacts network rigidity and connectivity, plays on the transport of particles through cytoskeleton composites.

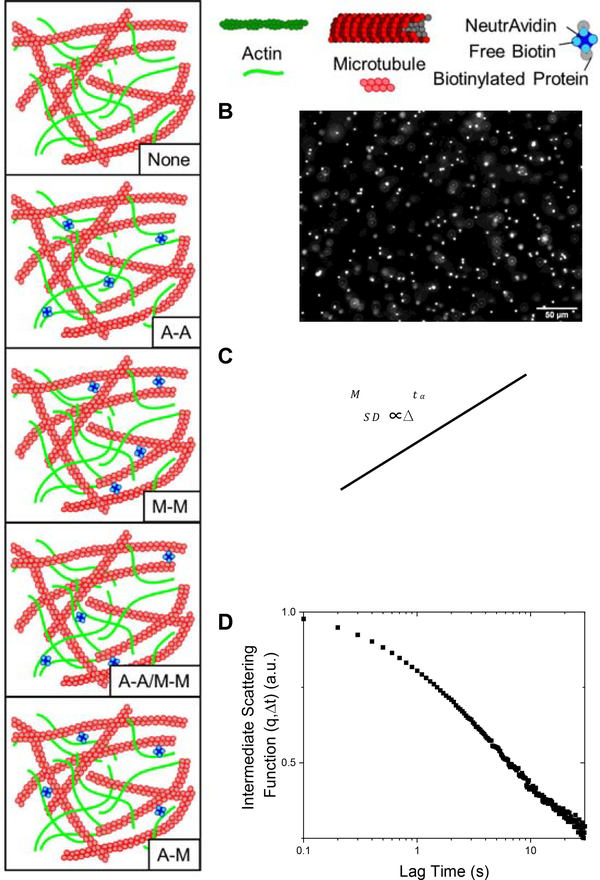
Here, we couple single-particle tracking (SPT) with differential dynamic microscopy (DDM) to elucidate the anomalous transport of microspheres through crosslinked cytoskeleton composites over a broad spatiotemporal range. To systematically determine the role of crosslinking on particle transport, we examine co-entangled actin-microtubule composites in which we fix the concentration of actin, microtubules and crosslinkers and vary the type of crosslinking to include actin crosslinked to actin (A-A), microtubules crosslinked to microtubules (M-M), actin crosslinked to microtubules (A-M), both actin crosslinked to actin and microtubules crosslinked to microtubules (A-A/M-M), and compare to networks without crosslinking (None) (Fig. 1).

Figure 1. Experimental approach to examine the impact of crosslinking on anomalous transport in cytoskeleton networks.

(A) Schematic of the different crosslinking motifs created in actin-microtubule networks: no crosslinkers (None), actin crosslinked to actin (A-A), microtubules crosslinked to microtubules (M-M), both actin-actin and microtubule-microtubule crosslinking (A-A/M-M), and actin crosslinked to microtubules (A-M). Biotinylated actin filaments and/or microtubules are crosslinked with NeutrAvidin to achieve the different motifs. (B) Videos of diffusing 1 μm fluorescent microspheres are collected and analyzed using single-particle tracking (SPT) (C) and differential dynamic microscopy (DDM) (D). (C) For SPT, the mean squared displacement (MSD) is plotted versus lag time ($\Delta t$) and fit to the power-law function $\mathrm{M}\mathrm{S}\mathrm{D}\propto (\Delta {t)}^{\alpha }$ that describes anomalous diffusion. (D) For DDM, intermediate scattering functions are generated and fit to $f\left(q,\Delta t\right)=\left(1-C\left(q\right)\right)\exp \left[-{\left(\frac{\Delta t}{\tau \left(q\right)}\right)}^{\gamma \left(q\right)}\right]+C\left(q\right)$ to extract the decay times $\tau \left(q\right)$, stretching exponents $\gamma \left(q\right)$, and nonergodicity parameters $C\left(q\right)$ for each condition. Data shown in (C) and (D) are for particles diffusing in the network without crosslinking (None).

We previously examined the transport of linear and ring DNA through similar crosslinked cytoskeleton composites, and found that both DNA types exhibited anomalous diffusion arising from threading of ring DNA by cytoskeleton filaments and caging and hopping of linear DNA^14,46. However, due to the complexity of these studies, it was difficult to parse the contributions from the DNA itself versus the cytoskeleton matrix to the transport properties, and the generality of the results to other particles. This difficulty was a primary motivator for the current study. Further, in the previous DNA transport studies we only measured transport to 7 s – over an order of magnitude shorter than done here – and we did not evaluate important transport metrics such as the stretching exponent, non-ergodicity parameter from DDM, or the single particle trajectories.

We also previously examined the nonlinear microrheological response of similar crosslinked cytoskeleton composites⁴⁷. The mesoscale lengthscale of measurements as well as the far-from-equilibrium regime examined in Ref 47 is quite different from the regime investigated here. While we qualitatively examined the mobilities of the filaments themselves, the results of which have proved important to the results we present here within, we did not investigate particle transport or quantify near-equilibrium dynamics.

Here, we find that transport in all networks is subdiffusive, non-Gaussian and non-ergodic – as measured by both SPT and DDM. Further, crosslinking appreciably enhances subdiffusion, ergodicity-breaking and non-Gaussianity compared to unlinked networks. However, the degree to which each parameter is enhanced depends on the crosslinking motif, with networks with actin-microtubule crosslinking (A-M) inducing the strongest anomalous transport features and networks with actin-actin and microtubule-microtubule crosslinking (A-A/M-M) inducing the weakest. These findings dovetail with our previous work, wherein we show that the type of crosslinking causes surprising and distinct changes to actin and microtubule mobility^14,46–48. Taken collectively, our results indicate that the effect of crosslinking on transport is dictated by the suppression of microtubule mobility, whereas the relative impact of the crosslinking type on transport is modulated by actin mobility.

Results

We characterize the thermal transport of microscopic particles diffusing in cytoskeletal composites composed of co-entangled actin (A) and microtubules (M) with varying crosslinking motifs. We create composites with four different crosslinking motifs (A-A, M-M, A-M, A-A/M-M), as well as no crosslinking (None), utilizing single-particle tracking and differential dynamic microscopy to characterize the transport of microspheres diffusing in the various composites (Fig. 1).

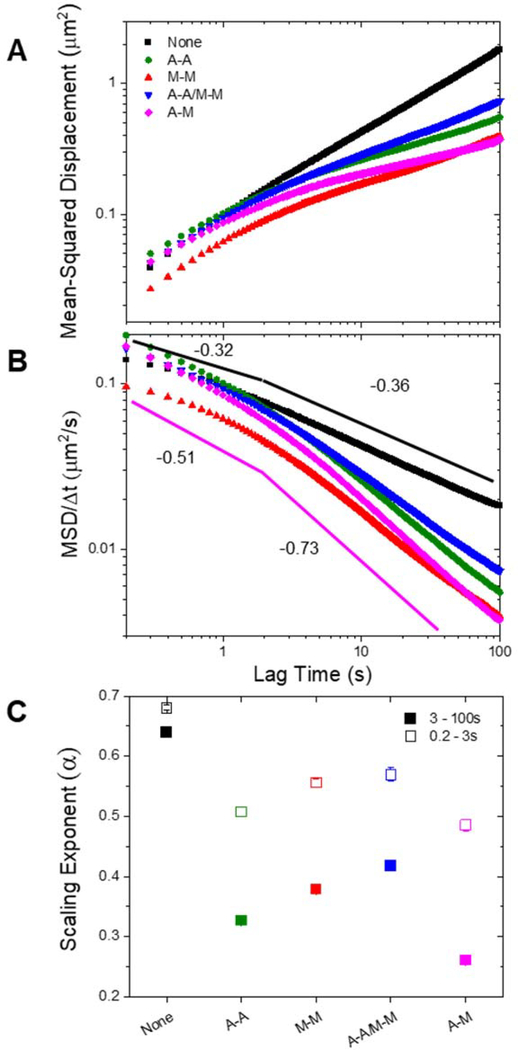
In Figure 2A, we plot the mean-squared displacement as a function of lag time for particles diffusing in all five types of networks. As shown, all composites, with and without crosslinking, display anomalous subdiffusion, i.e. $\mathrm{M}\mathrm{S}\mathrm{D}~\Delta t^{\alpha }$ where $\alpha <1$. However, all crosslinked networks are significantly more subdiffusive than the purely entangled case, especially at greater lag times. Further, in the crosslinked networks, the transport becomes more subdiffusive with increasing lag time, while in the unlinked network the degree of subdiffusion, as measured by $\alpha$, is relatively constant. This effect is more readily shown by plotting the MSDs scaled by lag time ($\mathrm{M}\mathrm{S}\mathrm{D}/\Delta t$) versus the lag time for each of the five composites (Fig. 2B). The solid lines in Fig. 2B act as a guide for $\alpha -1$ scaling, which is negative for subdiffusion.

Figure 2. Crosslinking of cytoskeleton networks leads to multi-phase particle transport with more subdiffusive behavior at long times.

(A) Mean-squared displacement (MSD) plotted as a function of lag time ($\mathrm{\Delta }t$) for each condition specified in the legend. (B) MSD scaled by lag time ($\mathrm{M}\mathrm{S}\mathrm{D}/\Delta t$) versus lag time ($\Delta t$) for each condition. Pink and black lines are power-laws with scaling exponents ($1–\alpha$) determined from fits to the A-M and None curves, respectively, for $\Delta t=0.2–3\mathrm{s}$ and $\Delta t=3–100\mathrm{s}$. Steeper negative slopes indicate more subdiffusive transport. (C) Anomalous scaling exponents α from power-law fits of the MSDs. Open squares show the initial fitting region (0.2–3 s) and closed squares represent the long-time (3–100 s) fits. Error bars are the standard error calculated from four random subsets of data for each condition.

Due to the temporally variant characteristic of the subdiffusion for crosslinked networks, we fit the MSDs with power law functions ($\mathrm{M}\mathrm{S}\mathrm{D}~\Delta t^{\alpha }$) over two distinct time regimes: 0.2–3 s and 3–100 s (Fig. 2C). We chose 3 s to demarcate the two regimes as it is the shortest time after which there is no detectable change in power-law scaling for all network types. We note that for the time regime below 3 s there is not a single power-law behavior for some of the data, so the exponent we show in Fig. 2C should be considered a lower limit. For both time regimes, the non-linked composite exhibits a significantly higher scaling exponent than the crosslinked networks. Additionally, by quantifying the scaling exponent, it becomes clear that the non-homologous crosslinked network, in which actin and microtubules are crosslinked to each other (A-M), is the most subdiffusive over the entire spatiotemporal range. Conversely, the network in which both filaments are homologously crosslinked (A-A/M-M) appears to be the least subdiffusive, with scaling exponents that are higher than for networks in which only one filament type is crosslinked (A-A and M-M). We note that for all networks, the molar ratio of crosslinkers to protein is held fixed. This is a critical detail, as it results in the actin and microtubules having twice as many crosslinkers per unit length in the A-A and M-M networks, respectively, as in the A-A/M-M network in which the crosslinkers are distributed among both filament types. However, this is not to say that we expect that doubling the number of crosslinkers in the A-A/M-M network would lead to transport properties similar to the A-A or M-M network. We previously observed such a network to display much more elastic properties than any of the composites studied here, and found that the corresponding filament mobilities were also much slower⁴⁷. We would expect both of these properties to cause more anomalous transport characteristics relative to the A-A or M-M composites studied here.

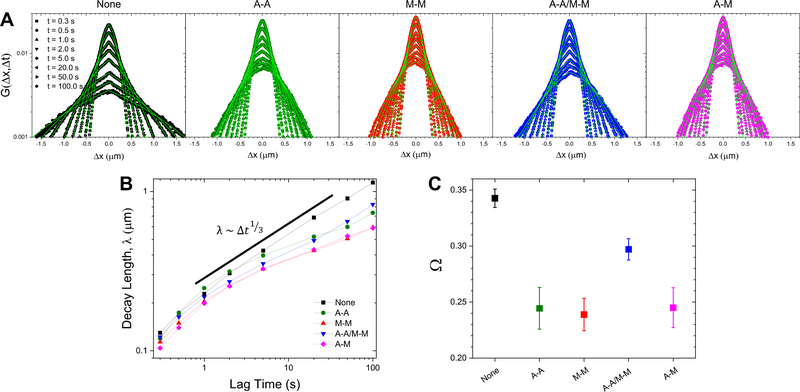
To examine potential mechanisms that give rise to the anomalous subdiffusion shown in Fig. 2, we evaluate the probability distributions of particle displacements, i.e. the van Hove distributions $G(\Delta x,\Delta t)$, measured from SPT. Figure 3 shows van Hove distributions for a range of lag times from 0.3 s to 100 s for each network type. For reference, displacement distributions for particles undergoing normal Brownian motion are expected to be Gaussian⁴⁰. However, as shown in Fig. 3, the distributions for all networks are distinctly non-Gaussian, with significant broad tails for large displacements. This phenomenon is commonly seen in crowded media in both synthetic and biological systems, and is a hallmark of dynamic heterogeneity^{36–40,49,50}. However, in these systems, non-Gaussian transport is often transient and reverts to Gaussian at long enough times^51–53. Conversely, we note the absence of a crossover to Gaussian transport in our systems at long lag times (100 s), suggesting that the dynamical processes governing transport in these networks have relaxation times longer than our measurement timescale.

Figure 3. van Hove distributions reveal non-Gaussian, heterogeneous particle transport in all networks.

(A) van Hove distributions ($G\left(\mathrm{\Delta }x,\mathrm{\Delta }t\right)$) for microspheres in composite networks without crosslinkers (None; black), with actin-actin crosslinking (A-A; green), microtubule-microtubule crosslinking (M-M; red), actin-actin and microtubule-microtubule crosslinking (A-A/M-M; blue), and actin-microtubule crosslinking (A-M; magenta) on a semi-log scale. Shown are the distributions for 0.3, 0.5, 1, 2, 5, 20, 50, and 100 seconds. The displacement distributions are distinctly non-Gaussian and were fit to a sum of a Gaussian and exponential distribution, $G\left(\Delta x,\mathrm{\Delta }t\right)=A{e}^{-0.5{\left(\frac{\Delta x}{w}\right)}^2}+B{e}^{-\left(\frac{\left|\Delta x\right|}{\lambda }\right)}$, shown in bright green. (B) The characteristic length, $\lambda$, obtained from the exponential fits shown in (A), plotted against lag time. Points are connected with a line to guide the eye. (C) Scaling exponents, $\mathrm{\Omega }$, obtained from fitting the curves in (B) to a power-law $\lambda \left(\mathrm{\Delta }t\right)~(\mathrm{\Delta }{t)}^{\mathrm{\Omega }}$.

We and others have previously found that non-Gaussian distributions in similar crowded and confined networks could be well-described by a sum of a Gaussian and exponential where the exponential,$G_{exp}\left(\Delta x,\Delta t\right)\propto e^{\left(-\frac{\left|\Delta x\right|}{\lambda \left(\mathrm{\Delta }t\right)}\right)}$, describes the large displacement tails^14,24,54. The decay length $\lambda \left(\mathrm{\Delta }t\right)$, is therefore best understood as the mean of length scales associated with the various relaxation processes that contribute to the exponential tails in the distributions. Moreover, this characteristic length has been shown to exhibit a power-law dependence on lag time with exponents of ~1/4 – 1/3^14,55. To ascertain whether or not this decay length is sensitive to crosslinking motif, we plot $\lambda \left(\mathrm{\Delta }t\right)$ against lag time and fit these curves to a power law, $\lambda ~\mathrm{\Delta }{t}^{\mathrm{\Omega }}$ (Fig. 3B). This decay length scales as a power law for all networks, though in the crosslinked networks the increase in the decay length with increasing lag time is smaller (smaller scaling exponent $\mathrm{\Omega }$). In order to quantify this scaling, we plot the scaling exponent $\mathrm{\Omega }$ for each network type (Fig. 3C), which highlights the decreased growth of the characteristic length for the crosslinked networks relative to the unlinked network. Further, the decay length in the network with both filaments crosslinked (A-A/M-M) grows faster than in the homologous (A-A, M-M) or non-homologous (A-M) crosslinked networks (Fig. 3C). Finally, we note that the relevant timescale when the entangled and crosslinked networks diverge is similar to the timescale over which the MSDs deviate from a single power law and become increasingly subdiffusive (Fig. 2). This timescale of ~3 s is quite close to the longest relaxation timescales that we previously measured for these crosslinked composites (~3–8 s), which we attributed to facilitated reptation, whereby filaments undergo a combination of curvilinear diffusion, confined by the surrounding entangled filaments (i.e. reptation), and lateral confinement-hopping at instances when entanglements are momentarily released via thermal fluctuations⁴⁷. As we demonstrated in Ref 47, below ~3 s, the filaments in all networks undergo internal relaxation modes related to hydrodynamic effects and bending. Above this timescale, unlinked composites relax nearly all of their imposed stress while crosslinked networks maintain varying amounts of stress for the duration of the measurement time (minutes). This difference between the stress relaxation of linked and unlinked networks, due to the nearly permanent nature of biotin-NeutrAvidin linking, is likely the phenomenon that drives the deviation at 3 s that we observe here.

To further connect our transport properties in the long-time regime (>3 s) to the rheological properties of the composites at these timescales, we compute the frequency-dependent elastic and viscous moduli, G’ and G”, from the MSDs for 3–100 s using the well-validated generalized Stokes-Einstein relation as previously described^56–58. Fig. S1 shows G’ as well as the loss tangent G”/G’ averaged over the entire frequency range. Generally speaking, more viscoelastic, rigid networks (i.e., higher G’) tend to result in more anomalous transport features^15,59, while more viscous ones (higher G”/G’) tend towards normal diffusion. Our results align with this expectation, with all crosslinked composites exhibiting higher <G’> and lower < G”/G’> than the unlinked composite and the variations among crosslinked composites tracking with our results described above.

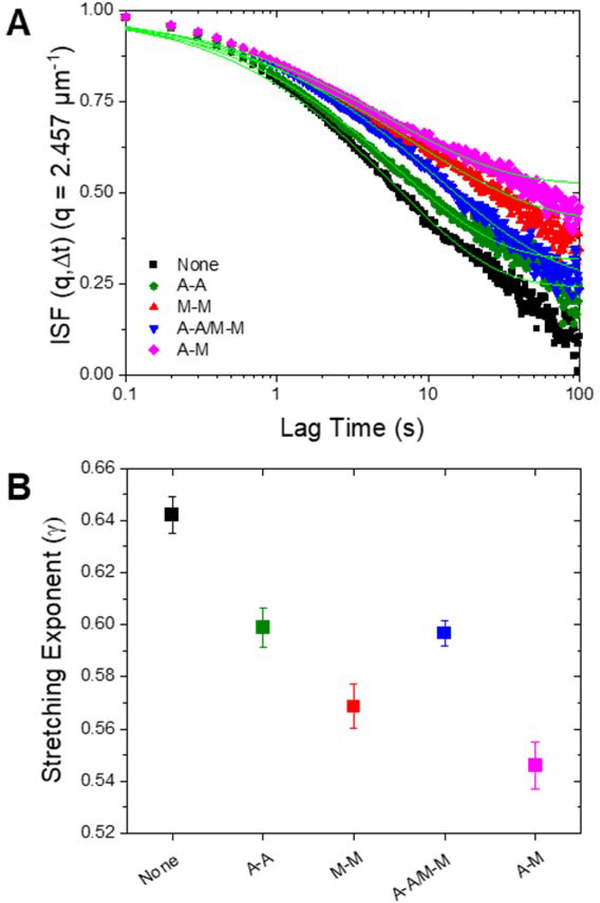
To further investigate the network-dependent anomalous transport, we complement our SPT measurements with differential dynamic microscopy (DDM) analysis that we perform on the same samples we use for SPT. Specifically, we analyze the decay time, $\tau$, of density fluctuations of an ensemble of particles across a range of spatial frequencies, $q$. As described in Methods, we fit the intermediate scattering function $f\left(q,\Delta t\right)$ to a stretched exponential while also taking into consideration the nonergodicity of the sample in order to extract dynamical information about the network. The stretching exponents (γ) we extract indicate the extent to which diffusion is anomalous. As seen in Figure 4, we find $\gamma <1$ (~0.5 to 0.7) for all conditions, indicative of diffusion in confined media⁴⁴. Further, the dependence of $\gamma$ on the type of crosslinking follows a similar trend to that found for the SPT anomalous scaling exponent. Namely, the introduction of crosslinkers causes a significant decrease in the stretching exponent and non-homologous crosslinking leads to the smallest stretching exponent. While the smaller anomalous scaling exponent found in SPT analysis (Fig. 2) indicates more subdiffusion, a smaller stretching exponent represents a wider distribution of decay times that is indicative of more dynamic heterogeneity in the environment^41,42,44. This trend supports our displacement distribution data (Fig. 3), which indicates substantial transport heterogeneity in all networks that is most apparent for A-M networks and least apparent for the non-crosslinked networks. We note that this apparent heterogeneity is not a result of spatial heterogeneities in the composites, as we have previously shown these networks to be well mixed and largely homogenous, with no sign of bundling, aggregation or other wide-spread spatial heterogeneities⁶⁰. Rather the heterogeneity lies in the individual particle trajectories which exhibit diverse combinations of caging, hopping, and randomly sampling the environment; a behavior that has been shown to occur more readily in more rigid networks (SI Fig. S2)^31,61.

Figure 4. DDM analysis reveals heterogenous, non-ergodic transport amplified in crosslinked networks.

(A) Intermediate scattering functions (ISF) are fit to a stretched exponential with a nonergodicity component, as described in Methods. The fits to the ISFs for each condition are plotted in bright green. The height of the long-time plateau reflects the nonergodicity of the transport. (B) DDM analysis shows increased dynamic heterogeneity in crosslinked networks through decreasing stretching exponents ($\gamma$). The stretching exponent ($\gamma$) from the intermediate scattering functions for each condition is plotted. A stretching exponent less than 1 indicates the presence of heterogeneous crowded media. Error bars are the standard error calculated from the different videos taken for each sample.

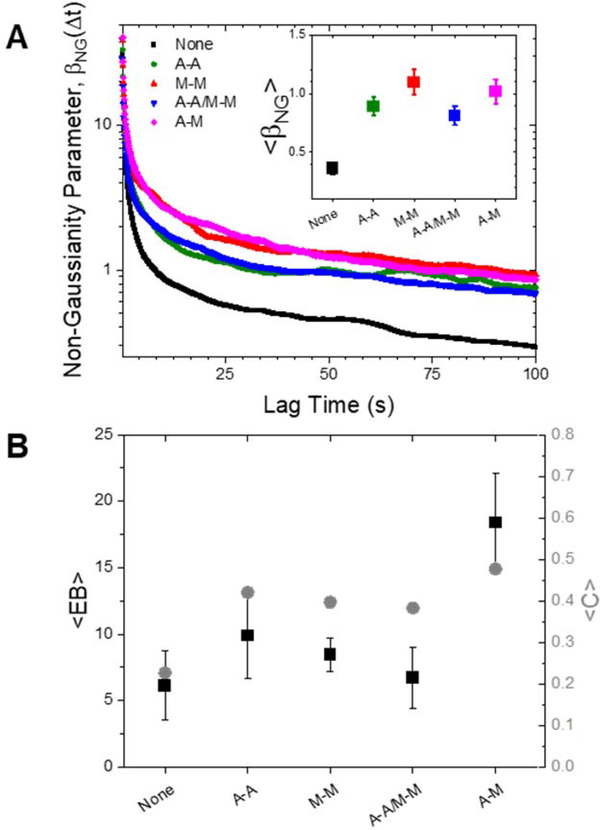
Finally, to further quantify the extent to which the transport we report is anomalous, we evaluate three dimensionless parameters: the non-Gaussianity parameter ${\beta }_{NG}$ determined via SPT data, the ergodicity-breaking parameter $EB$ generated via SPT, and the non-ergodicity parameter $C$ computed via DDM analysis (Fig. 5). For a particle undergoing Brownian motion, an ergodic process obeying Gaussian statistics, ${\beta }_{NG}=EB=C=0$ for long times. As shown in Fig. 5A, ${\beta }_{NG}\left(\mathrm{\Delta }t\right)$ for all conditions decreases from an initial absolute maximum $~O\left(10\right)$ to a nearly time-independent plateau of $~O\left(1\right)$. However, the long-time plateau is significantly higher for the crosslinked networks relative the unlinked network, further evidenced by the time-average of ${\beta }_{NG}\left(\mathrm{\Delta }t\right)$ shown in the inset. We also compare the ensemble-averaged MSDs with the time-averaged MSDs through the ergodicity breaking parameter $EB$, computed via SPT and defined in the Methods. We observe that $EB$ is non-zero for all conditions, indicating that the ensemble-averaged and time-averaged MSDs are not equivalent (Fig. 5B). Further, the non-homologously crosslinked network (A-M) is the least ergodic by a factor of ~2. The nonergodicity parameter, $C$, found independently through DDM analysis, shows strikingly similar trends to $EB$ (Fig. 5B). $C$ is a measure of the long-time plateau of the intermediate scattering functions and as such can vary between 0 and 1, with 0 indicating ergodic motion. Again, we find that the non-homologously crosslinked network (A-M) deviates the most from an ergodic process while the unlinked network deviates the least. The dependence of this deviation on the crosslinking motif follows a similar trend as our previously described parameters (subdiffusive scaling exponent, characteristic decay length and scaling, and DDM stretching exponent), wherein the unlinked network is consistently the least anomalous while the A-M network is the most anomalous.

Figure 5. Metrics from both SPT and DDM show that crosslinking increases the non-Gaussianity and non-ergodicity of particle transport.

(A) Non-Gaussianity parameter, ${\beta }_{NG}\left(\mathrm{\Delta }t\right)$, as function of time for each crosslinking type. Inset: Time-average of ${\beta }_{NG}$. (B) Black, left axis: Time-average of the ergodicity breaking term $EB$ as measured from SPT. Error bars represent the standard error calculated from the separate videos taken for each sample. Gray, right axis: Non-ergodicity parameter C averaged over wave vectors $1.37$ to $3.48\mu {\mathrm{m}}^{-1}$. Error bars represent the standard error calculated for the different wave vectors (see SI Fig S3).

Discussion

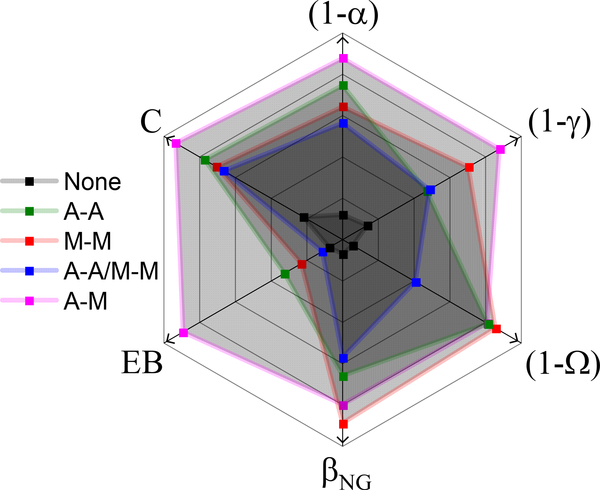
We use two independent techniques, SPT and DDM, to characterize the transport of microscopic particles in in vitro cytoskeleton networks with varying types of crosslinking. With these complementary techniques, we evaluate the degree to which the networks lead to deviations from normal Brownian diffusion with six different transport metrics to quantitatively characterize the network-dependent anomalous transport (Fig. 6). Collectively, our results indicate that particles undergo anomalous, non-Gaussian subdiffusion that is nonergodic in all networks. However, the degree to which these transport phenomena manifest is highly dependent on the type of crosslinking in the actin-microtubule composites.

Figure 6. Multiple transport metrics highlight the degree to which crosslinking motif drives deviations from normal Brownian motion in composite cytoskeleton networks.

Using the same color scheme as in previous figures, we show how the type of crosslinking, or lack thereof (black), influences subdiffusion ($\alpha$), spatiotemporal heterogeneity ($\gamma ,\mathrm{\Omega },{\beta }_{NG}$), and ergodicity ($EB,C$) across complementary, independent measurement techniques (SPT, DDM). A greater distance from the center (in the direction of the arrows) represents a greater deviation from normal Brownian diffusion. Each metric is scaled separately.

The unlinked network is consistently the least anomalous by all metrics (Fig. 6). While it may be intuitively expected that the least restricted network would have the least deviation from normal transport, this result is not trivial considering all networks have the same mesh size ($\xi =0.81\mu \mathrm{m}$) due to the fixed molar concentrations of actin and microtubules^47,60. Further, the transport in the unlinked network is still complex, i.e., it is subdiffusive (Fig. 2) and non-Gaussian (Figs. 3, 4, 5), and exhibits ergodicity-breaking (Fig. 5). To understand the distinct transport characteristics in crosslinked versus unlinked networks we turn to our previous analysis of the filament dynamics in these networks⁴⁷ which revealed that, upon crosslinking, the mobility of microtubules is significantly and equally suppressed by all crosslinking motifs, and the distribution of measured mobilities is narrowed. We note that while, in this case, the suppression of microtubule mobility is coupled with a narrowing of the corresponding mobility distributions, we also find instances in which reduced mobility of actin filaments is seen along with a broadening of mobility distributions, as we describe further below. This decrease in microtubule mobility likely acts to restrict or ‘cage’ the motion of the microsphere tracers to the local network mesh. This phenomenon is evidenced by the long-time limits in the MSD (Fig. 2A) and characteristic decay length $\lambda$ curves (Fig. 3B). In nearly all crosslinked networks the particle MSDs do not exceed the square of the mesh size ${\xi }^2$ and the decay lengths do not exceed the mesh size, indicating that trapping in the network mesh dominates transport in crosslinked networks, further evidenced by the decrease in proxies for ergodicity, $EB$ and $C$ (Figs. 5B, 6). Conversely, while transport in the unlinked network is indeed subdiffusive and non-Gaussian, MSDs exceed ${\xi }^2$ and characteristic decay lengths, $\lambda$, are greater than $\xi$ (Figs. 2A, 3B). This result suggests that the enhanced microtubule mobility in unlinked networks allows for faster network rearrangement to reduce caging, and instead couples microsphere transport to slow rearrangements of the local network⁶². This interpretation is bolstered by weaker ergodicity-breaking in the unlinked network compared to crosslinked networks (Fig. 5), as motion in a highly crowded, slowly evolving, biological environment without caging is an ergodic process⁶³.

While we attribute the difference between crosslinked and unlinked networks to the suppression of microtubule bending fluctuations, this effect cannot explain the differences among networks with varying crosslinking motifs. As shown in Figures 2–6, anomalous transport features are strongest for the non-homologous actin-microtubule crosslinked networks (A-M), followed by microtubule-microtubule (M-M), actin-actin (A-A) and A-A/M-M crosslinked networks. To understand this trend we look to our previous image analysis studies described above in which we found that, while microtubule mobility was equally reduced by all crosslinking types, the magnitude and distribution of actin mobilities were dependent on the crosslinking type and displayed a similar trend to our transport metrics⁴⁷. In particular, actin filaments displayed the slowest and broadest distribution of thermal fluctuations in A-M networks, followed by M-M and A-A networks, and the fastest and narrowest fluctuation distribution in A-A/M-M networks⁴⁷. The reduced mobility of actin in A-M networks likely arises from coupling actin to rigid microtubules. In all other cases, actin filaments, which is the more flexible component of the composite, only interact with microtubules sterically. Thus, the ability of the microtubules to slow actin fluctuations is weaker than in the case when actin filaments are chemically linked to the microtubules in a nearly permanent fashion. Conversely, relative to the other crosslinked networks, transport within the A-A/M-M network is more weakly subdiffusive at long times and the temporal evolution of the decay length is steeper, suggesting that faster actin filament fluctuations lead to weaker deviations from normal Brownian motion.

We expect our results to be generally valid for particle transport in biopolymer composites when the particle size is larger than the mesh size^{35,41,61,64–66}. Particles much smaller than the mesh size will primarily sample the solute rather than the network, so we would expect transport to be much faster and less anomalous³¹. Beads much larger than the mesh, while sampling the network and nominally being able to reproduce the results we present, would move too slowly to accurately measure MSDs and particle displacements in a reasonable window of time^67,68.

Conclusion

The cytoskeleton is a widely studied, complex network comprised, in part, of semiflexible actin filaments and rigid microtubules, along with myriad crosslinking proteins that crosslink actin to actin (e.g. alpha-actinin, filamin, spectrin, etc)^69–73, microtubules to microtubules (e.g. MAP65, XCTK2, Tau, etc)^74–76 and actin to microtubules (e.g. MAP2, APC, proflin, plectin, etc)^77–80. The diversity of crosslinking patterns possible with these crosslinkers not only directly alters the structure and dynamics of the cytoskeleton network, but, in turn, modulates the diffusion of biomacromolecules and particles in the cell. However, due to the complexity of the cytoskeleton, isolating the impact of different crosslinking motifs on diffusion through the cytoskeleton has proven difficult in vivo.

Here, we couple single-particle tracking with differential dynamic microscopy to elucidate the transport of microspheres in composite actin-microtubule networks in which we fix the concentrations of actin, microtubules and crosslinkers and only vary the type of crosslinking. Using both SPT and DDM allows us to buttress our results between the two complementary techniques, as well as capture transport properties over a spatiotemporal scale from single particles to the ensemble. Using these techniques, we have analyzed a robust suite of anomalous transport metrics to characterize particle dynamics in actin-microtubule networks with actin-actin, microtubule-microtubule and actin-microtubule crosslinking. We find that transport in all networks, even the network without crosslinkers, is subdiffusive, non-Gaussian and nonergodic. By introducing crosslinking, the transport becomes significantly more anomalous, per our metrics, which we suggest arises from the significant decrease in microtubule mobility, which, in turn, acts to increase the propensity for particle caging. The type of crosslinking also plays an important role in particle transport with actin-microtubule crosslinking resulting in the most extreme anomalous characteristics while networks in which both actin and microtubules are crosslinked to themselves but not each other exhibiting the least anomalous transport. Our previous results suggest that the dependence in transport characteristics on the crosslinking motif is a second order effect of varying actin mobility in the different networks. Namely, as the actin mobility decreases and exhibits greater variance, particle transport becomes more anomalous and increasingly controlled by the trapping of the particles within the network, as evidenced by the non-ergodicity and non-Gaussianity metrics.

Our results provide insight into particle transport in the cytoskeleton – important for processes such as viral infection, gene therapy, and drug delivery. We note that our bead size is indeed larger than the size of many vesicles, liposomes, cargo and macromolecules in the cell. However, our chosen composite mesh size is also larger than that found in the cytoskeleton^81–83. Because it is well established that transport properties are highly dependent on the size of the probe relative to the mesh size of the network,^{31,35,62,66,67,84,85} our results likely still apply to cytoskeleton transport in cases where the particle is larger than the cytoskeleton mesh size. We further note that our in vitro composite system is far less complex that the cytoskeleton in cells. However, much of the power of in vitro constitution studies lies in the ability to simplify very complex biological systems. We strive to create networks that simulate some of the hallmarks of the cytoskeleton – i.e., actin-microtubule interactions and various types of crosslinking – without adding too many complexities such as motor proteins, dynamic crosslinkers, and intermediate filaments. In this way, we can better isolate and evaluate the effect of changing key interactions such as crosslinking. In future work, we will continue to add in complexity into our in vitro systems, layer by layer, to better mimic the in vivo cytoskeleton and be able to best parse the contributions from each added component.

More generally, our results have direct implications towards understanding micro-particle transport in crowded environments, polymeric materials and synthetic hydrogels. Finally, our measurement approaches, comprehensive suite of metrics, and well-characterized and controlled actin-microtubule composites serve as much-needed platforms for screening the transport properties of a wide array of tracer particles and network architectures.

Methods

Sample Preparation.

Rabbit skeletal actin monomers and porcine brain tubulin dimers are purchased from Cytoskeleton (AKL99, T240) and suspended in G-buffer [2.0 mM Tris (pH 8), 0.2 mM ATP, 0.5 mM DTT, 0.1 mM CaCl₂] and PEM-100 [100 mM piperazine-N,N′-bis(ethanesulfonic acid) (pH 6.8), 2 mM MgCl2, 2 mM EGTA], respectively. Resuspended actin and tubulin solutions are flash-frozen and stored at −80°C at concentrations of 2 and 5 mg/mL, respectively. To form crosslinked networks, we mix actin monomers and tubulin dimers at a 1:1 molar ratio in an aqueous buffer composed of PEM-100, 2 mM ATP, 1 mM GTP, and 5 μM Taxol, to a final protein concentration of c = 5.8 μM, as described previously^14,47,48,60. To crosslink filaments, biotin-NeutrAvidin complexes with a 2:2:1 ratio of biotinylated protein (actin and/or tubulin) to free biotin to NeutrAvidin are preassembled and added to the solution at a crosslinker to protein molar ratio of R_cp = 0.02. We control the type of linking by varying the type(s) of biotinylated proteins (actin, tubulin, or both) we include in the crosslinker complexes^47,48. We are confident in the efficacy and selectivity of our crosslinking protocols based on very careful experimental design and protocols that we developed over several years. These protocols, and the demonstrated measurable effects of the varying crosslinking motifs, have been extensively vetted via peer-reviewed publications by our groups and others^{14,46,47,86–90}. The measurable effects have been shown in these works through confocal microscopy, optical tweezers and magnetic tweezers microrheology, single particle tracking, and differential dynamic microscopy. We chose the protein concentrations and molar ratios to best compare our results with previous studies^6,14,46,47. We chose the crosslinker densities to be large enough to induce measurable differences from unlinked networks but low enough to not induce bundling⁶. Further, at these protein and crosslinker concentrations, the networks are well-entangled and highly viscoelastic but still exhibit enough mobility to allow for measurable transport and rheological phenomena. Further, this regime is the most complex in terms of having aspects of rigidity and long-lived interactions as well as ample filament fluctuations, so requires the most intense investigation.

For SPT and DDM measurements, we add a trace amount of 1 μm diameter carboxylated fluorescent YG microspheres (Polysciences) which we coat with BSA to prevent nonspecific binding^91,92. Based on our previous works and those of others we are confident that this bead passivation is effective (Ref 91, 92). Further, if the beads were interacting with the filaments, we would not expect to measure so many hopping events (evidenced by the large-displacement tails in the displacement distributions and the trajectories in SI Fig S2) as the beads would be stuck in the mesh. We choose 1 μm particles such that they are larger than the mesh size of our networks, but still small enough to accurately measure transport properties^31,41,67,85. We verified the bead size, which was supplied by the manufacturer, by measuring the diffusion coefficient of the beads in water. We pipette final solutions into a sample chamber consisting of a glass slide and coverslip separated by ∼100 μm with double-sided tape. We add 0.05% Tween to the solutions prior to loading into the sample chamber to inhibit non-specific adsorption of proteins to the chamber surfaces. We seal chambers with epoxy and incubate at 37°C for 60 min to polymerize cytoskeletal proteins and form crosslinked networks.

Imaging.

For both single-particle tracking and DDM experiments, we image the microspheres using an Olympus IX73 inverted fluorescence microscope with a 20× 0.4 NA objective and a Hamamatsu ORCA-Flash 2.8 CMOS camera (320 nm/pixel). For SPT, we collect 20 1920×1440 pixel videos of 2000 frames at 10 fps for each condition. For each of the videos, we observe >40 trackable particles, producing a total of >800 particles tracked. For DDM, we collect 12 512×512 pixel videos of 5000 frames at 10 fps across two samples. Videos are analyzed by examining regions of interest (ROI) of 256×256 pixels. For each sample condition, the experiment is carried out on two independently prepared samples. The sample-to-sample variation we observe and measure is indistinguishable from video-to-video variation within a single sample. Error bars presented throughout are determined by analyzing 3 random subsets of videos from each sample and calculating the standard error in values from all 6 subsets (3 from each sample). We see no statistically significant differences in the magnitudes or distributions of these subset values when comparing the two different samples.

Single Particle Tracking.

We use custom-written particle-tracking scripts (Python) to track the particle trajectories and measure the frame-to-frame x- and y- displacements (Δx, Δy) of the beads. From the displacements, we compute mean-squared displacements <Δx²> and <Δy²>. The average of <Δx²> and <Δy²> (MSD) as a function of lag time Δt is fit to a power-law function MSD $\propto {\mathrm{\Delta }t}^{\alpha }$ where α is the subdiffusive scaling exponent. For a system exhibiting normal Brownian diffusion, $\alpha =1$, while $\alpha <1$ indicates anomalous subdiffusion.

We also evaluate probability distributions of the measured displacements (Δx, Δy) for various lag times (Δt) to generate van Hove distributions (Fig. 3). These distributions are fit to a combination of a Gaussian and exponential function $G\left(\Delta x,\mathrm{\Delta }t\right)=A{e}^{-0.5{\left(\frac{\Delta x}{w}\right)}^2}+B{e}^{-\left(\frac{\left|\Delta x\right|}{\lambda }\right)}$, where A is the amplitude of the Gaussian, w is the Gaussian width, B is the amplitude of the exponential, and λ is the decay length. To further characterize the transport, we compute the non-Gaussianity parameter ${\beta }_{NG}=\frac{1}{3}\frac{〈\overline{{\delta }^4\left(\Delta t\right)}〉}{{〈\overline{{\delta }^2\left(\Delta t\right)}〉}^2}-1$ and the ergodicity breaking parameter $EB=\frac{{〈{\left(\overline{{\delta }^2(\Delta t)}\right)}^2〉-〈\overline{{\delta }^2\left(\Delta t\right)}〉}^2}{{〈\overline{{\delta }^2\left(\Delta t\right)}〉}^2}$ where ${\delta }^2\left(\Delta t\right)$ is the time-averaged MSD for the entire ensemble of trajectories^35,93 (Fig. 5). For normal diffusion, both ${\beta }_{NG}$ and $EB$ trend towards zero, whereas anomalous transport manifests as ${\beta }_{NG}>0$ and/or $EB>0$.

Microrheology:

We determine the viscoelastic properties of the composites from our SPT data using previously described particle-tracking microrheology methods^56–58 as done in our prior work¹⁵. As described in detail in Refs 56–58, we generate the elastic modulus, $G\text{'}\left(\omega \right)$, and viscous modulus, $G^{\text{'}\text{'}}\left(\omega \right),$ from the MSDs via the generalized Stokes-Einstein relation

$$G^{\mathrm{*}}\left(\omega \right)=G^{\mathrm{\text{'}}}\left(\omega \right)+i{G}^{\mathrm{\text{'}}\mathrm{\text{'}}}\left(\omega \right)=\frac{k_{B}T}{i\omega 〈\mathrm{\Delta }{r}^2\left(\omega \right)〉\pi a}$$

where $k_B$ is the Boltzmann constant, T is the absolute temperature, $〈\mathrm{\Delta }{r}^2\left(\omega \right)〉$ is the Fourier transform of $〈\mathrm{\Delta }{r}^2\left(t\right)〉$, the MSD, and a is the bead radius.

Differential Dynamic Microscopy.

Following our previously described methods,^94,95 we obtain the image structure function $D(q,\Delta t)$, where q is the magnitude of the wave vector and Δt is the lag time. The image structure function, or DDM matrix, can then be expressed as $D\left(q,\Delta t\right)=A\left(q\right)\left[1-f\left(q,\Delta t\right)\right]+B\left(q\right)$, where $A\left(q\right)$ depends on the optical properties of the sample and microscope and $B\left(q\right)$ is a function of the camera noise. The intermediate scattering function $f\left(q,\Delta t\right)$ is then described as

$$f\left(q,\Delta t\right)=\left(1-C\left(q\right)\right)\exp \left[-{\left(\frac{\Delta t}{\tau \left(q\right)}\right)}^{\gamma \left(q\right)}\right]+C\left(q\right)$$

where $C\left(q\right)$ is the nonergodicity parameter, $\tau \left(q\right)$ is the decay time, and $\gamma \left(q\right)$ is the stretching exponent. Using methods similar to those described by Cho et al.⁴², we obtain both $A\left(q\right)$ and $B\left(q\right)$ prior to curve fitting. We find that $D(q,\Delta t)$ is independent of both q and $\Delta t$ in the highest q domains (q > 7.37 μm⁻¹) as $A\left(q\right)$ approaches zero. This is expected, as the value of $B\left(q\right)$ is independent of q if camera noise is uncorrelated in space and time⁹⁶. Thus, we take the minimum of the DDM matrix in this q regime and equate this value to $B\left(q\right)$. To calculate $A\left(q\right)$, we rely on the fact that, in linear space invariant imaging, the ensemble-averaged squared modulus of the Fourier-transformed images can be expressed as ${〈{\left|\widehat{i}\left(q\right)\right|}^2〉}_E\cong \frac{A\left(q\right)}{2}+\frac{B\left(q\right)}{2}$, if the contributions from imperfections in the optical path are negligible to those in the sample⁴³. Therefore, we calculate ${〈{\left|\widehat{i}\left(q\right)\right|}^2〉}_E$ and, with $B\left(q\right)$ already obtained, calculate $A\left(q\right)$. In our previous work, we fit the image structure functions to extract the decay times and stretching exponents. Here, having obtained A(q) and B(q), we fit the intermediate scattering functions (ISFs) directly to extract $C\left(q\right)$, $\tau \left(q\right)$, and $\gamma \left(q\right)$ using a combination of least squares and Levenberg-Marquardt curve fitting in Python. Only ISFs with q values in the range of $1.37$ to $3.48\mu {\mathrm{m}}^{-1}$ are well-fit to the stretched exponential equation above, so we restrict our analyses to this range.

Data Availability Statement

The datasets generated and/or analyzed during the current study are available from the corresponding author upon request.