Multi-generational SIR modeling: Determination of parameters, epidemiological forecasting and age-dependent vaccination policies

Abstract

We use an age-dependent SIR system of equations to model the evolution of the COVID-19. Parameters that measure the amount of interaction in different locations (home, work, school, other) are approximated from in-sample data using a random optimization scheme, and indicate changes in social distancing along the course of the pandemic. That allows the estimation of the time evolution of classical and age-dependent reproduction numbers. With those parameters we predict the disease dynamics, and compare our results with out-of-sample data from the City of Rio de Janeiro. Finally, we provide a numerical investigation regarding age-based vaccination policies, shedding some light on whether is preferable to vaccinate those at most risk (the elderly) or those who spread the disease the most (the youngest). There is no clear upshot, as the results depend on the age of those immunized, contagious parameters, vaccination schedules and efficiency.

1. Introduction

Several months after the onset of the COVID-19 pandemic it became clear that good numerical modeling is useful to understand the dynamics of the disease. In particular, simple compartmental epidemiological models are convenient, depending on few parameters and still capturing with reasonable precision essential aspects of the dynamics of infectious diseases (Brauer, 2017; Hethcote, 2000; Wang et al., 2021).

The Susceptible-Infected-Recovered (SIR) model in its simplest form depends on two parameters, the average number of sufficient contacts (those sufficient for transmission) and the mean waiting period during which patients are contagious. It relies on the assumption that the population is homogeneous both in terms of behavior and biological susceptibility. It also assumes, in its simplest instance, that demographic aspects as age structure, birth and death rates do not matter for the dynamics of the disease.

Some of the above assumptions appear to hold well in the case of the COVID-19 pandemic. For instance, demographic changes appear to be of less importance due to difference in time scales, compared with the evolution of the pandemic. However, dropping the homogeneity hypothesis allows a more realistic model, as age and location of contacts are important factors in understanding the dynamics of the disease. For instance, the disease's severity and lethality is age-dependent, among other factors (Bhopal & Bhopal, 2020; Jin et al., 2020; Verity et al., 2020; Wu & McGoogan, 2020).

Mathematical epidemiology has a somewhat long history, with (Hamer, 1906; M'Kendrick, 1925; Kermack, McKendrick, & Walker, 1927) being among the earliest contributions. See (Brauer, 2017; Hethcote, 2000) for a thorough review of mathematical modeling of infectious diseases, and (Albani et al., 2021a, 2021b,bib_Albani_et_al_2021a,bib_Albani_et_al_2021b; Iannelli & Milner, 2017; Klepac & Caswell, 2011; Klepac et al., 2009; bib_Li_et_al_2020Li, Yang, & Martcheva, 2020, pp. 1–21; Prem et al., 2020; Sun, 2010; Towers & Feng, 2012) for multi-group models. Some other models consider spatial aspects of infectious diseases, as (Bertaglia & Pareschi, 2020; Besse & Faye, 2020; Lang, De Sterck, Kaiser, & Miller, 2018; Paeng & Lee, 2017; Peixoto, Marcondes, Peixoto, & Oliva, 2020; Takács & Hadjimichael, 2019; Viguerie et al., 2020). Theoretical aspects of models are covered in (Kuniya & Wang, 2018; Wen, Ji, & Li, 2018; Wu & Zou, 2016). For the control related models for COVID-19 see for instance (Perkins & España, 2020) and references therein.

After the onset of the COVID-19 pandemic, a massive amount of articles related to the topic materialized. Several articles considered compartmental models to forecast different scenarios (Albani et al., 2021a, 2021b,bib_Albani_et_al_2021a,bib_Albani_et_al_2021b; Amaku et al., 2021a, 2021b,bib_Amaku_et_al_2021a,bib_Amaku_et_al_2021b; Atkeson, 2020; Coelho et al., 2020; Kimathi, Mwalili, Ojiambo, & Gathungu, 2021; Komatsu & Menezes-Filho, 2020; Prem et al., 2020; Viguerie et al., 2020; Walker et al., 2020).

Socioeconomic costs of imposing social distancing are combined with compartmental models in (Acemoglu, Chernozhukov, Werning, & Whinston, 2020; Alvarez, Argente, & Lippi, 2020; Atkeson, 2020), and the interplay between economics and individual decisions are considered in (Borelli & Góes, 2020; Brotherhood, Kircher, Santos, & Tertilt, 2020; Eichenbaum, Rebelo, & Trabandt, 2020). See (Kremer, 1996; d’Onofrio & Manfredi, 2020, pp. 185–203; Funk et al., 2015; Manfredi and d’Onofrio, 2013; Perrings et al., 2014; Soofi, Najafi, & Karami-Matin, 2020) for a description of behavioral- and economic-epidemiology ideas. Also, macro-economic aspects of the pandemic appears, e.g., in (Guerrieri, Lorenzoni, Straub, & Werning, 2020).

Population heterogeneity and its influence on herd immunity is considered in (Aguas et al., 2020; 2020Britton, Ball, & Trapman, ; Cui, Zhang, & Feng, 2019; Gomes et al., 2020). Also, different aspects of vaccination are considered in the literature (Albani et al., 2021b; Amaku et al., 2021a; d’Onofrio & Manfredi, 2020, pp. 185–203; Meehan et al., 2020; Chen & Toxvaerd, 2014; González & Villena, 2020; Jia et al., 2020; May & Anderson, 1984). Finally, alternative approaches, as agent-based, statistical models and a combination of these techniques with compartmental models (specially to gather data), are also commonly employed (Amaral, Casaca, Oishi, & Cuminato, 2021; Bendtsen Cano et al., 2020; Calvetti, Hoover, Rose, & Somersalo, 2020; Donnat & Holmes, 2004; Ferguson, Laydon, & Nedjati-Gilani, 2020; Roda, Varughese, Han, & Li, 2020).

In the present paper, we consider a modification of the age-structured SIR model (Britton et al., 2020; Towers & Feng, 2012), in particular allowing for age-dependent probabilities of patients being sub-clinical (asymptomatic or symptomatic patients that does not require hospitalization) or clinical (Albani et al., 2021b; Prem et al., 2020). We use contact matrices (Prem, Cook, & Jit, 2017) which differentiates not only age but also location (home, work, school, other); see also (Kimathi et al., 2021). Random searches approximate some key parameters that are related to social distancing in different locations, computing their values for some Brazilian regions. Following the approximation of those parameters, we are able to forecast long term best/worst case scenarios. We gauge the efficiency of the scheme comparing our predictions with available data using in-sample/out-of-sample testing.

We next use the model to compare age-dependent vaccination policies (Meehan et al., 2020). In a simple setting, we compare vaccinating the young or the older population, since the model allows the immunization of specific age groups. The outcome depends on the values of certain parameters, including how aggressive is the transmission and how late after the start of the pandemic the vaccinations take place.

In general, for a short term period, vaccination prioritizing the elderly population is the best option with respect to the total number of deaths. But that might not be the case in the long run if extra vaccine supplies are not provided.

Disclaimer: It is not our intention to propose real-life epidemiological policies or to provide predictions upon which policies could be developed. Our intention is solely to investigate possible patterns of the disease evolution and raise possible alternatives in terms of vaccination policies.

2. The model

In the spirit of compartmental modeling (Hethcote, 2000; Wang et al., 2021), we divide the whole population among susceptible (S), infected (I), removed (R). Due to the short time scale of the disease, we can assume that demographic changes are not relevant. The number of deaths are estimated a posteriori, from the removed R. The above quantities are 16-dimensional vectors, stratified by age, running from 0 to 4 (first components), 5–9 (second components), etc, up to 75-above (16th components). There are P_i individuals for each age group, and the total population $P={\sum }_{i=1}^{16}{P}_i$ is constant.

The equations governing the dynamics of the disease is as follows,1 for i = 1 …, 16 and $t\in \mathbb{N}$:

$$\begin{array}{l}{S}_i(t+1)=S_i(t)-{\beta }_i(\mathit{I})S_i(t),\hfill \\ I_i(t+1)=I_i(t)+{\beta }_i(\mathit{I})S_i(t)-\gamma I_i(t),\hfill \\ R_i(t+1)=R_i(t)+\gamma I_i(t),\hfill \end{array}$$ (1)

plus initial conditions. The model is “conservative” in the sense that S_i + I_i + R_i = P_i is constant for all ages i.

The term β_iS_i is the rate of new infections of the i-population, and we remark that β depends on the number of patients of all ages, making the model coupled and nonlinear. These patients are removed from their condition at rate γI_i (they either recover or die). We further divide the infectious into two groups, those that are asymptomatic or sub-clinical $I_i^{\text{sc}}=(1-{\rho }_i)I_i$ in the sense that they do not require medical care. The clinical group $I_i^{\text{c}}={\rho }_i{I}_i$ corresponds to those that get ill, requiring medical attention. The age-dependent fractions of those who become sub-clinical or clinical are ρ_i ∈ [0, 1].

To fully describe the model, we ought to define β and the other parameters.

• (i)the components of the incidence function β are given by the formula

$${\beta }_i(\mathit{I})=\sum _{j=1}^{16}\frac{{\alpha }^{\text{sc}}{I}_j^{\text{sc}}+{\alpha }^{\text{c}}{I}_j^{\text{c}}}{P_j}{C}_{i,j}^e=\sum _{j=1}^{16}\left({\alpha }^{\text{sc}}(1-{\rho }_j)+{\alpha }^{\text{c}}{\rho }_j\right)\frac{I_j}{P_j}{C}_{i,j}^e,$$

where C^e is an effective contact matrix that measures the number of contacts between age groups. It depends on the amount and choices of lock-down imposed, as we describe further ahead. The age-independent parameters α^sc and α^c correspond to the fraction of those that are infective, having the potential to infect others due to social behavior or biology. For convenience, we also write the vector β(I) = C^eDI, where D is a diagonal matrix defined by

$$D_{jj}=\frac{{\alpha }^{\text{sc}}(1-{\rho }_j)+{\alpha }^{\text{c}}{\rho }_j}{P_j}.$$

• (ii)The time dependent effective contact matrix C^e is defined by

$$C^e(t)={\beta }_h(t)C^{\text{home}}+{\beta }_w(t)C^{\text{work}}+{\beta }_s(t)C^{\text{school}}+{\beta }_o(t)C^{\text{other}},$$ (2)

where the exogenous data C^home, C^work, C^school, C^other are 16 × 16 matrices, where $C_{ij}^{\ell }$ indicates the average number of different people from the age group j that someone from the age group i contacted per day at ℓ ∈{home, work, school, other}, as compiled by (Mossong et al., 2008; Prem et al., 2017). The parameters β_ℓ control the fraction of contacts that are “adequate”, in the sense that they lead to infections.

• (iii)Each component of ρ gives the risk that an infectious will become a sub-clinical or a clinical case. Since COVID-19 symptoms are more aggressive for older patients, ρ_i grows with i.
• (iv)$\gamma =1-e^{-1/d_I}$ is the daily probability that someone stays infected, where d_I is the average duration of infection (Prem et al., 2017). For simplicity, we assume that the period in which one is infective is independent of age and disease severity. These hypotheses are commonly, but not always, assumed in the literature (Acemoglu et al., 2020; Albani et al., 2021a, 2021b,bib_Albani_et_al_2021a,bib_Albani_et_al_2021b; Britton et al., 2020; Prem et al., 2020); see (Levin et al., 2020; Walsh et al., 2020; Zhou, She, Wang, & Ma, 2020) for related discussions based on medical data.
• (v)The contagious parameters α^sc and α^c correspond to fractions of sub-clinical and clinical infected patients that still spread the virus.

2.1. Reproduction and replacement numbers

The basic reproduction number ${\mathcal{R}}_0$ is understood as the secondary cases produced by an infective patient introduced in a totally susceptible population (1002Barril, Calsina, Cuadrado, & Ripoll, ; Delamater, Street, Leslie, Yang, & Jacobsen, 2019; Diekmann, Heesterbeek, & Metz, 1990; Hethcote, 2000). Hence, suppose that the whole population with distribution P is susceptible (S = P), and we represent the infective patients by $\widehat{\mathit{I}}$, a vector belonging to the canonical basis {e₁, …, e₁₆}. The number of patients in the first day belonging to the i-th group is

$$\sum _{k=1}^{16}{\delta }_{ik}{\beta }_k(\widehat{\mathit{I}})P_k=\sum _{k,j,\ell =1}^{16}{\delta }_{ik}{P}_k{C}_{kj}^e{D}_{jl}{\widehat{\mathit{I}}}_l=\sum _{m,j,\ell =1}^{16}{\mathbb{P}}_{im}{C}_{mj}^e{D}_{jl}{\widehat{\mathit{I}}}_l$$

where δ_ik denotes the Kronecker delta, which equals one if i = j and zero otherwise, and we define $\mathbb{P}$ as the diagonal matrix such that ${\mathbb{P}}_{kk}=P_k$. Let $A=\mathbb{P}{C}^{e}D$. Then the vector containing the contaminated individuals in the first day is $A\widehat{\mathit{I}}$, and we can bound its Euclidean norm as

$$\Vert A\widehat{\mathit{I}}{\Vert }_2\le {\lambda }_{\text{max}}\Vert \widehat{\mathit{I}}{\Vert }_2={\lambda }_{\text{max}},$$ (3)

where λ_max is the largest eigenvalue of A. Note that only the fraction ${(1-\gamma )}^{d-1}\widehat{\mathit{I}}$ of the infective outsider remains infected on the d-th day. This fraction infect less than (1 − γ)^d−1λ_max, as in (3), and adding up all days, we gather that the total number of infective agents is bounded by the basic reproduction number

$${\mathcal{R}}_0≔\sum _{d=1}^{\infty }{(1-\gamma )}^{d-1}{\lambda }_{\text{max}}=\frac{1}{\gamma }{\lambda }_{\text{max}}.$$ (4)

Reasoning in a similar fashion, we define the replacement number

$${\mathcal{R}}_t≔\frac{1}{\gamma }{\lambda }_{\text{max}}(t),$$ (5)

where λ_max(t) is defined as the maximum eigenvalue of the matrix $\mathbb{S}{C}^{e}D$ and $\mathbb{S}$ is the diagonal matrix with the diagonal given by S_j for j = 1, …, 16.

The above definitions of ${\mathcal{R}}_0$ and ${\mathcal{R}}_t$ rely on the Euclidean and spectral norms. However, if one is interested in considering age-dependent quarantine or vaccination policies, it might be interesting to consider a slightly different approach. An infective patient of the age group ℓ ∈{1, …, 16} would contaminate, on a single day,

$$\mathit{\beta }({\mathit{e}}_{\ell })\cdot \mathit{P}=C^{e}D{\mathit{e}}_{\ell }\cdot \mathit{P}=\sum _{i=1}^{16}{C}_{i\ell }^e{D}_{\ell \ell }{P}_i.$$ (6)

As before, adding up the days and considering that at the jth day there will be a fraction (1 − γ)^d−1e_ℓ of the infective outsider, we gather that the total number of infective agents is the age-dependent basic reproduction number

$${\mathcal{R}}_{0,\ell }≔\sum _{d=1}^{\infty }{(1-\gamma )}^{d-1}{({\mathit{P}}^T{C}^{e}D)}_{\ell }=\frac{1}{\gamma }{({\mathit{P}}^T{C}^{e}D)}_{\ell }.$$ (7)

Similarly, we define the corresponding age-dependent replacement number

$${\mathcal{R}}_{t,\ell }≔\frac{1}{\gamma }{({\mathit{S}}^T{C}^{e}D)}_{\ell }.$$ (8)

The above number ${\mathcal{R}}_{t,\ell }$ indicates how many people would be contaminated by an infective patient from the age group ℓ introduced in the community at time t.

2.2. Modeling the lethality

Mortality is not part of the dynamics,2 resulting from the number of infectious. We postulate that only those clinically infected die, at an age-dependent rate. So, among the “recovered” patients,

$$d(t)=\gamma \mu (t){\mathit{w}}_d\cdot {\mathit{I}}^{\text{c}}(t)$$ (9)

die, where the constant vector w_d is the age-dependent lethality weights of the disease (Levin et al., 2020), and the lethality strength μ is a scalar that captures how lethality varies with time. Note that the lethality proportion between different ages is constant.

2.3. Data

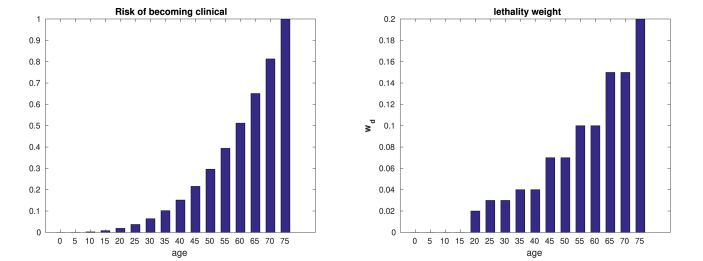
The transmission parameters α^sc and α^c are such that the transmission rate of symptomatic is higher than those asymptomatic (Byambasuren et al., 2020; Prem et al., 2020), and we stipulate that the proportion of symptomatic patients follows the same pattern of the hospitalized patients in (Verity et al., 2020). However, the proportion of asymptomatic patients is far from being settled (Byambasuren et al., 2020; Heneghan, Brassey, & Jefferson, 2020), with estimates ranging from 5% to 80%. Also, we assume that profile of the lethality rates follow Fig. 1, based on (Brazeau et al., 2020; Verity et al., 2020).

Fig. 1.

Probability of being clinical among infectives ρ (left) and lethality weight w_d (right).

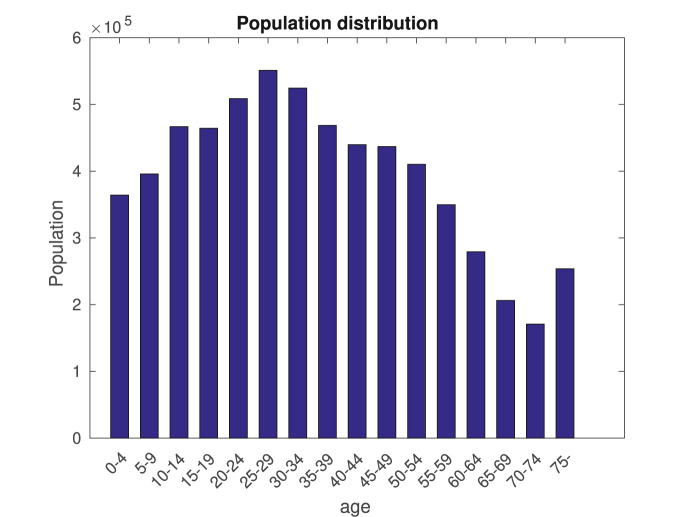
The contact matrices C^home, C^work, C^school, C^other are from (Prem et al., 2017), and population data, as seen in Fig. 10, is from the Instituto Brasileiro de Geografia e Estatística (IBGE). The average number of days d_I that a patient is infective is set to 12.

Fig. 10.

Population profile of Rio. The last column corresponds to the total population above 75 years old.

We use the available data (number of new cases and deaths) from each location to estimate the lethality strength μ(t), and β_h(t), β_w(t), β_s(t), β_o(t), which are necessary to compute the effective matrix C^e. These functions are transient since not only individuals change behavior with time (Brotherhood et al., 2020), but also lethality changes with medical conditions and virus mutations.

For a simple SIR model, the available data uniquely determines the parameters (Bakhta, Boiveau, Maday, & Mula, 2020). In general, that is not the case for our model, for instance if one of the four contact matrices vanish or if C^work = C^other. We reduce the possibility of parameter indeterminations by assuming that β_w = β_o, i.e., the behavior at work is equal to the behavior at other locations. We also make then some further simplifying hypotheses. First, we assume that β_h is constant, as there is no reason to expect that the amount of contacts at home varies significantly with time. The second assumption is that β_s(t) is identically zero, since schools were closed during the period of data gathering.

Consider that data is available for the period $\{1,\dots ,T\}\subseteq \mathbb{N}$, and let and ${\mathcal{N}}_{\mathcal{I}}^{\text{data}}(j)$ and ${\mathcal{N}}_{\mathcal{D}}^{\text{data}}(j)$ be the number of new cases and new deaths at the j-th day. For simplicity, assume that T = Nδt where δt = 10, and consider the partition ${\mathcal{T}}_{\delta t}$ of $\{1,\dots ,T\}={\cup }_{j=1}^N{I}_j$ where

$${\mathcal{T}}_{\delta t}=\left\{I_j:j=1,\dots ,N\right\},I_j=\left\{(j-1)\delta t+1,\dots ,j\delta t\right\}.$$

Let $P_0({\mathcal{T}}_{\delta t})$ be the space of piecewise constant functions with respect to the above partition. To determine β_w we pose the problem of finding (β_h, β_w) that solves

$${\min }_{({\widehat{\beta }}_h,{\widehat{\beta }}_w)\in \mathbb{R}\times P_0({\mathcal{T}}_{\delta t})}J({\widehat{\beta }}_h,{\widehat{\beta }}_w),\text{where }J({\widehat{\beta }}_h,{\widehat{\beta }}_w)=\frac{\Vert {\mathcal{N}}_{\mathcal{I}}^{\text{sir}}({\widehat{\beta }}_h,{\widehat{\beta }}_w)-{\mathcal{N}}_{\mathcal{I}}^{\text{data}}{\Vert }_{{\mathbb{R}}^T}}{\Vert {\mathcal{N}}_{\mathcal{I}}^{\text{data}}{\Vert }_{{\mathbb{R}}^T}},$$ (10)

and $\Vert \cdot {\Vert }_{{\mathbb{R}}^T}$ is the Euclidean norm in ${\mathbb{R}}^T$. Above, ${\mathcal{N}}_{\mathcal{I}}^{\text{sir}}({\widehat{\beta }}_h,{\widehat{\beta }}_w)(t)$ is the number of new infected clinical patients that the SIR model (1) yields at the t-th day if one replaces β_h and β_w by ${\widehat{\beta }}_h$ and ${\widehat{\beta }}_w$ in (2).

The above problem has finite dimension N + 1 since any function $\beta \in P_0({\mathcal{T}}_{\delta t})$ can be written as

$${\beta }_w(t)=\sum _{j=1}^N{b}_j{\chi }_{I_j}(t)$$ (11)

for some unknown coefficients $b_1,\dots ,b_N\in \mathbb{R}$. Here, ${\chi }_{I_j}(t)$ is the characteristic function of I_j, which equals one if t ∈ I_j, and zero otherwise. Note that the coefficients uniquely define a function in $P_0({\mathcal{T}}_{\delta t})$ and vice-versa.

To solve (10) we employ a random optimization approach (Matyaš, 1965; Sarma, 1990)

• (i)Choose a initial guess (β_h, β_w)
• (ii)
  While some convergence criteria is not reached

  • (a)
    Define $({\widehat{\beta }}_h,{\widehat{\beta }}_w)$ from (β_h, β_w) by adding noise
  • (b)
    If $J({\widehat{\beta }}_h,{\widehat{\beta }}_w)<J({\beta }_h,{\beta }_w)$, then $({\beta }_h,{\beta }_w)\leftarrow ({\widehat{\beta }}_h,{\widehat{\beta }}_w)$

The estimation of the lethality strength μ is based on the number of daily deaths data ${\mathcal{N}}_{\mathcal{D}}^{\text{data}}$. The total number of deaths simulated by the SIR model is given by γμ(t)w_d ⋅I^c(t). Equating both quantities we compute

$$\mu (t)=\frac{{\mathcal{N}}_{\mathcal{D}}^{\text{data}}(t)}{\gamma {\mathit{w}}_d\cdot {\mathit{I}}^{\text{c}}(t)}.$$ (12)

Of course, parameter determination could be pursued using more sophisticated methods, e.g. (Albani et al., 2021a).

3. Simulation of the dynamics of the disease

In what follows we show the results coming out of parameter estimations. We then show results addressing how well the model predicts the number of new cases. We compare with real daily data for new cases and deaths,3 and, to smooth out oscillations, we present the data using a 7-day moving average.

One of the hurdles for compartmental models is the definition of initial conditions. Indeed, both the exact “first day” of the disease and how many people were infected in that first day are unknown. As a initial condition of our model, we assume that the first infection occurred 30 days before the official recordings. Indeed, the first day of the official data logs 489 cases; cf. (Lourenço et al., 2020), who speculates that the epidemic in Italy and UK started one month before the first reported death. We also stipulate that there were 10 infectious at each age group at day one.

Such uncertainty of initial conditions makes the results unreliable at the initial periods of simulations. In particular, the computation of (12) is not feasible for the lack of data. Thus, we impose μ(j) = 1 at the initial stages.

3.1. Parameter estimations, and prediction analysis

We consider results for the City of Rio de Janeiro, henceforward simply called Rio. The results presented are for the sum of all ages:

$$\begin{array}{c}S(t)=\sum _{j=1}^{16}{S}_j(t),I^{\text{sc}}(t)=\sum _{j=1}^{16}{I}_j^{\text{sc}}(t),\\ I^{\text{c}}(t)=\sum _{j=1}^{16}{I}_j^{\text{c}}(t),R(t)=\sum _{j=1}^{16}{R}_j(t).\end{array}$$

We recall the assumption that the contacts might lead to infections at home are time independent, and the contacts at work and other locations are identical, i.e., β_w = β_o. Also, schools are closed, thus β_s = 0.

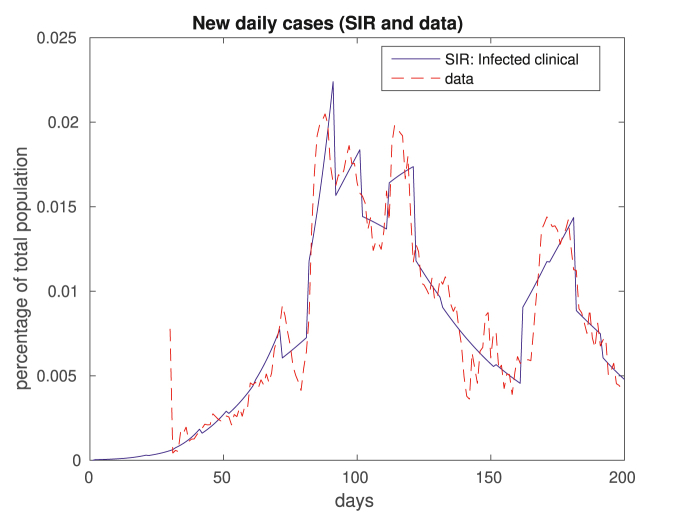
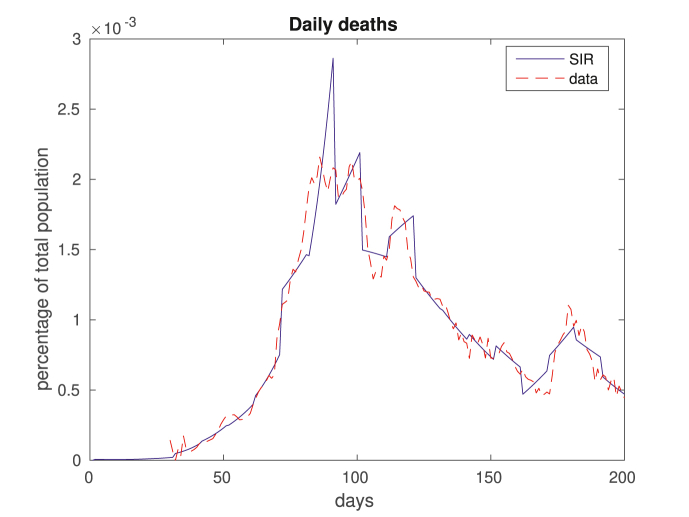
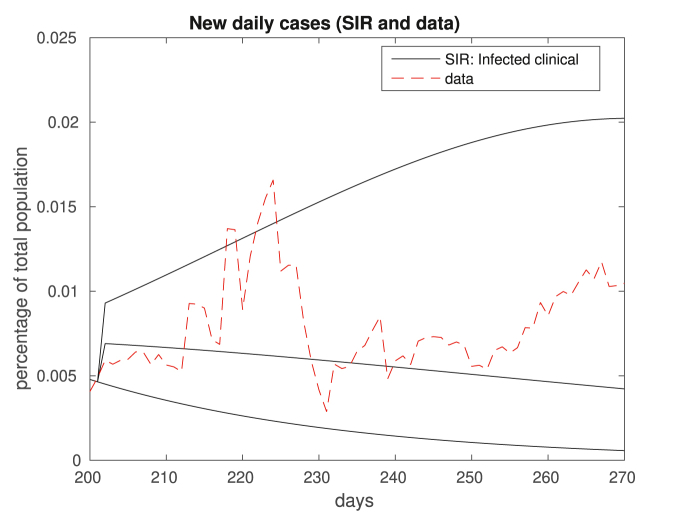
We compare in Fig. 2, Fig. 3 the results of our in-sample approximation of the dynamics of the disease. Note that the actual daily numbers of new cases (Fig. 2) and deaths (Fig. 3) are well approximated by the model.

Fig. 2.

In this figure we plot the 7-day moving average data on new daily cases. The dashed red plot corresponds to real data, and the solid blue plot depicts clinical cases modeled by SIR. Above, and in all figures that follow, what we call data is actually a 7-day moving average of the real data.

Fig. 3.

This figure is related to fatalities, displaying daily deaths. Again, real data is in dashed red, and computed daily deaths by the model come in solid blue.

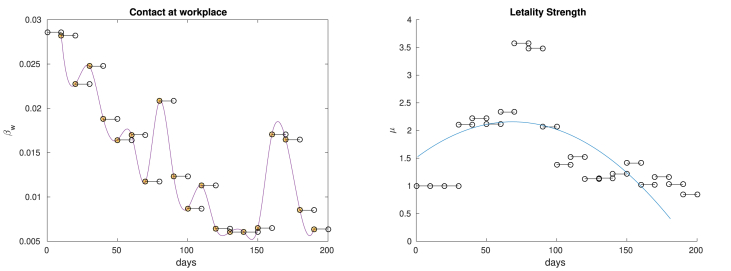
In Fig. 4 we display the values of β_w and μ, estimated by our random search. We see in particular that β_w oscillates following the “macroscopic” oscillations of daily cases. Regarding the lethality strength μ, note that it seems to decrease after day 90, in line with what was presented by (Dennis, McGovern, Vollmer, & Mateen, 2020; Horwitz et al., 2020). Such aspect is captured by the concave least square parabola.

Fig. 4.

On the left we plot the estimated values of β_w, except for the first one (that has a value roughly ten times bigger than the others). For visualization purposes we interpolated the discontinuous function β_w using cubic splines. On the right we display the values of the lethality strength μ, defined in (12). The blue curve is the least square quadratic curve.

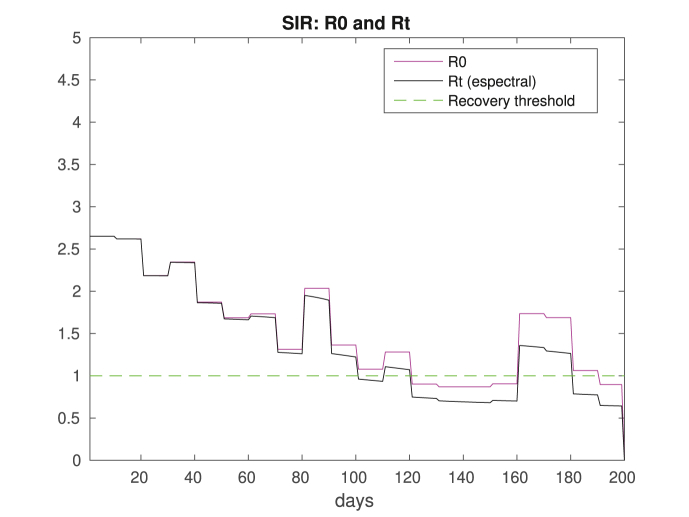
Two important pieces of information coming out of the model are the values of the reproduction and replacement numbers ${\mathcal{R}}_0$ and ${\mathcal{R}}_t$. Their computations follow easily from (4), (5), and we display the results in Fig. 5. Note that values of ${\mathcal{R}}_0$ is characterized only by the population's profile and the contact matrix C^e. On the other hand, ${\mathcal{R}}_t$ depends also on the dynamics of the disease through the susceptible population. That is important since even if ${\mathcal{R}}_0>1$, having ${\mathcal{R}}_t$ smaller than one is enough to have a declining number of infectious.

Fig. 5.

Reproduction and replacement numbers, ${\mathcal{R}}_0$ and ${\mathcal{R}}_t$. Note that ${\mathcal{R}}_0$ is transient since it depends on the time dependent contact matrix. We also draw a line at y = 1 highlighting the recovering threshold. Comparing with Fig. 2, we see that there is a correspondence between ${\mathcal{R}}_t$ crossing the threshold (up or down) and the number of new cases increasing or decreasing.

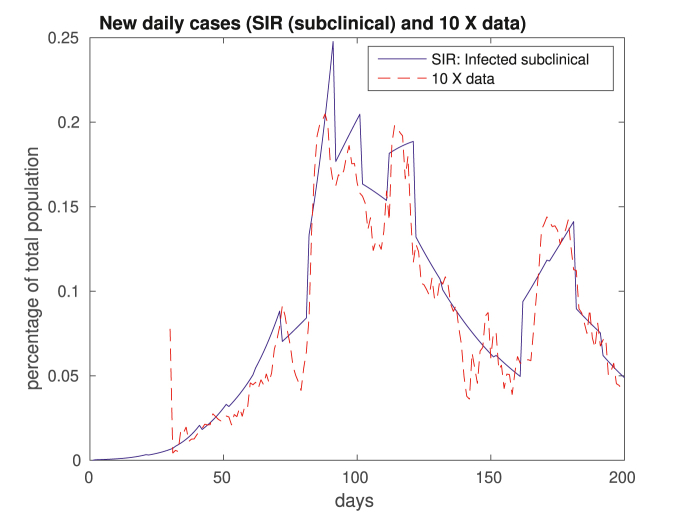
Another issue that is worth discussing is that we fit the number of clinically infective patients I^c to the data. However, we discussed nothing thus far about the sub-clinical patients I^sc. It turns out that the number of sub-clinical patients is, in this case, roughly ten times the number of registered patients, as shown in Fig. 6. Such difference resonates well with claims that there is a significant sub-notification. For instance (Havers et al., 2020), reports that the number of cases in the US might be at least 10 times of what is registered. It would not come as a surprise if this difference is even greater in Rio. Also, the WHO states that 80% of infections are mild or asymptomatic,4 in particular among children, as discussed by (DeBiasi & Delaney, 2770; Han et al., 2019). Recall that children are often not tested.

Fig. 6.

Number of sub-clinical cases in solid blue, corresponding roughly to ten times the number of official cases in dashed red.

Next, we investigate numerically if this model can make reasonable predictions. To do so, after the day 200, we run the simulations based on an in-sample (days 1–200) calculated β_w and μ, and compare with available data. We perform experiments considering the best and worst scenarios, i.e. lowest and highest number of cases and deaths. We also consider an intermediary case. The main idea shares similarities with some Value at Risk analyses used in risk management, where the past dynamics of investments help in predicting the future; see (Jorion, 2006).

We make the predictions by going back j 10-day periods and performing simulations with the highest and lowest values of β_w and μ in the period 200 − 10j and 200. Choosing j = 4, we show in Fig. 7, Fig. 8, Fig. 9 the predicted number of daily and accumulated cases and deaths, with 70 days in advance. Note that, for most of the period of interest, the data is in between the best/worst case scenarios. We also plot the intermediary case, corresponding to the choice of β_w and μ being the average of the extreme values, often yielding more accurate predictions.

Fig. 7.

Number of daily new cases. The dashed red plot indicates the data and the solid black plot represents the simulation results for frozen β_w and μ corresponding to the best/intermediary/worst case scenarios. Note that, for most of the 70-day forecast, that data lie within the interval predicted by the model.

Fig. 8.

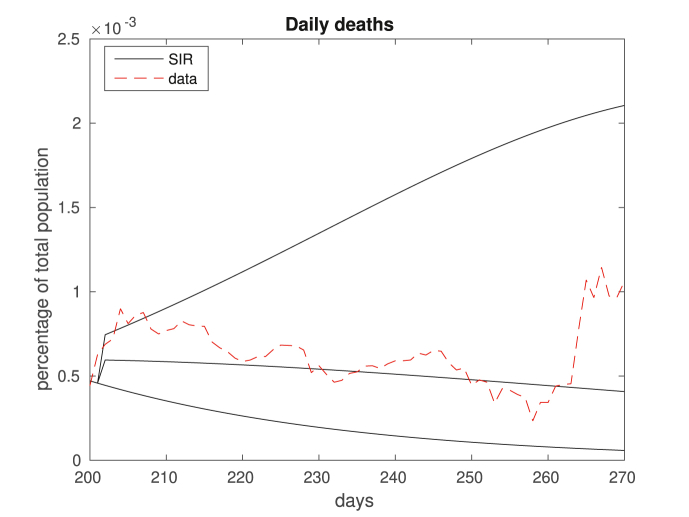
Similarly to Fig. 7, the figure displays the number of daily deaths, dashed red being data and solid black being the best/intermediary/worst cases predicted by the model.

Fig. 9.

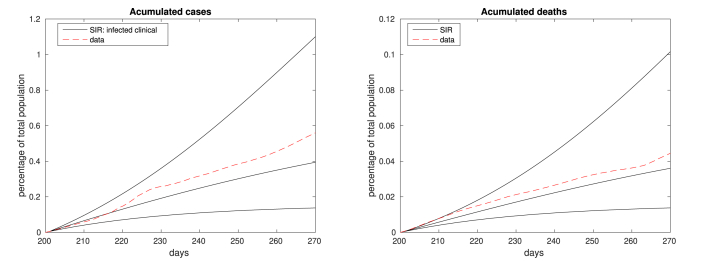
We present here the accumulated number of cases (left) and deaths (right). In both figures, the dashed red plots correspond to real data and the solid black plots represent the simulation results for frozen β_w and μ, for the best/intermediary/worst case scenarios.

4. Vaccination

We explore in this section simple immunization policies, shedding some light on the following question: if an age-based vaccination strategy should be implemented, who should be protected first? Certainly, real-life policies are never as simple as that, since other aspects as economics, logistics, ethics, politics, etc, play significant roles.5 Not only that, but also it is not even clear that vaccinations schemes should be devised based on age groups (Pastor-Satorras & Vespignani, 2002). However, vaccination policies based on age are easy to implement in practice.

Based on the age-dependent reproduction and replacement numbers ${\mathcal{R}}_{0,\ell }$ and ${\mathcal{R}}_{t,\ell }$, we find out which age group contaminates most people. Consider for instance the dynamics of the disease in Rio, with a population profile as in Fig. 10.

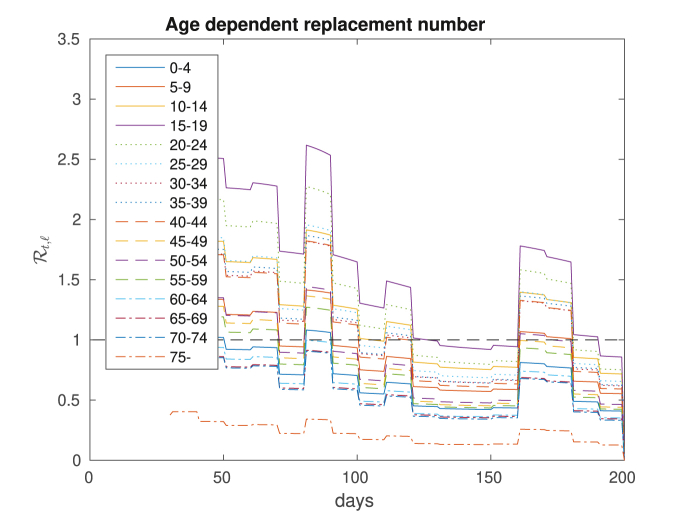
Based on the evolution of the COVID-19 in the first 200 days in Rio, we computed the age-dependent replacement numbers ${\mathcal{R}}_{t,\ell }$, displaying the results in Fig. 11. Note that as far as spreading the disease is concerned, individuals of younger age are the most dangerous. And individuals above 60, which are the ones most affected by the disease, contribute less for its spreading.

Fig. 11.

Age-dependent replacement numbers corresponding to the dynamics of the disease in Rio.

Such heterogeneity leads to interesting immunization policy possibilities. People in the age group 15–19 (around 500 k people in Rio) have the most impact on virus dissemination, but few of them die. On the other hand, those above 60 (around 900 k people) are at high risk, but they have little impact on the spreading of the disease.

To offer a glimpse on these issues, we modify our effective contact matrix C^e, allowing for the possibility of immunization. Let us redefine (2) by

$$C^e(t)=V(t)\left({\beta }_h(t)C^{\text{home}}+{\beta }_w(t)C^{\text{work}}+{\beta }_s(t)C^{\text{school}}+{\beta }_o(t)C^{\text{other}}\right)V(t),$$ (13)

where the transient diagonal matrix V(⋅) models the vaccinated age groups. Its j-th diagonal element is zero if the corresponding age group is protected, and one otherwise. Of course, it is also possible to consider partial immunization by setting values between zero and one.

Consider the hypothetical situation of having β_h and β_w as computed before (see Fig. 4) and the population of Rio. Between the days 200–500, we assume that β_w = β_opt = 0.0064 or β_w = β_max = 0.0117, and a constant lethality strength μ = 1.

Suppose that there is a limited supply of vaccines, which are made available only at a certain moment, that is, the vaccination campaign takes place at a single day. In our examples, this is 100, 150 or 200 days after the pandemic starts. Of course, the timing of vaccination campaigns impacts its effectiveness, and there is an important body of literature investigating this issue (Albani et al., 2021b; Amaku et al., 2021a; Quach and Deeks, 2021).

To better compare experiments, we define an utility function that takes into account the number of lost lives. For ϒ ∈ (0, 1), we define the ϒ-discounted cost of death as

$$\sum _{t=1}^{+\infty }{{\rm Y}}^{t}d\left(t\right),$$ (14)

where d(⋅) is the number of daily fatalities. We consider ϒ = 0.996^1/365 in the numerical tests.

In our numerical experiments, we first assume that a single shot of the vaccine induces a perfect immunization and stop the virus spreading. In a second example, we consider partial immunization. Consider three age groups of similar size as targets of an immunization campaign: those aged 15–34 (≈1,584 people), 40–59 (≈1,636 people) and those above 50 (≈1,670 people). In all tested situations, the groups with best results were either the 15–34 or those above 50.

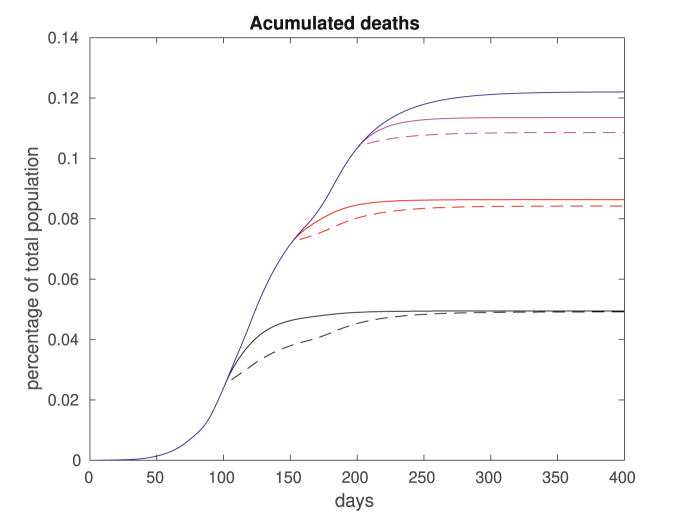
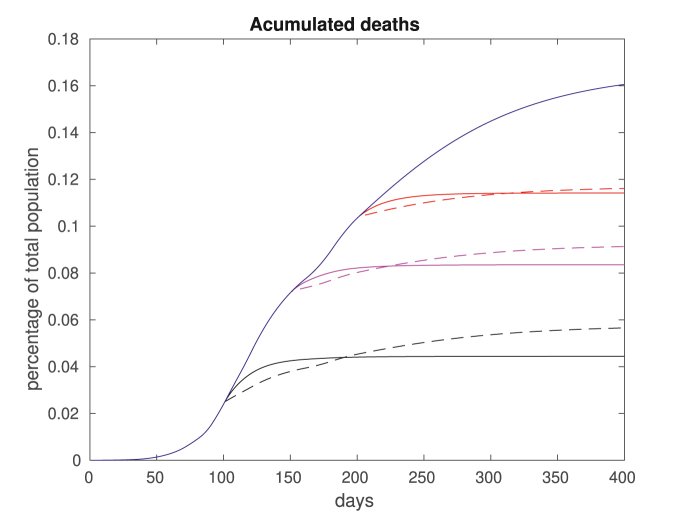
In Fig. 12, we plot the accumulated deaths considering full immunization of the groups aged 15–34 or over 50, for a fixed β_w = 0.0064 after day 200. In solid blue we plot the total deaths if no vaccination takes place. The remaining plots correspond to the total deaths if vaccination occur on day 100 (black), 150 (red) or 200 (magenta). The solid lines correspond to vaccinating the young and the dashes lines corresponding to vaccination of the elderly. In Fig. 13, we repeat the computations fixing a higher β_w = 0.0117 after day 200.

Fig. 12.

Accumulated deaths for β_w = 0.0064. We assume no vaccination (solid blue), vaccination for group aged 15–34 (solid plots) and over 50 (dashed plots). The vaccination takes place on day 100 (black), 150 (red) or 200 (magenta). Note that vaccinating the elderly population is always optimal in the short term, but not necessarily in the long run.

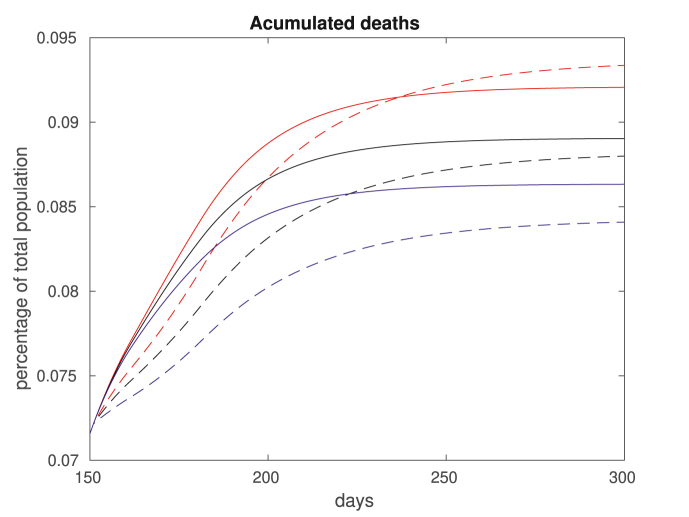
Fig. 13.

Accumulated deaths for β_w = 0.0117, a higher rate of transmission. As before, we assume no vaccination (solid blue), vaccination for group aged 15–34 (solid plots) and over 50 (dashed plots). The vaccination takes place on day 100 (black), 200 (red) or 300 (magenta). Note that vaccinating the elderly population is always optimal in the short term, but not necessarily in the long run.

Basically, two different policies are possible: stop the spreading corresponds to vaccinating those in the 15–34 age group, and protect the vulnerable corresponds to vaccinating those above 50. Note from the results that the impact of stop the spreading decreases as the vaccination date is delayed. That is because the percentage of young population already contaminated at later dates is larger, and vaccinating the young group ends up not being so effective. Such effect is amplified for higher transmission rates, as one can see by comparing Fig. 12, Fig. 13. Note also that for short terms, it is always preferable to protect the vulnerable, indicating that vaccinating the elderly population might be a wise option if a continuous supply of vaccines is available.

Considering the total amount of casualties in the long run, for lower transmission rates it is always better to vaccinate the elders (Fig. 12). For higher transmission rates, these results are reversed (Fig. 13). However, when considering the cost of death (14), the results are mixed, as shown in Table 1. For related results, see (Meehan et al., 2020; 1093Giubilini, Savulescu, & Wilkinson, ; Zhao et al., 2020). We also remark that although most countries are pursuing policies that prioritize the elderly, there are exceptions (The Japan Times, 2020).

Table 1.

Numerical investigation of immunization policies based on age. In each line we present the values of the death cost functional (14) assuming different age groups are vaccinated. The second column contains the population of the groups. In the three columns that follow, we present the results considering the vaccination takes place on the days 100, 150 or 200 and assuming that β_w = 0.0064. The following three columns display the results for β_w = 0.0117 and vaccination on the days 100, 150 or 200. For each column, we highlight the best results.

		βw = 0.0064 after day 200			βw = 0.0117 after day 200
		Vaccination day
Age group	# vaccines	100	150	200	100	150	200
none	0	7.4 k			9.6 k
15–34	1,584 k	3 k	5.2 k	5.9 k	3 k	5.3 k	7.1 k
40–59	1,636 k	3.3 k	5.3	6.7	3.7 k	5.7 k	7.1 k
50-	1,670 k	3 k	5.1 k	6.6	3.4 k	5.5 k	7 k

We consider in a second example the possibility that the vaccines are not perfect, and display the results in Fig. 14. Assume that a immunization campaign happens at day 150, and that either those aged 15–34 (solid lines) or those over 50 (dashed plots) are vaccinated. Assume also that the immunization is perfect (in blue), or has partial efficiency of 70% (black) or 50% (red). Note that, as expected, as the vaccine efficiency decreases the number of casualties increase. It is maybe more surprising to realize that this effect is more aggravated for the elderly.

Fig. 14.

Accumulated deaths for β_w = 0.0064, under varying vaccination efficiencies. Assume that at day 150, a vaccination campaign targets either the young (aged 15–34, solid plots) or those over 50 (dashed plots). The vaccination efficiency varies as follows: 100% (blue), 70% (black) or 50% (red).

5. Discussions and conclusion

Epidemics as the COVID-19 are hard to model, not only because of biological factors, but also due to the unpredictability of human responses. Political, economical, social and individual factors influence the behavior of people, leading to various degrees of risk behavior. Making long term predictions is riskier than in general (non-human) biological systems, but they are crucial for planning non-pharmaceutical interventions, allocation of resources, economical decisions, etc.

We propose in the work a general form to predict possible values of crucial parameters based on their history. Our method has two steps. Based on the dynamics of the disease on a multi-generational SIR model, we first determine the values of some time-dependent parameters, using a random optimization algorithm. Then, we feed the SIR model using extreme values of such parameters, and predict best/worst case scenarios. We are also consider a prediction that is in between the two extreme cases.

Our methodology is general and can be applied to other systems and circumstances, and might be useful to make long-term predictions in situations where unexpected occurrences might change the behavior of the system.

We also explore age-based immunization strategies, under simplifying hypotheses. For instance, while we assume the behavior of the population as known, the very existence of vaccines changes people's behavior. Moreover, several important aspects of vaccination are not considered here, as ethical problems, logistics, etc. We also point out that other policies might be better, as targeting certain classes of workers or individuals with comorbidities.

In our limited setting, we find out that optimal policies depend, among other things, on transmission rates, the vaccination efficiency and its timing. Earlier vaccination dates, low vaccine efficiency and higher transmission indices increase the impact of vaccinating the young. Under most conditions however, it pays off to vaccinate the elderly, although they contribute the least for spreading the viruses. Indeed, for short terms, protecting the older population is always preferred. That seems to indicate that under a continuous supply of vaccines, protecting the elderly is a wise option.

It is clear that the model provides different indications under different scenarios, and we shall explore more detailed policies in a future work.

As we point out in our Disclaimer, our goal is not to predict actual number of cases and deaths or to propose general policies, but instead to investigate limited aspects of the disease dynamics and raise possibilities of immunization strategies.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Handling editor: Dr Lou Yijun