Tuna robotics: hydrodynamics of rapid linear accelerations

Abstract

Fish routinely accelerate during locomotor manoeuvres, yet little is known about the dynamics of acceleration performance. Thunniform fish use their lunate caudal fin to generate lift-based thrust during steady swimming, but the lift is limited during acceleration from rest because required oncoming flows are slow. To investigate what other thrust-generating mechanisms occur during this behaviour, we used the robotic system termed Tunabot Flex, which is a research platform featuring yellowfin tuna-inspired body and tail profiles. We generated linear accelerations from rest of various magnitudes (maximum acceleration of $3.22\hspace{0.17em}\mathrm{m}\hspace{0.17em}{\mathrm{s}}^{-2}$ at $11.6\hspace{0.17em}\mathrm{Hz}$ tail beat frequency) and recorded instantaneous electrical power consumption. Using particle image velocimetry data, we quantified body kinematics and flow patterns to then compute surface pressures, thrust forces and mechanical power output along the body through time. We found that the head generates net drag and that the posterior body generates significant thrust, which reveals an additional propulsion mechanism to the lift-based caudal fin in this thunniform swimmer during linear accelerations from rest. Studying fish acceleration performance with an experimental platform capable of simultaneously measuring electrical power consumption, kinematics, fluid flow and mechanical power output provides a new opportunity to understand unsteady locomotor behaviours in both fishes and bioinspired aquatic robotic systems.

1. Introduction

Fish exhibit a wide variety of locomotor patterns that include steady swimming, escaping from predators, feeding strikes and a diversity of manoeuvres. Accelerations that provide the ability to change locomotor speed are routinely present in most of these swimming activities, yet little is known about the dynamics of acceleration in fishes [1,2]. Manoeuvres such as fast-start escape responses require strong accelerations to avoid predators [3,4], and these high accelerations typically result from quickly bending the body into a C-shape followed by a change in direction. Acceleration also occurs as part of the burst-and-coast swimming style of a multitude of fish species in which short periods of acceleration interrupt high-speed, steady swimming [5]. Fish also accelerate when shifting between different steady swimming speeds while maintaining their average heading, a behaviour termed as linear acceleration. The most common type of linear acceleration occurs when fish start swimming [6], as starting with zero velocity necessarily means that acceleration is required to reach a steady swimming speed.

Despite the abundance of studies on steady fish swimming, there are few analyses of the accelerations present throughout the routine locomotion. Previous research has addressed how swimming eels accelerate by increasing tail tip velocities [1]. In another study, incorporating 51 anguilliform and carangiform swimming fish species, it was shown that undulating fishes show increased tail beat amplitudes during linear accelerations compared to steady swimming [5]. This finding was corroborated by detailed analyses of bluegill sunfish showing increased head and tail amplitudes [7] and lamprey showing higher amplitudes along the entire body [6] during linear acceleration. Wise et al. [7] also found indications of larger force production rather than the reorientation of axial forces during acceleration compared to steady swimming patterns, which differs slightly from the conclusions of [5] who documented vortex wake reorientation during acceleration. Whereas fish show increased tail beat amplitudes during linear accelerations, Akanyeti et al. [5] also showed that different amounts of accelerations are largely modulated by the tail beat frequency. Thus, to increase acceleration, fish beat their tails faster.

Despite ongoing progress in understanding swimming acceleration dynamics [8–11], analyses of locomotor accelerations in living fishes are challenging. Obtaining consistent acceleration magnitudes while controlling for variables such as heading, the power used to generate the acceleration and kinematics ranges from difficult to impossible when studying live animals. As a result, a few investigators have turned to mechanical and robotic systems to provide a highly controlled experimental platform in which acceleration dynamics can be quantified [2,12–15]. These robotic systems have shed new light on the effects of the dorsal and anal fin on linear accelerations and have helped to design new mechanical systems to emulate and understand the impressive acceleration performance of fast-starting fish. Such platforms are convenient for quantifying performance effects thanks to their ability to control for variables while deliberately altering others (e.g. body flexibility, the magnitude of acceleration or kinematics). These platforms also afford more options for experimental instrumentation and manipulation compared with their biological counterparts.

In this study, we use a newly developed robotic platform inspired by yellowfin tuna (the Tunabot Flex [16]) to extend current analyses of acceleration patterns in fish swimming by inducing linear accelerations from an initial rest position at zero velocity. Thunniform swimmers heavily rely on lift-based propulsion generated by their lunate-shaped caudal fins. This mechanism is thought to generate thrust well at higher swimming speeds, whereas at slower swimming speeds, mechanisms based on reaction forces from accelerating the surrounding fluid along the body via undulations produce more thrust [17]. By investigating linear accelerations from rest with a tuna-like robot, where swimming speed is initially zero, we were able to quantify to what extent thrust is generated along the body and contributes to forward motion in thunniform swimmers. The Tunabot Flex robotic system is able to accurately measure instantaneous electrical power consumption and to alter the magnitude of acceleration. These capabilities provide a unique analytical opportunity to compare electrical power input with acceleration performance output. We also quantify body kinematics and fluid flow patterns throughout acceleration. Using these flow patterns around the body, we calculate the body surface pressure distribution and from this the force and energy imparted to the fluid. The ability to directly measure the sources of thrust generation in a biomimetic, accelerating, physical fish model provides new insights into the acceleration dynamics of fish.

2. Methods

(a). Tuna-like robot

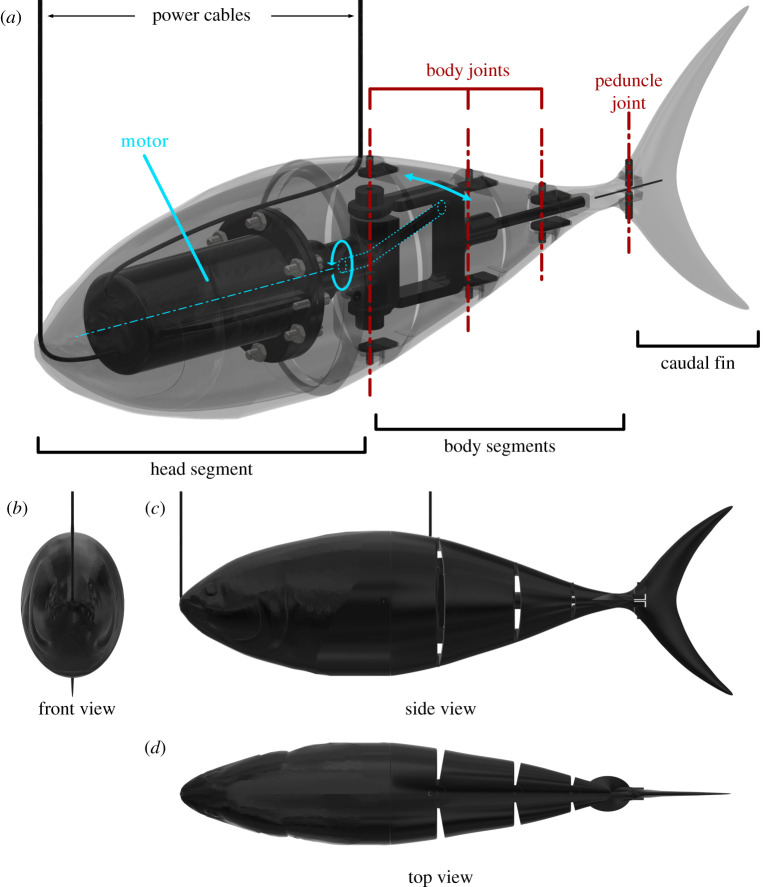
We used the Tunabot Flex platform presented by White et al. [16] to conduct experiments measuring instantaneous electrical power consumption, body kinematics and fluid flow patterns during linear acceleration from rest. This single-motor-actuated, robotic system (figure 1) possesses three jointed segments in addition to a flexible joint at the caudal peduncle that together allows body bending. The angled anterior surfaces of these joints also serve as mechanical stops at the limit of lateral bending, which ensures that the amplitude of body motion, by design, is constant across tested conditions (figure 1d). The Tunabot Flex platform was preceded by the Tunabot [18], which demonstrated high-frequency tail beats up to 15 Hz and steady swimming speeds up to 4 body lengths sec⁻¹ with a similar actuation mechanism. Tunabot Flex improved the mechanical and bioinspired designs of its predecessor, including variable body flexibility, while using the same external dimensions and motor. Added body flexibility was accomplished using a design that also enabled the generation of constant tail beat amplitudes at all tested frequencies, and the addition of body segments greatly increased swimming performance [16]. This body segment design involves small gaps between segments that open and close during swimming (figure 1), but visualization of flow in these regions indicated that water rapidly moved both in and out and did not reduce swimming performance. In addition, White et al. [16] demonstrated that steady swimming performance improved even when the number of gaps increased, and that passive body drag variations among models with different numbers of gaps were negligible.

Figure 1.

Tuna-like robot. The swimming Tunabot Flex robot (25.5 cm total length) is powered by a single motor that induces a continuously rotatory motion which is translated to an oscillatory flapping motion of the tail (blue arrows in (a)). The robot consists of three body joints plus a fourth peduncle joint that incorporates an internal spring for torsional stiffness. Complete details of Tunabot Flex can be found in [16].

One key feature of the Tunabot Flex system is the ability to produce multiple conditions of linear acceleration from rest by varying the tail beat frequency and holding all other parameters constant. In particular, we were able to keep the tail beat amplitude constant due to the hard-stop limits on the side to side motion. The tail beat frequency is varied by modulating the pulse width of the voltage signal input to the DC motor to produce four different duty cycles: 15, 30, 45 and 95%. The duty cycle indicates the percentage of time that the voltage is on and thus the tail beat frequency increases with duty cycle. A second key aspect of Tunabot Flex is our ability to quantify a time history of electrical power consumption ($P(t)\hspace{0.17em}=U(t)\times I(t)$: power P(t), voltage U(t) and current I(t)) throughout each experimental test (e.g. figure 2c), thereby permitting time-correlated analyses of power consumption, motions of the body and tail, fluid flow patterns in the wake, and calculated body surface pressures (see below). Complete details of power measurement methodology (e.g. circuitry and calculations) and tail beat frequency control are presented in [16].

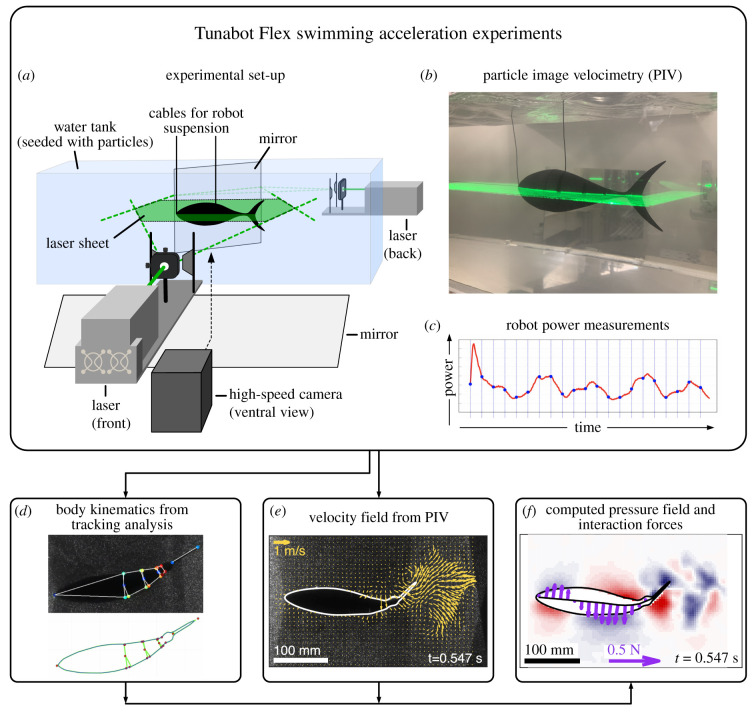
Figure 2.

Overview of acceleration analysis with the Tunabot Flex system. (a) Experimental set-up with the suspended robot in a water tank seeded with particles, two laser sheets for PIV (b) and a high-speed camera to record the movements of the robot and the fluid. In parallel, detailed electrical power measurements are obtained throughout the acceleration (c). High-speed video recordings are used to extract kinematics (d) as well as velocity fields (e), which are in turn used to compute pressure fields and interaction forces (f). (Online version in colour.)

(b). Experimental set-up

We carried out Tunabot Flex linear acceleration experiments in a custom water tank (28 cm × 28 cm × 90 cm). The robot was suspended in the middle of the tank using two power cables guided out of the nose and the mid-body (figures 1 and 2a). Each acceleration experiment was initiated in still water and recorded for 2–3 tail beats to provide sufficient time for body acceleration to peak and then decline. The flexible power cables suspending the robot within the flow tank did not restrict acceleration from rest and the robot was free to move forward over the short period of acceleration analysed in our study. The vertical swinging of the suspended robot (see tunabot_piv_lasersheet.mp4) was very small during data collection due to the length of power cables; since the foremost cable measured 0.36 m in length, the vertical displacement of the robot is 7 mm with a forward displacement of 70 mm. The elevation of 7 mm is within the limits that ensure that the mid-section of the robot can be consistently captured in the laser sheet used in our particle image velocimetry approach but the elevation of the body by this amount only occurred during the last stages of movement.

(c). Particle image velocimetry

We quantified flow patterns around the accelerating robot using particle image velocimetry (PIV) as in our previous research [18–20]. We seeded the water with near-neutrally buoyant plastic particles (approx. 50 µm mean diameter) that were illuminated by a laser light sheet through the middle (= half span) of the tunabot body (figure 2a,b). As indicated above, vertical swinging was very small. This was also confirmed by examining the robot outline profile in the recorded ventral view video which was consistently maintained across the acceleration manoeuvre (figure 2e). If the robot mid-section had been outside the laser sheet, we would notice gaps filled with fluid particles starting to appear at the peduncle as the robot is lifting up because of the cables. To avoid shadows caused by occlusion of the swimming robot and encompass the entire field around the robot, we generated the laser sheet with two lasers aligned in height that projected laterally from both sides of the robot (figure 2a). To avoid image overexposure at the edges of the robot and to simplify postprocessing of the obtained videos, we painted the robot black for this study (figure 2b). We recorded the movements of the particles in the light sheet from a ventral view using a high-speed camera at frame rates of 2000–4000 frames per second and shutter speeds of 1/2000–1/8000 s depending on the magnitude of acceleration. Finally, we processed the high-speed videos to extract both detailed body kinematics as well as the flow fields surrounding the swimming robot.

(d). Automated tracking and model fitting

We used the high-speed video recordings to extract body kinematics of the accelerating robot with the help of characteristic landmark points that were tracked throughout the videos. We automatically tracked a total of 20 points along the body (figure 2d) using DeepLabCut [21]. This method involved minimal training (18 frames from a single video) of a deep neural network to determine marker coordinates for a given input video frame. The tracked points included landmarks on both the midline and the outline of the body.

For the second step, we fitted a two-dimensional model (electronic supplementary material, figure S1) of the robot into the tracked points to obtain midline kinematics and the body outline, which was required for computing the surrounding pressure field. The two-dimensional model was composed of five polygons which together approximate the 2D projection of the robot: one head segment, two body segments, one peduncle segment and one tail segment. We further parametrized the model using five angles for the orientation of each polygon and the position of Tunabot Flex's mid-body joint. Thus, this set of seven parameters fully determined the position and posture of the robot in our recorded video frames. To obtain the kinematics, we fitted this model for each frame into the tracking points by minimizing the sum of squared errors:

$${\mathit{\Theta }}^{\ast }=\arg \underset{\mathit{\Theta }}{min}\left(\sum _i^n{(x_i-x_{m,i})}^2+{(y_i-y_{m,i})}^2\right),$$ 2.1

where $\mathit{\Theta }$ (and the solution ${\mathit{\Theta }}^{\ast }$) describes the set of 7 model parameters, $(x_i,y_i)$ and $(x_{m,i},y_{m,i})$ represent the two-dimensional position of the $i$-th tracking point and the corresponding tracking point in the model, respectively, and $n=20$ denotes the number of tracking points. We implemented the minimization procedure in MATLAB using the fminsearch function and initialized each search using the solution of the previous frame. The search in the initial frame was initialized by a straight body posture anchored in the tracking point of the first joint. We obtained the body outline by using the corresponding polygon points around the robot, resampling and connecting the outline with 500 points, and finally smoothing with a Savitzky-Golay filter and a window size of 41 points.

(e). Forward direction, acceleration and lateral displacement

To quantify the linear forward acceleration, it was necessary to compute the swimming direction first. For this purpose, for each acceleration manoeuvre, we applied a principal component analysis to the point cloud of the centre of mass (COM) locations across all the frames within that manoeuvre. The COM was estimated from the three-dimensional CAD robot model at 0.32 body lengths from the snout. The swimming direction was then identified as the first principal component. This method is preferred as it is robust against bias resulting from denser regions in the point cloud stemming from the fact that the body movement is slower in the beginning of the manoeuvre.

Using the computed forward direction, we determined the forward displacement $x_f(t)$ by projecting the COM locations in this direction. Given a constant tail beat frequency, the general dynamics of acceleration from rest involve an increase of acceleration from zero in a first phase and a decrease of acceleration towards (close to) zero in a second phase once steady cruising speed is reached. In our study here, we focused on the first phase and therefore analysed the first 2–3 tail beats because the COM forward speed showed a clear increase during this period. Specifically, we tested the hypothesis that acceleration in this initial phase was constant. For this purpose, we implemented a model of constant acceleration a from zero initial speed $(x(t=0)=\dot{x}(t=0)=0)$, and determined this forward acceleration by linearly regressing the following quadratic model to the forward displacement:

$$x_{\hspace{0.17em}f,\mathrm{model}}(t)\hspace{0.17em}=\hspace{0.17em}\frac{1}{2}\cdot a\cdot t^2.$$ 2.2

Lateral displacement profiles were computed by projecting the midline points to the direction perpendicular to the forward direction and computing the amplitude of the projected displacement along the body.

(f). Pressure forces and thrust

To obtain the interaction forces between the robot and water during acceleration manoeuvres, we followed the methodology detailed in [20]. This procedure starts with the computation of velocity fields in DaVis 8.3 (LaVision Inc.) and is followed by the computation of pressure fields using the Queen 2.0 software [22]. The necessary fluid–structure interface that is needed to compute the pressure acting on the robot was provided by the body outlines obtained from our two-dimensional robot model as described before. This approach to compute the pressure field assumes that shear forces are small and that pressure forces between the body and the fluid dominate, which is justified at the high Reynolds numbers observed in our experiments ranging from 17 512 to 160 326 (table 1). We then divided the body into 20 segments along the midline to obtain the distributed forces by multiplying the pressure with the surface area as described in [20]. These estimations assume an equal pressure distribution along with the depth of the body. We excluded the caudal fin (figure 1a) and only considered the first 16 segments in our analysis of pressure forces. This measure was taken (i) to isolate the contributions of the head and body segments on thrust during accelerations, and (ii) because a more elaborate analysis of the force generation is required for the caudal fin that includes the corresponding vortex generation at the leading edge of the caudal fin. We also provide more details on this second aspect in the discussion.

Table 1.

Summary of acceleration performance. Maximum wake speed is presented as the maximum magnitude in the velocity field occurring within an experiment. Peak power measurements are indicated by mechanical power peak $P_M$, initial electrical power peak $P_E^{(1)}$ (maximum electrical power value at first spike during acceleration), secondary electrical power peak $P_E^{(2)}$ (maximum electrical power value of the oscillating power signal after initial spike in power), and $t_{\mathrm{peak}}$denotes the time to reach the initial electrical power peak. Measurements are presented as mean ± s.d. The Reynolds number ($Re=(uL/\nu )$) was computed based on the final (forward) velocity u, characteristic body length $L=0.255\hspace{0.17em}\mathrm{m}$ and kinematic viscosity $\nu ={10}^{-6}\hspace{0.17em}{\mathrm{m}}^2{\mathrm{s}}^{-1}$.

n	duty cycle [%]	tail beat frequency [Hz]	acceleration [m s−2]	final velocity [m s−1]	Re [-]	max. wake speed [m s−1]	peak axial force [N]	$P_M^{\hspace{0.17em}}$ [W]	$P_E^{(1)}$ [W]a	$P_E^{(2)}$ [W]a	$t_{\mathrm{peak}}$ [ms]a
2	15	1.98 ± 0.06	0.09 ± 0.01	0.07 ± 0.00	18 088 ± 815	0.32 ± 0.06	0.04 ± 0.02	0.015 ± 0.003	0.84	0.59	5.28
2	30	3.96 ± 0.06	0.46 ± 0.02	0.24 ± 0.04	61 265 ± 9450	0.55 ± 0.11	0.12 ± 0.01	0.079 ± 0.016	3.38	2.17	5.66
2	45	5.90 ± 0.03	0.91 ± 0.14	0.35 ± 0.03	87 985 ± 8366	0.74 ± 0.09	0.23 ± 0	0.182 ± 0.049	7.55	4.24	6.09
1	95	11.59	3.22	0.63	160 326	1.58	0.637	0.753	17.31	17.56	4.01

^adenote measurements taken for a single test case only.

For the 16 segments, we computed thrust and drag forces by projecting these distributed interaction forces parallel to the swimming direction; forces pointing forward contribute to thrust, and forces pointing backwards contribute to drag. Using the distributed forces and torques together with the translational and angular velocities of each segment, we computed the instantaneous mechanical power ($P={\sum }_i{F}_i\cdot v_i+{\tau }_i\cdot {\omega }_i$; power P, force $F_i$, velocity $v_i$, torque ${\tau }_i$, angular velocity ${\omega }_i$ for the $i$-th segment) of the robot's main body by summation across the segments [20].

3. Results

(a). Acceleration performance and body kinematics

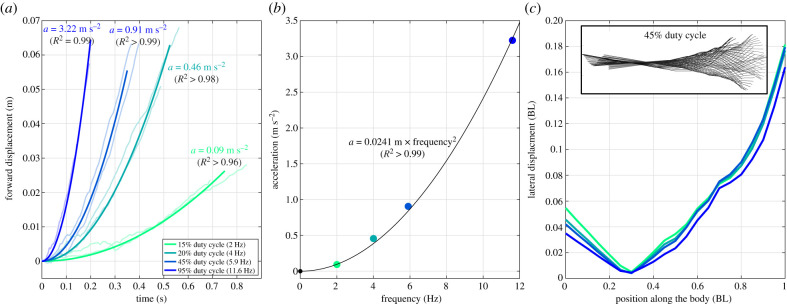
We quantified the acceleration performance of Tunabot Flex for a series of different tail beat frequencies. In all experiments, the robot started from a rest position (zero velocity in still water) and was recorded for 2–3 tail beat cycles. We validated our hypothesis of constant acceleration with the regressions showing $R^2>0.96$ across all trials (figure 3a). We measured a maximum acceleration of $3.22\hspace{0.17em}\mathrm{m}\hspace{0.17em}{\mathrm{s}}^{-2}$at a tail beat frequency of $11.6\hspace{0.17em}\mathrm{Hz}$. This maximum performance corresponds to an increase of 1.09 BL s⁻¹ (BL = body length) in speed within each tail beat cycle. Our experiments further indicate that the flapping frequency and acceleration share a quadratic relationship ($R^2>0.99$; figure 3b); the magnitude of acceleration significantly increases with the tail beat frequency.

Figure 3.

Acceleration performance and body kinematics. (a) Forward displacement over time for different flapping frequencies. Faint lines indicate raw data of the different runs, bold lines show average of regressed models of constant acceleration. (b) Mean accelerations for different frequencies show a quadratic relationship. (c) Body amplitude (i.e. lateral displacement) with respect to position along the body's midline. The black and white inset illustrates the midline kinematics of a representative trial. Coloured lines and points correspond to the four different duty cycles, and hence accelerations, studied. (Online version in colour.)

The robot was actuated by a single motor that translates the rotatory motion of a shaft into oscillatory movements of the tail. As such, tail beat frequency is modulated through control of the motor's angular velocity [16] and was intentionally varied throughout testing (figure 3). Body amplitudes and therefore lateral displacements remain similar to frequency increases (figure 3c) due to the predefined angles and locations of the four body joints [16]. Furthermore, we found that the minimum body amplitude of $(4.39\pm 0.48)\hspace{0.17em}{10}^{-3}\hspace{0.17em}\mathrm{BL}$ (mean ± s.d.) occurred at 0.3 BL (figure 3c), whereas the snout (head tip) amplitudes across frequencies were significantly greater compared to this minimum ($(44.3\pm 8.2)\hspace{0.17em}{10}^{-3}$ BL, p < 0.005 one-sided t-test). As expected, maximum body amplitudes occurred at the tail tip with amplitudes measuring $0.175\pm 0.008\hspace{0.17em}\mathrm{BL}$.

(b). Fluid flow patterns during acceleration

In addition to the kinematics of acceleration, we sought to understand and characterize the flow patterns surrounding the robot during the swimming start from rest. We used PIV to visualize fluid structures and extracted velocity and vorticity fields for subsequent analysis (figure 4; electronic supplementary material). Water is accelerated backwards in the wake of the robot as it accelerates forward in accordance with Newton's third law. Simultaneously, the sideways motion of the flapping tail generates lateral flows. As a result, we consistently observed a reverse Kármán vortex street (figure 4) characteristic of fish propulsion [20,23] in all our experiments across different flapping frequencies. Each vortex was shed at the instant of maximum tail tip excursion.

Figure 4.

Flow and pressure patterns during acceleration. Representative example of an acceleration manoeuvre at 45% duty cycle (5.9 Hz tail beat frequency). The columns show (a) velocity fields, the (b) axial and (c) lateral components of the velocity field, (d) the vorticity field and (e) the calculated pressure field including the distributed interaction forces (purple arrows) along the robot's length. Each row illustrates the different fields at the same time instance, which is displayed in the lower right corner of each panel. Circular arrows in the bottom row vorticity field panel indicate the reverse Kármán vortex street. Similar analyses for the other duty cycles tested are presented in the electronic supplementary material. (Online version in colour.)

Furthermore, we identified two characteristic regions in the wake when we looked at the axial flow speed components (i.e. in direction of the robot movement). The first region encompassed fluid that has a strong flow component in the backward direction with respect to the robot (figure 4b, red coloured areas). The second type of region consisted of fluid that has a flow component in the same forward direction as the robot (figure 4b, blue coloured regions). These regions were located at the edges of the vortex street. Table 1 presents the maximum wake flow speeds that we found for different frequencies with a maximum wake flow speed of 1.58 m s⁻¹ for the fastest acceleration experiments.

(c). Pressure, forces and thrust generation

Throughout the acceleration manoeuvre, we found consistent pressure patterns along the robot body for the different flapping frequencies. We identified three regions with characteristic pressure distributions where, for a given time instance and lateral side, the signs matched at the head and caudal fin but showed the opposite sign at the middle region of the body (figure 4e). Throughout the acceleration manoeuvre, we found that these regions collectively travel downstream toward the tail. Moreover, our pressure computations allowed us to characterize the wake of the robot, not only in terms of the fluid flow speeds, but also in terms of regions of positive and negative pressure: Large areas of negative pressure (figure 4e) are consistently present across our experiments in the wake immediately behind the accelerating robot. These regions are associated with the strong vortices shed from the tail fin which induces low pressures at the respective vortex cores.

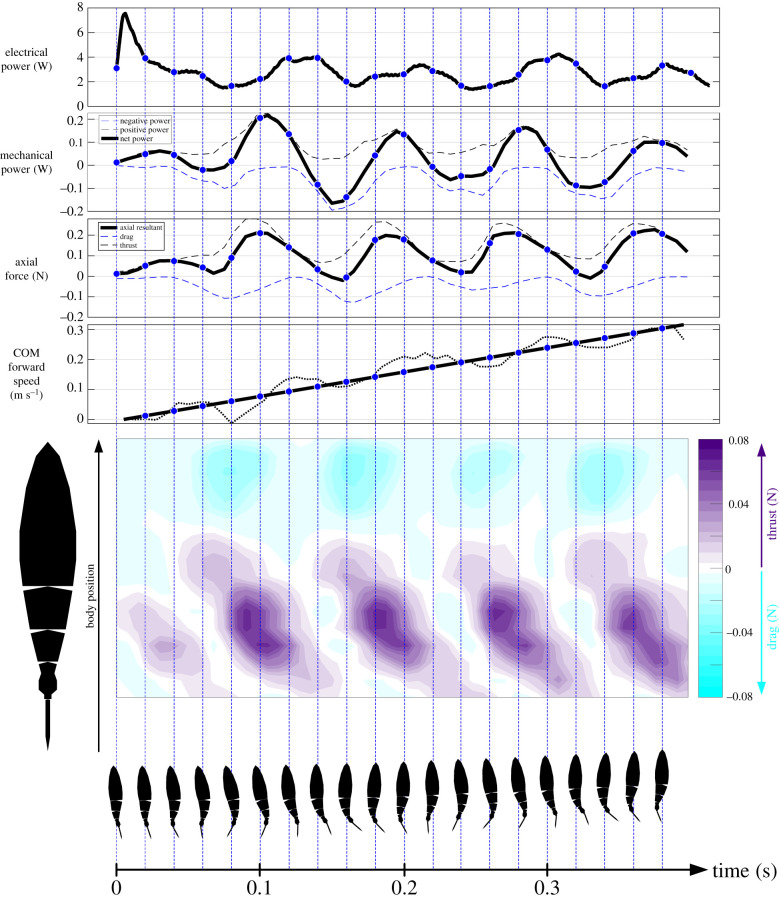
In addition to the pressure calculations, we were able to compute the distributed interaction forces between the robot body from head to peduncle and the surrounding fluid (see Methods, and [20]). Apart from the propulsive forces at the caudal fin which are not included in this analysis, we found that the robot generates forward thrust in the posterior half of the main body (figure 5). The underlying forces are largely pointed perpendicular (i.e. lateral) to the forward swimming direction such that the ratio of axial and lateral forces equals $0.23\pm 0.11$ (electronic supplementary material, figure S2). The left and right lateral force components cancel each other out on average, which is expected since the flapping motion is symmetric, causing the robot to stay constrained laterally. In the axial direction, however, a net forward thrust force is present that supports the forward acceleration. This net forward thrust oscillates over the course of the manoeuvre with peaks shortly after the maximum lateral tail tip excursion. Drag forces that oppose the direction of movement are also present and predominantly located at the head region (figure 5).

Figure 5.

Power and thrust forces during an acceleration manoeuvre (45% duty cycle, 5.9 Hz tail beat frequency). The four graphs at the top indicate the electrical power input to the robot, mechanical power output to the fluid (excl. caudal fin), axial forces generated (excl. caudal fin) and the centre of mass (COM) forward speed during this representative acceleration from rest. The blue dots and vertical dashed lines denote the same time instance in all graphs indicated by the body images below. The initial rapid increase in power is evident within the first 6 ms, followed by power oscillations starting at around 150 ms. Dashed lines on the mechanical power graph indicate positive (black) and negative (blue) power, where positive power corresponds to the work done by the body on the fluid per time and negative power vice versa. Similar figures for all trials and frequencies are provided in the electronic supplementary material. (Online version in colour.)

(d). Power during robot acceleration

Finally, our experimental platform allowed us to measure electrical power consumption during acceleration manoeuvres. By recording the voltage and current signals during these manoeuvres, we obtained the electrical power input that was provided to the motor of Tunabot Flex. We observed a strong initial power peak that was reached in the first 6 ms across the different frequencies (table 1). Subsequently, the electrical power shows an oscillatory behaviour albeit with smaller peaks (except for 11.59 Hz, 95% duty cycle, table 1) compared to the initial spike (figure 5). In addition, we also computed the mechanical power output (see Methods), which describes how much net work per time is done by the main body of the swimming robot (excluding the caudal fin). Here, we noticed that the mechanical power output has a phase shift and is an order of magnitude smaller than the electrical power input (figure 5, table 1).

4. Discussion

In order to steadily swim (i.e. zero mean acceleration averaged over a tail beat period), fish must first accelerate. Coordinated body and tail movements linearly accelerate the fish forward rapidly. Nearly all previous analyses of linear fish acceleration consider accelerations while transitioning between steady swimming speeds and accelerations from rest have rarely been studied [6]. Fish typically alter their tail beat frequency and amplitude to accelerate between different steady swimming speeds, generating a vortex wake with geometry and orientation that differ from those of steady swimming [1,5,7]. However, the dynamics of fish accelerating from rest are far less understood and have only been studied in lamprey [6]. Using the Tunabot Flex platform, we are able to generate linear accelerations of variable magnitude and analyse the resulting wake flow patterns of fish-like propulsion. Additionally, this robotic system allows us to assess the power transfer from the electrical power consumption of the motor to mechanical power output to the fluid. We achieve this by simultaneously measuring the body kinematics and electrical power input and by calculating the surface pressures of the body and tail. This furthers our understanding of the dynamics of fish linear accelerations from rest before steady swimming is established.

Thunniform swimmers are typically characterized by their narrow peduncle and lunate caudal fin. The caudal fin is thought to produce most of the forward swimming thrust using a lift-based mechanism. We illustrate this mechanism in a separate analysis (electronic supplementary material, figure S3) where we show an example of the tunabot steadily swimming. By carrying out PIV at the quarter span, we found a strong leading-edge vortex (LEV) at the caudal fin. Given the low pressure at the vortex core and the angle of attack of the tail at this time, the LEV most likely makes a significant contribution to forward thrust. In order for this LEV to form, oncoming flow is required in addition to the lateral shedding movement of the leading edge of the caudal fin. When a thunniform swimmer performs linear accelerations from rest this LEV will require some time to form before thrust forward can be generated. In our study, we therefore asked to what extent other parts of the body including the head and body segments before the peduncle can contribute to thrust during linear accelerations. Our analysis of pressure forces revealed that the posterior main body strongly contributes to forward thrust during this manoeuvre. Interestingly, these forces result from a so-called drag-based mechanism that involves the acceleration of adjacent fluid backwards resulting in forward thrust forces. Such drag-based mechanisms are typically found in anguilliform swimmers that exhibit slower swimming speeds. In our study, we show that also a thunniform swimmer benefits from drag-based propulsion at low swimming speeds that occur during linear acceleration from rest.

Our analysis of pressure forces showed that the head segment incurred drag forces and did not generate thrust during linear accelerations. This stands in contrast with steadily swimming fish-like trout [24] that can generate thrust on their anterior body via negative pressures around the head. However, our study investigates accelerations and not steady swimming. Similarly, albeit for a strongly different swimming mode, studies on steadily swimming and accelerating lamprey [6,25] have shown that the corresponding dynamics of thrust generation for these two behaviours are different: the head and anterior body of lamprey generates thrust during steady swimming, but not during acceleration from rest. Nonetheless, our results indicate that linear accelerations from rest appear to use, perhaps exclusively during the acceleration phase, a posterior-body and tail thrust generating mechanism that differs from steady swimming. Detailed analysis of the transition in kinematics and thrust generating mechanisms between the end of acceleration and steady swimming would be a promising area for future study.

Our kinematic analysis showed a minimum of the lateral displacement profiles at 0.3 BL, very close to the centre of the mass location at 0.32 BL, with increased amplitudes at the head and maximal amplitudes at the tail. These amplitude envelopes of Tunabot Flex qualitatively matched the corresponding lateral displacements profiles observed in fish [5,7]. The kinematic analysis further revealed a quadratic relationship between flapping frequency and forward acceleration of Tunabot Flex despite its deliberately constant tail beat amplitude. This is consistent with fish increasing acceleration by increasing tail beat frequency [5]; however, fishes additionally increase their tail beat amplitude to linearly accelerate compared to steady swimming [1,5,6]. In our experiments, the tail beat amplitude was fixed to focus on tail beat frequency changes and isolate their effects on acceleration performance. Variable tail beat amplitudes can be included in testing Tunabot Flex [16], and future experiments will investigate the effect of tail beat amplitude on acceleration performance.

Peak acceleration magnitudes occurred during the 95% duty cycle tests and reached 3.2 m s⁻². This maximum value exceeds the values of less than 2 m s⁻² reported for lamprey in the single study available for fish acceleration from rest [6]. Wen et al. [2] reviewed linear acceleration magnitudes of fish and robotic systems and showed that previously recorded fish linear accelerations ranged from 0.2 to 2.3 m s⁻². Both burst-and-coast swimming, which tends to occur during the highest steady swimming speeds, and fast-start escape responses involve much higher accelerations (up to 15 and 521 m s⁻², respectively) with the highest accelerations observed for fishes with smaller body lengths [2].

In addition to axial thrust and drag forces, we also computed lateral force magnitudes in the main body before the peduncle and found that these forces are about four times larger than the axial forces (electronic supplementary material, figure S2; figure 5). The ratio of lateral to thrust force in fish swimming has been discussed previously in a number of publications. Nauen & Lauder [26] studied the vortex wake structure in swimming mackerel (a tuna relative) and found that the magnitudes of lateral forces were twice those of thrust forces. Relative magnitudes between side and axial forces similar to this have been measured in other species [23]. This may be a consequence of an undulatory propulsive system in which side forces are necessarily relatively large with respect to thrust. But the relatively large values of side forces during Tunabot Flex linear acceleration from rest stand in contrast with the vortex wake observed during acceleration from one speed to another by Akanyeti et al. [5] where a reduction in the ratio of side to thrust force was observed. This suggests that acceleration from rest may involve different dynamics than accelerations to change swimming speed. This conclusion is also supported by the fact that we found drag-based thrust generation during acceleration from rest, whereas accelerations between swimming speeds would likely involve predominantly lift-based mechanisms for thunniform swimmers. Additional analyses of fish accelerating from rest would be valuable in determining the extent to which the vortex patterns differ between these two types of accelerations.

The initial spike in electrical power consumption within the first 6 ms (figure 5; electronic supplementary material, figures) can probably be attributed to electrical effects and inertia. Back electromotive force (emf) voltage of a DC motor is proportional to its angular velocity and is zero upon start-up. This condition allows for large inrush current and a corresponding surge in power consumption as the motor's shaft begins to rotate. This surge is exacerbated by the inertia of the stationary robot and surrounding fluid that the shaft must overcome. The back emf voltage rapidly increases as the motor's shaft accelerates and body actuation begins, causing the electrical power to decrease again in a matter of milliseconds. After the transition from linear acceleration to steady swimming, electrical power consumption decreases while mechanical power output increases, and both begin to oscillate around consistent mean values. The tail then beats back to the opposite side to complete the first full beat. At this time, forward motion has begun (figures 3 and 5). Energy demands decrease when the oscillatory pattern seen during steady swimming begins (figure 5).

Mechanical power output to the fluid stemming from the main body via drag-based forces was only about 5% of the electrical input power on average. In addition, we expect that lift-based forces at the tail contribute to mechanical power output and also play an important role during acceleration, albeit not as strong during acceleration from rest compared to steady swimming. Lift-based forces at the tail as the LEV forms require time for the flow to separate and roll up on the tail surface during the first beats, and thrust resulting from the LEV probably only begins to contribute to overall thrust after one to two tail beats have occurred. These lift-based forces and the associated mechanical output power of the caudal fin could be estimated in future work by analysing more planar flow fields at different span sections and using interpolation. Furthermore, we are not aware of other experimental systems capable of simultaneously measuring electrical power input and computing the mechanical output to the fluid through body surface calculations. This approach allows the effectiveness of mechanical swimming designs to be evaluated and betters our understanding of the overall propulsion dynamics. As such, we suggest that the approach demonstrated herein may be an important future direction for research in aquatic locomotion.

Data accessibility

Data used in this study, electronic supplementary material figures and movies are available on figshare: https://doi.org/10.6084/m9.figshare.c.5192591.

Authors' contributions

Conceptualization was done by R.T., G.V.L. and C.H.W.; methodology and experimental data acquisition were done by R.T., G.V.L. and C.H.W.; software was done by R.T.; formal analysis was done by R.T.; the original draft was written by R.T.; review and editing were done by R.T., G.V.L., C.H.W. and H.B.-S.; visualization was done by R.T.; funding acquisition was done by R.T., G.V.L. and H.B.-S. All authors gave final approval for publication and agree to be held accountable for the work performed therein.

Competing interests

The authors declare no competing or financial interests.

Funding

This research was funded by a Swiss National Science Foundation Early Postdoc Mobility Fellowship (P2ELP3_181755) to R.T., Office of Naval Research grant no. N000141410533 to G.V.L, N00014-15-1-2234 to H.B.-S. and G.V.L. and the David and Lucile Packard Foundation to H.B.-S.