Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 May 25;6(22):14639–14647. doi: 10.1021/acsomega.1c01747

Effects of Strain and Electric Field on Molecular Doping in MoSSe

Jincheng Zeng 1, Gang Liu 1,*, Yu Han 1, Wenwei Luo 1, Musheng Wu 1, Bo Xu 1, Chuying Ouyang 1
PMCID: PMC8190909  PMID: 34124487

Abstract

graphic file with name ao1c01747_0011.jpg

Recently, synthesized Janus MoSSe monolayers have attracted tremendous attention in science and technology due to their novel properties and promising applications. In this work, we investigate their molecular adsorption-induced structural and electronic properties and tunable doping effects under biaxial strain and external electric field by first-principles calculations. We find an effective n-type or p-type doping in the MoSSe monolayer caused by noncovalent tetrathiafulvalene (TTF) or tetracyanoquinodimethane (TCNQ) molecular adsorption. Moreover, the concentration of doping carrier with respect to the S or Se side also exhibits Janus characteristics because of the electronegativity difference between S and Se atoms and the intrinsic dipole moment in the MoSSe monolayer. In particular, this n-type or p-type molecular doping effect can be flexibly tuned by biaxial strain or under external electric field. By analyzing the valence band maximum (VBM) and conduction band minimum (CBM) in the band structure of MoSSe/TTF under strain, the strain-tunable band gap of MoSSe and the n-type molecular doping effect is revealed. Further explanation of charge transfer between TTF or TCNQ and the MoSSe monolayer by an equivalent capacitor model shows that the superimposition of external electric field and molecular adsorption-induced internal electric field plays a crucial role in achieving a controllable doping concentration in the MoSSe monolayer.

1. Introduction

Two-dimensional (2D) transition-metal dichalcogenides (TMDs) MX2 (M = Mo, W; X = S, Se, and Te) have attracted great interest in nanoelectronic and nano-optoelectronic devices due to their excellent physical and chemical properties, such as superior stability,1 high carrier mobility,2 strong spin–orbit coupling effects,3 and proper band gap values (1–3 eV) with a visible range of electromagnetic spectrum.4 In particular, benefiting from their atomic-scale thicknesses and sizeable band gaps, these materials provide a possibility to realize the electrostatic control in the field-effect transistors (FETs), and because of this reason they have been proposed as potential alternatives for next-generation semiconductor devices. For instance, transport with an excellent Ion/Ioff switching ratio (∼108) and a carrier mobility of up to 200 cm2/(V s) at room temperature has been observed in MoS2-based transistors.2 Other research efforts also have been devoted to explore the use of WS2, MoSe2, and WSe2 as active layers in FETs.5−7

For manufacturing transistors and p–n junctions with reproducible electrical characteristics or minimizing detrimental Schottky barriers at metal–semiconductor interfaces, one of the most important challenges is how to achieve a systematic control over charge-carrier type and doping level in these materials. Undoubtedly, conventional doping techniques, such as ion implantation and dopant diffusion, are unsuitable for these ultrathin crystals because the doping processes would greatly and unavoidably damage their structures and electronic properties. Thus, it is very urgent to look for some alternatives to realize this one goal. Compared with alloying,8 transition-metal and chalcogen substitution,9,10 and plasma-assisted doping,11 noncovalent molecular adsorption12,13 on these 2D semiconductor surfaces performs better due to its effectiveness and safety. In fact, many molecular approaches based on noncovalent interactions between molecules and TMDs have been reported in the last few years. Experimentally, Kiriya et al. reported an effective n-type doping in MoS2 by benzyl viologen (BV) adsorption14 and obtained a high electron sheet density of ∼1.2 × 1013 e/cm2. By BV doping of MoS2 at the metal junctions, the contact resistances were shown to be reduced by a factor of >3. Moreover, de la Rosa et al. demonstrated an effective doping in MoS2 thin-film field-effect transistors by oleylamine molecular adsorption.15 The doping of the MoS2 FETs induced an increase of Ion by an average factor of 1.9 in a set of nine devices by increasing the carrier concentration while not changing the mobility of the device. Theoretically, as typical electron donor and acceptor (EDA) molecules, tetrathiafulvalene (TTF) and tetracyanoquinodimethane (TCNQ) are widely used to act as ideal carriers due to their electrophilic or electrophobic characteristics. For instance, Y. Jing et al. investigated molecular doping induced by the adsorption of four organic molecules, including TCNQ, tetracyanoethylene (TCNE), TTF, and benzyl viologen (BV), on the basal plane of the MoS2 monolayer.16 Besides these, TMD sheets were also indicated to be highly sensitive to a large number of molecules, such as oleylamine, DNA, octadecyltrichlorosilane, and so on.15,17,18 All of these studies clearly demonstrate that the use of molecular adsorption on the TMD monolayer is emerging as a promising nondestructive method not only for controlling the charge-carrier doping in these 2D semiconductor materials but also for tailoring their optical properties and imparting them novel functionalities.

Recently, a well-organized Janus MoSSe monolayer with 2H phase was successfully synthesized by fully replacing the S (Se) layers with Se (S) atoms within MoS2 (MoSe2) at an appropriate temperature through the chemical vapor deposition method.19,20 Unlike 2D MX2 such as MoS2 with mirror symmetry, the Janus MoSSe monolayer reveals an intrinsic out-of-plane dipole moment due to the mirror asymmetry, leading to some different electronic properties from MX2, such as large Rashba band splitting and out-of-plane piezoelectricity.21,22 Motivated by the successful experimental synthesis of MoSSe, increasingly more research focuses on engineering the properties of MoSSe by stacking, adsorbing atoms or molecules, combining with other 2D materials to form heterostructures, applying external strain or electrical field, and so on,23−31 aiming to tailor its physical and chemical properties for practical applications. However, the molecular adsorption-induced doping effect in MoSSe has yet to be explored. Due to the two different chalcogenide sides in the Janus MoSSe monolayer, it is expected that MoSSe would possess several advantages over MoS2, such as enhanced sensitivity, higher charge-carrier concentration induced by its interior dipole moment, and tunable selectivity originating from its Janus structure, making it more suitable and flexible for acting as an active layer in nanoelectronic devices.

In this work, we investigate the effects of TTF and TCNQ molecular adsorption on the structural and electronic properties of the Janus MoSSe monolayer by first-principles calculations. We find that the noncovalent molecular adsorption of TTF or TCNQ on the MoSSe monolayer could introduce a donor state or an acceptor state into the band structure of MoSSe, resulting in a typical n-type or p-type doping effect. Interestingly, the carrier doping concentration induced by molecular adsorption is greatly dependent on the side of MoSSe. Moreover, this molecular adsorption-induced n-type or p-type doping effect can be flexibly tuned using biaxial strain or applying an external electric field. These findings could raise promising prospects of developing new Janus MoSSe-based nanodevices, such as FETs or sensors.

2. Results and Discussion

2.1. Molecular Adsorption of TTF on Different Sides of MoSSe

A 6 × 6 × 1 supercell of MoSSe monolayer is selected for acting as an adsorption substrate because the size of the 6 × 6 × 1 supercell is large enough to avoid the image influence due to the boundary conditions. The lattice constants of its unit cell are a = 3.250 Å and Δ = 3.233 Å, as shown in Figure S1a. Here, Δ is defined as the difference between S and Se atoms along the Z direction in the MoSSe monolayer. The bond lengths of Mo–S and Mo–Se are 2.423 and 2.538 Å, respectively. The angle of S–Mo–Se is 81.29°. These parameters are consistent with previous reports.32 The band gap of 1.545 eV clearly shows the semiconductor characteristics, as shown in Figure S1b.

Due to the asymmetric structure of MoSSe, there are two adsorption sides for the TTF molecule, named S and Se sides. Four typical adsorption sites based on the symmetrically geometrical structure of the TTF molecule are considered in our calculations for the S side as well as for the Se side, which are hollow site (molecular center located above the center of a hexagon in MoSSe), top site (molecular center located above the S or Se atom), bridge site (molecular center located above the midpoint of Mo–S or Mo–Se bond), and valley site (molecular center located above the Mo atom). Moreover, considering the graphene-liked structure of MoSSe, there are eight initial adsorption configurations of the TTF molecule on MoSSe, as shown in Figure S2, which can be denoted H1, H2, T1, T2, B1, B2, V1, and V2 sites. By comparing the adsorption energies of TTF under different adsorption sites, the most stable adsorption configurations of TTF on the S or Se side are obtained, as shown in Figure 1a,e. Here, the adsorption energy is defined as the energy difference between the total energy of reactants and the energy of product, which can be described as follows

2.1. 1

where EMoSSe, ETTF, and EMoSSe+TTF are the energies of isolated MoSSe, isolated molecule TTF, and TTF-adsorbed MoSSe, respectively.

Figure 1.

Figure 1

Open in a new tab

(a) Most stable adsorption configuration of TTF on the S side of the MoSSe monolayer. (b) Band structure of TTF/SMoSe. (c) Differential charge density of TTF/SMoSe. (d) HOMO of TTF/SMoSe. (e) Most stable adsorption configuration of TTF on the Se side of the MoSSe monolayer. (f) Band structure of TTF/SeMoS. (g) Differential charge density of TTF/SeMoS. (h) HOMO of TTF/SeMoS.

In Figure 1a,e, one can clearly see that the favorable adsorption site of TTF on the S side is H site, while it is V site on the Se side. The adsorption distance (defined as the difference between the molecular center and the average of the substrate along the Z direction) of TTF on the S side is 3.00 Å, and its corresponding adsorption energy is 0.82 eV. In contrast, the adsorption energy and the adsorption distance of TTF on the Se side are 0.85 eV and 3.62 Å, respectively. Due to the considerable adsorption distance of TTF on the S or Se side, there only exists weakened interaction between the TTF and substrate MoSSe. Thus, the structural and electronic properties of MoSSe are slightly influenced by the adsorption of TTF. For the case of S side-adsorbed TTF, the band structure of MoSSe/TTF is changed somewhat compared with its freestanding state except for the decrease in band gap from 1.545 to 1.536 eV. However, it is worthwhile to note that there exists a flat energy dispersion between valence band maximum (VBM) and conduction band minimum (CBM) below the Fermi level, as shown in Figure 1b, resulting in a typical donor energy state in the band structure of MoSSe. To investigate the origin of this flat energy dispersion, we calculate the highest occupied molecular orbital (HOMO) and find that the charge basically surrounds the TTF molecule, as seen in the graphical representation of HOMO in Figure 1d. It shows that the flat energy dispersion below the Fermi level is contributed by the TTF molecule. To further illustrate this donor energy state induced by TTF, we plot the differential charge density of MoSSe/TTF, as shown in Figure 1c. Here, the differential charge density is defined as follows

2.1. 2

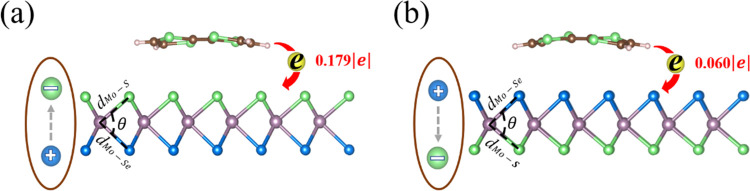
where ρMoSSe and ρTTF are the isolated charge densities of MoSSe and TTF, respectively, and ρMoSSe/TTF is the total charge density of TTF-adsorbed MoSSe. Obviously, the charge transfers from the TTF molecule to MoSSe, resulting in TTF losing the charge and MoSSe gaining it. Moreover, a numerical value of 0.179 electron in Bader analysis also shows the charge transfer. Therefore, as a typical electron donor, the TTF molecule transfers the charge from itself to MoSSe and then provides a filled band with the highest occupied energy, in favor of forming an n-type doping effect in MoSSe. In addition, the energy difference between the filled band maximum of the dopant and the conduction band minimum for electron excitation (defined as En) is only 0.017 eV. It implies that, even under room temperature, the electron would easily excite from the highest occupied state to the conduction band. More importantly, the charge transfer of 0.179 e from TTF to MoSSe further indicates that the order of magnitude for carrier doping induced by TTF in MoSSe is high, up to ∼1013 cm2, which is similar to the case of benzyl viologen (BV) doping in MoS2.14 Such a high concentration of carrier doping and such a low energy gap for the electron excitation would be very helpful for designing MoSSe-based sensors or optoelectronic devices.

Similar to the case of TTF adsorbed on the S side, the structural and electronic properties of MoSSe-adsorbed TTF on the Se side are also changed barely. From Figure 1e–h, it can be seen that the band gap of 1.538 eV is almost unchanged compared with the case of TTF adsorbed on the S side (1.536 eV). Moreover, the n-type molecular doping induced by noncovalent molecular adsorption can also be achieved. Meanwhile, TTF still acts as an electron donor. However, the En value of 0.635 eV is much higher than that of 0.017 eV in the S side case, while the charge transfer between MoSSe and TTF is only 0.06 e. This indicates that the concentration of carrier doping in MoSSe is highly dependent on the adsorption side for the TTF molecule, and the molecular doping effect also exhibits Janus characteristics like its geometrical structure.

To deeply understand the difference of charge transfer between TTF and MoSSe under different adsorption sides, we plot the diagrammatic sketch of charge transfer between MoSSe and TTF on S and Se sides, which can be seen in Figure 2a,b. As we know, sulfur and selenium both belong to the same main group. However, the electronegativity of S is greater than that of Se due to the difference in atomic radius. Thus, when TTF adsorbs on the S side, more charge would be transferred from TTF to the MoSSe surface. Moreover, the intrinsic dipole moment pointed from the Se to S side in MoSSe maybe also plays a key role in the process of charge transfer and redistribution. When the direction of charge transfer between TTF and MoSSe is opposite to the direction of intrinsic dipole moment, the total potential difference for transferred electrons would be increased, which would promote the charge transfer from TTF to MoSSe, as shown in Figure 2a. On the contrary, when the direction of charge transfer between TTF and MoSSe is the same as the direction of intrinsic dipole moment, the total potential difference for transferred electrons would be decreased, which would restrain the charge transfer from TTF to MoSSe, as shown in Figure 2b. Thus, the charge transfer of TTF adsorbed on the S side is much higher than in the case of TTF adsorbed on the Se side.

Figure 2.

Figure 2

Open in a new tab

Intrinsic dipole moment in MoSSe and the charge transfer between MoSSe and TTF on the (a) S side and (b) Se side.

Until now, we can confirm that, compared with the adsorption energy of 0.67 eV, the adsorption distance is 3.04 Å and charge transfer is 0.13 e in the case of TTF adsorbed on MoS2.33 MoSSe actually exhibits some advantages over MoS2, such as higher adsorption energy of 0.82/0.85 eV on the S/Se side (enhanced sensitivity), higher charge transfer of 0.179 e on the S side (higher charge-carrier concentration), and tunable selectivity originated from its Janus structure. Thus, it may be more suitable and flexible for acting as an active layer in nanoelectronic devices.

2.2. Strain-Tunable Molecular Doping Induced by TTF in MoSSe

It is well known that the tunable molecular doping effects induced by TTF in MoSSe, including the concentration of carrier doping and the energy difference for the electron excitation, are very important for its potential applications. Thus, we expect to find an efficient way to achieve this goal. In previous reports, we note that the biaxial strain can flexibly tune the band structure of MoSSe because the hybridization between electronic states of Mo atoms and S or Se atoms would be changed along with the biaxial strain.34 Therefore, we attempt to tune this n-type doping effect as well as the band structure of MoSSe/TTF using biaxial strain. Considering the stronger doping effect of TTF on the S side and the actual strain realized in experiment,35 a biaxial strain ranging from −3 to 1% is applied to investigate the strain-tunable molecular doping of TTF adsorbed on the S side.

Figure 3 depicts the band structures of MoSSe/TTF under the biaxial strain ranging from −3 to 1%. It is found that, when tensile strain of 1% is applied, Eg (the energy difference between VBM and CBM at the Γ point in the band structure of MoSSe) is decreased from 1.536 to 1.324 eV. However, the CBM at the Γ point passes through the Fermi level, resulting in MoSSe/TTF exhibiting metal characteristics, as shown in Figure 3e. In contrast, when a compressive strain of 1% is applied, Eg is increased from 1.536 to 1.657 eV and En is also increased from 0.017 to 0.161 eV, as shown in Figure 3c. With a further increase in the compressive strain from 1 to 3% (seen in Figure 3a–c) Eg is decreased from 1.657 to 1.571 eV instead. The corresponding En values under different compressive strains ranging from 1 to 3% are 0.161, 0.188, and 0.175 eV. Compared with the case of 0.017 eV without strain (seen in Figure 3d), the En value of 0.188 eV under the biaxial strain of −2% means that a relatively broad emission spectrum over the visible wavelengths can be obtained under biaxial strain, which is useful for designing the organic electroluminescence based on MoSSe/TTF. Moreover, from the different values of Eg under biaxial strain ranging from −3 to 1% (seen in Figure 3f), we find that it is similar to the previous report of freestanding MoSSe under biaxial strain.34 Maybe because there only exists noncovalently weakened interaction between TTF and MoSSe, the Eg value of MoSSe/TTF under biaxial strain only changes like its freestanding case. Besides the strain-tunable Eg and En values, the concentration of doping carrier can also be tuned by strain. In particular, it can be changed suddenly under a tensile strain of 1%. The corresponding concentration of doping carrier can be increased up to 0.721 × 1013/cm2. This sudden change just corresponds to the transition of MoSSe/TTF from semiconductor to metal and it maybe plays a fundamental role for this transition.

Figure 3.

Figure 3

Open in a new tab

(a–e) Band structures of MoSSe/TTF (S side) under the biaxial strain ranging from −3 to 1%. (f) En, Eg, and concentration of doping carrier as a function of biaxial strain ranging from −3 to 1%.

What is the underlying mechanism for strain-tunable electronic properties of MoSSe/TTF? To reveal the intrinsic essence, we calculate the structural parameters of MoSSe/TTF under different strains (seen in Table S1) and then we plot Figure 4 to explain it. Because the largest band gap of MoSSe/TTF is only increased under the biaxial strain of −1% while the others are both decreased, we start the analysis from this case. Figure 4 shows the electronic properties of MoSSe including PDOS and partial charge densities of VBM and CBM at the Γ point under biaxial strains of −1, 0, and 1%, respectively.

Figure 4.

Figure 4

Open in a new tab

(a–c) PDOS and partial charge densities of VBM and CBM at the Γ point of MoSSe/TTF under biaxial strains of −1, 0, and 1%, respectively.

From Figure 4a, one can clearly see that the VBM in the band structure of MoSSe is mainly contributed by the in-plane orbital dx2–y2 of Mo atoms while the CBM is originated from the hybridization of vertical orbital dz2 and in-plane orbital dx2–y2 of Mo atoms. When tensile strain is applied, the bond length of Mo–S is elongated while the distance between S and Se atoms as well as the angle of S–Mo–Se are reduced. That is to say, S atoms shift down to the plane of Mo atoms and then the overlapping of vertical orbitals composed of S pz and Mo dz2 would be strengthened, resulting in the fact that the bandwidth of vertical orbitals is widened. Thus, the energy levels of S pz and Mo dz2 in the valence band both shift up to the Fermi level, while the energy level of Mo dz2 in the conduction band drops down to the Fermi level. When the energies of S pz and Mo dz2 in the valence band exceed the energy of Mo dx2–y2 ultimately, the VBM is contributed by vertical orbitals S pz and Mo dz2 instead of the in-plane orbitals Mo dx2–y2. Simultaneously, the CBM is only contributed by vertical orbitals Mo dz2 instead of the hybridization of Mo dz2 and Mo dx2–y2, as shown in Figure 4b. Further increasing the tensile strain to 1%, the CBM even passes through the Fermi level and the system exhibits metal characteristics, as shown in Figure 4c. Meanwhile, the interaction between in-plane Mo atoms becomes more weakened, which would further narrow the bandwidth of in-plane orbitals Mo dx2–y2. Therefore, the energy of Mo dx2–y2 orbitals shifts far away from the Fermi level, only leaving Mo dz2 near the Fermi level. For the case of compressive strain exceeding 1%, an opposite trend for the shift of these energy levels can be observed.

2.3. Electric Field-Tunable Molecular Doping Induced by TTF in MoSSe

Except for using biaxial strain to tune the electronic properties of MoSSe, applying an external electric field is another effective way.36 To find the effect of the electric field on the electronic properties of MoSSe/TTF and molecular doping, we apply an external electric field ranging from −0.2 to 0.2 V/Å to MoSSe/TTF. The corresponding band structures of MoSSe/TTF can be seen in Figure 5. The band gaps of MoSSe/TTF are 1.549, 1.544, 1.536, and 1.535 eV under an external electric field ranging from −0.2 to 0.1 V/Å and the corresponding En values are 0.216, 0.064, 0.017, and 0.011 eV, as shown in Figure 5a–d.

Figure 5.

Figure 5

Open in a new tab

(a–e) Band structures of MoSSe/TTF (on S side) under the external electric field ranging from −0.2 to 0.2 V/Å. (f) En, Eg, and concentration of doping carrier as a function of external electric field ranging from −0.2 to 0.2 V/Å.

When a positive electric field of 0.2 V/Å is applied, the CBM can pass through the Fermi level, exhibiting metal characteristics like the case under biaxial strain of 1%, as shown in Figure 5e. In the whole range from −0.2 to 0.2 V/Å, we can see that both Eg and En are monotonously decreased with increasing electric field while the concentration of doping carrier can be almost linearly tuned by the external electric field, as shown in Figure 5f. Compared with the fact that Eg is nonmonotonic under the biaxial strain ranging from −3 to 1%, the monotonicity of Eg under the external electric field can be understood by the change of the MoSSe/TTF structure in a different way. When we use biaxial strain to tune the electronic properties of MoSSe, the distance between S and Se atoms is evidently changed. Thus, the CBM and VBM are also changed accordingly due to the contribution of different orbitals and the shifts of their energy levels. On the contrary, the distance between S and Se atoms is almost unchanged under different electric fields, resulting in that the CBM and VBM are still retained like the case without the external electric field, which can be seen from Figure 5a–e. The external electric field only plays an important role for changing the potential energy and adjusting the energy levels of MoSSe/TTF with respect to vacuum level.

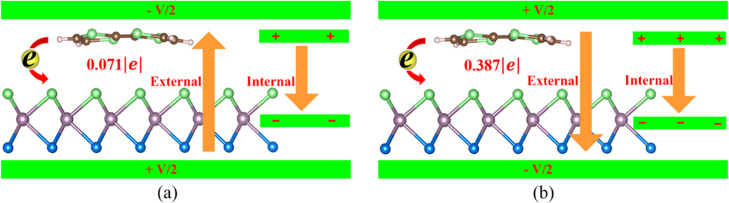
To explain the different values of Eg and En under the external electric field ranging from −0.2 to 0.2 V/Å, we plot the energies of CBM, VBM, and TTF with respect to Fermi level under different electric fields, as shown in Figure 6. It can be seen that, when a positive electric field of 0.1 V/Å is applied, the corresponding energy of CBM is 0.001 eV, while that of VBM is −1.534 eV. In contrast, when negative electric fields of 0.1 and 0.2 V/Å are applied, the corresponding energies of CBM are 0.030 and 0.172 eV, while those of VBM are −1.514 and −1.377 eV. Accordingly, the Eg value is decreased monotonously under the electric field ranging from −0.2 to 0.2 V/Å. Meanwhile, the amount of charge transferred from TTF to MoSSe is increased from 0.071e to 0.387 e when the external electric field ranging from −0.2 to 0.2 V/Å is applied. Thus, the energy of TTF becomes closer to the Fermi level.

Figure 6.

Figure 6

Open in a new tab

Energies of CBM, VBM, and TTF with respect to Fermi level under the external electric field ranging from −0.2 to 0.2 V/Å.

To further explain the electric field-tunable charge transfer between TTF and MoSSe, we use an equivalent capacitor model to illustrate it, as shown in Figure 7. As we know, when TTF adsorbs on the MoSSe surface, the charge of 0.179 e is transferred from TTF to MoSSe. It means that TTF loses the charge while MoSSe gains the charge. In other words, TTF is tantamount to schlepping positive charge while MoSSe is tantamount to schlepping negative charge. Thus, the direction of molecular adsorption-induced internal electric field in MoSSe/TTF is pointed from TTF to MoSSe. When an external electric field of −0.2 V/Å that has an opposite direction to the internal electric field is applied to MoSSe/TTF, it would restrain the charge transfer, as shown in Figure 7a. Thus, the amount of charge transfer between MoSSe and TTF would be decreased from 0.179 to 0.071 e compared with the case without the external electric field. In contrast, when an external electric field of 0.2 V/Å which has the same direction as internal electric field is applied to MoSSe/TTF, it would promote the charge transfer, as shown in Figure 7b. Accordingly, the amount of charge transfer between MoSSe and TTF is increased from 0.179 e to 0.387 e and the corresponding concentration of doping carrier is increased from 0.542 × 1013 to 1.172 × 1013/cm2, resulting in more positive and negative electric charges distributing on two polar plates of the equivalent plate capacitor. In addition, the amount of charge transfer is proportional to the strength of the superimposed electric field composed of internal and external electric fields, and this has been demonstrated in previous reports.36 Thus, the concentration of doping carrier, which corresponds to the amount of charge transfer between TTF and MoSSe, can be almost linearly tuned by the external electric field.

Figure 7.

Figure 7

Open in a new tab

(a, b) Mechanism of charge transfer between MoSSe and TTF under a negative or positive external electric field of 0.2 V/Å. An equivalent capacitor model of TTF/MoSSe and the sketch of charge transfer are inserted into the diagrammatic sketch for explaining the process. The direction of internal electric field always points from TTF to MoSSe.

2.4. Molecular Adsorption of TCNQ on MoSSe

As a typical electron acceptor, TCNQ can also noncovalently adsorb on the MoSSe surface like TTF, and it can induce a p-type doping effect in MoSSe. However, the molecular doping of TCNQ is in favor of the Se side instead of the S side, which is different from the case of TTF. The most stable adsorption site of TCNQ on the Se side is T1 site, which can be seen in Figure S3. Moreover, the biaxial strain ranging from −2 to 2% and the external electric field ranging from −0.2 to 0.2 V/Å can also flexibly tune the electronic properties of MoSSe/TCNQ. The strain-tunable Ep, Eg, and concentration of doping carrier are shown in Figure 8. The corresponding band structures of MoSSe/TCNQ (Se side) under biaxial strain can be seen in Figure S4.

Figure 8.

Figure 8

Open in a new tab

Ep, Eg, and concentration of doping carrier as a function of biaxial strain ranging from −2 to 2%.

It is found that the largest band gap of 1.658 eV is also increased under the biaxial strain of −1%, similar to the case of TTF. Moreover, if the strain is larger or smaller than −1%, the band gap of MoSSe/TCNQ would be both decreased. In addition, like the variation trend of Eg, Ep can be increased from 0.033 to 0.036 eV under the strain changing from −2 to 0% and then can be decreased from 0.036 to 0.009 eV under the strain changing from 0 to 2%. The biaxial strain of 0% just corresponds to the break point over the whole range. Compared with Eg and Ep, the strain-tunable concentration of doping carrier looks much more interesting. The fact is that not only can the compressive strain linearly tune the doping concentration but also the tensile strain can do it.

With respect to the effects of the electric field on the electronic properties of MoSSe/TCNQ, one can clearly see that Eg and the concentration of doping carrier can be linearly modulated by applying an external electric field ranging from −0.2 to 0.2 V/Å, as shown in Figure 9. The band structures of MoSSe/TCNQ (Se side) under the external electric field can be seen in Figure S5. The intrinsic mechanism of the tunable electric field can also be explained like the case of TTF under the electric field. In addition, the concentration of doping carrier induced by TCNQ can be as high up to 1.13 × 1013/cm2 under the electric field of 0.2 V/Å.

Figure 9.

Figure 9

Open in a new tab

Ep, Eg, and concentration of doping carrier as a function of external electric field ranging from −0.2 to 0.2 V/Å.

3. Conclusions

In this paper, the effects of TTF and TCNQ adsorption on the electric properties of MoSSe and the strain/electric field-tunable molecular doping are systematically studied using the first-principles calculation. The results show that both TTF and TCNQ molecules could noncovalently interact with MoSSe and they can induce a typical n-type or p-type doping in MoSSe. More importantly, the concentration of doping carrier induced by the same molecular adsorption is greatly dependent on the side of MoSSe, which also exhibits Janus characteristics like its structure. In addition, the n-type or p-type doping effect induced by TTF or TCNQ molecular adsorption can be flexibly tuned by using a biaxial strain or applying an external electric field. By analyzing the orbital contribution of Mo and S atoms, it is found that the in-plane Mo dx2–y2 orbitals and the vertical S pz and Mo dz2 orbitals play a crucial role in the band structure of MoSSe/TTF, similar to the case of freestanding MoSSe under biaxial strain. To further reveal the intrinsic mechanism of electric field-tunable concentration of doping carrier, the equivalent capacitor model is used for illustrating the process of charge transfer. The fact is that the superimposed electric field composed of the internal electric field induced by molecular adsorption and the external electric field would play a key role in tuning the charge transfer between the adsorbate and substrate. Such multiple effects of biaxial strain and external electric field on the electronic properties of MoSSe/TTF or MoSSe/TCNQ would greatly facilitate further experimental studies on this intriguing 2D material for more potential applications in the future.

4. Computational Methods

Our first-principles calculations were based on density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP)37 and with the projector augmented-wave (PAW) approach.38 The exchange–correlation interaction was treated within the generalized gradient approximations (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional.39 The freestanding MoSSe was modeled with a 6 × 6 × 1 supercell, which was separated with a 20 Å vacuum layer in the z-axis direction to avoid the interaction between two adjacent images. A plane-wave basis set with a cutoff energy of 470 eV was used for the valence electron wave functions. The entire systems were relaxed by the conjugate gradient method until the force on each atom was less than 0.02 eV/Å. The corresponding Monkhorst–Pack k point meshes40 were used with grid sizes of 2 × 2 × 1 for structural relaxation and 5 × 5 × 1 for electronic structure computations. The effect of van der Waals (vdW) interaction was included by using the DFT-D2 correction method proposed by Grimme,41 which was a good description of long-range vdW interactions. The Bader charge analysis was used to illustrate the charge transfer between the adsorbate and substrate.42

Acknowledgments

This work was financially supported by the National Natural Science Foundation of China (grant nos. 11664013 and 11664012).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01747.

  • Description of a 6 × 6 × 1 supercell for MoSSe including its geometrical and band structures and the electronic properties of MoSSe/TCNQ under strain and external electric field (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao1c01747_si_001.pdf (607.7KB, pdf)

References

  1. Ataca C.; Sahin H.; Ciraci S. Stable, Single-Layer MX2 Transition-Metal Oxides and Dichalcogenides in a Honeycomb-Like Structure. J. Phys. Chem. C 2012, 116, 8983–8999. 10.1021/jp212558p. [DOI] [Google Scholar]
  2. Radisavljevic B.; Radenovic A.; Brivio J.; Giacometti V.; Kis A. Single-layer MoS2 transistors. Nat. Nanotechnol. 2011, 6, 147–150. 10.1038/nnano.2010.279. [DOI] [PubMed] [Google Scholar]
  3. Cheng Y. C.; Zhu Z. Y.; Tahir M.; Schwingenschlogl U. Spin-orbit-induced spin splittings in polar transition metal dichalcogenide monolayers. Europhys. Lett. 2013, 102, 57001 10.1209/0295-5075/102/57001. [DOI] [Google Scholar]
  4. Feng J.; Qian X. F.; Huang C. W.; Li J. Strain-engineered artificial atom as a broad-spectrum solar energy funnel. Nat. Photonics 2012, 6, 866–872. 10.1038/nphoton.2012.285. [DOI] [Google Scholar]
  5. Fang H.; Chuang S.; Chang T. C.; Takei K.; Takahashi T.; Javey A. High-Performance Single Layered WSe2 p-FETs with Chemically Doped Contacts. Nano Lett. 2012, 12, 3788–3792. 10.1021/nl301702r. [DOI] [PubMed] [Google Scholar]
  6. Hwang W. S.; Remskar M.; Yan R. S.; Protasenko V.; Tahy K.; Chae S. D.; Zhao P.; Konar A.; Xing H. L.; Seabaugh A. Transistors with chemically synthesized layered semiconductor WS2 exhibiting 105 room temperature modulation and ambipolar behavior. Appl. Phys. Lett. 2012, 101, 013107 10.1063/1.4732522. [DOI] [Google Scholar]
  7. Larentis S.; Fallahazad B.; Tutuc E. Field-effect transistors and intrinsic mobility in ultra-thin MoSe2 layers. Appl. Phys. Lett. 2012, 101, 223104 10.1063/1.4768218. [DOI] [Google Scholar]
  8. Zhang M.; Wu J. X.; Zhu Y. M.; Dumcenco D. O.; Hong J. H.; Mao N. N.; Deng S. B.; Chen Y. F.; Yang Y. L.; Jin C. H.; Chaki S. H.; Huang Y. S.; Zhang J.; Xie L. M. Two-Dimensional Molybdenum Tungsten Diselenide Alloys: Photoluminescence, Raman Scattering, and Electrical Transport. ACS Nano 2014, 8, 7130–7137. 10.1021/nn5020566. [DOI] [PubMed] [Google Scholar]
  9. Tedstone A. A.; Lewis D. J.; O’Brien P. Synthesis, Properties, and Applications of Transition Metal-Doped Layered Transition Metal Dichalcogenides. Chem. Mater. 2016, 28, 1965–1974. 10.1021/acs.chemmater.6b00430. [DOI] [Google Scholar]
  10. Lin Z.; Carvalho B. R.; Kahn E.; Lv R.; Rao R.; Terrones H.; Pimenta M. A.; Terrones M. Defect engineering of two-dimensional transition metal dichalcogenides. 2D Mater. 2016, 3, 022002 10.1088/2053-1583/3/2/022002. [DOI] [Google Scholar]
  11. Wi S.; Kim H.; Chen M. K.; Nam H.; Guo L. J.; Meyhofer E.; Liang X. G. Enhancement of Photovoltaic Response in Multilayer MoS2 Induced by Plasma Doping. ACS Nano 2014, 8, 5270–5281. 10.1021/nn5013429. [DOI] [PubMed] [Google Scholar]
  12. Pang Q.; Li L.; Gao D.-l.; Chai R.-p.; Zhang C.-l.; Song Y.-l. Tuning the electronic and magnetic properties of germanene by surface adsorption of small nitrogen-based molecules. Phys. E 2017, 88, 237–242. 10.1016/j.physe.2017.01.018. [DOI] [Google Scholar]
  13. Wang X.; Liu G.; Liu R. F.; Luo W. W.; Wu M. S.; Sun B. Z.; Lei X. L.; Ouyang C. Y.; Xu B. Strain-tunable molecular doping in germanane: a first-principles study. Nanotechnology 2018, 29, 465202 10.1088/1361-6528/aae046. [DOI] [PubMed] [Google Scholar]
  14. Kiriya D.; Tosun M.; Zhao P. D.; Kang J. S.; Javey A. Air-Stable Surface Charge Transfer Doping of MoS2 by Benzyl Viologen. J. Am. Chem. Soc. 2014, 136, 7853–7856. 10.1021/ja5033327. [DOI] [PubMed] [Google Scholar]
  15. de la Rosa C. J. L.; Phillipson R.; Teyssandier J.; Adisoejoso J.; Balaji Y.; Huyghebaert C.; Radu I.; Heyns M.; De Feyter S.; De Gendt S. Molecular doping of MoS2 transistors by self-assembled oleylamine networks. Appl. Phys. Lett. 2016, 109, 253112 10.1063/1.4972781. [DOI] [Google Scholar]
  16. Jing Y.; Tan X.; Zhou Z.; Shen P. W. Tuning electronic and optical properties of MoS2 monolayer via molecular charge transfer. J. Mater. Chem. A. 2014, 2, 16892–16897. 10.1039/C4TA03660C. [DOI] [Google Scholar]
  17. Kang D. H.; Shim J.; Jang S. K.; Jeon J.; Jeon M. H.; Yeom G. Y.; Jung W. S.; Jang Y. H.; Lee S.; Park J. H. Controllable Nondegenerate p-Type Doping of Tungsten Diselenide by Octadecyltrichlorosilane. ACS Nano 2015, 9, 1099–1107. 10.1021/nn5074435. [DOI] [PubMed] [Google Scholar]
  18. Zhang Y.; Zheng B.; Zhu C. F.; Zhang X.; Tan C. L.; Li H.; Chen B.; Yang J.; Chen J. Z.; Huang Y.; Wang L. H.; Zhang H. Single-Layer Transition Metal Dichalcogenide NanosheetBased Nanosensors for Rapid, Sensitive, and Multiplexed Detection of DNA. Adv. Mater. 2015, 27, 935–939. 10.1002/adma.201404568. [DOI] [PubMed] [Google Scholar]
  19. Zhang J.; Jia S.; Kholmanov I.; Dong L.; Er D. Q.; Chen W. B.; Guo H.; Jin Z. H.; Shenoy V. B.; Shi L.; Lou J. Janus Monolayer Transition-Metal Dichalcogenides. ACS Nano 2017, 11, 8192–8198. 10.1021/acsnano.7b03186. [DOI] [PubMed] [Google Scholar]
  20. Lu A. Y.; Zhu H. Y.; Xiao J.; Chuu C. P.; Han Y. M.; Chiu M. H.; Cheng C. C.; Yang C. W.; Wei K. H.; Yang Y. M.; et al. Janus monolayers of transition metal dichalcogenides. Nat. Nanotechnol. 2017, 12, 744–749. 10.1038/nnano.2017.100. [DOI] [PubMed] [Google Scholar]
  21. Yao Q. F.; Cai J.; Tong W. Y.; Gong S. J.; Wang J. Q.; Wan X. G.; Duan C. G.; Chu J. H. Manipulation of the large Rashba spin splitting in polar two-dimensional transition-metal dichalcogenides. Phys. Rev. B 2017, 95, 165401 10.1103/PhysRevB.95.165401. [DOI] [Google Scholar]
  22. Dong L.; Lou J.; Shenoy V. B. Large In-Plane and Vertical Piezoelectricity in Janus Transition Metal Dichalchogenides. ACS Nano 2017, 11, 8242–8248. 10.1021/acsnano.7b03313. [DOI] [PubMed] [Google Scholar]
  23. Li F. P.; Wei W.; Wang H.; Huang B. B.; Dai Y.; Jacob T. Intrinsic Electric Field-Induced Properties in Janus MoSSe van der Waals Structures. J. Phys. Chem. Lett. 2019, 10, 559–565. 10.1021/acs.jpclett.8b03463. [DOI] [PubMed] [Google Scholar]
  24. Tao S. D.; Xu B.; Shi J.; Zhong S. Y.; Lei X. L.; Liu G.; Wu M. S. Tunable Dipole Moment in Janus Single-Layer MoSSe via Transition-Metal Atom Adsorption. J. Phys. Chem. C 2019, 123, 9059–9065. 10.1021/acs.jpcc.9b00421. [DOI] [Google Scholar]
  25. Jin C.; Tang X.; Tan X.; Smith S. C.; Dai Y.; Kou L. Z. A Janus MoSSe monolayer: a superior and strain-sensitive gas sensing material. J. Mater. Chem. A 2019, 7, 1099–1106. 10.1039/C8TA08407F. [DOI] [Google Scholar]
  26. Chen D. C.; Lei X. L.; Wang Y. N.; Zhong S. Y.; Liu G.; Xu B.; Ouyang C. Y. Tunable electronic structures in BP/MoSSe van der Waals heterostructures by external electric field and strain. Appl. Surf. Sci. 2019, 497, 143809 10.1016/j.apsusc.2019.143809. [DOI] [Google Scholar]
  27. Li F. P.; Wei W.; Zhao P.; Huang B. B.; Dai Y. Electronic and Optical Properties of Pristine and Vertical and Lateral Heterostructures of Janus MoSSe and WSSe. J. Phys. Chem. Lett. 2017, 8, 5959–5965. 10.1021/acs.jpclett.7b02841. [DOI] [PubMed] [Google Scholar]
  28. Guo S.-D.; Dong J. Biaxial strain tuned electronic structures and power factor in Janus transition metal dichalchogenide monolayers. Semicond. Sci. Technol. 2018, 33, 085003 10.1088/1361-6641/aacb11. [DOI] [Google Scholar]
  29. Yang X.-Y.; Hussain T.; Wärnå J. P. A.; Xu Z.; Ahuja R. Exploring Janus MoSSe monolayer as a workable media for SOF6 decompositions sensing based on DFT calculations. Comput. Mater. Sci. 2021, 186, 109976 10.1016/j.commatsci.2020.109976. [DOI] [Google Scholar]
  30. Panigrahi P.; Jini D.; Bae H.; Lee H.; Ahuja R.; Hussain T. Two-dimensional Janus monolayers of MoSSe as promising sensor towards selected adulterants compounds. Appl. Surf. Sci. 2021, 542, 148590 10.1016/j.apsusc.2020.148590. [DOI] [Google Scholar]
  31. Idrees M.; Din H. U.; Ali R.; Rehman G.; Hussain T.; Nguyen C. V.; Ahmad I.; Amin B. Optoelectronic and solar cell applications of Janus monolayers and their Van der Waals heterostructure. Phys. Chem. Chem. Phys. 2019, 21, 18612–18621. 10.1039/C9CP02648G. [DOI] [PubMed] [Google Scholar]
  32. Kandemir A.; Peeters F. M.; Sahin H. Monitoring the effect of asymmetrical vertical strain on Janus single layers of MoSSe via spectrum. J. Chem. Phys. 2018, 149, 084707 10.1063/1.5043207. [DOI] [PubMed] [Google Scholar]
  33. Jing Y.; Tan X.; Zhou Z.; Shen P. Tuning electronic and optical properties of MoS2 monolayer via molecular charge transfer. J. Mater. Chem. A 2014, 2, 16892–16897. 10.1039/C4TA03660C. [DOI] [Google Scholar]
  34. Guan X. X.; Zhu G. J.; Wei X. L.; Cao J. X. Tuning the electronic properties of monolayer MoS2, MoSe2 and MoSSe by applying z-axial strain. Chem. Phys. Lett. 2019, 730, 191–197. 10.1016/j.cplett.2019.06.007. [DOI] [Google Scholar]
  35. Huang M. Y.; Yan H. G.; Heinz T. F.; Hone J. Probing Strain-Induced Electronic Structure Change in Graphene by Raman Spectroscopy. Nano Lett. 2010, 10, 4074–4079. 10.1021/nl102123c. [DOI] [PubMed] [Google Scholar]
  36. Ye J. P.; Liu G.; Han Y.; Luo W. W.; Sun B. Z.; Lei X. L.; Xu B.; Ouyang C. Y.; Zhang H. L. Electric-field-tunable molecular adsorption on germanane. Phys. Chem. Chem. Phys. 2019, 21, 20287–20295. 10.1039/C9CP04122B. [DOI] [PubMed] [Google Scholar]
  37. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  38. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  39. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  40. Monkhorst H. J.; Pack J. D. Special points for Brillonin-zone integrations. Phys. Rev. Lett. 1976, 13, 5188–5192. 10.1103/physrevb.13.5188. [DOI] [Google Scholar]
  41. Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
  42. Henkelman G.; Arnaldsson A.; Jonsson H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. 10.1016/j.commatsci.2005.04.010. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c01747_si_001.pdf (607.7KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES