Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2021 May 26;6(22):14533–14541. doi: 10.1021/acsomega.1c01517

Prediction and Classification of Formation Energies of Binary Compounds by Machine Learning: An Approach without Crystal Structure Information

Yuanqing Mao †, Hongliang Yang †, Ye Sheng §, Jiping Wang †, Runhai Ouyang §, Caichao Ye †,‡,∥,*, Jiong Yang §,*, Wenqing Zhang †,⊥
PMCID: PMC8190927  PMID: 34124476

Abstract

graphic file with name ao1c01517_0008.jpg

It is well believed that machine learning models could help to predict the formation energies of materials if all elemental and crystal structural details are known. In this paper, it is shown that even without detailed crystal structure information, the formation energies of binary compounds in various prototypes at the ground states can be reasonably evaluated using machine-learning feature abstraction to screen out the important features. By combining with the “white-box” sure independence screening and sparsifying operator (SISSO) approach, an interpretable and accurate formation energy model is constructed. The predicted formation energies of 183 experimental and 439 calculated stable binary compounds (Ehull = 0) are predicted using this model, and both show reasonable agreements with experimental and Materials Project’s calculated values. The descriptor set is capable of reflecting the formation energies of binary compounds and is also consistent with the common understanding that the formation energy is mainly determined by electronegativity, electron affinity, bond energy, and other atomic properties. As crystal structure parameters are not necessary prerequisites, it can be widely applied to the formation energy prediction and classification of binary compounds in large quantities.

Introduction

The formation energy and the Gibbs free energy of materials have great significance in judging their stability. The rapid and accurate prediction of the formation energy of materials is of great scientific significance for their applications. To obtain precise formation energy and phase diagrams, scientists usually use first-principles calculations combined with experimental data, but exact crystal structure data is the prerequisite for calculations. However, as there are plenty of types of materials, the accurate crystal structure information of existing materials is limited, and first-principles calculation of formation energy is time-consuming and expensive as well.1 In addition, it is not realistic to systematically measure the formation energy of large amounts of material systems by experiments. A few studies focus on obtaining formation energy without structure data. Hence, the accurate prediction and calculation method of formation energy, as an efficient way for the screening of new materials without integral structure data, are of great significance.

In recent years, in terms of screening of new materials, high-throughput calculations have significantly accelerated the material design and discovery process.2 Many computational or predicted material property databases have been established (including electronic structures, thermodynamics, structural properties, etc.).3 These methods do help to improve the speed for screening materials with better performance. However, high-throughput computing often consumes a lot of computing resources, and there exists a large structural space with new atomic combinations yet to be explored beyond the current high-throughput efforts. Therefore, machine learning (ML), i.e., mining useful information from a mass of material data for performance prediction of unknown materials, has become a new approach for material scientists.4

There have been great advances recently in the application of machine learning algorithms to predict material properties, such as molecular prediction,5 characteristics of the periodic system,6,7 melting temperature,8 ionic conductivity,9 phase stability,10 molecular atomization energy,11 potential energy,12 crystal structure,12,13 band structure prediction,14−16 etc. In addition, multiple machine learning methods were applied to find a predictive model.14−17 Zhang et al. developed a strategy for machine learning to predict the band gap of binary semiconductors, lattice thermal conductivity, and elastic properties of zeolites based on small data sets.18 Ong et al. designed and optimized technological materials for energy storage, energy efficiency, and high-temperature alloys using machine learning on the experiments and high-throughput density functional theory calculations.19 Volker et al. used machine learning to analyze the electronic-structure data. Their ML-based interatomic potentials gave quick access to atomistic simulations.20 Dey et al.14 used ordinary least-squares regression (OLSR), sparse partial least-squares regression (SPLSR), and lasso algorithm. They predicted the direct band gap of 200 ternary chalcopyrite compounds, based on 28 compounds with experimental band gaps. Lee et al.15 used OLSR, Lasso, and support vector regression (SVR) to create G0W0 bands of 156 AX binary compounds’ predictive model. Pilania et al.16 evaluated more than 1.2 million attributes and finally used the lowest occupied Kohn–Sham level and elemental electronegativity of atomic species as statistical learning feature descriptors for developing a gap prediction model for perovskite bands using the kernel ridge regression (KRR) model. Ye et al.21 used neural networks to analyze the formation energy of an ABO3 perovskite system and concluded that the formation energy could be described by the two factors of Pauling electronegativity and ionic radii. To discover interpretable models, Bartel et al.22 used the sure independence screening and sparsifying operator (SISSO)23 approach to identify a simple and accurate equation to predict Gibbs energy of formation against temperature for inorganic compounds. As a general data-driven method, SISSO can be used to predict the formation energy as well. Bartel et al.24 used thousands of computed formation energy with different machine learning models to predict the stability of inorganic materials, including both stable and unstable materials. Jha et al.25 used a deep learning approach to predict materials’ chemistry from the elemental composition, and Goodall et al.26 used stoichiometry as the sole input and automatically learned appropriate and systematically improvable descriptors by Random Forest (RF), ElemNet, and Roost methods.

The goal of this work is to use a machine learning technique to reveal the underlying mechanism at an elemental level that affects the formation energy (ΔHf) without the material crystal structure information. We use machine learning algorithms to predict the formation energy of materials at the most stable configuration (the lower limit of materials’ formation energy); in other words, the most stable formation energy of a specific component of materials. For this purpose, binary compounds were chosen as examples since the data of their experimental properties are relatively easy to be collected, and the values of formation energy vary greatly (from 4 to 400 kJ·mol–1·atom–1). In this paper, an effective and reliable formation energy predictive model is developed to map the formation energy with few key parameters. In this work, the primary descriptors of a material sample are composed of multiple different material-related attributes that uniquely describe the sample. Instead of giving all of the material’s attributes for machine learning, we choose the information that is relevant and easily available. For example, no structure data is included, which means our formation energy prediction can be available without comprehensive material structure data. We performed feature selection using Random Forest. Then, we performed subsequent equation learning using SISSO.23 The SISSO method can broadly combine the primary features (i.e., the input parameters) to form a huge feature space, and then it determines the best low-dimensional descriptor through sparse regression. An interpretable and accurate descriptor was identified, which can facilitate future research on the formation energy and Gibbs free energy of multicomponent compounds as well.

Results and Discussion

Data Learning and Feature Selection by Machine Learning

For the prediction results generated by different regression models, the mean absolute error (MAE) and coefficient of determination (R2) are used to measure the prediction accuracy of each model on the test set. We evaluated the predictive performance of each supervised ML method (support vector machine (SVMs), KRR, Random Forest) using 80% of the data as a training set to predict the remaining 20% (test set). Table S3 (see the Supporting Information) shows the performance of each supervised ML method for the formation energy prediction of binary compounds. All of the three methods show good performance of prediction, and the Random Forest model shows the best score for the test set.

To easily understand the ML results, we used the “importance weights,” which is obtained by the “SelectFromModel” module based on the Random Forest model by scikit-learn, to measure the impact of each feature and filter the best ones for the formation energy prediction. The features that are not important for the formation energies of binary compounds can be excluded. The top important features are listed in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Random Forest analysis: (a) best training and test set performance for formation energy prediction and (b) top features determined by the Random Forest value importance weights analysis on the formation energy prediction.

The top five most important features are anion electronegativity (BEN), anion’s electron affinity (BEA), both anion’s and cation’s highest occupied and lowest unoccupied Kohn–Sham levels (A/BHKL), and cation’s radii of p orbitals (AP). As the feature importance of RF can be strongly affected by the distribution of datasets, further RF important features rank by a different range of formation energies (split the dataset by their formation energy by 50%), as shown in Figure S6, and indicates that the top identified features related to formation energy are physically relevant. The key features such as anion electronegativity and anion’s electron affinity can also be found in the top of the rank list of RF important features (Figure S6). From the rank list, it is obvious that the formation energy is related to materials’ atom property, electronic structure, and so on. But so far, the mathematical relationship between the key factors and the formation energy is not clear due to the complex mathematical expression of the abovementioned ML methods. In the next section, these top 20 features (Random Forest importance weights above 0.02) will be used in the analysis of the combination descriptor, and a concise descriptor will be shown.

Besides selecting important descriptors from ML analysis of the experimental sample set, comparability of experimental and calculated formation energy data is also analyzed. To use the MP-calculated data as a test set to test the accuracy of following SISSO trained models by experimental data, we first need to evaluate the consistency of experimental and calculated formation energy data. From the Materials Project (MP), formation energies of 170 stable binary compounds are calculated and are compared with their experimental ones in our 183 experimental sample set. To make sure the materials found on MP are stable, their Ehull values are analyzed. Ehull represents the energy of a material that decomposes into the set of most stable materials with the same chemical composition (in eV·atom–1), and the Ehull values of these 170 materials are zero, indicating that they are the most stable materials at their compositions. The coefficient of determination (R2 = 0.987 and root-mean-square error (RMSE) = 0.175) of the experimental and calculated formation energy shows good consistency, as shown in Figure 2. This shows that the large calculated formation energies of other binary compounds dataset from the MP database can be used as a test set for our further justification of the selection for ML training using an experimental sample set.

Figure 2.

Figure 2

Open in a new tab

Consistency analysis of the experimental formation energies (ΔHf/atom_exp) and the calculated formation energies (ΔHf/atom_MP_calc) of binary compounds of the experimental sample set.

As the experimental and MP-calculated formation energies show good consistency, we further collected the MP-calculated formation energies of binary compounds whose Ehull = 0 (indicates the most stable materials at their compositions). After filtering by the element types of A and B in AmBn and the feature’s range based on the experimental sample, finally, new 439 kinds of binary compounds, which do not appear in the 183 experimental materials, were obtained and used for testing our models based on a small experimental data set. As the data frequency and distribution of training and test sets can greatly affect the accuracy of prediction, frequency and distribution analyses are also performed. The results showed the same trend of training and test sets, which indicates that the set of new 439 kinds of binary compounds used as the test set is reasonable; see Figure S2. All MP-calculated data trained SISSO comprehensive descriptors and key features are also shown in Figure S3.

Identification of Comprehensive Descriptors

The three ML models above tend to pursue the most accurate data prediction, resulting in less model interpretability. In contrast, SISSO models are used to find a balance between the model accuracy and complexity for an understanding of the problem in addition to accurate prediction. The SISSO method was used to identify the best low-dimensional comprehensive descriptors for formation energy prediction, providing an advanced alternative path to reveal the correlation of multidimensional parameters with stability (formation energy). Here, dimensionality is defined as the number of fitting coefficients of a linear model (excluding the intercept).

After the SISSO analysis, the obtained best one-dimensional (1D) descriptor is

graphic file with name ao1c01517_m001.jpg

where AEN is the electronegativity of A and AHL/BHL is the highest occupied Kohn–Sham level of A/B.

The 1D descriptor can be used for searching the low formation energies of binary compounds, which are usually stable. The SISSO-predicted formation energy based on the 1D descriptor (ΔHf/atom 1D SISSO), the experimental formation energy data (ΔHf/atom_exp), and the calculated formation energy (ΔHf/atom_MP_calc) are shown in Figure 3. The quantitative relationship of ΔHf/atom 1D SISSO and D1 is shown in eq 1

graphic file with name ao1c01517_m002.jpg 1

In D1, only three features are used to describe the formation energy, and the coefficient of determination (R2) of the training set is 0.902, while the test set R2 is 0.795. Our D1 descriptor can only represent the formation energy of the most stable compound made of two different elements to a certain degree. While D1 is underfitting, the simple functional form enables good interpretability. To improve the prediction accuracy of formation energy, the identified best two-dimensional (2D) descriptors are

graphic file with name ao1c01517_m003.jpg

The quantitative relationship of ΔHf/atom 2D SISSO, D21, and D22 is shown in eq 2

graphic file with name ao1c01517_m004.jpg 2

In the 2D descriptors, AEN/BEN is the electronegativity of A/B, BEA is the electron affinity of B, ALL is the lowest unoccupied Kohn–Sham level of A, AHL is the highest occupied Kohn–Sham level of A, nB is the amount of n in AmBn, and NB is the atomic number of B.

Figure 3.

Figure 3

Open in a new tab

SISSO-model-predicted formation energy performance plots based on the 1D descriptor. SISSO-model-predicted formation energy based on the 1D descriptor (ΔHf/atom 1D SISSO, Y-axis), the experimental formation energy (183 training sets, ΔHf/atom_exp, X-axis) and the calculated formation energy from Materials Project (439 test sets, ΔHf/atom_MP_calc, X-axis); unit: J·mol–1·atom–1.

SISSO efficiently selects these comprehensive descriptors from a space of ∼107 candidate two-dimensional descriptors. The identification of these descriptors agrees well with intuition regarding the properties that most significantly affect the formation energy. The formation energy is related to electronegativity, the highest occupied Kohn–Sham level, etc. The SISSO-predicted formation energy based on 2D descriptors (ΔHf/atom 2D SISSO), the experimental formation energy data (ΔHf/atom_exp), and the calculated formation energy (ΔHf/atom_MP_calc) are shown in Figure 4. Compared with the 1D descriptor’s prediction performance, 2D descriptors’ accuracy (R2) increases to 0.938 for the train set, and its test set accuracy (R2) is also increased to 0.852. The cross-validations for the SISSO 2D prediction model are also performed. The training experimental sample set was randomly divided into five groups: any four groups (80%) were set as the training set and the remaining one group (20%) as the test set. The best training R2 is 0.953 (RMSE = 0.317) and the test R2 is 0.945 (RMSE = 0.370), while the average training R2 is 0.941 (RMSE = 0.350) and the average test R2 is 0.920 (RMSE = 0.414); see Table S4. Furthermore, out-of-domain cross-validations (k-fold forward cross-validation) are performed. The training experimental sample set was divided into five groups by the formation energy; see Table S5. Group 1 represents the relatively most stable materials (low experimental formation energy), whereas a higher group number represents relatively higher experimental formation energy. Increasing test R2 means the formation energy of stable materials can be well predicted by the formation energy of other less stable materials with increasing training size. The improved prediction accuracy of the SISSO 2D prediction model indicates that this 2D descriptor could better quantitatively predict the binary compounds’ formation energies compared to that of the 1D prediction model. It also shows that there must be some mechanism that can be explained by physics under these prediction functions. The prediction performance of the crystal graph convolutional neural networks (CGCNN)27 model is also shown in Figure S7. The CGCNN model uses only the crystal structure data to predict the formation energy, as the SISSO models in this work do not need any structure information. We use pretrained CGCNN to fit our experimental sample set. The performance (R2 = 0.904, RMSE = 0.287) is similar to our SISSO prediction model and worse than the SVM, KRR, and Random Forest models (in which all elemental and crystal structural information are trained). Since our SISSO model uses fewer features (without crystal structure data) and gives concise descriptors, it can be widely applied to the formation energy prediction and classification of binary compounds in large quantities.

Figure 4.

Figure 4

Open in a new tab

SISSO-model-predicted formation energy performance plots based on the 2D descriptor. SISSO-model-predicted formation energy based on the 2D descriptor (ΔHf/atom 2D SISSO, Y-axis), experimental formation energy (183 training sets, ΔHf/atom_exp, X-axis), and the calculated formation energy from Materials Project (439 test sets, ΔHf/atom_MP_calc, X-axis); unit: J·mol–1·atom–1.

Besides giving a quantitative prediction function for formation energy, the binary compounds can be classified by 2D descriptors into different groups. A 3D formation energy ΔHf/atom (J·mol–1·atom–1) map is shown in Figure 5a, indicating that a smaller D21 and a larger D22 will result in a lower formation energy (dark red area in the formation energy ΔHf/atom map). As shown in Figure 5a, a good prediction map for the formation energy by 2D descriptors is demonstrated. From the predicted ΔHf/atom 2D SISSO, classification lines for formation energy are also set up, as shown in Figure 5b. Using these lines in the real experimental sample set, the stabilities of binary compounds could be well judged qualitatively. From the above results, we can infer the implications for formation energy, which will be discussed in detail in the next section.

Figure 5.

Figure 5

Open in a new tab

Visualized results for the 2D descriptor. (a) Color map of 2D comprehensive descriptors for the predicted formation energy (ΔHf/atom 2D_SISSO) by 183 experimental sample set trained SISSO model. The color shows the value of formation energy: red area, low formation energy; blue and purple area: high formation energy. (b) Calculated formation energy differences lines used to classify the experimental formation energy (ΔHf/atom exp) according to the optimal 2D comprehensive descriptors. The classification formation energy value is listed above. The classification lines’ value is based on eq 2. The 2D descriptors’ extrapolation to classify the calculated formation energies of the Materials Project binary compounds is shown in Figure S4.

Atomic and Physical Implications by Descriptors

As discussed above, we demonstrated the best (i.e., lowest RMSE) 1D and 2D descriptors.

graphic file with name ao1c01517_m005.jpg
graphic file with name ao1c01517_m006.jpg

As for the D1 descriptor, it can be expressed as A’s highest occupied Kohn–Sham level plus the product of A and B’s highest occupied Kohn–Sham level divided by A’s electronegativity; the unit is eV, which is also the unit of the formation energy. As for the D21 descriptor, it is the electronegativity difference between the anion and cation multiplied by the sum of anion’s electron affinity and cation’s lowest unoccupied level; the unit is eV2. For the D22 descriptor, the first part is number y of B in AmBn divided by the atomic number of B. The second part in the D22 descriptor is A’s lowest unoccupied Kohn–Sham level divided by its highest occupied Kohn–Sham level. The meaning of all symbols, range, and units are listed in Table 1, and the visualized relationships of 2D descriptors (D21 and D22) with 183 experimental formation energies of the training sample set are shown in Figure 6. The visualized relationships of the key features with the experimental formation energies are shown in Figure S5.

Table 1. Meaning and Unit of Symbols in Descriptors for Binary Compound AmBn.

symbol meaning for binary compound AmBn rangea unit
AHL, BHL highest occupied Kohn–Sham level of A or B –11.29 to −2.22 eV
AEN, BEN electronegativity of A or B 2.29–11.84 eV
AEA electron affinity of A –2.751 to 1.081 eV
BEA electron affinity of B –4.27 to −0.11 eV
ALL lowest unoccupied Kohn–Sham level of A –2.13 to 3.06 eV
mA, nB m and n of AmBn 1–5  
NB atomic number of B 3–53  
Open in a new tab
a

The feature’s range based on the experimental sample.

Figure 6.

Figure 6

Open in a new tab

Visualized relationships of 2D descriptors (D21 and D22) with 183 experimental formation energies of the training sample set (the visualized relationships of key features with formation energy are shown in Figure S5).

From the results obtained by machine learning, stable binary compounds should fulfil these conditions:

  • (a)

    The cation’s ability of attracting electrons should be lower.

  • (b)

    The electronegativity difference between the cation and anion should be higher.

  • (c)

    The sum of anion’s electron affinity and cation’s lowest unoccupied level should be lower.

  • (d)

    The amount of the anion percentage should be higher.

  • (e)

    The atomic number of anions should be lower.

  • (f)

    The ratio of cation’s highest occupied Kohn–Sham level and lowest unoccupied level should be lower.

Most properties are consistent with physical ideas for the material design. For example, when the cation’s electronegativity is low, the material will be more likely stable. When the electronegativity difference between the cation and anion is high, the bond between them tend to be strong, thus leading to a more stable structure.

Physical Insights behind the Descriptors

For the D1 descriptor, the atom’s negative value of the highest occupied level, AHL, has the same trend with its electronegativity in the periodic table of elements. Both the values increase when the element goes to the upper right corner in the periodic table. Generally, when the element is more likely to lose the electron to become a cation, which also means its electronegativity28 is low, the binary compound is more stable. The highest occupied level of the cation, having the same trend with the negative electronegativity, should be higher for stable materials. In the second term, 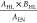Inline graphic, the ratio of cation’s highest occupied level and its electronegativity is around −1, so the anion’s highest occupied level should be lower, which shows agreements with the D1 descriptor’s result.

In the first term of D21, |AEN – BEN |, as the bigger difference between anion and cation’s electronegativity, the interaction between them is stronger, and the material is more stable. In the second term, BEA + ALL, the electron affinity of the anion atom should be lower for the low formation energy materials. Most materials’ D21 is below 0, but the cation atom’s lowest unoccupied level may not be less than zero, and the D21 descriptor will be larger than 0 in the boron-containing system, for example BN and BP. For the D22 descriptor, the first term, 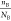Inline graphic, is the ratio of the anion content and the anion atomic number. As the element’s electronegativity decreases, the element’s period number and atomic number increases. The atomic number for the same group of anion elements should be lower to construct a more stable binary compound, which is reflected in this part. In the second term, Inline graphic, cation’s ratio of its lowest unoccupied level and its highest occupied level has a periodic trend in each element period (except that the ratio of cations with high ability to lose electrons is negative; in each element period, as the atomic number increases, the ratio of ALL and AHL becomes larger). The D21 and D22 descriptors demonstrate the theory that for more stable materials, the lowest unoccupied level should be relatively low and the highest occupied level should be relatively high.

Further, we verify that the bond energy29 can greatly affect the materials’ formation energy, and the electronegativity can intuitively show the power of bond energy, represented in the first term of D21 (|AEN – BEN|). The second term (BEA + ALL) can identify different kinds of bonds. In our SISSO model, usually, the ionic bond materials get a lower value for it than the covalent bond materials. It can be used for SISSO prediction to classify the bonds. For D22, the larger nB represents lower B’s valence, as well as larger electronegativity. In addition, the first term(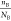Inline graphic) for B can filter the heavy elements apart, mostly for alloy (alloy’s 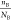Inline graphic is relatively low). On the other hand, the second term (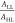Inline graphic) of D22 focuses on A’s electronegativity and gives a bonus for some A elements with low-to-average electronegativity (for example, B, Ge, N, etc.). This value can be used to fix the formation energy data of some relatively low formation energy materials with these A elements (such as GeO2).

All of these descriptors help not only to predict the range of formation energies in a mathematical way but also to understand the mechanism of formation energy from a different perspective by machine learning. Furthermore, the SISSO algorithm numerically connects all of these physical insights to representative descriptors for formation energy.

Conclusions

In this paper, we have demonstrated the power of machine learning in predicting the formation energies of binary compounds and their classification, which is based on a series of collected binary compounds’ experimental data. The important features (e.g., electronegativity, electron affinity, highest occupied Kohn–Sham level) are screened by ML, and a formation energy prediction model of binary compounds based on SISSO without the prerequisite of crystal structure parameters is established. ML has an excellent ability to analyze massive amounts of data, and it reveals trends and principles behind the complicated data. Since the experimental formation energy sample set is relatively small, the calculated formation energy data from Materials Project are collected. After verifying the good consistency of the experimental and calculated formation energies (R2 = 0.987 and RMSE = 0.175), the large amount of calculated formation energies of other binary compounds from the MP database was used as a test set to justify the ML models trained using the experimental sample set, which represent a good performance for formation energy prediction. One-dimensional and two-dimensional comprehensive descriptors for materials’ formation energy are obtained by SISSO algorithm analysis. These descriptors can greatly help to understand the mechanisms that affect the formation energy from atomic properties and physical implications. The descriptors give the logical result of formation energy from the ML perspective. Moreover, as crystal structure parameters are not necessary prerequisites, it can be widely applied to the formation energy prediction and classification of binary compounds in large quantities and accelerates the design and optimization process for new materials, which have important scientific significance as well. The application of machine learning would convert our ways of exploring new materials from a labor-intensive practice to an intellectual work. This work would lay the foundation for exploring other attribute descriptors for multielement materials.

Materials and Methods

Procedure for Acquisition of Data and Features of Binary Compounds

The experimental formation energies (ΔHf, kJ·mol–1) of binary compounds used as the training set to construct the ML models in this work are obtained from Materials Thermochemistry by Kubaschewski.30 The complementary calculated formation energies of binary compounds used as the test set to justify the models are obtained from Materials Project (MP).31 The MP-calculated formation energies of binary compounds were the formation energies of the materials whose Ehull is 0 (energy above hull: the energy of decomposition of a material into the set of most stable materials at its chemical composition is zero, which indicates that the chosen material is the most stable material at its composition), which is to ensure that all of the MP materials in the test set are the most stable materials at their compositions. Then, the formation energies are decomposed to ΔHf/atom (kJ·mol–1·atom–1), which shows every atom’s contribution to formation energy, as shown in eq 3.

graphic file with name ao1c01517_m013.jpg 3

E(A) and E(B) are the formation energies per atom for the corresponding stable elementary substance A and B, respectively, and E(AmBn) is the formation energy for the AmBn binary compound. The formation energies of the experimental materials here are at 298 K, and the calculated formation energies are at 0 K and 0 atm level. This quantity is often a good approximation for the formation energy at ambient conditions as well.31

The atomic parameters for a single atom10 are considered, such as the radial probability density of the valence of s, p, and d orbitals, ionization potential, electron affinity, etc. In addition, we use detailed crystal structure information as little as possible for model training and feature selection, and only the crystal structure parameters (such as lattice constant, volume, nearest-neighbor distance, etc.) are exported or analyzed from.cif files based on the ICSD crystal library.32 Surprisingly, although many crystal structure parameters were collected, none of them is evaluated to be the most important for the formation energy prediction from the importance analysis. The above parts combine as potential features for the initial study. After removing the missing data, 183 binary compounds with the experimental formation energies are selected, along with 91 features collected for machine learning (the sample set is listed in the Supporting Information). In the sample set, for each material, 91 features and a target variable (ΔHf/atom) are listed. These features are mainly derived from a plurality of different attributes at the atomic level in the binary compounds, along with the lattice structure parameters and crystal volume. The information of atomic properties of cations and anions are also listed, such as ionization potential, electron affinity, electronegativity, etc. Besides the 183 experimental formation energy dataset of the binary compounds, a large calculated formation energy dataset from the MP database is collected to justify the selection of using a small experimental dataset. After screening by the element types of A and B in AmBn and the feature’s range based on the experimental sample, 439 kinds of binary compounds, which have not appeared in the 183 experimental materials, were obtained, and their calculated formation energies and related features were used to construct a test set for further model testing. All this information is gained from Materials Thermochemistry,30ICSD,32Materials Project,31 and Ghiringhelli’s work.10

Machine Learning Algorithms

The supervised ML algorithms (SVR, KRR, Random Forest) are implemented with Python scripts using scikit-learn,33 a Python machine learning package, and a model based on the crystal structure data to predict the formation energy-CGCNN27 is implemented. The Random Forest (RF),34 support vector machines (SVMs),35 and kernel ridge regression (KRR)36 algorithms are tested (performances of different algorithms are compared in Figure S1 in the Supporting Information). SISSO was used to identify the best low-dimensional comprehensive descriptors, which provides insight into the correlation between multidimensional parameters and the formation energy.23 As we know, besides accuracy, interpretability is also crucial in machine learning models. In particular, when the models are mathematically expressed as simple, explicit, and analytic functions that only require basic physical quantities, they have the advantages of being more easily understood in their generalization ability and scientific insights and are able to work with small datasets as well. There have been methods to deliver such models, e.g., symbolic regression,37 sparse regression,10,38 and the SISSO that combines both symbolic regression and sparse regression.23 We chose SISSO in this work because it can improve the solutions by efficiently managing the immensity of feature spaces that challenges the usual sparse regression and symbolic regression methods. The SISSO-identified descriptors enable accurate prediction on the target property (formation energy), and more importantly, reveal the key factors of determining the formation energies for binary compounds. The SISSO prediction results are compared with other models in Table S6.

For all of the fitting figures listed in our work, we fit our SISSO-predicted formation energy and the experiment formation energy with y = x. R2 (the coefficient of determination)39 and root-mean-square error (RMSE) are used to express the accuracy of prediction. Their formulation 4 and 5 are as follows

graphic file with name ao1c01517_m014.jpg 4
graphic file with name ao1c01517_m015.jpg 5

where yi are the observed values of the experiments, y̅ is the corresponding average, ŷi are the ML predicted values, and m is the number of external sets.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.1c01517.

  • Results of three different ML methods; cross-validation analysis; the SISSO results on MP-calculated data; visualization for key features; feature importance on split data by formation energy and CGCNN model comparison (PDF)

  • Test MP dataset (XLSX)

  • Training experimental dataset (XLSX)

Author Contributions

C.Y. and W.Z. conceived this project. Y.M. and J.W. performed the data and features collection. Y.M. performed machine learning modeling, SISSO analysis. H.Y., Y.S., and R.O. provided helpful discussion in algorithm coding. Y.M. and C.Y. co-wrote the manuscript. W.Z., J.Y., and R.O. revised the manuscript. W.Z. secured funding.

Financial supports were provided by the Key-Area Research and Development Program of Guangdong Province (2019B010940001), Guangdong Provincial Key Laboratory of Computational Science and Material Design (2019B030301001) and Fundamental Research Program of Shenzhen (JCYJ20190809174203802), W.Z. also acknowledges the support from the Guangdong Innovation Research Team Project (2017ZT07C062) and Shenzhen Municipal Key-Lab program (ZDSYS20190902092905285). Computing resources were supported by the Center for Computational Science and Engineering at Southern University of Science and Technology.

The authors declare no competing financial interest.

Supplementary Material

ao1c01517_si_001.pdf (1.3MB, pdf)
ao1c01517_si_002.xlsx (63.5KB, xlsx)
ao1c01517_si_003.xlsx (103KB, xlsx)

References

  1. Kramer A.; Put M. L. V. D.; Hinkle C. L.; Vandenberghe W. G. In Trigonal Tellurium Nanostructure Formation Energy and Band Gap, 2019 International Conference on Simulation of Semiconductor Processes and Devices (SISPAD), IEEE, 2019.
  2. Sharma V.; Wang C. C.; Lorenzini R. G.; Ma R.; Zhu Q.; Sinkovits D. W.; Pilania G.; Oganov A. R.; Kumar S.; Sotzing G. A.; et al. Rational Design of All Organic Polymer Dielectrics. Nat. Commun. 2014, 5, 4845 10.1038/ncomms5845. [DOI] [PubMed] [Google Scholar]
  3. Landis D. D.; Hummelshoj J. S.; Nestorov S.; Greeley J.; Dulak M.; Bligaard T.; Norskov J. K.; Jacobsen K. W. The Computational Materials Repository. Comput. Sci. Eng. 2012, 14, 51–57. 10.1109/MCSE.2012.16. [DOI] [Google Scholar]
  4. Service R. F. Computational Science Materials Scientists Look to a Data-Intensive Future. Science 2012, 335, 1434–1435. 10.1126/science.335.6075.1434. [DOI] [PubMed] [Google Scholar]
  5. Rupp M.; Tkatchenko A.; Muller K. R.; von Lilienfeld O. A. Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning. Phys. Rev. Lett. 2012, 108, 058301 10.1103/PhysRevLett.108.058301. [DOI] [PubMed] [Google Scholar]
  6. Meredig B.; Agrawal A.; Kirklin S.; Saal J. E.; Doak J. W.; Thompson A.; Zhang K.; Choudhary A.; Wolverton C. Combinatorial Screening for New Materials in Unconstrained Composition Space with Machine Learning. Phys. Rev. B 2014, 89, 094104 10.1103/PhysRevB.89.094104. [DOI] [Google Scholar]
  7. Faber F. A.; Lindmaa A.; von Lilienfeld O. A.; Armiento R. Machine Learning Energies of 2 Million Elpasolite (AbC2D6) Crystals. Phys. Rev. Lett. 2016, 117, 135502 10.1103/PhysRevLett.117.135502. [DOI] [PubMed] [Google Scholar]
  8. Seko A.; Maekawa T.; Tsuda K.; Tanaka I. Machine Learning with Systematic Density-Functional Theory Calculations: Application to Melting Temperatures of Single- and Binary-Component Solids. Phys. Rev. B 2014, 89, 054303 10.1103/PhysRevB.89.054303. [DOI] [Google Scholar]
  9. Kishida I. The Graph-Theoretic Minimum Energy Path Problem for Ionic Conduction. AIP Adv. 2015, 5, 107107 10.1063/1.4933052. [DOI] [Google Scholar]
  10. Ghiringhelli L. M.; Vybiral J.; Levchenko S. V.; Draxl C.; Scheffler M. Big Data of Materials Science: Critical Role of the Descriptor. Phys. Rev. Lett. 2015, 114, 105503 10.1103/PhysRevLett.114.105503. [DOI] [PubMed] [Google Scholar]
  11. Pilania G.; Wang C. C.; Jiang X.; Rajasekaran S.; Ramprasad R. Accelerating Materials Property Predictions Using Machine Learning. Sci. Rep. 2013, 3, 2810 10.1038/srep02810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Behler J. Atom-Centered Symmetry Functions for Constructing High-Dimensional Neural Network Potentials. J. Chem. Phys. 2011, 134, 074106 10.1063/1.3553717. [DOI] [PubMed] [Google Scholar]
  13. Takahashi K.; Takahashi L. Creating Machine Learning-Driven Material Recipes Based on Crystal Structure. J. Phys. Chem. Lett. 2019, 10, 283–288. 10.1021/acs.jpclett.8b03527. [DOI] [PubMed] [Google Scholar]
  14. Dey P.; Bible J.; Datta S.; Broderick S.; Jasinski J.; Sunkara M.; Menon M.; Rajan K. Informatics-Aided Bandgap Engineering for Solar Materials. Comput. Mater. Sci. 2014, 83, 185–195. 10.1016/J.COMMATSCI.2013.10.016. [DOI] [Google Scholar]
  15. Lee J.; Seko A.; Shitara K.; Nakayama K.; Tanaka I. Prediction Model of Band Gap for Inorganic Compounds by Combination of Density Functional Theory Calculations and Machine Learning Techniques. Phys. Rev. B 2016, 93, 115104 10.1103/PhysRevB.93.115104. [DOI] [Google Scholar]
  16. Pilania G.; Mannodi-Kanakkithodi A.; Uberuaga B. P.; Ramprasad R.; Gubernatis J. E.; Lookman T. Machine Learning Bandgaps of Double Perovskites. Sci. Rep. 2016, 6, 19375 10.1038/srep19375. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Butler K. T.; Davies D. W.; Cartwright H.; Isayev O.; Walsh A. Machine Learning for Molecular and Materials Science. Nature 2018, 559, 547–555. 10.1038/s41586-018-0337-2. [DOI] [PubMed] [Google Scholar]
  18. Zhang Y.; Ling C. A Strategy to Apply Machine Learning to Small Datasets in Materials Science. npj Comput. Mater. 2018, 4, 25 10.1038/s41524-018-0081-z. [DOI] [Google Scholar]
  19. Ong S. P. Accelerating Materials Science with High-Throughput Computations and Machine Learning. Comput. Mater. Sci. 2019, 161, 143–150. 10.1016/j.commatsci.2019.01.013. [DOI] [Google Scholar]
  20. Deringer V. L.; Caro M. A.; Csanyi G. Machine Learning Interatomic Potentials as Emerging Tools for Materials Science. Adv. Mater. 2019, 31, 1902765 10.1002/adma.201902765. [DOI] [PubMed] [Google Scholar]
  21. Ye W. K.; Chen C.; Wang Z. B.; Chu I. H.; Ong S. P. Deep Neural Networks for Accurate Predictions of Crystal Stability. Nat. Commun. 2018, 9, 3800 10.1038/s41467-018-06322-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Bartel C. J.; Millican S. L.; Deml A. M.; Rumptz J. R.; Tumas W.; Weimer A. W.; Lany S.; Stevanovic V.; Musgrave C. B.; Holder A. M. Physical Descriptor for the Gibbs Energy of Inorganic Crystalline Solids and Temperature-Dependent Materials Chemistry. Nat. Commun. 2018, 9, 4168 10.1038/s41467-018-06682-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Ouyang R. H.; Curtarolo S.; Ahmetcik E.; Scheffler M.; Ghiringhelli L. M. Sisso: A Compressed-Sensing Method for Identifying the Best Low-Dimensional Descriptor in an Immensity of Offered Candidates. Phys. Rev. Mater. 2018, 2, 083802 10.1103/PhysRevMaterials.2.083802. [DOI] [Google Scholar]
  24. Bartel C. J.; Trewartha A.; Wang Q.; Dunn A.; Jain A.; Ceder G. A Critical Examination of Compound Stability Predictions from Machine-Learned Formation Energies. npj Comput. Mater. 2020, 6, 97 10.1038/s41524-020-00362-y. [DOI] [Google Scholar]
  25. Jha D.; Ward L.; Paul A.; Liao W. K.; Choudhary A.; Wolverton C.; Agrawal A. Elemnet: Deep Learning the Chemistry of Materials from Only Elemental Composition. Sci. Rep. 2018, 8, 17593 10.1038/s41598-018-35934-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Goodall R. E. A.; Lee A. A. Predicting Materials Properties without Crystal Structure: Deep Representation Learning from Stoichiometry. Nat. Commun. 2020, 11, 6280 10.1038/s41467-020-19964-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Xie T.; Grossman J. C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301 10.1103/PhysRevLett.120.145301. [DOI] [PubMed] [Google Scholar]
  28. Jensen W. B. Electronegativity from Avogadro to Pauling: Part 1: Origins of the Electronegativity Concept. J. Chem. Educ. 1996, 73, 11 10.1021/ed073p11. [DOI] [Google Scholar]
  29. Christian J. D. Strength of chemical bonds. J. Chem. Educ. 1973, 50, 176 10.1021/ed050p176. [DOI] [Google Scholar]
  30. Kubaschewski O.; Alcock C. B.; Spencer P. J.. Materials Thermochemistry; 6th ed.; Pergamon, New York, 1993. [Google Scholar]
  31. Jain A.; Ong S. P.; Hautier G.; Chen W.; Richards W. D.; Dacek S.; Cholia S.; Gunter D.; Skinner D.; Ceder G.; et al. Commentary: The Materials Project: A Materials Genome Approach to Accelerating Materials Innovation. APL Mater. 2013, 1, 011002 10.1063/1.4812323. [DOI] [Google Scholar]
  32. Belsky A.; Hellenbrandt M.; Karen V. L.; Luksch P. New Developments in the Inorganic Crystal Structure Database (Icsd): Accessibility in Support of Materials Research and Design. Acta Crystallogr., Sect. B: Struct. Sci. 2002, 58, 364–369. 10.1107/S0108768102006948. [DOI] [PubMed] [Google Scholar]
  33. Pedregosa F.; Varoquaux G.; Gramfort A.; Michel V.; Thirion B.; Grisel O.; Blondel M.; Prettenhofer P.; Weiss R.; Dubourg V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  34. Svetnik V.; Liaw A.; Tong C.; Culberson J. C.; Sheridan R. P.; Feuston B. P. Random Forest: A Classification and Regression Tool for Compound Classification and Qsar Modeling. J. Chem. Inf. Comput. Sci. 2003, 43, 1947–1958. 10.1021/ci034160g. [DOI] [PubMed] [Google Scholar]
  35. Cortes C.; Vapnik V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. 10.1007/BF00994018. [DOI] [Google Scholar]
  36. Murphy K. P.Machine Learning: A Probabilistic Perspective; The MIT Press, Cambridge, Massachusetts, 2012. [Google Scholar]
  37. Schmidt M.; Lipson H. Distilling Free-Form Natural Laws from Experimental Data. Science 2009, 324, 81–85. 10.1126/science.1165893. [DOI] [PubMed] [Google Scholar]
  38. Rudy S. H.; Brunton S. L.; Proctor J. L.; Kutz J. N. Data-Driven Discovery of Partial Differential Equations. Sci. Adv. 2017, 3, e1602614 10.1126/sciadv.1602614. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Gramatica P.; Sangion A. A Historical Excursus on the Statistical Validation Parameters for QSAR Models: A Clarification Concerning Metrics and Terminology. J. Chem. Inf. Model. 2016, 56, 1127–1131. 10.1021/acs.jcim.6b00088. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao1c01517_si_001.pdf (1.3MB, pdf)
ao1c01517_si_002.xlsx (63.5KB, xlsx)
ao1c01517_si_003.xlsx (103KB, xlsx)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES