Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 May 24;17(6):3426–3434. doi: 10.1021/acs.jctc.1c00212

Tailoring CIPSI Expansions for QMC Calculations of Electronic Excitations: The Case Study of Thiophene

Monika Dash †, Saverio Moroni ‡,*, Claudia Filippi †,*, Anthony Scemama §,*
PMCID: PMC8190955  PMID: 34029098

Abstract

graphic file with name ct1c00212_0007.jpg

The perturbatively selected configuration interaction scheme (CIPSI) is particularly effective in constructing determinantal expansions for quantum Monte Carlo (QMC) simulations with Jastrow–Slater wave functions: fast and smooth convergence of ground-state properties and balanced descriptions of ground and excited states of different symmetries have been reported. In particular, accurate excitation energies have been obtained by the pivotal requirement of using CIPSI expansions with similar second-order perturbation corrections for each state, that is, a similar estimated distance to the full configuration interaction limit. Here, we elaborate on the CIPSI selection criterion for excited states of the same symmetry as the ground state, generating expansions from a common orbital set. Using these expansions in QMC as determinantal components of Jastrow–Slater wave functions, we compute the lowest, bright excited state of thiophene, which is challenging due to its significant multireference character. The resulting vertical excitation energies are within 0.05 eV of the best theoretical estimates, already with expansions of only a few thousand determinants. Furthermore, we relax the ground- and excited-state structures following the corresponding root in variational Monte Carlo and obtain bond lengths that are accurate to better than 0.01 Å. Therefore, while the full treatment at the CIPSI level of this system is quite demanding, in QMC, we can compute high-quality excitation energies and excited-state structural parameters building on affordable CIPSI expansions with relatively few, well-chosen determinants.

1. Introduction

The accurate description of photoinduced phenomena relies on the balanced treatment of the multiple electronic states involved in the excitation process. Recently, we have demonstrated the ability of quantum Monte Carlo (QMC) methods to yield chemically accurate ground- and excited-state structures as well as vertical and adiabatic excitation energies for small, prototypical molecules.1,2 We used wave functions of the Jastrow–Slater form, where the determinantal component was generated in an automatic manner with the configuration interaction using a perturbative selection made iteratively (CIPSI) approach. When these expansions were fully optimized together with the Jastrow factor in QMC,3,4 we found that a handful of CIPSI determinants were sufficient to yield well-converged geometries and excitation energies.

Importantly, we showed2,5 that a balanced QMC description of the ground and excited states also at different geometries could be achieved by generating CIPSI expansions characterized by the same second-order perturbation (PT2) energy correction, that is, the same “error” with respect to the full CI limit. Furthermore, these “iso-PT2” expansions were found to have similar values of the CI variance, which is another useful measure of the error of a CIPSI wave function.

If the excited states investigated belong to a different symmetry class than the ground state, one can perform the expansions either separately, stopping when the same target PT2 energy correction or CI variance is reached5 or concurrently, with a common set of orbitals. In the latter case, the difference in symmetry and the relatively dominant single-reference character of the states investigated aided the CIPSI selection, and we heuristically found that a rather straightforward common selection criterion closely approaches the iso-PT2 condition.2 On the other hand, if the states are of the same symmetry and concurrent CIPSI expansions on a common set of orbitals are used to guarantee orthogonality, rendering their balanced description is more difficult and the simple selection scheme of ref (2) proves inadequate, especially if some of the relevant states are strongly multiconfigurational.

Here, we propose a simple and effective modification of the selection criterion to enable the construction of nearly iso-PT2 CIPSI expansions for multiple states of the same symmetry and illustrate the scheme on the challenging case of thiophene. This molecule forms the backbone of a class of π-conjugated donor polymers in organic solar-cell devices6−11 and the computation of its electronic excited states has been the subject of several theoretical investigations.12−21 In particular, the accurate prediction of the lowest, bright excited state of thiophene is difficult for traditional ab initio methods (e.g., density functional theory, multiconfigurational perturbation approaches), with different levels of theory spanning a range of about 0.5 eV, as we also illustrate in this work. The multireference character of this state calls, in fact, for the use of highly correlated electronic structure methods, and its inherent complexity renders this a perfect test case for our modified CIPSI selection approach.

By simply assigning a higher weight in the CIPSI selection criterion to the state showing a slower convergence, we succeed in generating CIPSI expansions for the ground and excited states of thiophene fulfilling the basic condition of similar PT2 energy corrections and CI variances. The resulting Jastrow–Slater wave functions yield variational Monte Carlo (VMC) vertical excitation energies, which are lower and in closer agreement with the diffusion Monte Carlo (DMC) counterparts than those provided by the default selection scheme. Furthermore, we obtain converged estimates of the QMC vertical excitation energy already with compact expansions containing a few thousand determinants, and our best estimates are within 0.05 eV of the reference coupled cluster (CC) value. Finally, we compute the optimal ground- and excited-state geometries in VMC, following the relevant root and generating CIPSI expansions with similar PT2 corrections for both states along the optimization path. The optimal VMC structural parameters are in excellent agreement with the CASPT2 or CC estimates, namely, within 0.01 Å for the bond lengths and, in the excited state, 1° for the bond angles.

This article is organized as follows: we describe the modified CIPSI selection procedure for multiple states of the same symmetry in Section 2 and present the computational details in Section 3. The construction procedure of the wave functions with the modified selection scheme is detailed in Section 4.1. We present the QMC vertical excitation energies in Section 4.2 and the optimal ground- and excited-state VMC structures in Section 4.4. We conclude in Section 5.

2. Methods

In this work, we consider excited states that are not the lowest in their symmetry class. In the QMC calculations, we describe them together with the lower-energy states of the same symmetry via a set of Jastrow–Slater wave functions with different CI coefficients but the same Jastrow and orbital parameters

2. 1

where Ndet is the total number of determinants and n is an electronic-state index. We use a Jastrow factor, which describes electron–nucleus and electron–electron correlations (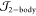Inline graphic), and guarantees that Kato’s cusp conditions are satisfied at the interparticle coalescence points.

To ensure that the common nonlinear (Jastrow and orbital) parameters offer a reasonable description of all states of interest, we optimize them by minimizing the state-average (SA) energy22 defined as

2. 2

where the weights, wnQMC, sum up to one and are kept fixed during the optimization. Orthogonality between the states is maintained through the (linear) CI coefficients whose optimal values are obtained by solving a generalized eigenvalue problem in the basis of the determinants multiplied by the Jastrow factor.

As described in ref (5), we alternate a number of optimization steps of the nonlinear parameters with a step of optimization of the linear coefficients. For the former, we follow the down-hill gradient of the SA energy in a scheme inspired by the stochastic reconfiguration approach for a single state23 and solve the relevant equations in a low-memory conjugate-gradient implementation.24 For the latter, we use a memory-efficient Davidson diagonalization method that allows the computation of the lowest-energy eigenvalues without explicit construction of the entire Hamiltonian and overlap matrices.24,25 Combining this optimization scheme with the fast generation of the quantities needed in the QMC estimators,3,4 we can optimize QMC wave functions for ground and excited states containing large determinantal expansions and several thousand parameters.

To construct the determinantal component of these wave functions, we employ an improved CIPSI approach that allows us to iteratively select the most important determinants required for the balanced description of multiple electronic states. Starting from an initial reference subspace, 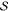Inline graphic, given by the union of determinants describing the states of interest, an external determinant |α⟩ is selected based on its weighted second-order perturbation (PT2) energy contribution obtained via the Epstein–Nesbet partitioning of the Hamiltonian26,27

2. 3

where

2. 4

and ΨnCIPSI is the current normalized CIPSI wave function for state n. In this partitioning scheme, the first-order energy correction is zero by definition. The determinant |α⟩ is added to 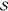Inline graphic if its energy contribution eα is higher than a given threshold, and the threshold is automatically adjusted so that the number of determinants in Inline graphic is increased by a certain percentage at every iteration.

We have recently shown that the use of iso-PT2 CIPSI expansions results in a balanced description of the relevant states when complemented by a Jastrow factor and fully optimized in QMC; these expansions were found to yield accurate QMC estimates of the excitation energies for relatively small numbers of determinants.2

When interested in the lowest-energy states of different symmetries, one can, in principle, perform the expansion separately for each state until the corresponding perturbation energy contribution is equal to a target value. Alternatively, one can generate the expansions using one set of orbitals for all states and enlarging the union space, 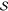Inline graphic, through a single threshold. Following this last scheme, we were able to obtain matched PT2 corrections2 by simply choosing the weights in the selection step eq 3 as

2. 5

where the index k runs over all determinants in the current ΨnCIPSI. Such a choice follows ref (28), with modifications due to the fact that we perform the CIPSI selection in the basis of determinants and not of configuration state functions (CSFs). The resulting expansions for states of different symmetries have different sizes since they do not share any common determinant (determinants of a given symmetry have zero coefficients in the expansion for a state belonging to a different symmetry class).

Here, we are interested in states of the same symmetry expanded on the same set of determinants, where a CSF may have nonzero and non-negligible overlap with all states of interest. In this case, we find that the use of the simple weights, eq 5, does not yield iso-PT2 expansions. To improve this balance, we explore a simple modification to the selection scheme where we multiply the weights of eq 5 by user-given “state-average” weights, wnSA, i.e.,

2. 6

In addition to the PT2 correction, we investigate the behavior of the CI variance, σCI2, which is defined as the variance of the full CI (FCI) Hamiltonian

2. 7

and goes to zero as the CIPSI wave function approaches the FCI limit. Since the CI variance is also an indicator of the quality of the CIPSI wave function, one can match the CI variances of the states of interest together with the PT2 energy correction or as an alternative to the PT2 criterion. We note that the CI variance should not be confused with the QMC variance, which is defined in terms of the exact Hamiltonian.

3. Computational Details

All QMC calculations are performed using the program package CHAMP.29 We employ the Burkatzki–Filippi–Dolg (BFD) scalar-relativistic energy-consistent Hartree–Fock (HF) pseudopotentials and correlation-consistent Gaussian basis sets that have been specifically constructed for these pseudopotentials.30,31 When unclear, we append the “(BFD)” suffix to these basis sets to avoid confusion with the corresponding all-electron basis sets. For most test QMC calculations, we use a minimally augmented double-ζ (maug-cc-pVDZ) basis set, where the basis on the heavy atoms is augmented with s and p diffuse functions. Final calculations are computed with the fully augmented double (aug-cc-pVDZ) and triple (aug-cc-pVTZ) basis sets. All diffuse functions are obtained from the corresponding all-electron Dunning’s correlation-consistent basis sets.32 We employ a two-body Jastrow factor including electron–electron and electron–nucleus correlation terms.33

We optimize all parameters (Jastrow, orbital, and CI coefficients) of the Jastrow–Slater wave function in VMC, as described above. We employ equal weights wnQMC in the state-average energy of eq 2 and a guiding wave function Ψg = ∑n|Ψn|2 in the sampling to ensure a reasonable overlap with all states of interest.22 In the VMC geometry optimization, we relax the structure without symmetry constraints and simply follow the path of steepest descent for the root of interest by appropriately rescaling the interatomic forces and using an approximate constant diagonal Hessian. After convergence, we perform 40 additional optimization steps to estimate the optimal average structural parameters. In the DMC calculations, we treat the pseudopotentials beyond the locality approximation using the T-move algorithm34 and employ an imaginary time step of 0.02 a.u. with single-electron moves. This time step yields DMC excitation energies converged to better than 0.01 eV also for the simplest wave function employed here (see S2).

We carry out the CIPSI calculations with Quantum Package35 using orbitals obtained from complete active space self-consistent field (CASSCF) calculations performed with the program GAMESS(US),36,37 correlating six electrons in five π orbitals in a minimal CAS(6,5). The CIPSI expansions are constructed to be eigenstates of Ŝ2 and are mapped into the basis of CSFs, effectively reducing the number of optimization parameters in VMC. The PSI4 package38 is used to compute the reference ground-state geometry and the Dalton package39,40 is used to compute the vertical excitation energies within the iterative approximate coupled cluster singles, doubles, and triples (CC3) approach. We perform the n-electron valence perturbation theory (NEVPT2) calculations using the Molpro 2019.2 code.41,42

All vertical excitation energies are computed on the fixed ground-state structure optimized at the CC3 level with an all-electron aug-cc-pVTZ basis and the frozen-core (FC) approximation. Unless explicitly stated, the calculations presented below are computed with the BFD pseudopotentials and the corresponding basis sets, irrespective of the level of theory.

4. Results and Discussion

We focus here on the lowest-lying, bright π → π* singlet excited state of the thiophene molecule (C4H4S). The ground-state structure of thiophene has C2v symmetry and the ground and the targeted excited state belong to the A1 irreducible representation. The accurate computation of this excited state is challenging because of its multireference character: in a CASSCF calculation with the minimal active space correlating six electrons in five π orbitals, one finds that the two dominant transitions, HOMO-1 → LUMO and HOMO → LUMO + 1, account for almost 60 and 20% of the wave function, respectively, while higher-order double excitations with four unpaired electrons make up for another 7%. The ground state, on the other hand, is single reference, dominated by the HF determinant, which alone accounts for more than 90% of the wave function in the same calculation.

The nature of this excited state leads to difficulties in estimating the corresponding vertical excitation energy, which we find to span a range of about 0.5 eV, between 5.60 and 6.07 eV, across different levels of theory as illustrated in Figure 1. Time-dependent density functional theory (TDDFT) in combination with different exchange-correlation functionals incorrectly places a π → π* state of B2 symmetry lower than the A1 state by about 0.1 eV or less.19 All tested wave function methods (CASPT2, NEVPT2, QMC, and CC3), instead, identify our state of interest as the energetically lowest singlet excited state, in qualitative agreement with experimental observations;17,43−45 however, they yield very different excitation energies.

Figure 1.

Figure 1

Open in a new tab

Vertical excitation energy of thiophene for the π → π* singlet transition to the lowest, bright excited state, computed with different approaches. All calculations are performed with the BFD pseudopotentials and the corresponding aug-cc-pVTZ basis set with the exception of the all-electron CC3/aug-cc-pVTZ (FC) calculation. We also include schematic representation of thiophene, where yellow, blue, and white denote sulfur, carbon, and hydrogen, respectively.

Estimating the FCI excitation energy of thiophene at the CIPSI level is challenging because of the size of the FCI space. Consequently, CIPSI calculations are limited to relatively small basis sets and yield extrapolated energy differences characterized by uncertainties as large as 0.08 eV:46 the ground state converges faster than the excited state, and the excited-state energy displays a change in the slope at very large determinantal expansions, rendering the extrapolation to the FCI limit difficult. Within a small basis set, CC3 yields excitation energy of thiophene compatible with the FCI estimate,46 and a T1 analysis of this CC3 excitation energy yields a T1 value of 0.87. Based on extensive benchmarking of similar cases,46,47 these combined findings suggest that the excitation energy computed at the CC3 level is likely accurate to better than 0.05 eV, and we, therefore, use this level of theory to provide the reference excitation energy for this state of thiophene. As regards the choice of basis, the CC3/aug-cc-pVTZ value was shown to differ from the complete basis set limit at the same level of theory by only 0.02 eV.47 In conclusion, since we use a slightly different geometry than those of refs (46, 47) and the QMC calculations are done with pseudopotentials, we compare our QMC results to the CC3/aug-cc-pVTZ(BFD) excitation energy computed with our geometry, which we believe to be an accurate estimate of the exact vertical excitation energy for our study.

4.1. Modified Selection Criterion for CIPSI

For the ground and excited states of thiophene, we construct CIPSI expansions of increasing length from subsequent CIPSI iterations. To test the different selection criteria, we use the maug-cc-pVDZ basis set and the common set of CAS(6,5) orbitals.

We first adopt the simple reweighting scheme, eq 5, that we successfully used for states of different symmetries2 and plot in panels (b) and (c) of Figure 2 the resulting differences ΔEPT2 between the PT2 energy corrections and ΔσCI2 between the CI variances of the ground and excited states (black symbols labeled “cmax”). We find that the convergence of the ground state is faster than that of the excited state: ΔEPT2 decreases and ΔσCI increases over the whole range of expansion sizes considered (also see Table S3). The faster convergence of the ground state is further reflected in the excitation energy ΔECI , shown in panel (d), which also grows with the expansion size. This is consistent with the observation that partitioning the determinants in each expansion based on the relative contribution to each state gives an insufficient number of “excited-state” determinants, namely, about 1.3–1.6 times more determinants contributing to the excited than to the ground state (see Table S4) compared to a significantly higher ratio of about 2.4–2.9 in our previous calculations with matched PT2 energy corrections for formaldehyde and thioformaldehyde.2 Therefore, all indications are that the description of the states is increasingly unbalanced in favor of the ground state as the number of determinants gets larger, at least within the range explored.

Figure 2.

Figure 2

Open in a new tab

CI results for the ground state (GS) and the excited state (ES) of thiophene with CIPSI expansions of increasing size: total energy (a); difference of the ground- and excited-state PT2 energy corrections ΔEPT2 (b) and CI variances ΔσCI2 (c); and vertical excitation energy ΔECI (d). We employ two reweighting schemes in the selection criterion, namely, wn and wncmax ×wn, and different choices of state-average weights, wnSA. The maug-cc-pVDZ basis set is used.

To achieve a more even description of the two states, we therefore modify the selection criterion by introducing the state-average weights, wnSAeq 6, and place a larger weight on the excited state. We show the resulting difference of the ground- and excited-state PT2 energy corrections and CI variances for sets of expansions generated with different choices of the state-average weights (“cmax × SA”) in Figure 2. The modified scheme clearly represents an improvement on the bare “cmax” criterion, and the use of 0.425 and 0.575 as wn weights for the ground and the excited state, respectively, leads to nearly optimal matching of PT2 corrections and CI variances for all expansion sizes.

Partitioning the determinants based on their dominant relative contributions to the two states reveals that the ratio between “excited-state” and “ground-state” determinants is now increased to about 1.9–2.1, as shown in Table S4. Furthermore, an inspection of the CI energies ECI obtained with both schemes, plotted in the panel (a) of Figure 2, shows that, for comparable sizes of the expansion, the modified selection criterion slows down the convergence of the ground state and, to a much lesser extent, speeds up the convergence of the excited state. The CI excitation energy, compared in panel (d) with the CC3 value obtained in the same basis, is also significantly reduced from about 6.6 eV with the “cmax” criterion to 5.9 eV for the larger expansions considered here. For comparison, the CC3/aug-cc-pVTZ excitation energy is 5.65 eV. Importantly, we find that the ideal weights depend rather weakly on the orbital basis employed in the determinant selection (see Figure S1) and also on the basis set (see Figures S2 and S3), being always very close to 0.4 and 0.6. Finally, we note that, while we set here the state-average weights manually, one can, in principle, devise a scheme where the values of wnSA are dynamically adjusted during the CIPSI iterations to enforce the iso-PT2 condition as closely as possible.

4.2. Impact of Selection on QMC-CIPSI Excitation Energies

In Figure 3, we illustrate the impact of the CIPSI selection on the VMC and DMC vertical excitation energies of thiophene computed with the corresponding Jastrow-CIPSI wave functions fully optimized at the VMC level. To this aim, we consider the CIPSI expansions generated with the old “cmax” and the new “cmax × SA” scheme and the ideal weights.

Figure 3.

Figure 3

Open in a new tab

VMC (filled) and DMC (empty symbols) vertical excitation energies ΔEQMC of thiophene versus the number of determinants for CIPSI determinantal expansions generated with the “cmax” (black) and “cmax × SA” (red) schemes with state-average weights 0.425 and 0.575. The horizontal dashed lines are drawn as guides and correspond to the average of the last five values of the VMC or DMC excitation energies. We also show VMC and DMC results for the CAS determinantal expansions (6,5), (10,9), and (10,14) in order of increasing number of determinants. The maug-cc-pVDZ basis set is used for all QMC calculations.

For all but the smallest expansion sizes, the VMC excitation energies corresponding to the “cmax” determinantal components settle around about 5.9 eV. Performing DMC calculations for these Jastrow-CIPSI wave functions decreases the excitation energy, which remains, however, more than 0.1 eV higher than the CC3 reference. Therefore, while both VMC and DMC substantially improve on the starting CIPSI excitation energy, which is as high as 6.6 eV for the largest expansions considered here (see Figure 2), the bias of the CIPSI selection toward the ground state is reflected in the QMC overestimation of the excitation energy.

When we use the expansions obtained with the “cmax × SA” reweighting scheme, we observe that the convergence of the ground state is somewhat slowed down with respect to “cmax” expansions of comparable size, while the VMC excited-state energies are largely unaffected (see Table S1). This leads to reduced VMC excitation energies, which quickly converge to about 5.8 eV. The VMC correction on the CIPSI excitation energy is now smaller and the same holds for the improvement of DMC upon VMC.

For comparison, in Figure 3, we also plot the QMC excitation energies computed with Jastrow–Slater wave functions built with three different CAS expansions: the minimal CAS(6,5), a CAS(10,9) correlating two additional occupied σ and two unoccupied σ* orbitals on the C–S bonds, and a CAS(10,14) that further includes the five 3d orbitals of the S atom. For the largest active space, the expansions are truncated with a threshold of 5 × 10–4 on the CSF coefficients and the union of the CSFs of the ground and excited states is retained. While increasing the active space lowers the QMC total energies (see Table S1), in all three cases, the VMC excitation energies are compatible within statistical errors and rather comparable to their DMC counterparts, which remain higher than the DMC values obtained with the CIPSI expansions and either criterion.

4.3. Best-Quality QMC Excitation Energy

The use of the “cmax × SA” criterion to generate iso-PT2 CIPSI expansions has the desired effect of yielding a more balanced description of the two states also at the QMC level. Furthermore, the calibration of the state-average weights we have carried out for the small maug-cc-pVDZ basis also helps us in selecting an appropriate range of values when constructing wave functions with other basis sets.

In particular, since the use of a maug-cc-pVDZ basis set is not sufficient for an accurate treatment of the vertical excitation energy of thiophene, we generate new CIPSI expansions with both the aug-cc-pVDZ and aug-cc-pVTZ basis sets, using the “cmax × SA” scheme, and find that the choice of weights, 0.4 and 0.6, leads to well-matched PT2 contributions and CI variances for both basis sets. As shown in Figure 4, the resulting VMC and DMC excitation energies are red-shifted relative to comparable expansions in the smaller maug-cc-pVDZ basis, and lie within less than 0.05 eV of our best CC3 reference value for both basis sets.

Figure 4.

Figure 4

Open in a new tab

VMC (filled) and DMC (empty circles) vertical excitation energies ΔEQMC of thiophene versus the number of determinants for CIPSI expansions generated with the aug-cc-pVDZ (aug-D) and aug-cc-pVTZ (aug-T) basis sets and the “cmax × SA” scheme. The VMC excitation energy with the aug-T basis is also estimated as the difference ΔEVMCfit = EES(σ2) – EGSfit(σ2) of the fits of the energies against the VMC variance of the two states (inset; the line of the fit difference is solid over the range of variances covered by the wave function used, with lower values of σ2 corresponding to a larger number of determinants).

Finally, we also estimate the vertical excitation energies by matching the VMC variances for the wave functions.48,49 To this aim, we linearly fit the VMC ground- and excited-state energies separately against their corresponding VMC variances σ2 (see Figure S4) and then compute the excitation energy as EESfit(σ2) – EGS(σ2). As shown in the inset of Figure 4, we find that the estimate of the excitation energy falls below the CC3 reference and decreases with increasing number of determinants, deviating for the largest expansions by about 0.1 eV. Therefore, while the adoption of the iso-PT2 “cmax × SA” reweighting scheme yields a more consistent estimate of the excitation energies, we observe a somewhat less predictable behavior when matching the VMC variances.

4.4. Optimal Ground- and Excited-State Structures

To optimize the structure of thiophene in the ground and excited states in VMC, the maug-cc-pVDZ basis set is found to be sufficiently accurate as verified with the use of the aug-cc-pVDZ basis set in Table S7, and we will therefore proceed with this cheaper basis set to determine the structural parameters of the minima.

For the ground state, we start from the geometry and wave functions previously employed to compute the vertical excitation energies of Table 1, for selected values of the number of determinants. For all chosen expansion sizes, we obtain very accurate geometries with differences of about 5 mÅ in the bond lengths with respect to the reference values, as shown in Table 2.

Table 1. VMC and DMC Ground- and Excited-State Energies (a.u.) and Vertical Excitation Energies (eV) of Thiophene for Increasing CIPSI Expansions in Fully Optimized Jastrow–Slater Wave Functions and Different Basis Setsa.

    VMC
 DMC
no. det no. param E(GS) E(ES) ΔE E(GS) E(ES) ΔE
aug-cc-pVDZ
1023 3084 –35.28511(30) –35.07512(31) 5.714(12) –35.35234(29) –35.14325(29) 5.690(11)
5116 6389 –35.29685(29) –35.08692(30) 5.712(11) –35.35678(27) –35.14731(27) 5.700(10)
11122 9412 –35.30335(28) –35.09350(29) 5.710(11) –35.35884(26) –35.14943(26) 5.698(10)
30615 16370 –35.31022(28) –35.09988(28) 5.724(11) –35.36062(28) –35.15117(28) 5.699(11)
aug-cc-pVTZ
1019 7442 –35.29270(28) –35.08212(29) 5.730(11) –35.35744(28) –35.14760(28) 5.710(11)
5051 14656 –35.30375(27) –35.09326(28) 5.728(11) –35.36164(26) –35.15294(27) 5.679(10)
10755 19674 –35.30913(27) –35.09948(27) 5.705(10) –35.36438(22) –35.15464(22) 5.707(09)
31581 33363 –35.31600(26) –35.10596(27) 5.715(10) –35.36534(46) –35.15666(44) 5.678(17)
               
CC3/aug-cc-pVDZ (BFD)         5.678
CC3/aug-cc-pVTZ (BFD)         5.65
Open in a new tab
a

“cmax × SA” selection criterion is used.

Table 2. Optimal VMC Ground- and Excited-State Bond Lengths (Å) and Angles (deg) of Thiophene Using “cmax × SA” CIPSI Expansions and the maug-cc-pVDZ Basis Set.

state δEPT2 no. det no. param C–C C=C C–S δCCCS
GS –0.67 1037 2002 1.4281(2) 1.3662(1) 1.7201(2) 0.06(5)
  –0.64 2614 2823 1.4282(2) 1.3681(2) 1.7202(1) 0.09(3)
  –0.59 5605 4106 1.4290(2) 1.3669(1) 1.7218(1) -0.08(3)
  –0.54 11003 6326 1.4279(4) 1.3676(4) 1.7223(4) 0.05(4)
CASPT2a 1.430 1.372 1.720 0.00
CCSD(T) (BFD)b 1.425 1.368 1.717 0.00
CCSD(T) (FC)b 1.430 1.372 1.728 0.00
CC3 (FC)b 1.430 1.372 1.729 0.00
ES –0.67 1663 3630 1.4396(7) 1.4161(6) 1.7626(5) 24.84(2)
  –0.63 3752 4957 1.4388(7) 1.4151(3) 1.7655(4) 25.58(3)
  –0.59 8304 7271 1.4383(1) 1.4144(2) 1.7709(1) 25.75(2)
  –0.546 15815 10278 1.4422(7) 1.4112(4) 1.7725(6) 26.01(7)
CASPT2a 1.448 1.423/1.416 1.782/1.778 26.7
ADC(2)c 1.422 1.419 1.796 28.2
DFT/MRCId 1.436 1.394 1.799 27.4
Open in a new tab
a

MS-CASPT2(10,8)/6-31G** from ref (16).

b

CC/aug-cc-pVTZ either all-electron (FC) or pseudotpotential (BFD).

c

ADC(2)/cc-pVTZ from ref (19).

d

DFT/MRCI/TZVP from ref (15).

The excited-state global minimum is the S-puckered structure of symmetry Cs shown in Figure 5 as obtained in previous studies employing the ADC(2),19 DFT/MRCI,15,50 and MS-CASPT216 approaches. It is interesting to note that TDDFT predicts instead a C-puckered minimum with the S-puckered structure actually being a transition state.18 Since the excited state has the same symmetry as the ground state also when the molecular symmetry is lowered from C2v to Cs, we need to follow the path of steepest descent for the second root in optimizing the excited-state structure. We do not impose any symmetry constraints and start from a slightly distorted geometry, where we reoptimize the same wave functions of Table 1 selected for the ground-state structural optimization. In the subsequent steps, we generate iso-PT2 CIPSI wave functions along the whole minimization path for both the ground and the excited state.

Figure 5.

Figure 5

Open in a new tab

Optimal ground- and excited-state structures of thiophene.

The final converged structural parameters are shown in Table 2: the optimized geometry is S-puckered in agreement with previous correlated calculations, with an elongation of all bonds, in particular, of the former C=C and the C–S bonds. The bond lengths and angles obtained with Jastrow-CIPSI wave functions are within 10 mÅ and 1° of the corresponding CASPT2 values, respectively.

5. Conclusions

In this work, we present a systematic investigation on how to obtain balanced CIPSI expansions for multiple states of the same symmetry and corresponding high-quality QMC excitation energies and optimal excited-state geometries. We focus on a case, the lowest-energy bright state of thiophene, which is characterized by a significant multireference character.

To this aim, we modify here the CIPSI selection scheme to treat multiple states of the same symmetry with wave functions expressed on a common set of determinants by introducing additional weights in the energy threshold for the selection step. This enables us to obtain expansions for the two states with the same PT2 energy corrections and CI variances, that is, similar estimated errors with respect to the full configuration interaction limit. Importantly, we find that the additional weights introduced in the selection scheme are largely independent of the basis set size and the orbital choice as the rate of convergence of the energy appears to be governed by the intrinsic multireference character of the excited state.

In practice, for thiophene, the new criterion slows down the convergence of the ground state at every CIPSI iteration and, to a lesser extent, accelerates that of the excited state, making the quality of the two CI wave functions more similar. Using these expansions as determinantal components in Jastrow–Slater wave functions leads to DMC excitation energies within 0.05(2) eV of the theoretical best estimate available, already when the expansions comprise only about 5000 determinants. With these Jastrow-CIPSI wave functions, structural relaxation in the ground state yields VMC bond lengths, which are compatible with the reference values to better than 0.01 Å. Following the second root in the geometry optimization while maintaining an iso-PT2 description of the ground and excited states, we obtain optimal VMC excited-state bond lengths and angles, which are within less than 0.01 Å and 1° of the best available estimates, respectively.

In summary, also in a case like thiophene where a reliable treatment fully at the CIPSI level is quite demanding, we are able to generate balanced Jastrow–Slater wave functions for multiple states and determine accurate excited-state properties in QMC, using relatively short CIPSI expansions. Therefore, when increasing the number of electrons or the size of the basis set, we expect that QMC in combination with compact and balanced CIPSI expansions will remain a viable route to deliver high-quality excited-state potential energy surfaces in the domain of applications where selected configuration interaction becomes instead intractable.

Acknowledgments

This work is part of the Industrial Partnership Programme (IPP) “Computational sciences for energy research” of the Netherlands Organisation for Scientific Research (NWO-I, formerly FOM). This research program is cofinanced by Shell Global Solutions International B.V. The work is also partially supported by the European Centre of Excellence in Exascale Computing TREX, Targeting Real Chemical Accuracy at the Exascale, which has received funding from the European Union’s Horizon 2020, Research and Innovation program, under grant agreement no. 952165. The calculations have been carried out on the Dutch national supercomputer Cartesius with the support of SURF Cooperative.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.1c00212.

  • CIPSI energies, PT2 energy corrections, and CI variances; VMC and DMC ground- and excited-state energies and vertical excitation energies computed with the maug-cc-pVDZ and aug-cc-pVTZ basis sets; dependence of the DMC energies on the time step; dependence of the wnSA weights on the choice of orbitals and the basis set; partitioning of the CSFs between the two states; comparison with other levels of theory; ground- and excited-state VMC geometries obtained with the aug-cc-pVDZ basis set; and ground-state CC3 geometry (PDF)

The authors declare no competing financial interest.

Supplementary Material

ct1c00212_si_001.pdf (928KB, pdf)

References

  1. Dash M.; Moroni S.; Scemama A.; Filippi C. Perturbatively Selected Configuration-Interaction Wave Functions for Efficient Geometry Optimization in Quantum Monte Carlo. J. Chem. Theory Comput. 2018, 14, 4176–4182. 10.1021/acs.jctc.8b00393. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Dash M.; Feldt J.; Moroni S.; Scemama A.; Filippi C. Excited States with Selected Configuration Interaction-Quantum Monte Carlo: Chemically Accurate Excitation Energies and Geometries. J. Chem. Theory Comput. 2019, 15, 4896–4906. 10.1021/acs.jctc.9b00476. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Filippi C.; Assaraf R.; Moroni S. Simple formalism for efficient derivatives and multi-determinant expansions in quantum Monte Carlo. J. Chem. Phys. 2016, 144, 194105 10.1063/1.4948778. [DOI] [PubMed] [Google Scholar]
  4. Assaraf R.; Moroni S.; Filippi C. Optimizing the Energy with Quantum Monte Carlo: A Lower Numerical Scaling for Jastrow-Slater Expansions. J. Chem. Theory Comput. 2017, 13, 5273–5281. 10.1021/acs.jctc.7b00648. [DOI] [PubMed] [Google Scholar]
  5. Cuzzocrea A.; Scemama A.; Briels W. J.; Moroni S.; Filippi C. Variational principles in quantum Monte Carlo: The troubled story of variance minimization. J. Chem. Theory Comput. 2020, 16, 4203–4212. 10.1021/acs.jctc.0c00147. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Roncali J. Conjugated poly (thiophenes): synthesis, functionalization, and applications. Chem. Rev. 1992, 92, 711–738. 10.1021/cr00012a009. [DOI] [Google Scholar]
  7. Zhang F.; Wu D.; Xu Y.; Feng X. Thiophene-based conjugated oligomers for organic solar cells. J. Mat. Chem. 2011, 21, 17590–17600. 10.1039/c1jm12801a. [DOI] [Google Scholar]
  8. Bian L.; Zhu E.; Tang J.; Tang W.; Zhang F. Recent progress in the design of narrow bandgap conjugated polymers for high-efficiency organic solar cells. Prog. Polym. Sci. 2012, 37, 1292–1331. 10.1016/j.progpolymsci.2012.03.001. [DOI] [Google Scholar]
  9. Xu Y.-X.; Chueh C.-C.; Yip H.-L.; Chang C.-Y.; Liang P.-W.; Intemann J. J.; Chen W.-C.; Jen A. K.-Y. Indacenodithieno [3, 2-b] thiophene-based broad bandgap polymers for high efficiency polymer solar cells. Polym. Chem. 2013, 4, 5220–5223. 10.1039/c3py00121k. [DOI] [Google Scholar]
  10. Meerheim R.; Körner C.; Leo K. Highly efficient organic multi-junction solar cells with a thiophene based donor material. Appl. Phys. Lett. 2014, 105, 063306 10.1063/1.4893012. [DOI] [Google Scholar]
  11. Duan C.; Gao K.; Colberts F. J.; Liu F.; Meskers S. C.; Wienk M. M.; Janssen R. A. Thiophene rings improve the device performance of conjugated polymers in polymer solar cells with thick active layers. Adv. Energy Mater. 2017, 7, 1700519 10.1002/aenm.201700519. [DOI] [Google Scholar]
  12. Wan J.; Hada M.; Ehara M.; Nakatsuji H. Electronic excitation spectrum of thiophene studied by symmetry-adapted cluster configuration interaction method. J. Chem. Phys. 2001, 114, 842–850. 10.1063/1.1332118. [DOI] [Google Scholar]
  13. Kleinschmidt M.; Tatchen J.; Marian C. M. Spin-orbit coupling of DFT/MRCI wavefunctions: Method, test calculations, and application to thiophene. J. Comput. Chem. 2002, 23, 824–833. 10.1002/jcc.10064. [DOI] [PubMed] [Google Scholar]
  14. Pastore M.; Angeli C.; Cimiraglia R. A multireference perturbation theory study on the vertical electronic spectrum of thiophene. Theor. Chem. Acc. 2007, 118, 35–46. 10.1007/s00214-006-0239-5. [DOI] [Google Scholar]
  15. Salzmann S.; Kleinschmidt M.; Tatchen J.; Weinkauf R.; Marian C. M. Excited states of thiophene: ring opening as deactivation mechanism. Phys. Chem. Chem. Phys. 2008, 10, 380–392. 10.1039/B710380H. [DOI] [PubMed] [Google Scholar]
  16. Stenrup M. Theoretical study of the radiationless deactivation mechanisms of photo-excited thiophene. Chem. Phys. 2012, 397, 18–25. 10.1016/j.chemphys.2011.12.004. [DOI] [Google Scholar]
  17. Holland D.; Trofimov A.; Seddon E.; Gromov E.; Korona T.; De Oliveira N.; Archer L.; Joyeux D.; Nahon L. Excited electronic states of thiophene: high resolution photoabsorption Fourier transform spectroscopy and ab initio calculations. Phys. Chem. Chem. Phys. 2014, 16, 21629–21644. 10.1039/C4CP02420F. [DOI] [PubMed] [Google Scholar]
  18. Prlj A.; Curchod B. F.; Corminboeuf C. Excited state dynamics of thiophene and bithiophene: new insights into theoretically challenging systems. Phys. Chem. Chem. Phys. 2015, 17, 14719–14730. 10.1039/C5CP01429H. [DOI] [PubMed] [Google Scholar]
  19. Prlj A.; Curchod B. F.; Fabrizio A.; Floryan L.; Corminboeuf C. Qualitatively incorrect features in the TDDFT spectrum of thiophene-based compounds. J. Phys. Chem. Lett. 2015, 6, 13–21. 10.1021/jz5022087. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Kölle P.; Schnappinger T.; de Vivie-Riedle R. Deactivation pathways of thiophene and oligothiophenes: internal conversion versus intersystem crossing. Phys. Chem. Chem. Phys. 2016, 18, 7903–7915. 10.1039/C5CP07634J. [DOI] [PubMed] [Google Scholar]
  21. Schnappinger T.; Kölle P.; Marazzi M.; Monari A.; González L.; de Vivie-Riedle R. Ab initio molecular dynamics of thiophene: the interplay of internal conversion and intersystem crossing. Phys. Chem. Chem. Phys. 2017, 19, 25662–25670. 10.1039/C7CP05061E. [DOI] [PubMed] [Google Scholar]
  22. Filippi C.; Zaccheddu M.; Buda F. Absorption spectrum of the green fluorescent protein chromophore: a difficult case for ab initio methods?. J. Chem. Theory Comput. 2009, 5, 2074–2087. 10.1021/ct900227j. [DOI] [PubMed] [Google Scholar]
  23. Sorella S.; Casula M.; Rocca D. Weak binding between two aromatic rings: Feeling the van der Waals attraction by quantum Monte Carlo methods. J. Chem. Phys. 2007, 127, 014105 10.1063/1.2746035. [DOI] [PubMed] [Google Scholar]
  24. Neuscamman E.; Umrigar C. J.; Chan G. K.-L. Optimizing large parameter sets in variational quantum Monte Carlo. Phys. Rev. B 2012, 85, 045103 10.1103/PhysRevB.85.045103. [DOI] [Google Scholar]
  25. Sabzevari I.; Mahajan A.; Sharma S. An accelerated linear method for optimizing non-linear wavefunctions in variational Monte Carlo. J. Chem. Phys. 2020, 152, 024111 10.1063/1.5125803. [DOI] [PubMed] [Google Scholar]
  26. Epstein P. S. The stark effect from the point of view of Schroedinger’s quantum theory. Phys. Rev. 1926, 28, 695. 10.1103/PhysRev.28.695. [DOI] [Google Scholar]
  27. Nesbet R. K. Configuration interaction in orbital theories. Proc. R. Soc. Lond. A. 1955, 312–321. 10.1098/rspa.1955.0134. [DOI] [Google Scholar]
  28. Angeli C.; Persico M. Multireference perturbation CI II. Selection of the zero-order space. Theor. Chem. Acc. 1997, 98, 117–128. 10.1007/s002140050285. [DOI] [Google Scholar]
  29. CHAMP is a quantum Monte Carlo program package written by C. J. Umrigar, C. Filippi, S.Moroni and collaborators..
  30. Burkatzki M.; Filippi C.; Dolg M. Energy-consistent pseudopotentials for quantum Monte Carlo calculations. J. Chem. Phys. 2007, 126, 234105 10.1063/1.2741534. [DOI] [PubMed] [Google Scholar]
  31. For the hydrogen atom, we use a more accurate BFD pseudopotential and basis set. Dolg, M.;Filippi, C., private communication.
  32. Kendall R. A.; Dunning T. H. Jr; Harrison R. J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. 10.1063/1.462569. [DOI] [Google Scholar]
  33. As Jastrow factor, we use the exponential of the sum of two fifth-order polynomials of the electron–nuclear and the electron–electron distances, respectively, and rescale the inter-particle distances as R = (1 – exp(−κr))/κ with κ set to 0.6 a.u. We employ different electron–nucleus Jastrow factors to describe the correlation of an electron with C, S, and H. The total number of free parameters to be optimized in the 2-body Jastrow factor is 17 for thiophene.
  34. Casula M. Beyond the locality approximation in the standard diffusion Monte Carlo method. Phys. Rev. B 2006, 74, 161102 10.1103/PhysRevB.74.161102. [DOI] [Google Scholar]
  35. Garniron Y.; Applencourt T.; Gasperich K.; Benali A.; Ferté A.; Paquier J.; Pradines B.; Assaraf R.; Reinhardt P.; Toulouse J.; Barbaresco P.; Renon N.; David G.; Malrieu J.-P.; Véril M.; Caffarel M.; Loos P.-F.; Giner E.; Scemama A. Quantum Package 2.0: An Open-Source Determinant-Driven Suite of Programs. J. Chem. Theory Comput. 2019, 15, 3591–3609. 10.1021/acs.jctc.9b00176. [DOI] [PubMed] [Google Scholar]
  36. Schmidt M. W.; Baldridge K. K.; Boatz J. A.; Elbert S. T.; Gordon M. S.; Jensen J. H.; Koseki S.; Matsunaga N.; Nguyen K. A.; Su S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. 10.1002/jcc.540141112. [DOI] [Google Scholar]
  37. Gordon M. S.; Schmidt M. W.. Theory and Applications of Computational Chemistry; Elsevier, 2005; pp 1167–1189. [Google Scholar]
  38. Parrish R. M.; Burns L. A.; Smith D. G.; Simmonett A. C.; DePrince A. E. III; Hohenstein E. G.; Bozkaya U.; Sokolov A. Y.; Di Remigio R.; Richard R. M.; et al. Psi4 1.1: An open-source electronic structure program emphasizing automation, advanced libraries, and interoperability. J. Chem. Theory Comput. 2017, 13, 3185–3197. 10.1021/acs.jctc.7b00174. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Aidas K.; Angeli C.; Bak K. L.; Bakken V.; Bast R.; Boman L.; Christiansen O.; Cimiraglia R.; Coriani S.; Dahle P.; Dalskov E. K.; Ekström U.; Enevoldsen T.; Eriksen J. J.; Ettenhuber P.; Fernández B.; Ferrighi L.; Fliegl H.; Frediani L.; Hald K.; Halkier A.; Hättig C.; Heiberg H.; Helgaker T.; Hennum A. C.; Hettema H.; Hjertenæs E.; Høst S.; Høyvik I.-M.; Iozzi M. F.; Jansík B.; Jensen H. J. Aa.; Jonsson D.; Jørgensen P.; Kauczor J.; Kirpekar S.; Kjærgaard T.; Klopper W.; Knecht S.; Kobayashi R.; Koch H.; Kongsted J.; Krapp A.; Kristensen K.; Ligabue A.; Lutnæs O. B.; Melo J. I.; Mikkelsen K. V.; Myhre R. H.; Neiss C.; Nielsen C. B.; Norman P.; Olsen J.; Olsen J. M. H.; Osted A.; Packer M. J.; Pawlowski F.; Pedersen T. B.; Provasi P. F.; Reine S.; Rinkevicius Z.; Ruden T. A.; Ruud K.; Rybkin V. V.; Sałek P.; Samson C. C. M.; de Merás A. S.; Saue T.; Sauer S. P. A.; Schimmelpfennig B.; Sneskov K.; Steindal A. H.; Sylvester-Hvid K. O.; Taylor P. R.; Teale A. M.; Tellgren E. I.; Tew D. P.; Thorvaldsen A. J.; Thøgersen L.; Vahtras O.; Watson M. A.; Wilson D. J. D.; Ziolkowski M.; Ågren H. The Dalton quantum chemistry program system. WIREs Comput. Mol. Sci. 2014, 4, 269–284. 10.1002/wcms.1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Dalton, A Molecular Electronic Structure Program, Release v2016.2, 2016.
  41. Werner H.-J.; Knowles P. J.; Knizia G.; Manby F. R.; Schütz M. Molpro: a general-purpose quantum chemistry program package. WIREs Comput. Mol. Sci. 2012, 2, 242–253. 10.1002/wcms.82. [DOI] [Google Scholar]
  42. Werner H.-J.; Knowles P. J.; Knizia G.; Manby F. R.; Schütz M.; Celani P.; Györffy W.; Kats D.; Korona T.; Lindh R.; Mitrushenkov A.; Rauhut G.; Shamasundar K. R.; Adler T. B.; Amos R. D.; Bennie S. J.; Bernhardsson A.; Berning A.; Cooper D. L.; Deegan M. J. O.; Dobbyn A. J.; Eckert F.; Goll E.; Hampel C.; Hesselmann A.; Hetzer G.; Hrenar T.; Jansen G.; Köppl C.; Lee S. J. R.; Liu Y.; Lloyd A. W.; Ma Q.; Mata R. A.; May A. J.; McNicholas S. J.; Meyer W.; Miller T. F. III; Mura M. E.; Nicklass A.; O’Neill D. P.; Palmieri P.; Peng D.; Pflüger K.; Pitzer R.; Reiher M.; Shiozaki T.; Stoll H.; Stone A. J.; Tarroni R.; Thorsteinsson T.; Wang M.; Welborn M.. MOLPRO, Version 2019.2, a Package of Ab Initio Programs, 2019, https://www.molpro.net,.
  43. Rolf H.; Nordén B.; Thulstrup E. W.; et al. Magnetic circular dichroism of heterocycles: thiophene. Chem. Phys. Lett. 1977, 50, 306–308. 10.1016/0009-2614(77)80187-5. [DOI] [Google Scholar]
  44. Nordén B.; HÅkansson R.; Pedersen P. B.; Thulstrup E. W. The magnetic circular dichroism of five-membered ring heterocycles. Chem. Phys. 1978, 33, 355–366. 10.1016/0301-0104(78)87085-2. [DOI] [Google Scholar]
  45. Igarashi N.; Tajiri A.; Hatano M. The Magnetic Circular Dichroism of the Conjugated O-and S-Heterocycles. Bull. Chem. Soc. Jpn. 1981, 54, 1511–1516. 10.1246/bcsj.54.1511. [DOI] [Google Scholar]
  46. Véril M.; Scemama A.; Caffarel M.; Lipparini F.; Boggio-Pasqua M.; Jacquemin D.; Loos P.-F. QUESTDB: A database of highly accurate excitation energies for the electronic structure community. WIREs Comput. Mol. Sci. 2021, e1517 10.1002/wcms.1517. [DOI] [Google Scholar]
  47. Loos P.-F.; Lipparini F.; Boggio-Pasqua M.; Scemama A.; Jacquemin D. A Mountaineering Strategy To Excited States: Highly Accurate Energies and Benchmarks for Medium Sized Molecules. J. Chem. Theory Comput. 2020, 16, 1711–1741. 10.1021/acs.jctc.9b01216. [DOI] [PubMed] [Google Scholar]
  48. Robinson P. J.; Pineda Flores S. D.; Neuscamman E. Excitation variance matching with limited configuration interaction expansions in variational Monte Carlo. J. Chem. Phys. 2017, 147, 164114 10.1063/1.5008743. [DOI] [PubMed] [Google Scholar]
  49. Pineda Flores S. D.; Neuscamman E. Excited State Specific Multi-Slater Jastrow Wave Functions. J. Phys. Chem. A 2019, 123, 1487–1497. 10.1021/acs.jpca.8b10671. [DOI] [PubMed] [Google Scholar]
  50. Grimme S.; Waletzke M. A combination of Kohn-Sham density functional theory and multi-reference configuration interaction methods. J. Chem. Phys. 1999, 111, 5645–5655. 10.1063/1.479866. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ct1c00212_si_001.pdf (928KB, pdf)

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES