Abstract
Early afterdepolarizations (EADs) are abnormal depolarizations during the repolarizing phase of the action potential, which are associated with cardiac arrhythmogenesis. EADs are classified into phase‐2 and phase‐3 EADs. Phase‐2 EADs occur during phase 2 of the action potential, with takeoff potentials typically above −40 mV. Phase‐3 EADs occur during phase 3 of the action potential, with takeoff potential between −70 and −50 mV. Since the amplitude of phase‐3 EADs can be as large as that of a regular action potential, they are also called triggered activities (TAs). This also makes phase‐3 EADs and TAs much more arrhythmogenic than phase‐2 EADs since they can propagate easily in tissue. Although phase‐2 EADs have been widely observed, phase‐3 EADs and TAs have been rarely demonstrated in isolated ventricular myocytes. Here we carry out computer simulations of three widely used ventricular action potential models to investigate the mechanisms of phase‐3 EADs and TAs. We show that when the T‐type Ca2+ current (ICa,T) is absent (e.g., in normal ventricular myocytes), besides the requirement of increasing inward currents and reducing outward currents as for phase‐2 EADs, the occurrence of phase‐3 EADs and TAs requires a substantially large increase of the L‐type Ca2+ current and the slow component of the delayed rectifier K+ current. The presence of ICa,T (e.g., in neonatal and failing ventricular myocytes) can greatly reduce the thresholds of these two currents for phase‐3 EADs and TAs. This implies that ICa,T may play an important role in arrhythmogenesis in cardiac diseases.
Keywords: afterdepolarizations, model
Phase‐3 early afterdepolarizations (EADs) and triggered activities (TAs) are widely observed in Purkinje fiber cells but rarely in isolated ventricular myocytes. Computer simulations using ventricular action potential models are carried out to investigate the underlying mechanisms of phase‐3 EADs and TAs. In the absence of ICa,T, such as in normal ventricular myocytes, unrealistically large ICa,L and IKs conductances are needed for phase‐3 EADs and TAs to occur. However, the presence of ICa,T can substantially lower these conductance thresholds. Unlike phase‐2 EADs which are suppressed by increasing IKs, increasing IKs promotes phase‐3 EADs and TAs. ICa,T is a key current for the genesis of phase‐3 EADs and TAs and may play an important role in arrhythmogenesis in cardiac diseases, such as in heart failure in which ICa,T is present.

1. INTRODUCTION
Early afterdepolarizations (EADs), which are associated with lethal arrhythmias in cardiac diseases (Cranefield & Aronson, 1988; El‐Sherif et al., 1990; Rosen et al., 1984; Volders et al., 2000; Vos et al., 2000; Weiss et al., 2010), are abnormal depolarizations during the plateau or repolarizing phase of an action potential (AP). Early afterdepolarizations (EADs) are traditionally classified into phase‐2 EADs and phase‐3 EADs. Phase‐2 EADs are depolarizations during the plateau phase or phase 2 of the AP with takeoff potentials typically above −40 mV. Figure 1a shows an AP with normal repolarization (dashed line) and an AP with phase‐2 EADs (solid line) recorded from an isolated rabbit ventricular myocyte (Liu et al., 2012). In the one with EADs, when the voltage decays to below 0 (~−10 mV), it begins to oscillate, resulting in EADs. The takeoff potential of the EADs decreases and the amplitude increases to a maximum before repolarizing to the resting potential. The lowest takeoff potential is around −20 mV. Phase‐3 EADs are depolarizations during phase 3 of the AP with takeoff potentials typically ranging from −50 to −70 mV. Figure 1b shows an example of phase‐3 EADs recorded from an isolated Purkinje fiber (Damiano & Rosen, 1984). Traditionally, the large depolarizations are called phase‐3 EAD‐induced triggered activities (TAs). The ones with small depolarization amplitudes (even if there is no depolarization but just a slow repolarization, such as the last one in Figure 1b) are called phase‐3 EADs (Damiano & Rosen, 1984; Szabo et al., 1994, 1995). Similar to that of phase‐2 EADs, the takeoff potential also decreases with time, but the voltage of each TA reaches the same peak.
FIGURE 1.

Phase‐2 and phase‐3 EADs recorded in experiments. (a). Phase‐2 EADs recorded from an isolated rabbit ventricular myocyte (Liu et al., 2012). (b). Phase‐2 and phase‐3 EADs, and phase‐3 EAD induced triggered activities recorded from an isolated canine Purkinje fiber (Damiano & Rosen, 1984)
Due to the difference in their takeoff potentials and amplitudes, phase‐2 EADs and phase‐3 EADs and TAs exhibit different arrhythmogenic consequences. For example, experimental studies of Purkinje fibers have shown that phase‐2 EADs cannot conduct, but phase‐3 EAD induced TAs can conduct to form PVCs and trigger ventricular arrhythmias (El‐Sherif et al., 1990; Kupersmith & Hoff, 1985; Méndez & Delmar, 1985), indicating the importance of phase‐3 EADs and TAs in cardiac arrhythmogenesis. The mechanisms of phase‐2 EADs have been widely investigated and well understood (Qu et al., 2013), but the mechanisms of phase‐3 EADs and TAs remain to be elucidated. Therefore, understanding the mechanisms of phase‐3 EADs and TAs may provide important insights into the genesis and prevention of cardiac arrhythmias.
Phase‐2 EADs have been widely demonstrated in experiments of isolated myocytes and intact tissue. Phase‐3 EADs and TAs have been recorded in isolated Purkinje fiber experiments (Bailie et al., 1988; Damiano & Rosen, 1984; Davidenko et al., 1989; Gilmour & Moise, 1996; Roden & Hoffman, 1985; Szabo et al., 1994, 1995), promoted by hypokalemia and block of outward currents. They were also observed in ventricular tissue in some experiments (Bailie et al., 1988; Ben‐David & Zipes, 1988; El‐Sherif et al., 1990; Hwang et al., 2020), but it is unclear if they were oscillations caused by a single‐cell mechanism or by a tissue‐scale mechanism due to repolarization gradients (Huang et al., 2016; Maruyama et al., 2011). However, phase‐3 EADs and TAs have been rarely observed in isolated ventricular myocytes [low amplitude phase‐3 EADs with take‐off potential around −50 mV but not TAs were reported in isolated mice ventricular myocytes (Edwards et al., 2014; Tazmini et al., 2020)]. This was supported by a literature survey by Huang et al (Huang et al., 2018), which showed that the vast majority of the EADs recorded in experiments of isolated ventricular myocytes are phase‐2 EADs (see table 1 in Huang et al), no phase‐3 EADs and TAs were observed. Moreover, phase‐3 EADs and TAs were also not observed in computer simulations of ventricular AP models, and only phase‐2 EADs were reported [see EAD takeoff potentials in our previous study for different AP models (Huang et al., 2018), as well as EADs shown in many other computer simulation studies (Clancy & Rudy, 1999; Kurata et al., 2017, 2020; Pueyo et al., 2011; Song et al., 2015; Tanskanen et al., 2005; Varshneya et al., 2018)]. This leads to a question why phase‐3 EADs and TAs have rarely been observed in ventricular myocytes.
In this study, we carry out computer simulations of three widely used ventricular AP models to investigate the mechanisms for the genesis of phase‐3 EADs and TAs in single ventricular myocytes. We show that differing from phase‐2 EADs which are promoted by increasing inward currents (e.g., ICa,L) and reducing outward currents (e.g., IKr and IKs), the occurrence of phase‐3 EADs and TAs requires a reduction of IKr but a substantial increase of both ICa,L and IKs. They also require a large reduction of IK1 and increase of INCX. However, when the T‐type Ca2+ current, ICa,T, is present (such as in neonatal or failing ventricular myocytes), the thresholds of ICa,L and IKs conductance for phase‐3 EADs and TAs can be greatly reduced. This implies that ICa,T may play an important role in arrhythmogenesis in cardiac diseases.
2. METHODS
Single‐cell simulations were carried out in this study. The governing differential equation for voltage (V) is:
| (1) |
where C m = 1 μF/cm2 and I ion is the total ionic current density. The I ion formulations are different for different AP models. In this study, we used the 2011 O’Hara et al (ORd) human ventricular AP model (O'Hara et al., 2011), the 2004 ten Tusscher et al (TP04) human ventricular AP model (ten Tusscher et al., 2004), and the 2004 Hund and Rudy (HRd) canine ventricular AP model (Hund & Rudy, 2004). The original codes for the AP models were downloaded from the authors’ websites and incorporated into our own C++ codes. I stim is the stimulus current density, which is a short pulse. The durations and strengths of the stimulation pulses as well as the initial conditions were the same as in the authors’ original codes of the AP models. In all simulations, a single pacing stimulus was applied at t = 100 ms to elicit an AP to observe EADs.
We varied the maximum conductance of the major ionic currents in the AP models and used α to denote the fold change of a parameter from its value in the original model. For example, indicates that the maximum conductance of ICa,L is α fold of that in the original model, and thus corresponds to the maximum conductance of ICa,L in the original model. To search different EAD behaviors in these AP models, we randomly draw the α values uniformly distributed in the pre‐assigned intervals for the following ionic currents: ICa,L, IKs, IKr, IK1, Ito, and INCX. To ensure the occurrence of phase‐3 EADs and TAs in the model, we chose very (maybe unphysiologically) large intervals for some of the α values. For the ORd model, and . For the TP04 model, and . For the HRd model, and . For all three models, , , , and .
We performed parameter sensitivity analyses for EADs using the logistic regression method proposed by Morotti and Grandi (Morotti & Grandi, 2017).
Simulations were carried out using a fixed timestep, Δt = 0.01 ms. All the models were programed in CUDA C++ and simulations were performed on Nvidia Tesla K80 GPU cards (NVIDIA corporation).
3. RESULTS
3.1. Phase‐3 EADs and TAs
In general, one can increase the inward currents or decrease the outward currents to promote phase‐2 EADs in many of the ventricular AP models. However, the same strategy does not work for observing phase‐3 EADs and TAs. To search for phase‐3 EADs and TAs, we randomly draw maximum conductance of the major ionic currents from assigned intervals (see Methods). For each parameter set, we detected the lowest EAD takeoff potential if EADs occurred in the AP. We plotted the histograms of EAD takeoff potentials in Figure 2a,d for the ORd model and the TP04 model, respectively. For both models, the histograms exhibit bimodal distributions, which are distinctly separated into two groups. For the ORd model (Figure 2a), the takeoff potentials of the phase‐2 EADs are between −35 and −15 mV. An example of phase‐2 EADs is shown in Figure 2b. The takeoff potentials of the phase‐3 EADs and TAs are between −65 and −50 mV. An example of phase‐3 EADs and TAs is shown in Figure 2c. For the TP04 model (Figure 2d), the takeoff potentials of the phase‐2 EADs are between −15 and 0 mV, and those of phase‐3 EADs and TAs are between −60 and −45 mV. Examples of phase‐2 EADs and phase‐3 EADs and TAs from the TP04 model are shown in Figure 2e,f, respectively. The EAD takeoff potentials from these two models agree well with those observed in experiments.
FIGURE 2.

Phase‐2 EADs and phase‐3 EADs and TAs in the ORd and TP04 models. (a) Histogram of EAD takeoff potential for the ORd model obtained by randomly drawing parameters from the assigned intervals (see Methods). The total number of parameter sets resulting in phase‐2 EADs is 16,165 and that for phase‐3 EADs and TAs is 617 in this histogram. (b) An example AP exhibiting phase‐2 EADs in the ORd model. α (PCa) = 11.364, α (GKs) = 1.675, α (GKr) = 0.858, α (GK1) = 0.846, α (Gto) = 1.583, and α (vNCX) = 4.676. (c) An example AP exhibiting a phase‐3 EAD and TA in the ORd model. α (PCa) = 17.994, α (GKs) = 96.302, α (GKr) = 0.003, α (GK1) = 0.612, α (Gto) = 1.727, and α (vNCX) = 3.26. (d) Histogram of EAD takeoff potential for the TP04 model. The total number of parameter sets resulting in phase‐2 EADs is 1,295 and that for phase‐3 EADs and TAs is 10,695 in this histogram. (e) An example AP exhibiting phase‐2 EADs in the TP04 model. α (PCa) = 11.023, α (GKs) = 0.445, α (GKr) = 0.42, α (GK1) = 1.926, α (Gto) = 0.354, and α (vNCX) = 1.633. (f) An example AP exhibiting phase‐3 EAD and TA in the TP04 model. α (PCa) = 18.808, α (GKs) = 3.536, α (GKr) = 0.018, α (GK1) = 0.611, α (Gto) = 1.575, and α (vNCX) = 1.757. Events in A and B are the parameter sets giving rise to EADs. Vtakeoff is the lowest takeoff potential for each parameter set. The takeoff potential of an EAD is defined by the voltage at which dV/dt changes from negative to positive preceding the EAD
To show the difference in ionic currents for the two types of EADs, we plotted the APs and the major ionic currents during an AP with phase‐2 EADs and an AP with phase‐3 EADs and TAs from the ORd model in Figure 3. For the case of phase‐2 EADs (Figure 3a), the takeoff potentials of the EADs decrease and the amplitudes of the EADs increase with time, agreeing with the general EAD features observed in experiments (e.g., Figure 1a). During the EADs, no INa is activated. The peak ICa,L increases with time and reaches maximum during the last EAD. Note that the peak ICa,L in the last EAD is much larger than that in the regular depolarization, which is a feature of the ORd model (Kurata et al., 2017; Yang et al., 2017). The peak IKs increases with time and reaches maximum in the last EAD, but the peak IKr remains unchanged. The increase of IKs is responsible for the termination of the EAD. INCX and [Ca2+]i also oscillate during the EADs.
FIGURE 3.
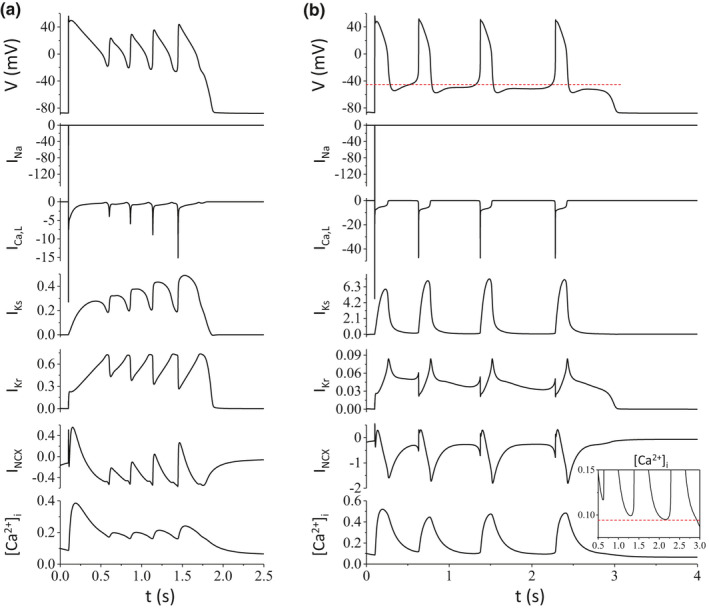
Ionic currents and Ca2+ transients during phase‐2 EADs and phase‐3 EADs and TAs from the ORd model. Shown are V, INa, ICa,L, IKs, IKr, INCX, and [Ca2+]i versus time. (a) Phase‐2 EADs. The parameters are the same as for Figure 2b. (b) Phase‐3 EADs. Inset in the bottom panel is an amplified view of the diastolic [Ca2+]i from t = 0.5–3 s. The dashed horizontal lines are for references. The parameters are: α (PCa) = 18.861, α (GKs) = 78.447, α (GKr) = 0.095, α (GK1) = 0.51, α (Gto) = 1.928, and α (vNCX) = 4.965
For the case of phase‐3 EADs and TAs (Figure 3b), the takeoff potentials decrease but only slightly (a dashed line was added on the top panel for reference), but the peak voltages remain the same. The time interval between two consecutive TAs also increases. These features agree with those observed in experiments (e.g., Figure 1b). During the phase‐3 EADs and TAs, no INa is activated. The amplitudes of other currents remain almost unchanged during the TAs (compare those in the last two TAs). However, the diastolic [Ca2+]i becomes progressively lower during the TAs (see the inset on the bottom panel for a blowup view). The reason for this decay may be that Ca2+ entry is fixed (since ICa,L remains the same) but Ca2+ extrusion is increased due to the increase in the time interval between TAs. A lower diastolic [Ca2+]i reduced the inward mode of NCX, which reduces INCX, resulting in the lowering of the takeoff potential and eventually terminating the TAs.
3.2. Key ionic currents for the genesis of phase‐3 EADs and TAs
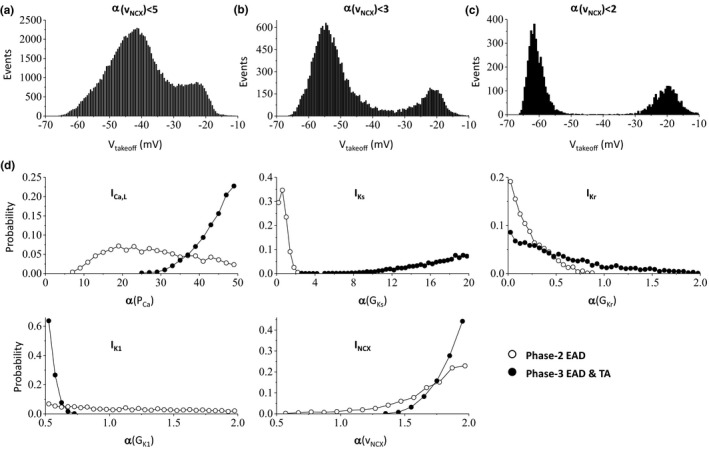
Since phase‐2 EADs and phase‐3 EADs and TAs are separately grouped in the histograms shown in Figure 2, we can then separate the parameter sets for the two types of EADs. This allows us to dissect the differential contributions of the ionic currents in the genesis of phase‐2 EADs and phase‐3 EADs and TAs. Figure 4 shows the parameter (maximum conductance) distributions of phase‐2 EADs and phase‐3 EADs and TAs for the ORd model. Both types of EADs occur more frequently as the maximum ICa,L conductance increases but phase‐3 EADs and TAs requires a much higher ICa,L conductance (Figure 4a). As expected, phase‐2 EADs are promoted by reducing IKs conductance, but surprisingly phase‐3 EADs and TAs are promoted by increasing the maximum IKs conductance (Figure 4b). Both types of EADs are promoted by reducing IKr conductance but more reduction is needed for phase‐3 EADs and TAs (Figure 4c). Phase‐2 EADs are insensitive to IK1 but phase‐3 EADs and TAs require reduction of IK1 conductance (Figure 4d). Increasing NCX activity slightly increases the occurrence of phase‐2 EADs but phase‐3 EADs and TAs require a much larger INCX (Figure 4e). For the TP04 model (Figure 5), the histograms are qualitatively the same but exhibit certain quantitative difference from the ORd model. For example, phase‐3 EADs and TAs only require a slightly larger ICa,L conductance than phase‐2 EADs and increasing INCX tends to promote phase‐3 EADs and TAs but suppress phase‐2 EADs. Similarly, phase‐2 EADs are promoted by reducing IKs conductance but phase‐3 EADs and TAs are promoted by increasing IKs conductance.
FIGURE 4.

Distributions of maximum conductance for phase‐2 EADs and phase‐3 EADs and TAs in the ORd model. Data are from the same simulations as in Figure 2a. Shown are probability of events (the fraction of the parameter sets giving rise to EADs) versus α (fold of the control value of the maximum conductance) for phase‐2 EADs (open circles) and phase‐3 EADs and TAs (filled circles). (a) ICa,L. (b) IKs. (c) IKr. (d) IK1. (e) INCX
FIGURE 5.

Distributions of maximum conductance for phase‐2 EADs and phase‐3 EADs and TAs in the TP04 model. Data are from the same simulations as in Figure 2d. Shown are probability of events (the fraction of the parameter sets giving rise to EADs) versus α (fold of the control value of the maximum conductance) for phase‐2 EADs (open circles) and phase‐3 EADs and TAs (filled circles). (a) ICa,L. (b) IKs. (c) IKr. (d) IK1. (e) INCX
We did the same simulations for the HRd model with similar assigned intervals for the maximum conductance (see Methods). The histogram of takeoff potentials also exhibits a bimodal distribution but there is no distinct separation for the two types of EADs (Figure 6a). In this set of simulations, we used the maximum NCX activity to be 5 folds of the control value. When we allowed the maximum fold of INCX activity to be 3 folds of the control value, the bimodal distribution is more prominent (Figure 6b). When we reduced it to 2 folds, the two types of EADs are separated (Figure 6c). Using the parameter sets in Figure 6c, we did the same statistics as in Figures 4 and 5, which are shown in Figure 6d. The parameter distributions for the occurrence of phase‐2 EADs and for phase‐3 EADs and TAs show the same dependences on the maximum conductance of the ionic currents as for the other two models.
FIGURE 6.
Phase‐3 EADs and TAs in the HRd model. (a) Histogram of Vtakeoff for . The total parameter sets (events) exhibiting EADs are 101,410 in this panel. (b) Histogram of Vtakeoff for . The total parameter sets (events) exhibiting EADs are 18,230 in this panel. (c) Histogram of Vtakeoff for . The total parameter sets (events) exhibiting EADs are 5,975 in this panel. (d) Probability of events (the fraction of the parameter sets giving rise to EADs) versus α (fold of the control value of the maximum conductance) for phase‐2 EADs (open circles) and phase‐3 EADs and TAs (filled circles) for ICa,L, IKs, IKr, IK1, and INCX from the same dataset in panel c
3.3. Roles of T‐type Ca2+ current
ICa,T is expressed in normal sinoatrial node cells and Purkinje fiber cells, not in normal adult ventricular myocytes (Ono & Iijima, 2010; Rosati et al., 2007; Shorofsky & January, 1992; Vassort et al., 2006). However, it has been shown that ICa,T is present in neonatal and failing ventricular myocytes (Cribbs, 2010; Ferron et al., 2003; Huang et al., 2000) as well as IPSC derived cardiac myocytes (Kernik et al., 2019). Since the voltage for ICa,T activation is much lower than that for ICa,L activation, we hypothesize that ICa,T may play a key role in the genesis of phase‐3 EADs and TAs. We incorporated an ICa,T model (Puglisi & Bers, 2001; Wang & Sobie, 2008) to the three AP models to investigate the roles of ICa,T in the genesis of phase‐3 EADs and TAs.
We first performed the same random parameter selections as in Figures 4, 5, 6 except that GCa,T was fixed at different values. Figure 7a shows the distributions of the maximum conductance of ICa,L and IKs for different GCa,T values for the ORd model. In the presence of ICa,T, the thresholds of ICa,L and IKs for phase‐3 EADs and TAs are substantially reduced. The requirements for other currents also become less stringent. Moreover, if ICa,T is large enough, no ICa,L or IKs is needed for phase‐3 EADs and TAs. We observed similar effects in the HRd model but in a less extent (Figure 7c) and the effects in the TP04 model are very small (Figure 7b). Note that for the latter two models, the ICa,L conductance for phase‐2 EADs have to be many folds larger than the control values (see the ICa,L conductance thresholds for phase‐2 EADs in Figures 5 and 6), and it seems that adding ICa,T cannot reduce the threshold to be much lower than that for phase‐2 EADs. Moreover, in all models, phase‐3 EADs and TAs are still promoted by increasing IKs in the presence of ICa,T.
FIGURE 7.

Roles of T‐type Ca2+ current in the genesis of phase‐3 EADs. Shown are probability of events (the fraction of the parameter sets giving rise to EADs) versus α (fold of the control value of the maximum conductance) when the ICa,T is absent (black circles) and present (colored circles). The same GCa,T values as labeled in panel c are used for all three AP models. (a) The ORd model. The total number of events (the parameter sets giving rise to phase‐3 EADs and TAs) is 617, 2,577, 5,414, and 17,347 for the four GCa,T values. (b) The TP04 model. The total number of events (the parameter sets giving rise to phase‐3 EADs and TAs) is 10,695, 35,295, 44,517, and 66,942 for the four GCa,T values. (c) The HRd model. The total number of events (the parameter sets giving rise to phase‐3 EADs and TAs) is 3,909, 3,006, 5,945, and 16,349 for the four GCa,T values
Figure 8 shows the parameter sensitivities of phase‐2 EADs and phase‐3 EADs and TAs in the absence (Figure 8a) and presence (Figure 8b) of ICa,T using the regression methods as in previous studies (Morotti & Grandi, 2017; Sobie, 2009). In the absence of ICa,T, phase‐2 EADs are positively correlated with PCa and vNCX, strongly negatively correlated with GKs and GKr, and very weakly correlated with GK1 and Gto. Phase‐3 EADs and TAs are strongly positively correlated with PCa, GKs, and vNCX, strongly negatively correlated with GKr and GK1. The presence of ICa,T exhibits almost no change in the parameter sensitivities for phase‐2 EADs. However, the presence of ICa,T substantially reduces the strong correlations of phase‐3 EADs and TAs with PCa, GKs, GK1, and vNCX for the ORd model although it has a much smaller effects in the other two models. These correlations agree with the histograms shown in Figures 4, 5, 6, 7.
FIGURE 8.

Parameter sensitivities of phase‐2 EADs and phase‐3 EADs and TAs to the maximum conductance of different ionic currents. (a) No ICa,T presence. (b) With ICa,T presence. The assigned intervals of the maximum conductance were the same as described in methods and the GCa,T range was set as [0, 0.11] mS/μF
4. DISCUSSION
In this study, we carried out computer simulations of three ventricular AP models to investigate the cellular mechanisms of phase‐3 EADs and TAs. We show that differing from phase‐2 EADs which are promoted by increasing inward currents (e.g., ICa,L) and reducing outward currents (e.g., IKr and IKs), the occurrence of phase‐3 EADs and TAs requires a reduction of IKr but a substantial increase of both ICa,L and IKs. Moreover, phase‐3 EADs and TAs also require a large reduction of IK1 and increase of INCX while phase‐2 EADs are much less sensitive to the changes of these currents. When ICa,T is present (such as in Purkinje fibers or neonatal and failing ventricular myocytes), the thresholds of ICa,L and IKs for phase‐3 EADs and TAs can be greatly reduced. Based on many previous studies on phase‐2 EADs and our present study on phase‐3 EADs and TAs, we discuss the mechanisms of the two types of EADs and the conditions for observing phase‐3 EADs and TAs in cardiac myocytes in the sections below.
4.1. Mechanisms of phase‐2 EADs
Phase‐2 EADs have been widely investigated in experimental and computer simulation studies and the dynamical mechanisms and the required key currents have been revealed in recent theoretical studies (Huang et al., 2018; Kügler, 2016; Kurata et al., 2017; Tran et al., 2009; Xie et al., 2014). Here we briefly summarize the mechanisms of phase‐2 EADs (with a schematic diagram in Figure 9a), which were also discussed in our previous publications (Qu et al., 2013; Song et al., 2015). The purpose is to compare the mechanism of the phase‐3 EADs and TAs with that of the phase‐2 EADs. For phase‐2 EADs, the latency of the first EAD from the AP upstroke is usually >200 ms [see table 1 in Huang et al (Huang et al., 2018)]. At 200 ms or a longer time after the AP upstroke, most of the currents reach their steady states or near their steady states except the slow ones, such as IKs. The total steady‐state inward current (e.g., summation of the window ICa,L, late INa, and INCX) and the total outward current (including the steady‐state and slowly changing outward currents) are roughly equal at the plateau voltage, forming a quasi‐equilibrium state (indicated by the filled dots in Figure 9a). As the time progresses, more IKs slowly activates, destabilizing the quasi‐equilibrium state (the open dot inside the arrowed circle) to result in oscillations. The transition from the stable equilibrium state to the unstable equilibrium state is called a Hopf bifurcation (Qu et al., 2013). The oscillation cycle can be understood as follows: the window ICa,L (or late INa and INCX) prevents the voltage to decay into phase 3, and once enough LCCs recover, they open to cause voltage elevation. When voltage is high enough, the LCCs are inactivated and the outward K+ currents (IKr and IKs) causes the voltage to decay until the window ICa,L stops further decay, forming a cycle. As IKs increases, the lowest voltage in a cycle becomes lower, causing more LCCs available to open and thus a higher peak voltage (large EAD amplitude, see ICa,L and IKs in Figure 3a). As IKs increase even further, the system approaches to another bifurcation point, called homoclinic bifurcation at which the oscillation can no longer be sustained. This is because the window ICa,L is not strong enough to compete against IKs to prevent the voltage decaying into phase 3 and thus repolarizing to the resting potential. As shown in our previous analyses (Huang et al., 2018; Qu et al., 2013; Tran et al., 2009), the key determinant of the stability of the quasi‐equilibrium steady state (the plateau phase) and the voltage oscillations (or the Hopf bifurcation) is the activation and inactivation kinetics of ICa,L with other currents playing auxiliary roles. Note that when the window ICa,L is too large, the quasi‐equilibrium state become a true equilibrium state, repolarization failure occurs. Therefore, increasing inward currents may reduce the occurrence of phase‐2 EADs, which may be the reason that increasing ICa,L conductance (e.g., Figure 6d) or INCX (e.g., Figure 5e) can also reduce the propensity of phase‐2 EADs.
FIGURE 9.

Schematic diagrams of dynamical mechanisms for phase‐2 EADs and phase‐3 EADs and TAs. See text for a detailed description. (a) Phase‐2 EADs. (b) Phase‐3 EADs and TAs. [Ca2+]o is the extracellular Ca2+ concentration and [Ca2+]i is the intracellular Ca2+ concentration
Therefore, in the core of the genesis of phase‐2 EADs, the activation and inactivation kinetics of ICa,L generate the oscillations while the slow increase of IKs [can be the slow increase of IKr, such as in the condition of LQT1 (Choi et al., 2018)] competes with the window ICa,L (and late INa) to bring the system into and out of the oscillatory regime. Other currents play auxiliary roles in facilitating the genesis and termination of EADs.
4.2. Mechanisms of phase‐3 EADs and TAs
In this study, we used computer simulations to investigate the key ionic currents responsible for phase‐3 EADs and TAs, which largely agrees with the experimental conditions for phase‐3 EADs and TAs in Purkinje fibers (Bailie et al., 1988; Damiano & Rosen, 1984; Davidenko et al., 1989; Gilmour & Moise, 1996; Roden & Hoffman, 1985; Szabo et al., 1994, 1995). But surprisingly, the occurrence of phase‐3 EADs and TAs requires a substantial increase of IKs, which seems to be nonintuitive based on the traditional understanding for the genesis of EADs. A rigorous analysis as for phase‐2 EADs (Tran et al., 2009) is still needed to pinpoint the mechanism and the necessary and sufficient conditions for the genesis and termination of the oscillations manifesting as phase‐3 EADs and TAs. Here we use a schematic diagram (Figure 9b) to postulate a cellular mechanism of phase‐3 EADs. The left panel in Figure 9b describes an oscillation cycle for a phase‐3 EAD or a TA. During this cycle, INCX outcompetes IK1 to hold the voltage at phase 3, preventing it from decaying to the resting potential. Moreover, it slowly elevates the voltage (see Figure 3b) to the threshold for ICa,L activation, at which a full depolarization occurs. This depolarization activates more outward K+ currents (mainly IKs, see Figure 3b) which then repolarizes the cell back into the phase 3 of the AP. This cycle repeats to result in voltage oscillations manifesting as phase‐3 EADs and TAs. During this cycle, LCCs bring in Ca2+ from outside and NCX extrudes Ca2+, the two competes to maintain a proper [Ca2+]i level to keep the cycle going. As time progresses, the amount of Ca2+ brought in by the LCCs remains the same in each cycle but more Ca2+ is extruded by NCX due to that the cycle length becomes longer and longer (see Figure 3b). This results in a decrease in the diastolic [Ca2+]i level, and thus a smaller inward INCX. Because of the reduction of INCX, it can no longer outcompete IK1 to maintain the voltage above phase 3, and thus the oscillations terminate and the voltage decays to the resting potential (as illustrated in the right panel in Figure 9b). Sustained oscillations can be maintained when the amount of Ca2+ entering the cell is equal to the amount of Ca2+ leaving the cell, resulting in a pacemaker.
Since the activation threshold of ICa,L is high (around −40 mV), it requires an inward current to depolarize the cell from phase 3 (in the range from −70 to −60 mV) to phase 2 (above −40 mV) for ICa,L activation. This can be achieved by different ways. One way is to substantially increase the ICa,L conductance since there is still some LCCs that can be opened below −40 mV. However, a very large ICa,L conductance may result in repolarization failure, and thus a very large IKs is then needed for repolarization. This is why very large ICa,L and IKs conductances are needed for phase‐3 EADs and TAs to occur in the AP models simulated in this study. The reason that a large IKs but not IKr is required is because IKs is almost fully deactivated during phase 3 but IKr does not (see Figure 3). Therefore, if IKr is large, then the voltage will decay from phase 3 to the resting potential, suppressing phase‐3 EADs and TAs. Another way is to increase INCX, but as shown in Figures 4, 5, 6, large INCX does not bring the ICa,L and IKs conductance thresholds to the normal levels. The third way is to increase ICa,T. Since its activation threshold is in the range of −60 mV, it provides the inward current needed to depolarize the cell from the −60 mV range to the −40 mV range, greatly reducing the conductance thresholds of ICa,L and INCX for phase‐3 EADs and TAs. Because of the reduction of the ICa,L conductance threshold, the IKs conductance threshold is also greatly reduced. Note that if ICa,T is large enough, phase‐3 EADs and TAs can occur without the presence of ICa,L (see Figure 7).
Therefore, in the core of the genesis of phase‐3 EADs and TAs, INCX outcompetes IK1 to prevent the voltage from decaying from phase 3 to the resting potential. INCX and ICa,T elevate the voltage from phase 3 to phase 2 for ICa,L activation. ICa,L activation depolarizes the voltage to the peak. Activation of IKs is then required to bring the voltage back to phase 3. The process repeats to result in the oscillations manifesting as phase‐3 EADs and TAs. The slow decrease of the diastolic Ca2+ level due to mismatch of Ca2+ entry via LCCs and Ca2+ extrusion via NCX terminates the oscillations, repolarizing the cell to the resting potential. Differing from phase‐2 EADs in which oscillations are mainly caused by the activation and inactivation of ICa,L while IKs always remains activated, phase‐3 EADs and TAs require activation and deactivation of IKs during the oscillation cycle. Note that Figure 9b is only a schematic diagram, a rigorous mathematical analysis as for phase‐2 EADs (Huang et al., 2018; Kügler, 2016; Kurata et al., 2017; Tran et al., 2009; Xie et al., 2014) is needed to pinpoint the bifurcations leading to and the minimally ionic currents needed for the oscillations.
4.3. Implications for the genesis of phase‐3 EADs and TAs in ventricular myocytes
Phase‐3 EADs and TAs have been widely observed in isolated Purkinje fibers (Damiano & Rosen, 1984; Davidenko et al., 1989; Gilmour & Moise, 1996; Roden & Hoffman, 1985; Szabo et al., 1994, 1995). These experiments have shown that phase‐3 EADs and TAs are promoted by hypokalemia and blocking outward currents with Cs+ (Bailie et al., 1988; Damiano & Rosen, 1984; Szabo et al., 1994, 1995) or quinidine (Davidenko et al., 1989; Roden & Hoffman, 1985). However, the type of phase‐3 EADs and TAs as shown in Figure 1b has been rarely reported in experiments of isolated ventricular myocytes. Phase‐3 EADs and TAs were observed in ventricular tissue experiments (Bailie et al., 1988; Ben‐David & Zipes, 1988; El‐Sherif et al., 1990; Hwang et al., 2020), however, it is unclear if they were oscillations caused by a single‐cell mechanism or by a tissue‐scale mechanism. As shown in both simulation and experimental studies (Huang et al., 2016; Maruyama et al., 2011), phase‐3 EADs and TAs can be generated by a tissue‐scale instability due to heterogeneous repolarization. Late phase‐3 EADs and TAs have been shown in atrial and ventricular tissue (Burashnikov & Antzelevitch, 2003; Maruyama et al., 2014), which are caused by Ca2+ overload and lengthening of the Ca2+ transient duration. This mechanism can only give rise to a single TA after a regular AP, not multiple TAs or oscillations as shown in Figure 1b. Another type of phase‐3 EADs has been observed in mouse ventricular myocytes (Edwards et al., 2014) and rat atrial and ventricular myocytes (Tazmini et al., 2020). Nonequilibrium reactivation of INa was shown to drive this type of EADs (Edwards et al., 2014; Morotti et al., 2016), which was observed for triangulated APs with short APDs, such as for mice and rats. However, no phase‐3 EAD induced TAs (as the ones in Figure 1b) were observed, and the features of this type of phase‐3 EADs, such as the EAD amplitude and oscillation period, are similar to those of phase‐2 EADs despite lower takeoff potentials (from −55 to −35 mV). Another type of phase‐3 EADs was shown in computer simulations (de Lange et al., 2012; Xie et al., 2010), which was generated by adding a Ca2+‐activated nonselective cation current [Ins(Ca)] to the AP model. Although Ins(Ca) has been identified in different species (Doerr et al., 1990; Ehara et al., 1988; Giles & Shimoni, 1989), its existence is controversial and its physiological or pathophysiological roles remain unclear.
Our current simulations demonstrate that in the absence of ICa,T, besides lower IK1 and IKr conductance, it requires a very large ICa,L conductance and a very large IKs conductance for phase‐3 EADs and TAs. But in the presence of ICa,T, the thresholds of these two currents can be greatly reduced. However, in normal ventricular myocytes in which no ICa,T is present, based on our simulations, it will require a very large ICa,L conductance and a very large IKs conductance to cause phase‐3 EADs and TAs. These conductances may be too large to be realistic in real ventricular myocytes. This may explain why no phase‐3 EADs and TAs have been observed in isolated ventricular myocyte experiments. On the other hand, ICa,T is expressed in neonatal and failing ventricular myocytes. Under hypokalemia (which lowers IK1) and infusion of isoproterenol [which increases both ICa,L and IKs (Liu et al., 2012), and loads the cell with more Ca2+ to increase INCX], phase‐3 EADs and TAs may be observed in neonatal and failing ventricular myocytes. In fact, phase‐3 EADs and TAs were observed in IPSC derived cardiac myocytes with infusion of isoproterenol (Spencer et al., 2014), which may benefit from the presence of ICa,T (Kernik et al., 2019). Since ICa,T is expressed in Purkinje fiber cells (Ono & Iijima, 2010; Rosati et al., 2007; Shorofsky & January, 1992; Vassort et al., 2006), it may also play an important role in phase‐3 EADs and TAs in Purkinje fiber cells. However, the ionic currents differ substantially between Purkinje fiber cells and ventricular myocytes, whether ICa,T is key to the genesis of phase‐3 EADs and TAs in Purkinje fiber cells needs to be investigated in future studies.
5. LIMITATIONS
Although we obtained the same general conclusions from the simulations of three widely used AP models, they do exhibit differences. For example, their susceptibilities to phase‐2 EADs and to phase‐3 EADs and TAs are very different, and their responses to ICa,T are also very different. Future studies are needed to pinpoint the causes giving rise to these differences, which will be helpful for a better understanding of the mechanisms of phase‐3 EADs and TAs in ventricular myocytes. We only simulated three AP models, our conclusions need to be examined in other AP models, and in particular validated in future experiments.
6. CONCLUSIONS
Our computer simulations of ventricular myocyte models show that besides the known promoting factors (e.g., blocking IK1 and increasing INCX), extensive increase of both ICa,L and IKs is needed for the genesis of phase‐3 EADs and TAs in the absence of ICa,T. However, in the presence of ICa,T, these requirements can be substantially weakened. Our results imply that it will become easier to observe phase‐3 EADs and TAs in neonatal and failing myocytes as well as IPSC derived cardiac myocytes where ICa,T is present. Due to the importance of ICa,T for the genesis of phase‐3 EADs and TAs, ICa,T may play an important role in arrhythmogenesis in cardiac diseases.
AUTHOR CONTRIBUTIONS
ZQ conceived the overall study and drafted the manuscript, ZZ performed the simulations, ZQ and ZZ analyzed the data and edited the manuscript.
ACKNOWLEDGMENTS
This work was supported by NIH grants R01 HL134709 and R01 HL139829.
Zhang Z, Qu Z. Mechanisms of phase-3 early afterdepolarizations and triggered activities in ventricular myocyte models. Physiol Rep. 2021;9:e14883. 10.14814/phy2.14883
DATA AVAILABILITY STATEMENT
The data and source codes that support the findings of this study are available from the corresponding author upon reasonable request.
References
- Bailie, D. S. , Inoue, H. , Kaseda, S. , Ben‐David, J. , & Zipes, D. P. (1988). Magnesium suppression of early afterdepolarizations and ventricular tachyarrhythmias induced by cesium in dogs. Circulation, 77, 1395–1402. [DOI] [PubMed] [Google Scholar]
- Ben‐David, J. , & Zipes, D. P. (1988). Differential response to right and left ansae subclaviae stimulation of early afterdepolarizations and ventricular tachycardia induced by cesium in dogs. Circulation, 78, 1241–1250. [DOI] [PubMed] [Google Scholar]
- Burashnikov, A. , & Antzelevitch, C. (2003). Reinduction of atrial fibrillation immediately after termination of the arrhythmia is mediated by late phase 3 early afterdepolarization‐induced triggered activity. Circulation, 107, 2355–2360. [DOI] [PubMed] [Google Scholar]
- Choi, B.‐R. , Li, W. , Terentyev, D. , Kabakov, A. Y. , Zhong, M. , Rees, C. M. , Terentyeva, R. , Kim, T. Y. , Qu, Z. , Peng, X. , Karma, A. , & Koren, G. (2018). Transient outward K+ Current (Ito) underlies the right ventricular initiation of polymorphic ventricular tachycardia in a transgenic rabbit model of long‐QT syndrome type 1. Circulation: Arrhythmia and Electrophysiology, 11, e005414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clancy, C. E. , & Rudy, Y. (1999). Linking a genetic defect to its cellular phenotype in a cardiac arrhythmia. Nature, 400, 566–569. [DOI] [PubMed] [Google Scholar]
- Cranefield, P. F. , & Aronson, R. S. (1988). Torsade de Pointes and other pause‐induced ventricular tachycardias: the short‐long‐short sequence and early afterdepolarizations. Pacing and Clinical Electrophysiology, 11, 670–678. [DOI] [PubMed] [Google Scholar]
- Cribbs, L. (2010). T‐type calcium channel expression and function in the diseased heart. Channels, 4, 447–452. [DOI] [PubMed] [Google Scholar]
- Damiano, B. P. , & Rosen, M. R. (1984). Effects of pacing on triggered activity induced by early afterdepolarizations. Circulation, 69, 1013–1025. [DOI] [PubMed] [Google Scholar]
- Davidenko, J. M. , Cohen, L. , Goodrow, R. , & Antzelevitch, C. (1989). Quinidine‐induced action potential prolongation, early afterdepolarizations, and triggered activity in canine Purkinje fibers. Effects of stimulation rate, potassium, and magnesium. Circulation, 79, 674–686. [DOI] [PubMed] [Google Scholar]
- de Lange, E. , Xie, Y. , & Qu, Z. (2012). Synchronization of early afterdepolarizations and arrhythmogenesis in heterogeneous cardiac tissue models. Biophysical Journal, 103, 365–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doerr, T. , Denger, R. , Doerr, A. , & Trautwein, W. (1990). Ionic currents contributing to the action potential in single ventricular myocytes of the guinea pig studied with action potential clamp. Pflugers Archiv: European Journal of Physiology, 416, 230–237. [DOI] [PubMed] [Google Scholar]
- Edwards, A. G. , Grandi, E. , Hake, J. E. , Patel, S. , Li, P. , Miyamoto, S. , Omens, J. H. , Heller Brown, J. , Bers, D. M. , & McCulloch, A. D. (2014). Non‐equilibrium reactivation of na+ current drives early afterdepolarizations in mouse ventricle. Circulation. Arrhythmia and Electrophysiology, 7(6), 1205–1213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehara, T. , Noma, A. , & Ono, K. (1988). Calcium‐activated non‐selective cation channel in ventricular cells isolated from adult guinea‐pig hearts. Journal of Physiology, 403, 117–133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El‐Sherif, N. , Craelius, W. , Boutjdir, M. , & Gough, W. B. (1990). Early Afterdepolarizations and Arrhythmogenesis. Journal of Cardiovascular Electrophysiology, 1, 145–160. [Google Scholar]
- Ferron, L. , Capuano, V. , Ruchon, Y. , Deroubaix, E. , Coulombe, A. , & Renaud, J.‐F. (2003). Angiotensin II signaling pathways mediate expression of cardiac T‐type calcium channels. Circulation Research, 93, 1241–1248. [DOI] [PubMed] [Google Scholar]
- Giles, W. , & Shimoni, Y. (1989). Comparison of sodium‐calcium exchanger and transient inward currents in single cells from rabbit ventricle. Journal of Physiology, 417, 465–481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmour, R. F. Jr , & Moise, N. S. (1996). Triggered activity as a mechanism for inherited ventricular arrhythmias in German shepherd dogs. Journal of the American College of Cardiology, 27, 1526–1533. [DOI] [PubMed] [Google Scholar]
- Huang, B. , Qin, D. , Deng, L. , Boutjdir, M. , & El‐Sherif, N. (2000). Reexpression of T‐type Ca2+ channel gene and current in post‐infarction remodeled rat left ventricle. Cardiovascular Research, 46, 442–449. [DOI] [PubMed] [Google Scholar]
- Huang, X. , Kim, T. Y. , Koren, G. , Choi, B.‐R. , & Qu, Z. (2016). Spontaneous initiation of premature ventricular complexes and arrhythmias in type 2 long QT syndrome. American Journal of Physiology ‐ Heart and Circulatory Physiology, 311, H1470–H1484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang, X. , Song, Z. , & Qu, Z. (2018). Determinants of early afterdepolarization properties in ventricular myocyte models. PLOS Computational Biology, 14, e1006382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hund, T. J. , & Rudy, Y. (2004). Rate dependence and regulation of action potential and calcium transient in a canine cardiac ventricular cell model. Circulation, 110, 3168–3174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang, J. , Kim, T. Y. , Terentyev, D. , Zhong, M. , Kabakov, A. Y. , Bronk, P. , Arunachalam, K. , Belardinelli, L. , Rajamani, S. , Kunitomo, Y. , Pfeiffer, Z. , Lu, Y. , Peng, X. , Odening, K. E. , Qu, Z. , Karma, A. , Koren, G. , & Choi, B.‐R. (2020). Late INa blocker GS967 supresses polymorphic ventricular tachycardia in a transgenic rabbit model of long QT type 2. Circulation: Arrhythmia and Electrophysiology, 13, e006875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kernik, D. C. , Morotti, S. , Wu, H. , Garg, P. , Duff, H. J. , Kurokawa, J. , Jalife, J. , Wu, J. C. , Grandi, E. , & Clancy, C. E. (2019). A computational model of induced pluripotent stem‐cell derived cardiomyocytes incorporating experimental variability from multiple data sources. The Journal of Physiology, 597, 4533–4564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kügler, P. (2016). Early afterdepolarizations with growing amplitudes via delayed subcritical Hopf bifurcations and unstable manifolds of saddle foci in cardiac action potential dynamics. PLoS One, 11, e0151178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kupersmith, J. , & Hoff, P. (1985). Occurrence and transmission of localized repolarization abnormalities in vitro. Journal of the American College of Cardiology, 6, 152–160. [DOI] [PubMed] [Google Scholar]
- Kurata, Y. , Tsumoto, K. , Hayashi, K. , Hisatome, I. , Kuda, Y. , & Tanida, M. (2020). Multiple dynamical mechanisms of phase‐2 early afterdepolarizations in a human ventricular myocyte model: involvement of spontaneous SR Ca2+release. Frontiers in Physiology, 10, 1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurata, Y. , Tsumoto, K. , Hayashi, K. , Hisatome, I. , Tanida, M. , Kuda, Y. , & Shibamoto, T. (2017). Dynamical mechanisms of phase‐2 early afterdepolarizations in human ventricular myocytes: insights from bifurcation analyses of two mathematical models. American Journal of Physiology ‐ Heart and Circulatory Physiology, 312, H106–H127. [DOI] [PubMed] [Google Scholar]
- Liu, G. X. , Choi, B. R. , Ziv, O. , Li, W. , de Lange, E. , Qu, Z. , & Koren, G. (2012). Differential conditions for early after‐depolarizations and triggered activity in cardiomyocytes derived from transgenic LQT1 and LQT2 rabbits. Journal of Physiology, 590, 1171–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama, M. , Ai, T. , Chua, S.‐K. , Park, H.‐W. , Lee, Y.‐S. , Shen, M. J. , Chang, P.‐C. , Lin, S.‐F. , & Chen, P.‐S. (2014). Hypokalemia promotes late phase 3 early afterdepolarization and recurrent ventricular fibrillation during isoproterenol infusion in Langendorff perfused rabbit ventricles. Heart Rhythm: the Official Journal of the Heart Rhythm Society, 11, 697–706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama, M. , Lin, S. F. , Xie, Y. , Chua, S. K. , Joung, B. , Han, S. , Shinohara, T. , Shen, M. J. , Qu, Z. , Weiss, J. N. , & Chen, P. S. (2011). Genesis of phase 3 early afterdepolarizations and triggered activity in acquired long‐QT syndrome. Circulation: Arrhythmia and Electrophysiology, 4, 103–111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Méndez, C. , & Delmar, M. (1985). Triggered activity: its possible role in cardiac arrhythmias. In Zipes D. P., & Jalife J. (Eds.), Cardiac Electrophysiology and Arrhythmias (pp. 311–313). Grune & Stratton Inc. [Google Scholar]
- Morotti, S. , & Grandi, E. (2017). Logistic regression analysis of populations of electrophysiological models to assess proarrythmic risk. MethodsX, 4, 25–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morotti, S. , McCulloch, A. D. , Bers, D. M. , Edwards, A. G. , & Grandi, E. (2016). Atrial‐selective targeting of arrhythmogenic phase‐3 early afterdepolarizations in human myocytes. Journal of Molecular and Cellular Cardiology, 96, 63–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Hara, T. , Virag, L. , Varro, A. , & Rudy, Y. (2011). Simulation of the undiseased human cardiac ventricular action potential: model formulation and experimental validation. PLoS Computational Biology, 7, e1002061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ono, K. , & Iijima, T. (2010). Cardiac T‐type Ca2+ channels in the heart. Journal of Molecular and Cellular Cardiology, 48, 65–70. [DOI] [PubMed] [Google Scholar]
- Pueyo, E. , Corrias, A. , Virag, L. , Jost, N. , Szel, T. , Varro, A. , Szentandrassy, N. , Nanasi, P. P. , Burrage, K. , & Rodriguez, B. (2011). A multiscale investigation of repolarization variability and its role in cardiac arrhythmogenesis. Biophysical Journal, 101, 2892–2902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Puglisi, J. L. , & Bers, D. M. (2001). LabHEART: an interactive computer model of rabbit ventricular myocyte ion channels and Ca transport. American Journal of Physiology. Cell Physiology, 281, C2049–2060. [DOI] [PubMed] [Google Scholar]
- Qu, Z. , Xie, L.‐H. , Olcese, R. , Karagueuzian, H. S. , Chen, P.‐S. , Garfinkel, A. , & Weiss, J. N. (2013). Early afterdepolarizations in cardiac myocytes: beyond reduced repolarization reserve. Cardiovascular Research, 99, 6–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roden, D. M. , & Hoffman, B. F. (1985). Action potential prolongation and induction of abnormal automaticity by low quinidine concentrations in canine Purkinje fibers. Circulation Research, 56, 857–867. [DOI] [PubMed] [Google Scholar]
- Rosati, B. , Dun, W. , Hirose, M. , Boyden, P. A. , & McKinnon, D. (2007). Molecular basis of the T‐ and L‐type Ca2+ currents in canine Purkinje fibres. The Journal of Physiology, 579, 465–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosen, M. R. , Moak, J. P. , & Damiano, B. (1984). The clinical relevance of afterdepolarizations. Annals of the New York Academy of Sciences, 427, 84–93. [DOI] [PubMed] [Google Scholar]
- Shorofsky, S. R. , & January, C. T. (1992). L‐ and T‐type Ca2+ channels in canine cardiac Purkinje cells. Single‐channel demonstration of L‐type Ca2+ window current. Circulation Research, 70, 456–464. [DOI] [PubMed] [Google Scholar]
- Sobie, E. A. (2009). Parameter sensitivity analysis in electrophysiological models using multivariable regression. Biophysical Journal, 96, 1264–1274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song, Z. , Ko, C. Y. , Nivala, M. , Weiss, J. N. , & Qu, Z. (2015). Calcium‐voltage coupling in the genesis of early and delayed afterdepolarizations in cardiac myocytes. Biophysical Journal, 108, 1908–1921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer, C. I. , Baba, S. , Nakamura, K. , Hua Ethan, A. , Sears Marie, A. F. , Fu, C.‐C. , Zhang, J. , Balijepalli, S. , Tomoda, K. , Hayashi, Y. , Lizarraga, P. , Wojciak, J. , Scheinman Melvin, M. , Aalto‐Setälä, K. , Makielski Jonathan, C. , January Craig, T. , Healy Kevin, E. , Kamp Timothy, J. , Yamanaka, S. , & Conklin, B. R. (2014). Calcium transients closely reflect prolonged action potentials in iPSC models of inherited cardiac arrhythmia. Stem Cell Reports, 3, 269–281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szabo, B. , Kovacs, T. , & Lazzara, R. (1995). Role of calcium loading in early afterdepolarizations generated by Cs+ in Canine and Guinea Pig Purkinje Fibers. Journal of Cardiovascular Electrophysiology, 6, 796–812. [DOI] [PubMed] [Google Scholar]
- Szabo, B. , Sweidan, R. , Rajagopalan, C. V. , & Lazzara, R. (1994). Role of Na+:Ca2+ exchange current in Cs(+)‐induced early afterdepolarizations in Purkinje fibers. Journal of Cardiovascular Electrophysiology, 5, 933–944. [DOI] [PubMed] [Google Scholar]
- Tanskanen, A. J. , Greenstein, J. L. , O'Rourke, B. , & Winslow, R. L. (2005). The role of stochastic and modal gating of cardiac L‐type Ca2+ channels on early after‐depolarizations. Biophysical Journal, 88, 85–95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tazmini, K. , Frisk, M. , Lewalle, A. , Laasmaa, M. , Morotti, S. , Lipsett, D. B. , Manfra, O. , Skogested, J. , Aronsen, J. M. , Sejersted, O. M. , Sjaastad, I. , Edwards, A. G. , Grandi, E. , Niederer, S. A. , Øie, E. , & Louch, W. E. (2020). Hypokalemia promotes arrhythmia by distinct mechanisms in atrial and ventricular myocytes. Circulation Research, 126, 889–906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ten Tusscher, K. H. , Noble, D. , Noble, P. J. , & Panfilov, A. V. (2004). A model for human ventricular tissue. American Journal of Physiology. Heart and Circulatory Physiology, 286, H1573–H1589. [DOI] [PubMed] [Google Scholar]
- Tran, D. X. , Sato, D. , Yochelis, A. , Weiss, J. N. , Garfinkel, A. , & Qu, Z. (2009). Bifurcation and chaos in a model of cardiac early afterdepolarizations. Physical Review Letters, 102, 258103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varshneya, M. , Devenyi, R. A. , & Sobie, E. A. (2018). Slow delayed rectifier current protects ventricular myocytes from arrhythmic dynamics across multiple species. Circulation: Arrhythmia and Electrophysiology, 11, e006558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vassort, G. , Talavera, K. , & Alvarez, J. L. (2006). Role of T‐type Ca2+ channels in the heart. Cell Calcium, 40, 205–220. [DOI] [PubMed] [Google Scholar]
- Volders, P. G. , Vos, M. A. , Szabo, B. , Sipido, K. R. , de Groot, S. H. , Gorgels, A. P. , Wellens, H. J. , & Lazzara, R. (2000). Progress in the understanding of cardiac early afterdepolarizations and torsades de pointes: time to revise current concepts. Cardiovascular Research, 46, 376–392. [DOI] [PubMed] [Google Scholar]
- Vos, M. A. , Gorenek, B. , Verduyn, S. C. , van der Hulst, F. F. , Leunissen, J. D. , Dohmen, L. , & Wellens, H. J. (2000). Observations on the onset of Torsade de Pointes arrhythmias in the acquired long QT syndrome. Cardiovascular Research, 48, 421–429. [DOI] [PubMed] [Google Scholar]
- Wang, L. J. , & Sobie, E. A. (2008). Mathematical model of the neonatal mouse ventricular action potential. American Journal of Physiology. Heart and Circulatory Physiology, 294, H2565–H2575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiss, J. N. , Garfinkel, A. , Karagueuzian, H. S. , Chen, P. S. , & Qu, Z. (2010). Early afterdepolarizations and cardiac arrhythmias. Heart Rhythm: the Official Journal of the Heart Rhythm Society, 7, 1891–1899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie, Y. , Izu, L. T. , Bers, D. M. , & Sato, D. (2014). Arrhythmogenic transient dynamics in cardiac myocytes. Biophysical Journal, 106, 1391–1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie, Y. , Sato, D. , Garfinkel, A. , Qu, Z. , & Weiss, J. N. (2010). So little source, so much sink: requirements for afterdepolarizations to propagate in tissue. Biophysical Journal, 99, 1408–1415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, P.‐C. , Perissinotti, L. L. , López‐Redondo, F. , Wang, Y. , DeMarco, K. R. , Jeng, M.‐T. , Vorobyov, I. , Harvey, R. D. , Kurokawa, J. , Noskov, S. Y. , & Clancy, C. E. (2017). A multiscale computational modelling approach predicts mechanisms of female sex risk in the setting of arousal‐induced arrhythmias. The Journal of Physiology, 595, 4695–4723. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The data and source codes that support the findings of this study are available from the corresponding author upon reasonable request.


