Lesions to the left lateral prefrontal cortex impair decision threshold adjustment for lexical selection

Abstract

Patients with lesions in the left prefrontal cortex (PFC) have been shown to be impaired in lexical selection, especially when interference between semantically related alternatives is increased. To more deeply investigate which computational mechanisms may be impaired following left PFC damage due to stroke, a psychometric modelling approach is employed in which we assess the cognitive parameters of the patients from an evidence accumulation (sequential information sampling) modelling of their response data. We also compare the results to healthy speakers. Analysis of the cognitive parameters indicates an impairment of the PFC patients to appropriately adjust their decision threshold, in order to handle the increased item difficulty that is introduced by semantic interference. Also, the modelling contributes to other topics in psycholinguistic theory, in which specific effects are observed on the cognitive parameters according to item familiarization, and the opposing effects of priming (lower threshold) and semantic interference (lower drift) which are found to depend on repetition. These results are developed for the blocked-cyclic picture naming paradigm, in which pictures are presented within semantically homogeneous (HOM) or heterogeneous (HET) blocks, and are repeated several times per block. Overall, the results are in agreement with a role of the left PFC in adjusting the decision threshold for lexical selection in language production.

Introduction

Lexical selection may be broadly defined as the process of selecting a lexical target from a number of alternatives, such as when one names an object or a concept. Patients with chronic left prefrontal cortex (PFC) damage due to stroke often have lexical selection impairment. In particular, it has been proposed that these patients have difficulties in overcoming interference caused by semantically related alternatives in lexical selection (e.g. Riès, Greenhouse, Dronkers, Haaland, & Knight, 2014; Schnur, Schwartz, Brecher, & Hodgson, 2006; Schnur et al., 2009). However, the mechanism by which the left PFC operates to help overcome interference between semantically related alternatives is unclear. In this study, we use evidence accumulation modelling to investigate which computational mechanism may be impaired in left PFC patients when performing a lexical selection task.

The left PFC, and especially the left inferior frontal gyrus, have been proposed to play a role in resolving interference between semantically related alternatives for lexical selection (e.g. Riès et al., 2014; Schnur et al., 2006, 2009; Thompson-Schill, D’Esposito, Aguirre, & Farah, 1997; Thompson-Schill et al., 1998). This has been shown in both picture naming and verb generation tasks. For example in the blocked-cyclic picture naming task (Damian, Vigliocco, & Levelt, 2001), left PFC patients are particularly impaired in naming pictures when presented in semantically homogeneous (HOM) versus heterogeneous (HET) blocks (e.g. Schnur et al., 2006, 2009). In this paradigm, pictures are repeated several times per block and performance is typically impaired in HOM versus HET blocks from the second presentation onwards, leading to a semantic interference effect. This semantic interference effect has been shown to be larger in left PFC patients than in controls, which has been interpreted as being due to a greater difficulty for these patients to overcome interference between semantically related alternatives.

Different mechanisms have been suggested to underlie the capacity of the left PFC in resolving this interference, including a “booster” mechanism helping to tease lexical representation apart (Oppenheim, Dell, & Schwartz, 2010), a top-down mechanism allowing bias of the levels of activation of the task-relevant alternatives (Belke & Stielow, 2013), or more generally a proactive interference control mechanism proposed to operate across cognitive domains (Jonides & Nee, 2006; Kan & Thompson-Schill, 2004; Riès et al., 2014). However, additional developments are needed for the assessment of these mechanisms, as none of them have yet been integrated into quantitative models that can, for example, rigorously analyse PFC patient data at the response time (RT) distributional level. In this paper, we demonstrate such a development by using evidence accumulation modelling as a means to analyse PFC patient data at this level of granularity. So far, the approach most closely corresponds to a means of implementing, or further researching, a style of the “booster” mechanism suggested by Oppenheim et al. (2010, p. 8) in PFC patient performance data.

This project builds upon recent work by Anders, Riès, van Maanen, & Alario (2015), who in the context of traditional psycholinguistic theories (e.g. see Chen & Mirman, 2012; Howard, Nickels, Coltheart, & Cole-Virtue, 2006; Levelt, Roelofs, & Meyer, 1999; Oppenheim et al., 2010), advanced a theory that evidence accumulation may be an underlying component of the lexical selection process (see also Roelofs, 1992; Van Maanen & Van Rijn, 2007). Furthermore, with experimental data, they newly demonstrate how the cognitive parameters of psychometric applications of evidence accumulation models can be used to progress psycholinguistic theory. Evidence accumulation (also known as sequential sampling) may be defined as an information processing paradigm for how behaviours are selected in the context of time. Particularly, the paradigm postulates that behaviours, or processing choices across cognitive domains, are enabled through a sequential sampling of signal information (with noise at each sample) that accumulates toward a triggering threshold (Busemeyer & Townsend, 1992, 1993). Such sequential sampling approaches which are aimed at modelling signal interpretation, have experienced continued support since their conception in the 1960s (Gerstein & Mandelbrot, 1964; Laming, 1968; Ratcliff, 1978; Stone, 1960) in both theoretical (e.g. simulation exploration) and real data applications of experimental psychology (e.g. Anders, Alario, & Van Maanen, 2016; Buckley & Gillman, 1974; Donkin & Van Maanen, 2014; Mulder et al., 2013; Ratcliff, Gomez, & McKoon, 2004; Ratcliff & McKoon, 2008; Ratcliff, Van Zandt, & McKoon, 1999), as well as neuroscience research (e.g. Dehaene, 2008; Kelly & O’Connell, 2013; Mulder, Van Maanen, & Forstmann, 2014; O’Connell, Dockree, & Kelly, 2012).

The evidence accumulation approach has a number of advantages. Specifically, the approach can provide cognitive psychometrics (Batchelder, 1998; Riefer, Knapp, Batchelder, Bamber, & Manifold, 2002) and quantitative modelling contributions for observed RT data that can be tied to existent psycholinguistic theory. Furthermore, the observed RT distributions can be simultaneously measured with the approach (e.g. see Anders et al., 2016), providing advancements over classical measurement (mean, standard deviation (SD)) approaches (Balota & Yap, 2011; Luce, 1986). Evidence accumulation can be implemented to analyse lexical selection, by quantitatively modelling the appropriate experimental tasks that can elicit a minimally biased (e.g. from language-neutral stimuli) lexical selection procedure, such as the sequential picture naming task (Cattell, 1886; Carroll & White, 1973; Oldfield & Wingfield, 1964) previously discussed.

In summary, Anders et al. (2015) provide the first application of evidence accumulation to the domain of lexical selection (in healthy speakers). Then in this study, we provide a first application of the approach to the domain of PFC patients performing lexical selection. Furthermore we examine replicability of the previous findings for healthy speakers. The paper is organized as follows. First, a description of the evidence accumulation paradigm and the psychometric model used to analyse the data is developed. Then the methods are outlined for the picture-naming experiment that contains the PFC patients and healthy speakers. Next, specifics are detailed regarding how the proposed cognitive-behavioural modelling is applied: Fitting methods are outlined, and appropriate model fit is assessed, according to proper correspondence with the observed data. Then the model analysis results are interpreted in relation to the underlying cognitive mechanisms. Finally, the paper concludes with a general discussion.

Evidence accumulation for lexical selection

In this section, we acquaint the reader with the paradigm of evidence accumulation, and specifically a model previously proposed to analyse lexical selection in the context of picture-naming, the shifted Wald model (SWM; Anders et al., 2016; Folks & Chhikara, 1978; Heathcote, 2004; Luce, 1986; Ricciardi, 1977). The SWM, which involves only one accumulator with one threshold, and positive drift rates, could be considered a canonical, simplest case of racing accumulation that models the activation of the lexical target spoken, and not the alternatives (see Anders et al., 2015). Racing accumulation may hence consist of many SWM accumulators that are involved in a single trial (for each alternative), and the first that reaches the threshold is the lexical item activated. The race versions have been respectively proposed and simulated by LaBerge (1962) and Usher, Olami, & McClelland (2002); however, these approaches are currently not developed as quantitative data analysis techniques (e.g. psychometric modelling approaches) in present lexical selection experiments, due to data limitations of insufficient observation numbers. Lastly, it is also worth noting that the accumulation process of the SWM involves nearly exactly the same kind of random-walk process as the popular drift diffusion model (or diffusion decision model, DDM; Ratcliff, 1978; Ratcliff & McKoon, 2008; Ratcliff et al., 1999), except there is only one absorbing threshold, and the drift rates are positive. While the DDM is appropriate for two-alternative forced choice paradigms, the SWM is appropriate for paradigms in which one characteristic response is observed across varying latencies (e.g. a picture’s name).

An illustration of the SWM, and how it may be used as a simple cognitive-behavioural model for lexical target activation, is provided in Figure 1. In the left plot of the figure, a single trial is modelled. The fluctuating black line is a representation of evidence (or activation) that is accumulating over time for the lexical target, X_t; note that the evidence begins at a value of 0, and increases (with noise) over time, until it hits the necessary threshold value, here a value of 40. The evidence accumulates at every time step (t ms) with sequential samples from a Gaussian signal distribution, with mean signal γ, and noise modelled by a SD of 1.^1,2 Upon reaching the threshold, the lexical target has been sufficiently activated, and the verbal response behaviour is hence initiated. Parameter γ indicates the rate of activation accumulation, α is the value of the threshold needed to initiate the behaviour, and θ is the time to perform the behaviour, such as for response encoding to execution (here abbreviated “TEA” for “time external to the accumulation process”), and may also include time for perceptual processes.

Figure 1.

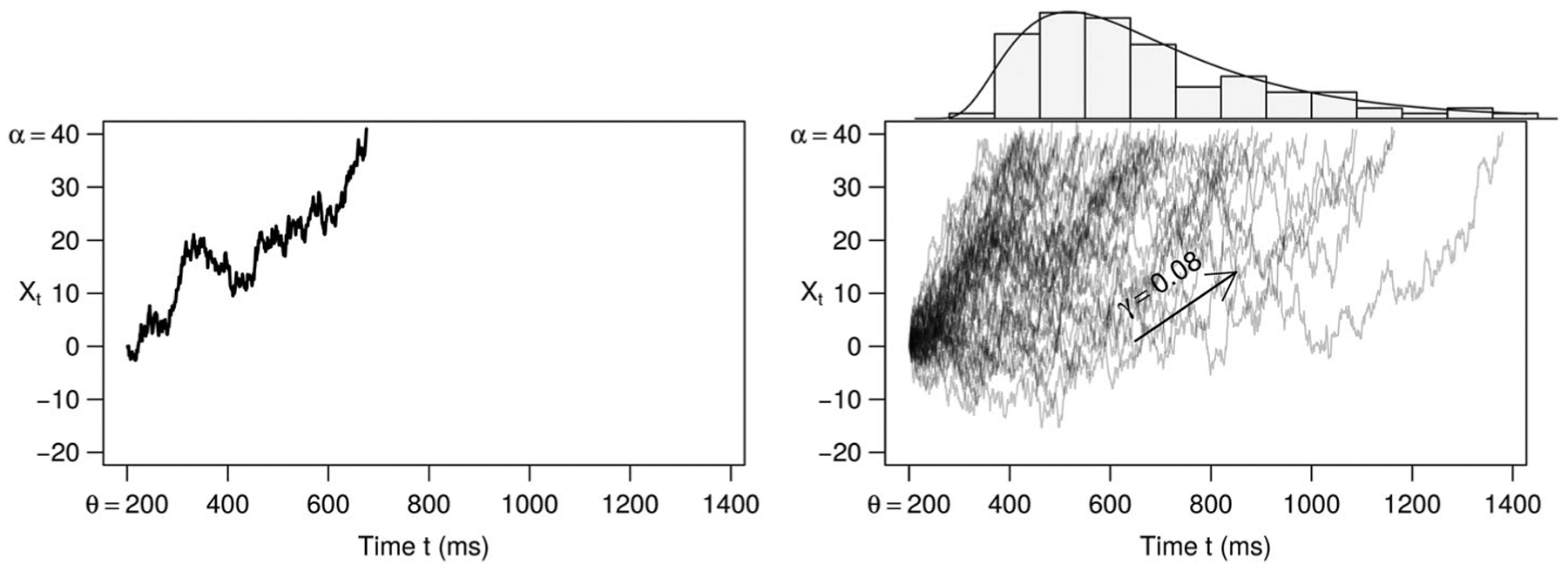
The SW as a cognitive-behavioural model, describing the RT data in the context of a latent quantity (e.g. signal) accumulating to threshold α at rate γ, where θ accounts for the time lapsed outside of (around) this process. Left, a single trial is modelled with the parameters. Right, many trials (e.g. an experimental design cell) are modelled with the same parameter values, and these ultimately form a SW distribution shaped with the same signal accumulation parameters.

In the right plot of Figure 1, many trials (e.g. a subject within an experimental design cell) are modelled with the same three parameters that simulated the single trial in the left plot. Note that all of these finishing times, of when the evidence accumulates to the necessary threshold, plus the TEA (θ),³ are the RTs, and these are quantified directly by the probability density function of the shifted Wald (SW) distribution, also known as the three-parameter inverse Gaussian distribution. Then, quantitatively one can think of any given RT_j, j ∈ 1 … N, N being the number of RT observations, as having a probabilistic likelihood of arising based on the evidence accumulation parameters of the corresponding experimental design cell c in which RT_j resides, as

$${\text{RT}}_j~\text{Shifted Wald}\left({\gamma }_c,{\alpha }_c,{\theta }_c\right),$$ (1)

in which each cell c may have various contributions based on experimental factors f, participant p, and item i. Hence in this kind of fitting approach (Anders et al., 2016), parameters are estimated per cell, as γ_c, α_c, θ_c, and these cells may vary according to such contributions. Each cell may be considered as corresponding to the right plot of Figure 1. The likelihood function of the SWM for a given RT_j in the context of an experimental design cell c is

$$\begin{gathered} f\left({\text{RT}}_j\mid {\gamma }_c,{\alpha }_c,{\theta }_c\right) \\ =\frac{{\alpha }_c}{\sqrt{2\pi {\left({\text{RT}}_j-{\theta }_c\right)}^3}} \\ \cdot \text{exp}\left\{-\frac{{\left[{\alpha }_c-{\gamma }_c\left({\text{RT}}_j-{\theta }_c\right)\right]}^2}{2\left({\text{RT}}_j-{\theta }_c\right)}\right\}, \end{gathered}$$ (2)

with expected value α_c/γ_c + θ_c, and variance ${\alpha }_c/{\gamma }_c^3$, for RT_j ∈ (θ_c, ∞) and γ_c, α_c, θ_c > 0.

Herein, each evidence accumulation parameter distinctly quantifies a unique RT distribution shape effect: γ for distribution tail length, α for variance around the mode, and θ for the distribution onset. Furthermore, it is important to note that each of these shape qualities can uniquely change an RT mean, as E(RT) = α_c/γ_c + θ_c (see Figure 2 in Anders et al., 2016). Hence this kind of analysis goes beyond assessing the RT mean, which is not identified in the case of skewed distributions (like RT distributions). For example, an RT mean can be greater due to a later distribution onset, a bigger tail, or more variance around the mode; two RT means can be equal (500 ms) but one distribution can have a larger tail and a faster onset E(RT) = (10/0.1) + 400 = 500 ms, while the other can have a smaller tail and a later onset E(RT) = (10/0.2) + 450 = 500 ms (the threshold, though equal in both cases to value 10 here, could also play a role in this issue). Furthermore, these opposing effects can be linked to distinct experimental predictors, and potentially disentangled. In the case of lexical selection experimental conditions (blocked-cyclic picture naming), which indeed has been proposed to have experimental predictors with opposing facilitatory and interference effects (e.g. semantic context and repetition; Navarrete, Del Prato, Peressotti, & Mahon, 2014; Oppenheim et al., 2010), then such a disentanglement provided by this modelling approach can be a notable advantage of the technique (see also Anders et al., 2015).

Figure 2.

Lesion overlay of the six patients. The colour coding indicates the amount of overlap between the different patients’ lesions (red corresponds to 100% overlap and purple to 0% overlap). Adapted with permission from Riès et al. (2014). To view this figure in colour, please see the online version of this journal.

Lexical target activity versus activity of alternatives

The succinctness and tractability of the SWM makes it a useful cognitive psychometric model for the empirical data that can inform psycholinguistic theory, and how experimental predictors (e.g. semantic context, repetition) may affect lexical activation dynamics. Furthermore, since the model does not require many observations, we can fit these predictors jointly, and also simultaneously account for between-trial effects (e.g. lag), which can improve model fit validity (see Baayen, 2004; Baayen, Davidson, & Bates, 2008; Barr, Levy, Scheepers, & Tily, 2013). Picture naming typically consists of correct responses among n-thousand possible alternatives, the correct responses having variability in latency. The model provides a sufficient, though simplistic, account (activation rate, threshold, non-selection time) of the observed behaviour (the lexical target), particularly via its accumulation dynamics. This kind of approach is compatible with research by Zandbelt, Purcell, Palmeri, Logan, & Schall (2014), who demonstrate how focusing on the relevant, single accumulator among a large ensemble (e.g. thousands)—such as the behaviour-triggering accumulator—can provide a sufficient cognitive-behavioural account of an observed response.

Though we gain a suitable, tractible process model for measurement through parameter succinctness (γ, α, θ), and through focusing on only the lexical target’s accumulation, it is worthwhile clarifying that other neurologically plausible dynamics (e.g. decay, inhibition, or competition) that may often be sourced by modelling the activation of lexical alternatives can still be integrated into the fitted model parameter results (if present). That is, the SWM fit is non-discriminating in the sense that it does not force the presence or absence of competition dynamics (e.g. by additional/constraining parameters), but will rather integrate these effects within the existing accumulation parameters {γ, α, θ} that provide an account of the overall accumulation trends. For example, if inhibition from lexical alternatives occurs, depending on how these factors manifest in accumulation dynamics, this may reduce the overall drift rate fitted by the SWM, and/or alternatively may increase the threshold needed—we note that psycholinguistic theories have different accounts on whether or not inhibition occurs, and how so (Dell, 1986; La Heij, 1988; Levelt et al., 1999; Mahon, Costa, Peterson, Vargas, & Caramazza, 2007; Oppenheim et al., 2010; Roelofs, 2003)—these will be discussed later after our data modelling results.

We note that in contrast to having high tractability by modelling only the behaviour-triggering accumulator, there exist multi-accumulator racing models that could simulate the n-thousand alternatives in lexical selection, and have added parameters that quantify decay/inhibition dynamics (e.g. McMillen & Holmes, 2006; Usher & McClelland, 2001). These models can resemble single-layer neural networks, and, similarly, some also do not include motor/non-selection time parameters. However, these more complex models are currently too intractable or demanding of observation numbers to be fit as psychometric models along experimental predictors, even for n ≥ 4 alternatives.⁴ However, it would be ideal if one could use these models as data measurement tools, and this is therefore a desirable goal for future work.

Hence, a primary difference between the SWM and these more complicated evidence accumulation models is that it does not have additional parameters that will parse out these more specific dynamics separately (e.g. a repeated decay on drift, or by inhibition, a repeated reduction on drift, or increase in threshold) from the three standard accumulation dynamics parameters, {γ, α, θ}. Therefore, to learn about the potential presence of competition (e.g. lateral inhibition) and its effects on the accumulation dynamics of lexical selection (drift rate, threshold, non-selection time) with the SWM (psychometrically), appropriately planned experimental predictors may be used. For example, by holding target difficulty constant (e.g. easy), one could examine changes in {γ, α, θ} for the lexical target between two experimental conditions, where one condition has another alternative(s) that is likely to be partially activated, but rarely selected. Fortunately, in the case of lexical selection, observing unrelated versus shared semantic context conditions across trial repetitions has been the corollary for this kind of analysis. Specifically, they have been the precedent experimental manipulations for examining the effects of partial activation of alternatives, and if activation of these alternatives provides interference (Damian et al., 2001). Therefore we will utilize these kinds of manipulations to demonstrate how a psychometric modelling of these predictors may help us learn about the activation dynamics of the target, as well as how it may be influenced (e.g. inhibition) by non-target activations.

Experiment methods

This study uses a subset of the data published in Riès et al. (2014) and only includes the data of the participants tested at UC Berkeley. This study differs from the previous work in that the analyses performed are of a completely different nature. To more deeply investigate how computational mechanisms may be impaired, or altered, in left PFC patients following damage due to stroke, herein a psychometric modelling approach is employed in which we assess the cognitive parameters of left PFC patients, which are obtained through a sequential information sampling (evidence accumulation) modelling analysis of their response data. Furthermore we compare the PFC patient results to healthy speakers in the experiment, assess replicability of previous analyses performed on healthy speakers (Anders et al., 2015), and interpret the findings in the context of current psycholinguistic theory.

Participants

The study was performed in agreement with the Declaration of Helsinki. All subjects gave informed consent approved by the University of California Berkeley Committee for Protection of Human Subjects. The data of nine PFC patients (five females; mean age: 59, SD = 12.09 years old) and 14 healthy speakers (eight females; mean age: 66, SD = 8.79 years old, t(13.41) = 1.50, p = 0.158) matched in age, gender, and education were collected. Patients had on average 17 years of education (SD = 2.30) and controls had on average 16 years of education (SD = 1.74; t(13.81) = −1.21, p = 0.245).

All patients had left PFC lesions due to stroke caused by infarction of the left precentral branch of the middle cerebral artery (providing the major blood supply to the left PFC). All were tested on the neuropsychological tests mentioned below and for the current study were at least six months post-stroke (chronic stage). Their lesions were delineated onto the MRIcro templates by a neurologist using input from T1, T2, and Flair scans acquired at least six months post-stroke on a Siemens Allegra 3.0 T MRI scanner. Of the nine patients tested, three PFC patients (two males) could not perform the experimental tasks adequately due to markedly poor performance: They either did not understand the instructions properly or their error rate on the experimental tasks was over 40% (mean score on Sequential Commands: 68/80, SD = 6.08, individual scores: 64, 65, and 75; mean score for Spontaneous Speech: 18/20, SD = 1.00, individual scores: 18, 17, and 19, respectively). The data of these three left PFC patients were excluded from the analysis. The remaining six left PFC patients had a mean Spontaneous Speech score of 18.83/20 (SD = 0.75), reflecting overall good production abilities despite some articulation problems (two patients had a score of 18 reflecting a lack of detail in the picture description or in answering one of the questions). The mean Sequential Command score was 74.9/80 (SD = 8.88 based on the five patients for which we had the Sequential Command score. The last patient had an overall Comprehension score of 9.8/10 reflecting good comprehension abilities). We note that three out of the six patients had a perfect score of 80, only one had a relatively low score of 59.5 and the other had a score of 75. The patient with the low comprehension score was nevertheless able to perform the naming task correctly. Thus the language production deficits of the left PFC patients included in the analysis were overall mild in nature allowing the patients to perform the task adequately. Lesion overlaps of the six patients included in the analyses are presented in Figure 2, and Table 1 provides information on total lesion volume and percentage damage in and outside the left PFC, by patient. Particularly, the left PFC patient lesions were centred in both the inferior frontal gyrus and the middle frontal gyrus.

Table 1.

Percentage damage in the PFC and outside the PFC (to the insula, basal ganglia, or temporal lobe) derived from manual delimitation onto the MRIcro templates by a neurologist, and total lesion volume per patient included in the study.

		% Damage outside the PFC
	% Damage in PFC	Insula	Basal ganglia	Temporal lobe	Total lesion volume (cm3)
P1	82.85	9.45	2.47	5.23	134.02
P2	81.46	7.00	8.40	3.14	72.53
P3	78.68	6.42	6.63	8.27	187.29
P4	69.35	4.46	0.52	25.67	96.98
P5	44.87	6.99	3.83	44.31	167.00
P6	70.20	10.89	0.25	18.66	59.96
Average	71.24	7.54	3.68	17.55	119.63
Standard deviation	14.10	2.29	15.68	16.37	51.62

Materials and design

As described in Riès et al. (2014), the stimuli were 252 line drawings of common objects or animals selected from published collections (Bonin, Peereman, Malardier, Méot, & Chalard, 2003; Snodgrass & Vanderwart, 1980), the Internet, or constructed by us (mean name agreement: 91.25%, SD = 8%). For purposes unrelated to the present study, participants also performed a Simon task (Simon & Rudell, 1967) using the same stimuli as in the picture naming task. Therefore, the stimuli were coloured in green or purple presented on the left or on the right of the fixation cross. These dimensions were however not relevant here. The stimuli were issued from six semantic categories (e.g. human dwellings, means of transportation). Each member (e.g. house) was represented by seven different items (e.g. six different houses: Five used as experimental items, one for familiarization). In the blocked-cyclic naming task as generally used, pictures are repeated several times per block (five or six most often; e.g. Damian et al., 2001; Maess, Friederici, Damian, Meyer, & Levelt, 2002). The semantic interference effect emerges only after the first presentation of the stimuli. We reasoned that repeating the same pictures several times may cause the stimulus–response associations to be over-learned. Therefore, we used different pictures to represent the same member of a category (e.g. different types of houses) to minimize stimulus–response associations that could bypass lexical access. Importantly, the semantic interference effect has been shown to extend to new items (Belke, Meyer, & Damian, 2005). We were therefore confident this design would give us a reliable semantic interference effect. The items were presented in a pseudo-random order (using the software MIX; Van Casteren & Davis, 2006) within each experimental run with the constraints that consecutive items were phonologically unrelated (i.e. two pictures in a row never had the same initial phoneme) and items sharing the same name would be at least three trials away from one another.

Procedure

The procedure was the same as described in S.K. Riès, Xie, Haaland, Dronkers, & Knight (2013), S. Riès et al. (2014), and S. Riès, Karzmark, Navarrete, Knight, & Dronkers (2015). We repeat relevant aspects for the current study. Participants responded by making verbal answers to pictures presented on a computer screen situated 148 cm in front of them while seated comfortably in a sound-attenuated dimly lit environment. Stimuli were presented using Eprime 2.0 Professional (Psychology Software Tools, Inc., Pittsburgh, PA), allowing online recording of verbal responses. A trial consisted of the following events: (1) A fixation point (“plus” sign presented at the centre of the screen) for 500 ms; (2) a picture for 2000 ms; (3) a blank screen for 2000 ms. The following trial started automatically. As mentioned above, participants also performed a Simon task but did so in separate blocks. The order in which the tasks were performed was counter-balanced across participants. In both tasks, participants had to add the possessive determiner “my” (e.g. “my house”) before their answer. This was done to reduce variability in vocal onsets and because we also recorded the electromyography (EMG) activity of three facial articulators for unrelated purposes. The response-onset measure was the vocal onsets. The task was split into four blocks of 108 trials each. Participants could take breaks whenever they needed and two built-in pauses were equally spaced within each block. Participants had to respond as fast and as accurately as possible. Before the experiment, participants were familiarized with the picture names.

The results of the Simon task are not considered here. In the Simon task, participants were asked to say “my right” or “my left” depending on the colour of the picture while ignoring the side on which the picture was presented. Thus interference is greater for a picture presented on the left of the fixation cross when the response to be given is “my right” and vice versa. The stimulus–response association rule (i.e. saying “my right” for a green picture and “my left” for a purple picture or vice versa) and the order in which the tasks were performed were counter-balanced across participants.

Data post-processing and analysis

Response accuracy and verbal RTs were measured offline using CheckVocal (Protopapas, 2007). Trials were excluded from the analysis if the participant did not respond, or produced any kind of verbal error: Partial or complete production of incorrect words, omission of the pronoun “my”, verbal dysfluencies (e.g. stuttering, utterance repairs: 4%), and hesitations (e.g. if the experimenter perceived the production of the possessive pronoun to be abnormally lengthened or separated from the production of the noun by a pause). Finally in the main effects and interactions analyses, and also to provide results that translate to previous analyses (Anders et al., 2015), we follow the common practice of excluding the first occurrence of each stimulus (namely, repetition cycle 1) on each block (Ewald, Aristei, Nolte, & Rahman, 2012) in the context of analysing semantic interference, as the semantic interference effect can be absent or even reversed in the first presentation (e.g. Belke et al., 2005; Damian et al., 2001; Rahman & Melinger, 2007). However, we provide a supplementary analysis afterward that indeed examines the contrasts between repetition cycle 1 and subsequent repetitions (e.g. 2–3 and 4–6), with semantic context, in order to bridge our model-based results to more recent literature that involves the topic (e.g. Mahon et al., 2007; Navarrete et al., 2014; Rabovsky, Schad, & Rahman, 2016).

Application to lexical retrieval patient data

Fitting approach

The fitting method utilized for the SWM combines techniques of maximum likelihood and deviance criterion minimization. In this approach (see Anders et al., 2016, for a tutorial and code), an independent SWM is fitted for each unique experimental design cell (each possessing an RT distribution), in which main effects and interactions can be observed on the parameters of evidence accumulation. Note that for every design cell, the cognitive parameters drift γ, threshold α, and TEA θ are estimated. The design cells consist of the possible combinations of the relevant factors of the task: Semantic context, repetition, and lag between item repetition. Furthermore, we fit these cells by participant (20 total), in which six participants are PFC patients, and the other 14 are healthy speakers. In order to provide comparison and replicability analysis of the modelling with the previous data researched (Anders et al., 2015), we similarly collapsed the repetition factor into two levels (2–3 and 4–6) and the lag factor into two levels (2–5 and 6–12). Then the result is N = 20 × 2 × 2 × 2 = 160 experimental cells fitted, each having an appropriate average cell size of 40 trials, with SD of trials 10, and range (20, 64). A supplementary analysis also compares semantic context effects of pictures in their first repetition (naming) with the other two repetition levels (2–3 and 4–6) for both healthy speakers and patients, resulting in 40 = 20 × 2 additional experimental cells (one lag level), with average cell size of 28 trials, SD 6, and range (14, 35). This totals 200 experimental cells being fitted by the model.

Finally before fitting, on each cell a very light processing of potential contaminant RTs (see Barnett & Lewis, 1994; Ratcliff & Tuerlinckx, 2002) was performed by an elimination criterion of below three or above six median absolute deviations (see Leys, Ley, Klein, Bernard, & Licata, 2013) from the cell RT median (preserving the long tail RT values), resulting in 6506 trials for analysis out of the original 6543 (0.5% of trials omitted). Then to fit the model, for each cell, maximum likelihood method of moment estimators were used to calculate the three SWM parameters when a shape parameter is proposed (β, as in Anders et al., 2016). Then searching across the near-entire range β, the optimal parameter set is selected according to the minimal difference between the data to model-predicted RT quantiles, by 100 equally spaced quantile points in the range (0.01, 0.99).

Illustration of the observed response time distributions by design cell

The analysis approach hence consists of modelling the observed RT distributions corresponding to each experimental design cell (partitioned by subject as well). After the model is fit, values for the process parameters are obtained for each of these cells. Then a formal comparative analysis of these parameters (e.g. an analysis of variance, ANOVA), can quantify the significant differences and/or interactions between the experimental conditions. Particularly, we obtain information on how these conditions modulate the dynamics of the underlying process modelled. In this section, we illustrate the observed RT distributions of the experimental design cells from sample subjects of each group: Healthy speakers and left PFC patients.

The top row of Figure 3 provides the observed data distributions obtained from four example subjects of the healthy speakers group, and the bottom row provides the same for four subjects of the left PFC patient group. The four distributions in each subject’s plot respectively correspond to the HET and HOM conditions at repetition levels 1 (cycles 2–3) and 2 (cycles 4–6) for a single lag level (>5).⁵ Keeping in mind that of the SWM parameters, γ quantifies the tail length, α quantifies the variance around the mode value, and θ quantifies the onset of the distribution, some elementary predictions can be made about what one might see when the model is fitted to this data. For example, in comparing the healthy speakers versus patients (top and bottom rows), the healthy speakers clearly show an improvement in RTs at the second repetition of HET conditions by narrower distributions/higher modes, while the patients do not. This distribution effect would most likely correspond to a lower α value obtained in the model fit with increased HET repetitions for healthy speakers. Another observable difference between healthy speakers and patients exists in how the healthy speakers have notably slower RT distributions between the HET versus HOM conditions (by being wider around the mode), while the patients do not have this specific modulation in their distributions. This is another effect in which one could expect that the model fit will derive an α change (here increased) for HOM conditions in healthy speakers, and this kind of threshold adjustment would not be present in patients.

Figure 3.

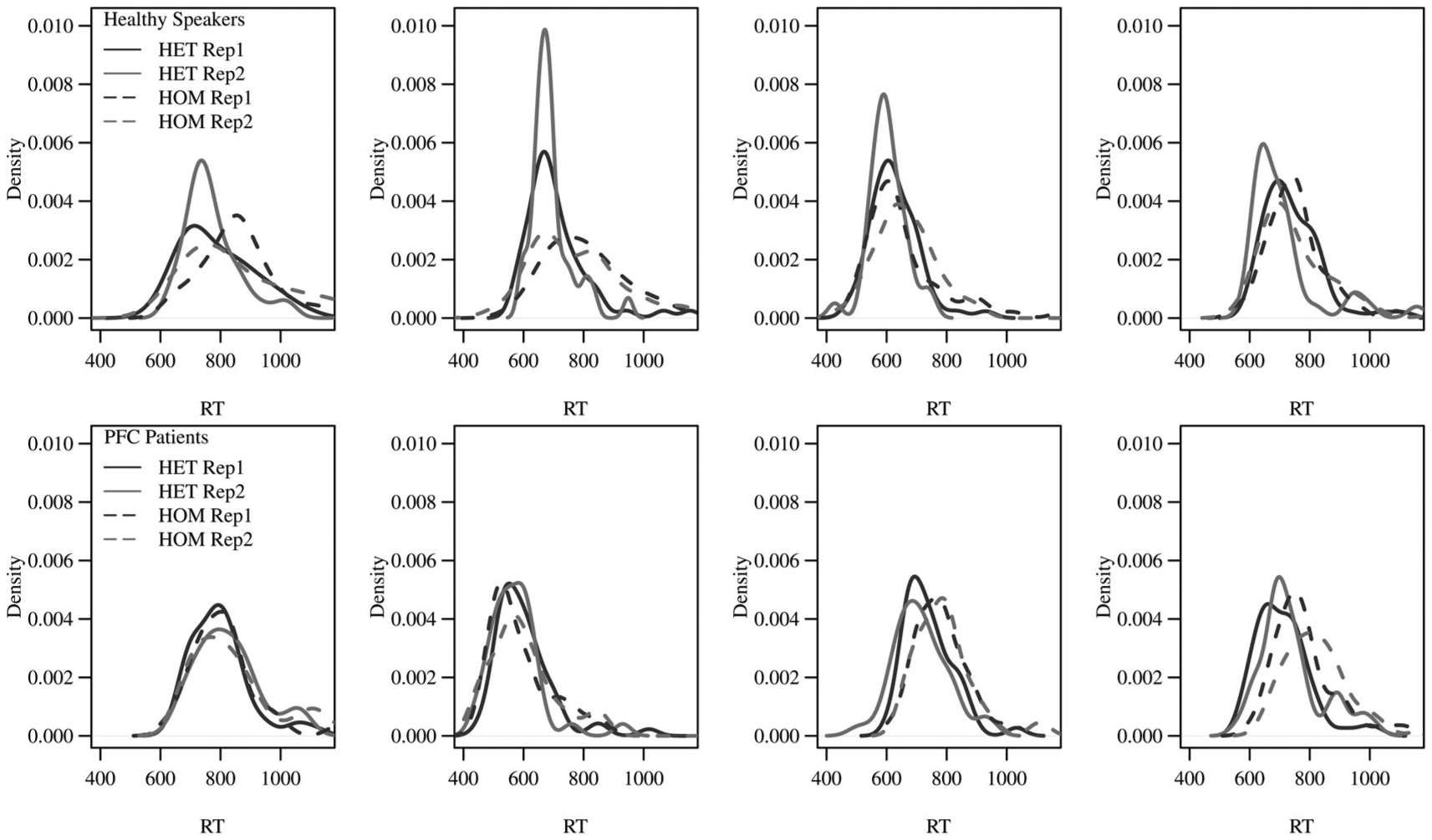
An illustration of the experimental cell distributions by subject that the SWM fits. The four distributions in each subject’s plot respectively correspond to the HET/HOM conditions at repetition levels 1 (cycles 2–3) and 2 (cycles 4–6) for one lag level (>5).

Through visually inspecting these by-cell observed RT distributions, these are just a few examples of speculations one could make about the results that will be obtained by the model fit. However, from only eye-balling these plots, it is difficult to capture all such differences, and be right about them, especially when one is tasked also with considering changes in distribution tail and onset. This is especially the case since the unique cells provide for as many as 200 distributions in total. Alternatively if one wanted to reduce these cells into a single distribution across subjects in order to make such conclusions, unfortunately this can blur the precision of the distributions (widen them) and can hence can mask or distort the underlying effects. In contrast, the proposed approach consists of applying a model to these distinct data cells, which will quantify each of these distribution features according to an objective function. Then comparison analyses of the posterior results will indicate what significant differences there are between the conditions and subject groups for the parameters. First, before examining these posterior parameter results however, the following section provides important model fit diagnostics based on quantifying the fit error (observed distributions vs the estimated distributions) at the specificity of all of the distribution deciles (e.g. 0.1, 0.2, …, 0.9). This is done for every cell (200 total). These diagnostics hence provide a systematic method for assessing quality of fit (and if the parameter results are appropriate to interpret).

Model fit checks

In this section, model fit diagnostics are examined to assess the degree to which the model appropriately fits the data, and hence if the parameter results may be appropriate to interpret. Then following a satisfactory fit, the next section reports the main parameter differences. Thirdly, an interpretation of these parameters and their relationships to psycholinguistic theory is provided.

The first plot in Figure 4 provides the quantile–quantile (QQ) matching of the deciles of the fit-simulated distributions against the observed distributions; it contains all 200 cells. The QQ plot may show overall trends in systematically misfitting quantiles of the distribution, as well as misfit outliers. It also gives an idea about the scale and range of the data. The importance of this check is to observe critically any curvatures in the plot, which is a strong sign of misfit. As one can see in the figure, there is no systematic curvature in the plot and the SWM performs systematically well on the data set, with minimal outliers.

Figure 4.

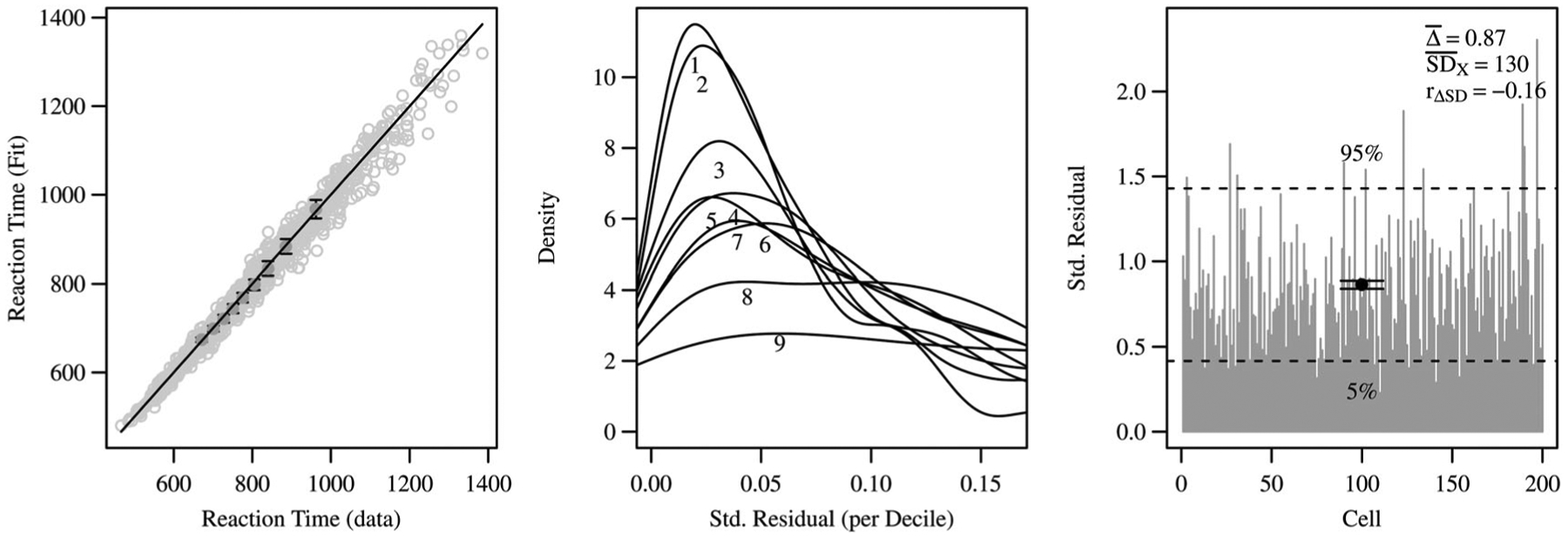
Diagnostics for the SWM fit to the observed data. The left plot shows the QQ match for the nine deciles (0.1 to 0.9) for each of the 200 cells. The middle plot shows the distribution of residuals for each these nine deciles across the 200 cells, where the residual is the absolute difference (in ms) between the observed decile and the model-predicted decile, and here the residuals are standardized (divided) by the corresponding cell’s model-estimated standard deviation. The right plot provides the sum of these standardized residuals of the nine deciles (by cell); including statistics respectively for the mean cell residual $\overline{\Delta }$, the mean cell standard deviation ${\overline{\text{SD}}}_{\text{X}}$, and the correlation between the two across cells.

The middle plot provides the distribution of standardized residuals for each of the nine deciles across the 200 cells fitted. In this model fit check, one might optimally see a distinct ordering of decile residual distributions, due to the property that residual magnitude tends to correlate with RT data variance and magnitude (e.g. see Anders et al., 2016). In this application, such an ordering is present, and it is nicely shown that most standardized residuals are near 0.05 and below, similar to previous applications. Finally the third plot provides the sum standardized residual, Δ, by cell. One can see that there are not many large residual outliers, the mean cell standardized residual $\overline{\Delta }=0.87$ is suitably low, and the correlation between the cells’ standardized residuals and the deviation of the data within each cell, r_ΔSD = −0.16, is also satisfactorily low (see Anders et al., 2016). Thus the three model fit diagnostics demonstrate appropriate results.

Results

In the model fit analysis of the 14 healthy speakers (left) and six left PFC patients (right) of Figure 5, the following results were observed. Firstly, overall group differences were shown to have marginal effects: The PFC patients were found to have overall higher accumulation rates γ (or excitability) than healthy speakers t(104) = −1.8, p = 0.07, which may be compensating for their overall slower non-accumulation delays θ (e.g., motor output) than healthy speakers t(73) = −1.5, p = 0.12. Then the most substantial effects were found along the experimental factors, as well as their interactions.

Figure 5.

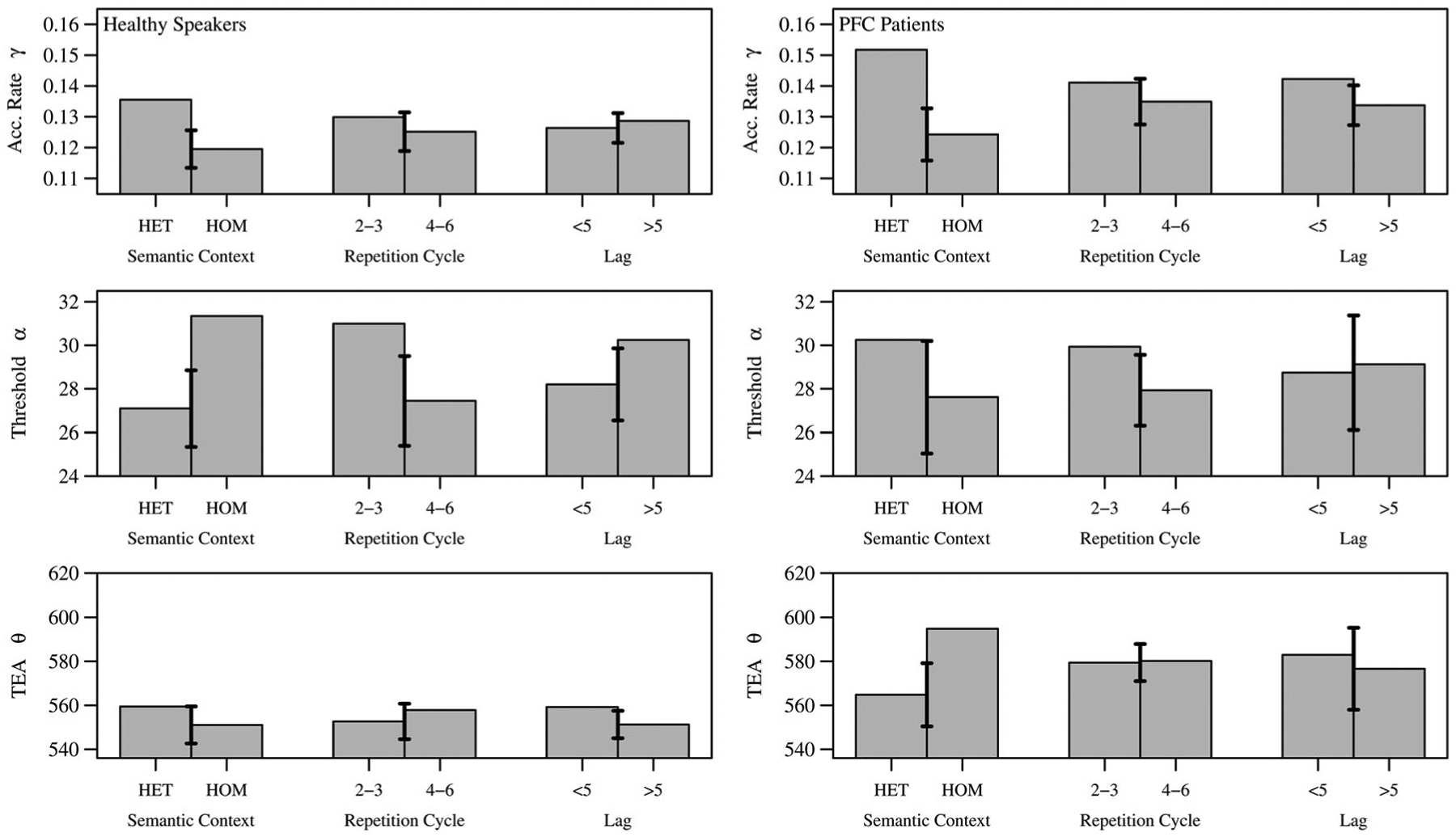
Left column: Healthy speakers; right column: Left PFC patients. The cognitive parameters from the model fit for each experimental condition: Semantic context for semantically unrelated conditions (HET) and semantically related conditions (HOM), repetition level (2–3, 4–6), and lag (<5, >5).

At the detail of the experimental manipulations, a main effect of semantic context (HET vs HOM blocks) was found, providing a decrease in the signal accumulation rate parameter, γ (F_γ(1, 18) = 15.3, p = 0.001, ${\eta }_p^2=0.46$, ${\eta }_G^2=0.080$),⁶ and an increase in the threshold parameter, α (F_α(1, 18) = 2.26, p = 0.15, ${\eta }_p^2=0.11$, ${\eta }_G^2=0.012$) for HOM over HET, but no effect in external time θ (F_θ(1, 18) = 0.18, p = 0.69, ${\eta }_p^2=0.01$, ${\eta }_G^2=0.000$). Critically, a significant interaction was discovered between groups regarding this α effect (F_interα(1,18) = 4.36, p = 0.04, ${\eta }_p^2=0.21$, ${\eta }_G^2=0.026$); in particular that PFC patients have an impairment to appropriately adjust their threshold according to semantic context. Hence this increase in threshold by HOM versus HET blocks occurs only in the healthy speakers (t(110) = −2.2, p = 0.032). Furthermore, a significant interaction was found between groups concerning θ (F_interθ(1,18) = 5.84, p = 0.03, ${\eta }_p^2=0.24$, ${\eta }_G^2=0.011$), suggesting semantic interference (HOM) for the PFC patients also introduces added motor output difficulties.

In regard to repetition between levels 2–3 and 4–6, a main effect was also found, providing a decrease in signal criterion level α (F_α(1, 18) = 4.05, p = 0.06, ${\eta }_p^2=0.18$, ${\eta }_G^2=0.025$) with increased repetition, which could be interpreted as a residually higher starting activation for the lexical target by its repetition. Here, no significant interaction was found between groups in regard to repetition. However, a significant interaction was evident for repetition crossed with semantic context, on accumulation rate γ (F_interγ(1, 18) = 7.32, p = 0.01, ${\eta }_p^2=0.29$, ${\eta }_G^2=0.014$). In particular semantic interference (HOM) provides decreased accumulation rate over repetition levels t(73) = 2.1, p = 0.037; see Figure 6 (row 1, HOM 2–3 to 4–6). Lastly, no significant effects were found in lag.

Figure 6.

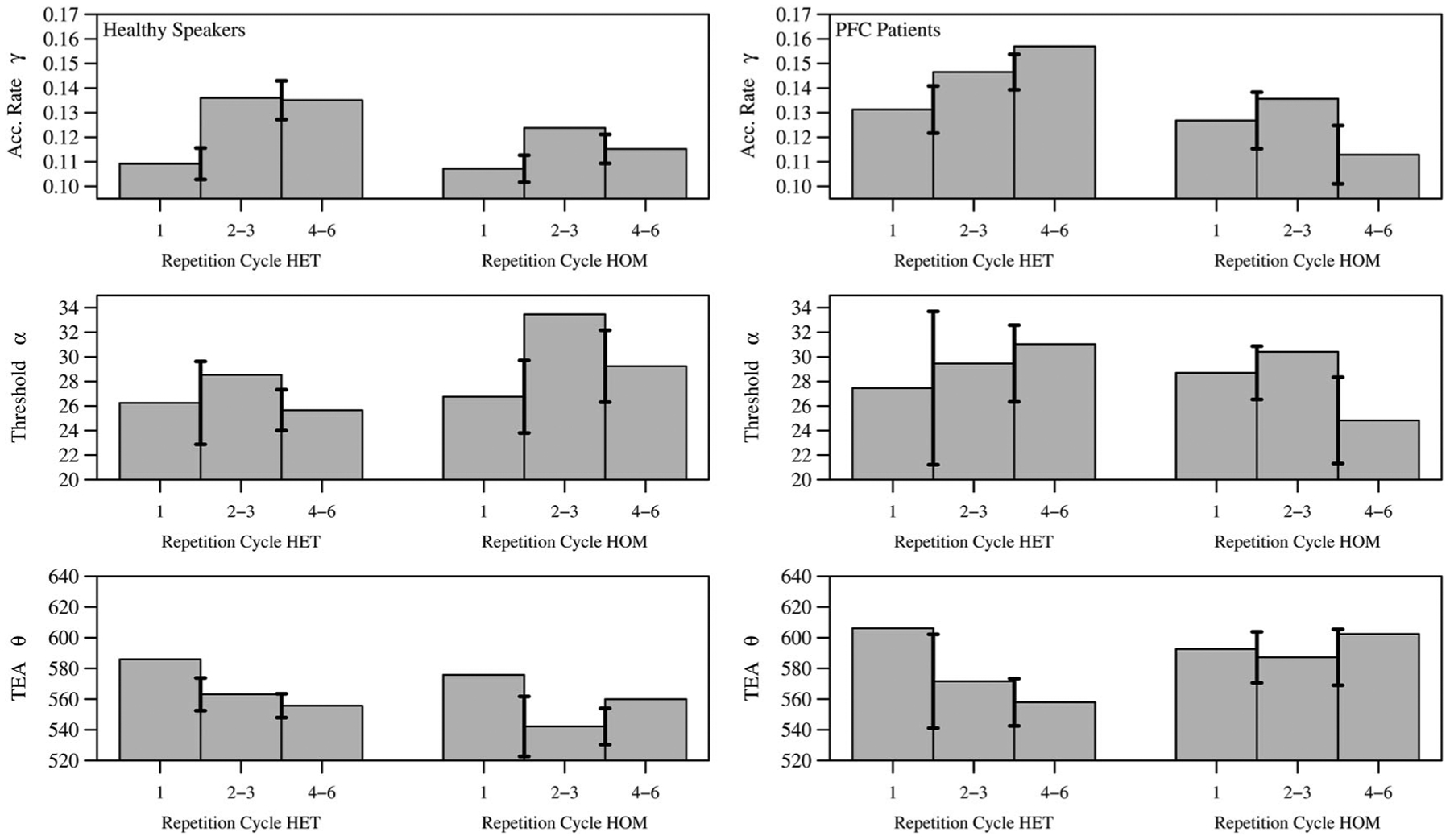
Left column: Healthy speakers; right column: Left PFC patients. A more detailed contrast provided for the semantically unrelated conditions (HET) and semantically related conditions (HOM) over each repetition level modelled (1, 2–3, 4–6). Used to further examine how the cognitive model parameters for HET/HOM adjust over repetition, and by subject group.

Supplementary analysis with first repetition (naming) level

In an ANOVA of the model parameters between the first repetition level and the next, crossed with semantic context and group, the model-based analysis accounts for the “known” boost (or notable improvement) in RTs after the first repetition, through the main effects of enhanced activation rate γ (F_γ(1, 18) = 18.64, p < .001, ${\eta }_p^2=0.51$, ${\eta }_G^2=0.107$) and reduced TEA θ (F_θ(1, 18) = 8.25, p = 0.01, ${\eta }_p^2=0.31$, ${\eta }_G^2=0.029$); see Figure 6 (rows 1 and 3). In contrast, a slowing in RTs occurs by increased threshold α (F_α(1, 18) = 3.58, p = 0.07, ${\eta }_p^2=0.17$, ${\eta }_G^2=0.056$), up to a level that corresponds to relative condition difficulty (lower for HET vs larger for HOM; see Healthy Speakers), as in Figure 6; while the left PFC patients have increased threshold means (from 1 to 2–3) as well in HET/HOM, these levels do not adequately adjust for semantic context difficulty like in healthy speaker levels. Thirdly, no significant interactions were found. Finally, no significant pairwise differences were found between first repetitions in HOM versus HET.

Summary

Replication.

Regarding the healthy speakers, we replicated the findings described by Anders et al. (2015): Shared semantic context (HOM, or semantic interference) reduces the rate of lexical target activity accumulation (γ) and increases the amount of activation needed for the lexical target to be selected (α). Repetition decreases the amount of activation needed for the lexical target to be selected (α), and, likewise, no significant effects were found in lag. Though similar to the previous study, a mean increase in threshold was observed with increased lag levels. We wonder if non-significance here is an issue to do with power, and if improvements in experimental design that balance observation numbers per lag level may improve analysis of this predictor and/or its interactions. Alternatively, we note that in previous analyses based on RT means, lag has not been found to have a significant effect.

Accounting for differences between PFC patients and healthy speakers.

New findings in left PFC patient data are the following. With respect to semantic context, left PFC patients have an impairment from healthy speakers in appropriate threshold adjustment. Although the patients have a much more pronounced drop in evidence accumulation rate between semantic context conditions HET/HOM than healthy speakers, they do not differ significantly from healthy speakers in accumulation rate during semantic interference. Rather, they fail to up-adjust the threshold to deal with the increased difficulty that semantic interference provides, as in healthy speakers, and instead appear to need less activation to select the lexical target (threshold) α during semantic interference, but are then slowed by the interference at either a process before this decision process can take place, or during the post-selection stages (e.g. articulation), by θ.

Although parameter θ includes both pre- and post-selection delays, given the location of these patients’ lesions, it may be reasonable to infer that the additional slowing in θ occurs post-selection (such as in articulation) for these patients. This is because their left PFC lesions also encompassed part of the premotor cortex and, in some cases, the insula. Several studies (e.g. Dronkers, 1996; Guenther, Ghosh, & Tourville, 2006) have discussed the relevant role of these regions in speech motor programming/functioning. Here (and as in Fink, Oppenheim, & Goldrick, 2017; Kello, Plaut, & MacWhinney, 2000), we are suggesting that these regions operating downstream from the word selection process are affected by word retrieval difficulty, with the idea that processing difficulty in lexical selection can cascade into articulation difficulties.

Another notable difference involves that over all conditions PFC patients have higher accumulation rates and non-accumulation times than healthy speakers. This tentatively suggests that PFC patients may compensate for such pre- and post lexical selection difficulties (increased θ) by exhibiting an increased overall excitability (γ) in the lexical network, which in combination with their impairment in appropriate threshold (α) modulation during semantic interference could potentially account for their higher error rates. For example, Usher et al. (2002) demonstrate how in racing accumulation models an increased threshold is needed to maintain accuracy levels when relevant alternative numbers are increased, which has also been replicated in fits to real data by Van Maanen et al. (2012); correspondingly, PFC patients do not appropriately increase the threshold in the case of semantic context, which has more alternatives active, and hence according to this modelling framework this finding predicts a higher error rate. Additional applications of this modelling (and advancements thereof) to patient data may further sharpen these inferences.

Disentangling Facilitatory and interference effects through different dynamics in lexical activation.

Next, the significant interaction analyses between semantic context and repetition have revealed valuable findings for psycholinguistic theory. Navarrete et al. (2014) have argued that semantic interference (from shared semantic context, HOM) in cyclic naming depends on (and hence accumulates with) repetition. We have reproduced this result (in both healthy speakers and PFC patients), and furthermore we newly link this repetition-based interference with decreases in the lexical target activity accumulation rate, γ.⁷ Secondly, Navarrete, Del Prato, & Mahon (2012) relate this accumulated interference not as through competition, but by the negative effects of incremental learning: Through naming semantically related targets that overcome the positive learning effects, as forwarded by Oppenheim, Dell, & Schwartz (2007) and Oppenheim et al. (2010).

While Oppenheim et al. (2010) consider two kinds of possible racing mechanisms, one competitive and one non-competitive (the latter having a threshold that is not forced to be negatively correlated to the booster accumulation rate), Anders et al. (2015) showed that the non-competitive version is supported by their similar psychometric modelling of these experimental data predictors in a different data set. Our work herein also supports/replicates these results of our previous modelling analysis, and further disentangles how these opposing effects of learning may be occurring in the lexical activation dynamics. That is, a deeper analysis of the cognitive parameters derived from the data here shows how they are able to disentangle the positive effects of learning (reduced thresholds, by repetition priming in general) from the negative effects of learning (reduced activation rate, by weakening closely related-but-incorrect targets by repetition priming in semantic context).

These results, that cumulative semantic interference occurs with repetition (by a reduction in lexical activation rate, γ) in patients with left PFC lesions as in healthy speakers, may shed more light on the argument put forward by Belke (2008) and Belke and Stielow (2013). Belke and colleagues observed that semantic interference is typically not cumulative in healthy young speakers in the blocked cyclic picture naming paradigm. They proposed that healthy speakers are able to keep the accumulation of the interference under control through frontal top-down biasing on the task set. This difference between our study and theirs regarding observing cumulative interference in healthy controls may be attributed to several reasons. First, Belke and colleagues’ argument pertains mainly to young healthy speakers, in which our study involved older healthy adults—though we note that Anders et al. (2015) and Navarrete et al. (2014) have observed the cumulative interference effect for young healthy speakers in their experimental data using the blocked cyclic picture naming paradigm. Secondly, Belke & Stielow’s conclusions pertain to analyses involving mean RT analyses. We argue that our response process (and RT distributional) modeling allows to disentangle the priming effect of repetition (quickening) from the semantic interference effect (slowing) on RTs better than an analysis on RT means and that our methodology is in this respect less prone to Type II errors (see the final paragraph of the SWM explanation section). Hence, we believe that more information on this debate might be yielded by re-analyzing Belke & Stielow’s discussed data sets with this kind of modeling, and seeing if similar opposing effects (facilitation and interference) occur on the RT means.

Accounting for how a network may be calibrated, adjusted for difficulty.

The supplementary analysis across repetition levels demonstrates how a naming system (or lexical activation) can become quickly calibrated after the first repetition. First, a commonly known result is a large boost (reduction) in RTs after the first repetition (Belke, 2013; Belke et al., 2005; Navarrete et al., 2012, 2014). Here the model-based results specify that the dynamics of this boost relate to a quickly calibrated network (e.g. through positive learning) by increased target activation rates γ and decreased external times θ (e.g. articulation preparation). Secondly, we show how the network is also simultaneously calibrated to the difficulty, in a way that slows RTs for increased selection caution by a magnitude relative to the difficulty level. For instance, while the initial threshold α states are nearly the same between HET/HOM conditions during the first naming (repetition), afterwards the network adjusts the threshold according to the condition difficulty (e.g. by learned interference), such as increasing the threshold to be more cautious in HOM than in HET. This idea ties into work by Navarrete et al. (2014) who demonstrate how different “baselines” may be determined according to the presence or absence of semantic context within the first repetition, from which subsequent positive/negative incremental learning effects may act regularly.

Discussion

A number of current psycholinguistic theories consider lexical selection as a process related to selecting a lexical target from a number of lexical alternatives which each have varying activations (or signal supports) that are largely resultant from an initial stimulus recognition. How these activations develop into influencing the decision process of selecting the appropriate lexical target can be described as a racing evidence accumulation process (e.g. see Anders et al., 2015). Herein we utilized data-derived (or psychometric) implementations of evidence accumulation modelling to provide a mechanistic account of lexical selection dynamics, as modulated by factors of semantic context and repetition cycles in the data, for the blocked-cyclic naming paradigm. We hence focus on studying the mechanics of the increased semantic interference effect observed in left PFC patients versus controls, through cognitive parameters that are estimated from the experimental data. Using this paradigm, our results suggest that it is the decision threshold adjustment that is specifically impaired in these patients. These results therefore shed light on the computational role of the left PFC in lexical selection.

A cognitive psychometric modelling of left PFC patients and healthy speakers.

We hence provide a first psychometric evidence accumulation application to left PFC patients performing semantic (e.g. picture/concept) lexical retrieval. We do so by applying a simplest case model of racing noisy evidence accumulation (due to observed data size constraints), called the SWM, and examine the cognitive parameters along the experimental predictors (both main effects and interactions). We also apply the SWM to a control group of healthy speakers on the task, examining the replicability of the SWM parameters in a previous experimental study of only healthy speakers by Anders et al. (2015).

Left PFC patients.

The left PFC patients primarily differed from the healthy speakers in regard to semantic interference effects. While healthy speakers are slowed in both evidence accumulation rate (γ) and threshold (α) during semantic interference, the left PFC patients appear to show only a slowing effect in evidence accumulation rate (γ), and hence have an impairment in decision threshold adjustment (α). It may therefore be reasonable to speculate that for these patients, a module in the pre-frontal cortex may not be accumulating semantic interference any more in a similar way to in healthy speakers. Furthermore, left PFC patients suffer semantic interference through difficulties (or modulations) of prior or posterior processes to lexical selection (e.g. lexical target articulation), as suggested by our finding of their slower non-accumulation function times (θ) during semantic interference contexts. A third finding is that the left PFC patients may be compensating for these slowings/impairments by exhibiting an increased overall excitability (or lexical target activation rate, γ) in the lexical network. This increased excitability, in combination with the other impairments, primarily the threshold modulation impairment of left PFC patients, may lead to increased error rates. For example, Usher et al. (2002) demonstrate how in racing accumulation models an increased threshold is needed to maintain accuracy levels when relevant alternative numbers are increased, which has also been replicated in fits to real data by Van Maanen et al. (2012). Correspondingly, PFC patients do not appropriately increase the threshold in the case of semantic context, which has more alternatives active, and hence this finding predicts a higher error rate.

Healthy speakers.

In the healthy speakers, the main effects in the previous experiment by Anders et al. (2015) were replicated, and through deeper analyses here, notable interaction effects were newly revealed. For example, while repetition itself provides a priming benefit in less activation needed (α) for the lexical target to be selected, it is the increasing semantic interference that reduces the evidence accumulation rate (γ) with increased repetition. Furthermore, we provided a new supplementary analysis that examined the first repetition (previously excluded) and its transition to subsequent repetitions. The parameters for first repetitions were close (nearly equal) between unrelated and related contexts, however, the large boost in faster RTs occurring in subsequent repetitions (commonly observed in such experiments; see Belke, 2013; Belke et al., 2005; Navarrete et al., 2012, 2014) were accounted for by the model with faster drift (γ) and TEA (θ) acquired after the first repetition cycle. In contrast, subsequent repetitions also have a slowing effect: Thresholds are heightened in accordance with condition difficulty—this can relate to the kind of “baseline” adjustment for semantic context that Navarrete et al. (2014) refer to. Furthermore, PFC patients had similar patterns to healthy speakers in calibration between the first repetition and subsequent ones (see Figure 6), but failed to set a heightened threshold to account for difficulty, which is compatible with the main results of the patient analysis.

Going deeper into modelling left PFC patient errors.

Although we were able to obtain psychometric indications for why PFC patients may make more errors, unfortunately, due to observation size limits, we were not able to fit the errors themselves, and more deeply analyse them with cognitive modelling. Hence an important development for future work is to collect enough observations to jointly fit the PFC patient errors as another contrast for comparison, either as another mixture (or factor) added onto the current modelling, or ideally with a racing evidence accumulation model, which can jointly model multiple kinds of errors (e.g. articulation, or specific word alternatives; LaBerge, 1962; Usher et al., 2002). While full racing models (e.g. quantifying n ≥ 4 alternative accumulators) are technically not used as data measurement models for experimental data (at least not currently), we can certainly learn from them instead as data-producing models for comparing PFC patients with healthy speakers and their errors. For example, one could examine simulated data for two groups: One a model that adjusts the threshold higher for semantic context (healthy speakers), and another group in which thresholds remain the same (PFC patients). Alternatively, to maintain the data-derived cognitive modelling approach used herein, perhaps a doubly sized experiment with PFC patients may provide enough errors to fit them as another mixture/factor. However, we note that since many kinds of errors (articulation, studder, semantic vs phonological, etc.) are possible, it is difficult to obtain enough observations of any single error type in order to study it with such modelling across the experimental predictors. Ideally larger experimental studies with more patients, and more observations, should be performed to more sharply develop these results.

Implications for current psycholinguistic theory.

One of our primary experimental findings here, that left PFC patients have threshold adjustment impairment during semantic interference contexts of lexical retrieval, builds upon current interpretations for how lesions to the left PFC may impair word selection processes in language production (reported for example in Schnur et al., 2006, 2009; Thompson-Schill et al., 1997, 1998). In particular, our finding sits well with the proposal that the left PFC, and especially the left inferior frontal gyrus, is involved in modulating a proactive interference control mechanism, which has been considered to operate across cognitive domains (Kan & Thompson-Schill, 2004; Riès et al., 2014, 2015, and see also Jonides & Nee, 2006). In this way, the adjustment of response threshold could be operating in response to interference that arises from closely related semantic contexts, and maintains a similar accuracy rate despite greater task difficulty, at the cost of higher caution (slower RTs). However, if this mechanism is indeed more domain-general than previously believed, then it may be less specialized to just lexical networks than the mechanisms proposed by Oppenheim et al. (2010) and Belke & Stielow (2013), though may still be modulated by such interference dynamics. For example, the lower lexical activation rates, γ, probably do not scale up the threshold as in learned interference (Oppenheim et al., 2010), since we observe how repetition priming instead scales down the threshold (in both HET and HOM) while γ scales down only during semantic interference (HOM; see Figure 6).

Relationships to broader model-based neuroscience literature.

Our findings can also be related as being in agreement with the broader neuroscience literature that also combines neurosciences and evidence accumulation, and similarly find the PFC to be principally implicated in decision threshold adjustment—particularly in perceptual decision-making (Boehm, van Maanen, Forstmann, & van Rijn, 2014; Domenech & Dreher, 2010; Forstmann et al., 2008, 2010). These recent studies, which also discuss decision threshold modulation by the PFC, are in turn similarly grounded by much earlier work. For example, as described by (chapter 7, Luria, 1997), one of the primary functions of the frontal cortex is to regulate mental activity, or cortical tone, depending on the task to be accomplished, notably supported by the discovery of “expectancy waves”, or contingent negative variation, initially found by Walter, Cooper, Aldridge, McCallum, & Winter in 1964. This specific electroencephalographic potential, shown to originate from the frontal lobes, arises in preparation for the processing of a task-relevant stimulus, and disappears when this stimulus stops being reinforced—with the interpretation that cortical activity is increased to facilitate the processing of task-relevant information.

Such previous studies, with evidence accumulation models similar to the one we used (e.g. DDM, linear ballistic accumulator), provide support that the frontal cortex, and especially the medial frontal cortex, are engaged in decision threshold adjustment in perceptual decision-making (Boehm et al., 2014; Domenech & Dreher, 2010). In particular, trial-by-trial modulations of medial PFC activity (electroencephalographic theta power, 4–8 Hz) have been related to an increase in decision threshold adjustment as a function of conflict (Cavanagh et al., 2011). In our study, the patients tested generally did not have medial frontal damage. It is therefore possible that the distinction between the roles of the left lateral PFC and the medial PFC may be somewhat different in lexical selection compared to the more traditionally used two forced choice tasks in cognitive control studies outside of language. After all, the choices made in language production and in picture naming (as opposed to two-choice perceptual decision) include a larger number of alternatives and the neuronal basis underlying this type of choice may be different. Another possibility may be linked to the connectivity patterns between the left lateral PFC and the medial PFC in the patients we studied. Indeed, given the damage to the lateral PFC, connections between these two regions were also damaged. It is therefore possible that the deficit in decision threshold adjustment we observe may be a consequence of this disruption. Further studies will need to be conducted to specify the precise frontal anatomical basis for decision threshold adjustment in lexical selection for speech production.

Data-derived sequential sampling models for brain-damaged patient cognition study.

This study has provided an important first step for how evidence accumulation models may provide insight into brain-damaged patient cognition and their observed data—here specifically on left PFC patients and their threshold-adjustment impairments in a multiple choice lexical retrieval task (picture naming). The precedent for such a development on how evidence accumulation may be extended to patients in general is set by several previous works which have also demonstrated success in using quantitative model parameters, rather than raw performance data comparisons, to account for aspects of patient cognition. For example, a diffusion model study on low- and high-anxiety individuals in a two-alternative lexical decision task (White, Ratcliff, Vasey, & McKoon, 2010) also found principal effects in threshold adjustment. There is also the notable related work of the neural network model designs by Dell, Schwartz, Nozari, Faseyitan, & Coslett (2013), which use quantitative model parameters to handle the accuracy patterns of aphasic patients in a word-repetition task well, and in tandem also draw relationships to neural structures. Hence an interesting development may be to consider integrating elements of this proposed evidence accumulation approach into these kinds of neural network models (see Anders et al., 2015), to further develop the networks into accounting for the RT distributions as well (see Oppenheim et al., 2010 for a beginning development in accounting for mean RT with accuracy). The limiting factor for achieving such advanced methodologies however, as well as the reliability of the patient cognition conclusions (as ours reported here), is the problem of often working with few patients or patient observations, and hence future work would do well to pursue augmented numbers.

Limitations and possible improvements for future work.

We propose therefore that the current results be used to advance theory, and stimulate subsequent psychometric modelling applications to explore further replication. While we did replicate previous results on healthy speakers, it is worthwhile noting how various modifications to the fitting approach may be used in future work to sharpen results or improve reliability. Firstly, the most straightforward method would be to include more brain-lesioned PFC patients. We note that our analysis involved only six left PFC patients, and therefore power in the significance tests was more difficult to achieve. Secondly, in contrast to augmenting patient numbers, one can perform more reliable (and advanced) modelling by augmenting observation numbers in the experimental design. Specifically, increased observation numbers would allow jointly modelling additional factors in tandem, which would parse out variance assigned to the experimental predictors that may actually be due to other factors (Barr et al., 2013). For instance, our modelling here and that by Anders et al. (2015) experienced better model fit along the experimental predictors, semantic context and repetition, by parsing out (jointly modelling also) lag effects, also known as trial distance (see Barr et al., 2013). Hence, along these lines, a modelling improvement for future work is also to jointly model the items (here 36) with the subjects and experimental predictors (see Baayen, 2004; Baayen et al., 2008), though here it was not possible, as it would leave near only one observation per experimental design cell, and three model parameters to fit it. Lastly, one should also note that the strength of the conclusions provided by these data-derived cognitive models also depends on the quality of the model fit, for which there are a variety of estimation options (e.g.hierarchical Bayesian by likelihood functions, or quantile-residual minimization; Brown & Heathcote, 2003; Rouder & Lu, 2005), each with their respective strengths (e.g. how error can be constrained by grouping assumptions; Rouder et al., 2007) and weaknesses (e.g. to what extent outliers perturb model fit; Ratcliff & Tuerlinckx, 2002).