Heritability of Brain Resilience to Perturbation in Humans

Abstract

Resilience is the capacity of complex systems to persist in the face of external perturbations and retain their functional properties and performance. In the present study, we investigated how individual variations in brain resilience, which might influence response to stress, aging and disease, are influenced by genetics and/or the environment, with potential implications for the implementation of resilience-boosting interventions. Resilience estimates were derived from in silico lesioning of either brain regions or functional connections constituting the connectome of healthy individuals belonging to two different large and unique datasets of twins, specifically: 463 individual twins from the Human Connectome Project and 453 individual twins from the Colorado Longitudinal Twin Study. As has been reported previously, moderate heritability was found for several topological indexes of brain efficiency and modularity. Importantly, evidence of heritability was found for resilience measures based on removal of brain connections rather than specific single regions, suggesting that genetic influences on resilience are preferentially directed toward region-to-region communication rather than local brain activity. Specifically, the strongest genetic influence was observed for moderately weak, long-range connections between a specific subset of functional brain networks: the Default Mode, Visual and Sensorimotor networks. These findings may help identify a link between brain resilience and network-level alterations observed in neurological and psychiatric diseases, as well as inform future studies investigating brain shielding interventions against physiological and pathological perturbations.

1. Introduction

Resilience describes a capacity of complex systems to sustain damage, failure, or other external perturbations while still maintaining a proficient level of functioning (Gao et al., 2016). When applied to the brain, resilience often describes the individual capacity to sustain a higher degree of damage, and for a longer time, before the display of overt symptoms, as well as the capacity to recruit additional regions not yet affected by the pathology to better compensate and so defer, or offset, cognitive consequences (Satz, 1993; Stern, 2009). A deeper understanding of the brain’s ability to resist external perturbations comes from the study of its underlying topological organization. A popular framework for studying the topology of the brain – graph theory - treats brain regions and their structural or functional coupling as nodes and edges (connections) serving as paths of information flow (Bullmore and Bassett, 2011). We have gained insights about the strengths and weaknesses of many complex systems —such as the brain, the World Wide Web, the organization of highways, and power grids— by removing nodes and edges from such networks via in silico simulations. These simulations reveal a strong link between the organization of a system and its resultant degree of resilience to targeted or random attacks (Achard et al., 2006; Barabasi and Bonabeau, 2003). In particular, networks in which connections between nodes are equally probable, as in random graphs, have high levels of resilience but poor communication efficiency, whereas networks whose information pathways are highly dependent upon major hubs, such as airline systems relying on major airports’ connectedness, are highly susceptible to the loss of central cores (Achard et al., 2006; Barabasi and Bonabeau, 2003). Complex biological networks, such as the brain, are characterized by a trade-off between those properties, as they display unique organization profiles that ensure efficient local processing and global integration between their components (Rubinov and Sporns, 2010), which in turn guarantee high levels of resilience (Achard et al., 2006; Joyce et al., 2013).

The use of topological measures not only provides insight on the propagation of information flow at a global level, but also allows analysis of the role of local brain regions and connections in complex ensembles. Such an approach contrasts with analyses that focus on univariate associations between brain activation levels and cognitive functions, which are more common in the cognitive neuroscience literature. Considering the high potential that graph theory analysis might hold for the study of aberrant or deviant topological structures in many neurological and psychiatric diseases, prior studies have queried the extent of genetic influences in shaping network topology. Indeed, thanks to genetic imaging techniques, it is now known that there is a close association between the expression of selective genes and structural properties of the brain, as well as their association with cognitive functions and general intelligence (Giddaluru et al., 2016; Grasby et al., 2020; Toga and Thompson, 2005). Initial studies have revealed modest heritability for several integration and segregation measures derived from the individual functional connectome (Sinclair et al., 2015). However, studies in the past focused on measures representing a static picture of the network organization, instead of looking at its dynamic ability to respond to external perturbations. In this sense, resilience may have distinct genetic and environmental influences on the connectome than this static network organization because its represents the brain’s ability for adaptive reconfiguration.

In the present study we assessed the extent to which variation in brain resilience is influenced by environmental and genetic factors. Since the degree of individual exposure to enriching environments (e.g., learning opportunities, access to healthy foods, opportunities for regular exercise) has indeed long been reported to favor greater system plasticity and robustness to a variety of pathological conditions (Quach et al., 2017), we hypothesize that resilience might be substantially influenced by the environment. Still, determining the heritable component of brain resilience might provide future insights into individual differences in conferred vulnerability to brain topology phenotypes associated with neurological and psychiatric disorders. To our knowledge, this is the first paper addressing the heritability of different resilience metrics. In this study, we first check that our samples are representative by determining whether they yield heritability estimates of global measures of network topology in line with prior reports. Then we derive heritability estimates of resilience across two large independent samples of twins. Finally due to somewhat discrepant findings across these two samples, we consider how scanning acquisition parameters may influence heritability analyses.

2. Methods

2.1. Human Participants

Two independent large datasets of young adult twins were employed in this study: the Human Connectome Project (HCP) (https://www.humanconnectome.org/), whose participants were drawn from a large sample (n=1200) of healthy young adults, including twins (Van Essen et al., 2013); and the Colorado Longitudinal Twin Study (LTS) (https://www.colorado.edu/ibg/research/human-research-studies/specific-twin-studies/longitudinal-twin-study), whose participants were recruited based on birth records between 1968 and 1990 (for a reference see (Corley et al., 2019; Rhea et al., 2013, 2006)). In the present study, 463 individual twins were selected from the HCP dataset (males= 194, age: M=29.16, SD=±3.45; monozygotic (MZ): n=287, M=29.42, SD= ±3.39; dizygotic (DZ): n=176, M=28.79, SD=3.53) and 453 individual twins from LTS dataset (males= 189, age: M=28.6, SD=±0.62; MZ: n=229, M=28.6, SD= ±0.62; DZ: n=216, M=28.7, SD=0.63). The racial make-up of the HCP dataset is 83.8% White, 10.4% African-American; 3.7% Asian/Hawaiian Native or other Pacific Islander, <1% American Indian/ Alaskan Native, <1% unknown and about 1% reported more than one race. The racial make-up of the LTS sample is 92.6% White, <1% American Indian/Alaskan Native, <1% Pacific Islander, 1.2% unknown and about 5% more than one race. In the HCP dataset, zygosity was determined based on both self-report and genotyping, derived from either blood or saliva samples, which is made available via the dbGAP repository (https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs001364.v1.p1); for the LTS dataset, zygosity was determined via testers’ ratings with an at least 85% agreement, as well as via DNA tests following cheek swabs.

Raw and preprocessed data of the HCP dataset are available at https://www.humanconnectome.org/; de-identified functional connectivity matrices are available at http://tmslab.org/netconlab.php. Heritability models estimates and LTS functional connectivity matrices are available at https://github.com/AReineberg/genetic_connectome.

2.2. Functional Connectome Extraction

Procedural details on fMRI data acquisition and preprocessing steps for both the HCP and LTS dataset are available in the Supplementary Materials. For examining the functional connectome, changes in the functional activity of the brain are represented by fluctuations in the Blood Oxygen Level Dependent (BOLD) signal, whose variation over time was extracted from each of the 1cm spherical regions of interest (ROIs) of the Power’s Atlas (Power et al., 2011). Furthermore, the Power Atlas distinguishes the brain as organized into the following discernable networks: Sensorimotor (SMN), Auditory (AUD), Visual (VIS), Frontoparietal (FPN), Salience (SN), Cingulo-opercular (CING), Dorsal Attention (DAN) and Ventral Attention (VAN), Default Mode (DMN), Memory (MEM), Subcortical (SUB) and Cerebellar (CEREB) networks (Power et al., 2011). For each participant, a 264×264 functional connectivity matrix was extracted from the Pearson’s r correlation between each pair of ROIs, upon which the Fischer’s z transformation was then applied (Figure 1, panels A, B, C). It is worth noting that in many rs-fMRI studies, the Global Signal Regression (GSR) is often employed as an additional preprocessing step to remove unspecific and globally distributed sources of variance, which are treated as noise (Murphy et al., 2009). However, the use of GSR has been criticized in the literature because it relies on a mathematical approach responsible for introducing negative activations in fMRI data (Murphy et al., 2009), which can systematically alter resting-state correlations and hence conclusions about brain functional connectedness (Saad et al., 2012). Based on these prior studies, no GSR was applied to derive the functional connectivity matrices.

Figure 1. Methodological Workflow.

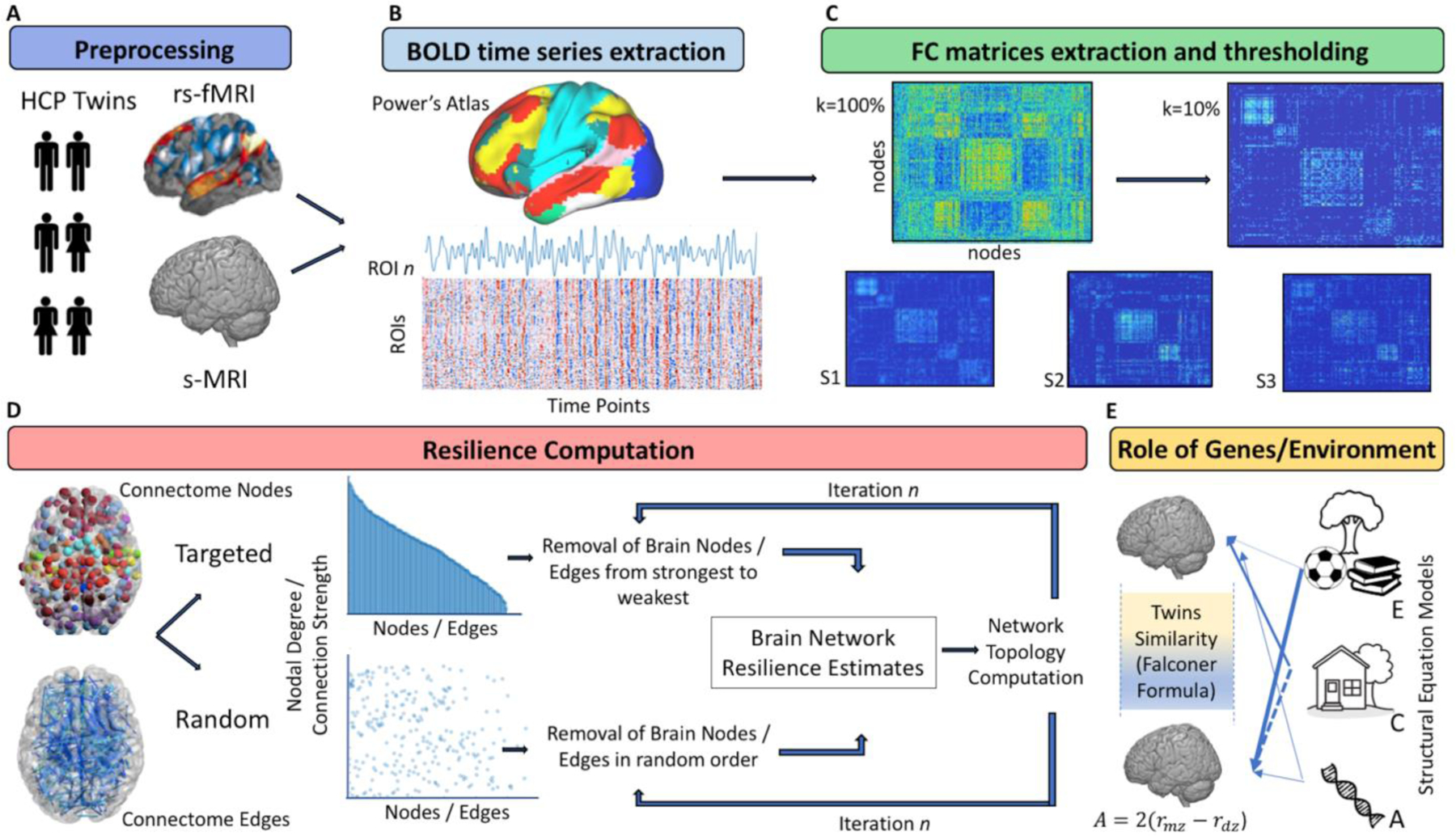
A. Resting state functional magnetic resonance imaging (rs-fMRI) and structural (s-MRI) data underwent standard preprocessing steps. B. Time series extraction was performed from each of the 264 cortical and subcortical parcels of the Power’s Atlas. C. Functional connectivity matrices were extracted from the Pearson’s r correlation between each pair of ROIs and were normalized through Fischer’s z transformation. Matrices were then thresholded to retain only 10% of the overall connections’ density, from which graph theory measures and brain resilience estimates were computed. D. Resilience measures were extracted following the random and targeted (strongest-to-weakest) removal of nodes and edges from each individual matrix. At each iteration, nodes and edges order of removal was recalculated, and the order of removal adjusted based on the effect of prior lesioning. E. Heritability estimates were computed looking at the phenotypic similarity between each pair of twins (Falconer Formula), as well as by means of structural equation models specifically looking at the influence of genetics (A), unique (E) and common (C) environmental exposure.

2.3. Standard Brain Topology Measures

A range of connection densities (top 5–25%) is usually tested to examine variation in graph theory metrics as a function of the threshold used. The rationale for the use of such high threshold values stems from the fact that very high connection density (~100%) results in graph metrics that tend to behave more similarly to that of random graphs, whereas the use of lower connection densities ensures only the most relevant connections are retained and allows one to clearly distinguish the single units constructing the network (Sinclair et al., 2015).

Prior big cohort studies have indicated that genetic contributions are better examined at connection density around 10% and in the absence of additional factors, such as GSR (Sinclair et al., 2015). Furthermore, 10% sparsity threshold has been associated with higher test-retest reproducibility for global metrics (Wang et al., 2011). For this reason, we thresholded our functional matrices to retain only the 10% of the original connection density (nodes surviving thresholding: M=259.28, SD= 4.42; edges surviving thresholding: M=6640.8, SD= 175.43; heritability estimates at different threshold values are reported in the Supplementary Materials)(Figure 1, panel C). Weighted adjacency matrices were then computed, where each node (N) represents an input in the square matrix:

$$A=\left|N\right|\times \left|N\right|$$

and where the assigned value to the edge A_ij is equal to the Fisher’s z value between node i and j when the connection exists, or zero otherwise.

Classic graph theory measures were extracted from the individual adjacency matrix based on Brain Connectivity Toolbox (https://sites.google.com/site/bctnet/) functions running in MATLAB 2017b. A selection of ground graph theory metrics that represent the efficiency of the information flow in the system was chosen, identifying measures of integration:

• iNodal Degree: the total number of edges that are connected to a given node;
• iiCharacteristic Path Length: the average distance between a node and all the other nodes of the system;
• iiiGlobal Efficiency: the inverse of the average shortest path;

and also measures of segregation:

• ivClustering Coefficient: the fraction of nodes being neighbors with the surrounding nodes, forming triangular triplets.
• vModularity: the extent for which a network can be divided into distinct units based on greater within-unit, rather than between-units, edges;
• viLocal Efficiency: the inverse of the average shortest path connecting a node to all other nodes of the system.
• viiSmall-Worldness: the property of a system to have concomitant high clustering coefficient and low path length.

For a more in-depth explanation of classic graph theory measures, the reader is referred to (Rubinov and Sporns, 2010). Mathematical formulas for the computation of the graph theory metrics used in this study are available in the Supplementary Materials.

2.4. Resilience Metrics

Resilience of the brain graph was computed through the sequential removal of nodes and edges from the weighted adjacency matrix, a procedure well established by prior studies (Achard et al., 2006; Albert et al., 2000; Albert and Barabási, 2002; Joyce et al., 2013). More specifically, nodes and edges were ordered in descending fashion based on their nodal degree and edge strength (Fischer’s z value). One by one, nodes or edges were removed from the graph and the drop in the largest connected component (LCC) computed as measure of the inferred damage. In a graph, the LCC refers to the biggest set of nodes, whose pairs are connected by an edge. In a completely connected graph, the LCC is the graph itself, but as we remove its nodes or edges, it partitions into several components. At each iteration, nodes’ degree was recalculated and the order of removal adjusted based on the effect of prior lesioning (Figure 1, panel D). The study of network robustness was tackled from different perspectives, first focusing on the broad effects of matrix lesioning according to standard literature approaches, and then further digging into the fine-grained mechanisms of resilience. Based on this rationale, the following resilience metrics were computed:

• iRandom Node Removal: mean reduction necessary to bring the LCC to a value of zero following the progressive removal of nodes in random order;
• iiTargeted Node Removal: mean reduction necessary to bring the LCC to a value of zero following the progressive removal of nodes based on their nodal degree (from highest to lowest);
• iiiTargeted Edge Removal: mean reduction necessary to bring the LCC to a value of zero following the progressive removal of edges based on their strength (from strongest to weakest).

It has generally been observed that biological networks are more resilient to the occurrence of random errors rather than of targeted attacks (Achard et al., 2006). Within that, particularly well-organized brain networks, subserving better cognitive performance, show further benefit of more distributed processing that ensure the system has higher resilience to targeted removal as well (Santarnecchi et al., 2015).

The study of classic resilience measures was then further broken down into the understanding of more fine-grained mechanisms, specifically looking at additional measures:

• ivSpeed of Drop: the individual pace of matrix lesioning, computed as the slope of decay of the LCC following the targeted removal of edges, whereby more negative values are interpreted as index of faster decay;
• vEarly Edges Drop: the overall amount of connections that needed to be lost before the individual LCC showed a reduction in its size (i.e. the degree of edges’ loss necessary to bring the LCC from a value of 1 to that of a value minor than 1, where 1 represents full integrity of the component, prior to any edge removal);
• viLate Edges Drop: the overall amount of connections’ loss necessary to completely deplete the LCC (i.e., the degree of edges’ loss necessary to bring the LCC from a value of 1 to a value of 0).
• viiCritical Point: the point of maximum deflection in the lesioning curve of the LCC, based on the removal of edges according to a strongest-to-weakest gradient.

Our logic is that more resilient individuals will not only show slower paths of degradation, but will show greater robustness to the inferred damage before any decay in their LCC becomes visible. Similarly, higher resilience should also be expressed in the form of greater maintenance capacity, such as that both the point of maximum deflection and the point of complete matrix depletion should occur at the more advances stages, thus later, than that observed for less resilient systems.

The code used for resilience measures extraction is available at http://tmslab.org/netconlab.php.

2.5. Statistical Analyses

2.5.1. Twin Models

Measures of heritability (the proportion of variance attributable to additive genetic influences [A]) were computed based on the notion that MZ twins share 100% of their genes whereas DZ share on average 50% of their segregating genes. Both types of twins are raised together, so their correlations are assumed to be equally influenced by the common or shared environment (C: environmental influences that lead siblings to correlate on a measure of interest). Thus, the MZ twin correlation can be estimated as A + C, and the DZ correlation as 0.5*A + C. Any difference in their correlations are attributable to A (Mayhew and Meyre, 2017); DZ correlations that are greater than half the MZ correlations are indicative of C; and MZ correlations that are less than unity indicate nonshared environmental influences (E; environmental influences that lead siblings to be uncorrelated, including measurement error) (Figure 1, panel E). A first approach to estimate heritability (h² or A) is thus given by Falconers’ Formula (Mayhew and Meyre, 2017):

$$A=2\left(r_{mz}-r_{dz}\right)$$

Estimates of the contribution of each factor and their confidence intervals can also be obtained with structural equation models, which have the advantage of enabling model comparisons (Mayhew and Meyre, 2017). We used OpenMx (Neale et al., 2016) to estimate univariate twin models with likelihood-based confidence intervals. The bounds of a likelihood-based confidence interval are the values of the parameter at which significant worsening of model fit occurs; that is, the interval includes all values for the parameter that would not lead to a significantly lower likelihood of having observed the data. Variance components were not bound at zero. Although negative variances are nonsensical, allowing estimates to be negative (which can occur due to sampling variation when parameters are likely zero) results in unbiased parameter estimates and confidence intervals (Verhulst et al., 2019). As is typical in the behavioral genetic literature, we have included output from 4 models: a model that estimated A, C, and E, a model that drops A (providing only estimates for C and E), a model that drops C (providing only estimates for A and E) and an E-only model. If model 1 is the best fitting model, there is evidence that that brain measure has genetic, shared environmental, and non-shared environmental influences whereas if the best fitting model is one of the other three, the data indicates there is no evidence for one or more of the influences. In this study, the Akaike Information Criterion (AIC) was used to compare model fit while penalizing model complexity; whereby lower values indicate better fit (Akaike, 1973).

In the present study, the degree of heritability was computed on all the graph theory metrics (characteristic path length, global and local efficiency, clustering coefficient, modularity and small-worldness) as well as on the computed metrics of resilience (random node removal, targeted node removal, targeted edge removal, speed of drop, early edges drop, late edges drop and critical point). A brief overview of the methodological workflow of the study is presented in Figure 1.

3. Results

3.1. Heritability of the Network Connectome Structure

In this study, the heritability of integration and segregation patterns of the functional brain topology were examined first to determine if we could replicate prior published results on the heritability of network topology (Fornito et al., 2011; Sinclair et al., 2015; van den Heuvel et al., 2013). Table 1 and 2 include MZ and DZ twin correlations, which provide an initial check on genetic influences. Similarly, they also include outputs from structural equation twin models, which enable statistical tests of the A, C and E parameters.

Table 1: Heritability of Network Connectome Structure in the HCP Dataset.

Twin correlations and ACE structural equation model estimates are displayed. For correlation analyses, heritability is suggested when the correlation between MZ twins is greater than the correlation between DZ twins. ACE variances were unbounded so could be negative. The upper and lower bound of the likelihood-based 95% confidence intervals are displayed inside the squared brackets for the A, C and E parameters. AIC= Akaike’s information criterion, a measure of model fit; lower AIC values indicate better fit, marked in bold in the table.

Measure	Twin correlations			ACE Structural Models
	rmz	rdz	Diff	Model	A [A−,A+]	C [C−,C+]	E [E−,E+]	AIC
Characteristic path length	0.573	0.393	0.18	ACE	0.287 [−0.15,0.83]	0.26[−0.26,0.64]	0.45[0.35,0.59]	326.274
				AE	0.56 [0.43,0.66]	NA	0.44 [0.34,0.57]	325.388
				CE	NA	0.5[0.39,0.6]	0.5 [0.4,0.61]	325.854
				E	NA	NA	1	375.020
Clustering Coefficient	0.485	0.255	0.23	ACE	0.49[0.04,0.59]	−0.03[−0.59,0.44]	0.54 [0.42,0.69]	341.632
				AE	0.46 [0.32,0.58]	NA	0.54[0.41,0.68]	339.644
				CE	NA	0.39[0.26,0.51]	0.61[0.49, 0.74]	342.912
				E	NA	NA	1	369.665
Global efficiency	0.291	0.101	0.19	ACE	0.44 [0.16,1.06]	−0.17[−0.72,0.35]	0.72[0.57,0.89]	417.56
				AE	0.26 [0.1,0.41]	NA	0.74[0.59,0.9]	415.929
				CE	NA	0.21[0.06,0.34]	0.79[0.66,0.94]	417.642
				E	NA	NA	1	423.465
Local efficiency	0.411	0.151	0.26	ACE	0.44[0.14,1.08]	−0.05[−0.64,0.45]	0.62[0.48,0.77]	375.833
				AE	0.38 [0.23,0.52]	NA	0.62[0.48,0.77]	373.866
				CE	NA	0.33 [0.19,0.45]	0.67[0.55,0.81]	376.0203
				E	NA	NA	1	393.164
Modularity	0.287	−0.045	0.33	ACE	0.65 [0.07,1.22]	−0.34[−0.83,0.14]	0.69 [0.53,0.87]	345.842
				AE	0.26[0.09,0.43]	NA	0.73[O.57,0.91]	345.741
				CE	NA	0.17[0.03,0.31]	0.83[0.69,0.97]	348.758
				E	NA	NA	1	352.092
Small Worldness	−0.095	−0.032	−0.06	ACE	−0.1[−0.72,0.51]	0 [−0.51,0.51]	1.1[0.91,1.28]	437.859
				AE	−0.1 [−0.27,0.08]	NA	1.1[0.92,1.27]	435.859
				CE	NA	−0.08 [−0.23,0.07]	1.08[0.93,1.23]	435.957
				E	NA	NA	1	435.06

Table 2: Heritability of Network Connectome Structure in the LTS dataset.

Twins’ correlations and ACE structural equation model estimates are displayed. For correlation analyses, heritability is suggested when the correlation between MZ twins is greater than the correlation between DZ twins. ACE variances were unbounded so could be negative. The upper and lower bound of the likelihood-based 95% confidence intervals are displayed inside the squared brackets for the A, C and E parameters. AIC = Akaike’s information criterion, a measure of model fit; lower AIC values indicate better fit, marked in bold in the table.

Measure	Twins’ Correlations			ACE Structural Model
	rmz	rdz	Diff	Model	A [A−,A+]	C [C−,C+]	E [E−,E+]	AIC
Characteristic path length	0.121	0.083	0.04	ACE	0.08[−0.5,0.67]	0.04[−0.43,0.49]	0.87[0.68,1.08]	689.168
				AE	0.13[−0.05,0.31]	NA	0.87[0.69,1.05]	687.197
				CE	NA	0.1[−0.04,0.25]	0.9[0.75,1.04]	687.247
				E	NA	NA	1	687.134
Clustering Coefficient	0.076	0.032	0.04	ACE	0.09[−0.49,0.67]	−0.01[−0.47,0.44]	0.92[0.73,1.13]	449.035
				AE	0.07[−0.11,0.25]	NA	0.93[0.75,1.11]	447.039
				CE	NA	0.05[−0.09,0.2]	0.95[0.8,1.09]	447.128
				E	NA	NA	1	445.635
Global efficiency	−0.003	0.005	−0.01	ACE	−0.02[−0.61,0.58]	0.01[−0.44,0.47]	1[0.79,1.22]	361.762
				AE	0[−0.19,0.19]	NA	1[0.81,1.19]	359.765
				CE	NA	0[−0.15,0.15]	1[0.85,1.15]	359.765
				E	NA	NA	1	357.766
Local efficiency	0.218	0.114	0.1	ACE	0.17[−0.39,0.74]	0.04[−0.44,0.48]	0.79[0.62,0.98]	591.985
				AE	0.21[0.04,0.37]	NA	0.79[0.63,0.96]	590.008
				CE	NA	0.17[0.03,0.3]	0.83[0.7,0.97]	590.337
				E	NA	NA	1	593.680
Modularity	−0.047	0.155	−0.2	ACE	−0.35[−0.92,0.24]	0.31[−0.12,0.73]	1.03[0.81,1.25]	464.684
				AE	0.05[−0.14,0.24]	NA	0.95[0.76,1.14]	464.719
				CE	NA	0.07[−0.07,0.21]	0.93[0.79,1.07]	464.038
				E	NA	NA	1	463.036
Small Worldness	0.138	−0.126	0.26	ACE	0.43[−0.16,1]	−0.32[−0.75,0.13]	0.89[0.69,1.11]	469.122
				AE	0.04[−0.15,0.22]	NA	0.96[0.78,1.15]	469.028
				CE	NA	−0.01[−0.15,0.14]	1.01[0.86,1.15]	469.167
				E	NA	NA	1	467.174

For the HCP dataset, the MZ correlation was nominally higher than the DZ correlation in all measures except one. In particular, a genetic influence appears to be present in shaping the traits of the characteristic path length (r_mz=0.573; r_dz=0.393), clustering coefficient (r_mz=0.485; r_dz=0.255), modularity (r_mz=0.287; r_dz=−0.045), global (r_mz=0.291; r_dz=0.101) and local (r_mz=0.411; r_dz=0.151) efficiency of the brain functional connectome. On the other hand, small-worldness showed twin correlations close to zero (r_mz=−0.095; r_dz=−0.032) (see Table 1). Based on the structural equation model comparisons, the best models were the ones that considered the contribution of A and E only (see Table 1). Moderate genetic effects were indeed observed in most graph theory metrics: characteristic path length (A=0.56 [0.43,0.66]), clustering coefficient (A=0.46 [0.32,0.58]), modularity (A=0.26 [0.09,0.43]), and global (A=0.26 [0.1,0.41]) and local (A=0.38 [0.23,0.52]) efficiency. On the other hand, small-worldness was best explained by the contribution of E alone.

For the LTS dataset, heritability estimates computed on the graph theory metrics mostly failed to show any significant evidence of a genetic component. The only exception was represented by the measure of Local Efficiency (r_mz=0.218, r_dz=0.114; A=0.21[0.04,0.37]), where a moderate genetic influence could be observed (Table 2).

3.2. Heritability of Brain Resilience

For all our resilience metrics, heritability analyses were run to determine the extent of genetic and environmental influences. For the HCP dataset, moderately higher correlational values were observed between MZ twins, compared to DZ twins, for the measures of Targeted Edge Removal (r_mz=0.249; r_dz=0.061) and Critical Point (r_mz=0.362; r_dz=0.048), suggesting moderate heritability of such traits. ACE models confirmed genetic influences for the Targeted Edge Removal (A=0.22 [0.06,0.37]) and Critical Point (A=0.35 [0.18,0.49]) measures. It is worth noticing that for the measure of Random Node Removal, a relatively strong influence of A was also reported (A=0.72 [0.07,1.31]). However, when the same measure was tested after removing factor C, the estimate of A dropped to a nonsignificant level (A=0.05 [−0.12,0.22]), suggesting that the aforementioned effect was driven by the negative estimate of C and thus should not be considered reliable evidence of heritability (see Table 3). For this reason, only the measures of Targeted Edge Removal and Critical Point are discussed in terms of heritability.

Table 3: Heritability of Brain Network Resilience in the HCP Dataset.

Twin correlations and ACE structural equation model estimates are displayed. For correlation analyses, heritability is suggested when the correlation between MZ twins is greater than the correlation between DZ twins. ACE variances were unbounded so could be negative. The upper and lower bound of the likelihood-based 95% confidence intervals are displayed inside the squared brackets for the A, C and E parameters. AIC = Akaike’s information criterion, a measure of model fit; lower AIC values indicate better fit, marked in bold in the table.

Measure	Twin Correlations			ACE Structural Models
	rmz	rdz	Diff	Model	A [A−,A+]	C [C−,C+]	E [E−,E+]	AIC
Random Node Removal	0.12	−0.238	0.36	ACE	0.72[0.07,1.31]	−0.61[−1.09,0.04]	0.88[0.71,1.07]	703.093
				AE	0.05[−0.12,0.22]	NA	0.95[0.78,1.12]	705.624
				CE	NA	0[−0.15,0.15]	1[0.85,1.15]	705.932
				E	NA	NA	1	703.932
Targeted Node Removal	0.204	0.136	0.07	ACE	0.19[−0.38,0.79]	−0.004[−0.52,0.48]	0.8[0.64,0.98]	618.403
				AE	0.19[0.03,0.35]	NA	0.81[0.65,0.97]	616.403
				CE	NA	0.16[0.02,0.3]	0.84[0.7,0.98]	616.843
				E	NA	NA	1	619.664
Targeted Edge Removal	0.249	0.061	0.19	ACE	0.39[0−0.19,1]	−0.16[−0.69,0.35]	0.76[0.61,0.93]	494.201
				AE	0.22[0.06,0.37]	NA	0.78[0.63,0.94]	492.568
				CE	NA	0.17[0.03,0.31]	0.83[0.69,0.97]	493.902
				E	NA	NA	1	497.460
Speed of Drop	0.007	−0.131	0.14	ACE	0.19[−0.42,0.79]	−0.17[−0.6,0.26]	0.98[0.74,1.22]	680.745
				AE	−0.04[−0.24,0.16]	NA	1.04[0.84,1.24]	679.343
				CE	NA	−0.04[−0.19,0.1]	1.04[0.9,1.19]	679.115
				E	NA	NA	1	677.479
Early Edges Drop	0.139	−0.051	0.19	ACE	0.35[−0.27,0.97]	−0.22[−0.75,0.31]	0.87[0.7,1.05]	568.216
				AE	0.1[−0.07,0.27]	NA	0.9[0.73,1.07]	566.879
				CE	NA	0.07[−0.08,0.22]	0.93[0.78,1.08]	567.439
				E	NA	NA	1	566.270
Critical Point	0.362	0.048	0.31	ACE	0.63[0.02,1.26]	−0.26[−0.83,0.27]	0.63[0.48,0.8]	643.684
				AE	0.35[0.18,0.49]	NA	0.65[0.51,0.82]	642.569
				CE	NA	0.27[0.12,0.4]	0.73[0.6,0.88]	645.876
				E	NA	NA	1	655.747
Late Edges Drop	0.225	0.246	−0.021	ACE	−0.18[−0.77,0.53]	0.4[−0.26,0.89]	0.78[0.62,0.95]	713.583
				AE	0.24[0.07,0.39]	NA	0.76[0.61,0.93]	713.123
				CE	NA	0.24[0.09,0.38]	0.76[0.62,0.91]	711.886
				E	NA	NA	1	719.085

For the LTS dataset, estimates of brain resilience to in-silico network lesioning failed to show any evidence of heritability (Table 4). In the latter, the models did not converge for the measures of Targeted Edge Removal and Speed of Drop.

Table 4: Heritability of Brain Network Resilience in the LTS Dataset.

Twins’ correlations and ACE structural equation model estimates are displayed. For correlation analyses, heritability is suggested when the correlation between MZ twins is greater than the correlation between DZ twins. ACE variances were unbounded so could be negative. The upper and lower bound of the likelihood-based 95% confidence intervals are displayed inside the squared brackets for the A, C and E parameters. AIC = Akaike’s information criterion, a measure of model fit; lower AIC values indicate better fit, marked in bold in the table. The models did not converge for the measures of Targeted Edge Removal and Speed of Drop.

Measure	Twins’ Correlations			ACE Structural Model
	r mz	rdz	Diff	Model	A [A−,A+]	C [C−,C+]	E [E−,E+]	AIC
Random Node Removal	0.045	−0.007	0.05	ACE	0.14[−0.45,0.71]	−0.09[−0.52,0.35]	0.95[0.74,1.17]	417.629
				AE	0.03[0.16,0.22]	NA	0.97[0.78,1.16]	415.783
				CE	NA	0.01[−0.13,0.15]	0.99[0.84,1.13]	415.85
				E	NA	NA	1	413.875
Targeted Node Removal	−0.076	0.092	−0.17	ACE	−0.35[−0.93,0.27]	0.25[−0.17,0.66]	1.1[0.84,1.33]	461.323
				AE	0[−0.2,0.2]	NA	1[0.8,1.2]	460.692
				CE	NA	0.03[−0.11,0.16]	0.97[0.8,1.11]	460.563
				E	NA	NA	1	458.693
Targeted Edge Removal	0.045	0.15	−0.1	ACE	NA	NA	NA
				AE	NA	NA	NA
				CE	NA	NA	NA
				E	NA	NA	NA
Speed of Drop	−0.069	−0.013	−0.06	ACE	NA	NA	NA
				AE	NA	NA	NA
				CE	NA	NA	NA
				E	NA	NA	NA
Early Edges Drop	−0.21	−0.004	−0.21	ACE	−0.38[−0.95,0.19]	0.19[−0.29,0.66]	1.19[1.01,1.36]	368.881
				AE	−0.16[0.33,0]	NA	1.17[0.99,1.33]	367.452
				CE	NA	−0.11[−0.25,0.02]	1.12[0.98,1.26]	368.586
				E	NA	NA	1	369.298
Critical Point	0.054	0.025	0.03	ACE	0.12[−0.52,0.72]	−0.03[−0.47,0.41]	0.92[0.68,1.18]	324.655
				AE	0.07[0.13,0.27]	NA	0.93[0.73,1.14]	322.678
				CE	NA	0.41[−0.1,0.19]	0.96[0.81,1.1]	322.784
				E	NA	NA	1	321.1
Late Edges Drop	0.022	0.048	−0.03	ACE	0[−0.65,0.63]	0.04[−0.39,0.48]	0.96[0.69,1.23]	317.146
				AE	0.06[−0.15,0.27]	NA	0.94[0.73,1.15]	315.182
				CE	NA	0.04[−0.1,0.18]	0.96[0.82,1.1]	315.146
				E	NA	NA	1	313.507

3.3. Impact of Scan Acquisition Time in Resting State Data on Heritability Estimates

As shown in Tables 2 and 4, no evidence of heritability was found for all measures computed on the LTS dataset, in which a shorter resting state scan (6.25min) was collected compared to the HCP dataset (30min). Such findings appear in line with the already expressed concerns in the literature, that too short acquisition times might yield unreliable results as they may fail to capture the slow wave dynamics of the functional fluctuations occurring in cycles of several minutes (Birn et al., 2013) (see Figure 2).

Figure 2. Dynamic Resilience Over Time.

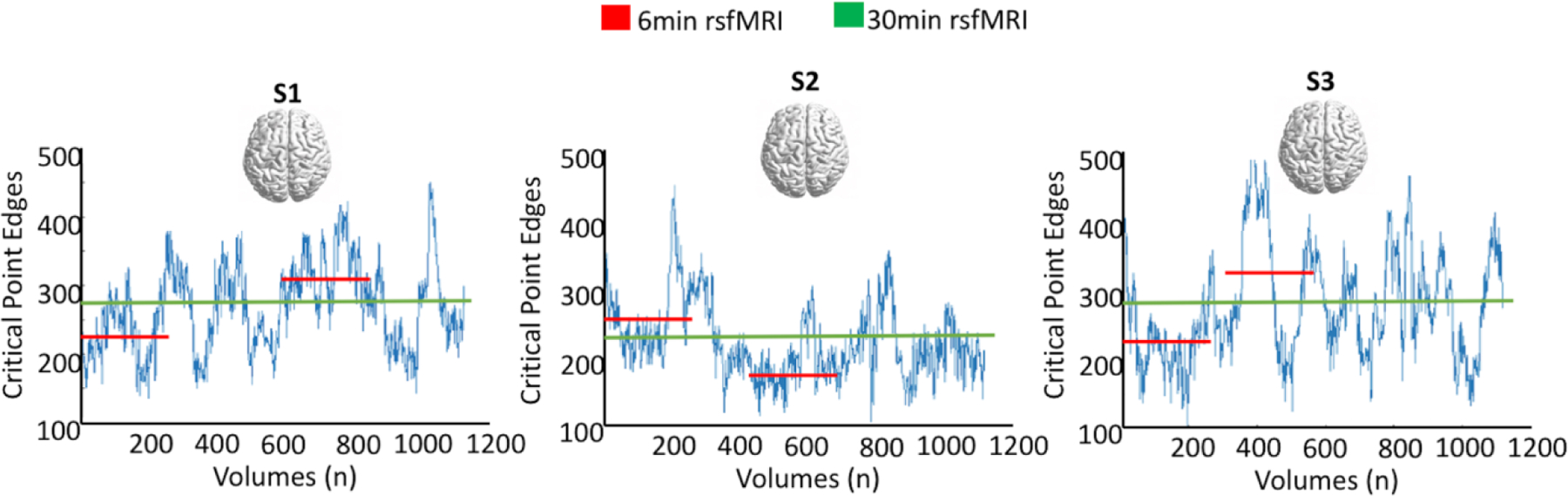
Oscillatory dynamics captured by rsfMRI occur in the scale of several minutes. The brain resilience estimates, secondarily computed from such measures, also shows high variability over time. Here, the measure of Critical Point dynamically computed overtime is shown for 3 example subjects. When the average of such signal fluctuations is taken, reliable estimates are achieved for longer scanning time only (green line), whereas state-dependent variability is introduced for shorter scanning times (red line), resulting in over- or under-estimation of the resilience metrics.

To examine this issue, we estimated how the reliability of our measures changes as a function of analyzing short (6 min) as compared to long (30 min) data sets (see Table 5). To do so, we separated the HCP time series into shorter batches of 6 min of data each, from which both graph theory and resilience metrics were computed again. The correlation between the measures of the two short batches was used to determine the reliability for a 6 min section of data (comparable to the LTS scan length). The Spearman-Brown formula was then applied to estimate reliability for the longer 30 min data (i.e., a scan length five times longer).

Table 5: Reliability measures as a function of scan times.

Reliability estimates were computed as the correlation for the metric computed on two separate 6 min scans in HCP dataset. The 30 min reliability estimates were obtained by adjusting the 6 min reliability estimates with the Spearman-Brown prophecy formula.

Measure	6min Reliability	Estimated 30 min Reliability
Resilience Metrics
Random Node Removal	0,019	0,088
Targeted Node Removal	0,128	0,423
Targeted Edge Removal	0,57	0,869
Speed of Drop	−0,003	−0,015
Early Edges Drop	0,152	0,473
Critical Point	0,157	0,482
Late Edges Drop	0,231	0,600
Graph Theory Measures
Characteristic path length	0,526	0,847
Clustering Coefficient	0,451	0,804
Global Efficiency	0,321	0,703
Local Efficiency	0,496	0,831
Modularity	0,392	0,763
Small Worldness	−0,032	−0,183

The reliability of a measure constrains the upper limit for its heritability, and unreliability is included in the nonshared environmental variance estimate. Given the low reliability estimates for many of the measures based on the 6 min scans, particularly the resilience measures, the lower heritability in the LTS is likely to be at least partially attributed to the shorter scan length. Thus, the lack of replication across the two datasets may be explained by this difference in length of the scan and as such differences in the stability and reliability of data acquired across the two data sets.

3.4. Functional Mapping of Network Resilience

In the HCP dataset, of all the tested network-derived resilience estimates, evidence of a stable genetic involvement was found only for resilience computed with the edge removal procedure. We explored the anatomical properties (e.g. strength, length, anatomical location) of those connections for which additive genetic influences on resilience were most prominent. This approach was possible only for the heritable measure of Critical Point, which provides information on the exact edge underlying the maximum point of deflection in the lesioning curve. The measure of Targeted Edge Removal, for which a moderate genetic component was also found, represents a general measure of the individual connectome robustness to lesioning and does not capitalize on the definition of single edges’ role. For this reason, it could not be graphically represented.

As shown in Figure 3, the type of edges representing the individual Critical Point consisted mainly of brain connections with a relatively weak connectivity value (M= 0.31 Fischer’s z value, SD=0.03 ) (Figure 3, panel A). Correlational values below 0.5 are indeed considered representative of weak connections in the human brain (Santarnecchi et al., 2014), with an important role in supporting network integrity and long-range information transfer (Granovetter, 1983; Santarnecchi et al., 2014).

Figure 3. Critical Point Edges’ Characterization.

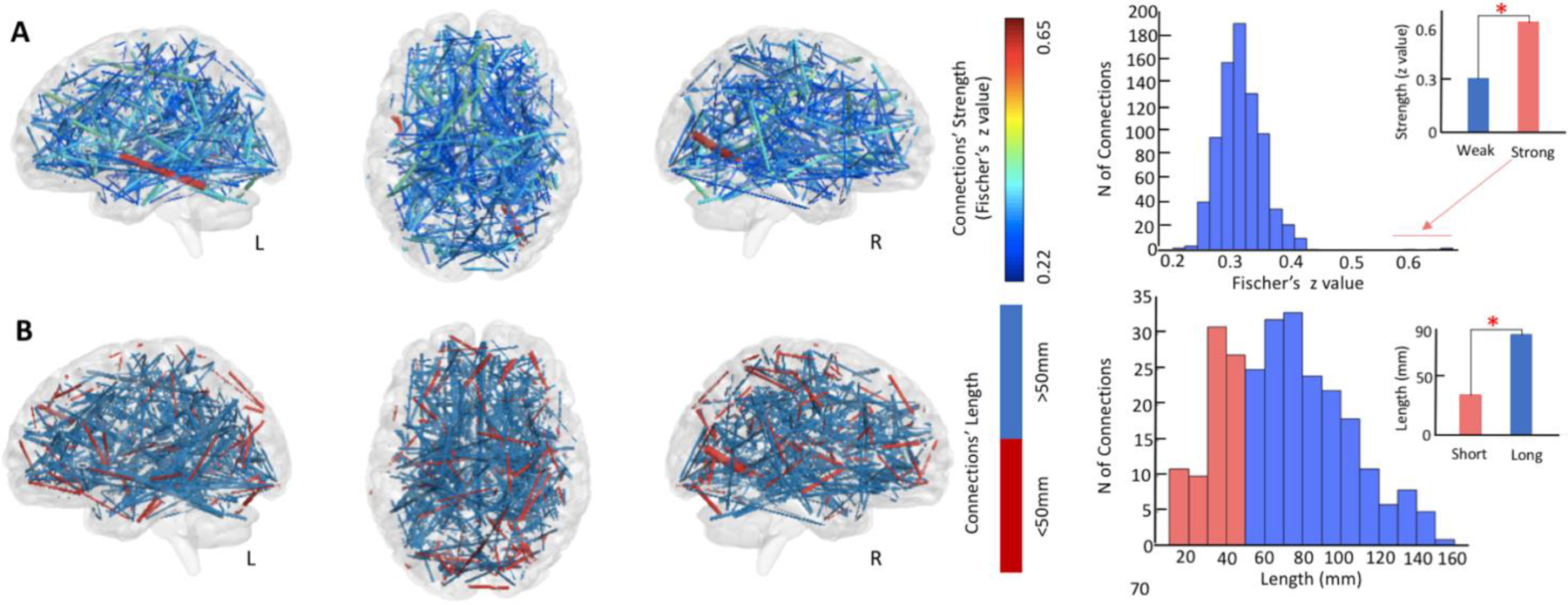
A. Edges accounting for the most heritable trait of resilience, the Critical Point, represent generally weaker ties, with the mean average strength of connections around 0.3 Fischer’s z value. B. From a functional perspective, these edges represent the long-range coupling between distant (>50mm) cortical sites. In panels A and B, the thickness of the edge is representative of its weight, also shown in color-code in panel A (colder colors are indicative of weaker strengths).

As a second characteristic, the majority of edges accounting for the individual Critical Point present a length greater than 50mm (Figure 3, panel B) (n_long=332, n_short=131; M_long= 85.42mm, SD_long=24.02mm; M_short=34.12mm, SD_short=10.98mm; t₍₂₆₂₎=−18.17, p<0.01), suggesting a role in connecting distant cortical regions based on prior studies looking at the specific role of short and long functional connections (Alexander-Bloch et al., 2013; Santarnecchi et al., 2014).

3.5. Cortical Networks Underlying Heritable Resilience

The functional connections underlying the resilience metric of Critical Point, which showed the highest heritability value in the HCP dataset, were mapped to determine if they belong to specific cortical resting state networks. To do so, we first created a weighted matrix in which nodes were represented by the brain’s ROIs from which the Critical Point’s edges originated, or from which the edges terminated. Edges in the weighted matrix were represented by the Fisher’s z-values of the individuals’ Critical Point. We then computed the nodal degree of the weighted matrix, such as that nodes with higher nodal degree have more Critical Point’s edges crossing them. The sum of the nodal degree of all nodes belonging to the same functional cluster was used to rank all networks’ involvement. As a result, we observed that the majority (>75%) of edges pertaining to the Critical Point originated from or terminated in the Default Mode (DMN) and Visual (VIS) networks (Figure 4, panel A). The nodal degree of the DMN was significantly higher than the mean nodal degree of all the other networks in the brain (t₍₆₇₎=−12.69, p<0.01). Of those connections, only a small number served as links between brain regions of the same network (intra-network connections-27%), whereas the majority acted in bridging distant cortical sites belonging to different networks (inter-networks connections-73%) (Figure 4, panel B and C).

Figure 4. Cortical Networks Associated with Heritable Resilience Estimates.

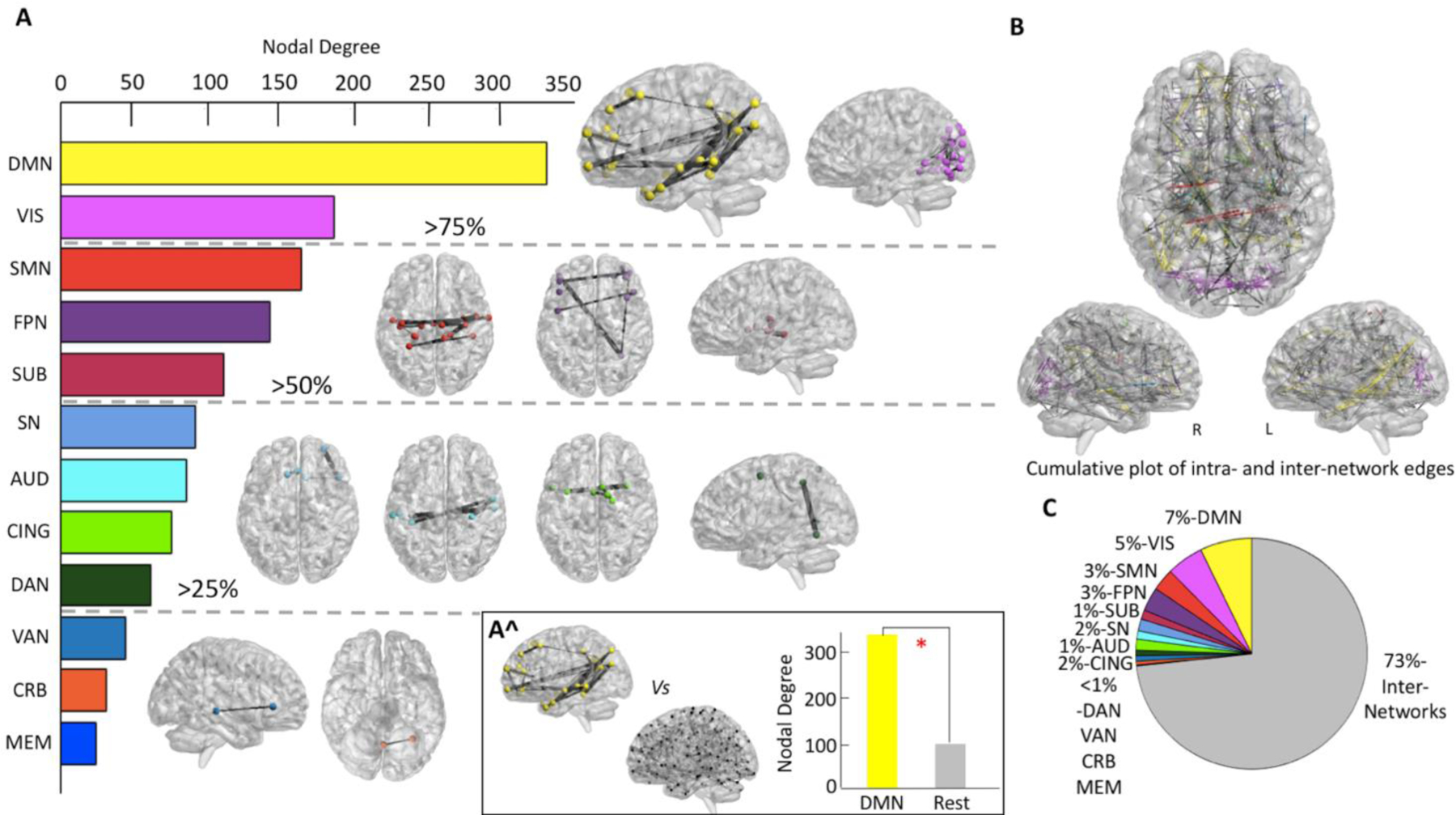
The nodal degree of the weighted matrix originating from all edges in the Critical Point was computed to assess the allocation of the functional connections. A. Over 75% of edges in the Critical Point originated from or terminated in nodes belonging to the DMN and VIS networks, followed by edges originating/ending in the SMN, FPN, and SUB networks. The SN, AUD, CING and DAN networks accounted for the observed probability distribution of edges between 25% and 50%. Finally, fewer than the 25% of edges were observed to fall in the VAN, CRB and MEM networks. A^. Overall, the number of connections belonging to the DMN was significantly higher than the number of connections belonging to other resting state networks. B. The overall distribution of all connections (intra and inter-modules) mapped in the brain. Intra-network edges are colored with the assigned color of the network, whereas inter-network edges are depicted in grey. C. The distribution of all connections (intra and inter-modules) is shown in form of pie chart distribution to depict how the majority of brain connections in the Critical Point consists of inter-networks ties.

[DMN= Default Mode Network, VIS= Visual Network, SMN= Sensorimotor Network, FPN= Frontoparietal Network, SUB= Subcortical Network, SN = Salience Network, AUD= Auditory Network, CING= Cingulo-Opercular Network, DAN= Dorsal Attention Network, VAN= Ventral Attention Network, CRB= Cerebellar Network, MEM= Memory Network]

4. Discussion

In the present study, we evaluated the pattern of genetic and environmental influence on both brain topology and its degree of resilience, a measure particularly relevant to mental health (Davydov et al., 2010), neurological diseases (Menardi et al., 2019; Perneczky et al., 2019), and stress (Santarnecchi et al., 2018). To do so, resting state fMRI data of 463 twins from the HCP dataset (Van Essen et al., 2013) and 453 twins from the LTS dataset (Corley et al., 2019; Rhea et al., 2013, 2006) were analyzed to exploit the underlying organization of the individual functional connectome and its response to the random or targeted (from strongest to weakest) removal of its nodes and edges. The progressive patterns of disaggregation were tackled from different perspectives to reveal the gross and fine-grained responses to simulated damage. Finally, both the computed ground topological measures and the resilience metrics were compared across pairs of MZ and DZ twins to examine genetic and environmental effects. For the HCP dataset, our results revealed, similar to prior studies, the presence of moderate heritability of several integration and segregation indexes, including clustering coefficient, characteristic path length, modularity, local and global efficiency measures. Importantly the novel finding of our study was that the brain’s resilience computed through the targeted removal of connections also showed moderate heritability, both in terms of the overall damage that needs to be sustained to cause a complete destruction of the functional graph (Targeted Edges Removal), as well as in terms of the point of maximum deflection in the lesioning process (Critical Point).

The heritability of resilience appears to depend more on the targeted lesioning of edges, and not on the random or targeted removal of nodes. This pattern may be attributable to the internal organization of the brain connectome itself. Its topology ensures a high level of robustness to the occurrence of random lesions, as well as great resilience when the most critical hubs of the network (i.e. the central cores/regions of the system) are selectively attacked (Achard et al., 2006; Joyce et al., 2013). Regardless of the targeted or random approach used, resilience estimates computed solely on the impact of node lesions might therefore not be particularly informative, as the brain appears to be capable of proficiently adjusting to such events.

On the other hand, the loss of important communication highways might be more detrimental to the overall network functioning. A parallel is seen in the impact of focal lesions versus diffuse axonal damage or functional disaggregation patterns. For instance, strokes can result in severe modular deficits, including selective attentional shortfalls (e.g. visuospatial neglect) (Bowen et al., 2013), loss of speech (e.g. aphasia) (Pedersen et al., 2004; Shafi and Carozza, 2018), sensory (e.g. cortical blindness, visual alterations, anosmia or loss of smell) (Gaber, 2010; Lotsch et al., 2016) and motor (e.g. loss of muscle control) (Langhorne et al., 2009) deficits, which although severe, can have reasonable potential for the individual to return to a good level of independence and life satisfaction (Vargo, 2011; Wolfenden and Grace, 2009). In contrast, lesions affecting structural and functional paths are associated with more widespread damage characterizing many neurological and psychiatric conditions. The structural connectome is responsible for global aspects of cognition, such as processing speed (Turken et al., 2008), cognitive flexibility and metastable dynamics (Hellyer et al., 2015). Its lesioning is a hallmark of widespread diseases like multiple sclerosis (Griffa et al., 2013) and diffuse axonal tearing following traumatic brain injury (Imms et al., 2019). The functional connectome relies on the coupling from the synchronous activity of distant regions, resulting in solid, yet modifiable, connections. The functional connectome shows strong correlation with the individual functioning (Finn et al., 2015), such as that its alteration has been observed in many pathological conditions, including schizophrenia (Garrity et al., 2007), depression (Wise et al., 2017), autism (Hogeveen et al., 2018), and even Alzheimer’s disease(Buckner, 2005). Furthermore, the loss of interhemispheric functional connections has been shown to be strongly related to the extent of behavioral impairment following a stroke (Corbetta et al., 2018; Siegel et al., 2016). These pieces of evidence have led to the term of “disconnecting syndromes” (Geschwind, 1970) to capitalize on the notion that many symptoms arise not from the damage of selective cortical nodes, but rather to abnormalities in their interactions. For this reason, focus on the study of the individual response to the selective lesioning of edges and its degree of heritability might be highly informative in guiding our understanding of the pathophysiological mechanisms of many diseases and for the development of therapeutic interventions, similarly to what has already been done in regard of the study of nodes lesioning (Aerts et al., 2016; Warren et al., 2014). Finally, lesioning approaches solely looking at the effects of nodes removal might fail to exploit the importance of strong and weak ties in the brain, as they will cause depletion of all connections regardless of their strength. From this perspective, edge-based lesioning approaches may be more informative on the fine-grained specifics of resilience in the human brain.

Indeed, as we further explored the anatomical characteristic of the brain connections subserving heritable resilience traits, we observed that the majority of them consisted of moderately weak, long, internetwork ties. Interest in the role of weak edges has a long history in network science, starting from the definition in social networks of “the strength of weak ties”, reflecting the role that one common acquaintance (i.e. weak connection) has in maintaining complex social dynamics by binding two separate groups otherwise relying on the strong connections between their members (Granovetter, 1983). Similarly, at the neural level, weak brain connections have been found to play a critical role in preserving the efficiency of the information flow with minimum wiring costs (Gallos et al., 2012). Weak ties might be the primary element capable of ensuring small-world properties to neural networks, similar to what has been observed in social ensembles, as such ties guarantee the passage of information between the backbones of highly knitted modules(Gallos et al., 2012). Not surprisingly, their role in bridging cortical modules has been thought to be accountable for observed variations in cognitive efficiency as well, for example in the form of higher intelligence relying on more distributed communication pathways mediated by weaker ties (Santarnecchi et al., 2014).

The role of weak connections in inter-network binding is in line with the results observed in the present study, where the majority of the edges subserving the individual Critical Point to the lesioning process was found to occur mainly at inter-modular connections. Indeed, network analyses revealed that most of those heritable edges originated from or terminated in nodes of the DMN (followed by the VIS and SMN), with the other end linking to nodes belonging to a different network (Figure 4). Notably, prior work has detailed the mapping of genetic and environmental influences on the human functional connectome, describing the genetic profile underpinning the synchronous activity of resting state networks (Richiardi et al., 2015). Based in part on data from the HCP, differences in the degree of heritability across brain networks have also been demonstrated, showing higher heritability for the connections between DMN and sensory-related clusters, especially the VIS network (Reineberg et al., 2019).

However, none of these results were replicated in the LTS dataset, except for the graph theory measure of Local Efficiency, which showed mild evidence of heritability. Resting state measurements reflect the low-frequency (<0.1Hz) synchronization of spontaneous neural activity underlying the functional coupling of distant regions in the brain (Fox and Raichle, 2007). As those fluctuations oscillate slowly, concerns have been raised regarding the minimum scan length necessary to measure them with sufficient quality to reliably detect interindividual differences (Anderson et al., 2011; Birn et al., 2013). Indeed, although the majority of studies use of acquisition lengths around 5–7 min, Birn and colleagues (Birn et al., 2013) have demonstrated how doubling the acquisition time (12 min) leads to substantially increased reliability of the derived functional connectivity. As graph theory metrics are secondarily computed from the functional connectome, major concerns have also been raised regarding the possibility that insufficiently long acquisition times might be under-powered for statistical tests performed upon those measures (Sinclair et al., 2015). In this sense, the HCP dataset has been specifically designed to optimize all acquisition parameters, with not only longer acquisition runs (30 min) (Glasser et al., 2013; Van Essen et al., 2012), but also fast TRs with multiband pulse sequences, allowing higher spatial resolution and greater number of scans to be acquired (Glasser et al., 2013). Since the LTS Dataset uses even higher TR than the HCP, this does not seem the reason of the difference, but it may apply for other rs-fMRI data with no multiband acquisition. Indeed, as no slice time correction is needed for those data, robustness against noise confounds (e.g., rapid head movement) are also highly increased, again ensuring a more stable signal (Glasser et al., 2013). The effect of shorter TR is therefore an adjunctive factor in favor of measure reliability in functional connectivity studies, improving the sensitivity of connections’ detection (Birn et al., 2013).

From a neurologic perspective, the concept of resilience has been addressed by two main independent theories: the Brain Reserve (Satz, 1993) and the Cognitive Reserve (Stern, 2009) hypotheses. According to the former, the amount of individual cerebral substrate is determined by a genetic predisposition and acts as a passive threshold, such that the greater the neural redundancy (e.g., higher number of neurons and synapses, larger brain and overall abundancy of brain tissue) the greater the damage it can sustain(Satz, 1993). On the other hand, the Cognitive Reserve hypothesis recognizes a more active role of the environment to which the individual is exposed, such as that the greater the life involvement in cognitive demanding jobs and activities, combined with a healthy diet and regular physical activity, the greater the individual potential to significantly counteract damage to vulnerable regions (Stern, 2002). These hypotheses are not mutually exclusive but rather see resilience as determined by the combined contribution of both genetic predisposition and favorable environmental influences. However, our results remain too preliminary to draw any conclusion about the relationship between in silico derived measures of resilience and what has been reported in clinical human studies in terms of brain and cognitive reserve. It would be desirable for future studies to address this possible association.

The present study is not free of other limitations. The first is that the unique environmental estimate, or “E”, includes measurement error. Moreover, E is an estimate of variance, so the specific environmental influences that it captures are not detailed. They most likely reflect the accumulation of many small environmental effects (Plomin, 2011). Second, it was beyond the scope of the present paper to test the association between resilience estimates and cognitive performance in this sample. Still, prior work has emphasized the link between cognition and resilience for both in-silico network lesioning and real life scenarios, revealing a positive association between higher cognitive performance and higher resilience (Deary, 2008; Deary et al., 2004; Santarnecchi et al., 2015; Simeon et al., 2007).

A final limitation to this study is represented by the sensitivity of graph theory metrics to a variety of data acquisition and preprocessing variables, including the length of scanning and the use of global signal regression, whereby the mean activity of the brain is regressed with the scope of further reducing noise confounds. Prior work has covered these issues, for example showing that the use of global signal regression substantially decreases the heritability of graph theory metrics and that short scans times (5–7min) also negatively impact the reproducibility of the results, which tend instead to stabilize with longer scans times (8–12min) (Birn et al., 2013; Sinclair et al., 2015). In line with these prior studies, we failed to fully replicate our findings in the LTS dataset, in which acquisition times were significantly reduced compared to the HCP (6min versus 30min). We believe these pieces of evidence should guide extra care in the acquisition parameters of future studies using similar approaches. Due to the high dynamicity of the brain, future studies could also address how topology and resilience estimates vary in time and are paralleled by the occurrence of specific brain states’ transitions.

5. Conclusions

Accurate understanding of brain topological properties and the degree to which genetic and environmental influences shape its resilience to external perturbation is of major interest for the understanding of healthy and pathological brain functioning. In the present study, we found mild-to-moderate heritability of resilience traits; still, the biggest contribution to those traits appears to be driven by environmental factors. From this evidence, future therapies aiming at increasing resilience might advocate in favor of interventions based on individual exposure to favorable environmental conditions. Evidence from both animal and human studies have indeed highlighted the importance of enriched environments for neural development and subsequent neuroprotective effects (Pham et al., 2002; Tost et al., 2015). For instance, future studies might compare the positive impact of such environmental factors (both socially and naturally driven) to more experimentally controlled scenarios, such as those based on the exposure of the brain to repetitive brain stimulation sessions. In this regard, knowledge of the neuroanatomical paths upon which brain resilience mechanisms preferentially load is of foremost importance. Hence, future scenarios might consider the development of interventions aimed at boosting individual strength in face of a variety or psychiatric and neurological disorders.

Highlights.

• Strokes, traumatic lesions, tumors and neurodegenerative disorders are all examples of neurological conditions that can severely impair the normal functioning of the human brain.

• Given the same amount of damage, a lot of variability exists in individual outcomes, a phenomenon often attributed to so-called “brain resilience”.

• By simulating brain lesions in a large dataset of twins, we investigated whether brain resilience is mainly influenced by genetic factor or by environmental factors.

• Results imply both heritable and environmental components of brain resilience, which may be important for designing interventions to help build individual resilience.