Neurophysiological and functional neuroanatomical coding of statistical and deterministic rule information during sequence learning

Abstract

Humans are capable of acquiring multiple types of information presented in the same information stream. It has been suggested that at least two parallel learning processes are important during learning of sequential patterns—statistical learning and rule‐based learning. Yet, the neurophysiological underpinnings of these parallel learning processes are not fully understood. To differentiate between the simultaneous mechanisms at the single trial level, we apply a temporal EEG signal decomposition approach together with sLORETA source localization method to delineate whether distinct statistical and rule‐based learning codes can be distinguished in EEG data and can be related to distinct functional neuroanatomical structures. We demonstrate that concomitant but distinct aspects of information coded in the N2 time window play a role in these mechanisms: mismatch detection and response control underlie statistical learning and rule‐based learning, respectively, albeit with different levels of time‐sensitivity. Moreover, the effects of the two learning mechanisms in the different temporally decomposed clusters of neural activity also differed from each other in neural sources. Importantly, the right inferior frontal cortex (BA44) was specifically implicated in visuomotor statistical learning, confirming its role in the acquisition of transitional probabilities. In contrast, visuomotor rule‐based learning was associated with the prefrontal gyrus (BA6). The results show how simultaneous learning mechanisms operate at the neurophysiological level and are orchestrated by distinct prefrontal cortical areas. The current findings deepen our understanding on the mechanisms of how humans are capable of learning multiple types of information from the same stimulus stream in a parallel fashion.

We investigated parallel processes in visual sequence learning, for that, EEG signal decomposition and source localization were used. Statistical and rule‐based learning were distinguishable in the decomposed signal, moreover, decomposed EEG and source analyses suggest distinct neural learning mechanisms. We suggest that parallel learning mechanisms are controlled by different prefrontal areas.

1. INTRODUCTION

How the human brain encodes regularities of the environment is a current topic in cognitive neuroscientific research. It has been proposed that learning of patterns includes at least two parallel processes (Batterink, Paller, & Reber, 2019; Conway, 2020; Maheu, Meyniel, & Dehaene, 2020; Nemeth, Janacsek, & Fiser, 2013). One of them is called statistical learning and refers to an automatic acquisition of associative relations and frequencies of external stimuli (Conway, 2020). Another attention‐dependent mechanism plays a role in controlling the learning process and integrating rule‐based regulations. This second process is often labelled as higher‐order sequence learning (Howard & Howard, 1997; Nemeth, Janacsek, & Fiser, 2013), deterministic rule‐learning (Maheu et al., 2020), or order‐based learning (Simor et al., 2019). It has been proposed that humans organize the temporal regularities in their environment in two distinct hypothesis spaces (Conway, 2020; Maheu et al., 2020): one is based on the estimation of probabilities, and works as statistical bias; the other one is based on deterministic relations or rules. Importantly, in situations where both statistical and rule‐like regularities occur in parallel (e.g., in language or music), not only competition can occur, but rules can induce statistical biases and vice versa (Maheu et al., 2020). That is, a high‐frequency continuation of a melody can be remembered as a rule (i.e., generalization from high probability to hundred percent probability), while not knowing the lyrics can be compensated by common rhymes (i.e., using high frequency associations in a deterministic context). Either way, singing the song might be a success or a catastrophe, depending on many factors, including the interaction between statistical and rule‐like predictions.

Parallel learning of different types of regularities can be studied with variations of sequence learning tasks, in which rules and interstimulus dependencies are repeated in the stimulus stream (Conway, 2020; Dehaene, Meyniel, Wacongne, Wang, & Pallier, 2015; Howard & Howard, 1997; Nissen & Bullemer, 1987). A short sequence can be memorized as an arbitrary order of items and stored in declarative memory (Conway, 2020). However, when the information stream becomes longer and more complicated, humans can only encode frequently co‐occurring patterns (statistical information) and hierarchical structures within the sequences (rule‐based learning) (Conway, 2020; Nemeth, Janacsek, & Fiser, 2013). While statistical learning reaches its plateau quickly, learning of sequential rules is characterized by a gradual change (Kóbor et al., 2018; Simor et al., 2019). Importantly, statistical information is not limited to adjacent relations (e.g., the probability of B following A) but also nonadjacent probabilities (e.g., A‐x‐B, where B follows A with high probability) can be detected by humans (Frost, Isbilen, Christiansen, & Monaghan, 2019; Gebhart, Newport, & Aslin, 2009; Hsu, Tomblin, & Christiansen, 2014; Kóbor et al., 2019; Nemeth, Janacsek, & Fiser, 2013; Szegedi‐Hallgató, Janacsek, & Nemeth, 2019) Consequently, the more complex and/or opaque a perceived sequence is, the larger employment of different computational processes are needed to detect and learn its structure (Conway, 2020; Dehaene et al., 2015; Maheu et al., 2020; Szegedi‐Hallgató et al., 2019). Thus, human sequence learning is inherently complex, not just in terms of (sub)processes but also in their relations to the wider cognitive architecture.

For instance, statistical learning is thought to be a largely stimulus‐dependent, bottom‐up process, and therefore, many aspects of it are modality‐specific (Batterink et al., 2019; Conway, 2020; Frost, Armstrong, Siegelman, & Christiansen, 2015). Learning of probabilistic information relies on local computations in separate networks for auditory, visual, and somatosensory regularities: this is also supported by the lack of intermodal correlations within individuals (Batterink et al., 2019; Frost et al., 2015). The functional significance of this relative independence across perceptual domains possibly lies in the nature of the stimulus: while auditory information is typically organized in time series, visual ones are more easily processed in a parallel fashion (Batterink et al., 2019). On the other hand, the higher‐order integration of sequential information is thought to be domain‐general (Fedorenko, Duncan, & Kanwisher, 2012). The domain‐specific versus domain‐general nature of different sequence learning processes are also related to the different level of involvement of attention and executive functions. Namely, statistical learning can be viewed as a result of sensory experience that created representations in specific sensory areas (Reber, 2013), and as such, it has limited or even inhibited access from top‐down functions (Ambrus et al., 2020; Conway, 2020; Filoteo, Lauritzen, & Maddox, 2010; Nemeth, Janacsek, Polner, & Kovacs, 2013). In contrast, sequential rules might be also accessed and even modified in a top‐down manner, thus, different learning processes also constitute differences in the implicit‐explicit dimension (Batterink et al., 2019; Conway, 2020). Notably, the common overlap between implicit and statistical, and rule‐based and explicit learning does not rule out exceptions (Batterink et al., 2019). Despite the growing interest in these simultaneous learning mechanisms (Conway, 2020), the neurophysiological processes behind them remain largely unknown (Kóbor et al., 2018, 2019) and it is an open question how these parallel learning mechanisms are coded at the neurophysiological level.

However, solving this puzzle represents a methodological challenge. Namely, different aspects of task‐related information and spontaneous background activities are present simultaneously in the EEG recordings of the scalp (Folstein & Van Petten, 2008; Nunez, Pilgreen, Westdorp, Law, & Nelson, 1991; Ouyang & Zhou, 2020; Stock, Gohil, Huster, & Beste, 2017) and overlapping brain areas are involved in processing them (Mückschel, Chmielewski, Ziemssen, & Beste, 2017). Furthermore, coding levels are more likely to get intermixed if the task requires manipulations of stimulus‐ and response‐related representations at the same time, such as in interference suppression (Mückschel, Chmielewski, et al., 2017) or stimulus–response binding (Opitz, Beste, & Stock, 2020; Takacs et al., 2020; Takacs, Mückschel, Roessner, & Beste, 2020). Using averaged trials of EEG data (Kóbor et al., 2018), it has been demonstrated that the frontal N2 event‐related potential (ERP) component reflects a rapid automatic detection of statistical properties in the sequence, and a rule‐based (pattern vs. random) learning with a longer time course of development. The P3 ERP‐component seems to be sensitive only to rule‐based differences and not to statistical properties (Kóbor et al., 2018). Therefore, the N2 is an ideal candidate to study the simultaneous mechanisms during sequence learning (Kóbor et al., 2018). In the EEG, the N2 is not a unitary component: it can be divided into different subcomponents related to cognitive control and stimulus‐related detection of novelty information processing (Adelhöfer et al., 2018; Adelhöfer, Gohil, Passow, Beste, & Li, 2019; Chmielewski, Mückschel, & Beste, 2018; Folstein & Van Petten, 2008; Mückschel, Chmielewski, et al., 2017). Specifically, subprocesses in the N2 time window that are affected by stimulus‐related information can be expected to show sensitivity to statistical learning. On the other hand, subprocesses related to control and monitoring may show modulations in relation to rule‐based learning of sequential information, reflecting this process' reliance on top‐down functions. Since statistical learning and deterministic rule‐based learning are supposed to occur in parallel (Conway, 2020), it is likely that these different information encoding principles are concomitantly coded in the neurophysiological signal. To solve this problem, we employed a signal decomposition method to disentangle the proposed simultaneous mechanisms.

A powerful method to disentangle intermixed coding levels in EEG data is the residue iteration decomposition (RIDE; Chmielewski et al., 2018; Mückschel, Chmielewski, et al., 2017; Mückschel, Dippel, & Beste, 2017; Ouyang, Sommer, & Zhou, 2015; Ouyang & Zhou, 2020). Instead of a traditional averaging of single trial data, RIDE can dissociate between three main activity clusters which preserve the dynamical response pattern of the single trial data. These activity clusters are the stimulus‐related S‐cluster, the response‐related R‐cluster, and finally the C‐cluster which captures the not strictly perceptual or motor aspects of the signal. That is, the C‐cluster reflects the translational aspect that is related to the association of stimuli with the appropriate response (Ouyang, Hildebrandt, Sommer, & Zhou, 2017). Among these aspects, response selection (Takacs, Zink, et al., 2020), stimulus‐distractor binding (Opitz et al., 2020), response inhibition (Mückschel, Dippel, & Beste, 2017), and interference suppression (Adelhöfer & Beste, 2020) have been linked to the C‐cluster EEG signal, revealing its sensitivity to action control.

The method postulates that parallel processes have different latency characteristics: perceptual and posterior attention processes are more likely tied to the stimulus presentation (S‐cluster), while motor execution is locked to the response (R‐cluster) (Ouyang, Herzmann, Zhou, & Sommer, 2011). Furthermore, higher‐order mechanisms, such as visuo‐motor integration, memory, retrieval, and decision making have variable latencies (C‐cluster), and, therefore, the related neurophysiological signals are smeared in the undecomposed EEG recording. In a previous study, different N2 effects related to conflict detection and response control could be differentiated by temporal signal decomposition (Mückschel, Chmielewski, et al., 2017). Based on the parallel subprocesses notion of Conway [2020; see also Kóbor et al., 2018], it is expected that statistical learning as an automatic, stimulus‐driven process is reflected by the S‐cluster activity, while the attention‐related, higher‐order rule‐based learning is mainly reflected by the C‐cluster activity. If this is the case, the current study would be the first to relate cognitive distinctions of statistical and rule‐based learning to distinct coding processes at the neurophysiological level. Learning of sequential patterns has been tied to widespread activations including the parietal cortex, the prefrontal cortex (PFC), the hippocampus, the cerebellum, and the basal ganglia (Conway, 2020). Yet, at least two networks can be differentiated from each other: a more perceptual, posterior one, and a prefrontal one (Conway, 2020). Especially the lateral PFC is important in the processing of rule‐based information in temporal sequences (Conway, 2020; Janacsek, Ambrus, Paulus, Antal, & Nemeth, 2015). Prefrontal functions, such as response selection and selective attention likely play a role not only in the production of sequential action, but also in learning of sequenced information (Conway, 2020). For instance, learning of nonadjacent, long‐distance regularities involves the inferior frontal gyrus (IFG; Barascud, Pearce, Griffiths, Friston, & Chait, 2016; Conway, 2020; López‐Barroso et al., 2013; Maheu et al., 2020; McNealy, Mazziotta, & Dapretto, 2006; Southwell & Chait, 2018). Specifically, the left IFG has been proposed as a supra‐modal hierarchical processor of sequence information (Tettamanti & Weniger, 2006), especially when sequences consisted of grammar‐like structures or verbal stimuli (Maheu et al., 2020). Learning of statistical information in the auditory domain involves a wide network: this includes functional connections between IFG and adjacent Broca's area and superior temporal cortex and Wernicke's area, indicating that efficient communication between temporal and (left) frontal areas is crucial in extracting probabilities from language‐like stimuli (Batterink et al., 2019; López‐Barroso et al., 2013; Maheu et al., 2020; McNealy et al., 2006). However, musical syntax is related to activations both in left and right IFG (Koelsch & Siebel, 2005). Importantly, processing sequences of visuospatial or visuomotor items seem to show right hemisphere dominance (Janacsek et al., 2015; Jarret, Stockert, Kotz, & Tillmann, 2019; Roser, Fiser, Aslin, & Gazzaniga, 2011), and data from brain stimulation experiments have shown that the right dorsolateral prefrontal cortex (DLPFC), but not the left DLPFC is associated with learning and retention of visuomotor sequences (Janacsek et al., 2015). Given the bottom‐up nature of sequence learning (Conway, 2020), and the importance of left IFG in language (Amunts et al., 2010; Friederici, 2006), a difference in laterality between visual and auditory sequences is conceivable. However, as the current study does not compare different modalities, it cannot contribute to this ongoing debate. Rather, potential laterality effects will be reported with tentative explanations only.

Additionally, prefrontal functions, such as attention and inhibitory control have been suggested to have an orthogonal relationship with statistical learning (Conway, 2020; Filoteo et al., 2010; Nemeth, Janacsek, Polner, & Kovacs, 2013). That is, performance on prefrontal functions negatively correlates with statistical learning abilities; moreover, temporary decrease of executive functions can enhance statistical learning (Ambrus et al., 2020; Nemeth, Janacsek, Polner, & Kovacs, 2013; Virag et al., 2015). The controversy between the role of frontal neural activity, particularly in the IFG in statistical learning and the opposing relation between prefrontal executive functions and learning of probabilistic information can be solved by considering alternative functions for the right IFG (Erika‐Florence, Leech, & Hampshire, 2014). Specifically, the alternative attentional rule‐processing (ARP) account of the right IFG postulates that this structure is not specific for inhibitory (or other executive) functions, but houses general task‐related functions, such as detecting novelty and frequency information in task settings, and gating of learning through attention control (Erika‐Florence et al., 2014; Southwell & Chait, 2018). Thus, the orthogonal relationship between statistical learning and prefrontal executive functions does not exclude the possibility of the involvement of IFG in learning, especially when the sequence is presented visually. In such sequences, detection of mismatch between internal models of the sequence and unexpected new items in the information stream contributes to surprise detection, which process has been linked to the right IFG (Barascud et al., 2016; Southwell & Chait, 2018). Moreover, it has been proposed that learning of nonadjacent dependencies relies on IFG (Amunts et al., 2010; Batterink et al., 2019) as opposed to adjacent regularities that are associated with activations in the (ventral) premotor cortex (Friederici, 2006; Opitz & Kotz, 2012). Thus, the statistical complexity of the sequence could influence the loci of frontal activations during learning.

In the current study, statistical learning effects are studied by temporally decomposed ERP components. Among these components, the S‐cluster N2 is expected to show the mismatch function related to distinguishing between predictable (frequent) and unpredictable (rare) stimuli. Since learning of statistical regularities is functionally related to detecting novelty in the stimuli, based on the ARP model (Erika‐Florence et al., 2014), we expected that learning of statistical probabilities as an S‐cluster N2 effect is related to the right IFG (Barascud et al., 2016; Conway, 2020; Maheu et al., 2020; Southwell & Chait, 2018). In contrast, we expected more widespread prefrontal activations related to rule‐based learning effect in the C‐cluster N2 in accordance with previous brain stimulation studies (Conway, 2020). The current study is a re‐analysis of the research by Kóbor et al. (2018). The undecomposed time‐domain data suggested that anterior negative deflections in the N2 time window were sensitive to both statistical learning and rule‐based learning albeit with different development as learning progressed (Kóbor et al., 2018). However, the conclusion was drawn based on overlapping time windows due to latency differences in the EEG data. To overcome this limitation, the current study employs temporal signal decomposition that is particularly suitable for studying simultaneous processes in the EEG signal (Ouyang et al., 2011; Ouyang & Zhou, 2020). Moreover, to further evaluate the independence of statistical learning and rule‐based learning at the neurophysiological level (Southwell & Chait, 2018), we have compared their neural source information, as well. In sum, to dissociate between neurophysiological markers of parallel learning mechanisms within sequence learning, we employed temporal signal decomposition and subsequent source localization of the RIDE‐decomposed components. Of note, while our hypotheses are specific to the decomposed N2, as in the original study (Kóbor et al., 2018), we also present related analyses of the P3 time window.

2. METHODS

2.1. Participants

The current study is a re‐analysis of the sample of 40 undergraduate students (21.4 years ± 1.6) as reported in Kóbor et al. (2018). All participants reported their vision to be normal or corrected‐to‐normal, the lack of any neurological or psychiatric condition, or taking any psychoactive medication. Further details of the participants, including handedness, years of education, and performance on standard neuropsychological tests are reported in the original study (Kóbor et al., 2018).

2.2. Ethics statement

Before the experiment started, participants were informed about the procedures of measurement and data collection. All participants provided written informed consent prior to participating, for which they received either payment or course credit. The study received approval from the United Ethical Review Committee for Research in Psychology in Hungary (EPKEB). The experiment was conducted in accordance with the Declaration of Helsinki.

2.3. Task

To measure sequence learning, a modified version of the Alternating Serial Reaction Time (ASRT) task (Howard & Howard, 1997) was presented to the participants, while EEG was recorded. This variation of the task is called the cued ASRT (Nemeth, Janacsek, & Fiser, 2013) and it has been successfully adapted for EEG measurement before (Kóbor et al., 2018). In this version of the task, a target stimulus (either a black or a red arrow facing left, up, down, or right) was presented on the display. The stimuli were always arranged to a central position of the screen. The task's instruction asked for pressing the corresponding button on the response box (indicating the four possible directions, see Figure 1) as accurately and as fast as possible. The stimuli appeared according to an eight‐element alternating sequence. The alternating sequence determined that random elements were always followed by pattern elements, and vice versa. Following this rule of stimulus presentation, if the sequence was 1–2‐4‐3, the stimuli appeared as 1‐r‐2‐r‐4‐r‐3‐r, where the four numbers correspond to the arrow's possible directions and “r” stands for a random direction. To visually indicate the task's rule, the black arrows represented pattern elements and the red arrows represented random elements. The instruction explicitly stated that the black arrows always followed a pattern, while red arrows appeared in random directions. Thus, the sequential rule was made explicit beforehand for the participants, and this information stayed salient during the task with the use of different colors for the two types of stimuli. Participants were asked to find the pattern in how the black arrows were presented to perform better in the task.

FIGURE 1.

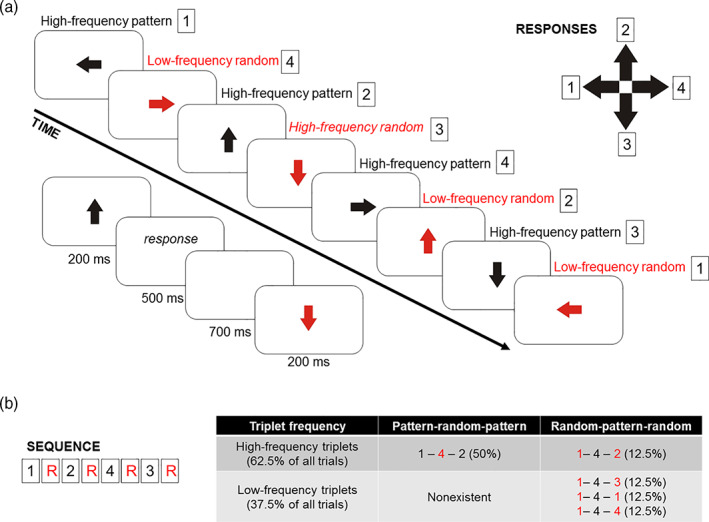
Experimental design. (a) In the current version of the Alternation Serial Reaction Time (ASRT) task, participants saw an arrow in the middle of the screen. The arrows' presentation followed an eight‐element sequence, in which pattern and random (R) elements alternate. Regularity of the sequence (e.g., the task rule) has been marked by black color for pattern and red color for random elements. Numbers denote the four possible directions of the arrows (1—left, 2—up, 3—down, 4—right). These directions correspond to the configuration of the response pad as presented in the top right corner of the figure. Timing of the task is presented below the thick black arrow (timeline). (b) Some series of consecutive elements (triplets) occur frequently in the task than others. High‐frequency triplets could either end with pattern or with random elements, while low‐frequency triplets always end with a random element

The structure of alternating black and red arrows means that some three‐element series of consecutive stimuli (“triplets”) appeared with different levels of probabilities, that is, triplets with high and low frequencies could be identified. In the example of 1‐r‐2‐r‐4‐r‐3‐r, the combinations of 1‐X‐2, 2‐X‐4, 4‐X‐3, 3‐X‐1 (X stands for any middle stimulus within the triplet) are frequent ones. However, series as 3‐X‐2 or 4‐X‐2 are less common. In these latter examples, the third element of the triplet can never occur as part of the sequence (pattern element), while in the former, frequent ones, the triplet can end either as a pattern or as a random stimulus. Triplets that are more probable to occur are called high‐frequency triplets, while less probable ones are called low‐frequency triplets. The designations also refer to the transition probabilities within the triplets. That is, in a high‐frequency triplet, the third element is highly predictable based on the first element (with 62.5% probability). In the case of the low‐frequency triplet, the predictability of the last element is lower (12.5%). In addition, each element can be categorized according to its sequential position, that is, whether it is a pattern element or a random element. If the last element is a pattern one, the explicit knowledge of the sequential rule contributes to predicting the direction of the next arrow. Therefore, the combination of the alternating sequence structure and the frequency information of the triplets results in a three‐way categorization of regularities within the task: high‐frequency triplets with either pattern or random endings and low‐frequency triplets that always end with random elements.

Consequently, based on the frequency and structure of the triplets, three types of trials can be distinguished: (a) high‐frequency pattern trials, (b) high‐frequency random trials, and (c) low‐frequency random trials. These types of trials can be analyzed to track the course of the two most important learning mechanisms in the ASRT task: sequence or rule‐based learning and statistical learning. Learning of sequential rule is quantified as a difference in response times between high‐frequency pattern and high‐frequency random elements. These elements are the last parts of a high‐frequency triplet, thus, they represent the same frequency information across the task. However, they differ in terms of sequential position, as one is part of the reoccurring pattern, while the other appears randomly. Therefore, faster responses to the pattern compared to the random trials indicates better learning of the sequential rule. To calculate the acquisition of frequency‐based information, that is, statistical learning, response times for high‐frequency random, and low‐frequency random trials are compared. Here, the elements carry the same information of the sequential rule (both random) but differ in frequencies, since they appear either in a high‐frequency or a low‐frequency triplet. Therefore, faster response time to high‐frequency random elements than to low‐frequency random elements is considered as a behavioral marker for successful statistical learning. In summary, statistical learning captures purely probability‐based learning, while learning of the sequential rule captures order‐based learning. In other words, the alternating regularity between nonadjacent items of the sequence creates more and less frequent (less predictable) chunks with either pattern‐random‐pattern or random‐pattern‐random configurations (triplets). In statistical learning, a second‐order transitional probability is being learnt: in one triplet, the first two items always followed by one frequently occurring and some less frequent endings within the stimulus chunk (Szegedi‐Hallgató et al., 2017; Szegedi‐Hallgató et al., 2019). That is, in high‐frequency triplets, the final item is more predictable by the first item compared to the low‐frequency triplets (the middle item does not have predictive value, hence, nonadjacent dependency). While in rule‐based learning, the second‐order transitional probability is always one: if the sequence has been learnt, pattern elements can be predicted with 100% certainty based on the previous pattern elements (Nemeth, Janacsek, & Fiser, 2013; Szegedi‐Hallgató et al., 2017, 2019).

Stimuli were presented in blocks, each of them containing 85 trials. Participants could take a short break between them, as the start of the blocks was self‐paced. In a block, first five warm‐up random trials were presented, then the eight‐element sequence appeared ten times. After a block was completed, explicit sequence knowledge was assessed. Participants were asked to type the order of the black (pattern) stimuli with the corresponding buttons, that is, as a continuous sequence that leaves out the red (random) arrows. The sequence report was finished after twelve button presses. If a participant reported at least ten correct continuous responses from the sequence, and they were able to keep this performance for the rest of the task, the original block where the sequence was first correctly reported was labelled as the timing of the discovery of the sequence. A more continuous measure of emerging sequence knowledge was calculated as a sequence knowledge score. In each postblock sequence report, each correct sequence item worth one point, then the sum of correct items was averaged across the thirty blocks of the experiment. After the sequence report has been completed, participants received feedback on the display for 4,000 ms that informed them about their general performance (average RT and accuracy on sequence stimuli). Of note, the feedback was not informative about the statistical learning performance nor about the rule‐based learning. After the feedback, participants took a short break before starting the next block. In sum, participants completed 2,550 trials over 30 blocks. The experiment lasted about 2.5 hr, including dimming the electrode cap and individual breaks.

2.4. EEG recording and analysis

Scalp EEG was recorded with 64 Ag/AgCl electrodes from an elastic cap (EasyCap, Germany), using Synamps amplifier and Neuroscan recording software (Compumedics Neuroscan, USA). For reference and ground, the tip of the nose and AFz electrode were employed. EEG recording was performed with a sampling rate of 1,000 Hz and with an online filter of 70 Hz low‐pass, 24 dB/oct. Impedance levels of electrodes were kept below the threshold of 10 kΩ. The recordings were analyzed in BrainVision Analyzer 2.0 (Brain Products, Germany). The EEG data were band‐passed filtered (0.5–30 Hz, 48 dB/oct), and a notch filter was applied (50 Hz). Then, independent component analysis (ICA, Infomax) was performed to remove only those components that were identified either as eye‐movement artifacts or as pulse artifacts based on their temporal properties and spatial distributions (Delorme, Sejnowski, & Makeig, 2007). As a result, two to four components have been removed per person (M = 3.2 ± 0.7). Then, the channel‐based EEG data were re‐referenced to the average of all electrodes. The preprocessed EEG was segmented according to time‐on‐task and experimental conditions, which required two consecutive steps. First, six equal length time bins or epochs were created. Second, the data were segmented into the three experimental conditions in each epoch. That is, high‐frequency pattern, high‐frequency random, and low‐frequency random segments were created. Segments with incorrect responses or without response markers (misses) were not included in the segmentation to ensure that only those trials are analyzed which were correctly identified by the participants. These segments were 800 ms long, starting −200 ms before the stimulus presentation, and ending 600 ms after that. Following the segmentation, automatic artifact rejection (as implemented in BrainVision Analyzer 2.0) was used to remove the remaining artifacts (with a voltage threshold of ±100 μV at any channels). The percentage of removed segments across conditions was 1.4% ± 3.7. None of the participants had to be removed because of a low number of kept segments. The kept segments were then baseline corrected based on the activity in a 200‐ms‐long interval before the stimulus presentation. The final segments represented the experimental conditions in six consecutive time stages of the task with correct responses. Further details of the EEG processing, including justification of these steps, can be found in Kóbor et al. (2018). The original analysis identified a frontal N2 component (time window of 200–300 ms) and a P3 component with a maximum activity on the electrode Pz (time window of 250–350 ms). Results of the original ERP analysis are reported in Kóbor et al. (2018). In the current study, the preprocessed, segmented, cleaned, and baseline‐corrected data was re‐analyzed with RIDE temporal decomposition.

2.5. Residue iteration decomposition

The RIDE temporal decomposition method was used for trial‐to‐trial variability‐based analysis of the stimulus‐locked ERPs. RIDE aims to distinguish components with variable intercomponent delays based on the single trial latency variability information (Ouyang et al., 2015; Ouyang & Zhou, 2020). The single‐trial ERPs are decomposed into different components with differential latency variability. Temporal decomposition is achieved in an iterative way. RIDE assesses latency variability in a channel‐specific fashion, thus, differences between individual electrodes remain valid in the identified components (Ouyang et al., 2015). In the current study, we used the RIDE toolbox in Matlab (Mathworks, Inc., MA), and followed the protocols of earlier studies (Mückschel, Chmielewski, et al., 2017; Ouyang et al., 2011; Verleger, Metzner, Ouyang, Śmigasiewicz, & Zhou, 2014). For a review of previous RIDE applications, see Ouyang and Zhou (2020). In two cluster types, latency information was extracted based on existing marker information. That is, stimulus onset was used to create the S‐cluster (“stimulus cluster”) and response markers for the R‐cluster (“response cluster”). The C‐cluster (“central cluster”) was estimated and iterated in each trial, assuming a nonconstant latency. That is, virtual time markers were created to decompose the last cluster. RIDE uses an iterative decomposition with an L1‐norm minimization. The resulting median waveforms represent the dynamics of single trials more reliably than traditional averaging of ERP components (Ouyang et al., 2017; Ouyang & Zhou, 2020). To estimate the first decomposed cluster, RIDE subtracts the other two from each trial and adjusts the residual of all trials for the latency information of the first one. As a result, median waveform is created for all time points in the cluster's search interval. The procedure is then repeated to create the remaining two clusters. The whole process iterates until convergence to better estimate the sub‐components. To extract the waveforms of each cluster, search windows should be predefined (Ouyang et al., 2011, 2015). The following time‐intervals were specified: for the S‐cluster up to 500 ms after the stimulus presentation; for the R‐cluster 300 ms before and after the correct response marker; for the C‐cluster 150 to 600 ms after the stimulus. Based on the original study (Kóbor et al., 2018), we selected the electrode Fz for the N2 component, and the electrode Pz for the P3 component. The selected channels were then visually inspected to determine the time window of these two components separately for the three RIDE clusters. The N2 component was identified between 200 and 300 ms after the stimulus presentation in the S‐cluster (similar to the undecomposed N2 in Kóbor et al. (2018). In the C‐cluster, the N2 was visible between 240 and 340 ms after the stimulus onset. In the R‐cluster, the N2 could not be identified by visual inspection, however, it was analyzed in the time window corresponding to the undecomposed N2 and the S‐cluster N2 time window (200–300 ms). The original study reported the P3 component between 250 and 350 ms after the stimulus presentation (Kóbor et al., 2018). We selected the identical time window in the S‐cluster data. In the C‐cluster, the P3 was detected between 250 and 400 ms, and in the R‐cluster, between 280 and 440 ms after the stimulus onset. Within the selected time intervals, the mean amplitude was quantified and extracted at the single‐subject level.

2.6. Source localization

The standard low resolution brain electromagnetic tomography (sLORETA) (Pascual‐Marqui, 2002) was used to examine the estimated neural sources of the effects of statistical learning and rule learning for the temporally decomposed EEG data. sLORETA provides neural source information based on images of standardized current source density. The standard electrode coordinates according to the 10/20 system were used as input. Then, a three‐shell spherical head model and the covariance matrix were calculated using the baselines at the single subject level. Within the head model, the intra‐cerebral volume is partitioned into 6,239 voxels using a spatial resolution of 5 mm. The standardized current density is calculated for each voxel, using an MNI152 head model template. sLORETA provides a single linear solution for the inverse problem without localization bias (Marco‐Pallarés, Grau, & Ruffini, 2005; Pascual‐Marqui, 2002; Sekihara, Sahani, & Nagarajan, 2005). Sources identified with using the sLORETA have been validated in combined MRI/EEG and TMS/EEG studies (Dippel & Beste, 2015; Ocklenburg et al., 2018; Sekihara et al., 2005). Comparisons against zero were used for the sLORETA contrasts. To calculate the statistics on the sLORETA sources, we used voxel‐wise randomization tests with 2,500 permutations and statistical nonparametric mapping procedures. Locations of voxels that were significantly different (p <.05) are shown in the MNI‐brain. Significant activations represent critical t‐values corrected for multiple comparisons as implemented in the sLORETA software.

2.7. Statistics

Statistical analyses were performed by using IBM SPSS Statistics, and followed the established procedure of analyzing the ASRT task (Kóbor et al., 2018; Nemeth, Janacsek, & Fiser, 2013; Song, Howard, & Howard, 2007). The two main learning processes, statistical learning and rule‐based learning were quantified for the behavioral and EEG analyses. Statistical learning was defined as the difference between high‐frequency random and low‐frequency random trials in reaction time, and mean activity of the RIDE clusters. Better statistical learning means shorter reaction time for high‐frequency random than for low‐frequency random trials. This learning index is expected to become larger as the learning progresses. Rule‐based learning was quantified as a difference between high‐frequency pattern and high‐frequency random trials in reaction time, and mean activity of the RIDE clusters. Better rule‐based learning means shorter reaction time for the pattern than for high‐frequency random trials. This learning index also becomes larger as the learning progresses (revealed by a significant interaction with the epoch). The two learning mechanisms were analyzed in two‐way repeated measures ANOVAs with “type” (high‐frequency pattern, high‐frequency random, and low‐frequency random) and “epoch” (from one to six) as within‐subject factors on reaction time, and the mean amplitude of the N2 and P3 components in the three RIDE clusters. When the interaction between type and epoch was significant, statistical learning was tested with a type by epoch ANOVA, in which the type factor included high‐frequency random and low‐frequency random trials. Similarly, rule‐based learning was analyzed as a type by epoch ANOVA, in which the type factor included high‐frequency random and high‐frequency pattern trials. In these ANOVA models, the Greenhouse–Geisser epsilon correction was used when the lack of sphericity necessitated it. Effect sizes are reported as partial eta‐squared. Post hoc pairwise comparisons of the behavioral measures and the decomposed N2 and P3 mean amplitudes were Bonferroni‐corrected, if necessary.

3. RESULTS

3.1. Behavioral results

Details of the behavioral results, including main effects and descriptive data are reported and illustrated in Kóbor et al. (2018). Overall accuracy separately for conditions has also been reported in the original manuscript. Crucially for the current study, the error rate was low in the entire sample (6.0% ± 2.0, range: 2.4–11.4%), thus, no participant had to be excluded based on low task performance. Here we summarize only those behavioral results that indicate learning effects and are necessary to interpret the neurophysiological results. Importantly, the type (high‐frequency pattern, high‐frequency random, and low‐frequency random) by epoch (1–6) ANOVA on the reaction time data showed a significant type by epoch interaction (F _{(10, 390)} = 15.25, ε = .382, p < .001, η _p ² = .281). This indicates that participants' responses changed between triplet types during the task. In the case of rule‐based learning, the type by epoch ANOVA revealed a significant type by epoch interaction (F _{(5, 195)} = 16.78, ε = .617, p <.001, η _p ² = .301). Participants' responses were faster in high‐frequency pattern than in high‐frequency random condition in all six epochs (p <.001), and this difference gradually increased from the first to the fourth epoch (smaller in the first epoch than in the other epochs ps <.004; smaller in the second epoch than in the fourth, and sixth ones p <.019; smaller in the third epoch than in sixth p <.001; for descriptive data, see Kóbor et al. (2018). That is, participants showed rule‐based learning from the beginning of the task, and this learning effect became larger as the task progressed. In the case of statistical learning, the type by epoch ANOVA did not reveal a significant type by epoch interaction (p = .643), however, the main effect of type was significant (F _{(1, 39)} = 123.53, p <.001, η _p ² = .760). Participants were faster in high‐frequency random than in low‐frequency random condition, throughout the task. That is, while rule‐based learning showed a gradual adaptation to the task starting from the first epoch, sensitivity to statistical regularities developed quickly and remained stable (i.e., reached its plateau more quickly). According to the collected sequence reports during the task, participants gained explicit knowledge about the sequence of the black arrows from around the fourth block (3.68 ± 6.15, that is, before reaching the end of the first epoch). Furthermore, the mean score of the sequence knowledge was 11.56 ± 0.82. After the first block, the majority (28 participants, 70% of the whole sample) responded with the maximum of 12 correct items (see also Kóbor et al., 2018).

3.2. Neurophysiological results

Analyses of the decomposed N2 and P3 components are presented as follows. First, type by epoch repeated measure ANOVAs are described. Second, separate ANOVAs investigating statistical learning or rule‐based learning are described.

3.2.1. Decomposed N2 (S‐cluster)

Grand‐averages of ERP waveforms in the S‐cluster N2 time window split by triplet type and epoch are presented in Figure 2 and statistical results are summarized in Table 1.

FIGURE 2.

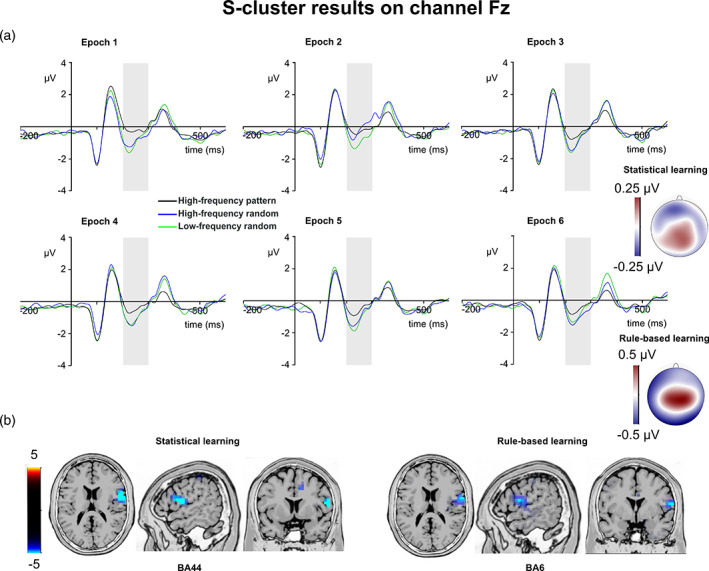
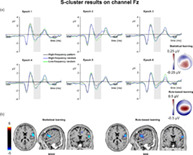
S‐cluster N2. (a) S‐cluster data is presented on channel Fz. Time point zero represents the stimulus presentation. The analyzed time window (200–300 ms) is marked with a shaded area. The S‐cluster N2 is presented across three conditions: high‐frequency pattern (black), high‐frequency random (blue), and low‐frequency random (green). The six panels depict the six consecutive epochs of the task. The scalp topography plots show the distribution of the mean activity of the two main contrasts: statistical learning as a difference between low‐frequency random and high‐frequency random and rule‐based learning as a difference between high‐frequency pattern and high‐frequency random conditions. (b) Voxels with significant differences for the statistical learning and rule‐based learning effects according to the standard low resolution brain electromagnetic tomography (sLORETA) analysis are presented. The sLORETA color bar presents critical t values

TABLE 1.

Summary of the decomposed N2 findings

	S‐cluster		C‐cluster			R‐cluster
Analysis and effects	F	p	η p 2	F	p	η p 2	F	p	η p 2
General
Type	10.73	<.001	.216	9.2	.001	.191	0.79	.409	.020
Epoch	3.97	.002	.092	1.27	.287	.032	1.58	.169	.039
Interaction	2.2	.036	.053	3.98	<.001	.092	0.22	.967	.006
Statistical learning
Type	1.52	.226	.037	4.54	.039	.104	0.82	.372	.020
Epoch	2.99	.020	.071	0.48	.755	.012	1.55	.189	.038
Interaction	3.14	.016	.074	1.93	.105	.047	0.11	.990	.003
Rule‐based learning
Type	9.53	.004	.196	7.48	.009	.161	1.18	.285	.029
Epoch	5.33	<.001	.120	2.6	.044	.062	0.78	.565	.020
Interaction	1.98	.101	.048	3.81	.003	.089	0.28	.926	.007

Note: p values ≤ .001 are presented in bold.

The type by epoch ANOVA on the mean amplitude of the S‐cluster N2 showed that the main effect of type was significant (F _(2,78) = 10.73, ε = .809, p <.001, η _p ² = .216). Similarly, the main effect of epoch was significant (F _(5,195) = 3.97, p = .002, η _p ² = .092). Importantly, the type by epoch interaction was also significant (F _(10,390) = 2.20, ε = .674, p = .036, η _p ² = .053), suggesting that the mean amplitude of the S‐cluster N2 changed between triplet types during the task.

In case of statistical learning, the type by epoch ANOVA showed that the main effect of triplet type was not significant (F _(1,39) = 1.52, p = .226, η _p ² = .037). However, the main effect of epoch was significant (F _(5,195) = 2.99, ε = .811, p = .020, η _p ² = .071). The S‐cluster N2 was larger in the fifth (−1.07 μV ± .26) than in the second epoch (−0.54 μV ± .28, p = .027). None of the other differences between epochs were significant (p >.070). However, the type by epoch interaction was significant (F _(5,195) = 3.14, ε = .796, p = .016, η _p ² = .074). In the second epoch, the S‐cluster N2 amplitude was larger in the low‐frequency random (−0.90 μV ± .26) than in the high‐frequency random (−0.19 μV ± .32, p <.001) condition. Triplet types did not differ from each other in other epochs (ps >.155). The sLORETA analysis revealed that the statistical learning effect across all epochs was reflected by activation modulations in the right IFG (BA44; MNI [x,y,z]: 60, 5, 15). Thus, in the S‐cluster N2, statistical learning was observed as a rapid effect occurring between the first and second epochs of the experiment. Additionally, statistical learning during the task was related to right IFG activation.

In case of rule‐based learning, the type by epoch ANOVA showed that the main effect of type was significant (F _(1,39) = 9.53, p = .004, η _p ² = .196). The S‐cluster N2 was larger in the high‐frequency random (−0.83 μV ± .24) than in the high‐frequency pattern (−0.41 μV ± .23) condition. Similarly, the main effect of epoch was significant (F _(5,195) = 5.33, p <.001, η _p ² = .120). The S‐cluster N2 was smaller in the second epoch (−0.21 μV ± .26) than in the third (−0.68 μV ± .23, p = .008), fourth (−0.69 μV ± .23, p = .037), fifth (−0.78 μV ± .24, p = .001), and sixth epochs (−0.80 μV ± .24, p <.001), consecutively. None of the other epochs differed from each other (p >.296). The type by epoch interaction was not significant (F _(5,195) = 1.98, ε = .796, p = .101, η _p ² = .048). According to the sLORETA analysis, the rule‐based learning effect during the task was reflected by activation modulations in the right prefrontal gyrus (BA6; MNI [x,y,z]: 65, 0, 15). Thus, rule‐based learning showed time‐invariant effect in the S‐cluster N2 mean amplitude. Triplets ending with pattern or random elements with the same frequency were dissociated through the whole task, and this difference was related to prefrontal activity.

3.2.2. Decomposed N2 (C‐cluster and R‐cluster)

Grand‐averages of ERP waveforms in the C‐cluster N2 time window split by triplet type and epoch are presented in Figure 3 and statistical results are summarized in Table 1.

FIGURE 3.

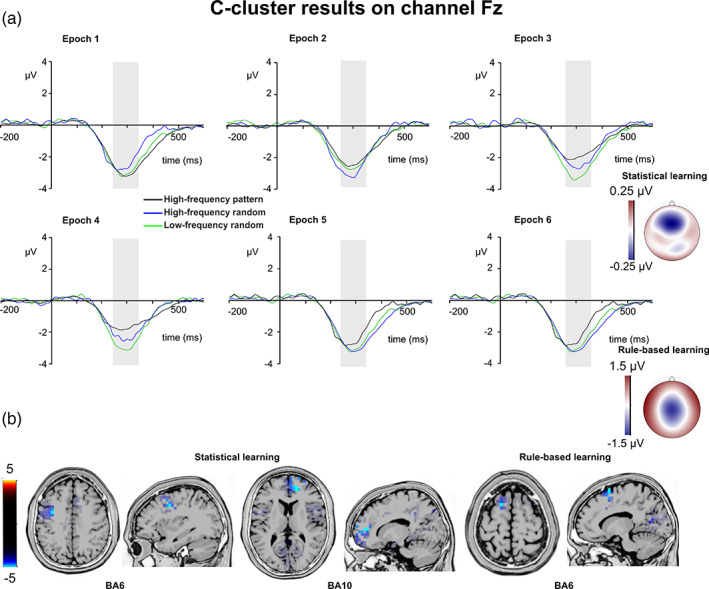
C‐cluster N2. (a) C‐cluster data is presented on channel Fz. Time point zero represents the stimulus presentation. The analyzed time window (240–340 ms) is marked with a shaded area. The C‐cluster N2 is presented across three conditions: high‐frequency pattern (black), high‐frequency random (blue), and low‐frequency random (green). The six panels depict the six consecutive epochs of the task. The scalp topography plots show the distribution of the mean activity of the two main contrasts: statistical learning as a difference between low‐frequency random and high‐frequency random and rule‐based learning as a difference between high‐frequency pattern and high‐frequency random conditions. (b) Voxels with significant differences for the statistical learning and rule‐based learning effects according to the standard low resolution brain electromagnetic tomography (sLORETA) analysis are presented. The sLORETA color bar presents critical t values

The type by epoch ANOVA on the mean amplitude of the C‐cluster N2 showed that the main effect of type was significant (F _(2,78) = 9.20, ε = .715, p = .001, η _p ² = .191). However, the main effect of epoch was not significant (F _(5,195) = 1.27, ε = .679, p = .287, η _p ² = .032). Importantly, the type by epoch interaction was significant (F _(10,390) = 3.98, ε = .695, p < .001, η _p ² = .092), which suggests that the mean amplitude of the C‐cluster N2 changed between triplet types during the task. In case of statistical learning, the type by epoch ANOVA showed that the main effect of triplet was significant (F _(1,39) = 4.54, p = .039, η _p ² = .104). The C‐cluster N2 was larger in the low‐frequency random (−2.91 μV ± .36) than in the high‐frequency random (−2.65 μV ± .33) condition. However, the main effect of epoch was not significant (F _(5,195) = 0.48, ε = .832, p = .755, η _p ² = .012). Similarly, the triplet by epoch interaction was not significant (F _(5,195) = 1.93, ε = .827, p = .105, η _p ² = .047). The sLORETA analysis revealed that the statistical learning effect was reflected by activation modulations in the left middle frontal gyrus (BA6; MNI [x,y,z]: −35, 0, 40) and in the right medial frontal gyrus (BA10; MNI [x,y,z]: 15, 50, 10). Thus, statistical learning effect occurred as a difference between low‐frequency random and high‐frequency random triplets irrespective of time on task, and this effect of the C‐cluster N2 was related to prefrontal activities.

In case of rule‐based learning, the type (high‐frequency random vs. high‐frequency pattern) by epoch (1–6) ANOVA showed that the main effect of type was significant (F _(1,39) = 7.48, p = .009, η _p ² = .161). The C‐cluster N2 was larger in the high‐frequency random (−2.65 μV ± .33) than in the high‐frequency pattern (−2.12 μV ± .33) condition. Similarly, the main effect of epoch was significant (F _(5,195) = 2.60, ε = .725, p = .044, η _p ² = .062). The C‐cluster N2 was smaller in the third epoch (−2.20 μV ± .35) than in the first (−2.78 μV ± .34, p = .017) and second (−2.66 μV ± .34, p = .017), and it was smaller in the fourth epoch (−2.03 μV ± .40) than in the first (p = .009), and second epochs (p = .015). None of the other epochs differed from each other (p >.082). The type by epoch interaction was also significant (F _(5,195) = 3.81, p = .003, η _p ² = .089). The C‐cluster N2 was more negative in the high‐frequency random than in the high‐frequency pattern condition in the fifth (−2.83 μV ± .37 vs. −2.01 μV ± .37, p = .019) and sixth epochs (−2.78 μV ± .39 vs. −1.68 μV ± .37, p = .001). The difference between conditions was not significant in the other epochs (p >.061). The sLORETA analysis revealed that the rule‐based learning effect was reflected by activation modulations in the left superior frontal gyrus (BA6; MNI [x,y,z]: −15, 10, 70). Thus, rule‐based learning was detected in the C‐cluster N2 mean amplitude data as a gradually increasing difference between random and pattern elements with the same frequency. This difference became the largest by the end of the learning. Additionally, rule‐based learning during the task was related to activation in the superior frontal gyrus.

The type (high‐frequency pattern, high‐frequency random, and low‐frequency random) by epoch (1–6) ANOVA on the mean amplitude of the R‐cluster N2 showed that the main effects of type (F _(2,78) = 0.79, ε = .641, p = .409, η _p ² = .020) and epoch (F _(5,195) = 1.58, p = .169, η _p ² = .039) were not significant. Similarly, the type by epoch interaction was not significant either (F _(5,195) = 0.22, ε = .590, p = .967, η _p ² = .006). Thus, the response‐related R‐cluster N2 did not show any modulation related to either statistical learning or rule‐based learning. For the complete comparisons, we provide the details of the follow‐up analyses (statistical learning and rule‐based learning) in Table 1.

3.2.3. Decomposed P3 (S‐cluster)

Grand‐averages of ERP waveforms in the S‐cluster P3 time windows split by triplet type and epoch are presented in Figure 4 and statistical results are summarized in Table 2.

FIGURE 4.

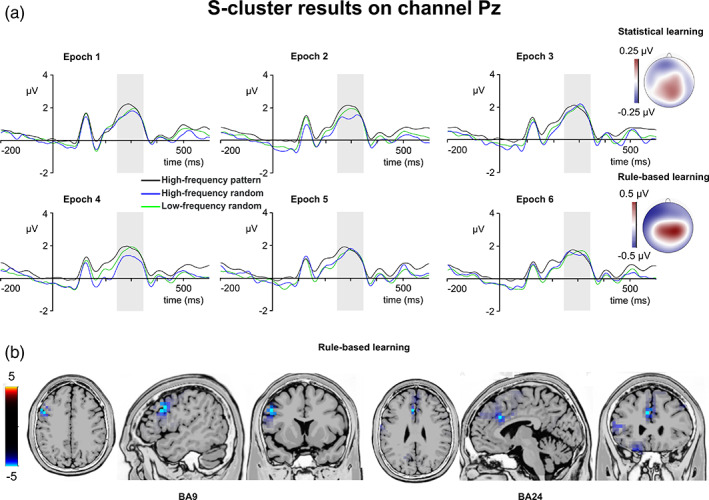
S‐cluster P3. S‐cluster P3. (a) S‐cluster data is presented on channel Pz. Time point zero represents the stimulus presentation. The analyzed time window (250–350 ms) is marked with a shaded area. The S‐cluster P3 is presented across three conditions: high‐frequency pattern (black), high‐frequency random (blue), and low‐frequency random (green). The six panels depict the six consecutive epochs of the task. The scalp topography plots show the distribution of the mean activity of the two main contrasts: statistical learning as a difference between low‐frequency random and high‐frequency random and rule‐based learning as a difference between high‐frequency pattern and high‐frequency random conditions. (b) Voxels with significant differences for the statistical learning and rule‐based learning effects according to the standard low resolution brain electromagnetic tomography (sLORETA) analysis are presented. The sLORETA color bar presents critical t values

TABLE 2.

Summary of the decomposed P3 findings

	S‐cluster			C‐cluster			R‐cluster
Analysis and effects	F	p	η p 2	F	p	η p 2	F	p	η p 2
General
Type	4.85	.010	.111	10.10	<.001	.206	10.71	<.001	.215
Epoch	2.57	.028	.062	4.40	.002	.101	3.05	.018	.073
Interaction	1.36	.198	.034	1.43	.196	.035	3.61	.001	.085
Statistical learning
Type	3.41	.072	.080	1.05	.312	.026	2.06	.160	.050
Epoch	1.62	.157	.040	2.56	.029	.062	1.17	.328	.029
Interaction	1.20	.311	.030	1.11	.355	.028	1.23	.295	.031
Rule‐based learning
Type	9.16	.004	.190	14.27	.001	.268	16.66	<.001	.299
Epoch	2.49	.033	.060	3.26	.008	.077	4.94	<.001	.112
Interaction	1.89	.098	.046	2.14	.063	.052	3.69	.007	.086

Note: p values ≤ .001 are presented in bold.

The type by epoch ANOVA on the mean amplitude of the S‐cluster P3 showed that the main effect of type was significant (F _(2,78) = 4.85, p = .010, η _p ² = .111). Similarly, the main effect of epoch was significant (F _(5,195) = 2.57, p = .028, η _p ² = .062). However, the type by epoch interaction was not significant (F _(10,390) = 1.36, p = .198, η _p ² = .034). In case of statistical learning, the type by epoch ANOVA showed that the main effects of type (F _(1,39) = 3.41, p = .072, η _p ² = .080) and epoch (F _(5,195) = 1.62, p = .157, η _p ² = .040) were not significant. Similarly, the type by epoch interaction was not significant (F _(5,195) = 1.20, p = .311, η _p ² = .030). Thus, the S‐cluster P3 did not show any modulation related to statistical learning. In case of rule‐based learning, the type by epoch ANOVA showed that the main effect of type was significant (F _(1,39) = 9.16, p = .004, η _p ² = .190). The S‐cluster P3 was larger in the high‐frequency pattern (1.74 μV ± .18) than in the high‐frequency random (1.48 μV ± .21) condition. Similarly, the main effect of epoch was significant (F _(5,195) = 2.49, p = .033, η _p ² = .060). The S‐cluster P3 was smaller in the fourth epoch (1.47 μV ± .21) than in the third (1.80 μV ± .21, p = .023). None of the other epochs differed from each other (p >.402). However, the type by epoch interaction was not significant (F _(5,195) = 1.89, p = .098, η _p ² = .046). The sLORETA analysis revealed that the rule‐based learning effect was reflected by activation modulations in the left IFG (BA9; MNI [x,y,z]: −50, 10, 35) and in the left anterior cingulate cortex (BA24; MNI [x,y,z]: −5, 25, 30). Thus, the S‐cluster P3 was sensitive the rule‐based learning.

3.2.4. Decomposed P3 (C‐cluster)

Grand‐averages of ERP waveforms in the C‐cluster P3 time windows split by triplet type and epoch are presented in Figure 5 and statistical results are summarized in Table 2.

FIGURE 5.

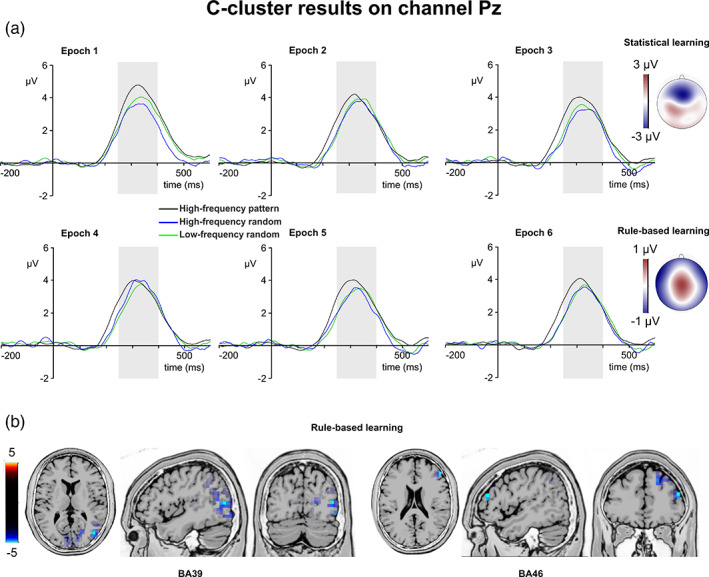
C‐cluster P3. (a) C‐cluster data is presented on channel Pz. Time point zero represents the stimulus presentation. The analyzed time window (250–400 ms) is marked with a shaded area. The C‐cluster P3 is presented across three conditions: high‐frequency pattern (black), high‐frequency random (blue), and low‐frequency random (green). The six panels depict the six consecutive epochs of the task. The scalp topography plots show the distribution of the mean activity of the two main contrasts: statistical learning as a difference between low‐frequency random and high‐frequency random and rule‐based learning as a difference between high‐frequency pattern and high‐frequency random conditions. (b) Voxels with significant differences for the statistical learning and rule‐based learning effects according to the standard low resolution brain electromagnetic tomography (sLORETA) analysis are presented. The sLORETA color bar presents critical t values

The type by epoch ANOVA on the mean amplitude of the C‐cluster P3 showed that the main effect of type was significant (F _(2,78) = 10.10, ε = .862, p <.001, η _p ² = .206). Similarly, the main effect of epoch was significant (F _(5,195) = 4.40, ε = .822, p = .002, η _p ² = .101). However, the type by epoch interaction was not significant (F _(10,390) = 1.43, ε = .662, p = .196, η _p ² = .035). In case of statistical learning, the type by epoch ANOVA showed that the main effect of triplet type (F _(1,39) = 1.05, p = .312, η _p ² = .026) was not significant. The main effect of epoch (F _(5,195) = 2.56, p = .029, η _p ² = .062) was significant, however, after Bonferroni‐correction, none of the pair‐wise differences between the epochs were significant (ps >.182). The type by epoch interaction was not significant either (F _(5,195) = 1.11, p = .355, η _p ² = .028). In case of rule‐based learning, the type (high‐frequency random vs. high‐frequency pattern) by epoch (1–6) ANOVA showed that the main effect of type was significant (F _(1,39) = 14.27, p = .001, η _p ² = .268). The C‐cluster P3 was larger in the high‐frequency pattern (3.60 μV ± .24) than in the high‐frequency random (3.05 μV ± .25) condition. Similarly, the main effect of epoch was significant (F _(5,195) = 3.26, p = .008, η _p ² = .077). The C‐cluster P3 was smaller in the fifth epoch (3.15 μV ± .25) than in the first one (3.64 μV ± .27, p = .028). None of the other epochs differed from each other (ps >.231).

The type by epoch interaction was not significant (F _(5,195) = 2.14, p = .063, η _p ² = .052). The sLORETA analysis revealed that the rule‐based learning effect was reflected by activation modulations in the right middle frontal gyrus (BA46; MNI [x,y,z]: 50, 40, 20) and in the right middle temporal gyrus (BA39; MNI [x,y,z]: 45, −75, 10). Thus, rule‐based learning modulated the C‐cluster P3 mean amplitude. High‐frequency pattern and random triplets were dissociated through the whole task, and this difference was related to frontotemporal activities.

3.2.5. Decomposed P3 (R‐cluster)

Grand‐averages of ERP waveforms in the R‐cluster P3 time windows split by triplet type and epoch are presented in Figure 6 and statistical results are summarized in Table 2.

FIGURE 6.

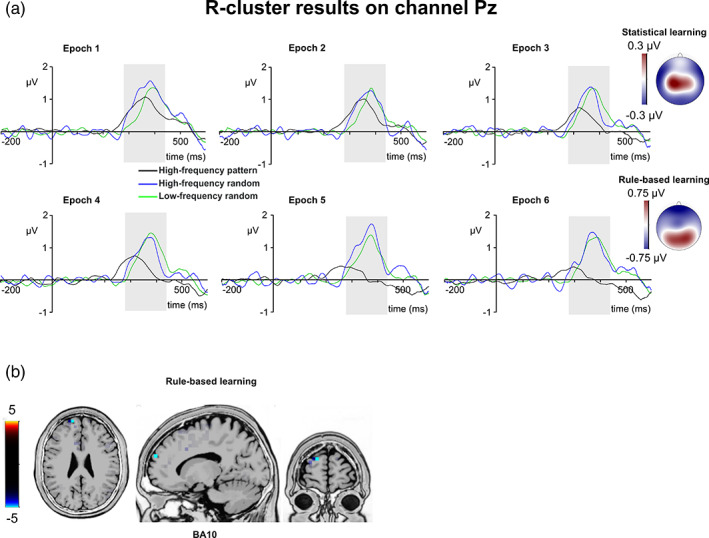
R‐cluster P3. (a) R‐cluster data is presented on channel Pz. Time point zero represents the stimulus presentation. The analyzed time window (280–440 ms) is marked with a shaded area. The R‐cluster P3 is presented across three conditions: high‐frequency pattern (black), high‐frequency random (blue), and low‐frequency random (green). The six panels depict the six consecutive epochs of the task. The scalp topography plots show the distribution of the mean activity of the two main contrasts: statistical learning as a difference between low‐frequency random and high‐frequency random and rule‐based learning as a difference between high‐frequency pattern and high‐frequency random conditions. (b) Voxels with significant differences for the statistical learning and rule‐based learning effects according to the standard low resolution brain electromagnetic tomography (sLORETA) analysis are presented. The sLORETA color bar presents critical t values

The type by epoch ANOVA on the mean amplitude of the R‐cluster P3 showed that the main effect of type was significant (F _(2,78) = 10.71, ε = .853, p <.001, η _p ² = .215). Similarly, the main effect of epoch was significant (F _(5,195) = 3.05, ε = .813, p = .018, η _p ² = .073). Importantly, the type by epoch interaction was also significant (F _(10,390) = 3.61, ε = .649, p = .001, η _p ² = .085). In case of statistical learning, the type by epoch ANOVA showed that the main effects of triplet type (F _(1,39) = 2.06, p = .160, η _p ² = .050) and epoch (F _(5,195) = 1.17, p = .328, η _p ² = .029) were not significant. Similarly, the type by epoch interaction was not significant either (F _(5,195) = 1.23, ε = .804, p = .295, η _p ² = .031). In case of rule‐based learning, the type by epoch ANOVA showed that the main effect of type was significant (F _(1,39) = 16.66, p <.001, η _p ² = .299). The R‐cluster P3 was larger in the high‐frequency random (0.91 μV ± .15) than in the high‐frequency pattern (0.41 μV ± .12) condition. Similarly, the main effect of epoch was also significant (F _(5,195) = 4.94, p <.001, η _p ² = .112). The R‐cluster P3 was larger in the first epoch (0.96 μV ± .14) than in the fifth (0.58 μV ± .13, p = .014) and sixth epochs (0.49 μV ± .12, p = .012). None of the other epochs differed from each other (ps >.066). Importantly, the type by epoch interaction was also significant (F _(5,195) = 3.69, ε = .794, p = .007, η _p ² = .086). The R‐cluster P3 was larger for high‐frequency random (1.13 μV ± .18) than for high‐frequency pattern trials in the first epoch (0.79 μV ± .14, p = .042). The same difference occurred in the third (0.78 μV ± .20 vs. 0.42 μV ± .16, p = .039), fourth (0.81 μV ± .19 vs. 0.40 μV ± .15, p = .027), fifth (1.05 μV ± .19 vs. 0.11 μV ± .14, p <.001), and sixth epochs (0.87 μV ± .17 vs. 0.10 μV ± .15, p <.001). The two conditions did not differ from each other in the second epoch (p = .333). The sLORETA analysis revealed that the rule‐based learning effect was reflected by activation modulations in the left superior frontal gyrus (BA10; MNI [x,y,z]: −15, 60, 25). Thus, rule‐based learning was detected in the R‐cluster P3 mean amplitude. Moreover, the interaction revealed a gradually increasing difference between high‐frequency random and pattern elements. This difference grew the largest by the end of the experiment, similarly to the C‐cluster N2 results (see above).

4. DISCUSSION

We compared temporally decomposed neurophysiological correlates of parallel learning processes, namely statistical learning and rule‐based learning in a visuomotor sequence learning task. The temporal decomposition successfully differentiated between S‐ and C‐cluster activities in the time windows of the N2 component, and between S‐, C‐, and R‐cluster activities in the time windows of the P3 component. We expected that statistical learning is reflected by the S‐cluster activity, while rule‐based learning is reflected by the C‐cluster activity. The results partially confirmed these hypotheses; however, the difference was more gradual than categorical between the learning mechanisms. In the following sections, we discuss how statistical learning and rule‐based learning effects modulated the temporally decomposed EEG signal. After reviewing the results of the RIDE clusters, we compare the two mechanisms and discuss the associated functional neuroanatomical sources.

4.1. Statistical learning

Statistical learning occurred incidentally, reflecting stimulus‐driven, implicit process that has reached its plateau quickly (Kóbor et al., 2018). This was reflected by both S‐cluster and C‐cluster N2 activities, as random triplets were distinguishable according to their predictability (e.g., probability information) in these two clusters. Importantly, the C‐cluster N2 did not show any modulation by statistical learning as the task progressed. This is in line with the results of Kóbor et al. (2018), where the N2 statistical learning effect was time‐invariant, thus, it did not show a gradual accumulation of statistical knowledge. However, the statistical learning effect of the S‐cluster N2 was time‐variant, as the difference between triplet types increased between the first and second epochs. Notably, this rapidly occurring effect decreased by the next epoch, which then showed similar activity to the beginning of the task. Thus, changes in the S‐cluster N2 were rapid and short lasting, while the C‐cluster N2 statistical learning effect was constant during the task. This is in line with the behavioral results that showed a rapid acquisition of statistical information early in the task, which then remained stable during the experiment (Kóbor et al., 2018). Both the C‐cluster N2 and the S‐cluster N2 mean amplitudes were larger for low‐frequency random than for high‐frequency random triplets. Thus, less predictable stimuli triggered larger N2 responses both as a function of mismatch or novelty detection (S‐cluster) and as a signal of response conflict (C‐cluster). Detecting statistical learning effects both in S‐cluster N2 and C‐cluster N2 promotes the notion of Koelsch, Busch, Jentschke, and Rohrmeier (2016) that processing transitional probabilities goes beyond sensory capacities. However, it is likely that a rare sequence of events signals a potential need for a higher cognitive load (Friston, 2010; Friston & Kiebel, 2009; Koelsch et al., 2016). This explanation also fits the current study, in which low‐frequency random triplets were associated with slower responses, thus the stimuli that was the hardest to predict increased the processing load (Kóbor et al., 2018). This increased load was detected not only in the undecomposed N2 (Kóbor et al., 2018), but also in the C‐cluster N2. It has been suggested, that a neurophysiological marker for statistical learning inevitably has a dual role: it can signal both increased processing load and a prediction error signal (Koelsch et al., 2016). Importantly, temporal signal decomposition could provide a meaningful distinction between these roles, as the S‐cluster reflects the stimulus‐driven aspects of novelty or mismatch detection, and the C‐cluster reflects the increased cognitive load and response conflict (Adelhöfer & Beste, 2020; Mückschel, Chmielewski, et al., 2017; Takacs, Zink, et al., 2020). Thus, statistical learning operates at a perceptual level, but not exclusively. Central aspects of statistical learning likely provide signals for the higher‐order functions for adaptive behavior (Conway, 2020). Unlike previous approaches with the undecomposed EEG (Kóbor et al., 2018; Koelsch et al., 2016), the temporally decomposed clusters could differentiate between these two functions of statistical learning. Even though these simultaneous processes occur in similar and overlapping time windows, the differences between them in latency variability reveal that one is directly triggered by the visual presentation of the stimulus while the other one represents a more variable mental chronometry. Thus, the multifaceted role of learning of probabilistic information was confirmed at the neurophysiological level.

4.2. Rule‐based learning

While statistical learning effects were specific to the S‐cluster and C‐cluster N2s, rule‐based learning was detected in a wide range of temporally decomposed components, such as the S‐cluster and C‐cluster N2s, S‐cluster, C‐cluster, and R‐cluster P3s. This pervasive effect likely indicates that the global integration of the acquired sequential rule‐based information involves sensory, translational, and motor aspects concurrently. That is, rule‐based learning provides a general access to summary statistics. This includes the distribution of statistics which originates from statistical learning, and a general knowledge of the uncertainty of the information stream (Conway, 2020; Daikoku, 2018). In the following, we discuss how temporal signal decomposition helped to differentiate between these set of functions.

Curiously, the S‐cluster N2 showed a time‐insensitive effect of rule‐based learning. The component was larger for high‐frequency random than for high‐frequency pattern triplets. Thus, despite the same level of stimulus probability, sequential position triggered a stimulus‐driven mismatch response. However, this effect has to be taken with caution, since in this version of the paradigm, random and pattern elements were visually distinguishable from each other, marked by red and black colors, respectively. Visible distinctions (cues) have been employed in the ASRT task before to help participants learn the sequence structure in a faster, intentional manner (Kóbor et al., 2018; Nemeth, Janacsek, & Fiser, 2013; Simor et al., 2019; Szegedi‐Hallgató et al., 2017). This is motivated by earlier studies showing that without such cues, rule‐based sequential knowledge requires several hours of practice to develop (Howard & Howard, 1997). Therefore, cues and explicit instruction was given to participants to speed up learning and enable us to compare different learning processes in the same time frame (Nemeth, Janacsek, & Fiser, 2013; Simor et al., 2019). While visual cues could have had an effect on the S‐cluster results, the advantage of decomposition is that this effect was potentially dampened in the C‐ and R‐cluster, respectively (Ouyang et al., 2011; Ouyang & Zhou, 2020). Crucially, rule‐based learning was detected in the C‐cluster N2, as well. High‐frequency random stimuli which is harder to predict elicited a larger component compared to the easy to predict high‐frequency pattern condition. Unlike statistical learning, the rule‐based learning effect on the C‐cluster N2 increased with practice, showing a gradual accumulation of sequence knowledge. This is in line with the undecomposed N2 results (Kóbor et al., 2018) and earlier reports of ERP correlates of sequence learning (Eimer, Goschke, Schlaghecken, & Stürmer, 1996; Ferdinand, Mecklinger, & Kray, 2007; Rüsseler, Kuhlicke, & Münte, 2003). The time‐sensitive nature of rule‐based learning also reflects the behavioral results that showed continuous learning as the task progressed, starting from the very first epoch (Kóbor et al., 2018). Thus, the C‐cluster N2 showed evidence for the changing level of response conflict between predictable (learnt) and less predictable random triplets.

Rule‐based learning effects were detected in the decomposed P3 components, as well. Effect of attention on detecting irregularities in the information stream is traditionally linked to the P3 (Chennu & Bekinschtein, 2012; Kóbor et al., 2018; Kóbor et al., 2019). Regularities, such as sequential patterns evoke attention (Zhao, Al‐Aidroos, & Turk‐Browne, 2013). Importantly, in a sequence in which pattern and random elements alternate with each other and are visually distinguishable, attention can be both endogenous and exogenous (Zhao et al., 2013). Exogenous attention evoked by the different colors of pattern and random elements is likely captured by the rule‐based learning effect in the S‐cluster P3, similarly to the rule‐based learning effect in the S‐cluster N2. Moreover, endogenous attention evoked by internal goal might be reflected by the C‐cluster P3 effect. Prioritizing a regular stimulus event over irregular ones is not a strictly stimulus‐driven process since it relies on the internal representation of the regularities (Zhao et al., 2013). Interestingly, both the S‐cluster P3 and the C‐cluster P3 effects were constant: high‐frequency pattern elements (targets according to the goal of the task) evoked larger P3s than high‐frequency random elements through the task. However, this time‐invariant nature of the rule‐based learning effects contradict the gradual learning curve seen in the behavioral data (Kóbor et al., 2018). This contradiction was resolved by the R‐cluster results. Importantly, the R‐cluster P3 provided a type by epoch interaction, which showed a growing difference between sequential and random triplets with the same stimulus frequencies. That is, neurophysiological dynamics similar to the behavioral learning curve was observed in the C‐cluster N2 and R‐cluster P3. Thus, these two decomposed components reflected the adaptation to the sequential regularities through response conflict and response preparation mechanisms. In sum, the pervasive effect of rule learning on the temporally decomposed clusters confirm the complex nature of this learning mechanism (Conway, 2020). The learning of higher‐order visual sequential information includes selective attention to different stimulus categories (S‐cluster P3), goal‐directed effort allocation (C‐cluster P3), and gradually more effective response management (R‐cluster P3). These various functions highlight the main characteristics of rule‐based learning. Namely, it is an attention‐dependent system which serves as a gating or control mechanism over the learning of sequential information (Conway, 2020).

4.3. Comparison between statistical learning and rule‐based learning

The main goal of the current study was to differentiate between parallel learning mechanisms in the neurophysiological signal. To characterize the differences between the types of learning at a single trial level, we employed temporal signal decomposition. This was successful as statistical learning in the visuomotor domain was detected specifically in the mean amplitudes of the S‐cluster N2 and C‐cluster N2, while rule‐based learning effect occurred in the mean amplitudes ranging from the S‐cluster N2 to the R‐cluster P3. Thus, statistical learning was identified as a learning mechanism related to mismatch‐detection and early response conflict. In contrast, rule‐based learning as a higher‐order process was reflected by every aspect of the decomposed N2 and P3 signals except of the R‐cluster N2. Thus, it was confirmed that rule‐based learning builds upon the acquired statistical regularities, and contributes to the control of the learning (Conway, 2020). However, a specific statistical learning effect and a more general rule‐based learning also raises the possibility that the two learning mechanisms are the same process albeit with different levels of complexity. This alternative explanation was ruled out by the source localization analyses. An important validation whether the decomposed components are related to distinct processes is differentiating between their neural sources. Specifically, we have expected that statistical learning effect of the S‐cluster N2 is associated with right IFG activity, while rule‐based learning as reflected by the C‐cluster N2 is associated with a more widespread dorsolateral activity. This was partially confirmed by the source localization, which revealed that the statistical learning effect in a visuomotor sequence on the S‐cluster N2 was related to activation modulations in the right IFG. In contrast, rule‐based learning effect was reflected by the right prefrontal gyrus' activation. The C‐cluster N2 also showed differences in the neural sources of the two forms of learning: statistical learning effect was reflected by changes of activation in the left middle frontal gyrus and in the right medial frontal gyrus, while rule‐based learning was reflected by activation modulations in the left superior frontal gyrus. Thus, the right IFG was mainly implicated in statistical learning, providing further evidence about this region's importance in acquiring probabilistic information (Barascud et al., 2016; Conway, 2020; Maheu et al., 2020; Southwell & Chait, 2018). Furthermore, this association was specific for the S‐cluster, while the C‐cluster N2 showed more widespread prefrontal activations both for statistical and rule learning. This pattern is in line with earlier research showing that frontal sources are associated with the learning of hierarchical rule‐based information (Southwell & Chait, 2018). In the current study, the alternation between sequence and random items corresponds to such hierarchical structure (Nemeth, Janacsek, & Fiser, 2013).

Taken together, the different coding levels in the N2 time window during the task are also related to different functional neuroanatomical structures. Moreover, similar to the N2 results, the S‐ and C‐cluster sources also differed in the P3 time windows. Note that, the P3 was only sensitive to the rule‐based learning effect. This effect in the S‐cluster showed activation modulations in the left IFG and in the left anterior cingulate cortex. In contrast, the C‐cluster's activity indicated the right middle frontal gyrus and the right middle temporal gyrus. In sum, different sources related to statistical learning and rule‐based learning effects suggest that sequence learning does not rely on a single mechanism of predicting the upcoming stimuli. Rather, this distinction in neural sources implicates that different levels of predictions are organized in different stages of the processing hierarchy (Southwell & Chait, 2018). Thus, statistical learning and rule‐based learning can be distinguished at the neurophysiological level. Additionally, the difference in neural sources does not only imply the existence of parallel processing mechanisms while learning a sequence. The specific contribution of the right IFG to the statistical learning effect of the S‐cluster N2 also suggests that this region is not specific to inhibitory functions. Rather, stimulus‐driven mismatch detection may characterize the right IFG (Barascud et al., 2016; Erika‐Florence et al., 2014; Southwell & Chait, 2018).

Please note that neural sources associated with statistical and rule‐based learning in the current study are linked to the average‐referenced and decomposed EEG signal of the time windows of N2 and P3. Thus, while the current study highlights the roles of the right IFG in statistical learning and wider prefrontal areas in rule‐based learning, these sources do not rule out the involvement of a wider network, especially in the temporal areas. For instance, statistical regularities presented in an auditory stimuli are associated with activations in the left IFG (including Broca's area), the premotor cortex, and the left superior temporal gyrus (Batterink et al., 2019; Maheu et al., 2020; McNealy et al., 2006). Moreover, the complexity of the sequence and the related computational processes could also influence the source localization results. Learning a sequence can require five different levels: processing of transitions and timing between items, chunking of sequences, ordering the items (independently of timing), understanding algebraic patterns, and finally, nested structures (Dehaene et al., 2015). In the current study, transitions and chunking were essential, and participants were capable of ordering the items as evidenced by the sequence reports. Additionally, the alternation of random and pattern items constituted an algebraic pattern. However, nested, tree‐like structures were not introduced in the sequence; and, therefore, this level of complexity was not needed for successful learning. Nested structures are typical in language and music, and humans have a tendency to discover or even impose to tree structures (Dehaene et al., 2015). In the language domain, learning of nested nonadjacent relations is related to the IFG while simpler, local regularities are linked to the ventral premotor cortex (Amunts et al., 2010; Friederici, 2006; Opitz & Kotz, 2012). This type of dissociation was not shown in the current study, which highlights the need of studying the acquisition of environmental regularities not just in different computational complexities, but also in different modalities (Conway, 2020; Frost et al., 2015).

Notably, the difference between statistical learning and rule‐based learning is not only the type of information that was acquired in the task, but also the level of awareness that was gained during learning. Participants were told to look for a pattern in the stream of black arrows, that is, the learning was intentional, and participants developed explicit knowledge of the sequence as shown by the sequence reports. In contrast, statistical learning about the deeper structure of the task (i.e., triplet probabilities) emerged without instruction or visual cues, that is, learning was incidental. Previous studies with the same paradigm have shown that learning of statistical properties is also implicit (Nemeth, Janacsek, & Fiser, 2013; Szegedi‐Hallgató et al., 2017). However, the focus of the current study was how the learning of parallel information embedded in the same sequences differ and not the awareness involved in their learning. For the latter, another study is warranted that compares incidental (implicit) and intentional (explicit) learning situations with a particular emphasis on the knowledge transition between them (Szegedi‐Hallgató et al., 2017).

Importantly, the comparison between the neurophysiological correlates of statistical learning and rule‐based learning in the current study strengthens and widens the results of Kóbor et al. (2018). The re‐analysis confirmed the notion of parallel learning mechanisms; furthermore, it proved that the results can be generalized at a single‐trial level. Moreover, the similarity between the original undecomposed and the current S‐cluster and C‐cluster N2 results suggests that potential smearing effects of the averaged trials caused by the moving latencies did not contribute to differences between learning effects. Rather, statistical learning and rule‐based learning are separable but simultaneous mechanisms that likely build upon each other (Conway, 2020). The existence of separable mechanisms was further confirmed by the source localization analysis. Given the overlapping time windows (Kóbor et al., 2018), distinct neural sources provide much warranted evidence of intertwined but differently driven learning types in the acquisition of sequential regularities (Southwell & Chait, 2018). Crucially, the re‐analysis shed light on the specificity of statistical learning. The original study proposed that the N2 is sensitive to both statistical and rule‐based learning with the difference between them is how fast they show asymptote (Kóbor et al., 2018). At the same time, the peak of the P3 showed solely a rule‐based learning effect (Kóbor et al., 2018). In contrast, in the temporally decomposed data, statistical learning was specific to mismatch‐related S‐cluster N2 and conflict‐related C‐cluster N2, while rule‐based learning effects were shown across S‐cluster and C‐cluster N2, and all the P3 clusters. Thus, we provided evidence of a specific statistical learning mechanism that operates at the levels of perceptual mismatch and early conflict detection and a more complex rule‐based learning that may be placed higher in the hierarchy of sequence learning (Conway, 2020; Kóbor et al., 2018; Nemeth, Janacsek, & Fiser, 2013). Notably, separating the neurophysiological mechanisms between different learning processes not only enriches our knowledge of human cognition, but also has implications on understanding atypical development. Specifically, the neuroanatomical differences between the two learning mechanisms may deepen our understanding of atypical forms of sequence learning, such as in specific language impairment (Lum, Conti‐Ramsden, Morgan, & Ullman, 2014), developmental dyslexia (Hedenius, Lum, & Bölte, 2020), or Gilles de la Tourette syndrome (Shephard, Groom, & Jackson, 2019; Takács et al., 2018).

4.4. Conclusion

In summary, we successfully identified functionally distinguishable clusters of neurophysiological activity in the N2 and P3 time range in sequence learning. The current analyses deepen our understanding how humans are capable of learning multiple types of information from the same stimulus stream in a parallel fashion. We have demonstrated that concomitant but distinct aspects of information coded in the N2 time window play a role in these mechanisms: mismatch detection and response control underlie statistical learning and rule‐based learning, respectively, albeit with different levels of time‐sensitivity. Moreover, the two learning effects in the different temporally decomposed clusters of neural activity also differed from each other in neural sources. Importantly, the right inferior frontal cortex (BA44) was specifically implicated in statistical learning in a visuomotor sequence, confirming its role in the acquisition of transitional probabilities. In contrast, rule‐based learning was associated with the prefrontal gyrus (BA6). The results show how parallel learning mechanisms operate at the neurophysiological level and are orchestrated by distinct prefrontal cortical areas. Understanding the neural mechanisms behind primary information processing functions, such as statistical and rule‐based sequence learning is crucial to gain a close‐up picture of how simultaneous learning develop both in typical and atypical cognition.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

Takács Á, Kóbor A, Kardos Z, et al. Neurophysiological and functional neuroanatomical coding of statistical and deterministic rule information during sequence learning. Hum Brain Mapp. 2021;42:3182–3201. 10.1002/hbm.25427

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available from the corresponding author upon reasonable request.