Temperature-based MRI safety simulations with a limited number of tissues

Abstract

Purpose:

Demonstrate ability to produce reasonable simulations of temperature using numerical models of the human body with a limited number of tissues.

Methods:

For both a male and female human body model, numerical simulations were used to calculate temperature distributions in three different models of the same human body: the original model with 35 tissues for the male model and 76 tissues for the female model, a simplified model having only three tissues (muscle, fat, and lung), and a simplified model having six tissues (muscle, fat, lung, bone, brain, and skin).

Results:

Although a three-tissue model gave reasonable specific absorption rate estimates in comparison to an original with many more tissues, because of tissue-specific thermal and physiological properties that do not affect specific absorption rate, such as rate of perfusion by blood, the three-tissue model did not provide temperature distributions similar to those of the original model. Inclusion of a few additional tissues, as in the six-tissue model, produced results in much better agreement with those from the original model.

Conclusion:

Reasonable estimates of temperature can be simulated with a limited number of tissues, although this number is higher than the number of tissues required to produce reasonable simulations of specific absorption rate. For exposures primarily in the head and thorax, six tissues may be adequate for reasonable estimates of temperature.

1 |. INTRODUCTION

In MRI systems, RF magnetic (B₁) fields are used to excite atomic nuclei throughout tissues. Concomitant RF electric fields induce currents in conductive tissues, resulting in heating of the tissues, which can be a source of discomfort or even tissue damage during MRI. For this reason, safety guidelines recommend limits on the maximum whole body, head average, partial body, and local power absorbed per mass of tissue (specific absorption rate, or SAR), as well as the maximum core and local temperature reached during an MRI exam. While whole body, head average, and partial body SAR can be estimated based on various measurements,^1–4 such as by measuring the transmitted and the reflected power and dividing by the mass of the subject or exposed portion of the subject,^3,4 local SAR and temperature are usually predicted with the use of prior electromagnetic simulations considering the geometry and electrical property distribution of the system, including the patient and RF coils. Patient morphometry and the position on the patient table of different human subjects result in different field distributions in the patient,^5,6 and consequently different SAR and temperature distributions. It is therefore important to use body models that match the shape of the individual patient as closely as possible, to have accurate estimations of both SAR and temperature.

It was previously shown that specific fast MRI acquisitions and automatic segmentation can be used to provide a simplified segmented model of a specific patient in whom all of the tissues have been assigned to a few different categories, and that simulations of SAR with just these few tissues produced reasonable estimates of SAR simulated with many more tissues.^7–12 In this work we use electromagnetic and temperature simulations to examine the impact on the temperature distributions when a detailed body model and various simplified body models are simulated within a birdcage coil for a 3T MRI system. Although a preliminary report related to this work was presented previously,¹³ here we present a corrected and more thorough comparison that includes additional tissues, to provide better agreement between the simplified model and the full tissue model.

2 |. METHODS

Temperature distributions were computed with a modified numerical implementation of the Pennes’ bioheat equation as follows¹⁴

$$\rho c\frac{\partial T}{\partial t}=\nabla \cdot (k\nabla T)-W{\rho }_{bl}{c}_{bl}\left(T-T_{bl}\right)+Q+\rho SAR,$$

where c denotes the heat capacity; Q denotes the heat rate generated by metabolism; W denotes the blood perfusion rate; k denotes the thermal conductivity; ρ denotes the mass density; and the subscript bl denotes the values for blood.

In our implementation, W and Q are allowed to change with local temperature, to include various local and whole-body physiological responses.^15,16 As in some other temperature computation models, such as the Generic Bioheat Transfer Model,¹⁷ core body temperature T_bl was allowed to change through time. In our model, it was dependent on many factors such as whole-body SAR, perspiration, respiration, heat lost by radiation, conduction, and convection through time.^15,16 In our simulations that included all tissues, temperature of blood (which is only identified in fairly large vessels and in the chambers of the heart) was assigned to that of core body temperature. While there have been some attempts to allow for the temperature of blood to vary with position in the model based on thermal exchange with tissues as it flows through the body, as well as to more realistically represent this thermal exchange at each location in tissue,^17,18 in practice this is not commonly done due to the challenges in defining vasculature throughout the body model.

The electromagnetic fields were generated with a body-sized birdcage coil having 16 rungs of 40-cm length and 60-cm diameter end rings operating at 123 MHz, with fields normalized so that the whole-body SAR is equal to 2 W/kg (maximum level under normal operating mode¹⁹) in each model. The coil was driven with current sources in place of capacitors positioned across gaps in the end rings and with currents corresponding to expectations for ideal mode 1 quadrature resonance of the birdcage coil.

For our simulations we used numerical models based on two different human subjects: a large-sized adult male model²⁰ and an average-sized adult female model.²¹ The models had a resolution of 5 mm in each dimension, to match that of previously published automatic segmentation of rapidly acquired whole-body data sets.⁷ For each body model, simulations were performed with the coil at two locations: one with the coil center near the base of the cervical spine, primarily exposing the tissues of the head and thorax to the RF fields, and another with the coil center near the lumbar spine, primarily exposing the tissues of the abdomen to RF Fields (Figure 1). The electromagnetic fields were computed with the commercial software xFDTD (Remcom, State College, PA). For all cases, fields were applied for 1 hour to models with three different levels of distinction of different tissues (Figure 2):

1. The original body model,^20,21 in which all 35 tissues of the male model and all 76 of the female model are represented.

2. A simplified model in which only three tissues are present⁷: muscle, fat, and lung.

3. A simplified model in which six tissues are present: muscle, fat, lung, skin, brain, and bone.

FIGURE 1.

Geometry of the simulations, with a 16-rung birdcage coil positioned to expose the tissues of the head and thorax (top row) and positioned to expose tissues of the abdomen (bottom row), loaded with a male (left column) and female (right column) human body model

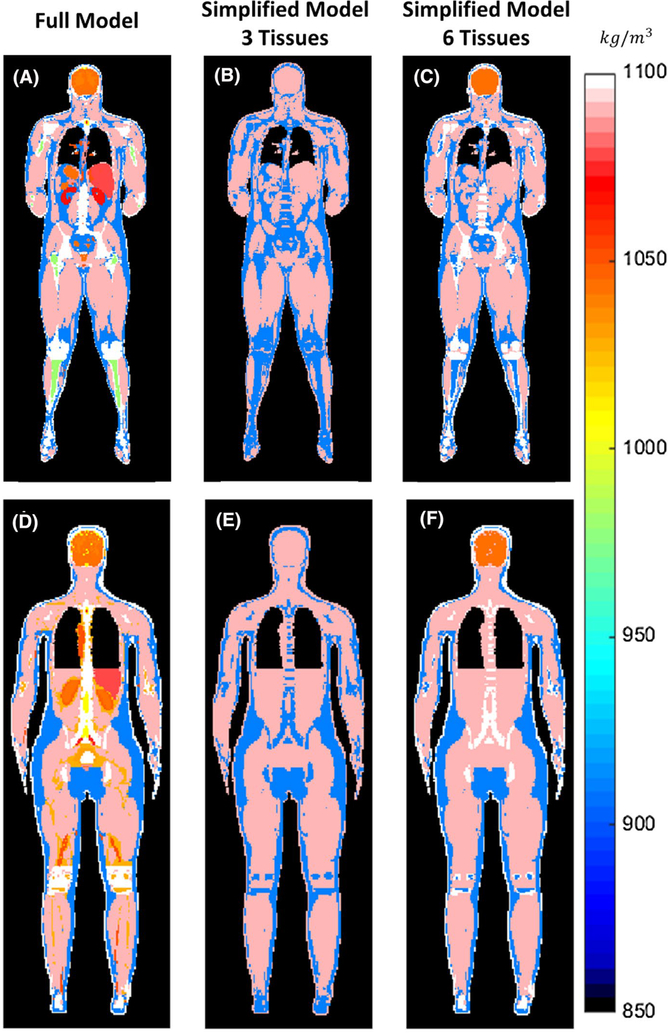
FIGURE 2.

For the two human body models, male (top row) and female (bottom row): distribution of tissue mass density of the original body model with all of the tissues (left column), simplified model with three tissues (center column), and simplified model with six tissues (right column)

Tissues with mass density lower than that of water were assigned properties of fat in the three-tissue simplified model.⁷ Bone was also assigned properties of fat in the three-tissue model,⁷ but is identified separately in the six-tissue model. In the IT’IS tissue properties database,²² red marrow (defined only in the female model) has a density greater than that of water, but an electrical permittivity close to that of fat. In our simplified models, red marrow was assigned the properties of fat. A detailed description of all electrical and thermal properties of the tissues in the models is provided in Supporting Information Tables S1 and S2. In the original body model, because some tissues are assigned identical electric and thermal properties, the number of effective tissue definitions is smaller: 34 tissues for the male model, and 53 for the female model (Supporting Information Tables S1 and S2).

The additional tissues in the third model were selected considering both their effect on the temperature distribution and the anticipated ease with which these tissues could be identified automatically, to allow the rapid segmentation of image data in a few minutes,⁷ and consequently facilitate patient-specific safety assessment. A skin layer was added to the outer surface of the body with an automated approach.^13,20 White matter, gray matter, and cerebellum were together identified as brain tissue and assigned properties equal to the average of the three with the expectation that previously published automated tools could be used to identify the brain accordingly in image data.^23,24 Moreover, fat and bone were distinguished from each other with the expectation that this should be easily done in image data based on their very different signal profiles, and it was observed that some local maxima in temperature better agreed with the full-tissue model with fat and bone treated differently. In all cases, the electric permittivity and conductivity of tissues were set according to the operating frequency of the coil, and thermal properties of the tissues set according to the values reported in the online IT’IS tissue properties database.²²

Temperature simulations were performed with an in-house finite-difference code.¹⁶ Local 10g average SAR values were computed throughout the body models using an averaging method with spherical adaptive masks described previously.^25,26

For all models, the average SAR and temperature values for the whole head were also computed.

3 |. RESULTS

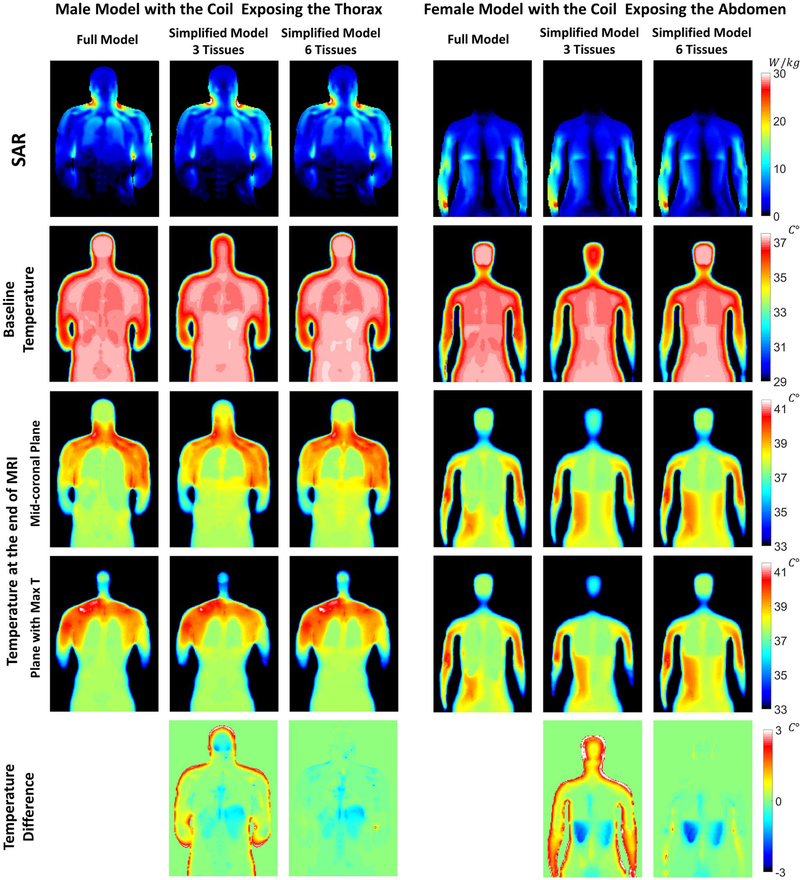
Distributions of 10g average SAR and temperature values both before and immediately after the imaging period are shown in Figure 3 for all simulated models. The most visible differences are in the head for the three-tissue simplified model when compared with the other two models.

FIGURE 3.

Distributions of specific absorption rate (SAR), baseline temperature, and maximum temperature on a midcoronal plane through each of the three body models simulated for the male body model, with the coil positioned to expose the head and thorax (left three columns), and for the female body model, with the coil positioned to expose the abdomen (right three columns). The difference in the maximum temperature between the simplified models and the full-tissue model is reported in the last row

For all of the human body models and coil positions, a comparison of the SAR and temperature values averaged over the whole head for all three models simulated is presented in Table 1.

TABLE 1.

Average of SAR, baseline temperature, final temperature, and temperature increase over the head for the 12 cases simulated

	Full model	Three-tissue simplified model	Six-tissue simplified model
Male body model—coil centered in thorax
Head-average SAR (W/kg)	3.58	3.88	3.68
Head-average baseline temperature (°C)	35.11	33.84	35.09
Head-average final temperature (°C)	36.16	35.29	36.20
Head-average temperature increase (°C)	1.05	1.45	1.10
Male body model—coil centered in abdomen
Head-average SAR (W/kg)	0.14	0.14	0.14
Head-average baseline temperature (°C)	35.11	33.84	35.09
Head-average final temperature (°C)	35.46	34.14	35.44
Head-average temperature increase (°C)	0.35	0.30	0.35
Female body model—coil centered in thorax
Head-average SAR (W/kg)	2.25	2.38	2.19
Head-average baseline temperature (°C)	34.39	33.15	34.45
Head-average final temperature (°C)	35.12	34.05	35.24
Head-average temperature increase (°C)	0.72	0.91	0.80
Female body model—coil centered in abdomen
Head-average SAR (W/kg)	0.08	0.08	0.08
Head-average baseline temperature (°C)	34.39	33.15	34.45
Head-average final temperature (°C)	34.72	33.41	34.77
Head-average temperature increase (°C)	0.32	0.26	0.32

Similarly, Table 2 provides the baseline temperature, temperature increase, and maximum temperature at the location where the maximum temperature occurs, which is consistently in the shoulder for both the male and the female models when the coil center is near the cervical spine, and it is located in the pelvis bone for the male model and in the arm for the female model when the coil center is near the lumbar spine. The specific locations where the maximum temperature occurs vary slightly depending on the model. Temperature distributions, including the plane with the maximum temperature, are shown in Figure 3 for the male model with the coil center near the cervical spine, and for the female model with the coil center near the lumbar spine. In all cases, the most prominent differences in temperature between the full-tissue model and the six-tissue model occur in blood vessels in the extremities (as seen in the forearm on the right of the corresponding plot), where temperature in the full-tissue model is assigned that of core temperature, and is therefore higher than the temperature at the corresponding location in the extremities when the tissue is defined as muscle rather than blood.

TABLE 2.

Baseline temperature, temperature increase, and maximum temperature at the location of maximum temperature for the 12 cases simulated

	Full model	Three-tissue simplified model	Six-tissue simplified model
Male body model—coil centered in thorax
Baseline temperature (°C)	36.76	36.61	36.76
Max final temperature (°C)	42.12	40.98	42.43
Temperature increase (°C)	5.36	4.37	5.68
Male body model—coil centered in abdomen
Baseline temperature (°C)	36.76	36.61	36.76
Max final temperature (°C)	42.12	40.98	42.43
Temperature increase (°C)	5.36	4.37	5.68
Female body model—coil centered in thorax
Baseline temperature (°C)	36.55	35.35	36.54
Max final temperature (°C)	40.75	40.23	40.74
Temperature increase (°C)	4.21	4.88	4.20
Female body model—coil centered in abdomen
Baseline temperature (°C)	35.79	35.00	35.35
Max final temperature (°C)	40.78	40.21	40.80
Temperature increase (°C)	4.99	5.22	5.45

4 |. DISCUSSION

Although temperature distributions in Figure 3 are similar, simplification of the model affects temperature more than it does SAR. Minor variations in SAR can also be observed in the whole-head average values reported in Table 1. However, adding a few additional tissues to the simplified model helps to produce temperature distributions more similar to the full model. While only electrical permittivity, electrical conductivity, and mass density affect SAR distribution, temperature also depends on thermal tissue properties, such as heat capacity and thermal conductivity, and on physiological parameters such as rate of blood perfusion and metabolic heat generation. In particular, blood perfusion has a significant effect on temperature distribution, especially in the brain and other highly perfused tissues.

Although the baseline temperature in the region associated with brain is lower in the three-tissue simplified model, lower average perfusion results in greater temperature increase in this model, such that the final temperature in much of the region of brain is higher than in the other models, and the head average increase in temperature is greater than in the other models. This is also evident from the values reported in Table 1. The addition of the brain in the six-tissue simplified model provides temperature distributions in the head very similar to the original model.

The addition of skin, which has a higher rate of perfusion than muscle, was found to increase baseline and final temperatures in much of the thorax and near the surface of the body, better approximating the values in the original model. This can be observed in the last row of Figure 3, where temperature difference with respect to the full-tissue model is reported. We also found that using two different tissues for fat and bone helps to improve accuracy in temperature calculations, especially regarding the location and amount of peak temperature increase. Although electrical properties of fat and bone are very similar, their thermal properties are different. These differences are very evident in the results of Table 2, where modeling the bone as fat (as in the three-tissue model) provides higher values of perfusion, and therefore smaller temperature estimations with respect to the more accurate full-tissue model.

Remaining differences between the temperature distribution in the original models and their simplified versions occur in other high-perfusion tissues, such as the liver and kidneys, as is particularly evident from the simulations in which the coil is centered in the abdomen. While the six-tissue model produced results for maximum temperature similar to the original model in the configuration with the coil exposing the thorax, for other configurations, including different coils or frequencies, it may be necessary to include additional tissues. Although there are various readily available software solutions to identify the brain,¹⁵ showing clear differences in signal intensity between fat and bone, and simple algorithms for ensuring a continuous layer of skin,²⁰ identification of additional organs for patient-specific models would require further development.

All simulations were performed for a birdcage coil in a 3T system, we expect that the conclusion that a greater number of tissues are required for accurate temperature simulations than for accurate SAR simulations can be extended to other coils and field strengths. However, the strategy for which tissues to include may depend on these variables and may require some coil-specific and frequency-specific investigation.

Simulations of temperature with a relatively low number of tissues have been performed previously,¹⁰ but without reference to results from simulations including many tissues. In some of these simulations, tissues with high perfusion, such as the brain, were excluded.¹⁰ We hope that the results shown here will help guide strategy regarding which tissues are most important to include in thermal simulations, especially when rapid segmentation of imaging data might be used to produce subject-specific models.^7,9