Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Apr 9;21(11):4887–4893. doi: 10.1021/acs.nanolett.0c04946

Quantum Transport of the 2D Surface State in a Nonsymmorphic Semimetal

Xue Liu †,‡,*, Chunlei Yue ‡, Sergey V Erohin §,∥, Yanglin Zhu ‡, Abin Joshy ‡, Jinyu Liu ‡, Ana M Sanchez ⊥, David Graf #, Pavel B Sorokin §,∥, Zhiqiang Mao ○,‡, Jin Hu △,*, Jiang Wei ‡,*
PMCID: PMC8193637  PMID: 33834787

Abstract

graphic file with name nl0c04946_0005.jpg

In a topological semimetal with Dirac or Weyl points, the bulk-boundary correspondence principle predicts a gapless edge mode if the essential symmetry is still preserved at the surface. The detection of such topological surface state has been considered as the fingerprint prove for crystals with nontrivial topological bulk band. On the contrary, it has been proposed that even with symmetry broken at the surface, a new surface band can emerge in nonsymmorphic topological semimetals. The symmetry reduction at the surface lifts the bulk band degeneracies and produces an unusual “floating” surface band with trivial topology. Here, we first report quantum transport probing to ZrSiSe thin flakes and directly reveal transport signatures of this new surface state. Remarkably, though topologically trivial, such a surface band exhibits substantial two-dimensional Shubnikov–de Haas quantum oscillations with high mobility, which signifies a new protection mechanism and may open applications for quantum computing and spintronic devices.

Keywords: 2D topological nodal line semimetal, nonsymmorphic symmetry, surface transport, SdH quantum oscillation

The surface electronic state has been a central focus of condensed matter physics. Distinct electrical properties from a well-protected surface (or edge) state, such as quantum Hall or quantum spin Hall effects, provide ample opportunities for the surface state-based device applications.1−5 The conventional surface states, resulting from the termination of the three-dimensional (3D) bulk periodic potential, are susceptible to defects or impurities, which appear nearly inevitably in crystals. Recently, there have been significant breakthroughs in the search for robust surface states along with the search for new topological quantum materials. Topological surface states found in bulk topological insulators6−11 eliminates backscattering due to the spin-momentum locking, which is originated from the chiral linear energy dispersion as protected by the time-reversal or lattice symmetries. In Weyl semimetals and Dirac semimetals,1,2 unusual surface states appear as disconnected or jointed Fermi arcs curving in opposite directions, respectively. Experimentally, there has been extensive characterization on the transport properties of surface states in topological insulators.7 For 3D topological semimetals, Weyl orbit on the surface of bulk Dirac semimetal Cd3As2 has recently been observed showing quantum oscillations12,13 and quantum Hall effect14,15 in the nanostructured device owing to the enhanced transport signal ratio of surface to bulk. In contrast to the above topologically protected surface states, a new 2D floating surface state can emerge in ZrSiM (M = S, Se, or Te) nonsymmorphic topological semimetals.4 Such a new surface state originates from the symmetry reduction at the surface, thus distinct from the well-known “conventional” topological surface state arising from the bulk-boundary correspondence principle in topological materials.

ZrSiM belongs to the recently discovered WHM-type (W = Zr, Hf, or rare-earth; H = Si, Ge, Sn)16−25 topological semimetal family. These materials crystallize in layered tetragonal structure (Figure 1a) and possess two types of Dirac states: the nodal-line Dirac state protected by the C2v symmetry and gapped by spin–orbit coupling16,17 and the 2D gapless nodal-point Dirac state protected by the nonsymmorphic symmetry.16,26−28 The different combinations of W, H, and M elements further give rise to high tunability in spin–orbit coupling,29−31 magnetism,22,23 and structural dimensionality,17,21,30 leading to rich electronic properties of various WHMs such as large magnetoresistance,32,33 high Dirac Fermion density,20,21 strong spin splitting,20 and magnetic field-mediated tunable Dirac and Weyl states.23 These properties, together with the feasibility in obtaining the atomically thin crystals, make this material family a versatile platform for investigating exotic phenomena of relativistic Fermions in nanostructures. In this work, taking advantage of the suppressed bulk contributions in the exfoliated ZrSiSe flakes, we have successfully probed transport of the surface floating band. Unlike the topological nontrivial surface states in many other topological nodal point semimetals, such a floating surface band is topologically trivial4 but surprisingly exhibits quantum oscillations with high mobility, which is not generally expected. The robustness of the surface state, as demonstrated both from our transport measurements and density functional theory (DFT) calculations, pave a way for surface-related device applications in quantum computing and spintronics.

Figure 1.

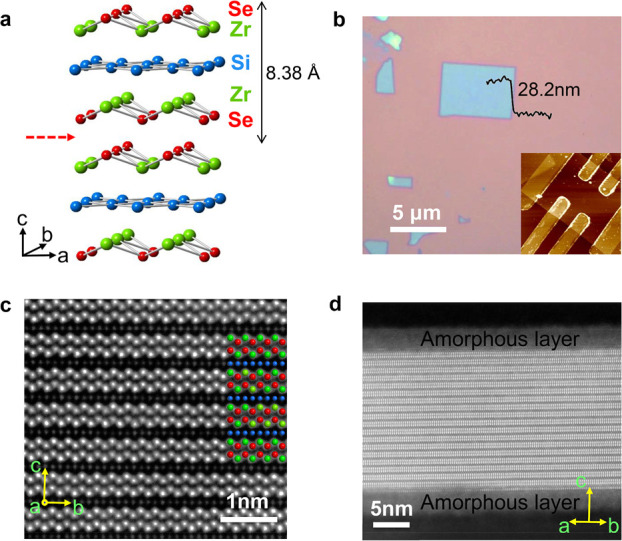
Figure 1

Open in a new tab

ZrSiSe crystal structure and microscopy characterizations. (a) Crystal structure of ZrSiSe, showing the Se–Zr–Si–Zr-Se slabs and the cleavage plane (red arrow). (b) Optical microscope image of a 28.2 nm ZrSiSe nanoflake on Si/SiO2 wafer obtained through micromechanical exfoliation. Inset, atomic force microscope image of a Hall bar device. (c, d) Atomic resolution annular dark-field (ADF) aberration-corrected scanning transmission electron microscopy (STEM) images of (c) the bulk along the [100] zone and (d) exfoliated ZrSiSe flakes along the [110] zone. Inset in c, the [100] zone (cross-section) image matches well with the crystal structure.

Figure 1a shows the crystal structure of ZrSiSe, which can be viewed as the stacking of Se–Zr–Si–Zr–Se slabs. The weak interslab binding strength allows for the mechanical exfoliation of ZrSiSe to atomically thin layers,21 as demonstrated in Figure 1b. The atomic resolution scanning transmission electron microscope (STEM) images of the as-exfoliated flakes reveal good crystallinity for the inner parts (Figure 1c) with shallow amorphous oxidation layers (∼5 nm) on the top and bottom surface (Figure 1d and Figure S1). The stacking of Zr, Si, and Se atoms precisely matches the expected lattice structure of ZrSiSe (Figure 1c, inset).

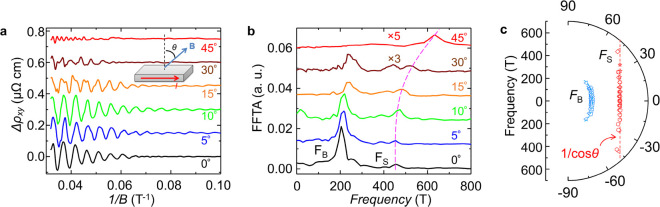
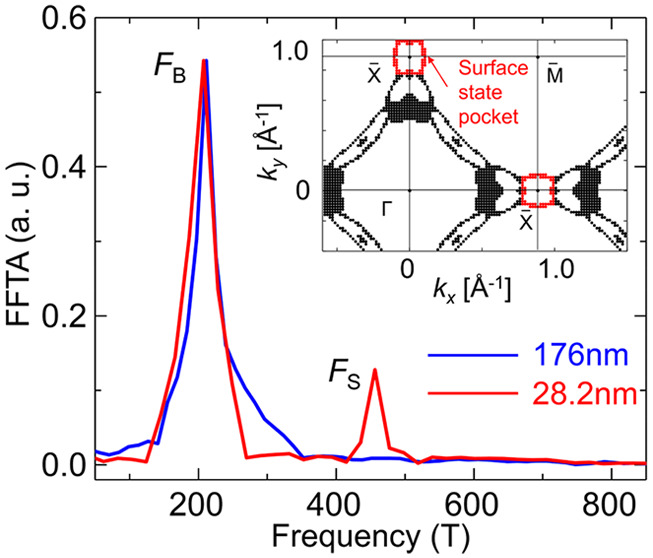
ZrSiSe devices (Figure 1b, inset) are fabricated through the standard electron beam lithography. With the magnetic field applied perpendicular to the sample surface (i.e., along the c-axis), we observed clear Shubnikov-de Haas (SdH) oscillations in magnetoresistance (MR) for all ZrSiSe thin flakes with various thickness at low temperatures (see Figure S3). Surprisingly, the oscillatory components of the longitudinal resistivity Δρxx, obtained by subtracting background, exhibit different signatures between very thick and thin flakes. In Figure 2a, we present the Δρxx for typical thick (176 nm) and thin (28.2 nm) samples. For the thicker sample (176 nm), the oscillation pattern contains only a single frequency of FB = 210 T as revealed by the fast Fourier transform (FFT) analysis (Figure 2a, inset), which is consistent with the observation in the single crystal bulks.21 In contrast, the oscillation pattern of the thinner sample (28.2 nm) deviates from the “bulk-like” behavior (Figure 2a) with an additional frequency occurring around FS = 445 T (Figure 2a, inset). Although FS appears to be close to 2 × FB, it should not be regarded as a harmonic frequency of FB because of their distinct angular dependencies, as will be shown later. Such a surprising, additional frequency component is reproducible for all thin flakes below 60 nm (see Figures S4 and S5). It is worth noting that multiple frequencies in quantum oscillations in bulk WHM crystals have been discovered,20,21,30,32−34 but our observation of the emergence of a new frequency upon reducing thickness is unique.

Figure 2.

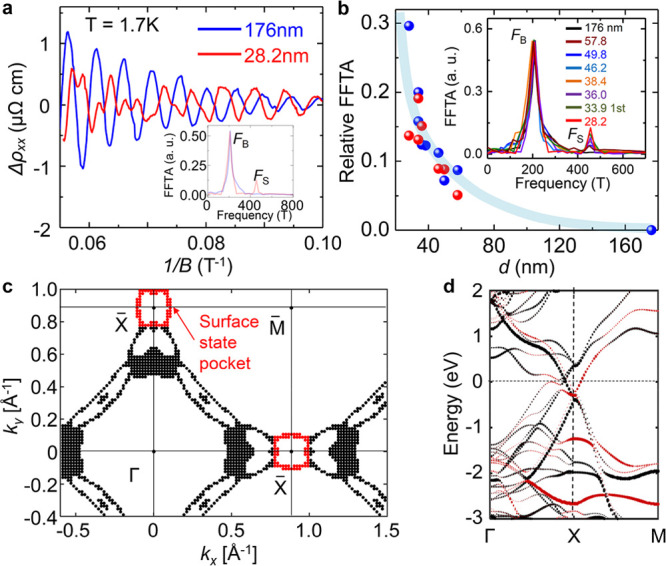
Figure 2

Open in a new tab

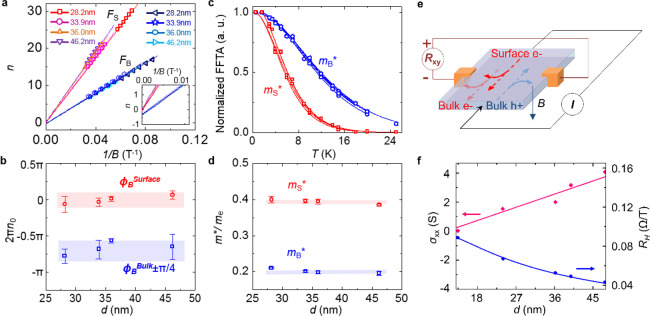
Thickness-dependent SdH oscillations. (a) Oscillatory components Δρxx of thick (176 nm) and thin (28.2 nm) ZrSiSe samples with magnetic field normal to the sample surface. Inset, the fast Fourier transform of the corresponding oscillation patterns. The FFT for the 28.2 nm sample is normalized to the 176 nm sample according to the FB for clarity. The additional frequency of FS = 445 T appears for the thin sample. (b) Thickness dependence of the relative FFT amplitude (FFTA) between FS and FB bands. The blue and red solid dots are based on the longitudinal and transverse resisitivity analysis, respectively. Inset, corresponding FFT spectra for different thicknesses, normalized to the 176 nm sample according to the FB peak and only the first 33.9 nm sample is included for clarity, other FFT analysis can be found in the Supporting Information. (c) Calculated Fermi surface cross-section at kz = 0 of a three-layer ZrSiSe. The surface Fermi pocket is labeled in red. (d) Calculated energy band dispersion of a three-layer slab ZrSiSe near X. The red color denotes the contribution from the surface state.

In principle, a quantum oscillation pattern with a specific frequency corresponds to an extremal Fermi surface cross-section. Therefore, the additional frequency in thin samples indicates that an additional electronic band starts to play a substantial role in transport only in the samples with reduced thickness. The modification of band structure due to 2D quantum confinement is widely observed in 2D materials by reaching the monolayer limit. However, it is unlikely that quantum confinement takes effect at a thickness of ∼60 nm, where the FS component already becomes visible (Figure 2b). Instead, this unusual frequency is most likely a manifestation of a new surface state owing to a few characteristics. First of all, the signal weight of the FS band in the transport measurement grows with the decreasing sample thickness. As shown in Figure 2b, the relative ratio between the FFT peak amplitudes of FS and FB increases significantly when the flake thickness is reduced, indicating the increased weight of the FS component in thinner samples. This result agrees well with the surface origin of the FS band and is a natural consequence of the enhanced surface-to-bulk ratio with reducing the thickness, which has also been observed in Cd3As2.13

In addition, the 2D character of the FS band is in line with a surface state. As shown in Figure 3a, for a typical sample with a moderate thickness of about 36 nm, the SdH oscillation weakens when the magnetic field is rotated away from the perpendicular direction (θ = 0°), which is consistent with observations in bulk ZrSiSe21 and other WHM compounds.30,33,35 However, as shown in Figure 3b, the angular dependences of FB and FS obtained from FFT are entirely different: FS varies significantly with θ, which is distinct from the very weak angular-dependence of FB, and indicates it is not a second-order harmonic of FB. Such angular dependences for FB and FS are highly reproducible with various sample thicknesses (Figure S5). To better illustrate the angular dependences of both frequencies in various samples, we have summarized the data in the polar plot shown in Figure 3c. FB (blue) appears to be nearly θ-independent up to θ = 45°, consistent with the previous studies on bulk samples.21 In contrast, FS at various θ obtained from different samples are well-aligned to a vertical line (red dashed lines) in the polar plot, i.e., showing a 1/cos θ dependence. Such a 1/cos θ dependence implies 2D nature for the FS band, expected for surface state.13

Figure 3.

Figure 3

Open in a new tab

Angular-dependent SdH oscillations. (a) Angular-dependent oscillatory components Δρxy of the 36 nm ZrSiSe device at T = 0.6 K. Inset, the measurement setup. (b) Fast Fourier transform of the SdH oscillation pattern shown in panel a, with a field range 1/B from 0.0318 to 0.1 T–1. Note: the 30 and 45° spectra have been multiplied by 3 and 5 times, respectively. (c) Polar plot of the angular-dependence of bulk frequency FB (blue) and surface frequency FS (red) from all measured devices (see Figures S4 and S5 for oscillation patterns and their FFTs). The dashed straight line (red) indicates the 1/cos θ dependence for FS.

Furthermore, the agreement of the oscillation frequency with our DFT calculations and previous ARPES observations36,37 provides further support for the surface origin of FS. According to the Onsager relation (F = ℏA/2πe), the observed FS frequency at θ = 0° corresponds to a Fermi surface cross-section area A of 4.25 nm–2, which matches well with the area of the ellipse-like surface-derived electron pocket around the Brillouin zone X point estimated in our DFT calculations (∼4.32 nm–2, Figure 2c), as well as that probed in ARPES experiment (∼4.58 nm–2, estimated from ref (36).). Given no other Fermi pocket with comparable size can be found either in our DFT calculations or ARPES reports,36,37 the FS frequency most likely reflects such an electron pocket of a surface-related state inferred in WHM compounds.4

Now, we discuss the mechanism of forming such a surface band. Generally, a surface state is expected to be formed as a result of the termination of the bulk potential or surface defects/adsorbates in conventional materials. This possibility can be easily excluded because quantum oscillations, which rely on the formation of complete cyclotron orbits and high mobility (i.e., sharp Landau levels), are generally not expected for “dirty” materials. Given defects or adsorbates are strong scattering centers, quantum oscillation from a surface state is often easily destroyed in conventional materials. However, in ZrSiSe, FS and its angular dependence in thin flakes are prominent and highly reproducible, even with significant amorphous surface layers observed by STEM (Figure 1d). Such observations are clearly inconsistent with extrinsic origins such as surface degradation, unintentional doping, and strain effect.

In addition, in a typical nodal-point topological semimetal with isolated bulk Dirac or Weyl points, the bulk-boundary correspondence principle results in a gapless mode at the edge when the symmetry group protecting the topology of bulk bands is unbroken on the edge.3 However, this possibility can also be excluded. ZrSiSe and related WHM compounds exhibit the coexistence of nodal-line and nodal-point Dirac states protected by different symmetries,16,17,26 but neither of them should lead to a topological surface state. In WHM compounds, topological surface states originated from band inversion-induced Weyl-like states38 and other gapless Dirac state39 have been reported. However, a topological surface state arising from the gapped nodal-line band has not been revealed in either first-principles calculations17 or ARPES experiments.16,18,36 Similarly, a topological surface state relevant to the nodal-point Dirac state arising from the bulk-boundary correspondence principle is not expected, as the corresponding nonsymmorphic symmetry is not preserved at the (001) plane of the crystal.3

After ruling out the possibility of surface chemistry and bulk-boundary correspondence, we argue that this robust FS surface band revealed in our quantum oscillation experiments represents the recently proposed novel floating surface states derived from the surface symmetry reduction in nonsymmorphic semimetals.4 Topp et al. showed that the ZrSiS bulk symmetry with nonsymmorphic space group P4/nmm is reduced to the symmorphic wallpaper group P4mm at the natural cleavage (001) surface. Such nonsymmorphic symmetry reduction significantly deforms the orbital, which lifts the degeneracy of the bulk bands at Brillouin zone X point and consequently causes an unpinned surface band floating on top of the bulk band.4 Such a proposed floating surface state is quantitatively consistent with the ARPES observations of the Fermi pocket with the 2D character at X.4,16 The isostructural compound ZrSiSe studied in this work also exhibits electron pocket at X point with similar surface states, as revealed by our DFT calculations (see Figure 2c, d and Supplementary Note 1).

The properties of the FS band provide further support for this argument. The surface floating band is formed by lifting the degeneracy of the bulk band and is thus topological trivial,4 which can be revealed by the Berry phase analysis. We have separated the FB and FS oscillation components and extracted the Berry phase for both bands using the Landau fan diagram (see Methods). As shown in Figure 4a, for ZrSiSe flakes with a range of thickness, the linear fits of the Landau indices n yield intercepts n0 around 0 and −0.5 for FS and FB bands, respectively. Berry phase ϕB can be derived via 2π(n0+δ), where δ = ± 1/8 for the 3D band (e.g., the bulk FB band) and 0 for the 2D band (e.g., the surface FS band). As summarized in Figure 4b, the Berry phase is trivial (ϕBsurface ≈ 0) for the surface FS band in each sample, in sharp contrast with that of the bulk FB band which exhibits an average Berry phase of ϕBBulk ≈ −0.68π ± 1/4 π. This result is further verified through directly fitting the oscillation pattern using the multiband Lifshitz-Kosevich model (see the Supporting Information), which confirms the distinct topology of the bulk and the surface floating bands in ZrSiSe.

Figure 4.

Figure 4

Open in a new tab

Property comparison between the bulk and surface bands. (a) Landau Level (LL) fan diagram for the bulk FB and surface FS states of four ZrSiSe nanodevices with thicknesses of 28.2, 33.9, 36, and 46.2 nm. The solid lines represent linear fits of the Landau indices, which intercept around 0 for the surface band and −0.34 for the bulk band. Inset, zoom-in view showing different intercepts for surface and bulks. (b) Berry phases derived from the LL fan diagram shown in (a) for samples with different thicknesses. (c) Temperature dependence of the FFT amplitude for bulk and surface bands for the same four samples in panel a. The solid lines indicate the fits to the thermal damping term of the LK-model. (d) Effective masses for bulk and surface states derived from the fitting shown in panel c. (e) Schematic drawing of the multichannel contributions to the Hall effect. Here, bulk e-, bulk h+, and surface e- denote contributions from bulk electron, bulk hole, and surface electron, respectively. (f) Thickness-dependent longitudinal conductivity and Hall coefficient. The solid lines show the fits to the three-channel model (see the Supporting Information).

Furthermore, the effective cyclotron mass of the FS band also agrees with the scenario of the surface floating band. The formation of the floating band at the surface of our material can be modeled by breaking the nonsymmorphic glide plane symmetry and introducing a large mass for S and Zr orbitals,4 so such surface state is expected to be more massive, which is indeed observed in ZrSiSe. We have extracted effective masses for both bulk FB and surface FS bands from the temperature dependence of FFT amplitude for ZrSiSe samples with various thicknesses (see Methods) (Figure 4c). As summarized in Figure 4d, the effective cyclotron mass for the surface floating band mS* is around 0.39m0 (m0 denotes free electron mass) for all analyzed samples, which is around twice as large as that of the bulk band (mB* ∼ 0.19m0).

The above discussions have established that the additional FS component observed in the quantum oscillation of ZrSiSe nanoflakes originates from the surface floating band. The observation of quantum oscillations caused by such topological trivial surface state is unusual because the lack of a protection mechanism is generally expected to lead to a vulnerable surface state with low mobility that is not favorable to quantum oscillations. Despite of the apparent surface degradations (Figure 1d and Figure S1), the LK-fitting (see the Supporting Information) has revealed high quantum mobility of 1.20 × 103 cm2 V–1 s–1 at 1.7 K for the topologically trivial surface FS band, which is comparable with the topologically protected bulk band (1.74 × 103 cm2 V–1 s–1). The high quantum mobility for the surface band is consistent with the transport mobility of 1.84 × 103 cm2 V–1 s–1 estimated from the multichannel model of Hall effect (Figure 4e, f) (see the Supporting Information). This result implies minimized surface scattering of charge carriers caused by surface deformation or disorders. Indeed, it is consistent with our STEM observations in Figure 1d, which shows an atomically sharp interface between the oxidized amorphous layer and the inner crystalline layer. The formation of such amorphous layer also explains why the ARPES observations varies strongly with the sample preparation methods. Because ARPES is an extremely surface sensitive technique, so that any oxidation or degradation of the topmost layer may significantly affect the spectra, as has been observed in ref.40 However, the surface floating band originates from the symmetry breaking at the surface so that it can exists even in the presence of surface oxidization. As discussed in Supplementary Note 2, the surface band is still preserved even by replacing all the Se atoms in the topmost surface with [OH] or [O4]. Therefore, in our samples, such surface state can occur at the interface between the inner crystalline layer and the outer amorphous layer where the bulk symmetry is broken, and manifest in quantum oscillations in thin flakes. The robustness of the surface band itself is unexpected and may benefit from a sort of protection mechanism that deserves further investigations. One possible interpretation could be the connection with the bulk topological band: given the surface floating band for nonsymmorphic ZrSiSe is caused by lifting degeneracy of the bulk band at the surface, it could be robust when the corresponding bulk band is topologically protected. In ZrSiSe, the surface floating band is related to the bulk Dirac band protected by the nonsymmorphic symmetry. Therefore, an “indirectly” protected surface bands with trivial topology could appear in ZrSiSe, which represents a novel protection mechanism in crystalline solid with similar nonsymmorphic symmetry.

In summary, we have systematically studied quantum oscillations of exfoliated ZrSiSe nanoflakes and successfully detected a new 2D, trivial surface state, which can be attributed to the surface floating state caused by symmetry reduction at the surface. Our results also suggest such a surface is trivial but robust and likely protected via a new mechanism. Our findings provide a new arena for the study of exotic surface states in topological quantum materials, which is an important step toward practical application in modern electronics and surface-related devices such as quantum computing and spintronics.

Methods

Sample Preparation

The ZrSiSe single crystal was synthesized by using a chemical vapor transport (CVT) method. The stoichiometric mixture of Zr, Si, and Se powder was sealed in a quartz tube with iodine being used as a transport agent (2 mg/cm3). Platelike single crystals with metallic luster can be obtained via the vapor transport growth with a temperature gradient from 950 to 850 °C. The composition and phase of the single crystals were examined by energy-dispersive X-ray spectroscopy and X-ray diffraction, respectively. The thin flakes of ZrSiSe were obtained through a micromechanical exfoliation. The thickness of thin flakes was precisely determined by an atomic force microscope. The ZrSiSe devices with the standard four-terminal resistivity or six-terminal Hall bar geometry were fabricated by using the standard electron beam lithography, followed by the deposition of 5 nm Ti/50 nm Au as contacts via electron beam evaporation. Ohmic contacts of devices were achieved by current annealing before the transport measurement (see the Supporting Information).

Scanning Transmission Electron Microscopy

Atomic-resolution annular dark field STEM images of the flakes were recorded with a JEOL ARM200F over collection angles 45–180 mrad. High signal-to-noise images were formed by averaging multiple, rapidly acquired frames to remove scan distortions.

Magnetotransport Measurements

Before the high field experiments, the ZrSiSe devices were tested by an in house 9T-PPMS. The high field magnetotransport measurements were performed at National High Magnetic Field Laboratory (NHMFL) in Tallahassee by using an 18T superconducting magnet and a 31T resistive magnet. The AC current used for all devices was between 20 and 50 μA supplied by Keithley 6221 AC and DC Current Source. The longitudinal/transverse voltages were measured using lock-in amplifiers with the frequencies triggered by the AC currents. The noise ratio was reduced by twisted pairs between two voltage cables and two current cables, respectively.

Landau Level Fan Diagrams

To examine the Berry phase ϕB accumulated along cyclotron orbits for bulk and surface bands, we performed Landau Level (LL) fan diagram analysis using the longitudinal conductivity σxx, which was derived via σxx= ρxx/(ρxx2+ρxy) where ρxx and ρxy are longitudinal and transverse resistivity, respectively, as shown in Supplementary Figure S6. Quantum oscillations arising from bulk and surface bands are separated by FFT filters to build the LL fan diagram for each band. We assigned the integer LL index to the oscillation maximum of σxx according to the previous quantum oscillation study on this family of materials,20 and extracted Berry phase for each band from the intercept of the linear fit of the LL fan diagram. Detailed analysis is provided in the Supporting Information. Although there are debates on the assignment of the integer LL indices, we intend to emphasize an observed Berry phase difference between bulk and surface band, which does not depend on the way of assigning integer LL indices and implies distinct topology of the bulk and the surface floating bands in ZrSiSe.

Effective Mass

The effective masses of bulk and surface bands for various samples were obtained from the temperature dependence of the quantum oscillations (1.7 to 20 K), as shown in Figure S10, by fitting the FFT peak intensity to the thermal damping term of the LK-formula.41

Acknowledgments

The work at Tulane is supported by the U.S. Department of Energy under grant DE-SC0014208. The work at the University of Arkansas (quantum oscillation, topological physics, and surface state analyses) is supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, under Award DE-SC0019467. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement DMR-1157490, DMR-1644779, and the State of Florida. S.V.E. and P.B.S. acknowledge the financial support of the Ministry of Education and Science of the Russian Federation in the framework of Increase Competitiveness Program of NUST “MISiS” (K2-2020-023). The calculations were performed at the supercomputer cluster provided by the Materials Modeling and Development Laboratory at NUST “MISiS” and Joint Supercomputer Center of the Russian Academy of Sciences.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.0c04946.

  • Materials include cross-sectional STEM and corresponded element mapping analysis, current annealing process, details of all measured samples and corresponding data analysis, in-plane conductivity and hall conductivity analysis, Berry phase analysis, transport mobility analysis, temperature-dependent FFT spectra, DFT calculations of the ZrSiSe band structure and surface state, and robustness discussions of the ZrSiSe surface state (PDF)

The authors declare no competing financial interest.

Supplementary Material

nl0c04946_si_001.pdf (1.4MB, pdf)

References

  1. Yan B.; Felser C. Topological Materials: Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337–354. 10.1146/annurev-conmatphys-031016-025458. [DOI] [Google Scholar]
  2. Armitage N. P.; Mele E. J.; Vishwanath A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 2018, 90, 015001. 10.1103/RevModPhys.90.015001. [DOI] [Google Scholar]
  3. Fang C.; Weng H.; Dai X.; Fang Z. Topological nodal line semimetals. Chin. Phys. B 2016, 25, 117106. 10.1088/1674-1056/25/11/117106. [DOI] [Google Scholar]
  4. Topp A.; Queiroz R.; Grüneis A.; Müchler L.; Rost A. W.; Varykhalov A.; Marchenko D.; Krivenkov M.; Rodolakis F.; McChesney J. L.; Lotsch B. V.; Schoop L. M.; Ast C. R. Surface Floating 2D Bands in Layered Nonsymmorphic Semimetals: ZrSiS and Related Compounds. Phys. Rev. X 2017, 7, 041073. 10.1103/PhysRevX.7.041073. [DOI] [Google Scholar]
  5. Kou X.; Fan Y.; Wang K. L. Review of Quantum Hall Trio. J. Phys. Chem. Solids 2017, 128, 2. 10.1016/j.jpcs.2017.10.016. [DOI] [Google Scholar]
  6. Hasan M. Z.; Kane C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. 10.1103/RevModPhys.82.3045. [DOI] [Google Scholar]
  7. Qi X.-L.; Zhang S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. 10.1103/RevModPhys.83.1057. [DOI] [Google Scholar]
  8. Xu S. Y.; Liu C.; Kushwaha S. K.; Sankar R.; Krizan J. W.; Belopolski I.; Neupane M.; Bian G.; Alidoust N.; Chang T. R.; Jeng H. T.; Huang C. Y.; Tsai W. F.; Lin H.; Shibayev P. P.; Chou F. C.; Cava R. J.; Hasan M. Z. Observation of Fermi arc surface states in a topological metal. Science 2015, 347, 294–298. 10.1126/science.1256742. [DOI] [PubMed] [Google Scholar]
  9. Lv B. Q.; Weng H. M.; Fu B. B.; Wang X. P.; Miao H.; Ma J.; Richard P.; Huang X. C.; Zhao L. X.; Chen G. F.; Fang Z.; Dai X.; Qian T.; Ding H. Experimental Discovery of Weyl Semimetal TaAs. Phys. Rev. X 2015, 5, 031013. 10.1103/PhysRevX.5.031013. [DOI] [Google Scholar]
  10. Lv B. Q.; Xu N.; Weng H. M.; Ma J. Z.; Richard P.; Huang X. C.; Zhao L. X.; Chen G. F.; Matt C. E.; Bisti F.; Strocov V. N.; Mesot J.; Fang Z.; Dai X.; Qian T.; Shi M.; Ding H. Observation of Weyl nodes in TaAs. Nat. Phys. 2015, 11, 724–727. 10.1038/nphys3426. [DOI] [Google Scholar]
  11. Xu S.; Belopolski I.; Alidoust N.; Neupane M.; Bian G.; Zhang C.; Sankar R.; Chang G.; Yuan Z.; Lee C.; et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 2015, 7, 613–617. 10.1126/science.aaa9297. [DOI] [PubMed] [Google Scholar]
  12. Potter A. C.; Kimchi I.; Vishwanath A. Quantum oscillations from surface Fermi arcs in Weyl and Dirac semimetals. Nat. Commun. 2014, 5, 5161. 10.1038/ncomms6161. [DOI] [PubMed] [Google Scholar]
  13. Moll P. J. W.; Nair N. L.; Helm T.; Potter A. C.; Kimchi I.; Vishwanath A.; Analytis J. G. Transport evidence for Fermi-arc-mediated chirality transfer in the Dirac semimetal Cd3As2. Nature 2016, 535, 266–270. 10.1038/nature18276. [DOI] [PubMed] [Google Scholar]
  14. Zhang C.; Zhang Y.; Yuan X.; Lu S.; Zhang J.; Narayan A.; Liu Y.; Zhang H.; Ni Z.; Liu R.; Choi E. S.; Suslov A.; Sanvito S.; Pi L.; Lu H.-Z.; Potter A. C.; Xiu F. Quantum Hall effect based on Weyl orbits in Cd3As2. Nature 2019, 565, 331–336. 10.1038/s41586-018-0798-3. [DOI] [PubMed] [Google Scholar]
  15. Wang C. M.; Sun H. P.; Lu H.; Xie X. C. 3D Quantum Hall Effect of Fermi Arcs in Topological Semimetals. Phys. Rev. Lett. 2017, 119, 136806. 10.1103/PhysRevLett.119.136806. [DOI] [PubMed] [Google Scholar]
  16. Schoop L. M.; Ali M. N.; Straßer C.; Topp A.; Varykhalov A.; Marchenko D.; Duppel V.; Parkin S. S. P.; Lotsch B. V.; Ast C. R. Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in ZrSiS. Nat. Commun. 2016, 7, 11696. 10.1038/ncomms11696. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Xu Q.; Song Z.; Nie S.; Weng H.; Fang Z.; Dai X. Two-dimensional oxide topological insulator with iron-pnictide superconductor LiFeAs structure. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 205310. 10.1103/PhysRevB.92.205310. [DOI] [Google Scholar]
  18. Neupane M.; Belopolski I.; Hosen M. M.; Sanchez D. S.; Sankar R.; Szlawska M.; Xu S.-Y.; Dimitri K.; Dhakal N.; Maldonado P.; Oppeneer P. M.; Kaczorowski D.; Chou F.; Hasan M. Z.; Durakiewicz T. Observation of Topological Nodal Fermion Semimetal Phase in ZrSiS. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 201104. 10.1103/PhysRevB.93.201104. [DOI] [Google Scholar]
  19. Takane D.; Wang Z.; Souma S.; Nakayama K.; Trang C. X.; Sato T.; Takahashi T.; Ando Y. Dirac-node arc in the topological line-node semimetal HfSiS. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 121108. 10.1103/PhysRevB.94.121108. [DOI] [Google Scholar]
  20. Hu J.; Tang Z.; Liu J.; Zhu Y.; Wei J.; Mao Z. Nearly massless Dirac fermions and strong Zeeman splitting in the nodal-line semimetal ZrSiS probed by de Haas-van Alphen quantum oscillations. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96, 045127. 10.1103/PhysRevB.96.045127. [DOI] [Google Scholar]
  21. Hu J.; Tang Z.; Liu J.; Liu X.; Zhu Y.; Graf D.; Myhro K.; Tran S.; Lau C. N.; Wei J.; Mao Z. Evidence of Topological Nodal-Line Fermions in ZrSiSe and ZrSiTe. Phys. Rev. Lett. 2016, 117, 016602. 10.1103/PhysRevLett.117.016602. [DOI] [PubMed] [Google Scholar]
  22. Hosen M. M.; Dhakal G.; Dimitri K.; Maldonado P.; Aperis A.; Kabir F.; Sims C.; Riseborough P.; Oppeneer P. M.; Kaczorowski D.; Durakiewicz T.; Neupane M. Discovery of topological nodal-line fermionic phase in a magnetic material GdSbTe. Sci. Rep. 2018, 8, 13283. 10.1038/s41598-018-31296-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Schoop L. M.; Topp A.; Lippmann J.; Orlandi F.; Müchler L.; Vergniory M. G.; Sun Y.; Rost A. W.; Duppel V.; Krivenkov M.; Sheoran S.; Manuel P.; Varykhalov A.; Yan B.; Kremer R. K.; Ast C. R.; Lotsch B. V. Tunable Weyl and Dirac states in the nonsymmorphic compound CeSbTe. Sci. Adv. 2018, 4, eaar2317 10.1126/sciadv.aar2317. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Hosen M. M.; Dimitri K.; Aperis A.; Maldonado P.; Belopolski I.; Dhakal G.; Kabir F.; Sims C.; Hasan M. Z.; Kaczorowski D.; Durakiewicz T.; Oppeneer P. M.; Neupane M. Observation of gapless Dirac surface states in ZrGeTe. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 97, 121103. 10.1103/PhysRevB.97.121103. [DOI] [Google Scholar]
  25. Lodge M. S.; Chang G. Q.; Huang C. Y.; Singh B.; Hellerstedt J.; Edmonds M. T.; Kaczorowski D.; Hosen M. M.; Neupane M.; Lin H.; Fuhrer M. S.; Weber B.; Ishigami M. Observation of effective pseudospin scattering in ZrSiS. Nano Lett. 2017, 17, 7213–7217. 10.1021/acs.nanolett.7b02307. [DOI] [PubMed] [Google Scholar]
  26. Topp A.; Lippmann J. M.; Varykhalov A.; Duppel V.; Lotsch B. V.; Ast C. R.; Schoop L. M. Non-symmorphic band degeneracy at the Fermi level in ZrSiTe. New J. Phys. 2016, 18, 125014. 10.1088/1367-2630/aa4f65. [DOI] [Google Scholar]
  27. Zhu Z.; Chang T. R.; Huang C. Y.; Pan H. Y.; Nie X. A.; Wang X. Z.; Jin Z. T.; Xu S. Y.; Huang S. M.; Guan D. D.; Wang S. Y.; Li Y. Y.; Liu C. H.; Qian D.; Ku W.; Song F. Q.; Lin H.; Zheng H.; Jia J. F. Quasiparticle interference and nonsymmorphic effect on a floating band surface state of ZrSiSe. Nat. Commun. 2018, 9, 4153. 10.1038/s41467-018-06661-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Su C. C.; Li C. S.; Wang T. C.; Guan S. Y.; Sankar R.; Chou F. C.; Chang C. S.; Lee W. L.; Guo G. Y.; Chuang T. M. Surface termination dependent quasiparticle scattering interference and magneto-transport study on ZrSiS. New J. Phys. 2018, 20, 103025. 10.1088/1367-2630/aae5c8. [DOI] [Google Scholar]
  29. Chen C.; Xu X.; Jiang J.; Wu S. C.; Qi Y. P.; Yang L. X.; Wang M. X.; Sun Y.; Schröter N. B. M.; Yang H. F.; Schoop L. M.; Lv Y. Y.; Zhou J.; Chen Y. B.; Yao S. H.; Lu M. H.; Chen Y. F.; Felser C.; Yan B. H.; Liu Z. K.; Chen Y. L. Dirac line nodes and effect of spin-orbit coupling in the nonsymmorphic critical semimetals MSiS (M = Hf, Zr). Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 125126. 10.1103/PhysRevB.95.125126. [DOI] [Google Scholar]
  30. Hu J.; Zhu Y. L.; Graf D.; Tang Z. J.; Liu J. Y.; Mao Z. Q. Quantum oscillation studies of topological semimetal candidate ZrGeM (M = S, Se, Te). Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 205134. 10.1103/PhysRevB.95.205134. [DOI] [Google Scholar]
  31. Topp A.; Vergniory M. G.; Krivenkov M.; Varykhalov A.; Rodolakis F.; McChesney J. L.; Lotsch B. V.; Ast C. R.; Schoop L. M. The effect of spin-orbit coupling on nonsymmorphic square-net compounds. J. Phys. Chem. Solids 2019, 128, 296–300. 10.1016/j.jpcs.2017.12.035. [DOI] [Google Scholar]
  32. Singha R.; Pariari A.; Satpati B.; Mandal P. Large nonsaturating magnetoresistance and signature of nondegenerate Dirac nodes in ZrSiS. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 2468–2473. 10.1073/pnas.1618004114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Ali M. N.; Schoop L. M.; Garg C.; Lippmann J. M.; Lara E.; Lotsch B.; Parkin S. Butterfly Magnetoresistance, Quasi-2D Dirac Fermi Surfaces, and a Topological Phase Transition in ZrSiS. Sci. Adv. 2016, 2, e1601742 10.1126/sciadv.1601742. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Wang X. F.; Pan X. C.; Gao M.; Yu J. H.; Jiang J.; Zhang J. R.; Zuo H. K.; Zhang M. H.; Wei Z. X.; Niu W.; Xia Z. C.; Wan X. G.; Chen Y. L.; Song F. Q.; Xu Y. B.; Wang B. G.; Wang G. H.; Zhang R. Evidence of both surface and bulk Dirac bands and anisotropic nonsaturating magnetoresistance in ZrSiS. Adv. Electron. Mater. 2016, 2, 1600228. 10.1002/aelm.201600228. [DOI] [Google Scholar]
  35. Kumar N.; Manna K.; Qi Y.; Wu S.-C.; Wang L.; Yan B.; Felser C.; Shekhar C. Unusual magnetotransport from Si-square nets in topological semimetal HfSiS. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 121109(R) 10.1103/PhysRevB.95.121109. [DOI] [Google Scholar]
  36. Hosen M. M.; Dimitri K.; Belopolski I.; Maldonado P.; Sankar R.; Dhakal N.; Dhakal G.; Cole T.; Oppeneer P. M.; Kaczorowski D.; Chou F.; Hasan M. Z.; Durakiewicz T.; Neupane M. Tunability of the topological nodal-line semimetal phase in ZrSiX-type materials (X = S, Se, Te). Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 161101. 10.1103/PhysRevB.95.161101. [DOI] [Google Scholar]
  37. Gatti G.; Crepaldi A.; Puppin M.; Tancogne-Dejean N.; Xian L.; De Giovannini U.; Roth S.; Polishchuk S.; Bugnon Ph; Magrez A.; Berger H.; Frassetto F.; Poletto L.; Moreschini L.; Moser S.; Bostwick A.; Rotenberg E.; Rubio A.; Chergui M.; Grioni M. Light-induced renormalization of the Dirac quasiparticles in the Nodal-line semimetal ZrSiSe. Phys. Rev. Lett. 2020, 125, 076401. 10.1103/PhysRevLett.125.076401. [DOI] [PubMed] [Google Scholar]
  38. Markovic I.; Hooley C. A.; Clark O. J.; Mazzola F.; Watson M. D.; Riley J. M.; Volckaert K.; Underwood K.; Dyer M. S.; Murgatroyd P. A. E.; et al. Weyl-like points from band inversions of spin-polarised surface state in NbGeSb. Nat. Commun. 2019, 10, 5485. 10.1038/s41467-019-13464-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Hosen M. M.; Dimitri K.; Aperis A.; Maldonado P.; Belopolski I.; Dhakal G.; Kabir F.; Sims C.; Hasan M. Z.; Kaczorowski D.; Durakiewicz T.; Oppeneer P. M.; Neupane M. Observation of gapless Dirac surface states in ZrGeTe. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 97, 121103(R) 10.1103/PhysRevB.97.121103. [DOI] [Google Scholar]
  40. Fu B. B.; Yi C. J.; Zhang T. T.; Caputo M.; Ma J. Z.; Gao X.; Lv B. Q.; Kong L. Y.; Huang Y. B.; Richard R.; Shi M.; Strocov V. N.; Fang C.; Weng H. M.; Shi Y. G.; Qian T.; Ding H. Dirac nodal surfaces and nodal lines in ZrSiS. Sci. Adv. 2019, 5, eaau6459 10.1126/sciadv.aau6459. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Hu J.; Xu S.; Ni N.; Mao Z. Electronic Transport and quantum oscillation of Topological Semimetals. Annu. Rev. Mater. Res. 2019, 49, 207–252. 10.1146/annurev-matsci-070218-010023. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nl0c04946_si_001.pdf (1.4MB, pdf)

Articles from Nano Letters are provided here courtesy of American Chemical Society

RESOURCES